| Issue |
A&A
Volume 598, February 2017
|
|
|---|---|---|
| Article Number | A90 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201629716 | |
| Published online | 07 February 2017 | |
Aeronomical constraints to the minimum mass and maximum radius of hot low-mass planets
1 Space Research Institute, Austrian Academy of Sciences, Schmiedlstrasse 6, 8042 Graz, Austria
e-mail: luca.fossati@oeaw.ac.at
2 Federal Research Center “Krasnoyarsk Science Center” SB RAS, “Institute of Computational Modelling”, Krasnoyarsk 36, Russian Federation
3 Max Planck Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
4 Institut für Geophysik, Astrophysik und Meteorologie, Karl-Franzens-Universität, Universitätsplatz 5, 8010 Graz, Austria
Received: 14 September 2016
Accepted: 15 December 2016
Stimulated by the discovery of a number of close-in low-density planets, we generalise the Jeans escape parameter taking hydrodynamic and Roche lobe effects into account. We furthermore define Λ as the value of the Jeans escape parameter calculated at the observed planetary radius and mass for the planet’s equilibrium temperature and considering atomic hydrogen, independently of the atmospheric temperature profile. We consider 5 and 10 M⊕ planets with an equilibrium temperature of 500 and 1000 K, orbiting early G-, K-, and M-type stars. Assuming a clear atmosphere and by comparing escape rates obtained from the energy-limited formula, which only accounts for the heating induced by the absorption of the high-energy stellar radiation, and from a hydrodynamic atmosphere code, which also accounts for the bolometric heating, we find that planets whose Λ is smaller than 15–35 lie in the “boil-off” regime, where the escape is driven by the atmospheric thermal energy and low planetary gravity. We find that the atmosphere of hot (i.e. Teq ⪆ 1000 K) low-mass (Mpl ⪅ 5 M⊕) planets with Λ< 15–35 shrinks to smaller radii so that their Λ evolves to values higher than 15–35, hence out of the boil-off regime, in less than ≈500 Myr. Because of their small Roche lobe radius, we find the same result also for hot (i.e. Teq⪆ 1000 K) higher mass (Mpl ⪅ 10 M⊕) planets with Λ< 15–35, when they orbit M-dwarfs. For old, hydrogen-dominated planets in this range of parameters, Λ should therefore be ≥15–35, which provides a strong constraint on the planetary minimum mass and maximum radius and can be used to predict the presence of aerosols and/or constrain planetary masses, for example.
Key words: planets and satellites: atmospheres / planets and satellites: fundamental parameters / planets and satellites: gaseous planets
© ESO, 2017
1. Introduction
Thanks to the large number of extra-solar planets (exoplanets) discovered to date by ground- and space-based facilities, such as SuperWASP (Pollacco et al. 2006), HATNet (Bakos et al. 2004), CoRoT (Auvergne et al. 2009), Kepler (Borucki et al. 2010), and K2 (Howell et al. 2014), we are beginning to classify the large variety of detected exoplanets on the basis of their properties. One of the greatest recent surprises in planetary sciences was the discovery of a large population of planets with mass and radius in between that of terrestrial and giant planets of the solar system (Mullally et al. 2015). These planets, hereafter sub-Neptunes, typically have masses and radii in the 1.5–17 M⊕ and 1.5–5 R⊕ range. Sub-Neptunes fill a gap of physical parameters that are absent from the solar system. Accurately deriving their masses and radii is therefore crucial to our overall understanding of planets.
The high quality of the Kepler light curves allowed us to obtain precise transit radii, even for small planets, but for most of them, the low mass and faint apparent magnitude of their host stars hampers a precise enough determination of the planetary mass through radial velocity. For several multi-planet systems, planetary masses have been inferred from transit-timing variations (TTVs), but some of the resulting values are at odds with those derived from radial velocity (e.g., Weiss & Marcy 2014). Sub-Neptunes for which both mass and radius have been measured present a large spread in bulk density (≈0.03–80 g cm-3; low average densities imply the presence of hydrogen-dominated atmospheres), which finding is currently greatly debated (e.g., Lopez et al. 2012; Howe et al. 2014; Howe & Burrows 2015; Lee & Chiang 2015, 2016; Owen & Morton 2015; Ginzburg et al. 2016).
It is therefore important to find external independent constraints to planetary masses and radii that could be applied to a large number of planets, for example to independently test the masses derived from TTVs, identify the possible presence of high-altitude aerosols, and estimate a realistic range of planetary radii/masses given a certain mass/radius. We show here how basic aeronomical considerations, supported by hydrodynamic modelling and previous results (Owen & Wu 2016), can constrain the mass/radius of old sub-Neptunes given their radius/mass and equilibrium temperature (Teq).
2. Generalisation of the Jeans escape parameter
The Jeans escape parameter λ is classically defined at the exobase and for a hydrostatic atmosphere. It is the ratio between the escape velocity υ∞ and the most probable velocity υ0 of a Maxwellian distribution at temperature T, squared (Jeans 1925; Chamberlain 1963; Öpik 1963; Bauer & Lammer 2004). We generalise the Jeans escape parameter at each atmospheric layer r and corresponding temperature T for a hydrodynamic atmosphere composed of atomic and molecular hydrogen as 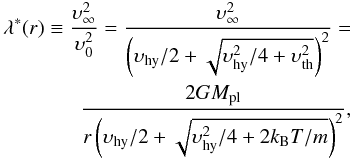 (1)where G is Newton’s gravitational constant, kB is Boltzmann’s constant, Mpl is the planetary mass, υth is the thermal velocity
(1)where G is Newton’s gravitational constant, kB is Boltzmann’s constant, Mpl is the planetary mass, υth is the thermal velocity 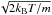 , and υhy is the bulk velocity of the particles at each atmospheric layer. In Eq. (1), m is the mean molecular weight
, and υhy is the bulk velocity of the particles at each atmospheric layer. In Eq. (1), m is the mean molecular weight 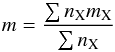 (2)where nX and mX are the density and mass of each atom/molecule (X) in the atmosphere. In this work, we consider atomic and molecular hydrogen.
(2)where nX and mX are the density and mass of each atom/molecule (X) in the atmosphere. In this work, we consider atomic and molecular hydrogen.
The value of υ0 in the hydrodynamic case is that of a shifted Maxwellian distribution, where υhy is the shift. The Maxwellian velocity distribution gives the number of particles between υ and υ + dυ and can be written as 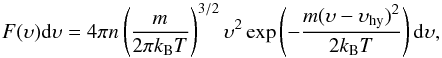 (3)where n is the number density and m the particle mass. The most probable velocity υ0 is found where Eq. (3) has its maximum and can therefore be derived by setting dF/ dυ = 0. This condition results in a quadratic equation for υ,
(3)where n is the number density and m the particle mass. The most probable velocity υ0 is found where Eq. (3) has its maximum and can therefore be derived by setting dF/ dυ = 0. This condition results in a quadratic equation for υ, 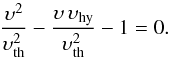 (4)The solution of this equation is
(4)The solution of this equation is 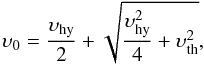 (5)
where only this positive solution is physical (the negative solution yields a negative υ0). Note that a direct derivation of υ0 by setting υhy = 0 in Eq. (3) or in Eq. (5) yields υ0 = υth. From Eq. (5) it also follows that if υth → 0, then υ0 → υhy, as expected.
(5)
where only this positive solution is physical (the negative solution yields a negative υ0). Note that a direct derivation of υ0 by setting υhy = 0 in Eq. (3) or in Eq. (5) yields υ0 = υth. From Eq. (5) it also follows that if υth → 0, then υ0 → υhy, as expected.
The formulation of the Jeans escape parameter given in Eq. (1) is reminiscent of the “solar breeze” used before Parker’s solar wind model was accepted (e.g., Chamberlain 1960, 1961). If υhy is negligible compared to υth (i.e. hydrostatic atmosphere), the Jeans escape parameter returns to the classical form of 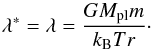 (6)We recall that for the classical Jeans escape parameter (hydrostatic atmosphere), a layer is completely bound to a planet for λ≳ 30 and escape is important for λ< 15, while for λ≲ 1.5 the atmosphere is in hydrodynamic “blow-off” (Jeans 1925; Chamberlain 1963; Öpik 1963; Bauer & Lammer 2004). This last condition occurs when the thermal energy of the gas is very close to, or even exceeds, the gravitational energy.
(6)We recall that for the classical Jeans escape parameter (hydrostatic atmosphere), a layer is completely bound to a planet for λ≳ 30 and escape is important for λ< 15, while for λ≲ 1.5 the atmosphere is in hydrodynamic “blow-off” (Jeans 1925; Chamberlain 1963; Öpik 1963; Bauer & Lammer 2004). This last condition occurs when the thermal energy of the gas is very close to, or even exceeds, the gravitational energy.
The vast majority of the exoplanets known to date orbits at close distance to their host stars. We therefore consider Roche-lobe effects. Following the procedure described in Sect. 2 of Erkaev et al. (2007), in Eq. (1) we substitute the gravitational potential difference between the planetocentric distance r and infinity (GMpl/r) by the gravitational potential difference between r and the Roche-lobe radius (Δφ). We therefore obtain 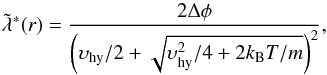 (7)where
(7)where ![\begin{equation} \Delta\phi = \phi_{\rm 0}\frac{\xi-1}{\xi}\left[1-\frac{1}{\delta}\frac{\xi}{\gamma^2}\frac{\gamma(1+\xi)-\xi}{(\gamma-1)(\gamma-\xi)}-\frac{\xi(1+\delta)(1+\xi)}{2\delta\gamma^3}\right] \label{eq:deltaphi} \end{equation}](/articles/aa/full_html/2017/02/aa29716-16/aa29716-16-eq42.png) (8)(see Eq. (7) of Erkaev et al. 2007) and
(8)(see Eq. (7) of Erkaev et al. 2007) and 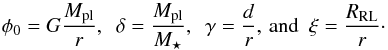 (9)In Eq. (9), M⋆ is the stellar mass, d is the semi-major axis, and RRL is the Roche lobe radius. Therefore, Eq. (7) gives the generalised form of the Jeans escape parameter.
(9)In Eq. (9), M⋆ is the stellar mass, d is the semi-major axis, and RRL is the Roche lobe radius. Therefore, Eq. (7) gives the generalised form of the Jeans escape parameter.
2.1. Planet atmosphere modelling
 |
Fig. 1 Left: synthetic transmission spectra calculated for a planet with Mpl = 5 M⊕, Rpl = 4 R⊕, and a 1000 K isothermal atmosphere with 0.01 (blue), 1.0 (orange), and 100 (green) times solar metallicity. The circles of corresponding colour denote the transmission curves integrated over the CoRoT spectral response curve (red dashed curve). Right: contribution functions for the vertical optical depth integrated over the CoRoT spectral response curve. |
To draw profiles of λ∗ and 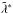 we derive the temperature, pressure, velocity, and density structure of planetary atmospheres employing a stellar high-energy (XUV; 1–920 Å) absorption and 1D hydrodynamic upper-atmosphere model that solves the system of hydrodynamic equations for mass, momentum, and energy conservation, and also accounts for ionisation, dissociation, recombination, and Lyα cooling. The full description of the hydrodynamic code adopted for the simulations is presented in Erkaev et al. (2016).
we derive the temperature, pressure, velocity, and density structure of planetary atmospheres employing a stellar high-energy (XUV; 1–920 Å) absorption and 1D hydrodynamic upper-atmosphere model that solves the system of hydrodynamic equations for mass, momentum, and energy conservation, and also accounts for ionisation, dissociation, recombination, and Lyα cooling. The full description of the hydrodynamic code adopted for the simulations is presented in Erkaev et al. (2016).
Hydrodynamic modelling is valid in presence of enough collisions, which occurs for Knudsen number Kn = l/H< 0.1 (Volkov et al. 2011), where l is the mean free path and H is the local scale height; in the domain of our models, from Rpl to RRL, this criterion is always fulfilled. Throughout our calculations, we adopt a net heating efficiency (η) of 15% (Shematovich et al. 2014) and use stellar XUV fluxes (IXUV) estimated from the average solar XUV flux (Ribas et al. 2005), scaled to the appropriate distance and stellar radius. We note that X-ray heating is not relevant in our case, because we do not consider active young stars (Owen & Jackson 2012). We also assumed that at Rpl hydrogen is completely in molecular form (i.e. H2), which is true for planets with Teq< 2000 K (Koskinen et al. 2010).
For all calculations, and throughout the paper, we consider that Rpl lies at a fiducial atmospheric pressure (p0) of 100 mbar. To justify this assumption, we calculated the photospheric deposition level using an updated version of the radiative transfer code described in Cubillos (2016) and Blecic (2016). The model considers opacities from line-by-line transitions from HITEMP for H2O, CO, and CO2 (Rothman et al. 2010) and HITRAN for CH4 (Rothman et al. 2013). In addition, it includes opacities for H2–H2 and H2–He collision-induced absorption from Borysow (2002), Borysow et al. (2001), and Jørgensen et al. (2000), H2 Rayleigh scattering from Lecavelier Des Etangs et al. (2008), and sodium and potassium doublets from Burrows et al. (2000).
In Fig. 1 we present transmission spectra for a fiducial sub-Neptune with Mpl = 5 M⊕, Rpl = 4 R⊕, and an isothermal atmosphere at 1000 K, in hydrostatic and thermochemical equilibrium. We explored three different cases varying the atmospheric elemental metallicities, considering 0.01, 1.0, and 100 times solar abundances (Figs. 1 and 2). We adjusted the pressure-radius reference level such that the resulting transmission radius (integrated over the optical band) matches the fiducial planetary radius, adopting the CoRoT spectral response curve, as an example. We find that the planetary transmission radii correspond to pressure levels of 130, 50, and 10 mbar for the 0.01, 1.0, and 100.0× solar-metallicity models, respectively (Fig. 1, left panel).
After we obtained the pressure-radius relationship, we computed the contribution functions (in the optical band) for the vertical optical depth. The barycenter (i.e., average) of the contribution functions indicate where the atmosphere becomes optically thick. This is the position of the planetary photosphere, where the lower boundary for the hydrodynamic calculation would need to be set. We find that for the planet considered here the photospheric deposition level is approximately located at 551, 159, and 33 mbar for the 0.01, 1.0, and 100.0× solar-metallicity models, respectively (Fig. 1, right panel).
We performed the same procedure for all planets analysed in this work and list the pressure corresponding to the barycenter of the contribution function in the fifth column of Table 1. The pressure values range between about 100 and 700 mbar, where the lower pressure values are obtained for the cooler, lower density planets. Figure 1 shows that a higher metallicity, as expected for low-mass planets, would lead to a slight decrease in pressure values, hence justifying our assumption of placing Rpl at an average 100 mbar pressure level.
 |
Fig. 2 Mole-mixing fractions of the atmospheric species (see legend in the bottom panel) in thermochemical equilibrium for isothermal (1000 K) models calculated for 0.01 (top), 1.0 (middle), and 100 (bottom) times solar metallicity. |
Our hydrodynamic model implicitly considers the stellar continuum absorption by setting the temperature at the lower boundary, hence at Rpl (i.e. where most of the stellar radiation is absorbed), equal to Teq. We return to the validity of this approximation in Sect. 3. The planets considered here are old, hence heating from the planet interior can be neglected.
Input parameters and results of the simulations performed with η = 15%.
2.2. λ∗ and 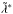 profiles
profiles
As an example to show the differences between λ∗ and 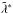 , we modelled a close-in low-density 5 M⊕ and 4 R⊕ (average density ρ of 0.4 g cm-3) planet with Teq of 1000 K, orbiting an early K-type star (see Table 1). The parameters adopted for this idealised planet are similar to those of Kepler-87c (Ofir et al. 2014). We derived the mean molecular mass at each atmospheric layer from the modelled H and H2 mixing ratios. Figure 3 shows the obtained profiles.
, we modelled a close-in low-density 5 M⊕ and 4 R⊕ (average density ρ of 0.4 g cm-3) planet with Teq of 1000 K, orbiting an early K-type star (see Table 1). The parameters adopted for this idealised planet are similar to those of Kepler-87c (Ofir et al. 2014). We derived the mean molecular mass at each atmospheric layer from the modelled H and H2 mixing ratios. Figure 3 shows the obtained profiles.
In the 1–2 Rpl range, λ∗ decreases with increasing r because the gravitational potential decreases and the H2 molecules dissociate under the action of the stellar XUV flux. All H2 molecules are dissociated at ~2 Rpl. Then, at larger radii, as the temperature continues to decrease due to adiabatic cooling, λ∗ increases and remains above 30 for radii grater than 6.5 Rpl. This implies that no particles could escape, regardless of their proximity to RRL, which is non-physical. Instead, 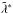 monotonically decreases with increasing r. The bottom panel of Fig. 3 shows that for such a close-in planet, despite the hydrodynamic nature of the atmosphere, in most layers υhy is negligible compared to υth, therefore λ∗≈λ and
monotonically decreases with increasing r. The bottom panel of Fig. 3 shows that for such a close-in planet, despite the hydrodynamic nature of the atmosphere, in most layers υhy is negligible compared to υth, therefore λ∗≈λ and 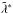 ≈
≈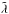 .
.
 |
Fig. 3 Top: temperature (black solid line) and pressure (red dashed line) profiles as a function of radius r in units of Rpl for a 5 M⊕ and 4 R⊕ planet with Teq=1000 K, orbiting an early K-type star (see Table 1). The right axis indicates the pressure scale. Middle: λ∗ (black solid line) and |
Figure 3 shows that the value of 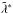 approaches unity at atmospheric layers where the pressure, hence density, is high enough to power high escape rates (see Table 1). These upper layers are in a blow-off regime where the escaping gas is continuously replenished by the hydrodynamically expanding atmosphere, with the expansion being driven by the high thermal energy and low planet gravity. This escape regime, here presented from an aeronomical point of view, has been discovered and thoroughly described by Owen & Wu (2016), who called it “boil-off”, in relation to the study of the evolution of young planets that are just released from the protoplanetary nebula (see also Ginzburg et al. 2016).
approaches unity at atmospheric layers where the pressure, hence density, is high enough to power high escape rates (see Table 1). These upper layers are in a blow-off regime where the escaping gas is continuously replenished by the hydrodynamically expanding atmosphere, with the expansion being driven by the high thermal energy and low planet gravity. This escape regime, here presented from an aeronomical point of view, has been discovered and thoroughly described by Owen & Wu (2016), who called it “boil-off”, in relation to the study of the evolution of young planets that are just released from the protoplanetary nebula (see also Ginzburg et al. 2016).
3. Using escape rates to identify planets in the boil-off regime
We define Λ as the Jeans escape parameter λ (without accounting for Roche-lobe effects and hydrodynamic velocities) at Rpl, evaluated at the Teq of the planet and for an atomic-hydrogen gas (see the full dot and the blue dotted lines in Fig. 3) 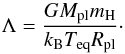 (10)This quantity, which we call the restricted Jeans escape parameter, is useful because it can be derived for any planet for which mass, transit radius, and Teq are measured, and without the need of any atmospheric modelling or calculation of RRL. We aim here at roughly finding the threshold Λ values (ΛT), as a function of Mpl, Rpl, and Teq, below which the atmosphere transitions towards the boil-off regime. For this we use escape rates, as described below.
(10)This quantity, which we call the restricted Jeans escape parameter, is useful because it can be derived for any planet for which mass, transit radius, and Teq are measured, and without the need of any atmospheric modelling or calculation of RRL. We aim here at roughly finding the threshold Λ values (ΛT), as a function of Mpl, Rpl, and Teq, below which the atmosphere transitions towards the boil-off regime. For this we use escape rates, as described below.
In addition to the escape rates derived from the hydrodynamic model (Lhy), we consider the maximum possible XUV-driven escape rates, which can be analytically estimated using the energy-limited formula (e.g., Watson et al. 1981; Erkaev et al. 2007), 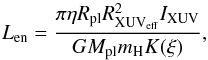 (11)where RXUVeff is the effective radius at which the XUV energy is absorbed in the upper atmosphere (see Table 1; Erkaev et al. 2007, 2015) and η is the heating efficiency (see Sect. 2.1). The factor
(11)where RXUVeff is the effective radius at which the XUV energy is absorbed in the upper atmosphere (see Table 1; Erkaev et al. 2007, 2015) and η is the heating efficiency (see Sect. 2.1). The factor 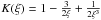 accounts for Roche-lobe effects (Erkaev et al. 2007). We note that Roche-lobe effects are also considered in the hydrodynamic model.
accounts for Roche-lobe effects (Erkaev et al. 2007). We note that Roche-lobe effects are also considered in the hydrodynamic model.
By construction, XUV heating and the intrinsic thermal energy of the atmosphere are considered in the computation of Lhy, while only XUV heating is taken into account when deriving Len. It follows that the boil-off regime, that is, when the intrinsic thermal energy of the atmosphere becomes the efficient main driver of the escape, occurs for Lhy greater than Len. For this situation, Lhy/Len>1 cannot be achieved purely from XUV heating, implying that the outflow must be driven by the heat present at the lower boundary of the atmosphere. We can therefore use the Lhy/Len≈1 as an empirical condition to estimate ΛT.
To identify the ΛT value, which is the Λ value satisfying the Lhy/Len≈1 condition, we ran a set of hydrodynamic simulations for two idealised old planets of 5 and 10 M⊕ orbiting an early G-, K-, and M-type star at distances such that Teq is equal to 500 and 1000 K, assuming a Bond albedo of 0.3. Table 1 lists the complete set of input parameters and results, which are visually displayed in Fig. 4.
 |
Fig. 4 Ratio between the hydrodynamic (Lhy) and energy-limited (Len) escape rates as a function of Λ for the modelled planets orbiting the G2 (top), K2 (middle), and M2 (bottom) star. Within each panel, the legend indicates the mass (in M⊕) and temperature (in K) of the modelled planets. The dashed line indicates the equality between Lhy and Len, while the dotted line indicates where the Lhy/Len ratio is equal to 2.0. The value of ΛT lies between 15 and 35. |
Figure 4 shows that the Lhy/Len≈1 condition is reached for Λ values between 15 and 35, with a slight dependence on stellar type and Teq. In particular, for the planets orbiting the G- and K-type stars, the ΛT values appear to be lower at higher temperature, hence ΛT decreases with increasing tidal gravity. This does not seem to be the case for the planets orbiting the M-type star, particularly for the 10 M⊕ planet.
We discuss here the uncertainties related to the computation of the Lhy/Len ratio. Since we do not consider real planets, there are no observational uncertainties connected to the system parameters. The RXUVeff value present in Eq. (11) is an output of the hydrodynamic code, and it is used to calculate Lhy as well. For these reasons, there are no uncertainties on the RXUVeff value. The heating efficiency η is therefore the only input parameter for which its uncertainties may affect the Lhy/Len ratio.
Generally, the heating efficiency varies with altitude, and Shematovich et al. (2014) concluded that for hot Jupiters the value of η in the thermosphere varies between ≈10% and 20%. Because our model does not self-consistently calculate η with height, we assume an average value of 15% (Sect. 2.1). This agrees well with calculations by Owen & Jackson (2012), who also estimated that η values higher than 40% are unrealistically high. More recently, Salz et al. (2016) calculated the average heating efficiency for a set of planets with different masses and radii. They concluded that for planets with log (GMpl/Rpl) smaller than 13.11 (the case of the planets considered here), η is about 23%, independent of the planet parameters.
As discussed by Lammer et al. (2016), the heating efficiency enters in the calculation of both Lhy and Len, although with a slightly different dependence. To quantitatively estimate the effects of the uncertainty on the heating efficiency on the Lhy/Len ratio, we ran a set of simulations for two planets orbiting the K2 star with two different Λ values (Λ = 21, Mpl = 5 M⊕, Rpl = 1.8 R⊕ and Λ = 8, Mpl = 5 M⊕, Rpl = 4.5 R⊕) and Teq = 1000 K, varying η between 10 and 40%, leaving all other parameters fixed. The results, displayed in Fig. 5, indicate that variations of η by a factor of two from the adopted value of 15% (e.g. between 10 and 30%) modify the Lhy/Len ratio by a factor of about 1.5 in the case of low Λ and of about 1.05 in the case of high Λ. The sensitivity of the Lhy/Len ratio on variations of η therefore decreases with increasing Λ. On the basis of these results, to be conservative, we consider the Lhy/Len≈1 condition to be fulfilled when Lhy/Len≤2.0.
 |
Fig. 5 Variation of the Lhy/Len ratio, normalised to the value of the Lhy/Len ratio obtained with η = 15% (adopted for our calculations), as a function of heating efficiency η for two planets orbiting the K2 star with two different Λ values (dashed line: Λ = 21, Mpl = 5 M⊕, Rpl = 1.8 R⊕; solid line: Λ = 8, Mpl = 5 M⊕, Rpl = 4.5 R⊕) and Teq = 1000 K. |
Figure 6 shows the atmospheric structure of the 5 M⊕ planet considered in Sect. 2.2, but with a radius of 1.8 R⊕ (i.e. out of the boil-off regime). Close to Rpl the atmosphere is hydrostatic, as indicated by the temperature increase (i.e. no adiabatic cooling), with the high-energy stellar flux providing a considerable amount of heating. The rise in temperature close to the lower boundary in Fig. 6 is caused by XUV heating, which is the driver of the outflow. In contrast, the monotonic temperature decrease (caused by adiabatic cooling) shown in Fig. 3 indicates that XUV heating is not important, implying that the outflow is driven by the high thermal energy of the planet. In our modelling we do not consider cooling from H . However, H
. However, H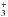 cooling is not relevant in our case, because it does not affect the thermally driven escape rates in the boil-off regime (H
cooling is not relevant in our case, because it does not affect the thermally driven escape rates in the boil-off regime (H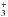 is produced much above the lower boundary of the atmosphere; Chadney et al. 2016).
is produced much above the lower boundary of the atmosphere; Chadney et al. 2016).
On the basis of detailed evolution modelling of young planets immediately after the disk dispersal, Owen & Wu (2016) concluded that planets exit the boil-off regime when their radius becomes smaller than 0.1 Bondi radii (RB). The Bondi radius is defined as 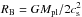 , where cs is the isothermal sound speed. The Rpl/RB = 0.1 condition for the occurrence of boil-off given by Owen & Wu (2016) is therefore mathematically identical to the ΛT=20 condition, when an adiabatic gas index γ equal to 1 is considered, or in other words, isothermal gas.
, where cs is the isothermal sound speed. The Rpl/RB = 0.1 condition for the occurrence of boil-off given by Owen & Wu (2016) is therefore mathematically identical to the ΛT=20 condition, when an adiabatic gas index γ equal to 1 is considered, or in other words, isothermal gas.
We arrived at a result similar to that of Owen & Wu (2016), who properly took into account the various heating and cooling sources, which indicates that the assumptions and simplifications we made for our modelling are robust. In particular, it shows the validity of (i) simplifying the processes leading to the planet’s thermal balance by setting the temperature of the atmosphere equal to Teq at the lower boundary; and (ii) setting the lower boundary at the pressure level where the optical depth is roughly unity, which is where most of the stellar radiation is absorbed1. We note that modifications to these two assumptions affect the shape of the atmospheric profiles, but not the escape rates, if Lhy is equal to or smaller than Len. For example, Fig. 2 of Lammer et al. (2016) shows that by varying the pressure at the lower boundary from 100 mbar to 1 bar only affects the Lhy/Len ratio in the boil-off regime (when Lhy>Len), while the radius at which the Lhy/Len≈1 condition is reached (namely the value of ΛT) is not affected. This implies that, within our scheme, the ΛT values are independent of the two assumptions described above. It should also be noted that our results apply to any planet, independent of the internal structure, for which the 100 mbar pressure level lies above the solid core, if any is present.
4. Constraints on Mpl and Rpl
To explore whether the knowledge of the value of ΛT, or equivalently of the Rpl/RB = 0.1 condition, can help to constrain the parameters of old planets, it is necessary to consider the atmospheric evolution of planets in the boil-off regime. To roughly estimate how much time the modelled planets need to evolve out of the boil-off regime, we follow the same procedure as adopted by Lammer et al. (2016) to study the case of CoRoT-24b.
As an example, we take the simulations we carried out for the Mpl = 5 M⊕ planet with Teq = 1000 K orbiting the K-type star. We assumed a core mass of 5 M⊕ and used formation and structure models by Rogers et al. (2011, see their Fig. 4) to estimate for each modelled radius the atmospheric mass fraction f. We then used the Lhy values to roughly estimate the evolution of the atmospheric mass over time. Figure 7 shows that the atmospheric mass for a radius above 1.8 R⊕ (where Lhy/Len≈ 1) would be lost within ≈500 Myr. This is therefore the timescale needed for this planet to evolve out of the boil-off regime.
 |
Fig. 7 Atmospheric mass MAT evolution normalised to the atmospheric mass corresponding to Rpl =1.8 R⊕ (where Lhy/Len≈1) estimated from the Lhy escape rates obtained for the Mpl = 5 M⊕ planet with Teq = 1000 K orbiting the K-type star. The dashed line indicates MAT = MAT(1.8 R⊕). The initial time is arbitrarily set at 0.1 Myr. The legend lists the atmospheric mass fraction corresponding to each radius. |
Table 2 lists the timescales for each modelled planet from Table 1. We find the shorter timescales for the less massive and hotter planets. In particular, for planets with Mpl = 5 M⊕ and Teq = 1000 K, the timescale to evolve out of boil-off is shorter than 500 Myr. The same also occurs for the hot (i.e. Teq = 1000 K) 10 M⊕ planet orbiting the M-type star, likely because of the effect of the smaller Roche-lobe radius compared to the case of the same planet orbiting the G- and K-type stars. In general, we therefore find that hot (i.e. Teq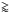 1000 K) low-mass (Mpl
1000 K) low-mass (Mpl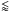 5 M⊕) planets with hydrogen-dominated atmospheres, unless very young, should not have Λ<ΛT. Because of their small Roche lobe, this conclusion also extends to hot (i.e. Teq
5 M⊕) planets with hydrogen-dominated atmospheres, unless very young, should not have Λ<ΛT. Because of their small Roche lobe, this conclusion also extends to hot (i.e. Teq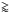 1000 K) higher mass (Mpl
1000 K) higher mass (Mpl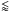 10 M⊕) planets if they are orbiting M-dwarfs.
10 M⊕) planets if they are orbiting M-dwarfs.
From the above considerations, it follows that for hot low-mass planets with hydrogen-dominated atmospheres with observed values leading to Λ< 15–35 there must be problems with the estimation/interpretation of the measured mass (i.e. too low), or radius (i.e. too large), or both. Large transit radii may be caused by the presence of aerosols lying far above Rpl or by an incorrect estimation of the stellar radius. We note, however, that the atmosphere of planets with a large enough atmospheric mass may stably lie in the boil-off regime, as described above.
 |
Fig. 8 Colour-scaled value of Λ as a function of planetary mass and radius for Teq = 1000 K. The white straight lines indicate equal Λ values given in the plot. The red solid lines indicate lines of equal average densities of 0.6, 1.6, 3.2, and 5.5 g cm-3. The symbols correspond to the observed (blue bar and arrow) and possible mass-radius combination (black points) for CoRoT-24b. |
The presence of aerosols may indeed lead to a misinterpretation of the observed transit radius. Lee et al. (2015), for example, calculated from first principles the formation of aerosols in the atmosphere of the hot Jupiter HD 189733 b (Teq≈1000 K, similar to that of the hottest planets considered in this work), obtaining that clouds start forming in the 10–100 μbar pressure range. For the planet considered in Fig. 6 (Mpl = 5 M⊕; Rpl = 1.8 R⊕; Teq = 1000 K), this pressure level corresponds to about 1.2–1.4 Rpl, that is, a radius of 2.2–2.5 R⊕ or 5.3–9.3 pressure scale heights above Rpl. The presence of high-altitude clouds/hazes in the atmosphere of such a planet would therefore lead to an overestimation of Rpl measured through broad-band optical transit observations of about 20–40%. Lee et al. (2015) investigated a hot Jupiter, which has physical characteristics different from those of the planets considered here, but this is what is currently available, showing that similar cloud formation calculations, tuned for lower-mass planets, are clearly needed for a more appropriate interpretation of the results.
For hot low-mass planets it is therefore possible to use the Λ≥ΛT condition to constrain the minimum mass, given a certain radius, or maximum radius, given a certain mass. The only assumptions are the presence of a hydrogen-dominated atmosphere, which is likely for low-density planets, and an old age (i.e. >1 Gyr). Most of the extremely low-density planets discovered by Kepler fall into this regime.
Figure 8 shows the Λ value as a function of planetary mass and radius (at the 100 mbar level) for Teq = 1000 K. We use the sub-Neptune CoRoT-24b as an example of the constraining power of this plot. CoRoT-24b has a mass lower than 5.7 M⊕, a transit radius of 3.7 ± 0.4 R⊕, and an equilibrium temperature of 1070 K (blue bar and arrow in Fig. 8; Alonso et al. 2014). CoRoT-24b therefore has a Λ value lower than 10.9, well below ΛT. For a value of ΛT of 25 and when we assume that Mpl is equal to 5.7 M⊕ (Lammer et al. 2016, excluded masses smaller than ≈5 M⊕), Fig. 8 (bottom black point) indicates that the 100 mbar pressure level, and hence where the transit radius would be if the planet were possessed of a clear atmosphere, lies around 2 R⊕ (≈1.7 R⊕ less than the transit radius), in agreement with the detailed analysis of Lammer et al. (2016). When we instead assume a clear atmosphere, hence RT = R100 mbar, Mpl should be 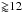 M⊕ (right black cross in Fig. 8), although this is unlikely given the non-detection of the planet in the radial-velocity measurements.
M⊕ (right black cross in Fig. 8), although this is unlikely given the non-detection of the planet in the radial-velocity measurements.
The atmospheric pressure profile of CoRoT-24b shown by Lammer et al. (2016) indicates that if we assume that the 100 mbar level lies at 2 R⊕, then the transit radius is at a pressure of 1–10 μbar, which is about 10 times smaller than the lowest pressure at which Lee et al. (2015) predicts cloud formation. For this particular planet, the most likely scenario is therefore a combined effect of the presence of aerosols and of a slight mass underestimation.
Table 2 shows that for most of the more massive planets (Mpl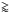 10 M⊕) and all the cooler (Teq
10 M⊕) and all the cooler (Teq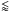 500 K) ones, the timescale for the atmosphere to evolve out of the boil-off regime is longer than 10 Gyr and in some cases even longer than the main-sequence life time of the host stars. This clearly shows that although the atmosphere of these planets may be in boil-off, the escape rates are not high enough to significantly affect the atmosphere in a short time, in agreement with the results of Ginzburg et al. (2016).
500 K) ones, the timescale for the atmosphere to evolve out of the boil-off regime is longer than 10 Gyr and in some cases even longer than the main-sequence life time of the host stars. This clearly shows that although the atmosphere of these planets may be in boil-off, the escape rates are not high enough to significantly affect the atmosphere in a short time, in agreement with the results of Ginzburg et al. (2016).
From the results of Table 2, it follows that in the 5–10 M⊕ planetary mass and 500–1000 K equilibrium temperature range with increasing temperature and/or decreasing mass the escape rates start affecting the long-term evolution of the atmosphere. This transition region depends not only on the planetary parameters, but also on the stellar properties and orbital separation, which affect the escape rates through the XUV flux and size of the Roche lobe. We will explore this transition region in detail in a forthcoming work.
5. Conclusions
We generalised the expression of the Jeans escape parameter to account for hydrodynamic and Roche-lobe effects, which is important for close-in exoplanets. We use a planetary upper atmosphere hydrodynamic code to derive the atmospheric temperature, pressure, and velocity structure of sub-Neptunes with various masses and radii and draw the profiles of the Jeans escape parameter as a function of height. We used our simulations and the generalised Jeans escape parameter to describe the boil-off regime (Owen & Wu 2016), which is characterised by very high escape rates driven by the planet’s high thermal energy and low gravity.
We introduce the restricted Jeans escape parameter (Λ) as the value of the Jeans escape parameter calculated at the observed planetary radius and mass for the planet’s equilibrium temperature, and considering atomic hydrogen. We used the Lhy/Len≤1 empirical condition, where Len is derived analytically from the energy-limited formula, to estimate ΛT, the critical value of Λ below which efficient boil-off occurs. We ran simulations with varying planetary mass, stellar mass, and equilibrium temperature, concluding that ΛT lies between 15 and 35, depending on the system parameters. This result, mostly based on aeronomical considerations, is in agreement with that obtained by Owen & Wu (2016), namely Rpl/RB> 0.1.
From the analysis of our simulations, we find that the atmosphere of hot (i.e. Teq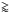 1000 K) low-mass (Mpl
1000 K) low-mass (Mpl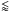 5 M⊕) planets with Λ<ΛT would be unstable against evaporation because they lie in an efficient boil-off regime that would shrink their radius within a few hundreds of Myr. We find the same result also for hot (i.e. Teq
5 M⊕) planets with Λ<ΛT would be unstable against evaporation because they lie in an efficient boil-off regime that would shrink their radius within a few hundreds of Myr. We find the same result also for hot (i.e. Teq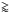 1000 K) higher mass (Mpl
1000 K) higher mass (Mpl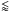 10 M⊕) planets with Λ<ΛT, when they orbit M-dwarfs. We conclude that for old hydrogen-dominated planets in this range of parameters, Λ should be ≥ΛT, which therefore provides a strong constraint on the planetary minimum mass/maximum radius.
10 M⊕) planets with Λ<ΛT, when they orbit M-dwarfs. We conclude that for old hydrogen-dominated planets in this range of parameters, Λ should be ≥ΛT, which therefore provides a strong constraint on the planetary minimum mass/maximum radius.
This information can be used to predict the presence of high-altitude aerosols on a certain planet without the need to obtain transmission spectra, or inform on the reliability of planetary masses. Our results could also be used to indicate the possible presence of contaminants in the images used to derive the transit light curves, which would lead to the measurement of a planetary radius larger than what is in reality (Dalba et al. 2017). Our results are relevant because of the various present and future ground- and space-based planet-finding facilities (e.g. K2, NGTS, CHEOPS, TESS, PLATO), which will detect sub-Neptunes orbiting bright stars, hence amenable to atmospheric characterisation. Our results will help prioritisation processes: for instance, hot low-density, low-mass planets, with masses measured through radial velocity, are good targets for transmission spectroscopy, but their large radii may be caused by high-altitude clouds, which would therefore obscure the atmospheric atomic and molecular features. An application of our results to the transiting sub-Neptune planets known to date is presented by Cubillos et al. (2017).
The simulations presented in this work, only sparsely cover the typical parameter space of the discovered systems hosting sub-Neptunes, also in terms of high-energy stellar flux. In the future, we will extend our work to a larger parameter space and aiming at its more homogeneous coverage. In particular, we will better identify the dependence of the ΛT value on the planetary (e.g. mass, radius, and temperature/pressure at the lower boundary) and stellar (e.g. mass and high-energy flux) parameters.
This is also how Owen & Wu (2016) set their upper boundary.
Acknowledgments
We acknowledge the Austrian Forschungsförderungsgesellschaft FFG projects “RASEN” P847963 and “TAPAS4CHEOPS” P853993, the Austrian Science Fund (FWF) NFN project S11607-N16, and the FWF project P27256-N27. N.V.E. acknowledges support by the RFBR grant Nos. 15-05-00879-a and 16-52-14006 ANF_a. We thank the anonymous referee for the comments that led to a considerable improvement of the manuscript.
References
- Alonso, R., Moutou, C., Endl, M., et al. 2014, A&A, 567, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bakos, G., Noyes, R. W., Kovács, G., et al. 2004, PASP, 116, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Bauer, S. J., & Lammer, H. 2004, Planetary aeronomy: atmosphere environments in planetary systems (Berlin: Springer) [Google Scholar]
- Blecic, J. 2016, Ph.D. Dissertation [arXiv:1604.02692] [Google Scholar]
- Borysow, A. 2002, A&A, 390, 779 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borysow, A., Jorgensen, U. G., & Fu, Y. 2001, J. Quant. Spec. Radiat. Transf., 68, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Burrows, A., Marley, M. S., & Sharp, C. M. 2000, ApJ, 531, 438 [NASA ADS] [CrossRef] [Google Scholar]
- Chadney, J. M., Galand, M., Koskinen, T. T., et al. 2016, A&A, 587, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chamberlain, J. W. 1960, ApJ, 131, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Chamberlain, J. W. 1961, ApJ, 133, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Chamberlain, J. W. 1963, Planet. Space Sci., 11, 901 [NASA ADS] [CrossRef] [Google Scholar]
- Cubillos, P. E. 2016, Ph.D. Dissertation [arXiv:1604.01320] [Google Scholar]
- Cubillos, P., Erkaev, N. V., Juvan, I. G., et al. 2017, MNRAS, 466, 1868 [NASA ADS] [CrossRef] [Google Scholar]
- Dalba, P. A., Muirhead, P. S., Croll, B., & Kempton, E. M.-R. 2017, AJ, 153, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Erkaev, N. V., Kulikov, Y. N., Lammer, H., et al. 2007, A&A, 472, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Erkaev, N. V., Lammer, H., Odert, P., Kulikov, Y. N., & Kislyakova, K. G. 2015, MNRAS, 448, 1916 [NASA ADS] [CrossRef] [Google Scholar]
- Erkaev, N. V., Lammer, H., Odert, P., et al. 2016, MNRAS, 460, 1300 [NASA ADS] [CrossRef] [Google Scholar]
- Ginzburg, S., Schlichting, H. E., & Sari, R. 2016, ApJ, 825, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Howe, A. R., & Burrows, A. 2015, ApJ, 808, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Howe, A. R., Burrows, A., & Verne, W. 2014, ApJ, 787, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Jeans, J. 1925, The Dynamical Theory of Gases (Cambridge University Press) [Google Scholar]
- Jørgensen, U. G., Hammer, D., Borysow, A., & Falkesgaard, J. 2000, A&A, 361, 283 [NASA ADS] [Google Scholar]
- Koskinen, T. T., Yelle, R. V., Lavvas, P., & Lewis, N. K. 2010, ApJ, 723, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Lammer, H., Erkaev, N. V., Fossati, L., et al. 2016, MNRAS, 461, L62 [NASA ADS] [CrossRef] [Google Scholar]
- Lecavelier Des Etangs, A., Pont, F., Vidal-Madjar, A., & Sing, D. 2008, A&A, 481, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, G., Helling, C., Dobbs-Dixon, I., & Juncher, D. 2015, A&A, 580, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, E. J., & Chiang, E. 2015, ApJ, 811, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, E. J., & Chiang, E. 2016, ApJ, 817, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, E. D., Fortney, J. J., & Miller, N. 2012, ApJ, 761, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Mullally, F., Coughlin, J. L., Thompson, S. E., et al. 2015, ApJS, 217, 31 [Google Scholar]
- Ofir, A., Dreizler, S., Zechmeister, M., & Husser, T.-O. 2014, A&A, 561, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Öpik, E. J. 1963, Geophys. J., 7, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, J. E., & Jackson, A. P. 2012, MNRAS, 425, 2931 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, J. E., & Morton, T. D. 2016, ApJ, 819, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, J. E., & Wu, Y. 2016, ApJ, 817, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Pollacco, D. L., Skillen, I., Collier Cameron, A., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Ribas, I., Guinan, E. F., Güdel, M., & Audard, M. 2005, ApJ, 622, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, L. A., Bodenheimer, P., Lissauer, J. J., & Seager, S. 2011, ApJ, 738, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Rothman, L. S., Gordon, I. E., Barber, R. J., et al. 2010, J. Quant. Spectr. Rad. Transf., 111, 2139 [NASA ADS] [CrossRef] [Google Scholar]
- Rothman, L. S., Gordon, I. E., Babikov, Y., et al. 2013, J. Quant. Spectr. Rad. Transf., 130, 4 [Google Scholar]
- Salz, M., Schneider, P. C., Czesla, S., & Schmitt, J. H. M. M. 2016, A&A, 585, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shematovich, V. I., Ionov, D. E., & Lammer, H. 2014, A&A, 571, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Volkov, A. N., Johnson, R. E., Tucker, O. J., & Erwin, J. T. 2011, ApJ, 729, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, A. J., Donahue, T. M., & Walker, J. C. G. 1981, Icarus, 48, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, L. M., & Marcy, G. W. 2014, ApJ, 783, L6 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Left: synthetic transmission spectra calculated for a planet with Mpl = 5 M⊕, Rpl = 4 R⊕, and a 1000 K isothermal atmosphere with 0.01 (blue), 1.0 (orange), and 100 (green) times solar metallicity. The circles of corresponding colour denote the transmission curves integrated over the CoRoT spectral response curve (red dashed curve). Right: contribution functions for the vertical optical depth integrated over the CoRoT spectral response curve. |
| In the text | |
 |
Fig. 2 Mole-mixing fractions of the atmospheric species (see legend in the bottom panel) in thermochemical equilibrium for isothermal (1000 K) models calculated for 0.01 (top), 1.0 (middle), and 100 (bottom) times solar metallicity. |
| In the text | |
 |
Fig. 3 Top: temperature (black solid line) and pressure (red dashed line) profiles as a function of radius r in units of Rpl for a 5 M⊕ and 4 R⊕ planet with Teq=1000 K, orbiting an early K-type star (see Table 1). The right axis indicates the pressure scale. Middle: λ∗ (black solid line) and |
| In the text | |
 |
Fig. 4 Ratio between the hydrodynamic (Lhy) and energy-limited (Len) escape rates as a function of Λ for the modelled planets orbiting the G2 (top), K2 (middle), and M2 (bottom) star. Within each panel, the legend indicates the mass (in M⊕) and temperature (in K) of the modelled planets. The dashed line indicates the equality between Lhy and Len, while the dotted line indicates where the Lhy/Len ratio is equal to 2.0. The value of ΛT lies between 15 and 35. |
| In the text | |
 |
Fig. 5 Variation of the Lhy/Len ratio, normalised to the value of the Lhy/Len ratio obtained with η = 15% (adopted for our calculations), as a function of heating efficiency η for two planets orbiting the K2 star with two different Λ values (dashed line: Λ = 21, Mpl = 5 M⊕, Rpl = 1.8 R⊕; solid line: Λ = 8, Mpl = 5 M⊕, Rpl = 4.5 R⊕) and Teq = 1000 K. |
| In the text | |
 |
Fig. 6 Same as Fig. 3, but for a 5 M⊕ planet with a radius of 1.8 R⊕. |
| In the text | |
 |
Fig. 7 Atmospheric mass MAT evolution normalised to the atmospheric mass corresponding to Rpl =1.8 R⊕ (where Lhy/Len≈1) estimated from the Lhy escape rates obtained for the Mpl = 5 M⊕ planet with Teq = 1000 K orbiting the K-type star. The dashed line indicates MAT = MAT(1.8 R⊕). The initial time is arbitrarily set at 0.1 Myr. The legend lists the atmospheric mass fraction corresponding to each radius. |
| In the text | |
 |
Fig. 8 Colour-scaled value of Λ as a function of planetary mass and radius for Teq = 1000 K. The white straight lines indicate equal Λ values given in the plot. The red solid lines indicate lines of equal average densities of 0.6, 1.6, 3.2, and 5.5 g cm-3. The symbols correspond to the observed (blue bar and arrow) and possible mass-radius combination (black points) for CoRoT-24b. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


