| Issue |
A&A
Volume 598, February 2017
|
|
|---|---|---|
| Article Number | A42 | |
| Number of page(s) | 7 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201629644 | |
| Published online | 27 January 2017 | |
Synchrotron radiation and absence of linear polarization in the colliding wind binary WR 146
1 National Radio Astronomy Observatory, PO Box 0, Socorro, NM 87801, USA
e-mail: chales@nrao.edu
2 Instituto Argentino de Radioastronomía, CCT-La Plata, CONICET, Argentina
3 Facultad de Ciencias Astronomicas y Geofisicas, Universidad Nacional de La Plata, Pasea del Bosque s/n, 1900 La Plata, Argentina
4 Australia Telescope National Facility, CSIRO Astronomy & Space Science, PO Box 76, Epping, NSW 1710, Australia
Received: 2 September 2016
Accepted: 21 October 2016
Context. Several massive early-type binaries exhibit non-thermal emission which has been attributed to synchrotron radiation from particles accelerated by diffusive shock acceleration (DSA) in the wind-collision region (WCR). If the magnetic field in the strong shocks is ordered, its component parallel to the shock front should be enhanced, and the resultant synchrotron radiation would be polarized. However, such polarization has never been measured.
Aims. We aim to determine the percentage of linearly polarized emission from the well-known non-thermal radio emitter WR 146, a WC6+O8 system.
Methods. We performed spatially-unresolved radio continuum observations of WR 146 at 5 cm and 20 cm with the Karl G. Jansky Very Large Array. We constructed a numerical model to investigate a scenario where particles are accelerated by turbulent magnetic reconnection (MR), and we performed a quantitative analysis of possible depolarization effects.
Results. No linearly polarized radio emission was detected. The data constrain the fractional linear polarization to less than 0.6% between 1 to 8 GHz. This is compatible with a high level of turbulence and a dominant random component in the magnetic field. In this case the relativistic particles could be produced by turbulent magnetic reconnection. In order for this scenario to satisfy the required non-thermal energy budget, the strength of the magnetic field in the WCR must be as high as ~ 150 mG. However, if the magnetic field is ordered and DSA is ongoing, then a combination of internal and external Faraday rotation could equally account for the depolarization of the emission.
Conclusions. The absence of polarization could be caused by a highly turbulent magnetic field, other depolarization mechanisms such as Faraday rotation in the stellar wind, or a combination of these processes. It is not clear whether it is possible to develop the high level of turbulence and strong magnetic fields required for efficient MR in a long-period binary such as WR 146. This scenario might also have trouble explaining the low-frequency cutoff in the spectrum. We therefore favor a scenario where particles are accelerated through DSA and the depolarization is produced by mechanisms other than a large ratio between random to regular magnetic fields.
Key words: polarization / radio continuum: stars / radiation mechanisms: non-thermal / stars: individual: WR 146 / stars: winds, outflows
© ESO, 2017
1. Introduction
Hot, early-type stars (O-B2, Wolf-Rayet) are commonly found in stellar systems. If the two components of the system exhibit strong winds, these can interact forming a wind collision region (WCR); we refer to such systems as colliding-wind binaries (CWBs). Colliding stellar winds are clearly detected at a few GHz using radio interferometers, as methodical studies such as Bieging et al. (1989) show. Observations of these systems over a range of radio frequencies show flux density decreasing with the observing frequency, something characteristic of non-thermal (NT) radiation. The recent catalog of particle-accelerating colliding-wind binaries (PACWB) compiled by De Becker & Raucq (2013) presents very detailed information of what is known about these systems. Their emission is interpreted as having a synchrotron origin (i.e. due to relativistic electrons moving in the presence of a magnetic field). Synchrotron radiation is expected to be polarized. However, to date there are no reports of polarized radio emission from a PACWB.
According to the PACWB catalog there are more than 40 known binary systems capable of producing synchrotron radiation. One of these is WR 146, the brightest WR star at radio wavelengths and the fourth to be associated with a NT radio source (Felli & Massi 1991). It is located at a distance of 1.2 kpc and is thought to be a WC6+O8 system (Niemela et al. 1998). MERLIN observations at 5 GHz (Dougherty et al. 1996) show a NT source located north of the primary star. The system was observed in 2004 with the VLA in combination with the VLBA Pie Town antenna, from 1.4 to 43 GHz (O’Connor et al. 2005). The 43 GHz observations reveal two components, separated by about 0.2 arcsec: a northern source coincident with the secondary star and a southern source coincident with the primary star. The 1.4 GHz observations reveal that the NT source is located part-way between the two components, close to the northern one. Only the NT source is detected at the lower frequencies (1.4 GHz, 5 GHz). The system was monitored over 10 yr with the WSRT at 350 MHz and 1.4 GHz. Variability with period 3.38 yr suggests the presence of a third component that modulates the O star wind (Setia Gunawan et al. 2000).
The polarization characteristics of a synchrotron source can potentially provide useful and unique information about physical conditions within the source (Cioffi & Jones 1980). An accurate determination of the polarization degree (PD) allows one, in principle, to distinguish among different scenarios. If the observed PD is between a few percent up to a few tens, this would provide decisive evidence of the synchrotron origin of the NT emission and constrain the degree of turbulence in the plasma. If an extremely high polarization (above 70%) is detected, the underlying physics of particle acceleration in CWBs will be shown to be different from what has been traditionally assumed in most theoretical models. Finally, if no polarization is detected (i.e., PD ≲ 1%), the main acceleration and emission mechanisms of the standard model of CWBs – diffusive shock acceleration (DSA) and synchrotron radiation, respectively – might need to be reconsidered. Therefore, polarization measurements can improve our knowledge of CWBs.
This work presents the first radio polarimetric study of a CWB, focusing on WR 146. We describe our observations and data reduction in Sect. 2. Results are presented in Sect. 3. In Sect. 4 we discuss acceleration processes and interpret our polarization findings. Concluding remarks and directions for future research are presented in Sect. 5.
2. Observations and data reduction
We observed WR 146 with the Karl G. Jansky Very Large Array (VLA) on 2015 May 4 under Project Code 15A-480. The array was in B configuration. Full polarization observations were performed in two frequency bands. These were centered at 1.5 GHz (20 cm, L-band) and 6 GHz (5 cm, C-band) spanning bandwidths of 1 GHz and 4 GHz, respectively. In the 20 cm band, the correlator was configured to deliver 16 spectral windows with 64 × 1 MHz channels. The 5 cm band was configured to deliver 32 spectral windows with 64 × 2 MHz channels. The time sampling was 3 s for both bands. The total observing time on WR 146 was 19 min at L-band and 14 min at C-band. We observed 3C 138 for the purpose of flux density and position angle calibration, J2007+4029 for amplitude and phase calibration, and the unpolarized source J2355+4950 for instrumental leakage calibration. J2355+4950 is less than 0.25% polarized at L-band and C-band.
The data were reduced using version 4.3.0 of the CASA package (McMullin et al. 2007). Hanning smoothing was performed. RFI was identified manually and conservatively flagged. The flux density scale was referenced to the most recent 2012 value for 3C 138 from Perley & Butler (2013a). The position angle of 3C 138 was assumed to be −11° on all spatial scales across L-band and C-band. This is within a few degrees of the values presented by Perley & Butler (2013b) based on D configuration observations. However, their values are only loosely appropriate for translation to our B configuration data because 3C 138 exhibits polarization structure on sub-arcsecond scales (Cotton et al. 1997). We conservatively estimate that any intrinsic rotation measure (RM) left unaccounted in our model of 3C 138 is no worse than 2 rad m-2. No dedicated corrections were performed to account for atmospheric Faraday rotation taking place within the ionosphere and plasmasphere (the necessary CASA functionality contained an error in version 4.3.0, so it was not used). Line of sight atmospheric RMs throughout our observation were approximately constant at ~ 6 rad m-2, estimated by combining GPS-derived total electron content data from the International GNSS Service with the International Geomagnetic Reference Field model of the Earth’s magnetic field. Without correction, this atmospheric RM was absorbed into our position angle calibration, imparting a residual ~ 1 rad m-2 on our target data. Combining these two uncertainties, we estimate that our WR 146 data are affected by a systematic RM of no more than approximately 2 rad m-2. This is negligible given our resolution in Faraday depth space, described below. We performed one round of phase self-calibration on WR 146 in each band.
The total intensity data were imaged per band as well as per spectral window, the latter every 64 MHz in the 20 cm band (minus 3 windows affected by RFI) and every 128 MHz in the 5 cm band (minus 4 windows affected by RFI). The continuum rms noises in the full-band 20 cm and 5 cm images are 40 μJy beam-1 and 12 μJy beam-1, respectively. These values are worse than theoretical expectations (almost double) due to unusually disruptive RFI. However, taking into account observational contingencies, the sensitivities are sufficient for the objectives in this work. The spatial resolutions in the full-band 20 cm and 5 cm images are ~ 4′′ and ~ 1′′, respectively. Flux density measurements in the full-band and per spectral window images were performed using BLOBCAT (Hales et al. 2012b).
We imaged the Stokes Q and U data by pre-averaging every 2 input spectral channels to form an output image cube with 2 MHz channels across L-band and 4 MHz channels across C-band. Each image plane was then smoothed to a common spatial resolution of 14′′ × 6′′, set by the lowest frequency. Using this data we performed RM synthesis (Brentjens & de Bruyn 2005). We examined the data in four different frequency ranges: the combined 1−2 GHz and 4−8 GHz data, and subsets 1−2 GHz, 4−8 GHz, and 6−8 GHz. The resolution in Faraday depth space for each of these frequency ranges is approximately 40 rad m-2, 50 rad m-2, 900 rad m-2, and 3000 rad m-2, respectively. The effective rms noise (σQU; Hales et al. 2012a) for each of the respective ranges is 22 μJy beam-1, 30 μJy beam-1, 34 μJy beam-1, and 51 μJy beam-1.
3. Results
We detect WR 146 as a single spatially-unresolved source in the 20 cm and 5 cm total intensity images. The flux density is 79.8 ± 1.6 mJy at 1.52 GHz and 35.7 ± 0.7 mJy at 6.00 GHz, obtained from the full-band images. The errors include a systematic absolute flux density uncertainty of 2% added in quadrature to the statistical errors previously quoted.
The spectrum obtained from the per spectral window data is displayed in Fig. 1 and tabulated in the appendix. The figure shows marginal evidence for a turnover below 1.5 GHz. The spectral index (α such that Sν ∝ να) is −0.58 ± 0.02 when fit to the flux densities from all spectral windows. It is possible that the flux densities at the lower frequencies are affected by absorption. To account for this, we fit only the higher frequency data from spectral windows within the 5 cm band, obtaining a softer value of −0.62 ± 0.02 (Fig. 1). To highlight the putative turnover, in Fig. 1 (and later in Fig. 2) we also plot measurements at 327 MHz from Benaglia & Ishwara-Chandra (priv. comm.; observed with GMRT in Oct. 2014) and Taylor et al. (1996), where the cutoff becomes more pronounced. Note, however, that their observations are not contemporaneous with those presented in this work, so their data points are not expected to correspond with our spectral fit.
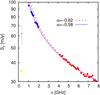 |
Fig. 1 Radio observations at L-band (blue points) and C-band (red points). We show the spectral fit Sν ∝ να to the whole data set (solid purple line) and only to the C-band data (dashed orange line). We also show the flux densities measured at 327 MHz by Taylor et al. (1996) (grey triangle) and Benaglia & Ishwara-Chandra (priv. comm., observed in Oct. 2014, yellow square). |
 |
Fig. 2 Luminosities in the 20 cm and 5 cm bands from our per spectral window data (red points). The solid green curve is the simulated emission considering acceleration by MR, and synchrotron emission suffering free-free absorption in the stellar wind. We also include data points from Taylor et al. (1996) (grey triangle) and Benaglia & Ishwara-Chandra (priv. comm., observed in Oct. 2014, yellow circle), and from O’Connor et al. (2005) for the total flux density (dark grey squares) and the WR emission (orange squares). The straight lines represent the separated (dashed) and summed (solid) free-free emission from the winds using Eq. (8) from Wright & Barlow (1975). |
We do not detect any linearly polarized emission from WR 146 within the 4 frequency ranges examined. Upper bounds1 are reported in Table 1. In each case, the statistical significance is below the Gaussian equivalent of a 4 sigma detection (Hales et al. 2012a). Combining these results with total intensity flux densities, the PD at L-band is less than 0.15% (<120 μJy/80 mJy), at C-band it is less than 0.5% (<180 μJy/36 mJy), and within the upper half of C-band (6–8 GHz) it is less than 0.6% (<190 μJy/32 mJy). Thus overall, the WR 146 emission exhibits less than 0.6% fractional polarization across 1-8 GHz.
Upper bounds on the linearly polarized flux density (LPFD) for different portions of the data.
4. Discussion
Since the pioneering studies of Eichler & Usov (1993), the NT radio emission of PACWBs has been explained as synchrotron radiation produced by a population of relativistic electrons interacting with the local magnetic field. It has been suggested that the most suitable mechanism to account for the acceleration of electrons in PACWBs is DSA through a first-order Fermi process (Romero et al. 1999; Benaglia & Romero 2003; Pittard & Dougherty 2006; Reitberger et al. 2014), although magnetic reconnection (MR) is also possible (Jardine et al. 1996). For DSA to operate efficiently, a strong shock, a turbulent motion of the plasma, and a disordered magnetic field are required. The plasma is expected to develop instabilities near the contact discontinuity (Stevens et al. 1992), which would provide the required turbulence for this scenario, although a very high turbulence might debilitate the shock and therefore reduce the efficiency of DSA. On the other hand, for MR to be efficient, small-scale turbulent motions are necessary (Lazarian & Vishniac 1999). Hence, this mechanism cannot be discarded in a very turbulent regime (Falceta-Gonçalves & Abraham 2012). The magnetic field is not required to be high for DSA (Bosch-Ramon & Rieger 2012), in contrast to the case of MR.
In any case, the high-energy electrons are expected to obtain a power-law distribution in energy with a spectral index p ~ 2. The resultant synchrotron radiation is intrinsically polarized up to a value of Πi(p) ~ 70%. However, a turbulent magnetic field greatly decreases the PD. If the random component of the field is Br and the ordered field is B0, the observed PD becomes (Burn 1966): 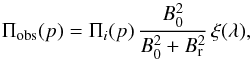 (1)where the function ξ(λ) takes into account possible depolarization effects (wavelength-dependent in some cases; Sect. 4.2). Since the magnetic field lines are frozen in the plasma, the random component of the magnetic field is linked to the degree of turbulence in the WCR, measured by the ratio Br/B0. Therefore, the PD is strictly related to the degree of turbulence, and a small polarization could be indirect evidence of a highly turbulent medium. Considering solely this effect, our result of non-detection of polarization in WR 146 points to a very high ratio Br/B0> 8. DSA is not expected to be efficient under such conditions due to the consequently weaker shocks, which leads to the conclusion that MR could be the principal acceleration mechanism acting on this PACWB.
(1)where the function ξ(λ) takes into account possible depolarization effects (wavelength-dependent in some cases; Sect. 4.2). Since the magnetic field lines are frozen in the plasma, the random component of the magnetic field is linked to the degree of turbulence in the WCR, measured by the ratio Br/B0. Therefore, the PD is strictly related to the degree of turbulence, and a small polarization could be indirect evidence of a highly turbulent medium. Considering solely this effect, our result of non-detection of polarization in WR 146 points to a very high ratio Br/B0> 8. DSA is not expected to be efficient under such conditions due to the consequently weaker shocks, which leads to the conclusion that MR could be the principal acceleration mechanism acting on this PACWB.
4.1. Turbulent magnetic reconnection
MR is a process that develops when two converging flows meet. If the magnetic fields carried by the flows have opposite polarity, the magnetic field lines reconnect and magnetic energy is released. This energy can be converted to kinetic energy, i.e., sheating and/or particle acceleration, in multiple small-scale MR events that develop in turbulent plasmas. In such case particles are accelerated in multiple magnetic islands (Kowal et al. 2011). The acceleration timescale is 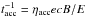 , where ηacc ~ 0.3(vrec/c)2 is the acceleration efficiency, vrec the reconnection velocity, e and E the charge and energy of the particle, respectively, and B the ambient magnetic field. Depending on the conditions in the plasma, the spectral index can be p< 2.5 (Drury 2012), which is in agreement with the injection spectral index derived from our observations, p = −2α + 1 ≃ 2.3 ± 0.1.
, where ηacc ~ 0.3(vrec/c)2 is the acceleration efficiency, vrec the reconnection velocity, e and E the charge and energy of the particle, respectively, and B the ambient magnetic field. Depending on the conditions in the plasma, the spectral index can be p< 2.5 (Drury 2012), which is in agreement with the injection spectral index derived from our observations, p = −2α + 1 ≃ 2.3 ± 0.1.
We applied the NT emission model described in del Palacio et al. (2016) to test whether turbulent MR can account for the accelerated particles in WR 146. This model considers the adiabatic wind shocks to be thin enough to neglect their width, and that the relativistic particles are attached to the flow streamlines through the chaotic B-component. The NT particle content is modeled as sets of linear-emitters. In each linear-emitter, a population of relativistic particles is injected at a given location with a distribution Q(E) ∝ E− p, and evolve until reaching the stationary particle distribution at positions along the streamline. The relevant energy losses (IC scattering and synchrotron for electrons; p-p interactions for protons) and the advection of particles are taken into account when computing the particle evolution. The adopted system parameters are summarized in Table 2. The adopted parameters yield a linear distance of D ~ 200 AU. The small value of η means that the shocked structure is much closer to the secondary star.
Parameters of the WR 146 system for the primary (sub-index 1) and the secondary (sub-index 2).
The WCR consists of the shocked stellar wind from the primary (S1) and the shocked stellar wind from the secondary (S2), each with different properties. Magnetic field notation is as follows: B∗ 1 and B∗ 2 are the stellar surface magnetic fields, and B1 and B2 are the compressed fields in the shocks S1 and S2 which are (in our simple model) the WCR. In both shocks we considered a reconnection velocity given by vrec = 0.6vA (del Valle & Romero 2012), where vA is the Alfvén velocity. We also assumed that ~ 4% of the released magnetic energy goes to accelerating electrons (del Valle et al. 2011, and references therein).
Under the mentioned conditions, our results show that as long as the WR star is not extremely magnetized (surface magnetic field B∗ 1 < 2000 G), or that no highly efficient B-amplification is taking place in S1, then the NT emission is completely dominated by S2 (i.e. B2 is the only relevant magnetic field). Fitting the observed energy fluxes requires that in S2 the magnetic field energy density is 38% of the thermal energy density, which corresponds to a magnetic field intensity of B2 ~ 150 mG, and ηacc ~ 10-7. For typical values of the Alfvén radius rA = R2 and rotational speed Vrot = 250 km s-1, this yields a maximum value for the stellar surface magnetic field B∗ 2< 800 G; this condition is relaxed if magnetic field amplification is taking place in the shocks. Figure 2 shows a good agreement between our model and the new radio observations. Features of the non-simultaneous observations are also reproduced qualitatively, although it is not clear if the cut-off at lower energies can be explained by free-free absorption in the stellar wind (suppression due to Razin-Tsytovich effect is negligible due to the high value of B; we further discuss this in Sect. 4.3).
In the MR model, the acceleration time depends heavily on B. In S1 no efficient acceleration takes place, while in S2 electrons can reach energies up to ~ 100 GeV, this being the maximum energy limited by IC losses with stellar photons. The expected IC luminosity is not very high and falls below the gamma-ray detector sensitivities of the LAT on board the Fermi satellite (4-yr of integration time) and the Cherenkov Telescope Array (CTA, 50-h).
4.2. Depolarization processes
Synchrotron radiation can be depolarized by various radiation transfer effects. In transparent radio sources the main effect is Faraday rotation (FR). FR alters the plane of polarization and can reduce the observed PD. Sokoloff et al. (1998) reviewed the different mechanisms that produce depolarization of synchrotron radio emission. In what follows we will analyze the most relevant of these processes in CWBs, besides the one presented above. To be more conservative, we assume a classical DSA scenario. In such case, the available energy to accelerate NT particles is larger, as it is provided by the wind kinetic energy instead of the magnetic field. Moreover, the acceleration timescale in the fast shocks is shorter than in the MR scenario. To fit the observed synchrotron fluxes, a value of B2 ~ 40 mG is then sufficient.
-
1.
Reduced polarization due to thermal fraction: a significantcontribution from thermal (unpolarized) emission can reduce theobserved PD. However, the thermal contribution in L-band isbelow 1% of the total emission, while in C-band it is lower than 5%.This effect can therefore be neglected.
-
2.
Differential (depth) FR: when synchrotron emission originates in a thermal plasma containing a regular magnetic field, the polarization plane of the radiation produced at different depths within the source is rotated over different angles by the Faraday effect. The emission from deeper regions in the volume is Faraday rotated along the line of sight, and cancels out the polarization from the surface layers of the volume, resulting in a decrease in the PD of the integral emission observed (e.g. see Velusamy & Kundu 1975, for a study of this effect in supernova remnants). This is a wavelength-dependent depolarization process that is likely to require a more laminar flow than present in the WCR. In the case of WR 146, the large separation between the stars means that the shocks in the WCR will be adiabatic, and therefore reasonably thin (although a high level of turbulence could widen them). The shock width can be estimated as ~ 0.1 times its distance to the respective star, yielding Δl1 ≈ 20 AU and Δl2 ≈ 5 AU. Typical values for the physical parameters at the shocks in the WCR are an electron number density of ne1 ~ 105 cm-3 and ne2 ~ 106 cm-3, and a magnetic field of B1 ~ 3 mG and B2 ~ 40 mG. Considering the simplest case of a uniform slab, we can construct a rough estimate of the maximum intrinsic RM ~ KRMneBzΔl, where the constant KRM is equal to 81 cm pc-1 G-1 and
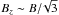 is the component of the magnetic field in the direction of the line of sight (LOS). We obtain values of RM1 ~ 5 × 103 rad m-2 and RM2 ≈ 30RM1. The depolarization factor in this case is ξ2(λ) ≈ sin(RM2λ2)/(RM2λ2) < 0.3% for λ> 5 cm, which shows that this effect could be relevant in the case of a dominant ordered magnetic field. A detailed analysis of this process will be addressed in a forthcoming work, with an improved modeling of the quantities ne and Bz along the LOS through the shock.
is the component of the magnetic field in the direction of the line of sight (LOS). We obtain values of RM1 ~ 5 × 103 rad m-2 and RM2 ≈ 30RM1. The depolarization factor in this case is ξ2(λ) ≈ sin(RM2λ2)/(RM2λ2) < 0.3% for λ> 5 cm, which shows that this effect could be relevant in the case of a dominant ordered magnetic field. A detailed analysis of this process will be addressed in a forthcoming work, with an improved modeling of the quantities ne and Bz along the LOS through the shock. -
3.
Internal Faraday Dispersion: in the WCR the synchrotron emitting electrons and thermal plasma coexist. In the case the latter is turbulent, nearby lines of sight experience a random walk in FR. If the telescope beam encompasses many turbulent cells, the observed PD diminishes. This is a wavelength-dependent process. Using the simple formulas given by Burn (1966) for the case of a uniform slab, one has S = 2(KRMneBr)2(δL)2λ4 ~ 10-2RM2λ4, where we assumed δL ~ 0.1ΔL and Br ~ Bz. This yields ξ2(5 cm) ≈ (1−e− S) /S< 0.1%. Once again, this very simple approximation just shows that the depolarization could be strong, although a more careful analysis is needed.
-
4.
External Faraday Dispersion: this is similar to the internal effect above, but in this case the FR takes place in a thermal plasma (the stellar wind) external to the synchrotron emitting volume (the WCR). To properly account for this process, one has to solve numerically the value of RM = Kλ2∫nBzdz for each emitting region in the WCR. This integral depends on both the intensity and the geometry of the stellar magnetic field. In the case of a toroidal magnetic field (which is expected at large distances from massive stars) supported by a surface stellar magnetic field of B∗ ~ 200 G, the value of RM can be in the range (3−40) × 104 rad m-2, with significant dependence on the LOS for the particular surface element. However, this condition can be considerably relaxed if the stellar magnetic field is much lower; in particular, the strength of B2 could be due to a high local amplification. Other external Faraday screens in the interstellar medium are most likely negligible on the angular scales of interest here.
-
5.
Gradients in RM across the beam: this is similar to the dispersion effects above, but here describes variations in RM originating from systematic gradients within the telescope beam rather than from a random walk. In our case, we are looking at a curved shock that is completely unresolved within the beam of our observations. Then, if there is a gradient in RM along the shock, polarization vectors within the beam may cancel, leading to depolarization. However, one would expect that this effect does not lead to a complete depolarization of the emission as long as the LOS does not coincide with the axis of symmetry of the WCR (which would seldom occur and only if the orbit is seen edge-on at inclination ~90°). Future high resolution (VLBI) polarimetric observations may be used to examine this effect. Spatially resolved fractional polarization measurements of the shock could be used to discriminate between two cases: (i) the emission appears polarized, in which case the acceleration mechanism is likely DSA due to coherent B-fields; or (ii) the emission is still depolarized, in which case either MR or external depolarization could be responsible.
4.3. Source variability and possible contamination
The WR 146 system is a variable radio source (Setia Gunawan et al. 2000). Orbital modulation could play a significant role in its variability if the eccentricity and/or the inclination of the orbit are large (Eichler & Usov 1993). If the orbit is eccentric, conditions in the shocked plasma will vary, as will the medium in which the synchrotron photons propagate. If the orbital inclination is large, this will affect the degree to which low-frequency photons emitted in the WCR will be absorbed within the stellar wind, depending on the photon path to the observer and the orbital phase. If the binary is seen approximately edge-on (i ~ 90°), the absorption will be maximum when one of the stars is in front of the WCR (conjunction) and minimum when they are near quadrature. However, as VLBI observations of the system have revealed a C-shaped WCR (O’Connor et al. 2005), this points to a rather small orbital inclination, unless those observations of the binary correspond to rather specific positions of the orbit near quadrature (if the system were near conjunction, the WCR would look like more circular; e.g. see Fig. 4 in del Palacio et al. 2016). To explain the steep low-frequency cutoff in the spectrum seen in Fig. 2, there are two other possibilities: (i) the effect is mostly due to the eccentricity of the orbit, in which case both observations at 325 MHz should correspond to orbital phases different to those of the observations at 5 GHz (some coincidence is demanded, as the observations were performed at random phases); or (ii) the low-frequency cutoff is related to the Razin-Tsytovich effect, which produces a cutoff at νRT ~ 20ne/B Hz (in c.g.s. units). Given that typically ne2 ~ 106 in S2, this requires B2 ~ 50 mG. This value of B2 is too small for MR, and therefore the cutoff is more consistent within a DSA scenario. Nevertheless, we remark that our interpretation of the low-frequency cutoff solely in terms of free-free absorption is subject to the unknown orbital parameters; simultaneous observations at low (<1 GHz) and high (> 1 GHz) frequencies would help to disentangle this ambiguity.
Moreover, it is still under debate whether the secondary in WR 146 is an O8V star or another binary (Setia Gunawan et al. 2000). Despite this uncertainty in the composition of the secondary, the very high resolution image from O’Connor et al. (2005) shows signs of only one WCR, so it seems unlikely that our results are biased by the behavior of the secondary. Instead, the most reasonable explanation is that there is only one dominant WCR whose variability (especially at low frequencies) is due to geometrical modulations. Long-term monitoring is needed to confirm this.
5. Conclusions
We presented the first radio polarimetric study of a colliding-wind binary. Our VLA observations of WR 146 reveal the absence of linearly polarized emission down to a fractional level of 0.6% across 1 to 8 GHz. If acceleration were due predominantly to DSA in strong shocks, as usually assumed, then the magnetic field component parallel to the shock front would be enhanced, and the resultant emission would be polarized. The absence of polarization can be explained in terms of a highly turbulent magnetic field, in which case turbulent magnetic reconnection would account for non-thermal particle acceleration, or depolarization effects, for example due to Faraday rotation in the stellar wind, or perhaps a combination of these effects. We have shown that, in principle, either scenario is plausible. If turbulent MR is taking place, a high value of the magnetic field in the WCR ~ 150 mG is required to account for the synchrotron emission. On the other hand, if DSA is the main acceleration mechanism, a magnetic field of ≈ 40 mG is sufficient to account for the synchrotron emission. However, even this relatively low magnetic field was shown to be enough to produce significant FR and consequently strong depolarization. Moreover, a lower value of the magnetic field in the WCR also helps to reproduce the low-frequency cutoff seen in the spectrum, as in this case the Razin-Tsytovich suppression is more effective. Our analysis seems to favor a scenario where DSA and a partially ordered B-field are responsible for the synchrotron emission, while various depolarization processes account for the very low PD in the radiation. Future high resolution observations of the shock could be used to reveal polarized emission, where the angular scale at which the shock appears polarized would be an important diagnostic discriminant between MR and DSA. An RM detection would also help to distinguish between MR and DSA by providing constraints on magnetic field strengths, and thus checking if MR remains plausible. In a forthcoming work we will investigate the depolarization effects in more detail, and study if the detection of polarization remains elusive in other particle-accelerating colliding-wind binaries.
Adhering to the terminology regarding bound versus limit from Kashyap et al. (2010).
Acknowledgments
P.B. and G.E.R. are members of the CIC, CONICET. G.E.R. acknowledges support by the Spanish Ministerio de Economía y Competitividad (MINECO/FEDER, UE) under grant AYA2016-76012-C3-1-P and CONICET grant PIP 0338. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc.
References
- Benaglia, P., & Romero, G. E. 2003, A&A, 399, 1121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bieging, J. H., Abbott, D. C., & Churchwell, E. B. 1989, ApJ, 340, 518 [NASA ADS] [CrossRef] [Google Scholar]
- Bosch-Ramon, V., & Rieger, F. M. 2012, in Astroparticle, Particle, Space Physics and Detectors For Physics Applications – Proc. of the 13th ICATPP Conf. (World Scientific Publishing Co. Pte. Ltd.), eds. S. Giani, et al., 219 [Google Scholar]
- Brentjens, M. A., & de Bruyn, A. G. 2005, A&A, 441, 1217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burn, B. J. 1966, MNRAS, 133, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Cioffi, D. F., & Jones, T. W. 1980, AJ, 85, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Cotton, W. D., Dallacasa, D., Fanti, C., et al. 1997, A&A, 325, 493 [NASA ADS] [Google Scholar]
- De Becker, M., & Raucq, F. 2013, A&A, 558, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- del Palacio, S., Bosch-Ramon, V., Romero, G. E., & Benaglia, P. 2016, A&A, 591, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- del Valle, M. V., & Romero, G. E. 2012, A&A, 543, A56 [Google Scholar]
- del Valle, M. V., Romero, G. E., Luque-Escamilla, P. L., Martí, J., & Ramón Sánchez-Sutil, J. 2011, ApJ, 738, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Dougherty, S. M., & Williams, P. M. 2000, MNRAS, 319, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Dougherty, S. M., Williams, P. M., van der Hucht, K. A., Bode, M. F., & Davis, R. J. 1996, MNRAS, 280, 963 [NASA ADS] [CrossRef] [Google Scholar]
- Drury, L. O. 2012, MNRAS, 422, 2474 [NASA ADS] [CrossRef] [Google Scholar]
- Eichler, D., & Usov, V. 1993, ApJ, 402, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Falceta-Gonçalves, D., & Abraham, Z. 2012, MNRAS, 423, 1562 [NASA ADS] [CrossRef] [Google Scholar]
- Felli, M., & Massi, M. 1991, in Wolf-Rayet Stars and Interrelations with Other Massive Stars in Galaxies, eds. K. A. van der Hucht, & B. Hidayat, IAU Symp., 143, 87 [Google Scholar]
- Hales, C. A., Gaensler, B. M., Norris, R. P., & Middelberg, E. 2012a, MNRAS, 424, 2160 [NASA ADS] [CrossRef] [Google Scholar]
- Hales, C. A., Murphy, T., Curran, J. R., et al. 2012b, MNRAS, 425, 979 [NASA ADS] [CrossRef] [Google Scholar]
- Jardine, M., Allen, H. R., & Pollock, A. M. T. 1996, A&A, 314, 594 [NASA ADS] [Google Scholar]
- Kashyap, V. L., van Dyk, D. A., Connors, A., et al. 2010, ApJ, 719, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Kowal, G., de Gouveia Dal Pino, E. M., & Lazarian, A. 2011, ApJ, 735, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Lazarian, A., & Vishniac, E. T. 1999, ApJ, 517, 700 [NASA ADS] [CrossRef] [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Data Analysis Software and Systems XVI, eds. R. A. Shaw, F. Hill, & D. J. Bell, ASP Conf. Ser., 376, 127 [Google Scholar]
- Niemela, V. S., Shara, M. M., Wallace, D. J., Zurek, D. R., & Moffat, A. F. J. 1998, AJ, 115, 2047 [NASA ADS] [CrossRef] [Google Scholar]
- O’Connor, E. P., Dougherty, S. M., Pittard, J. M., & Williams, P. M. 2005, in Proc. Massive Stars and High-Energy Emission in OB Associations, eds. G. Rauw, Y. Nazé, R. Blomme, & E. Gosset, 81 [Google Scholar]
- Perley, R. A., & Butler, B. J. 2013a, ApJS, 204, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, R. A., & Butler, B. J. 2013b, ApJS, 206, 16 [Google Scholar]
- Pittard, J. M., & Dougherty, S. M. 2006, MNRAS, 372, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Reitberger, K., Kissmann, R., Reimer, A., Reimer, O., & Dubus, G. 2014, ApJ, 782, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Romero, G. E., Benaglia, P., & Torres, D. F. 1999, A&A, 348, 868 [NASA ADS] [Google Scholar]
- Setia Gunawan, D. Y. A., de Bruyn, A. G., van der Hucht, K. A., & Williams, P. M. 2000, A&A, 356, 676 [NASA ADS] [Google Scholar]
- Sokoloff, D. D., Bykov, A. A., Shukurov, A., et al. 1998, MNRAS, 299, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Stevens, I. R., Blondin, J. M., & Pollock, A. M. T. 1992, ApJ, 386, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, A. R., Goss, W. M., Coleman, P. H., van Leeuwen, J., & Wallace, B. J. 1996, ApJS, 107, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Velusamy, T., & Kundu, M. R. 1975, A&A, 41, 307 [NASA ADS] [Google Scholar]
- Wright, A. E., & Barlow, M. J. 1975, MNRAS, 170, 41 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional table
Table A.1 presents our VLA flux density measurements for WR 146, as displayed in Fig. 1.
VLA flux densities for WR 146 measured across L-band and C-band within 64 MHz and 128 MHz spectral windows, respectively.
All Tables
Upper bounds on the linearly polarized flux density (LPFD) for different portions of the data.
Parameters of the WR 146 system for the primary (sub-index 1) and the secondary (sub-index 2).
VLA flux densities for WR 146 measured across L-band and C-band within 64 MHz and 128 MHz spectral windows, respectively.
All Figures
 |
Fig. 1 Radio observations at L-band (blue points) and C-band (red points). We show the spectral fit Sν ∝ να to the whole data set (solid purple line) and only to the C-band data (dashed orange line). We also show the flux densities measured at 327 MHz by Taylor et al. (1996) (grey triangle) and Benaglia & Ishwara-Chandra (priv. comm., observed in Oct. 2014, yellow square). |
| In the text | |
 |
Fig. 2 Luminosities in the 20 cm and 5 cm bands from our per spectral window data (red points). The solid green curve is the simulated emission considering acceleration by MR, and synchrotron emission suffering free-free absorption in the stellar wind. We also include data points from Taylor et al. (1996) (grey triangle) and Benaglia & Ishwara-Chandra (priv. comm., observed in Oct. 2014, yellow circle), and from O’Connor et al. (2005) for the total flux density (dark grey squares) and the WR emission (orange squares). The straight lines represent the separated (dashed) and summed (solid) free-free emission from the winds using Eq. (8) from Wright & Barlow (1975). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


