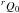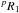| Issue |
A&A
Volume 598, February 2017
|
|
|---|---|---|
| Article Number | A9 | |
| Number of page(s) | 8 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201629508 | |
| Published online | 24 January 2017 | |
Laboratory detection of the rotational-tunnelling spectrum of the hydroxymethyl radical, CH2OH
1 Univ. Lille, CNRS, UMR 8523 – PhLAM – Physique des Lasers, Atomes et Molécules, 59000 Lille, France
e-mail: stephane.bailleux@univ-lille1.fr
2 Instituto de Ciencia de Materiales de Madrid, CSIC, Group of Molecular Astrophysics, C/Sor Juana Inés de la Cruz 3, 28049 Cantoblanco, Madrid, Spain
Received: 9 August 2016
Accepted: 30 October 2016
Context. Of the two structural isomers of CH3O, methoxy is the only radical whose astronomical detection has been reported through the observation of several rotational lines at 2 and 3 mm wavelengths. Although the hydroxymethyl radical, CH2OH, is known to be thermodynamically the most stable (by ~3300 cm-1), it has so far eluded rotational spectroscopy presumably because of its high chemical reactivity.
Aims. Recent high-resolution (~10 MHz) sub-Doppler rovibrationally resolved infrared spectra of CH2OH (symmetric CH stretching a-type band) provided accurate ground vibrational state rotational constants, thus reviving the quest for its millimeter-wave spectrum in laboratory and subsequently in space.
Methods. The search and assignment of the rotational spectrum of this fundamental species were guided by our quantum chemical calculations and by using rotational constants derived from high-resolution IR data. The hydroxymethyl radical was produced by hydrogen abstraction from methanol by atomic chlorine.
Results. Ninety-six b-type rotational transitions between the v = 0 and v = 1 tunnelling sublevels involving 25 fine-structure components of Q branches (with Ka = 1 ← 0) and 4 fine-structure components of R branches (assigned to Ka = 0 ← 1) were measured below 402 GHz. Hyperfine structure alternations due to the two identical methylenic hydrogens were observed and analysed based on the symmetry and parity of the rotational levels. A global fit including infrared and millimeter-wave lines has been conducted using Pickett’s reduced axis system Hamiltonian. The recorded transitions (odd ΔKa) did not allow us to evaluate the Coriolis tunnelling interaction term. The comparison of the experimentally determined constants for both tunnelling levels with their computed values secures the long-awaited first detection of the rotational-tunnelling spectrum of this radical. In particular, a tunnelling rate of 139.73 ± 0.10 MHz (4.6609(32) × 10-3 cm-1) was obtained along with the rotational constants, electron spin-rotation interaction parameters and several hyperfine coupling terms.
Conclusions. The laboratory characterization of CH2OH by millimeter-wave spectroscopy now offers the possibility for its astronomical detection for the first time.
Key words: molecular data / ISM: molecules / submillimeter: ISM
© ESO, 2017
1. Introduction
The hydroxymethyl radical, CH2OH, is involved as an intermediate species in many chemical reaction systems, and its study spans a wide range of fields, such as in tropospheric chemistry (Atkinson 1990; Pagsberg et al. 1989; Nesbitt et al. 1989) and hydrocarbon (e.g. methane and methanol) oxidation processes (Lin et al. 1999, 2000; Rissanen et al. 2013; Rasmussen et al. 2008). It is also supposed to be an abundant molecule in space because of the ubiquitous methanol molecule, where its less stable structural isomer radical, CH3O, has recently been unexpectedly detected by Cernicharo et al. (2012) towards the cold dark core B1-b. In such cold dark regions a significant CH3O/CH2OH ratio in the gas phase would be indicative of either CH3O/CH2OH photo-desorption or their direct formation in the gas phase. Laboratory experiments have indeed revealed that CH2OH (in contrast to CH3O) is formed by UV photolysis of interstellar ice analogues containing CH3OH (see e.g. Gerakines et al. 1996). Other similar experiments (see e.g. Watanabe & Kouchi 2002; Watanabe et al. 2007) indicated that the detections of H2CO and CH3OH by UV/ion irradiation of CO:H2O ices suggest that CH3O and/or CH2OH are the intermediate species following the chain reaction H2CO + H → CH3O/CH2OH + H → CH3OH. Therefore, taking into account the large methanol abundance in B1-b (Öberg et al. 2010), the possibility to form both methoxy and hydroxymethyl radicals has to be considered.
The high chemical reactivity of CH2OH under laboratory conditions makes it difficult to study experimentally, and its rotational spectrum has always eluded microwave spectroscopists, a fact that has so far hampered its radioastronomical discovery.
In view of its general chemical importance as an intermediate species, especially in modelling the chemistry of interstellar medium, this radical has been the subject of very many studies. An exhaustive list of bibliographic references can be found in Johnson & Hudgens (1996) and in Roberts et al. (2013), for example. In this latter spectroscopic work, which was done in the Nesbitt Laboratory, accurate B and C rotational constants in the ground state were derived from the analysis of the high-resolution, sub-Doppler, near-infrared (NIR) spectrum of the ν3 symmetric CH stretching band.
Our research presented in this paper, the first identification of the rotational-tunnelling spectrum of CH2OH, relies for the most part on this recent fully rotationally resolved high-resolution IR spectra of the hydroxymethyl radical.
2. Prediction of the spectrum
2.1. Quantum chemical calculations
The rotational spectrum of CH2OH was predicted on the basis of ab initio geometrical structure optimization to provide the molecular parameters that are needed to assist with the search for and identification of this spectrum. These are the rotational and quartic centrifugal distortion constants, the electron spin-rotation interaction tensor that is due to the unpaired electron, and the isotropic (Fermi contact) and anisotropic contributions (magnetic dipole-dipole interaction) of the three protons that account for the hyperfine structures. At equilibrium, CH2OH is a non-planar species belonging to the C1 point group with unequal CH bond lengths. However, it is well accepted (Johnson & Hudgens 1996; Kamarchik et al. 2012) that this radical in its ground vibrational state effectively behaves as a planar molecule of Cs symmetry with a 2A″ electronic ground state. Therefore the Cs symmetry-constrained geometry optimization has been performed by employing the B3LYP/6-311++G(d, p) method. The Gaussian package (Frisch et al. 2009) has been used, and the resulting geometry, in close agreement with that of Kamarchik et al. (2012), is cast in Table 1.
Structure of CH2OH optimized at Cs symmetry calculated at the B3LYP/6-311++G(d, p) level of theory.
The computed components of the electric dipole moment are −0.13 D and + 1.64 D for μa and μb, respectively. The molecular parameters derived from the structure are given in Tables 2–4. Roberts et al. (2013) obtained from high-resolution (~10 MHz) sub-Doppler rovibrationally resolved IR spectra the B and C rotational constants in the ground vibrational state (29 832(18) and 25 950(15) MHz, respectively), and our quantum chemically computed values compare well (Table 2). The asymmetry parameter κ = −0.95 inferred from the rotational constants shows that CH2OH is a near-prolate symmetric rotor with an electric dipole moment that is mainly imposed by the OH bond.
Energy separation between tunnelling substates ΔE01, rotational (MHz) and quartic centrifugal distortion constants (kHz) of CH2OH in the A reduction, Ir representation.
Electron spin-rotation (MHz) and their quartic centrifugal distortion coupling constants (MHz) of CH2OH in the A reduction, Ir representation.
2.2. Tunnelling splitting and nuclear spin statistics
At Cs conformation, CH2OH has a double minimum potential with a finite torsional barrier height (~1650 cm-1, Johnson & Hudgens 1996), allowing tunnelling of the hydroxyl proton between two isoenergetic mirror frameworks. The tunnelling doublings were clearly brought to light in the high-resolution NIR spectra of ν1 (OH stretching, Wang et al. 2014a), ν2 (CH asymmetric stretching, Chang et al. 2014), and ν3 (CH symmetric stretching, Wang et al. 2014b) bands measured in the Nesbitt laboratory. An upper limit of 10-3cm-1 (30 MHz) for the tunnelling rate was also estimated for the ground vibrational state using high-level (CCSD(T)/VnZ-F12 with n = 2,3) ab initio computations (Nesbitt et al. 2014). To clarify the allowed electric dipole rotational-tunnelling transitions in the ground vibrational state, the two tunnelling sublevels of the rigid rotor levels of CH2OH (Cs symmetry) can be labelled with the symmetry species of the C2v(M) molecular symmetry group. This group is isomorphic with the permutation-inversion symmetry group (G4) of this non-rigid radical (Bunker & Jensen 1998). Fermi-Dirac statistics dictates that the complete internal wavefunction Φtot = Φelec Φrot Φtun Φvib Φns must change in sign under the sole exchange of the two identical methylenic hydrogen atoms, corresponding to the C2a operation. Therefore the symmetry of Φtot is B1 or B2. The electronic wavefunction Φelec is of B1 symmetry since the C2v radical has an X 2B1 ground state Bruna & Grein (1998; the subscript 1 means symmetric with respect to the σv(ab) operator). The ground vibrational state being always symmetric, Φvib is A1. Regarding the tunnelling wavefunction Φtun, states of A′ symmetry in the rigid radical correlate with those of A1 and B2 symmetry when tunnelling is feasible, while A′′ states separate into A2 and B1 states. Thus Φtun belongs to A1 for the lower (v = 0) and B2 for the higher (v = 1) tunnelling components. Coupling the two identical methylenic proton spin angular momenta to yield IH, nuclear spin states having IH = 1 produce three states of A1 symmetry, and those having IH = 0 give rise to one state of symmetry B1. Then the total nuclear spin wavefunction Φns generates the representation 3A1 ⊕ B1. Finally, the rotational wavefunctions Φrot are A1 or A2 if Ka is even and B1 or B2 for odd Ka. The symmetry labelling of the complete internal wavefunction obtained for each KaKc parity is summarized in Table 5, where the nuclear spin weights (in the case of unresolved hyperfine structure) are also indicated. The ν3 (symmetric CH stretch) vibrationally excited state being also of A1 symmetry, the selection rules for the rovibrational-tunnelling transitions (inserted in the global fit) are identical to those in the ground vibrational state.
Isotropic (Fermi-contact terms aF) and anisotropic (Tij) hyperfine interaction constants (MHz) of the three protons of CH2OH.
Symmetry species and statistical weights of the complete internal wavefunction for the lower (v = 0) and upper (v = 1) tunnelling sublevels for each NKaKc level.
Figure 1 depicts the energy level diagram of the CH2OH radical. The sublevels of B1 symmetry have the lowest tunnelling energy (v = 0) when Ka + Kc is even, with a statistical weight of 3 (1) if Ka is even (odd). The situation is reversed for odd Ka + Kc, that is, these sublevels correspond to those with the highest tunnelling energy (v = 1), with a statistical weight of 1 (3) if Ka is even (odd).
 |
Fig. 1 Energy level diagram showing the doubling of the rigid rotor levels (identified by NKaKc) for Ka = 0,1 into tunnelling sublevels labelled with the symmetry species of the complete internal wavefunction of CH2OH in the C2v(M) group. The statistical weights arising from the permutation of the two identical methylenic hydrogen nuclei are indicated between parentheses. Levels with a weight of 3 correspond to ortho-CH2OH and those with a weight of 1 correspond to the para isomer of the radical. Examples of a-type transitions (not observed) are depicted as black, dashed lines, while representatives of b-type (observed) Q- and R-branch transitions are displayed in green and red, respectively. For clarity the tunnelling splittings (Δ) are 800 times the actual ones, and the fine- and hyperfine-structure splittings are not illustrated. |
The allowed electric dipole transitions are between B1 and B2 levels of identical statistical weights, meaning (Table 5) that a-type transitions occur within a given tunnelling state, while those of b-type take place between tunnelling levels. Clearly, the tunnelling effect essentially modulates the b component of the dipole moment.
Spectral lines falling in the 170–500 GHz frequency range have been predicted using the computed energy difference between the rotationless (N = 0) levels of the two tunnelling substates ΔE01 ≈ 30 MHz (Nesbitt et al. 2014) together with the ab initio molecular parameters given in Tables 2–4 except for the B and C ground vibrational state rotational constants, which were obtained by fitting reported IR lines of the ν3 CH symmetric stretching band (Roberts et al. 2013). These correspond to transitions from the lower tunnelling state (v = 0). All ground-state molecular parameters were taken to be identical in the two tunnelling states.
3. Experimental details
3.1. Spectrometer
Millimeter-wave (mmw) b-type transitions belonging to Q and R branches were recorded using the Lille spectrometer, which is devoted to the study of short-lived species. We failed to detect rotational-tunnelling transitions of a-type. The spectrometer was adapted for the production of the CH2OH radical, and the salient features are summarised here. It now employs an all-solid-state frequency multiplier chain for emission between 170–500 GHz. Mmw radiation was obtained by the frequency multiplication of an E8257D synthesizer with option UNX for improved phase noise performance (Agilent, 8.88–13.89 GHz). It was referenced to a GPS-locked Rubidium atomic clock (FS725, Stanford Research Systems) to secure its frequency accuracy. The output of the synthesizer fed a WR9.0 Amplifier Multiplier Chain (Virginia Diodes Inc.) capable of delivering an output power up to 14 dBm in the 80–125 GHz frequency band. It was used to drive two active broadband frequency doublers (models WR4.3 and WR2.2) and one passive full-band tripler (WR2.8) to cover the 170–500 GHz region entirely. For improved sensitivity, the synthesizer was frequency-modulated at 27 kHz, and phase-sensitive detection at twice this frequency was accomplished with a lock-in amplifier (SR830, Stanford Research Systems), resulting in second-derivative line shapes. The fine-tuning of the modulation depth to the line widths and line strengths ensured full optimization of signal detection, which was achieved using a fast liquid-helium-cooled InSb hot-electron bolometer (QMC Instruments Ltd). This multiplier chain was controlled by a custom-made data acquisition program running in the Igor Pro environment (Wavemetrics) also employed for signal processing. The E8257D synthesizer was either digitally swept step-by-step for spectral search or analogically fast-scanned upwards and downwards. This latter mode of operation, in combination with a 12-bit resolution HDO4034 oscilloscope (Teledyne Lecroy) equipped with a low-noise system architecture, is especially advantageous to efficiently accumulate weak spectra. Accuracy of the measurements was checked against known lines of formaldehyde, and is estimated to be in the 50–150 kHz range depending on the signal-to-noise (S/N) ratio obtained for each line.
3.2. Production of CH2OH
The CH2OH radical was generated in a fast flow system by hydrogen abstraction from CH3OH by Cl. The single-pass absorption cell consisted of a 2 m long double jacketed Pyrex tubing to cool the gas mixture by flowing liquid-nitrogen between the two jackets. Off-axis parabolic mirrors were placed at either end of the cell to optimize the injection of mmw radiation into the cell and to focus the beam onto the bolometer. It was equipped with a solenoid coil used for creating an axial magnetic field to distinguish paramagnetic lines through the observation of the Zeeman effect by successive on/off measurements. The stationary component of the Earth’s magnetic field was not compensated for by the use of Helmholtz coils. At the one end (close to the mmw source), a horizontal Pyrex crosspiece (25 cm long, 20 cm wide) was connected to introduce upstream methanol vapour and chlorine separately (the two inlets were facing each other). Cl2 diluted with He (3.8%) was used as a source for atomic chlorine. The cylinder containing the He/Cl2 gas mixture was agitated on a daily basis to keep the gaseous mixture homogeneous. Cl atoms were generated in a microwave discharge in a small quartz tube (16 cm long, 9 mm inner diameter) placed at one inlet and surrounded by an Evenson-type cavity fed by radiation from a magnetron operating at 2450 MHz. The power of the microwave discharge was kept to the minimum (20 W). Inlet connections to the Pyrex element were made using Teflon flanges to avoid metal in the chemical reaction zone. At the other end, a vertical Pyrex crosspiece was used to connect to a half-choked diffusion pump below the cell and to a pressure gauge above the cell. The outer end of each crosspiece was sealed by a Teflon window mounted at a Brewster angle to improve transmission of polarized mmw radiation and to reduce standing waves. The optimized partial pressure for methanol was 1.2 × 10-3 mBar and the total pressure measured downstream was 7.0 × 10-3 mBar. A brownish deposit located on the inner wall surfaces of the horizontal crosspiece formed rapidly after a few hours of experimentation. Once it began to darken, the detection of CH2OH became impossible and the periodic elimination of this deposit was ineluctable. Cooling the 2 m long tubing element, although not absolutely necessary, was very helpful to efficiently trap the many diamagnetic species generated and otherwise detected, such as unreacted methanol, H2CO, H2O, HClCO, CO, and HCOOH. Several unidentified diamagnetic lines were also detected. The lifetime of CH2OH in our experimental setup was short enough that the magnetic field created by the solenoid coil, which did not surround the horizontal crosspiece, was inefficient in disturbing the energy levels of the CH2OH radical by the Zeeman interaction. Instead, it was appropriate to place strong permanent magnets near the horizontal crosspiece to confirm that the lines belong to this paramagnetic species. Lines of HCO (formyl radical, Blake et al. 1984), which we also observed during our spectral search, needed an additional magnetic field generated by the solenoid coil (~200 G) to completely disappear. The observed weakness of the lines of the hydroxymethyl radical can presumably be imputed to its short lifetime, which is partly due to the fast reaction of CH2OH with Cl to yield H2CO and HCl, about one order of magnitude faster than the reaction of CH3OH with Cl (Aristov et al. 2000; Pagsberg et al. 1988), and to the distribution of the radical population between the tunnelling, fine and hyperfine sublevels.
3.3. Identification of the spectrum
In the very early stage of the experiment, aiming at testing the chemical reactions, we found it impossible to observe the N,J = 3,3.5 ← 2,2.5, K = 1, F = 5 ← 4 upper component transition of CH3O in the 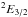 state (192 603.84 MHz). It is known that Cl atoms exclusively attack one of the three methyl protons in methanol (Dóbé et al. 1994). Formaldehyde was easily detected, and the optimized partial pressure of methanol is slightly below the maximum of formaldehyde detected (observing the JKa,Kc = 31,2 ← 21,1 line near 225 697.8 MHz). We then searched for the 615 ← 606 and 716 ← 707 transitions, which were predicted to lie around 209.45 and 225.65 GHz. Lines corresponding to the various tunnelling and fine-structure sublevels were expected to appear within a few hundred MHz around these values. We continuously scanned the 208–228.0 GHz frequency region. The only paramagnetic line detected lies near 227.330 GHz (~1.9 GHz above the predicted frequency for the 716 ← 707 transition) and appears as a doublet whose components are separated by ~2.3 MHz and have imbalanced intensities. We were not able to detect any other line sensitive to the Zeeman effect within ±700 MHz. We afterwards decided to scan between 243.5–247.5 GHz to search for the 817 ← 808 transition, which was predicted to occur at 245.04 GHz. We only found one paramagnetic line that showed itself as a triplet near 247.242 GHz. Again we failed to observe another fine-structure component of any tunnelling levels. However, we were convinced that they were due to the CH2OH radical because of the comparable frequency offset of ~2 GHz compared with predictions, and predominantly because of the hyperfine structure and of the chemical conditions for them to be discovered. The search for the 918 ← 909 transition proved to be decisive in the identification of the rotational spectrum of CH2OH. Another doublet was found at 270.105 GHz, ~2.2 GHz above the predicted frequency (267.87 GHz). Scaling the frequency offsets with N led us to conclude that the triplet seen at 247.242 GHz corresponds to the J = N + S fine-structure component of the v = 1 ← 0 level, while the doublets observed at 227.330 GHz and 270.105 GHz are the J = N + S transitions arising from the v = 1 tunnelling level. The averaged frequencies of the hyperfine components were least-squares analysed in a preliminary fit with the reported IR lines of the ν3 band (Roberts et al. 2013), which allowed us to predict and detect within several MHz the remaining fine-structure components of the 918 ← 909 transition (arising from the two tunnelling levels), except for the one occurring near 270.530 GHz that corresponds to J = N−S, v = 0 ← 1, which overlaps with unidentified diamagnetic lines. The fine-structure components of the 716 ← 707 and 817 ← 808 transitions that we initially missed are either too weak or masked by lines of diamagnetic species. The triplet detected at 247.242 GHz is composed of six hyperfine components, and only four of them could be discovered in a single scan (two of which are blended, plus two adjacent lines).
state (192 603.84 MHz). It is known that Cl atoms exclusively attack one of the three methyl protons in methanol (Dóbé et al. 1994). Formaldehyde was easily detected, and the optimized partial pressure of methanol is slightly below the maximum of formaldehyde detected (observing the JKa,Kc = 31,2 ← 21,1 line near 225 697.8 MHz). We then searched for the 615 ← 606 and 716 ← 707 transitions, which were predicted to lie around 209.45 and 225.65 GHz. Lines corresponding to the various tunnelling and fine-structure sublevels were expected to appear within a few hundred MHz around these values. We continuously scanned the 208–228.0 GHz frequency region. The only paramagnetic line detected lies near 227.330 GHz (~1.9 GHz above the predicted frequency for the 716 ← 707 transition) and appears as a doublet whose components are separated by ~2.3 MHz and have imbalanced intensities. We were not able to detect any other line sensitive to the Zeeman effect within ±700 MHz. We afterwards decided to scan between 243.5–247.5 GHz to search for the 817 ← 808 transition, which was predicted to occur at 245.04 GHz. We only found one paramagnetic line that showed itself as a triplet near 247.242 GHz. Again we failed to observe another fine-structure component of any tunnelling levels. However, we were convinced that they were due to the CH2OH radical because of the comparable frequency offset of ~2 GHz compared with predictions, and predominantly because of the hyperfine structure and of the chemical conditions for them to be discovered. The search for the 918 ← 909 transition proved to be decisive in the identification of the rotational spectrum of CH2OH. Another doublet was found at 270.105 GHz, ~2.2 GHz above the predicted frequency (267.87 GHz). Scaling the frequency offsets with N led us to conclude that the triplet seen at 247.242 GHz corresponds to the J = N + S fine-structure component of the v = 1 ← 0 level, while the doublets observed at 227.330 GHz and 270.105 GHz are the J = N + S transitions arising from the v = 1 tunnelling level. The averaged frequencies of the hyperfine components were least-squares analysed in a preliminary fit with the reported IR lines of the ν3 band (Roberts et al. 2013), which allowed us to predict and detect within several MHz the remaining fine-structure components of the 918 ← 909 transition (arising from the two tunnelling levels), except for the one occurring near 270.530 GHz that corresponds to J = N−S, v = 0 ← 1, which overlaps with unidentified diamagnetic lines. The fine-structure components of the 716 ← 707 and 817 ← 808 transitions that we initially missed are either too weak or masked by lines of diamagnetic species. The triplet detected at 247.242 GHz is composed of six hyperfine components, and only four of them could be discovered in a single scan (two of which are blended, plus two adjacent lines).
4. Spectral analysis
With a doublet electronic ground state (S = 1/2), each tunnelling level for N> 0 exhibits a fine structure of rotational J sublevels with J = N ± 1/2. For N = 0, J = 1/2 is the only possible spin sublevel. The electron spin-rotation coupling tensor, which contains five non-zero elements (the two off-diagonal terms ϵab and ϵba in addition to the three diagonal ϵii, Brown & Sears 1979) causes the fine structure. From the Pauli exclusion principle it follows (Table 5) that levels with a statistical weight of 3(1) are associated with IH = 1(0) and correspond to the ortho-(para-) isomer of the CH2OH radical. Even and odd values of Ka in the v = 0 and 1 tunnelling levels, respectively, connect with the ortho species (Table 5). Consequently, the above-mentioned fine-structure levels of para-CH2OH further split into two hyperfine sublevels that are due solely to the hydroxyl hydrogen nucleus, while those of the ortho isomer split into six hyperfine sublevels owing to the additional two equivalent methylenic proton spins. Figures 2 and 3 illustrate such a hyperfine pattern alternation observed in the para- and ortho-isomer of the hydroxymethyl radical, respectively.
 |
Fig. 2 Hyperfine structure of para-CH2OH for the |
 |
Fig. 3 Hyperfine structure of ortho-CH2OH for the |
 |
Fig. 4 Expected line intensities for the two strongest series of hyperfine lines for a cold prestellar core with a column density N(CH2OH) = 1012 cm-2, full line width at half power Δv = 1 km s-1, and TK = 12 K. The predictions have been obtained with the MADEX code (Cernicharo 2012). The upper panel corresponds to the fundamental R-branch transition 111−000 around 220.5 GHz and the lower one to the Q-branch transition 110−101 near 168.6 GHz. Quantum numbers for the selected hyperfine components can be found in Table 6. We have assumed that the source fills the main beam of the telescope. |
We employed the following coupling scheme of angular momenta: J = N + S, F1 = J + IH1 for para-CH2OH, and J = N + S, F1 = J + IH1, IH = IH2 + IH3 and F = F1 + IH for the ortho isomer. Then each rotational-tunnelling level is identified with N, Ka, Kc, J, F1, F, and v as quantum numbers, the latter one describing the tunnelling substate. The Hamiltonian used in the analysis is that for an asymmetric top radical in a doublet state including the energy separation between the tunnelling levels, that is to say, no interaction terms connecting the two tunnelling substates were needed to account for the observed spectrum: H = Hrot + Hsr + Hns + H01. Details on these terms can be found in Tanaka et al. (2004). Briefly, Hrot and Hsr stand for the Watson A reduction in the Ir representation of the rotational and of the electron-spin rotational coupling tensors, respectively, both including the centrifugal distortion effects. Hns (=Hns(H1) + Hns(H2) + Hns(H3)) describe the Fermi contact (isotropic, aF) and the magnetic dipole-dipole (anisotropic, T) electron spin-nuclear spin interactions owing to the three hydrogen nuclei contributions. Bowater et al. (1973) have shown for a paramagnetic species of Cs symmetry that the tensors T contain only one (Tab) non-zero off-diagonal coupling constants. The observed transitions did not permit us to determine any of the off-diagonal parameters. The last contribution to the Hamiltonian, H01, contains ΔE01, the energy difference between the rotationless (N = 0) levels of the two tunnelling substates. The observed transitions limited to ΔKa = ± 1 (i.e. odd ΔKa) prevented the Coriolis tunnelling interaction Hamiltonian from being included in the analysis (Schäfer et al. 2003).
In total, 96 mmw lines were recorded between 197–402 GHz and assigned to b-type Q- and R-branches transitions, involving N′′ = 5−13, 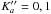 . They were subjected to a global least-squares analysis with available IR lines of the ν3 band, with the modified version of Pickett’s program SPFIT (to circumvent the size limitation of the Hamiltonian) using 21 adjustable parameters (Pickett 1991; Kisiel 2001). The measured frequencies were weighted proportionally to the inverse square of their experimental uncertainties. In the least-squares analysis, the A rotational constant was constrained to be identical in all states (i.e. in the tunnelling levels of the ground- and ν3 vibrational states). Because of strong correlations between the C rotational constants of the two tunnelling levels (and to a less extent between the two B), we instead fitted B and C of the lower tunnelling level (v = 0) and the differences of those in the upper level (v = 1) relatively to the lower level values. The standard deviations of the fit are 77 kHz and 0.09 × 10-3 cm-1 for the mmw and IR transitions, respectively. The ground-state constants derived are provided in Tables 2–4 for comparison with their computed values. Generally speaking, excellent agreement is found between them, and the nearly identical values of the B and C rotational constants in the two tunnelling substates are consistent with a high OH torsional barrier height and small energy difference between the tunnelling levels, as in the case of the CHF2 radical (Inada et al. 1998). The molecular parameters that we obtained have been used to predict lines of astronomical interest using the MADEX code (Cernicharo 2012), namely the NKaKc = 110−101 and the fundamental one, 111−000, whose upper energy levels lie below 10 K. The most intense of them are supplied in Table 6. A supplementary spectrum to this table is plotted in Fig. 4, which lists expected line intensities for cold prestellar cores around 168.6 and 220.5 GHz. The list of obs. and obs.−cal. transition frequencies is supplied in Table A.1.
. They were subjected to a global least-squares analysis with available IR lines of the ν3 band, with the modified version of Pickett’s program SPFIT (to circumvent the size limitation of the Hamiltonian) using 21 adjustable parameters (Pickett 1991; Kisiel 2001). The measured frequencies were weighted proportionally to the inverse square of their experimental uncertainties. In the least-squares analysis, the A rotational constant was constrained to be identical in all states (i.e. in the tunnelling levels of the ground- and ν3 vibrational states). Because of strong correlations between the C rotational constants of the two tunnelling levels (and to a less extent between the two B), we instead fitted B and C of the lower tunnelling level (v = 0) and the differences of those in the upper level (v = 1) relatively to the lower level values. The standard deviations of the fit are 77 kHz and 0.09 × 10-3 cm-1 for the mmw and IR transitions, respectively. The ground-state constants derived are provided in Tables 2–4 for comparison with their computed values. Generally speaking, excellent agreement is found between them, and the nearly identical values of the B and C rotational constants in the two tunnelling substates are consistent with a high OH torsional barrier height and small energy difference between the tunnelling levels, as in the case of the CHF2 radical (Inada et al. 1998). The molecular parameters that we obtained have been used to predict lines of astronomical interest using the MADEX code (Cernicharo 2012), namely the NKaKc = 110−101 and the fundamental one, 111−000, whose upper energy levels lie below 10 K. The most intense of them are supplied in Table 6. A supplementary spectrum to this table is plotted in Fig. 4, which lists expected line intensities for cold prestellar cores around 168.6 and 220.5 GHz. The list of obs. and obs.−cal. transition frequencies is supplied in Table A.1.
Finally, the inertial defect has been inferred from the rotational constants, Δ0 = −0.0406 amu Å2, a low value compatible with a planar structure. The fact that Δ0 is negative deserves a last comment. Oka (1995) gave a semi-empirical formula relating the zero-point inertial defect, the lowest out-of-plane vibration νl (in unit of cm-1), and 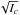 , where Ic is the principal moment of inertia along the c axis:
, where Ic is the principal moment of inertia along the c axis: 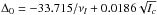 . Hence very low out-of-plane vibration can give a dominant negative contribution to the inertial defect. We obtained νl = 274cm-1, a value in excellent agreement with the observed one at 234 ± 5cm-1 for the ν9-CH2 wag mode (Johnson & Hudgens 1996).
. Hence very low out-of-plane vibration can give a dominant negative contribution to the inertial defect. We obtained νl = 274cm-1, a value in excellent agreement with the observed one at 234 ± 5cm-1 for the ν9-CH2 wag mode (Johnson & Hudgens 1996).
Strongest lines of astrophysical interest predicted for a cloud at T = 10 K.
5. Conclusion
The rotational-tunnelling spectrum of the CH2OH radical has been identified for the first time. Several molecular parameters have been accurately determined, not the least of which is the energy difference between the rotationless levels of the two tunnelling substates (139.73 ± 0.10 MHz). The height of the OH torsional barrier potential can in principle be obtained from this tunnelling rate, but this determination is beyond the scope of this study. The observed hyperfine structure alternation with 3:1 statistical weights depending on the symmetry and parity of the rotational levels revealed a tunnelling CH2OH radical with B1 symmetry in the C2v(M) permutation-inversion molecular symmetry group (A″ symmetry assuming a Cs planar and rigid molecular framework). It is worth mentioning that the works reported by the Nesbitt group (Roberts et al. 2013; Wang et al. 2014b) were invaluable to us to accomplish this research. Several hyperfine transitions have been predicted with enough accuracy to enable the radioastronomical detection of this species, which is important in astrochemistry. Ongoing efforts are underway to increase the radical production efficiency to allow for measurements of higher Ka transitions and/or above 400 GHz. If successful, these observations will help refine the molecular constants and hence the prediction of lines of astrophysical interest. A direct measure of the CH2OH radical abundance will be of high relevance for the modelling of the rich chemistry that results in the formation of complex organic molecules in cold dark cores, such as B1-b and TMC1, and also in hot cores and corinos, where dust ice mantles are submitted to strong desorption processes. A first check in Orion using IRAM 30 m observations and ALMA Science Verification data provided an upper limit to the column density of CH2OH of 1/1000 that of methanol. In cold dark clouds the higher partition function and lower dipole moment than CH3O will translate into lines weaker than those of methoxy by a factor of 3–4. These results will be published in a forthcoming paper.
Acknowledgments
This research was supported in part by the National French Program “Physique et Chimie du Milieu Interstellaire” (PCMI) and the French National Research Agency (ANR-13-BS05-0008-02 “IMOLABS”). The Laboratoire d’Excellence “Chemical and Physical Properties of the Atmosphere” (CaPPA) is also acknowledged. The CaPPA project is funded by the French National Research Agency under contract ANR-11-LABX-0005-01, by the Regional Council “Hauts de France” and by the European Regional Development Fund (ERDF). J. Cernicharo thanks the European Research Council and the Spanish Ministry of Science and Innovation through the NANOCOSMOS (SyG-610256) and ASTROMOL (CSD2009-00038) projects, respectively, and the Spanish Ministry of Economy and Competitiveness through the projects AYA2009-07304, and AYA2012-32032. The referee is also thanked for the valuable comments concerning the hyperfine structure.
References
- Aristov, V., Conroy, D., & Reisler, H. 2000, Chem. Phys. Lett., 318, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Atkinson, R. 1990, Atmos. Environ. Part A, 24, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Blake, G. A., Sastry, K. V. L. N., & de Lucia, F. C. 1984, J. Chem. Phys., 80, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Bowater, I. C., Brown, J. M., & Carrington, A. 1973, Proc. Roy. Soc. London A, 333, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. M., & Sears, T. J. 1979, J. Mol. Spectrosc., 75, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Bruna, P. J., & Grein, F. 1998, J. Phys. Chem. A, 102, 3141 [CrossRef] [Google Scholar]
- Bunker, P. R., & Jensen, P. 1998, Molecular Symmetry and Spectroscopy, 2nd edn. (Cambridge: NRC Researcch Press) [Google Scholar]
- Cernicharo, J. 2012, in ECLA-2011: Proc. European Conference on Laboratory Astrophysics, eds. C. Stehl, C. Joblin, & L. d’Hendecourt, EAS Pub. Ser., 58, 251 [Google Scholar]
- Cernicharo, J., Marcelino, N., Roueff, E., et al. 2012, ApJ, 759, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, C.-H., Wang, F., & Nesbitt, D. J. 2014, 69 International Symposium on Molecular Spectroscopy, http://hdl.handle.net/2142/50829 [Google Scholar]
- Dóbé, S., Bérces, T., Temps, F., Wagner, H. C., & Ziemer, H. 1994, 25th Symp. (Int.) Combust. [Proc.], 25, 755 [Google Scholar]
- Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2009, Gaussian 09 Revision E.01, Gaussian Inc. Wallingford CT 2009 [Google Scholar]
- Gerakines, P. A., Schutte, W. A., & Ehrenfreund, P. 1996, A&A, 312, 289 [NASA ADS] [Google Scholar]
- Inada, N., Saito, K., Hayashi, M., Ozeki, H., & Saito, S. 1998, Chem. Phys. Lett., 284, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, R. D., & Hudgens, J. W. 1996, J. Phys. Chem., 100, 19874 [CrossRef] [Google Scholar]
- Kamarchik, E., Rodrigo, C., Bowman, J. M., Reisler, H., & Krylov, A. I. 2012, J. Chem. Phys., 136, 084304 [NASA ADS] [CrossRef] [Google Scholar]
- Kisiel, Z. 2001, Spectroscopy from Space, Proc. NATO Advanced Research Workshop held 31 October4 November 2000, in Bratislava, Slovakia, eds. J. Demaison, K. Sarka, & E. A. Cohen (Dordrecht: Kluwer Academic Publishers), 91 [Google Scholar]
- Lin, J. J., Harich, S., Lee, Y. T., & Yang, X. 1999, J. Chem. Phys., 110, 10821 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, J. J., Shu, J., Lee, Y. T., & Yang, X. 2000, J. Chem. Phys., 113, 5287 [NASA ADS] [CrossRef] [Google Scholar]
- Nesbitt, D. J., Chang, C.-H., & Wang, F. 2014, 69th International Symp. on Molecular Spectroscopy, http://hdl.handle.net/2142/50831 [Google Scholar]
- Nesbitt, F. L., Payne, W. A., & Stief, L. J. 1989, J. Phys. Chem., 93, 5158 [CrossRef] [Google Scholar]
- Öberg, J. K., Bottinelli, S., Jörgensen, J. K., & van Dischoek, E. F. 2010, ApJ, 716, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Oka, T. 1995, J. Mol. Struct., 352, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Pagsberg, P., Munk, J., & Sillesen, A. 1988, Chem. Phys. Lett., 146, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Pagsberg, P., Munk, J., Anastasi, C., & Simpson, V. J. 1989, J. Phys. Chem., 93, 5162 [CrossRef] [Google Scholar]
- Pickett, H. M. 1991, J. Mol. Spectrosc., 148, 371 [Google Scholar]
- Rasmussen, C. L., Wassard, K. H., Dam-Johansen, K., & Glarborg, P. 2008, Int. J. Chem. Kinet., 40, 423 [CrossRef] [Google Scholar]
- Rissanen, M. P., Arppe, S. L., & Timonen, R. S. 2013, J. Phys. Chem. A, 117, 3902 [CrossRef] [Google Scholar]
- Roberts, M. A., Sharp-Williams, E. N., & Nesbitt, D. J. 2013, J. Phys. Chem. A, 117, 7042 [CrossRef] [Google Scholar]
- Schäfer, M., Ha, T.-H., & Bauder, A. 2003, J. Chem. Phys., 119, 8404 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, K., Toshimitsu, M., Harada, K., & Tanaka, T. 2004, J. Chem. Phys., 120, 3604 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, F., Chang, C.-H., & Nesbitt, D. J. 2014a, 69th International Symp. on Molecular Spectroscopy, http://hdl.handle.net/2142/50881 [Google Scholar]
- Wang, F., Chang, C.-H., & Nesbitt, D. J. 2014b, 69th International Symp. on Molecular Spectroscopy, http://hdl.handle.net/2142/50878 [Google Scholar]
- Watanabe, N., & Kouchi, A. 2002, ApJ, 571, L173 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, N., Mouri, O., Nagaoka, A., et al. 2007, ApJ, 668, 1001 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional table
List of obs. and obs.−cal. transition frequencies.
All Tables
Structure of CH2OH optimized at Cs symmetry calculated at the B3LYP/6-311++G(d, p) level of theory.
Energy separation between tunnelling substates ΔE01, rotational (MHz) and quartic centrifugal distortion constants (kHz) of CH2OH in the A reduction, Ir representation.
Electron spin-rotation (MHz) and their quartic centrifugal distortion coupling constants (MHz) of CH2OH in the A reduction, Ir representation.
Isotropic (Fermi-contact terms aF) and anisotropic (Tij) hyperfine interaction constants (MHz) of the three protons of CH2OH.
Symmetry species and statistical weights of the complete internal wavefunction for the lower (v = 0) and upper (v = 1) tunnelling sublevels for each NKaKc level.
All Figures
 |
Fig. 1 Energy level diagram showing the doubling of the rigid rotor levels (identified by NKaKc) for Ka = 0,1 into tunnelling sublevels labelled with the symmetry species of the complete internal wavefunction of CH2OH in the C2v(M) group. The statistical weights arising from the permutation of the two identical methylenic hydrogen nuclei are indicated between parentheses. Levels with a weight of 3 correspond to ortho-CH2OH and those with a weight of 1 correspond to the para isomer of the radical. Examples of a-type transitions (not observed) are depicted as black, dashed lines, while representatives of b-type (observed) Q- and R-branch transitions are displayed in green and red, respectively. For clarity the tunnelling splittings (Δ) are 800 times the actual ones, and the fine- and hyperfine-structure splittings are not illustrated. |
| In the text | |
 |
Fig. 2 Hyperfine structure of para-CH2OH for the |
| In the text | |
 |
Fig. 3 Hyperfine structure of ortho-CH2OH for the |
| In the text | |
 |
Fig. 4 Expected line intensities for the two strongest series of hyperfine lines for a cold prestellar core with a column density N(CH2OH) = 1012 cm-2, full line width at half power Δv = 1 km s-1, and TK = 12 K. The predictions have been obtained with the MADEX code (Cernicharo 2012). The upper panel corresponds to the fundamental R-branch transition 111−000 around 220.5 GHz and the lower one to the Q-branch transition 110−101 near 168.6 GHz. Quantum numbers for the selected hyperfine components can be found in Table 6. We have assumed that the source fills the main beam of the telescope. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.