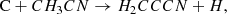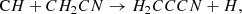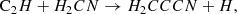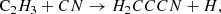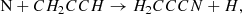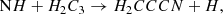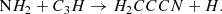| Issue |
A&A
Volume 676, August 2023
|
|
|---|---|---|
| Article Number | L5 | |
| Number of page(s) | 9 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202347385 | |
| Published online | 31 July 2023 | |
Letter to the Editor
Laboratory and astronomical discovery of the cyanovinyl radical H2CCCN⋆,⋆⋆
1
Departamento de Astrofísica Molecular, Instituto de Física Fundamental (IFF-CSIC), C/ Serrano 121, 28006 Madrid, Spain
e-mail: carlos.cabezas@csic.es; jose.cernicharo@csic.es
2
Institute of Global Human Resource Development and Graduate School of Natural Science and Technology, Okayama University, 3-1-1 Tsushima-naka, Kita-ku, Okayama, 700-8531
Japan
e-mail: jtang@okayama-u.ac.jp
3
Department of Basic Science, The University of Tokyo, 3-8-1 Komaba, Meguro-ku, Tokyo, 153-8902
Japan
4
Division of Pure and Applied Science, Graduate School of Science and Technology, Gunma University, 4-2 Aramaki, Maebashi, Gunma, 371-8510
Japan
5
Department of Chemistry, School of Science, Tokyo Institute of Technology, Ookayama 2-12-1, Meguro, Tokyo, 152-8550
Japan
6
Observatorio Astronómico Nacional (IGN), C/ Alfonso XII 3, 28014 Madrid, Spain
7
Observatorio de Yebes (IGN), Cerro de la Palera s/n, 19141 Yebes, Guadalajara, Spain
8
Department of Applied Chemistry, Science Building II, National Yang Ming Chiao Tung University, 1001 Ta-Hsueh Rd., Hsinchu, 300098
Taiwan
Received:
6
July
2023
Accepted:
18
July
2023
We report the first laboratory and interstellar detection of the α-cyano vinyl radical (H2CCCN). This species was produced in the laboratory by an electric discharge of a gas mixture of vinyl cyanide, CH2CHCN, and Ne. Its rotational spectrum was characterized using a Balle-Flygare narrowband-type Fourier-transform microwave spectrometer operating in the frequency region of 8–40 GHz. The observed spectrum shows a complex structure due to tunneling splittings between two torsional sublevels of the ground vibronic state, 0+ and 0−, derived from a large-amplitude inversion motion. In addition, the presence of two equivalent hydrogen nuclei makes it necessary to discern between ortho- and para-H2CCCN. A least-squares analysis reproduces the observed transition frequencies with a standard deviation of ca. 3 kHz. Using the laboratory predictions, this radical was detected in the cold dark cloud TMC-1 using the Yebes 40 m telescope and the QUIJOTE1 line survey. The 40, 4-30, 3 and 50, 5-40, 4 rotational transitions, composed of several hyperfine components, were observed in the 31.0–50.4 GHz range. Adopting a rotational temperature of 6 K, we derived a column density of (1.4±0.2)×1011 cm−2 and (1.1±0.2)×1011 cm−2 for ortho-H2CCCN and para-H2CCCN, respectively. The reaction of C + CH3CN emerges as the most likely route to H2CCCN in TMC-1, and possibly that of N + CH2CCH as well.
Key words: molecular data / methods: laboratory: molecular / line: identification / ISM: molecules / astrochemistry / ISM: individual objects: TMC-1
Tables A.3 and A.4 are only available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/676/L5
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Vinyl cyanide, CH2CHCN, is a well-known interstellar molecule that was detected in the interstellar medium (ISM) for the first time in 1973 toward the Sagittarius B2 (Sgr B2) molecular cloud (Gardner & Winnewisser 1975). Since then, vinyl cyanide has been detected toward different sources, such as Orion (Schilke et al. 1997), the dark cloud TMC-1 (Matthews & Sears 1983), the circumstellar envelope of the late-type star IRC+10216 (Agúndez et al. 2008), and the Titan atmosphere (Capone et al. 1981). Vinyl cyanide is one of the molecules, whose high abundance and significant dipole moment allow radioastronomical detection even of its rare isotopologue species and vibrationally excited states (López et al. 2014). Thus, the cyanovinyl radical (CVR) is a promising candidate for its interstellar detection given its similarity to the aforementioned vinyl cyanide. This hypothesis is strengthened by the recent detection of the H2C4N radical (Cabezas et al. 2021) with the QUIJOTE1 line survey (Cernicharo et al. 2021, 2023).
The CVR has two structural isomers depending on whether the α- or β-hydrogen, -CH or CH2, respectively, of vinyl cyanide is removed. The molecular formula H2CCCN corresponds to the α-CVR, while the HCCHCN formula is that for β-CVR, which further allows the cis and trans isomers. Quantum chemical calculation indicate that the α-CVR is more stable in energy than the β-CVR by 30–45 kJ mol−1 (Balucani et al. 2000; Huang et al. 2000; Johansen et al. 2019). The rotational spectra of both isomers of the β-CVR have been investigated by Johansen et al. (2019) and Nakajima et al. (2022). In their study, Johansen et al. (2019) observed several rotational transitions for both cis and trans isomers of β-CVR in the 5–75 GHz frequency range but no conclusive assignments of the fine and hyperfine components was reported. On the other hand, Nakajima et al. (2022) reported precise molecular constants for the cis isomer of β-CVR thanks to the deep analysis of all the fine and hyperfine components observed in the 10–55 GHz region. However, no spectroscopic data for the α-CVR have been reported before in the literature, beyond our preliminary results (Tang et al. 2000).
In this Letter, we report the first rotational investigation study of the α-CVR, hereafter, H2CCCN, and the discovery of this radical in space towards TMC-1. The laboratory characterization was carried out using Fourier transform microwave (FTMW) spectroscopy in combination with electric discharges techniques. The identification of this radical in space has been done using the on-going QUIJOTE line survey (Cernicharo et al. 2021, 2023).
2. Laboratory FTMW spectroscopy of H2CCCN
The rotational spectrum of H2CCCN was observed using a Balle-Flygare narrowband type FTMW spectrometer operating in the frequency region of 4–40 GHz (Endo et al. 1994; Cabezas et al. 2016). The short-lived species H2CCCN was produced in a supersonic expansion by a pulsed electric discharge of a gas mixture of CH2CHCN (0.2%) diluted in Ne. This gas mixture was flowed through a pulsed-solenoid valve that is accommodated in the backside of one of the cavity mirrors and aligned parallel to the optical axis of the resonator. A pulse voltage of 900 V with a duration of 450 μs was applied between stainless steel electrodes attached to the exit of the pulsed discharge nozzle (PDN), resulting in an electric discharge synchronized with the gas expansion. The resulting products generated in the discharge were supersonically expanded, rapidly cooled to a rotational temperature of ∼2.5 K between the two mirrors of the Fabry-Pérot resonator, and then probed by FTMW spectroscopy. For the measurements of the paramagnetic lines, the Earth’s magnetic field was cancelled out by using three sets of Helmholtz coils placed perpendicular to one another. Since the PDN is arranged parallel to the cavity of the spectrometer, it is possible to suppress the Doppler broadening of the spectral lines, allowing to resolve small hyperfine splittings. The spectral resolution is 5 kHz and the frequency measurements benefit from an estimated accuracy better than 3 kHz.
3. Astronomical observations
New receivers, built within the Nanocosmos2 project and installed at the Yebes 40 m radiotelescope, were used for the observations of TMC-1 (αJ2000 = 4h41m41.9s and δJ2000 = +25° 41′27.0″). A detailed description of the telescope, receivers, and backends is given by Tercero & López-Pérez (2021). Briefly, the receiver consists of two cold high electron mobility transistor amplifiers covering the 31.0–50.3 GHz band with horizontal and vertical polarizations. The backends are 2 × 8 × 2.5 GHz fast Fourier transform spectrometers with a spectral resolution of 38.15 kHz providing the whole coverage of the Q-band in both polarisations. The observations, carried out during different observing runs, were performed using the frequency-switching mode with a frequency throw of 10 MHz in the very first observing runs, during November 2019 and February 2020, 8 MHz over the duration of the observations taken between January and November 2021, and alternating these frequency throws in the last observing runs between October 2021 and February 2023. The total on-source telescope time is 850 h in each polarization (385 and 465 h for the 8 MHz and 10 MHz frequency throws, respectively). The sensitivity of the QUIJOTE line survey varies between 0.09 and 0.25 mK in the 31–50.3 GHz domain. The intensity scale used in this work, antenna temperature (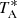 ), was calibrated using two absorbers at different temperatures and the atmospheric transmission model ATM (Cernicharo 1985; Pardo et al. 2001). Calibration uncertainties have been adopted to be 10%. The beam efficiency of the Yebes 40 m telescope in the Q-band is given as a function of frequency by Beff = 0.797 exp[−(ν(GHz)/71.1)2]. The forward telescope efficiency is 0.95. The telescope beam size varies from 56.7′ at 31 GHz to 35.6′ at 49.5 GHz. All data were analyzed using the GILDAS package3.
), was calibrated using two absorbers at different temperatures and the atmospheric transmission model ATM (Cernicharo 1985; Pardo et al. 2001). Calibration uncertainties have been adopted to be 10%. The beam efficiency of the Yebes 40 m telescope in the Q-band is given as a function of frequency by Beff = 0.797 exp[−(ν(GHz)/71.1)2]. The forward telescope efficiency is 0.95. The telescope beam size varies from 56.7′ at 31 GHz to 35.6′ at 49.5 GHz. All data were analyzed using the GILDAS package3.
4. Results
4.1. Quantum chemical calculations of H2CCCN
Several theoretical calculations for H2CCCN radical have been previously reported. Fenistein et al. (1969) and Hinchliffe (1977) calculated only the C2v-symmetry structure in that two protons are equivalent relative to the linear carbon-chain backbone. Later, Mayer et al. (1998) and Parkinson et al. (1999) predicted a stable Cs-symmetry structure, both using density functional theory calculations, with the bending angle ∠CCC = 164.9° and in the standard coupled cluster approach level with ∠CCC = 149.1° (Parkinson et al. 1999). The energy barrier from the Cs minimum to the C2v saddle point of H2CCCN was calculated to be 1190 cm−1 (Parkinson et al. 1999).
We optimized the geometry of the H2CCCN radical at the spin-restricted coupled cluster method with single, double, and perturbative triple excitations (RCCSD(T)) and an explicitly correlated (F12A) approximation (Adler et al. 2007; Knizia et al. 2009) with all electrons (valence and core) correlated and the Dunning’s correlation consistent basis sets with polarized core-valence triple-ζ for explicitly correlated calculations (cc-pCVTZ-F12; Hill et al. 2010; Hill & Peterson 2010). At the optimized geometry, electric dipole moment components were calculated at the same level of theory as that of the geometrical optimization. We derived a value for μa of 3.6 D. The H2CCCN radical in the 2A′ ground electronic state adopts a bent geometry with a ∠CCC angle of 147°, as can be seen in Fig. 1. Using RCCSD(T)-F12/cc-pCVTZ-F12 level of theory we obtained the inversion barrier of Vi = 356 cm−1 at the C2v saddle point. These calculations were performed using the Molpro 2020 ab initio program package (Werner & Knizia 2020).
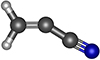 |
Fig. 1. Molecular structure of the H2CCCN radical. |
The fine and hyperfine coupling constants were estimated using the B3LYP hybrid density functional (Becke 1993) with the augmented diffuse basis set (aug-cc-pVTZ; Woon & Dunning 1995). Harmonic and anharmonic vibrational frequencies were computed using second-order Møller-Plesset perturbation (MP2; Møller & Plesset 1934) with the cc-pVTZ basis set (Woon & Dunning 1995) level of theory to estimate the centrifugal distortion constants and the vibration-rotation interaction contribution to the rotational constants. These calculations were performed using the Gaussian16 program package (Frisch et al. 2016). The calculated molecular parameters are summarized in Table 1.
Spectroscopic parameters of H2CCCN (all in MHz).
4.2. Rotational spectrum of H2CCCN
Due to the bent geometry for H2CCCN radical in the 2A′ ground state, there are two equivalent configurations corresponding to different minima of the double minimum potential of the inversion motion. This pair of tunneling inversion states νinv = 0±, will originate a doublet pattern in the rotational spectrum for H2CCCN. Required by the Pauli’s exclusion principle, ortho and para species due to two hydrogen nuclei in H2CCCN correspond to the inversion states 0+ and 0−, respectively, in the even Ka rotational levels. For odd Ka rotational levels ortho and para changes and 0+ is para, while 0− is ortho. The 0+ level is considered to be always the lower splitting sublevel.
A total of four groups of paramagnetic lines around 8.7 GHz, 17.4 GHz, 26.2 GHz, and 34.9 GHz were observed in our experiment. An example is shown in Fig. 2. The H2CCCN radical was readily confirmed as the spectral carrier based on the following arguments. (i) The observed transition frequencies agree well with the calculated frequencies, (ii) each transition has a hyperfine spectral structure similar to that expected for an open-shell species with three coupling nuclei, and (iii) the lines exhibit the paramagnetic behavior.
 |
Fig. 2. FTMW spectrum for the H2CCCN radical showing the 40, 4-30, 3 rotational transition at 34.9 GHz. Much weaker additional hyperfine components, which are not shown in this figure, were also observed. The abscissa corresponds to the frequency of the lines in MHz. The spectra were achieved by 200 shots of accumulation and a step scan of 1 MHz with a repetition rate of 10 Hz. The coaxial arrangement of the adiabatic expansion and the resonator axis produces an instrumental Doppler doubling. The resonance frequencies are calculated as the average of the two Doppler components. |
Assignment of the fine and hyperfine structure was first achieved for the spectrum of para-H2CCCN (Ka = 0 transitions for 0− sublevel), in which the higher-N transitions presented relatively simple structures. By a least-squares fitting, the spin-rotation interaction constants and the hyperfine interaction constants for the nitrogen nucleus were determined, where hyperfine interaction constants for the two hydrogen nuclei cannot be determined due to I(2H) = 0 in para-H2CCCN, since this species has parity +1 for the a-axis rotation. Then, the remaining H2CCCN transition lines were assigned to the ortho-H2CCCN (Ka = 0 transitions for 0+ sublevel) spectrum. Slightly different effective molecular constants from the ones of para-H2CCCN including the hyperfine interaction constants for the two hydrogen nuclei were obtained for ortho-H2CCCN with I(2H) = 1, parity -1 for the a-axis rotation. A total of 36 and 137 hyperfine components from Ka = 0 rotational transitions were measured for para-H2CCCN and ortho-H2CCCN species, respectively (see Tables A.1 and A.2).
All the lines for each species were independently analyzed using a standard Hamiltonian for an asymmetric top molecule with a doublet electronic state (2A′) and three non-zero-spin nuclei. The coupling scheme for angular momenta of rotation N, electron spin S, and nuclear spins I of two equivalent protons and one nitrogen nucleus is J = N + S, F1 = J + IH, and F = F1 + IN. The molecular constants derived from the analysis are shown in Table 1.
Although we have succeeded in assigning and analyzing the H2CCCN spectra of the Ka = 0 transitions by considering a tunneling inversion effect and by applying an effective Hamiltonian to the ortho/para species, information of the tunneling inversion motion, such as inversion barrier Vi, inversion-vibration frequency νi, and inversion-vibration splitting 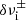 , could not be obtained directly from our spectral analysis. The abnormally large inversion-vibration dependence of the (B + C)/2 constant indicated that there is a strong rotation-dependent perturbation in this radical.
, could not be obtained directly from our spectral analysis. The abnormally large inversion-vibration dependence of the (B + C)/2 constant indicated that there is a strong rotation-dependent perturbation in this radical.
4.3. Detection of H2CCCN in TMC-1
Using the molecular constants derived for ortho- and para-H2CCCN, we predicted the rotational spectra of each species. We considered the ortho and para species separately as there are no radiative or collisional transitions between them. The predictions for ortho-H2CCCN include the rotational transitions with Ka even for the 0+ sublevel and those with Ka odd for 0− sublevel, while para-H2CCCN predictions contain the rotational transitions, with Ka even for the 0− sublevel and those with Ka odd for 0+ sublevel. Predictions for Ka = 0 transitions have uncertainties smaller than 30 kHz up to N = 10. They were implemented in the MADEX code (Cernicharo 2012) to compute column densities. We adopted a dipole moment of 3.60 D as derived from our calculations. The catalog files with the predicted frequencies and the calculated intensities up to N = 30 and at 300 K are provided in Tables A.3 and A.4 at the CDS.
Two rotational transitions for H2CCCN with Ka = 0 are covered by our QUIJOTE survey, at 34.9 and 43.6 GHz. We observed two groups of lines at the predicted frequencies for the 40, 4–30, 3 and 50, 5–40, 4 transitions. Figure 3 shows the lines corresponding to these rotational transitions. More than 30 hyperfine components are observed in TMC-1 with a sensitivity of 0.09 mK for N = 4 and of 0.14 mK for N = 5. Our frequency switching observing procedure affects to some of these lines. The forest of lines for each transition covers more than 10 MHz (see Fig. 3) and, hence, the hyperfine components separated by 8 or 10 MHz, namely, the frequency throws of the observations, will affect each other. In addition, at this level of sensitivity, transitions from other species and from unidentified lines could also affect the observed intensities. Some of the blends arising between the lines and their negative features at ±8 MHz and ±10 MHz produced in the folding of the frequency switching, have been identified and blanked in the data. As an example, the lines of C6H and H2C6 appearing around 34 918 MHz in the bottom left panel of the figure, will have negative counterparts at 34 926 and 34 928 MHz, which are within the frequency range of the 40, 4 − 30, 3 transition. The corresponding channels have been cleaned in the top panel of Fig. 3. Three hyperfine components labelled as A, B, and C in Fig. 3 are affected by other lines of H2CCCN and by unidentified lines. For other blending situations, the removal of the negative feature is much more delicate and has not been performed on the final data presented in Fig. 3. It is worth to note that each of the negative features produced by a line will have half of its intensity, which for the strongest features of Fig. 3 points to intensities of 0.3–0.4 mK. Nevertheless, the number of detected lines is large enough to support the identification of H2CCCN in TMC-1 and to ensure a reliable determination of the column density.
 |
Fig. 3. Observed rotational transitions of H2CCCN in TMC-1 in the 31.0–50.4 GHz range. The abscissa corresponds to the rest frequency, assuming a local standard of rest velocity of 5.83 km s−1. The ordinate is antenna temperature in millikelvins. Curves shown in red are the computed synthetic spectra for Trot = 6 K, N(ortho-H2CCCN) = 1.4×1011 cm−2, and N(para-H2CCCN) = 1.1×1011 cm−2. |
The observed lines of H2CCCN correspond to transitions with upper energy levels of 4.2 and 6.3 K for N = 4 and 5, respectively. Hence, the rotational temperature (Trot) can not be derived in a reasonable way from the observations, except in cases where it is rather low. We have explored values for Trot between 5 and 10 K and found that the derived column density for the two inversion states is not very sensitive to the adopted value for Trot (see e.g., Cernicharo et al. 2021). In order to estimate the expected rotational temperature of the 40, 4–30, 3 and 50, 5–40, 4 transitions of H2CCCN, we have analyzed the excitation conditions of a similar molecule, H2CCC. For this species, the collisional rates are available (Khalifa et al. 2019), and the dipole moment is also similar to that of our molecule. For a volume density of 2–3×104 cm−3, typical of TMC-1, and assuming optically thin emission, we obtain rotational temperatures between 5.6–7 K for the Ju = 4 and 5 transitions of H2CCC. Adopting a value of 6 K for the two observed transitions of H2CCCN, we derive a column density of (1.4±0.2)×1011 cm−2 and of (1.1±0.2)×1011 cm−2 for ortho-H2CCCN and para-H2CCCN, respectively. These column densities indicate that, within the uncertainties, both inversion states are equally populated. Adopting a rotational temperature of 7 K introduces an increase of the column density of ∼10%.
Two additional transitions for each value of N corresponding to Ka = 1 could be also within the QUIJOTE frequency coverage. However, the frequency predictions for these lines are unreliable as the A rotational constant value has not been determined from the laboratory data. Moreover, using the value of the constant A estimated from our calculations, the upper rotational levels of these Ka = 1 transitions will be around 14 K. Hence, for rotational temperatures below 10 K the intensity of these lines is expected to be much lower than those of the transitions with Ka = 0, and below the sensitivity of QUIJOTE.
5. Chemistry of H2CCCN
There are several chemical reactions that can form H2CCCN in TMC-1, although there is little experimental or theoretical information on most of them. In fact, the chemical databases UMIST (McElroy et al. 2013) and KIDA (Wakelam et al. 2015) do not contain any reaction of formation of H2CCCN. Among the potential routes to H2CCCN, we can consider the following neutral-neutral reactions that occur with H atom elimination:
To evaluate whether these reactions can produce H2CCCN with an abundance similar to that of the observations, we plugged them into a chemical model. As a starting point, we used the chemical model built by Cabezas et al. (2021) to study the chemistry of CH2CCCN, which uses the chemical network RATE12 from the UMIST database (McElroy et al. 2013), with updates from Loison et al. (2014) and Marcelino et al. (2021). The physical parameters assumed are the typical ones of cold dark clouds, namely, a density of H nuclei of 2 × 104 cm−3, gas kinetic temperature of 10 K, cosmic-ray ionization rate of H2 of 1.3 × 10−17 s−1, visual extinction of 30 mag, and the set of low-metal elemental abundances (see, e.g., Agúndez & Wakelam 2013). We added H2CCCN in as a new species and included the above seven neutral–neutral reactions with a rate coefficient of 10−10 cm3 s−1, which is typical of neutral-neutral reactions that are fast at low temperature. We considered that H2CCCN is destroyed by reacting with neutral atoms, such as H, O, N, and C, with a rate coefficient of 10−10 cm3 s−1, and with abundant positive cations, such as H+ and C+, with a rate coefficient of 10−9 cm3 s−1 at 300 K and a dependence with temperature of the type T−0.5.
Our results are shown in Fig. 4. The first conclusion is that H2CCCN is indeed produced with a peak abundance of the order of the observed value at a time of a few 105 yr. The second conclusion is that the main reactions of formation of H2CCCN are by far reactions (1) and (5), because they involve as reactants atomic carbon and atomic nitrogen, respectively, which are very abundant (see Fig. 4). Interestingly, reaction (1) was recently studied by Hickson et al. (2021). These authors measured the rate coefficient to be (3–4) × 10−10 cm3 s−1 in the temperature range 50–296 K and the H atom yield to be 0.63 at 177 K. They also carried out quantum chemical calculations, which point to H2CCCN and H2CCNC as the most likely products on the triplet potential energy surface. Reaction (5) has not been studied to our knowledge. Loison et al. (2017) suggest that the reaction is fast, although they favor C2H2 + HCN and HC3N + H2 as products. It would be interesting to investigate whether this reaction can produce H2CCCN at low temperature. In summary, the reaction C + CH3CN, and perhaps also the reaction N + CH2CCH, emerge as the most likely routes to H2CCCN. The species H2CCNC is also predicted to be formed in the C + CH3CN reaction and thus it is an interesting target to be searched for in TMC-1.
 |
Fig. 4. Abundances calculated with the chemical model for H2CCCN and for its potential precursors. The horizontal dashed lines correspond to the values observed in TMC-1: H2CCCN (this work), CH3CN (Cabezas et al. 2021), and CH2CCH (Agúndez et al. 2022). |
Alternatively, the cyanovinyl radical could also be formed in the dissociative recombination with electrons of positive ions such as H3C3N+ or H4C3N+. The astrochemical databases UMIST and KIDA consider that the dissociative recombination of H4C3N+ produces vinyl cyanide (CH2CHCN). However, the product distribution of this reaction has not been measured and H2CCCN could also be formed.
6. Conclusions
We report the detection in TMC-1 of the radical H2CCCN, based on an accurate laboratory spectroscopy of the N = 1, 2, 3 and 4 Ka = 0 rotational transitions of this species, as well as on the QUIJOTE line survey of this prestellar cold core. We have identified 30 hyperfine components in TMC-1. Chemical modeling indicates that the reaction of C + CH3CN, as well as possibly N + CH2CCH, are the most likely paths to H2CCCN in TMC-1.
ERC grant ERC-2013-Syg-610256-NANOCOSMOS. https://nanocosmos.iff.csic.es/
Acknowledgments
The present study was supported by ERC through the grant ERC-2013-Syg-610256-NANOCOSMOS, Ministry of Science and Technology of Taiwan through project MOST 104-2113-M-009-202, JSPS KAKENHI through Grant 06640644, and Ministerio de Ciencia e Innovación of Spain through projects PID2019-106110GB-I00, PID2019-107115GB-C21/AEI/10.13039/501100011033, and PID2019-106235GB-I00. C.C., M.A, Y.E. and J.C. thank Ministry of Science and Technology of Taiwan and Consejo Superior de Investigaciones Científicas for funding support under the MOST-CSIC Mobility Action 2021 (Grant 11-2927-I-A49-502 and OSTW200006). J.T. thanks the JSPS Postdoctoral Fellowship for Foreign Researchers and Grant-in-Aid for JSPS Fellows.
References
- Adler, T. B., Knizia, G., & Werner, H.-J. 2007, J. Chem. Phys., 127, 221106 [Google Scholar]
- Agúndez, M., & Wakelam, V. 2013, Chem. Rev., 113, 8710 [Google Scholar]
- Agúndez, M., Fonfría, J. P., Cernicharo, J., et al. 2008, A&A, 479, 493 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Agúndez, M., Marcelino, N., Cabezas, C., et al. 2022, A&A, 657, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balucani, N., Asvany, O., Huang, L. C. L., et al. 2000, ApJ, 545, 892 [Google Scholar]
- Becke, A. D. 1993, J. Chem. Phys., 98, 1372 [Google Scholar]
- Cabezas, C., Guillemin, J.-C., & Endo, Y. 2016, J. Chem. Phys., 145, 184304 [Google Scholar]
- Cabezas, C., Agúndez, M., Marcelino, N., et al. 2021, A&A, 654, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Capone, L. A., Prasad, S. S., Huntress, W. T., et al. 1981, Nature, 293, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J. 1985, Internal IRAM report (Granada: IRAM) [Google Scholar]
- Cernicharo, J. 2012, in European Conference on Laboratory Astrophysics, eds. C. Stehlé, C. Joblin, & L. d’Hendecourt, EAS Publ. Ser., 58, 251 [Google Scholar]
- Cernicharo, J., Agúndez, M., Kaiser, R., et al. 2021, A&A, 652, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Pardo, J. R., Cabezas, C., et al. 2023, A&A, 670, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Endo, Y., Kohguchi, H., & Ohshima, Y. 1994, Faraday Discuss., 97, 341 [Google Scholar]
- Fenistein, S., Marx, R., Moreau, C., & Serre, J. 1969, Theor. Chim. Acta., 14, 339 [CrossRef] [Google Scholar]
- Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2016, Gaussian 16 Revision A.03 [Google Scholar]
- Gardner, F. F., & Winnewisser, G. 1975, ApJ, 195, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Hickson, K. M., Loison, J.-C., & Wakelam, V. 2021, ACS Earth Space Chem., 5, 824 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, J. G., & Peterson, K. A. 2010, Phys. Chem. Chem. Phys., 12, 10460 [Google Scholar]
- Hill, J. G., Mazumder, S., & Peterson, K. A. 2010, J. Chem. Phys., 132, 054108 [Google Scholar]
- Hinchliffe, A. 1977, J. Mol. Struct., 39, 123 [Google Scholar]
- Huang, L. C. L., Asvany, O., Chang, A. H. H., et al. 2000, J. Chem. Phys., 113, 8656 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, S. L., Martin-Drumel, M.-A., & Crabtree, K. N. 2019, J. Phys. Chem. A, 123, 5171 [NASA ADS] [CrossRef] [Google Scholar]
- Khalifa, M. B., Sahnoun, E., Wiesenfeld, L., et al. 2019, PCCP, 21, 1443 [NASA ADS] [CrossRef] [Google Scholar]
- Knizia, G., Adler, T. B., & Werner, H.-J. 2009, J. Chem. Phys., 130, 054104 [Google Scholar]
- Loison, J.-C., Wakelam, V., & Hickson, K. M. 2014, MNRAS, 443, 398 [Google Scholar]
- Loison, J.-C., Agúndez, M., Wakelam, V., et al. 2017, MNRAS, 470, 4075 [Google Scholar]
- López, A., Tercero, B., Kisiel, Z., et al. 2014, A&A, 572, A44 [Google Scholar]
- Marcelino, N., Tercero, B., Agúndez, M., & Cernicharo, J. 2021, A&A, 646, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matthews, H. E., & Sears, T. J. 1983, ApJ, 267, L53 [CrossRef] [Google Scholar]
- Mayer, P. M., Parkinson, C. J., Smith, D. M., & Radom, L. 1998, J. Cosmol. Phys., 108, 604 [Google Scholar]
- McElroy, D., Walsh, C., Markwick, A. J., et al. 2013, A&A, 550, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Møller, C., & Plesset, M. S. 1934, Phys. Rev., 46, 618 [Google Scholar]
- Nakajima, M., Liu, Y.-T., Chang, C.-H., et al. 2022, PCCP, 24, 11585 [NASA ADS] [CrossRef] [Google Scholar]
- Pardo, J. R., Cernicharo, J., & Serabyn, E. 2001, IEEE Trans. Antenn. Propag., 49, 12 [Google Scholar]
- Parkinson, C. J., Mayer, P. M., & Radom, L. 1999, Theor. Chem. Acc., 102, 92 [CrossRef] [Google Scholar]
- Schilke, P., Groesbeck, T. D., Blake, G. A., & Philips, T. G. 1997, ApJS, 108, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Tang, J., Seiki, K., Sumiyoshi, Y., et al. 2000, Bunshi Kozo Sogo Toronkai 2000 Koen Yoshishu, 11 (1A4)(in Japanese) [Google Scholar]
- Tercero, F., López-Pérez, J. A., Gallego, , et al. 2021, A&A, 645, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakelam, V., Loison, J.-C., Herbst, E., et al. 2015, ApJS, 217, 20 [Google Scholar]
- Werner, H. J., Knowles, P. J., Knizia, G., et al. 2020, MOLPRO, version 2020.2 [Google Scholar]
- Woon, D. E., & Dunning, T. H. 1995, J. Chem. Phys., 103, 4572 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Laboratory transition frequencies for H2CCCN
The laboratory measurements of H2CCCN described in Sect. 2 have permitted to measure 137 and 36 hyperfine components for ortho-H2CCCN and para-H2CCCN, respectively. The observed frequencies and quantum number assignments are given in Tables A.1 and A.2.
Observed transition frequencies for ortho-H2CCCN.
Observed transition frequencies for para-H2CCCN.
All Tables
All Figures
 |
Fig. 1. Molecular structure of the H2CCCN radical. |
| In the text | |
 |
Fig. 2. FTMW spectrum for the H2CCCN radical showing the 40, 4-30, 3 rotational transition at 34.9 GHz. Much weaker additional hyperfine components, which are not shown in this figure, were also observed. The abscissa corresponds to the frequency of the lines in MHz. The spectra were achieved by 200 shots of accumulation and a step scan of 1 MHz with a repetition rate of 10 Hz. The coaxial arrangement of the adiabatic expansion and the resonator axis produces an instrumental Doppler doubling. The resonance frequencies are calculated as the average of the two Doppler components. |
| In the text | |
 |
Fig. 3. Observed rotational transitions of H2CCCN in TMC-1 in the 31.0–50.4 GHz range. The abscissa corresponds to the rest frequency, assuming a local standard of rest velocity of 5.83 km s−1. The ordinate is antenna temperature in millikelvins. Curves shown in red are the computed synthetic spectra for Trot = 6 K, N(ortho-H2CCCN) = 1.4×1011 cm−2, and N(para-H2CCCN) = 1.1×1011 cm−2. |
| In the text | |
 |
Fig. 4. Abundances calculated with the chemical model for H2CCCN and for its potential precursors. The horizontal dashed lines correspond to the values observed in TMC-1: H2CCCN (this work), CH3CN (Cabezas et al. 2021), and CH2CCH (Agúndez et al. 2022). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.