| Issue |
A&A
Volume 598, February 2017
|
|
|---|---|---|
| Article Number | A64 | |
| Number of page(s) | 7 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201629385 | |
| Published online | 01 February 2017 | |
Evolution of lithium abundance in the Sun and solar twins
1 Université de La Côte d’Azur, OCA, Laboratoire Lagrange CNRS, BP. 4229, 06304 Nice Cedex, France
2 Sternberg Astronomical Institute, Lomonosov Moscow State University, 119992 Moscow, Russia
e-mail: avo@sai.msu.ru
Received: 23 July 2016
Accepted: 8 November 2016
Evolution of the 7Li abundance in the convection zone of the Sun during different stages of its life time is considered to explain its low photospheric value in comparison with that of the solar system meteorites. Lithium is intensively and transiently burned in the early stages of evolution (pre-main sequence, pMS) when the radiative core arises, and then the Li abundance only slowly decreases during the main sequence (MS). We study the rates of lithium burning during these two stages. In a model of the Sun, computed ignoring pMS and without extra-convective mixing (overshooting) at the base of the convection zone, the lithium abundance does not decrease significantly during the MS life time of 4.6 Gyr. Analysis of helioseismic inversions together with post-model computations of chemical composition indicates the presence of the overshooting region and restricts its thickness. It is estimated to be approximately half of the local pressure scale height (0.5HP) which corresponds to 3.8% of the solar radius. Introducing this extra region does not noticeably deplete lithium during the MS stage. In contrast, at the pMS stage, an overshooting region with a value of approximately 0.18HP is enough to produce the observed lithium depletion. If we conclude that the dominant lithium burning takes place during the pMS stage, the dispersion of the lithium abundance in solar twins is explained by different physical conditions, primarily during the early stage of evolution before the MS.
Key words: Sun: abundances / Sun: interior / Sun: evolution / stars: solar-type
© ESO, 2017
1. Introduction
The solar photospheric lithium abundance measured spectroscopically is 160 times less than the solar system’s meteoritic abundance (see for example Asplund et al. 2009). This discrepancy was already noticed by Greenstein & Richardson (1951) and has been widely discussed in the literature (see for example Hughes et al. 2007, and references therein). The meteoritic abundance is usually accepted as the initial lithium abundance in the Sun. Lithium depletion inside a star occurs in thermonuclear reactions of proton capturing with subsequent nuclear decay into two α-particles: 7Li(p,α) 4He. The solar lithium problem consists of reproducing the low photospheric abundance as a result of evolutionary model computations starting from the high initial value.
If one considers standard solar modelling, which includes only the main sequence (MS) stage and one does not consider any additional mixing beneath the convection zone (CZ), then the observed lithium abundance in the photosphere cannot be predicted (see, for example, Fig. 1 in Meléndez et al. 2010; D’Antona & Mazzitelli 1984). The photospheric lithium abundance is determined by the temperature and density at the base of the CZ. This is because matter in the CZ is efficiently mixed and the abundance of lithium through the whole CZ is identical and equal to that of the photosphere. The temperature is the main parameter controlling the nuclear reaction rates, so the maximum rate of lithium burning is achieved at the base of CZ, where the temperature is hottest and reaches 2.2 MK in the present-day Sun (e.g. model S Christensen-Dalsgaard et al. 1991, 1996, defacto accepted as the standard one). But even at this temperature, the rate of depletion is low, and its abundance does not decrease significantly during the MS stage.
However, the base of the CZ is remarkably hotter when a radiative core arises during the early stage of evolution, before the MS. The maximal temperature in the CZ can reach 3.9 MK (see, for example Piau & Turck-Chièze 2002). As a result, the lithium depletion rate during the pre-main sequence (pMS) is several times higher than during the MS, athough it still cannot entirely explain the observed depletion in the frame of standard physics (Morel et al. 1995). The modelling of the evolution of the lithium abundance has to take into account the pMS stage where the depletion is intensive, especially if we observe significant lithium depletion during the MS stage.
Let us note that non-standard models considering other hypotheses can lead to changes at the base of the CZ and help to solve the problem. Several approaches have been proposed to describe extra mixing: by overshooting (Böhm 1963; Ahrens et al. 1992), by internal waves (Montalban 1994) or by turbulent diffusion (Baglin et al. 1985; Zhang & Li 2012). This mixing is also influenced by differential rotation (Zahn 1983; Lebreton & Maeder 1987; Brun et al. 1999) and magnetic field (McIntyre 2007). Additional lithium depletion can also be caused by other mechanisms such as stellar wind (Vauclair & Charbonnel 1995; Morel et al. 1997), circumstellar disks at the early stage of evolution (Piau & Turck-Chièze 2002) as well as activity during the early MS lifetime (Turck-Chièze et al. 2011).
Models of the Sun should be consistent with helioseismic data, in particular with respect to the sound speed profile. Such discussions on the sound speed profiles in models with overshooting have been considered in detail by Christensen-Dalsgaard et al. (2011); Zhang & Li (2012, and references therein).
In this article, we estimate the rate of lithium depletion of the present-day Sun using helioseismic constraints at the base of the solar CZ. Usually helioseismic constraints are based on analysis of the sound speed profile and determination of the depth of the CZ (Christensen-Dalsgaard et al. 1991) and allow us to limit the temperature in the CZ by 2.2 MK (Christensen-Dalsgaard et al. 1996). Our analysis method applied to the sound speed gradient is much more sensitive to details of additional mixing and to the gradient of the hydrogen abundance below the CZ affected by mixing. Our modelling predicts only small rates of lithium depletion at the present stage of the solar evolution and this argues in favour of a dominate role of the pMS stage in lithium evolution.
Sometimes photospheric beryllium abundance is used to test model computations, but for the Sun, Be is a much weaker constraint on the modelling than lithium. Moreover, the measurement of the beryllium abundance is difficult. A brief review of this problem can be found in (Andrássy & Spruit 2015), for example.
We describe the modelling of the Sun in Sect. 2, and constrain the region of additional mixing below the CZ in Sect. 3. Then we analyse the rate of lithium burning during various stages of the evolution in Sect. 4. Our results on solar twins are discussed in Sect. 5, before concluding.
2. Standard evolutionary model in CESAM
Evolutionary modelling has been performed using the 1D CESAM2k code (Morel & Lebreton 2008). Quasi-hydrostatic solar evolution has been computed until age 4.6 Gyr, including the pMS. The duration of pMS stage is approximately 30 Myr.
On the basis of the evolutionary computations, we trace the lithium abundance in CZ. Initial chemical composition of the Sun is adopted according to Grevesse & Sauval (1998), in particular for the lithium A(Li) = 3.31. Here, logarithmic abundance is defined as A(Li) = log (NLi/NH) + 12 where NLi and NH are the number densities of lithium and hydrogen.
The input physics is relatively common. The temperature gradient in CZ is calculated using the mixing length theory formalism (Böhm-Vitense 1958). Rates of thermonuclear reactions are computed by Angulo et al. (1999). Microscopic diffusion of a wide set of chemical isotopes is traced along evolution following methods by Michaud & Proffitt (1993). The traced isotopes, besides main species (hydrogen and helium), are 6Li, 7Li, 9Be and others components of the CNO cycle. Equation of state is OPAL2001 (Rogers et al. 1996) and opacity is OPAL1993 (Iglesias & Rogers 1996). More details on the standard solar model in CESAM have been given by Brun et al. (1998).
 |
Fig. 1 Evolution of the Sun during pMS and MS stages. a) solar radius (R) and coordinate of the convection zone base (rczb); b) temperature at the solar centre (Tc) and at the CZ base (Tczb); c) density at the solar centre (ρc) and at the CZ base (ρczb); d) lithium abundance in CZ in the standard model (solid line) and with additional mixing (dashed line). Grey vertical lines separate pMS and MS stages. Grey rectangles highlight time of intensive lithium burning. |
In the Solar System, lithium abundance is composed of two stable isotopes 7Li and 6Li. The percentage of 7Li is 92.41% (Asplund et al. 2009). The main thermonuclear reactions with lithium are capturing protons with subsequent nuclear decay: 7Li(p,α) 4He and 6Li(p,α) 3He. The rate of 6Li burning is approximately two orders of magnitude higher than that of 7Li. Thus, the initial abundance of 6Li is small and the rate of its burning is high; it quickly disappeared during the early stages of evolution. Therefore, we consider only 7Li hereafter.
Two different stages in the solar evolution are considered. The short initial pMS stage of hydrostatic evolution starts from collapse of a completely convective star (Fig. 1a). The temperature of the contracting proto-star increases and achieves approximately 4 MK in the core (Fig. 1b), the matter becomes transparent and convection ceases, as a result the radiative core appears. It happens at an age of 1.3 Myr. Then, the radiative-convective star continues to contract and heat up, the radiative core occupies more space and the convective envelope becomes shallower (Iben 2013). From view of lithium evolution, the temperature at the base of CZ is a principal value and decreases from 3.9 to 2.3 MK during radiative core growth on pMS. At the same time, behaviour of density at the CZ base is more complicate and finally reduced to 0.3 g/cm3 (Fig. 1c).
The second stage is a quasi-stationary evolution on the MS which lasts billions of years for the Sun. Stellar parameters are changing slowly at this stage, particularly the temperature and position of the base of CZ. In Fig. 1, the grey vertical line conditionally separates these two stages. It corresponds to the zero age main sequence (ZAMS) and characterises change of the source of luminosity from gravitational contraction to the thermonuclear reactions (Clayton 1968). At the MS stage, the convective zone continues very slowly shallowing and the temperature and density at the CZ base decrease from 2.3 to 2.2 MK and from 0.3 to 0.2 g/cm3 , respectively.
Our standard computations result in lithium depletion in the solar CZ by a factor of seven during the whole evolution, while its main part is depleted during the stage of the pMS (Fig. 1d, solid curve).
3. Helioseismic model of slow diffusive mixing at the stage of MS
Our main statement is that the rate of lithium burning in the present solar envelope is too slow to provide the necessary depletion value. We make this conclusion because the temperature at the CZ base according to the standard modelling is not high enough to provide effective lithium depletion, and because according to our estimation, the thickness of additional mixing region below CZ could not be extended to reach high-temperature layers.
The first statement is based on the fact that the temperature at the base of CZ is fixed by the helioseismic determination (Christensen-Dalsgaard et al. 1991) of the Schwarzschild point position at the r = 0.713 R⊙ and the suggestion that the temperature profile T(r) in the adiabatic solar CZ is well defined in Model S (Christensen-Dalsgaard et al. 1996).
The second statement about additional mixing below the CZ base is more complex and we outline here the scheme of consideration.
Basic helioseismic information about solar interior is the sound speed profile c(r) and it is obtained from the eigenfrequencies with a procedure named helioseismic inversion. The deviation of the model sound-speed profile from the inverted one is considered as a measure of quality of the model. But this direct comparison is adequate in the radiative (i.e. convectively stable) region below CZ, whereas sound-speed profiles inside adiabatic CZ are generally very close to one another in different models. Therefore, models can hardly be distinguished by this criterion.
Instead of analysing the c(r) itself, we use a gradient of sound speed as a more physically meaningful value. The idea of using the gradient of sound speed came from early helioseismic work (Gough 1984), where the author considered the expression 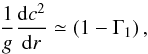 (1)which is well satisfied inside the adiabatic CZ. Here r is a radius-coordinate, g is gravity acceleration and Γ1 is an adiabatic exponent. It is clear from Eq. (1) that the gradient of the sound speed is directly connected with thermodynamic properties via Γ1.
(1)which is well satisfied inside the adiabatic CZ. Here r is a radius-coordinate, g is gravity acceleration and Γ1 is an adiabatic exponent. It is clear from Eq. (1) that the gradient of the sound speed is directly connected with thermodynamic properties via Γ1.
Having the sound speed profile, one is able (at least in principle) to get a gradient of sound speed, but this can be problematic due to ill-posed numerical differentiation. In our study, we use results of inversion by Vorontsov et al. (2013) to acquire an “inverted gradient of squared sound speed”.
The first step of our analysis is to obtain information regarding the gradient of hydrogen abundance ∇X from the gradient of sound speed based on a general expression for the gradient of sound speed via three other gradients. During deduction of the expression, the differential of dlnρ(lnP,lnT,X) is used, and after a number of transformations we acquire 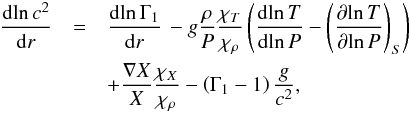 (2)where P is plasma pressure, T is temperature, ρ is density, X is hydrogen mass fraction and χρ ≡ (∂lnP/∂lnρ)T,X, χT ≡ (∂lnP/∂lnT)ρ,X, χX ≡ (∂lnP/∂lnX)T,ρ are thermodynamic derivatives of the pressure.
(2)where P is plasma pressure, T is temperature, ρ is density, X is hydrogen mass fraction and χρ ≡ (∂lnP/∂lnρ)T,X, χT ≡ (∂lnP/∂lnT)ρ,X, χX ≡ (∂lnP/∂lnX)T,ρ are thermodynamic derivatives of the pressure.
For the region below CZ, we neglect the gradient of the adiabatic exponent Γ1 and suppose that Γ1 in the last term of the right side of Eq. (2) is adequately prescribed by the equation of state.
We infer an appropriate gradient of hydrogen from Eq. (2), keeping the gradient of temperature dlnT/ dlnP as it is in the model. This inverted ∇Xinv should provide a good consistency of model data with helioseismic inversion data.
The second step of our analysis consists of comparison of the inverted ∇Xinv with model ∇Xmod. Then we can conclude whether an additional mixing occurs beneath the convection zone and we can apply possible constraints on its value.
Standard evolutionary computations provide model ∇Xmod without additional mixing. To study abundance gradient profile ∇X in more common cases of mixing, we use an effective and robust method of post-model computations proposed in (Baturin et al. 2006; Gorshkov & Baturin 2014; Baturin et al. 2015).
The method consists of numerical solution of the evolutionary Eq. (3) while the pressure and temperature profiles are given by some evolutionary sequence and fixed during integration. In our calculations, model profiles have been adopted from the Model S (Christensen-Dalsgaard et al. 1996).
The evolutionary equation is 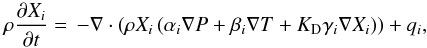 (3)
(3)
where Xi is the mass fraction of a chemical element, αi,βi,γi are the coefficients of baro-, thermo-, and concentration diffusion computed following Michaud & Proffitt (1993) and KD is a coefficient for describing mixing. In the standard model without extra-mixing, KD = 1 in the radiative zone and KD ≫ 1 in CZ, where mixing is much faster than diffusion. The last term qi is rate of elements changing in nuclear reactions. All the values in Eq. (3) depend on radius-coordinate r and time t.
As a result, a set of ∇Xmod profiles has been obtained for various profiles of mixing coefficient KD. Among this set, we look for a profile of KD which provides the best agreement with the inverted profile ∇Xinv.
An example of such a comparison is shown by Fig. 2. The hydrogen abundance and its gradient resulting from the matching procedure is presented by dashed curves in Figs. 2a,b. The corresponding coefficient KD is in Fig. 2c. The convection zone is marked by the roman numeral I on all panels.
The main results of the matching procedure are the following. Firstly, below level r ≈ 0.6 R⊙, agreement between inverted ∇Xinv (pointed line) and standard model ∇Xmod (solid line) is very good without assumption of additional mixing. However, in the range from 0.6 R⊙ to convection zone base, discrepancy is evident. There seems to be a necessity for additional mixing in the model. Secondly, our main conclusion is the possibility to fit model gradient ∇Xmod to the inverted ∇Xinv in the zone III (≈0.615−0.67 R⊙) by supposing slow mixing with KD = 2. Thirdly, in the zone II, an increase of KD is needed to reach an agreement. However, further growth of KD> 10 does not provide better agreement in the vicinity of the CZ base. This high value of KD, however, means that we reach the fast mixing (overshooting) region. This region is limited by depth 0.038 R⊙, that is 0.5HP, where HP = −(dr/ dP)P is the local pressure scale height.
 |
Fig. 2 Profiles of hydrogen abundance a), its gradient b) and coefficient KDc) beneath the convection zone in the present-day Sun. Dashed and solid lines describe the model with and without additional mixing, respectively. The thin, solid, horizontal line on the plot a) is hydrogen distribution at the ZAMS. The pointed line on the plot b) is inverted gradient of hydrogen abundance obtained from the observed sound-speed profile. Vertical dashed-pointed lines separate three regions with different mixing: I is convection zone, II and III are zones with additional mixing. |
This new increased coefficient of diffusion has been used to compute the lithium evolution on the Sun. In our model, the profile KD(r,t) translates along the radius keeping its shape with convection zone base evolution. Radius-coordinate of the base of the convection zone and that of the zone of additional slow mixing are shown as functions of time in Fig. 3a. The temperature at the base of the mixing zone is higher than that at the CZ base by 0.7 MK (Fig. 3b). This leads to additional lithium burning of approximately 5%, that is, its present abundance is 80% of the initial one (Fig. 3c, dashed line). Even if we assume mixing in the poorly known region II to be as fast as in the convection zone, the envelope lithium abundance decreases insignificantly at the MS stage. We obtain 65% of the initial abundance after 4.6 Gyr evolution (pointed line); this is not enough to explain our observational value.
So, the present helioseismic data do not allow the mixing process to be deep and fast enough to deplete lithium at the MS stage, supposing the rate is constant.
 |
Fig. 3 Evolution of the convection zone during the MS stage. Solid lines indicate classical Model S, dashed ones indicate the model with additional helioseismic mixing beneath the convection zone. a) Radius-coordinate of the base of CZ and zone of the additional mixing; b) temperature at the bases; c) lithium depletion in both models. The dotted line indicates lithium depletion in the case of fast mixing. |
4. Fast mixing during the pMS stage
In contrast to the MS stage, an assumption about additional mixing during the pMS can efficiently explain lithium depletion in the CZ by a factor of 160 (Fig. 1d, dashed curve). Computations with CESAM2k show that the depletion is achieved with a thickness of the extra-mixing region of approximately 0.18HP. The extra-mixing (convective overshooting) is modelled assuming a large diffusion coefficient KD ≫ 1. The thickness of the overshooting region is constant during the whole evolutionary computation. The extra-mixing increases lithium depletion only slightly during the MS stage. In contrast, the rate of lithium burning during the pMS stage is increased significantly because the maximum temperature at the overshooting region base achieves 4.2 MK, whereas it is 3.9 MK at the CZ base (Fig. 4a).
Figure 4b shows the characteristic times τ of thermonuclear reaction 7Li(p,α) 4He:
![$$ \tau \equiv \frac{N(\element[][]{Li})}{{\partial}N(\element[][]{Li})/{\partial t}}, $$](/articles/aa/full_html/2017/02/aa29385-16/aa29385-16-eq62.png) where N(Li) is number density of lithium. The characteristic times are computed for the convection zone base (solid curve) and for the overshooting region base (dashed curve). The grey straight line corresponds to characteristic time τ equal to the current age t of a star. When the characteristic time of the reaction is longer than the current age of a star (i.e. the curve is above the straight line), the reaction is slow; it does not change the element abundance on the considered timescale. If the characteristic time is less (the curve is below the straight line), then the reaction is significant for the abundance evolution.
where N(Li) is number density of lithium. The characteristic times are computed for the convection zone base (solid curve) and for the overshooting region base (dashed curve). The grey straight line corresponds to characteristic time τ equal to the current age t of a star. When the characteristic time of the reaction is longer than the current age of a star (i.e. the curve is above the straight line), the reaction is slow; it does not change the element abundance on the considered timescale. If the characteristic time is less (the curve is below the straight line), then the reaction is significant for the abundance evolution.
We see, firstly, that during the pMS stage, from 1 to 20 Myr, the overshooting leads to a decrease in characteristic time of lithium burning by a factor of three. Moreover, it prolongs the time when the characteristic time of reaction is smaller than the age of a star. Secondly, during the MS, overshooting value is not important because characteristic time of burning is much longer than the current age in both cases.
We may notice that overshooting is not the unique factor which can lead to efficient lithium burning. Higher opacity, for example, can play the same role. The key factor of the lithium evolution is the maximum temperature at the mixing zone base during the pMS stage.
 |
Fig. 4 Temperature (a) and characteristic times (b) for lithium burning in reaction 7Li(p, α)4He during the evolution of the Sun. The solid line is obtained for conditions of the convection zone base, dashed line – for the base of the overshooting region. The grey straight line corresponds to τ equal to the current age t of a star. |
5. Solar twins
Solar twins are defined as MS stars with effective temperature, surface gravity and metallicity close to the solar values, but independent of age. The mass is assumed to be close to the solar mass.
We study a set of solar twin stars with measured lithium abundances. Two different scenarios of lithium depletion in solar twins during their MS evolution are discussed. The first scenario considers a low Li depletion rate where A(Li) remains almost unchanged on the MS: (| dA(Li)/dt | ~ 0.01 dex/Gyr). We refer to this untraditional scenario as early depletion evolution course. The second considers a depletion rate during the MS stage larger than some limit (| dA(Li)/dt | ~ 0.2 dex/Gyr), and we refer to this as the traditional scenario. Assuming the traditional scenario, one could expect a noticeable difference in the lithium abundance between young and old stars.
Li abundances of several solar twins have recently been published. Observations of this kind could be used to estimate the MS depletion rate of lithium abundance and could help to distinguish between the two scenarios. Meléndez et al. (2014) describe five solar twins and these are shown in Fig. 5 (black circles). A similar analysis is also presented by Carlos et al. (2016). The authors demonstrated a strong correlation between A(Li) and the age of 21 selected solar twins. These stars are shown by grey circles and triangles in the figure. The authors show that the lithium depletion rate during the MS is high. There are several evolutionary model predictions in the framework of the traditional scenario (Charbonnel & Talon 2005; Do Nascimento et al. 2009; Xiong & Deng 2009; Denissenkov 2010; Andrássy & Spruit 2015). An example is represented by the dashed curve.
 |
Fig. 5 Evolution of lithium abundance in solar twins. Solid lines indicate our models of early depletion scenario with different overshooting values (see Table 1) leading to significant lithium depletion during the pMS stage. The dashed line qualitatively illustrates the traditional scenario with significant lithium depletion during the stage of MS. Black circles are solar twins taken from (Meléndez et al. 2014). Grey and unfilled circles and triangles are twins from (Carlos et al. 2016); triangles are the upper limits on lithium abundance; three unfilled circles are twins-exceptions which can be interpreted in the framework of the early depletion scenario. |
We note that the traditional scenario predicts lithium abundance decreasing rapidly until the present-day Sun, in contradiction with our results, which are based on an analysis of the sound speed gradient. Comparing the sound speed profiles in the theoretical models introduced above with the helioseismically inverted model is not enough to make any conclusions regarding the depth of the region where additional mixing takes place. In other words, sound speed profiles may somewhat agree for different models but the sound speed gradient may show specific peculiarities. We estimate that the rate of lithium depletion is too small in the Sun and that this therefore favours the early depletion scenario.
The early depletion scenario does not predict any correlation between Li and age when starting simulations from a random set of stars after the pMS. The dispersion of the lithium abundances in solar twins can be explained through the various physical conditions during the early pMS stage, for example, different overshooting values. Assuming this scenario we can interpret the solar twins which do not show the strong Li/age correlation, for example HD 96423, HD 38277, and 16 Cyg A (shown as unfilled circles in Fig. 5). In Table 1 we list the values of overshooting that have been adjusted in the stellar evolution models to match the observed lithium abundances for the given ages. These values do not follow from any physical model and are merely auxiliary parameters. In the case of evolution of 16 Cyg A, lithium abundance decreases rapidly after 8 Gyr because of a hydrogen-fusing shell arising in this star earlier than in others due to its relatively higher mass. Thus, the lithium-age strong correlation itself does not reject the early depletion scenario.
Overshooting values used to compute evolution of the solar twins.
We should also remark that it is hard to explain why a random sample of solar twins could demonstrate such a strong correlation between lithium abundance and age. The traditional scenario predicts some correlation between A(Li) and age, but it is not strong. Statistically it would lead to a strong correlation only if the dispersion of lithium abundance after the pMS stage was small meaning that the process of lithium burning during the pMS stage is strictly identical for all solar twins. Moreover, the strong correlation implies that the rate of lithium burning during the MS stage is also well defined, even if stars have slightly different masses, metallicities and surface gravity as in the example of Carlos et al. (2016). As a result, we conclude that both scenarios do not predict the strong correlation for a random set of stars.
Considering the different lithium abundance after pMS, we note that different mixing conditions beneath the CZ can be explained by, for example, the hydrodynamic instability below the CZ, which can be affected by rotation as well as protoplanetary discs (Eggenberger et al. 2012). Observations show that young stars (up to 500 Myr) can rotate ten times faster than the Sun (Gallet & Bouvier 2013). The observed dispersion in the rotational velocities and/or life-time of a disk can explain different overshooting values in different stars.
Dispersion of pMS lithium abundance can also be caused by spreading of convective efficiency in the presence of rotation and/or a magnetic field (Somers & Pinsonneault 2014). Another possibility is an episodic accretion on young (less than approximately 30 Myr) low-mass stars (Baraffe & Chabrier 2010). After hydrogen burning has started, stars with the same age and mass may have different lithium abundance depending on the accretion history. These mechanisms demonstrate the crucial role of the pMS stage in lithium evolution.
Extensive observations of solar twins (including those re-analysed by Carlos et al. 2016) is also provided by Delgado Mena et al. (2014). We selected stars with parameters in the range of Carlos et al. (2016): Teff = 5690−6870 K, log (g) = 4.25−4.50 dex, [Fe/H] = −0.11−( + 0.11), and also M = (0.94−1.07) M⊙. The selected stars are shown in Fig. 6, presenting different lithium abundances in both young and old stars. Moreover, there is no significant correlation between A(Li) and age. In the context of early depletion scenario they can be explained by various physical conditions during the early stage of evolution, for example, by different overshooting values as shown in Fig. 6, or different A(Li) in the clouds from which stars are born.
Discussions about determining ages of stars of Carlos et al. (2016) and Delgado Mena et al. (2014) are very interesting but this is outside the scope of this work.
 |
Fig. 6 Evolution of lithium abundance in solar twins. Solid lines show two examples of our computations in framework of early depletion scenario: thin line shows standard solar model without overshooting, thick line shows solar model with overshooting 0.18Hp. Circles and triangles indicate solar twins considered by (Delgado Mena et al. 2014), and selected over the ranges of parameters proposed by (Carlos et al. 2016); triangles are upper limits on lithium abundance. |
6. Conclusions
Considering the general evolution of solar-type stars, we make conclusions about the prevailing role of the early pMS stage on the present-day lithium abundance in the convective envelope.
In the solar surface envelope, the lithium abundance decreases by a factor of seven during the whole evolution in models without extra mixing while the lithium is mainly depleted during the pMS stage.
When we assume the mixing model under the CZ in the present-day Sun restricted by helioseismic analysis, the lithium depletion increases only by 5% during the MS stage.
Low observed lithium abundance on the Sun can be explained by the existence of regions with additional mixing during the early stage of evolution, before the MS stage. The thickness of extra-mixing regions is estimated as 0.18HP.
Dispersion of lithium abundance in solar twins could be explained by variation of physical conditions during the pMS stage whilst keeping lithium abundance almost stable during the MS stage.
Acknowledgments
Part of this work was supported by a research project “Modélisation Cesam2k” of Observatoire de la Côte d’Azur.
References
- Ahrens, B., Stix, M., & Thorn, M. 1992, A&A, 264, 673 [NASA ADS] [Google Scholar]
- Andrássy, R., & Spruit, H. C. 2015, A&A, 579, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Baglin, A., Morel, P., & Schatzman, E. 1985, A&A, 149, 309 [Google Scholar]
- Baraffe, I., & Chabrier, G. 2010, A&A, 521, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baturin, V. A., Gorshkov, A. B., & Ayukov, S. V. 2006, Astron. Rep., 50, 1001 [NASA ADS] [CrossRef] [Google Scholar]
- Baturin, V. A., Gorshkov, A. B., & Oreshina, A. V. 2015, Astron. Rep., 59, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm, K.-H. 1963, ApJ, 138, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm-Vitense, E. 1958, ZAp, 46, 108 [NASA ADS] [Google Scholar]
- Brun, A. S., Turck-Chièze, S., & Morel, P. 1998, ApJ, 506, 913 [NASA ADS] [CrossRef] [Google Scholar]
- Brun, A. S., Turck-Chièze, S., & Zahn, J. P. 1999, ApJ, 525, 1032 [NASA ADS] [CrossRef] [Google Scholar]
- Carlos, M., Nissen, P. E., & Meléndez, J. 2016, A&A, 587, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charbonnel, C., & Talon, S. 2005, Science, 309, 2189 [Google Scholar]
- Christensen-Dalsgaard, J., Gough, D. O., & Thompson, M. J. 1991, ApJ, 378, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J., Dappen, W., Ajukov, S. V., et al. 1996, Science, 272, 1286 [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J., Monteiro, M. J. P. F. G., Rempel, M., & Thompson, M. J. 2011, MNRAS, 414, 1158 [NASA ADS] [CrossRef] [Google Scholar]
- Clayton, D. D. 1968, Principles of stellar evolution and nucleosynthesis (New York: McGraw-Hill) [Google Scholar]
- D’Antona, F., & Mazzitelli, I. 1984, A&A, 138, 431 [Google Scholar]
- Delgado Mena, E., Israelian, G., González Hernández, J. I., et al. 2014, A&A, 562, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Denissenkov, P. A. 2010, ApJ, 719, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Do Nascimento, Jr., J. D., Castro, M., Meléndez, J., et al. 2009, A&A, 501, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, P., Haemmerlé, L., Meynet, G., & Maeder, A. 2012, A&A, 539, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallet, F., & Bouvier, J. 2013, A&A, 556, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gorshkov, A. B., & Baturin, V. A. 2014, in Proc. XVIII All Russian Conf. with Int. Participation Solar and Solar-Terrestrial Physics, eds. A. V. Stepanov, & Y. Nagovitsyn, 109 [Google Scholar]
- Gough, D. O. 1984, Mem. Soc. Astron. Ital., 55, 13 [Google Scholar]
- Greenstein, J. L., & Richardson, R. S. 1951, ApJ, 113, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [Google Scholar]
- Hughes, D. W., Rosner, R., & Weiss, N. O. 2007, The Solar Tachocline (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Iben, Jr., I. 2013, Stellar Evolution Physics, Volume 1: Physical Processes in Stellar Interiors (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Lebreton, Y., & Maeder, A. 1987, A&A, 175, 99 [Google Scholar]
- McIntyre, M. E. 2007, in The Solar Tachocline, eds. D. W. Hughes, R. Rosner, & N. O. Weiss (Cambridge, UK: Cambridge University Press), 183 [Google Scholar]
- Meléndez, J., Ramírez, I., Casagrande, L., et al. 2010, Ap&SS, 328, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Meléndez, J., Schirbel, L., Monroe, T. R., et al. 2014, A&A, 567, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michaud, G., & Proffitt, C. R. 1993, in IAU Colloq. 137, Inside the Stars, eds. W. W. Weiss, & A. Baglin, ASP Conf. Ser., 40, 246 [Google Scholar]
- Montalban, J. 1994, A&A, 281, 421 [NASA ADS] [Google Scholar]
- Morel, P., & Lebreton, Y. 2008, Ap&SS, 316, 61 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Morel, P., Provost, J., Berthomieu, G., Matias, J., & Zahn, J. P. 1995, in Proc. of the 32nd Liège Int. Astrophysical Colloq., 395 [Google Scholar]
- Morel, P., Provost, J., & Berthomieu, G. 1997, A&A, 327, 349 [NASA ADS] [Google Scholar]
- Piau, L., & Turck-Chièze, S. 2002, ApJ, 566, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., Meléndez, J., Cornejo, D., Roederer, I. U., & Fish, J. R. 2011, ApJ, 740, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, F. J., Swenson, F. J., & Iglesias, C. A. 1996, ApJ, 456, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Somers, G., & Pinsonneault, M. H. 2014, ApJ, 790, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Turck-Chièze, S., Piau, L., & Couvidat, S. 2011, ApJ, 731, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Vauclair, S., & Charbonnel, C. 1995, A&A, 295, 715 [NASA ADS] [Google Scholar]
- Vorontsov, S. V., Baturin, V. A., Ayukov, S. V., & Gryaznov, V. K. 2013, MNRAS, 430, 1636 [NASA ADS] [CrossRef] [Google Scholar]
- Xiong, D. R., & Deng, L. 2009, MNRAS, 395, 2013 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J. P. 1983, in Saas-Fee Advanced Course 13: Astrophysical Processes in Upper Main Sequence Stars, eds. A. N. Cox, S. Vauclair, & J. P. Zahn (Switzerland: Geneva Observatory), 253 [Google Scholar]
- Zhang, Q. S., & Li, Y. 2012, ApJ, 746, 50 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Evolution of the Sun during pMS and MS stages. a) solar radius (R) and coordinate of the convection zone base (rczb); b) temperature at the solar centre (Tc) and at the CZ base (Tczb); c) density at the solar centre (ρc) and at the CZ base (ρczb); d) lithium abundance in CZ in the standard model (solid line) and with additional mixing (dashed line). Grey vertical lines separate pMS and MS stages. Grey rectangles highlight time of intensive lithium burning. |
| In the text | |
 |
Fig. 2 Profiles of hydrogen abundance a), its gradient b) and coefficient KDc) beneath the convection zone in the present-day Sun. Dashed and solid lines describe the model with and without additional mixing, respectively. The thin, solid, horizontal line on the plot a) is hydrogen distribution at the ZAMS. The pointed line on the plot b) is inverted gradient of hydrogen abundance obtained from the observed sound-speed profile. Vertical dashed-pointed lines separate three regions with different mixing: I is convection zone, II and III are zones with additional mixing. |
| In the text | |
 |
Fig. 3 Evolution of the convection zone during the MS stage. Solid lines indicate classical Model S, dashed ones indicate the model with additional helioseismic mixing beneath the convection zone. a) Radius-coordinate of the base of CZ and zone of the additional mixing; b) temperature at the bases; c) lithium depletion in both models. The dotted line indicates lithium depletion in the case of fast mixing. |
| In the text | |
 |
Fig. 4 Temperature (a) and characteristic times (b) for lithium burning in reaction 7Li(p, α)4He during the evolution of the Sun. The solid line is obtained for conditions of the convection zone base, dashed line – for the base of the overshooting region. The grey straight line corresponds to τ equal to the current age t of a star. |
| In the text | |
 |
Fig. 5 Evolution of lithium abundance in solar twins. Solid lines indicate our models of early depletion scenario with different overshooting values (see Table 1) leading to significant lithium depletion during the pMS stage. The dashed line qualitatively illustrates the traditional scenario with significant lithium depletion during the stage of MS. Black circles are solar twins taken from (Meléndez et al. 2014). Grey and unfilled circles and triangles are twins from (Carlos et al. 2016); triangles are the upper limits on lithium abundance; three unfilled circles are twins-exceptions which can be interpreted in the framework of the early depletion scenario. |
| In the text | |
 |
Fig. 6 Evolution of lithium abundance in solar twins. Solid lines show two examples of our computations in framework of early depletion scenario: thin line shows standard solar model without overshooting, thick line shows solar model with overshooting 0.18Hp. Circles and triangles indicate solar twins considered by (Delgado Mena et al. 2014), and selected over the ranges of parameters proposed by (Carlos et al. 2016); triangles are upper limits on lithium abundance. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


