| Issue |
A&A
Volume 598, February 2017
|
|
|---|---|---|
| Article Number | A7 | |
| Number of page(s) | 20 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201527203 | |
| Published online | 24 January 2017 | |
eXtended CASA Line Analysis Software Suite (XCLASS) ⋆,⋆⋆
1 I. Physikalisches Institut, Universität zu Köln, Zülpicher Str. 77, 50937 Köln, Germany
e-mail: moeller@ph1.uni-koeln.de
2 Max-Planck-Institut für extraterrestrische Physik, Giessenbachstrasse 1, 85748 Garching, Germany
Received: 17 August 2015
Accepted: 22 September 2016
The eXtended CASA Line Analysis Software Suite (XCLASS) is a toolbox for the Common Astronomy Software Applications package (CASA) containing new functions for modeling interferometric and single dish data. Among the tools is the myXCLASS program which calculates synthetic spectra by solving the radiative transfer equation for an isothermal object in one dimension, whereas the finite source size and dust attenuation are considered as well. Molecular data required by the myXCLASS program are taken from an embedded SQLite3 database containing entries from the Cologne Database for Molecular Spectroscopy (CDMS) and JPL using the Virtual Atomic and Molecular Data Center (VAMDC) portal. Additionally, the toolbox provides an interface for the model optimizer package Modeling and Analysis Generic Interface for eXternal numerical codes (MAGIX), which helps to find the best description of observational data using myXCLASS (or another external model program), that is, finding the parameter set that most closely reproduces the data.
Key words: editorials, notices / line: identification / methods: analytical / methods: data analysis / methods: numerical
A copy of the code is available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/598/A7
© ESO, 2017
1. Introduction
The CASA package (McMullin et al. 2007) provides a powerful tool for data post-processing for ALMA and JVLA, but contains only rudimentary functions for modeling the data. But modeling astronomical data is essential to derive physical parameters such as column densities and rotational temperatures, as well as information on the location and the kinematics of the emitting gas component for each observed molecular species.
The toolbox described in this paper offers not only the possibility to model data by using the myXCLASS program (Schilke et al. 2001; Comito et al. 2005; Zernickel et al. 2012; Crockett et al. 2014a,b; Neill et al. 2014), which computes synthetic spectra by solving the detection equation similar to software packages like Weeds (Maret et al. 2011) and CASSIS1, but also makes use of the optimization package MAGIX (Möller et al. 2013). MAGIX provides a framework of an easy interface between existing codes and an iterating engine that attempts to minimize deviations of the model results from available observational data, constraining the values of the model parameters and providing corresponding error estimates. In addition to the myXCLASS program many external model programs2 such as RADEX (Van der Tak et al. 2007), RADMC-3D3 or LIME (Brinch & Hogerheijde 2010) can be plugged into MAGIX to explore their parameter space and find the set of parameter values that best fits observational data. Most of the optimization algorithms included in the MAGIX package are available as an OpenMP4 and an MPI5 version to speed up the computation. Furthermore, the toolbox includes two new functions which provide a simplified interface for MAGIX in conjunction with myXCLASS to model single spectra and complete data cubes, respectively. Once installed, it is seamlessly integrated into CASA, so the tasklist command within CASA lists all the new functions. In addition, the help command followed by the name of the function provides a short description of the corresponding function with a short overview of all input parameters. In addition, the XCLASS interface can be used without CASA, wherefore the following python packages has to be installed: numpy, scipy, pyfits, matplotlib and sqlite3.
The Splatalogue database6 is accessible from within the viewer in CASA. We have opted to use our own SQLite3 database based on the VAMDC7 implementation, mostly because this allows the user to augment the data by providing the partition function between 1.072 and 1000 K at 110 different temperatures in contrast to seven temperatures in the Splatalogue database, which is derived from the traditional JPL8 and CDMS9 catalogs. It is hoped that the content of Splatalogue and the VAMDC database will at some point be homogenized.
The XCLASS interface for CASA is mostly written in python, whereas the myXCLASS program and most of the algorithms included in the MAGIX package are written in Fortran 90. All required Python modules are already included in the CASA package, so no further software package except the GNU compiler10 (gfortran and gcc) with OpenMP/OpenMPI extension has to be installed. The XCLASS interface for CASA is available for Linux and Mac OS 10.11 (64 bit).
In the next sections we describe the myXCLASS program and its algorithms, assumptions, and shortcomings in detail. Afterwards, we describe the SQLite3 database used for the myXCLASS program and the related functions provided by the XCLASS interface. In the following we briefly present the MAGIX package with a short overview of the included algorithms. Finally, we give a detailed description of the new functions myXCLASSFit and myXCLASSMapFit used for modeling data with myXCLASS and MAGIX.
2. myXCLASS
The XCLASS interface for CASA contains the myXCLASS program, originally developed by P. Schilke (Schilke et al. 2001; Comito et al. 2005; Zernickel et al. 2012; Crockett et al. 2014a,b; Neill et al. 2014) based on the GILDAS11 package CLASS, which models a spectrum by solving the radiative transfer equation for an isothermal object in one dimension, the detection equation (Stahler & Palla 2005). Here, LTE is assumed, that is, the source function is given by the Planck function of an excitation temperature, which does not need to be the physical temperature, but is constant for all transitions. The myXCLASS function is designed to describe line-rich sources which are often dense, so that LTE is a reasonable approximation. Also, a non-LTE description requires collision rates which are available only for a few molecules.
The myXCLASS function is able to model a spectrum with an arbitrary number of molecules where the contribution of each molecule is described by an arbitrary number of components. The 1d assumption imposes a very simplistic geometrical structure. We recognize two classes of components.
One, the core objects (in earlier implementations called emission component), consists of an ensemble of objects centered at the middle of the beam. These could be identified with clumps, hot dense cores etc. which overlaps but do not interact either because they do not overlap in physical or in velocity space. For computational convenience, they are assumed to be centered in the beam, as shown in Fig. 1. It is also assumed that the dust emission emanates (partly) from these components. Their intensities are added, weighted with the beam filling factor, see Eq. (2).
The second class, foreground objects (in earlier implementations called absorption components), are assumed to be in layers in front of the core components. In the current 1d implementation, they would have a beam averaged intensity of the core sources as background, and would fill the whole beam. Examples for such structures would be source envelopes in front of dense cores, or absorption components along the line-of-sight.
As shown in Fig. 1, we assume that core components do not interact with each other radiatively, that is, one core layer is not influenced by the others. But the core layers may overlap to offer the possibility to model sources consisting of several molecules and compounds. The solution of the radiative transfer equation for core layers is12, ![\begin{eqnarray} \label{myXCLASS:modelEm} T_{\rm mb}^{\rm core}(\nu) &=& \sum_m \sum_{c} \Bigg[\eta \left(\theta^{m,c}\right) \left[S^{m,c}(\nu) \left(1 - {\rm e}^{-\tau_{\rm total}^{m,c}(\nu)} \right) \right.\nonumber\\ && \quad + \left. I_{\rm bg}^{\rm core} (\nu) \left({\rm e}^{-\tau_{\rm total}^{m,c}(\nu)} - 1 \right)\right]\Bigg] \nonumber\\ && \quad + \left(I_{\rm bg}^{\rm core} (\nu) - J_\mathrm{CMB} \right), \end{eqnarray}](/articles/aa/full_html/2017/02/aa27203-15/aa27203-15-eq1.png) (1)where the sums go over the indices m for molecule, and c for (core) component, respectively. In the following we briefly describe each term in Eq. (1).
(1)where the sums go over the indices m for molecule, and c for (core) component, respectively. In the following we briefly describe each term in Eq. (1).
 |
Fig. 1 Sketch of a distribution of core layers within the Gaussian beam of the telescope (black ring). Here, we assume three different core components 1, 2, and 3, centered at the middle of the beam with different source sizes, excitation temperatures, velocity offsets etc. indicated by different colors. Additionally, we assume that all core components have the same distance to the telescope, i.e., all core layers are located within a plane perpendicular to the line of sight. Furthermore, we assume that this plane is located in front of a background Layer 4 with homogeneous intensity |
The beam filling (dilution) factor η(θm,c) of molecule m and component c in Eq. (1)for a source with a Gaussian brightness profile, see below, and a Gaussian beam is given by13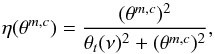 (2)where θm,c and θt represents the source and telescope beam full width half maximum (FWHM) sizes, respectively. The sources beam FWHM sizes θm,c for the different components are defined by the user in the molfit file, described in Sect. 2.1. Additionally, we assume for single dish observations, that the telescope beam FWHM size is related to the diameter of the telescope by the diffraction limit
(2)where θm,c and θt represents the source and telescope beam full width half maximum (FWHM) sizes, respectively. The sources beam FWHM sizes θm,c for the different components are defined by the user in the molfit file, described in Sect. 2.1. Additionally, we assume for single dish observations, that the telescope beam FWHM size is related to the diameter of the telescope by the diffraction limit 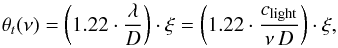 (3)where D describes the diameter of the telescope, clight the speed of light, and ξ = 3600 × 180 π-1 a conversion factor to get the telescope beam FWHM size in arcsec. For interferometric observations, the user has to define the interferometric beam FWHM size directly. In contrast to single dish observations we assume a constant interferometric beam FWHM size for the whole frequency range.
(3)where D describes the diameter of the telescope, clight the speed of light, and ξ = 3600 × 180 π-1 a conversion factor to get the telescope beam FWHM size in arcsec. For interferometric observations, the user has to define the interferometric beam FWHM size directly. In contrast to single dish observations we assume a constant interferometric beam FWHM size for the whole frequency range.
In general, the brightness temperature of radiation temperature J(T,ν) is defined as 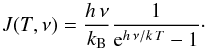 (4)The expression JCMB used in Eq. (1), describes the radiation temperature Eq. (4)of the cosmic background Tcbg = 2.7 K, that is, JCMB ≡ J(Tcbg,ν).
(4)The expression JCMB used in Eq. (1), describes the radiation temperature Eq. (4)of the cosmic background Tcbg = 2.7 K, that is, JCMB ≡ J(Tcbg,ν).
In Eq. (1), the expression Sm,c(ν) represents the source function and is according to Kirchhoff’s law of thermal radiation given by ![\begin{eqnarray} \label{myXCLASS:SourceFunction} S^{m,c}(\nu) &= &\frac{\epsilon_{\rm l}^{m,c}(\nu) + \epsilon_{\rm d}^{m,c}(\nu)}{\kappa_{\rm l}^{m,c}(\nu) + \kappa_{\rm d}^{m,c}(\nu)} \nonumber \\[3mm] &=& \frac{\kappa_{\rm l}^{m,c}(\nu) \, J(T_\mathrm{ex}^{m,c}, \nu) + \kappa_{\rm d}^{m,c}(\nu) \, J(T_{\rm d}^{m,c}, \nu)}{\kappa_{\rm l}^{m,c}(\nu) + \kappa_{\rm d}^{m,c}(\nu)}\nonumber \\[3mm] &=& \left(1 - \delta_{\gamma, 0}\right) \cdot \left[\frac{\tau_{\rm l}^{m,c}(\nu) \, J(T_\mathrm{ex}^{m,c}, \nu) + \tau_{\rm d}^{m,c}(\nu) \, J(T_{\rm d}^{m,c}, \nu)}{\tau_{\rm l}^{m,c}(\nu) + \tau_{\rm d}^{m,c}(\nu)}\right]\nonumber \\[3mm] && \quad + \delta_{\gamma, 0} \, J(T_\mathrm{ex}^{m,c}, \nu), \end{eqnarray}](/articles/aa/full_html/2017/02/aa27203-15/aa27203-15-eq23.png) (5)where
(5)where  and
and 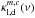 are the core and foreground coefficients for line and dust, respectively. Additionally, the optical depth is given by
are the core and foreground coefficients for line and dust, respectively. Additionally, the optical depth is given by 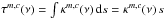 . This assumes that molecules and dust are well mixed, that is, it would not be correct if the molecule exists only in part of the cloud, but the dust everywhere. In older versions, the background temperature could only be defined as the measured continuum offset, which corresponds to the beam-averaged continuum brightness temperature. At the same time, the dust, as agent of line attenuation, was described by column density and opacity. This is practical, because the observable Tbg is used, but does not constitute a self-consistent and fully physical description. Therefore, we now use optionally either a physical (γ ≡ 1) or phenomenological (γ ≡ 0) description of the background indicated by the Kronecker delta δγ,0, that is,
. This assumes that molecules and dust are well mixed, that is, it would not be correct if the molecule exists only in part of the cloud, but the dust everywhere. In older versions, the background temperature could only be defined as the measured continuum offset, which corresponds to the beam-averaged continuum brightness temperature. At the same time, the dust, as agent of line attenuation, was described by column density and opacity. This is practical, because the observable Tbg is used, but does not constitute a self-consistent and fully physical description. Therefore, we now use optionally either a physical (γ ≡ 1) or phenomenological (γ ≡ 0) description of the background indicated by the Kronecker delta δγ,0, that is, 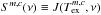 for γ ≡ 0. (Here, the phrase “background” means the “layer” with intensity
for γ ≡ 0. (Here, the phrase “background” means the “layer” with intensity 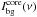 which is located behind the core components, that is, the background of the core layers, see Fig. 1.) We note that, if γ ≡ 0, the definition of the dust temperature
which is located behind the core components, that is, the background of the core layers, see Fig. 1.) We note that, if γ ≡ 0, the definition of the dust temperature 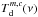 , Eq. (13), is superfluous.
, Eq. (13), is superfluous.
The total optical depth 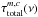 of each molecule m and component c is defined as the sum of the optical depths
of each molecule m and component c is defined as the sum of the optical depths 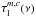 of all lines of each molecule m and component c plus the dust optical depth
of all lines of each molecule m and component c plus the dust optical depth 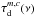 , that is,
, that is, 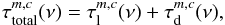 (6)where the dust optical depth
(6)where the dust optical depth 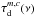 takes the dust attenuation into account and is given by
takes the dust attenuation into account and is given by 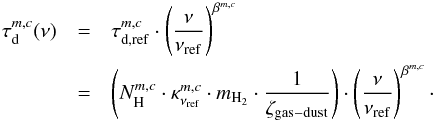 (7)Here,
(7)Here, 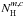 describes the hydrogen column density,
describes the hydrogen column density, 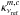 the dust mass opacity for a certain type of dust (Ossenkopf & Henning 1994) at the reference frequency νref, and βm,c the spectral index of
the dust mass opacity for a certain type of dust (Ossenkopf & Henning 1994) at the reference frequency νref, and βm,c the spectral index of 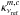 . These parameters are defined by the user, see Sect. 2.1. In addition, νref = 230 GHz indicates the reference frequency of the reference dust opacity
. These parameters are defined by the user, see Sect. 2.1. In addition, νref = 230 GHz indicates the reference frequency of the reference dust opacity 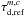 , mH2 describes the mass of a hydrogen molecule, and
, mH2 describes the mass of a hydrogen molecule, and 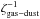 describes the dust to gas ratio and is set here to (1/100) (Hillebrand 1983). The equation is valid for dust and gas well mixed.
describes the dust to gas ratio and is set here to (1/100) (Hillebrand 1983). The equation is valid for dust and gas well mixed.
The optical depth 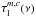 of all lines for each molecule m and component c is described as14
of all lines for each molecule m and component c is described as14![\begin{eqnarray} \label{myXCLASS:tau} \tau_{\rm l}^{m,c}(\nu) &=& \sum_t \Bigg[\frac{c_{\rm light}^2}{8 \pi \nu^2} \, A_{\rm ul}^t \, N_{\rm tot}^{m,c} \, \frac{g_{\rm u}^t \, {\rm e}^{-E_{\rm l}^t/k_{\rm B} \, T_{\rm ex}^{m,c}}}{Q \left(m, T_{\rm ex}^{m,c} \right)} \left(1 - {\rm e}^{-h \, \nu^t /k_{\rm B} \, T_{\rm ex}^{m,c}} \right) \nonumber\\ && \quad \times \phi^{m,c,t}(\nu)\Bigg], \end{eqnarray}](/articles/aa/full_html/2017/02/aa27203-15/aa27203-15-eq46.png) (8)where the sum with index t runs over all spectral line transitions of molecule m within the given frequency range. The Einstein Aul coefficient15, the energy of the lower state El, the upper state degeneracy gu, and the partition function
(8)where the sum with index t runs over all spectral line transitions of molecule m within the given frequency range. The Einstein Aul coefficient15, the energy of the lower state El, the upper state degeneracy gu, and the partition function 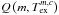 of molecule m are taken from the embedded SQLite3 database, described in Sect. 3. (Because the database usually does not describe the partition functions at the given excitation temperature
of molecule m are taken from the embedded SQLite3 database, described in Sect. 3. (Because the database usually does not describe the partition functions at the given excitation temperature 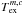 , the value of
, the value of 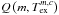 is computed from a linear interpolation. With the new catalog, extrapolation should not be necessary for most conditions encountered in molecular cores.) In addition, the values of the excitation temperatures
is computed from a linear interpolation. With the new catalog, extrapolation should not be necessary for most conditions encountered in molecular cores.) In addition, the values of the excitation temperatures 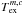 and the column densities
and the column densities 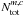 for the different components and molecules are taken from the user defined molfit file, see Sect. 2.1.
for the different components and molecules are taken from the user defined molfit file, see Sect. 2.1.
In order to take broadening of lines caused by the thermal motion of the gas particles and micro-turbulence into account we assume in Eq. (8)a normalized Gaussian line profile, that is, 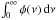 = 1, for a spectral line t:
= 1, for a spectral line t: 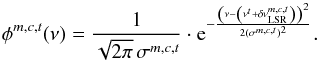 (9)The source frequency
(9)The source frequency 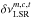 for each component c of a molecule m is related to the user defined velocity offset
for each component c of a molecule m is related to the user defined velocity offset 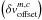 taken from the aforementioned molfit file, by the following expression
taken from the aforementioned molfit file, by the following expression 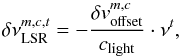 (10)where νt indicates the frequency of transition t taken from the SQLite3 database mentioned above. Additionally, the standard deviation σm,c of the profile is defined by the velocity width
(10)where νt indicates the frequency of transition t taken from the SQLite3 database mentioned above. Additionally, the standard deviation σm,c of the profile is defined by the velocity width 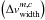 described in the molfit file for each component c of a molecule m:
described in the molfit file for each component c of a molecule m: 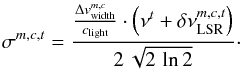 (11)The beam-averaged continuum background temperature
(11)The beam-averaged continuum background temperature 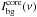 is parametrized as
is parametrized as 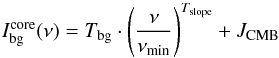 (12)to allow the user to define the continuum contribution for each frequency range, individually. Here, νmin indicates the lowest frequency of a given frequency range. Tbg and Tslope, defined by the user, describe the background continuum temperature and the temperature slope, respectively. Here, the treatment of the dust is not entirely self-consistent. To amend that, we would need to define the sub-beam scale structure of the source, which we consider to be outside the scope of the current effort, although it is envisioned to provide this as an option in the future.
(12)to allow the user to define the continuum contribution for each frequency range, individually. Here, νmin indicates the lowest frequency of a given frequency range. Tbg and Tslope, defined by the user, describe the background continuum temperature and the temperature slope, respectively. Here, the treatment of the dust is not entirely self-consistent. To amend that, we would need to define the sub-beam scale structure of the source, which we consider to be outside the scope of the current effort, although it is envisioned to provide this as an option in the future.
In Eq. (1), the continuum contribution is described through the source function Sm,c(ν), Eq. (5), by an effective dust temperature 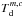 (through
(through 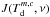 ) for each component which is given by
) for each component which is given by 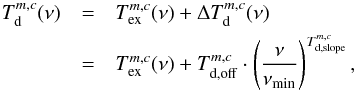 (13)where
(13)where 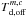 and
and 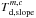 can be defined by the user for each component in the molfit. If
can be defined by the user for each component in the molfit. If 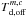 and
and 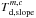 are not defined for a certain component, we assume
are not defined for a certain component, we assume 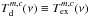 for all components. For a physical (γ ≡ 1) description of the background intensity, see Eq. (5), the user can define the dust opacity, Eq. (7), and dust temperature, Eq. (13), for each component.
for all components. For a physical (γ ≡ 1) description of the background intensity, see Eq. (5), the user can define the dust opacity, Eq. (7), and dust temperature, Eq. (13), for each component.
Finally, the last term JCMB in Eq. (1)describes the OFF position for single dish observations, where we have an intensity caused by the cosmic background JCMB. For interferometric observations, the contribution of the cosmic background is filtered out and has to be subtracted as well.
In contrast to core layers, foreground components may interact with each other, as shown in Fig. 2, where absorption takes places only, if the excitation temperature for the absorbing layer is lower than the temperature of the background.
Hence, the solution of the radiative transfer equation for foreground layers can not be given in a form similar to Eq. (1). Foreground components have to be considered in an iterative manner. The solution of the radiative transfer equation for foreground layers can be expressed as 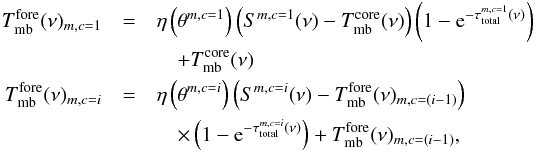 (14)where m indicates the index of the current molecule and i represents an index running over all foreground components c of all molecules. Additionally, we assume that each foreground component covers the whole beam, that is,
(14)where m indicates the index of the current molecule and i represents an index running over all foreground components c of all molecules. Additionally, we assume that each foreground component covers the whole beam, that is, 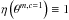 for all foreground layer. Thus, Eq. (14)simplifies to
for all foreground layer. Thus, Eq. (14)simplifies to ![\begin{eqnarray} \label{myXCLASS:modelAbsFinal} T_{\rm mb}^{\rm fore}(\nu)_{m,c=1} &=& \Big[ S^{m,c=1}(\nu) \left(1 - {\rm e}^{-\tau_{\rm total}^{m,c=1}(\nu)}\right) + T_{\rm mb}^{\rm core}(\nu) {\rm e}^{-\tau_{\rm total}^{m,c=1}(\nu)}\Big] \nonumber\\ T_{\rm mb}^{\rm fore}(\nu)_{m,c=i} &=& \Big[S^{m,c=i}(\nu) \left(1 - {\rm e}^{-\tau_{\rm total}^{m,c=i}(\nu)}\right) \nonumber\\ && \quad + T_{\rm mb}^{\rm fore}(\nu)_{m,c=(i-1)} {\rm e}^{-\tau_{\rm total}^{m,c=i}(\nu)}\Big], \end{eqnarray}](/articles/aa/full_html/2017/02/aa27203-15/aa27203-15-eq77.png) (15)where
(15)where 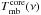 describes the core spectrum, see Eq. (1), including the beam-averaged continuum background temperature
describes the core spectrum, see Eq. (1), including the beam-averaged continuum background temperature 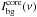 . For foreground lines the contribution by other components is considered by first calculating the contribution of core objects and then use this as new continuum for foreground lines reflecting the fact that cold foreground layers are often found in front of hotter emission sources. We assume, that the cosmic background describes together with the core components one end of a stack of layers. Additionally, the foreground components are located between this plane and the telescope, see Fig. 2. The total column density
. For foreground lines the contribution by other components is considered by first calculating the contribution of core objects and then use this as new continuum for foreground lines reflecting the fact that cold foreground layers are often found in front of hotter emission sources. We assume, that the cosmic background describes together with the core components one end of a stack of layers. Additionally, the foreground components are located between this plane and the telescope, see Fig. 2. The total column density 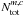 depends on the abundance of a certain molecule and on the thickness of a layer containing the molecule. The order of components along the line of sight is defined by the occurrence of a certain foreground component in the molfit file.
depends on the abundance of a certain molecule and on the thickness of a layer containing the molecule. The order of components along the line of sight is defined by the occurrence of a certain foreground component in the molfit file.
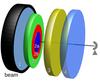 |
Fig. 2 Sketch of a distribution of core and foreground layers within the Gaussian shaped beam of the telescope (black ring). Here, we assume three different core components 2a, 2b, and 2c located in a plane perpendicular to the line of sight which lies in front of the background layer 1 with intensity |
By fitting all species and their components at once, line blending and optical depth effects are taken into account. The modeling can be done simultaneously with isotopologues (and higher vibrational states) of a molecule assuming an isotopic ratio stored in the so-called iso ratio file, see Sect. 2.2. Here, all parameters are expected to be the same except the column density which is scaled by one over the isotopic ratio for each isotopologue.
 |
Fig. 3 myXCLASS function used to calculate a spectrum for three different step sizes. |
In order to correctly take instrumental resolution effects into account in comparing the modeled spectrum with observations myXCLASS integrates the calculated spectrum over each channel. Thereby, myXCLASS assumes that the given frequencies ν describe the center of each channel, respectively. This is particularly important if the instrumental channel width is in the order of, or even larger, than intrinsic line widths. The resulting value is than given as 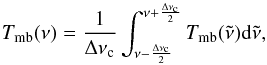 (16)where Δνc represents the width of a channel. Due to the complexity of Eqs. (1)and (15)the integration in Eq. (16)can not be done analytically. Therefore, myXCLASS performs a piecewise integration of each component and channel using the trapezoidal rule and sums up the resulting values to get the final value used in Eq. (16). Internal resampling guarantees that even if the line width is smaller than the channel width the integration is done correctly, see Fig. 3.
(16)where Δνc represents the width of a channel. Due to the complexity of Eqs. (1)and (15)the integration in Eq. (16)can not be done analytically. Therefore, myXCLASS performs a piecewise integration of each component and channel using the trapezoidal rule and sums up the resulting values to get the final value used in Eq. (16). Internal resampling guarantees that even if the line width is smaller than the channel width the integration is done correctly, see Fig. 3.
2.1. The molfit file
Within the molfit file the user defines both which molecules are taken into account and the number of components for each molecule. Additionally, the user has to define for each component the source size θm,c in arcsec (size), the excitation temperature Tex in K (T_ex), the column density Ntot in cm-2 (N_tot), the velocity width (FWHM) Δν in km s-1 (V_width), the velocity offset in km s-1 (V_off), which is via Eq. (10)connected to the source velocity νLSR, and the flag (CFFlag) indicating if a component is considered for core c or foreground f. The definition of the source size θm,c for a foreground component will be ignored, because we assume that all foreground layers cover the whole beam. So, the definition of this parameter is not necessary.
Example of a molfit file:
CS;v=0; 3 48.47 80.00 3.91E+17 2.86 -20.56 c 21.80 51.03 6.96E+17 8.07 30.68 c 81.70 68.11 1.46E+17 5.16 -10.12 cHCS+;v=0; 2 150.00 1.10E+18 5.00 -0.15 f 200.00 2.20E+17 3.10 -2.15 fThe definition of parameters for a molecule starts with a line describing the name of the molecule, which must be identical to the name of the molecule included in the database, see Sect. 3, followed by the number of components N for this molecule. The following N lines describe the parameters for each components, separately. Generally, all parameters have to be separated by blanks, comments are marked with the % character.
In order to define the dust temperature for each component, the molfit file has to contain two additional columns between columns V_off and CFFlag, describing the parameters 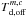 and
and 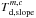 , Eq. (13), respectively.
, Eq. (13), respectively.
Additionally, the myXCLASS program allows to define a hydrogen column density NH (in cm-2), dust mass opacity κνref (in cm2 g-1), and the spectral index β for each component or globally, that is, 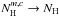 ,
, 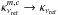 , and βm,c → β. In order to define these parameters individually for each component, the molfit file has to contain additional columns on the left side of column CFFlag.
, and βm,c → β. In order to define these parameters individually for each component, the molfit file has to contain additional columns on the left side of column CFFlag.
For globally defined dust parameters, the myXCLASS program assumes that all core components do not contain dust except the core component with the largest beam filling factor, see Eq. (2). This avoids an overestimation of the dust contribution caused by the overlap of the core components.
2.2. The iso ratio file
As mentioned above, the myXCLASS program offers the possibility to define isotopologues of a molecule and their abundance ratios to reduce the number of input parameters. For that purpose the user has to create an iso ratio file which consists of three columns, where the first two columns indicates the isotopologue and the corresponding molecule, respectively. The third column defines the assumed isotopic ratio. The columns are separated by blanks and comments are marked with the % character.
Example of an iso ratio file:
S-33-O2;v=0; SO2;v=0; 30.0S-34-O2;v=0; SO2;v=0; 5.0SO2;v2=1; SO2;v=0; 1.0SOO-17;v=0; SO2;v=0; 750.0SOO-18;v=0; SO2;v=0; 500.0Here, we assume that the abundance of molecule "SO2;v=0;" is 30 times higher than the abundance of its isotopologue "S-33-O2;v=0;".
2.3. The myXCLASS function
The myXCLASS function calculates a synthetic spectrum for a user defined frequency range, see Fig. 4. The function returns the calculated myXCLASS spectrum, a list of all transition frequencies within the defined range, and the intensities and optical depths for each molecule and component as python arrays, which can be used for further analysis. An example call of the myXCLASS function is given in Appendix A.2.
 |
Fig. 4 myXCLASS function used to model HIFI data of Sgr B2m (black) using SO2 (with three different components), SO (with one component), and HNO (with one component). The intensities of each component are shown in the bottom half. |
3. Database
The XCLASS interface contains a SQLite3 database including spectroscopic data from CDMS (Müller et al. 2001, 2005) and JPL (Pickett et al. 1998). Data can be retrieved and updated via VAMDC, which is an interoperable e-Infrastructure for the exchange of molecular and atomic data between different databases. In principle, all databases which support the VAMDC standard and which contain the required spectroscopic information can be accessed via myXCLASS. A local database was chosen to be able to run the program without network access. CDMS also provides the latest version of the SQLite3 database, which is updated when new entries to the CDMS or JPL are made. In addition, the XCLASS interface allows in principle to add private entries (e.g., unpublished new spectroscopic data) to the database. New functions which facilitate adding private entries will be included in one of the next releases of the XCLASS package.
The spectroscopic data is stored in two tables: The table partitionfunctions contains the partition functions Q(m,Tex) for more than 1000 molecules for 110 different temperatures between 1.072 and 1000 K, which widely extends the standard range of the CDMS/JPL entries. This feature was deemed desirable because particularly for foreground lines with an excitation temperature Tex of 2.7 K, extrapolation from the canonical values (lowest calculated temperature of the partition function 9.75 K) could be wrong in either direction by large factors. Additonally, the table transitions contains more than 5 415 000 transitions and includes the frequency νt (in MHz) with its uncertainty, the Einstein Aul coefficient (in s-1), the upper state degeneracy gu, the energy of the lower state El (in K), and the quantum numbers for each transition.
Entries in the tables are related by the species name, which are different from the names used in the Splatalogue catalog, for example, we use "HC-13-N;v=0;" instead of "HC(13)N v=0" (Splatalogue). In one of the next releases the Splatalogue names will be usable as well.
Furthermore, the XCLASS interface provides functions to update and manage the myXCLASS database: the function UpdateDatabase updates the existing database file by downloading the latest changes from the databases via VAMDC or by downloading a complete new database file from the CDMS server. The first option adds new entries to the tables and overwrites existing entries with new data. Private entries remain unchanged. The second option is much faster but removes all private entries by overwriting the database file with the most recent file from the CDMS server. In addition the function DatabaseQuery offers the possibility to send an user defined SQL query string to the database, for example, to add private entries or query about species names, content etc. Also, the interface contains functions ListDatabase, see Appendix A.1, and GetTransitions, see Fig. 5, to display information about transitions within an user defined range. The GetTransitions function allows the user to select a region on the displayed spectrum, and prints out all the lines from the catalog around the region selected. Additionally, the function offers the possibility to set filters in frequency and energy range.
 |
Fig. 5 Graphical user interface (GUI) of the GetTransitions function. Here, the user has to define a frequency range by selecting a single frequency in the shown spectrum. This frequency represents the central frequency of the range. The width of the range is given by an user defined parameter. XCLASS prints out informations (name of molecule, transition frequency, uncertainty of transition frequency, Einstein A coefficient, quantum number for lower and upper state, and energy of lower state) of all transitions in the selected molecule list located in the given frequency range, see screen output of ListDatabase described in Appendix A.1. |
4. MAGIX
So far, we have discussed how to use XCLASS to produce synthetic spectra. In fact, what the user usually desires is a description of data that provides a fit to a set of observational data. In many packages, this is done by manually changing the parameters until the fit looks good. In XCLASS, we use an optimizer that provides the parameter set for a given model which best matches the data. Due to the large number of input parameters required by the myXCLASS program it is essential to use a powerful optimization package to achieve a good description of observational data by the myXCLASS program. Therefore, the XCLASS interface contains the MAGIX package (Möller et al. 2013) which is a model optimizer providing an interface between existing codes and an iterating engine. The package attempts to minimize deviations of the model results from observational data, constraining the values of the model parameters and providing corresponding error estimates.
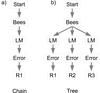 |
Fig. 6 Example of an a) algorithm chain and b) algorithm tree. In both cases, we start with the bees swarm algorithm and use the best a) and the three best results b) as starting values for the Levenberg-Marquardt local optimization algorithm (LM), respectively. Afterwards, we apply the error estimation algorithm (Error) to the result(s) of the Levenberg-Marquardt algorithm. In case of an algorithm chain we get one final result (R1), whereas we get three different results (R1, R2, R3) for an algorithm tree. |
MAGIX offers the possibility to model physical and chemical data using an arbitrary external model program, not only myXCLASS, explore their parameter space and find the set of parameter values that best fits observational data. The goodness of a fit is described by the χ2 distribution which is a function of relative quadratic differences between observational and model values. MAGIX is able to explore the landscape of the χ2 function without the knowledge of starting values. Additionally, MAGIX can calculate probabilities for the occurrence of minima in the χ2 distribution and give information about confidence intervals for the parameters. The package provides optimization through one of the following algorithms or via a combination of several of them (an algorithm chain or tree, see Fig. 6): the Levenberg-Marquardt (conjugate gradient) method, which is fast, but can get stuck in local minima, simulated annealing, which is slower, but more robust against local minima. Other global optimization algorithms, such as bees, genetic, particle swarm optimization, nested sampling, or interval nested sampling algorithms are included as well for exploring the solution landscape, checking for the existence of multiple solutions, and giving confidence ranges. Additionally, MAGIX provides an interface to make several algorithms included in the scipy16 package available.
Using an algorithm chain or tree offers the possibility to send the results of the optimization process performed by one algorithm to another optimization loop through some different algorithm. The simulated annealing as well as the Levenberg-Marquardt algorithm require starting values of the parameters that are not too far from the final solution, otherwise the algorithm might stray so far away from the solution that it never converges, that is, the user has to find an acceptable fit by hand before applying these algorithms produces useful results. Often, the location of the minimum can be guessed with sufficient accuracy to give good starting values, but sometimes one is completely in the dark. Using an algorithm chain or tree, the user can first apply one of the swarm algorithms, for example, the bees or interval nested sampling algorithm, to determine the starting values for the subsequent local optimization algorithm using simulated annealing or the Levenberg-Marquardt algorithm, see Fig. 6a. But MAGIX does not only allow one to use the best but also the second best etc. result of a swarm algorithm as starting values for other algorithms (algorithm tree), see Fig. 6b. Therefore, MAGIX is able to find multiple minima of models.
Since this can, depending on the data set and the number of free parameters, be quite computing intensive, OpenMP and OpenMPI parallelization for simultaneous evaluations of the external program is available for most of the algorithms. In addition to the normal MAGIX package which can be used with an arbitrary external model program, the XCLASS interface contains a further MAGIX version optimized for the usage with the myXCLASS program. This optimized MAGIX version is used by the myXCLASSFit and myXCLASSMapFit (myXCLASSMapRedoFit) functions and we are exploring the use of graphics processing units (GPUs).
Generally, MAGIX is controlled by different XML files: The so-called instance file includes the names, initial values (and ranges) for all model parameters. Additionally, the instance file indicates the parameters which should be optimized by MAGIX. In addition the experimental XML file containing settings for the import of observational data, that is, path(s) and name(s) of the data file(s), format(s), range(s) etc. Furthermore, the algorithm control file, defining the algorithm or algorithm sequence which should be used for the optimization together with the settings for each algorithm.
The new MAGIX function offers the possibility to use MAGIX within CASA with a previously registered external model program. For that purpose, the user has to provide the XML files, described above, and passes their path and file names to the MAGIX function, see Appendix A.3.
In general, XCLASS creates job directories for some functions (MAGIX, myXCLASSFit, and myXCLASSMapFit) where all log and output files are stored. The job directories are created in the XCLASS run directory defined by the environment variable myXCLASSRunDirectory. The name of a job directory contains the date and time of the function execution followed by a unique job number.
5. Other functions
The XCLASS interface for CASA includes two new functions (myXCLASSFit and myXCLASSMapFit) which provide a simplified interface for MAGIX using the myXCLASS program.
The myXCLASSFit function offers the possibility to fit multiple ranges in multiple files from multiple telescopes simultaneously using MAGIX in conjunction with the myXCLASS program. It starts MAGIX using the Levenberg-Marquardt algorithm to optimize the input parameters defined in an extended molfit file to achieve a good description of the observational data. The user has to specify the maximum number of iterations, the path and file name of the observational data file (or of a MAGIX experimental XML file, see Sect. 4), and the path and name of an extended molfit file. In contrast to the molfit file described in Sect. 2.1, the extended molfit file, see Appendix A.4, contains one additional column on the left side of each parameter (except for the core/foreground flag) of each component. The additional column defines the range for each parameter. The definition of ranges guarantees that the fits does not run out of the defined parameter ranges. The limits, that is, the lowest and highest allowed values, for the parameters source size θm,c, column density Ntot, and hydrogen column density NH are determined by 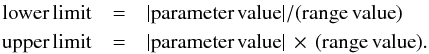 The limits for the other parameters are calculated by simply adding or subtracting the value of the additional column to or from the value itself. All calculated lower limits which are less than zero are set to zero (except for velocity offset). If the range of a certain parameter is set to zero, the corresponding parameter is kept constant and is not optimized by the myXCLASSFit function. Additionally, the myXCLASSFit function offers the possibility to fit the iso ratios in the same fit process as well. For that purpose, the user has to add two additional columns in the iso ratio file on the right side of the third column. The fourth and fifth column defines the lower and upper limit for each iso ratio, respectively. If the lower limit is equal to the upper limit or if the lower limit is higher than the upper limit, the corresponding iso ratio is not optimized by the myXCLASSFit function. In general, the fit procedure stops, if the maximum number of iterations is reached, or if χ2 drops below 10-7 (or an user defined value). Additionally, the myXCLASSFit function offers the possibility to use another algorithm or an algorithm chain or tree by defining the path and name of a MAGIX algorithm XML file, see Sect. 4. Furthermore, the function offers the possibility to fit multiple frequency ranges simultaneously by using a MAGIX experimental XML file, see Sect. 4. Finally, the myXCLASSFit function returns the optimized molfit file from the best fit and the corresponding modeled spectra as python arrays. (Here, the phrase “best fit” is connected to the application of an algorithm chain or tree: using an algorithm chain or tree offers the possibility to use more than one algorithm to fit the data. Each application of an algorithm is connected with a fit represented by a certain χ2 value. The myXCLASSFit function reads in the χ2 values of all optimization loops of all applied algorithm and determines the lowest χ2 value. The result of the “best fit” is than given by the parameter vector which belongs to the lowest χ2 value.)
The limits for the other parameters are calculated by simply adding or subtracting the value of the additional column to or from the value itself. All calculated lower limits which are less than zero are set to zero (except for velocity offset). If the range of a certain parameter is set to zero, the corresponding parameter is kept constant and is not optimized by the myXCLASSFit function. Additionally, the myXCLASSFit function offers the possibility to fit the iso ratios in the same fit process as well. For that purpose, the user has to add two additional columns in the iso ratio file on the right side of the third column. The fourth and fifth column defines the lower and upper limit for each iso ratio, respectively. If the lower limit is equal to the upper limit or if the lower limit is higher than the upper limit, the corresponding iso ratio is not optimized by the myXCLASSFit function. In general, the fit procedure stops, if the maximum number of iterations is reached, or if χ2 drops below 10-7 (or an user defined value). Additionally, the myXCLASSFit function offers the possibility to use another algorithm or an algorithm chain or tree by defining the path and name of a MAGIX algorithm XML file, see Sect. 4. Furthermore, the function offers the possibility to fit multiple frequency ranges simultaneously by using a MAGIX experimental XML file, see Sect. 4. Finally, the myXCLASSFit function returns the optimized molfit file from the best fit and the corresponding modeled spectra as python arrays. (Here, the phrase “best fit” is connected to the application of an algorithm chain or tree: using an algorithm chain or tree offers the possibility to use more than one algorithm to fit the data. Each application of an algorithm is connected with a fit represented by a certain χ2 value. The myXCLASSFit function reads in the χ2 values of all optimization loops of all applied algorithm and determines the lowest χ2 value. The result of the “best fit” is than given by the parameter vector which belongs to the lowest χ2 value.)
 |
Fig. 7 Example of parameter maps created by the myXCLASSMapFit function. Here, the K-ladder structure of the CH3CN(12-11) transition (plus isotopologues) in G75.78+0.34 was fitted at around 220 GHz (observed with the SMA). The temperature gradient is expected as also seen in different NH3 lines (Sanchez-Monge 2011; Sanchez-Monge et al. 2013). |
In addition to the myXCLASSFit function which is useful to fit single spectra, the XCLASS interface for CASA contains the myXCLASSMapFit function which fits one or more complete (FITS) data cubes. Here, the myXCLASSMapFit function reads in the data cube(s), extracts the spectra for each pixel and fits these spectra separately using the Levenberg-Marquardt (or another) algorithm (chain or tree). The optimization procedure for each pixel stops, if the maximum number of iterations is reached, or if the χ2 value drops below 10-7 (or below an user defined value). In analogous to the myXCLASSFit function the fit parameters and their ranges for the myXCLASSMapFit function are defined in an extended molfit (and iso ratio) file as well. Additionally, the myXCLASSMapFit function offers the possibility to limit the fit to certain frequency ranges of a spectrum and to an user defined region of the cube(s). In order to reduce the computation effort, the user can exclude pixels by defining a threshold for the min. intensity of a pixel, that is, if the maximum intensity of a pixel is below the user defined threshold, the corresponding pixel is not fitted by the myXCLASSMapFit function. In general, the myXCLASSMapFit function assumes, that the first three axes of the data cube(s) describe the right ascension, the declination, and the frequency, respectively. If the frequencies are not given in MHz, the FITS header has to contain the definition of the CUNIT3 command which defines the unit of the frequency axis. If more than one data cube is specified in the XML file, the data cubes must describe the same map, that is, covered spatial area and the resolution have to be identical. The different data cubes are allowed to differ only in the frequency axis. At the end of the whole fit procedure, the myXCLASSMapFit function creates FITS images for each free parameter of the best fit, where each pixel corresponds to the value of the optimized parameter taken from the best fit for this pixel, see Fig. 7. Furthermore, the myXCLASSMapFit function creates FITS cubes for each fitted data cube, where each pixel contains the modeled spectrum. Finally, the myXCLASSMapFit function creates one FITS image which describes the quality of the fit for each pixel. Here, each pixel corresponds to the χ2 value of the best fit for this pixel. Applications of this are temperature maps, but also first and second moment maps, which are based on the simultaneous fitting of many lines, and are fairly robust against line confusion and blending of single lines.
In order to improve the results of a previous application of the myXCLASSMapFit function the XCLASS interface contains the myXCLASSMapRedoFit function which offers the possibility to redo one or more so-called pixel fits of a previous myXCLASSMapFit run. The function performs fits for the selected pixels and recreates the different parameter maps using the new optimized parameter values.
6. Example application
 |
Fig. 8 Result of the spectral line survey of the high-mass star-forming region Orion KL between 325 to 360 GHz using the myXCLASSFit function. Here, we used 24 molecules in conjunction with 245 isotopologues. In panel a) the whole spectral line survey (back) is shown together with the result of myXCLASSFit function (red). Panels b), c) and d) show fit examples around 332.5 GHz, 338.15 GHz, and 358.0 GHz, respectively. |
The XCLASS interface for CASA was used to redo the analysis of the spectral line survey of the high-mass star-forming region Orion KL from 325 to 360 GHz as reported by Schilke et al. (1997), which was done without using the myXCLASS program nor optimization packages like MAGIX.
In our fit, shown in Fig. 8, we used the following 25 molecules: C2H3CN, C2H5CN, CCH, CH3CCH, CH3CN, CH3OCH3, CH3OCHO, CH3OH, CN, CO, CS, H2CO, H2CS, H2O, HCCCN, HCN, HCO+, HCS+, HDO, HNCO, NO, OCS, SiO, SO2, and SO. The different molecules were described by 44 components in total, see Table 1. Additionally, we have taken 241 isotopologues and higher vibrated states into account where we assumed the following ratios: [12C]/[13C] = 45 (Crockett et al. 2014a), [16O]/[18O] = 250 (Crockett et al. 2014a), [16O]/[17O] = 2625 (Tercero et al. 2010), [32S]/[33S] = 75 (Crockett et al. 2014a), [32S]/[34S] = 22.5 (Schilke et al. 1997), [14N]/[15N] = 234 (Crockett et al. 2014a), [28Si]/[29Si] = 20 (Schilke et al. 1997), and [28Si]/[30Si] = 30 (Anders & Grevesse 1989). In order to reduce the computational effort, we assumed a ratio of one for all vibrational excited transitions, that is, we used the same column densities as for the corresponding molecules.
Additionally, we were able to (partly) identify 35 of the 57 unidentified lines (U-lines) reported by Schilke et al. (1997), see Table 2. Here, we marked an unidentified line as (partly) identified, if the modeled integrated intensity of a component 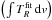 covers at least 10% of the integrated line intensity
covers at least 10% of the integrated line intensity 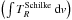 . We note that, the majority of the unidentified lines contain contributions from more than one component. Contributions of more than 100% are caused by inaccuracies in the fit. For 19 U-lines the modeled spectrum describes less than 50% of the integrated line intensity. Nevertheless, we are able to (partly) describe all unidentified lines, except the line at 348 358 MHz, with an integrated line intensity of more than 10 K km s-1. The improved identification may caused by an updated and enhanced line catalog.
. We note that, the majority of the unidentified lines contain contributions from more than one component. Contributions of more than 100% are caused by inaccuracies in the fit. For 19 U-lines the modeled spectrum describes less than 50% of the integrated line intensity. Nevertheless, we are able to (partly) describe all unidentified lines, except the line at 348 358 MHz, with an integrated line intensity of more than 10 K km s-1. The improved identification may caused by an updated and enhanced line catalog.
In the following we compare our fit results, given in Table 1, with those reported by Schilke et al. (1997). Our calculated errors describe the 2σ credibility interval for each parameter, respectively. Large asymmetric error ranges for some column densities (e.g., SO) are caused by the fact that some lines start to become optically thick which prevents an accurate parameter estimation. For these lines we can only determine lower limits of the corresponding column densities.
Fit results of the molfit file parameters used for the Orion-KL model.
New identified lines.
In contrast to Schilke et al. (1997) we were not able to identify NH2CHO, C2H5OH, and HCOOH because of their weak lines which do not allow a distinct estimation of their contribution to the given spectrum. But we took CCH, CN, and NO into account.
Our derived excitation temperatures and beam averaged column densities for H2CS and CH3OCHO agree (within the given error ranges) with Schilke’s result. In order to achieve a good description for HCCCN, HDO, and OCS we used two components, respectively. For HCCCN and HDO we find that the second components show similar temperatures and column densities compared to Schilke’s results. Due to the large error ranges for OCS we are not able to identify the corresponding component for Schilke’s result although the temperatures as well as column densities are comparable within the given error ranges.
Additionally, we used H2CO with two components instead of H CO with one component. Using the aforementioned isotopologue ratio of [12C]/[13C] = 45 we find that the temperature and column density for the first component of H2CO agree with those described by Schilke et al. (1997).
CO with one component. Using the aforementioned isotopologue ratio of [12C]/[13C] = 45 we find that the temperature and column density for the first component of H2CO agree with those described by Schilke et al. (1997).
As shown in Table 1, we used three components to describe the contribution of CH3OH and SO2. Schilke’s result for CH3OH corresponds to our second component whereas the excitation temperature and beam averaged column density for the first component of SO2 agree with those reported by Schilke et al. (1997). Furthermore, the described temperatures and column densities (after scaling with the isotopologue ratios, mentioned above) for 34SO2 match our results nicely. For 33SO2 the derived excitation temperature do not coincide with Schilke’s result.
In order to model the contribution of HNCO we used only two instead of four components. We see that the temperatures and column densities of Schilke’s first, third, and fourth component match our results for the first component. But, the column density of Schilke’s second component clearly does not agree with our column density for the second component although the excitation temperatures are comparable.
Although we find similar results for the majority of molecules we derived different excitation temperatures for CH3CN, CH3CCH, SO, CH3OCH3, C2H3CN, and C2H5CN. In contrast to CH3CCH, SO, C2H3CN, C2H5CN, and CH3OCH3 where we find discrepancies with less than 24 K we find a striking difference for CH3CN. Already Schilke et al. (1999) noticed that the value of 445 K based on rotation diagram analysis was wrong due to a neglect of the line opacity. They presented a corrected fit using the opacities derived from CH3CN/CH CN, yielding 160 K, which differs from the present value because (i) a [12C]/[13C] ratio of 60 (instead of 45) was used then – which increases the correction due to opacity; and (ii) the correction was done by hand, not taking the individual lines as well into account as the present study. Not taking into account the opacities also underestimates the column density, by an order of magnitude in the present case. Additionally, we derived a column density for CH3CCH which is nearly an order of magnitude higher than Schilke’s result.
CN, yielding 160 K, which differs from the present value because (i) a [12C]/[13C] ratio of 60 (instead of 45) was used then – which increases the correction due to opacity; and (ii) the correction was done by hand, not taking the individual lines as well into account as the present study. Not taking into account the opacities also underestimates the column density, by an order of magnitude in the present case. Additionally, we derived a column density for CH3CCH which is nearly an order of magnitude higher than Schilke’s result.
For optically thin, unblended lines (like for H2S and CH3OCHO), the rotation diagram method gives the same results as the XCLASS fit, but requires more effort through manual fitting of all lines. High opacities, while they can be corrected in rotation diagrams (Schilke et al. 1997; Goldsmith & Langer 1999), this is very cumbersome to do by hand, and is much more robustly achieved through the use of XCLASS – in this data set, CH3CN and CH3OH are prominent examples. Lastly, the identification of species with weak features is only possible reliably in line-rich spectra if all the other species are modeled as well, as can be seen by the XCLASS fits reported in Belloche et al. (2008, 2009, 2013). All this together with the capability of producing credibility intervals demonstrates that the methods of XCLASS give much more accurate and reliable results than those achieved with rotational diagram methods.
7. Conclusions
We presented the XCLASS interface for CASA which provides powerful new functions for the CASA distribution for analyzing spectral surveys. The toolbox includes the myXCLASS program which models observational data by solving the radiative transfer equation for an isothermal object in one dimension (detection equation). The myXCLASS program is able to model a huge number of molecules simultaneously, whereat the contribution of each molecule can be described by an arbitrary number of components. These can usually be distinguished by different radial velocities and do not interact with each other radiatively but superimpose in the model. The myXCLASS program depends on a number of parameters, which are partially taken from an embedded SQLite3 database containing entries from CDMS and JPL through the VAMDC portal. The other input parameters are read from an user defined ASCII file containing parameters for each molecule and component. In order to achieve a reasonable description of observational data one has to partially optimize the user defined parameters. For that purpose the toolbox contains an interface for the model optimizer package MAGIX, which helps to find the best description of the data using a certain model, that is, finding the parameter set that most closely reproduces the data. Therefore, the toolbox provides two functions to model one or more single spectra or data cubes simultaneously using the myXCLASS program in conjunction with one of the optimization algorithms (or combinations of them in an algorithm chain or tree) included in the MAGIX package. The combination of myXCLASS and MAGIX prepare the way for an automatic line identification routine which is essential for a spectral survey on large spectral cubes produced by ALMA. Additionally, the MAGIX package offers the possibility to apply more elaborate programs (such as LIME) to model astronomical data as well.
Enhancements are being worked on a 3d version for defining sub-beam structure. Additionally, we work on an automatic line identification function for XCLASS, which will be described in a subsequent paper.
A derivation of the expression can be found in Appendix B.1.
A derivation of the expression is given in Appendix B.3.
Acknowledgments
The authors would like to thank Anika Schmiedeke, Álvaro Sánchez-Monge, and Alexander Zernickel for intensive testing and helpful suggestions. We acknowledge funding from BMBF/Verbundforschung through the Projects ALMA-ARC 05A11PK3 and 05A14PK1.
References
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Belloche, A., Menten, K. M., Comito, C., et al. 2008, A&A, 482, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Garrod, R. T., Müller, H. S. P., et al. 2009, A&A, 499, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Müller, H. S. P., Menten, K. M., et al. 2013, A&A, 559, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brinch, C., & Hogerheijde, M.R. 2010, A&A, 523, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Comito, C., Schilke, P., Phillips, T. G., et al. 2005, ApJS, 156, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Crockett, N., Bergin, E., Neill, J., et al. 2014a, ApJ, 787, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Crockett, N., Bergin, E., Neill, J., et al. 2014b, ApJ, 781, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P.F., & Langer, W.D., 1999, ApJ, 517, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Hillebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
- Maret, S., Hily-Blant, P., Pety, J., et al. 2011, A&A, 526, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Data Analysis Software and Systems XVI, eds. R. A. Shaw, F. Hill, & D. J. Bell (San Francisco, CA: ASP), ASP Conf. Ser., 376, 127 [Google Scholar]
- Möller, T., Bernst, I., Panoglou, D., et al. 2013, A&A, 549, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Neill, J. L., Bergin, E. A., Lis, D. C., Schilke, P., et al. 2014, ApJ, 789, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spectr. Radiat. Transf., 60, 883 [Google Scholar]
- Sanchez-Monge, A. 2011, Ph.D. Thesis, Universitat de Barcelona [Google Scholar]
- Sanchez-Monge, A., Kurtz, S., Palau, A., et al. 2013, ApJ, 766, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Schilke, P., Groesbeck, T. D., Blake, G. A., & Phillips, T. G., et al. 1997, ApJS, 108, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Schilke, P., Phillips, T. G., & Mehringer, D. M. 1999, in The Physics and Chemistry of the Interstellar Medium, Proc. of the 3rd Cologne-Zermatt Symp., held in Zermatt, September 22–25, eds. V. Ossenkopf, J. Stutzki, & G. Winnewisser (GCA-Verlag Herdecke) [Google Scholar]
- Schilke, P., Attallah, F., Beckert, K., et al. 2001, ApJS, 132, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Stahler, S. W., & Palla, F. 2005, The Formation of Stars (Wiley-VCH) [Google Scholar]
- Tercero, B., Cernicharo, J., Pardo, J. R., & Goicoechea, J. R. 2010, A&A, 517, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van der Tak, F. F. S., Black, J. H., Schier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zernickel, A., Schilke, P., Schmiedeke, A., et al. 2012, A&A, 546, 87 [Google Scholar]
Appendix A: Examples
Appendix A.1: ListDatabase function
This function reads in entries from the table transitions, see Sect. 3, located in the SQLite3 database file and prints out the contents (name of molecule, quantum number for lower and upper state, transition frequency, uncertainty of transition frequency, Einstein A coefficient, and energy of lower state) to the screen or file (defined by the input parameter OutputDevice). The user can limit the output by defining a minimum and maximum for the frequency (or for the lower energy) for the transitions or by selecting one or more molecule(s) by using the input parameter SelectMolecule.
Input within CASA:
FreqMin = 20000.0
FreqMax = 990000.0
ElowMin = 100.0
ElowMax = 2000.0
SelectMolecule = ["CO;v=0;"]
OutputDevice = ""
Contents = ListDatabase()
Screen output (shortened):
Name: upper state: lower state: Freq. [MHz]: Error Freq. [MHz]: Einstein A[s-1]: E_low [K]:
CO;v=0; X;v=0;J=7; X;v=0;J=6; 806651.80600 5.0000e-03 3.422e-05 115.354
CO;v=0; X;v=0;J=8; X;v=0;J=7; 921799.70000 5.0000e-03 5.134e-05 153.798
Appendix A.2: myXCLASS function
The function calculates a spectrum based on a user defined molfit file described in Sect. 2.1. The function returns the modeled spectrum as well as the intensities and optical depths for each component.
In the example described below, we use the molfit file CH3OH__pure.molfit located in “demo/myXCLASS/” to create a spectrum between 580 102.0 and 580 546.5 MHz with a step size of 0.5 MHz. Additionally, we use global definitions for Tbg, Tslope, NH, κνref, and β (indicated by t_back_flag = T and nH_flag = T). Furthermore, we use the iso ratio file iso_names.txt and set the diameter of the telescope to 3.5 m. In addition, we set the rest frequency to 0.0 MHz with a reference velocity of 0 km s-1. The output parameter modeldata contains the modeled spectrum described by a python array with two columns, where the first column indicates the frequencies (in MHz) and the second column the corresponding intensities (in K). For a rest frequency unequal zero, the myXCLASS function adds a further column to parameter modeldata describing the velocities (in km s-1).
The output parameter log contains some informations about the calculation and parameter trans describes the transition frequencies of all molecules used in the molfit file within the given frequency range. The intensities and optical depths for each component and molecule is stored in parameter IntOptical. Finally, parameter jobDir indicates the path and name of the corresponding job directory containing all files produced during the calculation process. We note that the user is free to define other names for the output parameters.
Input within CASA:
FreqMin = 580102.0 FreqMax = 580546.5 FreqStep = 5.0000000000E-01 TelescopeSize = 3.5 Inter_Flag = F t_back_flag = T tBack = 1.1 tslope = 0.0000000000E+00 nH_flag = T N_H = 3.0000000000E+24 beta_dust = 2.0 kappa_1300 = 0.02 MolfitsFileName = "demo/myXCLASS/CH3OH__pure.molfit" iso_flag = T IsoTableFileName = "demo/myXCLASS/iso_names.txt" RestFreq = 0.0 vLSR = 0.0 modeldata, log, TransEnergies, IntOptical, jobDir = myXCLASS()
Appendix A.3: MAGIX function
The function starts the MAGIX program. The user has to define the paths and names of the registration, instance, experimental, and algorithm xml file, respectively. The parameter MAGIXOption indicates if informations are printed to screen (None) or not (quiet). The results, that is, the optimized instance file(s) etc., are stored in a job directory described by parameter JobDir, mentioned above.
Input within CASA:
MAGIXExpXML = "demo/MAGIX/TwoOscillators_RefFit_R.xml" MAGIXInstanceXML = "demo/MAGIX/parameters.xml" MAGIXFitXML = "demo/MAGIX/Levenberg-Marquardt_Parameters.xml" MAGIXRegXML = "Fit-Functions/Drude-Lorentz_conv/xml/" MAGIXRegXML += "Conventional_Drude-Lorentz.xml" MAGIXOption = "" JobDir = MAGIX()
Appendix A.4: myXCLASSFit function
This function provides a simplified interface for MAGIX using the myXCLASS program. The function returns the contents of the molfit file containing the parameters for the best fit and the corresponding model function values for each data point.
Here we fit observational data stored in file band1b.dat using the molfit file CH3OH__old.molfit, see below, without isotopologues (indicated by iso_flag = F) and the Levenberg-Marquardt algorithm with maximum ten iterations.
Input within CASA:
NumberIteration = 10
MolfitsFileName = "demo/myXCLASSFit/CH3OH__old.molfit"
experimentalData = "demo/myXCLASSFit/band1b.dat"
TelescopeSize = 3.5
Inter_Flag = F
t_back_flag = T
tBack = 1.1
tslope = 0.0000000000E+00
nH_flag = T
N_H = 3.0000000000E+24
beta_dust = 2.0
kappa_1300 = 0.02
iso_flag = F
IsoTableFileName = ""
RestFreq = 0.0
vLSR = 0.0
newmolfit, modeldata, JobDir = myXCLASSFit()
Extended molfit file CH3OH__old.molfit used in the example described above:
CH3OH;v=0; 1
% limit: s_size: limit: T_rot: limit: N_tot: limit: V_width: limit: V_off: CFFlag:
10.00 1.153 50.00 115.1219 50.00 1.648e+17 10.00 7.463 0.00 -7.900 c
Appendix A.5: myXCLASSMapFit function
The myXCLASSMapFit function uses the myXCLASS program in conjunction with MAGIX to fit complete data cubes instead of single spectra. In the example described below, we fit a part of the FITS cube Orion.methanol.cbc.contsub.image.fits described by the region file region__box__ds9.reg. (In order to fit the whole data cube, the parameter regionFileName has to be cleared, that is, regionFileName = "".) Here, we set the threshold to 0.001, that is, we fit all pixels which have a maximum intensity of 0.001 K (or higher). Additionally, we use the molfit file CH3OH.molfit together without an iso ratio file and set the diameter of the telescope to 3.5 m. Furthermore, we use the Levenberg-Marquardt algorithm with maximum 15 iterations for each pixel fit. In order to use another algorithm (or algorithm combination) the parameter AlgorithmXMLFile has to describe the path and name of a MAGIX algorithm XML file. The myXCLASSMapFit function returns the path and the name of the job directory described by parameter JobDir containing subdirectories for each pixel fit and the parameter FITS images.
Input within CASA:
NumberIteration = 15
AlgorithmXMLFile = "demo/myXCLASSMapFit/algorithm-settings.xml"
MolfitsFileName = "demo/myXCLASSMapFit/CH3OH__new.molfit"
experimentalData = "demo/myXCLASSMapFit/Orion.methanol.cbc.contsub.image.fits"
regionFileName = "demo/myXCLASSMapFit/ds9_phys.reg"
FreqMin = 0.0
FreqMax = 0.0
TelescopeSize = 3.5
Inter_Flag = F
t_back_flag = T
tBack = 9.5000000000E-01
tslope = 0.0000000000E+00
nH_flag = T
N_H = 3.0000000000E+24
beta_dust = 1.4
kappa_1300 = 0.02
iso_flag = F
IsoTableFileName = ""
RestFreq = 0.0
vLSR = 0.0
Threshold = 0.001
UsePreviousResults = T
clusterdef = "demo/myXCLASSMapFit/clusterdef.txt"
JobDir = myXCLASSMapFit()
Appendix A.6: myXCLASSMapRedoFit function
This function offers the possibility to improve the result of a previous performed myXCLASSMapFit run using another molfit file and/or other algorithms.
In the example given below, the myXCLASSMapRedoFit function will re-fit the pixels (83.201,-15.1345) and (83.111,-15.221) of the previous myXCLASSMapFit run with job number 1234 using the molfit file "CH3OH.molfit".
Input within CASA:
JobNumber = 1234
PixelList = [[83.201, -15.1345], [83.111, -15.221]]
NumberIteration = 10
AlgorithmXMLFile = ""
MolfitsFileName = "demo/myXCLASSMapFit/CH3OH.molfit"
experimentalData = ""
Threshold = 0.0
FreqMin = 0.0
FreqMax = 0.0
t_back_flag = T
tBack = 9.5000000000E-01
tslope = 0.0000000000E+00
nH_flag = T
N_H = 3.0000000000E+24
beta_dust = 2.0
kappa_1300 = 0.02
iso_flag = T
IsoTableFileName = "demo/myXCLASSMapFit/iso_names.txt"
RestFreq = 0.0
vLSR = 0.0
myXCLASSMapRedoFit()
Appendix B: Derivations
Appendix B.1: Detection equation
In absence of scattering, the radiative transfer equation 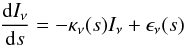 (B.1)describes the propagation of radiation which passes through a medium. During the propagation photons are absorbed and emitted indicated by the emission and absorption coefficients ϵν and κν, respectively.
(B.1)describes the propagation of radiation which passes through a medium. During the propagation photons are absorbed and emitted indicated by the emission and absorption coefficients ϵν and κν, respectively.
The optical depth τν(s) which measures the distance in units of the mean free path, is given by 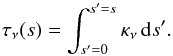 (B.2)By using the source function
(B.2)By using the source function 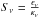 , the radiative transfer equation can be expressed as
, the radiative transfer equation can be expressed as 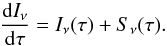 (B.3)Within the local thermodynamic equilibrium (LTE) the source function is described by Planck’s law for black body radiation Bν(T).
(B.3)Within the local thermodynamic equilibrium (LTE) the source function is described by Planck’s law for black body radiation Bν(T).
Integrating Eq. (B.3)over τ leads to 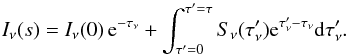 (B.4)Assuming a constant source function, that is, constant emission and absorption coefficients through the medium, the transfer equation can be written as
(B.4)Assuming a constant source function, that is, constant emission and absorption coefficients through the medium, the transfer equation can be written as 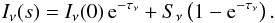 (B.5)Additionally, we have to take into account that the different components may not cover the whole beam, that is, that the background behind a certain component might contribute as well. So, we have to extend Eq. (B.5)by introducing the beam filling factor η, Eq. (2), which describes the fraction of the beam covert by a component
(B.5)Additionally, we have to take into account that the different components may not cover the whole beam, that is, that the background behind a certain component might contribute as well. So, we have to extend Eq. (B.5)by introducing the beam filling factor η, Eq. (2), which describes the fraction of the beam covert by a component ![\appendix \setcounter{section}{2} \begin{equation} \label{DE:finalExt} I_{\nu}(s) = \eta \, \left[I_{\nu}(0) \, {\rm e}^{-\tau_{\nu}} + S_{\nu} \left(1 - {\rm e}^{-\tau_{\nu}} \right)\right] + \left(1 - \eta\right) \, I_{\nu}(0). \end{equation}](/articles/aa/full_html/2017/02/aa27203-15/aa27203-15-eq335.png) (B.6)Here, the term ηIν(0) e− τν indicates the attenuated radiation from the background Iν(0). The second term ηSν(1−e− τν) describes the self attenuated radiation emitted by a certain component. Finally, the last term (1−η) Iν(0) represents the contribution of the background which is not covert by a component.
(B.6)Here, the term ηIν(0) e− τν indicates the attenuated radiation from the background Iν(0). The second term ηSν(1−e− τν) describes the self attenuated radiation emitted by a certain component. Finally, the last term (1−η) Iν(0) represents the contribution of the background which is not covert by a component.
In real observations, we do not measure absolute intensities but only differences of intensities, that is, we have to subtract the OFF-position for single dish observations from Eq. (B.6)as well, where we have an intensity caused by the cosmic background JCMB. So, we achieve ![\appendix \setcounter{section}{2} \begin{eqnarray} \label{DE:FinalEq} I_{\nu}(s) &=& \eta \, \left[I_{\nu}(0) \, {\rm e}^{-\tau_{\nu}} + S_{\nu} \left(1 - {\rm e}^{-\tau_{\nu}} \right)\right] + \left(1 - \eta\right) \, I_{\nu}(0) - J_\mathrm{CMB}\nonumber\\ &=& \eta \, \left[\left(S_{\nu} - I_{\nu}(0)\right)\left(1 - {\rm e}^{-\tau_{\nu}} \right)\right] + I_{\nu}(0) - J_\mathrm{CMB}. \end{eqnarray}](/articles/aa/full_html/2017/02/aa27203-15/aa27203-15-eq340.png) (B.7)
(B.7)
Appendix B.2: Beam filling factor
 |
Fig. B.1 a) A single two-dimensional Gaussian function, Eq. (B.8), with σx = σy = 1.9 and μx = μy = 0 representing a Gaussian beam of a telescope. b) Cut through the Gaussian function described in a) at half height. c) A single two-dimensional Gaussian function, with σx = σy = 1.1 and μx = 0.5 and μy = 0.9 representing a Gaussian beam of a point source. d) Cut through the Gaussian function described in c) at half height. e) Convolved Gaussian of telescope and point source as given by Eq. (B.10). f) Cut through the convolved Gaussian function described in e) at half height. |
The derivation of the beam filling factor (2)starts with the normalized two-dimensional Gaussian function 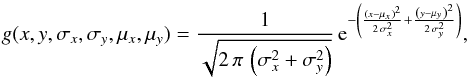 (B.8)where
(B.8)where 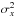 and
and 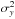 describe the variances and μx and μy the center along the x and y axis, respectively.
describe the variances and μx and μy the center along the x and y axis, respectively.
Observing a Gaussian shaped extended source with a telescope is described by a convolution of two two-dimensional Gaussian functions: 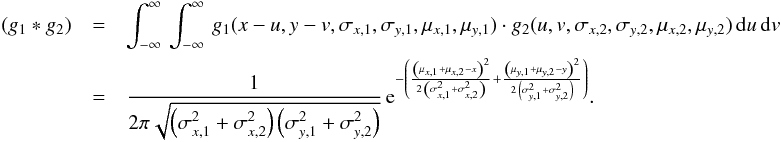 (B.9)Assuming that g1 describes the telescope with μx,1 = μy,1 ≡ 0 and that telescope and extended source are described by non-elliptical Gaussians, that is, σx,1 = σy,1 ≡ σ1 and σx,2 = σy,2 ≡ σ2, Eq. (B.9)can be simplified to17
(B.9)Assuming that g1 describes the telescope with μx,1 = μy,1 ≡ 0 and that telescope and extended source are described by non-elliptical Gaussians, that is, σx,1 = σy,1 ≡ σ1 and σx,2 = σy,2 ≡ σ2, Eq. (B.9)can be simplified to17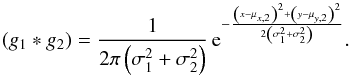 (B.10)The FWHM of the resulting Gaussian is given by
(B.10)The FWHM of the resulting Gaussian is given by 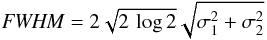 (B.11)which describes an area of
(B.11)which describes an area of 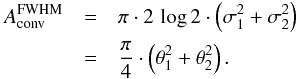 (B.12)In the last line we used the relation between the variances σ1,2 and the user defined FWHM of telescope (θ1 ≡ θt) and source size (θ2 ≡ θm,c) which is given by
(B.12)In the last line we used the relation between the variances σ1,2 and the user defined FWHM of telescope (θ1 ≡ θt) and source size (θ2 ≡ θm,c) which is given by 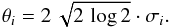 (B.13)The beam filling factor Eq. (2)is defined as ratios of areas
(B.13)The beam filling factor Eq. (2)is defined as ratios of areas 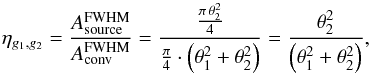 (B.14)which is completely independent of the position μx and μy of the extended source within the telescope beam.
(B.14)which is completely independent of the position μx and μy of the extended source within the telescope beam.
If more extended sources are observed with the telescope, we have to convolve the already convolved Gaussian Eq. (B.10)with a further two-dimensional Gaussian function with variance σx,3 = σy,3 ≡ σ3 and center μx,3 and μy,3. We get 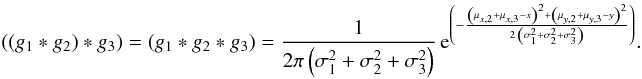 (B.15)The FWHM of the resulting Gaussian is given by
(B.15)The FWHM of the resulting Gaussian is given by 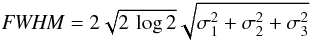 (B.16)which describes an area of
(B.16)which describes an area of 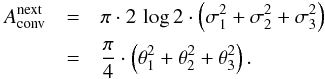 (B.17)In the last line we used again the relation between the variances and FWHM, Eq. (B.13). Now, we can again define a beam filling factor similar to Eq. (2)and get
(B.17)In the last line we used again the relation between the variances and FWHM, Eq. (B.13). Now, we can again define a beam filling factor similar to Eq. (2)and get 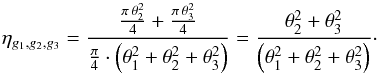 (B.18)When we observe more than three extended sources with a telescope we have to iteratively convolve the resulting Gaussian with a further two-dimensional Gaussian function and we can generalize Eq. (B.18)to
(B.18)When we observe more than three extended sources with a telescope we have to iteratively convolve the resulting Gaussian with a further two-dimensional Gaussian function and we can generalize Eq. (B.18)to 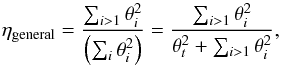 (B.19)where θ1 ≡ θt describes the FWHM of the Gaussian shaped beam of the telescope, defined by the diffraction limit, Eq. (3).
(B.19)where θ1 ≡ θt describes the FWHM of the Gaussian shaped beam of the telescope, defined by the diffraction limit, Eq. (3).
Appendix B.3: Optical depth
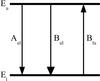 |
Fig. B.2 Transitions between the lower l and the upper u level with the corresponding Einstein coefficients. |
In order to derive Eq. (8)we consider a system which involves radiative transitions between a lower l and an upper u level only. As shown in Fig. B.2, the lower level has an energy El and the upper level an energy Eu>El. With 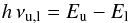 (B.20)describing the energy difference between these two levels we can express the emissivity due to spontaneous radiative decay as
(B.20)describing the energy difference between these two levels we can express the emissivity due to spontaneous radiative decay as 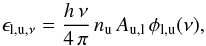 (B.21)where Au,l describes the Einstein A-coefficient, or radiative decay rate for the transition from the lower l to the upper u level. The expression
(B.21)where Au,l describes the Einstein A-coefficient, or radiative decay rate for the transition from the lower l to the upper u level. The expression 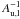 gives the averaged time, that a quantum mechanical system can stay in level u before radiatively decaying to level l, where we assume no collisional (de-)excitation. The expression φl,u(ν) describes the line profile of the transition of photons of frequency ν and is normalized to one, that is,
gives the averaged time, that a quantum mechanical system can stay in level u before radiatively decaying to level l, where we assume no collisional (de-)excitation. The expression φl,u(ν) describes the line profile of the transition of photons of frequency ν and is normalized to one, that is, 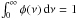 .
.
Similar to Eq. (B.21)we can write the extinction coefficient, which describes the radiative excitation from the lower to the upper level 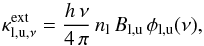 (B.22)where Bl,u describes the Einstein B-coefficient for extinction.
(B.22)where Bl,u describes the Einstein B-coefficient for extinction.
In addition to spontaneous emission and extinction we have to take the stimulated emission into account, which can be described by adding a negative opacity contribution to Eq. (B.22): 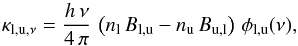 (B.23)where Bu,l represents the Einstein B-coefficient for stimulated emission. So, for nlBl,u<nuBu,l we get laser (maser) emission.
(B.23)where Bu,l represents the Einstein B-coefficient for stimulated emission. So, for nlBl,u<nuBu,l we get laser (maser) emission.
The different Einstein coefficients are related to each other by the Einstein relations: 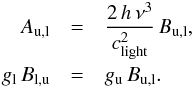 (B.24)Following Eq. (B.2), the differential optical depth τν is defined as
(B.24)Following Eq. (B.2), the differential optical depth τν is defined as 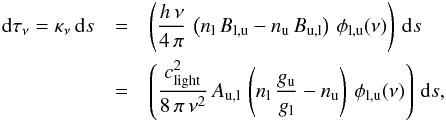 (B.25)where we used the Einstein relations Eq. (B.24)in the last line. By assuming LTE conditions and therefore Boltzmann population distribution
(B.25)where we used the Einstein relations Eq. (B.24)in the last line. By assuming LTE conditions and therefore Boltzmann population distribution 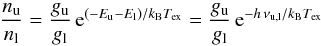 (B.26)we can rewrite Eq. (B.25)by using Eq. (B.20)
(B.26)we can rewrite Eq. (B.25)by using Eq. (B.20)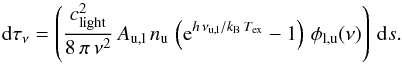 (B.27)Finally, we have to integrate along the line of sight and obtain the optical depth τν
(B.27)Finally, we have to integrate along the line of sight and obtain the optical depth τν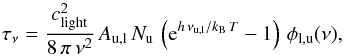 (B.28)where
(B.28)where 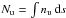 describes the column density of a certain molecule in the upper state.
describes the column density of a certain molecule in the upper state.
In order to express Eq. (B.28)in terms of the total column density 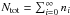 we start again with the Boltzmann population distribution
we start again with the Boltzmann population distribution 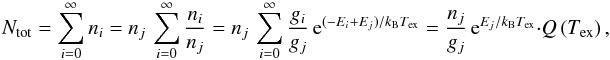 (B.29)where we used the partition function Q(Tex), which is defined as sum over all states
(B.29)where we used the partition function Q(Tex), which is defined as sum over all states 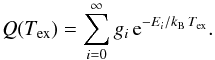 (B.30)For our purpose we rewrite Eq. (B.29)in terms of Nu and Ntot:
(B.30)For our purpose we rewrite Eq. (B.29)in terms of Nu and Ntot: 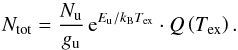 (B.31)Inserting this expression into Eq. (B.28)gives
(B.31)Inserting this expression into Eq. (B.28)gives ![\appendix \setcounter{section}{2} \begin{eqnarray} \label{od:tauFinal} \tau_{\nu} &=& \frac{c_{\rm light}^2}{8 \, \pi \, \nu^2} \, A_{\rm u,l} \, \left[\frac{N_{\rm tot} \, g_{\rm u}}{Q \left(T_{\rm ex} \right)} \, {\rm e}^{-E_{\rm u}/k_{\rm B} T_{\rm ex}} \right] \, \left({\rm e}^{h \, \nu_{\rm u,l}/k_{\rm B} \, T} - 1 \right) \, \phi_{\rm l,u} (\nu) \nonumber\\ &=& \frac{c_{\rm light}^2}{8 \, \pi \, \nu^2} \, A_{\rm u,l} \, N_{\rm tot} \, \frac{g_{\rm u} \, {\rm e}^{-E_{\rm l}/k_{\rm B} T_{\rm ex}}}{Q \left(T_{\rm ex} \right)} \, \left(1 - {\rm e}^{-h \, \nu_{\rm u,l}/k_{\rm B} \, T} \right) \, \phi_{\rm l,u} (\nu), \end{eqnarray}](/articles/aa/full_html/2017/02/aa27203-15/aa27203-15-eq399.png) (B.32)where we used Eq. (B.20)to achieve Eq. (8)for a single line of a certain component and molecule.
(B.32)where we used Eq. (B.20)to achieve Eq. (8)for a single line of a certain component and molecule.
All Tables
All Figures
 |
Fig. 1 Sketch of a distribution of core layers within the Gaussian beam of the telescope (black ring). Here, we assume three different core components 1, 2, and 3, centered at the middle of the beam with different source sizes, excitation temperatures, velocity offsets etc. indicated by different colors. Additionally, we assume that all core components have the same distance to the telescope, i.e., all core layers are located within a plane perpendicular to the line of sight. Furthermore, we assume that this plane is located in front of a background Layer 4 with homogeneous intensity |
| In the text | |
 |
Fig. 2 Sketch of a distribution of core and foreground layers within the Gaussian shaped beam of the telescope (black ring). Here, we assume three different core components 2a, 2b, and 2c located in a plane perpendicular to the line of sight which lies in front of the background layer 1 with intensity |
| In the text | |
 |
Fig. 3 myXCLASS function used to calculate a spectrum for three different step sizes. |
| In the text | |
 |
Fig. 4 myXCLASS function used to model HIFI data of Sgr B2m (black) using SO2 (with three different components), SO (with one component), and HNO (with one component). The intensities of each component are shown in the bottom half. |
| In the text | |
 |
Fig. 5 Graphical user interface (GUI) of the GetTransitions function. Here, the user has to define a frequency range by selecting a single frequency in the shown spectrum. This frequency represents the central frequency of the range. The width of the range is given by an user defined parameter. XCLASS prints out informations (name of molecule, transition frequency, uncertainty of transition frequency, Einstein A coefficient, quantum number for lower and upper state, and energy of lower state) of all transitions in the selected molecule list located in the given frequency range, see screen output of ListDatabase described in Appendix A.1. |
| In the text | |
 |
Fig. 6 Example of an a) algorithm chain and b) algorithm tree. In both cases, we start with the bees swarm algorithm and use the best a) and the three best results b) as starting values for the Levenberg-Marquardt local optimization algorithm (LM), respectively. Afterwards, we apply the error estimation algorithm (Error) to the result(s) of the Levenberg-Marquardt algorithm. In case of an algorithm chain we get one final result (R1), whereas we get three different results (R1, R2, R3) for an algorithm tree. |
| In the text | |
 |
Fig. 7 Example of parameter maps created by the myXCLASSMapFit function. Here, the K-ladder structure of the CH3CN(12-11) transition (plus isotopologues) in G75.78+0.34 was fitted at around 220 GHz (observed with the SMA). The temperature gradient is expected as also seen in different NH3 lines (Sanchez-Monge 2011; Sanchez-Monge et al. 2013). |
| In the text | |
 |
Fig. 8 Result of the spectral line survey of the high-mass star-forming region Orion KL between 325 to 360 GHz using the myXCLASSFit function. Here, we used 24 molecules in conjunction with 245 isotopologues. In panel a) the whole spectral line survey (back) is shown together with the result of myXCLASSFit function (red). Panels b), c) and d) show fit examples around 332.5 GHz, 338.15 GHz, and 358.0 GHz, respectively. |
| In the text | |
 |
Fig. B.1 a) A single two-dimensional Gaussian function, Eq. (B.8), with σx = σy = 1.9 and μx = μy = 0 representing a Gaussian beam of a telescope. b) Cut through the Gaussian function described in a) at half height. c) A single two-dimensional Gaussian function, with σx = σy = 1.1 and μx = 0.5 and μy = 0.9 representing a Gaussian beam of a point source. d) Cut through the Gaussian function described in c) at half height. e) Convolved Gaussian of telescope and point source as given by Eq. (B.10). f) Cut through the convolved Gaussian function described in e) at half height. |
| In the text | |
 |
Fig. B.2 Transitions between the lower l and the upper u level with the corresponding Einstein coefficients. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


