| Issue |
A&A
Volume 597, January 2017
|
|
|---|---|---|
| Article Number | A73 | |
| Number of page(s) | 11 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201629400 | |
| Published online | 03 January 2017 | |
HARPS-N high spectral resolution observations of Cepheids I. The Baade-Wesselink projection factor of δ Cep revisited⋆
1 Université Côte d’Azur, OCA, CNRS, Lagrange, France
e-mail: Nicolas.Nardetto@oca.eu
2 INAF–Osservatorio Astronomico di Brera, via E. Bianchi 46, 23807 Merate (LC), Italy
3 Institute of Astronomy of the Russian Academy of Sciences, 48 Pjatnitskaya Str., 109017 Moscow, Russia
4 Université de Toulouse, UPS-OMP, Institut de Recherche en Astrophysique et Planétologie, 31400 Toulouse, France
5 CNRS, UMR 5277, Institut de Recherche en Astrophysique et Planétologie, 14 avenue Édouard Belin, 31400 Toulouse, France
6 Department of Physics and Astronomy, The Johns Hopkins University, 3400 N. Charles St, Baltimore, MD 21218, USA
7 European Southern Observatory, Alonso de Córdova 3107, Casilla 19001, Santiago 19, Chile
8 Departamento de Astronomía, Universidad de Concepción, Casilla 160-C, Concepción, Chile
9 Millenium Institute of Astrophysics, Santiago, Chile
10 Nicolaus Copernicus Astronomical Center, Polish Academy of Sciences, ul. Bartycka 18, 00-716 Warszawa, Poland
11 LESIA (UMR 8109), Observatoire de Paris, PSL, CNRS, UPMC, Univ. Paris-Diderot, 5 place Jules Janssen, 92195 Meudon, France
12 Unidad Mixta Internacional Franco-Chilena de Astronomía, CNRS/INSU, France (UMI 3386) and Departamento de Astronomía, Universidad de Chile, Camino El Observatorio 1515, Las Condes, Santiago, Chile
13 Department of Astronomy & Astrophysics, University of Toronto, 50 St. George Street, Toronto, ON, M5S 3H4, Canada
14 Leibniz Institute for Astrophysics, An der Sternwarte 16, 14482 Potsdam, Germany
Received: 26 July 2016
Accepted: 21 October 2016
Context. The projection factor p is the key quantity used in the Baade-Wesselink (BW) method for distance determination; it converts radial velocities into pulsation velocities. Several methods are used to determine p, such as geometrical and hydrodynamical models or the inverse BW approach when the distance is known.
Aims. We analyze new HARPS-N spectra of δ Cep to measure its cycle-averaged atmospheric velocity gradient in order to better constrain the projection factor.
Methods. We first apply the inverse BW method to derive p directly from observations. The projection factor can be divided into three subconcepts: (1) a geometrical effect (p0); (2) the velocity gradient within the atmosphere (fgrad); and (3) the relative motion of the optical pulsating photosphere with respect to the corresponding mass elements (fo−g). We then measure the fgrad value of δ Cep for the first time.
Results. When the HARPS-N mean cross-correlated line-profiles are fitted with a Gaussian profile, the projection factor is pcc−g = 1.239 ± 0.034(stat.) ± 0.023(syst.). When we consider the different amplitudes of the radial velocity curves that are associated with 17 selected spectral lines, we measure projection factors ranging from 1.273 to 1.329. We find a relation between fgrad and the line depth measured when the Cepheid is at minimum radius. This relation is consistent with that obtained from our best hydrodynamical model of δ Cep and with our projection factor decomposition. Using the observational values of p and fgrad found for the 17 spectral lines, we derive a semi-theoretical value of fo−g. We alternatively obtain fo−g = 0.975 ± 0.002 or 1.006 ± 0.002 assuming models using radiative transfer in plane-parallel or spherically symmetric geometries, respectively.
Conclusions. The new HARPS-N observations of δ Cep are consistent with our decomposition of the projection factor. The next step will be to measure p0 directly from the next generation of visible interferometers. With these values in hand, it will be possible to derive fo−g directly from observations.
Key words: stars: oscillations / techniques: spectroscopic / stars: individual: delta Cep / stars: distances / stars: atmospheres / stars: variables: Cepheids
Table A.1 is also available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/597/A73
© ESO, 2017
Non-exhaustive history of the determination of the Baade-Wesselink projection factor in the case of δ Cep.
1. Introduction
Since their period-luminosity (PL) relation was established (Leavitt & Pickering 1912), Cepheid variable stars have been used to calibrate the distance scale (Hertzsprung 1913) and then the Hubble constant (Riess et al. 2011; Freedman et al. 2012; Riess et al. 2016). The discovery that the K-band PL relation is nearly universal and can be applied to any host galaxy whatever its metallicity (Storm et al. 2011a) is a considerable step forward in the use of Cepheids as distance indicators. Determining the distances to Cepheids relies on the Baade-Wesselink (BW) method, which in turn relies on a correct evaluation of the projection factor p. This is necessary to convert the radial velocity variations derived from the spectral line profiles into photospheric pulsation velocities (Nardetto et al. 2004).
The projection factor of δ Cep, the eponym of the Cepheid variables, has been determined by means of different techniques, which we summarize here (see Table 1 and the previous review by Nardetto et al. 2014b):
-
Purely geometric considerations lead to the identification of twocontributing effects only in the projection factor, i.e., the limbdarkening of the star and the motion (expansion or contraction) ofthe atmosphere. Nardettoet al. (2014b) described thisclassical approach and its recent variations (e.g., Gray &Stevenson 2007; Hadravaet al. 2009).
-
To improve the previous method we should consider that Cepheids do not pulsate in a quasi-hydrostatic way and the dynamical structure of their atmosphere is extremely complex (Sanford 1956; Bell & Rodgers 1964; Karp 1975; Sasselov & Lester 1990; Wallerstein et al. 2015). Therefore, improving the determination of the BW projection factor requires a hydrodynamical model that is able to describe the atmosphere. To date, the projection factor has been studied with two such models: the first is based on a piston in which the radial velocity curve is used as an input (Sabbey et al. 1995) and the second is a self-consistent model (Nardetto et al. 2004). Sabbey et al. (1995) found a mean value of the projection factor p = 1.34 (see also Marengo et al. 2002, 2003). However, this value was derived using the bisector method of the radial velocity determination (applied to the theoretical line profiles). This makes it difficult to compare this value with other studies. As commonly done in the literature, if a Gaussian fit of the cross-correlated line-profile is used to derive the radial velocity RVcc−g (“cc” for cross-correlated and “g” for Gaussian), then the measured projection factor tends to be about 11% smaller than the initial geometrical projection factor is found, i.e., p = 1.25 ± 0.05 (Nardetto et al. 2009).
-
As an approach entirely based on observations, Mérand et al. (2005) applied the inverse BW method to infrared interferometric data of δ Cep. The projection factor is then fit, where the distance of δ Cep is known with 4% uncertainty from the HST parallax (d = 274 ± 11 pc; Benedict et al. 2002). They found p = 1.273 ± 0.021 ± 0.050 using RVcc−g for the radial velocity. The first error is the internal one due to the fitting method. The second is due to the uncertainty of the distance. Groenewegen (2007) found p = 1.245 ± 0.030 ± 0.050 when using almost the same distance (273 instead of 274 pc), a different radial velocity dataset and a different fitting method of the radial velocity curve. Recently, Merand et al. (2015) applied an integrated inverse method (SPIPS) to δ Cep (by combining interferometry and photometry) and found p = 1.29 ± 0.02 ± 0.05. These values agree closely with the self-consistent hydrodynamical model. Another slightly different approach is to apply the infrared surface brightness inverse method to distant Cepheids (see Fouque & Gieren 1997; Kervella et al. 2004a, for the principles) in order to derive a period projection factor relation (Pp). In this approach the distance to each LMC Cepheid is assumed to be the same by taking into account the geometry of LMC. This constrains the slope of the Pp relation. However, its zero-point is alternatively fixed using distances to Cepheids in Galactic clusters (Gieren et al. 2005b), HST parallaxes of nearby Cepheids derived by van Leeuwen et al. (2007; Laney & Joner 2009; Storm et al. 2011b), or a combination of both (Groenewegen 2013). Laney & Joner (2009) also used high-amplitude δ Scuti stars to derive their Pp relation (see also Fig. 10 in Nardetto et al. 2014a). The projection factors derived by Laney & Joner (2009) and Groenewegen (2013) are consistent with the interferometric values, while the projection factors from Gieren et al. (2005b) and Storm et al. (2011b) are significantly greater (see Table 1).
-
Pilecki et al. (2013) constrained the projection factor using a short-period Cepheid (P = 3.80 d, similar to the period of δ Cep) in a eclipsing binary system. They found p = 1.21 ± 0.04.
This non-exhaustive review shows just how complex the situation regarding the value of the BW projection factor of δ Cep is. This paper is part of the international “Araucaria Project”, whose purpose is to provide an improved local calibration of the extragalactic distance scale out to distances of a few megaparsecs (Gieren et al. 2005a). In Sect. 2 we present new High Accuracy Radial velocity Planet Searcher for the Northern hemisphere (HARPS-N) observations. Using these spectra together with the Mérand et al. (2005) data obtained with the Fiber Linked Unit for Optical Recombination (FLUOR, Coudé du Foresto et al. 1997) operating at the focus of the Center for High Angular Resolution Astronomy (CHARA) array (ten Brummelaar et al. 2005) located at the Mount Wilson Observatory (California, USA), we apply the inverse BW method to derive the projection factor associated with the RVcc−g radial velocity and for 17 individual spectral lines (Sect. 3). In Sect. 4, we briefly describe the hydrodynamical model used in Nardetto et al. (2004) and review the projection factor decomposition into three sub-concepts (p = p0fgradfo−g, Nardetto et al. 2007). In Sect. 4.1, we compare the observational and theoretical projection factors. We then compare the hydrodynamical model with the observed atmospheric velocity gradient (Sect. 4.2) and the angular diameter curve of FLUOR/CHARA (Sect. 4.3). In Sect. 5 we derive the fo−g quantity from the previous sections. We conclude in Sect. 6.
2. HARPS-N spectroscopic observations
HARPS-N is a high-precision radial-velocity spectrograph installed at the Italian Telescopio Nazionale Galileo (TNG), a 3.58-m telescope located at the Roque de los Muchachos Observatory on the island of La Palma, Canary Islands, Spain (Cosentino et al. 2012). HARPS-N is the northern hemisphere counterpart of the similar HARPS instrument installed at the ESO 3.6 m telescope at La Silla Observatory in Chile. The instrument covers the wavelength range from 3800 to 6900 Å with a resolving power of R ≃ 115 000. A total of 103 spectra were secured between 27 March and 6 September 2015 in the framework of the OPTICON proposal 2015B/015 (Table A.1). In order to calculate the pulsation phase of each spectrum, we used P = 5.366208 d (Engle et al. 2014) and T0 = 2 457 105.930 d, the time corresponding to the maximum approaching velocity determined from the HARPS-N radial velocities. The data are spread over 14 of the 30 pulsation cycles elapsed between the first and last epoch. The final products of the HARPS-N data reduction software (DRS) installed at TNG (on-line mode) are background-subtracted, cosmic-corrected, flat-fielded, and wavelength-calibrated spectra (with and without merging of the spectral orders). We used these spectra to compute the mean-line profiles by means of the least-squares deconvolution (LSD) technique (Donati et al. 1997). As can be seen in Fig. 1, the mean profiles reflect the large-amplitude radial pulsation by distorting the shape in a continuous way.
The DRS also computes the star’s radial velocity by fitting a Gaussian function to the cross-correlation functions (CCFs). To do this, the DRS uses a mask including thousands of lines covering the whole HARPS-N spectral ranges. The observer can select the mask among those available online and the G2 mask was the closest to the δ Cep spectral type. As a further step, we re-computed the RV values by using the HARPS-N DRS in the offline mode on the Yabi platform, as in the case of τ Boo (Borsa et al. 2015). We applied both library and custom masks, ranging spectral types from F5 to G2. We obtained RV curves fitted with very similar sets of least-squares parameters showing only some small changes in the mean values. Table A.1 lists the RVcc−g values obtained from the custom F5I mask, also plotted in panel a) of Fig. 2 with different symbols for each pulsation cycle. The RV curve shows a full amplitude of 38.4 km s-1 and an average value (i.e., the A0 value of the fit) of Vγ = −16.95km s-1 . As a comparison, we calculate the centroid of the mean line profiles RVcc−c (“cc” for cross-correlated and “c” for centroid) and plot the residuals in panel b) of Fig. 2. The RVcc−c curve has an amplitude 1.2 km s-1 lower than that of the RVcc−g value. This result is similar to that reported in the case of β Dor (Fig. 2 in Nardetto et al. 2006). The implications of this difference on the projection factor is discussed in Sect. 3.1.
Consistent with Anderson et al. (2015), we find no evidence for cycle-to-cycle differences in the RV amplitude as exhibited by long-period Cepheids (Anderson 2014; Anderson et al. 2016). We also investigated the possible effect of the binary motion due to the companion (Anderson et al. 2015). Unfortunately, the HARPS-N observations are placed on the slow decline of the RV curve and they only span 160 days. We were able to detect a slow drift of −0.5 ± 0.1 m s-1 d-1. The least-squares solution with 14 harmonics leaves a r.m.s. residual of 49 m s-1. Including a linear trend did not significantly reduce the residual since the major source of error probably lies in the fits of the very different shapes of the mean-line profiles along the pulsation cycle (Fig. 1). We also note that surface effects induced by convection and granulation (Neilson & Ignace 2014) could contribute to increasing the residual r.m.s. These effects are also observed in the light curves of Cepheids (Derekas et al. 2012, 2017; Evans et al. 2015; Poretti et al. 2015).
 |
Fig. 1 Mean line profile changes during the pulsation cycle of δ Cep. The line profile with the highest receding motion is highlighted in red, the one with the highest approaching motion in blue. |
 |
Fig. 2 Panel a): HARPS-N radial velocities associated with the Gaussian fit of the cross-correlated line profile (RVcc−g using F5I template) plotted as a function of the pulsation phase of the star after correction of the γ-velocity (i.e., Vγ = −16.95km s-1 ). The cycle of observations are shown in different colors. The data are reproduced from one cycle to the other. The precision on the measurements is between 0.5 and 1.5 m s-1 (error bars are lower than symbols). Panel b) residuals between RVcc−c (F5I) and RVcc−g (F5I) after correction of their respective γ-velocities. |
3. Inverse Baade-Wesselink projection factors derived from observations
3.1. Using the cross-correlated radial velocity curve
We describe the interferometric version of the BW method as follows. We apply a classical χ2 minimization 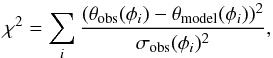 (1)where
(1)where
-
θobs(φi) are the interferometric limb-darkened angular diameters obtained from FLUOR/CHARA observations (Mérand et al. 2005), with φi the pulsation phase corresponding to the ith measurement (Fig. 3);
σobs(φi) are the statistical uncertainties corresponding to FLUOR/CHARA measurements;
θmodel(φi) are the modeled limb-darkened angular diameters, defined as
![\begin{equation} \label{diam_mod} \theta_{\rm model}(\phi_{i}) = \overline{\theta} + 9.3009\,\frac{p_\mathrm{cc-g}}{d} \left(\int RV_\mathrm{cc-g}(\phi_{i}) {\rm d}\phi_{i}\right) [{\rm mas}], \end{equation}](/articles/aa/full_html/2017/01/aa29400-16/aa29400-16-eq47.png) (2)
(2)
The RVcc−g(φi) is the interpolated HARPS-N cross-correlated radial velocity curve shown in panel a) of Fig. 2. It is obtained using the Gaussian fit, i.e., the most common approach in the literature. The parameters 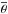 and pcc−g are the mean angular diameter of the star (in mas) and the projection factor (associated with the Gaussian fit of the CCFs), respectively, while d is the distance to the star. The quantities
and pcc−g are the mean angular diameter of the star (in mas) and the projection factor (associated with the Gaussian fit of the CCFs), respectively, while d is the distance to the star. The quantities 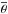 and pcc−g are fit in order to minimize χ2, while d is fixed to d = 272 ± 3(stat.) ± 5(syst.) pc (Majaess et al. 2012).
and pcc−g are fit in order to minimize χ2, while d is fixed to d = 272 ± 3(stat.) ± 5(syst.) pc (Majaess et al. 2012).
We find 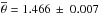 mas and pcc−g = 1.239 ± 0.031, where the uncertainty on the projection factor (hereafter σstat−fluor) is about 2.5% and stems from FLUOR/CHARA angular diameter measurements. If we apply this procedure 10 000 times using a Gaussian distribution for the assumed distance that is centered at 272 pc and has a half width at half maximum (HWHM) of 3 pc (corresponding to the statistical precision on the distance of Majaess et al. 2012), then we obtain a symmetric distribution for the 10 000 values of pcc−g with a HWHM σstat−d = 0.014. If the distance is set to 277 pc and 267 pc (corresponding to the systematical uncertainty of ± 5 pc of Majaess et al. 2012), we find p = 1.262 and p = 1.216, respectively. We have a systematical uncertainty σsyst−d = 0.023 for the projection factor. We thus find pcc−g = 1.239 ± 0.031 (σstat−fluor) ± 0.014 (σstat−d) ± 0.023 (σsyst−d). These results are illustrated in Fig. 4. Interestingly, if we use the RVcc−c curve in Eq. (2) (still keeping d = 272 pc), we obtain pcc−c = 1.272 while the uncertainties remain unchanged.
mas and pcc−g = 1.239 ± 0.031, where the uncertainty on the projection factor (hereafter σstat−fluor) is about 2.5% and stems from FLUOR/CHARA angular diameter measurements. If we apply this procedure 10 000 times using a Gaussian distribution for the assumed distance that is centered at 272 pc and has a half width at half maximum (HWHM) of 3 pc (corresponding to the statistical precision on the distance of Majaess et al. 2012), then we obtain a symmetric distribution for the 10 000 values of pcc−g with a HWHM σstat−d = 0.014. If the distance is set to 277 pc and 267 pc (corresponding to the systematical uncertainty of ± 5 pc of Majaess et al. 2012), we find p = 1.262 and p = 1.216, respectively. We have a systematical uncertainty σsyst−d = 0.023 for the projection factor. We thus find pcc−g = 1.239 ± 0.031 (σstat−fluor) ± 0.014 (σstat−d) ± 0.023 (σsyst−d). These results are illustrated in Fig. 4. Interestingly, if we use the RVcc−c curve in Eq. (2) (still keeping d = 272 pc), we obtain pcc−c = 1.272 while the uncertainties remain unchanged.
The distance of δ Cep obtained by Majaess et al. (2012) is an average of Hipparcos (van Leeuwen 2007) and HST (Benedict et al. 2002) trigonometric parallaxes, together with the cluster main sequence fitting distance. If we rely on the direct distance to δ Cep obtained only by HST (Benedict et al. 2002), i.e., 273 ± 11 pc, then σstat−d is larger with a value of 0.050 (compared to 0.014 when relying on Majaess et al. 2012). A distance d = 244 ± 10 pc was obtained by Anderson et al. (2015) from the reanalysis of the Hipparcos astrometry of δ Cep. It leads to a very small projection factor pcc−g = 1.14 ± 0.031 ± 0.047 compared to other values listed in Table 1.
 |
Fig. 3 Inverse BW method applied to FLUOR/CHARA data (Mérand et al. 2005) considering a distance for δ Cep of d = 272 ± 3 ± 5 pc (Majaess et al. 2012) and the HARPS-N cross-correlated radial velocity curve. The black dotted line corresponds to the best fit. |
 |
Fig. 4 Inverse BW method described in Sect. 3 applied considering a Gaussian distribution for the distance. The resulting projection factor distributions are shown in three particular cases: when using the cross-correlated radial velocity curve RVcc−g (red), the RVc radial velocity curve of line 7 (blue), and the RVc radial velocity curve of line 10 (green). The quantities σstat−d and σsyst−d are the uncertainties on the projection factor due to the statistical and systematical uncertainties on the distance, respectively. The quantity σstat−fluor stems from the statistical uncertainties on the FLUOR/CHARA interferometric measurements. |
Spectral lines used this study.
 |
Fig. 5 a) First moment radial velocity curves (RVc) associated with the 17 lines of Table 2. The γ-velocity associated with the cross-correlated radial velocity curve, RVcc−g in Fig. 2a, has been removed from these curves, i.e., Vγ = −16.95km s-1 . The γ offset residuals are known to be related to the k-term (Nardetto et al. 2008). The residuals between the RVc curves and the RVcc−g in Fig. 2a (resp. RVcc−c) are plotted in panel b) (resp. c)) after correcting each RVc curve from its Vγ value. |
3.2. Using the first moment radial velocity curves corresponding to individual spectral lines
We use the 17 unblended spectral lines (Table 2) that were previously selected for an analysis of eight Cepheids with periods ranging from 4.7 to 42.9 d (Nardetto et al. 2007). These lines remain unblended for every pulsation phase of the Cepheids considered. Moreover, they were carefully selected in order to represent a wide range of depths, hence to measure the atmospheric velocity gradient (Sect. 4.2). For each of these lines, we derive the centroid velocity (RVc), i.e., the first moment of the spectral line profile, estimated as 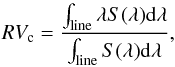 (3)where S(λ) is the observed line profile. The radial velocity measurements associated with the spectral lines are presented in Fig. 5a together with the interpolated RVcc−g curve. The RVc curves plotted have been corrected for the γ-velocity value corresponding to the RVcc−g curve, i.e., Vγ = −16.95km s-1 . The residuals, i.e., the γ-velocity offsets, between the curves of Fig. 5a are related to the line asymmetry and the k-term value (see Nardetto et al. 2008, for Cepheids; and Nardetto et al. 2013, 2014a, for other types of pulsating stars). This will be analyzed in a forthcoming paper. The final RVc curves used in the inverse BW approach are corrected from their own residual γ-velocity in such a way that the interpolated curve has an average of zero. The residual of these curves compared to the RVcc−g and RVcc−c curves are shown in panel b and c, respectively. We then apply the same method as in Sect. 3.1. The measured projection factor values pobs(k) associated with each spectral line k are listed in Table 3. The statistical and systematical uncertainties in the case of individual lines are the same as those found when using the RVcc−g curve. The projection factor values range from 1.273 (line 7) to 1.329 (line 10), whereas the value corresponding to the cross-correlation method is 1.239 (see Fig. 4). This shows that the projection factor depends significantly on the method used to derive the radial velocity and the spectral line considered. To analyze these values it is possible to use hydrodynamical simulations and the projection factor decomposition into three terms introduced by Nardetto et al. (2007).
(3)where S(λ) is the observed line profile. The radial velocity measurements associated with the spectral lines are presented in Fig. 5a together with the interpolated RVcc−g curve. The RVc curves plotted have been corrected for the γ-velocity value corresponding to the RVcc−g curve, i.e., Vγ = −16.95km s-1 . The residuals, i.e., the γ-velocity offsets, between the curves of Fig. 5a are related to the line asymmetry and the k-term value (see Nardetto et al. 2008, for Cepheids; and Nardetto et al. 2013, 2014a, for other types of pulsating stars). This will be analyzed in a forthcoming paper. The final RVc curves used in the inverse BW approach are corrected from their own residual γ-velocity in such a way that the interpolated curve has an average of zero. The residual of these curves compared to the RVcc−g and RVcc−c curves are shown in panel b and c, respectively. We then apply the same method as in Sect. 3.1. The measured projection factor values pobs(k) associated with each spectral line k are listed in Table 3. The statistical and systematical uncertainties in the case of individual lines are the same as those found when using the RVcc−g curve. The projection factor values range from 1.273 (line 7) to 1.329 (line 10), whereas the value corresponding to the cross-correlation method is 1.239 (see Fig. 4). This shows that the projection factor depends significantly on the method used to derive the radial velocity and the spectral line considered. To analyze these values it is possible to use hydrodynamical simulations and the projection factor decomposition into three terms introduced by Nardetto et al. (2007).
4. Comparing the hydrodynamical model of δ Cep with observations
Our best model of δ Cep was presented in Nardetto et al. (2004) and is computed using the code by Fokin (1991). The hydrodynamical model requires only five input fundamental parameters: M = 4.8 M⊙, L = 1995 L⊙, Teff = 5877 K, Y = 0.28, and Z = 0.02. At the limit cycle the pulsation period is 5.419 d, very close (1%) to the observed value.
4.1. Baade-Wesselink projection factors derived from the hydrodynamical model
The projection factors are derived directly from the hydrodynamical code for each spectral line of Table 2 following the definition and procedure described in Nardetto et al. (2007). The computed projection factors range from 1.272 (line 7) to 1.328 (line 2). In Fig. 6 we plot the theoretical projection factors (phydro) as a function of the observational values (listed in Table 3). In this figure the statistical uncertainties on the observational projection factors, i.e., σstat−fluor and σstat−d, have been summed quadratically (i.e., σ = 0.034). The agreement is excellent since the most discrepant lines (10 and 17, in red in the figure) show observational projection factor values only about 1σ larger than the theoretical values.
 |
Fig. 6 Observational projection factors derived using the inverse BW approach described in Sect. 3 compared to the theoretical values obtained from the hydrodynamical model (Sect. 4.1). |
4.2. Atmospheric velocity gradient of δ Cep
In Nardetto et al. (2007), we split the projection factor into three quantities: p = pofgradfo−g, where p0 is the geometrical projection factor (linked to the limb darkening of the star); fgrad, which is a cycle-integrated quantity linked to the velocity gradient in the atmosphere of the star (i.e., between the considered line-forming region and the photosphere); and fo−g, which is the relative motion of the optical pulsating photosphere with respect to the corresponding mass elements.
We derive fgrad directly from HARPS-N observations. In Nardetto et al. (2007), we showed that the line depth taken at the minimum radius phase (hereafter D) traces the height of the line-forming regions in such a way that the projection factor decomposition is possible. By comparing ΔRVc with the depth, D, of the 17 selected spectral lines listed in Table 2, we directly measure fgrad. If we define a0 and b0 as the slope and zero-point of the linear correlation (the photosphere being the zero line depth), 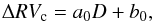 (4)then the velocity gradient correction on the projection factor is
(4)then the velocity gradient correction on the projection factor is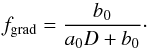 (5)In Anderson (2016) the atmospheric velocity gradient is defined as the difference between velocities determined using weak and strong lines at each pulsation phase. In our description of the projection factor, fgrad is calculated with Eqs. (4) and (5), i.e., considering the amplitude of the radial velocity curves from individual lines. In the following we thus refer to fgrad as a cycle integrated quantity.
(5)In Anderson (2016) the atmospheric velocity gradient is defined as the difference between velocities determined using weak and strong lines at each pulsation phase. In our description of the projection factor, fgrad is calculated with Eqs. (4) and (5), i.e., considering the amplitude of the radial velocity curves from individual lines. In the following we thus refer to fgrad as a cycle integrated quantity.
 |
Fig. 7 Amplitude of the radial velocity curves for the 17 spectral lines listed in Table 2 plotted versus the line depth for the hydrodynamical model (magenta squares), and for the HARPS-N spectroscopic observations (blue dots, except lines 10 and 17 plotted with filled red squares). A rescale of the model with a multiplying factor (i.e., fc) is necessary to fit the data (light blue circles). |
In Fig. 7 we plot the HARPS-N measurements with blue dots, except for lines 10 and 17 for which we use red squares. These two values are about 2σ below the other measurements, as already noted in Fig. 6. After fitting all measured ΔRVc [obs] with a linear relation we find ![\begin{equation} \label{Eq_grad_O} \Delta RV_{\mathrm{c}}\mathrm{[obs]}= [2.86 \pm 0.84] D + [35.40 \pm 0.36] . \end{equation}](/articles/aa/full_html/2017/01/aa29400-16/aa29400-16-eq126.png) (6)The reduced χ2 is 1.4 and decreases to 1.1 if lines 10 and 17 are not considered (but with approximately the same values of a0 and b0). For comparison, the reduced χ2 is 2.5 if a horizontal line is fitted. The same quantities derived from the hydrodynamical model are shown in Fig. 7 (ΔRVc [mod], magenta squares). The corresponding relation is
(6)The reduced χ2 is 1.4 and decreases to 1.1 if lines 10 and 17 are not considered (but with approximately the same values of a0 and b0). For comparison, the reduced χ2 is 2.5 if a horizontal line is fitted. The same quantities derived from the hydrodynamical model are shown in Fig. 7 (ΔRVc [mod], magenta squares). The corresponding relation is ![\begin{equation} \label{Eq_grad_M} \Delta RV_{\mathrm{c}}\mathrm{[mod]}= [2.90 \pm 0.39] D + [32.84 \pm 0.13] . \end{equation}](/articles/aa/full_html/2017/01/aa29400-16/aa29400-16-eq129.png) (7)The slopes of Eqs. (6) and (7) are consistent, while the theoretical zero-point is about 2.6 km s-1 below the corresponding observational value, which means that the amplitudes of the theoretical radial velocity curves are 2.6 km s-1 (or 7.8%) smaller on average. Such disagreement occurs because our code is self-consistent, i.e., the radial velocity curve is not used as an input like in a piston code, and because the treatment of convection in the code is missing which can slightly bias (by a few percent) the input fundamental parameters. The two- or three-dimensional models that properly describe the coupling between the pulsation and the convection (Geroux & Deupree 2015; Houdek & Dupret 2015) are currently not providing synthetic profiles, hence preventing the calculation of the projection factor. Therefore, we rely on our purely radiative hydrodynamical code (as previously done in Nardetto et al. 2004, 2007) to study the atmosphere of Cepheids. Its consistency with the spectroscopic and interferometric observables is satisfactory as soon as we consider a multiplying correcting factor of fc = 1.078. Consequently, Eq. (7) becomes
(7)The slopes of Eqs. (6) and (7) are consistent, while the theoretical zero-point is about 2.6 km s-1 below the corresponding observational value, which means that the amplitudes of the theoretical radial velocity curves are 2.6 km s-1 (or 7.8%) smaller on average. Such disagreement occurs because our code is self-consistent, i.e., the radial velocity curve is not used as an input like in a piston code, and because the treatment of convection in the code is missing which can slightly bias (by a few percent) the input fundamental parameters. The two- or three-dimensional models that properly describe the coupling between the pulsation and the convection (Geroux & Deupree 2015; Houdek & Dupret 2015) are currently not providing synthetic profiles, hence preventing the calculation of the projection factor. Therefore, we rely on our purely radiative hydrodynamical code (as previously done in Nardetto et al. 2004, 2007) to study the atmosphere of Cepheids. Its consistency with the spectroscopic and interferometric observables is satisfactory as soon as we consider a multiplying correcting factor of fc = 1.078. Consequently, Eq. (7) becomes ![\begin{equation} \label{Eq_grad_M_res} \Delta RV_{\mathrm{c}}\mathrm{[mod]}= [2.90 D + 32.84] *f_\mathrm{c}. \end{equation}](/articles/aa/full_html/2017/01/aa29400-16/aa29400-16-eq131.png) (8)The corresponding values are shown in Fig. 7 with light blue squares, and the agreement with observations is now excellent. If the theoretical amplitudes of the radial velocity curves are underestimated, why do we obtain the correct values of the projection factors in Sect. 4.1? The answer is that the projection factor depends only on the ratio of pulsation to radial velocities. If the pulsation velocity curve has an amplitude that is 7.8% larger, then the radial velocity curve (whatever the line considered) and the radius variation (see Sect. 4.3), also have amplitudes that are 7.8% larger and the derived projection factor remains the same.
(8)The corresponding values are shown in Fig. 7 with light blue squares, and the agreement with observations is now excellent. If the theoretical amplitudes of the radial velocity curves are underestimated, why do we obtain the correct values of the projection factors in Sect. 4.1? The answer is that the projection factor depends only on the ratio of pulsation to radial velocities. If the pulsation velocity curve has an amplitude that is 7.8% larger, then the radial velocity curve (whatever the line considered) and the radius variation (see Sect. 4.3), also have amplitudes that are 7.8% larger and the derived projection factor remains the same.
Small differences in the velocity amplitudes between the RVcc−c and RVc curves (Fig. 5c) are due to the use of different methods and line samples (a full mask and 17 selected lines, respectively).
4.3. Angular diameter curve
 |
Fig. 8 FLUOR/CHARA limb-darkened angular diameter curve compared to the hydrodynamical model (see the text). |
In Fig. 8, we compare our best-fit infrared angular diameters from FLUOR/CHARA (same curve as Fig. 3) with the photospheric angular diameters derived directly from the model assuming a distance of d = 272 pc (Majaess et al. 2012). Following the projection factor decomposition, this photospheric angular diameter is calculated by integrating the pulsation velocity associated with the photosphere of the star. We consider this to be the layer of the star for which the optical depth in the continuum (in the vicinity of the Fe i 6003.012 Å spectral line) is 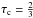 . However, to superimpose the computed photospheric angular diameter curve on the interferometric one, we again need a correction factor fc. We find that the rescaled model (magenta open squares) is consistent with the solid line, which corresponds to the integration of the HARPS-N RVcc−g curve (multiplied consistently by pcc−g).
. However, to superimpose the computed photospheric angular diameter curve on the interferometric one, we again need a correction factor fc. We find that the rescaled model (magenta open squares) is consistent with the solid line, which corresponds to the integration of the HARPS-N RVcc−g curve (multiplied consistently by pcc−g).
We rescaled the outputs of the hydrodynamical code, i.e., the atmospheric velocity gradient (Sect. 4.2), the radial velocity, and the angular diameter curves, by the same quantity fc in order to reproduce the observations satisfactorily. This scaling leaves the hydrodynamical projection factors unchanged and in agreement with the observational values (Table 2). This can be seen using Eq. (2): if we multiply each part of this equation by fc, the result in terms of the projection factor is unchanged.
5. Determining fo-g
The variable fo−g is linked to the distinction between the optical and gas photospheric layers. The optical layer is the location where the continuum is generated (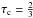 ). The gas layer is the location of some mass element in the hydrodynamic model mesh where, at some moment in time, the photosphere is located. Given that the location of the photosphere moves through different mass elements as the star pulsates, the two layers have different velocities, hence it is necessary to define fo−g in the projection factor decomposition. The fo−g quantity is independent of the spectral line considered and is given by
). The gas layer is the location of some mass element in the hydrodynamic model mesh where, at some moment in time, the photosphere is located. Given that the location of the photosphere moves through different mass elements as the star pulsates, the two layers have different velocities, hence it is necessary to define fo−g in the projection factor decomposition. The fo−g quantity is independent of the spectral line considered and is given by 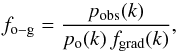 (9)where k indicates the spectral line considered. From the previous sections, we now have the ability to derive fo−g. In Sect. 3, we derived the projection factors pobs(k) for 17 individual lines. In Sect. 4.2, we determined
(9)where k indicates the spectral line considered. From the previous sections, we now have the ability to derive fo−g. In Sect. 3, we derived the projection factors pobs(k) for 17 individual lines. In Sect. 4.2, we determined 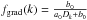 using Eq. (5) (see Table 3). The last quantity required to derive fo−g is the geometric projection factor po (see Eq. (9)). There is currently no direct estimation of po for δ Cep. If we rely on the hydrodynamical model, po can be inferred from the intensity distribution next to the continuum of each spectral line. The list of geometric projection factors are listed in Table 3 and plotted in Fig. 9 with magenta dots. These calculations are done in the plane-parallel radiative transfer approximation. On the other hand, Neilson et al. (2012) showed that the p-factor differs significantly as a function of geometry where those from plane-parallel model atmospheres are 3−7% greater then those derived from spherically symmetric models. Using their Table 1, we find for δ Cep a spherically symmetric geometrical projection factor of 1.342 in the R-band (i.e., with an effective wavelength of 6000 Å). In Fig. 9, if we shift our results (magenta dots) by 0.043 in order to get 1.342 at 6000 Å (a decrease of 3.2%), we roughly estimate the geometrical projection factors in spherical geometry as a function of the wavelength (red open triangles). In Fig. 9, we now plot the
using Eq. (5) (see Table 3). The last quantity required to derive fo−g is the geometric projection factor po (see Eq. (9)). There is currently no direct estimation of po for δ Cep. If we rely on the hydrodynamical model, po can be inferred from the intensity distribution next to the continuum of each spectral line. The list of geometric projection factors are listed in Table 3 and plotted in Fig. 9 with magenta dots. These calculations are done in the plane-parallel radiative transfer approximation. On the other hand, Neilson et al. (2012) showed that the p-factor differs significantly as a function of geometry where those from plane-parallel model atmospheres are 3−7% greater then those derived from spherically symmetric models. Using their Table 1, we find for δ Cep a spherically symmetric geometrical projection factor of 1.342 in the R-band (i.e., with an effective wavelength of 6000 Å). In Fig. 9, if we shift our results (magenta dots) by 0.043 in order to get 1.342 at 6000 Å (a decrease of 3.2%), we roughly estimate the geometrical projection factors in spherical geometry as a function of the wavelength (red open triangles). In Fig. 9, we now plot the 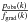 quantity for each individual spectral line with their corresponding uncertainties (blue open squares). If we divide the
quantity for each individual spectral line with their corresponding uncertainties (blue open squares). If we divide the 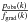 quantities obtained for each individual spectral line by the corresponding value of po(k) calculated in plane-parallel geometry, we obtain fo−g = 0.975 ± 0.002, with a reduced χ2 of 0.13. This indicates that our uncertainties (the quadratic sum of σstat−fluor, σstat−d and the statistical uncertainty on fgrad) are probably overestimated. This value is several σ greater than that found directly with the hydrodynamical model of δ Cep: fo−g = 0.963 ± 0.005 (Nardetto et al. 2007, their Table 5). Using the values of po from Neilson et al. (2012) (blue open triangles), we obtain fo−g = 1.006 ± 0.002. Thus, fo−g depends significantly on the model used to calculate po.
quantities obtained for each individual spectral line by the corresponding value of po(k) calculated in plane-parallel geometry, we obtain fo−g = 0.975 ± 0.002, with a reduced χ2 of 0.13. This indicates that our uncertainties (the quadratic sum of σstat−fluor, σstat−d and the statistical uncertainty on fgrad) are probably overestimated. This value is several σ greater than that found directly with the hydrodynamical model of δ Cep: fo−g = 0.963 ± 0.005 (Nardetto et al. 2007, their Table 5). Using the values of po from Neilson et al. (2012) (blue open triangles), we obtain fo−g = 1.006 ± 0.002. Thus, fo−g depends significantly on the model used to calculate po.
 |
Fig. 9 Geometric projection factors calculated using radiative transfer in plane-parallel and in spherical geometry used together with the observational quantity |
6. Conclusion
Our rescaled hydrodynamical model of δ Cep is consistent with both spectroscopic and interferometric data modulo a rescaling factor that depends on the input parameters of the model (M,L,Teff,Z). In particular, it reproduces the observed amplitudes of the radial velocity curves associated with a selection of 17 unblended spectral lines as a function of the line depth in a very satisfactory way. This is a critical step for deriving the correct value of the projection factor. This strongly suggests that our decomposition of the projection factor into three physical terms is adequate. The next difficult step will be to measure p0 directly from the next generation of visible-wavelength interferometers. With such values in hand, it will be possible to derive fo−g directly from observations.
The projection factor is a complex quantity that is particularly sensitive to the definition of the radial velocity measurement. More details should be given and perhaps a standard procedure applied in future analyses. For instance, the CCFs are generally fitted with a Gaussian. This produces a velocity value sensitive to stellar rotation and to both the line width and depth (Nardetto et al. 2006). Thus, additional biases in the distance determination are introduced, in particular when comparing the projection factors of different Cepheids. Conversely, investigating the projection factor of individual lines is useful for learning how to mitigate the impact of the radial velocity modulation (Anderson 2014) and the possible angular-diameter modulation (Anderson et al. 2016) on the BW distances.
In this study, we found pcc−g = 1.24 ± 0.04 a value that is consistent with the Pp relation of Nardetto et al. (2009), i.e., pcc−g = 1.25 ± 0.05. However, a disagreement is still found between the interferometric and the infrared surface-brightness approaches (and their respective projection factors) in the case of δ Cep (Ngeow et al. 2012), while an agreement is found for the long-period Cepheid ℓ Car (Kervella et al. 2004b). This suggests that the p-factors adopted in these approaches might be affected by something not directly related to the projection factor itself but rather to other effects in the atmosphere or close to it, such as a static circumstellar environment (Nardetto et al. 2016). However, it is worth mentioning that the two methods currently provide absolutely the same results in terms of distances. After a long history (since Getting 1934), the BW projection factor remains a key quantity in the calibration of the cosmic distance scale, and one century after the discovery of the Period-Luminosity relation (Leavitt 1908), Cepheid pulsation is still a distinct challenge. With Gaia and other high-quality spectroscopic data, it will soon be possible to better constrain the Pp relation.
Acknowledgments
The observations leading to these results have received funding from the European Commission’s Seventh Framework Programme (FP7/2013−2016) under grant agreement No. 312430 (OPTICON). The authors thank the GAPS observers F. Borsa, L. Di Fabrizio, R. Fares, A. Fiorenzano, P. Giacobbe, J. Maldonado, and G. Scandariato. The authors thank the CHARA Array, which is funded by the National Science Foundation through NSF grants AST-0606958 and AST-0908253 and by Georgia State University through the College of Arts and Sciences, as well as the W. M. Keck Foundation. This research has made use of the SIMBAD and VIZIER Available at http://cdsweb.u- strasbg.fr/ databases at CDS, Strasbourg (France), and of the electronic bibliography maintained by the NASA/ADS system. W.G. gratefully acknowledges financial support for this work from the BASAL Centro de Astrofisica y Tecnologias Afines (CATA) PFB-06/2007, and from the Millenium Institute of Astrophysics (MAS) of the Iniciativa Cientifica Milenio del Ministerio de Economia, Fomento y Turismo de Chile, project IC120009. We acknowledge financial support for this work from ECOS-CONICYT grant C13U01. Support from the Polish National Science Center grant MAESTRO 2012/06/A/ST9/00269 is also acknowledged. E.P. and M.R. acknowledge financial support from PRIN INAF-2014. N.N., P.K., A.G., and W.G. acknowledge the support of the French-Chilean exchange program ECOS- Sud/CONICYT (C13U01). The authors acknowledge the support of the French Agence Nationale de la Recherche (ANR), under grant ANR-15-CE31-0012- 01 (project UnlockCepheids) and the financial support from “Programme National de Physique Stellaire” (PNPS) of CNRS/INSU, France.
References
- Anderson, R. I. 2014, A&A, 566, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anderson, R. I. 2016, MNRAS, 463, 1707 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, R. I., Sahlmann, J., Holl, B., et al. 2015, ApJ, 804, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, R. I., Mérand, A., Kervella, P., et al. 2016, MNRAS, 455, 4231 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, R. A., & Rodgers, A. W. 1964, MNRAS, 128, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Benedict, G. F., McArthur, B. E., Fredrick, L. W., et al. 2002, AJ, 124, 1695 [NASA ADS] [CrossRef] [Google Scholar]
- Borsa, F., Scandariato, G., Rainer, M., et al. 2015, A&A, 578, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burki, G., Mayor, M., & Benz, W. 1982, A&A, 109, 258 [NASA ADS] [Google Scholar]
- Cosentino, R., Lovis, C., Pepe, F., et al. 2012, in SPIE Conf. Ser., 8446, 1 [Google Scholar]
- Coudé du Foresto, V., Ridgway, S., & Mariotti, J.-M. 1997, A&AS, 121, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Derekas, A., Szabó, G. M., Berdnikov, L., et al. 2012, MNRAS, 425, 1312 [NASA ADS] [CrossRef] [Google Scholar]
- Derekas, A., Plachy, E., Molnar, L., et al. 2017, MNRAS, 464, 1553 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., Semel, M., Carter, B. D., Rees, D. E., & Collier Cameron, A. 1997, MNRAS, 291, 658 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Engle, S. G., Guinan, E. F., Harper, G. M., Neilson, H. R., & Remage Evans, N. 2014, ApJ, 794, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, N. R., Szabó, R., Derekas, A., et al. 2015, MNRAS, 446, 4008 [NASA ADS] [CrossRef] [Google Scholar]
- Fokin, A. B. 1991, MNRAS, 250, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Fouque, P., & Gieren, W. P. 1997, A&A, 320, 799 [NASA ADS] [Google Scholar]
- Freedman, W. L., Madore, B. F., Scowcroft, V., et al. 2012, ApJ, 758, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Geroux, C. M., & Deupree, R. G. 2015, ApJ, 800, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Getting, I. A. 1934, MNRAS, 95, 139 [NASA ADS] [Google Scholar]
- Gieren, W., Pietrzynski, G., Bresolin, F., et al. 2005a, The Messenger, 121, 23 [NASA ADS] [Google Scholar]
- Gieren, W., Storm, J., Barnes, III, T. G., et al. 2005b, ApJ, 627, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F., & Stevenson, K. B. 2007, PASP, 119, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Groenewegen, M. A. T. 2007, A&A, 474, 975 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groenewegen, M. A. T. 2013, A&A, 550, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hadrava, P., Šlechta, M., & Škoda, P. 2009, A&A, 507, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hertzsprung, E. 1913, Astron. Nachr., 196, 201 [NASA ADS] [Google Scholar]
- Houdek, G., & Dupret, M.-A. 2015, Liv. Rev. Sol. Phys., 12, 8 [CrossRef] [Google Scholar]
- Karp, A. H. 1975, ApJ, 201, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Kervella, P., Bersier, D., Mourard, D., Nardetto, N., & Coudé du Foresto, V. 2004a, A&A, 423, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Fouqué, P., Storm, J., et al. 2004b, ApJ, 604, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Laney, C. D., & Joner, M. D. 2009, in AIP Conf. Ser. 1170, eds. J. A. Guzik, & P. A. Bradley, 93 [Google Scholar]
- Leavitt, H. S. 1908, Annals of Harvard College Observatory, 60, 87 [Google Scholar]
- Leavitt, H. S., & Pickering, E. C. 1912, Harvard College Observatory Circular, 173, 1 [Google Scholar]
- Majaess, D., Turner, D., & Gieren, W. 2012, ApJ, 747, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Marengo, M., Sasselov, D. D., Karovska, M., Papaliolios, C., & Armstrong, J. T. 2002, ApJ, 567, 1131 [NASA ADS] [CrossRef] [Google Scholar]
- Marengo, M., Karovska, M., Sasselov, D. D., et al. 2003, ApJ, 589, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Merand, A., Kervella, P., Breitfelder, J., et al. 2015,A&A, 584, A80 [Google Scholar]
- Mérand, A., Kervella, P., Coudé du Foresto, V., et al. 2005, A&A, 438, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Fokin, A., Mourard, D., et al. 2004, A&A, 428, 131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Mourard, D., Kervella, P., et al. 2006, A&A, 453, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Mourard, D., Mathias, P., Fokin, A., & Gillet, D. 2007, A&A, 471, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Stoekl, A., Bersier, D., & Barnes, T. G. 2008, A&A, 489, 1255 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Gieren, W., Kervella, P., et al. 2009, A&A, 502, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Mathias, P., Fokin, A., et al. 2013, A&A, 553, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Poretti, E., Rainer, M., et al. 2014a, A&A, 561, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Storm, J., Gieren, W., Pietrzyński, G., & Poretti, E. 2014b, in Precision Asteroseismology, eds. J. A. Guzik, W. J. Chaplin, G. Handler, & A. Pigulski, IAU Symp., 301, 145 [Google Scholar]
- Nardetto, N., Mérand, A., Mourard, D., et al. 2016, A&A, 593, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neilson, H. R., & Ignace, R. 2014, A&A, 563, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neilson, H. R., Nardetto, N., Ngeow, C.-C., Fouqué, P., & Storm, J. 2012, A&A, 541, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ngeow, C.-C., Neilson, H. R., Nardetto, N., & Marengo, M. 2012, A&A, 543, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilecki, B., Graczyk, D., Pietrzyński, G., et al. 2013, MNRAS, 436, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Poretti, E., Le Borgne, J. F., Rainer, M., et al. 2015, MNRAS, 454, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Prša, A., Harmanec, P., Torres, G., et al. 2016, AJ, 152, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Macri, L., Casertano, S., et al. 2011, ApJ, 730, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Macri, L. M., Hoffmann, S. L., et al. 2016, ApJ, 826, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Sabbey, C. N., Sasselov, D. D., Fieldus, M. S., et al. 1995, ApJ, 446, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Sanford, R. F. 1956, ApJ, 123, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Sasselov, D. D., & Lester, J. B. 1990, ApJ, 362, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Storm, J., Gieren, W., Fouqué, P., et al. 2011a, A&A, 534, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Storm, J., Gieren, W., Fouqué, P., et al. 2011b, A&A, 534, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- ten Brummelaar, T. A., McAlister, H. A., Ridgway, S. T., et al. 2005, ApJ, 628, 453 [NASA ADS] [CrossRef] [Google Scholar]
- van Hoof, A., & Deurinck, R. 1952, ApJ, 115, 166 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, Astrophys. Space Sci. Libr., 350 [Google Scholar]
- van Leeuwen, F., Feast, M. W., Whitelock, P. A., & Laney, C. D. 2007, MNRAS, 379, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Wallerstein, G., Albright, M. B., & Ritchey, A. M. 2015, PASP, 127, 503 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional table
HARPS-N spectroscopic data of δ Cep.
All Tables
Non-exhaustive history of the determination of the Baade-Wesselink projection factor in the case of δ Cep.
All Figures
 |
Fig. 1 Mean line profile changes during the pulsation cycle of δ Cep. The line profile with the highest receding motion is highlighted in red, the one with the highest approaching motion in blue. |
| In the text | |
 |
Fig. 2 Panel a): HARPS-N radial velocities associated with the Gaussian fit of the cross-correlated line profile (RVcc−g using F5I template) plotted as a function of the pulsation phase of the star after correction of the γ-velocity (i.e., Vγ = −16.95km s-1 ). The cycle of observations are shown in different colors. The data are reproduced from one cycle to the other. The precision on the measurements is between 0.5 and 1.5 m s-1 (error bars are lower than symbols). Panel b) residuals between RVcc−c (F5I) and RVcc−g (F5I) after correction of their respective γ-velocities. |
| In the text | |
 |
Fig. 3 Inverse BW method applied to FLUOR/CHARA data (Mérand et al. 2005) considering a distance for δ Cep of d = 272 ± 3 ± 5 pc (Majaess et al. 2012) and the HARPS-N cross-correlated radial velocity curve. The black dotted line corresponds to the best fit. |
| In the text | |
 |
Fig. 4 Inverse BW method described in Sect. 3 applied considering a Gaussian distribution for the distance. The resulting projection factor distributions are shown in three particular cases: when using the cross-correlated radial velocity curve RVcc−g (red), the RVc radial velocity curve of line 7 (blue), and the RVc radial velocity curve of line 10 (green). The quantities σstat−d and σsyst−d are the uncertainties on the projection factor due to the statistical and systematical uncertainties on the distance, respectively. The quantity σstat−fluor stems from the statistical uncertainties on the FLUOR/CHARA interferometric measurements. |
| In the text | |
 |
Fig. 5 a) First moment radial velocity curves (RVc) associated with the 17 lines of Table 2. The γ-velocity associated with the cross-correlated radial velocity curve, RVcc−g in Fig. 2a, has been removed from these curves, i.e., Vγ = −16.95km s-1 . The γ offset residuals are known to be related to the k-term (Nardetto et al. 2008). The residuals between the RVc curves and the RVcc−g in Fig. 2a (resp. RVcc−c) are plotted in panel b) (resp. c)) after correcting each RVc curve from its Vγ value. |
| In the text | |
 |
Fig. 6 Observational projection factors derived using the inverse BW approach described in Sect. 3 compared to the theoretical values obtained from the hydrodynamical model (Sect. 4.1). |
| In the text | |
 |
Fig. 7 Amplitude of the radial velocity curves for the 17 spectral lines listed in Table 2 plotted versus the line depth for the hydrodynamical model (magenta squares), and for the HARPS-N spectroscopic observations (blue dots, except lines 10 and 17 plotted with filled red squares). A rescale of the model with a multiplying factor (i.e., fc) is necessary to fit the data (light blue circles). |
| In the text | |
 |
Fig. 8 FLUOR/CHARA limb-darkened angular diameter curve compared to the hydrodynamical model (see the text). |
| In the text | |
 |
Fig. 9 Geometric projection factors calculated using radiative transfer in plane-parallel and in spherical geometry used together with the observational quantity |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.