EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 596 (December 2016) A&A, 596 (2016) L3 Full HTML
Free Access
Issue
A&A
Volume 596, December 2016
Article Number L3
Number of page(s) 5
Section Letters
DOI https://doi.org/10.1051/0004-6361/201629680
Published online 23 November 2016

© ESO 2016

1. Introduction

Determining the fate of solids in protoplanetary disks is key for understanding the birth and growth of planets and planetary systems. While small grains are coupled to the disk gas, large particles drift inward as a consequence of angular momentum loss by aerodynamical gas drag. For meter sizes (assuming compact grains), the inward drift velocity is ~10-2 au/yr (e.g., Weidenschilling 1980; Nakagawa et al. 1981). For small dust grains, growth through pairwise collisions is faster than drift so that they grow in situ until they reach 1 to 100 cm, at which point drift starts to dominate (e.g., Okuzumi et al. 2012; Lambrechts & Johansen 2014). These so-called pebbles then drift rapidly with limited growth, implying that without a mechanism to suppress the drift, they would be lost to the central star.

Planetesimals would form directly by gravitational instability (GI) in the dust disk if it is sufficiently thin and dense (e.g., Goldreich & Ward 1973). However, even in low-turbulence disks, the Kelvin-Helmholtz (KH) instability generated by the vertical shear between the dust subdisk and the gas prevents the development of a disk that is thin enough (e.g., Weidenschilling 1995; Sekiya 1998). Youdin & Shu (2002) proposed that migrating dust (or pebbles) would pile up in the inner disk to become gravitationally unstable (see also Laibe et al. 2012), but they neglected grain growth, which was then shown to prevent this pile-up (see Krijt et al. 2016).

Another possibility to form planetesimals is to invoke streaming instabilities (SI) in the drifting pebble flow: when their density is high enough, clumps can form, and because they undergo relatively less gas drag, they accrete individual pebbles to rapidly form planetesimals of 100 to 1000 km (Youdin & Goodman 2005; Johansen et al. 2007). However, this mechanism requires a high solid-to-gas ratio (Z) and has also been shown to be difficult to achieve in realistic disks (Krijt et al. 2016).

With analytical calculations, we examine here the formation of planetesimals from drifting pebbles in smooth disks (i.e., without pressure bumps, gaps, or vortexes) through these two mechanisms. We highlight the importance of sublimation across the snow line. Instead of examining the consequence of ice deposition beyond the snow line in turbulent disks (e.g., Stevenson & Lunine 1988; Ros & Johansen 2013; Armitage et al. 2016), following Saito & Sirono (2011), we concentrate on the region inside the snow line where dust grains ejected from sublimated pebbles are present.

2. Pebble-to-gas surface density ratio

We consider a protoplanetary disk characterized by a steady gas accretion rate Ṁ∗ in which the solids are in the form of pebbles migrating inward at a mass flux Ṁpeb. The surface density of the migrating pebbles Σp and the disk gas Σg are given by 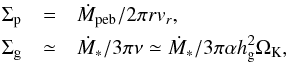Σp=Ṁpeb/2πrvr,Σg≃\begin{eqnarray} \sigp & = & \mdotf/2\pi r \vr, \nonumber\\ \sigg & \simeq & \dot{M}_*/3\pi \nu\simeq \dot{M}_*/3\pi \alpha \hg^2 \Omega_{\rm K}, \label{eq:Sigma} \end{eqnarray}(1)where ν is the turbulent viscosity of the gas disk, hg the gas scale height, ΩK the Keplerian frequency, and vr is the pebble migration speed. 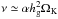We use the α-prescription, that is, ν≃αhg2ΩK\hbox{$\nu \simeq \alpha \hg^2 \Omega_{\rm K}$}.

The inward radial drift speed of solids was calculated in the limit of a static disk by Nakagawa et al. (1986) and in the limit of a low solid-to-gas ratio by Guillot et al. (2014). Combining the two yields 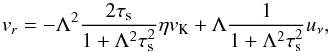vr=−Λ22τs1+Λ2τs2ηvK+Λ11+Λ2τs2uν,\begin{equation} \vr = -\Lambda^2 \frac{2\st}{1+\Lambda^2 \st^2}\eta \vk + \Lambda \frac{1}{1+\Lambda^2 \st^2}u_\nu, \label{eq:vr} \end{equation}(2)where the back-reaction of the gas to the motion of solids has been included through Λ ≡ ρg/ (ρg + ρp), and ρg and ρp are the mid-plane densities of gas and solids, respectively. We included the Λ-dependence of uν as well for later purposes. In Eq. (2), the size of the solids is defined through their Stokes number τs, which is the ratio of their stopping time due to gas drag (tstop) to the Kepler frequency as 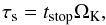τs=tstopΩK,\begin{equation} \st = t_{\rm stop}\Omega_{\rm K}, \end{equation}(3)uν is the radial velocity of the accreting disk gas, which in the inner regions of a vertically uniform disk may be approximated by 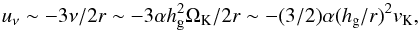uν~−3ν/2r~−3αhg2ΩK/2r~−(3/2)α(hg/r)2vK,\begin{equation} u_\nu \sim - 3\nu/2r \sim - 3 \alpha \hg^2 \Omega_{\rm K}/2r \sim - (3/2) \alpha (\hg/r)^2 \vk, \label{eq:ur} \end{equation}(4)and η(≪ 1) is the deviation fraction of the gas orbital angular velocity (Ω) relative to the Keplerian angular velocity (ΩK) that is due to the radial pressure gradient in the disk, 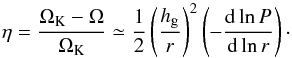η=ΩK−ΩΩK≃12(hgr)2(−dlnPdlnr)·\begin{equation} \eta = \frac{\Omega_{\rm K}-\Omega}{\Omega_{\rm K}}\simeq \frac{1}{2} \left(\frac{\hg}{r}\right)^2 \left( - \frac{{\rm d} \ln P}{{\rm d} \ln r} \right)\cdot \label{eq:eta0} \end{equation}(5)From Eqs. (2), (4), and (5), vr≃−11+Λ2τs2[Λ2τs(−dlnPdlnr)+Λ3α2](hgr)2vK.\begin{equation} \vr \simeq - \frac{1}{1+\Lambda^2\st^2} \left[ \Lambda^2 \st \left( -\frac{{\rm d} \ln P}{{\rm d} \ln r} \right) + \Lambda \frac{3\alpha}{2} \right] \left(\frac{\hg}{r}\right)^2 \vk. \label{eq:vr2} \end{equation}(6)Using Eq. (1), we then obtain the solid-to-gas ratio as Z=ΣpΣg≃3α2(hgr)2vKvrṀpebṀ∗≃\begin{eqnarray} Z = \frac{\sigp}{\Sigma_g} & \simeq & \frac{3 \alpha}{2} \left(\frac{\hg}{r}\right)^2 \frac{\vk}{\vr} \frac{\mdotf}{\dot{M}_*} \nonumber \\ & \simeq & \left(1+\Lambda^2 \st^2\right) \left[ \frac{2 \st}{3 \alpha} \Lambda^2 \left(- \frac{{\rm d} \ln P}{{\rm d} \ln r} \right) + \Lambda \right]^{-1} \frac{\mdotf}{\dot{M}_*} \cdot \label{eq:solid_to_gas} \end{eqnarray}(7)

Now, the parameter Λ may be estimated in the limit of a vertically isothermal disk as 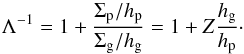Λ-1=1+Σp/hpΣg/hg=1+Zhghp·\begin{equation} \Lambda^{-1} = 1 + \frac{\sigp/\hp}{\sigg/\hg} = 1 + Z\frac{\hg}{\hp}\cdot \label{eq:Lambda} \end{equation}(8)This thus leads to the following second-order equation in Z: 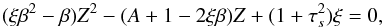(ξβ2−β)Z2−(A+1−2ξβ)Z+(1+τs2)ξ=0,\begin{equation} (\xi\beta^2-\beta)Z^2-(A+1-2\xi \beta)Z+(1+\tau_s^2)\xi=0,\label{eq:Z-eq} \end{equation}(9)where we have defined a few quantities, 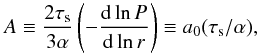A≡2τs3α(−dlnPdlnr)≡a0(τs/α),\begin{equation} A \equiv \frac{2\st}{3\alpha} \left(-\frac{{\rm d}\ln P}{{\rm d}\ln r}\right)\equiv a_0(\st/\alpha), \end{equation}(10)and we adopt a0 ≈ 1.75 as a0 is estimated to be ≈1.70−1.85 for radially smooth disks with both viscous heating and stellar irradiation (see Ida et al. 2016), β is the ratio of the gas-to-dust pressure scale heights (Dubrulle et al. 1995; Youdin & Lithwick 2007), 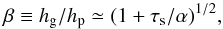β≡hg/hp≃(1+τs/α)1/2,\begin{equation} \beta \equiv \hg/\hp\simeq (1+\st/\alpha)^{1/2}, \end{equation}(11)and ξ is the ratio of the solid mass flux to the gas mass flux: 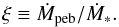ξ≡Ṁpeb/Ṁ∗.\begin{equation} \xi \equiv \dot{M}_{\rm peb}/ \dot{M}_*. \end{equation}(12)The solutions to Eq. (9)are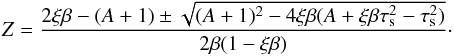Z=2ξβ−(A+1)±(A+1)2−4ξβ(A+ξβτs2−τs2)2β(1−ξβ)·\begin{equation} Z=\frac{2\xi\beta - (A+1) \pm \sqrt{(A+1)^2-4\xi\beta (A+\xi\beta\st^2-\st^2)}}{2\beta(1- \xi\beta)}\cdot \label{eq:Z} \end{equation}(13)

Figure 1 shows the solutions to Eq. (13) obtained for Z as a function of τs for different values of the pebble-to-gas-mass flux ratio ξ. For pebbles, we expect τs ~ 0.1 (Sato et al. 2016; Ida et al. 2016), so that τs ≫ α and hence A/a0 ≃ β2 ≫ 1, yielding the approximate solution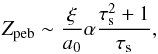Zpeb~ξa0ατs2+1τs,\begin{equation} Z_{\rm peb}\sim \frac{\xi}{a_0}\alpha\frac{\st^2+1}{\st}, \label{eq:Zpeb} \end{equation}(14)which fits the lower-Z solutions in Fig. 1 for τs ≳ 10-2. This approximate solution can be easily derived from Eq. (7) with τs ≫ α and Λ ≃ 1. The dependence on α appears because, as shown by Eq. (1), Σg ∝ 1 /α and Σp is independent of α for τs ~ 0.1. The fast drift of pebbles is responsible for the small Zpeb.

thumbnail Fig. 1

Steady-state solutions for the solid-to-gas mixing ratio Z as a function of the Stokes number of solid particles τs for different values of the solid-to-dust-mass flux ratio ξ (as labeled), assuming a value of the turbulent viscosity α = 10-3. The values of τs corresponding to expected pebble sizes are highlighted with larger symbols. The two solutions provided by Eq. (13)are indicated by filled and open symbols, respectively. The gray area highlights the region in which planetesimals should form by a streaming instability (Carrera et al. 2015).

We expect planetesimal formation to occur either by GI in the dust disk when ρp ≳ ρR, where ρR ~ M∗/r3 is the Roche density, independently of the dust size, or by SI with Z as low as ~0.02 but a limited range of τs values (Dra¸żkowska & Dullemond 2014; Carrera et al. 2015, also see Fig. 1). In general, the condition for GI, ρp ≳ ρR, is difficult to reach because of the vertical shear that is due to KH instabilities and thus requires very high values of Z.

We see in Fig. 1 that the formation of pebbles by SI is possible but requires high values of ξ. The criterion for planetesimals to form directly from τs ~ 0.1 pebbles is Zpebble~>0.02. From Eq. (14), this implies 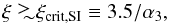ξ~>ξcrit,SI≡3.5/α3,\begin{equation} \xi\wig{>} \xi_{\rm crit,SI} \equiv 3.5 /\alpha_3, \end{equation}(15)where α3 = α/ 10-3. We show below that this condition, which requires the mass flux of pebbles to be equivalent to the mass flux of gas, is difficult to reach (see also Krijt et al. 2016). One possibility is to advocate high values of α (see Armitage et al. 2016), but this is generally not favored by the latest magnetohydrodynamical simulations of protoplanetary disks (e.g., Bai 2015). Other possibilities exist that require local perturbations in the disk to modify the pressure gradient term (e.g., Johansen et al. 2014, and references therein) or favorable conditions in terms of fragmentation threshold velocity and disk properties (Laibe 2014; Drazkowska et al. 2016). We show below that the conditions necessary to form planetesimals can be reached at lower ξ values and for small α-disks next to a snow line. Before we examine this possibility, it is worth noting that for small particles (with τs ≲ 10-3), no solution is found for ξ ≳ 1, meaning that no steady-state exists: if there were a way to have small particles drift in at a very high rate or to deplete disk gas preferentially, the particles would pile up and accumulate, eventually forming planetesimals by direct gravitational instability.

3. Solid-to-gas density ratio inside of the snow line

When the inward-drifting pebbles cross the snow line, they progressively sublimate until only small refractory (silicate dust) seeds remain (e.g., Saito & Sirono 2011; Morbidelli et al. 2016). Observations of the interstellar medium and of interplanetary dust particles indicate that these dust seeds should be of submicron size, corresponding to τs ~ 10-7−10-5. Even for the much larger millimeter-sized chondrules, we expect τs to be between 10-4 and 5 × 10-2 at most in a rarefied disk. The presence of a snow line is thus a way of transforming a high-mass flux of fast-drifting pebbles into a flux of small, slow-drifting dust particles.

Two additional factors need to be considered. First, the sublimation of the ice decreases the amount of solid material by a factor ζ0 ~ 1/3 corresponding to the ratio of the mass of dust (silicate components) to the total mass of condensates (dust+ice) (Lodders 2003). By assuming for simplicity that the pebbles instantaneously form small dust particles, the flux of material to inside of the snow line that is to be considered in Eq. (13)is now therefore ξ → ζ0ξpeb, where ξpeb corresponds to the ratio of the non-sublimated pebble mass flux to the gas mass flux.

Second, we expect dust grains to retain a memory of the vertical scale height of the pebbles. Their vertical mixing timescale can be estimated to be 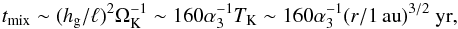tmix~(hg/ℓ)2ΩK-1~160α3-1TK~160α3-1(r/1 au)3/2yr,\begin{equation} t_{\rm mix} \sim (\hg/\ell)^2 \Omega_{\rm K}^{-1} \sim 160 \alpha_3^{-1} T_{\rm K} \sim 160 \alpha_3^{-1} (r/1{\,\rm au})^{3/2}~{\rm yr}, \label{eq:t_mix} \end{equation}(16)where 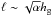ℓ~αhg\hbox{$\ell \sim \sqrt{\alpha} \hg$} is the estimated vertical mean free path and TK is Kepler period. Comparing a sublimation timescale with a migration timescale for pebbles, we can derive the radial width for completion of the sublimation as Δr ~ 10-2(R/ 10 cm)1/2r (see also Ciesla & Cuzzi 2006). With Eq. (1), the timescale for the pebble flux to establish Z ≳ 1 in the sublimation region is estimated as 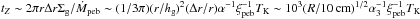tZ~2πrΔrΣg/Ṁpeb~(1/3π)(r/hg)2(Δr/r)α-1ξpeb-1TK~103(R/10 cm)1/2α3-1ξpeb-1TK\hbox{$t_Z \sim 2\pi r \Delta r \sigg/\dot{M}_{\rm peb} \sim (1/3\pi) (r/\hg)^2(\Delta r/r)\alpha^{-1}\xi_{\rm peb}^{-1} T_{\rm K} \sim 10^3 (R/10\,{\rm cm})^{1/2} \alpha_3^{-1}\xi_{\rm peb}^{-1} T_{\rm K}$}. Although tZ for R = 10 cm is 10−100 times longer than tmix, the effective R for sublimation would be much smaller and tZ would be much shorter for more realistic fluffy pebbles (e.g., Kataoka et al. 2013). We can thus assume that the dust seeds released by the sublimating pebbles have the same vertical thickness as the pebbles themselves. This is done in Eq. (13)by replacing β by the value set by the pebble subdisk β → β0 ~ (1 + τs,peb/α)1/2.

thumbnail Fig. 2

Steady-state solutions for the solid-to-gas mixing ratio Z as a function of the solid-to-gas-mass flux ratio ξ for different values of the Stokes number of solid particles τs (from 10-5 to 10-2, as labeled), assuming two values of the turbulent viscosity α = 10-4 (in blue) and α = 10-3 (in red). Equation (13) is numerically solved. In contrast to Fig. 1, we now consider that initially icy pebbles with τs,peb ~ 0.1 and containing a mass fraction ζ0 = 1/3 in dust sublimate inside of the snow line. The thicker lines corresponds to the preferred value for the dust particles, τs = 10-4.

As shown in Fig. 2, the situation is now much more favorable toward the development of GI of the layer of sublimated pebbles. As pointed out by Saito & Sirono (2011) and Birnstiel et al. (2012), the release of small slow-drifting dust by fast-drifting pebbles naturally yields values of Z that are much higher than for pebbles. It first increases linearly with ξpeb. However, when the pebble flux is high enough to yield ρp/ρg ≳ 1, the dust migration velocity decreases as a result of the inertia of the dust, which further enhances ρp/ρg. The value of Z then increases more than linearly with ξpeb until the positive feedback becomes so strong that no steady-state solution can be found. At this point, we expect ρp to rapidly exceed ρR, and planetesimals are formed by GI.

It is useful at this point to rederive Eq. (13) for these small grains, that is, in the limit of A ≪ 1 and τs ≪ 1: 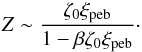Z~ζ0ξpeb1−βζ0ξpeb·\begin{eqnarray} Z \sim \frac{\zeta_0 \xi_{\rm peb}}{1-\beta \zeta_0 \xi_{\rm peb}}\cdot \label{eq:Z2} \end{eqnarray}(17)For these small grains, the critical value ξcrit above which no steady-state solution exists can be easily derived by calculating when the denominator of Eqs. (13) or (17) becomes zero, that is, 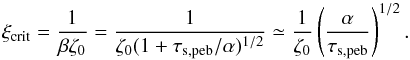ξcrit=1βζ0=1ζ0(1+τs,peb/α)1/2≃1ζ0(ατs,peb)1/2.\begin{equation} \xi_{\rm crit} = \frac{1}{\beta \zeta_0} = \frac{1}{\zeta_0 (1+\tau_{\rm s,peb}/\alpha)^{1/2}} \simeq \frac{1}{\zeta_0}\left(\frac{\alpha}{\tau_{\rm s,peb}}\right)^{1/2}. \label{eq:xi_crit} \end{equation}(18)The critical value ξcrit is thus independent of the local pressure gradient. This is because the small dust grains ejected from sublimating pebbles are coupled to the disk gas motion and migrate with disk gas accretion and not by gas drag.

As shown by Fig. 2, higher values of ξcrit are possible for τs ≫ α, a possibility that we do not consider here because we expect seed grains to be such that τs ≲ 10-5. Typically, we thus obtain ξcrit ≃ 0.3 for α = 10-3, ζ0 = 1/3 and τs,peb = 0.1. The fact that ξcrit scales with α1/2 is governed by the height of the dust and pebble subdisk. The formation of dust-rich planetesimals inside of the snow line is thus favored in weakly turbulent disks.

4. Pebble flux and planetesimal formation

The pebble mass flux is calculated by the mass in dust swept by the pebble formation front at r ≃ rpeb per unit time (Lambrechts & Johansen 2014; Ida et al. 2016), Ṁpeb≃2πrpeb×Z0Σg(rpeb)×drpebdt,\begin{equation} \dot{M}_{\rm peb} {\displaystyle \simeq 2\pi r_{\rm peb} \times Z_0 \Sigma_g(r_{\rm peb}) \times \frac{{\rm d}r_{\rm peb}}{{\rm d}t}}, \label{eq:M_F_est} \end{equation}(19)where Z0 is the solid-to-gas ratio in the pebble formation region. The growth time of pebbles from μm sized dust grains is given by (Takeuchi & Lin 2005; Okuzumi et al. 2012; Ida et al. 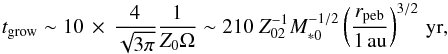2016) tgrow~10 × 43π1Z0Ω~210Z02-1M∗0−1/2(rpeb1 au)3/2 yr,\begin{equation} t_{\rm grow} \sim 10 \, \times \, \frac{4}{\sqrt{3\pi}} \frac{1}{Z_0 \Omega}\sim 210 \; Z_{02}^{-1} M_{*0}^{-1/2} \left(\frac{r_{\rm peb}}{1\,\au}\right)^{3/2}\,{\rm yr}, \label{eq:t_grow} \end{equation}(20)where Z02 = Z0/ 0.01. From this equation, the pebble formation front radius is given by 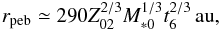rpeb≃290Z022/3M∗01/3t62/3 au,\begin{equation} r_{\rm peb} \simeq 290 Z_{02}^{2/3} M_{*0}^{1/3}t_6^{2/3}\,\au, \end{equation}(21)where t6 = t/ 106 yr. Because ice needs to condense, rpeb ≳ 1 au, implying that pebbles may start forming when t ≳ 200 yr. Substituting this relation into Eq. (19) with ṙpeb/rpeb = (2/3tgrow), we obtain 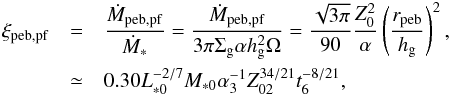ξpeb,pf=Ṁpeb,pfṀ∗=Ṁpeb,pf3πΣgαhg2Ω=3π90Z02α(rpebhg)2,≃\begin{eqnarray} \xi_{\rm peb,pf} & =& \frac{\dot{M}_{\rm peb,pf}}{\dot{M}_*} = \frac{\dot{M}_{\rm peb,pf}}{3 \pi \sigg \alpha \hg^2 \Omega} = \frac{\sqrt{3\pi}}{90}\frac{Z_0^2}{\alpha} \left(\frac{r_{\rm peb}}{\hg}\right)^2, \nonumber \\ & \simeq& 0.30 L_{*0}^{-2/7}M_{*0} \alpha_3^{-1} Z_{02}^{34/21} t_6^{-8/21}, \label{eq:xi_pf} \end{eqnarray}(22)where L∗ 0 = L∗/L⊙, M∗ 0 = L∗/M⊙, α3 = α/ 10-3, and we considered the irradiation-dominated regime with 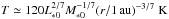T≃120L∗02/7M∗0−1/7(r/1 au)−3/7K\hbox{$T \simeq 120 L_{*0}^{2/7}M_{*0}^{-1/7} (r/1\,\au)^{-3/7}\; {\rm K}$}, for the pebble formation region in the outer disk. This corresponds to the disk aspect ratio, 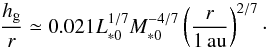hgr≃0.021L∗01/7M∗0−4/7(r1 au)2/7·\begin{equation} \frac{\hg}{r} \simeq 0.021 L_{*0}^{1/7}M_{*0}^{-4/7} \left(\frac{r}{1\,\au}\right)^{2/7}\cdot \label{eq:h_irr} \end{equation}(23)(The expressions are slightly simplified compared to Ida et al. 2016.) The pebble mass flux is given by ξpeb,pfṀ∗, implying 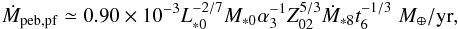Ṁpeb,pf≃0.90×10-3L∗0−2/7M∗0α3-1Z025/3Ṁ∗8t6−1/3M⊕/yr,\begin{equation} \dot{M}_{\rm peb,pf} \simeq 0.90 \times 10^{-3} L_{*0}^{-2/7}M_{*0} \alpha_3^{-1} Z_{02}^{5/3}\dot{M}_{*8} t_6^{-1/3} \;\mearth/{\rm yr}, \label{eq:M_F_est2} \end{equation}(24)where Ṁ∗ 8 = Ṁ∗/ (10-8M⊙/ yr). This mass flux is higher than obtained by Lambrechts & Johansen (2014) because they assumed a lower initial surface density in the gas disk (Σg = 500 g/cm2 at 1 au, not tied to the mass flux in the disk) and a 1/2 coagulation probability.

When rpeb exceeds the disk size rout, that is, when t ≳ 2 × 105(rout/ 100 au)3/2 yr, we would expect Ṁpeb to decay more rapidly than Ṁ∗ because most of the solid material has been made into pebbles and drifted in (Sato et al. 2016). This may be inconsistent with the observational data that show that mm or cm sized particles survive in the disks for several million years (Brauer et al. 2007). However, we expect strong turbulence due to GI of the gas disk (not GI of the dust subdisk) to limit this fast spread of the pebble front, which could explain the presence of mm or cm sized particles for relatively long times.

Disks with Σg given by Eq. (1) are gravitationally unstable in their outer parts unless the disk is compact. In the unstable parts, their surface density should evolve to become marginally unstable so that 1 ~ Q = csΩ /πGΣg,GI, or equivalently 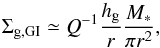Σg,GI≃Q-1hgrM∗πr2,\begin{equation} \Sigma_{\rm g,GI} \simeq Q^{-1} \frac{h_{\rm g}}{r} \frac{M_*}{\pi r^2}, \label{eq:GI} \end{equation}(25)where Q is a factor on the order of unity. In these regions, the turbulence generated by gravitational waves (assumed to lead to αGI ~ 0.1) may be high enough that collisions between icy grains result in fragmentation rather than coalescence. Typical collision velocities are estimated to be 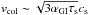vcol~3αGIτscs\hbox{$v_{\rm col}\sim \sqrt{3 \alpha_{\rm GI} \st} c_{\rm s}$} (Sato et al. 2016). Assuming a sound speed cs ~ 270(r/ 100 au)− 3/14 m/s implies vcol ~ 50(αGI/ 0.1)1/2(τs/ 0.1)1/2(r/ 100 au)− 3/14 m/s. The threshold velocity for fragmentation of icy particles is predicted to be around 20−100 m/s (e.g., Blum & Wurm 2000; Zsom et al. 2011; Wada et al. 2011). We therefore assume that pebbles may form only in the stable parts of the disks, that is, for r<rGI, implying that the location of the pebble formation front is given by min(rpeb,rGI).

Since Σg given by Eq. (1) is equal to Σg,GI at r = rGI, we obtain Q(rGI/hg)3 ≃ 3α(M∗/Ṁ∗)Ω, where α is the turbulence parameter for the inner regions. With Eq. (23), 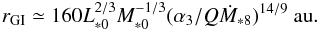rGI≃160L∗02/3M∗0−1/3(α3/QṀ∗8)14/9au.\begin{equation} r_{\rm GI} \simeq 160 L_{*0}^{2/3}M_{*0}^{-1/3}(\alpha_3/Q \dot{M}_{*8})^{14/9}~\au.\label{eq:r_GI} \end{equation}(26)As Ṁ∗ decreases with time, rGI increases. From (drGI/ dt) /rGI ~ −(14/9)(dṀ∗/ dt) /Ṁ∗ and Eq. (25), the pebble mass flux that is due to the outward spread of rGI is 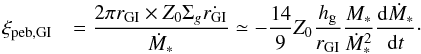ξpeb,GI=2πrGI×Z0ΣgrGI˙Ṁ∗≃−149Z0hgrGIM∗Ṁ2∗dṀ∗dt·\begin{equation} \begin{array}{ll} \xi_{\rm peb,GI} & {\displaystyle = \frac{2\pi r_{\rm GI} \times Z_0 \Sigma_g \dot{r_{\rm GI}} }{\dot{M}_*} \simeq - \frac{14}{9} Z_0 \frac{h_{\rm g}}{r_{\rm GI}} \frac{M_*}{\dot{M}_*^2} \frac{{\rm d} \dot{M}_*}{{\rm d}t}\cdot } \end{array} \label{eq:xi_GI} \end{equation}(27)We now use the relation between accretion rate and age suggested by the observations of young clusters, 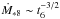Ṁ∗8~t6−3/2\hbox{$\dot{M}_{*8} \sim t_6^{-3/2}$} (Hartmann et al. 1998). This yields 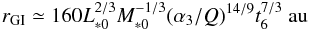rGI≃160L∗02/3M∗0−1/3(α3/Q)14/9t67/3au\begin{equation} r_{\rm GI} \simeq 160 L_{*0}^{2/3}M_{*0}^{-1/3} (\alpha_3/Q)^{14/9} t_6^{7/3}\ \au \end{equation}(28)and 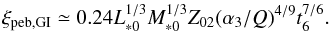ξpeb,GI≃0.24L∗01/3M∗01/3Z02(α3/Q)4/9t67/6.\begin{equation} \xi_{\rm peb,GI} \simeq 0.24 L_{*0}^{1/3}M_{*0}^{1/3} Z_{02} (\alpha_3/Q)^{4/9} t_6^{7/6}. \label{eq:xi_pebGI} \end{equation}(29)Equivalently, 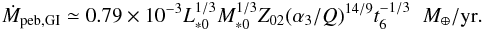Ṁpeb,GI≃0.79×10-3L∗01/3M∗01/3Z02(α3/Q)14/9t6−1/3M⊕/yr.\begin{equation} \dot{M}_{\rm peb,GI} \simeq 0.79 \times 10^{-3} L_{*0}^{1/3}M_{*0}^{1/3}Z_{02} (\alpha_3/Q)^{14/9} t_6^{-1/3} \;\;\mearth/{\rm yr}. \end{equation}(30)

Figure 3 shows the evolution of the pebble formation front, the pebble mass flux Ṁper , and ξpeb. The mass flux ratio ξpeb reaches a maximum when rGI = rpeb. This maximum value is proportional to α− 29/45, whereas ξcrit ∝ α1/2. For the α = 10-3 case, we see that ξpeb becomes equal to ξcrit obtained from Eq. (18)only for a very short time. The α = 10-4 case, in contrast, leads to a prolonged period in which planetesimals can form inside the snow line. Thus, direct formation of planetesimals is possible in low-turbulence disks. Conversely, in high-turbulence disks, the relatively low maximum values of ξpeb obtained imply that other mechanisms have to be sought so that planetesimals can form. This may involve disk photoevaporation, disk winds, or growth of pebbles by ice condensation.

thumbnail Fig. 3

Time evolution of a) radius of the pebble formation front, b) pebble accretion rate (Ṁpeb), and c) ξpeb = Ṁpeb/Ṁ∗ for two values of α, 10-4 (red) and 10-3 (blue). The lines labeled “grow” (dotted) and “GI” (dashed) represent the pebble growth and disk GI limits, respectively. The thick solid lines express the actual values obtained by the minima of the two limits. Here we assumed τs,peb = 0.1 and Z0 = 0.01. In panel c), the small squares represent the points with ξpeb>ξcrit, see Eq. (18).

When formed by GI, the mass of a clump is 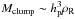Mclump~hp3ρR\hbox{$M_{\rm clump}\sim \hp^3 \rho_{\rm R}$}, where ρR ~ M∗/r3 is the Roche density. If the clump shrinks into a planetesimal with physical radius R and bulk density ρs ( ~1 g cm-3), then for the solar case, 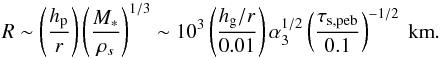R~(hpr)(M∗ρs)1/3~103(hg/r0.01)α31/2(τs,peb0.1)−1/2km.\begin{equation} R \sim \left(\frac{\hp}{r}\right)\left(\frac{M_*}{\rho_s}\right)^{1/3} \sim 10^3 \left(\frac{\hg/r}{0.01}\right) \alpha_3^{1/2} \left(\frac{\stpeb}{0.1}\right)^{-1/2}\ {\rm km}. \end{equation}(31)Although a more detailed analysis would be required, it appears that the planetesimals formed through this mechanism are as large as those formed by SI (e.g., Johansen et al. 2014).

5. Discussion and conclusion

With a simple model of pebble growth, drift, and sublimation at the snow line, we have examined the conditions for the formation of planetesimals in protoplanetary disks.

We first showed that forming planetesimals from streaming instability in the flow of icy pebbles requires both a high level of turbulence (α ≳ 0.01) and an unrealistically high pebble flux. We note that for these high turbulence levels, water vapor diffusion can decrease the requirement on the pebble mass flux (e.g., Ros & Johansen 2013; Armitage et al. 2016).

By including the often neglected mass-loading factor in the equations for the drift of solids, we have shown that the pile-up of solids inside of the snow line leads to the formation of dust-rich planetesimals directly by gravitational instability in the dust subdisk. This instability exists for relatively high values of ξ, the pebble-to-gas-mass flux ratio, and for relatively low values of α.

With a simple model of the formation of pebbles, we have demonstrated that super-critical values of the pebble-to-gas mass flux ξ ≥ ξcrit are reached in disks with α ≲ 10-3. This condition may be reached more easily, that is, for higher values of α or lower values of ξ, by taking into account disk gas depletion mechanisms other than viscous disk accretion such as photoevaporation or disk winds. The planetesimals that are formed in this way are expected to be large, probably larger than 100 km in radius.

During that time, the H2O snow line could move from several au to inside of 1au (e.g., Oka et al. 2011). These planetesimals are expected to be composed of a high fraction of dust (silicates), which may explain why the rock-to-ice fractions inferred in minor planets and moons in the outer solar system (e.g., Schubert et al. 2010) or the dust-to-ice ratio in comets (e.g., Rotundi et al. 2015; Lorek et al. 2016) are often significantly higher than the expected 1/2 to 1/3 value obtained from purely solar composition (e.g., Lodders 2003).

Our model requires a fast breakup of pebbles, however, so that the dust particles are released over a small annulus. Given that we expect these pebbles to be porous (e.g., Kataoka et al. 2013), this should be verified. We note that the possibility that disks have flow in the midplane that are directed outward (Takeuchi & Lin 2005) or are stochastic (Suzuki & Inutsuka 2014) will favor the mechanism that we propose.

Finally, this process may apply to other sublimation lines (e.g., Drozdovskaya et al. 2016) if these lead to the breakup of fluffy pebbles into much smaller grains. Indeed, sintering has been shown to have this effect and thus might explain the rings that were recently observed in young disks (Okuzumi et al. 2016). The pile-up and planetesimal formation mechanism that we propose may thus naturally explain the formation of rings of planetesimals in low-turbulence disks.

Acknowledgments

We thank Chris Ormel, Anders Johansen, Satoshi Okuzumi, and an anonymous referee for helpful comments. S. I. thanks for the hospitality he experienced during his visit to the Observatoire de la Côte d’Azur, which was made possible thanks to support from OCA BQR. S.I. is also supported by MEXT Kakenhi grant 15H02065. We acknowledge support by the French ANR, project number ANR-13-13-BS05- 0003-01 projet MOJO (Modeling the Origin of JOvian planets).

References

  1. Armitage, P. J., Eisner, J. A., & Simon, J. B. 2016, ApJ, 828, L2 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bai, X.-N. 2015, ApJ, 798, 84 [NASA ADS] [CrossRef] [Google Scholar]
  3. Birnstiel, T., Klahr, H., & Ercolano, B. 2012, A&A, 539, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Blum, J., & Wurm, G. 2000, Icarus, 143, 138 [NASA ADS] [CrossRef] [Google Scholar]
  5. Brauer, F., Dullemond, C. P., Johansen, A., et al. 2007, A&A, 469, 1169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Carrera, D., Johansen, A., & Davies, M. B. 2015, A&A, 579, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Ciesla, F. J., & Cuzzi, J. N. 2006, Icarus, 181, 178 [NASA ADS] [CrossRef] [Google Scholar]
  8. Drążkowska, J., & Dullemond, C. P. 2014, A&A, 572, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Drazkowska, J., Alibert, Y., & Moore, B. 2016, A&A, 594, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Drozdovskaya, M. N., Walsh, C., van Dishoeck, E. F., et al. 2016, MNRAS, 462, 977 [NASA ADS] [CrossRef] [Google Scholar]
  11. Dubrulle, B., Morfill, G., & Sterzik, M. 1995, Icarus, 114, 237 [NASA ADS] [CrossRef] [Google Scholar]
  12. Goldreich, P., & Ward, W. R. 1973, ApJ, 183, 1051 [NASA ADS] [CrossRef] [Google Scholar]
  13. Guillot, T., Ida, S., & Ormel, C. W. 2014, A&A, 572, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [NASA ADS] [CrossRef] [Google Scholar]
  15. Ida, S., Guillot, T., & Morbidelli, A. 2016, A&A, 591, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Johansen, A., Oishi, J. S., Mac Low, M.-M., et al. 2007, Nature, 448, 1022 [Google Scholar]
  17. Johansen, A., Blum, J., Tanaka, H., et al. 2014, Protostars and Planets VI, 547 [Google Scholar]
  18. Kataoka, A., Tanaka, H., Okuzumi, S., & Wada, K. 2013, A&A, 557, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Krijt, S., Ormel, C. W., Dominik, C., & Tielens, A. G. G. M. 2016, A&A, 586, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Laibe, G. 2014, MNRAS, 437, 3037 [NASA ADS] [CrossRef] [Google Scholar]
  21. Laibe, G., Gonzalez, J.-F., & Maddison, S. T. 2012, A&A, 537, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Lambrechts, M., & Johansen, A. 2014, A&A, 572, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
  24. Lorek, S., Gundlach, B., Lacerda, P., & Blum, J. 2016, A&A, 587, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Morbidelli, A., Bitsch, B., Crida, A., et al. 2016, Icarus, 267, 368 [NASA ADS] [CrossRef] [Google Scholar]
  26. Nakagawa, Y., Nakazawa, K., & Hayashi, C. 1981, Icarus, 45, 517 [NASA ADS] [CrossRef] [Google Scholar]
  27. Nakagawa, Y., Sekiya, M., & Hayashi, C. 1986, Icarus, 67, 375 [NASA ADS] [CrossRef] [Google Scholar]
  28. Oka, A., Nakamoto, T., & Ida, S. 2011, ApJ, 738, 141 [NASA ADS] [CrossRef] [Google Scholar]
  29. Okuzumi, S., Tanaka, H., Kobayashi, H., & Wada, K. 2012, ApJ, 752, 106 [NASA ADS] [CrossRef] [Google Scholar]
  30. Okuzumi, S., Momose, M., Sirono, S.-I., Kobayashi, H., & Tanaka, H. 2016, ApJ, 821, 82 [NASA ADS] [CrossRef] [Google Scholar]
  31. Ros, K., & Johansen, A. 2013, A&A, 552, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Rotundi, A., Sierks, H., Della Corte, V., et al. 2015, Science, 347, aaa3905 [Google Scholar]
  33. Saito, E., & Sirono, S.-I. 2011, ApJ, 728, 20 [NASA ADS] [CrossRef] [Google Scholar]
  34. Sato, T., Okuzumi, S., & Ida, S. 2016, A&A, 589, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Schubert, G., Hussmann, H., Lainey, V., et al. 2010, Space Sci. Rev., 153, 447 [NASA ADS] [CrossRef] [Google Scholar]
  36. Sekiya, M. 1998, Icarus, 133, 298 [CrossRef] [Google Scholar]
  37. Stevenson, D. J., & Lunine, J. I. 1988, Icarus, 75, 146 [NASA ADS] [CrossRef] [Google Scholar]
  38. Suzuki, T. K., & Inutsuka, S.-i. 2014, ApJ, 784, 121 [Google Scholar]
  39. Takeuchi, T., & Lin, D. N. C. 2005, ApJ, 623, 482 [NASA ADS] [CrossRef] [Google Scholar]
  40. Wada, K., Tanaka, H., Suyama, T., Kimura, H., & Yamamoto, T. 2011, ApJ, 737, 36 [NASA ADS] [CrossRef] [Google Scholar]
  41. Weidenschilling, S. J. 1980, Icarus, 44, 172 [NASA ADS] [CrossRef] [Google Scholar]
  42. Weidenschilling, S. J. 1995, Icarus, 116, 433 [NASA ADS] [CrossRef] [Google Scholar]
  43. Youdin, A. N., & Goodman, J. 2005, ApJ, 620, 459 [NASA ADS] [CrossRef] [Google Scholar]
  44. Youdin, A. N., & Lithwick, Y. 2007, Icarus, 192, 588 [NASA ADS] [CrossRef] [Google Scholar]
  45. Youdin, A. N., & Shu, F. H. 2002, ApJ, 580, 494 [NASA ADS] [CrossRef] [Google Scholar]
  46. Zsom, A., Sándor, Z., & Dullemond, C. P. 2011, A&A, 527, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Figures

thumbnail Fig. 1

Steady-state solutions for the solid-to-gas mixing ratio Z as a function of the Stokes number of solid particles τs for different values of the solid-to-dust-mass flux ratio ξ (as labeled), assuming a value of the turbulent viscosity α = 10-3. The values of τs corresponding to expected pebble sizes are highlighted with larger symbols. The two solutions provided by Eq. (13)are indicated by filled and open symbols, respectively. The gray area highlights the region in which planetesimals should form by a streaming instability (Carrera et al. 2015).
In the text
thumbnail Fig. 2

Steady-state solutions for the solid-to-gas mixing ratio Z as a function of the solid-to-gas-mass flux ratio ξ for different values of the Stokes number of solid particles τs (from 10-5 to 10-2, as labeled), assuming two values of the turbulent viscosity α = 10-4 (in blue) and α = 10-3 (in red). Equation (13) is numerically solved. In contrast to Fig. 1, we now consider that initially icy pebbles with τs,peb ~ 0.1 and containing a mass fraction ζ0 = 1/3 in dust sublimate inside of the snow line. The thicker lines corresponds to the preferred value for the dust particles, τs = 10-4.
In the text
thumbnail Fig. 3

Time evolution of a) radius of the pebble formation front, b) pebble accretion rate (Ṁpeb), and c) ξpeb = Ṁpeb/Ṁ∗ for two values of α, 10-4 (red) and 10-3 (blue). The lines labeled “grow” (dotted) and “GI” (dashed) represent the pebble growth and disk GI limits, respectively. The thick solid lines express the actual values obtained by the minima of the two limits. Here we assumed τs,peb = 0.1 and Z0 = 0.01. In panel c), the small squares represent the points with ξpeb>ξcrit, see Eq. (18).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.