| Issue |
A&A
Volume 596, December 2016
|
|
|---|---|---|
| Article Number | A111 | |
| Number of page(s) | 18 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201629576 | |
| Published online | 12 December 2016 | |
The habitability of Proxima Centauri b
I. Irradiation, rotation and volatile inventory from formation to the present
1 Institut de Ciències de l’Espai (IEEC-CSIC), C/Can Magrans, s/n, Campus UAB, 08193 Bellaterra, Spain
e-mail: iribas@ice.cat
2 NaXys, Department of Mathematics, University of Namur, 8 rempart de la Vierge, 5000 Namur, Belgium
3 Laboratoire d’Astrophysique de Bordeaux, Univ. Bordeaux, CNRS, B18N, allée Geoffroy Saint-Hilaire, 33615 Pessac, France
4 Institut für Astrophysik, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
5 Department of Astrophysics and Planetary Science, Villanova University, Villanova, PA 19085, USA
6 LUPM, Université de Montpellier, CNRS, Place E. Bataillon, 34095 Montpellier, France
7 Laboratoire de Météorologie Dynamique, IPSL, Sorbonne Universités, UPMC Univ. Paris 06, CNRS, 4 place Jussieu, 75005 Paris, France
8 School of Physics and Astronomy, Queen Mary University of London, 327 Mile End Rd, London E1 4NS, UK
Received: 24 August 2016
Accepted: 26 September 2016
Proxima b is a planet with a minimum mass of 1.3M⊕ orbiting within the habitable zone (HZ) of Proxima Centauri, a very low-mass, active star and the Sun’s closest neighbor. Here we investigate a number of factors related to the potential habitability of Proxima b and its ability to maintain liquid water on its surface. We set the stage by estimating the current high-energy irradiance of the planet and show that the planet currently receives 30 times more extreme-UV radiation than Earth and 250 times more X-rays. We compute the time evolution of the star’s spectrum, which is essential for modeling the flux received over Proxima b’s lifetime. We also show that Proxima b’s obliquity is likely null and its spin is either synchronous or in a 3:2 spin-orbit resonance, depending on the planet’s eccentricity and level of triaxiality. Next we consider the evolution of Proxima b’s water inventory. We use our spectral energy distribution to compute the hydrogen loss from the planet with an improved energy-limited escape formalism. Despite the high level of stellar activity we find that Proxima b is likely to have lost less than an Earth ocean’s worth of hydrogen (EOH) before it reached the HZ 100–200 Myr after its formation. The largest uncertainty in our work is the initial water budget, which is not constrained by planet formation models. We conclude that Proxima b is a viable candidate habitable planet.
Key words: stars: individual: Proxima Cen / planets and satellites: individual: Proxima b / planets and satellites: atmospheres / X-rays: stars / planet-star interactions
© ESO, 2016
1. Introduction
The discovery and characterization of Earth-like planets is among the most exciting challenges in science today. A plethora of rocky planets have been discovered in recent years by both space-based missions such as Kepler (Borucki et al. 2010; Batalha et al. 2013) and by ground-based radial velocity monitoring (Mayor et al. 2011). Anglada-Escudé et al. (2016) have announced the discovery of Proxima b, a planet with a minimum mass of 1.3 M⊕ orbiting Proxima Centauri, the closest star to the Sun. Table 1 shows the characteristics of Proxima and its discovered planet.
Here – as well as in a companion paper (Turbet et al. 2016, hereafter Paper II) – we address a number of factors related to the potential habitability of Proxima b.
Defining planet habitability is not straightforward. In the context of the search for signs of life on exoplanets, the presence of stable liquid water on a planet’s surface represents an important specific case of habitability. There are strong thermodynamic arguments to consider that the detection of a biosphere that is confined into a planetary interior with no access to stellar light will require in-situ exploration and may not be achieved by remote observations only (Rosing 2005). Surface habitability requires water but also an incoming stellar flux low enough to allow part of the water to be in the liquid phase but sufficient to maintain the planetary surface (at least locally) above 273 K. These two limits in stellar flux determine the edges of the habitable zone (HZ) as defined by Kasting et al. (1993). Proxima b orbits its star at a distance that falls well within its HZ limits, with a radiative input of 65–70% of the Earth’s value (S⊕) based on the measured orbital period, and on estimates of the stellar mass (Delfosse et al. 2000) and bolometric luminosity (Demory et al. 2009; Boyajian et al. 2012). The inner and outer limits of a conservative HZ are indeed estimated at 0.9 and 0.2 S⊕, respectively (Kopparapu 2013). For a synchronized planet, the inner edge could be as close as 1.5 S⊕ (Yang et al. 2013; Kopparapu et al. 2016).
Although Proxima b’s insolation is similar to Earth’s, the context of its habitability is very different. Proxima is a very low mass star, just 12% as massive as the Sun. Proxima’s luminosity changed considerably during its early evolution, after Proxima b had already formed. As a consequence, and in contrast with the evolution of the solar system, the HZ of Proxima swept inward as the star aged. Proxima b spent a significant amount of time interior to the HZ before its inner edge caught up with the planet’s orbit (e.g., Ramirez & Kaltenegger 2014). This phase of strong irradiation has the potential to induce water loss, with the potential for Proxima b entering the HZ as dry as present-day Venus. We return to this question in Sect. 4. Rotation represents another difference between Proxima b and Earth: while Earth’s spin period is much shorter than its orbital period, Proxima b’s rotation has been affected by tidal interactions with its host star. The planet is likely to be in one of two resonant spin states (see Sect. 4.6).
In this paper we focus on the evolution of Proxima b’s volatile inventory using all available information regarding the irradiation of the planet over its lifetime and taking into account how tides have affected the planet’s orbital and spin evolution. More specifically, we address the following issues:
-
We first estimate the initial water content of the planet bydiscussing the important mechanisms for water deliveryoccurring in the protoplanetary disk (Sect. 2).
-
To estimate the atmospheric loss rates, we need to know the spectrum of Proxima at wavelengths that photolyse water (FUV, H Lyα) and heat the upper atmosphere, powering the escape (soft X-rays and extreme-UV, hereafter EUV), as well as its stellar wind properties. For such purpose, we provide measurements of Proxima’s high energy emissions and wind at the orbital distance of the planet (Sect. 3).
-
To better constrain the system, we investigate the history of Proxima and its planet. We first reconstruct the evolution of its structural parameters (radius, luminosity), the evolution of its high-energy irradiance and particle wind. We then investigate the tidal evolution of the system, including the semi-major axis, eccentricity, and rotation period. This allows us to infer the possible present day rotation states of the planet (Sect. 4).
-
With all the previous information, we can estimate the loss of volatiles of the planet, namely the loss of water and the loss of the background atmosphere prior to entering in the HZ (the runaway phase) and while in the HZ. To compute the water loss, we use an improved energy limited escape formalism (Lammer et al. 2003; Selsis et al. 2007a) based on hydrodynamical simulations (Owen & Alvarez 2016). This model was used by Bolmont et al. (2016) to estimate the water loss from planets around brown dwarfs and the planets of TRAPPIST-1 (Gillon et al. 2016, Sect. 5).
Following up on the results, in Paper II we study the possible climate regime that can exist on the planet as a function on the volatile reservoirs and the rotation rate of the planet.
Adopted stellar and planetary characteristics of the Proxima system.
2. The initial water inventory on Proxima b
Proxima b’s primordial water content is essential for evaluating the planet’s habitability as well as its water loss and, thus, its present-day water content. One can easily imagine an unlucky planet located in the habitable zone that is completely dry, and such situations do arise in simulations of planet formation (Raymond et al. 2004). Of course, Earth’s water content is poorly constrained. Earth’s surface water budget is ~1.5 × 1024 g, defined as one “ocean” of water. The water abundance of Earth’s interior is not well known. Estimates for the amount of water locked in the mantle range between ≲0.3 and 10 oceans (Lécuyer et al. 1998; Marty 2012; Panero 2016). The core is not thought to contain a significant amount of hydrogen (e.g., Badro et al. 2014).
In this section we discuss factors that may have played a role in determining the planet’s water content. Our discussion is centered on theoretical arguments based on our current understanding of planet formation.
It is thought that Earth’s water was delivered by impacts with water-rich bodies. In the Solar System, the division between dry inner material and more distant hydrated bodies is located in the asteroid belt, at ~2.7 AU, which roughly divides S-types and C-types (Gradie & Tedesco 1982; DeMeo & Carry 2013). Earth’s D/H and 15N/14N ratios are a match to carbonaceous chondrite meteorites (Marty & Yokochi 2006) associated with C-type asteroids in the outer main belt. Primordial C-type bodies are the leading candidate for Earth’s water supply1.
Models of terrestrial planet formation (see Morbidelli et al. 2012; Raymond et al. 2014, for recent reviews) propose that Earth’s water was delivered by impacts from primordial C-type bodies. In the classical model of accretion, water-rich planetesimals originated in the outer asteroid belt (Morbidelli et al. 2000; Raymond et al. 2007a, 2009; Izidoro et al. 2015). Earth’s feeding zone was several AU wide and encompassed the entire inner Solar System (see Fig. 3 from Raymond et al. 2006). In the newer Grand Tack model, water was delivered to Earth by C-type material, but those bodies actually condensed much farther from the Sun and were both implanted into the asteroid belt and scattered to the terrestrial planet-forming region during Jupiter’s orbital migration (Walsh et al. 2011; O’Brien et al. 2014).
If the Proxima system formed by in-situ growth like our own terrestrial planets, then there are reasons to think that planet b might be drier than Earth. First, the snow line is farther away from the habitable zone around low-mass stars (Lissauer 2007; Mulders et al. 2015). Viscous heating is the main heat source for the inner parts of protoplanetary disks. The location of the snow line is therefore determined not by the star but by the disk. However, the location of the habitable zone is linked to the stellar flux. Thus, while Proxima’s habitable zone is much closer-in than the Sun’s, its snow line was likely located at a similar distance. Water-rich material thus had a far greater dynamical path to travel to reach Proxima b, and, as expected, water delivery is less efficient at large dynamical separations (Raymond et al. 2004). But protoplanetary disks are not static. They cool as the bulk of their mass is accreted by the star. The snow line therefore moves inward in time, (e.g., Lecar et al. 2006; Kennedy & Kenyon 2008; Podolak 2010; Martin & Livio 2012). Models for the Sun’s early evolution suggest that the Solar System’s snow line may have spent time as close in as 1 AU (e.g., Sasselov & Lecar 2000; Garaud & Lin 2007). Yet the Solar System interior to 2.7 AU is extremely dry. One explanation for this apparent contradiction is that the inward drift of water-rich bodies was blocked when Jupiter formed (Morbidelli et al. 2015). The dry/wet boundary at 2.7 AU may be a fossil remnant of the position of the snow line at the time of Jupiter’s growth.
One can imagine that in systems without a Jupiter the situation might be quite different. In principle, if the snow line swept all the way in to the habitable zone, it may have snowed on the planet late in the disk’s lifetime. As concluded by the UVES M-dwarf survey (Zechmeister et al. 2009), it is highly unlikely that Proxima hosts a gas giant within a few AU. Even at longer orbital distances, such planet would cause acceleration that would likely be detectable with radial velocity data. The Doppler method is only sensitive to the orbital motions along the line-of-sight, so there is always a chance that a large planet is hidden to Doppler detection on a face-on orbit. As a rule of thumb, we estimate the chance of hiding a gas giant within 10 AU at <10%. As reported in Anglada-Escudé et al. (2016) there is unconfirmed evidence for an additional planet exterior to Proxima b but stellar activity might still be the cause of the observed Doppler variability. Even if such a planet is confirmed in the future, its minimum mass would be in the range of ~3–6 M⊕. The presence of such planet would likely have an impact on the evolution of the putative atmosphere and state of Proxima b, especially due to the induction of a non-zero eccentricity and resulting non-trivial tidal state (Van Laerhoven et al. 2014). However, we consider that adding an additional planet and all the associated degrees of freedom to an already complex model is an unnecessary complication given the limited information we have on the system and the tentative nature of this additional companion. Proxima is possibly the star on which the Gaia space mission has highest sensitivity to small planets (Neptune-mass objects should be trivially detectable for P> 100 days irrespective of the inclination), so it will not be long before the question about the presence or absence of long-period gas giants is finally settled.
Second, the impacts involved in building Proxima b were more energetic than those that built the Earth. The collision speed between two objects in orbit scales with the local velocity dispersion (as well as the two bodies’ mutual escape speed). The random velocities for a planet located in the habitable zone are directly linked to the local orbital speed as 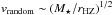 , where M⋆ is the stellar mass (Lissauer 2007). For Proxima, the impacts that built planets in the habitable zone would have been a few times more energetic on average than those that built the Earth. This may have led to significant loss of the planet’s atmosphere and putative oceans (Genda & Abe 2005).
, where M⋆ is the stellar mass (Lissauer 2007). For Proxima, the impacts that built planets in the habitable zone would have been a few times more energetic on average than those that built the Earth. This may have led to significant loss of the planet’s atmosphere and putative oceans (Genda & Abe 2005).
Third, Proxima b likely took less time than Earth to grow. Assuming a surface density large enough to form an Earth-mass planet, simple scaling laws and N-body simulations show that planets in the habitable zones of ~0.1 M⊙ stars form in 0.1 to a few Myr (Raymond et al. 2007b; Lissauer 2007). Even if the planets formed very quickly, the dissipation of the gaseous disk after a few Myr (Haisch et al. 2001; Pascucci et al. 2009) may have triggered a final but short-lived phase of giant collisions. Although it remains to be demonstrated quantitatively, the concentration of impact energy in a much shorter time than Earth may have contributed to increased water loss.
Yet simulations have shown that in-situ growth can indeed deliver water-rich material in to the habitable zones of low-mass stars (Raymond et al. 2007b; Ogihara & Ida 2009; Montgomery & Laughlin 2009; Hansen 2015; Ciesla et al. 2015). However, these simulations did not focus on very low-mass stars such as Proxima. The water-depleting effects discussed above are expected to increase in importance for the lowest-mass stars, so the retention of water remains in question.
It also remains a strong possibility that Proxima b formed farther from the star and migrated inward. Bodies more massive than ~0.1–1 M⊕ are subject to migration from tidal interactions with the protoplanetary disk (Goldreich & Tremaine 1980; Paardekooper et al. 2011). Given that the mass of Proxima b is on this order, migration is a plausible origin. Indeed, the population of “hot super-Earths” can be explained if planetary embryos formed at several AU, migrated inward to the inner edge of the protoplanetary disk and underwent a late phase of collisions (Terquem & Papaloizou 2007; Ida & Lin 2010; McNeil & Nelson 2010; Swift et al. 2013; Cossou et al. 2014; Izidoro & et al. 2016). If Proxima b or its building blocks formed much farther out and migrated inward, then their compositions may not reflect the local conditions in the disk. Rather, they could be extremely water-rich (Kuchner 2003; Léger et al. 2004). If migration did indeed take place it must have happened very early, during the gaseous disk phase. Migration would not have affected the planet’s irradiation or tidal evolution, just its initial water budget.
Other mechanisms may have affected Proxima b’s water budget throughout the planet’s formation. For example, if Proxima’s protoplanetary disk underwent external photoevaporation, the snow line may have stayed far from the star (Kalyaan & Desch 2016), thus inhibiting water delivery to Proxima b. The short-lived radionuclide 26Al is thought to play a vital role in determining the thermal structure and water contents of planetesimals, especially those that accrete quickly (as may have been the case for Proxima b’s building blocks; e.g., Grimm & McSween 1993; Desch & Leshin 2004). Finally, we cannot rule out a late bombardment of water-rich material on Proxima b, although it would have to have been 1–2 orders of magnitude more abundant than the Solar System’s late heavy bombardment to have delivered an ocean’s worth of water (Gomes et al. 2005).
To summarize, there are several mechanisms by which water may have been delivered to Proxima b. Yet it is unclear how much water would have been delivered or retained. We can imagine a planet with Earth-like water content that was delivered somewhat more water than Earth but lost a higher fraction. We can also picture an ocean-covered planet whose building blocks condensed beyond the snow line. Finally, we can imagine a dry world whose surface water was removed by impacts and early heating. In the following sections, we therefore consider a broad range of initial water contents for Proxima b.
3. High-energy irradiation
High-energy emissions and particle winds have been shown to play a key role in shaping the atmospheres of rocky planets. Numerous studies (e.g., Lammer et al. 2009) have highlighted the impact of the so-called XUV flux on the volatile inventory of a planet, including water. The XUV range includes emissions from the X-rays (starting at ~0.5 nm–2.5 keV) out to the far-UV (FUV) just short of the H Lyα line. Here we extend our analysis out to 170 nm, which is a relevant interval for photochemical studies.
One unavoidable complication of estimating the XUV fluxes is related to their intrinsic variability. Proxima is a well-known flare star (e.g., Haisch et al. 1983; Güdel et al. 2004; Fuhrmeister et al. 2011) and thus its high-energy emissions are subject to strong variations (of up to 2 orders of magnitude in X-rays) over timescales of a few hours and longer. Further, optical photometry of Proxima indicates a long-term activity cycle of ~7.1 yr (Engle & Guinan 2011). For a nearby planet, both the so-called quiescent activity and the flare rate of Proxima are relevant. X-ray emission of Proxima was observed with ROSAT and XMM. Hünsch et al. (1999) report log LX = 27.2 erg s-1 from a ROSAT observation, and Schmitt & Liefke (2004) report log LX = 26.9 erg s-1 for ROSAT PSPC and log LX = 27.4 erg s-1 for an XMM observation. It is interesting to note that Proxima’s X-ray flux is quite similar to the solar one, which is between log LX = 26.4 and 27.7 erg s-1, corresponding to solar minimum and maximum, respectively.
High-energy fluxes received currently by Proxima b and the Earth in units of erg s-1 cm-2.
In the present study we estimate the average XUV luminosity over a relatively long timescale in an attempt to measure the overall dose on the planetary atmosphere, including the flare contribution. This is based on the assumption of a linear response of the atmosphere to different amounts of XUV radiation, which is certainly an oversimplification, but should be adequate for an approximate evaluation of volatile loss processes.
High-energy observations of Proxima have been obtained from various facilities and covering different wavelength intervals. In the X-ray range we use XMM-Newton observations with Observation IDs 0049350101, 0551120201, 0551120301, and 0551120401. The first dataset, with a duration of 67 ks, was studied by Güdel et al. (2004) and contains a very strong flare with a total energy of ≈2 × 1032 erg. The other three (adding to a total of 88 ks), were studied by Fuhrmeister et al. (2011), and include several flares, the strongest of which has an energy of about 2 × 1031 erg.
The flare distribution of Proxima can be crudely approximated using the analysis of Audard et al. (2000) for CN Leo, which has similar X-ray luminosity and spectral type. Audard et al. (2000) find a cumulative flare distribution of CN Leo that can be described by a power law with the form N( >E) = 3.7 × 1037E-1.2, where N is the number of flares per day, and E is the total (integrated) flare energy in erg. Thus, CN Leo has flares with energies greater than about 2 × 1031 erg over a timescale of 1 day. Interestingly, this is in agreement with the 88-ks dataset of Proxima, and thus this seems to be quite representative of the daily average X-ray flux. The (time-integrated) average flux from the XMM 88-ks dataset between 0.65 and 3.8 nm yields a value at the orbital distance of Proxima b of 87 erg s-1 cm-2.
Using the expressions in Audard et al. (2000) we can estimate a correction factor to account for the total energy produced by more energetic flares. The integrated flux value of 87 erg s-1 cm-2 should represent the average flux between energies of 2 × 1029 erg (minimum energy as found by Audard et al. 2000) and 2 × 1031 erg, and should be compared with the flux produced by flares up to 2 × 1032 erg, which is the strongest flare observed for Proxima. The integration of the cumulative flare distribution above indicates that the X-ray dose produced by energetic flares increases the typical 1-day average by about 25%. Thus, this implies an extra flux of 22 erg s-1 cm-2, and a total average of 109 erg s-1 cm-2 with the energetic flare correction. This value and those following in this section are listed in Table 2 and illustrated in Fig. 1.
 |
Fig. 1 High-energy spectral irradiance received by Proxima b and the Earth. The values correspond to those in Table 2 but calculated per unit wavelength (i.e., divided by the width of the wavelength bin; 0.5 nm is adopted for H Lyα). |
We note that a comparison of the results in Walker (1981) and Kunkel (1973) indicates the Proxima has about 60% of the flare rate of CN Leo as measured in comparable energy bands. However, this small difference does not affect our calculations since we are interested in estimating the relative contribution of the energetic flares with respect to the background of lower energy flare events. The methodology assumes a power law slope as given above for CN Leo (and should apply to Proxima as well) and some flare energy intervals that are appropriate for Proxima.
ROSAT observations were used in the wavelength range from 3.8 to 10 nm. Four suitable datasets are available from the ROSAT archive, with Dataset IDs RP200502A01, RP200502A02, RP200502A03, and RP200502N00, and integration times ranging from 3.8 to 20 ks. After flare events were filtered out, quiescent fluxes were calculated by fitting a two temperature (2-T) MEKAL collisional ionization equilibrium model (Drake et al. 1996) with solar abundance (Neves et al. 2013) and NH value of 4 × 1017 cm-2. This was done within the XSPEC (v11) X-ray Spectral Fitting Package, distributed by NASA’s HEASARC. Because of the short integration times, substantial differences between datasets exist depending on the flare properties. We employed the RP200502N00 dataset because it has a 0.6–3.8 nm integrated flux closer to the XMM values (and this ensured similar spectral hardness). A modest scaling of 1.28 was used to bring the actual fluxes into agreement, including the flare correction. Using this prescription, we calculated that the 3.8–10 nm flux of Proxima at the distance of its planet is 43 erg s-1 cm-2 in quiescence and 54 erg s-1 cm-2 with the flare correction. Thus, the total X-ray dose of Proxima b from 0.6 to 10 nm is 163 erg s-1 cm-2, including an energetic flare correction of 33 erg s-1 cm-2.
An alternative approach to estimate the flare-corrected X-ray flux of Proxima is to use the similarity with the Sun. Proxima’s cumulative energy distribution can be compared to the solar and other stellar distributions in Drake et al. (2015). The cumulative flare energy output of the quiet Sun is 2 × 1025 erg s-1 (Hudson 1991), i.e., 3.1 erg s-1 cm-2 at the distance of Proxima b. The current Sun, as well as average Sun-like stars observed by Kepler, and Proxima, are flaring at roughly the same rate, which is a factor of ~10 higher than solar minimum (Shibayama et al. 2013). This results in a flux of about 31 erg s-1 cm-2 at the distance of Proxima b, nicely consistent with the estimate above.
For the extreme-UV range we use the EUVE spectrum available from the mission archive with Data ID proxima_cen__9305211911N, corresponding to an integration time of 77 ks. This dataset was studied by Linsky et al. (2014), who measured an integrated (and corrected for interstellar medium – ISM – absorption) flux between 10 and 40 nm of 89 erg s-1 cm-2 at the distance of Proxima b. No information on the flare status of the target is available, and we applied the same correction obtained for the X-rays to obtain a flux value of 111 erg s-1 cm-2 at the distance of Proxima b.
FUSE observations are used to obtain the flux in part of the far-UV range. We employed the spectrum with Data ID D1220101000 with a total integration time of 45 ks. A concern related to FUSE observations is the contamination by geocoronal emission. We made sure that the spectrum had little or no visible geocoronal features but the H Ly lines always show some degree of contamination. Such flux increase competes with the significant ISM absorption, which diminishes the intrinsic stellar flux. We measured the integrated flux in the 92–118 nm interval excluding the H Ly series and obtained 10 erg s-1 cm-2. Following Guinan et al. (2003) and Linsky et al. (2014), we estimate the H Ly series contribution, except H Lyα, to be of the same order and thus the 92–118 nm flux at the distance of Proxima b is ≈20 erg s-1 cm-2. We note that Christian et al. (2004) found 3 flare events in the FUSE dataset, which produce an increase of up to one order of magnitude in the instantaneous flux. The integrated effect of such flares is about 20–30% relative to the quiescent emission, which appears to be reasonable given our X-ray estimates and thus no further correction was applied.
A high-quality HST/STIS spectrum obtained from the StarCAT catalog (Ayres 2010) was used to estimate the fluxes between 118 and 170 nm (except for H Lyα). The flux integration yielded a value of 17 erg s-1 cm-2 at the distance of Proxima b. A flare analysis of this dataset was carried out by Loyd & France (2014), who identified a number of flare events in the stronger emission lines. These flares contribute some 25–40% of the integrated flux (Loyd, priv. comm.) and thus represent similar values to those found in the X-ray domain. No further corrections were made. The same base spectrum was used by Wood et al. (2005) to estimate the intrinsic H Lyα stellar line profile and the integration results in a flux of 130 erg s-1 cm-2 at the orbital distance of Proxima b. The relative flare contribution corrected for ISM absorption is estimated to be of ~10% (Loyd, priv. comm.).
The interval between 40 and 92 nm cannot be observed from Earth due to the very strong ISM absorption, even for a star as nearby as Proxima. To estimate the flux in this wavelength range we make use of the theoretical calculations presented by Linsky et al. (2014), who show that it can be approximated as being about 10% of the H Lyα flux, i.e., 13 erg s-1 cm-2.
Thus, the total integrated flux today that is representative of the time-averaged high-energy radiation on the atmosphere of Proxima b is of 307 erg s-1 cm-2 between 0.6 and 118 nm. To compare with the current Earth XUV irradiation we employ the Thuillier et al. (2004) solar spectrum corresponding to medium solar activity and the average of the maximum and minimum Solar Irradiance Reference Spectrum (SIRS) as given by Linsky et al. (2014). Both data sources provide very similar results. Integration in the relevant wavelength interval yields a total XUV flux at Earth of 5.1 erg s-1 cm-2. Thus, Proxima b receives 60 times more XUV flux than the current Earth, which we refer to as XUV⊕. Also, the far-UV flux on Proxima b between 118 nm and 170 nm is 147 erg s-1 cm-2, which is about 10 times higher than the flux received by the Earth, namely FUV⊕. The H Lyα flux alone received by Proxima is 15 times stronger than Earth’s. We note that the high-energy emission spectrum of Proxima is significantly harder than that of the Sun today. If we consider that the current X-ray luminosities of the Sun and Proxima are similar, the distance scaling from 1 AU to 0.048 AU represents a factor of 435 in the flux, which is much higher than our measured value of 60. All the values measured for Proxima as well as the comparison with the Sun are listed in Table 2 and illustrated in Fig. 1.
4. Co-evolution of Proxima b and its host star
The observations of the Proxima system (Anglada-Escudé et al. 2016) show that Proxima b is located in the classical insolation HZ (as defined in Kasting et al. 1993; Selsis et al. 2007b; Kopparapu 2013; Kopparapu et al. 2014). However, as Proxima is a low-mass star, it spent a non-negligible time decreasing its luminosity during the early evolution, which means that the HZ moved inwards with time. If Proxima b’s orbit remained the same with time, and assuming it was formed with a non-zero water reservoir, it would have experienced a runaway greenhouse phase, which means water was in gaseous phase prior to entering the HZ. Planets orbiting very low-mass stars could be desiccated by this hot early phase and enter the HZ as dry worlds (as shown by the works of Barnes & Heller 2013; Luger & Barnes 2015). In contrast, the detailed analysis of the TRAPPIST-1 system (Gillon et al. 2016) by Bolmont et al. (2016), using a mixture of energy-limited escape formalism together with hydrodynamical simulations (Owen & Alvarez 2016), shows that the planets could have retained their water during the runaway phase. We apply a similar scheme to Proxima b to evaluate this early water loss.
4.1. The early evolution of Proxima
Proxima’s physical properties, such as its mass, radius, luminosity and effective temperature are given in Table 1. We used the evolutionary tracks provided by Baraffe et al. (2015) in order to reproduce these values at the age of the star (4.8 Gyr). As M⋆ = 0.123M⊙ is not tabulated, we performed a linear interpolation between the evolutionary tracks corresponding to 0.1 M⊙ and 0.2 M⊙. We tested the following masses: 0.120, 0.123, 0.125, 0.130 M⊙. None of these interpolated tracks allow to reproduce simultaneously the exact values of the adopted radius, luminosity and effective temperature simultaneously. The best agreement for the luminosity is found for a mass of 0.120 M⊙ but the best agreement for the effective temperature is found for a mass of 0.130 M⊙. For the radius, all masses lead to an agreement. This apparent (minor) disagreement between luminosity, effective temperature and mass may come from the fact that the models of Baraffe et al. (2015) use a solar metallicity while Proxima is more metal rich than the Sun ([Fe/H] = 0.21, Anglada-Escudé et al. 2016). In the following we assume a mass of 0.123 M⊙. Figure 2 shows the evolution of the bolometric luminosity of Proxima, according to our adopted model.
 |
Fig. 2 Evolution of the HZ inner edge, bolometric luminosity and XUV luminosity for Proxima. Top panel: evolution of the inner edge of the HZ for two different assumptions: Sp = 0.9S⊕ (dashed blue line), Sp = 1.5S⊕ (full blue line). The full black line corresponds to Proxima’s measured orbital distance. Bottom panel: evolution of the luminosity for a 0.1M⊙ star (in orange), for 0.2 M⊙ (in red) and 0.123 M⊙ (in blue). The gray area corresponds to the observed value (see Table 1). The black vertical dashed line corresponds to the estimated age of Proxima. |
To estimate the location of the inner edge of the HZ, we considered two possible scenarios for the rotation of the planet, as discussed in Sect. 4.6: a synchronous rotation and a 3:2 spin-orbit resonance. For a non-synchronous planet we considered an inner edge at Sp = 0.9S⊕, where S⊕ = 1366 W m-2 is the flux received by the Earth (e.g., Kopparapu 2013; Kopparapu et al. 2014). For a synchronized planet, we locate the inner edge at Sp = 1.5S⊕ (the protection of the substellar point by clouds allows the planet to be much closer, e.g., Yang et al. 2013; Kopparapu et al. 2016). The top panel of Fig. 2 shows the evolution of the inner edge of the HZ for both prescriptions compared to the semi-major axis of Proxima b.
4.2. History of XUV irradiance
In addition to the average flux that Proxima b receives today given in Sect. 3, having an approximate description of the history of XUV emissions is key to investigate the current atmospheric properties of the planet and its potential habitability. While the variation of XUV emissions with time is relatively well constrained for Sun-like stars (Ribas et al. 2005; Claire et al. 2012), the situation for M dwarfs (and especially mid-late M dwarfs) is far from understood. Some results were presented and discussed by Selsis et al. (2007b) and, more recently, by Guinan et al. (2016) within the “Living with a Red Dwarf” program. Qualitatively, these works present a picture of a time-evolution in which log LX/Lbol shows a flat regime starting at the ZAMS and extending out to about 1 or a few Gyr, and known as saturation (e.g., Jardine & Unruh 1999), followed by a regime in which the decrease shows a power law form. The timescales in this approximation are notoriously uncertain. For example, models of low-mass star angular momentum evolution predict that braking timescales in low-mass stars are substantially longer than in Sun-like stars. Reiners & Mohanty (2012) estimate a timescale of roughly 7 Gyr until activity in a star like Proxima falls below the saturation limit, which is often assumed to be around a few tens of days. From there, the star would need a few more Gyr to reach the observed value of P = 83 d. This would imply an age of about 10 Gyr or so, which is clearly inconsistent with the estimate of 4.8 ± 1 Gyr by Bazot et al. (2016). A way out is that Proxima started its rotational evolution with less initial angular momentum or was kept at fixed rotation rate by a surrounding disk for longer than the canonical 10 Myr. The saturation limit itself is not well constrained in stars of such low masses. For example, extrapolating the luminosity scaling law from Reiners et al. (2014, Eq. (10)), the saturation limit would be at Psat ≈ 40 d. However, the radius-luminosity relation used in that paper cannot readily be extended to very low masses and a calculation using their saturation criterion yields Psat ≈ 80 d. The latter would imply that Proxima is still exhibiting saturated activity and probably did so over its entire lifetime. Reiners et al. (2014) also suggest that the amount of X-ray emission may slightly depend on P in saturated stars such that Proxima would have had a higher value of LX/Lbol when it was young.
Clearly, there are significant uncertainties in low-mass star angular momentum evolution. In any case, all models and observations of rotational braking tend to agree that stars like Proxima exhibit saturated activity from early ages until an age of several Gyr, perhaps even until today. If today’s rotation period is below the saturation limit, exponential rotational braking on timescales of Gyr and LX ∝ P-2 is expected. We calculate two scenarios to estimate the effect of angular momentum evolution on the history of XUV irradiance. In the first scenario, we estimate that Proxima stayed saturated at a level of log LX/Lbol = −3.3 until an age of 3 Gyr and spent another 2 Gyr until its rotation decreased to 83 d as observed (both values with uncertainties of about 1 Gyr) and its X-ray radiation diminished to log LX/Lbol = −3.8 as observed in quiescence. Since in this scenario the spectral hardness of the high-energy emissions has likely decreased with time (as happens for Sun-like stars; see Ribas et al. 2005), we adopt an approximate slope of −2 for the XUV and we suggest the following relationship: ![\begin{eqnarray} &&F_{\rm XUV}=7.8\times10^2 \hspace*{20mm} \mbox{for }\tau < \tau_\circ\nonumber\\ &&F_{\rm XUV}=7.8\times10^2 \: [\tau/\tau_\circ]^{-2} \hspace*{7.5mm} \mbox{for }\tau > \tau_\circ, \end{eqnarray}](/articles/aa/full_html/2016/12/aa29576-16/aa29576-16-eq68.png) (1)with τ° = 3 Gyr and FXUV (0.6–118 nm) in erg s-1 cm-2 at 0.048 AU. Thus, in our first scenario, Proxima b was probably irradiated by XUV photons at a level ~150 XUV⊕ during the first 3 Gyr of its lifetime. This functional relationship is shown in Fig. 3. We provide a second scenario in which we assume that Proxima has remained in a saturated activity state for its entire lifetime and that the saturation level is the same as the one observed today, log LX/Lbol = −3.8. This is clearly a lower limit to the XUV radiation emitted by Proxima and it is also shown in Fig. 3.
(1)with τ° = 3 Gyr and FXUV (0.6–118 nm) in erg s-1 cm-2 at 0.048 AU. Thus, in our first scenario, Proxima b was probably irradiated by XUV photons at a level ~150 XUV⊕ during the first 3 Gyr of its lifetime. This functional relationship is shown in Fig. 3. We provide a second scenario in which we assume that Proxima has remained in a saturated activity state for its entire lifetime and that the saturation level is the same as the one observed today, log LX/Lbol = −3.8. This is clearly a lower limit to the XUV radiation emitted by Proxima and it is also shown in Fig. 3.
 |
Fig. 3 XUV flux evolution for Proxima and the Sun at the orbital distance of Proxima b and Earth, respectively. The two scenarios discussed in the text, namely a flat regime and a power-law decrease and a constant value throughout, are represented, with the gray area indicating a realistic possible range. Such relationships show that Proxima b has been irradiated at a level significantly higher than the Earth throughout most of their lifetimes and the integrated XUV dose is between 7 and 16 times higher, depending on the assumed XUV flux evolution for Proxima. |
We can also compare the integrated XUV irradiance that Proxima b and the Earth have likely received over the course of their lifetimes. For the Earth and the Sun, we use the expressions in Ribas et al. (2005) with a slight correction to reflect the updated XUV current solar irradiance value discussed in Sect. 3. This corresponds to FXUV = 5.6 × 102 erg s-1 cm-2 up to 0.1 Gyr and FXUV = 33τ-1.23 erg s-1 cm-2 beyond. The calculations show that Proxima b has received, in total, between 7 and 16 times more XUV radiation than Earth, with this range corresponding to the two XUV evolution scenarios described above.
4.3. Particle wind
The analysis of Wood et al. (2001) using the astrospheric absorption of the H Lyα feature provided an upper limit of the mass loss rate of Proxima of 0.2 Ṁ⊙ (4 × 10-15M⊙ yr-1). For the Sun, the latitudinal particle flux depends on the activity level, ranging from nearly spherically symmetric during solar maximum to being significantly higher at the ecliptic (Solar) equator with respect to the poles during solar minimum (Sokół et al. 2013). Nothing is known on the geometry of particle emissions for other stars. Thus, to scale the mass loss rate from the solar value at Earth to the value that Proxima b receives, we adopt two different geometrical prescriptions, namely, a spherical distribution (i.e., flux scaling with distance squared) and an equatorial distribution (i.e., flux scaling with distance). Following these recipes, we estimate that Proxima b is receiving a particle flux that could be within a factor of ≈4 and ≈80 of today’s Earth value. We note that the methodology of determining mass loss rates from the observation of the astrospheric absorption assumes a constant or quasi-steady mass loss rate (Linsky & Wood 2014) and should represent a time-averaged value, comprising both the quiescent stellar particle emissions and coronal mass ejections possibly related to flare events.
Regarding the history of the particle fluxes, not much is known on the evolution of stellar wind over time. The observations of Wood et al. (2014), in good agreement with the recent semi-empirical analyses of do Nascimento et al. (2016) and Airapetian & Usmanov (2016), reveal a picture in which the mass loss rate of Sun-like stars was quite similar to today’s during the early evolution (up to about 0.7 Gyr in the case of the Sun), then there is evidence of much stronger wind fluxes of about 50–100 times today’s value, and the subsequent evolution follows a power-law relationship with age with an exponent of about −2. In this picture, which is based on the surface X-ray flux, Proxima would still be in the initial low-flux regime and therefore the upper limit of 4–80 times today’s Earth value can be assumed to apply to its entire lifetime.
4.4. The magnetopause radius of Proxima b
In order to provide a first estimate of the position of the magnetopause of Proxima b we follow the approach of Vidotto et al. (2013). This method assumes an equilibrium between the magnetic pressures associated with the stellar and planetary magnetic fields. By doing so we neglect the effect of the ram pressure of the stellar wind and only consider the stellar magnetic pressure – which Vidotto et al. (2013) found to be important for M dwarfs – and we therefore derive an upper limit for the magnetopause radius. Starting from the basic Eq. (2) of Vidotto et al. (2013), which defines the pressure balance at the nose of the magnetopause, and rescaling with respect to the Earth case (for a balance driven by the wind ram pressure of the stellar wind in that case) we obtain the following expression for the radius of the magnetopause relative to the planetary radius: ![\begin{equation} \dfrac{r_M}{r_{\rm p}} = K \left( \dfrac{R_{\rm orb}}{{\rm [1~AU]}} \right)^{2/3} \left( \dfrac{R_\star}{R_\odot} \right)^{-2/3} \left( \dfrac{B_{\rm p,0}}{f_1 f_2 B_\star} \right)^{1/3} \text{,} \label{eq:rmag_numeric} \end{equation}](/articles/aa/full_html/2016/12/aa29576-16/aa29576-16-eq75.png) (2)where K = 15.48, Bp,0 is the polar magnetic field of the planet taken at the surface, B⋆ is the average stellar magnetic field taken at photosphere, and f1 and f2 are two scaling factors. We use the values f1 = 0.2 if the large-scale component of the stellar magnetic field is dipole-dominated and f1 = 0.06 if it is multipolar. From the stellar sample of Vidotto et al. (2013) we find f2 = 1/15 for most stars and larger values for stars with a very non-axisymmetric field, we use f2 = 1/50 as a representative value of this case. The derivation of Eq. (2) and the meaning of the factors f1 and f2 are detailed in Appendix A. As in Vidotto et al. (2013), we compute B⋆ using the parametrization of Reiners & Mohanty (2012) :
(2)where K = 15.48, Bp,0 is the polar magnetic field of the planet taken at the surface, B⋆ is the average stellar magnetic field taken at photosphere, and f1 and f2 are two scaling factors. We use the values f1 = 0.2 if the large-scale component of the stellar magnetic field is dipole-dominated and f1 = 0.06 if it is multipolar. From the stellar sample of Vidotto et al. (2013) we find f2 = 1/15 for most stars and larger values for stars with a very non-axisymmetric field, we use f2 = 1/50 as a representative value of this case. The derivation of Eq. (2) and the meaning of the factors f1 and f2 are detailed in Appendix A. As in Vidotto et al. (2013), we compute B⋆ using the parametrization of Reiners & Mohanty (2012) : 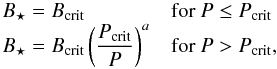 (3)where we use Bcrit = 3 kG and a = 1.7 as in Vidotto et al. (2013). In line with the discussion in Sect. 4.2, we adopt two scenarios for the magnetic properties of Proxima. One in which the star is still very near the saturation rotation period Pcrit and another one by which it stayed saturated until about 2 Gyr ago, which would roughly correspond to Pcrit = 40 d and thus B⋆ ≈ 1 kG.
(3)where we use Bcrit = 3 kG and a = 1.7 as in Vidotto et al. (2013). In line with the discussion in Sect. 4.2, we adopt two scenarios for the magnetic properties of Proxima. One in which the star is still very near the saturation rotation period Pcrit and another one by which it stayed saturated until about 2 Gyr ago, which would roughly correspond to Pcrit = 40 d and thus B⋆ ≈ 1 kG.
In order to provide a more realistic estimate, we also take into account the impact of the stellar wind ram pressure on the magnetopause radius of Proxima b. The detail of the calculations is provided in Appendix A. From our estimate in Sect. 4.3 that the wind particle flux at Proxima is 4–80 times that at Earth, it ensues that the ram pressure exerted by the stellar wind of Proxima at Proxima b is also 4–80 times the ram pressure of the solar wind at Earth, if we assume that both stars have the same wind velocity (this assumption is used for instance in Wood et al. 2001).
Assuming a planetary magnetic field equal to the value for the Earth 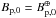 , we derive rM/rp values ranging from 2.2 to 6.9. For a weaker field
, we derive rM/rp values ranging from 2.2 to 6.9. For a weaker field 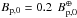 , more in line with Zuluaga et al. (2013) for a tidally-locked planet, we obtain values ranging from 1.3 to 4.1. These results are summarized in Table 3. In the cases with a dipole-dominated stellar magnetic field the wind ram pressure has virtually no impact on the magnetopause radius, while for the multipolar stellar magnetic field cases considered we provide a range of values for rM/rp representing various values for the wind ram pressure (varying by a factor of 20). We note that for a star star such as Proxima in the low-wind flux regime, even in those cases where the ram pressure is non-negligible, the magnetic pressure of the stellar wind remains the dominant term, in contrast with the case of the Earth.
, more in line with Zuluaga et al. (2013) for a tidally-locked planet, we obtain values ranging from 1.3 to 4.1. These results are summarized in Table 3. In the cases with a dipole-dominated stellar magnetic field the wind ram pressure has virtually no impact on the magnetopause radius, while for the multipolar stellar magnetic field cases considered we provide a range of values for rM/rp representing various values for the wind ram pressure (varying by a factor of 20). We note that for a star star such as Proxima in the low-wind flux regime, even in those cases where the ram pressure is non-negligible, the magnetic pressure of the stellar wind remains the dominant term, in contrast with the case of the Earth.
4.5. Orbital tidal evolution
As Proxima b is located close to its host star, its orbit is likely to have suffered tidal evolution. To investigate this possibility, we adopted a standard equilibrium tide model (Hut 1981; Mignard 1979; Eggleton et al. 1998), taking into account the evolution of the host star (as in Bolmont et al. 2011, 2012). We tested different dissipation values for the star: from the dissipation in a Sun-like star to the dissipation in a gas giant following Hansen (2010), which differ by several orders of magnitude. We assume an Earth composition for the planet, which gives us a radius of ~1.1 R⊕ for a mass of 1.3M⊕ (Fortney et al. 2007) and a resulting gravity g = 10.5 m s-2. Finally, we explored tidal dissipation factors for the planet ranging from ten times lower than that of Earth (Neron de Surgy & Laskar 1997, hereafter noted σp) to the Earth’s value. The Earth is thought to be very dissipative due to the shallow water reservoirs (as in the bay of Biscay, Gerkema et al. 2004). In the absence of surface liquid layers, that is, before reaching the HZ, the dissipation of the planet would therefore be smaller than that of the Earth. Considering this range in tidal dissipation should encompass what we expect for this planet.
As in Bolmont et al. (2011, 2012), we compute the effect of both the tide raised by the star on the planet (planetary tide) and by the planet on the star (stellar tide). In agreement with Bolmont et al. (2012), we find that, even when assuming a high dissipation in the star, no orbital evolution is induced by the stellar tide. The semi-major axis and inclination of the planet remain constant throughout the evolution and are thus independent of the wind prescription governing the spin evolution of the star. The planet is simply too far away.
The planetary tide leads mainly to an evolution of the planet’s rotation period and obliquity (see Sect. 4.6). The eccentricity evolves on much longer timescales so that it does not decrease significantly over the 4.8 Gyr of evolution. Assuming a dissipation of 0.1σp, we can reproduce the observed upper limit eccentricity (0.35, given by Anglada-Escudé et al. 2016) and semi-major axis at present day with a planet initial semi-major axis and eccentricity of ~0.05 AU and ~0.37, respectively. The current eccentricity of 0.35 would imply a tidal heat flux in the planet on the order of 2.5 W m-2, that is, comparable to the one of Io (Spencer et al. 2000). This would imply an intense volcanic activity on the planet. The average flux received by the planet would also be increased by 6–7% compared to a circular orbit with the same semi-major axis.
An orbital eccentricity of 0.37 at the end of accretion may be too high. Let us assume Proxima b is alone in the system, its eccentricity could thus be excited only by α Centauri. Given the structure of the system (Kaib et al. 2013; Worth & Sigurdsson 2016), this excitation should not be responsible for eccentricities higher than 0.1. We therefore computed the tidal evolution of the system with an initial eccentricity of 0.1. By the age of the system and assuming a dissipation of 0.1σp, the eccentricity would have decreased to 0.097, and the tidal heat flux would be ~0.07 W m-2, which is of the order of the heat flux of the Earth (Pollack et al. 1993). Assuming a dissipation as the one of the Earth, we find that the eccentricity would have decreased to 0.07, which corresponds to a tidal heat flux of ~0.03 W m-2.
4.6. Is Proxima b synchronously rotating?
Although it has been shown that the final dynamical state of an isolated star-planet system subjected only to gravitational tides should be a circular orbit and the synchronization of both spins (Hut 1980), there are several reasons for not finding a real system in this end state:
-
Tidal evolution timescales may be too long for the system to reachequilibrium. In the case at hand, it has indeed been shown abovethat circularization is expected to take longer than the system’slifetime. The spin evolution, however, is expected to be muchfaster so that synchronous rotation would be expected2.
-
Venus, for example, tells us that thermal tides in the atmosphere can force an asynchronous rotation (Gold & Soter 1969; Ingersoll & Dobrovolskis 1978; Correia & Laskar 2001; Leconte et al. 2015). However, due to its scaling with orbital distance, this process seems to lose its efficiency around very low mass stars such as Proxima (Leconte et al. 2015).
-
Finally, if the orbit is still eccentric as might be the case here, trapping into a spin-orbit resonance, such as the 3:2 resonance of Mercury, becomes possible (Goldreich & Peale 1966).
The goal of this section is to quantify the likelihood of an asynchronous, resonant spin-orbit state. For sake of simplicity and concision, we will assume that the planet started with a rapid prograde spin. Because of the short spin evolution timescale, we will also assume that the obliquity has been damped early in the life of the system. We note, however, that trapping in Cassini states may be possible if the precession of the orbit is sufficient and tidal damping not too strong (Fabrycky et al. 2007). This possibility is left out for further investigations.
4.6.1. Probability of capture in spin-orbit resonance
For a long time, only few unrealistic parameterizations of the tidal dissipation inside rocky planets were available (Darwin 1880; Love 1909; Goldreich 1963). At moderate eccentricities, models based on those parameterizations almost always predicted an equilibrium rotation rate – where the tidal torque would vanish – that was either synchronous or with a much slower rotation than the slowest spin-orbit resonance. As a result, tides would always tend to spin down a quickly rotating planet and persistence into a given resonance could only occur through trapping. In this mechanism, the gravitational torque over a permanent, non-axisymetric deformation – the triaxiality – of the planet creates an effective “potential well” in which the planet can be trapped (Goldreich & Peale 1966).
In this framework, consider a planet with a rotation angle θ and a mean anomaly M (with the associated mean rotation rate, 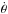 , and mean motion n) around an half integer resonance p. Defining γ ≡ θ−pM, the equation of the spin evolution averaged over an orbit is given by
, and mean motion n) around an half integer resonance p. Defining γ ≡ θ−pM, the equation of the spin evolution averaged over an orbit is given by 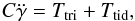 (4)where
(4)where 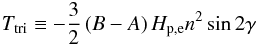 (5)is the torque due to the triaxiality (B−A) /C where A,B, and C are the three principal moments of inertia of the planet (in increasing magnitude), Hp,e is a Hansen coefficient that depends on the resonance and the eccentricity (e), and Ttid is the dissipative tidal torque. In their very elegant calculation, Goldreich & Peale (1966) demonstrated that the probability of capture only depends on the ratio of the constant part of the tidal torque that acts to traverse the resonance to the linear one that needs to damp enough energy during the first resonance passage to trap the planet. This theory was further generalized by Makarov (2012) who showed that this is actually between the odd and the even part of the torque (where
(5)is the torque due to the triaxiality (B−A) /C where A,B, and C are the three principal moments of inertia of the planet (in increasing magnitude), Hp,e is a Hansen coefficient that depends on the resonance and the eccentricity (e), and Ttid is the dissipative tidal torque. In their very elegant calculation, Goldreich & Peale (1966) demonstrated that the probability of capture only depends on the ratio of the constant part of the tidal torque that acts to traverse the resonance to the linear one that needs to damp enough energy during the first resonance passage to trap the planet. This theory was further generalized by Makarov (2012) who showed that this is actually between the odd and the even part of the torque (where 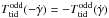 and
and 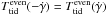 ) that the separation needs to be done. With these notations, the capture probability simply writes
) that the separation needs to be done. With these notations, the capture probability simply writes 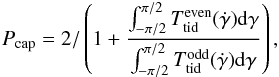 (6)where the integral should be performed over the separatrix between the librating (trapped) and circulating states given by
(6)where the integral should be performed over the separatrix between the librating (trapped) and circulating states given by 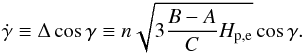 (7)For further reference, Δ will be called the width of the resonance, as this is the maximum absolute value that
(7)For further reference, Δ will be called the width of the resonance, as this is the maximum absolute value that 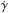 can reach inside the resonance.
can reach inside the resonance.
Equation (6) is completely general and can readily be used with any torque. Hereafter, we will only use a tidal torque that is representative of the rheology of solid planets, i.e., the Andrade model generalized by Efroimsky (2012). Specifically, we will use the implementation in Eq. (10) of Makarov (2012). All model parameters are exactly the same as in this article (in particular, the Maxwell time is τM = 500 yr), except that we fix the Andrade time to be equal to the Maxwell time for simplicity. We note that although this model and these parameter values fairly reproduce some features from the tidal response of the Earth, it does not consistently account for the effect of the oceans2. The numerical results for the capture probability are shown where applicable for the 3:2 resonance in Fig. 4.
 |
Fig. 4 Probability of capture in the 3:2 resonance as a function of orbital eccentricity and triaxiality of the planet (numbered contours with color shadings). White regions depict areas of certain capture due to the tidal torque. Black regions show where the triaxial torque is too weak to enforce capture. Labeled curves are: (a) tidal torque at the lower boundary of the separatrix is negative and greater in magnitude than the maximum restoring torque; (b) tidal torque at the lower boundary of the separatrix is positive; (c) maximal tidal torque inside the resonance is greater than the maximum triaxial torque. Being above (c) and/or (b) leads to certain capture. Below (c) and (a) capture is impossible. |
4.6.2. Is capture always possible?
An interesting property of the solution above is that because it involves the ratio of two components of the torque, any overall multiplicative constant, that is, the overall strength of tides, cancels out. At first sight, this seems to simplify greatly the survey of the whole parameter space because explicit dependencies on the stellar mass and orbital semi-major axis, among other parameters, disappear. The capture probability only depends on the eccentricity of the orbit, the triaxiality of the planet, and the ratio of the orbital period to the Maxwell time. This completely hides the fact that capture may be impossible even when the capture probability is not zero. Indeed, as pointed out by Goldreich & Peale (1966), another condition must be met for trapping to occur: the maximum restoring torque due to triaxiality must overpower the maximum tidal torque inside the resonance. If not, even if the energy dissipation criterion is met, the tidal torque is just strong enough to pull the planet out of the potential well of the resonance.
In our specific case, the maximum restoring torque and the maximum tidal torque trying to extract the planet from the resonance both occur at the lowest boundary of the resonance (when 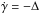 and γ = −π/ 4). This point is reached on the first swing of the planet inside the resonance, when it moves along a trajectory close to the separatrix. So, notwithstanding the value of Pcap, capture is impossible whenever
and γ = −π/ 4). This point is reached on the first swing of the planet inside the resonance, when it moves along a trajectory close to the separatrix. So, notwithstanding the value of Pcap, capture is impossible whenever 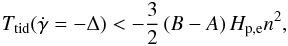 (8)both quantities being negative. This condition, hereafter referred to as condition (a), is verified below the curve with the same label in Fig. 4.
(8)both quantities being negative. This condition, hereafter referred to as condition (a), is verified below the curve with the same label in Fig. 4.
4.6.3. Non-synchronous equilibrium rotation
Contrary to simplified parametrizations of tides, the more realistic frequency dependence of the Andrade torque entails that synchronous rotation is not the only equilibrium rotation state. As illustrated by Fig. 5, depending on the eccentricity, the tidal torque can vanish for several rotation states, although only the ones near half integer resonances are stable. As this process does not involve the same processes as the usual resonance capture, the ratio of equilibrium rotation rates to the mean motion are not exactly half integers (see Makarov 2012 for details). For Proxima b’s orbital period and with τM = 500 yr, the ω ≈ 3n/ 2 rotation becomes stable for an eccentricity greater than 0.06–0.07, and the ω ≈ 2n above e = 0.16.
In the absence of any triaxiality, the planet would always be stopped in the fastest stable equilibrium rotation state available for a given eccentricity. When triaxiality is finite, it entails libration around the resonance, inside the area delimited by dashed gray curves in Fig. 5. This can actually cause the planet to traverse the resonance. In such a case, the capture is probabilistic and its probability can be computed using Eq. (6). There are however two conditions for which capture becomes certain:
-
(b)
If the tidal torque is positive at the lower boundary of theseparatrix (
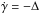 , that is, along the dashed curve at the left of each resonance in Fig. 5), the planet is always brought back toward the equilibrium rotation.
, that is, along the dashed curve at the left of each resonance in Fig. 5), the planet is always brought back toward the equilibrium rotation. -
(c)
If anywhere in the resonance the tidal torque is positive and greater than the maximum triaxial torque, then the rotation rate can never decrease below that point. If this situation occurs, the planet will never reach the bottom of the separatrix. Therefore, capture will ensue, even though the condition (a) is not met.
These two conditions are met above the black curves labeled (b) and (c) respectively in Fig. 4.
 |
Fig. 5 Sketch of the equilibrium eccentricity, whence the tidal torque vanishes, as a function of planetary rotation rate (blue curve). Solid portions of the curve near resonances depict stable equilibria, whereas dotted portions show unstable ones. Areas of positive torque are in gray, and of negative torque in blue. Dashed gray curves show the area covered by librations inside the resonances, that is, the resonance width (see Eq. (7)). With realistic values for the triaxiality and the Maxwell time, both the kink around the resonances and the resonance width would be much narrower and difficult to see. |
4.6.4. Summary and implications for climate
Figure 4 summarizes the chances of capture in the 3:2 resonance as a function of its triaxiality and eccentricity at the resonance crossing. The white area shows where capture is certain, and the black area, where capture is impossible. In the remaining part of the parameter space, capture probability is computed using Eq. (6). If capture does not occur, which may occur in the color shaded area and is certain in the black one, the planet ends up in synchronous rotation.
As expected, capture probability increases with eccentricity. We also recover the fact that, at low eccentricities (here below ~0.06), capture can only occur if the triaxiality is sufficient to counteract the spin down due to tidal friction. To put these numbers into context, let us note than triaxiality shows variability from one planet to another, but seems to decrease with increasing mass, from ~1.4 × 10-4 for Mercury, as derived from the gravity moments (in particular C2,2) measured by Smith et al. (2012), to ~2 × 10-5 for the Earth, and ~6 × 10-6 for Venus (Yoder 1995). Being a little more massive, Proxima b’s triaxiality is likely to be smaller still. As a consequence, capture is rather unlikely for an eccentricity below 0.06.
A slightly less intuitive result is that, at higher eccentricities, capture probability decreases when triaxiality increases. Again, this is due to the fact that, although a 3:2 rotation rate might be an equilibrium configuration, triaxiality induced librations can help the planet get through the resonance. In this regime, the likely low triaxiality of the planet will probably trap the latter in the 3:2 asynchronous rotation resonance.
In conclusion, let us recall that the final rotational state of an initially fast rotating planet will be the result of the encounter of several resonances. Moreover, both the eccentricity and the triaxiality of the planet could vary from one resonance encounter to the other. The final rotational state thus depends on the orbital history of the system. However, considering the range of eccentricities discussed above, it seems that resonances higher than 3:2 (or maybe 2:1) are rather unlikely. At eccentricities lower than 0.06, the most probable state becomes the synchronous one. This highlights the need for further constraints on the eccentricity of the planet, its possible evolution, and the existence of additional planets.
As shown by Yang et al. (2013) and Kopparapu et al. (2016), the inner edge of the HZ depends on the rotation rate of the planet. In particular, simulated atmospheres of synchronous planets with large amounts of water develop a massive convective updraft sustaining a high-albedo cloud deck in the substellar region. Based on these studies and the characteristics of Proxima, the runaway threshold is expected to be reached at 0.9 and 1.5S⊕, for a non-synchronous and a synchronous planet, respectively (S⊕ being the recent Solar flux at 1 AU). Assuming the planet’s orbit did not evolve during the Pre-Main Sequence phase, it would have entered the HZ at ~90 Myr if the rotation of the planet is synchronous, or at ~200 Myr if the rotation of the planet is non-synchronous. Thus, before reaching the HZ, the planet could have spent 100–200 Myr in a region too hot for surface liquid water to exist. This can be compared to the Earth, which is thought to have spent a few Myr in runaway after the largest giant impact(s) (Hamano et al. 2013). During this stage all the water is in gaseous form in the atmosphere, and therefore it can photo-dissociate and the hydrogen atoms can escape.
5. Water loss and volatile inventory
Proxima b has experienced a runaway phase that lasted up to ~200 Myr, during which water is thought to have been able to escape. We discuss here the processes of water loss as well as the processes responsible for the erosion of the background atmosphere.
5.1. Modeling water loss
In order to estimate the amount of water lost, we use the method of Bolmont et al. (2016) which is an improved energy-limited escape formalism. The energy-limited escape mechanism requires two types of spectral radiation: FUV (100–200 nm) to photo-dissociate water molecules and XUV (0.1–100 nm) to heat up the exosphere. We consider here that the planet is on a circular orbit at the end of the protoplanetary disk phase, its orbit thus remains constant throughout the evolution. The mass loss is given by (Lammer et al. 2003; Selsis et al. 2007a): 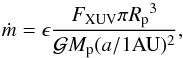 (9)where a is the planet’s semi-major axis, Rp its radius and Mp its mass. ϵ is the fraction of the incoming energy that is transferred into gravitational energy through the mass loss. As in Bolmont et al. (2016), we estimate ϵ using 1D radiation-hydrodynamic mass-loss simulations based on the calculations of Owen & Alvarez (2016). For incoming XUV fluxes between 0.3 and 200 erg s-1 cm-2, the efficiency is higher than 0.1, but for incoming XUV fluxes higher than 200 erg s-1 cm-2, the efficiency decreases (down to 0.01 at 105 erg s-1 cm-2, see Fig. 2 of Bolmont et al. 2016). t0 is the initial time taken to be the time at which the protoplanetary disk dissipates. We consider that when the planet is embedded in the disk, it is protected and does not experience mass loss. We assume that protoplanetary disks around dwarfs such as Proxima dissipate after between t0 = 3 Myr and 10 Myr (Pascucci et al. 2009; Pfalzner et al. 2014; Pecaut & Mamajek 2016).
(9)where a is the planet’s semi-major axis, Rp its radius and Mp its mass. ϵ is the fraction of the incoming energy that is transferred into gravitational energy through the mass loss. As in Bolmont et al. (2016), we estimate ϵ using 1D radiation-hydrodynamic mass-loss simulations based on the calculations of Owen & Alvarez (2016). For incoming XUV fluxes between 0.3 and 200 erg s-1 cm-2, the efficiency is higher than 0.1, but for incoming XUV fluxes higher than 200 erg s-1 cm-2, the efficiency decreases (down to 0.01 at 105 erg s-1 cm-2, see Fig. 2 of Bolmont et al. 2016). t0 is the initial time taken to be the time at which the protoplanetary disk dissipates. We consider that when the planet is embedded in the disk, it is protected and does not experience mass loss. We assume that protoplanetary disks around dwarfs such as Proxima dissipate after between t0 = 3 Myr and 10 Myr (Pascucci et al. 2009; Pfalzner et al. 2014; Pecaut & Mamajek 2016).
We consider here that the atmosphere is mainly composed of hydrogen and oxygen. From the mass loss given by Eq. (9), we can compute the ratio of the escape flux of oxygen and hydrogen (Hunten et al. 1987; Luger & Barnes 2015). The ratio of the escape fluxes of hydrogen and oxygen in such hydrodynamic outflow is given by: 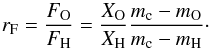 (10)This ratio depends on the crossover mass mc given by:
(10)This ratio depends on the crossover mass mc given by: 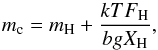 (11)where T is the temperature in the exosphere, g is the gravity of the planet and b is a collision parameter between oxygen and hydrogen. In the oxygen and hydrogen mixture, we consider XO = 1/3, XH = 2/3, which corresponds to the proportion of dissociated water.
(11)where T is the temperature in the exosphere, g is the gravity of the planet and b is a collision parameter between oxygen and hydrogen. In the oxygen and hydrogen mixture, we consider XO = 1/3, XH = 2/3, which corresponds to the proportion of dissociated water.
5.2. Water loss in the runaway phase
To calculate the flux of hydrogen atoms, we need an estimation of the XUV luminosity of the star considered, as well as an estimation of the temperature T. We use the two different XUV luminosity prescriptions as in Sect. 4.2, namely Proxima having had a saturation phase up to 3 Gyr and then a power-law decrease and another one with a constant value during its entire lifetime representing that saturation still lasts today (see Fig. 3). We adopt an exosphere temperature of 3000 K (given by hydrodynamical simulations, e.g., Bolmont et al. 2016). In the following, we give the mass loss from the planet in units of Earth Ocean equivalent content of hydrogen (EOH).
We calculated the hydrogen loss using three different methods:
-
(1)
assumingrF = 0.5, and calculating the mass loss as in Bolmont et al. (2016);
-
(2)
assuming rF = f(FXUV), and calculating the mass loss as in Bolmont et al. (2016);
-
(3)
computing the loss of hydrogen and oxygen atoms by integrating the expressions of FO and FH (see the equations in Bolmont et al. 2016).
Using method (1) and (2) allows to bracket the hydrogen loss without doing the integration of method (3). Indeed, using rF = 0.50 allows to compute the best case scenario: the loss is stoichiometric, 1 atom of oxygen is lost every 2 atoms of hydrogen. However, using rF = f(FXUV) allows to compute the mass loss assuming an infinite initial water reservoir: whatever the loss of hydrogen and oxygen, the ratio XO/XH remains the same and rF only depends on FXUV.
 |
Fig. 6 Hydrogen loss and O2 pressure for Proxima-b for an initial time of t0 = 3 Myr. Top panel: hydrogen loss computed with method (1) and (2) in full red lines and with method (3) in colored dashed lines. The gray areas correspond to the amount of hydrogen created by photolysis for two different efficiencies ϵα = 1.0 (all the incoming energy is used for photolysis) and ϵα = 0.1 (only 10% of the incoming energy is used). The edges of the gray areas were calculated using two different assumptions on the wavelength range important for photolysis: the lower edge corresponds to the energy flux in the H Ly α band (Table 2), the upper edge corresponds to the energy flux in a wider band: 10–170 nm. The vertical lines represent the time at which the planet reaches the 1.5 S⊕ HZ inner edge, the 0.9 S⊕ HZ inner edge and the age of the system (4.8 Gyr). Bottom panel: O2 pressure building up in the atmosphere computed with method (3). |
Lost hydrogen (in EOH), lost oxygen (in bar) and atmospheric build-up O2 pressure when Proxima b reaches the HZ and at the age of the system.
With this method we can compute the hydrogen loss from Proxima b. Figure 6 shows the evolution of the hydrogen loss with time for an initial time of protoplanetary disk dispersion of 3 Myr assuming different initial water reservoirs and with the different methods. Table 4 summarizes the results for the two different XUV prescriptions: FXUV = cst and FXUV = evol (as given in Sect. 4.2). We used for these calculations the minimum mass of Proxima b (1.3 M⊕). If a mass corresponding to an inclination of 60° is adopted (≈1.6 M⊕; the most probable one) the resulting losses are slightly higher but by no more than about 10%, which is negligible given the uncertainties in other parameters.
We find that for the evolving XUV luminosity the water loss from the planet is below 0.42 EOH at THZ (1.5 S⊕) and below ~1 EOH at THZ (0.9 S⊕). The loss of hydrogen does not significantly change when considering different initial time of protoplanetary disk dispersion (3 or 10 Myr here). The calculations thus suggest that the planet does not lose a very high amount of water during the runaway phase.
Figure 6 also shows the hydrogen produced by photo-dissociation (gray areas in top panel). If all the incoming FUV photons do photolyse H2O molecules with ϵα = 1 (100% efficiency) and if all the resulting hydrogen atoms then remain available for the escape process then photolysis is not limiting the loss process. However, when considering a smaller efficiency (ϵα = 0.1), we can see that photo-dissociation is the limiting process, indeed hydrogen is being produced at a slower rate than the escape rate. We find that for ϵα< 0.2, photo-dissociation becomes the limiting process for the stronger hypothesis on the FUV incoming flux (i.e., when we consider all that is emitted between 10 and 170 nm).
Because oxygen is lost at a much slower rate than hydrogen (but is still lost quite fast, see Table 4: up to 50 bar of O2 is lost before the planet reaches the 1.5 S⊕ HZ), the loss of hydrogen results in a build-up of oxygen in the atmosphere. We calculated the amount of remaining oxygen (that may be removed from the atmosphere by chemical reactions with surface minerals and recycling of the crust) as a potential O2 pressure in the atmosphere. If the inner edge of the HZ is defined by Sp = 1.5S⊕, the resulting O2 pressure is of the order of 30 to 43 bar. Assuming the planet initially has a water content equal to 1 Earth ocean, the O2 pressure starts decreasing as the hydrogen becomes scarce and oxygen becomes the only species to escape. This explains the wide range of O2 pressures at THZ (0.9 S⊕): from 55 bar to almost 100 bar. Of course, had we assumed an atmosphere with more species, we expect that the species reaching sufficiently high up in the atmosphere to escape as well. The presence of a background atmosphere would probably slow down the escape of hydrogen, which means our calculations are an upper value on the hydrogen loss.
5.3. Nitrogen loss associated with the hydrogen escaping flow
Just as oxygen atoms, nitrogen atoms can be dragged away by collision with the outflow of hydrogen. Compared with other volatile elements, and assuming a carbonaceous chondrite origin, nitrogen is depleted on Earth by one order of magnitude. There is about as much nitrogen in the atmosphere and in the mantle of the Earth (Marty 2012), the missing part being possibly trapped into the core (Roskosz et al. 2013) since the differentiation of the planet. Unless Proxima b accreted a much larger initial nitrogen amount and/or suffered less nitrogen segregation into its core, the atmospheric escape of nitrogen – an element essential to life as we know it – represents a major threat to its habitability.
Oxygen loss rates computed in the previous section show that hydrodynamic escape of hydrogen can potentially exhaust several bars of nitrogen reservoir in a few Myr. By the time the planet reaches the HZ defined by 1.5 S⊕, the equivalent of 50 bar of O2 can be lost (see Table 4). A similar quantity of N2 could be lost, which represents more than 30 times the reservoir of nitrogen in the Earth’s atmosphere and mantle. Two effects should however protect the nitrogen reservoir. First, during the runaway phase, the atmospheric content is in equilibrium with the magma ocean and a fraction of the nitrogen reservoir is therefore in solution in the interior. This partition is not sufficient in itself to protect nitrogen from escaping. Indeed, equilibrium between the silicates and the atmosphere implies that mantle outgassing compensates for the loss to space, which therefore exhausts both reservoirs. Vertical transport and fractionation within the mantle may, however, deplete the upper mantle that exchanges with the atmosphere and bury nitrogen at depth by the same process that may have enriched the core of the Earth in nitrogen. If part of this nitrogen is lost into the core another part is outgassed when the mantle solidify after water condensation at the end of the runaway (Elkins-Tanton 2008). As the solubility of nitrogen into silicates depends strongly on the redox state of the mantle and its water content (Roskosz et al. 2013) it is difficult to draw quantitative conclusions but current geochemistry tells us that part of the nitrogen should indeed be released only once the planet enters the HZ.
Another strong limitation of nitrogen escape is the photolysis of N2. Due to its triple bond, N2 is photodissociated only in the 40–100 nm wavelength range. But there appear to be sufficient photons (even with the current stellar emission) to photolyze 1 bar of N2 in a few Myrs. Assuming that no other species absorbs and that atoms released by N2 photolysis do not recombine, this is about enough to feed the computed loss rates. However, losing N atoms through the hydrogen outflows implies that the atmosphere is dominated by H2O and that H2O is efficiently photolysed to produce H atoms at least as fast as they are lost. Water vapor absorbs at the wavelengths photolyzing N2 (40–100 nm) with a similar cross-section (~10-17 cm2) and photons are thus absorbed by a column of 1017 cm-2 of either of the two species. If such column is found above the N2–H2O homopause then H2O, which has a 50% larger scale height, absorbs most of the incoming radiation even if both species have similar mixing ratios at the homopause. To determine the total concentration at the homopause we must assume a value for the eddy mixing coefficient KZZ. Near the homopause of the terrestrial planets of the solar system KZZ spans values from 3 × 105 cm2 s-1 on Earth to 108 cm2 s-1 on Mars (Atreya 1999). Using a H2O–N2 diffusion parameter of 6 × 1018 cm-1 s-1 (Chamberlain & Hunten 1987) we can determine the homopause concentration nh as well as the column of H2O and N2 assuming a temperature at the homopause (we take 300 K) and a mixing ratios Xh2o, Xn2 for the two species below the homopause. We find a H2O column density between Xh2o × 8.5 × 1016 and Xh2o × 2.8 × 1019 cm-2 and a N2 column density between Xn2 × 5.4 × 1016 and Xn2 × 1.8 × 1019 cm-2. For low values of KZZ, photons are absorbed above the homopause by H2O even for significant N2 mixing ratios. (We note that in this case, we verified that the altitude of absorption always remains negligible compared with the radius of the planet, even for hot expanded thermospheres, so that the UV absorption section of the planet is not enhanced by the expansion of the upper atmosphere). For high values of KZZ, photolysis of H2O and N2 occurs within the well mixed atmosphere and photolyzing photons will be absorbed in majority by the most abundant species. In models of Earth early atmosphere in equilibrium with a magma ocean, the water vapor pressure is estimated at several hundreds of bars. Assuming the present silicate and atmosphere partition for nitrogen (which, as said previously could have been in fact dominated by the mantle reservoir) yields a mixing ratio of less than 0.01. Accounting also for the recombination of nitrogen atoms, the integrated loss rate of nitrogen falls well below a bar of N2 in 100 Myr.
Carbon atoms can also be dragged by hydrogen but are expected to be protected by the same processes as nitrogen. Details would be quantitatively different because carbon dioxide – assumed to be the carrier – absorbs over a different wavelength range (still overlapped by that of H2O) and has mass 60% larger than N2. Based on Venus and Earth carbon inventories (equivalent to more than 90 bars of CO2 for Venus and 150 bars for the Earth), we know that the carbon reservoir can exceed by far the nitrogen content and the amount that can be exhausted by hydrogen drag alone.
5.4. Water loss while in the HZ
Let us consider a scenario where Proxima b enters the HZ with enough water to condense into an ocean but with only a tenuous background atmosphere of 10 mbar or less. Turbet et al. (2016) show that this configuration is still compatible with surface habitability for large amounts of water preventing its trapping at the poles (3:2 spin-orbit resonance) or on the night side (synchronous rotation). But they also show that the tropospheric cold trap of water is no longer efficient in this case resulting in a H2O-rich upper atmosphere. This is due to the fact that, in the substellar region, the vapor pressure at the surface exceeds the pressure of the background gas and the decrease vapor pressure with altitude (following the temperature) is not steeper than the decrease of the background pressure. The upper atmosphere is therefore fed with H2O through substellar warm vapor-rich columns.
In the absence of a dense enough background atmosphere, the escape of oxygen and hydrogen could therefore continue on much longer timescales without being limited by the diffusion of water vapor. If we integrate the water loss with the same assumptions used for the runaway phase (except for the evolution of the XUV flux, which is accounted for) over the whole history of the planet (4.8 Gyr) we find that the planet loses as much as ~21 EOH by the age of the star (see Table 4). Considering the constant XUV luminosity assumption, the loss decreases to ~16 EOH at the current age of the system. As a consequence, a situation with Proxima b in the HZ with a global ocean but a surface pressure lower than a few tens of mbars is likely to result in the rapid (<1 Gyr) total loss of water and volatiles. Indeed, it would be difficult to imagine a reservoir of water larger than 16 EOH with such a depletion of all other atmospheric species.
5.5. Other mechanisms for the loss of heavy elements
Heavy elements like carbon,oxygen and nitrogen escape at much slower rate than hydrogen under similar conditions but, at the exception of O/H2O, the transport of their main carrier (N2, CO2) toward the upper atmosphere is not limited by condensation like water. Therefore their loss proceeds through the whole history of the planet and not only when they are carried away by a hydrogen outflow as discussed in Sect. 5.3. In the absence of hydrogen, however, a significant erosion of the CO2 or N2 reservoir of an Earth-like planet would require XUV fluxes much higher than that experienced by Proxima b. Tian (2009) estimated for instance that a flux of 150 XUV⊕ would erode less than 0.5% of the Earth carbon reservoir from a 5.9 M⊕ planet during 1 Gyr. Although this calculation was done for a large terrestrial planet, with twice the gravity of a 1.3M⊕ rocky planet, other calculations by Tian (2009) show that the loss becomes weakly gravity-dependent at very high XUV fluxes and that only fluxes higher than 1000 XUV⊕ could erode more than half the Earth carbon reservoir. Therefore, if an initial reservoir of heavy volatile elements comparable to that of Earth or Venus was present on Proxima b at the end of its accretion, the majority of it should not have been lost through thermal escape alone.
The loss process that represents the main threat for the survival of a dense atmosphere on Proxima b is the joint effect of EUV-driven atmospheric thermal expansion and non-thermal losses, mainly ion pick-up by particles from the stellar wind (Lammer et al. 2011) and CMEs (coronal mass ejections Khodachenko et al. 2007; Lammer et al. 2007). When the Sun has a low activity, the Earth exobase (the limit above which collisions become negligible) is found at ~500 km far below the magnetopause at ~15 planetary radii (96 000 km). Inside the magnetopause the plasma dynamics are controlled by Earth magnetic field while outside they are driven by the solar wind. During high activity phases of the Sun, the EUV flux received by the Earth increases by a factor of two. As a consequence the exobase rises to ~1000 km while the magnetopause moves inward, down to ~7 R⊕ (45 000 km) due to an increased solar wind pressure. Under higher EUV fluxes and stellar wind pressure the magnetopause can be compressed below the exobase and neutral species ionized above the magnetopause by either charged particle impacts or XUV irradiation are efficiently picked-up through open magnetic field lines.
The exposure of Proxima b to stellar wind could be moderate to severe, with a particle flux 4–80 times higher than that received by the Earth (see Sect. 4.2). Non-thermal losses depend therefore more on the atmospheric expansion driven by XUV heating relative to the magnetopause distance maintained by the magnetic field of the planet. We found that the magnetopause radius of Proxima b could be between 1.3 to 7 planetary radii depending on the values of the intrinsic magnetic moment, on the stellar wind pressure and on whether the stellar magnetic field is dipole-dominated or multipolar (see Sect. 4.4). Tian et al. (2008) found that Earth exobase would rise to 4.8 and 12.7 planetary radii for 10 and 20 EUV⊕, respectively. This result depends, however, strongly on the details of the atmospheric composition and in particular on infrared coolants. Tian (2009) calculated that a pure CO2 atmosphere requires much higher EUV fluxes to expand to similar distances (for instance, 1000 EUV⊕ for an exobase at 5 planetary radii). We can see that, within the possible range of magnetopause and exobase distances, the magnetosphere could penetrate or could not the atmosphere. A similar question exists for the early Earth: using estimates for the evolution of Solar EUV/wind Lichtenegger et al. (2010) calculated that the magnetopause could have been as close as 2–4 R⊕ during the first Gyr of Earth evolution (when the Solar wind at Earth distance is assumed to have been much stronger than it is now and was at Proxima b). Whether this distance provided a protection against non-thermal escape depends on the atmospheric composition. Lichtenegger et al. (2010) claimed that a CO2-rich atmosphere could have withstood erosion while a N2-rich atmosphere with a low CO2 content (few percent or less) would have resulted in the loss of Earth’s nitrogen reservoir. Estimating the loss by this process would require to explore the response of different types of atmospheres to EUV heating for different planetary magnetic moments. But it means also that the Earth kept an atmosphere despite a severely compressed magnetosphere and the expanded atmosphere predicted by models.
In addition to the stellar wind itself, particles emitted by CMEs impact the planet sporadically, potentially compressing the magnetosphere within the atmosphere and eroding it by ion pick-up (Khodachenko et al. 2007; Lammer et al. 2007). These authors estimated that CMEs could prevent terrestrial planets in the habitable zone of low-mass stars like Proxima from having a dense atmosphere. This conclusion is based on the combination of enhanced stellar wind pressures, high XUV heating and inefficient magnetic protection due to the slow rotation of tidally-evolved planets and the weak resulting dynamo. They estimated the loss rate from a CO2-rich atmosphere as a function of the XUV flux and for different magnetopause distances. If we consider the present XUV flux at Proxima b (60 XUV⊕) and a magnetopause at 2 R⊕, less than 1 bar of atmosphere would be lost per Gyr. A less magnetized planet with a magnetopause at 1.5 R⊕ would lose a few bars and a non-magnetized planet would be stripped off its atmosphere at a rate of more than 100 bars per Gyr. If we assume that the XUV flux was higher in the past, up to 150 XUV⊕, then even a magnetopause at 2 R⊕ could not prevent the planet to lose hundreds of bars/Gyr.
We should note, however, that these pioneer attempts to calculate non-thermal losses still need to be improved in several ways. First, they lack a determination of an energy balance that would allow to determine what the maximum mass loss rate is and what limits the loss in a particular case. For instance, in the case of infinitely efficient thermal loss above the magnetopause, the mass loss would become limited by the expansion of the atmosphere above the magnetopause and would thus be related with the thermal hydrodynamic expansion and the XUV energy-limited loss rate, unless particles contribute also to this expansion.
In addition, in the absence of an intrinsic magnetic moment, ionospheric motions induce a magnetic field. On Venus for instance, the stellar wind does not penetrate the atmosphere that remains protected by this induced field (Zhang et al. 2007). It should be noted that the stellar magnetic activity that results in non-thermal escape also contributes to shield the atmosphere. For this reason, the magnetopause is more extended during active phases of the Sun than at Solar minimum (Zhang et al. 2007). Theoretical studies concluded that a magnetic field of 0.03–0.3 G is induced in the ionosphere even when Earth’s magnetic moment disappears during magnetic reversals (Birk et al. 2004). Atmospheres exposed to a strong ionizing environment as well as a strong stellar wind or CMEs are expected to develop induced magnetic moments much stronger than those found in the solar system. In particular, the formation of so-called circumplanetary plasma-disks is now studied as a natural consequence of such exposition for close-in planets (Khodachenko et al. 2012). Previous estimates of non-thermal losses will have to be revisited to account for this additional and, potentially efficient, protection.
Thermal and non-thermal loss rates that have been estimated in previous studies are usually given as a function of EUV⊕ or XUV⊕. Soft X-rays and EUV have, however, very different absorption cross-sections and interact differently with atmospheric atoms and molecules. The fraction of incoming energy that actually powers the atmospheric expansion strongly depends on the altitude of absorption. Proxima b receives 250, 30 and 15 times more flux than the Earth in of X-rays, EUV and Lyα, respectively, and 60 times more in the overall XUV range. Results from the literature are therefore not directly applicable to Proxima b when they are given only in terms of EUV⊕ or XUV⊕, especially when they are based on solar or early-Sun spectra.
5.6. Lessons from planet Earth
As highlighted above, estimates of volatile loss to space are subject to large and even unknown uncertainties. First, they rely on complex models that were never confronted to actual observations of massive escape. None of the available models include all the mechanisms controlling the loss rate, for example, the photochemistry of the upper atmosphere and its detailed interaction with the wavelength-dependent stellar emission, non-LTE cooling processes, and an accurate description of the outflow beyond the exobase where hydrodynamics no longer apply. Some key data are not known, like the intrinsic planetary magnetic moment, now and in the past, the detailed evolution of the atmospheric composition, of the high-energy spectrum and of stellar wind properties. Maybe more importantly, the erosion of the volatile inventory critically depends on the time-dependent distribution of the volatiles between the atmosphere and the different layers of the interior, which is currently beyond predictive modeling.
Considering this situation let us discuss another approach by comparing Earth and Proxima b early history. It took about 100 Myr to build the Earth by colliding tens of Moon- to Mars-sized protoplanets (see Morbidelli et al. 2012; Raymond et al. 2014). Each of these giant collisions resulted in a runaway and magma-ocean phase that lasted 1 to a few Myr (Hamano et al. 2013). Therefore, protoplanets that eventually became the Earth spent a large fraction of these 100 Myr in such runaway phase while exposed to the early Sun high-energy radiation. At that time, the Sun was likely to be in its saturated phase, characterized by a maximum LX/Lbol ratio. The XUV irradiation and stellar wind on the proto-Earth was therefore comparable, and possibly higher, than that of Proxima b. Proxima b spent 100–200 Myr in runaway before entering the HZ, which is longer than the runaway phases experienced by the proto-Earth by a small factor only (<10). Models predict that early Earth suffered massive volatile losses: hydrodynamic escape of hydrogen dragging away heavier species and non thermal losses under strong stellar wind exposure and CMEs (Lammer et al. 2012). Nonetheless, no clear imprint of these losses is found in the present volatile inventory.
The main source of Earth volatiles is believed to be carbonaceous chondrite (CC) material that, on average, shares with our planet a similar volatile pattern both in terms of relative abundances and isotopic signatures, in particular with identical D/H and 14N/15N ratios (Marty 2012). No mixture of other known sources of volatiles (for instance cometary and solar) can reproduce these patterns. Nitrogen found in the silicate Earth and the atmosphere is depleted by one order of magnitude compared with a CC composition, but there is mounting evidence that this missing nitrogen was segregated into the core (Roskosz et al. 2013). Some lighter hydrogen leaks from the deep mantle but is attributed to a solar nebula origin as confirmed by associated noble gases (Marty 2012). From geochemical evidence alone there is no indication of a significant erosion of the Earth volatile inventory and one possible conclusion is that the volatile loss from the Earth was very limited. The only depleted and (slightly) fractionated species is Xenon. This could have been caused by atmospheric escape but considering that lighter species like Krypton are not depleted nor fractionated, it requires some complex scenario coupling preferential exchanges with mantle (e.g., Tolstikhin et al. 2014) and/or non-thermal escape processes affecting only Xenon. For instance Xenon could be the only noble gas that can escape as an ion (Zahnle 2015). This scenario should, in addition, apply to the completely different history of Mars where Xenon presents the same puzzling properties. Until a robust explanation is found for the missing Xenon, its case cannot really provide any constraints on atmospheric escape.
Overall, escape processes produced negligible fractionation and preserved CC volatile patterns. Integrating these losses – that did not alter Earth’s volatile inventory in a measurable way – over a runaway period about ten times longer on Proxima b does not appear as an overwhelming threat to habitability.
6. Conclusions
This paper presents a first assessment of the potential habitability of the recently announced Earth-like planet Proxima b. Different aspects including the initial water inventory, history of the stellar XUV and particle emissions, orbital evolution, volatile losses, including water and the background atmosphere before and after entering the HZ, have been evaluated. The main summary and conclusions from our study are:
-
We cannot currently constrain Proxima b’sinitial water content. The planet’s water budget was determinedby the planet’s feeding zone during its formation. Given its muchsmaller orbital radius it must have accreted much faster thanEarth. We can envision a range of plausible formation scenariosthat cover a broad range of volatile contents, from nearly dryplanets to Earth-like water contents to waterworlds.
-
Using observations of Proxima, we estimate its high-energy emission in several wavelength ranges (from 0.6 to 170 nm). The total XUV irradiation that Proxima b receives today is of 307 erg s-1 cm-2 between 0.6 and 118 nm, and 147 erg s-1 cm-2 in the far-UV between 118 nm and 170 nm. We note that, on a short timescale, the high-energy flux is composed of quiescent emission plus short-term flare events covering a variety of energy levels. The value we provide is a time average over a timescale of years that can be used as energy input to the planetary atmosphere.
-
Proxima b receives 60 times more XUV flux than the current Earth, and ten times more far-UV flux. We note that the high-energy emission spectrum of Proxima is significantly harder than that of the Sun today, i.e., the relative contribution of X-rays compared to EUV is much higher.
-
We also give a prescription for the XUV-flux evolution of Proxima on nuclear timescales (from the time of stellar formation until the present age – 4.8 Gyr). We adopt two different scenarios that should represent the extreme cases bracketing the real behavior. One is an XUV irradiation on Proxima b ~150 times stronger that the Earth today during the first 3 Gyr of its lifetime followed by a decay in the form of a power-law relationship. The other one is a constant flux in time, namely ~60 times stronger than the Earth today. The total integrated XUV dose of Proxima b should be in the range 7–16 times what Earth has received.
-
Indirect observations yield an upper limit of the mass loss rate of Proxima of 0.2 Ṁ⊙. Assuming different geometries, we estimate that Proxima b is receiving a particle flux that should be at most a factor 4–80 higher than today’s Earth value and roughly constant for the entire lifetime of the planet.
-
We carry out a tidal analysis of the system by taking into account the host star Proxima. On the one hand, the tidal evolution of Proxima induced by the stellar tide is negligible even when assuming a very high dissipation factor for the star. Therefore, the history of the star, and in particular the history of its rotation period, does not have an influence on the orbit of Proxima b. On the other hand, we find that the tide raised by Proxima in the planet leads to a very small decrease in eccentricity and semi-major axis. We therefore find that, at the age of the system, Proxima b may have retained most of its initial eccentricity (which could be as high as 0.1).
-
We determine the possible spin states of Proxima b at the age of the system. Due to the possible remnant eccentricity, the planet could have been captured in a 3:2 spin-orbit resonance depending on its level of triaxiality. If the orbit is circular or near circular, the planet could be synchronized. For realistic triaxialities, the transition occurs around e = 0.06.
-
Proxima b experiences two distinct major phases in its evolution: (1) during the first few million years after the protoplanetary disk dispersion the planet is too hot for surface liquid water to exist; and (2) after the first few hundred million years the planet enters the HZ. During these two phases Proxima b experiences atmospheric loss.
-
We find that during the initial runaway phase the planet loses less than 1 EOH. We cannot provide strong constraints on the survival of the background atmosphere during the runaway phase: with the harshest constraints, up to ~100 bar of N2 could be lost. Under these circumstances, once in the HZ most water would be in the high atmosphere and susceptible to escape. In this case, Proxima b could have lost 16–21 EOH by the age of the system. It is also possible the planet has been able to keep its background atmosphere over the 4.8 Gyr of evolution. In this case the total water loss would far lower.
-
During the runaway phase the erosion of a significant water reservoir would have left large amounts of residual oxygen, possibly in the form of atmospheric O2, of up to 100 bar. This may have two important astrobiological consequences. First, the atmosphere, surface, ocean, and crust could have been strongly oxidized at the time the planet entered the HZ, which could prevent prebiotic chemical processes important for the origin of life. Second, a search for biosignatures must account for a possible abiotic build-up of O2 and the consequent formation of an ozone layer.
-
Due to XUV-driven atmospheric expansion and compression of the magnetopause by stellar wind, the planet could have lost a significant fraction of its volatile content by non-thermal losses. But quantifying the erosion depends on many unknown factors like the intrinsic and induced magnetic field, the actual stellar wind pressure on the planet, or the atmospheric composition. Further constraints are needed to assess whether Proxima b has suffered intense atmosphere losses via these mechanisms or whether it has been able to keep its volatile inventory during its lifetime.
Our results highlight the difficulty of assessing the habitability of a planet with an environment so different to Earth’s and with only a rough estimate of its past irradiation and orbital history. Some of the scenarios we consider lead to a massive loss of volatiles, including water and the background atmosphere, and thus to a desiccated, inhospitable planet. But when other, equally plausible, constraints are used, the current state of Proxima b turns out to be one in which a dense atmosphere is still present and that only a modest amount of water (perhaps less than 1 Earth Ocean) has been lost to space. Of course, it all depends on the initial volatile content and on the efficiency of processes that counteract themselves, namely in protecting or enhancing the erosion of the atmosphere subject to high-energy irradiation and particle wind. Although we have been able to present new, quantitative information on the high-energy and particle environment of Proxima b, significant uncertainties in the initial state and subsequent evolution remain. The case of Venus and the Earth in the Solar System also provide interesting comparisons. In spite of the strong solar emissions in the past, they both have managed to keep dense atmospheres and no conclusive evidence of massive volatile loss has been found. This is even so in the case of Venus, which has no protection from an intrinsic magnetic field.
Much research is still due, but the main general conclusion from our study is that Proxima b could have liquid water on its surface today and thus can be considered a viable candidate habitable planet. Future observations as those discussed in Paper II will allow us to further characterize Proxima b (e.g., spectral properties, orbital phase variations) and investigate the hypothetical presence of a thick atmosphere, which would open the exciting possibility for the planet hosting a liquid water reservoir. If this turned out to be the case, it would be noteworthy that the nearest star to the Sun also hosts the nearest habitable (perhaps inhabited?) planet.
Two Jupiter-family comets and one Oort cloud comet have been measured to have Earth-like D/H ratios (Hartogh et al. 2011; Lis et al. 2013; Biver et al. 2016) although the Jupiter-family comet 67P/Churyumov-Gerasimenko has a D/H ratio three times higher than Earth’s (Altwegg et al. 2015). Jupiter-family comets also do not match Earth’s 15N/14N ratio (e.g., Marty et al. 2016).
For a slightly eccentric planet, some simple tidal models predict a slow “pseudosynchronous rotation”, whose rate depends on the eccentricity. This possibility seems to be precluded for solid, homogeneous planets with an Andrade rheology (Makarov & Efroimsky 2013). However, let us note that planets with oceans may strongly depart from this predicted tidal response. What is the frequency dependence of the tidal response of an ocean-covered planet or of an “ocean planet”, or even what is inventory of water necessary to transition from one regime to the other remains poorly constrained. Pseudosynchronous rotation thus remains a possibility to be investigated.
Acknowledgments
B. E. Wood is thanked for kindly providing the reduced HST/STIS H Ly α spectrum and model for Proxima. I.R. acknowledges support by the Spanish Ministry of Economy and Competitiveness (MINECO) through grant ESP2014-57495-C2-2-R. E.B. acknowledges that this work is part of the F.R.S.-FNRS “ExtraOrDynHa” research project. The work of E.B. was supported by the Hubert Curien Tournesol Program. E.F.G. and S.E. acknowledge support by the NSF and NASA through grants NSF/RUI-1009903, HST-GO-13020.001-A and Chandra Award GO2-13020X to Villanova University. S.N.R. acknowledges support from the Agence Nationale de la Recherche via grant ANR-13-BS05-0003-002 (project MOJO). We are grateful to the referees, Dr. Jason W. Barnes and an anonymous referee, for constructive, insightful, and timely reports.
References
- Airapetian, V. S., & Usmanov, A. V. 2016, ApJ, 817, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Altwegg, K., Balsiger, H., Bar-Nun, A., et al. 2015, Science, 347, 1261952 [Google Scholar]
- Anglada-Escudé, G., Amado, P. J., Barnes, J., et al. 2016, Nature, 536, 437 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Atreya, S. K. 1999, EOS Transactions, 80, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Audard, M., Güdel, M., Drake, J. J., & Kashyap, V. L. 2000, ApJ, 541, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Ayres, T. R. 2010, ApJS, 187, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Badro, J., Cote, A., & Brodholt, J. 2014, PNAS, 132, 94 [Google Scholar]
- Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barnes, R., & Heller, R. 2013, Astrobiology, 13, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Batalha, N. M., Rowe, J. F., Bryson, S. T., et al. 2013, ApJS, 204, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Bazot, M., Christensen-Dalsgaard, J., Gizon, L., & Benomar, O. 2016, MNRAS, 460, 1254 [NASA ADS] [CrossRef] [Google Scholar]
- Birk, G. T., Lesch, H., & Konz, C. 2004, A&A, 420, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biver, N., Moreno, R., Bockelée-Morvan, D., et al. 2016, A&A, 589, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolmont, E., Raymond, S. N., & Leconte, J. 2011, A&A, 535, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolmont, E., Raymond, S. N., Leconte, J., & Matt, S. P. 2012, A&A, 544, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolmont, E., Selsis, F., Owen, J. E., et al. 2016, MNRAS, submitted [arXiv:1605.00616] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Boyajian, T. S., von Braun, K., van Belle, G., et al. 2012, ApJ, 757, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Chamberlain, J. W., & Hunten, D. M. 1987, International Geophysics Series (Orlando FL Academic Press Inc.), 36 [Google Scholar]
- Christian, D. J., Mathioudakis, M., Bloomfield, D. S., Dupuis, J., & Keenan, F. P. 2004, ApJ, 612, 1140 [NASA ADS] [CrossRef] [Google Scholar]
- Ciesla, F. J., Mulders, G. D., Pascucci, I., & Apai, D. 2015, ApJ, 804, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Claire, M. W., Sheets, J., Cohen, M., et al. 2012, ApJ, 757, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Correia, A. C. M., & Laskar, J. 2001, Nature, 411, 767 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cossou, C., Raymond, S. N., Hersant, F., & Pierens, A. 2014, A&A, 569, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Darwin, G. H. 1880, Roy. Soc. Lond. Philosoph. Trans. Ser. I, 171, 713 [Google Scholar]
- Delfosse, X., Forveille, T., Ségransan, D., et al. 2000, A&A, 364, 217 [NASA ADS] [Google Scholar]
- DeMeo, F., & Carry, B. 2013, Icarus, 226, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Demory, B.-O., Ségransan, D., Forveille, T., et al. 2009, A&A, 505, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Desch, S. J., & Leshin, L. A. 2004, in Lunar and Planetary Science Conference, eds. S. Mackwell, & E. Stansbery, 35 [Google Scholar]
- do Nascimento, Jr., J.-D., Vidotto, A. A., Petit, P., et al. 2016, ApJ, 820, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, S. A., Singh, K. P., White, N. E., Mewe, R., & Kaastra, J. S. 1996, in Cool Stars, Stellar Systems, and the Sun, eds. R. Pallavicini, & A. K. Dupree, ASP Conf. Ser., 109, 263 [Google Scholar]
- Drake, S. A., Behar, E., Doyle, J. G., et al. 2015, ArXiv e-prints [arXiv:1501.02771] [Google Scholar]
- Efroimsky, M. 2012, ApJ, 746, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P., Kiseleva, L. G., & Hut, P. 1998, ApJ, 499, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Elkins-Tanton, L. T. 2008, Earth and Planetary Science Letters, 271, 181 [Google Scholar]
- Engle, S. G., & Guinan, E. F. 2011, in 9th Pacific Rim Conference on Stellar Astrophysics, eds. S. Qain, K. Leung, L. Zhu, & S. Kwok, ASP Conf. Ser., 451, 285 [Google Scholar]
- Fabrycky, D. C., Johnson, E. T., & Goodman, J. 2007, ApJ, 665, 754 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Marley, M. S., & Barnes, J. W. 2007, ApJ, 659, 1661 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhrmeister, B., Lalitha, S., Poppenhaeger, K., et al. 2011, A&A, 534, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garaud, P., & Lin, D. N. C. 2007, ApJ, 654, 606 [Google Scholar]
- Genda, H., & Abe, Y. 2005, Nature, 433, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Gerkema, T., Lam, F. A., & Maas, L. R. M. 2004, Deep Sea Research, Part II: Topical Studies in Oceanography, 51, 2995 [NASA ADS] [CrossRef] [Google Scholar]
- Gillon, M., Jehin, E., Lederer, S. M., et al. 2016, Nature, 533, 221 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gold, T., & Soter, S. 1969, Icarus, 11, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P. 1963, MNRAS, 126, 257 [NASA ADS] [Google Scholar]
- Goldreich, P., & Peale, S. 1966, AJ, 71, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Tremaine, S. 1980, ApJ, 241, 425 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Gomes, R., Levison, H. F., Tsiganis, K., & Morbidelli, A. 2005, Nature, 435, 466 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gradie, J., & Tedesco, E. 1982, Science, 216, 1405 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Grimm, R. E., & McSween, H. Y. 1993, Science, 259, 653 [NASA ADS] [Google Scholar]
- Güdel, M., Audard, M., Reale, F., Skinner, S. L., & Linsky, J. L. 2004, A&A, 416, 713 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guinan, E. F., Ribas, I., & Harper, G. M. 2003, ApJ, 594, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Guinan, E. F., Engle, S. G., & Durbin, A. 2016, ApJ, 821, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Haisch, B. M., Linsky, J. L., Bornmann, P. L., et al. 1983, ApJ, 267, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Haisch, Jr., K. E., Lada, E. A., & Lada, C. J. 2001, ApJ, 553, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Hamano, K., Abe, Y., & Genda, H. 2013, Nature, 497, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, B. M. S. 2010, ApJ, 723, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, B. M. S. 2015, Int. J. Astrobiol., 14, 267 [CrossRef] [Google Scholar]
- Hartogh, P., Lis, D. C., Bockelée-Morvan, D., et al. 2011, Nature, 478, 218 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hudson, H. S. 1991, Sol. Phys., 133, 357 [Google Scholar]
- Hünsch, M., Schmitt, J. H. M. M., Sterzik, M. F., & Voges, W. 1999, A&AS, 135, 319 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunten, D. M., Pepin, R. O., & Walker, J. C. G. 1987, Icarus, 69, 532 [NASA ADS] [CrossRef] [Google Scholar]
- Hut, P. 1980, A&A, 92, 167 [NASA ADS] [Google Scholar]
- Hut, P. 1981, A&A, 99, 126 [NASA ADS] [Google Scholar]
- Ida, S., & Lin, D. N. C. 2010, ApJ, 719, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Ingersoll, A. P., & Dobrovolskis, A. R. 1978, Nature, 275, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Izidoro, A., Raymond, S. N., Morbidelli, A., & Winter, O. C. 2015, MNRAS, 453, 3619 [NASA ADS] [CrossRef] [Google Scholar]
- Izidoro, A., et al. 2016, MNRAS, submitted [Google Scholar]
- Jardine, M., & Unruh, Y. C. 1999, A&A, 346, 883 [NASA ADS] [Google Scholar]
- Kaib, N. A., Raymond, S. N., & Duncan, M. 2013, Nature, 493, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Kalyaan, A., & Desch, S. 2016, in Am. Astron. Soc. Meet. Abstr., 228, 320.05 [Google Scholar]
- Kasting, J. F., Whitmire, D. P., & Reynolds, R. T. 1993, Icarus, 101, 108 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kennedy, G. M., & Kenyon, S. J. 2008, ApJ, 673, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Khodachenko, M. L., Ribas, I., Lammer, H., et al. 2007, Astrobiology, 7, 167 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Khodachenko, M. L., Alexeev, I., Belenkaya, E., et al. 2012, ApJ, 744, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Kopparapu, R. K. 2013, ApJ, 767, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Kopparapu, R. K., Ramirez, R. M., SchottelKotte, J., et al. 2014, ApJ, 787, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Kopparapu, R. K., Wolf, E. T., Haqq-Misra, J., et al. 2016, ApJ, 819, 84 [Google Scholar]
- Kuchner, M. J. 2003, ApJ, 596, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Kunkel, W. E. 1973, ApJS, 25, 1 [Google Scholar]
- Lammer, H., Selsis, F., Ribas, I., et al. 2003, ApJ, 598, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Lammer, H., Lichtenegger, H. I. M., Kulikov, Y. N., et al. 2007, Astrobiology, 7, 185 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lammer, H., Bredehöft, J. H., Coustenis, A., et al. 2009, A&ARv, 17, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Lammer, H., Kislyakova, K. G., Odert, P., et al. 2011, Origins of Life and Evolution of the Biosphere, 41, 503 [Google Scholar]
- Lammer, H., Güdel, M., Kulikov, Y., et al. 2012, Earth, Planets, and Space, 64, 179 [Google Scholar]
- Lecar, M., Podolak, M., Sasselov, D., & Chiang, E. 2006, ApJ, 640, 1115 [Google Scholar]
- Leconte, J., Wu, H., Menou, K., & Murray, N. 2015, Science, 347, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Lécuyer, C., Gillet, P., & Robert, F. 1998, Chem. Geol., 145, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Léger, A., Selsis, F., Sotin, C., et al. 2004, Icarus, 169, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Lichtenegger, H. I. M., Lammer, H., Grießmeier, J.-M., et al. 2010, Icarus, 210, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Linsky, J. L., & Wood, B. E. 2014, ASTRA Proc., 1, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Linsky, J. L., Fontenla, J., & France, K. 2014, ApJ, 780, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Lis, D. C., Biver, N., Bockelée-Morvan, D., et al. 2013, ApJ, 774, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Lissauer, J. J. 2007, ApJ, 660, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Love, A. E. H. 1909, MNRAS, 69, 476 [NASA ADS] [Google Scholar]
- Loyd, R. O. P., & France, K. 2014, ApJS, 211, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Luger, R., & Barnes, R. 2015, Astrobiology, 15, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Makarov, V. V. 2012, ApJ, 752, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Makarov, V. V., & Efroimsky, M. 2013, ApJ, 764, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, R. G., & Livio, M. 2012, MNRAS, 425, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Marty, B. 2012, Earth and Planetary Science Letters, 313, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Marty, B., & Yokochi, R. 2006, Rev. Mineral Geophys., 62, 421 [CrossRef] [Google Scholar]
- Marty, B., Avice, G., Sano, Y., et al. 2016, Earth and Planetary Science Letters, 441, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C., et al. 2011, A&A, submitted [arXiv:1109.2497] [Google Scholar]
- McNeil, D. S., & Nelson, R. P. 2010, MNRAS, 401, 1691 [NASA ADS] [CrossRef] [Google Scholar]
- Mignard, F. 1979, Moon and Planets, 20, 301 [Google Scholar]
- Montgomery, R., & Laughlin, G. 2009, Icarus, 202, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., Chambers, J., Lunine, J. I., et al. 2000, Met. Planet. Science, 35, 1309 [Google Scholar]
- Morbidelli, A., Lunine, J. I., O’Brien, D. P., Raymond, S. N., & Walsh, K. J. 2012, Ann. Rev. Earth Planet. Sci., 40, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., Lambrechts, M., Jacobson, S., & Bitsch, B. 2015, Icarus, 258, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Morin, J., Donati, J.-F., Petit, P., et al. 2010, MNRAS, 407, 2269 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Mulders, G. D., Ciesla, F. J., Min, M., & Pascucci, I. 2015, ApJ, 807, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Neron de Surgy, O., & Laskar, J. 1997, A&A, 318, 975 [NASA ADS] [Google Scholar]
- Neves, V., Bonfils, X., Santos, N. C., et al. 2013, A&A, 551, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Brien, D. P., Walsh, K. J., Morbidelli, A., Raymond, S. N., & Mandell, A. M. 2014, Icarus, 239, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Ogihara, M., & Ida, S. 2009, ApJ, 699, 824 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, J. E., & Alvarez, M. A. 2016, ApJ, 816, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S.-J., Baruteau, C., & Kley, W. 2011, MNRAS, 410, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Panero, W. 2016, Nature Geosciences, submitted [Google Scholar]
- Pascucci, I., Apai, D., Luhman, K., et al. 2009, ApJ, 696, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Pecaut, M. J., & Mamajek, E. E. 2016, MNRAS, 461, 794 [NASA ADS] [CrossRef] [Google Scholar]
- Pfalzner, S., Steinhausen, M., & Menten, K. 2014, ApJ, 793, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Podolak, M. 2010, in IAU Symp. 263, eds. J. A. Fernandez, D. Lazzaro, D. Prialnik, & R. Schulz, 19 [Google Scholar]
- Pollack, H. N., Hurter, S. J., & Johnson, J. R. 1993, Rev. Geophys., 31, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Ramirez, R. M., & Kaltenegger, L. 2014, ApJ, 797, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Raymond, S. N., Quinn, T., & Lunine, J. I. 2004, Icarus, 168, 1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Raymond, S. N., Quinn, T., & Lunine, J. I. 2006, Icarus, 183, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Raymond, S. N., Quinn, T., & Lunine, J. I. 2007a, Astrobiology, 7, 66 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Raymond, S. N., Scalo, J., & Meadows, V. S. 2007b, ApJ, 669, 606 [Google Scholar]
- Raymond, S. N., O’Brien, D. P., Morbidelli, A., & Kaib, N. A. 2009, Icarus, 203, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Raymond, S. N., Kokubo, E., Morbidelli, A., Morishima, R., & Walsh, K. J. 2014, Protostars and Planets VI, 595 [Google Scholar]
- Reiners, A., & Basri, G. 2009, A&A, 496, 787 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reiners, A., & Mohanty, S. 2012, ApJ, 746, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., Schüssler, M., & Passegger, V. M. 2014, ApJ, 794, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Ribas, I., Guinan, E. F., Güdel, M., & Audard, M. 2005, ApJ, 622, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Rosing, M. T. 2005, Int. J. Astrobiol., 4, 9 [CrossRef] [Google Scholar]
- Roskosz, M., Bouhifd, M. A., Jephcoat, A. P., Marty, B., & Mysen, B. O. 2013, Geochim. Cosmochim. Acta, 121, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Sasselov, D. D., & Lecar, M. 2000, ApJ, 528, 995 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitt, J. H. M. M., & Liefke, C. 2004, A&A, 417, 651 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Selsis, F., Chazelas, B., Bordé, P., et al. 2007a, Icarus, 191, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Selsis, F., Kasting, J. F., Levrard, B., et al. 2007b, A&A, 476, 1373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Semel, M. 1989, A&A, 225, 456 [NASA ADS] [Google Scholar]
- Shibayama, T., Maehara, H., Notsu, S., et al. 2013, ApJS, 209, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, D. E., Zuber, M. T., Phillips, R. J., et al. 2012, Science, 336, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Sokół, J. M., Bzowski, M., Tokumaru, M., Fujiki, K., & McComas, D. J. 2013, Sol. Phys., 285, 167 [Google Scholar]
- Spencer, J. R., Rathbun, J. A., Travis, L. D., et al. 2000, Science, 288, 1198 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Swift, J. J., Johnson, J. A., Morton, T. D., et al. 2013, ApJ, 764, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Terquem, C., & Papaloizou, J. C. B. 2007, ApJ, 654, 1110 [NASA ADS] [CrossRef] [Google Scholar]
- Thuillier, G., Floyd, L., Woods, T. N., et al. 2004, in Solar Variability and its Effects on Climate, Geophysical Monograph, eds. J. M. Pap, P. Fox, C. Frohlich, H. S., Hudson, et al. (Washington DC: American Geophysical Union), Geophysical Monograph Series, 141, 171 [Google Scholar]
- Tian, F. 2009, ApJ, 703, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, F., Kasting, J. F., Liu, H.-L., & Roble, R. G. 2008, J. Geophys. Res., 113, 05008 [Google Scholar]
- Tolstikhin, I., Marty, B., Porcelli, D., & Hofmann, A. 2014, Geochim. Cosmochim. Acta, 136, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Turbet, M., Leconte, J., Selsis, F., et al. 2016, A&A, 596, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Laerhoven, C., Barnes, R., & Greenberg, R. 2014, MNRAS, 441, 1888 [NASA ADS] [CrossRef] [Google Scholar]
- Vidotto, A. A., Jardine, M., Morin, J., et al. 2013, A&A, 557, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walker, A. R. 1981, MNRAS, 195, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, K. J., Morbidelli, A., Raymond, S. N., O’Brien, D. P., & Mandell, A. M. 2011, Nature, 475, 206 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wood, B. E., Linsky, J. L., Müller, H.-R., & Zank, G. P. 2001, ApJ, 547, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, B. E., Redfield, S., Linsky, J. L., Müller, H.-R., & Zank, G. P. 2005, ApJS, 159, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, B. E., Müller, H.-R., Redfield, S., & Edelman, E. 2014, ApJ, 781, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Worth, R., & Sigurdsson, S. 2016, ApJ, 831, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, J., Cowan, N. B., & Abbot, D. S. 2013, ApJ, 771, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Yoder, C. F. 1995, in Global Earth Physics: A Handbook of Physical Constants, ed. T. J. Ahrens (Washington DC: American geophysical Union), 1 [Google Scholar]
- Zahnle, K. J. 2015, in Lunar and Planetary Inst. Technical Report, Lunar and Planetary Science Conference, 46, 1549 [NASA ADS] [Google Scholar]
- Zechmeister, M., Kürster, M., & Endl, M. 2009, A&A, 505, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, T. L., Delva, M., Baumjohann, W., et al. 2007, Nature, 450, 654 [NASA ADS] [CrossRef] [Google Scholar]
- Zuluaga, J. I., Bustamante, S., Cuartas, P. A., & Hoyos, J. H. 2013, ApJ, 770, 23 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Magnetopause radius of Proxima b
Appendix A.1: Case without wind ram pressure
This is the approach of Vidotto et al. (2013, hereafter V13), which relies on the extrapolation of the large-scale surface magnetic field of a star – derived by means of Zeeman-Doppler Imaging (ZDI) – using the potential field source surface methods. The equation 2 of V13 defining the pressure balance at the nose of the magnetopause then becomes  (A.1)where Bss is the stellar magnetic field extrapolated at the source surface, Rss is the radius of the source surface, Rorb the orbital radius of the planet, and Bp,0, rp, rM have already been defined.
(A.1)where Bss is the stellar magnetic field extrapolated at the source surface, Rss is the radius of the source surface, Rorb the orbital radius of the planet, and Bp,0, rp, rM have already been defined.
We also rewrite the pressure balance equation in the case of the Earth where the solar wind magnetic pressure is negligible with respect to the wind ram pressure, in this case we obtain:  (A.2)where
(A.2)where 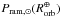 is the ram pressure of the solar wind at Earth, and the right-hand side of the equation is the same as in Eq. (A.1) with Earth values. Dividing Eq. (A.1) by (A.2) yields
is the ram pressure of the solar wind at Earth, and the right-hand side of the equation is the same as in Eq. (A.1) with Earth values. Dividing Eq. (A.1) by (A.2) yields ![\appendix \setcounter{section}{1} \begin{equation} \dfrac{r_M}{r_{\rm p}} = \dfrac{r_M^\oplus} {r_\oplus} \dfrac{\left[ 8\pi P_{\rm ram,\odot}(R_{\rm orb}^{\oplus}) \right]^{1/6}} {\left(f_1 f_2 B_{\star}\right)^{1/3} \left(\dfrac{R_{\rm ss}}{R_{\rm orb}} \right)^{2/3}} \left( \dfrac{B_{\rm p,0}}{B_{\rm p,0}^\oplus} \right)^{1/3} \cdot \label{eq:rmag} \end{equation}](/articles/aa/full_html/2016/12/aa29576-16/aa29576-16-eq208.png) (A.3)In this equation, we have expressed the value of the magnetic field at the source surface as
(A.3)In this equation, we have expressed the value of the magnetic field at the source surface as 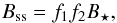 (A.4)where f1 = BZDI/B⋆ represents the fraction of the stellar surface magnetic “flux” that can be detected through ZDI (Semel 1989). Following Reiners & Basri (2009) and Morin et al. (2010) we take f1 = 0.2 if the large-scale component of the field is dipole-dominated and f1 = 0.06 in the multipolar case. The factor f2 = Bss/BZDI represents the ratio between the average magnetic field measured by ZDI and the average magnetic field at the source surface. From the sample of M dwarfs analyzed in V13 we find anaverage value of f2 = 1/15 with little scatter for most stars, while a few stars with very non-axisymmetric fields have much lower values. This can be considered as a favorable case allowing the development of a large planetary magnetosphere, in the present study we consider f2 = 1/50 as a representative value for this configuration. In Table 3, to encompass a wide range of physically meaningful values, we consider f1 = 0.2, f2 = 1/15 for a dipole-dominated stellar magnetic field and f1 = 0.06, f2 = 1/50 for a multipolar field.
(A.4)where f1 = BZDI/B⋆ represents the fraction of the stellar surface magnetic “flux” that can be detected through ZDI (Semel 1989). Following Reiners & Basri (2009) and Morin et al. (2010) we take f1 = 0.2 if the large-scale component of the field is dipole-dominated and f1 = 0.06 in the multipolar case. The factor f2 = Bss/BZDI represents the ratio between the average magnetic field measured by ZDI and the average magnetic field at the source surface. From the sample of M dwarfs analyzed in V13 we find anaverage value of f2 = 1/15 with little scatter for most stars, while a few stars with very non-axisymmetric fields have much lower values. This can be considered as a favorable case allowing the development of a large planetary magnetosphere, in the present study we consider f2 = 1/50 as a representative value for this configuration. In Table 3, to encompass a wide range of physically meaningful values, we consider f1 = 0.2, f2 = 1/15 for a dipole-dominated stellar magnetic field and f1 = 0.06, f2 = 1/50 for a multipolar field.
By replacing numerical constants and allowing to express Rss and Rorb in convenient units, one finally obtains the expression presented in Eq. (2), where ![\appendix \setcounter{section}{1} \begin{equation} K = \dfrac{r_M^\oplus}{r_\oplus} \dfrac{\left[ 8\pi P_{\rm ram,\odot}(R_{\rm orb}^{\oplus}) \right]^{1/6}} {\left( {B_{\rm p,0}^\oplus} \right)^{1/3} \left(\dfrac{R_{\rm ss}}{R_\star}\right)^{2/3}} \left(\dfrac{[1~{\rm AU}]}{R_\odot}\right)^{2/3} \cdot \label{eq:Krmag} \end{equation}](/articles/aa/full_html/2016/12/aa29576-16/aa29576-16-eq212.png) (A.5)The value of the non-dimensional constant K = 15.48 mentioned in the main text can be estimated by using the following values taken from V13:
(A.5)The value of the non-dimensional constant K = 15.48 mentioned in the main text can be estimated by using the following values taken from V13: 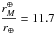 ;
; 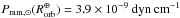 ;
; 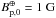 and
and 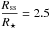 .
.
Appendix A.2: Case with wind ram pressure
In this case, Eq. (A.1) becomes 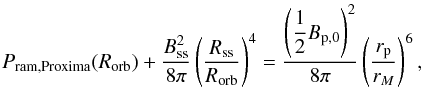 (A.6)where Pram,Proxima(Rorb) is Proxima’s wind ram pressure at the orbit of Proxima b. The expression of the magnetopause radius then becomes
(A.6)where Pram,Proxima(Rorb) is Proxima’s wind ram pressure at the orbit of Proxima b. The expression of the magnetopause radius then becomes ![\appendix \setcounter{section}{1} \begin{equation} \dfrac{r_M}{r_{\rm p}} = \dfrac{r_M^\oplus} {r_\oplus} \left[ \dfrac{1} {f_w + \dfrac{\left(f_1 f_2 B_{\star}\right)^{2} \left(\dfrac{R_{\rm ss}}{R_{\rm orb}} \right)^{4}} {8\pi P_{\rm ram,\odot}(R_{\rm orb}^{\oplus})}} \right]^{1/6} \left( \dfrac{B_{\rm p,0}}{B_{\rm p,0}^\oplus} \right)^{1/3} \text{,} \label{eq:rmag_full} \end{equation}](/articles/aa/full_html/2016/12/aa29576-16/aa29576-16-eq219.png) (A.7)where the ratio
(A.7)where the ratio  lies in the range 4–80 according to Sect. 4.3.
lies in the range 4–80 according to Sect. 4.3.
All Tables
High-energy fluxes received currently by Proxima b and the Earth in units of erg s-1 cm-2.
Lost hydrogen (in EOH), lost oxygen (in bar) and atmospheric build-up O2 pressure when Proxima b reaches the HZ and at the age of the system.
All Figures
 |
Fig. 1 High-energy spectral irradiance received by Proxima b and the Earth. The values correspond to those in Table 2 but calculated per unit wavelength (i.e., divided by the width of the wavelength bin; 0.5 nm is adopted for H Lyα). |
| In the text | |
 |
Fig. 2 Evolution of the HZ inner edge, bolometric luminosity and XUV luminosity for Proxima. Top panel: evolution of the inner edge of the HZ for two different assumptions: Sp = 0.9S⊕ (dashed blue line), Sp = 1.5S⊕ (full blue line). The full black line corresponds to Proxima’s measured orbital distance. Bottom panel: evolution of the luminosity for a 0.1M⊙ star (in orange), for 0.2 M⊙ (in red) and 0.123 M⊙ (in blue). The gray area corresponds to the observed value (see Table 1). The black vertical dashed line corresponds to the estimated age of Proxima. |
| In the text | |
 |
Fig. 3 XUV flux evolution for Proxima and the Sun at the orbital distance of Proxima b and Earth, respectively. The two scenarios discussed in the text, namely a flat regime and a power-law decrease and a constant value throughout, are represented, with the gray area indicating a realistic possible range. Such relationships show that Proxima b has been irradiated at a level significantly higher than the Earth throughout most of their lifetimes and the integrated XUV dose is between 7 and 16 times higher, depending on the assumed XUV flux evolution for Proxima. |
| In the text | |
 |
Fig. 4 Probability of capture in the 3:2 resonance as a function of orbital eccentricity and triaxiality of the planet (numbered contours with color shadings). White regions depict areas of certain capture due to the tidal torque. Black regions show where the triaxial torque is too weak to enforce capture. Labeled curves are: (a) tidal torque at the lower boundary of the separatrix is negative and greater in magnitude than the maximum restoring torque; (b) tidal torque at the lower boundary of the separatrix is positive; (c) maximal tidal torque inside the resonance is greater than the maximum triaxial torque. Being above (c) and/or (b) leads to certain capture. Below (c) and (a) capture is impossible. |
| In the text | |
 |
Fig. 5 Sketch of the equilibrium eccentricity, whence the tidal torque vanishes, as a function of planetary rotation rate (blue curve). Solid portions of the curve near resonances depict stable equilibria, whereas dotted portions show unstable ones. Areas of positive torque are in gray, and of negative torque in blue. Dashed gray curves show the area covered by librations inside the resonances, that is, the resonance width (see Eq. (7)). With realistic values for the triaxiality and the Maxwell time, both the kink around the resonances and the resonance width would be much narrower and difficult to see. |
| In the text | |
 |
Fig. 6 Hydrogen loss and O2 pressure for Proxima-b for an initial time of t0 = 3 Myr. Top panel: hydrogen loss computed with method (1) and (2) in full red lines and with method (3) in colored dashed lines. The gray areas correspond to the amount of hydrogen created by photolysis for two different efficiencies ϵα = 1.0 (all the incoming energy is used for photolysis) and ϵα = 0.1 (only 10% of the incoming energy is used). The edges of the gray areas were calculated using two different assumptions on the wavelength range important for photolysis: the lower edge corresponds to the energy flux in the H Ly α band (Table 2), the upper edge corresponds to the energy flux in a wider band: 10–170 nm. The vertical lines represent the time at which the planet reaches the 1.5 S⊕ HZ inner edge, the 0.9 S⊕ HZ inner edge and the age of the system (4.8 Gyr). Bottom panel: O2 pressure building up in the atmosphere computed with method (3). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


