| Issue |
A&A
Volume 596, December 2016
|
|
|---|---|---|
| Article Number | A40 | |
| Number of page(s) | 9 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201629059 | |
| Published online | 28 November 2016 | |
Uninterrupted optical light curves of main-belt asteroids from the K2 mission⋆
1 Konkoly Observatory, Research Centre for Astronomy and Earth Sciences, Hungarian Academy of Sciences, 1121 Budapest, Konkoly Thege Miklós út 15–17, Hungary
e-mail: rszabo@konkoly.hu
2 Eötvös Loránd Tudományegyetem, 1117 Pázmány Péter sétány 1/A, Budapest, Hungary
3 Gothard-Lendület Research Team, 9704 Szombathely, Szent Imre herceg út 112, Hungary
4 ELTE Gothard Astrophysical Observatory, 9704 Szombathely, Szent Imre herceg út 112, Hungary
5 Sydney Institute for Astronomy, School of Physics A28, University of Sydney, NSW 2006, Australia
Received: 5 June 2016
Accepted: 14 September 2016
Context. Because the second reaction wheel failed, a new mission was conceived for the otherwise healthy Kepler space telescope. In the course of the K2 mission, the telescope is staring at the plane of the Ecliptic. Thousands of solar system bodies therefore cross the K2 fields and usually cause additional noise in the highly accurate photometric data.
Aims. We here follow the principle that some person’s noise is another person’s signal and investigate the possibility of deriving continuous asteroid light curves. This is the first such endeavor. In general, we are interested in the photometric precision that the K2 mission can deliver on moving solar system bodies. In particular, we investigate space photometric optical light curves of main-belt asteroids.
Methods. We studied the K2 superstamps that cover the fields of M35, and Neptune together with Nereid, which were observed in the long-cadence mode (29.4 min sampling). Asteroid light curves were generated by applying elongated apertures. We used the Lomb-Scargle method to determine periodicities that are due to rotation.
Results. We derived K2 light curves of 924 main-belt asteroids in the M35 field and 96 in the path of Neptune and Nereid. The light curves are quasi-continuous and several days long. K2 observations are sensitive to longer rotational periods than typical ground-based surveys. Rotational periods are derived for 26 main-belt asteroids for the first time. The asteroid sample is dominated by faint objects (>20 mag). Owing to the faintness of the asteroids and the high density of stars in the M35 field, only 4.0% of the asteroids with at least 12 data points show clear periodicities or trends that signal a long rotational period, as opposed to 15.9% in the less crowded Neptune field. We found that the duty cycle of the observations had to reach ~60% to successfully recover rotational periods.
Key words: techniques: photometric / minor planets, asteroids: general
Full Tables 1–4 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/596/A40
© ESO, 2016
1. Introduction
 |
Fig. 1 Mosaic of the M35 open cluster (and NGC 2158) as seen by K2. The area is covered by 154 sub-apertures amounting to 800 × 550 pixels (53′ × 36′). |
The Kepler space telescope revolutionized time-domain astronomy, and its unique capabilities were demonstrated by the detection of short- (Sanchis-Ojeda et al. 2014) and long-period transiting exoplanets (Kipping et al. 2016), the application of stellar seismology (Chaplin et al. 2011), and the renewed interest in studying classical variable stars (Gilliland et al. 2010). In the latter case, for example, a new dynamical phenomenon was discovered in RR Lyrae stars (Szabó et al. 2010), whose detection had been previously hampered by the diurnal variations affecting ground-based observations.
In 1901, von Oppolzer first noted the brightness variation of an asteroid, (433) Eros (von Oppolzer 1901), and its first correct period was published in Bailey (1913) with those of several other minor planets. During the more than hundred years since then, the light variation of more than 10 000 main-belt asteroids were measured, but the length of the continuous observations has always been limited by the length of a winter night. The repurposed Kepler mission (K2; Howell et al. 2014) made it possible for the first time to quasi-continuously measure the brightness of a large number of main-belt asteroids. In this paper we show the results obtained from the photometry of almost 1000 main-belt asteroids, most of them followed continuously for up to 3–4 days or longer, a small fraction of them up to 6 days in two large superstamps of the K2 mission.
In a series of works we have been investigating the possibilities of high-precision space photometric observations of solar system objects with the rejuvenated Kepler space telescope (Howell et al. 2014). In Szabó et al. (2015) the effects of main-belt asteroid encounters on K2 photometry of stellar targets were investigated. Pál et al. (2015) analyzed the two faint trans-Neptunian objects 2002 GV31and 2007 JJ43 by measuring their rotation periods. They are among the faintest objects Kepler has measured so far. We also outlined the method for handling these moving targets that Kepler has not been designed for. Special masks were allocated to these targets, which enabled us to observe them continuously. By complementing recent K2 observations with archival Herschel data, we analyzed the thermophysical parameters of 2007 OR10 in Pál et al. (2016).
In this work we turn our attention to two special fields that K2 has observed, both of which have been covered by multiple sub-apertures, so that large enough fields were created to search for asteroids. In Campaign 0 (C0), the well-known bright open cluster M35 (NGC 2168) was observed with Kepler. It was covered with a mosaic of small stamps consisting of 154 50 × 50 pixels, which amounts to 800 × 550 pixels (53′ × 36′ on the sky); the EPIC IDs range from 2000000811 to 200000964. The observed field also includes the open cluster NGC 2158. By briefly investigating the images, it was immediately obvious that hundreds of asteroids crossed this field of view. We chose these observations because of the large contiguous field and the large number of asteroids available. Campaign 0 covers the period March 8 to May 30, 2014. It was implemented as a full-length engineering test to prove that K2 was a viable mission. The Kepler spacecraft was not in fine point for the first 16 days of C0, which caused large photometric scatter. Eventually, the Kepler spacecraft went into safe mode that lasted for about 24 days. After this, high-quality fine-point measurements began, which span 35 days. The data quality improved in the second half of the campaign. We used data from only this part of the campaign. Jupiter was crossing the field, but fell on the dead Module 3 and caused only increased background flux.
 |
Fig. 2 Mosaic covering the paths of Neptune and Nereid observed by the K2 mission. The length of the mosaic is approximately 20′. |
Campaign 3 (C3) started on November 15, 2014, and ended on January 23, 2015. In this campaign Neptune and its satellite, Nereid, was observed (GO IDs: 3057, 3060, 3115), their path was also tiled with 305 narrow strips of pixel masks (EPIC IDs 200004468–200004762). We refer to this field as Nereid field henceforth. While C0, and especially the vicinity of M35, contains a crowded field, this small stripe of the sky gave us the opportunity to analyze light curves of asteroids that are usually free of too many stellar sources. However, because of the proximity to Neptune, other problems arose (high background, saturation, etc.). The change in bandwidth for pointing control (from 50 to 20 s) for C3 resulted in an increase in signal-to-noise ratio for short cadence by a factor of roughly 4–9, with the greater improvement seen at the higher frequency end. Campaign 3 had a nominal duration of 80 days, but an actual duration of only 69.2 days. The campaign ended earlier than expected because the on-board storage filled up faster than anticipated because of the unusually poor data compression1.
A similar study about Jovian Trojan asteroids observed by the K2 mission will be published in a related paper (Szabó et al. 2016).
2. Data analysis
 |
Fig. 3 Photometric errors of the individual K2 asteroid measurements in the M35 field as a function of the apparent brightness of the asteroids (light blue dots). The red line plots the Kepler preflight estimate of the photometric precision (Van Cleeve & Caldwell 2016)2, the purple line shows the scaled Combined Differential Photometric Precision data (Christiansen et al. 2013), the black line represents the photometry of a faint RR Lyrae star in Leo IV for comparison (Molnár et al. 2015), and the dashed line shows the linear interpolation between the last two. |
In Fig. 1 we show the result of stitching the small sub-fields that cover the open cluster M35, while Fig. 2 displays the path covered by Nereid in the vicinity of Neptune.
2.1. Photometry
We used only long-cadence (29.4 min sampling) observations of the two fields. To prepare the light curves and derive photometry, we used the FITSH package (Pál 2012). Some aspects of obtaining precise photometry of moving targets with the Kepler space telescope during the K2 mission have been discussed by our group in Pál et al. (2015, 2016) and in Kiss et al. (2016). Here, we had to accommodate more elongated trails during the long-cadence observations because of the main-belt asteroid targets than for the trans-Neptunian objects in our earlier works. The method is based on a process that fits a circular aperture convolved with the apparent track of the asteroid. The track is approximated with a linear curve. The details of the method are described in Szabó et al. (2016). In Fig. 3 we plot the photometric error of each individual data point for every asteroids in the M35 field as a function of brightness. The error contains the noise from the background and the shot noise. The background noise is determined from a circular or elongated ring around the target, while the shot noise is computed from the known electron/ADU conversion rates. For the brightest targets we added a conservative upper error limit (0.001 mag for the brightest objects, 0.002 mag for slightly fainter observations, etc.), since the error computation gives an unrealistically low error limit because systematic errors are neglected (e.g., errors caused by passing through bright stellar objects). Our approach is an attempt to compensate for this underestimation. This choice probably does not affect the information content of the figure and affects only a negligible portion of the targets. The precision reaches a few mmag for the brightest objects, 0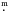 01 for an 18th magnitude object and 0
01 for an 18th magnitude object and 0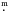 1 for an asteroid of the 20th magnitude. We note that the error values do not contain systematic errors. The precision we achieved is better than the conservative preflight estimate of Kepler, but slightly poorer than the precision derived from actual photometry of stellar targets. For the latter comparison we scaled the Combined Differential Photometric Precision (CDPP, Christiansen et al. 2013) values of the original Kepler mission to a single long-cadence exposure. However, these data only extended to 16 mag, therefore we also included the measurements of the extragalactic RR Lyrae EPIC 210282474, the only variable star in Leo IV that was not affected by blending (Molnár et al. 2015). Finally, we added a linear interpolation between the two data sets.
1 for an asteroid of the 20th magnitude. We note that the error values do not contain systematic errors. The precision we achieved is better than the conservative preflight estimate of Kepler, but slightly poorer than the precision derived from actual photometry of stellar targets. For the latter comparison we scaled the Combined Differential Photometric Precision (CDPP, Christiansen et al. 2013) values of the original Kepler mission to a single long-cadence exposure. However, these data only extended to 16 mag, therefore we also included the measurements of the extragalactic RR Lyrae EPIC 210282474, the only variable star in Leo IV that was not affected by blending (Molnár et al. 2015). Finally, we added a linear interpolation between the two data sets.
Sample table of the observed asteroids in the K2 M35 superstamp.
2.2. Period search
We searched for significant periodicities using the Lomb-Scargle periodogram functions of the gatspy Python package3. Although Fourier-based methods were considered as well, as implemented in the Period04 program package (Lenz & Breger 2005), we obtained very similar results in several test cases, therefore we decided to stick to the Lomb-Scargle method. We note that the errors of the individual photometric points are taken into account by the implementation of the Lomb-Scargle algorithm we used. Only those signals were considered that were significant on the 3σ-level compared to the background local noise in the Lomb-Scargle periodogram. We phase-folded the light curves with the best period and its double value, then decided which gives a better fit based on a visual inspection. In many cases there were significant deviations in odd and even cycles. In these cases the two-period folding was chosen. When the inspection was inconclusive or resulted in a dynamically untenable short period (i.e. shorter than two hours), we chose the double-period solution. Following this method, we did not retain any single-periodic solutions in accordance with other main-belt asteroid works. We note that the chosen two-hour limit is plausible, since K2 did not observe smaller asteroids in these fields. To demonstrate this we considered a close-by asteroid of the Hungaria family in the classical main belt. When its brightness in opposition is 21 mag (it is fainter than 22 mag in the K2 field), this corresponds to H = 19.0 absolute magnitude, which translates into a diameter of 300 m assuming an albedo of 0.5. We emphasize that this is a conservative estimate.
M35 field: out of 924 asteroids that crossed the M35 field, 867 had more than 12 data points. We retained only these asteroids to have a set of reasonably covered light curves. Although this number might vary from light curve to light curve depending on the distribution of data points, we found that this number covers the short-period asteroids well and still gives some information for longer rotational periods. Twenty-three of the 867 light curves showed clear periodicities, that is, above the 3σ limit. The periods ranged from 3.89 h to 88.41 h, with a median of 9.83 h. The length of the covered paths ranged from 0.26 days to 6.05 days with a median of 2.06 days. The median number of observations per asteroid was 48.
 |
Fig. 4 Light curve (left panel) and Lomb-Scargle periodogram (right panel) of (111) Ate, the brightest member of our sample. The periodogram shows three peaks, the largest of which corresponds to a period of 20.63 ± 0.60 h. |
Nereid field: out of 96 light curves, 88 had more than 12 points in their K2 C3 light curves, of which 14 showed periodicities above the 3σ limit. The shortest detected period is 3.71 h, while the longest is 14.63 h, the median being 4.96 h. The length of observation varied from a few data points (aboutone hour) to 14.45 days, the latter corresponds to an asteroid that moved parallel to the apparent path of Nereid. The median length was 1.25 days. Compared to the M35 field, here we found fewer asteroids because of the smaller field, but the light curves are more complete, meaning that fewer points had to be dropped. To put it quantitatively, the median number of retained observations per asteroid was 57. This is due to the less crowded nature of the field.
 |
Fig. 5 Duty cycle vs. length of observations for asteroids in the M35 K2 field. Blue dots are all the 924 asteroids crossing the superstamp, red dots are those that exhibit significant periodicity or trend. The histograms show the distribution of the observing length and the duty cycle. |
To end this section, we show the case of (111) Ate, an example where our period search did not result in an unambiguous period value. In the left panel of Fig. 4 we show the light curve. The three minima clearly define two periods in our light curve. The periodogram (right panel of the same figure) shows three significant peaks, but we were unable to determine the value based on this accurate but short light curve. The largest peak corresponds to 20.63 ± 0.60 h (significant at the 5σ level), which is clearly different from the 22.072 ± 0.001 h value found in the literature (Warner et al. 2009). None of the peaks in our periodogram corresponds to the literature value. This is the brightest asteroid in our sample, but most probably our data set is too short to define a clear rotational period. More observations are clearly needed to settle the question.
3. Results
3.1. Unbiased K2 main-belt asteroid sample
In Table 1 we present the asteroids identified in the M35 superstamp during the second half of C0. Only those objects are listed that showed at least 12 useful photometric data points. The table lists the identification, and the start and end date of the time interval during which the minor planet was passing through the superstamp. The number of useful long-cadence observations and the calculated duty cycle is also given. The duty cycle is 1.0 when all the photometric points were retained, and 0 when all had to be discarded. We also provide the median brightness transformed to the USNO R band (Pál et al. 2015). When reliable period and amplitude were found, these values were added to the table(s). In Table 2 the same parameters are given for the main-belt asteroids that cross the Nereid superstamp.
As we discussed in detail in Szabó et al. (2015), no (or very few) new main-belt asteroid discoveries are expected in the K2 campaign fields because of the available limiting magnitude. We did not seen unknown objects among the 1020 identified asteroids in the two fields. The procedure of prediction and identification of the main-belt asteroids as seen from Kepler was described in detail in Szabó et al. (2015) and was followed here as well.
Figure 5 shows the duty cycle (percentage of the number of observed 29.4 min cadences with respect to the maximal possible cadences during the length of observation), that is, the number of cadences lost due to technical problems originating mainly from the photometric pipeline (outliers, encountering too bright stars, stellar residuals, etc.) versus the length of observations in the case of the M35 asteroids. Most of our objects were observed for 1–4 days, and we were able to follow some of them for 5–6 days. The vast majority of our targets were observed with a duty cycle of between 20 and 80%, a handful of them above 80%. Only one asteroid was followed with 100% duty cycle, and in this case, no long-cadence observations had to be discarded.
Objects that exhibited significant periodicities are shown with red dots in Fig. 5. It is evident that the majority of the minor planets showing periodicities were found among those that were observed with a high duty cycle. We found all the periodicities or long periods (seen as trends) only where the duty cycle was close to or above 60%. Similarly, we found that the more continuous the light curve in the Nereid field, the higher the chance to detect variability at a statistically significant level.
Twelve asteroids in the M35 field exhibited long-term trends or incompletely covered half-rotation periods. We identified these with longer-period asteroids. One example was found with literature data, namely asteroid (3345), for which we found a rotational period that is longer than 34 h, and Benishek & Coley (2014) reported 187 h.
In Tables 3 and 4 we give the format and the content of the files that contain the K2 photometry for all the targets in the M35 and Nereid fields, respectively. The full tables are available online.
 |
Fig. 6 Examples of periodic long-cadence (29.4 min sampling) asteroid light curves ordered according to decreasing brightness. Left panels: asteroids crossing the M35 field, right panel: asteroids observed in the Neptune-Nereid path. In each case the left panel shows the K2 light curve with error bars folded by the adopted (double) period, the right panel is the Lomb-Scargle plot. The error bars for bright asteroids are smaller than the size of the symbols. The sine plotted in red is fit to the data to guide the eye. The adopted period and the ID of the asteroid is shown in the middle of the left and right panels, respectively. |
Photometry of main-belt asteroids observed in the M35 superstamp by K2 during Campaign 0.
3.2. Selected light curves
In the left panels of Fig. 6 we show a few selected main-belt asteroid light curves in the M35 field along with their Lomb-Scargle diagrams, demonstrating the high quality of K2 observations. The right panels of the same figure show asteroids crossing our Nereid field. Both the light curves and the periodograms are of better quality in the latter field, which underpins our suspicions that more crowding precludes obtaining high-quality light curves for main-belt asteroids with Kepler. This is also supported by us recovering light curves with clear periodicities, incomplete cycles, or long-term trends, which implies long rotational period for 35 out of 867 asteroids (4.0%) in the M35 superstamp, and 14 out of 88 objects (15.9%) in the Nereid field.
Tables 5, 6 show rotational periods and amplitudes along with literature data where available. In the cases where only trends or partially covered cycles were found, we were able to establish only lower limits for the rotational period. The agreement between our rotational periods and literature values is excellent in each case despite the differences in observational strategies (multiple nights with ground-based telescopes vs. quasi-continuous for a few nights in the K2 mission). One exception is (111) Ate, which we discussed earlier. For more than half of our objects in Tables 5, 6 (26/47 combined) we publish unambiguous rotational parameters for the first time thanks to the continuous coverage of Kepler. The observed amplitudes are also in satisfactory agreement with available literature values. The uncertainty of the rotational period (also given in Tables 5, 6) depends on a number of factors, such as the brightness of the object, the length of observations, and the number of observational points in the light curve.
3.3. Interesting light curves with three maxima
 |
Fig. 7 Light curve of asteroid (29628) with three different peaks observed in the Nereid field. Upper panel: light curve folded with triple periods, lower panel: same data folded by sixtuple period. The curved line is a sixth-order Fourier-fit. Bottom panel: the light curve of asteroid (37201). |
Trimodal (i.e., three maxima during one rotation) and complex light curves are still considered as peculiar asteroid light curve shapes, although they were investigated as early as in the 1950s (Gehrels & Owings 1962). The first known examples of complex light curves were detected among the brightest asteroids, for example, (16) Psyche, (21) Lutetia, (37) Fides, (39) Laetitia, (43) Ariadne, (52) Europa, and (532) Herculina (Zappalà et al. 1983; Cellino et al. 1989). It has also been recognized that the same asteroids exhibit bimodal or even unimodal light curves at varying phase and aspect angles, therefore, shading effects, phase effects, and/or unusual rotational geometry were usually invoked to explain the complex light variations (e.g., Zappalà et al. 1983; Michalowski 1996). More recently, Harris et al. (2014) derived the higher-order harmonics that are due to polygonal shapes and concluded that rotating triangles enhance the sixth harmonics, therefore leading to light curves with six maxima and not exceeding 0.156 mag full amplitude of the sixth harmonics. They also presented two examples, (5404) Uemura and 2010 RC130, where the composite light curve of six maxima was far more convincing than with three maxima. Moreover, they remarked that the solution with three maxima led to short rotation periods, near the break-up barrier, which is an additional argument for the longer periods and a light curve with six maxima.
Two light curves in our data were found to show this type of complexity. Asteroid (29628) 1998 TX30 was observed in the Nereid field, during 16.7 h. The peak-to-peak amplitude is 0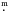 72, and the light curve suggests a triple or sextuple symmetry (Fig. 7). Assuming three humps, the rotational period is 8.04 h. Another solution with 16.08 h period is also possible. The overlapping region in the latter case (P = 16.08 h) extends only to five points, and despite their perfect fit to each other, drawing firm conclusions is not possible. However, the overall shape with six or eight humps is quite similar to the examples for complex light curves, in disfavor of trimodal solutions, by Harris et al. (2014). We note that other scenarios such as tumbling or albedo variegation may also play a role in this light variation, but a proper investigation would require a longer data set.
72, and the light curve suggests a triple or sextuple symmetry (Fig. 7). Assuming three humps, the rotational period is 8.04 h. Another solution with 16.08 h period is also possible. The overlapping region in the latter case (P = 16.08 h) extends only to five points, and despite their perfect fit to each other, drawing firm conclusions is not possible. However, the overall shape with six or eight humps is quite similar to the examples for complex light curves, in disfavor of trimodal solutions, by Harris et al. (2014). We note that other scenarios such as tumbling or albedo variegation may also play a role in this light variation, but a proper investigation would require a longer data set.
We retained 50 photometric data points of asteroid (37201) 2000 WS94, covering 25 h. The asteroid was also in the Nereid field. The light variation shows three humps with clearly incompatible shapes to each other, suggesting that this asteroid also has a complex light curve (Fig. 7, bottom panel). Because of the relatively short coverage, concluding about the rotation period is not possible. These two asteroids are therefore not included in Table 6.
 |
Fig. 8 Period-amplitude diagram of an unbiased sample of 35 asteroids from the M35 field (red points). The small green dots represent 16 000 asteroids from the Asteroid Lightcurve Database (Warner et al. 2009), while the thick black line shows the binned average of that large sample. |
3.4. Rotation statistics
Figure 8 shows the period-amplitude diagram of our sample of 35 asteroids with uninterrupted light curves from the M35 field. For comparison we plotted the parameters of over 16 000 asteroids taken from the Asteroid Lightcurve Database (Warner et al. 2009), which reflect the status of the database as of 20 February, 2016. We plot only the rotation frequencies above the Nyquist-frequency of K2 data, where the results are comparable. The thick black line shows the binned average of the large sample. The distribution of our limited sample nicely follows that of the underlying bulk sample. The median rotational period in the M35 field (9.83 h) clearly shows that we are sensitive to asteroids with relatively long periods compared to the bulk sample shown in Fig. 8, whose median rotational period is 7.00 h. This indicates that ground-based observations might usually be biased toward shorter rotational periods that are easier to detect from the ground. The average period depends on the size of the asteroids (see, e.g., Pravec 2000). Our sample is composed of some of the smallest known asteroids, where the average rotation period is predicted to be shorter than for the largest bodies. Since we observe the opposite, the difference in periods cannot be explained by these selection biases, but it really shows the power of space observations in the long-period range.
We tested whether the K2 long-cadence (29.4 min) sampling has any effect on the period (and amplitude) determination. Since we considered rotational periods that are longer than two hours (i.e., below the Nyquist-frequency limit), we expect that despite the long integration, we are still able to retrieve the periods. This is indeed the case, as was demonstrated by a series of Monte Carlo simulations. In the course of these simulations we computed to which fraction of the cases our algorithm can find the correct (injected) period, which was simulated by a pure sinus wave. In these tests the photometric noise (depending on the brightness), the observation length, the duty cycle, and the rotational period were varied. We found that our sensitivity does not decrease in the relevant period range (>2 h) because of the long integration times. The most important factors are instead the length of observations and the noise level. With the long-cadence sampling the measured amplitude decreases with respect to the true variation for short-period signals, but our simulations show that we do not loose asteroids as a result of this effect. The worst-case scenario is a decrease of the amplitude by 37% at a rotation period of two hours, which is still detectable in our K2 data in the case of an assumed 0.1 mag true variation down to the 20th mag.
 |
Fig. 9 Magnitude distribution of the asteroids in the M35 field seen by Kepler (924, blue columns), and the selected sample where a significant rotational signal (period or trend) could be derived (35, red columns). Two brighter objects were omitted from the figure for the sake of clarity. |
Rotational signal detected in asteroids observed in the K2 M35 superstamp.
4. Conclusions
We used the Kepler space telescope for the first time to derive quasi-continuous light curves of a large number of main-belt asteroids in long-cadence mode (29.4 min sampling). The main conclusions of this work are the following:
Out of 924 (96) asteroids in the M35 (Nereid) field in Campaign 0 (3), 867 (88) had twelve or more useful photometric data points and only 23 (14) exhibited clear periodicities, which is attributed to rotation. In addition, 12 (0) objects showed a slow trend or were observed through an incomplete rotational cycle; this implies a long rotational period.
By comparing the M35 and Nereid samples, we found a remarkable difference regarding the number of main-belt asteroids with detected rotational periods in the two fields. While in the dense M35 field only 4.0% of the asteroids showed clear periodicities or trend, in the Nereid field we recovered periodicities in 15.9% of the observed asteroids. The difference is significant given the large number of observed asteroids in both fields. To explain this difference, we propose two arguments:
First, we conclude that the dense stellar field precluded the derivation of meaningful photometry for many asteroids because too many points had to be discarded as a result of the disturbing effects of stellar residuals along the paths of the asteroids (see Fig. 5). This is partly explained by the undersampled PSFs delivered by the Kepler spacecraft.
Second, in Fig. 9 we plot the magnitude distribution of our full M35 asteroid sample (in blue) as seen from Kepler, and also those that showed periodicities or long-term trends in their light variations (red). The plot convincingly shows that our sample is heavily dominated by faint targets (>20 mag). Together with Fig. 3, this clearly demonstrates that there is a rather low chance to determine the rotational signal of asteroids below the 20th magnitude brightness limit. This reasoning helps to explain the relatively low rate of recovered rotational periods in our fields, especially in the M35 superstamp.
More sophisticated photometric methods may improve our results and provide more reliable space photometric data of moving objects. Testing of such methods is currently is under way.
Observed periods and amplitudes of the asteroids in the K2 Nereid field.
Tabulated values: http://keplergo.arc.nasa.gov/CalibrationSN.shtml
Acknowledgments
This project has been supported by the Lendület LP2012-31 Young Researchers Program, the Hungarian OTKA grants K-109276 and K-104607, the Hungarian National Research, Development and Innovation Office (NKFIH) grants K-115709 and PD-116175, the GINOP-2.3.2-15-2016-00003 grant, and by City of Szombathely under agreement no. S-11-1027. The research leading to these results has received funding from the European Community’s Seventh Framework Programme (FP7/2007–2013) under grant agreement No. 312844 (SPACEINN), the European Union’s Horizon 2020 Research and Innovation Programme, under Grant Agreement No. 687378 (SBNAF), and the ESA PECS Contract Nos. 4000110889/14/NL/NDe and 4000109997/13/NL/KML, and the European Union’s Horizon 2020 Research and Innovation Programme, Grant Agreement No. 687378. Gy.M.Sz., Cs.K. and L.M. were supported by the János Bolyai Research Scholarship. Funding for the K2 spacecraft is provided by the NASA Science Mission directorate. The authors thank the hospitality of the Veszprém Regional Centre of the Hungarian Academy of Sciences (MTA VEAB), where part of this project was carried out. We acknowledge the Kepler team and engineers for their efforts to keep this fantastic instrument alive and for allocating the large pixel mosaics. All of the data presented in this paper were obtained from the Mikulski Archive for Space Telescopes (MAST). STScI is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555. Support for MAST for non-HST data is provided by the NASA Office of Space Science via grant NNX13AC07G and by other grants and contracts. We thank the referee for the useful comments that helped to improve the paper significantly.
References
- Bailey, S. J. 1913, Ann. Harvard Coll. Obs., 72, 165 [NASA ADS] [Google Scholar]
- Benishek, V., & Coley, D. 2014, Minor Planet Bulletin, 41, 260 [NASA ADS] [Google Scholar]
- Behrend, R. 2009, Observatoire de Genève web site, http://obswww.unige.ch/~behrend/page_cou.html [Google Scholar]
- Cellino, A., Zappalà, V., & Farinella, P. 1989, Icarus, 78, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Chaplin, W. J., Kjeldsen, H., Christensen-Dalsgaard, J., et al. 2011, Science, 332, 213 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Christiansen J. L., Clarke, B. D., Burke, C. J., et al. 2013, Kepler Data Characteristics Handbook, VizieR On-line Data Catalog:J/ApJS/207/35 [Google Scholar]
- Cooney, W. R. 2005, Minor Planet Bulletin, 32, 15 [NASA ADS] [Google Scholar]
- Ditteon, R., Hirsch, B., Kirkpatrick, E., et al. 2004, Minor Planet Bulletin, 31, 54 [NASA ADS] [Google Scholar]
- Ferrero, A. 2010, Minor Planet Bulletin, 37, 145 [NASA ADS] [Google Scholar]
- Gehrels, T., & Owings, D. 1962, ApJ, 135, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Gilliland, R. L., Brown, T. M., Christensen-Dalsgaard, J., et al. 2010, PASP, 122, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Hanus, J., Ďurech, J., Oszkiewicz, D. A., et al. 2016, A&A, 586, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, A. W., Pravec, P., Galád, A., et al. 2014, Icarus, 235, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Ivarsen, K., Willis, S., Ingleby, L., et al. 2004, Minor Planet Bulletin, 31, 29 [NASA ADS] [Google Scholar]
- Kipping, D. M., Torres, G., Henze, C., et al. 2016, ApJ, 820, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Kiss, C., Pál, A., Farkas-Takács, A. I., et al. 2016, MNRAS, 457, 2908 [NASA ADS] [CrossRef] [Google Scholar]
- Lenz, P., & Breger, M. 2005, Commun. Asteroseismol., 146, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Michałowski, T. 1996, A&A, 309, 970 [NASA ADS] [Google Scholar]
- Molnár, L., Pál, A., Plachy, E., et al. 2015, ApJ, 812, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Pál, A. 2012, MNRAS, 421, 1825 [NASA ADS] [CrossRef] [Google Scholar]
- Pál, A., Szabó, R., Szabó, Gy. M., et al. 2015, ApJ, 804, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Pál, A., Kiss, Cs., Müller, T. G., et al. 2016, AJ, 151, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Polishook, D. 2009, Minor Planet Bulletin, 36, 104 [NASA ADS] [Google Scholar]
- Pravec, P., & Harris, A. W. 2000, Icarus, 148, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Sanchis-Ojeda, R., Rappaport, S., Winn, J. N., et al. 2014, ApJ, 787, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Skiff, B. A. 2011, http://www.minorplanet.info/call.html [Google Scholar]
- Szabó, R., Kolláth, Z., Molnár, L., et al. 2010, MNRAS, 409, 1244 [NASA ADS] [CrossRef] [Google Scholar]
- Szabó, R., Sárneczky, K., Szabó, Gy. M., et al. 2015, AJ, 149, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Szabó, R., Gy. M., Pál, A., et al. 2016, A&A, in press DOI: 10.1051/0004-6361/201629401 [Google Scholar]
- Van Cleeve, J. E., & Caldwell, D. A. 2016, Kepler Instrument Handbook [Google Scholar]
- von Oppolzer, E. 1901, Astron. Nachr., 154, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Warner, B. D., Harris, A. W., & Pravec, P. 2009, Icarus, 202, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Waszczak, A., Chang, C.-K., Ofeck, E. O., et al. 2015, AJ, 150, A75 [NASA ADS] [CrossRef] [Google Scholar]
- Wisniewski, W. Z., Michałowski, T. M., Harris, A. W., et al. 1997, Icarus, 126, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Zappalà, V., Martino, M. D., Scaltriti, F., et al. 1983, A&A, 123, 326 [NASA ADS] [Google Scholar]
All Tables
Photometry of main-belt asteroids observed in the M35 superstamp by K2 during Campaign 0.
All Figures
 |
Fig. 1 Mosaic of the M35 open cluster (and NGC 2158) as seen by K2. The area is covered by 154 sub-apertures amounting to 800 × 550 pixels (53′ × 36′). |
| In the text | |
 |
Fig. 2 Mosaic covering the paths of Neptune and Nereid observed by the K2 mission. The length of the mosaic is approximately 20′. |
| In the text | |
 |
Fig. 3 Photometric errors of the individual K2 asteroid measurements in the M35 field as a function of the apparent brightness of the asteroids (light blue dots). The red line plots the Kepler preflight estimate of the photometric precision (Van Cleeve & Caldwell 2016)2, the purple line shows the scaled Combined Differential Photometric Precision data (Christiansen et al. 2013), the black line represents the photometry of a faint RR Lyrae star in Leo IV for comparison (Molnár et al. 2015), and the dashed line shows the linear interpolation between the last two. |
| In the text | |
 |
Fig. 4 Light curve (left panel) and Lomb-Scargle periodogram (right panel) of (111) Ate, the brightest member of our sample. The periodogram shows three peaks, the largest of which corresponds to a period of 20.63 ± 0.60 h. |
| In the text | |
 |
Fig. 5 Duty cycle vs. length of observations for asteroids in the M35 K2 field. Blue dots are all the 924 asteroids crossing the superstamp, red dots are those that exhibit significant periodicity or trend. The histograms show the distribution of the observing length and the duty cycle. |
| In the text | |
 |
Fig. 6 Examples of periodic long-cadence (29.4 min sampling) asteroid light curves ordered according to decreasing brightness. Left panels: asteroids crossing the M35 field, right panel: asteroids observed in the Neptune-Nereid path. In each case the left panel shows the K2 light curve with error bars folded by the adopted (double) period, the right panel is the Lomb-Scargle plot. The error bars for bright asteroids are smaller than the size of the symbols. The sine plotted in red is fit to the data to guide the eye. The adopted period and the ID of the asteroid is shown in the middle of the left and right panels, respectively. |
| In the text | |
 |
Fig. 7 Light curve of asteroid (29628) with three different peaks observed in the Nereid field. Upper panel: light curve folded with triple periods, lower panel: same data folded by sixtuple period. The curved line is a sixth-order Fourier-fit. Bottom panel: the light curve of asteroid (37201). |
| In the text | |
 |
Fig. 8 Period-amplitude diagram of an unbiased sample of 35 asteroids from the M35 field (red points). The small green dots represent 16 000 asteroids from the Asteroid Lightcurve Database (Warner et al. 2009), while the thick black line shows the binned average of that large sample. |
| In the text | |
 |
Fig. 9 Magnitude distribution of the asteroids in the M35 field seen by Kepler (924, blue columns), and the selected sample where a significant rotational signal (period or trend) could be derived (35, red columns). Two brighter objects were omitted from the figure for the sake of clarity. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


