EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 596 (December 2016) A&A, 596 (2016) A53 Full HTML
Free Access
Issue
A&A
Volume 596, December 2016
Article Number A53
Number of page(s) 13
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201628425
Published online 29 November 2016

© ESO, 2016

1. Introduction

Quantifying differential surface rotation has proven difficult even for the Sun. Stellar observations are even more demanding and equally ambiguous are the results. However, quantitative detections are now possible for those stars where we are able to spatially resolve the stellar disk by means of Doppler imaging. Such observations (e.g. Korhonen et al. 2007; Weber 2007; Kővári et al. 2013, 2015) as well as theoretical considerations (Kitchatinov & Rüdiger 2004; Küker & Rüdiger 2012) imply that stellar surface rotation could probably be more complex for evolved stars than for main sequence stars like the Sun. Differential rotation (DR) for main sequence and pre-main sequence stars is found to decrease with effective temperature (Barnes et al. 2005; Reinhold et al. 2013) just as was predicted from mean-field models (Küker 2015). However, the situation seems to be less well defined for post-main sequence stars with their much deeper convective envelopes. Because many of these giants are components in RS CVn-type binary systems, their surfaces are possibly distorted by and respond to the orbital dynamics. Moreover, as a star evolves up the red giant branch (RGB), its core experiences a modification of nuclear reactions followed by core contraction and envelope expansion long before helium burning sets in. After the core hydrogen is exhausted, the hydrogen fusion keeps going in a surrounding shell, providing more helium onto the contracting inert core. The contraction heats up the core together with the interlocked shell, which expands inward, until the core becomes degenerate. The increasing density at the bottom of the H-rich shell yields a more efficient H-burning, which eventually inflates the envelope. The temperature of the envelope decreases and the outer layers become fully convective, transporting more flux outwards, which explains the rapidly increasing luminosity with decreasing surface temperature along the RGB. The shell material penetrates into the hotter regions below, decaying light elements and triggering a mixing process called the first dredge up, which is responsible for the dilution of the lithium. Indeed, according to Charbonnel (1994, 1995) in low-mass (≤2 M⊙) stars, further rotationally induced mixing occurs after the completion of the first dredge up (see also Zahn 1992). Such mixing episodes can be inferred from the lowering of the observed surface abundances of the most fragile elements (7Li, 12C) and the 12C/13C isotopic ratio (Gratton et al. 2000). Even the simple expansion appears to have an effect on the mixing of the convective envelope and eventually also alters the surface DR profile as well. In some cases, the DR profile can be even of anti-solar type, i.e. where the equator rotates slower than the poles (Vogt & Hatzes 1991; Strassmeier et al. 2003; Kővári et al. 2015, etc.). Whether such anti-solar DR was already present during the main sequence phase of such a star or explicitly developed during the expansion phase on the giant branch is not known. In addition, DR of either solar or anti-solar has been derived only for a handful of late-type evolved stars to date. A short list of the giant stars with known DR from Doppler imaging would include the following objects. Among the single (or effectively single) giants, solar-type DR has been reported for FK Com (Korhonen et al. 2007), V390 Aur (Konstantinova-Antova et al. 2012), and KU Peg (Weber & Strassmeier 2001), which is the star to be revisited in this paper, while anti-solar DR has been detected on HD 31993 (Strassmeier et al. 2003), DI Psc, and DP CVn (Kővári et al. 2013; Kriskovics et al. 2014). In binary systems solar-type DR has been found, for example on the evolved components of ζ And (Kővári et al. 2012), XX Tri (Künstler et al. 2015), and IL Hya (Kővári et al. 2014), while anti-solar DR has been found on σ Gem (Kővári et al. 2015), IM Peg, UZ Lib, etc. (see Kővári & Oláh 2014, and the references therein). Our foremost aim is to enlarge the observational sample of reliable DR detections on giant stars.

Time-series Doppler imaging has proven to be extremely useful for studying stellar DR (e.g. Vogt & Hatzes 1996; Donati & Collier Cameron 1997; Weber & Strassmeier 1998; Petit et al. 2004). When performing subsequent Doppler reconstructions of the spotted stellar surface, the rotation rates of individual spots can reveal the latitude-dependent stellar rotation profile. However, such Doppler reconstructions require high-resolution spectroscopic time-series data, covering at least two but preferably many consecutive rotation cycles. That this is indeed a challenge for stars with rotation periods of close to a month is obvious. A unique possibility for such long-term Doppler observations (see e.g. Kővári et al. 2015; Strassmeier et al. 2015; Künstler et al. 2015) is provided by the STELLA robotic observatory of the AIP in Tenerife (Strassmeier et al. 2010). In this paper we present and analyse such spectroscopic observations of the rapidly rotating (Prot ≈ 24 days) K-giant KU Peg (=HD 218153).

Chromospheric activity of KU Peg was recognized by Bidelman (1983) who reported strong Ca ii H&K emission. The large chromospheric fluxes were later confirmed with IUE observations by de Medeiros et al. (1992). Just recently, Aurière et al. (2015) have detected magnetic fields on KU Peg and found that the star follows the magnetic field strength-rotation relationship established for active giants, indicating that probably a solar-type magnetic dynamo was working inside. In addition, the authors reported an unusually strong X-ray luminosity of LX = 11.8 × 1030 erg s-1 confirming the existence of coronal activity as well. KU Peg was found to be a single-lined spectroscopic binary with an orbital period of ≈1400 days (de Medeiros et al. 1992), suggesting that it is effectively a single star. Because differential rotation is supposed to be weakened (or totally quenched) by tidal forces in close binaries (Scharlemann 1981, 1982), KU Peg is a good candidate for a comparison with theory. A projected rotational velocity of 29  km s-1 was measured by Fekel (1997), which placed the star among the possible Doppler-imaging candidates (Strassmeier et al. 2000).

The first and so far only Doppler-imaging study of KU Peg was carried out by Weber & Strassmeier (2001, hereafter Paper I) using high-resolution spectra taken with the McMath-Pierce solar telescope and the coudé feed telescope at Kitt Peak National Observatory over two months in 1996/97. The data allowed the reconstruction of two consecutive Doppler images that revealed an asymmetric polar spot and several other cool spots at lower latitudes. The time evolution of the spotted surface was followed by means of a cross-correlation analysis and revealed a complex DR profile that resembled the solar case only in the directional sense, i.e. lower latitudes rotating faster. Its lap time was twice as long as that of the Sun for the full pole to equator range but twice as short if only the latitudes where the Sun has spots were considered. Moreover, patterns of local meridional flows were detected, which also likely play an important role for stellar dynamos (Kitchatinov & Rüdiger 2004; Küker & Rüdiger 2011).

The current paper is organized as follows. In Sect. 2 we describe our photometric and spectroscopic observations. In Sect. 3 photometric data spanning more than 18 yr are employed to derive a precise average rotation period. These data are also used to search for photometric signals of surface DR. In Sect. 4, we first redetermine the basic astrophysical properties of KU Peg by including our new photometric and spectroscopic data. Then we give a brief description of our inversion code iMap and its data assumptions for image reconstruction. Finally, we present the time-series Doppler images. In Sect. 5 the consecutive Doppler images are used to derive the surface DR of KU Peg. Lithium abundance determination is carried out in Sect. 6. The results are summarized and discussed in Sect. 7.

2. Observations

2.1. Photometry

Photometric observations in this paper were obtained with the Amadeus 0.75 m automatic photoelectric telescope (T7-APT) of the AIP operated at Fairborn Observatory in southern Arizona (Strassmeier et al. 1997). The data set consists of 1243 measurements in Johnson V and 1306 measurements in the Johnson-Cousins IC band. To date, a total of 18 yr between JD 2 450 395 and 2 457 015 are covered. Differential photometric observations were carried out with respect to HD 218610 as the comparison star (, 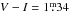), and HD 219050 as the check star. Mean photometric errors were in V and in IC. For more details on APT performance and operation, as well as its data reduction, we refer to Granzer et al. (2001).

2.2. Spectroscopy

A total of 193 high-resolution spectra were collected with the robotic 1.2 m STELLA-I telescope at the Izaña Observatory in Tenerife, Spain (Strassmeier et al. 2010) during 2006–2011. The STELLA robotic observatory (also containing a 1.2 m photometric telescope, now STELLA-I) runs fully autonomously without any personnel on site, guided only by weather and meteorological parameters and the target schedule. The STELLA-II telescope is equipped with the fibre-fed fixed-format STELLA Echelle Spectrograph (SES). We note that for most of the time span in the present paper, the SES fibre was connected to one of the two Nasmyth foci of STELLA-I but was moved to STELLA-II in 2010 after the wide-field imager was inaugurated. All SES spectra cover the wavelength range 3900–8800 Å with a two-pixel resolution of R = 55 000 corresponding to a spectral resolution of 0.12 Å at 6500 Å. For further details of the performance of the system and also for the detailed data-reduction procedures, we refer to Weber et al. (2008, 2012) and Weber & Strassmeier (2011). Table A.1 presents a log of all SES observations of KU Peg.

thumbnail Fig. 1

String-length Lafler-Kinman periodogram from APT V-band data covering ≈18 yr. Its best-fit period of 23.9045 d is interpreted as the rotation period of the star.

3. Refinement of the photometric period

Our extended photometric coverage of more than 18 yr allows us to derive a more precise rotation period. For the period determination we apply the string-length search using the Lafler-Kinman statistics (hereafter SLLK-method, Clarke 2002). This method phases the light curves with different periods and selects the period giving the smoothest light curve as the correct one. The SLLK-method is particularly useful for finding periods in non-sinusoidal data as compared to standard Fourier analysis. Figure 1 shows the resulting periodogram and suggests a long-term average photometric period of Pphot = Prot = 23.9045 ± 0.0014 d which we adopt as the best representation of the rotation period of KU Peg. All phase calculations in this paper use this period with the following ephemeris, (1)where the arbitrarily chosen zero point at HJD 2 450 385.5 is taken from Paper I for consistency reasons.

In Paper I a photometric period of 24.96 ± 0.04 d was derived from the first three years of APT V-band data. Its difference of almost one day, i.e. 25σ, is not only due to measuring errors, but also due to changing spot locations in combination with differential surface rotation. Photometric periods derived for individual observing seasons on a differentially rotating star are expected to differ from the period from longer-term data (see the review by Strassmeier 2009, and the many references therein). From the range of seasonal periods a rough estimation can be given for the average DR as first introduced by Hall (1972).

thumbnail Fig. 2

Johnson V observations (top) and seasonally derived photometric periods (bottom) of KU Peg. Each grey band indicates the time range of the data combined for the period determination in the lower panel. In the bottom panel the size of each dot is proportional to the amplitude of the frequency peak in the power spectrum; the vertical error bar represents the uncertainty of the period determination. The horizontal bar indicates the time coverage.

In order to determine seasonal periods for KU Peg, we first select adjacent light curves with the criterion that they have similar amplitude, mean brightness, and overall shape. Then, a period is determined for each of the ten seasonal subsets using our standard Fourier-transformation based frequency analyser program MuFrAn (Csubry & Kolláth 2004). Figure 2 shows the long-term V-band APT data along with the subsets time ranges and the period results. We note that in some cases the light curves were not suitable for deriving a reliable period because of their large scatter compared to the actual amplitude and/or their insufficient length. Table 1 lists the seasonal periods and their errors, which are estimated by increasing the residual scatter of the non-linear least-squares solutions a certain degree, which corresponds to 10% of the photometric accuracy (cf. Oláh et al. 2003).

We estimate a DR shear parameter 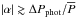, where ΔPphot is the full range of the seasonal period, while 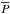is the long-term average. From the values listed in Table 1, we obtain | α | ≳ 0.13 ± 0.05. This result is similar to the value of +0.09 determined in Paper I from spectroscopy, but considering the errors of either the photometric or the spectroscopic methods, it is also in agreement with the corrected value of +0.03 proposed later by Weber et al. (2005). We note, however, that such a method based simply on photometric data does not allow the sign of the DR parameter α to be determined, but only the amount of the shear (but see Reinhold & Arlt 2015).

Table 1

Seasonal periods from our long-term APT photometry.

4. Doppler images for 2006–2011

4.1. Astrophysical parameters of KU Peg

In this section some of the astrophysical parameters are refined with respect to our earlier determinations in Paper I (Weber & Strassmeier 2001). Among these are the effective temperature (Teff), the surface gravity (log g), the metallicity ([Fe/H]), and the projected rotational velocity (vsini). We employ our SES spectra and the spectrum-synthesis code PARSES (Allende Prieto 2004; Jovanovic et al. 2013), which is implemented in the standard STELLA-SES data-reduction pipeline (Weber et al. 2008). A grid of synthetic ATLAS-9 spectra tailored to the stellar parameters of KU Peg and for up to 40 échelle orders around 500–750 nm were chosen and the result per spectral order combined on the basis of a weighted least-squares minimization. The average and the standard deviations then constitute our final values and their internal precisions. We found Teff = 4440 ± 10 K, log g = 2.0 ± 0.1, vsini = 29.4 ± 1.1  km s-1, and [Fe/H] = −0.37 ± 0.02 with a microturbulence of 1.8 km s-1 and a prefixed value for the macroturbulence of 3 km s-1. We note again that the errors are internal errors. External errors are difficult to obtain for spotted stars with broadened line profiles, but from past experience we estimate 70 K, 0.2 dex, and 0.1 dex for Teff, log g, and [Fe/H], respectively. We note that Teff is lower by 260 K compared to the value of 4700 K in Paper I. However, when taking 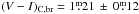for the brightest (i.e. unspotted) magnitude Vbr of 7760 ± 0.043, observed only just recently (see Fig. 2), a similarly low value of Teff of 4385 ± 20 K is obtained using the colour index vs. temperature calibration by Worthey & Lee 2011. Moreover, taking 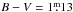(Strassmeier et al. 2000) together with [Fe/H] = −0.37 and using the metallicity-dependent Teff-colour calibrations by Huang et al. (2015) yields Teff = 4475 ± 83 K, i.e. again a significantly lower value compared to that in Paper I, but in alignment with the above-mentioned determination from (V−I)C.

Since this new set of fundamental parameters is in contrast with those from previous studies (cf. Lèbre et al. 2009; Aurière et al. 2015) we carried out a comparative study by using the spectrum synthesis code SPECTRUM by R. Gray (www.appstate.edu/~grayro/spectrum/spectrum.html). We calculated synthetic spectra from our new parameters (Teff = 4440 K, log g = 2.0, vsini = 29.4  km s-1, [Fe/H] = − 0.37, and micro- and macroturbulences of ξmic = 1.8  km s-1 and ξmac = 3.0  km s-1) and from the old parameter set taken from Lèbre et al. (2009), i.e. Teff = 5000 K, log g = 3.0, vsini = 27.1  km s-1, [Fe/H] = −0.15, ξmic = 2.0  km s-1, ξmac = 3.0  km s-1 (assumed value). The synthetic data sets were compared to the observations (an average of 94 high-quality spectra) over the 5950–6510 Å spectral range. We found at all times that, in terms of goodness-of-fit values, the synthetic spectra from our new input parameters fitted slightly better the observations. Moreover, the comparisons were extended to orders between 5000−5600 Å, which resulted in similarly better fits for the new parameters, however, with larger rms values due to the ambiguous continuum setting and the increasing line concentration. Accordingly, we believe that our new fundamental parameters for KU Peg with lower Teff and lower metallicity are more accurate and more consistent. This is strengthened by the colour-temperature calibrations from either B−V or V−I measurements, suggesting effective temperatures lower than 5000 K by 250–600 K, depending on the calibration method used (cf. Flower 1996; Kučinskas et al. 2006; Huang et al. 2015). In addition, our lower metallicity agrees better with the photometric metallicities of − 0.50 and − 0.39 determined by Eggen (1993). Finally, we note that most of the spectral type and luminosity classifications of KU Peg in the literature refer to one original determination of G8II by Heard (1956) based on the “general appearence” of objective prism spectra covering much narrower spectral range than ours.

The rotation period from photometry combined with the projected rotational velocity of 29.4 ± 1.1  km s-1 from PARSES, and the 50° ± 10° inclination angle taken from Paper I, leads to the most likely stellar radius of 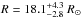. For a Teff of 4440 K, this radius is in good agreement with the expected size of a standard K2III giant star (Dyck et al. 1996). The bolometric magnitude from 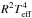is then 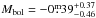(adopting ).

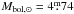The Hipparcos distance of 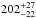 pc (van Leeuwen 2007) combined with Vbr and an interstellar extinction of 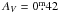(cf. Paper I) as well as a bolometric correction of 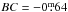from Flower (1996) yields 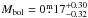. This value is only slightly larger than the value calculated from the radius and the effective temperature. As a trade-off we take , i.e. the mean of the two values, which yields a luminosity of 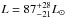for KU Peg.

Figure 3 shows the position of KU Peg in the Hertzsprung-Russell diagram (HRD) together with the stellar evolutionary tracks for Z = 0.008 of Bertelli et al. (2008). To determine the mass and age of KU Peg, a trilinear interpolation within the three-dimensional space (L, Teff, [Fe/H]) based on a Monte Carlo method is applied (Künstler et al. 2015). The values obtained are a mass of 1.1 ± 0.1 M⊙ and an age of 7.6 ± 2.9 Gyr, assuming the metallicity from PARSES. We note that the mass is about one-half of the former value in Paper I, thus increasing the age by a factor of ≈9. The refined absolute dimensions and astrophysical quantities summarized in Table 2 are more consistent and with generally smaller error bars than in Paper I.

thumbnail Fig. 3

Stellar evolutionary tracks around the RGB bump from Bertelli et al. (2008) for Z = 0.008 together with the position of KU Peg (dot with error bar). The numbers indicate the corresponding masses in M⊙. It suggests that M = 1.1 ± 0.1 M⊙ is the most likely mass for KU Peg.

Table 2

Astrophysical properties of KU Peg.

4.2. STELLA data subsets

The spectroscopic data cover up to three consecutive stellar rotations with fairly good phase sampling in all five observing seasons. The detailed time stamps (mid-HJDs) of the data subsets used for the Doppler reconstructions are listed in Table 3. For the 2006 and the 2008 seasons three consecutive data subsets are formed (S1, S2, and S3), each covering one single stellar rotation, i.e. each one suitable for Doppler reconstruction. For the 2009 and 2011 seasons, two consecutive subsets are formed (S1 and S2), while for season 2010 only one data set is available.

Table 3

Data subsets for the 11 individual Doppler reconstructions.

4.3. Image reconstruction code iMap

Our DI+ZDI code iMap used in this work performs multi-line inversion for a large number of photospheric line profiles simultaneously (Carroll et al. 2012). We note that in this particular case only the DI code is used. In the case of KU Peg 40 suitable absorption lines, mostly Fe i, were chosen between 5000−6750 Å (Künstler et al. 2015). In the course of the selection, the line depth, the blends, the continuum level, and the temperature sensitivity were taken into consideration.

thumbnail Fig. 4

Doppler images of KU Peg for the three data sets S1, S2, and S3 in 2006. The corresponding time stamps in mid-dates are 2006.61, 2006.67, and 2006.76, respectively. The maps are shown in four spherical projections with the corresponding temperature scale. The rotational phase is indicated above each image.

For the line profile calculation iMap solves the radiative transfer using an artificial neural network (Carroll et al. 2008). Individual atomic line parameters are taken from the VALD line database (Kupka et al. 1999). The code uses Kurucz model atmospheres (Castelli & Kurucz 2004) which are interpolated for each desired temperature, gravity and metallicity. The typical ill-posed nature of the surface inversion is tackled with an iterative regularization based on a Landweber algorithm (Carroll et al. 2012). Therefore, no additional constraints are imposed in the image domain. The surface grid is set to a 5° × 5° equal-degree partition. For each surface segment the full radiative transfer of all involved line profiles are calculated under the actual effective temperature and atmospheric model. The line profile discrepancy is reduced by adjusting the surface temperature of each segment according to the local temperature gradient information until the minimum χ2 is reached.

thumbnail Fig. 5

Doppler images of KU Peg for the three data sets S1, S2, and S3 in 2008. The corresponding mid-dates are 2008.45, 2008.52, and 2008.60, respectively. Otherwise, as in Fig. 4.

thumbnail Fig. 6

Doppler images of KU Peg for the two data sets S1 and S2 in 2009. The corresponding mid-dates are 2009.54, and 2009.61, respectively. Otherwise, as in Fig. 4.

thumbnail Fig. 7

Doppler image of KU Peg for the only available data set (S1/2010) in 2010. The corresponding mid-date is 2010.69. Otherwise, as in Fig. 4.

thumbnail Fig. 8

Doppler images of KU Peg for the two available data sets (S1 and S2) in 2011. The corresponding mid-dates are 2011.46 and 2011.52, respectively. Otherwise, as in Fig. 4.

4.4. Doppler image reconstructions

Our Doppler reconstructions for KU Peg in Figs. 4–8 reveal spots mostly at middle to high latitudes, sometimes covering the visible pole and sometimes a single spot appears at low latitudes. All in all, the images very much resemble the first Doppler images in Paper I. The temperature of the coolest spots range between ≈3650–3850 K, i.e. cooler by ≈800 K on average than the photosphere.

The three maps of the 2006 data (S1, S2, and S3 in Fig. 4) show spots centred at latitudes between 30°–80°. No polar spot is seen. There is also a bright spot at φ ≈ 0.5 in S1 with a temperature of ≈4700 K, i.e. ≈250 K warmer than the surrounding photosphere. This feature also appears in the subsequent independent images, but with decreasing size and contrast. The three maps in this mini time series already indicate the fast time evolution of the spotted surface. Short-term rearrangements are seen throughout, which finally result in a ring-like structure around the visible pole (seen in S3).

In the 2008 season the most prominent feature that appears in all three of the Doppler reconstructions (S1, S2, and S3 in Fig. 5) is the cool polar spot cross talking with another spot centred at around 45° latitude and 15° longitude (i.e. best seen at φ = 0.0). Again, there is a bright spot best seen at φ = 0.25. However, its contrast is weaker than the feature in 2006 and it almost completely vanishes in the last image of the time series. Most interestingly, a ring-like structure had formed by the end of this mini time series, similar to the one in the map S3/2006.

The most dominant feature in the two consecutive Doppler maps in 2009 (S1 and S2 in Fig. 6) is a cool spot at 50° latitude with a diameter of ≈30°. The small polar spot seen a year earlier is still there but is much weaker. Again there is a small bright spot at 60° latitude (best seen at φ = 0.25) which is bigger/warmer in the second image. Other even smaller features are consistently reconstructed in both images and are seen to evolve from S1 to S2.

For the one image in 2010 (S1 in Fig. 7) the polar spot had fully disappeared, while a high-latitude feature with an elongated bipolar structure remained and is now dominating the surface. A bright spot is also seen near 60° latitude, but is accompanied by a similarly sized cool spot along the same iso-radial line on either side of the central meridian, which makes its reality a little bit suspect. One of its cool counterparts, however, is a rather large and very significant spot, which is a counterargument because it is actually well constrained.

The two consecutive Doppler images in 2011 (S1 and S2 in Fig. 8) reveal dramatic changes in the spot morphology over just about one stellar rotation. The largest changes are seen at lower latitudes. The one cool spot located at around 45° latitude and 15° longitude in S1 seemed to have been shifted by more than 20° towards increased longitude in S2 or is a product of a merger. The other smaller spot centred at 10° latitude and 345° longitude seems to have either disappeared or merged with the spot at 15° longitude. Meanwhile, a minor displacement of the high-latitude bright feature between S1 and S2 is seen in the direction of forward rotation. The most dominant cool spot or spot group in S1 at 180° longitude (best seen at φ = 0.5) seems to have started dissolving or at least stretching towards other nearby spots. A weak polar spot seems to be getting stronger in the second map.

The line profile fits for the altogether 11 Doppler reconstructions in the five observing seasons are plotted in Figs. A.1, A.2.

thumbnail Fig. 9

Average cross-correlation function map showing the evidence for surface differential rotation. Darker shade represents better correlation. The average longitudinal cross-correlation functions in 5° bins are fitted by Gaussian curves. Gaussian peaks are indicated by dots, the corresponding Gaussian widths by horizontal lines. The continuous line is the best fit, suggesting solar-type differential rotation with Peq = 23.2051 d equatorial period and α = + 0.040 surface shear.

5. Surface differential rotation from Doppler images

Time-series Doppler images allow a determination of the surface DR by cross-correlating the consecutive maps with each other. We apply our cross-correlation technique ACCORD (Kővári et al. 2012), which combines all the available surface information in order to achieve an intensified signature of DR. In our case, we have a total of 11 Doppler images. In 2006 and 2008 we have three consecutive maps, while in 2009 and 2011 we have two consecutive maps. Therefore, we are able to create a total of eight pairs of maps, i.e. S1-S2, S2-S3, and S1-S3 for 2006 and 2008, and S1-S2 for 2009 and 2011. We cross-correlate the corresponding latitude stripes of the paired Doppler images for each latitude bin of 5°-width, obtaining eight cross-correlation function maps. These correlation maps are then combined in order to recover an average correlation pattern from which we determine the surface DR. For a more detailed description of the ACCORD technique we refer to our recent application in Kővári et al. (2015) and the references therein.

Figure 9 shows the average correlation pattern with the best-fit quadratic rotation law. We note that owing to the limited appearance of spots at low latitudes, the weak correlation pattern at latitudes below ≈ 40° must be rejected; however, the dashed-line function clearly represents a solar-type DR. The rotation law in the usual quadratic form takes the shape Ω(β) = Ωeq(1−αsin2β), where Ω(β) is the angular velocity at β latitude and Ωeq is the equatorial angular velocity, while α = ΔΩ/Ωeq is the surface shear coefficient and ΔΩ = Ωeq−Ωpol is the angular velocity difference between the equator and the pole. The best fit yields Ωeq = 15.5138°/d (or equivalently Peq = 23.2051 d) and α = + 0.040 ± 0.006. This can be converted to a lap time of ≈580 d, i.e. the time needed by the equator to lap the polar regions. This result is of the order of the empirical estimation of | α | ≈ Prot/ 360 d deduced by Kővári & Oláh (2014) from Doppler imaging studies of either single stars or members of binary systems. We note, however, that the statistically small sample of comparably fast rotating single giants with known surface DR does not make possible to obtain such a relationship for single giants only.

6. Li abundance determination

thumbnail Fig. 10

Li i 6708 Å spectral region of KU Peg. The observed spectrum is an average of 40 individual exposures taken in July/Aug 2009. The three sets of thin lines are synthetic spectra for three metallicities (see insert, for –1.00, –0.37 and 0.0) and for three Li abundances of log n = 0.0, 0.1, and 0.2. Our best estimate with a metallicity of –0.37 suggests an upper Li limit of log n = 0.1 ± 0.1.

In Fig. 10 the extracted spectral region around the Li i-6708 Å line is plotted. Visual inspection of individual exposures does not show any striking evidence of a Li i-6708 Å line, which is hampered by the large vsini (30  km s-1) and the comparably low signal-to-noise ratio (S/N, on average 100:1 for a single exposure). Only after co-adding 40 spectra from within two months in 2009 (July/Aug) a consistent asymmetry of the Fe i and CN blends appears. However, the averaging smears the line profile shapes due to the rotationally modulated spot contribution and makes the average line strength appear weaker than it is. This may be an effect of a few per cent in the equivalent width, but we believe it can be neglected because the uncertainty of the continuum setting is so much larger. A straightforward double Gaussian fit to the average spectrum centred at the average Li i-6708 Å line wavelength and the Fe i-6707.43 blend results in a mere ≈5 mÅ Li equivalent width. It converts to a logarithmic abundance of ≈0.1 ± 0.1 relative to hydrogen (log n(H) = 12.00) with the NLTE tables of Pavlenko & Magazzu (1996) if it is all due to Li and for the case that the models are error free. Such a low Li abundance is not seen on other rapidly rotating K giants of comparable luminosity and KU Peg may be an interesting target also for constraining the Li dredge-up problem.

We also compare our average spectrum with a small grid of forward synthetic Li spectra from 3D model atmospheres. A formal fit of the spectrum was not possible with the current set-up owing to the lack of the appropriate 3D models and the comparably large vsini and low S/N of the data. However, Fig. 10 compares three sets of synthetic spectra for metallicities between solar and ten times less than solar and with logarithmic Li abundances of A(Li) = 0.0, 0.1, and 0.2, i.e. approximately ten times below the solar value (log n⊙ = 1.05 ± 0.1; Asplund et al. 2009). We note that changing the continuum of the observed spectrum by just 1% already has a 0.2-dex impact on the Li abundance and the case for the metallicity is similar. Nevertheless, the 3D synthetic spectra agree with the equivalent width given above and constrain the Li abundance to an upper limit of log n = 0.1 ± 0.2. Its uncertainty is estimated from the case when the metallicity and the continuum location are assumed to be free of error. We adopted the new line list given in Caffau et al. (2015) with a total of 40 spectral lines plus the hyperfine structure of the Li resonance. Line computations were done from 3D CO5BOLD model atmospheres matching the temperature and gravity of KU Peg in Table 2.

7. Summary and discussions

Our new Doppler image reconstructions of KU Peg indicate that its surface spot distribution is indeed very active and dynamic, even when compared to other overactive stars, and so must be the underlying dynamo. According to the theoretical estimation by Aurière et al. (2015) the maximum convective turnover time of KU Peg should be around τ ≈ 100 d. This would yield a moderate Rossby number of Ro ≈ 0.24, indicating that the star operates an αΩ type dynamo. However, from the time evolution of the spotted surface, especially considering the polar spots between 2006–2011, we were only able to estimate a rough cycle length of a few years. On the other hand, from long-term photometry, such a cycle (of about 2–4 yr) can be inferred at a very weak significance level, i.e. not conclusively.

From our cross-correlation study, we derived a solar-like surface DR with a shear of α = + 0.040 ± 0.006 and a lap time of ≈580 days. A similar solar-like DR was found in Paper I with α = + 0.09 and a corresponding lap time of ≈260 days. We note that the higher value in Paper I came from a cross-correlation of only two consecutive Doppler maps and the use of a less-robust correlation routine which both resulted in a less pronounced correlation pattern. A redetermination of α with a different cross-correlation program but the same data as in Paper I by Weber et al. (2005), revealed an α of +0.03, in agreement with our new value. In the present paper, we applied a more robust cross-correlation technique for a total of eight cross-correlation maps and conclude that our new result is much more reliable and now has a reasonable error bar.

The time-series Doppler reconstructions revealed evidence for systematic spot displacements that may be interpreted as evidence for local meridional flows. Examples are the poleward drift of the dominant feature in Fig. 4 at φ = 0.25 or the displacement of the low latitude spot in Fig. 6 at φ = 0.25 (and in Fig. 8 at φ = 0.00 and φ = 0.25). Compared to the longitudinal displacements due to DR, the latitudinal displacements are more diffused and much weaker on average. At the same time the overall evolution of the spot distribution is generally more complex than thought and can have spots come and go from one rotation to the next (e.g. in 2011, Fig. 8).

Rapid rotation of an old, effectively single evolved star like KU Peg remains a theoretical challenge. If tidal effects did not play a role in the past of the star, the most likely explanation for its rapid rotation would be that a deepening convective envelope eventually reaches the high angular momentum material around a fast rotating core, and thus transports high angular momentum material up to the surface on a comparably short convective timescale (Endal & Sofia 1979). This dredge-up must take place before the star evolves up to the bump of the RGB. On the other hand, with the expanding envelope an increasing mass loss rate would be expected, which would again mean angular momentum loss. However, excessive mass loss can be excluded by the lack of any IR excess from a comparison of the measured (2MASS) J, H, and K magnitudes and the colour calibrations provided by Ramírez & Meléndez (2005). However, out-flowing material can also be coupled to closed surface magnetic fields generated by a dynamo, thus preventing the star from quickly losing angular momentum (cf. Cohen et al. 2010).

In any case, a rapidly rotating core on the main sequence is required to explain the spin-up by angular momentum transport from the deep. However, it is not likely that a star of 1.1 M⊙ could provide such a fast rotating core. Moreover, according to Privitera et al. (2016a) the dredge up may not produce enough acceleration of the surface to be a reasonable explanation at all.

As an alternative scenario, engulfment of one planet (or even more) may explain the rapid rotation (Siess & Livio 1999; Carlberg et al. 2012; Privitera et al. 2016b). Using the expression from Massarotti et al. (2008), we estimate the mass of the planet which would spin up the star to be ≈1.25 MJ, but this would also raise the Li abundance at the surface rather than lowering it, which is found for KU Peg. We note however, that according to Casey et al. (2016) any close giant planet is likely to be engulfed well before the host star is able to evolve up the RGB. This would explain the low surface Li abundance, since by the end of the dredge up phase the extra Li coming from the planet will be destroyed together with the primeval Li of the stellar envelope. However, lithium can be affected by other, even unknown processes too, thus the surface Li measurement itself can hardly account for or disprove any planetary interaction, as has been pointed out by Privitera et al. (2016b).

The position in the H-R diagram indicates that KU Peg is past the RGB luminosity bump. Only low-mass stars that have a highly degenerate He core on the RGB, and later undergo the He flash evolve through this phase (see Charbonnel & Balachandran 2000). At this time extra Li is produced and very high Li abundances are reached (e.g. HD 233517; Strassmeier et al. 2015). However, this phase is extremely short-lived because once the mixing extends deep enough the freshly synthesized Li is quickly destroyed. Immediately before the bump phase (and after the end of the first dredge-up), we expect relatively low Li abundances. The timescale of the bump for M = 1.1 M⊙ and Z = 0.008 (almost equivalent with [Fe/H] = −0.37) is ≈10 Myr; the time between the bump and the current position of KU Peg is ≈40 Myr according to the models of Bertelli et al. (2008). This must have been enough time to dilute KU Peg’s surface Li to basically zero.

Acknowledgments

We are thankful for the critical remarks by the referee, who helped to improve the manuscript. Authors from Konkoly Observatory are grateful to the Hungarian Scientific Research Fund for support through grants OTKA K-109276 and OTKA K-113117. This work is supported by the “Lendület-2011” Young Researchers’ Program of the Hungarian Academy of Sciences. The authors acknowledge the support of the German Deutsche Forschungsgemeinschaft, DFG through projects KO 2320/1 and STR645/1. We thank Alessandro Mott for computing the synthetic Li spectra for us. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.

References

  1. Allen de Prieto, C. 2004, Astron. Nachr., 325, 604 [NASA ADS] [CrossRef] [Google Scholar]
  2. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  3. Aurière, M., Konstantinova-Antova, R., Charbonnel, C., et al. 2015, A&A, 574, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Barnes, J. R., Collier Cameron, A., Donati, J.-F., et al. 2005, MNRAS, 357, L1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  5. Bertelli, G., Girardi, L., Marigo, P., & Nasi, E. 2008, A&A, 484, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Bidelman, W. P. 1983, AJ, 88, 1182 [NASA ADS] [CrossRef] [Google Scholar]
  7. Caffau, E., Mott, A., Steffen, M., et al. 2015, Astron. Nachr., 336, 968 [NASA ADS] [CrossRef] [Google Scholar]
  8. Carlberg, J. K., Cunha, K., Smith, V. V., & Majewski, S. R. 2012, ApJ, 757, 109 [NASA ADS] [CrossRef] [Google Scholar]
  9. Carroll, T. A., Kopf, M., & Strassmeier, K. G. 2008, A&A, 488, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Carroll, T. A., Strassmeier, K. G., Rice, J. B., & Künstler, A. 2012, A&A, 548, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Casey, A. R., Ruchti, G., Masseron, T., et al. 2016, MNRAS, 461, 3336 [NASA ADS] [CrossRef] [Google Scholar]
  12. Castelli, F., & Kurucz, R. L. 2004, IAU Symp., 210, poster A20 [Google Scholar]
  13. Charbonnel, C. 1994, A&A, 282, 811 [NASA ADS] [Google Scholar]
  14. Charbonnel, C. 1995, ApJ, 453, L41 [NASA ADS] [CrossRef] [Google Scholar]
  15. Charbonnel, C., & Balachandran, S. C. 2000, A&A, 359, 563 [NASA ADS] [Google Scholar]
  16. Clarke, D. 2002, A&A, 386, 763 [Google Scholar]
  17. Cohen, O., Drake, J. J., Kashyap, V. L., et al. 2010, ApJ, 719, 299 [NASA ADS] [CrossRef] [Google Scholar]
  18. Csubry, Z., & Kolláth, Z. 2004, in SOHO 14 Helio- and Asteroseismology: Towards a Golden Future, ed. D. Danesy, ESA SP, 559, 396 [Google Scholar]
  19. de Medeiros, J. R., Mayor, M., & Simon, T. 1992, A&A, 254, L36 [NASA ADS] [Google Scholar]
  20. Donati, J.-F., & Collier Cameron, A. 1997, MNRAS, 291, 1 [NASA ADS] [CrossRef] [Google Scholar]
  21. Dyck, H. M., Benson, J. A., van Belle, G. T., & Ridgway, S. T. 1996, AJ, 111, 1705 [NASA ADS] [CrossRef] [Google Scholar]
  22. Eggen, O. J. 1993, AJ, 106, 80 [NASA ADS] [CrossRef] [Google Scholar]
  23. Endal, A. S., & Sofia, S. 1979, ApJ, 232, 531 [NASA ADS] [CrossRef] [Google Scholar]
  24. Fekel, F. C. 1997, PASP, 109, 514 [NASA ADS] [CrossRef] [Google Scholar]
  25. Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
  26. Granzer, T., Reegen, P., & Strassmeier, K. G. 2001, Astron. Nachr., 322, 325 [NASA ADS] [CrossRef] [Google Scholar]
  27. Gratton, R. G., Sneden, C., Carretta, E., & Bragaglia, A. 2000, A&A, 354, 169 [NASA ADS] [Google Scholar]
  28. Hall, D. S. 1972, PASP, 84, 323 [NASA ADS] [CrossRef] [Google Scholar]
  29. Heard, J. F. 1956, Publications of the David Dunlap Observatory, 2, 107 [Google Scholar]
  30. Huang, Y., Liu, X.-W., Yuan, H.-B., et al. 2015, MNRAS, 454, 2863 [NASA ADS] [CrossRef] [Google Scholar]
  31. Jovanovic, M., Weber, M., & Allen de Prieto, C. 2013, Publ. Astron. Obs. Belgrade, 92, 169 [NASA ADS] [Google Scholar]
  32. Kitchatinov, L. L., & Rüdiger, G. 2004, Astron. Nachr, 325, 496 [Google Scholar]
  33. Konstantinova-Antova, R., Aurière, M., Petit, P., et al. 2012, A&A, 541, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Korhonen, H., Berdyugina, S. V., Hackman, T., et al. 2007, A&A, 476, 881 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Kővári, Zs., Korhonen, H., Kriskovics, L., et al. 2012, A&A, 539, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Kővári, Zs., & Oláh, K. 2014, Space Sci. Rev., 186, 457 [NASA ADS] [CrossRef] [Google Scholar]
  37. Kővári, Zs., Korhonen, H., Strassmeier, K. G., et al. 2013, A&A, 551, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Kővári, Zs., Kriskovics, L., Oláh, K., et al. 2014, in Magnetic Fields throughout Stellar Evolution, eds. P. Petit, M. Jardine, & H. C. Spruit, IAU Symp., 302, 379 [Google Scholar]
  39. Kővári, Zs., Kriskovics, L., Künstler, A., et al. 2015, A&A, 573, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Kriskovics, L., Kővári, Zs., Vida, K., Granzer, T., & Oláh, K. 2014, A&A, 571, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Küker, M. 2015, in Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, 18, eds. G. T. van Belle, & H. C. Harris, 535 [Google Scholar]
  42. Küker, M., & Rüdiger, G. 2011, Astron. Nachr., 332, 83 [NASA ADS] [CrossRef] [Google Scholar]
  43. Küker, M., & Rüdiger, G. 2012, Astron. Nachr., 333, 1028 [NASA ADS] [CrossRef] [Google Scholar]
  44. Künstler, A., Carroll, T. A., & Strassmeier, K. G. 2015, A&A, 578, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
  46. Kučinskas, A., Hauschildt, P. H., Brott, I., et al. 2006, A&A, 452, 1021 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Lèbre, A., Palacios, A., Do Nascimento, Jr., J. D., et al. 2009, A&A, 504, 1011 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Massarotti, A., Latham, D. W., Stefanik, R. P., & Fogel, J. 2008, AJ, 135, 209 [NASA ADS] [CrossRef] [Google Scholar]
  49. Oláh, K., Jurcsik, J., & Strassmeier, K. G. 2003, A&A, 410, 685 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Pavlenko, Y. V., & Magazzu, A. 1996, A&A, 311, 961 [NASA ADS] [Google Scholar]
  51. Petit, P., Donati, J.-F., & Collier Cameron, A. 2004, Astron. Nachr., 325, 221 [Google Scholar]
  52. Privitera, G., Meynet, G., Eggenberger, P., et al. 2016a, A&A, 591, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Privitera, G., Meynet, G., Eggenberger, P., et al. 2016b, A&A, 593, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Ramírez, I., & Meléndez, J. 2005, ApJ, 626, 465 [NASA ADS] [CrossRef] [Google Scholar]
  55. Reinhold, T., & Arlt, R. 2015, A&A, 576, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Reinhold, T., Reiners, A., & Basri, G. 2013, A&A, 560, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Scharlemann, E. T. 1981, ApJ, 246, 292 [NASA ADS] [CrossRef] [Google Scholar]
  58. Scharlemann, E. T. 1982, ApJ, 253, 298 [NASA ADS] [CrossRef] [Google Scholar]
  59. Siess, L., & Livio, M. 1999, MNRAS, 308, 1133 [NASA ADS] [CrossRef] [Google Scholar]
  60. Strassmeier, K. G. 2009, A&ARv, 17, 251 [NASA ADS] [CrossRef] [Google Scholar]
  61. Strassmeier, K. G., Boyd, L. J., Epand, D. H., & Granzer, T. 1997, PASP, 109, 697 [NASA ADS] [CrossRef] [Google Scholar]
  62. Strassmeier, K., Washuettl, A., Granzer, T., Scheck, M., & Weber, M. 2000, A&AS, 142, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Strassmeier, K. G., Kratzwald, L., & Weber, M. 2003, A&A, 408, 1103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Strassmeier, K. G., Granzer, T., Weber, M., et al. 2010, Adv. Astron., 2010, 19 [NASA ADS] [CrossRef] [Google Scholar]
  65. Strassmeier, K. G., Carroll, T. A., Weber, M., & Granzer, T. 2015, A&A, 574, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Vogt, S. S., & Hatzes, A. P. 1991, in The Sun and Cool Stars. Activity, Magnetism, Dynamos, IAU Colloq. 130, eds. I. Tuominen, D. Moss, & G. Rüdiger (Berlin: Springer Verlag), Lect. Notes Phys., 380, 297 [Google Scholar]
  68. Vogt, S. S., & Hatzes, A. P. 1996, in Stellar Surface Structure, eds. K. G. Strassmeier & J. L. Linsky, IAU Symp., 176, 245 [Google Scholar]
  69. Weber, M. 2007, Astron. Nachr., 328, 1075 [NASA ADS] [CrossRef] [Google Scholar]
  70. Weber, M., & Strassmeier, K. G. 1998, A&A, 330, 1029 [NASA ADS] [Google Scholar]
  71. Weber, M., & Strassmeier, K. G. 2001, A&A, 373, 974 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Weber, M., & Strassmeier, K. G. 2011, A&A, 531, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Weber, M., Strassmeier, K. G., & Washuettl, A. 2005, Astron. Nachr., 326, 287 [NASA ADS] [CrossRef] [Google Scholar]
  74. Weber, M., Granzer, T., Strassmeier, K. G., & Woche, M. 2008, in SPIE Conf. Ser., 7019 [Google Scholar]
  75. Weber, M., Granzer, T., & Strassmeier, K. G. 2012, in SPIE Conf. Ser., 8451 [Google Scholar]
  76. Worthey, G., & Lee, H.-c. 2011, ApJS, 193, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]

Appendix A: Observing log and line profile fits

Table A.1

Observing log of STELLA-I SES spectra taken between 2006–2011.

thumbnail Fig. A.1

Line profile fits for the Doppler reconstructions shown in Figs. 4, 5. The phases of the individual observations are listed on the right side of the panels.

thumbnail Fig. A.2

Line profile fits for the Doppler reconstructions shown in Figs. 6–8. The phases of the individual observations are listed on the right side of the panels.

All Tables

Table 1

Seasonal periods from our long-term APT photometry.

In the text
Table 2

Astrophysical properties of KU Peg.

In the text
Table 3

Data subsets for the 11 individual Doppler reconstructions.

In the text
Table A.1

Observing log of STELLA-I SES spectra taken between 2006–2011.

In the text

All Figures

thumbnail Fig. 1

String-length Lafler-Kinman periodogram from APT V-band data covering ≈18 yr. Its best-fit period of 23.9045 d is interpreted as the rotation period of the star.
In the text
thumbnail Fig. 2

Johnson V observations (top) and seasonally derived photometric periods (bottom) of KU Peg. Each grey band indicates the time range of the data combined for the period determination in the lower panel. In the bottom panel the size of each dot is proportional to the amplitude of the frequency peak in the power spectrum; the vertical error bar represents the uncertainty of the period determination. The horizontal bar indicates the time coverage.
In the text
thumbnail Fig. 3

Stellar evolutionary tracks around the RGB bump from Bertelli et al. (2008) for Z = 0.008 together with the position of KU Peg (dot with error bar). The numbers indicate the corresponding masses in M⊙. It suggests that M = 1.1 ± 0.1 M⊙ is the most likely mass for KU Peg.
In the text
thumbnail Fig. 4

Doppler images of KU Peg for the three data sets S1, S2, and S3 in 2006. The corresponding time stamps in mid-dates are 2006.61, 2006.67, and 2006.76, respectively. The maps are shown in four spherical projections with the corresponding temperature scale. The rotational phase is indicated above each image.

In the text
thumbnail Fig. 5

Doppler images of KU Peg for the three data sets S1, S2, and S3 in 2008. The corresponding mid-dates are 2008.45, 2008.52, and 2008.60, respectively. Otherwise, as in Fig. 4.
In the text
thumbnail Fig. 6

Doppler images of KU Peg for the two data sets S1 and S2 in 2009. The corresponding mid-dates are 2009.54, and 2009.61, respectively. Otherwise, as in Fig. 4.
In the text
thumbnail Fig. 7

Doppler image of KU Peg for the only available data set (S1/2010) in 2010. The corresponding mid-date is 2010.69. Otherwise, as in Fig. 4.
In the text
thumbnail Fig. 8

Doppler images of KU Peg for the two available data sets (S1 and S2) in 2011. The corresponding mid-dates are 2011.46 and 2011.52, respectively. Otherwise, as in Fig. 4.
In the text
thumbnail Fig. 9

Average cross-correlation function map showing the evidence for surface differential rotation. Darker shade represents better correlation. The average longitudinal cross-correlation functions in 5° bins are fitted by Gaussian curves. Gaussian peaks are indicated by dots, the corresponding Gaussian widths by horizontal lines. The continuous line is the best fit, suggesting solar-type differential rotation with Peq = 23.2051 d equatorial period and α = + 0.040 surface shear.
In the text
thumbnail Fig. 10

Li i 6708 Å spectral region of KU Peg. The observed spectrum is an average of 40 individual exposures taken in July/Aug 2009. The three sets of thin lines are synthetic spectra for three metallicities (see insert, for –1.00, –0.37 and 0.0) and for three Li abundances of log n = 0.0, 0.1, and 0.2. Our best estimate with a metallicity of –0.37 suggests an upper Li limit of log n = 0.1 ± 0.1.

In the text
thumbnail Fig. A.1

Line profile fits for the Doppler reconstructions shown in Figs. 4, 5. The phases of the individual observations are listed on the right side of the panels.
In the text
thumbnail Fig. A.2

Line profile fits for the Doppler reconstructions shown in Figs. 6–8. The phases of the individual observations are listed on the right side of the panels.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.