EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 595 (November 2016) A&A, 595 (2016) A59 Full HTML
Free Access
Issue
A&A
Volume 595, November 2016
Article Number A59
Number of page(s) 9
Section Galactic structure, stellar clusters and populations
DOI https://doi.org/10.1051/0004-6361/201629091
Published online 28 October 2016

© ESO, 2016

1. Introduction

Open clusters such as the Pleiades are of vital importance for our understanding of stellar evolution theory because of the assumption that stars form in groups within a common molecular cloud. Since clusters are composed of many stars, which are assumed to have the same chemical composition, distance, and age, but different initial masses and therefore reside at different evolutionary stages, they are ideal laboratories for testing stellar evolution models. An important output from these models is the intrinsic luminosity of a star. Given the theoretical luminosity and the observed flux, the model can be calibrated to a star when the distance of the star is known. This is because the observed flux of a star is proportional to the luminosity and inversely proportional to the distance.

The Hipparcos mission (ESA 1997) measured to a high accuracy trigonometric parallaxes of about 120 000 stars in the solar neighbourhood. We caution that the concept of stellar distance measurements from Hipparcos or Gaia is incorrect because distance is not a true astrometrical observable. The measured quantity is the parallax, ϖ, which is a annual angular variation of an object with respect to distant stars, and the parallax is related to the distance d of that object by d = 1 /ϖ.

thumbnail Fig. 1

Illustration of the twin method applied to the Pleiades cluster. The coordinates of the stars used in this work are shown in the upper panel. The blue circle represents the location of the Pleiades cluster, the black crosses are the reference Hipparcos field stars, and the black squares are the twins of the Pleiades stars found in the field. The bottom left panel shows the colour−magnitude diagram of the Pleiades, including the stars of the Seven Sister DANCe catalogue (Bouy et al. 2015) for reference with crosses. Circles correspond to the stars for which we took HARPS spectra, and the red triangles correspond to stars with twins in the field. A selection of Pleiades members with different spectra are shown around the Mg I triplet in red in the bottom right plot, together with a spectrum of a twin in the field as a dotted black line. The name of the Pleiades star and its corresponding twin are indicated, as well as its distance. Fast rotators are Pels 17, Pels 35, and Pels 174, which is seen in the greater broadening of their lines.

For most of the nearby open clusters, such as the Hyades, the distances obtained from Hipparcos parallaxes agree well with those inferred from stellar evolution models. For the Pleiades, however, the Hipparcosparallax is 8.32 ± 0.13 mas, corresponding to a distance of 120.3 ± 1.5 pc (van Leeuwen 2007, 2009; Perryman 2008; Palmer et al. 2014), while other methods, mainly using theoretical modelling, estimate a distance of approximately 134 pc, that is, a parallax of about 7.46 mas. These methods include isochrone fitting (Pinsonneault et al. 1998; Percival et al. 2005; An et al. 2007), empirical main-sequence fitting (Stello & Nissen 2001), astrometric solutions that are alternative to Hipparcos (Makarov 2002; Soderblom et al. 2005), analysing spectroscopic binaries (Munari et al. 2004; Zwahlen et al. 2004; Valls-Gabaud 2007; Groenewegen et al. 2007; Pan et al. 2004), and long-baseline interferometry (Melis et al. 2014). A recent comparison can be found in Melis et al. (2014), while an extensive discussion on the Pleiades distance controversy is reported in Perryman (2008).

Recently, we proposed the twin method as a reliable method for determining stellar distances (Jofré et al. 2015b) that is independent of stellar modelling. It assumes that if two stars at different locations in the sky have identical physical properties, then they are stellar twins. The difference in their apparent brightnesses is directly related to the difference in their distances. By knowing the distance of one star (e.g. from a Hipparcos parallax), it is then possible to know the distance of its twin. As the underlying assumption is that twin stars are physically identical, both stars must have the same spectra. The twin method involves only observational quantities (the apparent brightness and the observed spectra) in the distance determination. This is a great advantage compared to non-astrometric distance determination methods that rely on stellar evolution models and is therefore a powerful independent technique for estimating the distance of this important open cluster, under the condition that thespectra of Pleiades member stars are identical to spectra of field stars with accurate parallaxes.

A summary of this idea is illustrated in Fig. 1, in which the spectra of some of the field stars with accurate parallaxes located at different parts of the sky is identical to some of the spectra of Pleiades stars located at different parts of the HR diagram. The distance of each of the Pleiades spectroscopic twins can be measured independently. In this paper we present our procedure in detail and discuss our results for the distance of the Pleiades.

Table 1

Name, coordinates, apparent magnitudes in the visual, iSpec radial velocity, parallax and its standard error according to van Leeuwen (2007), and S/N of the Pleiades stars analysed in this work.

2. Data

The spectra used in this work were taken by the HARPS instrument, which is fibre-fed by the Cassegrain focus of the 3.6 m telescope in La Silla (Mayor et al. 2003). The spectra were reduced by the HARPS Data Reduction Software (version 3.1). A combination of data taken from the ESO public archive and observations taken by ourselves during four nights in November 2015 were considered in this analysis.

The new observations contain spectra of 23 stars in the Pleiades field, which have spectral types FGK. This spectral type is important for enhancing the chances to find twins in the sample of field Hipparcos stars available in the HARPS archive, which is composed mostly of FGK solar-type stars. Eleven of these 23 stars have Hipparcos parallaxes. The apparent magnitudes of these stars vary from V = 7 to 11 mag, and to achieve a signal-to-noise ratio (S/N) higher than 50, which is required for an accurate analysis, the exposure times of these stars were in the range of 1−2 h. In several cases, shorter exposures of about 10 min were carried out before these long-time observations to reject potential spectroscopic binaries that show double spectral lines. All observations for each star were stacked using iSpec (Blanco-Cuaresma et al. 2014). The basic information of the Pleiades targets can be found in Table 1.

The spectra of Pleiades stars were compared with a reference sample of HARPS spectra of field stars that have accurate Hipparcos parallaxes. Most of the Hipparcos field stars were taken from our previous work on twin distances (Jofré et al. 2015b), which were selected by cross-matching against the HARPS archive. The cross-matched 664 stars were required to have estimates of FGK spectral type (Soubiran et al. 2010). In addition, we requested 62 stars from the ESO archives1 that matched the photometric properties of the Pleiades targets. Finally, 143 Hipparcos targets that were not observed so far with HARPS were added to the reference sample and observed during the same run as the Pleiades observations. They were selected to have similar photometric properties as the Pleiades targets to enhance our opportunities of finding twins in both samples. These stars are very bright, and exposures times of around 10 min were therefore sufficient to achieve high S/N. The two additional requirements of a non-saturated photometry in the H and Ks band and a standard error of the Hipparcos parallax smaller than 7% reduced the reference sample to a total of 598 stars. The reference sample, which includes the name, coordinates, magnitude, and parallax of the stars, as well as the S/N, the date of the HARPS observation, and the programme ID in which the data were taken, can be found in Table A.1.

The dataset was prepared for analysis using iSpec functionalities, which resulted in a homogeneous set of spectra. The spectra were normalised by fitting cubic splines to the pseudo-continuum, were corrected for radial velocity by cross-correlating them with the solar atlas of Hinkle et al. (2000), were cleaned from cosmic and telluric lines, sampled to common wavelength ranges, and smoothed with a Gaussian kernel to a lower resolution of 70 000. Although reducing the resolution is not imperative, the smooth spectra had fewer data points, but very high resolution. This allowed us to resolve the key spectral lines under study and perform a faster pixel-by-pixel comparison of the entire dataset.

2.1. Selection of Pleiades members

We assessed the question on the cluster membership of the stars in the Pleiades field by comparing their radial velocities, which are listed in Table 1. We considered the radial velocities determined with iSpec, which was also used to process the spectra of the reference dataset. The Pleiades cluster has a radial velocity of approximately 5.7 km s-1 (van Leeuwen 2009). According to this value, the stars Pels 6, Pels 25, Pels 26, Pels 42, Pels 70, Pels 86, HII 948, and BD +20594 are not considered members of the cluster and were rejected from further analysis. After this membership classification, we had 15 Pleiades members in total for the twin distance determination.

2.2. Summary

The twin method was applied to a sample of 613 FGK stars with high-resolution spectra and non-saturated 2MASS photometry (Skrutskie et al. 2006) in the near-infrared Ks and H bands. The sample contained 15 Pleiades members and 598 fields stars distributed over the whole sky, each with a Hipparcos parallax with an accuracy of better than 7%. The Pleiades spectra were compared to the entire sample of field stars to search for potential stellar twins.

3. Method

To analyse homogeneously the slow- and fast-rotating stars in the Pleiades, we adopted a procedure to determine twin distances by comparing the spectra pixel-to-pixel instead of using equivalent widths as in Jofré et al. (2015b). The use of equivalent widths for high-precision studies of solar twins to determine chemical abundances (Meléndez et al. 2006; Datson et al. 2014; Nissen 2015; Spina et al. 2016) is very common and has shown to be very powerful, but it reaches its limitation for fast rotators (v sin i> 20 m/s). Our sample has such fast rotators, and therefore we developed a new procedure for this purpose.Key to this method is to take the difference of two spectra and evaluate the standard deviation σ of these differences. In this section we explain our procedure in detail.

3.1. Twin distance determination

In the absence of interstellar extinction, there is the well-known relation between the apparent brightness, m and fluxes, F, between two stars 1and2: 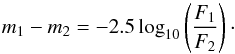(1)As the flux is a function of the luminosity L and the distance d of a star, that is, F ∝ L/d2, we have 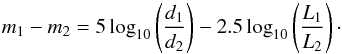(2)The main assertion of the twin distance determination is that twins have the same intrinsic physical properties. Therefore twin stars must have the same intrinsic luminosity, and consequently the second term on the right hand side of Eq. (2) vanishes. Another consequence is that twin stars must have the same intrinsic colour, allowing us to use the difference in observed colour as a proxy for interstellar extinction on the observed magnitudes (3)where RV is ratio of the total-to-selective extinction in filter V, and E(B−V) is the de-reddening. Part of the Pleiades cluster is known to be obscured by the Merope Nebula, producing a reddening that is not constant to all stars (Stauffer & Hartmann 1987). Such errors that are due to extinction can be minimised by using apparent brightnesses in the H and Ks filters of 2MASS, while they have the added advantage of employing a fully homogeneous sample for the photometry. In these filters, we considered RKs [(H−Ks)1−(H−Ks)2] as a proxy for extinction, with RKs = 0.3 according to Yuan et al. (2013). Including this colour correction, twin distances can be determined from the following equation (4)Since for the reference stars we have direct measurements of the parallax ϖ = 1 /d, we write Eq. (4) as (5)We note that the last equation only involves observable quantities.Thus, our expression to determine twin parallaxes has the form (6)where we determined the unknown parallax ϖ2 given the knowledge of the reference parallax ϖ1 and photometry in the H and Ks bands of the stars labelled with 1 and 2, respectively.

3.2. Spectral analysis: assessment of spectral similarity

We compared each spectrum of the reference sample with each of the 15 Pleiades spectra around 423 atomic transitions listed in Jofré et al. (2014) for Fe and in Jofré et al. (2015a) for Mg, Si, Ca, Ti, Sc, V, Cr Mn, Co, and Ni, which have been used for the abundance determination of the Gaia benchmark stars (see also Heiter et al. 2015; Hawkins et al. 2016). Furthermore, the strong features of the wings of the Mg I b triplet and the Balmer lines Hα and Hβ were also taken into account. These spectral regions are known to contain information on the stellar atmospheric parameters and therefore are well suited to assess the overall equality of spectra of FGK stars.

In theory, twin stars have identical spectra. In practice, this is not true because the spectra have noise and are observed under different conditions for different stars (Katz et al. 1998; Soubiran et al. 2003). Thus, critical to this work is a parameter that we call σ, with which we address the similarity of the spectra such that the twin parallax formula of Eq. (6) is satisfied within an accepted error in stellar distance. We define σ as the standard deviation of the pixel-to-pixel difference between the spectra in the regions mentioned above. The lower the value of σ, the more similar the two spectra.

thumbnail Fig. 2

Behaviour of the ratio of twin parallax and Hipparcos parallax as a function of σ using the Hipparcos reference sample. The inset shows a zoom of the region of the plot at low σ. The horizontal lines represent the range of 10% difference in parallaxes while the vertical line the value of σ = 0.015.

Table 2

Pleiades member stars and their twins in the field.

We investigated the threshold for σ such that we obtained a 10% error for the twin parallax. This threshold was found by comparing the spectra with the twin distances of the entire dataset of reference field stars with known Hipparcos parallaxes. That is, the ratio between the Hipparcos parallax ϖHIP and the twin parallax ϖtwin was related to σ for each pair of spectra in the data set. This is shown in Fig. 2, where we plot the ratio of the parallaxes obtained from Eq. (4) and the Hipparcos parallax as a function of σ for the set of field stars. We found that when a pair had very different spectra, the value of σ was high and the value (ϖHIP/ϖtwin) was also very different from unity. In the same way, when the spectra were very similar, σ had a low value and the ratio between Hipparcos and twin parallax was close to unity.

Figure 2 shows that for σ< 0.015, a typical error in parallax does not exceed 10%. We refer to this parallax error Δϖσ as the error of the twinness, that is, the relative error Δϖσ/ϖ< 0.1 for σ = 0.015 (see below). This error is similar to typical errors estimated using isochrone fitting when internal systematic errors on the models are neglected. The advantage here is that no stellar evolution models are required.

Hence, requiring σ< 0.015 for the Pleiades-field pairs yields individual parallaxes to the Pleiades targets with expected errors of 10%. We note that this includes both the twin assumption error and the errors of the Hipparcos parallax.

3.3. Uncertainties

Below we summarise the sources of uncertainties involved in this work regarding our distance determinations.

  • 1.

    Reference parallax: our reference sample is comprised of onlyparallaxes with accuracies better than 7% and typically of 3.5%,therefore the traditional law of error propagation can beapproximately applied in our case. An uncertainty in the parallaxassociated with the reference star was propagated to the twinparallax following Jofréet al. (2015b). As discussed in thatpaper, typical propagated errors are of about 5%.

  • 2.

    Photometry: in our sample, the median errors in the photometry of the stars for the H and Ks band are of 0.03 and 0.02 mag, respectively. In Jofré et al. (2015b) we showed that this introduces a negligible error in the final results lower than 1%.

  • 3.

    Twinness: the error of the twinness Δϖσ/ϖ arises because the stars may not be exact twins and because the spectra have noise as a result of different observational conditions. The latter was minimised by requiring a high S/N of the observed spectra. As explained in the previous section, the error of the twinness is lower than 10% when choosing σ< 0.015 in the comparison of the spectra.

  • 4.

    Multiple twins: when one star has more than one twin, different values for its parallax can be estimated using each of these twins as reference. This gives a distribution of almost independent parallax measurements, with an associated mean with its standard error. This uncertainty is dependent on the number of twins found for a given star, where the larger the number of twins, the more accurate the distance.

In summary, when several twins are found for a target (which applies to the case of the Pleiades), the reported standard errors correspond to the statistical error (point 4). When only one twin is found, then the reported standard error corresponds to the square root of the quadratic sum of the uncertainties explained in points 1 to 3.

Table 3

Our determinations of parallaxes and distances together with their error for the individual Pleiades members with twin candidates in the field.

4. Results

Applying the cut of σ< 0.015 to the difference of the spectra of the 8970 Pleiades-field-star pairs (this number is the product of 15 Pleiades stars and 598 field stars) resulted in 57 twin pairs, which are listed in Table 2. These pairs were used to determine the individual parallaxes of the Pleiades members, which are indicated in Table 3. Most of the Pleiades targets have more than one partner in the field. As multiple twins to an individual Pleiades star must then share the physical properties, these multiple partners should also be twins with each other. We compared their Hipparcos and twin parallax and found an agreement of better than 10%, which is consistent with the uncertainty obtained from the selection of σ. This comparison between the Hipparcos field stars implies that the reference parallaxes of the field twins are accurate. It further confirms the analysis of Kim et al. (2016), who found that Hipparcos parallaxes of FGK field stars similar to Pleiades member stars agree well with stellar models.

4.1. Parallaxes of individual Pleiades stars

Figure 3 shows the parallaxes of individual Pleiades stars, in which our results are compared with the literature (Makarov 2002; Soderblom et al. 2005; van Leeuwen 2007). The star HII 3179 has been analysed by Soderblom et al. (2005), who performed parallax measurements using the Hubble Space Telescope. Our twin parallax and the parallax from Soderblom et al. (2005) are in excellent agreement at 2%. This is encouraging given that these are independent works.

It is important to remark that not all the Hipparcos parallax measurements have the large error bars of the Hipparcos stars shown in Fig. 3. Several brighterPleiades members have significantly more accurate measurements. We show in Fig. 4 our Pleiades twin parallax with Hipparcos parallaxes of 54 Pleiades stars that are commonly considered for the astrometric solution (e.g. Makarov 2002; van Leeuwen 2007; Palmer et al. 2014). The bright stars (H< 7 mag) have accurate Hipparcos parallaxes with a low star-to-star scatter of 0.5 mas with an averaged parallax of 8.36 ± 0.09 mas (Fig. 4), suggesting that they might be better candidates for comparison. However, this is currently not possible, since these stars are mainly of A and B spectral type, to which the twin method is much more difficult to apply. First, the HARPS public archive contains mainly FGK stars spectra because of the bias towards searching for exoplanets around solar-like stars. For the AMBRE project (De Pascale et al. 2014) 70% of the HARPS archive were found to be FGK stars, while the remaining 30% were either binaries, had a too low S/N, or were outside the FGK-parameter space. Second, 20% of the brighter Pleiades stars are either variable or binary stars, so that their photometry could not be used to determine their distance with the twin method. Furthermore, AB stars are more massive than FGK stars and so evolve faster, implying that there are much fewer AB stars in the sky than there are FGK stars. However, the twin method might be applied to any spectral type, provided a good reference sample is available, as was recently shown for twin supernovae (Fakhouri et al. 2015).

thumbnail Fig. 3

In both panels, the pink band represents the values of the Hipparcos solution within its margin of error while the yellow band represents the range of the alternatives to Hipparcos. The upper panels show the parallaxes ofthe 57 field twins of each Pleiades member sorted by decreasing brightness, while the median and dispersion of the final twin parallaxes are illustrated with the blue line and band, respectively. The lower panel displays the averaged individual twin parallaxes (blue triangles), Hipparcos parallaxes (red squares, HIP vL07), the alternative astrometric solution of Makarov (2002) (cyan diamonds, HIP M02) and the parallax measurement with the Hubble Space Telescope of Soderblom et al. (2005) (pink star, S05).

thumbnail Fig. 4

Parallaxes of 54 Pleiades stars of the Hipparcos solution are indicated with black crosses. The mean and standard deviation of these Hipparcos parallaxes is shown by the grey band enclosed by a dotted line. Eleven of the Hipparcos stars have HARPS spectra and have been analysed in this work (red squares). Our results are indicated with blue triangles. The standard deviation of these values are shown with the blue band enclosed by the blue line. The pink band represents the values of the Hipparcos solution within its margin of error, while the yellow band represents the range of the alternatives to Hipparcos.

For fainter stars (H> 7 mag) the situation in Fig. 4 is very different. The Hipparcos parallaxes have large star-to-star scatter of up to 1.8 mas, while the twin parallax show a scatter of around 0.4 mas. For further comparison we calculated the weighted mean parallax of the Hipparcos stars with H> 7 mag. Taking the weighted mean is preferred because the parallax estimates of Hipparcos correlate with the errors of the measurements for fainter stars (van Leeuwen 2007, 2009). The weighted mean parallax obtained for the faint Hipparcos stars is 8.07 ± 0.20 mas, which still agrees within the errors with the value obtained from the bright stars. In turn, calculating the weighted mean of the 15 twin parallaxes gives a value of 7.42 ± 0.09 mas.

thumbnail Fig. 5

Difference of the Li equivalent widths and depth as a function of distance for the Pleiades-field twins. The red line indicates the linear fit of the data, with the slope and error of slope indicated in the legend. No correlation between the difference of Li abundance and distance has been found.

Since the literature regarding the Pleiades controversy is more commonly discussed in terms of distances in parsecs, we transformed our results of the individual parallaxes and mean parallax of the cluster to distance using d = 1 /ϖ. From this non-linear relation it is clear that a parallax with a symmetric error results in a distance with an asymmetric error. A recent discussion on how parallaxes, distances, and their errors are related can be found in Bailer-Jones (2015), where the standard error propagation law of 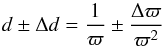(7)for translating errors in parallax to errors in distance can only be used when the error of the parallax is lower than 20%. As both the derived twins parallaxes and the weighted mean parallax have relative errors well below 20%, we are can apply Eq. (7). The individual distances of the Pleiades members and their errors are displayed in Table 3. Our main result is thus that the weighted mean parallax of the 15 stars obtained with the twin method yields a distance of 134.8 ± 1.7 pc to the Pleiades.

4.2. Lithium

In our comparison of Pleiades and field stars the problem arises that age differences add systematic uncertainties in the distance determination because the cluster stars are all young, while the field stars have different ages. van Leeuwen (2009) showed that the colour-colour diagrams of the Pleiades and other young clusters were different from those of the Hyades, suggesting an intrinsic difference in the luminosity and therefore distance modulus that is due to age. To study this potential systematic difference with our method, we examined the Li λ6707 Å line in our spectra, taking into account that Li abundances can be used as an age proxy (Jackson & Jeffries 2014; Kim et al. 2016), namely that a strong Li line indicates young stars. Using iSpec, we measured the equivalent width and the depth of the Li λ6707 Å line in our sample of twins and correlated their difference with distance (see Fig. 5). A linear fit to the data was performed, showing no indication of systematic difference in distance for stars with the same or different Li abundances (see also Kim et al. 2016, for a discussion of Li abundances of field stars with same photometric properties as Pleiades member stars). This shows that both young and older twins give the same result, which means that differential age effects are not significant in the method.

5. Conclusions

We have applied the twin method to determine distances of the Pleiades in a model-independent way. Our result of 134.8 ± 1.7 pc, based on Hipparcos parallaxes of field stars, disagrees with the value directly derived from Hipparcos parallaxes of Pleiades members (van Leeuwen 2007; Perryman 2008; van Leeuwen 2009; Palmer et al. 2014), but agrees well with the value provided by the model-based methods mentioned earlier (Pinsonneault et al. 1998; Percival et al. 2005; Valls-Gabaud 2007; Groenewegen et al. 2007; Pan et al. 2004; Melis et al. 2014). Since most of these methods (except for those of Stello & Nissen 2001; Makarov 2002; Soderblom et al. 2005; Melis et al. 2014) use stellar evolution models in their distance determination and because our observed stars are FGK stars, our derived value implies that the current stellar evolution models for FGK stars in the Pleiades are accurate.

Very soon the parallaxes from Gaia will confirm whether our prediction for the individual distances of the 15 Pleiades stars is correct, showing the power of the twin method in complementing Gaia and calibrating distance scales. The Gaia Data Release 1 will probably also show whether the star-to-star dispersion for the fainter Pleiades targets remains. It will further confirm whether the Pleiades distance controversy is a matter of individual distance accuracies, cluster morphology, astrometry, or the approximations in stellar evolution models. In this study, a distance estimate to some of the most difficult Hipparcos targets within the Pleiades has been determined. At the end of the Gaia mission, accurate parallaxes will be available for almost every star for which there is a high-resolution spectrum. Nevertheless, new larger telescopes are being constructed, such as the 39-m E-ELT, which will give us high-resolution spectra of very faint stars at the outskirts of our Galaxy and beyond. These ground-based instruments will provide new opportunities for complementing Gaia’s astrometric solutions and so to continue to climb the cosmic distance ladder with stellar twins.

1

Request number 192955.

Acknowledgments

We are grateful to the referee U. Bastian, whose comments helped us to significantly improve the article. It is our pleasure to thank T. Masseron, Q. Kral and A. Bonsor for fruitful discussions on the subject. This work was partly supported by the European Union FP7 programme through ERC grant No. 320360. C.W. acknowledges the Leverhulme Trust through grant RPG-2012-541. Based on data obtained from the ESO Science Archive Facility and on data. This research has made use of the SIMBAD and WEBDA databases.

References

  1. An, D., Terndrup, D. M., Pinsonneault, M. H., et al. 2007, ApJ, 655, 233 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bailer-Jones, C. A. L. 2015, PASP, 127, 994 [NASA ADS] [CrossRef] [Google Scholar]
  3. Blanco-Cuaresma, S., Soubiran, C., Heiter, U., & Jofré, P. 2014, A&A, 569, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bouy, H., Bertin, E., Sarro, L. M., et al. 2015, A&A, 577, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Datson, J., Flynn, C., & Portinari, L. 2014, MNRAS, 439, 1028 [NASA ADS] [CrossRef] [Google Scholar]
  6. De Pascale, M., Worley, C. C., de Laverny, P., et al. 2014, A&A, 570, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. ESA 1997, The Hipparcos and TYCHO catalogues. Astrometric and photometric star catalogues derived from the ESA Hipparcos Space Astrometry Mission, ESA SP, 1200 [Google Scholar]
  8. Fakhouri, H. K., Boone, K., Aldering, G., et al. 2015, ApJ, 815, 58 [NASA ADS] [CrossRef] [Google Scholar]
  9. Groenewegen, M. A. T., Decin, L., Salaris, M., & De Cat, P. 2007, A&A, 463, 579 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Hawkins, K., Jofre, P., Heiter, U., et al. 2016, A&A, 592, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Heiter, U., Jofré, P., Gustafsson, B., et al. 2015, A&A, 582, A49 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
  12. Hinkle, K., Wallace, L., Valenti, J., & Harmer, D. 2000, Visible and Near Infrared Atlas of the Arcturus Spectrum 3727−9300 Å (San-Francisco: ASP) [Google Scholar]
  13. Jackson, R. J., & Jeffries, R. D. 2014, MNRAS, 445, 4306 [NASA ADS] [CrossRef] [Google Scholar]
  14. Jofré, P., Heiter, U., Soubiran, C., et al. 2014, A&A, 564, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Jofré, P., Heiter, U., Soubiran, C., et al. 2015a, A&A, 582, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Jofré, P., Mädler, T., Gilmore, G., et al. 2015b, MNRAS, 453, 1428 [NASA ADS] [CrossRef] [Google Scholar]
  17. Katz, D., Soubiran, C., Cayrel, R., Adda, M., & Cautain, R. 1998, A&A, 338, 151 [NASA ADS] [Google Scholar]
  18. Kim, B., An, D., Stauffer, J. R., et al. 2016, ApJS, 222, 19 [NASA ADS] [CrossRef] [Google Scholar]
  19. Makarov, V. V. 2002, AJ, 124, 3299 [NASA ADS] [CrossRef] [Google Scholar]
  20. Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
  21. Meléndez, J., Dodds-Eden, K., & Robles, J. A. 2006, ApJ, 641, L133 [NASA ADS] [CrossRef] [Google Scholar]
  22. Melis, C., Reid, M. J., Mioduszewski, A. J., Stauffer, J. R., & Bower, G. C. 2014, Science, 345, 1029 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  23. Munari, U., Dallaporta, S., Siviero, A., et al. 2004, A&A, 418, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Nissen, P. E. 2015, A&A, 579, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Palmer, M., Arenou, F., Luri, X., & Masana, E. 2014, A&A, 564, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Pan, X., Shao, M., & Kulkarni, S. R. 2004, Nature, 427, 326 [NASA ADS] [CrossRef] [Google Scholar]
  27. Percival, S. M., Salaris, M., & Groenewegen, M. A. T. 2005, A&A, 429, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Perryman, M. 2008, Astronomical Applications of Astrometry: Ten Years of Exploitation of the Hipparcos Satellite Data (Cambridge: Cambridge University Press) [Google Scholar]
  29. Pinsonneault, M. H., Stauffer, J., Soderblom, D. R., King, J. R., & Hanson, R. B. 1998, ApJ, 504, 170 [NASA ADS] [CrossRef] [Google Scholar]
  30. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
  31. Soderblom, D. R., Nelan, E., Benedict, G. F., et al. 2005, AJ, 129, 1616 [NASA ADS] [CrossRef] [Google Scholar]
  32. Soubiran, C., Bienaymé, O., & Siebert, A. 2003, A&A, 398, 141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Soubiran, C., Le Campion, J.-F., Cayrel de Strobel, G., & Caillo, A. 2010, A&A, 515, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Spina, L., Meléndez, J., Karakas, A. I., et al. 2016, A&A, 593, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Stauffer, J. R., & Hartmann, L. W. 1987, ApJ, 318, 337 [NASA ADS] [CrossRef] [Google Scholar]
  36. Stello, D., & Nissen, P. E. 2001, A&A, 374, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Valls-Gabaud, D. 2007, in Binary Stars as Critical Tools Tests in Contemporary Astrophysics, eds. W. I. Hartkopf, P. Harmanec, & E. F. Guinan, IAU Symp., 240, 281 [Google Scholar]
  38. van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. van Leeuwen, F. 2009, A&A, 497, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Yuan, H. B., Liu, X. W., & Xiang, M. S. 2013, MNRAS, 430, 2188 [NASA ADS] [CrossRef] [Google Scholar]
  41. Zwahlen, N., North, P., Debernardi, Y., et al. 2004, A&A, 425, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

References

  1. An, D., Terndrup, D. M., Pinsonneault, M. H., et al. 2007, ApJ, 655, 233 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bailer-Jones, C. A. L. 2015, PASP, 127, 994 [NASA ADS] [CrossRef] [Google Scholar]
  3. Blanco-Cuaresma, S., Soubiran, C., Heiter, U., & Jofré, P. 2014, A&A, 569, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bouy, H., Bertin, E., Sarro, L. M., et al. 2015, A&A, 577, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Datson, J., Flynn, C., & Portinari, L. 2014, MNRAS, 439, 1028 [NASA ADS] [CrossRef] [Google Scholar]
  6. De Pascale, M., Worley, C. C., de Laverny, P., et al. 2014, A&A, 570, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. ESA 1997, The Hipparcos and TYCHO catalogues. Astrometric and photometric star catalogues derived from the ESA Hipparcos Space Astrometry Mission, ESA SP, 1200 [Google Scholar]
  8. Fakhouri, H. K., Boone, K., Aldering, G., et al. 2015, ApJ, 815, 58 [NASA ADS] [CrossRef] [Google Scholar]
  9. Groenewegen, M. A. T., Decin, L., Salaris, M., & De Cat, P. 2007, A&A, 463, 579 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Hawkins, K., Jofre, P., Heiter, U., et al. 2016, A&A, 592, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Heiter, U., Jofré, P., Gustafsson, B., et al. 2015, A&A, 582, A49 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
  12. Hinkle, K., Wallace, L., Valenti, J., & Harmer, D. 2000, Visible and Near Infrared Atlas of the Arcturus Spectrum 3727−9300 Å (San-Francisco: ASP) [Google Scholar]
  13. Jackson, R. J., & Jeffries, R. D. 2014, MNRAS, 445, 4306 [NASA ADS] [CrossRef] [Google Scholar]
  14. Jofré, P., Heiter, U., Soubiran, C., et al. 2014, A&A, 564, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Jofré, P., Heiter, U., Soubiran, C., et al. 2015a, A&A, 582, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Jofré, P., Mädler, T., Gilmore, G., et al. 2015b, MNRAS, 453, 1428 [NASA ADS] [CrossRef] [Google Scholar]
  17. Katz, D., Soubiran, C., Cayrel, R., Adda, M., & Cautain, R. 1998, A&A, 338, 151 [NASA ADS] [Google Scholar]
  18. Kim, B., An, D., Stauffer, J. R., et al. 2016, ApJS, 222, 19 [NASA ADS] [CrossRef] [Google Scholar]
  19. Makarov, V. V. 2002, AJ, 124, 3299 [NASA ADS] [CrossRef] [Google Scholar]
  20. Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
  21. Meléndez, J., Dodds-Eden, K., & Robles, J. A. 2006, ApJ, 641, L133 [NASA ADS] [CrossRef] [Google Scholar]
  22. Melis, C., Reid, M. J., Mioduszewski, A. J., Stauffer, J. R., & Bower, G. C. 2014, Science, 345, 1029 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  23. Munari, U., Dallaporta, S., Siviero, A., et al. 2004, A&A, 418, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Nissen, P. E. 2015, A&A, 579, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Palmer, M., Arenou, F., Luri, X., & Masana, E. 2014, A&A, 564, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Pan, X., Shao, M., & Kulkarni, S. R. 2004, Nature, 427, 326 [NASA ADS] [CrossRef] [Google Scholar]
  27. Percival, S. M., Salaris, M., & Groenewegen, M. A. T. 2005, A&A, 429, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Perryman, M. 2008, Astronomical Applications of Astrometry: Ten Years of Exploitation of the Hipparcos Satellite Data (Cambridge: Cambridge University Press) [Google Scholar]
  29. Pinsonneault, M. H., Stauffer, J., Soderblom, D. R., King, J. R., & Hanson, R. B. 1998, ApJ, 504, 170 [NASA ADS] [CrossRef] [Google Scholar]
  30. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
  31. Soderblom, D. R., Nelan, E., Benedict, G. F., et al. 2005, AJ, 129, 1616 [NASA ADS] [CrossRef] [Google Scholar]
  32. Soubiran, C., Bienaymé, O., & Siebert, A. 2003, A&A, 398, 141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Soubiran, C., Le Campion, J.-F., Cayrel de Strobel, G., & Caillo, A. 2010, A&A, 515, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Spina, L., Meléndez, J., Karakas, A. I., et al. 2016, A&A, 593, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Stauffer, J. R., & Hartmann, L. W. 1987, ApJ, 318, 337 [NASA ADS] [CrossRef] [Google Scholar]
  36. Stello, D., & Nissen, P. E. 2001, A&A, 374, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Valls-Gabaud, D. 2007, in Binary Stars as Critical Tools Tests in Contemporary Astrophysics, eds. W. I. Hartkopf, P. Harmanec, & E. F. Guinan, IAU Symp., 240, 281 [Google Scholar]
  38. van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. van Leeuwen, F. 2009, A&A, 497, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Yuan, H. B., Liu, X. W., & Xiang, M. S. 2013, MNRAS, 430, 2188 [NASA ADS] [CrossRef] [Google Scholar]
  41. Zwahlen, N., North, P., Debernardi, Y., et al. 2004, A&A, 425, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

Appendix A: Data of field stars

The information of the Hipparcos field stars used in this work is contained in Table A.1. The name and coordinates of the stars are given together with the 2MASS photometry with its quality flag, the Hipparcos parallax from van Leeuwen (2007), the S/N of the spectra, the date on which the spectra were taken, and the program ID.

Table A.1

Properties of reference field Hipparcos stars used in this sample.

All Tables

Table 1

Name, coordinates, apparent magnitudes in the visual, iSpec radial velocity, parallax and its standard error according to van Leeuwen (2007), and S/N of the Pleiades stars analysed in this work.

In the text
Table 2

Pleiades member stars and their twins in the field.

In the text
Table 3

Our determinations of parallaxes and distances together with their error for the individual Pleiades members with twin candidates in the field.

In the text
Table A.1

Properties of reference field Hipparcos stars used in this sample.

In the text

All Figures

thumbnail Fig. 1

Illustration of the twin method applied to the Pleiades cluster. The coordinates of the stars used in this work are shown in the upper panel. The blue circle represents the location of the Pleiades cluster, the black crosses are the reference Hipparcos field stars, and the black squares are the twins of the Pleiades stars found in the field. The bottom left panel shows the colour−magnitude diagram of the Pleiades, including the stars of the Seven Sister DANCe catalogue (Bouy et al. 2015) for reference with crosses. Circles correspond to the stars for which we took HARPS spectra, and the red triangles correspond to stars with twins in the field. A selection of Pleiades members with different spectra are shown around the Mg I triplet in red in the bottom right plot, together with a spectrum of a twin in the field as a dotted black line. The name of the Pleiades star and its corresponding twin are indicated, as well as its distance. Fast rotators are Pels 17, Pels 35, and Pels 174, which is seen in the greater broadening of their lines.

In the text
thumbnail Fig. 2

Behaviour of the ratio of twin parallax and Hipparcos parallax as a function of σ using the Hipparcos reference sample. The inset shows a zoom of the region of the plot at low σ. The horizontal lines represent the range of 10% difference in parallaxes while the vertical line the value of σ = 0.015.
In the text
thumbnail Fig. 3

In both panels, the pink band represents the values of the Hipparcos solution within its margin of error while the yellow band represents the range of the alternatives to Hipparcos. The upper panels show the parallaxes ofthe 57 field twins of each Pleiades member sorted by decreasing brightness, while the median and dispersion of the final twin parallaxes are illustrated with the blue line and band, respectively. The lower panel displays the averaged individual twin parallaxes (blue triangles), Hipparcos parallaxes (red squares, HIP vL07), the alternative astrometric solution of Makarov (2002) (cyan diamonds, HIP M02) and the parallax measurement with the Hubble Space Telescope of Soderblom et al. (2005) (pink star, S05).

In the text
thumbnail Fig. 4

Parallaxes of 54 Pleiades stars of the Hipparcos solution are indicated with black crosses. The mean and standard deviation of these Hipparcos parallaxes is shown by the grey band enclosed by a dotted line. Eleven of the Hipparcos stars have HARPS spectra and have been analysed in this work (red squares). Our results are indicated with blue triangles. The standard deviation of these values are shown with the blue band enclosed by the blue line. The pink band represents the values of the Hipparcos solution within its margin of error, while the yellow band represents the range of the alternatives to Hipparcos.

In the text
thumbnail Fig. 5

Difference of the Li equivalent widths and depth as a function of distance for the Pleiades-field twins. The red line indicates the linear fit of the data, with the slope and error of slope indicated in the legend. No correlation between the difference of Li abundance and distance has been found.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.