| Issue |
A&A
Volume 595, November 2016
|
|
|---|---|---|
| Article Number | A19 | |
| Number of page(s) | 14 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201628164 | |
| Published online | 24 October 2016 | |
Quantitative model for the generic 3D shape of ICMEs at 1 AU
1 Observatoire de Paris, LESIA, UMR 8109 (CNRS), 92195 Meudon, France
e-mail: Pascal.Demoulin@obspm.fr
2 Institut d’Astrophysique Spatiale, UMR8617, Univ. Paris-Sud-CNRS, Université Paris-Saclay, Bâtiment 121, 91405 Orsay Cedex, France
e-mail: mjanvier@ias.u-psud.fr
3 Departamento de Física and IFIBA, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires, 1428 Buenos Aires, Argentina
4 Instituto de Astronomía y Física del Espacio, UBA-CONICET, CC. 67, Suc. 28, 1428 Buenos Aires, Argentina
5 Departamento de Ciencias de la Atmósfera y los Océanos and Departamento de Física, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires, 1428 Buenos Aires, Argentina
Received: 20 January 2016
Accepted: 30 August 2016
Context. Interplanetary imagers provide 2D projected views of the densest plasma parts of interplanetary coronal mass ejections (ICMEs), while in situ measurements provide magnetic field and plasma parameter measurements along the spacecraft trajectory, that is, along a 1D cut. The data therefore only give a partial view of the 3D structures of ICMEs.
Aims. By studying a large number of ICMEs, crossed at different distances from their apex, we develop statistical methods to obtain a quantitative generic 3D shape of ICMEs.
Methods. In a first approach we theoretically obtained the expected statistical distribution of the shock-normal orientation from assuming simple models of 3D shock shapes, including distorted profiles, and compared their compatibility with observed distributions. In a second approach we used the shock normal and the flux rope axis orientations together with the impact parameter to provide statistical information across the spacecraft trajectory.
Results. The study of different 3D shock models shows that the observations are compatible with a shock that is symmetric around the Sun-apex line as well as with an asymmetry up to an aspect ratio of around 3. Moreover, flat or dipped shock surfaces near their apex can only be rare cases. Next, the sheath thickness and the ICME velocity have no global trend along the ICME front. Finally, regrouping all these new results and those of our previous articles, we provide a quantitative ICME generic 3D shape, including the global shape of the shock, the sheath, and the flux rope.
Conclusions. The obtained quantitative generic ICME shape will have implications for several aims. For example, it constrains the output of typical ICME numerical simulations. It is also a base for studying the transport of high-energy solar and cosmic particles during an ICME propagation as well as for modeling and forecasting space weather conditions near Earth.
Key words: Sun: coronal mass ejections (CMEs) / Sun: heliosphere / Sun: magnetic fields / solar-terrestrial relations
© ESO, 2016
1. Introduction
The coronal magnetic field recurrently accumulates magnetic field and free magnetic energy as a consequence of photospheric plasma motions and flux emergence. Through the process of photospheric cancellation of magnetic polarities, a sheared arcade is typically transformed into a twisted flux tube or flux rope (FR). At some point during its evolution, the FR can become unstable, erupting upward, with fast reconnection occurring underneath its structure, which leads to a flare (e.g., see the reviews of Forbes et al. 2006; Janvier et al. 2015a; Schmieder et al. 2015). If the downward magnetic tension of the overlying arcade is not strong enough, the flux rope is ejected, which creates a coronal mass ejection (CME).
Observations of CMEs by coronagraphs are extended in the interplanetary space with the heliospheric imagers of the STEREO spacecraft (e.g., see the review of Rouillard 2011). The interplanetary CMEs (ICMEs) are also detected in situ as an altered solar wind structure (e.g., see the review of Zurbuchen & Richardson 2006). Many differences have been found between ICMEs and ordinary solar wind properties: a low proton temperature (lower than half of what is expected for a typical solar wind with a similar velocity, Richardson & Cane 1995; Elliott et al. 2005; Démoulin 2009), an enhanced and coherent magnetic field (e.g., Burlaga et al. 1990), enhanced ion charge states (Lepri et al. 2001; Lepri & Zurbuchen 2004), an increase of bidirectional fluxes of suprathermal particles (e.g., Marsden et al. 1987; Gosling et al. 1987), etc. From the plasma parameters and the magnetic field reported in previous and recent ICME studies (and including the present one), a global picture for the structure of ICMEs has emerged. This is summarized in Fig. 1 with three key ingredients: the magnetic cloud (MC), the sheath, and the front shock.
An MC is identified by an enhanced magnetic field intensity, a large-scale and coherent magnetic field rotation, and proton temperatures lower than in the typical solar wind with the same radial speed (e.g., Burlaga et al. 1981; Dasso et al. 2005). These observations are typically interpreted as the crossing of an FR, which corresponds to the unstable magnetic configuration ejected from the Sun, a few days before it is detected in the interplanetary medium (e.g., see the review of Démoulin et al. 2008). MCs are typically present in a fraction (about one-third) of ICMEs (e.g., Richardson & Cane 2010). This is a lower limit, since the other fraction of cloud-like or no MC detected events could be due to a spacecraft crossing too far away from the nose or the center of the MC (hampering both the detection and the data fitting). The propagation process of MCs in the solar wind can also complicate the detection of MCs. For example, the FR erosion upon reconnection with the solar-wind magnetic field creates an asymmetric FR with part of the original FR connected to the solar wind (Dasso et al. 2006; Ruffenach et al. 2015).
Shocks are formed in front of ICMEs/MCs when they travel faster than the encountered solar wind, with a relative speed higher than the faster magnetohydrodynamics (MHD) mode speed (e.g., Bothmer & Schwenn 1998). At 1 AU, shocks are frequent in front of ICME sheaths. For example, shocks were present in front of 64% of the MCs studied by Feng et al. (2010) during the period 1995 to 2007. It is commonly thought that the shock is driven by the FR behind it (e.g., Lario et al. 2001; Oh et al. 2002; Marubashi & Lepping 2007). At 1 AU, the shocks have a moderate strength with a Mach number and density compression ratio both with a mean of just above 2 (Oh et al. 2007; Wang et al. 2010).
ICMEs are typically preceded by a sheath of compressed plasma and magnetic field collected on the way from the Sun (e.g., Gosling & McComas 1987; Démoulin 2010; Richardson 2011). A shock is typically present at the sheath front border where the plasma and the magnetic field are suddenly compressed. The sheath typically has a magnetic field strength comparable to or even exceeding that of the following MC (e.g., Zurbuchen & Richardson 2006; Masías-Meza et al. 2016). The magnetic field rapidly changes its orientation inside the sheath (because different solar wind structures are pressed together) and the proton temperature is typically much higher than in the solar wind and even higher than in MCs (because of strong compression and stronger heating).
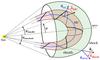 |
Fig. 1 Schema of an MC, its sheath, and its front shock. The MC axis is drawn in blue and its maximum angular extension as viewed from the Sun is 2ϕmax,MC while the shock extends up to 2ϕmax,shock. λ is defined by the angle between the radial direction from the Sun and the axis or the shock normal. |
It is important for several reasons to know the FR, sheath and shock shapes, and more generally the whole ICME structure. For example, they set global constraints on the results of numerical simulations. They are also important information for possible impact prediction with the Earth’s magnetosphere, their arrival time, and their journey in the interplanetary medium (e.g., Möstl & Davies 2013; Möstl et al. 2015). The ICME structure also affects the transport of energetic particles in the heliosphere over a wide range of energies (e.g., Cane et al. 2000). First, the global shape of MCs and their amount of twist determine the effective length for the travel of charged relativistic particles from the Sun to Earth, which produces delays in the observation of ground-level enhancements with respect to the expected time for a Parker-type solar wind (e.g., Kahler et al. 2011; Masson et al. 2012; Hu et al. 2015). Second, at higher energies (Galactic cosmic rays), the passage of an ICME frequently modifies the stationary flux of particles arriving at the Earth surface (e.g., producing a Forbush decrease, Cane et al. 2000), which can be observed from ground-level instruments such as neutron monitors (e.g., Simpson 1954, 2000) or water Cherenkov detectors (e.g., Abreu et al. 2011; Dasso et al. 2012; Asorey et al. 2016). Finally, ICMEs can produce changes in fluxes of suprathermal particles at lower energies, which can be observed in situ in the heliosphere by spacecraft (e.g., Mulligan et al. 2009). All in all, a better knowledge of the ICME generic structure helps the progress of ICME modeling and forecasting for space weather.
In a series of papers, the ICME generic structure was characterized from in situ data of large sample of events. Janvier et al. (2013) defined this new statistical method and deduced the mean shape of the MC axis from the local FR axis orientation of an MC set based on the results of Lepping & Wu (2010). Janvier et al. (2013) introduced the location angle λ defined as the angle between the radial direction from the Sun and the local normal to the MC axis (Fig. 1). λ defines the location of the spacecraft crossing along the flux-rope axis when its shape is known. The generic MC axis was deduced from the observed probability function,  . The authors found an axis shape close to an ellipse shape with an aspect ratio of 1.2 (lower extension in the radial direction). This statistical method was extended to shocks in front of ICMEs by Janvier et al. (2014b), with λ defined as the angle between the radial direction from the Sun and the local normal to the shock (Fig. 1). They showed that in situ data could be compatible with an axisymmetric shock shape around the direction of the Sun to the shock apex. They also showed that these statistical results agree with imager data of a well-observed ICME (Möstl et al. 2009). Next, while the relative directions of the MC axis and shock normal have a large dispersion when analyzed case by case (Feng et al. 2010), the above statistical method applied to the same sample of cases showed comparable results for the MC axis and shock shapes (Janvier et al. 2015b). More generally, the authors showed that MC axis and shock normals lead to comparable ellipsoidal shapes with all the in situ data sets analyzed. Finally, the ellipsoidal model has the closest probability,
. The authors found an axis shape close to an ellipse shape with an aspect ratio of 1.2 (lower extension in the radial direction). This statistical method was extended to shocks in front of ICMEs by Janvier et al. (2014b), with λ defined as the angle between the radial direction from the Sun and the local normal to the shock (Fig. 1). They showed that in situ data could be compatible with an axisymmetric shock shape around the direction of the Sun to the shock apex. They also showed that these statistical results agree with imager data of a well-observed ICME (Möstl et al. 2009). Next, while the relative directions of the MC axis and shock normal have a large dispersion when analyzed case by case (Feng et al. 2010), the above statistical method applied to the same sample of cases showed comparable results for the MC axis and shock shapes (Janvier et al. 2015b). More generally, the authors showed that MC axis and shock normals lead to comparable ellipsoidal shapes with all the in situ data sets analyzed. Finally, the ellipsoidal model has the closest probability,  , from the observed distributions for the three models.
, from the observed distributions for the three models.
In this paper we continue the effort of determining the generic structure of ICMEs by first exploring the effect of various shock surface shapes, and in particular some distortion effects, on the distribution of λ (Sect. 2). The comparison of this prediction to the observed distribution from shock normals sets some constraints on the generic shock structure. We next explore the possible observational constraints that can be set on ICME sheaths from in situ data (Sect. 3). Then, we combine the previous results with those obtained earlier to derive a global generic and quantitative structure of ICMEs (Sect. 4). Finally, in Sect. 5, we first summarize the main results and then conclude and outline potential applications.
2. Testing different shock shapes with in situ data
In this section we explore the implications of various 3D shock shapes and distortions effects on the probability distributions of the location angle λ (defined in Fig. 1). The main aim is to explore whether various shock shapes are compatible with the observed distribution of λ, and whether there could be generic shock shapes in front of ICMEs.
2.1. 3D shock shape
To simplify the description of the 3D shock shape, the model is described in Cartesian coordinates (x,y,z) with the x coordinate being the radial direction (direction of propagation) away from the Sun and y,z two orthogonal directions. The shock surface in general can be described by an equation of the type f(x,y,z) = 0. The shock normal 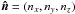 is along ∇f. The location angle, λ, is related to
is along ∇f. The location angle, λ, is related to 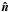 with
with 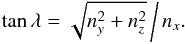 (1)Here λ is defined with respect to the fixed direction ûx, while in previous studies it was defined with respect to ûρ (Fig. 1). This approximation is better suited for narrower shocks (see below).
(1)Here λ is defined with respect to the fixed direction ûx, while in previous studies it was defined with respect to ûρ (Fig. 1). This approximation is better suited for narrower shocks (see below).
Next, we compute the probability of having λ ± dλ/ 2 during a spacecraft crossing the shock of a large number of CMEs. We assume a uniform probability of the spacecraft location in the y,z plane. This uniform probability is assumed since a spacecraft typically observes a large number of ICMEs launched from the Sun from a broad range of latitudes and longitudes (Sect. 2.3). Similarly, the ACE spacecraft crossed ICME shocks for several years without a privileged location. Numerically, we set a uniform grid in y,z, and compute λ from Eq. (1). The probability density function (PDF) of λ is then computed by normalizing the histogram of λ by the sum of bin counts.
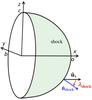 |
Fig. 2 Schema of the front shock in Cartesian coordinates. x is the propagation direction of the following ICME (not represented). λ is defined by the angle between the x direction and the shock normal. |
2.2. 3D ellipsoidal model
The shock front is described by the x> 0 half part of an ellipsoidal surface, shown in Fig. 2: 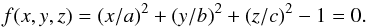 (2)tanλ, derived from Eq. (1), is a function of y,z and of the shock shape as
(2)tanλ, derived from Eq. (1), is a function of y,z and of the shock shape as 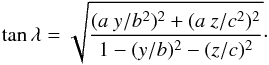 (3)In general, the analytical derivation of the probability
(3)In general, the analytical derivation of the probability  is complicated, therefore we computed it numerically. Two limits are still easily derived analytically, as follows.
is complicated, therefore we computed it numerically. Two limits are still easily derived analytically, as follows.
For the case with axisymmetry, that is, b = c, λ is a function of r with 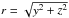 . The probability
. The probability 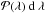 is proportional to the surface 2πr d r. The fraction dλ/ dr is computed by deriving Eq. (3). Finally,
is proportional to the surface 2πr d r. The fraction dλ/ dr is computed by deriving Eq. (3). Finally,  writes
writes 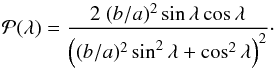 (4)A second analytical case is found in the limit c → ∞, which is the situation when the cross section of the shock in the xy-plane extends indefinitely in the z-direction (i.e., a semi-elliptic cylinder with its axis along the z-direction). In this limit, we derive
(4)A second analytical case is found in the limit c → ∞, which is the situation when the cross section of the shock in the xy-plane extends indefinitely in the z-direction (i.e., a semi-elliptic cylinder with its axis along the z-direction). In this limit, we derive 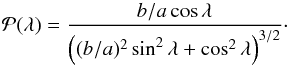 (5)These cases are used to test the numerical computations of
(5)These cases are used to test the numerical computations of  (brown dashed curves in Fig. 3).
(brown dashed curves in Fig. 3).
 |
Fig. 3 Probability of λ, |
 |
Fig. 4 Minimization of the difference between shock observations (blue histogram, Wang et al. 2010) and the 3D ellipsoidal model (Sect. 2.1). a) The difference function is defined by Eq. (6) and is plotted as a function of the aspect ratio b/a. b) The theoretical probability for the shock shape described by Eq. (2) and least-squares fitted to the observed distribution is shown for four values of the aspect ratio c/b (=1 for the axisymmetric case). Here, b/a is defined by the minimum of diff(obs.,mod.) of panel a) with the curve of the same color. |
Next, we compare  of the axisymmetric case, b = c to the axisymmetric model of Janvier et al. (2015b). This last model was derived in spherical geometry, Fig. 1, while the present model is derived in Cartesian geometry, Fig. 2. The difference is that the reference direction ûρ to compute λ is changing direction along the shock (Fig. 1), while ûx has a fixed direction. Then, the difference of computing λ between the models in spherical and Cartesian geometries is the angle between ûρ and ûx. When the shock is crossed at the nose, the radial direction (spacecraft crossing) is the same as the propagation direction, so that ûρ= ûx. If the spacecraft is crossed farther away from the nose, then the radial direction becomes quite different from the propagation direction, especially if the maximum angular extension of the shock ϕmax, defined in Fig. 1, is large. For low values of ϕmax, ûρ ≈ ûx, and therefore the 3D ellipsoidal model is suited for narrow ICMEs. Figure 3 shows that
of the axisymmetric case, b = c to the axisymmetric model of Janvier et al. (2015b). This last model was derived in spherical geometry, Fig. 1, while the present model is derived in Cartesian geometry, Fig. 2. The difference is that the reference direction ûρ to compute λ is changing direction along the shock (Fig. 1), while ûx has a fixed direction. Then, the difference of computing λ between the models in spherical and Cartesian geometries is the angle between ûρ and ûx. When the shock is crossed at the nose, the radial direction (spacecraft crossing) is the same as the propagation direction, so that ûρ= ûx. If the spacecraft is crossed farther away from the nose, then the radial direction becomes quite different from the propagation direction, especially if the maximum angular extension of the shock ϕmax, defined in Fig. 1, is large. For low values of ϕmax, ûρ ≈ ûx, and therefore the 3D ellipsoidal model is suited for narrow ICMEs. Figure 3 shows that  distributions are still comparable for a spherical model with a total angular width of 30° (black dashed line) and the 3D ellipsoidal model (blue line). This last numerical result is identical to Eq. (4) (brown dashed line).
distributions are still comparable for a spherical model with a total angular width of 30° (black dashed line) and the 3D ellipsoidal model (blue line). This last numerical result is identical to Eq. (4) (brown dashed line).
Finally, we analyzed the 3D ellipsoidal model to explore the effect of modifying the shock shape to non-axisymmetric configurations on  . Increasing the ratio c/b above 1 implies a flatter surface. For a given b/a (taken as 1.4, a value close to those derived from previous studies, see Janvier et al. 2015b; Möstl et al. 2015), this implies a shift of the peak in the
. Increasing the ratio c/b above 1 implies a flatter surface. For a given b/a (taken as 1.4, a value close to those derived from previous studies, see Janvier et al. 2015b; Möstl et al. 2015), this implies a shift of the peak in the  distribution to lower λ values as c/b increases (Fig. 3). In the limit of the high c/b ratio,
distribution to lower λ values as c/b increases (Fig. 3). In the limit of the high c/b ratio, 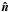 is mostly located in the x,y plane, and the distribution of λ is defined by the curvature of a surface nearly invariant in the z direction. Because of this invariance, the distributions of λ become similar to those found for a curve related to the same shape lying in the x-y plane. This distribution of λ is close to the distribution found for the MC axis (Janvier et al. 2013), but is significantly different from what is found for the shocks (Janvier et al. 2014b).
is mostly located in the x,y plane, and the distribution of λ is defined by the curvature of a surface nearly invariant in the z direction. Because of this invariance, the distributions of λ become similar to those found for a curve related to the same shape lying in the x-y plane. This distribution of λ is close to the distribution found for the MC axis (Janvier et al. 2013), but is significantly different from what is found for the shocks (Janvier et al. 2014b).
2.3. Comparison to observations
Below we compare the 3D ellipsoidal model to the in situ data of shocks studied by Wang et al. (2010). This study extends from February 1998 to August 2008, and the authors have analyzed 216 shocks. They derived the shock parameters, in particular the shock normal, by fitting the MHD Rankine-Hugoniot relations to the data in the vicinity of the shocks. One hundred and seventeen shocks are in front of ICMEs as identified by Richardson & Cane (2010), and the 99 remaining shocks have no detected ICMEs behind.
A small fraction of these last shocks is genereated by a fast solar wind stream that overtakes a slower solar wind (stream interaction regions, or SIRs). These shocks may represent as much as 20–30% of shocks measured at 1 AU during the time period 1995 to 2004 (Jian et al. 2006). Around solar maximum and at 1 AU such shocks are about ten times less numerous than ICME shocks (Lai et al. 2012). Janvier et al. (2014b) found comparable distributions  for shocks with and without an associated detected ICME, and the deduced mean shock shapes are very close. Of course this similarity of
for shocks with and without an associated detected ICME, and the deduced mean shock shapes are very close. Of course this similarity of  could also indicate that the physical processes involved in ICME and SIR shocks are similar because for both cases the driven structure (ICME or fast wind) mainly travels radially from the Sun and overtakes a slower plasma. However, we follow below the interpretation of Janvier et al. (2014b), who concluded that most shocks observed at 1 AU are associated with an ICME, although the ICME is not always detected because the shock has a broader spatial extension than the ICME. Then, we use below all the shock data set to derive the observed
could also indicate that the physical processes involved in ICME and SIR shocks are similar because for both cases the driven structure (ICME or fast wind) mainly travels radially from the Sun and overtakes a slower plasma. However, we follow below the interpretation of Janvier et al. (2014b), who concluded that most shocks observed at 1 AU are associated with an ICME, although the ICME is not always detected because the shock has a broader spatial extension than the ICME. Then, we use below all the shock data set to derive the observed  , called
, called 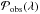 . The conclusions are similar for
. The conclusions are similar for  computed only from shocks associated to ICMEs.
computed only from shocks associated to ICMEs.
The analytical model described in Sect. 2.2 provides a continuous function of λ (e.g., Eqs. (4) and (5)). To compare this function with the observed probabilities, we first need to bin this analytical function, similarly as what is done for the observations (the probability function of this binned model is noted 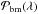 in the following). We also express both probabilities with the same unit, per unit of degree. The difference between the observed and the analytical probability is quantified by computing the least-squares difference with
in the following). We also express both probabilities with the same unit, per unit of degree. The difference between the observed and the analytical probability is quantified by computing the least-squares difference with 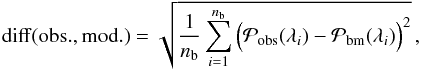 (6)where nb is the number of bins.
(6)where nb is the number of bins.
We explore below the effect of the ratio c/b on the fit of the modeled  to the observations by finding the ratio b/a that minimizes diff(obs.,mod.) for a fixed c/b value. We find that the maximum of
to the observations by finding the ratio b/a that minimizes diff(obs.,mod.) for a fixed c/b value. We find that the maximum of  shifts to lower λ values for larger c/b, Fig. 4b, as in Fig. 3. However, since a least-squares fit is made to a fixed observed distribution (blue histogram in Fig. 4), the effect of increasing c/b is softened by a reverse change of b/a (Fig. 4a). Decreasing values of b/a means that the shock shape is more bent in the xy-plane, then
shifts to lower λ values for larger c/b, Fig. 4b, as in Fig. 3. However, since a least-squares fit is made to a fixed observed distribution (blue histogram in Fig. 4), the effect of increasing c/b is softened by a reverse change of b/a (Fig. 4a). Decreasing values of b/a means that the shock shape is more bent in the xy-plane, then  decreases for lower λ values and increases at higher λ values, which moderates the
decreases for lower λ values and increases at higher λ values, which moderates the  changes outlined in Fig. 3 with an increasing c/b. Still, the values of
changes outlined in Fig. 3 with an increasing c/b. Still, the values of  are very different from that of
are very different from that of 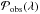 with increasing c/b values. For c/b = 3,9,and27, the minimum value of diff(obs.,mod.) grows by 2, 14, and 22% of its minimum value for c/b = 1. This growth is much larger in cases for which only the λ values close to the origin are used to compute diff(obs.,mod.), as illustrated in Fig. 4b with the larger distance between the curves at low λ values compared to higher ones. Then, shock configurations too far from the axisymmetric case are incompatible with observations. However, the upper limit set on c/b is high because case c/b = 3 fits the observed distribution nearly as well as case c/b = 1 (Fig. 4). This result is compatible with the equivalent ratio deduced from coronagraph observations of CMEs typically imaged at solar distances below half AU: Cremades & Bothmer (2005) and Cabello et al. (2016) deduced c/b ≈ 1.6 both from single-perspective observations performed on different CMEs and from a single CME observed in quadrature.
with increasing c/b values. For c/b = 3,9,and27, the minimum value of diff(obs.,mod.) grows by 2, 14, and 22% of its minimum value for c/b = 1. This growth is much larger in cases for which only the λ values close to the origin are used to compute diff(obs.,mod.), as illustrated in Fig. 4b with the larger distance between the curves at low λ values compared to higher ones. Then, shock configurations too far from the axisymmetric case are incompatible with observations. However, the upper limit set on c/b is high because case c/b = 3 fits the observed distribution nearly as well as case c/b = 1 (Fig. 4). This result is compatible with the equivalent ratio deduced from coronagraph observations of CMEs typically imaged at solar distances below half AU: Cremades & Bothmer (2005) and Cabello et al. (2016) deduced c/b ≈ 1.6 both from single-perspective observations performed on different CMEs and from a single CME observed in quadrature.
We conclude that the observed distribution 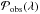 could still be compatible with front shocks that depart significantly from axisymmetry while coronagraph observations closer to the Sun point to a low asymmetry.
could still be compatible with front shocks that depart significantly from axisymmetry while coronagraph observations closer to the Sun point to a low asymmetry.
 |
Fig. 5 a), b) Theoretical distributions obtained with a 3D ellipsoidal model with a variable dip shape at its front as defined by Eq. (7) and shown in c) with a cut in the x-y plane. The color curves are for different dip depths (parameter d). a) The front is asymmetric around the x axis (direction of CME propagation) and b) the dip has no dependence on y. For all curves b/a = 1.4 and c/b = 1. |
2.4. Models with a front dip
Many numerical simulations of ICMEs show a shock front that at least globally has an ellipsoidal shape as modeled above (e.g., Manchester et al. 2004a; Xiong et al. 2006; Jacobs et al. 2007; Taubenschuss et al. 2010; Zhou et al. 2014). However, when the flux rope travels in a structured solar wind, with some dense and high plasma β regions, the front shock shape can be significantly deformed. In particular, the shock apex takes a concave-outward shape, or dips, for cases when the flux rope propagates in a slow wind that is edged on both sides by fast winds (Riley et al. 2003; Manchester et al. 2004b; Xiong et al. 2006; Taubenschuss et al. 2010). Such a dipped shape requires a very steady and bimodal solar wind, which is not present around solar maximum or with a succession of CMEs (e.g., Shen et al. 2014; Lugaz et al. 2007,respectively).
We investigate below the effect of such a shock deformation on the distribution  . First we rewrite x explicitly in function of y,z from Eq. (2), then we subtract a Gaussian shape:
. First we rewrite x explicitly in function of y,z from Eq. (2), then we subtract a Gaussian shape: 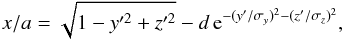 (7)with y′ = y/b and z′ = z/c. The depth of the dip is characterized by d and its extension in y,z by σy,σz, respectively. For example, with a slow and dense solar wind located around the x-y plane, surrounded by a faster solar wind at higher | z | values, the dip is expected to have σz ≪ σy with a higher d value for a denser slow solar wind.
(7)with y′ = y/b and z′ = z/c. The depth of the dip is characterized by d and its extension in y,z by σy,σz, respectively. For example, with a slow and dense solar wind located around the x-y plane, surrounded by a faster solar wind at higher | z | values, the dip is expected to have σz ≪ σy with a higher d value for a denser slow solar wind.
We show in Fig. 5 the results for two extreme cases: the axisymmetric case in panel (a), and the dipped case that only depends on the z coordinate in panel (b). They outline the range of possible cases obtained by varying the parameters d,σy,σz. Peaks in the distribution functions are present where the shock shape has an inflection point (Fig. 5c) because this implies that λ has nearly the same value in a wide range of y,z values. In this case,  is larger. This effect is more pronounced in the axisymmetric case, Fig. 5a, since the effect cumulates around circles of constant radius
is larger. This effect is more pronounced in the axisymmetric case, Fig. 5a, since the effect cumulates around circles of constant radius 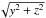 . On the other hand, for cases with σy significantly larger than σz, the inflection point is present on a wider range of λ values. In that case, the peak of
. On the other hand, for cases with σy significantly larger than σz, the inflection point is present on a wider range of λ values. In that case, the peak of  is broader, especially on its right side (e.g., see Fig. 5b for the limit σy → ∞).
is broader, especially on its right side (e.g., see Fig. 5b for the limit σy → ∞).
For moderate d values, the shock shape is nearly flat around the apex. This implies significant values of  near the origin (e.g., the green curves in Figs. 5a,b). This contrasts with the observation results, which show distributions of
near the origin (e.g., the green curves in Figs. 5a,b). This contrasts with the observation results, which show distributions of 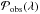 with low values near the origin (histogram in Fig. 4b and see other data sets in Janvier et al. 2015b).
with low values near the origin (histogram in Fig. 4b and see other data sets in Janvier et al. 2015b).
We next scan the parameter space of σy,σz and d. The results can be summarized as follows. Decreasing σy,σz values brings the peaks of  to lower λ values (not shown). This can be partly compensated for by increasing the dip depth (d), so that Fig. 5 gives a fair overview of the
to lower λ values (not shown). This can be partly compensated for by increasing the dip depth (d), so that Fig. 5 gives a fair overview of the  distributions obtained by scanning the space of parameters d,σy,σz. Then, the results of Fig. 5 also describe the typical results that we found with a full exploration of the parameter space (within the limits of plausible shapes, i.e., those found in numerical simulations).
distributions obtained by scanning the space of parameters d,σy,σz. Then, the results of Fig. 5 also describe the typical results that we found with a full exploration of the parameter space (within the limits of plausible shapes, i.e., those found in numerical simulations).
The results above show that flat and concave-outward shapes are not typical of observed ICME shocks. On the one hand, if a flat front were a common feature of their shapes, then the observed distribution 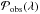 would not have low values close to the origin, as observed. On the other hand, if a dipped front with a characteristic shape were a common feature, then the observed distribution
would not have low values close to the origin, as observed. On the other hand, if a dipped front with a characteristic shape were a common feature, then the observed distribution 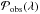 would have a pronounced peak around some λ values (which would characterize the dip shape). It is possible that the peaks at λ ≈ 10° and 28° in Fig. 4b could be due to an enhanced contribution of shocks with dips. However, they could also be due to statistical fluctuations due to the low statistics in each bin: there are around 14 cases per bin in the maximum region of
would have a pronounced peak around some λ values (which would characterize the dip shape). It is possible that the peaks at λ ≈ 10° and 28° in Fig. 4b could be due to an enhanced contribution of shocks with dips. However, they could also be due to statistical fluctuations due to the low statistics in each bin: there are around 14 cases per bin in the maximum region of 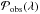 , that is, a statistical fluctuation of ± 4, which implies a probability fluctuating in the range [0.017,0.033], a range that is comparable to what is observed. That said, the interaction of ICMEs with different slow solar winds and different interacting configurations could smooth the observed distribution by creating a variety of dips. Finally, since various dip shapes imply very different
, that is, a statistical fluctuation of ± 4, which implies a probability fluctuating in the range [0.017,0.033], a range that is comparable to what is observed. That said, the interaction of ICMEs with different slow solar winds and different interacting configurations could smooth the observed distribution by creating a variety of dips. Finally, since various dip shapes imply very different  , the observed distribution
, the observed distribution 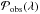 is not sufficient to set an estimate of the proportion of dipped cases or to estimate the dip shape distribution.
is not sufficient to set an estimate of the proportion of dipped cases or to estimate the dip shape distribution.
The conclusion that the concave-outward shapes are relatively rare agrees with the results of the STEREO spacecraft imagers, which show only a few observed cases (Savani et al. 2010; Lugaz & Roussev 2011). This is also an expected result since the characteristics of the deformation depend on many parameters, such as the geometry of the interaction, in particular the relative orientation of the flux-rope propagation direction and the slow wind layer region. The symmetric configurations analyzed in the numerical simulations (Manchester et al. 2004b; Xiong et al. 2006; Taubenschuss et al. 2010) are therefore not expected to represent typical ICME cases.
 |
Fig. 6 Correlations between the maximum velocity, Vmax, within ICMEs and the size of their sheaths, Ssha); and their sizes, Sicmeb), for the ICMEs studied by Richardson & Cane (2010) and those with a front shock studied by Wang et al. (2010). The blue straight line is the least-squares fit to the data points (black points). cp and cs are the Pearson and Spearman correlation coefficients, and σ is the standard deviation of the ordinate. |
3. Sheath and ICME properties
In this section we explore the statistical properties of ICMEs to obtain information on the global ICME parameters across the spacecraft trajectory. We first summarize the data used in Sect. 3.1, then we explore some global properties in Sect. 3.2 before introducing the new statistical method used in Sect. 3.3 and finally describing the results in Sect. 3.4.
3.1. Association of ICMEs with shocks and MCs
Richardson & Cane (2010) reported on 317 ICMEs observed from 1996 to 2009. In particular, they listed the beginning of the disturbance (tdist), associated with the time of the shock, the start (tstart) and the end (tend) times for each detected ICME. The time difference Δtsheath = tstart−tdist defines the observed duration of the sheath.
To gather complementary information on ICMEs, we associated them with shocks or/and MCs when they are observed. In particular, this provides an estimate of where each ICME was crossed by the spacecraft (see Sect. 3.3).
We associated shocks studied by Wang et al. (2010) with the beginning of ICME disturbances of Richardson & Cane (2010) using a time window of two hours following the procedure described in Sect. 2.3 of Janvier et al. (2014b). Wang’s list of shocks, observed by ACE spacecraft, extends from February 1998 to August 2008 and contains a total of 257 shocks with their main properties (e.g., shock strength and normal). This reduces to 117 pairs of associated ICMEs-shocks.
Next, we used an extended list of events (Table 2 at http://wind.nasa.gov/mfi/mag_cloud_S1.html) that is based on the fit by a Lundquist model of the in situ data (Lepping & Wu 2010). The list contains the parameters obtained for 121 MCs observed by the Wind spacecraft from February 1995 to December 2009. Following Janvier et al. (2013), we restricted Lepping’s list to 107 MCs (avoiding the cases with the poorest model fit to the data). The association with ICMEs was made by maximizing the overlapping time period between each MC and the ICMEs, with a minimum overlapping interval of ten hours. In the few cases where two MCs were associated with one ICME, we selected the MC with the longest common time interval. We also kept only the MCs that were crossed by the spacecraft at a distance of the flux-rope axis shorter than 70% of its radius (i.e., the absolute value of the impact parameter ≤0.7) to avoid uncertain fitted parameters for too distant encounters. The association and filtering provided 67 pairs of associated ICMEs-MCs.
The above ICMEs associated with a shock were then associated with MCs with the above procedure. This restricted the data to 30 triads of associated ICMEs-shocks-MCs. Since it limits the statistics, we instead present below the results with the pairs of ICMEs-shocks and ICMEs-MCs. The results with the triads are typically comparable while with larger uncertainties that are due to the limited number of cases.
3.2. Sheath global properties
We computed the ICME sheath thickness, Ssh, by taking the integral of the radial speed component in the time interval defined by Richardson & Cane (2010). We used the data from OMNI with spacecraft located at 1 AU. Some of the ICME sheaths have data gaps, therefore we can perform the computations on only 268 cases of Richardson and Cane list. We find a mean sheath thickness of 0.1 AU, which is comparable to the mean value of 0.082 AU found by Richardson & Cane (2010) for the same dataset and 0.11 AU found by Mitsakou & Moussas (2014) for ICMEs observed during 1996–2008.
The sheath thickness Ssh is very case dependent, with values in the range [0, 0.5] AU (e.g., Fig. 6). This is an expected result since CMEs near the Sun have a broad range of speeds (from ≈30 to more than ≈2000 km s-1, see Yashiro et al. 2004; Robbrecht et al. 2009; Wang et al. 2011), so that an efficient snow-plow effect is highly case dependent. Moreover, FRs are expected to reconnect with the overtaken solar wind with a variable efficiency (e.g., depending on the relative velocities and magnetic field orientations). The percentage of reconnected flux at 1 AU ranges from no significant reconnected flux to at least 60% in MCs (Dasso et al. 2006, 2007; Mandrini et al. 2007; Ruffenach et al. 2012, 2015). This variable amount of reconnection between the FR and the magnetic field accumulated in the sheath is another source of variable sheath thickness.
At first sight, faster ICMEs are expected to have an average larger sheath as they overcome more solar wind plasma during their travel from the Sun to D = 1 AU. For example, with a constant front velocity equal to Vmax and solar wind velocity, Vwind, the radial size of the overtaken solar wind is (1−Vwind/Vmax)D, which means a monotonously growing function of Vmax. However, including the shock properties, as deduced from hydrodynamics physics within a mass budget of the sheath, Siscoe & Odstrcil (2008) found a sheath thickness relative to the radius of curvature of the driver that is a decreasing function of the Mach number. With a comparable overtaken solar wind, the sheath thickness is therefore instead expected to decrease with Vmax. We find that the sheath thickness is weakly dependent on Vmax within the dispersion of individual cases (Fig. 6a). The large dispersion of Ssh, for example, due to reconnection, may wash out the expected dependency. The radius of curvature is not available from in situ data either, therefore we cannot normalize the sheath thickness as in Siscoe & Odstrcil (2008).
 |
Fig. 7 Variation of the sheath size, Ssh, along: a) the MC axis (| λMC |); b) across the MC axis (| pMC |); and c) along the shock (λshock). The drawing convention and added parameters are the same as in Fig. 6. Panels a) and b) are for the MCs of Lepping’s list, and panel c) shows the shocks studied by Wang et al. (2010). Both sets were associated with the ICMEs studied by Richardson & Cane (2010). The panels show that there is no global dependence on Ssh along and across the flux rope or along the shock. |
For comparison with the sheath, we also computed the ICME size Sicme. The faster ICMEs are typically larger (Fig. 6b). A comparable positive correlation, around 0.4 to 0.5, is found between Sicme and Vmax in different sub-groups of ICMEs, for example with/without MCs (not shown). These results agree with those in Fig. 12 of Richardson & Cane (2010), who found a positive correlation of the expansion speed with radial size and velocity of ICMEs. The next question is the origin of this positive correlation between Sicme and Vmax. Reconnection at the ICME front removes an equivalent amount of magnetic flux in the front of the FR as in the rear of the sheath, while the corresponding flux stays at the rear of the ICME. This back region is connected to the solar wind, with a mix of properties between MC and solar wind ones. In particular, this back region typically has a weaker magnetic field than in the FR (Dasso et al. 2007; Ruffenach et al. 2015), which means that when magnetic field reconnection is present, the back region is more extended than when it was still part of the FR. Then, the front reconnection decreases the ICME size at the front while it extends the rear, mitigating the effect of reconnection on the ICME size. We concluded that the positive correlation Vmax(Sicme) is the remains of an intrinsic correlation, most likely not affected strongly by the amount of front reconnection.
Finally, we note some high Ssh and Sicme values in Fig. 6. The large sheaths may be due to a merging process with the compressed plasma in an SIR, or they may contain an overtaken ICME that is compressed and hotter. Large ICMEs may be also due to the interaction and the merging of two ICMEs (e.g., Wang et al. 2002; Dasso et al. 2009; Liu et al. 2014; Lugaz & Farrugia 2014). It is difficult to filter such events without a detailed analysis of each case. However, such events do not depart from the general tendency (Fig. 6), and they are not numerous. Filtering the large events in practice, for example, by considering only cases with Ssh< 0.3 and Sicme< 0.5, therefore does not affect the least-squares fit significantly. This is also the case in the following analysis (e.g., as shown in Fig. 7).
 |
Fig. 8 Variation of the maximum radial velocity, Vmax, measured after the sheath within the ICME. The dependence is shown: a) along the MC axis (| λMC |); b) across the MC axis (| pMC |); and c) along the shock (λshock). The drawing convention and added parameters are the same as in Fig. 6. The graphs show that Vmax is independent of the crossing location. The red, green, and pink lines indicate the expectation of a self-similar expansion model (see Sect. 3.4). |
3.3. Statistical method for exploring across spacecraft trajectories
A single spacecraft explores the crossed ICME only along a line parallel to the main ICME global motion (nearly in the radial direction from the Sun). Moreover, the location of the crossing within the ICME is typically not known. Exploring the ICME properties in the ortho-radial directions would need an ensemble of spacecraft distributed over the ICME cross section, which is not available at present, or to have multi-crossing of a single spacecraft, which is impossible as the ICME is too fast and not massive enough to be orbited.
For most ICME shocks, λshock is a monotonic function of ϕ, the angular distance from the shock apex as seen from the Sun (Sect. 2.4). With a defined shock shape, for instance, with the generic ICME shock shape determined by Janvier et al. (2015b), λshock therefore defines where the shock is crossed. The same is true for λMC (Fig. 1) with the MC axis shape determined by Janvier et al. (2013): it provides an estimate of the location where the FR is crossed along its axis. We can then derive how physical quantities typically change along the MC axis together with the shock shape from sets of MCs and ICME shocks.
In summary, the generic dependence of physical parameters across and along the FR can be explored statistically using pMC and λMC, while λshock allows exploring the dependence away from the shock apex independently of the MC axis direction. The results are independent of each other because MC and shock data have been obtained separately, and the techniques used to derive the FR axis and shock normal are unrelated as well. However, we expect that the results are linked to each other from a physical point of view: exploring λshock is almost equivalent to exploring both pMC and λMC parameters, but without knowing the MC axis direction (this approach is less reliable for the side extensions of the shock, behind which there are no FRs).
While λshock is positive by definition, both pMC and λMC are signed quantities (indicating on which side the FR is crossed). However, as we are limited by the number of MCs, we report the results as a function of | pMC | and | λMC | to group the FR sides (the FR legs) together and increase the statistics.
The statistical study of a parameter in function of pMC, λMC, or λshock can reveal if this parameter has a global dependence across or along the MC axis or along the ICME front within the limit of the statistical dispersion (its standard deviation). More precisely, it can reveal a monotonous variation or one dominated by a positive or negative variation on the scale of the range of pMC, λMC, or λshock. However, the correlation coefficients and the slope (of the fitted straight line) cannot reveal significant variations on scales much smaller than the scale of the range studied, nor a more complex relation than the one given by a non-linear function (e.g., a relation with several branches). A summary of the statistical tests is presented in Appendix A.
Finally, it is also worth noting that the angles λMC and λshock have large errors, on the order of 20°, as deduced by comparing the results obtained with the same MCs/shocks but with different methods for deducing λMC and λshock (see Fig. 2 of Janvier et al. 2015b). The impact parameter has also large uncertainties (Lepping & Wu 2010; Démoulin et al. 2013). These large error bars of individual cases are decreased by the statistics, and compatible FR axis and shock shapes were found by Janvier et al. (2015b) from a statistical method, while in one-third of the same events the difference of relative orientation of the FR axis and shock normal was different from the expected (orthogonal) orientation by more than 25° (Feng et al. 2010).
 |
Fig. 9 Variation of the mean field strength, ⟨ Bicme ⟩, measured after the sheath within the ICME. The dependence is shown: a) along the MC axis (| λMC |); b) across the MC axis (| pMC |); and c) along the shock (λshock). The drawing convention and added parameters are the same as in Fig. 6. ⟨ Bicme ⟩ is uniform on average along the MC axis (| λMC |) and along the shock front (λshock), while ⟨ Bicme ⟩ decreases across the MC axis (| pMC |), as expected (stronger magnetic field in the MC core). |
3.4. Property variations along the ICME front
The sheath thickness, Ssh, shows a large variability for all | λMC |, | pMC | and λshock values (Fig. 7). All the correlation coefficients are low (≤0.11). We conclude that the sheath thickness has no global trend along the shock front within the limit of the observed standard deviation (≈0.1 AU). Some individual ICME sheaths may still vary along the shock front, but they are not generic for the majority of events. This result is compatible with the similar mean shape found for the MC axis and shock normals (Janvier et al. 2015b), see Sect. 4.2.
Next, we explored the global properties of ICMEs, such as the maximum, Vmax, and mean velocity, Vmean, computed after the sheath within each ICME. We found no correlation of Vmax (Fig. 8) and Vmean (not shown) with any of the location parameters. Next, we compared this with the expectation of a self-similar expansion model (e.g., Möstl et al. 2015,and references therein) where the shape (axis or shock surface) was rescaled with a function of time f(t), so r(λ,t) = f(t) r(λ,t0) where r(λ,t) is the distance to the Sun at λ and time t, and t0 is a reference time. Then the radial velocity is 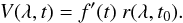 (8)We used the elliptical model of Janvier et al. (2013) with b/a = 1.3, a value very close to those deduced from the distributions of λ for MCs and shocks. For a given time, t, or a velocity weakly dependent on time around the spacecraft location (f′(t) ≈ constant), the self-similar expansion implies a decreasing function V(λ,t) of λ for any ϕmax value. This decrease is not observed (Figs. 8a,c), and it implies a lack of exact self-similar evolution.
(8)We used the elliptical model of Janvier et al. (2013) with b/a = 1.3, a value very close to those deduced from the distributions of λ for MCs and shocks. For a given time, t, or a velocity weakly dependent on time around the spacecraft location (f′(t) ≈ constant), the self-similar expansion implies a decreasing function V(λ,t) of λ for any ϕmax value. This decrease is not observed (Figs. 8a,c), and it implies a lack of exact self-similar evolution.
We interpret these differences as follows. Away from the Sun, the main force acting on the ICME is the drag force, which typically depends on the square of the velocity difference between the ICME and the encountered solar wind (e.g., Vršnak et al. 2013,and references therein). Then, the drag force tends to make the values of the velocity closer to the value of the encountered plasma, so that the dependence V(λ) becomes weaker with distances if the MC is embedded in the same type of solar wind. Finally, from the results of Fig. 8 and the same ones for Vmean, we conclude that the drag force was efficient enough during the travel to 1 AU to harmonize the ICME velocities in the ortho-radial directions.
Next, we analyzed the mean magnetic field strength, ⟨ Bicme ⟩, computed after the sheath within each ICME. There is no significant dependence of ⟨ Bicme ⟩ on | λMC | and λshock (Figs. 9a,c). However, ⟨ Bicme ⟩ decreases with the impact parameter (Fig. 9b) as expected in FR models since the field strength decreases away from the axis as a result of the inward magnetic tension. This provides a test for the statistical method: while there is a large variability of the quantities within the ICME cases, the statistical approach still shows a dependence when it is present. This result is supported by the tests summarized in Appendix A.
Finally, when the magnetic field strength Baxis on the FR axis is considered (derived from the fitted FR model to the in situ magnetic field data), we found only weak correlations with | λMC | and | pMC | (cp and cs are between −0.2 and −0.1). The low correlation with | λMC | agrees with the result of ⟨ Bicme ⟩ (Fig. 9), but limited to the MC part of the ICMEs. The low correlation of | pMC | with Baxis is expected if there is no bias in the results of the fitted FR model.
In conclusion, with a statistical approach on large sets of MCs, shocks, and ICMEs and with the estimated parameters | λMC |, | pMC | and λshock we were able to explore the behavior of global ICME quantities in directions orthogonal to the spacecraft trajectory. This new approach provides new results such as a sheath thickness and an ICME radial velocity, which show no global and systematic dependence along the ICME front within the limit of the observed standard deviation, meaning that there is no dependence that would be present in the majority of ICMEs. A priori we cannot exclude a situation with several groups of ICMEs with different dependencies that cancel on average, for instance. However, we explored this by dividing the ICME set into a few groups with common characteristics (e.g., velocity, field strength, or size), but we did not find any sub-group with specific properties.
4. Quantitative generic ICME structure
4.1. Relationship between the axis and shock angular extensions
In previous studies (Janvier et al. 2013, 2015b), two parameters could not be determined from in situ data: the maximum angular extension of the structures, ϕmax,MC and ϕmax,shock. However, under the assumptions that all ICMEs contain an FR and that all shocks are driven by ICMEs, we can use the relative number of detected FRs to that of shocks in a given time interval to constrain ϕmax,MC as a function of ϕmax,shock, as follows. For an FR with a constant radius R along its axis, its cross section, as seen from a spacecraft located at a distance D, is approximately the product of its diameter and its projected length 2 ϕmax,MCD (we assume that R ≪ D so that the cross section is a thin elongated band of the sphere of radius D). For an FR with a variable radius along its axis, its mean radius Rmean replaces R. Then the FR cross section seen by a spacecraft is 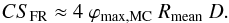 (9)The cross section of a shock with an ellipsoid shape, Eq. (2), is
(9)The cross section of a shock with an ellipsoid shape, Eq. (2), is 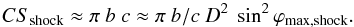 (10)We choose to define above ϕmax,shock with the largest extension c since we estimate ϕmax,shock below from the imager data. The 2D images do not provide the orientation of the FR, nor from which point of view the sheath is observed, which means that there is no indication whether the extension seen is closer to b or c. With a uniform distribution of the elongation orientation, the measured width is closer to the longest extension. From the imagers c = b is estimated for the axisymmetric case and 2c/π for the limit case of c ≫ b. Then, we define ϕmax,shock with c in Eq. (10) as the best approximation since c/b is unknown. Furthermore, there is the caveat that the shock extension is rarely traced in CME images, so that the observed angular extension is rather the extension of the dense sheath.
(10)We choose to define above ϕmax,shock with the largest extension c since we estimate ϕmax,shock below from the imager data. The 2D images do not provide the orientation of the FR, nor from which point of view the sheath is observed, which means that there is no indication whether the extension seen is closer to b or c. With a uniform distribution of the elongation orientation, the measured width is closer to the longest extension. From the imagers c = b is estimated for the axisymmetric case and 2c/π for the limit case of c ≫ b. Then, we define ϕmax,shock with c in Eq. (10) as the best approximation since c/b is unknown. Furthermore, there is the caveat that the shock extension is rarely traced in CME images, so that the observed angular extension is rather the extension of the dense sheath.
Because of the broad range of latitudes of the solar sources and the solar rotation, CMEs are randomly launched in a nearly uniform range of directions for a spacecraft observing at a fixed position for years. Then, the expected ratio of the number of FRs, NFR with shock, to the number of ICME front shocks, Nshock, is the ratio of their cross-sections. This provides a relationship between ϕmax,MC and ϕmax,shock of 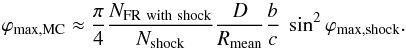 (11)Janvier et al. (2014b) associated 117 shocks with ICME sheath fronts from the lists of Richardson & Cane ICME and Wang et al. (see Sect. 3.1). Then, 99 other shocks were also considered. These shocks were not directly associated with ICME sheath fronts, but were also not found within ICME sheaths, within an ICME, or within six hours after an ICME. The authors argued that most of these remaining shocks were associated with ICMEs not detected in situ. Two reasons can be given. First, the frequency of shocks driven by stream interaction regions (SIRs) is much lower than the frequency of shocks driven by ICMEs at 1 AU, and second, the distribution of
(11)Janvier et al. (2014b) associated 117 shocks with ICME sheath fronts from the lists of Richardson & Cane ICME and Wang et al. (see Sect. 3.1). Then, 99 other shocks were also considered. These shocks were not directly associated with ICME sheath fronts, but were also not found within ICME sheaths, within an ICME, or within six hours after an ICME. The authors argued that most of these remaining shocks were associated with ICMEs not detected in situ. Two reasons can be given. First, the frequency of shocks driven by stream interaction regions (SIRs) is much lower than the frequency of shocks driven by ICMEs at 1 AU, and second, the distribution of 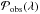 for those 99 shocks is similar to
for those 99 shocks is similar to 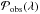 for shocks with a detected ICME behind. This result also agrees with the expectation that the lateral extension of the shock is broader than the driving ICME. In summary, we estimated a total of 216 shocks detected in front of ICME sheaths in the time interval 1998–2008.
for shocks with a detected ICME behind. This result also agrees with the expectation that the lateral extension of the shock is broader than the driving ICME. In summary, we estimated a total of 216 shocks detected in front of ICME sheaths in the time interval 1998–2008.
Within the same time interval, 45 MCs and 36 MC-like events were detected. Then, the number of FRs entering in Eq. (11) is between 45 and 81. Next, the mean FR radius for MCs is Rmean ≈ 0.12 AU (Lepping & Wu 2010). Although ϕmax,shock cannot be determined by the shape of 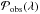 , we constrained ϕmax,shock< 60° following the analysis in Sect. 3.4 of Janvier et al. (2015b). Moreover, the mean half angular width of a limb CME is ≈30° (Wang et al. 2011). This angular width, corresponding to the CME sheath, is typically kept as CMEs propagate away from the Sun, so that ϕmax,shock is around 30°.
, we constrained ϕmax,shock< 60° following the analysis in Sect. 3.4 of Janvier et al. (2015b). Moreover, the mean half angular width of a limb CME is ≈30° (Wang et al. 2011). This angular width, corresponding to the CME sheath, is typically kept as CMEs propagate away from the Sun, so that ϕmax,shock is around 30°.
With this set of parameters, ϕmax,MC was estimated for a given ϕmax,shock. In Fig. 10 we show the conservative case where only MCs are considered for the number of FRs. For the axisymmetric case, b = c, the shock is typically broader by about 10° than the MC axis. As c/b increases, the shock becomes even broader by 20° to 30°. From the impact parameter distribution, Démoulin et al. (2013) showed that the typical FR cross section is indeed not circular but flattened in the radial direction by a factor ranging from 1.5 to 3 depending on the selected FR model. Taking this flattening into account would increase the Rmean value used above by this factor. It has the same effect as increasing c/b, as discussed above. Next, when we consider MCs and MC-like events, the estimate of ϕmax,MC needs to be multiplied by 81/45 = 1.8, so that ϕmax,MC and ϕmax,shock are much closer, with the possibility of a shock extending a shorter distance than the MC axis (ϕmax,shock−ϕmax,MC is in the range [− 10°,20°]). Finally, when we consider that only 70% of the shocks observed at 1 AU are driven by ICMEs (Jian et al. 2006), the estimate of ϕmax,MC is multiplied by 1/0.7 ≈ 1.43 so that it has the same effect, but weaker, as including the MC-like events.
 |
Fig. 10 ϕmax,MC in function of ϕmax,shock from Eq. (11). NFR with shock is estimated with the number of detected MCs (45) and Nshock is the total number of front ICME shocks (216) detected during the same period of time. The curves are for the shock-surface aspect ratio c/b defined in Fig. 2. |
 |
Fig. 11 Summary of the results of the axis and shock shapes providing a quantitative version of the sketch drawn in Fig. 1. a) Cut in the plane of the FR axis and b) cut in the plane orthogonal to the axis plane at the apex. ϕmax,shock is the only free parameter, set here to 30°. ϕmax,MC = 20° is estimated from Eq. (11) with NFR = 45 (Fig. 10). The aspect ratio b/a = 1.2 and 1.3 for axis and shock, respectively, are mean values of the results of Janvier et al. (2014b). At the apex, the sheath thickness is set to the mean value of 0.1 AU, but it is very case dependent (Fig. 7). The radial FR extension is deduced from Janvier et al. (2014b). The FR cross section is elliptic with an aspect ratio of 2 as estimated by Démoulin et al. (2013). The FR front is set at 1 AU, with the axis and shock shapes rescaled by their apex distances (0.87 and 1.1 AU, respectively). The two dotted lines mark the radial distance to the Sun at 0.5 and 1 AU. |
4.2. Quantitative generic ICME structure
With the quantitative information found above and in previous studies on the different parts of ICMEs (shock, sheath, and FR axis), we can derive a quantitative generic model of ICMEs based on the analyzed in situ observations, as follows. Since neither the imager nor in situ data are sufficient to define the aspect ratio of the shock surface in ortho-radial directions, we keep below the simplest solution compatible with the observations: an axisymmetric configuration. The global ICME configuration can be derived with other aspect ratios and another ϕmax,shock value, with the same procedure.
The generic shapes of the MC axis and shock shells have been determined with the ellipsoidal model, which provides the closest distribution  from the observed one,
from the observed one, 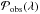 , both for MCs and shocks (Janvier et al. 2015b). While errors in the determination of MC axis and shock normals are large for individual events, we have shown that these errors have a small effect on the determination of the generic shapes. We set ϕmax,shock = 30° and, with a conservative approach, we included only MCs as detected flux ropes. This implies ϕmax,MC ≈ 20° (Fig. 10).
, both for MCs and shocks (Janvier et al. 2015b). While errors in the determination of MC axis and shock normals are large for individual events, we have shown that these errors have a small effect on the determination of the generic shapes. We set ϕmax,shock = 30° and, with a conservative approach, we included only MCs as detected flux ropes. This implies ϕmax,MC ≈ 20° (Fig. 10).
First, we considered the plane containing the FR axis (Fig. 11a). The FR radius of MCs, from Lepping’s list, was found to depend on λ (Janvier et al. 2014a). We used the approximation R(λ) = 0.13−10-5λ2 AU for this dependence. This radius was added or substracted in the direction orthogonal to the axis to derive the front or rear of the FR, respectively (Fig. 11a). This means that in the present model we did not take the amount of reconnected flux into account, which is the back region that is observed in some flux ropes. We normalized the front apex to 1 AU. The sheath thickness, ≈0.1 AU (Sect. 3.2, Fig. 7), was added radially to the FR front apex to define the shock apex. Then, the shock shape found in Janvier et al. (2014b), rescaled to the sheath apex, was added. Finally, we note that all observations were made at 1 AU, while Fig. 11 shows the FR, sheath, and shock around 1 AU. To draw Fig. 11 we assumed that their shapes are not significantly modified around 1 AU (only rescaled by a factor so that  is not changed). This hypothesis is stronger for high λ values with few detected cases so that the axis and shock shapes are less constrained by observations for higher λ values.
is not changed). This hypothesis is stronger for high λ values with few detected cases so that the axis and shock shapes are less constrained by observations for higher λ values.
We show an elliptical shape for the FR cross section with an intermediate aspect ratio of 2 in Fig. 11b. We included the sheath thickness at the apex as explained above, as well as the same shock shape (assuming axisymmetry).
A configuration qualitatively comparable to Fig. 11a was first derived from multi-spacecraft crossings of a single MC by Burlaga et al. (1990). Such favorable observations with multi-spacecraft crossings remain rare, however, because there are only a few spacecraft at most. Moreover, the various methods for reconstructing the FR from in situ data are prone to large uncertainties. Recent studies conducted by different authors have reached different conclusions on the axis shape even when the same multi-spacecraft data of an MC observed with favorable conditions were analyzed. For example, the differing results of Farrugia et al. (2011) and Ruffenach et al. (2012) on the axis shape are compared in Fig. 3 of Démoulin (2014). In contrast, our statistical approach allows us to minimize these uncertainties on the axis and shock normal directions and to derive a quantitative generic configuration for ICMEs (Fig. 11).
The result of Fig. 11 is also qualitatively comparable to the expected features of coronal mass ejections as frequently sketched (e.g., Zurbuchen & Richardson 2006, and references therein). However, our model, which is directly derived from observational data, differs quantitatively in the shapes of the different ICME components.
We emphasize that the FR axis and shock shapes are consistent with each other in Fig. 11 even though they are derived from different in situ data and modeling. Furthermore, the typical FR cross-section shape, the FR size, the FR axis, and shock shapes combined together imply a sheath thickness that is nearly independent of λshock, similarly as found from a direct analysis of observations (Fig. 7). This is compatible with the assumption of axisymmetry around the Sun-apex line used in our analysis of the shock shape. In other words, the two principal curvatures of FR boundary are comparable around the apex, then the FR obstacle drives a shock in front with an approximately axisymmetric shape around the FR mean motion direction.
5. Conclusion
Imager data only provide a 2D distribution of the mass density integrated along the line of sight. In situ measurements typically provide the magnetic field and plasma parameters along the 1D trajectory of the crossing spacecraft, while the crossing of the same ICME by several spacecraft is rare. Our understanding of the 3D structure of ICMEs is therefore partial.
In this study, we further developed a statistical approach of the in situ data to derive information on the 3D shape of ICMEs and their components. Since it uses single crossings of a large number of ICMEs, the results can only provide a generic description of the 3D shape, washing out all the peculiarities of single events.
We first investigated the generic shape of the front shock. In previous studies (Janvier et al. 2014b, 2015b) we derived its generic shape assuming a symmetry around the line from the Sun to shock apex, and we showed that an ellipsoid shape was the best-fit model of the shapes we tested to the observed distribution 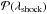 of the location angle λshock (defined in Fig. 1). Here, we tested how an asymmetric shock shape is compatible with the observed distribution of λshock by computing the distributions generated by a shock with a 3D ellipsoid shape. We showed that a stronger elongation of the ellipsoid in one direction can be partly compensated for by a more bent shape in the orthogonal direction for the computed λshock values. The observed
of the location angle λshock (defined in Fig. 1). Here, we tested how an asymmetric shock shape is compatible with the observed distribution of λshock by computing the distributions generated by a shock with a 3D ellipsoid shape. We showed that a stronger elongation of the ellipsoid in one direction can be partly compensated for by a more bent shape in the orthogonal direction for the computed λshock values. The observed 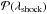 is then compatible with shock shapes with an aspect ratio (in the two orthogonal directions across the propagation direction) lower than or equal to 3, but not significantly higher. Then, the in situ data constrained the asymmetry around the Sun-apex line without determining it.
is then compatible with shock shapes with an aspect ratio (in the two orthogonal directions across the propagation direction) lower than or equal to 3, but not significantly higher. Then, the in situ data constrained the asymmetry around the Sun-apex line without determining it.
In numerical simulations where the ICME apex was directed into a dense and slow solar wind while its sides were located in a fast solar wind, the shock shape was bent around the apex to a degree that it reversed the curvature: the shock surface had a dip around the apex. We tested the implication of such a dipped shock surface on 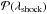 . A flattening of the shock front has already a strong effect on
. A flattening of the shock front has already a strong effect on 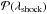 since low λshock values are more frequent because the shock front is flatter. Furthermore, as the dip of the surface is stronger, this effect is present at higher λshock values. This means that flat and even more dipped shock surfaces cannot be generically present in ICMEs, otherwise
since low λshock values are more frequent because the shock front is flatter. Furthermore, as the dip of the surface is stronger, this effect is present at higher λshock values. This means that flat and even more dipped shock surfaces cannot be generically present in ICMEs, otherwise 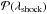 would be different than observed.
would be different than observed.
Next, the location angle λshock provides an estimate of where the shock was crossed by the spacecraft (λshock = 0 at the apex and λshock is a growing function of the distance to the apex). In the same way, λMC (see Fig. 1) provides an estimate of where the spacecraft is crossing the MC along its axis, while the impact parameter pMC provides a comparable information away from the axis. These quantities provide two independent ways, with shock and MC data, to localize the spacecraft trajectory within the encountered ICME. However, because of the large uncertainties on these three parameters, this information can only be used on a statistical basis. This approach allows deriving the generic variations of global ICME quantities along the shock front, the MC axis, and across the axis.
We found that the sheath thickness (1) has a mean value of 0.1 AU (comparable to other studies); (2) strongly varies between cases; and (3) has no global dependence along the FR/shock front within the limits of the observed standard deviation (Fig. 7). Third, the maximum and mean velocities (along the spacecraft crossing) are also almost constant along the shock front, contrary to the expected results of a self-similar expansion model. These uniform velocities were interpreted as the consequence of a strong coupling to the ambient solar wind by the drag force. Finally, we found that the average ICME magnetic field strength is uniform along the FR but decreases across it, as expected by FR models.
With all these results, we finally considered the generic shape of the whole ICME. The ellipsoidal model best fits the observed distributions 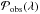 . It defines the axis and shock generic shapes up to the free angular extensions ϕmax,MC and ϕmax,shock (defined in Fig. 1) because
. It defines the axis and shock generic shapes up to the free angular extensions ϕmax,MC and ϕmax,shock (defined in Fig. 1) because  of the ellipsoidal model depends only weakly on this parameter (Janvier et al. 2014b). We related ϕmax,MC to ϕmax,shock using the observed numbers of ICME shocks with and without associated MCs. Next, ϕmax,shock was approximated by the mean angular extension of CMEs observed close to the solar limb (in this way, we minimized projection effects, but with the caveat that the sheath is observed, not the shock). Finally, the mean variation of the flux tube radius with λ and the typical shape of the FR cross section were taken from previous studies (Janvier et al. 2013; Démoulin et al. 2013,respectively). By combining all these results, we established a quantified generic ICME structure comprising a flux rope, a sheath, and an associated shock (Sect. 4). All the parts of this generic model, shown in Fig. 11, are constrained by observations. The results are in the line of some previous studies based on multi-spacecraft observations of one event (e.g., Burlaga et al. 1990; Ruffenach et al. 2012), with the advantage that using a large set of MCs and shocks crossed at various λ allows deriving a quantitative and generic model. As far as we know, this is the first time that a quantitative and generic 3D-shape of ICMEs and their sub-structures is derived from a statistical analysis. The derived ICME model can have several applications, some examples of which we describe below.
of the ellipsoidal model depends only weakly on this parameter (Janvier et al. 2014b). We related ϕmax,MC to ϕmax,shock using the observed numbers of ICME shocks with and without associated MCs. Next, ϕmax,shock was approximated by the mean angular extension of CMEs observed close to the solar limb (in this way, we minimized projection effects, but with the caveat that the sheath is observed, not the shock). Finally, the mean variation of the flux tube radius with λ and the typical shape of the FR cross section were taken from previous studies (Janvier et al. 2013; Démoulin et al. 2013,respectively). By combining all these results, we established a quantified generic ICME structure comprising a flux rope, a sheath, and an associated shock (Sect. 4). All the parts of this generic model, shown in Fig. 11, are constrained by observations. The results are in the line of some previous studies based on multi-spacecraft observations of one event (e.g., Burlaga et al. 1990; Ruffenach et al. 2012), with the advantage that using a large set of MCs and shocks crossed at various λ allows deriving a quantitative and generic model. As far as we know, this is the first time that a quantitative and generic 3D-shape of ICMEs and their sub-structures is derived from a statistical analysis. The derived ICME model can have several applications, some examples of which we describe below.
A first application of our results is to provide constraints for numerical simulations of ICMEs. In particular, the quantitative generic shock, sheath, and axis derived (Fig. 11) provide a landmark to compare with numerical simulations. Furthermore, the shock and FR axis distributions of  of these simulations can be compared with the observed distributions (as derived in Fig. 4 of Janvier et al. 2015b).
of these simulations can be compared with the observed distributions (as derived in Fig. 4 of Janvier et al. 2015b).
Another possible application of the results presented here is linked with the transport of energetic particles in the interplanetary medium. The most energetic solar particles produced during a flare can travel in interplanetary structures near or inside ICMEs (e.g., Masson et al. 2012,and references therein). Then, to improve the knowledge of the transport properties of these solar energetic particles (e.g., their time of travel), it is necessary to know the global shape of the ICME magnetic structure and the length of the FR field lines (Démoulin et al. 2016).
More global implications are related with depletions of Galactic cosmic ray fluxes arriving at Earth in association with the passage of an ICME (e.g., Masías-Meza et al. 2016). Two physical mechanisms are typically thought to explain the depletion of cosmic ray fluxes (which occur in two steps): the deflection of particles by the more intense ICME magnetic field and by the turbulence properties at the ICME shock (the so-called diffusive barrier, e.g., Cane et al. 2000). The quantification of these two effects requires knowing the global structure of ICMEs.
Finally, another application of our results is for space weather. The results summarized in Fig. 11 could be used to develop the ellipse evolution model of Möstl et al. (2015) by incorporating a typical FR and sheath. Depending on the available observations, the parameters of the model could be specific to the event studied, alternatively, the derived generic values found above can be used.
Acknowledgments
We thank the referee for the comments that improved the manuscript. M.J. acknowledges funding from the Northern Research Partnership with travel support to the Observatoire de Paris. S.D. acknowledges partial support from the Argentinian grants UBACyT 20020120100220 (UBA), PICT-2013-1462 (FONCyT-ANPCyT), PIP-CONICET-11220130100439CO, and PIDDEF 2014-2017 number 8. This work was partially supported by a one-month invitation of P.D. to the Instituto de Astronomía y Física del Espacio, and by a one-month invitation of S.D. to the Observatoire de Paris. S.D. is member of the Carrera del Investigador Científico, CONICET.
References
- Abreu, P., Aglietta, M., et al. (Pierre Auger Collaboration) 2011, J. Instrument., 6, 1003 [Google Scholar]
- Asorey, H., Dasso, S., & The LAGO Collaboration 2016, Proc. of Science, in press [Google Scholar]
- Bothmer, V., & Schwenn, R. 1998,Annales Geophysicae, 16, 1 [Google Scholar]
- Burlaga, L., Sittler, E., Mariani, F., & Schwenn, R. 1981, J. Geophys. Res., 86, 6673 [Google Scholar]
- Burlaga, L. F., Lepping, R. P., & Jones, J. A. 1990, in Physics of magnetic flux ropes (Washington DC: American Geophysical Union), 373 [Google Scholar]
- Cabello, I., Cremades, H., Balmaceda, L., & Dohmen, I. 2016, Sol. Phys., 291, 1799 [NASA ADS] [CrossRef] [Google Scholar]
- Cane, H. V., Richardson, I. G., & Cyr, O. C. S. 2000, Geophys. Res. Lett., 27, 3591 [Google Scholar]
- Cremades, H., & Bothmer, V. 2005, in Coronal and Stellar Mass Ejections, eds. K. Dere, J. Wang, & Y. Yan, IAU Symp., 226, 48 [Google Scholar]
- Dasso, S., Mandrini, C. H., Démoulin, P., Luoni, M. L., & Gulisano, A. M. 2005,Adv. Spa. Res., 35, 711 [Google Scholar]
- Dasso, S., Mandrini, C. H., Démoulin, P., & Luoni, M. L. 2006, A&A, 455, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dasso, S., Nakwacki, M. S., Démoulin, P., & Mandrini, C. H. 2007, Sol. Phys., 244, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Dasso, S., Mandrini, C. H., Schmieder, B., et al. 2009, J. Geophys. Res., 114, A02109 [NASA ADS] [CrossRef] [Google Scholar]
- Dasso, S., Asorey, H., & Pierre Auger Collaboration 2012,Adv. Spa. Res., 49, 1563 [Google Scholar]
- Démoulin, P. 2009, Sol. Phys., 257, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Démoulin, P. 2010, Twelfth Int. Solar Wind Conf., 1216, 329 [NASA ADS] [Google Scholar]
- Démoulin, P. 2014, in IAU Symp. 300, eds. B. Schmieder, J.-M. Malherbe, & S. T. Wu, 245 [Google Scholar]
- Démoulin, P., Nakwacki, M. S., Dasso, S., & Mandrini, C. H. 2008, Sol. Phys., 250, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Démoulin, P., Dasso, S., & Janvier, M. 2013, A&A, 550, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Démoulin, P., Janvier, M., & Dasso, S. 2016, Sol. Phys., 291, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Elliott, H. A., McComas, D. J., Schwadron, N. A., et al. 2005, J. Geophys. Res., 110, A04103 [NASA ADS] [CrossRef] [Google Scholar]
- Farrugia, C. J., Berdichevsky, D. B., Möstl, C., et al. 2011, J. Atmos. Sol. Terr. Phys., 73, 1254 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, H. Q., Wu, D. J., Chao, J. K., Lee, L. C., & Lyu, L. H. 2010, J. Geophys. Res., 115, A04107 [NASA ADS] [Google Scholar]
- Forbes, T. G., Linker, J. A., Chen, J., et al. 2006, Space Sci. Rev., 123, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Gosling, J. T., Baker, D. N., Bame, S. J., Feldman, W. C., & Zwickl, R. D. 1987, J. Geophys. Res., 92, 8519 [Google Scholar]
- Gosling, J. T., & McComas, D. J. 1987, Geophys. Res. Lett., 14, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, Q., Qiu, J., & Krucker, S. 2015, J. Geophys. Res., 120, 5266 [Google Scholar]
- Jacobs, C., van der Holst, B., & Poedts, S. 2007, A&A, 470, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janvier, M., Démoulin, P., & Dasso, S. 2013, A&A, 556, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janvier, M., Démoulin, P., & Dasso, S. 2014a, J. Geophys. Res., 119, 7088 [Google Scholar]
- Janvier, M., Démoulin, P., & Dasso, S. 2014b, A&A, 565, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janvier, M., Aulanier, G., & Démoulin, P. 2015a, Sol. Phys., 290, 3425 [NASA ADS] [CrossRef] [Google Scholar]
- Janvier, M., Dasso, S., Démoulin, P., Masías-Meza, J. J., & Lugaz, N. 2015b, J. Geophys. Res., 120, 3328 [CrossRef] [Google Scholar]
- Jian, L., Russell, C. T., Luhmann, J. G., & Skoug, R. M. 2006, Sol. Phys., 239, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Kahler, S. W., Krucker, S., & Szabo, A. 2011, J. Geophys. Res., 116, A01104 [NASA ADS] [CrossRef] [Google Scholar]
- Lai, H. R., Russell, C. T., Jian, L. K., et al. 2012, Sol. Phys., 278, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Lario, D., Haggerty, D. K., Roelof, E. C., et al. 2001, Space Sci. Rev., 97, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Lepping, R. P., & Wu, C. C. 2010, Annales Geophysicae, 28, 1539 [Google Scholar]
- Lepri, S. T., & Zurbuchen, T. H. 2004, J. Geophys. Res., 109, 1112 [CrossRef] [Google Scholar]
- Lepri, S. T., Zurbuchen, T. H., Fisk, L. A., et al. 2001, J. Geophys. Res., 106, 29231 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y. D., Yang, Z., Wang, R., et al. 2014, ApJ, 793, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Lugaz, N., & Farrugia, C. J. 2014, Geophys. Res. Lett., 41, 769 [Google Scholar]
- Lugaz, N., & Roussev, I. 2011, J. Atmos. Sol. Terr. Phys., 73, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- Lugaz, N., Manchester, IV, W. B., Roussev, I. I., Toth, G., & Gombosi, T. I. 2007, ApJ, 659, 788 [Google Scholar]
- Manchester, W. B., Gombosi, T. I., Roussev, I., et al. 2004a, J. Geophys. Res., 109, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Manchester, W. B. I., Gombosi, T. I., Roussev, I., et al. 2004b, J. Geophys. Res., 109, A02107 [Google Scholar]
- Mandrini, C. H., Nakwacki, M., Attrill, G., et al. 2007, Sol. Phys., 244, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Marsden, R. G., Sanderson, T. R., Tranquille, C., Wenzel, K.-P., & Smith, E. J. 1987, J. Geophys. Res., 92, 11009 [NASA ADS] [Google Scholar]
- Marubashi, K., & Lepping, R. P. 2007, Annales Geophysicae, 25, 2453 [Google Scholar]
- Masías-Meza, J. J., Dasso, S., Démoulin, P., Rodriguez, L., & Janvier, M. 2016, A&A, 592, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masson, S., Démoulin, P., Dasso, S., & Klein, K.-L. 2012, A&A, 538, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mitsakou, E., & Moussas, X. 2014, Sol. Phys., 289, 3137 [Google Scholar]
- Möstl, C., & Davies, J. A. 2013, Sol. Phys., 285, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Möstl, C., Farrugia, C. J., Temmer, M., et al. 2009, ApJ, 705, L180 [NASA ADS] [CrossRef] [Google Scholar]
- Möstl, C., Rollett, T., Frahm, R. A., et al. 2015, Nat. Com., 6, 7135 [CrossRef] [Google Scholar]
- Mulligan, T., Blake, J. B., Shaul, D., et al. 2009, J. Geophys. Res., 114, 7105 [CrossRef] [Google Scholar]
- Oh, S. Y., Yi, Y., Nah, J.-K., & Cho, K.-S. 2002, J. Kor. Astron. Soc., 35, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Oh, S. Y., Yi, Y., & Kim, Y. H. 2007, Sol. Phys., 245, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, J. D. 2011,J. Atmos. Sol. Terr. Phys., 73, 1385 [Google Scholar]
- Richardson, I. G., & Cane, H. V. 1995, J. Geophys. Res., 100, 23397 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, I. G., & Cane, H. V. 2010, Sol. Phys., 264, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Riley, P., Linker, J. A., Mikić, Z., et al. 2003, J. Geophys. Res., 108, 1272 [CrossRef] [Google Scholar]
- Robbrecht, E., Berghmans, D., & Van der Linden, R. A. M. 2009, ApJ, 691, 1222 [NASA ADS] [CrossRef] [Google Scholar]
- Rouillard, A. P. 2011,J. Atmos. Sol. Terr. Phys., 73, 1201 [Google Scholar]
- Ruffenach, A., Lavraud, B., Owens, M. J., et al. 2012, J. Geophys. Res., 117, A09101 [NASA ADS] [CrossRef] [Google Scholar]
- Ruffenach, A., Lavraud, B., Farrugia, C. J., et al. 2015, J. Geophys. Res., 120, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Savani, N. P., Owens, M. J., Rouillard, A. P., Forsyth, R. J., & Davies, J. A. 2010, ApJ, 714, L128 [Google Scholar]
- Schmieder, B., Aulanier, G., & Vršnak, B. 2015, Sol. Phys., 290, 3457 [Google Scholar]
- Shen, F., Shen, C., Zhang, J., et al. 2014, J. Geophys. Res., 119, 7128 [Google Scholar]
- Simpson, J. A. 1954, Phys. Rev., 94, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Simpson, J. A. 2000, Space Sci. Rev., 93, 11 [Google Scholar]
- Siscoe, G., & Odstrcil, D. 2008, J. Geophys. Res., 113, A00B07 [Google Scholar]
- Taubenschuss, U., Erkaev, N. V., Biernat, H. K., et al. 2010,Annales Geophysicae, 28, 1075 [Google Scholar]
- Vršnak, B., Žic, T., Vrbanec, D., et al. 2013, Sol. Phys., 285, 295 [Google Scholar]
- Wang, Y. M., Wang, S., & Ye, P. Z. 2002, Sol. Phys., 211, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, C., Li, H., Richardson, J. D., & Kan, J. R. 2010, J. Geophys. Res., 115, A09215 [NASA ADS] [Google Scholar]
- Wang, Y., Chen, C., Gui, B., et al. 2011, J. Geophys. Res., 116, 4104 [Google Scholar]
- Xiong, M., Zheng, H., Wang, Y., & Wang, S. 2006, J. Geophys. Res., 111, A08105 [Google Scholar]
- Yashiro, S., Gopalswamy, N., Michalek, G., et al. 2004, J. Geophys. Res., 109, 7105 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, Y., Feng, X., & Zhao, X. 2014, J. Geophys. Res., 119, 9321 [CrossRef] [Google Scholar]
- Zurbuchen, T. H., & Richardson, I. G. 2006, Space Sci. Rev., 123, 31 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Statistical tests
 |
Fig. A.1 Examples for the three cases c = 0,0.5,1 (from top to bottom) of Eq. (A.1) with the added noise with the StudentT distribution (ν = 2.1) and for three levels of noise (standard deviation σn = 0.1,0.5,1from left to right column). In each panel N = 60 points are selected with a different random seed. The blue straight line is the least-squares fit to the simulated points (in black). The correlation coefficients and the slope of the fitted straight line are written at the top of the panels. |
 |
Fig. A.2 Statistical results for the three cases c = 0,0.5,1 (from top to bottom) of Eq. (A.1) and the added noise with the StudentT distribution (ν = 2.1). The correlation coefficients and the slope of the fitted straight line are plotted as a function of the standard deviation σn of the added noise. The tests, shown in Fig. A.1, are repeated 1000 times with a modified random seed. The means are shown with black lines, and the error range, defined with the standard deviation, is shown with the red lines. |
We analyzed the correlation coefficients and the linear least-squares fits of various parameters in Sects. 3.3 and 3.4 with a limited number of cases (between 59 and 117) and with significant dispersions. To better characterize the results, we test the same statistical tools on models with added noise below.
With the limited number of available data and their dispersion, we cannot hope to derive more than global tendencies. We therefores considered a polynomial function ymod(x) to test the reliability of the Pearson and Spearman correlation coefficients, cp,cs, and of the slope of the linear fit. Since these three coefficients are insensitive to the mean of ymod(x), we skipped the constant of the polynomial. We defined the range of x variations to the normalized interval [0,1]. The y variable was also normalized so that y(1) = 1. We limit ourselves below to a polynomial of second order as it is sufficient to show the strengths and limits of the analysis. These constraints define the model function 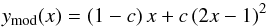 (A.1)where c is a free coefficient. For c = 0, ymod(x) is linear while for c = 1, ymod(x) is a parabola symmetric around the straight line x = 1/2.
(A.1)where c is a free coefficient. For c = 0, ymod(x) is linear while for c = 1, ymod(x) is a parabola symmetric around the straight line x = 1/2.
Next, we defined N values of x randomly selected in the range [0,1] with a uniform distribution. Then, we added noise to ymod(x) with a mean μn = 0 and a given standard deviation σn. We tested three distributions for the random noise: uniform, normal (or Gaussian), and StudentT. They are functions of μn and σn. Only the StudentT distribution has a third parameter called ν, and its standard deviation is ∝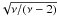 , so that it is defined only for ν> 2. The lower ν, the more extended the distribution tails (they behave as | x−μn | − ν−1).
, so that it is defined only for ν> 2. The lower ν, the more extended the distribution tails (they behave as | x−μn | − ν−1).
To illustrate the effect of outsider points, we selected cases with the StudentT distribution with ν = 2.1 as it has large tails. Different outsiders are present in the panels of Fig. A.1 since the random seeds are different. Comparing this with the results of other distributions (e.g., normal and uniform) with weak or without tails, we found comparable results. For a given noise magnitude, measured by σn, the correlation coefficients decrease less rapidly with σn for lower ν, that is, for distributions with more numerous outsiders and farther away from the mean, as the core of the distribution needs to be narrower to keep the same σn value.
The results derived from the examples shown in Fig. A.1 were checked by running different random distributions and
comparing the plots. Next a statistical analysis was performed by performing ntest cases. The mean and its associated standard deviation of the results are represented in Fig. A.2 with ntest = 1000 and again for the StudentT distribution with ν = 2.1, N = 60, and c = 0,0.5,1.
For a linear model, c = 0, the correlation coefficients detect the linear relation up to σn values about twice higher than the global variation (=1 here). The slope of the fit is more reliable than cp,cs since its mean is close to 1. Its error bar increases linearly with the noise level.
The case with c = 0.5 is also well detected by the correlation coefficients and the slope, also up to σn values about twice higher than the global variation (=0.5 here). The cases with uniform and normal distributions show similar curves, but with a faster decrease with increasing σn so that the threshold of σn is rather comparable to the global variation.
For both cases c = 0 and = 0.5, the Spearman coefficient decreases less rapidly than the Pearson coefficient for increasing σn because the ranks, and not the data values, are considered. The slope is also slightly less dispersed for lower ν. In contrast, Figs. 7–9 have far fewer prominent outsiders, so that their effects is even lower. The outsiders are not a problem in these data.
The case with c = 1 is an extreme case where no global dependence is present (the positive correlation part exactly cancels the negative correlation part). In this case the correlation coefficients and the slope are not able to detect a dependence between the axis variables. However, scatter plots such as in Fig. A.1 do show this dependence up to a noise level σn comparable to the maximal excursion of the function. In this case, the least-squares fit by a polynomial of second order (or higher if needed) would show the underlying dependence. However, since no such dependence is seen in the scatter plots of Figs. 7–9, this approach was not pursued. Still, these data show that there is no global linear trend, up to the limit of the data standard deviation.
To decrease these limitations, more numerous data are needed. For example, repeating the above test with N = 240, the results of Fig. A.2 are reproduced with less strongly fluctuating curves, and the error bars (distance between red curves) are about twice lower. Still, the mean tendency, shown with the black lines, is almost unchanged. We conclude that the results in Figs. 7–9 with N ≈ 60 and those with N ≈ 120 have a similar statistical significance (only a factor 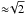 of differrence).
of differrence).
All Figures
 |
Fig. 1 Schema of an MC, its sheath, and its front shock. The MC axis is drawn in blue and its maximum angular extension as viewed from the Sun is 2ϕmax,MC while the shock extends up to 2ϕmax,shock. λ is defined by the angle between the radial direction from the Sun and the axis or the shock normal. |
| In the text | |
 |
Fig. 2 Schema of the front shock in Cartesian coordinates. x is the propagation direction of the following ICME (not represented). λ is defined by the angle between the x direction and the shock normal. |
| In the text | |
 |
Fig. 3 Probability of λ, |
| In the text | |
 |
Fig. 4 Minimization of the difference between shock observations (blue histogram, Wang et al. 2010) and the 3D ellipsoidal model (Sect. 2.1). a) The difference function is defined by Eq. (6) and is plotted as a function of the aspect ratio b/a. b) The theoretical probability for the shock shape described by Eq. (2) and least-squares fitted to the observed distribution is shown for four values of the aspect ratio c/b (=1 for the axisymmetric case). Here, b/a is defined by the minimum of diff(obs.,mod.) of panel a) with the curve of the same color. |
| In the text | |
 |
Fig. 5 a), b) Theoretical distributions obtained with a 3D ellipsoidal model with a variable dip shape at its front as defined by Eq. (7) and shown in c) with a cut in the x-y plane. The color curves are for different dip depths (parameter d). a) The front is asymmetric around the x axis (direction of CME propagation) and b) the dip has no dependence on y. For all curves b/a = 1.4 and c/b = 1. |
| In the text | |
 |
Fig. 6 Correlations between the maximum velocity, Vmax, within ICMEs and the size of their sheaths, Ssha); and their sizes, Sicmeb), for the ICMEs studied by Richardson & Cane (2010) and those with a front shock studied by Wang et al. (2010). The blue straight line is the least-squares fit to the data points (black points). cp and cs are the Pearson and Spearman correlation coefficients, and σ is the standard deviation of the ordinate. |
| In the text | |
 |
Fig. 7 Variation of the sheath size, Ssh, along: a) the MC axis (| λMC |); b) across the MC axis (| pMC |); and c) along the shock (λshock). The drawing convention and added parameters are the same as in Fig. 6. Panels a) and b) are for the MCs of Lepping’s list, and panel c) shows the shocks studied by Wang et al. (2010). Both sets were associated with the ICMEs studied by Richardson & Cane (2010). The panels show that there is no global dependence on Ssh along and across the flux rope or along the shock. |
| In the text | |
 |
Fig. 8 Variation of the maximum radial velocity, Vmax, measured after the sheath within the ICME. The dependence is shown: a) along the MC axis (| λMC |); b) across the MC axis (| pMC |); and c) along the shock (λshock). The drawing convention and added parameters are the same as in Fig. 6. The graphs show that Vmax is independent of the crossing location. The red, green, and pink lines indicate the expectation of a self-similar expansion model (see Sect. 3.4). |
| In the text | |
 |
Fig. 9 Variation of the mean field strength, ⟨ Bicme ⟩, measured after the sheath within the ICME. The dependence is shown: a) along the MC axis (| λMC |); b) across the MC axis (| pMC |); and c) along the shock (λshock). The drawing convention and added parameters are the same as in Fig. 6. ⟨ Bicme ⟩ is uniform on average along the MC axis (| λMC |) and along the shock front (λshock), while ⟨ Bicme ⟩ decreases across the MC axis (| pMC |), as expected (stronger magnetic field in the MC core). |
| In the text | |
 |
Fig. 10 ϕmax,MC in function of ϕmax,shock from Eq. (11). NFR with shock is estimated with the number of detected MCs (45) and Nshock is the total number of front ICME shocks (216) detected during the same period of time. The curves are for the shock-surface aspect ratio c/b defined in Fig. 2. |
| In the text | |
 |
Fig. 11 Summary of the results of the axis and shock shapes providing a quantitative version of the sketch drawn in Fig. 1. a) Cut in the plane of the FR axis and b) cut in the plane orthogonal to the axis plane at the apex. ϕmax,shock is the only free parameter, set here to 30°. ϕmax,MC = 20° is estimated from Eq. (11) with NFR = 45 (Fig. 10). The aspect ratio b/a = 1.2 and 1.3 for axis and shock, respectively, are mean values of the results of Janvier et al. (2014b). At the apex, the sheath thickness is set to the mean value of 0.1 AU, but it is very case dependent (Fig. 7). The radial FR extension is deduced from Janvier et al. (2014b). The FR cross section is elliptic with an aspect ratio of 2 as estimated by Démoulin et al. (2013). The FR front is set at 1 AU, with the axis and shock shapes rescaled by their apex distances (0.87 and 1.1 AU, respectively). The two dotted lines mark the radial distance to the Sun at 0.5 and 1 AU. |
| In the text | |
 |
Fig. A.1 Examples for the three cases c = 0,0.5,1 (from top to bottom) of Eq. (A.1) with the added noise with the StudentT distribution (ν = 2.1) and for three levels of noise (standard deviation σn = 0.1,0.5,1from left to right column). In each panel N = 60 points are selected with a different random seed. The blue straight line is the least-squares fit to the simulated points (in black). The correlation coefficients and the slope of the fitted straight line are written at the top of the panels. |
| In the text | |
 |
Fig. A.2 Statistical results for the three cases c = 0,0.5,1 (from top to bottom) of Eq. (A.1) and the added noise with the StudentT distribution (ν = 2.1). The correlation coefficients and the slope of the fitted straight line are plotted as a function of the standard deviation σn of the added noise. The tests, shown in Fig. A.1, are repeated 1000 times with a modified random seed. The means are shown with black lines, and the error range, defined with the standard deviation, is shown with the red lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


