| Issue |
A&A
Volume 594, October 2016
|
|
|---|---|---|
| Article Number | A103 | |
| Number of page(s) | 6 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201527917 | |
| Published online | 19 October 2016 | |
Observed and simulated power spectra of kinetic and magnetic energy retrieved with 2D inversions
1 Max-Planck-Institut für
Sonnensystemforschung, Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany
e-mail: danilovic@mps.mpg.de
2 High Altitude Observatory,
NCAR, PO Box 3000,
Boulder, CO
80307,
USA
Received:
8
December
2015
Accepted:
18
July
2016
Context. Information on the origin of internetwork magnetic field is hidden at the smallest spatial scales.
Aims. We try to retrieve the power spectra with certainty to the highest spatial frequencies allowed by current instrumentation.
Methods. To accomplish this, we use a 2D inversion code that is able to recover information up to the instrumental diffraction limit.
Results. The retrieved power spectra have shallow slopes that extend further down to much smaller scales than has been found before. They do not seem to show any power law. The observed slopes at subgranular scales agree with those obtained from recent local dynamo simulations. Small differences are found for the vertical component of kinetic energy that suggest that observations suffer from an instrumental effect that is not taken into account.
Conclusions. Local dynamo simulations quantitatively reproduce the observed magnetic energy power spectra on the scales of granulation down to the resolution limit of Hinode/SP, within the error bars inflicted by the method used and the instrumental effects replicated.
Key words: Sun: granulation / Sun: photosphere / Sun: magnetic fields
© ESO 2016
1. Introduction
Recent high-resolution observations, together with state-of-the-art magneto-hydrodynamic (MHD) simulations reinforced the hypothesis, first suggested by Petrovay & Szakaly (1993), that the small-scale dynamo is the dominant source of magnetic field in internetwork regions. Only indirect support was offered so far. It was shown that a small-scale dynamo can be efficiently sustained in strongly stratified, compressible, and nonhelical surface convection without enforced recirculation (Vögler & Schüssler 2007; Pietarila Graham et al. 2010). The overall structure of the magnetic field resulting from such an action seems to agree with observations, but fall short by about a factor of 2−3 in field strength (Schüssler & Vögler 2008; Danilovic et al. 2010). Small-scale dynamo solutions, which are in agreement with the field strength implied by observations, require a setup that mimics a deep magnetized convection zone and account for an upward directed Poynting flux in upflow regions at the bottom boundary (Rempel 2014). Additional support for a small-scale dynamo comes from observations in which it has been shown that the mean unsigned magnetic flux in the internetwork is not dependent on the solar cycle or location on the solar disk (Trujillo Bueno et al. 2004; Bühler et al. 2013). Furthermore, the net flux imbalance in internetwork is not correlated to the surrounding network (Lites 2011).
Demonstrating small-scale dynamo action is difficult. If the dynamo was operating in the kinematic regime, it would be sufficient to demonstrate that the magnetic power spectrum peaks at scales smaller than the kinetic power spectrum (Abramenko et al. 2012). However, in the saturated state, such as we find in most astrophysical contexts, the power in both the magnetic field and velocity moves to larger wavelengths and the peak in the magnetic power spectrum no longer needs to be at smaller wavelengths than the peak in the kinetic energy power spectrum (Moll et al. 2011). Nonetheless, the power spectra remain an important diagnostic, but retrieving them is in itself a challenging task. One is not only limited by instrumental effects, but also by methods and diagnostics used to obtain information on velocity and magnetic fields. Recent studies (Abramenko et al. 2001, 2012; Katsukawa & Orozco Suárez 2012; Stenflo 2012, and references therein) showed that the shallow magnetic energy spectrum tends to extend toward higher wavenumbers as the spatial resolution of the instrumentation improves, but the slope remains steep at subgranular scales.
The largest slope value of approximately −1 was fitted by Katsukawa & Orozco Suárez (2012), who accounted for the modulation transfer function (MTF) of the instrument. In their study, a simple deconvolution was applied that is not directly to the observables, but to the derivatives, such as proxies for line-of-sight (LOS) velocity and magnetic flux densities.
In this paper, we perform a power spectral analysis on the same Hinode/SP (Lites et al. 2001; Kosugi et al. 2007) data, but we use 2D inversions (van Noort 2012) to retrieve the magnetic field and the LOS velocity. As demonstrated by van Noort (2012), the advantage of this code over the simple deconvolution is that it uses the information contained in the full observed spectral range simultaneously. In this way, the 2D inversions are not only able to retrieve the information up to the instrumental diffraction limit, but also to minimize the influence of noise on the retrieved highest spatial frequencies. In Danilovic et al. (2016), we tested the code on three different simulations that give the same level of spectropolarimetric signals as the quiet Sun observations. We showed that the inversion code behaves well when a certain combination of node positions is chosen. We demonstrated that, in this case, the code is able to retrieve the overall distributions of the field strength and inclination.
In this paper we concentrate on kinetic and magnetic power spectra. We use the comprehensive MHD simulations to estimate how well and in what case can we recover the power spectra correctly. We also quantitatively compare our results with those obtained by Katsukawa & Orozco Suárez (2012).
2. Test on MHD simulations
We take two different local dynamo simulations produced by the MURaM code (Vögler et al. 2005). The first, called Sim 1 here, is the Run G (Rm ~ 5200) that was previously used in Danilovic et al. (2010) and Pietarila Graham et al. (2009, 2010). This run covers 4.86 × 1.4 × 4.86 Mm with the resolution of 5 km. It simulates dynamo action without any magnetic flux coming through the bottom boundary. Because of this, it reaches lower magnetic energy in the saturation phase than was necessary to quantitatively reproduce the observations. For this reason, we multiply the field strength by a factor of 2, following the same argument as in Danilovic et al. (2010). We also use one snapshot from the most recent local dynamo simulation (hereafter Sim 2), which takes into account the coupling between the top layers with the bulk of the convection zone (Rempel 2014). The computational domain, in this case, is 24 × 7.68 × 24 Mm, with about 1.5 Mm above τ500 = 1, and a resolution of 16 km in both the horizontal and vertical direction. This run uses an open bottom boundary condition that allows the presence of (small-scale) horizontal field in upflow regions in an attempt to mimic a deep magnetized convection zone that was implemented through a symmetric boundary condition for all three magnetic field components. It was shown by Rempel (2014) that only such a boundary condition or alternatively a closed bottom boundary with complete recirculation leads to the observationally inferred field strength of the quiet sun. In this case, the mean unsigned vertical field strength at τ = 1 is approximately 60 G.
 |
Fig. 1 Probability density functions (PDFs) for the longitudinal (upper panel) and transverse (lower panel) apparent magnetic flux density. PDFs from MHD simulations reduced to Hinode resolution (Sim1: black plus signs and Sim2: blue plus signs) are compared with the PDFs obtained from observations (red solid line). |
 |
Fig. 2 Sim 2: power spectra of the vertical component of kinetic (top panel) and magnetic energy (middle panel) and power spectra of the total magnetic energy (bottom panel). Blue lines indicate the original spectra before any spatial smearing at different heights (log τ = 0 solid and −2.0 dashed). Purple lines show the result of 2D inversions at the same optical depths. Black lines indicate spectra of the corresponding parameters obtained from Solarsoft routines (see the text) before (dashed line) and after (solid line) spatial smearing. Vertical line represent the resolution limit of Hinode/SP. |
Figure 1 shows the comparison of the synthesized observables and the Hinode/SP deep magnetogram observations. The simulations are treated in the same way as in Danilovic et al. (2010). After taking all instrumental effects into account, the longitudinal and transverse flux densities are calculated using the Solarsoft procedure (Lites & Ichimoto 2013). Figure 1 shows the comparison with data set II from Danilovic et al. (2010), where the noise level was reduced to 3 × 10-4Ic by extending the effective exposure time. The x-axis is chosen to be logarithmic so that distribution in the hG field range would be better visible and the results consistent with Danilovic et al. (2010). However, the values below the noise level (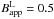 G and
G and 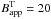 G) should be disregarded. The figure show that, compared to the local dynamo simulations with conservative boundary conditions (Sim 1), the snapshot of Sim 2 provides a better match to the observed magnetic flux densities. The tails of the observed distributions are better reproduced because of the deeper lower boundary that permits formation of stronger magnetic structures on larger spatial scales.
G) should be disregarded. The figure show that, compared to the local dynamo simulations with conservative boundary conditions (Sim 1), the snapshot of Sim 2 provides a better match to the observed magnetic flux densities. The tails of the observed distributions are better reproduced because of the deeper lower boundary that permits formation of stronger magnetic structures on larger spatial scales.
To retrieve the magnetic field and velocity from simulated observations, we used the same strategy as in Danilovic et al. (2016). The fitted model is described as a height dependent atmosphere at three nodes in optical depth with the following free parameters: temperature, magnetic field strength, magnetic field inclination with respect to the (LOS), azimuth of the magnetic field vector, LOS velocity, and a microturbulent velocity. The nodes are placed at log τ = 0, −0.8 and −2.0. This proved to give recovered velocity, field strength, and inclination closest to the original.
Figure 2 shows the original kinetic and magnetic energy power spectra, and the corresponding spectra retrieved with a 2D inversion. Since the full velocity field cannot be obtained from Hinode/SP maps, only the part associated with the vertical component 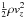 is discussed here. A similar plot is added for the vertical component of the magnetic energy to compare it to the results obtained in previous studies. For reference, Fig. 2 shows the same quantities derived by applying the standard sp_prep Solarsoft routines, which obtain the LOS velocity by fitting the Fe I 630.15 nm line and the apparent magnetic flux using the approximation given in Lites et al. (2008), to both unsmeared and instrumentally degraded simulated data.
is discussed here. A similar plot is added for the vertical component of the magnetic energy to compare it to the results obtained in previous studies. For reference, Fig. 2 shows the same quantities derived by applying the standard sp_prep Solarsoft routines, which obtain the LOS velocity by fitting the Fe I 630.15 nm line and the apparent magnetic flux using the approximation given in Lites et al. (2008), to both unsmeared and instrumentally degraded simulated data.
Since the core of the Fe I 630.15 nm line is formed fairly high, it is not a surprise that the power spectrum of the velocity obtained by fitting the core sits closer to the curve showing the power spectrum of the velocity at log τ = −2.0 than that at optical depth unity. The curves are not strictly parallel, which could be due to variations in the formation height of the Fe I 630.15 nm line core. After taking the instrumental spatial resolution into account, the slope at the subgranular scales becomes steep with a power-law index close to −4.5 as found by Katsukawa & Orozco Suárez (2012).
Similarly, the longitudinal apparent magnetic flux density shows significantly reduced power at subgranular scales after spatial smearing with a power-law index close to −2.7, in agreement with observations (Katsukawa & Orozco Suárez 2012). At the original resolution, the curve sits lower than the curve corresponding to the longitudinal component of magnetic field at log τ = −2.0. Given that the procedure for calculating the apparent flux density takes the full spectral range of Hinode/SP into account, it is hard to specify the height that the values correspond to without performing a detailed analysis. The power spectra suggest that the procedure seems to underestimate the field strength at all spatial scales.
The red curves in Fig. 2 show the result of a 2D inversion applied to a simulation snapshot. All parameters are retrieved well up to the resolution limit, but they diverge rapidly from the original beyond the smallest spatial scales (approximately around 250 km in this case). This is where the diffraction limit is located and thus no information on spatial frequencies higher than this is contained in the data. The departure from the original curve happens a bit sooner for the vertical component of velocity at log τ = −2.0. We ascribe this to the highly complex stratification of some of the simulated atmospheres, which cannot be always retrieved by an inversion that fits the physical quantities at only 3 nodes and/or to the low signal-to-noise ratio in the line core.
Fitting a slope of the power spectra can be very tricky and misleading as shown by Nordlund et al. (1997). To be on the safe side, a clear behavior over at least an order of magnitude for the whole time series is needed. Taken that we clearly do not have such a case, we deduce that none of the retrieved power spectra seem to follow a clear power law, but we give indices just to have some quantitative measure of the slopes. If we take the spatial scales around 1 Mm-1, we get −1.8 for the LOS kinetic energy power spectrum and a positive slope of 0.13 for the longitudinal component of the magnetic energy. Also, the transverse component of the magnetic field increases the power at both the largest and smallest spatial scales and makes the slope slightly negative, around −0.73 for the total magnetic energy, in good agreement with the slope of the original distribution.
In Danilovic et al. (2016), we tested how a slight change of the defocus accounted in the point spread function (PSF) affects the retrieved distributions of the field strength and inclination. We chose three different PSFs to estimate the impact. The first PSF assumed a defocus of seven steps away from the optimal focus position, which brings the simulated continuum contrast to the observed value, as shown in Danilovic et al. (2008). This PSF is also a reference PSF because it is also used to spatially smear the synthesized Stokes profiles and produce the simulated Hinode observations. The other two PSFs assumed a defocus that is ± 4 defocus steps away from the reference in both directions, i.e., toward the optimal focus position and away from it. When the defocus value that was accounted for in the PSF used in 2D inversion was changed by four defocus steps, the effect on the retrieved distributions of the field strength and inclination is found to be minimal. In this case, the impact was the largest in the weak end of the field strength distribution, where the field strengths were underestimated when the PSF used in the inversion is too compact. When looking at the power spectra, however, when the PSF used to invert the data is slightly wrong, the recovered power spectra diverge significantly from the original, especially for the velocity. Figure 3 shows the difference when the same test is applied on the power spectra. An underestimate of the width of the PSF, i.e. assuming PSF with a defocus that is four defocus steps smaller than it should be, leads to less magnetic power recovered on the granular and subgranular scales. At the same time, accounting for the wider PSF results in an overestimate at the same spatial scales. The kinetic power spectrum follows the same pattern, where the sensitivity to an underestimate of the width of the PSF seems to be larger than that to an overestimate.
Another potential source of systematic error is temporal averaging due to the finite exposure time, which has to be taken into account when comparing with observations. Figure 4 shows what happens with the retrieved power spectra after temporal averaging, demonstrated on Sim 1. As in Danilovic et al. (2016), we choose to integrate over 20 s, 2 min and 9 min. The upper panel shows the range of power coming from the quasi-periodic oscillations in the simulations. Every gray curve corresponds to the instantaneous original spectra obtained from each snapshot produced over the 10 min long run.
 |
Fig. 3 Sim 2: dependence of the inversion results on the PSF used. Power spectra of the vertical component of kinetic (top panel) and magnetic energy (middle panel) and power spectra of the total magnetic energy (bottom panel). Purple lines indicate the spectra inverted with the correct PSF. Solid and dashed lines correspond to different heights, log τ = 0 and −2.0, respectively. Blue and green lines show the result when the defocus accounted for is 4 defocus steps less or more, respectively, than the defocus used in degradation. |
 |
Fig. 4 Sim 1: influence of temporal averaging on the power spectra of the vertical component of kinetic (top panel) and magnetic energy (middle panel) and power spectra of the total magnetic energy (bottom panel). Different colors indidcate the power spectra obtained after integration over 0 s, 20 s, 2 min, and 9 min as denoted in the legend. |
 |
Fig. 5 Observations: power spectra of the vertical component of kinetic (top panel) and magnetic energy (middle panel) and power spectra of the total magnetic energy (bottom panel). Green lines indciate the results of 2D inversions at different heights (log τ = 0 solid and −2.0 dashed). Black lines represent spectra of the corresponding parameters obtained from Solarsoft routines (see the text). Purple lines indicate the curves obtained from Sim 2 (purple curves in Fig. 2). |
For the vertical components of the kinetic and magnetic energy, the temporal averaging reduces the power and steepens the slopes. When averaging over up to 2 min, the differences in the power spectra are visible only on subgranular scales. Continued averaging in time tends to shift the curves downward on all spatial scales, which are similar to the results of Kitiashvili et al. (2012) for horizontal velocities. The opposite effect is visible in the power spectra of magnetic energy. An increase in power comes from the horizontal component of magnetic field, whose contribution grows with exposure time, as found by Danilovic et al. (2016).
3. Power spectra of internetwork
We take the scan used in various studies starting with Lites et al. (2008) and Orozco Suárez et al. (2007a,b). This scan is obtained in normal mode with an exposure time of 4.8 s on March 10th 2007 between 11:37 and 14:37 UT. Since we are mainly interested in small scales, we limit our study to a small part of the whole scan, 70″ × 70″ wide. The power spectra of the parameters retrieved with a 2D inversion are shown in Fig. 5. Power spectra calculated from simulations are also overplotted. The parameters derived with the Solarsoft routines, applied to observations, show the same slopes as obtained by Katsukawa & Orozco Suárez (2012).
All the curves retrieved from observations have similar slopes as those from simulations. Although it appears to have the same slope, the observed velocity power spectrum differs considerably from the simulated power spectrum at granular and subgranular scales. The difference is slightly smaller for an optical depth of 0.01. The most obvious explanation for this is the presence of p-mode oscillations in the observations that cannot be easily filtered out from the scanned maps. Figure 4, on the other hand, shows that periodic osculations in the simulations result in a much smaller scatter of the kinetic energy power spectra, hence the difference we see in the observed and simulated power might be too big to be explained with p-mode oscillations alone. Additionally, the observed velocity power spectrum shows a strange plateau around the resolution limit. Given that the same feature is somewhat less visible but still present in the magnetic spectra, we are prone to conclude that this could be due to some instrumental effect that we did not take into account, for example, JPEG compression or some other source of noise not introduced in the simulations. Furthermore, the reduced power in the observed velocity power spectrum on the granular and subgranular scales might be due to a small error in the PSF used in the inversion. As demonstrated in Fig. 3, an over- or underestimate of the width of the PSF can result in a kinetic power spectrum with the observed slope.
Another, but smaller difference can be seen in the power spectrum of the vertical component of the magnetic field. The simulated and observed power spectra seem to diverge for spatial scales larger than the granular scale. The observed spectrum shows more power at these scales, which changes the slope from slightly positive to slightly negative. The difference comes from the strong network visible in the observed maps, but not present in simulations. Rempel (2014) showed that increasing the simulation domain size (both vertically and horizontally) leads to an increase of power on scales larger than granulation.
4. Conclusions
Applying a 2D inversion code to spectra synthesized from MHD simulated snapshots showed that all atmospheric parameters can be retrieved reliably up to the diffraction limit of the telescope when all instrumental effects are properly taken into account. The power spectra are recovered to much smaller spatial scales than any other method used before and are not significantly affected by the limited spatial resolution. Although we cannot claim that any of the spectra follow a power law, we find slopes that are much more gentle at subgranular scales than previous studies. The observed magnetic power spectra follow closely the power spectra obtained from the most recent local dynamo runs, however, a mismatch of the observed and simulated kinetic power spectra was still observed. The inherent sensitivity of this quantity to the instrumental properties suggests that perhaps some inaccuracies in the instrumental properties still remain. Although state-of-the-art simulations show that the effect of small-scale dynamo action has its peak at scales comparable to the resolution limit of Hinode, looking at smaller scales is of course still desirable. However, as the present study shows, to gain a reliable information on these scales, having an optical system whose properties are well known is essential.
Acknowledgments
The National Center for Atmospheric Research (NCAR) is sponsored by the National Science Foundation. We would like to acknowledge high-performance computing support from Yellowstone (http://n2t.net/ark:/85065/d7wd3xhc) provided by NCAR’s Computational and Information Systems Laboratory, sponsored by the National Science Foundation. Hinode is a Japanese mission developed and launched by ISAS/JAXA, with NAOJ as domestic partner and NASA and STFC (UK) as international partners. It is operated by these agencies in co-operation with ESA and NSC (Norway).
References
- Abramenko, V., Yurchyshyn, V., Wang, H., & Goode, P. R. 2001, Sol. Phys., 201, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Abramenko, V., Yurchyshyn, V., & Goode, P. R. 2012, 4th Hinode Science Meeting: Unsolved Problems and Recent Insights, 455, 17 [Google Scholar]
- Bühler, D., Lagg, A., & Solanki, S. K. 2013, A&A, 555, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovic, S., Gandorfer, A., Lagg, A., et al. 2008, A&A, 484, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovic, S., Schüssler, M., & Solanki, S. K. 2010, A&A, 509, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovic, S., van Noort, M., & Rempel, M. 2016, A&A, 593, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Katsukawa, Y., & OrozcoSuárez, D. 2012, ApJ, 758, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Kitiashvili, I., Abramenko, V., Goode, P. R., et al. 2012, IAU Special Session, 6, E1 [Google Scholar]
- Knobloch, E., & Rosner, R. 1981, ApJ, 247, 300 [NASA ADS] [CrossRef] [Google Scholar]
- Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W. 2011, ApJ, 737, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W., & Ichimoto, K. 2013, Sol. Phys., 283, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W., Elmore, D. F., & Streander, K. V. 2001, in Advanced Solar Polarimetry – Theory, Observation, and Instrumentation, ed. M. Sigwarth, ASP Conf. Ser., 236, 33 [NASA ADS] [Google Scholar]
- Lites, B. W., Kubo, M., Socas-Navaro, H., et al. 2008, ApJ, 672, 1237 [NASA ADS] [CrossRef] [Google Scholar]
- Moll, R., Pietari la Graham, J., Pratt, J., et al. 2011, ApJ, 736, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Nordlund, A., Spruit, H. C., Ludwig, H.-G., & Trampedach, R. 1997, A&A, 328, 229 [NASA ADS] [Google Scholar]
- Orozco Suárez, D., Bellot Rubio, L. R., Del Toro Iniesta, J. C., et al. 2007a, PASJ, 59, 837 [Google Scholar]
- Orozco Suárez, D., Bellot Rubio, L. R., del Toro Iniesta, J. C., et al. 2007b, ApJ, 670, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Petrovay, K., & Szakaly, G. 1993, A&A, 274, 543 [Google Scholar]
- Pietari la Graham, J., Danilovic, S., & Schüssler, M. 2009, ApJ, 693, 1728 [Google Scholar]
- Pietari la Graham, J., Cameron, R., & Schüssler, M. 2010, ApJ, 714, 1606 [NASA ADS] [CrossRef] [Google Scholar]
- Rempel, M. 2014, ApJ, 789, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Schüssler, M., Vögler, A. 2008, A&A, 481, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stenflo, J. O. 2012, A&A, 541, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trujillo Bueno, J., Shchukina, N., & Asensio Ramos, A. 2004, Nature, 430, 326 [Google Scholar]
- van Noort, M. 2012, A&A, 548, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vögler, A. & Schüssler, M. 2007, A&A, 465, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vögler, A., Shelyag, S., Schüssler, M., Cattaneo, F., Emonet, T., & Linde, T. 2005, A&A, 429, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Probability density functions (PDFs) for the longitudinal (upper panel) and transverse (lower panel) apparent magnetic flux density. PDFs from MHD simulations reduced to Hinode resolution (Sim1: black plus signs and Sim2: blue plus signs) are compared with the PDFs obtained from observations (red solid line). |
| In the text | |
 |
Fig. 2 Sim 2: power spectra of the vertical component of kinetic (top panel) and magnetic energy (middle panel) and power spectra of the total magnetic energy (bottom panel). Blue lines indicate the original spectra before any spatial smearing at different heights (log τ = 0 solid and −2.0 dashed). Purple lines show the result of 2D inversions at the same optical depths. Black lines indicate spectra of the corresponding parameters obtained from Solarsoft routines (see the text) before (dashed line) and after (solid line) spatial smearing. Vertical line represent the resolution limit of Hinode/SP. |
| In the text | |
 |
Fig. 3 Sim 2: dependence of the inversion results on the PSF used. Power spectra of the vertical component of kinetic (top panel) and magnetic energy (middle panel) and power spectra of the total magnetic energy (bottom panel). Purple lines indicate the spectra inverted with the correct PSF. Solid and dashed lines correspond to different heights, log τ = 0 and −2.0, respectively. Blue and green lines show the result when the defocus accounted for is 4 defocus steps less or more, respectively, than the defocus used in degradation. |
| In the text | |
 |
Fig. 4 Sim 1: influence of temporal averaging on the power spectra of the vertical component of kinetic (top panel) and magnetic energy (middle panel) and power spectra of the total magnetic energy (bottom panel). Different colors indidcate the power spectra obtained after integration over 0 s, 20 s, 2 min, and 9 min as denoted in the legend. |
| In the text | |
 |
Fig. 5 Observations: power spectra of the vertical component of kinetic (top panel) and magnetic energy (middle panel) and power spectra of the total magnetic energy (bottom panel). Green lines indciate the results of 2D inversions at different heights (log τ = 0 solid and −2.0 dashed). Black lines represent spectra of the corresponding parameters obtained from Solarsoft routines (see the text). Purple lines indicate the curves obtained from Sim 2 (purple curves in Fig. 2). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


