| Issue |
A&A
Volume 593, September 2016
|
|
|---|---|---|
| Article Number | A128 | |
| Number of page(s) | 16 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201628758 | |
| Published online | 05 October 2016 | |
Star-planet interactions
II. Is planet engulfment the origin of fast rotating red giants?
1 Geneva Observatory, University of Geneva, Chemin des Maillettes 51, 1290 Sauverny, Switzerland
e-mail: giovanni.privitera@unige.ch
2 Istituto Ricerche Solari Locarno, via Patocchi, 6605 Locarno-Monti, Switzerland
3 School of Physics, Trinity College Dublin, Dublin 2, Ireland
4 Department of Theoretical Physics, Universidad Autonoma de Madrid, Modulo 8, 28049 Madrid, Spain
Received: 21 April 2016
Accepted: 23 June 2016
Context. Fast rotating red giants in the upper part of the red giant branch have surface velocities that cannot be explained by single star evolution.
Aims. We check whether tides between a star and a planet followed by planet engulfment can indeed accelerate the surface rotation of red giants for a sufficiently long time to produce these fast rotating red giants.
Methods. We studied how the surface rotation velocity at the stellar surface evolves using rotating stellar models, accounting for the redistribution of the angular momentum inside the star by different transport mechanisms, the exchanges of angular momentum between the planet orbit and the star before the engulfment, and for the deposition of angular momentum inside the star at the engulfment. We considered different situations with masses of stars in the range between 1.5 and 2.5 M⊙, masses of the planets between 1 and 15 MJ (Jupiter mass), and initial semimajor axis between 0.5 and 1.5 au. The metallicity Z for our stellar models is 0.02.
Results. We show that the surface velocities reached at the end of the orbital decay due to tidal forces and planet engulfment can be similar to values observed for fast rotating red giants. This surface velocity then decreases when the star evolves along the red giant branch but at a sufficiently slow pace to allowing stars to be detected with such a high velocity. More quantitatively, star-planet interaction can produce a rapid acceleration of the surface of the star, above values equal to 8 km s-1, for periods lasting up to more than 30% the red giant branch phase. As found already by previous works, the changes of the surface carbon isotopic ratios produced by the dilution of the planetary material into the convective envelope is modest. The increase of the lithium abundance due to this effect might be much more important, however lithium may be affected by many different, still uncertain, processes. Thus any lithium measurement can hardly be taken as a support or argument against any star-planet interaction.
Conclusions. The acceleration of the stellar surface to rotation velocities above limits that depend on the surface gravity does appear at the moment to be the clearest signature of a star-planet interaction.
Key words: planetary systems / planet-star interactions / stars: rotation / stars: low-mass
© ESO, 2016
1. Introduction
It is well known that when stars evolve into the red giant branch after the main-sequence phase, the very large expansion of the envelope imposes very low surface rotation velocities. Indeed, early survey of projected rotational velocities vsini (Gray 1981, 1982) showed that giants cooler than about 5000 K are predominantly slow rotators and are characterized by vsini of a few km s-1 (see Fig. 7). However, there exists a small percentage of red giants that present much higher vsini (Fekel & Balachandran 1993; Massarotti et al. 2008; Carlberg et al. 2011; Tayar et al. 2015).
To explain the high rotation rates of (apparently) single red giants, two kinds of scenarios have been proposed. The first scenario involves a mechanism occurring in the star itself. Simon & Drake (1989) proposed that, at the time of the first dredge-up, the surface could be accelerated by the transfer through convection of angular momentum from the central fast spinning regions to the surface. Fekel & Balachandran (1993) explained the high rotation and high lithium abundance they observed in their sample of red giants as resulting from such a scenario. The dredge-up episode would bring to the surface not only angular momentum but also freshly synthesized lithium. It is interesting to underline here that this dredge-up scenario is expected to cause rapid rotation at a particular phase in giant stars evolution, namely when the first dredge-up occurs. In the large sample studied by Carlberg et al. (2011), a clustering of the rapid rotators at this phase (between Teff equal to ~4500 and 5500 K or log Teff between 3.732 and 3.740) is not seen. Moreover, we showed in Privitera et al. (2016) that the dredge-up actually produces no significant acceleration of the surface and thus cannot be a realistic reason for the high surface rotations that we are discussing here.
A second scenario proposed to explain the high rotation rates in giants involves the swallowing of planet (Peterson et al. 1983; Siess & Livio 1999a; Livio & Soker 2002; Massarotti et al. 2008; Carlberg et al. 2009). The phenomenon of planet and brown dwarf ingestion was studied theoretically by Sandquist et al. (1998, 2002) for main-sequence (MS) stars and by Soker et al. (1984), Siess & Livio (1999a,b), and recently by Passy et al. (2012) and Staff et al. (2016) for giant stars. Siess & Livio (1999a,b) studied the accretion of a gaseous planet by a red giant and an asymptotic giant branch star (AGB). They considered cases where the planet is destroyed in the stellar envelope. They focused their study on possible consequences of this engulfment on the luminosity and surface composition of the star. Here we want to study the impact on the surface rotation of the star.
In the first paper of this series (Privitera et al. 2016), we followed the orbital evolution of a planet accounting for all the main effects impacting the orbit, that is changes of masses of the star and the planet, frictional and gravitational drags, and tidal forces, and computed the changes of the stellar rotation due to the planet orbital changes. We used rotating stellar models allowing us to follow the angular momentum transport inside the star in a consistent way. In the present paper, we study what happens when the orbital decay causes the planet to be engulfed by the star. More precisely we address the following questions:
-
By how much can the surface rotation increase through a planetengulfment process?
-
How long is the period during which a rapid surface velocity can be observed after an engulfment?
-
Can the increase of the surface velocity trigger some internal mixing?
-
Are there other signatures in addition to fast surface rotation that are linked to a planet engulfment event?
In Sect. 2, we discuss the physics included in our models. Section 3 presents post-engulfment evolution of various stellar models. Comparisons with observations are discussed in Sect. 4. Finally in Sect. 5 the main results are listed.
2. Ingredients of the models
2.1. The stellar models
The rotating stellar models are computed using the Geneva stellar evolution code (for a detailed description see Eggenberger et al. 2008). Ekström et al. (2012) provides the details about the ingredients of the models, such as nuclear reaction rates, opacities, mass loss rates, initial composition, overshooting, and diffusion coefficients for rotation, and Privitera et al. (2016) explain how the exchanges of angular momentum between the planetary orbit and the star are treated.
The present models allow us to make predictions of the evolution of the surface and the interior velocity resulting from the following processes: shear turbulence and meridional currents in radiative zones, convection, changes of the structure, loss of angular momentum by stellar winds, changes of angular momentum of the star resulting from tidal forces between the star and the planet, and the process of planet engulfment. In convective zones, solid body rotation is assumed, while radial differential rotation can develop in the radiative zone.
2.2. The planet model
Some knowledge of the structure of the planet is needed to determine where, once engulfed, the planet dissolves and deposits its angular momentum into the star. More precisely, we need to know two quantities (see Eq. (2) below): the planet radius, Rpl, and the mean molecular weight of the planet gas, μpl.
The radius of the planet is determined using the mass-radius relation by Zapolsky & Salpeter (1969), ![\begin{equation} R_{\rm pl}\approx 0.105 \left( \frac{2x^{1/4}}{1+x^{1/2}}\right)\ \ [R_{\odot}], \end{equation}](/articles/aa/full_html/2016/09/aa28758-16/aa28758-16-eq10.png) (1)where x = Mpl/ (3.2 × 10-3) and Mpl is the planetary mass given in solar mass.
(1)where x = Mpl/ (3.2 × 10-3) and Mpl is the planetary mass given in solar mass.
The same initial chemical composition is considered for the star and the planet. Here we consider a mass fraction of hydrogen X = 0.707, a mass fraction of helium Y = 0.273, and a mass fraction of the heavy elements Z = 0.02. With that composition, μpl = 0.614. Below, we shall consider different compositions for the planet and star for what concerns carbon and lithium. These changes have however very limited impacts on the value of μpl and are neglected in the estimate of this quantity.
2.3. Physics of the engulfment
In Privitera et al. (2016), given a mass of a star and a mass of the planet, we studied the range of an initial semimajor axis that leads to a planet engulfment along the red giant branch. Now, we need some prescriptions for the fate of the planet inside the star to describe what happens next. According to the work by Soker et al. (1984), planets with masses inferior or equal to about 20 MJ are destroyed in the star. In the present work, we consider only planets with masses equal or below 15 MJ, and therefore we assume that they are destroyed.
 |
Fig. 1 Kippenhahn diagram during the red giant phase. The central radiative zone and the convective envelope are represented by a white area and an area with black dots, respectively. The horizontal axis is the age of the star minus its main-sequence lifetime (tMS). The four lines indicate the limit layers that can be reached by the planets of mass 1 MJ (red solid line), 5 MJ (blue dashed line), 10 MJ (green dash-dotted line), and 15 MJ (continuous cyan line). The vertical dashed lines labelled A, B, and C indicate when the engulfment occurs for the 15 MJ planet at an initial distance of 0.5 au, the 10 MJ planet at an initial distance of 1.0 au, and the 1 MJ planet at an initial distance of 1.5 au, respectively. All the other cases occur between the lines A and C. The left panel corresponds to a model star of 1.5 M⊙ and the right panel to a mass of 2 M⊙. |
We need to know two quantities to be able to compute the impact on the surface velocity of this destruction process. The first quantity is the timescale for the destruction of the planet and the second is the location of this destruction inside the star. For instance, if the destruction occurs in a very short timescale (much shorter than the evolutionary timescale) then, once engulfment occurs, the whole orbital angular momentum of the planet orbit is given to the star in one shot. Moreover, if the destruction occurs in the convective envelope, then this angular momentum can be added in a very simple way to the convective envelope (see below).
2.3.1. Destruction timescale
Livio & Soker (1984) studied the evolution of star-planet systems during the red giant phase. They found that the engulfed planets with masses equal or below 10 MJ are destroyed after a few thousand years (see their Fig. 3). This is very short with respect to the evolutionary timescale during the red giant phase. Indeed, the duration of the first ascent of the red giant branch branch (i.e. before the ignition of helium burning in the core) is 180 Myr for a 1.7 M⊙ star. Therefore, we can consider that the angular momentum that remains in the orbit of the planet at the moment of the engulfment is delivered to the star in one shot.
2.3.2. Where is the angular momentum deposited?
The location of the planet dissolution (i.e. the dissolution point) depends on the physical mechanism that is responsible for this dissolution. We can consider two main mechanisms: thermal and mechanical destruction of the planet. Thermal dissolution is obtained where the virial temperature of the planet becomes lower than the local stellar temperature. The thermal kinetic energy of the stellar material is higher than the binding energy of the planet more deeply beyond this point.
Knowing the internal structure of the star, it is possible to compare the local temperature in the star and the virial temperature of the planet (Siess & Livio 1999a) as follows: ![\begin{equation} T_{\rm v,pl}\sim \frac{GM_{\rm pl}\mu_{\rm pl}m_{\rm H}}{kR_{\rm pl}} \sim 10^5 \mu_{\rm pl} {M_{\rm pl}\over M_{\rm J}} {R_{\rm J} \over R_{\rm pl}}\rm [K] , \label{equa:tvirial} \end{equation}](/articles/aa/full_html/2016/09/aa28758-16/aa28758-16-eq19.png) (2)where k is the Boltzmann constant and MJ, RJ are the mass and radius of Jupiter.
(2)where k is the Boltzmann constant and MJ, RJ are the mass and radius of Jupiter.
Figure 1 indicates the regions where the stellar temperature is equal to the virial temperature of planets of various masses. Also, isothermal lines1 are indicated in Fig. 1. We also indicated by vertical dashed lines the engulfment time of planets of various masses and initial semimajor axes as obtained in Privitera et al. (2016). As indicated in Sect. 2.3.1, the migration time of the planet is very short, thus the destruction of those planets occurs at the intersection of the isothermal line for the planet mass considered with the corresponding vertical lines indicating the time of engulfment (only a few cases are shown for illustration). A few interesting points can be noted from Fig. 1:
-
When the star evolves, the dissolution points reach (in general)deeper layers in the stellar interior. This is a consequence of theexpansion of the envelope during the red giant phase, whichproduces a lowering of the temperature at a given Lagrangianmass. The dissolution point only shifts for a time outwards whenthe star contracts, for example during the bump. This explains thelocal minimum that can be seen for instance for the5 MJ mass planet at a time around 0.08 Gyr for the 2 M⊙ model (right panel of Fig. 1).
-
More massive planets go deeper inside the star. This is of course expected, since a more massive planet requires more extreme conditions to be destroyed than lighter planets.
-
Under the assumptions above, and in the light of Fig. 1, it is reasonable to assume that the planets are destroyed in the convective envelope of the star.
Siess & Livio (1999a) also examined the possibility that when the planet gets closer to the stellar core, tidal effects induce strong distortions of the planet that can destroy it. Using the elongation stress at the centre of the planet as approximated by Soker et al. (1987), we find in most cases that the planet would be destroyed in the convective envelope as is the case when the criterion based on the virial temperature is used. The planet would only be destroyed by tides just below the convective envelope in a few cases. In the following we consider only the criterion based on the virial temperature and thus assume that all our engulfed planets deliver their angular momentum in the convective envelope.
We call ℒpl the angular momentum of the planet orbit at the time of engulfment and ℒ⋆(ce) the angular momentum of the external convective envelope (ce) of the star just before engulfment. To obtain the new angular velocity of the envelope after engulfment, 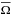 , we write
, we write 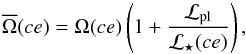 (3)where Ω(ce) is the angular velocity of the convective envelope just before the engulfment.
(3)where Ω(ce) is the angular velocity of the convective envelope just before the engulfment.
Equation (3) assumes that the moment of inertia of the convective envelope is not changed by the planet engulfment process. Actually the engulfment process might add thermal energy in the upper layers of the stellar envelope, making these layers expand for a while. But the excess of energy is rapidly radiated away and thus the star rapidly evolves back to its initial state. Just as a numerical example, in cases in which all the kinetic energy in the planetary orbit of a 15 MJ initially orbiting a 1.7 M⊙ at 0.5 au would be added as an increase of the internal energy in the outer layers, then the excess of energy would be radiated away in about 55 yr, thereby in a very short time compared to the evolutionary timescale.
2.4. Initial conditions considered
We consider stars with initial masses in the range between 1.5 and 2.5 M⊙, with a metallicity Z = 0.02 and an initial rotation equal to Ωini/ Ωcrit = 0.1 and 0.5, where Ωini is the initial angular velocity and Ωcrit the critical angular velocity on the zero age main sequence (ZAMS). These correspond to initial surface velocities of ~30 and 160 km s-1, respectively.
As explained in Privitera et al. (2016), we focused here on stellar masses that are larger or equal to 1.5 M⊙ because stars in this mass range do not have a sufficiently extended outer convective zone to activate a dynamo during the main sequence, so that unless they host a fossile magnetic field, they do not undergo any significant surface magnetic braking. The results obtained in the present work are thus not sensitive to the uncertainties related to the modelling of this braking during the main sequence. In contrast, lower initial mass stars have an extended outer convective zone during the main sequence. Therefore they can activate a dynamo and suffer strong magnetic braking. The evolution of the rotational properties of these lower initial mass stars is then different and will be the topic of another paper in this series (Privitera et al. 2016).
Planets with masses equal to 1, 5, 10, and 15 MJ were considered2. The initial semimajor axes (a0) were taken as equal to 0.5, 1, and 1.5 au and the eccentricities of the orbits are equal to 0. In Privitera et al. (2016), the evolution of the planetary orbit and the star were computed in a consistent way up to the point of engulfment. The end of the computation in Privitera et al. (2016) represents the initial conditions for the present work (see Table A.1).
3. Impact of planet engulfment on surface velocities of red giants
The impact of tides and engulfment on the surface velocity of a red giant depends at least on the following parameters: the mass of the planet, its initial distance to the star, and the mass of the star. Other parameters such as metallicity (which is not discussed here) and rotation (which is discussed here) of the star also affect the results.
 |
Fig. 2 Evolution of the surface velocity as a function of the logarithm of the surface gravity. Dotted (black) lines are for stars without engulfment. Cases for Ω / Ωini = 0.1 and 0.5 are shown. The black long-dashed line (labelled Vmax) corresponds to solid body rotation without engulfment starting with an initial rotation near the critical velocity (see text). Continuous lines correspond to cases with planet engulfment for stars with an initial velocity equal to 10% the critical value and the short-dashed lines correspond to the same cases but for an initial rotation equal to 50% of the critical value. The different colours for solid and dashed lines are for planet masses of 5 (red), 10 (magenta), and 15 MJ (blue) and initial orbital distances of 0.5, 1, and 1.5 au from left to right (see labels). The different panels are for different values of the mass of the star. In the case of 2.5 M⊙, the evolution is pursued until the end of the core He-burning phase, while for lower initial mass stars, the evolution is stopped at the tip of the red giant branch. |
 |
Fig. 3 Left panel: variation of the angular velocity as a function of the Lagrangian mass inside a 1.5 M⊙ model along the red giant branch just before (blue continuous line) and after the engulfment (red dashed line) of a 15 MJ mass planet at an initial distance of 0.5 au from the star. Right panel: evolution of the ratio between the angular velocity of the core and surface angular velocity as a function of the surface gravity along the red giant branch for the same models as in the left panel. |
Figure 2 shows the evolution of the surface equatorial velocities for the present stellar models with and without engulfment of a planet. Tables A.2 and A.3 present some characteristics of the star after an engulfment.
3.1. Planet engulfment by a 1.5 M⊙ star
We begin by discussing the case of the 1.5 M⊙ stellar model (upper left diagram in Fig. 2). The case of an engulfment of a 15 MJ initially at a distance of 0.5 au is considered for the purpose of the discussion. We note several features.
Planet engulfment may have a very strong effect on the surface rotation of a red giant. Compare for instance in the upper left panel, the (black) dotted line that shows the evolution of the surface velocity of a 1.5 M⊙ red giant that began its evolution with an angular velocity equal to 50% of the critical velocity (142 km s-1) and with no planet engulfment, with the (blue) dashed line showing the evolution of the surface velocity of a similar star engulfing a planet. While the isolated star has a surface velocity that remains below 7 km s-1 for log g below 2.8, the star that engulfed the planet shows an extremely rapid increase of the surface velocity up to a maximum value of about 40 km s-1.
The left panel of Fig. 3 shows the variation of the angular velocity inside the 1.5 M⊙ with an initial angular velocity equal to 10% of the critical velocity just before and just after the engulfment of a planet. The angular velocity in the convective zone extending from a mass equal to about 0.3 M⊙ up to the surface has its angular velocity increased by about 1.7 dex (a factor 50). At engulfment (around a log g equal to 2.5), the ratio between the angular velocity of the core and that of the envelope decreases from a value of about 32 000 to a value equal to 1000 (see the right panel of Fig. 3). Then the contrast increases again as a result of the expansion of the envelope and contraction of the core.
The present models cannot account for the small contrast of about one dex between the core and envelope rotation rates that have been obtained by asteroseismology for red giants at the base of the giant branch (Beck et al. 2012; Mosser et al. 2012; Deheuvels et al. 2012, 2014). In that respect, an additional internal angular momentum transport process is missing in the radiative interior of the present models (Eggenberger et al. 2012; Marques et al. 2013; Cantiello et al. 2014). This weakness has however no major impact on the process studied here. The missing transport mechanism would add a fraction of the angular momentum of the core to the envelope, but this does not accelerate the envelope much because the angular momentum in the core is quite small with respect to that contained in the envelope. Therefore the angular momentum coming from the planetary orbit remains in any case that is much larger than the angular momentum of the envelope, and the final result of a planet engulfment would remain nearly unchanged.
After the engulfment, the surface velocity decreases because the stellar envelope continues to expand, but it remains above 8 km s-1 for a time, i.e. nearly 36 Myr (see Table A.3), which means for about 15% of the total duration of the red giant branch phase. No significant changes of the structure of the star (i.e. change of the extent of the convective envelope and/or of the mixing of the chemical elements) is produced by the increase of the rotational speed of the convective envelope. So in our models, any changes of the surface abundances can only be attributed to the dilution of the planet material into the convective envelope. This is briefly investigated in the next section when comparisons with observations are discussed.
In Fig. 2 we also indicated the maximum value for the surface rotation that is expected during the red giant phase (see the black long-dashed line) for a star with no planet. This line has been obtained assuming that the star rotates near the critical velocity on the ZAMS and that a solid body rotation is maintained at every time. This is clearly an extremum. This case of solid body represents an extremum case in terms of efficiency of angular momentum transport and also in terms of surface velocities3. This means that any observed star with initial masses of about 1.5 M⊙ and with a surface velocity that is higher than that given by the curve Vmax in the left upper panel of Fig. 2 needs some acceleration process, which might come either from tidal forces or from an engulfment. We see that for a 1.5 M⊙ star at a metallicity Z = 0.02, this maximum velocity is well below the 40 km s-1 reached by the engulfment of a 15 MJ planet with an initial distance to the star equal to 0.5 au. Therefore planet engulfment may be a sufficiently strong mechanism to produce surface acceleration beyond any reasonable process that can occur in single stars. Of course not just any planet engulfment will produce such strong acceleration, but at least some events can produce surface velocities beyond what can be reasonably explained by single star evolution.
We see that decreasing the initial distance between the star and the planet produces higher surface velocities and longer periods during which high surface rotations can be observed. The main reason for this is that the smaller the initial distance, the engulfment occurrs earlier along the red giant branch. The earlier the engulfment occurs, the smaller the moment of inertia of the convective envelope, and the effect produced by the injection of the planetary angular momentum in the stellar convective envelope is thus more important. We could argue however that the larger the distance, the larger the amount of angular momentum in the planet orbit. However the effect indicated above (the small moment of inertia of the envelope) is the most important and clearly overcomes the effect of the larger angular momentum associated with a larger orbital radius. An interesting consequence of that point was noted already by Carlberg et al. (2009, 2011); planet engulfment produces the largest increases of the surface rotation when the engulfment occurs at the beginning of the red giant branch.
We see also that the higher the mass of the planet, the higher the maximum surface velocity reached (assuming identical initial distance of the planet to the star) and longer the period during which the surface velocity is superior to a given limit (see Tables A.2 and A.3).
If keeping all the other parameters equal, we change the initial rotation of the star, passing from Ωini/ Ωcrit = 0.1 to 0.5, we obtain very similar behaviors. This indicates that the outcome at least in the case of the 1.5 M⊙ does not depend much on the initial rotation of the star.
3.2. Planet engulfment by stars with masses between 1.7 and 2.5 M⊙
 |
Fig. 4 Evolution of the surface velocity of various initial mass stellar models during the red giant phase as a function of the surface gravity. The initial rotations are between 30 and 50 km s-1. Planets have a mass equal to 15 MJ and the orbits have an initial semimajor axis equal to 0.5 au. |
In Fig. 4, the increase of the surface velocity due to a planet engulfment is compared for stars with different initial masses. We see that in general, for a given planet mass and a given initial distance between the star and the planet, the engulfment occurs at a higher surface gravity when the mass of the star decreases. The maximum surface velocities that are reached are higher for lower initial mass stars. We added a track for a one solar mass model to provide a clear illustration of this. As explained in Sect. 2, such a star suffers magnetic braking during the main-sequence phase. This is introduced for the one solar mass model using a solar-calibrated value for the efficiency of this braking. As a result, the surface velocity at the base of the red-giant branch is much lower for the one solar mass model than for stars with higher initial masses. When the engulfment occurs, the acceleration is stronger for this model than for the more massive stars because of the larger ratio between the planetary orbital angular momentum and the stellar envelope angular momentum. Since the 2.5 M⊙ star does not evolve through the He flash, we pursued the evolution during the core He-burning phase. This is why its evolution looks so different from the lower initial mass stars (compare the lower right panel of Fig. 2 with the other panels). Actually, just after the engulfment, we can see a very similar behaviour as those we could see in the other panels. The surface velocity increases nearly vertically at engulfment and after engulfment decreases with surface gravity. When the tip of the red giant branch is reached, the star contracts and the track evolves again at high surface gravities, following first the same path as that used when the star was evolving up the red giant branch, passing again through the same point where engulfment occurred, and evolving to higher surface velocities still when it continues to contract. Most of the core He-burning phase occurs along the extremity of the loop at surface gravities between 2.7 and 3.0. After the core He-burning phase, the envelope of the star expands, the surface gravity decreases, and the star joins the asymptotic giant branch.
Interestingly, the surface velocity during the core He-burning phase remains quite high after an engulfment (above the curve Vmax in the lower right panel of Fig. 2). Therefore, the signature of planet engulfment may remain visible for the whole core He-burning phase. This would likely be the case for lower initial mass stars too that are evolving through a He flash, although this remains to be confirmed by computations.
In general, as was the case for the 1.5 M⊙ star, changing the initial rotation rate of the star does not have a very large impact on the results. We note, however, the very thin loop at engulfment in the lower left panel of Fig. 2 in the case of 2 M⊙ models with an initial rotation equal to 50% the critical angular velocity and with a 15 MJ at initial distance of 0.5 au. For this model, the time of engulfment coincides with the time when the bump occurs. During the bump, the star contracts (hence the increase of the surface gravity seen on Fig. 2). This contraction occurs when the H shell enters the domain whose composition has been enriched in hydrogen by the downwards extension of the external convective zone. As a consequence, the H-burning shell expands and reduces its temperature. By a mirror effect, the envelope contracts provoking an additional increase of the surface velocity and the thin loop that appears at the end of the engulfment process.
3.3. How long does a red giant star remain fast rotating after an engulfment?
 |
Fig. 5 Fraction of the total red giant branch duration spent with a surface equatorial rotation velocity that is higher than 8 km s-1 after an engulfment. Upper left panel: case of a 1.5 M⊙ with an initial rotation Ωini/ Ωcrit = 0.1. Upper right panel: same as the upper left panel, but with Ωini/ Ωcrit = 0.5. Lower left panel: same as the upper left panel, but for a star of mass 2.0 M⊙. Lower right panel: same as the lower left panel, but with Ωini/ Ωcrit = 0.5. |
In the literature, a value of υsini higher than 8 km s-1 is sometimes used as a criterion to qualify a red giant as fast rotating (see e.g. Carlberg et al. 2012). We see on Fig. 2 that indeed higher values than 8 km s-1 would definitively require some interaction with a second body for surface gravities that are smaller than log g equal 2.0 (1.5 M⊙), 2.1 (1.7 M⊙), 2.15 (2 M⊙), and 2.1 (2.5 M⊙). Of course, this does not exclude that stars showing surface velocities below this limit have not undergone any interaction, but in that case, alternative single star models could be proposed to explain the high velocity as well.
Figure 5 shows a synthetic view of the durations of the high surface velocity periods. We see that, for a given stellar model, the duration increases when the initial semimajor axis decreases and the mass of the planet increases (see also Tables A.2 and A.3). The conditions for, let us say, having a high surface velocity during about 10% of the red giant phase are less restricted when the mass of the star passes from 1.5 to 2 M⊙4. The same occurs when, keeping the stellar mass constant; the initial rotation passes from 10 to 50% of the critical velocity, although the impact is less important than changing the initial mass of the star.
3.4. Impact of tidal forces with respect to engulfment
 |
Fig. 6 Evolution of the surface velocity of a 2 M⊙ stellar model during the red giant phase as a function of the luminosity. The initial rotation of the star is 10% of the critical velocity (on the ZAMS). When evolution proceeds, the luminosity in general increases except at the bump visible in the left panel under the form of a small hook. Magenta lines indicate cases without planet engulfment, while blue, green, red, and cyan lines correspond to the engulfment of a planet with a mass equal to 1, 5, 10, and 15 MJ, respectively. The surface velocity reached just before engulfment, i.e. resulting only from tidal forces, is indicated by a small dot. Left panel: the initial semimajor axis is equal to 0.5 au. Right panel: the initial semimajor axis is equal to 1.5 au. |
The physics of what happens during the engulfment is not so well known and thus we may wonder about the reliability of the present results. An interesting point to mention in that context is the fact that the tidal forces may already lead to significant accelerations of the stellar surface. Figure 6 shows the evolution of the surface rotation as a function of the luminosity for a few selected models of 2 M⊙ stars. The small dots along the curves with engulfment indicate the surface velocity reached just before engulfment. The acceleration up to this point is only due to tidal forces. The acceleration after that point is due to the engulfment process itself.
We see that tides alone may be sufficient to accelerate the surface rotation of the star significantly. Since the acceleration due to tides is very rapid (see Privitera et al. 2016), as is the acceleration due to the engulfment, there is no chance that using the rotational velocity of the star to distinguish observationally between tides- and engulfment-acceleration processes, would both occur.
4. Comparisons with observations
The observed sample of Carlberg et al. (2011) (1287 stars) is shown in Fig. 7 superposed on the evolution of the surface velocities for different 2.5 M⊙ models as computed in the present work. A significant number of stars are rotating much faster than what is predicted by these models. An extreme case is the star Tyc5854-011526-1 that has a vsini of 84 km s-1, which corresponds to two-thirds of the critical velocity of a 2.5 M⊙ at the considered effective temperature. In the remainder of this section, we compare our theoretical predictions with the observations of red giants performed by Carlberg et al. (2012). We choose this sample since it gives surface velocities and surface gravities for a significant number of red giants (91 stars). Moreover, it also provides indications for some stars on the 12C/13C ratio at the surface and for lithium abundance. This allows us to check whether stars that are believed to have acquired their high surface rotation as a result of planet engulfment also show some special features in their surface composition.
We do not perform a very detailed analysis since that analysis was already carried out in Carlberg et al. (2012), but we want to address the following questions:
-
Are there among the observed stars, cases that cannot beexplained by single star models?
-
Can the observed surface velocities of such cases be reproduced by invoking a planet engulfment?
-
If yes, is it possible to deduce the initial conditions required to explain these systems by a planet engulfment?
-
Is there any chance of seeing some signatures of the planet engulfment in the surface composition?
Before investigating these points based on the present computations, we must see whether the metallicities and mass range of our stellar models are adequate for a comparison with the sample of Carlberg et al. (2012). For what concerns the metallicity, the correspondence between the metallicity of the observed sample and metallicity of the models is marginal. The [Fe/H] of the sample studied by Carlberg et al. (2012) is on average lower than solar, while the present computations were performed with a heavy mass fraction of Z = 0.020 which is over solar (Z⊙ = 0.014). However, whatever the metallicity, the engulfment would produce a strong acceleration of the surface. It may be that a given surface velocity would be reached with slightly different initial conditions, but the main outcomes are not changed.
In the left panel of Fig. 8, the observed sample is shown together with the tracks of the single (no engulfment) stellar models computed in the present work (case with Ωini/ Ωcrit = 0.1). In case we had made our computations of stellar models with a lower initial metallicity, the tracks would have been slightly shifted to the left, i.e. to the blue. Keeping this in mind, we see that the range of masses followed here, would more or less go through the averaged observed positions. It may be that some stars have lower initial mass than 1.5 M⊙ and some may have higher initial mass than 2.5 M⊙, but on the whole the mass range of the models is relatively well representative of most of the masses of the sample.
4.1. Stars with a clear signature of a past interaction
In many works, a red giant is considered as fast rotating and thus as a possible candidate for having gone through a planet engulfment process if its υsini is larger than 8 km s-1. This criterion is however too schematic. To understand this point, we point out the right panel of Fig. 8. We see that, actually, many of the red-filled points (υsini> 8 km s-1) are not very far from the line corresponding to the track for the 1.5 M⊙ with Ωini/ Ωcrit = 0.5, allowing such stars to be possibly explained without invoking any interaction with a companion. On the contrary, much lower surface velocities can be the indication of a planet engulfment. This can be seen looking at the magenta-dotted line, which is in the lower right corner in the right panel of Fig. 8. The tracks with no engulfment pass well below the slowly rotating points observed with surface gravities below about 1.6, while the track with an engulfment of a one Jupiter mass planet initially at a distance of 0.5 au of a 1.5 M⊙ star with Ωini/ Ωcrit = 0.5 would pass through at least part of these observed points. Thus, the surface rotation above which some interaction may be needed depends strongly on the surface gravity and cannot be given by only one number.
How can we distinguish stars that would nearly certainly require some interaction as the cause for their high surface velocities? The continuous (blue) line shows the evolution of the surface velocity for a 2.5 M⊙ that would begin its evolution at the critical velocity and evolves as a solid body rotating model. This evolution, as explained in the previous section, represents an extremum in terms of efficiency of the internal angular momentum transport and surface rotation. Actually, this is upper limit is very generous because we know that red giants are not rotating as solid body.
Turning now to stars that are found above this limit, we can be quite confident that, for these cases, an interaction with a companion must have occurred. These stars are shown as circled blue magenta filled points and individually labelled with a capital letter. Hence, this answers our first question above. We see that stars are indeed observed with surface velocities that cannot be explained by single star evolution5.
As a final remark, as already stated in the introduction, the bulk of stars with υsini lower than 8 km s-1 are in between the single star evolutionary tracks with Ωini/ Ωcrit = 0.1 and Ωini/ Ωcrit = 0.5. This shows that single star models can well account for the surface rotation of the bulk of red giants.
4.2. Can planet engulfment explain the cases likely resulting from an interaction?
 |
Fig. 7 Surface velocities υsini as a function of the effective temperature for the sample of red giants observed by Carlberg et al. (2011). The red dots correspond to stars with υsini larger than 8 km s-1. The lines indicate the evolutionary tracks for 2.5 M⊙ stellar models for different initial rotations (from bottom to top, the time-averaged velocities during the MS phases are ~20, 100, and 280 km s-1). The upper dotted line shows the critical velocity. |
Can planet engulfment reproduce the surface velocities observed for those red giants that have such large surface rotations that no single star models can reproduce them (see the points labelled by upper-case letters A to F in Figs. 9 and 8)? The answer is yes, as can be seen by comparing the locations of these stars in the right panel of Fig. 8 with the black continuous tracks. Only a few cases are shown for purpose of illustration, but there is no doubt that playing with the initial conditions (mass of the star, mass of the planet, and initial distance of the planet), it is indeed possible to produce a sufficient surface acceleration to reach these observed surface velocities for a sufficiently long duration to allow these high surface velocities to be observed.
4.3. Can the initial conditions be deduced from observations?
Can we determine the initial conditions needed to reproduce these systems? The solutions are unfortunately not unique. For instance, the positions of the points E and F could be reproduced by the engulfment of typically a 10 MJ planet initially at a distance of 0.5 au of a 2.5 M⊙ with Ωini/ Ωcrit = 0.5, or by the engulfment of a 10 MJ planet initially at a distance of 0.5 au from a 1.5 M⊙ with Ωini/ Ωcrit = 0.5, and there are likely other solutions. Of course, additional information can provide some further constraints. For instance, from the position in the HR diagram of the E and F stars (see left panel), the solution with the 2.5 M⊙ would be favoured with respect to that involving a 1.5 M⊙. In that case the star would be likely in the clump and not along the red giant branch.
4.4. The surface compositions after an engulfment
 |
Fig. 8 Left panel: surface gravities vs. effective temperatures. The continuous lines correspond to evolutionary tracks for single star models (no engulfment) for (from bottom to top) 1.5 (red), 1.7 (magenta), 2.0 (black), and 2.5 M⊙ (blue), starting with an initial angular velocity equal to 50% of the critical velocity. The dots show the observations by Carlberg et al. (2012), the black circles are for stars with υsini< 8 km s-1, the filled red and circled blue magenta points are for stars with υsini> 8 km s-1. The velocities of the circled blue magenta points cannot be explained by any reasonable model for single stars. The high rotation of these stars results with great probability from an interaction with an additional body. These points are labelled by letters (see text). The filled blue triangles are observations by Adamów et al. (2014), the filled blues square is the Li-rich star BD+48 740 discussed by Adamów et al. (2012a), and the blue star is the super Li-rich giant HD 107028 studied by Adamów et al. (2015). The two empty squares correspond to fast rotators obtained by Tayar et al. (2015) for stars with masses equal to 1.43 and 2.07 M⊙ along the red giant branch. Right panel: surface equatorial rotation vs. surface gravities for 1.5 M⊙ models. The two red tracks correspond to no planet engulfment cases starting with different initial rotations. The black curves show the evolution for stars with planet engulfment. The dots are the same observations as those shown in the left panel. |
 |
Fig. 9 Comparison between surface abundances and theoretical predictions. The points are observations (see caption of Fig. 8 for the meaning of the different symbols). Left panel: surface isotopic ratios 12C/13C vs. surface gravities. The continuous lines are the same evolutionary tracks as those shown in the left panel of Fig. 8. The dotted lines show the new isotopic ratios obtained when account is made for the dilution in the convective envelope of the planet material (see text for more details) starting from the models with Ωini/ Ωcrit = 0.5. Right panel: surface lithium abundance vs. surface gravities. The continuous (black) horizontal line shows the averaged lithium abundance observed at the surface of stars with υsini smaller than 8 km s-1. The dotted lines show the results of dilution of the planet material into the convective envelope. |
The left panel of Fig. 9 shows isotopic ratios at the surface of the observed stars and predictions of the theoretical models. The continuous lines show the predictions of the present stellar models without any planet engulfment. The predictions depend on the initial rotation. Higher initial rotations lead to lower 12C/13C ratios. Models with an initial rotation equal to 50% of the critical value go roughly through the middle of the observed points6.
We can deduce the following points looking at the left panel of Fig. 9:
-
The planet engulfment process decreases the shear between thecore and the convective envelope and thus weakens the shearmixing in that region. However this effect is negligible becauseeven in models without engulfment, which have a stronger shearin that region, we see no effect. Indeed, such an effect wouldproduce a continuous decrease of the 12C/13C ratio once the convective envelope has reached its deepest point. This is obviously not the case as shown in the left panel of Fig. 9.
-
Another process can change the isotopic ratio: the dilution of the planet material into the convective envelope. To estimate the importance of this process, we followed the same line of reasoning as presented in Carlberg et al. (2012). We applied their Eq. (3), which gives the new isotopic ratio, (12C /13C)new accounting for the dilution of the planetary material into the convective envelope
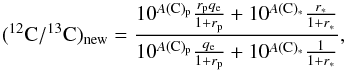 where A(C)p is Log(N(C) /N(H)) + 12 in the planet and A(C)∗ is the same quantity for the star (N(C) is the number of carbon per unit volume accounting for the two isotopes 12C and 13C). The ratio r is equal to N(12C) /N(13C) and qe is the ratio of the mass of the planet to the mass of the convective envelope. We took the values directly from our stellar models for the quantities concerning the star (∗). We considered the same values for the planet as in Carlberg et al. (2012) namely A(C)p = 8.87 dex (about three times the solar carbon abundance as determined by Wong et al. 2004) and rp = 89, which is a standard value for the solar system (Lodders & Fegley 1998). Using the above formula, we obtain after engulfment the level of 12C /13C shown by the dashed segments in Fig. 9. We see that since the planetary material has a higher 12C /13C ratio than the stellar envelope; this effect makes the surface isotopic ratio a bit larger. The effect is however small and thus the measure of this isotopic ratio appears as a poor indicator of a planet engulfment, especially that changes of the initial mass, rotation, and likely other possible mixing processes have stronger effects than the engulfment.
where A(C)p is Log(N(C) /N(H)) + 12 in the planet and A(C)∗ is the same quantity for the star (N(C) is the number of carbon per unit volume accounting for the two isotopes 12C and 13C). The ratio r is equal to N(12C) /N(13C) and qe is the ratio of the mass of the planet to the mass of the convective envelope. We took the values directly from our stellar models for the quantities concerning the star (∗). We considered the same values for the planet as in Carlberg et al. (2012) namely A(C)p = 8.87 dex (about three times the solar carbon abundance as determined by Wong et al. 2004) and rp = 89, which is a standard value for the solar system (Lodders & Fegley 1998). Using the above formula, we obtain after engulfment the level of 12C /13C shown by the dashed segments in Fig. 9. We see that since the planetary material has a higher 12C /13C ratio than the stellar envelope; this effect makes the surface isotopic ratio a bit larger. The effect is however small and thus the measure of this isotopic ratio appears as a poor indicator of a planet engulfment, especially that changes of the initial mass, rotation, and likely other possible mixing processes have stronger effects than the engulfment. -
Looking only at the observed points, we see that the fast rotators and those stars whose surface velocities cannot be explained by single star evolution do not present different carbon isotopic ratios than the rest of the sample, confirming that this isotopic ratio does not appear to be very sensitive to the engulfment.
In the right panel of Fig. 9, observed lithium abundances are shown. It seems as indicated by Carlberg et al. (2012), that the fast rotators present on average higher lithium abundances. However, if we consider the Li-rich giants observed by Adamów et al. (2012a, 2014, 2015), none of these stars have a υsini> 8 km s-1 (see the right panel of Fig. 8), which somewhat blurs the trend.
Similar estimates as that for the carbon isotopic ratio can be performed for the lithium abundance. Using Eq. (2) of Carlberg et al. (2012)
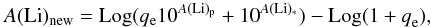 we estimate the new surface lithium abundance, A(Li)new, after accretion of the planetary material. In our stellar models, the abundance of lithium is not followed explicitly, thus we did as in Carlberg et al. (2012), considering for A(Li)∗ a value equal to −0.18 dex corresponding to the averaged abundance of lithium observed at the surface of slow rotators; see the horizontal continuous line in the right panel of Fig. 9. For A(Li)p, we took a value equal to 3.3 (Lodders & Fegley 1998), while for qe, we used the stellar models quantities. The results are shown by the dotted tracks in the right panel of Fig. 9. The lines represent the surface lithium abundances that would be observed in case the engulfment occurred at various surface gravities. When the outer convective zone begins to appear, the convective envelope is very small and the Li abundance that results from a planet dilution is very high. This makes the vertical part of the track. Then when the envelope increases in mass, the evolution goes to lower Li abundances and to lower gravities.
we estimate the new surface lithium abundance, A(Li)new, after accretion of the planetary material. In our stellar models, the abundance of lithium is not followed explicitly, thus we did as in Carlberg et al. (2012), considering for A(Li)∗ a value equal to −0.18 dex corresponding to the averaged abundance of lithium observed at the surface of slow rotators; see the horizontal continuous line in the right panel of Fig. 9. For A(Li)p, we took a value equal to 3.3 (Lodders & Fegley 1998), while for qe, we used the stellar models quantities. The results are shown by the dotted tracks in the right panel of Fig. 9. The lines represent the surface lithium abundances that would be observed in case the engulfment occurred at various surface gravities. When the outer convective zone begins to appear, the convective envelope is very small and the Li abundance that results from a planet dilution is very high. This makes the vertical part of the track. Then when the envelope increases in mass, the evolution goes to lower Li abundances and to lower gravities.
From the right panel of Fig. 9, we see that indeed the dilution of the planetary material into the convective envelope can have a strong effect on the surface Li abundance. The conditions at the base of the convective of our stellar models are not favourable to a rapid destruction of that element by proton captures, thus it is burned unless some mixing occurs below the convective envelope (see also Aguilera-Gómez et al. 2016).
The strong effect on lithium abundance found here after the planet engulfment confirms what was suggested by many authors in the past (see e.g. Alexander 1967; Siess & Livio 1999a; Carlberg et al. 2012; Adamów et al. 2012b), namely that the planet engulfment process can indeed produce lithium-rich red giants. However, the lithium signature of planet engulfment remains difficult to disentangle from other processes. Lithium is a fragile element that is destroyed at about 2.6 million degrees, so any surface enrichment might disappear rapidly in some stellar models. Lithium can also be produced in some red giant models, which completely blurs the picture for what concerns the origin of a high lithium abundance.
In that respect it is interesting to see the lithium surface abundances of those stars whose high surface velocities cannot be explained by single star models (see the circled blue magenta filled points in Fig. 9). Their positions are not very peculiar in the sense that slowly rotating stars are also found with similar levels of Li abundances. All these stars, however, are above the averaged level for the (apparently) slowly rotating stars, leaving open the possibility that they could have received some lithium from a planet.
On the other hand, as noted already above, none of the Li-rich giants observed by Adamów et al. (2012a, 2014, 2015) are apparently fast rotators. These kinds of stars are therefore difficult to be explained by a planet engulfment process unless some mechanism, not accounted for in the present models, such as a strong wind magnetic braking for instance, has occurred. In that case those red giants would have once been fast rotators, but the wind magnetic braking was efficient enough for the star to have lost memory of its post-engulfment fast rotating stage.
5. Perspectives and conclusions
As was already shown in Privitera et al. (2016), there are observed red giant stars whose high surface velocities cannot be explained by single star evolution. The upper velocities that can be reached by single star models of the considered mass are indicated as a function of the surface gravity in Fig. 2 by the long-dashed black line labelled Vmax. The use of such gravity dependent limits to isolate red giants that have likely engulfed a planet, or at least interacted with, it is probably more realistic than the commonly used limit of 8 km s-1.
The present models show that tidal interactions followed by planet engulfment can reproduce the high surface velocities of these stars during sufficiently long periods that allow these high rotations to be observable. Surface velocities beyond the upper limit allowed by single star evolution can be reached already just by tidal interaction.
We obtain also that the high rotation obtained after the engulfment is maintained beyond the end of the red giant branch for the 2.5 M⊙. It would be extremely interesting to check whether such a conclusion would hold for our lower initial mass models that go through a He-flash episode.
Conditions also exist for producing engulfments with much less spectacular impacts. The engulfment of a one MJ planet by a 1.5 M⊙ star would produce surface velocities of only a few km per seconds at gravities below about 1.6. This is quite small and these stars would hardly be recognized as having engulfed a planet.
The above conclusions make the link between observed fast rotating red giants and red giants that have engulfed a planet much less clear in the sense that not all fast rotating red giants need an interaction to have reached their surface velocities; this may reflect simply a high initial rotation rate of the progenitor. Also, not all slowly rotating red giants may be explained by single star evolution that is typically in the upper part of the red giant branch.
We discussed in a simple way the consequences of an engulfment on the surface composition of red giants and confirmed the results obtained by Carlberg et al. (2012) that the effect on the carbon isotopic ratios are very small and the impact on lithium might be quite large, although remaining difficult to interpret (see below).
We showed that the chemical signatures of an engulfment are still quite ambiguous because planet engulfment either produce too small signal as in the case of the carbon isotopic ratios, or produce signals that cannot be attributed in a non-ambiguous way to a planet engulfment. This makes the surface velocity of a red giant the most stringent observable feature indicating a past star-planet interaction.
The present results also show that the evolution after an engulfment is not very different from that obtained without any engulfment. The main difference is in the surface rotation (and of course the rotation as a whole of the external convective zone). A planet engulfment would somewhat lower the contrast between the angular velocity of the core and that of the envelope, but not at a level that could be useful to reproduce the small contrast as obtained by asteroseismology for a few red giants (e.g. Beck et al. 2012; Mosser et al. 2012; Deheuvels et al. 2012, 2014).
There are many other points that should be addressed in further works. In particular, we shall investigate whether the acceleration of the surface due to a planet engulfment may trigger a magnetic field.
These lines would not be isothermal lines in the case in which the structure of the planet were to change during its journey inside the star. Here it is assumed that during the very short migration time the planet structure does not change significantly. The only change occurs at the very end, when the planet dissolves.
In our models, we take planets with masses that are not larger than 15 MJ, which means below the limiting value Mcri ≃ 20 MJ estimated by Soker et al. (1984), above which the planet is no longer completely destroyed when engulfed by the stellar envelope. This limit is also consistent with the value found in the numerical simulations by Staff et al. (2016).
One could argue that, once the solid body rotation is reached, some processes might still advect angular momentum from the centre to the surface producing a negative gradient of Ω, i.e. a core rotating slower than the envelope, and increasing the surface velocity. However, this is not supported by asteroseismic determinations of the interior rotation of red giants (e.g. Beck et al. 2012; Mosser et al. 2012; Deheuvels et al. 2012, 2014), which show that red giants have a clear increase of rotation towards the central regions. In that respect, the hypothesis of solid body rotation gives a very conservative upper limit for the surface rotation of red giants.
The duration of the period during which the surface velocity remains superior to a given limit after an engulfment is larger in lower mass stars. However, when this period is normalized to the total duration of the red giant branch, then the fraction spent above a given limit decreases when the mass decreases.
The present models do not account for thermohaline mixing for instance, which has been proposed by Charbonnel & Zahn (2007) as causing an additional decrease of the 12C/13C ratio and of the lithium along the red giant branch (see also Charbonnel & Lagarde 2010).
Actually, this timescale changes a bit with the mass of the planet as can be seen in Fig. A.1, which is slightly shorter for the 5 than for the 15 MJ planet. On the other hand, the differences between the various planet masses are not very large.
Acknowledgments
This research has made use of the Exoplanet Orbit Database and the Exoplanet Data Explorer at exoplanets.org. The project has been supported by Swiss National Science Foundation grants 200021-138016, 200020-160119 and 200020-15710.
References
- Adamów, M., Niedzielski, A., Villaver, E., Nowak, G., & Wolszczan, A. 2012a, ApJ, 754, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Adamów, M., Niedzielski, A., Villaver, E., Nowak, G., & Wolszczan, A. 2012b, ApJ, 754, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Adamów, M., Niedzielski, A., Villaver, E., Wolszczan, A., & Nowak, G. 2014, A&A, 569, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adamów, M., Niedzielski, A., Villaver, E., et al. 2015, A&A, 581, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aguilera-Gómez, C., Chanamé, J., Pinsonneault, M., & Carlberg, J. 2016, ApJ, accepted [arXiv:1605.05332] [Google Scholar]
- Alexander, J. B. 1967, The Observatory, 87, 238 [NASA ADS] [Google Scholar]
- Beck, P. G., Montalban, J., Kallinger, T., et al. 2012, Nature, 481, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Cantiello, M., Mankovich, C., Bildsten, L., Christensen-Dalsgaard, J., & Paxton, B. 2014, ApJ, 788, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Carlberg, J. K., Majewski, S. R., & Arras, P. 2009, ApJ, 700, 832 [Google Scholar]
- Carlberg, J. K., Majewski, S. R., Patterson, R. J., et al. 2011, ApJ, 732, 39 [Google Scholar]
- Carlberg, J. K., Cunha, K., Smith, V. V., & Majewski, S. R. 2012, ApJ, 757, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonnel, C., & Lagarde, N. 2010, A&A, 522, A10 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Charbonnel, C., & Zahn, J.-P. 2007, A&A, 467, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deheuvels, S., García, R. A., Chaplin, W. J., et al. 2012, ApJ, 756, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Deheuvels, S., Doğan, G., Goupil, M. J., et al. 2014, A&A, 564, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, P., Meynet, G., Maeder, A., et al. 2008, Ap&SS, 316, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Eggenberger, P., Montalbán, J., & Miglio, A. 2012, A&A, 544, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fekel, F. C., & Balachandran, S. 1993, ApJ, 403, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F. 1981, ApJ, 251, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F. 1982, ApJ, 262, 682 [Google Scholar]
- Livio, M., & Soker, N. 1984, MNRAS, 208, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Livio, M., & Soker, N. 2002, ApJ, 571, L161 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K., & Fegley, B. 1998, The planetary scientist’s companion (Oxford University Press) [Google Scholar]
- Marques, J. P., Goupil, M. J., Lebreton, Y., et al. 2013, A&A, 549, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massarotti, A., Latham, D. W., Stefanik, R. P., & Fogel, J. 2008, AJ, 135, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012, A&A, 540, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Passy, J.-C., Mac Low, M.-M., & De Marco, O. 2012, ApJ, 759, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, R. C., Tarbell, T. D., & Carney, B. W. 1983, ApJ, 265, 972 [NASA ADS] [CrossRef] [Google Scholar]
- Privitera, G., Meynet, G., Eggenberger, P., et al. 2016, A&A, 591, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sandquist, E., Taam, R. E., Lin, D. N. C., & Burkert, A. 1998, ApJ, 506, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Sandquist, E. L., Dokter, J. J., Lin, D. N. C., & Mardling, R. A. 2002, ApJ, 572, 1012 [NASA ADS] [CrossRef] [Google Scholar]
- Siess, L., & Livio, M. 1999a, MNRAS, 304, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Siess, L., & Livio, M. 1999b, MNRAS, 308, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, T., & Drake, S. A. 1989, ApJ, 346, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Soker, N., Livio, M., & Harpaz, A. 1984, MNRAS, 210, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Soker, N., Regev, O., Livio, M., & Shara, M. M. 1987, ApJ, 318, 760 [NASA ADS] [CrossRef] [Google Scholar]
- Staff, J. E., De Marco, O., Wood, P., Galaviz, P., & Passy, J.-C. 2016, MNRAS, 458, 832 [NASA ADS] [CrossRef] [Google Scholar]
- Tayar, J., Ceillier, T., García-Hernández, D. A., et al. 2015, ApJ, 807, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Wong, M. H., Mahaffy, P. R., Atreya, S. K., Niemann, H. B., & Owen, T. C. 2004, Icarus, 171, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Zapolsky, H. S., & Salpeter, E. E. 1969, ApJ, 158, 809 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Detailed properties of the stellar models before and after engulfment
This Appendix contains three tables that list information on the characteristics of the star before and after an engulfment. Table A.1 indicates the properties of the stellar models just before the engulfment. The first column is the mass of the planet. Columns 2 to 5 give the mass of the star, its radius, surface angular velocity, mass loss rate, and mass of the convective envelope at this time.
Tables A.2 and A.3 present the changes occurring owing to the tides/engulfment processes. The first column is the mass of the planet. Columns 2 gives the equatorial surface velocity before the engulfment. This velocity is already significantly higher than that of the corresponding single star at that stage. Actually, the velocity indicated in that column would be the velocity acquired by the tidal forces alone. Column 3 gives the duration of the phases during which, starting from the velocity indicated in Col. 2, the surface velocity would be higher than 8 km s-1, Δtt(FR). To compute this duration we used the results shown in Fig. A.1. This figure shows the evolution as a function of time of the surface velocity just after an engulfment. We see that roughly the surface velocity varies as v(Δt) ~ vmax(1−0.04Δt), where Δt (in Myr) is t−tMS, with t the age of the star, tMS the age of the star at the end of the MS phase, and vmax the surface velocity reached just after the engulfment. This relation does not much depend on the mass of the planet, or equivalently on the value of vmax. It means that after 2.5 Myr, whatever the initial velocity, the surface velocity decreases by 10% with respect to its initial value7. We can use such a plot to estimate the time during which a star maintains a certain velocity after the engulfment evolving up along the red giant branch. This is how we estimated the time, Δtt(FR), indicated in Col. 3 of Tables A.2 and A.3 showing the duration of the period when the star has a surface velocity higher than 8 km s-1 when only the acceleration due to tides is accounted for.
In Tables A.2 and A.3, Cols. 4 to 6 indicate the surface velocity right after the engulfment; the duration of the phases during which the surface velocity, after an engulfment, is higher than 8 km s-1 (Δtt + e(FR)), and finally the fraction of the red giant branch phase spent with a surface velocity superior to 8 km s-1. Tables A.2 show the results obtained with stellar models that have an initial angular velocity equal to 10% of the critical velocity, and Tables A.3 show the results for models that have an initial angular velocity equal to 50% of the critical velocity.
 |
Fig. A.1 Evolution of the surface velocity (normalized to the velocity reached just after the engulfment, vmax) as a function of time for a 2 M⊙ stellar model with an initial rotation equal to 10% of the critical velocity. Various masses for the planets are considered. All planets started at a distance equal to 0.5 au from their parent star. |
Characteristics of the star at the time of engulfment; see also Privitera et al. (2016) for additional pieces of information.
Effect of planet engulfment on the surface rotation velocities of red giants.
All Tables
Characteristics of the star at the time of engulfment; see also Privitera et al. (2016) for additional pieces of information.
All Figures
 |
Fig. 1 Kippenhahn diagram during the red giant phase. The central radiative zone and the convective envelope are represented by a white area and an area with black dots, respectively. The horizontal axis is the age of the star minus its main-sequence lifetime (tMS). The four lines indicate the limit layers that can be reached by the planets of mass 1 MJ (red solid line), 5 MJ (blue dashed line), 10 MJ (green dash-dotted line), and 15 MJ (continuous cyan line). The vertical dashed lines labelled A, B, and C indicate when the engulfment occurs for the 15 MJ planet at an initial distance of 0.5 au, the 10 MJ planet at an initial distance of 1.0 au, and the 1 MJ planet at an initial distance of 1.5 au, respectively. All the other cases occur between the lines A and C. The left panel corresponds to a model star of 1.5 M⊙ and the right panel to a mass of 2 M⊙. |
| In the text | |
 |
Fig. 2 Evolution of the surface velocity as a function of the logarithm of the surface gravity. Dotted (black) lines are for stars without engulfment. Cases for Ω / Ωini = 0.1 and 0.5 are shown. The black long-dashed line (labelled Vmax) corresponds to solid body rotation without engulfment starting with an initial rotation near the critical velocity (see text). Continuous lines correspond to cases with planet engulfment for stars with an initial velocity equal to 10% the critical value and the short-dashed lines correspond to the same cases but for an initial rotation equal to 50% of the critical value. The different colours for solid and dashed lines are for planet masses of 5 (red), 10 (magenta), and 15 MJ (blue) and initial orbital distances of 0.5, 1, and 1.5 au from left to right (see labels). The different panels are for different values of the mass of the star. In the case of 2.5 M⊙, the evolution is pursued until the end of the core He-burning phase, while for lower initial mass stars, the evolution is stopped at the tip of the red giant branch. |
| In the text | |
 |
Fig. 3 Left panel: variation of the angular velocity as a function of the Lagrangian mass inside a 1.5 M⊙ model along the red giant branch just before (blue continuous line) and after the engulfment (red dashed line) of a 15 MJ mass planet at an initial distance of 0.5 au from the star. Right panel: evolution of the ratio between the angular velocity of the core and surface angular velocity as a function of the surface gravity along the red giant branch for the same models as in the left panel. |
| In the text | |
 |
Fig. 4 Evolution of the surface velocity of various initial mass stellar models during the red giant phase as a function of the surface gravity. The initial rotations are between 30 and 50 km s-1. Planets have a mass equal to 15 MJ and the orbits have an initial semimajor axis equal to 0.5 au. |
| In the text | |
 |
Fig. 5 Fraction of the total red giant branch duration spent with a surface equatorial rotation velocity that is higher than 8 km s-1 after an engulfment. Upper left panel: case of a 1.5 M⊙ with an initial rotation Ωini/ Ωcrit = 0.1. Upper right panel: same as the upper left panel, but with Ωini/ Ωcrit = 0.5. Lower left panel: same as the upper left panel, but for a star of mass 2.0 M⊙. Lower right panel: same as the lower left panel, but with Ωini/ Ωcrit = 0.5. |
| In the text | |
 |
Fig. 6 Evolution of the surface velocity of a 2 M⊙ stellar model during the red giant phase as a function of the luminosity. The initial rotation of the star is 10% of the critical velocity (on the ZAMS). When evolution proceeds, the luminosity in general increases except at the bump visible in the left panel under the form of a small hook. Magenta lines indicate cases without planet engulfment, while blue, green, red, and cyan lines correspond to the engulfment of a planet with a mass equal to 1, 5, 10, and 15 MJ, respectively. The surface velocity reached just before engulfment, i.e. resulting only from tidal forces, is indicated by a small dot. Left panel: the initial semimajor axis is equal to 0.5 au. Right panel: the initial semimajor axis is equal to 1.5 au. |
| In the text | |
 |
Fig. 7 Surface velocities υsini as a function of the effective temperature for the sample of red giants observed by Carlberg et al. (2011). The red dots correspond to stars with υsini larger than 8 km s-1. The lines indicate the evolutionary tracks for 2.5 M⊙ stellar models for different initial rotations (from bottom to top, the time-averaged velocities during the MS phases are ~20, 100, and 280 km s-1). The upper dotted line shows the critical velocity. |
| In the text | |
 |
Fig. 8 Left panel: surface gravities vs. effective temperatures. The continuous lines correspond to evolutionary tracks for single star models (no engulfment) for (from bottom to top) 1.5 (red), 1.7 (magenta), 2.0 (black), and 2.5 M⊙ (blue), starting with an initial angular velocity equal to 50% of the critical velocity. The dots show the observations by Carlberg et al. (2012), the black circles are for stars with υsini< 8 km s-1, the filled red and circled blue magenta points are for stars with υsini> 8 km s-1. The velocities of the circled blue magenta points cannot be explained by any reasonable model for single stars. The high rotation of these stars results with great probability from an interaction with an additional body. These points are labelled by letters (see text). The filled blue triangles are observations by Adamów et al. (2014), the filled blues square is the Li-rich star BD+48 740 discussed by Adamów et al. (2012a), and the blue star is the super Li-rich giant HD 107028 studied by Adamów et al. (2015). The two empty squares correspond to fast rotators obtained by Tayar et al. (2015) for stars with masses equal to 1.43 and 2.07 M⊙ along the red giant branch. Right panel: surface equatorial rotation vs. surface gravities for 1.5 M⊙ models. The two red tracks correspond to no planet engulfment cases starting with different initial rotations. The black curves show the evolution for stars with planet engulfment. The dots are the same observations as those shown in the left panel. |
| In the text | |
 |
Fig. 9 Comparison between surface abundances and theoretical predictions. The points are observations (see caption of Fig. 8 for the meaning of the different symbols). Left panel: surface isotopic ratios 12C/13C vs. surface gravities. The continuous lines are the same evolutionary tracks as those shown in the left panel of Fig. 8. The dotted lines show the new isotopic ratios obtained when account is made for the dilution in the convective envelope of the planet material (see text for more details) starting from the models with Ωini/ Ωcrit = 0.5. Right panel: surface lithium abundance vs. surface gravities. The continuous (black) horizontal line shows the averaged lithium abundance observed at the surface of stars with υsini smaller than 8 km s-1. The dotted lines show the results of dilution of the planet material into the convective envelope. |
| In the text | |
 |
Fig. A.1 Evolution of the surface velocity (normalized to the velocity reached just after the engulfment, vmax) as a function of time for a 2 M⊙ stellar model with an initial rotation equal to 10% of the critical velocity. Various masses for the planets are considered. All planets started at a distance equal to 0.5 au from their parent star. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


