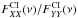| Issue |
A&A
Volume 593, September 2016
|
|
|---|---|---|
| Article Number | A44 | |
| Number of page(s) | 11 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201628176 | |
| Published online | 12 September 2016 | |
The 492 GHz emission of Sgr A* constrained by ALMA
1 European Southern Observatory
(ESO), Karl-Schwarzschild-Str.
2, 85748 Garching, Germany
e-mail: baobabyoo@gmail.com
2 Academia Sinica Institute of
Astronomy and Astrophysics, PO Box
23-141, 106
Taipei,
Taiwan
3 Department of Astronomy,
Campbell Hall, UC
Berkeley, Berkeley,
CA
94720,
USA
4 Harvard-Smithsonian Center for
Astrophysics, 60 Garden St., MS 78, Cambridge, MA
02138,
USA
5 National Radio Astronomy Observatory,
1003 Lopezville Rd,
Socorro, NM
87801,
USA
6 Space Telescope Science Institute,
3700 San Martin
Dr., Baltimore,
MD
21218,
USA
7 European Southern Observatory, 3107 Alonso de Córdova,
Vitacura, Santiago
8 Joint ALMA Observatory,
3107 Alonso de Córdova,
Vitacura, Santiago,
Chile
9 Dept. of Physics & Astronomy,
University of California, Los
Angeles, CA
90095-1547,
USA
10 Astrophysics Research Institute, Liverpool John Moores
University, 146 Brownlow Hill, L3 5RF, USA
11 Department of Astrophysics/IMAPP,
Radboud University, Nijmegen, PO
Box 9010, 6500
GL
Nijmegen, The
Netherlands
Received:
23
January
2016
Accepted:
13
June
2016
Aims. Our aim is to characterize the polarized continuum emission properties including intensity, polarization position angle, and polarization percentage of Sgr A* at ~492 GHz. This frequency, well into the submillimeter bump where the emission is supposed to become optically thin, allows us to see down to the event horizon. Hence the reported observations contain potentially vital information on black hole properties. We have compared our measurements with previous, lower frequency observations, which provides information in the time domain.
Methods. We report continuum emission properties of Sgr A* at ~492 GHz, based on Atacama Large Millimeter Array (ALMA) observations. We measured flux densities of Sgr A* from the central fields of our ALMA mosaic observations. We used calibration observations of the likely unpolarized continuum emission of Titan and the observations of Ci line emission, to gauge the degree of spurious polarization.
Results. The flux density of 3.6 ± 0.72 Jy which we measured during our run is consistent with extrapolations from previous, lower frequency observations. We found that the continuum emission of Sgr A* at ~492 GHz shows large amplitude differences between the XX and the YY correlations. The observed intensity ratio between the XX and YY correlations as a function of parallactic angle can be explained by a constant polarization position angle of ~158°± 3°. The fitted polarization percentage of Sgr A* during our observational period is 14% ± 1.2%. The calibrator quasar J1744-3116 we observed on the same night can be fitted to Stokes I = 252 mJy, with 7.9% ± 0.9% polarization at position angle PA = 14°± 4.2°.
Conclusions. The observed polarization percentage and polarization
position angle in the present work appear consistent with those expected from longer
wavelength observations in the period of 1999−2005. In particular, the polarization position angle at 492 GHz
expected from the previously fitted 167°±
7° intrinsic polarization
position angle and (−5.6
± 0.7) × 105 rotation measure is 155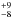 °, which is consistent with our new measurement of polarization
position angle within 1σ. The polarization percentage and the polarization
position angle may be varying over the period of our ALMA 12 m Array observations, which
demands further investigation with future polarization observations.
°, which is consistent with our new measurement of polarization
position angle within 1σ. The polarization percentage and the polarization
position angle may be varying over the period of our ALMA 12 m Array observations, which
demands further investigation with future polarization observations.
Key words: techniques: polarimetric / black hole physics / polarization / radiation mechanisms: non-thermal / Galaxy: nucleus
© ESO, 2016
1. Introduction
The sub-Eddington accretion of the nearest supermassive black hole, Sgr A* (~4 × 106M⊙, e.g., Schödel et al. 2002; Ghez et al. 2005; Gillessen et al. 2009), has inspired a tremendous amount of observational and theoretical activity (see Yuan & Narayan 2014, for a complete review of existing theories). This activity includes monitoring observations at multiple wavelengths to probe synchrotron emission, which may come from the innermost part of an accretion flow or the footpoint of a jet (Falcke et al. 2000, 2009; Liu et al. 2007; Huang et al. 2009; more below), and has motivated very long baseline millimeter interferometric observations (e.g., Johnson et al. 2015, and references therein).
Observed flux densities of Sgr A* (from a vector averaging at Sgr A* in the visibility domain prior to correction of primary beam attenuation).
Observations of polarization position angle and polarization percentage of the synchrotron emission over a broad range of frequencies may provide information about the geometry and the magnetic field configuration of the accretion flow (Bromley et al. 2001; Liu et al. 2007; Huang et al. 2009), and can help in determining the black hole accretion rate on small scales via deriving Faraday rotation (more below). Previously established strong observational constraints on the linear polarization percentage in the 4.8−112 GHz bands (Bower et al. 1999a,c, 2001) and the detected linear polarization at the 83−400 GHz bands (Aitken et al. 2000; Bower et al. 2003, 2005; Macquart et al. 2006; Marrone et al. 2006a, 2007) have given rise to a model in which linearly polarized radiation is emitted from within a few gravitational radii around Sgr A*, and is further Faraday depolarized by the ionized accretion flow foreground to Sgr A*. This model is supported by the detection of circularly polarized emission in the 1.4−15 GHz bands (Bower et al. 1999b, 2002; Sault & Macquart 1999; see also the measurements at 230 and 345 GHz by Muñoz et al. 2012). These observations have constrained the accretion rate of Sgr A* to be between 2 × 10-9 and 2 × 10-7M⊙ yr-1. On the other hand, the observed flux density variations of Sgr A*, including large millimeter flares (Zhao et al. 2003, 2004; Marrone et al. 2006), indicates that conditions in the accretion flow may not be stationary.
In this work, we report new constraints on the polarized emission of Sgr A* at 492 GHz, based on Atacama Large Millimeter Array (ALMA) 12 m Array and Compact Array (ACA) mosaic observations towards the Galactic center. Our new high-frequency observations provide long lever arms in the frequency and time domains for comparison with submillimeter, millimeter, and radio bands observations carried out between 1999 and 2005. In particular, our observing frequency is above the turnover frequency at which the emission becomes optically thin (Marrone et al. 2006b). Moreover, we are able to reliably derive polarizion properties, which make these the highest frequency interferometric polarization observations of Sgr A* done so far. These observations help us establish the intrinsic polarization of the inner accretion flow. Our work provides a starting point for future observations to probe polarization variability at high frequencies, which are crucial to understanding the physics of Sgr A*.
Details of our observations and data reduction are provided in Sect. 2. Our results are given in Sect. 3. In Sect. 4 we address potential systematic biases, and present the comparison of our results with previous observations. A brief conclusion is provided in Sect. 5.
2. Observations and data reduction
The ALMA 12 m Array (consisting of 12 m dishes) mosaic observations of 149 fields were carried out on 2015 April 30 (UTC 06:48:32.4–08:04:38.4) with 39 antennas. The array consists of 19 Alcatel antennas (DA), 18 Vertex antennas (DV), and 2 Mitsubishi antennas (PM). These observations covered approximately a 55′′ × 80′′ rectangular region on the sky. The pointing and phase referencing center of the central field was RA (J2000) = 17h45m40s.036, and Dec (J2000) = −29°00′28 17, which is approximately centered upon Sgr A*. We configured the correlator to provide four 1.875 GHz wide spectral windows (spws), covering the frequency ranges of 491.3−493.2 GHz (spw 0), 489.3−491.2 GHz (spw 1), 479.2−481.1 GHz (spw 2), and 481.0−482.9 GHz (spw 3). The observations were designed to cover the Ci line and the CS 10-9 line, the rest-frame frequencies of which are 492.16065 GHz and 489.75093 GHz, respectively. The frequency channel spacing was 1953.125 kHz (~1.2 km s-1). The receivers are aligned in a parallel-linear configuration, which yields the XX and YY linear correlations. The X polarization of the receivers is aligned radially in the receiver cryostat, with Y being aligned perpendicular to X (private communications with Ted Huang and Shin’ichiro Asayama). According to ALMA specifications, the accuracy of this alignment is within 2 deg. The absolute feed alignment was obtained from the raw data, using the CASA software package (McMullin et al. 2007) with command tb.getcol(“RECEPTOR_ANGLE”), and can be referenced from the ALMA Cycle 3 and Cycle 4 Technical Handbook1.
17, which is approximately centered upon Sgr A*. We configured the correlator to provide four 1.875 GHz wide spectral windows (spws), covering the frequency ranges of 491.3−493.2 GHz (spw 0), 489.3−491.2 GHz (spw 1), 479.2−481.1 GHz (spw 2), and 481.0−482.9 GHz (spw 3). The observations were designed to cover the Ci line and the CS 10-9 line, the rest-frame frequencies of which are 492.16065 GHz and 489.75093 GHz, respectively. The frequency channel spacing was 1953.125 kHz (~1.2 km s-1). The receivers are aligned in a parallel-linear configuration, which yields the XX and YY linear correlations. The X polarization of the receivers is aligned radially in the receiver cryostat, with Y being aligned perpendicular to X (private communications with Ted Huang and Shin’ichiro Asayama). According to ALMA specifications, the accuracy of this alignment is within 2 deg. The absolute feed alignment was obtained from the raw data, using the CASA software package (McMullin et al. 2007) with command tb.getcol(“RECEPTOR_ANGLE”), and can be referenced from the ALMA Cycle 3 and Cycle 4 Technical Handbook1.
The range of uv spatial frequencies sampled by the 12 m Array observations is 25−570 kλ. The system temperature (Tsys) ranged from ~500−1000 K. The mosaic field was Nyquist sampled in hexagonal packing, with an on-source integration time of 12.08 s for each of the 149 mosaic fields. We observed J1744-3116 approximately every 10 min for gain calibrations. We observed Titan and J1833-2103 for absolute flux and passband calibrations, respectively.
The Atacama Compact Array (ACA; consisting of ten 7 m dishes) observations were carried out on 2015 April 30 (UTC 05:35:00.0–07:30:00.1) with ten available antennas. All ten antennas shared an identical design (Mitsubishi, 7 m). The ACA observations covered approximately the same field of view as the 12 m-Array mosaic, with the pointing and phase referencing center of the central field also on Sgr A*. The correlator setup of the ACA observations was identical to that of the 12 m Array mosaic. The ACA observations sampled a uv spacing range of 14−80 kλ. The mosaic field was Nyquist sampled in hexagonal packing. Owing to unspecified technical issues, the ACA observations were terminated at the middle of the track. Therefore, the southeastern half of the observed region had an on-source integration time of 60.6 s for each mosaic field, while the northwestern half had an on-source integration time of 30.3 s for each mosaic field. This led to different sensitivity and uv coverages for the southeastern and the northwestern fields. Like the 12 m observations, Tsys values ranged from ~500−1000 K. We again observed J1744-3116 approximately every 10 minutes for gain calibrations, and observed Titan and J1517-2422 for absolute flux and passband calibrations, respectively. There are currently no available single-dish data to provide information on the zero-spacing fluxes for these observations.
A priori calibrations including the application of Tsys data, the water vapor radiometer (wvr) solutions (which are only provided for the 12 m Array observations), antenna based passband calibrations, gain amplitude and phase calibrations, and absolute flux scaling were carried out using the CASA software package (McMullin et al. 2007) version 4.3.1. To enhance the signal-to-noise ratio, we first solved for and applied phase offsets between the four spectral windows, based on scans on the passband calibrator. We then derived gain calibration solutions. The gain-phase solutions were derived separately for the XX and YY correlations, while the gain-amplitude solutions were derived from the average of the XX and YY correlations. We derived gain-phase solutions for all individual spectral windows and for the average of all spectral windows together. We ultimately chose to use the latter, as the wvr solutions for the 12 m Array data in spw 1 and 3 have poorer quality, which led to massive data flagging when deriving gain-phase solutions for the individual spectral windows independently. We also tested whether the application of the wvr solutions changed the quality of our final images; ultimately, although the difference was minimal, we chose to apply the wvr solutions to the 12 m data. We confirmed that the qualities of continuum images generated from all spectral windows are consistent (i.e., any differences are a result of the available bandwidths in spectral line-free channels). There was also significant interference due to atmospheric lines in spw 3, which degraded its continuum sensitivity.
The absolute flux scaling was derived incrementally from the gain-amplitude solutions, combining all scans. The scans on Titan were largely flagged owing to interference from spectral lines. Therefore, absolute flux referencing for both the 12 m Array and ACA observations is subject to a large uncertainty (~20%, empirically). This can explain the mismatched flux levels between the 12 m Array and the ACA observations, and the errors in the observed spectral indices.
We fitted the continuum baselines from line-free channels using the CASA task uvcontsub. We then generated a continuum data set for each spectral window by averaging the line-free channels. After this step, we exported the calibrated continuum data and the continuum-subtracted line data into standard fits format files, using the CASA task exportfits. Finally, we used the Miriad 4.3.8 (Sault et al. 1995) task fits to convert the fits format data into the Miriad data format for further analyses including imaging.
Using Miriad, we synthesized images (i.e., dirty images) of the continuum using naturally weighed data for the 12 m Array and ACA with beam widths (FWHM) 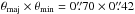 (PA = −88°) and
(PA = −88°) and 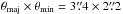 (PA = 78°), respectively. For the Ci line, we tapered the 12 m Array data using a Gaussian weighting function of
(PA = 78°), respectively. For the Ci line, we tapered the 12 m Array data using a Gaussian weighting function of 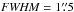 to enhance the signal-to-noise ratio of the line, and then generated the synthesized images. For all of these images we do not make deconvolved Ci line maps (i.e., cleaned) to avoid any possibility of uncertainties caused by the clean process.
to enhance the signal-to-noise ratio of the line, and then generated the synthesized images. For all of these images we do not make deconvolved Ci line maps (i.e., cleaned) to avoid any possibility of uncertainties caused by the clean process.
 |
Fig. 1 Central 7 mosaic fields of the 12 m-Array observations. The black circle shows the field (FWHM) centered on Sgr A*. Gray circles show the 6 fields which are the nearest to the central one. The diameter of these circles is |
3. Results
Throughout this manuscript, the X and Y polarization and Stokes Q are defined in the receiver coordinate frame if not explicitly mentioned otherwise. In close to ideal observational and instrumental conditions, the polarization percentage and the polarization position angle of a non-variable source are related to these quantities based on the formula: 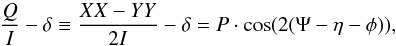 (1)where Q denotes the observed Stokes Q flux; δ (hereafter Q offset) is an assumed constant normalized offset of observed Stokes Q due to amplitude calibration errors or polarization leakage; P is the polarization percentage; Ψ, η, and φ are the polarization position angle in the sky (e.g., right ascension/declination) frame, the parallactic angle, and the angular separations between the X polarization and the local vertical (which is known as the E-vector). The E-vector of ALMA is 0° for the frequency band we observed. A wide coverage of η during the observations will allow for unambiguous fitting of δ, P, and Ψ.
(1)where Q denotes the observed Stokes Q flux; δ (hereafter Q offset) is an assumed constant normalized offset of observed Stokes Q due to amplitude calibration errors or polarization leakage; P is the polarization percentage; Ψ, η, and φ are the polarization position angle in the sky (e.g., right ascension/declination) frame, the parallactic angle, and the angular separations between the X polarization and the local vertical (which is known as the E-vector). The E-vector of ALMA is 0° for the frequency band we observed. A wide coverage of η during the observations will allow for unambiguous fitting of δ, P, and Ψ.
 |
Fig. 2 Top: flux density measurements of Sgr A*, from images made using only the inner 7 mosaic fields of the 12 m array, and the flux density of Sgr A* from an average of the ACA observations, are both plotted against time. Error bars in the horizontal direction represent the scan duration. Vertical error bars in the upper panel include both the uncertainty on the pointing (~1′′) and the uncertainty on the primary beam response function. The vertical error bar of the ACA data additionally includes a potential 20% absolute flux calibration uncertainty, relative to the 12 m array observations. The horizontal error bars for the continuum data of the 12 m-Array observations are shorter than the symbol size. Bottom: intensity ratio between the XX and the YY intensity maps derived from the continuum and the Ci line observations are plotted against time. Filled black and green symbols show the 12 m array measurements from Sgr A* and Titan, respectively. Errors are negligibly small for the snapshot on field 0, which is centered on Sgr A* (see Fig. 1). The Ci line measurements are averages from high S/N spectral channels (see also Fig. 6). Their vertical error bars are given by ±1 standard deviations of the intensity ratio, which were derived from those high S/N spectral channels. |
3.1. Continuum data
After a priori calibration, we found that the continuum emission from Sgr A* was significantly detected in the central 19 mosaic fields of the 12 m Array observations. To inspect the residual phase errors, we used the CASA task fixvis to shift the phase referencing centers of these fields to the position of Sgr A*. We observed up to ~±50° of residual phase offsets, and a phase RMS of ~16.5°. The phase offsets and phase rms of the XX and YY correlations are consistent with each other.
We attribute the phase errors partly to phase variations that are faster than our gain calibration cycle time, and partly to phase offsets between the gain calibrator and the target source fields. To correct for these phase errors we used the Miriad task demos, assuming the nominal ALMA primary beam shape, to generate models of Sgr A* for the central seven mosaic fields (Fig. 1). We removed the phase errors of the central seven fields using the Miriad task selfcal options=mosaic with a 0.01 min solution interval. Then, we used the Miriad task uvflux to fit the observed amplitudes from the visibility data. Our 12 m Array measurements for Sgr A* are summarized in Table 1 and Fig. 2. After self-calibration, the averaged flux density of Sgr A* at 492 GHz is 3.6 ± 0.72 Jy. The application of phase self-calibration solutions does not significantly change the observed amplitude (or flux density) ratios between the XX and the YY correlations. We do not present flux density measurements of Sgr A* from outside of the central seven mosaic fields because there is a potential for large amplitude uncertainties induced by antenna pointing errors (e.g., up to ~1′′ according to private communication among members in the ALMA Regional Centers) and the poorly understood primary beam phase responses.
 |
Fig. 3 Fittings of the (XX-YY)/I intensity ratio of quasar J1744-3116 to determine polarization percentages and polarization position angles. Observations from the four individual spectral windows are presented in separate panels. For each panel, the best fits of polarization percentage, polarization position angle (in the receiver frame; PA), and a constant normalized Stokes Q offsets (Q offset) are provided in the upper left, which are represented by a black curve. For each observed frequency, the errors of fitted quantities were determined by one standard deviation of fittings of 1000 random realizations of noisy data. The gray lines in each panel plot 1 in every 100 of the random realizations. |
The Stokes I intensity of Sgr A* may vary with time, but this variation cannot be clearly distinguished given our present flux calibration accuracy (Fig. 2). In addition, we find that Sgr A* and the gain calibrator J1744-3116 have fractional amplitude differences that are several times higher between the XX and the YY correlations than what is found for the continuum emission of Titan. From the <100 m baselines, the XX/YY flux ratios of Titan measured in spw 0, 1, 2, and 3, are 0.99, 0.98, 1.0, and 1.0, respectively. This indicates that the relative amplitude differences of Sgr A* and J1744-3116 cannot be attributed to decoherence due to phase errors. The observed XX and YY amplitudes of the gain calibrator J1744-3116 can be fitted to yield Stokes I = 252 mJy, with 7.9% ± 0.9% polarization in position angle PA = 14°± 4.2°, and a constant normalized Stokes Q offset δ = −0.02 ± 0.02, which may be caused by amplitude calibration errors or polarization leakage (Fig. 3). However, the XX and YY amplitudes of Sgr A* obtained from the inner seven mosaic fields do not vary smoothly with parallactic angle. To the first order, taking the intensity ratio of these two correlations removes the total intensity variations. Plotting the XX to YY intensity ratio versus parallactic angle from the 12 m Array observations shows a peak at a parallactic angle of −22°, with an intensity ratio close to 1 around parallactic angle +20°, From a least squares fit to a constant polarization position angle, the measured XX to YY intensity ratios for Sgr A* are consistent with the polarization percentage of ~14% ± 1.2% and a position angle of ~158°± 3° (Fig. 4). For comparison, previously measured polarization position angles at 340 GHz were ~136°−163°, and showed variations on daily timescales (Marrone et al. 2006a). The imperfect fits shown in Fig. 4, if not due to calibration issues (for further discussion see Sect. 4), may be attributed to time variation in the polarization percentage and position angles during the period of our ALMA observations. However, we cannot easily verify this without observing and calibrating the XY and YX cross-correlations. We refer to Bower et al. (2003) and Marrone et al. (2006a) for the observational evidence and discussion of polarization percentage variability at the 230 and the 340 GHz bands. We refer to Eckart et al. (2006), Fish et al. (2009), Zamaninasab et al. (2010) and references therein, for modeling frameworks of the polarized emission.
To determine whether there might be a spurious polarization signal due to the heterogeneity of dishes in the 12 m array, we split the 12 m array visibility data into subsets containing only correlation products between the DA antennas, only correlation products between the DV antennas, and a subset containing all correlation products between the DA and the DV antennas. We obtained identical measurements from these three subsets. Therefore, we are convinced that there is no detectable spurious polarization due to the different DA and DV antenna designs. There were only two PM antennas in our 12 m array observations, so we could not reliably check their cross-correlation products independently. Nevertheless, we found that including or excluding the PM antennas does not significantly change our measurements. The XX and YY intensity differences of Sgr A* observed in the four spectral windows are also consistent (Fig. 5).
 |
Fig. 4 Normalized intensity difference of the XX and YY correlations of Sgr A*, observed by the ALMA 12 m array (symbols), and a black curve representing our best fit to these data. The constant polarization percentage and polarization position angle obtained from our best fit model are 14% ± 1.2% and 158°± 3°, respectively. The gray curves show 50 independent random realizations of models with constant polarization percentage and polarization position angle, which characterize the error bars we give. We caution that these quantities are not fully constrained without the measurements of the XY and YX correlations. |
3.2. Spectral line data
We are not aware of any mechanism that can uniformly polarize Ci line emission to a high percentage over our mosaic field of view. Thermal continuum emission of Titan is also not known to be polarized. Therefore, we use these observations to gauge the magnitude of spurious polarization caused by the offset of antenna response in XX and YY, and polarization leakage.
We used the Miriad task imdiff to systematically estimate the multiplicative factor that minimizes the difference between the XX and YY synthesized images of Ci in a maximum likelihood sense. We note that this multiplicative factor (hereafter 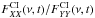 ) can depend on vlsr and time. To avoid the high noise at the edge of the 12 m array mosaic field, we limited the derivation of
) can depend on vlsr and time. To avoid the high noise at the edge of the 12 m array mosaic field, we limited the derivation of 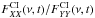 to a box-shaped region containing the most significant Ci emission. The coordinates of the bottom left and top right corners of this region are RA (J2000) = 17h45m41
to a box-shaped region containing the most significant Ci emission. The coordinates of the bottom left and top right corners of this region are RA (J2000) = 17h45m41 332, and Dec (J2000) = −29°00′56
332, and Dec (J2000) = −29°00′56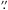 77 and RA (J2000) = 17h45m38
77 and RA (J2000) = 17h45m38 885, and Dec (J2000) = −28°59′56
885, and Dec (J2000) = −28°59′56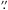 77, respectively. We verify that using the full images for estimating
77, respectively. We verify that using the full images for estimating 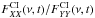 does not change the results, although it can affect the noise behavior. We also measured the XX to YY amplitude ratio of the 12 m array continuum observations of Titan, using the same method. The continuum emission from Titan shows a ~3% intensity difference between the XX and the YY correlations. The XX to YY continuum intensity ratios of both Sgr A* and Titan are shown in Fig. 2.
does not change the results, although it can affect the noise behavior. We also measured the XX to YY amplitude ratio of the 12 m array continuum observations of Titan, using the same method. The continuum emission from Titan shows a ~3% intensity difference between the XX and the YY correlations. The XX to YY continuum intensity ratios of both Sgr A* and Titan are shown in Fig. 2.
We define 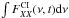 /∫dν =
/∫dν = 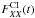 and
and 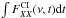 /∫dt =
/∫dt = 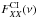 . In practice, we measured
. In practice, we measured 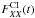 /
/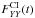 of the 12 m array observations from spectral channels which are dominated by Ci emission (the case in which it is dominated by absorption is described below), for each of the target source scans (i.e., every time period bracketed by two adjacent gain calibration scans).
of the 12 m array observations from spectral channels which are dominated by Ci emission (the case in which it is dominated by absorption is described below), for each of the target source scans (i.e., every time period bracketed by two adjacent gain calibration scans). 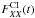 /
/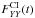 for the ACA observations were measured in the same way, but over the entire ACA observing period. We also measured
for the ACA observations were measured in the same way, but over the entire ACA observing period. We also measured 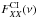 /
/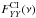 for every 2.5 km s-1 wide velocity channels by averaging over all 12 m array integrations. However, we were not able to obtain a meaningful constraint of
for every 2.5 km s-1 wide velocity channels by averaging over all 12 m array integrations. However, we were not able to obtain a meaningful constraint of 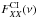 /
/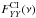 from the ACA observations owing to their limited sensitivity. Figure 6 shows the measured
from the ACA observations owing to their limited sensitivity. Figure 6 shows the measured 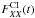 /
/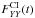 and
and 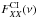 /
/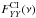 from our observations.
from our observations.
Extended emission from the Ci line is detected in channels over a range of velocities, following a similar velocity field to that of the molecular circumnuclear disk (Guesten et al. 1987; Wright et al. 2001; Liu et al. 2012, 2013, and references therein). Examples of the Ci line velocity channel synthesized images from the 12 m array observations, are given in Fig. 7. The CI emission will be discussed in more detail in a separate paper (Liu et al., in prep.). However, we found that for several velocity channels around vlsr ~ 20 km s-1, the extended CI line emission from the Galactic center is nearly completely absorbed by foreground gas. In these channels, the dominant feature is absorption against the continuum emission of Sgr A*, which is not spatially resolved by our observations.
 |
Fig. 5 Intensity ratio (XX-YY)/I of Sgr A*. Observations from each of the four spectral windows are presented in separate panels. The blue lines show the best fit in Fig. 4. |
At the same velocity as the absorption feature we detect a local maximum of 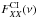 /
/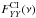 (Fig. 6). The local peak value of
(Fig. 6). The local peak value of 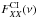 /
/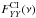 is ~1.3 (or 0.11 in logarithmic units). This peak value of
is ~1.3 (or 0.11 in logarithmic units). This peak value of 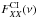 /
/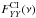 is consistent within 1σ with the XX and YY continuum intensity ratio of Sgr A* measured from the inner seven fields mosaic of the 12 m array observations. In fact, the three most prominent absorption line features of Ci against the continuum emission of the Sgr A*, consistently present a deeper absorption feature in XX correlation than in YY (Fig. 8). In the ACA observations, the difference of the absorption line intensities between the XX and the YY correlations are lower than the 1σ noise level of the ACA observations.
is consistent within 1σ with the XX and YY continuum intensity ratio of Sgr A* measured from the inner seven fields mosaic of the 12 m array observations. In fact, the three most prominent absorption line features of Ci against the continuum emission of the Sgr A*, consistently present a deeper absorption feature in XX correlation than in YY (Fig. 8). In the ACA observations, the difference of the absorption line intensities between the XX and the YY correlations are lower than the 1σ noise level of the ACA observations.
The ratio 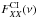 /
/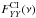 is close to 1 in the remaining velocity channels with significant emission. The standard deviation of
is close to 1 in the remaining velocity channels with significant emission. The standard deviation of 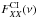 /
/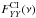 ,
, 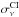 , measured from velocity channels away from vlsr = 20 km s-1 (Fig. 6), is 0.043. For the velocity range in which we significantly detected Ci, the value of [Max(
, measured from velocity channels away from vlsr = 20 km s-1 (Fig. 6), is 0.043. For the velocity range in which we significantly detected Ci, the value of [Max(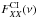 /
/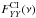 ) − Mean(
) − Mean(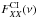 /
/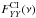 )]/
)]/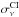 is 7.8 (Fig. 6). We have visually inspected the XX and YY intensity maps (IXX(ν,t), IYY(ν,t))2, and the residual R(ν,t)≡IXX(ν,t) – (
is 7.8 (Fig. 6). We have visually inspected the XX and YY intensity maps (IXX(ν,t), IYY(ν,t))2, and the residual R(ν,t)≡IXX(ν,t) – (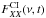 /
/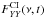 ) ×IYY(ν,t). Based on the statistics of pixel values and on our visual inspection of the images we found that R(ν,t) and its time integration are consistent with thermal noise. On the other hand, we found that for spectral channels away from vlsr ~ 20 km s-1, IXX(ν,t)−1.3 × IYY(ν,t) presents significant (i.e., >3σ) features of oversubtraction.
) ×IYY(ν,t). Based on the statistics of pixel values and on our visual inspection of the images we found that R(ν,t) and its time integration are consistent with thermal noise. On the other hand, we found that for spectral channels away from vlsr ~ 20 km s-1, IXX(ν,t)−1.3 × IYY(ν,t) presents significant (i.e., >3σ) features of oversubtraction.
Figure 6 and 8 may be understood considering the radiative transfer equation Tb = (Tex − Tbg)(1 − e− τ), where Tb is the observed Ci brightness temperature, Tex is the gas excitation temperature, Tbg is the background brightness temperature, and τ is the optical depth of the gas. For the foreground Ci absorption against the continuum emission of Sgr A*, it is safe to assume that Tex is negligible and that the gas optical depth τ is identical for the orthogonal linear polarizations X and Y. The assumption of the identical gas optical depth τ for the X and Y polarizations can be supported by the observed XX/YY ~ 1 from the emission line (Fig. 6). Therefore, the Ci absorption line ratio of the XX and YY correlations is expected to be nearly identical to the XX/YY flux ratio of the continuum emission of Sgr A*.
 |
Fig. 6 Top panel: derived intensity ratio between the XX and the YY correlations ( |
4. Discussion
The significant difference between the XX and YY correlations can be used to make a reliable determination of Stokes Q at 492 GHz. However lacking the cross-correlations XY and YX, which were not sampled in these observations, we are not able to determine Stokes U. Nevertheless, the ALMA observations give a meaningful lower limit on the linear polarization continuum emission from Sgr A* at this highest frequency that has been studied in polarization of any submillimeter bands available on interferometric arrays to date. The maximum of the intensity differences between the XX and the YY correlations observed from the ~492 GHz continuum emission of Sgr A* (diff(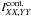 ), hereafter) implies a ~14% ± 1.2% lower limit on its polarization percentage.
), hereafter) implies a ~14% ± 1.2% lower limit on its polarization percentage.
Potential causes of the observed diff(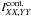 ) are synchrotron emission from ionized gas close to Sgr A* (Falcke et al. 1998; Aitken et al. 2000; Bower et al. 2001, 2003; Marrone et al. 2006a; Bromley et al. 2001; Liu et al. 2007; Huang et al. 2009), or instrumental effects including (1) beam squint; (2) relative drifts of instrumental gain-amplitude between the XX and YY correlations, (3) phase decoherence for a certain polarization; and (4) primary beam polarization. As addressed in Sect. 2, we find no evidence that the decoherence due to phase errors can lead to the differences of intensities measured by the XX and YY correlations. In addition, our analysis of the Ci line emission has ruled out the possibilities that the relative drifts of instrumental gain-amplitude and the effects of phase decoherence can lead to the observed diff(
) are synchrotron emission from ionized gas close to Sgr A* (Falcke et al. 1998; Aitken et al. 2000; Bower et al. 2001, 2003; Marrone et al. 2006a; Bromley et al. 2001; Liu et al. 2007; Huang et al. 2009), or instrumental effects including (1) beam squint; (2) relative drifts of instrumental gain-amplitude between the XX and YY correlations, (3) phase decoherence for a certain polarization; and (4) primary beam polarization. As addressed in Sect. 2, we find no evidence that the decoherence due to phase errors can lead to the differences of intensities measured by the XX and YY correlations. In addition, our analysis of the Ci line emission has ruled out the possibilities that the relative drifts of instrumental gain-amplitude and the effects of phase decoherence can lead to the observed diff(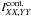 ) in continuum emission (Sect. 3.2). Beam squint does not apply to the observations on the central field (field 0, see Fig. 1). The observed diff(
) in continuum emission (Sect. 3.2). Beam squint does not apply to the observations on the central field (field 0, see Fig. 1). The observed diff(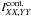 ) from the other mosaic fields also appears too big to be explained by beam squint, unless the actual primary beam response functions of the ALMA antennas seriously deviate from the present understanding. Nevertheless, the comparisons of the diff(
) from the other mosaic fields also appears too big to be explained by beam squint, unless the actual primary beam response functions of the ALMA antennas seriously deviate from the present understanding. Nevertheless, the comparisons of the diff(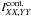 ) taken from the pairs of fields (18, 25), (94, 101), and (133, 134), which were observed closely in time, empirically provide a limit on the scale of beam squint effects (Fig. 2). Each two exposures of these three pairs of fields show rather consistent diff(
) taken from the pairs of fields (18, 25), (94, 101), and (133, 134), which were observed closely in time, empirically provide a limit on the scale of beam squint effects (Fig. 2). Each two exposures of these three pairs of fields show rather consistent diff(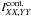 ), which may indicate that there is no significant variation of polarization on the very short timescales probed by their time separations. Primary beam polarization cannot explain the observed highest diff(
), which may indicate that there is no significant variation of polarization on the very short timescales probed by their time separations. Primary beam polarization cannot explain the observed highest diff(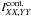 ) from the central field (i.e. Field 0, see Fig. 2), and cannot explain the frequency dependence of
) from the central field (i.e. Field 0, see Fig. 2), and cannot explain the frequency dependence of 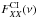 /
/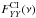 (Fig. 6). We are not aware of other instrumental defects that can cause similar effects, and consider polarized synchrotron emission as the most probable explanation for the diff(
(Fig. 6). We are not aware of other instrumental defects that can cause similar effects, and consider polarized synchrotron emission as the most probable explanation for the diff(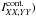 we measured from Sgr A*.
we measured from Sgr A*.
The ~14% ± 1.2% polarization percentage and 158°± 3° polarization position angle of the continuum emission of Sgr A* appear realistic when compared with previous (sub)millimeter observations in other frequency bands (Aitken 2000; Bower et al. 2003, 2005; Marrone et al. 2006a, 2007), despite the large time separation between these observations (Figs. 9, 10). In particular, Marrone et al. (2007) reported the fitted intrinsic polarization position angle χ0 = 167°± 7° and the rotation measure RM = (−5.6 ± 0.7) × 105 rad m-2, which implies a 155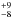 ° polarization position angle at 492 GHz. This is consistent with our new measurement of the polarization position angle within 1σ. Least squares fitting of our measured polarization position angle at 492 GHz, together with the records provided by Bower et al. (2003, 2005), Macquart et al. (2006), and Marrone (2006a, 2007), yield χ0 = 167°± 7° and RM = (−4.9 ± 1.2) × 105 rad m-2, which essentially cannot be distinguished from the fitting results of Marrone et al. (2007), and the results of χ0 = 168°± 8° and RM = (−4.4 ± 0.3) × 105 rad m-2 given by Macquart et al. (2006). We note that there is a discrepancy between the intrinsic polarization position angle determined with millimeter and submillimeter band observations, and the PA determined with near infrared observations (Eckart et al. 2006; Shahzamanian et al. 2015). Assuming a thin Keplerian rotating disk geometry of the accretion flow, and the toroidal magnetic field perpendicular to the rotating axis, this nearly 90° flip of polarization position angle may be interpreted by the spatially (projected) shifted dominant polarization emission area, when the observations move gradually from the optically thicker (low frequency) to the optically thinner (high frequency) regime (e.g., Bromley et al. 2001; Liu et al. 2007; Huang et al. 2009). Therefore, knowing the exact frequency at which the 90° polarization position angle flip occurs will provide a particularly important constraint on the accretion flow model. By comparing the Stokes I flux density we detected at 492 GHz with previous observations at lower frequencies (Marrone et al. 2006b), we found that the 492 GHz emission is very likely to be in the transition from the optically thick to the optically thin regime of the spectrum. Our 492 GHz measurement does not yet present the suggested 90° flip of polarization position angle, which may suggest that the blueshifted side of the accretion flow does not yet fully dominate the polarized emission at this observing frequency (Huang et al. 2009). Our observing frequency may not be high enough to research the turning point of polarization position angle, which is expected to be >1 THz in some recent radiative transfer modelings (Liu et al. 2007; Huang et al. 2009). In addition, the accuracy of the comparison of the Stokes I flux densities is affected by the large time separations of those measurements. Therefore, whether our 492 GHz observations were indeed probing the optically thin regime is uncertain. Resolving the nature of this discrepancy will require future coordinated monitoring observations.
° polarization position angle at 492 GHz. This is consistent with our new measurement of the polarization position angle within 1σ. Least squares fitting of our measured polarization position angle at 492 GHz, together with the records provided by Bower et al. (2003, 2005), Macquart et al. (2006), and Marrone (2006a, 2007), yield χ0 = 167°± 7° and RM = (−4.9 ± 1.2) × 105 rad m-2, which essentially cannot be distinguished from the fitting results of Marrone et al. (2007), and the results of χ0 = 168°± 8° and RM = (−4.4 ± 0.3) × 105 rad m-2 given by Macquart et al. (2006). We note that there is a discrepancy between the intrinsic polarization position angle determined with millimeter and submillimeter band observations, and the PA determined with near infrared observations (Eckart et al. 2006; Shahzamanian et al. 2015). Assuming a thin Keplerian rotating disk geometry of the accretion flow, and the toroidal magnetic field perpendicular to the rotating axis, this nearly 90° flip of polarization position angle may be interpreted by the spatially (projected) shifted dominant polarization emission area, when the observations move gradually from the optically thicker (low frequency) to the optically thinner (high frequency) regime (e.g., Bromley et al. 2001; Liu et al. 2007; Huang et al. 2009). Therefore, knowing the exact frequency at which the 90° polarization position angle flip occurs will provide a particularly important constraint on the accretion flow model. By comparing the Stokes I flux density we detected at 492 GHz with previous observations at lower frequencies (Marrone et al. 2006b), we found that the 492 GHz emission is very likely to be in the transition from the optically thick to the optically thin regime of the spectrum. Our 492 GHz measurement does not yet present the suggested 90° flip of polarization position angle, which may suggest that the blueshifted side of the accretion flow does not yet fully dominate the polarized emission at this observing frequency (Huang et al. 2009). Our observing frequency may not be high enough to research the turning point of polarization position angle, which is expected to be >1 THz in some recent radiative transfer modelings (Liu et al. 2007; Huang et al. 2009). In addition, the accuracy of the comparison of the Stokes I flux densities is affected by the large time separations of those measurements. Therefore, whether our 492 GHz observations were indeed probing the optically thin regime is uncertain. Resolving the nature of this discrepancy will require future coordinated monitoring observations.
 |
Fig. 7 Left to right columns: XX, YY, XX − YY, and XX – aCI(ν)YYsynthesized intensity maps of selected velocity channels. These images were generated using the 12 m array data only (Sect. 2), and were further tapered by a Gaussian weighting function of |
We note that the polarization position angle observed in the 230 GHz band is reported to present a larger time variability than that observed in the 340 GHz band (see also Fig. 9). Bower et al. (2005) favored an interpretation in which the variation is attributed to variations in the medium through which the polarization propagates (i.e. the variation of rotation measure), and thereby proposed a scenario of a hot and turbulent accretion flow. Contrary to this view, Marrone et al. (2007) argued that the observed time variation of the polarization position angle is more likely due to variation of the emission source itself. Since we only have a single epoch of observations at 492 GHz, it is possible that the consistency of our observed polarization position angle with the extrapolation of the previous observations is merely a coincidence. We cannot yet distinguish between these two proposed scenarios, This will require future multi-epoch observations. We note, however, that these two scenarios are not mutually exclusive.
As indicated in recent studies, Sgr A* is believed to be the source for major episodical events manifested by large flares that have luminosities up to 1041−42 erg s-1. The time interval between such events is about 100 yr, as suggested by the front of fluorescent X-ray emission propagating away from Sgr A* (Ponti et al. 2010; Clavel et al. 2013). Such extraordinary X-ray flares are also expected from the statistical analysis of Sgr A* flux density fluctuations observed in the past decades in the near-IR band (Witzel et al. 2012). In comparison to measurements made about 10 yr ago, our new measurements of the rotation measure with ALMA may imply that both the accretion rate to and the magnetic configuration around Sgr A* have not significantly changed in the past decade. No extraordinary flares have been found from the monitoring programs at multiple wavelengths ranging from radio, submillimeter, IR to X-ray performed over the past decade. Our current results may be expected given this inactivity of the source. We note that the total flux density may have varied by ~50% during our observations (see Fig. 2); however, this effect might also result from pointing errors or other calibration problems in these observations. More frequent calibrations in future observation will provide the robustness required for addressing this point.
Finally, our simple analysis technique can also be applied to ALMA observations of quasars used as gain calibrators in order to generate a large database of rotation measures. A similar technique has been used to estimate the rotation measure of PKS 1830-211. For details see Marti-Vidal et al. (2015, 2016; we note an updated instrumental parameter and thereby results from 2015 to 2016).
 |
Fig. 8 Line spectra of Ci taken from a single synthesized beam area surrounding Sgr A*. The blue and red lines present the XX and YY polarizations. |
 |
Fig. 9 Observed polarization position angle of Sgr A* at 492 GHz, compared with prior data from Aitken et al. (2000), Bower et al. (2003, 2005), the mean of Macquart et al. (2006), and Marrone et al. (2006a, 2007). The polarization position angles of the data from Macquart et al. (2006) were unwrapped by −180°. We overplot the mean fitted intrinsic polarization position angle the and rotation measure by Marrone et al. (2007), and the updated fit including our measurement at 492 GHz. Gray curves show 50 independent random realizations which characterize our fitting errors. We note that our fitting error is not well-defined, because our observations did not include the XY and YX cross correlations. We omit error bars due to the crowded data points. However, we note that the scattering of data points due to actually observed time variations (e.g. Bower et al. 2005; Marrone et al. 2006a, 2007), is more significant than the measurement errors. Therefore, the data we present in this figure are adequate for providing the sense of uncertainty in rotation measure. The same arguments are relevant to Fig. 10. |
 |
Fig. 10 Observed polarization percentage of Sgr A* at 492 GHz plotted together with prior data from Aitken et al. (2000), Bower et al. (2003, 2005), the mean of Macquart et al. (2006), and Marrone et al. (2006a, 2007). We overplot the power-law models with indices of 1.0, 2.0, 2.5 and 4, which were presented by Bower et al. (2003) using dashed lines. |
5. Conclusions
We have performed Band 8 (479−482 GHz; 489−493 GHz) mosaic observations of the Galactic center, using the ALMA 12 m array and the ACA. The observed Stokes I flux density of Sgr A* at 492 GHz is 3.6 ± 0.72 Jy. We hypothesize that the continuum emission of Sgr A* and the Ci absorption line against Sgr A* exhibit substantial intensity differences between the XX and the YY correlations. However, the XX and YY intensities of the Ci line emission are essentially identical, at all velocity channels for which there is significant emission and over the entire time period of the 12 m array observations. The maximum value of the observed intensity differences from Sgr A* implies a ~14% ± 1.2% lower limit on the polarization percentage. A comparable or even higher polarization percentage of the continuum emission of Sgr A* is expected from prior observations at other frequencies (Bower et al. 2003, 2005). The intrinsic polarization position angle we have derived from the observed XX to YY intensity ratios is ~167°, which is in surprisingly good agreement with the polarization position angles reported by the SMA observations at 230−340 GHz performed about one decade ago (Marrone et al. 2006a, 2007). Therefore, we attribute the observed intensity differences to linearly polarized synchrotron emission from hot ionized gas immediately surrounding Sgr A*. We found that the polarization percentage at our observing frequency may be varying over the time period of our 12 m array observations. Improved constraints on polarization will require new measurements that include the XY and YX correlations. We also detected 7.9% ± 0.9% polarization in position angle PA = 14°± 4.2° from the gain calibration quasar J1744-3116, which was observed on the same night as Sgr A*.
Acknowledgments
We thank our referee for the very precise and useful opinions. H.B.L. thanks ASIAA for support. H.B.L. thanks Yu-Nung Su for the help when organizing the observational proposal; and thanks Lei Huang for some basic discussion on the subject in 2004−2006. This paper makes use of the following ALMA data: ADS/JAO.ALMA 2013.1.00071.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada) and NSC and ASIAA (Taiwan), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. We thank Aaron Evans and Todd Hunter for providing information about the ALMA primary beams. We thank Shin’ichiro Asayama, Ted Huang, Hiroshi Nagai, Dirk Petry, George Moellenbrock and Charles Hull for providing clarification on the ALMA feed orientation.
References
- Aitken, D. K., Greaves, J., Chrysostomou, A., et al. 2000, ApJ, 534, L173 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, G. C., Backer, D. C., Zhao, J.-H., Goss, M., & Falcke, H. 1999a, ApJ, 521, 582 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, G. C., Falcke, H., & Backer, D. C. 1999b, ApJ, 523, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, G. C., Wright, M. C. H., Backer, D. C., & Falcke, H. 1999c, ApJ, 527, 851 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, G. C., Wright, M. C. H., Falcke, H., & Backer, D. C. 2001, ApJ, 555, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, G. C., Falcke, H., Sault, R. J., & Backer, D. C. 2002, ApJ, 571, 843 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, G. C., Wright, M. C. H., Falcke, H., & Backer, D. C. 2003, ApJ, 588, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, G. C., Falcke, H., Wright, M. C., & Backer, D. C. 2005, ApJ, 618, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Bromley, B. C., Melia, F., & Liu, S. 2001, ApJ, 555, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Clavel, M., Terrier, R., Goldwurm, A., et al. 2013, A&A, 558, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eckart, A., Schödel, R., Meyer, L., et al. 2006, A&A, 455, 1 [Google Scholar]
- Falcke, H., & Markoff, S. 2000, A&A, 362, 113 [NASA ADS] [Google Scholar]
- Falcke, H., Goss, W. M., Matsuo, H., et al. 1998, ApJ, 499, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Falcke, H., Markoff, S., & Bower, G. C. 2009, A&A, 496, 77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fish, V. L., Doeleman, S. S., Broderick, A. E., Loeb, A., & Rogers, A. E. E. 2009, ApJ, 706, 1353 [NASA ADS] [CrossRef] [Google Scholar]
- Ghez, A. M., Salim, S., Hornstein, S. D., et al. 2005, ApJ, 620, 744 [NASA ADS] [CrossRef] [Google Scholar]
- Gillessen, S., Eisenhauer, F., Trippe, S., et al. 2009, ApJ, 692, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Guesten, R., Genzel, R., Wright, M. C. H., et al. 1987, ApJ, 318, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, L., Liu, S., Shen, Z.-Q., et al. 2009, ApJ, 703, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, M. D., Fish, V. L., Doeleman, S. S., et al. 2015, Science, 350, 1242 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, S., Qian, L., Wu, X.-B., Fryer, C. L., & Li, H. 2007, ApJ, 668, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, H. B., Hsieh, P.-Y., Ho, P. T. P., et al. 2012, ApJ, 756, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, H. B., Ho, P. T. P., Wright, M. C. H., et al. 2013, ApJ, 770, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Macquart, J.-P., Bower, G. C., Wright, M. C. H., Backer, D. C., & Falcke, H. 2006, ApJ, 646, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Marrone, D. P., Moran, J. M., Zhao, J.-H., & Rao, R. 2006a, ApJ, 640, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Marrone, D. P., Moran, J. M., Zhao, J.-H., & Rao, R. 2006b, J. Phys. Conf. Ser., 54, 354 [Google Scholar]
- Marrone, D. P., Moran, J. M., Zhao, J.-H., & Rao, R. 2007, ApJ, 654, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Martí-Vidal, I., Muller, S., Vlemmings, W., Horellou, C., & Aalto, S. 2015, Science, 348, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Marti-Vidal, I., Vlemmings, W. H. T., & Muller, S. 2016, A&A, in press, DOI: 10.1051/0004-6361/201628225 [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, Astronomical Data Analysis Software and Systems XVI, 376, 127 [NASA ADS] [Google Scholar]
- Muñoz, D. J., Marrone, D. P., Moran, J. M., & Rao, R. 2012, ApJ, 745, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Ponti, G., Terrier, R., Goldwurm, A., Belanger, G., & Trap, G. 2010, ApJ, 714, 732 [NASA ADS] [CrossRef] [Google Scholar]
- Sault, R. J., & Macquart, J.-P. 1999, ApJ, 526, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Sault, R. J., Teuben, P. J., & Wright, M. C. H. 1995, Astronomical Data Analysis Software and Systems IV, 77, 433 [Google Scholar]
- Schödel, R., Ott, T., Genzel, R., et al. 2002, Nature, 419, 694 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Shahzamanian, B., Eckart, A., Valencia-S., M., et al. 2015, A&A, 576, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Witzel, G., Eckart, A., Bremer, M., et al. 2012, ApJS, 203, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, M. C. H., Coil, A. L., McGary, R. S., Ho, P. T. P., & Harris, A. I. 2001, ApJ, 551, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, F., & Narayan, R. 2014, ARA&A, 52, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Zamaninasab, M., Eckart, A., Witzel, G., et al. 2010, A&A, 510, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhao, J.-H., Young, K. H., Herrnstein, R. M., et al. 2003, ApJ, 586, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, J.-H., Herrnstein, R. M., Bower, G. C., Goss, W. M., & Liu, S. M. 2004, ApJ, 603, L85 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Observed flux densities of Sgr A* (from a vector averaging at Sgr A* in the visibility domain prior to correction of primary beam attenuation).
All Figures
 |
Fig. 1 Central 7 mosaic fields of the 12 m-Array observations. The black circle shows the field (FWHM) centered on Sgr A*. Gray circles show the 6 fields which are the nearest to the central one. The diameter of these circles is |
| In the text | |
 |
Fig. 2 Top: flux density measurements of Sgr A*, from images made using only the inner 7 mosaic fields of the 12 m array, and the flux density of Sgr A* from an average of the ACA observations, are both plotted against time. Error bars in the horizontal direction represent the scan duration. Vertical error bars in the upper panel include both the uncertainty on the pointing (~1′′) and the uncertainty on the primary beam response function. The vertical error bar of the ACA data additionally includes a potential 20% absolute flux calibration uncertainty, relative to the 12 m array observations. The horizontal error bars for the continuum data of the 12 m-Array observations are shorter than the symbol size. Bottom: intensity ratio between the XX and the YY intensity maps derived from the continuum and the Ci line observations are plotted against time. Filled black and green symbols show the 12 m array measurements from Sgr A* and Titan, respectively. Errors are negligibly small for the snapshot on field 0, which is centered on Sgr A* (see Fig. 1). The Ci line measurements are averages from high S/N spectral channels (see also Fig. 6). Their vertical error bars are given by ±1 standard deviations of the intensity ratio, which were derived from those high S/N spectral channels. |
| In the text | |
 |
Fig. 3 Fittings of the (XX-YY)/I intensity ratio of quasar J1744-3116 to determine polarization percentages and polarization position angles. Observations from the four individual spectral windows are presented in separate panels. For each panel, the best fits of polarization percentage, polarization position angle (in the receiver frame; PA), and a constant normalized Stokes Q offsets (Q offset) are provided in the upper left, which are represented by a black curve. For each observed frequency, the errors of fitted quantities were determined by one standard deviation of fittings of 1000 random realizations of noisy data. The gray lines in each panel plot 1 in every 100 of the random realizations. |
| In the text | |
 |
Fig. 4 Normalized intensity difference of the XX and YY correlations of Sgr A*, observed by the ALMA 12 m array (symbols), and a black curve representing our best fit to these data. The constant polarization percentage and polarization position angle obtained from our best fit model are 14% ± 1.2% and 158°± 3°, respectively. The gray curves show 50 independent random realizations of models with constant polarization percentage and polarization position angle, which characterize the error bars we give. We caution that these quantities are not fully constrained without the measurements of the XY and YX correlations. |
| In the text | |
 |
Fig. 5 Intensity ratio (XX-YY)/I of Sgr A*. Observations from each of the four spectral windows are presented in separate panels. The blue lines show the best fit in Fig. 4. |
| In the text | |
 |
Fig. 6 Top panel: derived intensity ratio between the XX and the YY correlations ( |
| In the text | |
 |
Fig. 7 Left to right columns: XX, YY, XX − YY, and XX – aCI(ν)YYsynthesized intensity maps of selected velocity channels. These images were generated using the 12 m array data only (Sect. 2), and were further tapered by a Gaussian weighting function of |
| In the text | |
 |
Fig. 8 Line spectra of Ci taken from a single synthesized beam area surrounding Sgr A*. The blue and red lines present the XX and YY polarizations. |
| In the text | |
 |
Fig. 9 Observed polarization position angle of Sgr A* at 492 GHz, compared with prior data from Aitken et al. (2000), Bower et al. (2003, 2005), the mean of Macquart et al. (2006), and Marrone et al. (2006a, 2007). The polarization position angles of the data from Macquart et al. (2006) were unwrapped by −180°. We overplot the mean fitted intrinsic polarization position angle the and rotation measure by Marrone et al. (2007), and the updated fit including our measurement at 492 GHz. Gray curves show 50 independent random realizations which characterize our fitting errors. We note that our fitting error is not well-defined, because our observations did not include the XY and YX cross correlations. We omit error bars due to the crowded data points. However, we note that the scattering of data points due to actually observed time variations (e.g. Bower et al. 2005; Marrone et al. 2006a, 2007), is more significant than the measurement errors. Therefore, the data we present in this figure are adequate for providing the sense of uncertainty in rotation measure. The same arguments are relevant to Fig. 10. |
| In the text | |
 |
Fig. 10 Observed polarization percentage of Sgr A* at 492 GHz plotted together with prior data from Aitken et al. (2000), Bower et al. (2003, 2005), the mean of Macquart et al. (2006), and Marrone et al. (2006a, 2007). We overplot the power-law models with indices of 1.0, 2.0, 2.5 and 4, which were presented by Bower et al. (2003) using dashed lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.