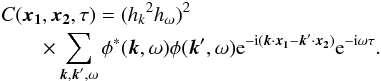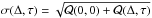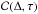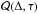| Issue |
A&A
Volume 593, September 2016
|
|
|---|---|---|
| Article Number | A41 | |
| Number of page(s) | 7 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201628129 | |
| Published online | 09 September 2016 | |
Statistics of the two-point cross-covariance function of solar oscillations
1 Max-Planck-Institut für
Sonnensystemforschung, Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany
e-mail: nagashima@mps.mpg.de
2 National Astronomical Observatory of
Japan, Mitaka,
Tokyo
181-8588,
Japan
3 Department of Astronomical Science,
SOKENDAI (the Graduate University for Advanced Studies), Mitaka, Tokyo
181-8588,
Japan
4 Institut für Astrophysik,
Georg-August-Universität Göttingen, Friedrich-Hund-Platz 1, 37077
Göttingen,
Germany
Received:
14
January
2016
Accepted:
17
June
2016
Context. The cross-covariance of solar oscillations observed at pairs of points on the solar surface is a fundamental ingredient in time-distance helioseismology. Wave travel times are extracted from the cross-covariance function and are used to infer the physical conditions in the solar interior.
Aims. Understanding the statistics of the two-point cross-covariance function is a necessary step towards optimizing the measurement of travel times.
Methods. By modeling stochastic solar oscillations, we evaluate the variance of the cross-covariance function as function of time-lag and distance between the two points.
Results. We show that the variance of the cross-covariance is independent of both time-lag and distance in the far field, that is, when they are large compared to the coherence scales of the solar oscillations.
Conclusions. The constant noise level for the cross-covariance means that the signal-to-noise ratio for the cross-covariance is proportional to the amplitude of the expectation value of the cross-covariance. This observation is important for planning data analysis efforts.
Key words: Sun: helioseismology / Sun: oscillations / methods: data analysis
© ESO, 2016
1. Introduction
Solar acoustic waves are randomly excited by turbulent convection in the upper convection zone. They propagate through the interior and are refracted by the increase of sound speed with depth. By measuring the travel times of wave packets between pairs of points on the solar surface we can probe the subsurface structure and dynamics of the Sun.
The travel time between any two points on the solar surface is measured from the cross-covariance of the oscillation signals observed at these two points. The definition of the temporal cross-covariance function between points x1 and x2 is 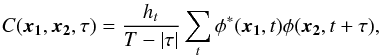 (1)where φ(xi,t) is the oscillation signal at time t and position xi on the solar surface, T is the duration of the observations, ht is the time sampling, and τ is the time lag. Duvall et al. (1993) demonstrated that wave travel times can be used to map flows and sound-speed heterogeneities in the solar interior (for a review see Gizon & Birch 2005). The cross-covariance function has, however, intrinsic noise due to the stochastic nature of solar oscillations. Understanding the statistical properties of this noise is crucial for interpreting measurements of wave travel times (Gizon & Birch 2004; Fournier et al. 2014).
(1)where φ(xi,t) is the oscillation signal at time t and position xi on the solar surface, T is the duration of the observations, ht is the time sampling, and τ is the time lag. Duvall et al. (1993) demonstrated that wave travel times can be used to map flows and sound-speed heterogeneities in the solar interior (for a review see Gizon & Birch 2005). The cross-covariance function has, however, intrinsic noise due to the stochastic nature of solar oscillations. Understanding the statistical properties of this noise is crucial for interpreting measurements of wave travel times (Gizon & Birch 2004; Fournier et al. 2014).
In practice, wave travel times are estimated by fitting a model to the cross-covariance function. In the standard approach, the fitting parameters p are obtained by minimizing a merit function X(p) using the least-squares method, where ![\begin{eqnarray} X(\vec{p}) = \sum_i f(t_i) \left[C_{\mathrm{obs}}(t_i)-C_{\mathrm{model}}(t_i; \vec{p}) \right]^2, \label{eq:chisq_constc} \end{eqnarray}](/articles/aa/full_html/2016/09/aa28129-16/aa28129-16-eq12.png) (2)and f(ti) is the window function (e.g., to isolate the first bounce part of the cross-covariance function). The function Cobs(ti) is the observed cross-covariance function at time lag ti and Cmodel(ti;p) is the model cross-covariance function. Duvall et al. (1997) and Kosovichev & Duvall (1997) used a Gabor wavelet with five parameters to model the cross-covariance function, while Gizon & Birch (2002) performed one-parameter fits to measure the time shift compared to a reference cross-covariance function. Gizon & Birch (2004) simplified the definition of Gizon & Birch (2002) in the limit of small travel-time shifts; this linearized form is more robust to noise.
(2)and f(ti) is the window function (e.g., to isolate the first bounce part of the cross-covariance function). The function Cobs(ti) is the observed cross-covariance function at time lag ti and Cmodel(ti;p) is the model cross-covariance function. Duvall et al. (1997) and Kosovichev & Duvall (1997) used a Gabor wavelet with five parameters to model the cross-covariance function, while Gizon & Birch (2002) performed one-parameter fits to measure the time shift compared to a reference cross-covariance function. Gizon & Birch (2004) simplified the definition of Gizon & Birch (2002) in the limit of small travel-time shifts; this linearized form is more robust to noise.
As an alternative procedure, Couvidat et al. (2006) proposed using ![\begin{equation} X(\vec{p}) = \sum_i \frac{f(t_i)}{\sigma_i^2} \left[C_{\mathrm{obs}}(t_i)-C_{\mathrm{model}}(t_i; \vec{p}) \right]^2 , \label{eq:chisq_sigma} \end{equation}](/articles/aa/full_html/2016/09/aa28129-16/aa28129-16-eq17.png) (3)where
(3)where 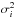 is the variance of the cross-covariance function at time lag ti. Couvidat et al. (2006) estimated the variance using a Monte-Carlo approach and the method proposed by Gizon & Birch (2004): many realizations of the cross-covariance function were generated using a model that depends only on the observed oscillation power spectrum. The assumptions of the model are temporal stationarity and spatial homogeneity. Couvidat et al. (2006) mentioned that Eqs. (2) and (3) lead to different travel times in the short-distance case, but did not explain why, nor did they discuss the dependence of σi on time lag ti.
is the variance of the cross-covariance function at time lag ti. Couvidat et al. (2006) estimated the variance using a Monte-Carlo approach and the method proposed by Gizon & Birch (2004): many realizations of the cross-covariance function were generated using a model that depends only on the observed oscillation power spectrum. The assumptions of the model are temporal stationarity and spatial homogeneity. Couvidat et al. (2006) mentioned that Eqs. (2) and (3) lead to different travel times in the short-distance case, but did not explain why, nor did they discuss the dependence of σi on time lag ti.
In this paper we discuss some properties of the noise in the cross-covariance function. First, we evaluate the variance and covariance of the cross-covariance function in a stochastic oscillation model. We then show that for some standard situations (far field) the variance of the cross-covariance function is nearly independent of both time lag and distance between the observation points, while this is not the case in the near field.
We note that in this paper we discuss the two-point (point-to-point) cross-covariance function. In typical helioseismology travel-time measurements, point-to-annulus cross-covariance functions are widely used to increase the signal-to-noise ratio; the oscillation signal averaged over an annulus and the oscillation signal at the central point of the annulus are used to calculate the cross-covariance function. Discussions on such geometry are found in Gizon & Birch (2004).
2. Variance of the cross-covariance function
In this paper we use a stochastic oscillation model to determine the variance and covariance of the cross-covariance function. We use the model of Gizon & Birch (2004), which is itself a generalization of the standard model for realization noise in global helioseismology (e.g., Woodard 1984; Appourchaux et al. 2000). Throughout this paper we use the notation of Gizon & Birch (2004).
The observed signal φ(x,t) is sampled with temporal cadence ht and spatial sampling hx over a duration T = Ntht and an area L2 with L = Nxhx. Using the horizontal wavevector k and the angular frequency ω, we denote the Fourier transform of the oscillation signal by 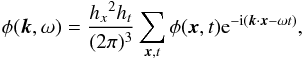 (4)and the inverse Fourier transform by
(4)and the inverse Fourier transform by 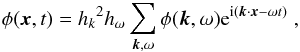 (5)where hk = 2π/L and hω = 2π/T. The notation ∑ t means that the sum is over times tj = jht where j is an integer in the range [− Nt/ 2,Nt/2−1]. Here we assume Nt is even. We note that since φ(x,t) is real, we have φ(−k, −ω) = φ∗(k,ω). Using the Fourier transform of φ, we can rewrite the cross-covariance function (Eq. (1)) as
(5)where hk = 2π/L and hω = 2π/T. The notation ∑ t means that the sum is over times tj = jht where j is an integer in the range [− Nt/ 2,Nt/2−1]. Here we assume Nt is even. We note that since φ(x,t) is real, we have φ(−k, −ω) = φ∗(k,ω). Using the Fourier transform of φ, we can rewrite the cross-covariance function (Eq. (1)) as
For the sake of simplicity we assumed φ is cyclic in t, that is, φ(t + T) = φ(t). A generalization is possible by applying zero-padding.
Let us define 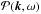 as the expectation value (ensemble average) of the power spectrum,
as the expectation value (ensemble average) of the power spectrum, ![\begin{eqnarray} \mathcal{P} (\vec{k},\omega) = E [| \phi (\vec{k},\omega) |^2] , \end{eqnarray}](/articles/aa/full_html/2016/09/aa28129-16/aa28129-16-eq42.png) (7)where E [X] denotes the expectation value of X. This quantity has the symmetry
(7)where E [X] denotes the expectation value of X. This quantity has the symmetry 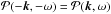 as the oscillation signal is real valued. Assuming every mode (k,ω) is excited stochastically and independently, we model the Fourier transform of the oscillation signal as
as the oscillation signal is real valued. Assuming every mode (k,ω) is excited stochastically and independently, we model the Fourier transform of the oscillation signal as 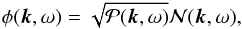 (8)where
(8)where 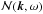 is a centered complex Gaussian random variable with unit variance and independent real and imaginary parts, i.e.,
is a centered complex Gaussian random variable with unit variance and independent real and imaginary parts, i.e., ![\hbox{$E[ \mathcal{N}(\vec{k},\omega)] =0$}](/articles/aa/full_html/2016/09/aa28129-16/aa28129-16-eq49.png) ,
, ![\hbox{$E[\mathcal{N}^*(\vec{k},\omega) \mathcal{N}(\vec{k},\omega)] =1$}](/articles/aa/full_html/2016/09/aa28129-16/aa28129-16-eq50.png) , and
, and ![\hbox{$E [ \mathcal{N}^* (\vec{k},\omega) \mathcal{N} (\vec{k}^{\prime},\omega^{\prime}) ] =0$}](/articles/aa/full_html/2016/09/aa28129-16/aa28129-16-eq51.png) if k ≠ k′ or ω ≠ ω′, but with the additional requirement that
if k ≠ k′ or ω ≠ ω′, but with the additional requirement that 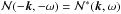 to comply with the condition that φ(x,t) is real. In this case, | φ(k,ω) | 2 has a chi-square distribution with two degrees of freedom. This model is rather general. In frequency space, it is known, from observations, to be a good description of solar oscillations (Woodard 1984; Appourchaux et al. 1998, 2000).
to comply with the condition that φ(x,t) is real. In this case, | φ(k,ω) | 2 has a chi-square distribution with two degrees of freedom. This model is rather general. In frequency space, it is known, from observations, to be a good description of solar oscillations (Woodard 1984; Appourchaux et al. 1998, 2000).
In this simple model (spatial homogeneity) the distribution function of the cross-covariance function is a normal distribution (Nagashima 2010). As a consequence, the statistical properties of the cross-covariance function are determined completely by its expectation value and variance. The expectation value of the cross-covariance function, 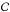 , is proportional to the inverse Fourier Transform of the power spectrum:
, is proportional to the inverse Fourier Transform of the power spectrum:
![\begin{eqnarray} &&\mathcal{C}(\vec{x_2} - \vec{x_1} , \tau) \equiv E[C(\vec{x_1},\vec{x_2},\tau)] = ({h_k}^2 h_{\omega})^2\nonumber\\ &&\qquad \qquad\times \sum_{\vec{k}, \omega} \mathcal{P} (\vec{k},\omega) {\rm e}^{{\rm i} \{\vec{k}\cdot (\vec{x_2} - \vec{x_1})-\omega \tau\}} = ({h_k}^2 h_{\omega})\mathcal{P}(\vec{x_2} - \vec{x_1} , \tau). \label{eq:EC} \end{eqnarray}](/articles/aa/full_html/2016/09/aa28129-16/aa28129-16-eq57.png) (9)The covariance of the cross-covariance function is given by
(9)The covariance of the cross-covariance function is given by ![\begin{eqnarray} &&\mathrm{Cov} [ C (\vec{x_1},\vec{x_2},\tau) ,C(\vec{x_1}^{\prime}, \vec{x_2}^{\prime}, \tau^{\prime})] = ({h_k}^2 {h_\omega})^4\nonumber\\ &&\qquad \times \sum_{\vec{k}, \vec{k}^{\prime}, \omega} \mathcal{P}(\vec{k},\omega) \mathcal{P}(\vec{k^{\prime}},\omega) \Bigl[ {\rm e}^{ -{\rm i} \{\vec{k}\cdot(\vec{x_1}-\vec{x_1}^{\prime} ) - \vec{k}^{\prime} \cdot (\vec{x_2} - \vec{x_2}^{\prime}) + \omega (\tau-\tau^{\prime})\}} \nonumber \\&&\qquad +{\rm e}^{ -{\rm i}\{ \vec{k}\cdot(\vec{x_1}-\vec{x_2}^{\prime} ) + \vec{k}^{\prime} \cdot (\vec{x_1}^{\prime} - \vec{x_2})+ \omega (\tau+\tau^{\prime}) \} } \Bigr] . \label{eq:covC} \end{eqnarray}](/articles/aa/full_html/2016/09/aa28129-16/aa28129-16-eq58.png) (10)Here the covariance of two complex variables X and Y is defined by Cov [X,Y] ≡ E [XY∗] − E [X] E [Y∗]. Detailed derivations of Eq. (10) are shown by Nagashima (2010) and Fournier et al. (2014). For the case when x1 = x1′, x2 = x2′ ≡ x1 + Δ, and τ = τ′, this simplifies to the variance of the cross-covariance function:
(10)Here the covariance of two complex variables X and Y is defined by Cov [X,Y] ≡ E [XY∗] − E [X] E [Y∗]. Detailed derivations of Eq. (10) are shown by Nagashima (2010) and Fournier et al. (2014). For the case when x1 = x1′, x2 = x2′ ≡ x1 + Δ, and τ = τ′, this simplifies to the variance of the cross-covariance function: ![\begin{eqnarray} \mathrm{Var} [ C(\vec{x_1},\vec{x_2},\tau)]&=& ({h_k}^2 {h_{\omega}})^4 \sum_{\vec{k},\vec{k}^{\prime},\omega} \mathcal{P} (\vec{k},\omega) \mathcal{P} (\vec{k^{\prime}},\omega)\nonumber\\ &&\times \left[ 1 + {\rm e}^{ {\rm i}\{ (\vec{k}+\vec{k}^{\prime}) \cdot \vec{\Delta} - \omega (2\tau)\} } \right] \nonumber \\ &=& \mathcal{Q} (\vec{0}, 0 )+ \mathcal{Q}(\vec{\Delta}, \tau ) , \label{eq:CCvariance} \end{eqnarray}](/articles/aa/full_html/2016/09/aa28129-16/aa28129-16-eq64.png) (11)where Var [X] ≡ Cov [X,X] and we have defined
(11)where Var [X] ≡ Cov [X,X] and we have defined 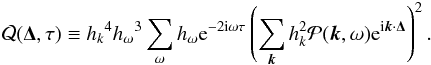 (12)The noise of the cross-covariance function is given by
(12)The noise of the cross-covariance function is given by 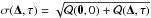 . We note that in Eq. (11) only the second term,
. We note that in Eq. (11) only the second term, 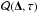 , depends on Δ and τ. This term
, depends on Δ and τ. This term 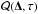 can be written in terms of
can be written in terms of 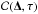 defined by Eq. (9):
defined by Eq. (9): 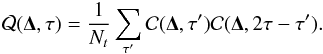 (13)This is consistent with the discussions in Gizon & Birch (2004), except that the terms involving ℱ of Eq. (C.8) of Gizon & Birch (2004) should vanish from the exact solution.
(13)This is consistent with the discussions in Gizon & Birch (2004), except that the terms involving ℱ of Eq. (C.8) of Gizon & Birch (2004) should vanish from the exact solution.
In the next section we compute 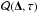 for some standard situations in helioseismology analyses. Note that
for some standard situations in helioseismology analyses. Note that  would imply that σ is independent of time lag and the distance.
would imply that σ is independent of time lag and the distance.
3. Examples
In this section, we consider two examples to show the behavior of 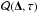 . First, we look at oscillations with a simple Gaussian distribution of power in k-ω space. Second, we consider oscillations with a solar-like power distribution. Also, by using Eq. (13), we provide a simple formula for
. First, we look at oscillations with a simple Gaussian distribution of power in k-ω space. Second, we consider oscillations with a solar-like power distribution. Also, by using Eq. (13), we provide a simple formula for 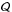 in terms of
in terms of  .
.
3.1. Wave power localized in wavenumber-frequency space
First, we consider the simplest power distribution: power localized around (kx,ky,ω) = ± (k0,0,ω0). Even in this simplest case, however, 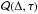 cannot be computed analytically. We simplify the computation of Eq. (12) by approximating the discrete sums over k and ω with continuous integrals. This approximation is good when 1) the wavenumber resolution (hk ∝ 1 /Nt) and frequency resolution (hω ∝ 1 /Nt) are small enough to capture the smallest scales in the power spectrum and 2) the spatial and temporal sampling rates (hx and ht) are small enough that the resulting Nyquist frequencies in space and time are larger than k0 and ω0.
cannot be computed analytically. We simplify the computation of Eq. (12) by approximating the discrete sums over k and ω with continuous integrals. This approximation is good when 1) the wavenumber resolution (hk ∝ 1 /Nt) and frequency resolution (hω ∝ 1 /Nt) are small enough to capture the smallest scales in the power spectrum and 2) the spatial and temporal sampling rates (hx and ht) are small enough that the resulting Nyquist frequencies in space and time are larger than k0 and ω0.
Consider a Gaussian power distribution of the form 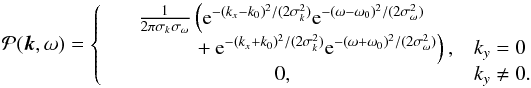 (14)The second peak of power is required to ensure that the oscillation signal is real. With this power distribution,
(14)The second peak of power is required to ensure that the oscillation signal is real. With this power distribution, ![\begin{equation} \mathcal{Q}(\Delta,\tau) = \frac{ {h_k}^4 {\rm e}^{-\sigma_k^2\Delta^2-\sigma_\omega^2 \tau^2}}{\sqrt{\pi}\sigma_\omega} \left( {\rm e}^{-\omega_0^2/\sigma_\omega^2} +\cos[2(\omega_0 \tau-k_0 \Delta)] \right) , \label{eq:inf_cont_Q_1Dgauss1} \end{equation}](/articles/aa/full_html/2016/09/aa28129-16/aa28129-16-eq85.png) (15)where Δ here is the distance in the x direction. This means that the ratio of the two terms that make up the variance of the cross-covariance function is given by
(15)where Δ here is the distance in the x direction. This means that the ratio of the two terms that make up the variance of the cross-covariance function is given by 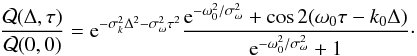 (16)Equation (16) shows that the variance of the cross-covariance function has a peak around the origin with a width of (1 /σk,1 /σω) in space and time, equal to the coherence scales of the oscillations. If Δ and τ are large compared to 1 /σk and 1 /σω, then the variance of the cross-covariance function (Eq. (11)) is independent of both Δ and τ. Therefore, the remaining task is to discuss the coherence length and coherence time.
(16)Equation (16) shows that the variance of the cross-covariance function has a peak around the origin with a width of (1 /σk,1 /σω) in space and time, equal to the coherence scales of the oscillations. If Δ and τ are large compared to 1 /σk and 1 /σω, then the variance of the cross-covariance function (Eq. (11)) is independent of both Δ and τ. Therefore, the remaining task is to discuss the coherence length and coherence time.
Figure 1 shows an example with a Gaussian power distribution in 2D. This example has a single Gaussian-shaped peak at (k0R⊙,ω0/ (2π)) = (600,3 mHz) with the widths of (σkR⊙,σω/ (2π)) = (100,0.5 mHz), where R⊙ is the solar radius. We chose these parameters as typical values of the Sun. We note that in Fig. 1a we show only k ≥ 0 and ω ≥ 0, but there is also the associated peak at (− k0, −ω0). In this case the widths in space and time (1 /σk and 1 /σω from Eq. (16)) are 7 Mm and 5 min, respectively (see vertical dotted lines in Figs. 1d and 1f). For the temporal and spatial scales larger than these coherence scales (a standard case in helioseismology analysis), the noise level is constant, that is,  .
.
Note that this simple Gaussian power distribution with typical solar values also explains the origin of the horizontal stripes that are seen in the near field (Fig. 2b) in the time-distance diagram.
 |
Fig. 1 Examples of the power spectrum in logarithmic gray scale (Panel a)) and the expectation value of the cross-covariance function (Panel b)) in the case of the Gaussian power spectrum. In Panel a) (and the same is true in Figs. 2a and 4a), larger and smaller power is indicated by black and white, respectively. The peak of the power is located at (k0R⊙,ω0/ (2π)) = (600,3 mHz) and the peak has widths (σkR⊙,σω/ (2π)) = (100,0.5 mHz). The cuts through the expectation value of the cross-covariance function at Δ = 0 and τ = 0 are shown in Panels c) and e), and the noise for the same cuts are shown in Panels d) and f). The cross-covariance (cc) function and the noise, |
Thus a Gaussian is a simple but useful model for the envelope of the power spectrum, which determines the coherence scales in time and space. The solar oscillation power spectrum has many peaks, however; we can calculate the detailed behavior of the cross-covariance function using Eq. (15) and model power spectra with multiple Gaussian peaks as well; more detailed investigation is found in Appendix A.
3.2. Solar-like oscillation power spectrum
Here we consider power spectra of solar oscillations observed by the Helioseismic and Magnetic Imager (HMI; Schou et al. 2012) on the Solar Dynamics Observatory. In one case we consider the full p-mode power spectrum. In another case we apply a phase-speed filter to isolate waves with a skip distance on the Sun of 2° (24.1 Mm) (Nagashima 2010): the filter is centered at the horizontal phase speed of vph = 36 km s-1 and has a width of 5 km s-1. For these two cases, the power spectra and the cross-covariance functions are shown in Figs. 2 and 4. To construct the power spectra, we used observations obtained from 18 UT on January 22, 2011 to 12 UT on January 26, 2011. We divided this data set into ten nine-hour segments, and in each segment we tracked the quiet region near disk center at the Carrington rotation rate using the code mtrack (Bogart et al. 2011). The mean of the azimuthally-averaged power spectra is an estimate of the expectation value 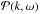 . The pixel scale is 0.03 heliographic degrees (0.36 Mm), the temporal sampling cadence is 45 s, and the field of view is 1024 pixels square. Before calculating the power spectra, we take the running difference in time for detrending, and apply spatial and temporal zero-padding to handle the non-cyclic functions in our formula.
. The pixel scale is 0.03 heliographic degrees (0.36 Mm), the temporal sampling cadence is 45 s, and the field of view is 1024 pixels square. Before calculating the power spectra, we take the running difference in time for detrending, and apply spatial and temporal zero-padding to handle the non-cyclic functions in our formula.
Figures 3 and 5 show cuts through the cross-covariance functions and the noise in cross-covariance function at Δ = 24.1 Mm and τ = 30 min. In these cases the non-constant part of the noise is small; for example, in Fig. 3b variations in noise are only 0.4% of the constant part of the noise. These examples show that the noise in the cross-covariance is independent of time lag (and thus that, in the far field, Eq. (3) can be reduced to Eq. (2)). As we mentioned in Sect. 3.1, the coherence scale of the solar oscillations is about 7 Mm and 5 min. In local helioseismology we usually care only about scales larger than these coherence scales.
By comparing Figs. 3b and 5b, or Figs. 3d and 5d, it is evident that the noise in the cross-covariance function is reduced by the phase-speed filter. Here we define a signal-to-noise ratio for the cross-covariance by ![\hbox{$\mathcal{C}(\Delta,\tau) = E[C(\Delta,\tau)]$}](/articles/aa/full_html/2016/09/aa28129-16/aa28129-16-eq119.png) is the signal and
is the signal and 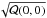 is the noise level. Since we choose the normalization factor throughout this paper as
is the noise level. Since we choose the normalization factor throughout this paper as 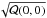 , the amplitude of the cross-covariance function in the figures directly gives the signal-to-noise ratio. The signal-to-noise ratio is 1.3 in the case without the phase-speed filter (Fig. 3a), while it is more than 5 in the case with the phase-speed filter (Fig. 5a). But with a phase-speed filter, the noise variations extend to larger time lags and the amplitude of the variations is larger as well. Therefore, we need to choose the filter carefully, considering the trade-off between the signal-to-noise ratio and the variation of the noise with time-lag and distance. This is consistent with what Duvall & Hanasoge (2013) reported about the width of the phase-speed filter and the signal-to-noise ratio of the travel time.
, the amplitude of the cross-covariance function in the figures directly gives the signal-to-noise ratio. The signal-to-noise ratio is 1.3 in the case without the phase-speed filter (Fig. 3a), while it is more than 5 in the case with the phase-speed filter (Fig. 5a). But with a phase-speed filter, the noise variations extend to larger time lags and the amplitude of the variations is larger as well. Therefore, we need to choose the filter carefully, considering the trade-off between the signal-to-noise ratio and the variation of the noise with time-lag and distance. This is consistent with what Duvall & Hanasoge (2013) reported about the width of the phase-speed filter and the signal-to-noise ratio of the travel time.
 |
Fig. 2 Example of the case of p-mode power spectrum of HMI Doppler observations: power spectra (Panel a)) in logarithmic gray scale, cross-covariance function |
 |
Fig. 3 Expectation value of the cross-covariance function (Panels a), c)) and its noise, σ(Δ,τ), (Panels b), d)) for the full p-mode power spectrum of HMI Doppler observations (Fig. 2). Panels a) and b) are cuts at Δ = 24.1 Mm, and Panels c) and d) are cuts at τ = 30.0 min. The cross-covariance (cc) function and the noise are both normalized by |
 |
Fig. 4 Similar to Fig. 2 but for the case of p-mode power spectrum of HMI Doppler observation datacube with a phase speed filter centered at vph = 36 km s-1 with the width of 5 km s-1. The central phase speed corresponds to a ray which has 2-degree (24.1-Mm) skip distance on the Sun. |
 |
Fig. 5 Expectation value of the cross-covariance function (Panels a), c)) and its noise (Panels b), d)) and for the power spectrum of HMI Doppler observation datacube with a phase speed filter (Fig. 4). Panels a) and b) are cuts at Δ = 24.1 Mm, and Panels c) and d) are cuts at τ = 30.0 min. Normalization factors are determined in the same way as Fig. 3. |
3.3. Noise estimate from the cross-covariance function
In time-distance helioseismology we measure travel times from the cross-covariance function. Therefore, it would be practical to be able to estimate the noise not from the power spectrum but instead from the cross-covariance function itself. Here we show a simple example.
Since Eq. (13) tells us that the noise function is written with a simple form using the expectation value of the cross-covariance function, in order to estimate the noise level of the cross-covariance function, namely 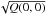 , in practice, we need to obtain the zero-distance cross-covariance function and fit it to obtain the parameters to estimate
, in practice, we need to obtain the zero-distance cross-covariance function and fit it to obtain the parameters to estimate 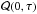 in addition to calculation of the cross-covariance functions at targeted distances. The cross-covariance function is often approximated by a Gabor wavelet (e.g., Duvall et al. 1997; Kosovichev & Duvall 1997). Therefore, if we fit the zero-distance cross-covariance function with
in addition to calculation of the cross-covariance functions at targeted distances. The cross-covariance function is often approximated by a Gabor wavelet (e.g., Duvall et al. 1997; Kosovichev & Duvall 1997). Therefore, if we fit the zero-distance cross-covariance function with 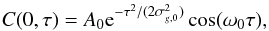 (17)then using Eq. (13)1 we obtain
(17)then using Eq. (13)1 we obtain 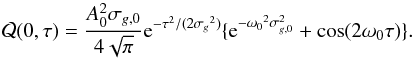 (18)Once the fitting parameters A0, σg,0 and ω0 are obtained, the noise level is estimated as
(18)Once the fitting parameters A0, σg,0 and ω0 are obtained, the noise level is estimated as ![\begin{equation} \sqrt{\mathcal{Q}(0,0)}= \frac{A_0 \sqrt{\sigma_{g,0}}}{2\sqrt[4]{\pi}} \sqrt{ {\rm e}^{-{\omega_0}^2 \sigma_{g,0}^2} +1}. \label{eq:Noisesimplewavelet} \end{equation}](/articles/aa/full_html/2016/09/aa28129-16/aa28129-16-eq133.png) (19)Moreover, when we use the cross-covariance function at a certain targeted distance Δc, we can also estimate the oscillations of the noise around
(19)Moreover, when we use the cross-covariance function at a certain targeted distance Δc, we can also estimate the oscillations of the noise around 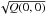 . In that case, if we consider a pair of Gabor wavelets as a symmetrical expectation value of the cross-covariance function at a certain distance Δc:
. In that case, if we consider a pair of Gabor wavelets as a symmetrical expectation value of the cross-covariance function at a certain distance Δc:
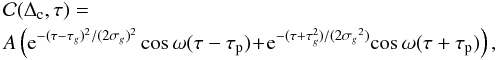 (20)where A,τg, σg, τp, σp are fitting parameters at Δ = Δc, according to Eq. (13)
(20)where A,τg, σg, τp, σp are fitting parameters at Δ = Δc, according to Eq. (13)
![\begin{eqnarray} &&\mathcal{Q}(\Delta_{\rm c}, \tau) = \frac{A^2 \sigma_g}{4\sqrt{\pi}} \biggl[ {\rm e}^{- (\tau-{\tau_g})^2/\sigma_g^2} \left\{\cos{2\omega(\tau-\tau_{\rm p})} + {\rm e}^{-\omega^2 {\sigma_g}^2} \right\} \nonumber\\ &&\quad \quad\quad\quad+ {\rm e}^{- (\tau+{\tau_g})^2/\sigma_g^2} \left\{\cos{2\omega(\tau+\tau_{\rm p})} + {\rm e}^{-\omega^2 {\sigma_g}^2} \right\} \nonumber \\ && \quad\quad\quad \quad + 2 {\rm e}^{-\tau^2/{\sigma_g}^2} \left\{\cos{(2\omega\tau)} + {\rm e}^{-\omega^2 {\sigma_g}^2} \cos{2\omega(\tau_{\rm p} -\tau_g ) } \right\} \biggr]. \label{eq:Qsimplewavelet} \end{eqnarray}](/articles/aa/full_html/2016/09/aa28129-16/aa28129-16-eq144.png) (21)Hence, the oscillatory part of the variance basically consists of Gaussians peaking at τ = τg, −τg, and 0. The width of these peaks is determined by the wavepacket width (σg), and the frequency of the oscillatory part of the noise is twice higher than that of the cross-covariance. This is consistent with the calculation results we showed in the previous subsection. The oscillation field with a narrower peak in the power distribution has a cross-covariance function with the broader wavelet form, and thus, the width of the noise is broader as well.
(21)Hence, the oscillatory part of the variance basically consists of Gaussians peaking at τ = τg, −τg, and 0. The width of these peaks is determined by the wavepacket width (σg), and the frequency of the oscillatory part of the noise is twice higher than that of the cross-covariance. This is consistent with the calculation results we showed in the previous subsection. The oscillation field with a narrower peak in the power distribution has a cross-covariance function with the broader wavelet form, and thus, the width of the noise is broader as well.
4. Conclusions and outlook
In this work, by modeling stochastic solar oscillations we calculated the variance of the point-to-point cross-covariance function as a function of time-lag and distance between the two observation points. As a result, we showed that the variance of the cross-covariance in the far-field is independent of both time-lag and distance. We also showed in the previous section that the constant noise level can be estimated using the fitting parameters of the zero-distance cross-covariance function. The fact that in the far field the noise is flat means that the signal-to-noise ratio for the cross-covariance function is proportional to the amplitude of the expectation value of the cross-covariance, and this is of importance in analysis.
As mentioned in the introduction, the full statistics of the cross-covariance function (e.g., Gizon & Birch 2004; Jackiewicz et al. 2012; Fournier et al. 2014) are needed to optimize the definition of travel time. In particular, it would be appropriate to obtain the parameters of the model, p, by minimizing the merit function ![\begin{eqnarray} X (\vec{p}) = \left\| \Lambda^{-1/2} f(t) [C(t)-C_{\mathrm{model}} (t; \vec{p})] \right\|^2, \label{eq:chisq_general} \end{eqnarray}](/articles/aa/full_html/2016/09/aa28129-16/aa28129-16-eq148.png) (22)where C(t) is the cross-covariance function at time lag t, Cmodel(t;p) is the model cross-covariance function, and
(22)where C(t) is the cross-covariance function at time lag t, Cmodel(t;p) is the model cross-covariance function, and ![\begin{eqnarray} \Lambda_{ij} = \mathrm{Cov}[C(t_i), C(t_j)] , \end{eqnarray}](/articles/aa/full_html/2016/09/aa28129-16/aa28129-16-eq151.png) (23)is the covariance matrix of the cross-covariance function. We note that the merit function, Eq. (22), is the general form of Eq. (3). The computation of Λ is future work. In the inversion process we cannot avoid the computation of Λ, and the covariance of the travel time. For those extended calculations we perhaps could use the concept of our calculation to simplify the computation of the variance of the covariance in this paper and Fournier et al. (2014). An alternative and simpler approach would be transform to the Fourier domain, where different frequencies are uncorrelated.
(23)is the covariance matrix of the cross-covariance function. We note that the merit function, Eq. (22), is the general form of Eq. (3). The computation of Λ is future work. In the inversion process we cannot avoid the computation of Λ, and the covariance of the travel time. For those extended calculations we perhaps could use the concept of our calculation to simplify the computation of the variance of the covariance in this paper and Fournier et al. (2014). An alternative and simpler approach would be transform to the Fourier domain, where different frequencies are uncorrelated.
Acknowledgments
We thank Damien Fournier and Jesper Schou for useful discussions. Part of this work was done while K.N. was supported by the Research Fellowship from the Japan Society for the Promotion of Science for Young Scientists. K.N. and L.G. acknowledge support from EU FP7 “Collaborative Project Exploitation of Space Data for Innovative Helio- and Asteroseismology” (SPACEINN). The HMI data used are courtesy of NASA/SDO and the HMI science team. The German Data Center for SDO (GDC-SDO), funded by the German Aerospace Center (DLR), provided the IT infrastructure to process the data.
References
- Appourchaux, T., Chang, H., Gough, D. O., & Sekii, T. 2000, MNRAS, 319, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Appourchaux, T., Gizon, L., & Rabello-Soares, M. 1998, A&AS, 132, 107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bogart, R. S., Baldner, C., Basu, S., Haber, D. A., & Rabello-Soares, M. C. 2011, J. Phys. Conf. Ser., 271, 012008 [NASA ADS] [CrossRef] [Google Scholar]
- Couvidat, S., Birch, A. C., & Kosovichev, A. G. 2006, ApJ, 640, 516 [NASA ADS] [CrossRef] [Google Scholar]
- Duvall, T. L., & Hanasoge, S. M. 2013, Sol. Phys., 287, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Duvall, Jr., T. L., Jefferies, S. M., Harvey, J. W., & Pomerantz, M. A. 1993, Nature, 362, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Duvall, Jr., T. L., Kosovichev, A. G., Scherrer, P. H., et al. 1997, Sol. Phys., 170, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Fournier, D., Gizon, L., Hohage, T., & Birch, A. C. 2014, A&A, 567, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gizon, L., & Birch, A. C. 2002, ApJ, 571, 966 [NASA ADS] [CrossRef] [Google Scholar]
- Gizon, L., & Birch, A. C. 2004, ApJ, 614, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Gizon, L., & Birch, A. C. 2005, Liv. Rev. Sol. Phys., 2, 6 [Google Scholar]
- Jackiewicz, J., Birch, A. C., Gizon, L., et al. 2012, Sol. Phys., 276, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Kosovichev, A. G., & Duvall, Jr., T. L. 1997, in SCORe’96: Solar Convection and Oscillations and their Relationship, eds. F. P. Pijpers, J. Christensen-Dalsgaard, & C. S. Rosenthal (Dordrecht: Kluwer), Astrophys. Space Sci. Libr., 225, 241 [Google Scholar]
- Nagashima, K. 2010, Ph.D Thesis, The Graduate University for Advanced Studies [Google Scholar]
- Schou, J., Scherrer, P. H., Bush, R. I., et al. 2012, Sol. Phys., 275, 229 [Google Scholar]
- Woodard, M. F. 1984, Ph.D. Thesis, University of California, San Diego [Google Scholar]
Appendix A: Analytical calculation of the noise for a multi-peak power distribution
If the power distribution has not only one pair of peaks, but multiple pairs of peaks, and if the number of the Gaussian peaks is Np, then the power is
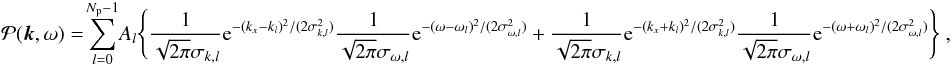 (A.1)at ky = 0 and zero at ky ≠ 0, where Al (l = 0,1,...Np − 1) are real-valued amplitudes.
(A.1)at ky = 0 and zero at ky ≠ 0, where Al (l = 0,1,...Np − 1) are real-valued amplitudes.
In this case, with a straightforward calculation
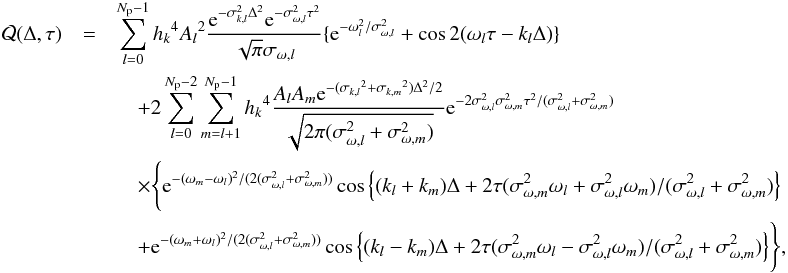 (A.2)where Δ is in the x direction, and
(A.2)where Δ is in the x direction, and 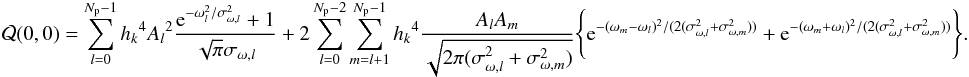 (A.3)Although the form of
(A.3)Although the form of 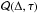 (Eq. (A.2)) is not that simple, all the terms in the summation have a Gaussian envelope centered at the origin in space and time. Since the oscillatory cosine functions have respective spatial and temporal frequencies, in the case of sufficiently many modes (large Np), the sum, and thus
(Eq. (A.2)) is not that simple, all the terms in the summation have a Gaussian envelope centered at the origin in space and time. Since the oscillatory cosine functions have respective spatial and temporal frequencies, in the case of sufficiently many modes (large Np), the sum, and thus 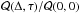 will damp more rapidly than each mode component, except near the origin.
will damp more rapidly than each mode component, except near the origin.
All Figures
 |
Fig. 1 Examples of the power spectrum in logarithmic gray scale (Panel a)) and the expectation value of the cross-covariance function (Panel b)) in the case of the Gaussian power spectrum. In Panel a) (and the same is true in Figs. 2a and 4a), larger and smaller power is indicated by black and white, respectively. The peak of the power is located at (k0R⊙,ω0/ (2π)) = (600,3 mHz) and the peak has widths (σkR⊙,σω/ (2π)) = (100,0.5 mHz). The cuts through the expectation value of the cross-covariance function at Δ = 0 and τ = 0 are shown in Panels c) and e), and the noise for the same cuts are shown in Panels d) and f). The cross-covariance (cc) function and the noise, |
| In the text | |
 |
Fig. 2 Example of the case of p-mode power spectrum of HMI Doppler observations: power spectra (Panel a)) in logarithmic gray scale, cross-covariance function |
| In the text | |
 |
Fig. 3 Expectation value of the cross-covariance function (Panels a), c)) and its noise, σ(Δ,τ), (Panels b), d)) for the full p-mode power spectrum of HMI Doppler observations (Fig. 2). Panels a) and b) are cuts at Δ = 24.1 Mm, and Panels c) and d) are cuts at τ = 30.0 min. The cross-covariance (cc) function and the noise are both normalized by |
| In the text | |
 |
Fig. 4 Similar to Fig. 2 but for the case of p-mode power spectrum of HMI Doppler observation datacube with a phase speed filter centered at vph = 36 km s-1 with the width of 5 km s-1. The central phase speed corresponds to a ray which has 2-degree (24.1-Mm) skip distance on the Sun. |
| In the text | |
 |
Fig. 5 Expectation value of the cross-covariance function (Panels a), c)) and its noise (Panels b), d)) and for the power spectrum of HMI Doppler observation datacube with a phase speed filter (Fig. 4). Panels a) and b) are cuts at Δ = 24.1 Mm, and Panels c) and d) are cuts at τ = 30.0 min. Normalization factors are determined in the same way as Fig. 3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.