EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 591 (July 2016) A&A, 591 (2016) A122 Full HTML
Free Access
Issue
A&A
Volume 591, July 2016
Article Number A122
Number of page(s) 8
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201628172
Published online 24 June 2016

© ESO, 2016

1. Introduction

The main reservoir of nitrogen-bearing species in most solar system bodies is unknown. The dominant form of nitrogen on these bodies is inherited from the chemical composition of the solar nebula when planetesimals were formed (Schwarz & Bergin 2014; Mumma & Charnley 2011). This composition strongly depends on the initial abundances, which are difficult to probe since N and N2 are not directly observable in the interstellar medium (ISM). The Spitzer program “Cores to Disks” found that on average 10% to 20% of nitrogen is contained in ices such as NH3, 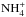NH4+\hbox{$\rm{NH_4^+}$}, and XCN, mostly in the form of OCN− (Öberg et al. 2011a). Water is the most abundant volatile in interstellar ices and cometary ices. The relative abundance of the main nitrogen-bearing species compared to water are on the order of a few percent; ~5% for ammonia and ~0.3% for XCN (Bottinelli et al. 2010; Öberg et al. 2011a). CN and HCN have been detected in later stages of star formation toward protoplanetary disks (see Dutrey et al. 1997; Thi et al. 2004; Öberg et al. 2011b; Guilloteau et al. 2013) along with resolved N2H+ emission in TW Hya (Qi et al. 2013) and unresolved N2H+ emission in several other disks (Dutrey et al. 2007; Öberg et al. 2010, 2011b). Although some upper limits exist for NH3 in protoplanetary disks in the near-infrared (Salyk et al. 2011; Mandell et al. 2012), there are currently no published detections.

Here we report the first detection of NH3 along with the N2H+ 6–5 line in the planet-forming disk around TW Hya using the HIFI instrument on the Herschel Space Observatory. This disk has already been well studied. It was first imaged by the Hubble Space Telescope (HST; Krist et al. 2000; Weinberger et al. 2002), which revealed a nearly face-on orientation. Roberge et al. (2005) took new HST images that confirmed this orientation and measured scattered light up to 280 au. Submillimeter interferometric CO data suggest an inclination of 6° to 7° (Qi et al. 2004; Rosenfeld et al. 2012). The age of TW Hya is estimated to be 8–10 Myr (Hoff et al. 1998; Webb et al. 1999; de la Reza et al. 2006; Debes et al. 2013) at a distance of 54 ± 6 pc (Rucinski & Krautter 1983; Wichmann et al. 1998; van Leeuwen 2007).

We here model the ammonia emission from TW Hya assuming that it is desorbed simultaneously with water. The thermal desorption characteristics of ammonia are similar to those of water (Collings et al. 2004). The nonthermal desorption of ammonia through photodesorption has a similiar rate to that of water, within a factor of three (Öberg 2009). Ammonia is frozen in water-rich ice layers on interstellar dust particles. Therefore, we can expect both molecules to be absent from the gas phase in similar regions. In order to properly constrain the NH3/H2O ratio we need to revisit past models of water emission in the disk surrounding TW Hya.

The ground-state rotational emission for both of the water spin isomers has been found around TW Hya by Hogerheijde et al. (2011, from now on H11), also using the HIFI instrument onboard the Herschel Space Observatory. The authors explained this emission using the physical model from Thi et al. (2010) to calculate the amount of water that can be produced by photodesorption from a hidden reservoir of water in the form of ice on dust grains (Bergin et al. 2010; van Dishoeck et al. 2014). Their model overestimates the total line flux by a factor of 3–5. They explored different ways to reduce the amount of water flux and concluded that settling of large icy grains is the only viable way to fit the data.

Here, we rederive estimates of the amount of water vapor, using an updated estimate of the disk gas mass. We also consider the effect of a more compact distribution of millimeter-sized grains that are moved by radial drift and settling. These dust processes are relevant for the molecular abundance of water because they can potentially move the bulk of the ice reservoir away from regions where photodesorption is effective. Simultaneously, we estimate the amount of NH3 using the detection of ammonia in the Herschel spectra and derive constraints on the NH3/H2O ratio in the disk gas, assuming that NH3 and H2O are co-spatial. We also estimate the amount of N2H+ and compare it to the amount of NH3 using a simple parametric model. Section 2 presents our data and their reduction. Section 3 contains our modeling approach and Sect. 4 the resulting ammonia and water vapor masses. Section 5 discusses the validity of our models and compares these predictions to standard values. Finally, Sect. 6 summarizes our conclusions.

thumbnail Fig. 1

Observed spectra of a) ortho-NH310−00, ortho-H2O 110−101 (previously presented by H11); and b) N2H+ 6–5, using Herschel WBS. The dashed line shows the continuum-subtracted spectral baseline. The o-H2O and o-NH3 lines are observed in opposite sidebands, causing the o-H2O to be detected at a velocity of −14 km s-1 in panel a).

2. Observations

Observations of TW Hya (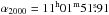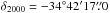α2000=11h01m51.s91\hbox{$\rm\alpha_{2000} = {\rm 11^h01^m51{\fs}91}$}, \hbox{$\delta_{2000} = -34^\circ42'17{\farcs}0$}) were previously presented by H11 and obtained using the Heterodyne Instrument for the Far-Infrared (HIFI) as part of the key program Water in Star-Forming Regions with Herschel (WISH; van Dishoeck et al. 2011). We now present observations taken on 2010 June 15 of the NH310−00 line at 572.49817 GHz simultaneously with o-H2O at 556.93607 GHz using receiver band 1b and a local oscillator tuning of 551.895 GHz (OBS-ID 1342198337). We also present the detection of N2H+ 6–5 at 558.96651 GHz in the same spectrum. With a total on-source integration of 326 min, the observation was taken with system temperatures of 360–400 K. The data were recorded in the Wide-Band Spectrometer (WBS) which covers 4.4 GHz with 1.1 MHz resolution. This corresponds to 0.59 km s-1 at 572 GHz. The data were also recorded in the High-Resolution Spectrometer (HRS) which covers 230 MHz at a resolution of 0.25 MHz resulting in 0.13 km s-1 at the observed frequency of the NH310−00 line. The calibration procedure is identical to the one of H11, but employs an updated beam efficiency of ηmb = 0.635 and a HPBW of 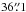\hbox{$36{\farcs}1$}1, which increases the reported water line fluxes by about 17% with respect to the values of H11. Table 1 summarizes the line fluxes of ammonia, water and N2H+ 6–5. Figure 1 shows the calibrated spectra of ortho-ammonia, ortho-water, and the N2H+ 6–5 lines.

Table 1

Observed line parameters.

3. Modeling approach

Since NH3 is intermixed with H2O on interstellar ices and is thought to desorb simultaneously (Öberg 2009), our modeling approach focuses on deriving a NH3/H2O ratio in the TW Hya disk assuming that the NH3 emission comes from the same location as the H2O emission. We adopt a physical model for the gas density and temperature and rederive the amount of water vapor from literature results (H11). After we define our H2O model, we use it to model NH3 emission by adopting the same spatial distribution as the water but scaling the overall abundance as a free parameter. We also take into account the effect of radial drift and vertical settling of dust grains on our abundance profiles. Additionally, we model the N2H+ 6–5 emission by assuming a constant abundance throughout the disk where the temperature is below the CO freeze-out temperature (17 K) following Qi et al. (2013). The total amount of N2H+ in this model is also a free parameter. The following sections describe the physical and chemical structure of our models.

3.1. Physical structure

Recently, Cleeves et al. (2015) used HD measurements (Bergin et al. 2013) to constrain the total gas mass for the disk of TW Hya of 0.04 ± 0.02 M⊙, which is twice as massive as the model used by H11. 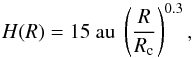We adopted the physical structure of their best-fit model defined by a dust surface density profile of Σd(R)=0.04gcm-2(RRc)-1exp[−(RRc)],\begin{equation} \Sigma_d(R) = 0.04~{\rm g~cm^{-2}}\left(\frac{R}{R_{\rm c}}\right)^{-1}{\rm exp}\left[-\left(\frac{R}{R_{\rm c}}\right)\right]{\rm,} \end{equation}(1)and a scale height for small grains (and gas) given by H(R)=15au(RRc)0.3,\begin{equation} H(R) = 15~{\rm au}~\left(\frac{R}{R_{\rm c}}\right)^{0.3}{\rm,} \end{equation}(2)where the critical radius Rc is 150 au. We also adopted their estimated temperature profile T(R,z) calculated from the ultraviolet radiation field throughout the disk (see Appendix A of Cleeves et al. 2015). Cleeves and collaborators did not consider a radial separation between large and small grains because the small grains dominate the dust surface area, which is most important for the chemistry. Many models for the TW Hya SED include an inner hole with a radius of a few au that is depleted of dust. Slight variations of this gap size have been proposed (Calvet et al. 2002; Eisner et al. 2006; Hughes et al. 2007; Ratzka et al. 2007; Arnold et al. 2012; Menu et al. 2014). However, the observations in the large Herschel beam are not sensitive to these small scales, and we ignore the inner hole in our model.

3.2. Chemical model

Gas temperatures throughout the disk in previous models and ours are typically below 200 K, which means that they exclude high-temperature gas-phase water formation. We consider thermal evaporation and photodesorption by ultraviolet radiation as H2O production mechanisms and ultraviolet photodissociation and freeze-out as the only H2O destruction mechanisms using the time-dependent chemical model of Cleeves et al. (2015). Thermal desorption is only dominant in the innermost disk up to a few au. Most of the water in this chemical model is released to the gas-phase through photodesorption in the outer disk. Compared to the chemistry used in H11, this model uses a more realistic water grain chemistry and updated gas-phase reactions. Figure 2 summarizes the physical conditions of the model and the location of the bulk of the water vapor. A significant decrease in the midplane abundance of water vapor can be seen in comparison to the model proposed by H11, which is due to a lower rate of cosmic-ray (CR) driven water formation. Two layers of water abundance can be distinguished in Fig. 2b. The upper layer is the product of gas-phase chemistry and photodesorption whereas the layer at larger radii but smaller height is dominated by photodesorption.

Since our observations are spatially unresolved and the disk is observed nearly face on, no information of the spatial location of the emitting molecules can be retrieved directly from our spectrally resolved data. The following sections describe two processes (radial drift and settling) that are due to grain growth that affects the radial and vertical configuration of dust grains. These in turn determine the distribution of the ices. We consider two scenarios for the vertical location and two scenarios for the radial location of the molecules, resulting in four different configurations.

thumbnail Fig. 2

Overview of the adopted model structure. a) Logarithm of the molecular hydrogen density in cm-3 with black contours. b) Logarithm of the water vapor density with white contours at 0.6 cm-3. c) Gas temperature in K. Black contours represent the logarithm of the water abundance at 0.6 cm-3.

3.2.1. Vertical settling

For the vertical distribution, we considered two extreme cases. In the first scenario (p), the vertical distribution of the ammonia and water follows that found by the location of water released through photodesorption (i.e., in the upper and intermediate disk layers) as described above. In the second extreme scenario (m) we assume that the H2O/H2 and NH3/H2 abundances are constant. We distribute the species vertically out to one scale height of the millimeter grains following Andrews et al. (2012),H(R)=10.31(R100au)1.25au.\begin{equation} H(R)= 10.31\left(\frac{R}{\rm 100~ au}\right)^{1.25}{\rm au.} \end{equation}(3)Because the column density is dominated by the dense layers near the midplane, this model represents emission dominated by the midplane (hence: model m). The latter is motivated by H11, where they tried to explain water emission from TW Hya using the physical model from Thi et al. (2010) to calculate the amount of water vapor that can be produced by photodesorption. But their model overestimates the total line flux by a factor of 3−5. They concluded that settling of large(r) icy grains could be acting as a mechanism to hide the icy grains from the reach of ultraviolet photons resulting in the lower-than-expected water line fluxes. We do not make any assumptions about the production mechanism of the gas-phase ammonia and water in the absence of photodesorption in the midplane (m), but discuss possible mechanisms in Sect. 5.

3.2.2. Radial drift

For the radial location we considered an extended model (E) with ammonia and water across the entire disk out to 196 au, corresponding to the extent of μ-size grains(Debes et al. 2013), and a compact model (C) with NH3 and H2O confined to the location of the millimeter grains (<60 au). Andrews et al. (2012) found that the millimeter-sized grains are located within 60 au, probably as the result of radial drift causing a separation between the large and small-size population of dust that remains coupled to the gas. The compact model (C) is also motivated by H11, since grain settling operates faster than drift because the vertical pressure gradient is larger than the radial one. Any grains large enough to drift radially will certainly have settled vertically first. This means that the molecules are already locked up in large(r) grains when they experience (or not) a radial drift. Our compact model (C) represents the extreme case where all water and ammonia ice has been transported to within 60 au and is (partially) returned to the gas phase only there. In the same way, our extended model (E) represents the other extreme where the water and ammonia reservoir, locked up in icy dust particles, extends across the full disk.

As Fig. 2 shows, water vapor is mostly present in a thin photo-dominated layer (models p) or near the midplane (models m) following total H2 density profile. Figure 3 summarizes the resulting four different scenarios (Em, Ep, Cm and Cp). In all scenarios, the total amount of ammonia and water vapor is a free parameter constrained by fitting the observed line fluxes. In particular, for the p-models, this means that we use the radial and vertical density distribution from the detailed calculations but scale the total amount of ammonia and water vapor up or down as necessary.

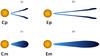thumbnail Fig. 3

Schematic illustration of the location of water vapor in our models: a) Compact photodesorption-layer configuration (Cp). b) Extended photodesorption-layer configuration (Ep). c) Compact with a constant abundance configuration (Cm). d) Extended with a constant abundance configuration (Em).

3.3. Line excitation and radiative transfer

We used LIME (v1.3.1), a non-LTE 3D radiative transfer code (Brinch & Hogerheijde 2010) that can predict line and continuum radiation from a source model. All of our models use 15 000 grid points. Doubling the number of grid points does not affect the outcome of the calculations. Grid points are distributed randomly in R using a logarithmic scale. This means in practice that inner regions of the disk have a finer sampling than the outer parts of the disk. Since it is difficult to establish reliable convergence criteria, LIME requires that the number of iterations of each point are set manually. We set this number to 12 and confirmed convergence in our models by performing consecutive iterations. Forty channels of 110 m s-1 each were used for all line models with 200 pixels of 0.05 arcsec. Because we aimed at comparing these models with spatially unresolved data, we calculated the total flux by summing all the pixels after subtracting the continuum.

Rate coefficients for ortho-ammonia, N2H+, and both spin isomers of water were taken from the Leiden Atomic and Molecular Database (Schöier et al. 2005)2. The excitation levels of para-H2O and ortho-H2O have separate coefficients for o-H2 and p-H2 (Daniel et al. 2011). The o-NH3 collision rates are only available for p-H2, therefore we considered the total H2 as p-H2 to calculate their population levels (see Danby et al. 1988). The N2H+ collision rates were adopted from HCO+ following Flower (1999). We assumed that the H2 ortho-to-para ratios are in local thermal equilibrium. Given the low dust temperatures, this implies H2 OPR <0.3. If instead we increase the H2 ortho-to-para ratio to 3, the high-temperature limit for formation on grains (Flower et al. 1996), it will increase the H2O line fluxes by a factor ~2. We discuss the effect of this on the inferred water vapor mass below.

thumbnail Fig. 4

Panels a), b) and c) show the LIME (Brinch & Hogerheijde 2010) output of the total line fluxes of ortho-NH3, ortho-H2O, and para-H2O, respectively, as a function of the total water vapor mass. The blue, green, red, and yellow curves correspond to the Em, Ep, Cm, and Cp models, respectively. The dashed lines and horizontal green bar show the observed line fluxes and their 3σ ranges, with sigma having two sources of noise added in quadrature; the systematic error of the observations, estimated to be about 20% of the total flux, and the rms of the spectra.

4. Results

Figure 4 shows the emerging line flux in the Herschel beam as a function of ammonia and water vapor mass. These curves of growth (flux (F) vs. mass ∝ column density(N)) are consistent with saturated lines: the slopes go from linear (F ∝ N) in the low-opacity regime to saturated (F∝ln(N)\hbox{$F\propto {\rm \sqrt{{\rm ln}(N)}}$}). The latter behavior is due to the line becoming gradually optically thick in its wings, resulting in a steady flux growth.

Our four models predict different asymptotic values for high vapor masses. In the asymptotic regimes, the lines are fully thick and probe only a very thin region near the surface of the disk. The larger E models therefore result in more flux than the smaller C models. The m models trace higher H2 densities but lower temperatures than the corresponding p models, resulting in different predicted fluxes. This has a strong effect on the water lines, which have critical densities and upper level energies higher than the conditions prevalent in the regions where the lines originate. This effect is strongest for the Cm models because in this regime densities are considerably higher and the lines become thermalized and opaque, resulting in higher required water-vapor masses.

Table 2

Summary table of our results in different regimes.

Table 2 summarizes the best-fit vapor masses; error estimates include statistical errors on the observations and the systematic errors on the total line flux, estimated to be about 20%. The ammonia-to-water ratios shown in Table 2 assume an OPR of ammonia of either ∞ or 1. As stated above in Sect. 3.3, we assumed that H2 ortho-to-para ratios are in local thermal equilibrium. If we increase this value to 3 (the high-temperature limit), the derived masses would decrease by a little more than one order of magnitude in our most massive and optically thick model (Cm) and by less than one order of magnitude in the remaining models (Cp, Em, and Ep). We do not include this in the error budget of our reported values because the NH3 and N2H+ might be equally affected.

All four models yield o-NH3 masses ranging from (0.7−1.2) × 1021 g for models Ep, Em, and Cp, to 1.1 × 1022 g. These correspond to ammonia abundances ranging from (2.0−9.5) × 10-12 (E models) to (0.6−1.7) × 10-10 (C models), relative to H2. For water, a higher range of masses is inferred, ranging from (2.2−4.5) × 1021 g for models Ep, Em, and Cp, to 1.6 × 1023 g for model Cm. These correspond to water abundances ranging from (1.1−3.0) × 10-11 (E models) to (4.5−9.0) × 10-10 (C models), relative to H2. The water OPR is found to range from 0.73 to 1.52. If the associated errors are considered, the range is much wider (0.2−3.0) with model Ep, Cp and Cm in agreement with the interstellar and cometary range of 2.0−3.0 for the OPR of water. 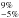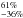The ammonia-to-water ratio ranges from 7%9%−5%\hbox{$^{9\%}_{-5\%}$} to 84%61%−36%\hbox{$^{61\%}_{-36\%}$}.

Calculations using a simple escape-probability code (RADEX, van der Tak et al. 2007) reproduce the observed line fluxes adopting the inferred vapor masses and using densities and temperatures representative for the emitting regions. But only a full 3D calculation can reproduce the exact line fluxes because of the wide range in densities and temperatures. These simple calculations also show that, under the conditions of the four models, equal amounts of o–H2O and o–NH3 give approximately equal line strengths (within 50%). This means that we can relate the observed line ratios of Fo−NH3/Fo−H2O ~ 0.6 to estimate the actual overall NH3/ H2O abundance fraction of about 0.35−0.65 as confirmed by the detailed LIME modeling below. The high NH3/H2O ratios suggested by most models are therefore a direct consequence of the near-equal observed line fluxes of H2O and NH3; only in the Cm model where lines are opaque, are much lower NH3/H2O values consistent with the observed fluxes.

Our best-fit model result for N2H+ is agrees with the N2H+ 4–3 emission reported in Qi et al. (2013). The fit to the N2H+ 6–5 emission yields a total N2H+ vapor mass of 4.9× 1021 g, which is ~50% higher than the model of Qi et al. (2013) obtained from integrating their best-fit model (zbig(H) = 3 in Table S2).

5. Discussion

5.1. Ice reservoirs and total gass masses

The inferred NH3 vapor masses from 7.0 × 1020 g to 1.1 × 1022 g are much lower than the potential ammonia ice reservoir of ~3.0 × 1028 g. This ice reservoir mass estimate was obtained assuming an elemental nitrogen abundance relative to H of 2.25 × 10-5 and a disk mass of 0.04 ± 0.02 M⊙, and assuming that 10% of nitrogen freezes out on grains as NH3 (Öberg et al. 2011a). In the same way, we estimate a water ice mass reservoir of 3.4 × 1029 g, adopting an oxygen elemental abundance of 3.5 × 10-4 relative to H, assuming that 70% of O is locked up in water (Visser et al. 2009) and all of it is frozen out. Both mass estimates indicate that the detected vapor masses are only tiny fractions (≲10-6) of the available ice reservoirs.

The total water mass of our original chemistry model (4.6 × 1024 g) is 2.5 to 25 times (Cm and Ep models respectively) more massive than the values derived from our reanalysis of the water detection toward TW Hya. H11 reported a model 16 times more massive than their original chemistry model to fit the water emission from the disk of TW Hya. This value is significantly lower than the value of our analogous Ep model, which indicates an even higher degree of settling of the icy grains than previously proposed. This is consistent with earlier conclusions that most volatiles are locked up in large grains near the midplane (Hogerheijde et al. 2011; Du et al. 2015).

5.2. Gas-phase chemistry

The reported ammonia-to-water ratios are considerably higher than those found for ices in solar system comets and interstellar sources (Mumma & Charnley 2011), which are typically below 5%. Our model-derived ratios assume that the NH3 and H2O emission originates from the same regions; however, if this is not the case, expressing the relative amounts of ammonia and water as a ratio is not very useful. Then, it is better to work with their (disk averaged) abundances of 0.2−17.0 × 10-11 and 0.1−9.0 × 10-10 respectively.

An obvious conclusion from the large amount of NH3 is that other routes exist for gas-phase NH3 in addition to evaporating NH3/H2O ice mixtures. In the colder outer disk the synthesis of ammonia in the gas phase relies on ion-molecule chemistry. This means that N2 needs to be broken apart (to release N or N+) first, but N2 can self-shield against photodissociation (Li et al. 2013). The chemistry in the disk of TW Hya seems to reflect an elevated X-ray state of the star (Cleeves et al. 2015). This strong X-ray field scenario could be invoked to break N2 apart. The models of Schwarz & Bergin (2014) for a typical T Tauri disk (with a FUV field measured in TW Hya) give values for the abundance of NH3 as high as ~10-8 (the models of Walsh et al. 2015, also produce the same abundance), which would be sufficient to explain the emission. Modeling tailored to TW Hya with the correct stellar and disk parameters, as well as appropriate initial conditions is required to fully address the question of the origin of the large NH3 abundance.

Of our four models, the Cm model stands out in that it yields much lower NH3/H2O ratios that are consistent with the low values found in solar system bodies and interstellar ices. It is also the only model where the (large uncertainties of the) derived water OPR overlap with the 2−3 range commonly found in solar system comets. Recent laboratory work by Hama et al. (2015) shows that water in ices efficiently attains an OPR of 3 upon release into the gas-phase, indicating that the OPR is not a reflection of the physical temperature and that high OPR values are naturally expected. The NH3/H2O values and the water OPR values together can be taken as evidence that the Cm model is a correct description for the distribution of H2O and NH3 in the disk. If so, a mechanism to release water in the midplane is required.

5.3. Collisions of large bodies as a production mechanism

In the midplane models (Em and Cm), photodesorption cannot explain the abundance of water and ammonia in the gas phase because ultraviolet radiation cannot penetrate these depths. CR-induced H2O desorption, such as modeled in H11, cannot produce the required amount of H2O. The typical water vapor abundances found in the H11 chemical model near the midplane are on the order of XH2O ~ 10-13, much smaller than the corresponding best-fit midplane abundances in the Em and Cm models of XH2O ~ 10-10−10-9. How can volatiles such as ammonia and water exist near the midplane where low temperatures and high densities would ensure rapid freeze-out?

One way of releasing such a vapor mass from the icy reservoir would be through collisions of larger icy bodies. We can calculate how much water needs to be released through these collisions if we assume steady-state with freeze-out to retain the observed amount of volatiles in the gas phase. Freeze-out is calculated using the freeze-out rate expression for neutral species derived in Charnley et al. (2001). For typical temperatures of 12 K and densities of 1.7 × 109 cm-3, the freeze-out rate of water vapor is 2.5 × 1013g s-1 if we consider the (Em) model to match the observations. That is equivalent to completely destroying ~7000 comets per year, with a mass similar to Halley’s comet and assuming they consist of 50% water. After 10 Myr roughly 5% of the water previously locked up in icy grains would be back to the gas phase if an ice reservoir of 3.4 × 1029g were present in the disk. In the case of the (Cm) model a higher production of water vapor 1.6 × 1016 g s-1 is needed to match the observations. This would mean destroying ~5 × 106 comets per year. After 10 Myr we would have produced ten times more water vapor than its total ice reservoir. Such large numbers of collisions and the significant (or even unrealistic) amount of released water suggest that collisions between icy bodies are an unlikely explanation for the observed amount of water and ammonia vapor in the midplane models.

The freeze-out rates used above have been calculated assuming a typical grain size distribution n(a) ∝ a-3.5 (Mathis et al. 1977) with smallest and largest grains sizes of 10-8 m and 10-1 m. Since the majority of the surface for freeze-out is on (sub)μm-size grains, we can expect this surface to be substantially reduced if these smaller grains are removed thus reducing the freeze-out rate significantly. Small grains may be removed by photoevaporating winds (Gorti et al. 2015), when transported to the upper layers by vertical mixing, or have coagulated into larger grains. In the extreme case where all of the μm-size grains have grown into larger bodies the freeze-out rate can be reduced by two orders of magnitude.

We can achieve a drop by a factor of 100 in the freeze-out rate by directly calculating the mean grain surface in Eq. (6) from Charnley et al. (2001) by setting amin = 10-4 m for our Em model, amin = 10-3 m for our Cm model (see calculations of Vasyunin et al. 2011) and amax = 10-1 m for both. If this assumption holds, then our model with the highest production rate (Cm) will have processed only 10% of its water reservoir into water vapor in the span of 10 Myr, equivalent to destroying only ~5000 comets per year. In the same way, the amount of water processed in the span of 10 Myr in our (Em) will be only 0.5% of its ice reservoir, equivalent to destroying only ~70 comets per year. These numbers are much more realistic, making this a viable mechanism for releasing volatiles in the midplane.

Nevertheless, for this scenario to be viable, the system must meet some criteria. First, the comets (or planitesimals) must have a high enough collision rate that accounts for the numbers estimated above. In the outer disk this can be enhanced through shepherding by planets, that is, sweeping up the planetesimals into one proto-debris belt. Acke et al. (2012) calculated a collision rate of 6.3 × 1013 g s-1 in Fomalhout’s debris disk to reproduce the thin dust belt seen in far-infrared images (70−500 μm). This rate is similar to our estimated rate even in the absence of a reduction in grain surface available for freeze-out. For Fomalhout, this rate corresponds to a population of 2.6 × 1011 comets with a size of 10 km, which is similar to the number of comets in the Oort cloud of 1012−1013 (Weissman 1991). Second, the collisions must release enough energy to sublimate the ices. This is only achieved if the relative velocities of the parent bodies are sufficiently high. If the colliding bodies have high eccentricities their relative velocities can be high. But in the presence of gas, we expect their orbits to be circularized. If this is the case, then the relative velocities will be dominated by the radial drift in the outer parts of the disk and enhanced in the very inner regions by turbulence. Finally, the small dust produced in the cometary (or planitesimal) collisions themselves must not provide a surface for the volatiles to freeze back onto.

If a sufficient number of small grains (≲μm) is removed by coagulation into larger grains (≳mm) and the relatives velocities and rates of the collisions between larger bodies (≳m) in the miplane are sufficiently high to meet the conditions above, then collisions between icy bodies are a plausible mechanism for releasing (and keeping in the gas phase for long enough) the amount of water and ammonia that we observe. The treatment above is simplistic and there are many other ways to achieve this (e.g., changing the slope of the grain distribution or by photoevaporation of grains along with the gas). A full treatment of the combined effect of grain growth, drift, settling, collisions and volatile freeze-out is needed to confirm this scenario, but is beyond the scope of this paper.

6. Conclusions

We have successfully detected NH3 and N2H+ in the disk surrounding TW Hya. We used a non-LTE excitation and radiative transfer code and a detailed physical and chemical disk structure to derive the amount of NH3, N2H+, and (for comparison) H2O adopting four different spatial distributions of the molecules. Our main conclusions are as follows.

  • 1.

    The NH3 emission corresponds to an ammonia vapor mass that ranges from 7.0 × 1020 g (Ep model) to 1.1 × 1022 g (Cm model).

  • 2.

    We used the above values and the same approach to derive H2O vapor masses to derive NH3/H2O ratios ranging from 7% to 15% (Cm model) and 42% to 84% (Cp model), adopting a NH3 OPR of ∞ or 1, respectively. These ratios are higher than those observed in solar system and interstellar ices, with the exception of our most massive and compact configuration (Cm model).

  • 3.

    Of our four models, only model Cm gives NH3/H2O ratios as low as observed in interstellar ices and solar system comets. It is also the only model that within the errors gives a water OPR of 2−3, which is similar to solar system comets. This can be taken as evidence that H2O and NH3 are indeed located near the midplane at radii <60 au.

  • 4.

    If the H2O and NH3 follow the Cp, Ep, or Em spatial distributions, the implied high NH3/H2O ratio requires an additional mechanism to produce gas-phase NH3. A strong X-ray field may provide the necessary N atoms or radicals to form NH3 in the gas.

  • 5.

    If NH3 and H2O emission comes from the midplane, where photodesorption does not operate (models m), collisions of larger bodies can release NH3 and H2O and explain the observed vapor. This requires a reduction of the total grain surface available for freeze-out, for example, through the growth of grains into pebbles and larger; and a sufficiently high collision rate and sufficiently violent collisions to release the volatiles.

  • 6.

    The ammonia vapor mass is similar to the N2H+ mass derived with our simple model and to that inferred by Qi et al. (2013) (see Sect. 4) within 50%.

Additional spatially resolved observations of ammonia would help to constrain the radial extent of ammonia (and perhaps vertical structure) and refine our current limits. We can observe ammonia isotopes with ALMA in band 7 (ortho-NH2D 101−000 at 332.781 GHz and para-NH2D 101−000 at 332.822 GHz) and band 8 (ortho-NH2D 110−000 at 470.271 GHz and para-NH2D 110−000 at 494.454 GHz). We used our models to predict line fluxes of about 1 Jy in band 8 and 30 mJy in band 7 using LIME in all of our models, and considering a value of 0.1 for ammonia deuterium fractionation as found toward protostellar dense cores (Roueff et al. 2005; Busquet et al. 2010), and an OPR ammonia of 1. ALMA can detect such line fluxes in a few hours3OA. Observations with JVLA or GBT of para-ammonia (para-NH311−10 at 23.694 GHz or para-NH321−20 at 23.722 GHz) are not possible since our predicted line fluxes are too low (~10 mJy).

3

Calculations performed with the ALMA sensitivity calculator (https://almascience.eso.org/proposing/sensitivity-calculator)

Acknowledgments

Herschel is a European Space Agency space observatory with science instruments provided by European-led principal investigator consortia and with important participation from NASA. HIFI has been designed and built by a consortium of institutes and university departments from across Europe, Canada, and the United States under the leadership of SRON Netherlands Institute for Space Research, Groningen, The Netherlands, and with major contributions from Germany, France, and the US. Consortium members are: Canada: CSA, U. Waterloo; France: IRAP (formerly CESR), LAB, LERMA, IRAM; Germany: KOSMA, MPIfR, MPS; Ireland, NUI Maynooth; Italy: ASI, IFSI-INAF, Osservatorio Astrofisico di Arcetri-INAF; Netherlands: SRON, TUD; Poland: CAMK, CBK; Spain: Observatorio Astronmico Nacional (IGN), Centro de Astrobiología (CSIC-INTA). Sweden: Chalmers University of Technology MC2, RSS & GARD; Onsala Space Observatory; Swedish National Space Board, Stockholm University Stockholm Observatory; Switzerland: ETH Zurich, FHNW; USA: Caltech, JPL, NHS. Support for this work was provided by NASA (Herschel OT funding) through an award issued by JPL/Caltech. This work was partially supported by grants from the Netherlands Organization for Scientific Research (NWO) and the Netherlands Research School for Astronomy (NOVA). The data presented here are archived at the Herschel Science Archive, http://archives.esac.esa.int/hda/ui, under OBSID 1342198337 and 1342201585.

References

  1. Acke, B., Min, M., Dominik, C., et al. 2012, A&A, 540, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Andrews, S. M., Wilner, D. J., Hughes, A. M., et al. 2012, ApJ, 744, 162 [NASA ADS] [CrossRef] [Google Scholar]
  3. Arnold, T. J., Eisner, J. A., Monnier, J. D., & Tuthill, P. 2012, ApJ, 750, 119 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bergin, E. A., Hogerheijde, M. R., Brinch, C., et al. 2010, A&A, 521, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bergin, E. A., Cleeves, L. I., Gorti, U., et al. 2013, Nature, 493, 644 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  6. Bottinelli, S., Boogert, A. C. A., Bouwman, J., et al. 2010, ApJ, 718, 1100 [NASA ADS] [CrossRef] [Google Scholar]
  7. Brinch, C., & Hogerheijde, M. R. 2010, A&A, 523, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Busquet, G., Palau, A., Estalella, R., et al. 2010, A&A, 517, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Calvet, N., D’Alessio, P., Hartmann, L., et al. 2002, ApJ, 568, 1008 [NASA ADS] [CrossRef] [Google Scholar]
  10. Charnley, S. B., Rodgers, S. D., & Ehrenfreund, P. 2001, A&A, 378, 1024 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Cleeves, L. I., Bergin, E. A., Qi, C., Adams, F. C., & Öberg, K. I. 2015, ApJ, 799, 204 [NASA ADS] [CrossRef] [Google Scholar]
  12. Collings, M. P., Anderson, M. A., Chen, R., et al. 2004, MNRAS, 354, 1133 [NASA ADS] [CrossRef] [Google Scholar]
  13. Danby, G., Flower, D. R., Valiron, P., Schilke, P., & Walmsley, C. M. 1988, MNRAS, 235, 229 [NASA ADS] [CrossRef] [Google Scholar]
  14. Daniel, F., Dubernet, M.-L., & Grosjean, A. 2011, A&A, 536, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. de la Reza, R., Jilinski, E., & Ortega, V. G. 2006, AJ, 131, 2609 [NASA ADS] [CrossRef] [Google Scholar]
  16. Debes, J. H., Jang-Condell, H., Weinberger, A. J., Roberge, A., & Schneider, G. 2013, ApJ, 771, 45 [NASA ADS] [CrossRef] [Google Scholar]
  17. Du, F., Bergin, E. A., & Hogerheijde, M. R. 2015, ApJ, 807, L32 [NASA ADS] [CrossRef] [Google Scholar]
  18. Dutrey, A., Guilloteau, S., & Guelin, M. 1997, A&A, 317, L55 [NASA ADS] [Google Scholar]
  19. Dutrey, A., Henning, T., Guilloteau, S., et al. 2007, A&A, 464, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Eisner, J. A., Chiang, E. I., & Hillenbrand, L. A. 2006, ApJ, 637, L133 [NASA ADS] [CrossRef] [Google Scholar]
  21. Flower, D. R. 1999, MNRAS, 305, 651 [NASA ADS] [CrossRef] [Google Scholar]
  22. Flower, D. R., Pineau des Forets, G., Field, D., & May, P. W. 1996, MNRAS, 280, 447 [NASA ADS] [CrossRef] [Google Scholar]
  23. Gorti, U., Hollenbach, D., & Dullemond, C. P. 2015, ApJ, 804, 29 [NASA ADS] [CrossRef] [Google Scholar]
  24. Guilloteau, S., Di Folco, E., Dutrey, A., et al. 2013, A&A, 549, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Hama, T., Kouchi, A., & Watanabe, N. 2015, Science, 351, 65 [Google Scholar]
  26. Hoff, W., Henning, T., & Pfau, W. 1998, A&A, 336, 242 [NASA ADS] [Google Scholar]
  27. Hogerheijde, M. R., Bergin, E. A., Brinch, C., et al. 2011, Science, 334, 338 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  28. Hughes, A. M., Wilner, D. J., Calvet, N., et al. 2007, ApJ, 664, 536 [NASA ADS] [CrossRef] [Google Scholar]
  29. Krist, J. E., Stapelfeldt, K. R., Ménard, F., Padgett, D. L., & Burrows, C. J. 2000, ApJ, 538, 793 [NASA ADS] [CrossRef] [Google Scholar]
  30. Li, X., Heays, A. N., Visser, R., et al. 2013, A&A, 555, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Mandell, A. M., Bast, J., van Dishoeck, E. F., et al. 2012, ApJ, 747, 92 [Google Scholar]
  32. Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
  33. Menu, J., van Boekel, R., Henning, T., et al. 2014, A&A, 564, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Mumma, M. J., & Charnley, S. B. 2011, ARA&A, 49, 471 [NASA ADS] [CrossRef] [Google Scholar]
  35. Öberg, K. I. 2009, Ph.D. Thesis, Leiden Observatory, Leiden University, The Netherlands [Google Scholar]
  36. Öberg, K. I., Qi, C., Fogel, J. K. J., et al. 2010, ApJ, 720, 480 [NASA ADS] [CrossRef] [Google Scholar]
  37. Öberg, K. I., Boogert, A. C. A., Pontoppidan, K. M., et al. 2011a, ApJ, 740, 109 [NASA ADS] [CrossRef] [Google Scholar]
  38. Öberg, K. I., Qi, C., Fogel, J. K. J., et al. 2011b, ApJ, 734, 98 [NASA ADS] [CrossRef] [Google Scholar]
  39. Qi, C., Ho, P. T. P., Wilner, D. J., et al. 2004, ApJ, 616, L11 [NASA ADS] [CrossRef] [Google Scholar]
  40. Qi, C., Öberg, K. I., Wilner, D. J., et al. 2013, Science, 341, 630 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  41. Ratzka, T., Leinert, C., Henning, T., et al. 2007, A&A, 471, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Roberge, A., Weinberger, A. J., & Malumuth, E. M. 2005, ApJ, 622, 1171 [NASA ADS] [CrossRef] [Google Scholar]
  43. Rosenfeld, K. A., Qi, C., Andrews, S. M., et al. 2012, ApJ, 757, 129 [NASA ADS] [CrossRef] [Google Scholar]
  44. Roueff, E., Lis, D. C., van der Tak, F. F. S., Gerin, M., & Goldsmith, P. F. 2005, A&A, 438, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Rucinski, S. M., & Krautter, J. 1983, A&A, 121, 217 [NASA ADS] [Google Scholar]
  46. Salyk, C., Pontoppidan, K. M., Blake, G. A., Najita, J. R., & Carr, J. S. 2011, ApJ, 731, 130 [NASA ADS] [CrossRef] [Google Scholar]
  47. Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Schwarz, K. R., & Bergin, E. A. 2014, ApJ, 797, 113 [NASA ADS] [CrossRef] [Google Scholar]
  49. Thi, W.-F., van Zadelhoff, G.-J., & van Dishoeck, E. F. 2004, A&A, 425, 955 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Thi, W.-F., Mathews, G., Ménard, F., et al. 2010, A&A, 518, L125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. van Dishoeck, E. F., Kristensen, L. E., Benz, A. O., et al. 2011, PASP, 123, 138 [NASA ADS] [CrossRef] [Google Scholar]
  53. van Dishoeck, E. F., Bergin, E. A., Lis, D. C., & Lunine, J. I. 2014, Protostars and Planets VI, 835 [Google Scholar]
  54. van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Vasyunin, A. I., Wiebe, D. S., Birnstiel, T., et al. 2011, ApJ, 727, 76 [NASA ADS] [CrossRef] [Google Scholar]
  56. Visser, R., van Dishoeck, E. F., Doty, S. D., & Dullemond, C. P. 2009, A&A, 495, 881 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Walsh, C., Nomura, H., & van Dishoeck, E. 2015, A&A, 582, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Webb, R. A., Zuckerman, B., Platais, I., et al. 1999, ApJ, 512, L63 [NASA ADS] [CrossRef] [Google Scholar]
  59. Weinberger, A. J., Becklin, E. E., Schneider, G., et al. 2002, ApJ, 566, 409 [NASA ADS] [CrossRef] [Google Scholar]
  60. Weissman, P. R. 1991, in IAU Colloq. 116: Comets in the post-Halley era, eds. R. L. Newburn, Jr., M. Neugebauer, & J. Rahe, Astrophys. Space Sci. Lib., 167, 463 [Google Scholar]
  61. Wichmann, R., Bastian, U., Krautter, J., Jankovics, I., & Rucinski, S. M. 1998, MNRAS, 301, 39L [Google Scholar]

All Tables

Table 1

Observed line parameters.

In the text
Table 2

Summary table of our results in different regimes.

In the text

All Figures

thumbnail Fig. 1

Observed spectra of a) ortho-NH310−00, ortho-H2O 110−101 (previously presented by H11); and b) N2H+ 6–5, using Herschel WBS. The dashed line shows the continuum-subtracted spectral baseline. The o-H2O and o-NH3 lines are observed in opposite sidebands, causing the o-H2O to be detected at a velocity of −14 km s-1 in panel a).
In the text
thumbnail Fig. 2

Overview of the adopted model structure. a) Logarithm of the molecular hydrogen density in cm-3 with black contours. b) Logarithm of the water vapor density with white contours at 0.6 cm-3. c) Gas temperature in K. Black contours represent the logarithm of the water abundance at 0.6 cm-3.
In the text
thumbnail Fig. 3

Schematic illustration of the location of water vapor in our models: a) Compact photodesorption-layer configuration (Cp). b) Extended photodesorption-layer configuration (Ep). c) Compact with a constant abundance configuration (Cm). d) Extended with a constant abundance configuration (Em).
In the text
thumbnail Fig. 4

Panels a), b) and c) show the LIME (Brinch & Hogerheijde 2010) output of the total line fluxes of ortho-NH3, ortho-H2O, and para-H2O, respectively, as a function of the total water vapor mass. The blue, green, red, and yellow curves correspond to the Em, Ep, Cm, and Cp models, respectively. The dashed lines and horizontal green bar show the observed line fluxes and their 3σ ranges, with sigma having two sources of noise added in quadrature; the systematic error of the observations, estimated to be about 20% of the total flux, and the rms of the spectra.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.