EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 591 (July 2016) A&A, 591 (2016) A83 Full HTML
Free Access
Issue
A&A
Volume 591, July 2016
Article Number A83
Number of page(s) 12
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201628152
Published online 20 June 2016

© ESO, 2016

1. Introduction

Blazars count among the most violent sources of high-energy emission in the known universe. They are characterized by highly variable nonthermal emission across the entire electromagnetic spectrum, strong radio and optical polarization, and apparent superluminal motion. The likely explanation of such observations is that they are a subclass of active galactic nuclei (AGNs) where the emission originates from a relativistic jet oriented close to the line of sight (Urry & Padovani 1995). Blazars are the dominant sources of high-energy radiation in the extragalactic sky with over 50 blazars1 detected in the VHE regime. Blazars are further subdivided into BL Lacertae (BL Lac) and flat-spectrum radio quasars (FSRQs), where BL Lacs are characterized by the absence of (or very weak) emission lines. The broadband spectral energy distribution (SED) of blazars is characterized by two peaks, one in the IR – X-ray regime and the second in the γ-ray regime. According to the location of the first peak, BL Lacs are further classified into low-energy peaked BL Lacs (LBL), intermediate peaked BL Lacs (IBL) and high-energy peaked BL Lacs (HBL; Padovani & Giommi 1995). Both leptonic and hadronic models have been used to explain the broadband SED with varying degrees of success. The origin of the low-energy component is well established to be caused by synchrotron emission from relativistic electrons gyrating in the magnetic field of the jet. However, the physical mechanisms responsible for the high-energy emission are still under debate. It can be produced either through inverse Compton (IC) scattering of low-frequency photons by the same electrons responsible for the synchrotron emission (leptonic models), or through hadronic processes initiated by relativistic protons, neutral and charged pion decays, or muon cascades (hadronic models). The seed photons for IC in leptonic models can be either the synchrotron photons themselves (synchrotron self-Compton; SSC) or from external sources such as the broad line region (BLR), the accretion disk, and the cosmic microwave background (external Compton, EC). For a comprehensive review of these mechanisms, see Böttcher (2007).

Mkn 421 is one of the closest (z = 0.031) and the best-studied TeV blazar. It is also the first detected extragalactic TeV source (Punch et al. 1992), and one of the brightest BL Lac objects seen in the UV and X-ray bands. This blazar is a HBL with the synchrotron spectrum peaking in the X-ray regime. It is highly variable on all timescales and across all wavelengths from radio to TeVs, and has been studied comprehensively during its various flaring episodes by several authors (Aleksić et al. 2012, 2010; Acciari et al. 2009; Shukla et al. 2012; Isobe et al. 2010; Krawczynski et al. 2001; Ushio et al. 2009; Tramacere et al. 2009; Horan et al. 2009; Lichti et al. 2008; Fossati et al. 2008; Albert et al. 2007; Brinkmann et al. 2003; Sinha et al. 2015; Paliya et al. 2015; Donnarumma et al. 2009). Abdo et al. (2011) studied the quiescent state emission from this source with the best-sampled SED to date. Liu et al. (1997) constructed the historical light curve of this object from 1900 to 1991 in the optical B band, the analysis of which revealed a possible time period of 23.1 ± 1.1 yrs in the flux variations. Tluczykont et al. (2010) compiled and studied the long-term VHE light curve and found significant correlation (~ 68%) with X-ray data from RXTE-ASM. Strong X-ray-TeV correlation has also been found at smaller timescales (Błażejowski et al. 2005; Katarzynski et al. 2005; jie Qian et al. 1998). Recently, Bartoli et al. (2016) have reported on extensive multiwavelength observations of this source from 2008−2013. They found the VHE flux to be strongly correlated with the X-ray flux, but partially correlated with the GeV flux. Such moderate X-ray-GeV correlation is typical of most HBLs (Li et al. 2013).

The High Altitude GAmma Ray (HAGAR) telescope system at Hanle, India has been regularly monitoring Mkn 421 since its inception in October 2008. In this paper we present the results of the long-term monitoring of this source for the past seven years, from 2009−2015. We use data in the radio, optical, X-ray, and gamma rays to characterize lognormality in the intrinsic flux variations across the multiwavelength spectrum. Correlation studies between different wavelengths are also performed. Spectral energy distribution during different flux states of the source have been constructed simultaneous with HAGAR observations, and fit with leptonic SSC models. The main aim of this paper is not to investigate the fast temporal and spectral variabilities, but to study the smooth variations over weekly and monthly timescales, which may throw light on the underlying jet environment.

2. Multiwavelength observations and data analysis

During the period from 2009−2015, Mkn 421 has been simultaneously observed by many instruments across the entire electromagnetic spectrum. Alongside data from HAGAR, we analyse data from the Fermi-LAT, Nuclear Spectroscopic Telescope Array (NuSTAR), Swift X-ray, and UV telescopes. In addition, we include X-ray observations by the Monitor of All-sky X-ray Image (MAXI) telescope, optical observations by SPOL CCD Imaging/Spectropolarimeter at Steward Observatory, and radio data from the Owens Valley Radio Observatory (OVRO) for the present study. The analysis procedures of these observations are described below.

2.1. HAGAR

The High Altitude GAmma Ray (HAGAR) array is a hexagonal array of seven atmospheric Cherenkov telescopes that uses the wavefront sampling technique to detect celestial gamma rays. It is located at the Indian Astronomical Observatory site (32°46′46′′N, 78° 58′35′′E), in Hanle, Ladakh in the Himalayan mountain ranges at an altitude of 4270 m. The Cherenkov photon density of a shower increases with altitude, and thus, a low-energy threshold is achieved by operating the telescope at such high altitudes. A schematic of the HAGAR telescope array is given in Fig. 1. The telescope structures are based on alt-azimuth design (details given in Gothe et al. 2013) and the separation between two nearest telescopes is 50 m. Each of the seven telescopes has seven para-axially mounted front coated parabolic mirrors of diameter 0.9 m with a UV-sensitive photo-multiplier tube (PMT) at the focus of individual mirrors. The opening angle (field of view) of the HAGAR telescopes is 3°. The pulses from the seven PMTs of each telescope are linearly added to form a telescope pulse for forming trigger and are brought to the control room through low attenuation co-axial cables. Data are recorded using a CAMAC based data acquisition system. The presence of at least four telescope pulses within a coincidence window of 60 ns is used as the trigger for data recording and the relative arrival time of the Cherenkov shower front at each telescope is recorded for each event using a 12-bit Phillips Time to Digital Converter (TDC). A VME based DAQ and an Acquiris digitizer has also been recently installed. Details of the HAGAR array can be found in Chitnis et al. (2011) and Shukla et al. (2012).

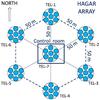thumbnail Fig. 1

Schematic of the HAGAR telescope array. The hexagonal array has a radius of 50 m, and each telescope has seven PMTs in a hexagonal array.

Table 1

The 21 states contemporaneous with HAGAR time periods for which SED has been constructed.

Observations are carried out in ON-OFF mode with a typical 60 min source run followed (or preceded) by a 60 min background run with the same zenith angle. The data analysis is performed using a toolkit developed in-house using IDL based routines. The relative arrival time of the Cherenkov shower front at each telescope is used to reconstruct the arrival direction of the incident cosmic or γ-ray. The relative arrival times are corrected for fixed time offsets (T0) arising as a result of the difference in the signal path length, propagation delay in processing electronics, and transit time of PMTs. We calculate T0s by pointing all the telescopes at a fixed angle (say 10° N) in a dark region of the sky, and minimizing the χ2 given by 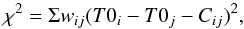χ2=Σwij(T0i−T0j−Cij)2,\begin{equation} \label{equn:t0} \chi^2 = \Sigma w_{ij}(T0_i -T0_j - C_{ij})^2 , \end{equation}(1)where T0i and T0j are the time offsets, wij the weight factor, and Cij the mean delay between the ith and jth telescope. The arrival direction of the Cherenkov shower front is reconstructed by assuming that it is a plane wavefront. Various data quality cuts are imposed to obtain clean data.

Detailed simulations for studying the performance parameters have been performed in Saha et al. (2013). The energy threshold for the HAGAR array for vertically incident γ-ray showers is 208 GeV with a sensitivity of detecting a Crab nebula-like source in 17 h for a 5σ significance. The integral flux of the Crab nebula above 208 GeV is 2.29 × 10-6 ph/cm2/s, corresponding to a mean count rate of 6.6 counts/min.

Mkn 421 has been regularly monitored by HAGAR since its setup in 2008. Analysis of all data up to 2015 yields 101 hrs of clean data. Monthly averaged T0s are used for reconstruction of arrival direction of the shower front and the source counts computed according to the procedure outlined in Shukla et al. (2012). We only retain events with signals in at least five telescopes to minimize systematic errors, for which the energy threshold is estimated to be ~ 250 GeV. Mkn 421 is detected at a mean level of 80% of the Crab flux, at a significance of 9.7σ. The excess counts over background in each HAGAR season are listed in Table 1.

To study the spectral variations, multiwavelength SEDs are constructed contemporaneously with each HAGAR season.

2.2. Fermi Large Area Telescope

Fermi-LAT data from 2009−2015 are extracted from a region of 20° centred on the source. The standard data analysis procedure as mentioned in the Fermi-LAT documentation2 is used. Events belonging to the energy range 0.2−300 GeV and SOURCE class are used. To select good time intervals, a filter “DATA_QUAL>0”, && “LAT_CONFIG==1” is used and only events with less than 105° zenith angle are selected to avoid contamination from the Earth limb γ-rays. The galactic diffuse emission component gll_iem_v05_rev1.fits and an isotropic component iso_source_v05_rev1.txt are used as the background models. The unbinned likelihood method included in the pylikelihood library of Science Tools (v9r33p0) and the post-launch instrument response functions P7REP_SOURCE_V15 are used for the analysis. All the sources lying within 10° region of interest (ROI) centred at the position of Mkn 421 and defined in the third Fermi-LAT catalog (Acero et al. 2015), are included in the xml file. All the parameters except the scaling factor of the sources within the ROI are allowed to vary during the likelihood fitting. For sources between 10° to 20° from the centre, all parameters were kept frozen at the default values. The source is modelled by a simple power law. The light curve is binned over ten days, and spectra are extracted in six logarithmically binned energy bins for the 21 different states contemporaneous with the HAGAR observation seasons.

2.3. NuSTAR

NuSTAR (Harrison et al. 2013) features the first focussing X-ray telescope to extend high sensitivity beyond 10 keV. NuStar observations for this source are available for the year 2013, amounting to a total of 24 pointings. The NuSTAR data are processed with the NuSTARDAS software package v.1.4.1 available within HEASOFT package (6.16). The latest CALDB (v.20140414) is used. After running nupipeline v.0.4.3 on each observation, nuproducts v.0.2.8 is used to obtain the light curves and spectra. Circular regions of 12 pixels centred on Mkn 421 and of 40 pixels centred on 165.96, 38.17 are used as source and background regions, respectively. The spectra from the two detectors, A and B, are combined using addascaspec. Data from various observations are added using addascaspec and then grouped (using the tool grppha v.3.0.1) to ensure a minimum of 30 counts in each bin. Spectra are available for the states s10−s14 and are analysed simultaneously with spectra from Swift-XRT (Sinha et al. 2015).

2.4. Swift observations

There are 594 Swift pointings between January 2009 and June 2015. Publicly available daily binned source counts in the 15−50 keV range are taken from the Swift-BAT webpage3.

The XRT data (Burrows et al. 2005) are processed with the XRTDAS software package (v.3.0.0) available within HEASOFT package (6.16). Event files are cleaned and calibrated using standard procedures (xrtpipeline v.0.13.0), and xrtproducts v.0.4.2 is used to obtain the light curves and spectra. Standard grade selections of 0−12 in the windowed timing (WT) mode are used. Circular regions of 20 pixels centred on Mkn 421 (at RA 166.113 and Dec 38.208) and of 40 pixels centred at 166.15, 38.17 are used as source and background regions, respectively. For the observations affected by pileup (counts > 100 cts/s) (Romano et al. 2006), an annular region with an inner radius of 2 pixels and an outer radius of 20 pixels is taken as the source region. The light curves are finally corrected for telescope vignetting and PSF losses with the tool xrtlccorr v.0.3.8. All pointings within each state are added using the tool addspec. The spectra are grouped to ensure a minimum of 30 counts in each bin by using the tool grppha v.3.0.1.

Since the X-ray data lies at the peak of the synchrotron spectrum, significant departure from a simple power law is needed to model the X-ray spectrum. Following (Sinha et al. 2015), we fit the observed spectrum with a log parabola given by 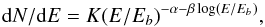dN/dE=K(E/Eb)−α−βlog(E/Eb),\begin{equation} {\rm d}N/{\rm d}E = K(E/E_b)^{-\alpha -\beta \log(E/E_{b})} , \end{equation}(2)where α gives the spectral index at Eb. The point of maximum curvature, Ep is given by 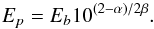Ep=Eb10(2−α)/2β.\begin{equation} \label{lp_phot} E_{p} = E_{b} 10^{(2-\alpha)/2\beta} . \end{equation}(3)During fitting, Eb is fixed at 1 keV, and the XRT and NuSTAR (where available) spectral parameters are tied to each other, except for the relative normalization between the two instruments. To correct for the line-of-sight absorption of soft X-rays due to the interstellar gas, the neutral hydrogen column density is fixed at NH = 1.92 × 1020 cm-2 (Kalberla et al. 2005).

Swift-UVOT (Roming et al. 2005) operated in imaging mode during this period, and for most of the observations, cycled through the UV filters UW1, UW2, and UM2. The tool uvotsource v.3.3 is used to extract the fluxes from each of the images using aperture photometry. The observed magnitudes are corrected for Galactic extinction (EB − V = 0.019 mag) using the dust maps of Schlegel et al. (1998) and converted to flux units using the zero-point magnitudes and conversion factors of Breeveld et al. (2011).

2.5. Other multiwavelength data

We supplement the above information with other available multiwavelength data, namely from:

  • (i)

    MAXI Publicly available daily binned sourcecounts in the 2−20 keV range from the Monitor of All-sky X-ray Image (MAXI) on board the International Space Station (ISS; Matsuoka et al. (2009)) are taken from their website4. MAXI orbital data are known to have some bad quality points due to fluctuations in the background or a shadow of solar-battery paddles. However, this should not affect our results significantly since we use daily binned count rates, where the fluctuations are expected to be averaged out.

  • (ii)

    SPOL The SPOL CCD Imaging/Spectropolarimeter at the Steward Observatory at the University of Arizona (Smith et al. 2009) regularly monitors Mkn 421 as a part of the Fermi multiwavelength support programme. The publicly available optical R-band and V-band photometric and linear polarization data are downloaded from the SPOL website5.

  • (iii)

    OVRO As a part of the Fermi monitoring programme, the Owens Valley Radio Observatory (OVRO; Richards et al. 2011) has been regularly observing this source since 2007. Flux measurements at 15 GHZ are taken directly from their website6.

3. Multiwavelength temporal study

The multiwavelength light curve of Mkn 421 from all available instruments during 2009-2015 is given in Fig. 2. The integration time for each panel is chosen according to the instrument sensitivities. HAGAR points are averaged over each observation season (~ 10 days), likewise the Fermi-LAT, Swift-BAT, and MAXI points are also averaged over 10 days. Each Swift-XRT and Swift-UVOT point corresponds to one pointing (~hours) and (~minutes), respectively, and the CCD-SPOL and OVRO points have integration times of a few seconds. As can be clearly seen, the source is variable across all wavelengths and many flares can be identified. The most dramatic flare in the GeV band occurred during in 2012 (MJD ~ 56 140−56 180; calendar dates 2012-08-01 to 2012-09-10), which is reflected in the radio band after a gap of one and half months (MJD ~ 56 193, Calendar date 2012-09-23). In contrast, the largest X-ray/optical flare happened during April 2013, which has been studied in detail by various authors (Sinha et al. 2015; Pian et al. 2014; Paliya et al. 2015). In this section, we study the flux correlations between the various frequencies and quantify the nature of the variability.

thumbnail Fig. 2

Multiwavelength light curve of Mkn 421 from 2009−2015 showing in panel 1): radio fluxes at 15 GHz from the OVRO; panel 2): optical V-band flux from the CCD-SPOL; panel 3): degree and angle of the optical polarization using data from CCD-SPOL; and panel 4): UV flux in the Swift-UVOT UW2 band. Fluxes in the UW1 and WM2 bands follow a similar trend, and thus only one band has been plotted to avoid cluttering. Panel 5): Swift-XRT count rates; panel 6): MAXI count rate (averaged over 10 days); panel 7): Swift-BAT count rates (10 days averaged); panel 8): Fermi-LAT flux in 10-7 ph/cm2/ s averaged over ten days; and panel 9): HAGAR counts/min, averaged over each observation season. The black dotted line denotes the Crab count rate.

3.1. Variability and correlations

We quantify the variability using the fractional variability amplitude parameter Fvar (Vaughan et al. 2003; Chitnis et al. 2009). It is calculated as 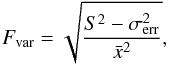Fvar=S2−σerr2x̅2,\begin{equation} F_{\rm var}=\sqrt{\frac{S^2-\sigma^2_{\rm err}}{\bar{x}^2}} , \end{equation}(4)where 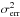σerr2\hbox{$\sigma^2_{\rm err}$} is the mean square error, 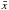\hbox{$\bar{x}$} the unweighted sample mean, and S2 the sample variance. The error on Fvar is given as 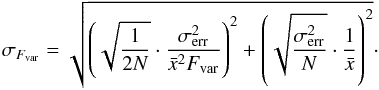σFvar=(12N·σerr2x̅2Fvar)2+(σerr2N·1x̅)2·\begin{equation} \sigma_{F_{\rm var}}= \sqrt{ \left( \sqrt{\frac{1}{2N}}\cdot\frac{\sigma^2_{\rm err}}{\bar{x}^2 F_{\rm var}} \right)^2 + \left( \sqrt{\frac{\sigma^2_{\rm err}}{N}}\cdot\frac{1}{\bar{x}} \right)^2} \cdot \end{equation}(5)Here, N is the number of points.

thumbnail Fig. 3

Fractional variability Fvar as a function of frequency.

The Fvar values derived from the light curves in Fig. 2 are plotted in Fig. 3. To investigate the dependence of variability on the range of timescales, Fvar was computed with 1-day, 10-day, 30-day and 3-month binning (Table 2). Owing to sensitivity issues, Fvar at daily binning cannot be computed for γ-rays, i.e, with the Fermi-LAT and HAGAR. The results remained roughly similar with differences showing up mainly in the X-ray bands. For the optical/GeV bands, the difference is ~ 5%. This shows that the low variability seen in the optical/GeV bands is not an artifact of the binning, but is intrinsic to the source. The variability is maximum in the X-ray/VHE bands, ~ 80%, and goes down with frequency. The GeV and UV data show a similar variability index of ~ 40%, which suggests a similar origin for the X-ray and VHE, and for the UV and GeV spectrum. Similar results have been reported in Aleksić et al. (2015).

Table 2

Fractional variability (Fvar) in different wavebands with different time binnings.

We compute the hardness ratios from Swift-XRT data, which are defined as the ratio of the flux in the 2−10 keV band to the flux in 0.3−2 keV band. As can be seen in Fig. 4, while there is clear trend of spectral hardening with flux seen in the X-ray band (ρ = 0.83, prob = 2.1 × 10-16), no such evidence is seen in the γ-ray band (ρ = 0.06prob = 0.33), again suggesting different origin for the X-ray and GeV data.

thumbnail Fig. 4

Hardness ratio in the X-ray(Swift-XRT) band and GeV (Fermi-LAT) bands. While the trend of spectral hardening with flux is clear in the X-ray band, no such trend is seen in the GeV band.

To study the lags between the various unevenly sampled energy bands, we use the z-transformed discrete cross correlation function, freely available as a FORTRAN 90 routine with the details of the method described in Alexander (1997). A minimum of 11 points are taken in each bin and points with zero lag are omitted. Since many of the HAGAR seasonal points correspond to upper limits, we avoid the use of HAGAR data in detailed temporal studies. The computed z-DCFs are plotted in Fig. 5. A lag of 73 ± 20 days is observed between the optical V band and the ultraviolet UW2 band with a strong correlation of 0.80 ± 0.04. The Fermi low- (0.2−2 GeV) and high- (2−300 GeV) energy bands are highly correlated (z-DCF = 0.67 ± 0.34) with no visible lag, whereas the low- (2−20 keV, MAXI) and high- (15−150 keV, Swift-BAT) energy X-ray bands are less strongly correlated (z-DCF = 0.28 ± 0.02) at a lag of 7.1 ± 0.5 days (Fig. 5a). There is no correlation between the Fermi and the X-ray bands (Fig. 5b). The Fermi flux does not show any lag with the optical flux (z-DCF = 0.52 ± 0.06), but leads the UV flux by 80 ± 1 days (z-DCF = 0.57 ± 0.07) (Fig. 5c). Interestingly, there is strong radio-γ-ray correlation (z-DCF = 0.69 ± 0.05) as seen in Fig. 5d, where the radio flux lags behind the γ-ray flux by 52 ± 20 days. Such strong radio-γ ray correlations due to large dominant flares have been previously seen in long-term studies of blazars (Mufakharov et al. 2015; Wu et al. 2014; Max-Moerbeck et al. 2014).

thumbnail Fig. 5

z-DCF between the various wavebands. A positive lag indicates the lower energy flare leads the high-energy flare.

3.2. Lognormality

Lognormality is an important statistical process found in many accreting sources like X-ray binaries (Uttley & McHardy 2001). Lognormal fluxes have fluctuations, that are, on average, proportional to the flux itself, and are indicative of an underlying multiplicative, rather than additive physical process. It has been suggested that a lognormal flux behaviour in blazars could be indicative of the variability imprint of the accretion disk onto the jet (McHardy 2008). This behaviour in blazars was first clearly detected in the X-ray regime in BL Lac (Giebels & Degrange 2009) and has been seen across the entire electromagnetic spectrum in PKS 2155+304 (Chevalier et al. 2015).

thumbnail Fig. 6

Histograms of the fluxes (shown in black) at different wavebands. In all of the cases, a lognormal distribution (blue line) fits better than the Gaussian distribution (red line). The reduced chi-squares are given in Table 3.

To investigate lognormality, we fit the histograms of the observed fluxes with a Gaussian and a lognormal function (Fig. 6). The reduced chi-squares from the fits are given in Table 3. The lognormal function is clearly preferred over the Gaussian, indicating a lognormal trend in the flux distribution. We further plot the excess variance, 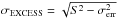σEXCESS=S2−σerr2\hbox{$\sigma_{\rm EXCESS}= \sqrt{S^2-\sigma^2_{\rm err}}$} versus the mean flux in Fig. 7. Data is binned over a period of 100 days to get sufficient statistics. To test the rms-flux relationship, following Giebels & Degrange (2009) and Chevalier et al. (2015), the scatter plot is fit by a constant and a linear function. The linear fit is clearly preferred over the constant with r as the measure of the correlation coefficient. Spearman’s rank correlation (ρ) is also computed, the result of which shows that the errors are generally proportional to the flux. While lognormality is clearly detected for the survey instruments, Fermi-LAT, Swift-BAT, and MAXI, the correlations decrease for the other instruments. This is likely because the observations from the pointing instruments are biased towards the flaring states. In fact, the histogram of the flux distribution clearly shows two peaks for the OVRO and the R-band data, the second of which can be attributed to the flare states. These flares may be caused by separate “short-term” phenomena, as compared to the long-term flux modulations. This hypothesis is supported by the fact that lognormality is clearly seen by MAXI, but not by Swift-XRT, where the two instruments sample similar energy regimes. Also, the measured radio flux from OVRO is the combined emission from the jet and radio lobes, the latter of which may contribute to the second component.

Table 3

Lognormal trends in the different wavebands.

thumbnail Fig. 7

Excess variance vs. the mean flux for the different wavebands. The black lines show the best-fit linear regression line.

4. Spectral modelling

Twenty-one SEDs were extracted over the past seven years. We do not bias our SEDs over any flare/quiescent states as in Bartoli et al. (2016), but choose epochs contemporaneous with HAGAR time periods. During these epochs, the total bolometric luminosity varied almost by a factor of 10. The broadband emission is assumed to originate from a single spherical zone of radius R filled with a tangled magnetic field B. A non-thermal population of electrons, with a broken power-law spectral shape, 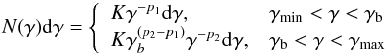N(γ)dγ={Kγ−p1dγ,γmin<γ<γbKγb(p2−p1)γ−p2dγ,γb<γ<γmax\begin{equation} \label{eq:bknpo} N (\gamma) {\rm d}\gamma =\left\{ \begin{array}{ll} K \gamma^{-p_1}{\rm d}\gamma,& \gamma_{\rm min}<\gamma<\gamma_{\rm b} \\ K \gamma^{(p_2-p_1)}_b \gamma^{-p_2}{\rm d}\gamma,& \gamma_{\rm b}<\gamma<\gamma_{\rm max} \end{array} \right. \end{equation}(6)is assumed to lose its energy through synchrotron and self-Compton (SSC) processes. As a result of the relativistic motion of the jet, the radiation is boosted along our line of sight by a Doppler factor δ. This simple model is most commonly used in literature to model the broadband spectrum (Ghisellini et al. 1996; Krawczynski et al. 2004). Correction for attenuation of TeV photons due to the extragalactic background light (EBL) is accounted for by deconvolving the obtained spectrum with the EBL model of (Franceschini et al. 2008). Mankuzhiyil et al. (2012) used the Levenburg-Marquadt algorthim to fit the numerical model to the observed spectrum. We incorporate the numerical SSC model of Saha & Bhattacharjee (2015) in the XSPEC spectral fitting software to perform a χ2 minimization. Swift-XRT data are binned to have ~ 6 points (and similarly for NuSTAR) to avoid biasing the fit towards the X-ray energies. The tool flx2xsp v.2.1 was used to convert the fluxes to pha files for use in XSPEC. Since we are dealing with several different instruments over a broad energy range, we assume model systematics of 5%.

A good sampling of the entire SED from radio to γ-rays allows one to perform a reasonable estimation of the physical parameters (Ghisellini et al. 1996; Tavecchio et al. 1998) in terms of the observed fluxes. The radius R of the emission region has to be independently estimated from the light travel time argument, R<cδtvar/ (1 + z), where tvar is the observed flux doubling timescale. However, Mkn 421 shows different flux doubling timescales over different time periods, and since we are dealing mainly with quiescent state emission, we keep R fixed at 6.0 × 1016 cm, which was used by Aleksić et al. (2015). This roughly corresponds to a tvar ~ 1 day for δ = 21, which is also frozen during the fitting. The minimum particle Lorentz factor, γmin can be fixed at a reasonably low value without affecting the modelling (Archambault et al. 2015), and is assumed to be 1000. The maximum Lorentz factor, γmax, is kept fixed at 10γb.

The ratio of the electric (UE) and magnetic (UB )field energy density is parameterized by the equipartition parameter η = UE/UB, where UB = B2/ 2μ0 and 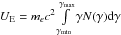UE=mec2γminγmin∫γmaxγmaxγminγmaxγN(γ)dγ\hbox{$U_{\rm E} = m_e c^2 \int\limits_{\gamma_{\rm min}}^{\gamma_{\rm max}} \gamma N(\gamma) {\rm d} \gamma$}. The results of the fit are shown in Fig. 8. The best-fit parameters and the reduced χ2 are listed in Table 4. During all the epochs, the energy density in the jet is matter dominated with the model parameters a factor of 10 away from equipartition. However, this ratio may be improved by choosing a lower value of δ or R. For all the SEDs studied here, the one-zone model provides a very good fit to the observed data and does not motivate the need for a second emitting region.

Table 4

Fit parameters for the different SED states with R = 6.0 × 1016 cm, δ = 21, γmin = 1000, and γmax = 10γb.

thumbnail Fig. 8

Model SEDs during the 21 states fit with a one-zone SSC, along with the model SED during the February 2010 flare (Shukla et al. (2012), plotted in thick black line for reference).

5. Results and discussions

The similar variability in the optical-GeV bands, and the X-ray-VHE bands indicates a similar origin for the optical and Fermi-LAT bands and for the X-ray-VHE bands. In the framework of the SSC model, this is attributed as the first index, p1 contributing to the optical-GeV bands (synchrotron and SSC respectively), and the second index p2 for the X-ray-VHE bands. As can be seen from the fit parameters in Table 4, some of the states require a very hard particle index p1< 2.0. Such an index cannot originate from a single shock acceleration, but may originate from multiple shocks (Malkov & Drury 2001), which can produce particle indices as hard as 1.5, which is close to the hardest spectrum (p1 = 1.6) obtained in our fits. Alternatively, stochastic acceleration in resonance with plasma wave turbulence behind the relativistic shock front can also harden the injection index (Vainio et al. 2004). The two indices, p1 and p2, show a weak correlation with ρ = 0.42, prob = 0.05 (Fig. 9a). In particular, p2 is much steeper than what would be expected from p2 = p1 + 1, thus ruling out the broken power-law spectrum as originating from a cooling break. There is a significant correlation between the total bolometric luminosity L and the first index (ρ = 0.66, prob = 0.001), and a very strong correlation between L and the particle break energy γb (ρ = 0.79, prob = 3.2 × 10-5) (Fig. 9b). However, no significant trend is seen between the magnetic field B and L. This implies that the variations in the different flux states occur mainly because of a change in the underlying particle distribution, rather than in the jet environment.

We observe that the γ-ray flares lead the radio flares, 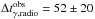Δtγ,radioobs=52±20\hbox{$\Delta t^{\rm obs}_{\gamma,{\rm radio}} = 52 \pm 20$} days. Pushkarev et al. (2010) explained this because of the synchrotron opacity in the nuclear region. Since the radio core is optically thick to synchrotron radiation up to a frequency dependant radius rc ∝ ν-1, the γ-ray emission zone should be located upstream with respect to the apparent radio core position. Assuming the flares to be caused by the same disturbance, the radio and γ-ray flares are not observed simultaneously because of the opacity effect. This information can be used to estimate the distance travelled by emission region dγ,radio using the relation (Ramakrishnan et al. 2015) 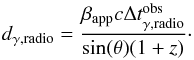dγ,radio=βappcΔtγ,radioobssin(θ)(1+z)·\begin{equation} d_{\gamma,{\rm radio}} = \frac{\beta_{\rm app} c \Delta t^{\rm obs}_{\gamma,{\rm radio}}}{\sin(\theta)(1+z)} \label{eq:dist} \cdot \end{equation}(7)Using βapp ~ 1.92 (Zhang & Bååth 1996), θ = tan-1(2βapp/ 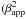(βapp2\hbox{$(\beta^2_{\rm app}$} + δ2−1)) ~ 0.5° (Ghisellini et al. 1993), and z = 0.031, we find the distance travelled by the emission region dγ,radio = 9.3 pc. This corresponds to a projected distance of 0.08 pc, equivalent to an angular size of 0.12 mas. Zhang & Baath (1991) studied the VLBI image of this source at a resolution of ~ 0.15 mas and found unresolved core. This, compared to our estimated size of 0.12 mas allows us to constrain the γ-ray emission site within the radio core.

thumbnail Fig. 9

Cross plot of the fit parameters for the one-zone SSC. The black dotted line in the first panel corresponds to the relation p2 = p1 + 1, which is what would have been expected from a synchrotron cooling break. The second panel shows the variation of the synchrotron peak frequency with the total bolometric luminosity. A strong correlation is clearly observed.

The observed lognormality of the flux distributions in the different bands and the proportionality between the fluctuations in the flux imply that the variations are lognormal. Similar trends have been found in several accreting galactic sources (Giebels & Degrange 2009) and also in the Seyfert 1 galaxy, Mkn 766, where the physical process responsible for the X-ray emission is most likely thermal emission from the galactic disk (Vaughan et al. 2003). The results of our SED modelling in Sect. 4 show that the flux variability in the source can be mainly attributed to changes in the particle spectrum rather than jet parameters such as the magnetic field or Doppler factor. This implies that the lognormal fluctuations in the flux are indicative of lognormal processes in the accretion disk, and the lognormal fluctuations in the accreting rate give rise to an injection rate with similar properties.

The one-zone SSC model used in this study provides a suitable fit to the observed SEDs for all epochs without motivating the need for any additional emitting regions. Interestingly, while the time-resolved UV-X-ray spectra during the April 2013 flare could not be explained by synchrotron emission from a single region (Sinha et al. 2015), the time averaged broadband spectrum during the same time (State s13) can be well fitted by our model (reduced χ2 = 1.5). This motivates a need for better time-resolved broadband spectra. The upcoming Major Atmospheric Cherenkov Experiment (MACE; Koul et al. 2011) at Hanle, Ladakh is expected to provide us with excellent time-resolved spectrum at VHE energies, which may throw new light onto the VHE emission from blazar jets.

Acknowledgments

We thank the scientific and technical personnel of HAGAR groups at IIA, Bengaluru and TIFR, Mumbai for observations with HAGAR system. A. Sinha would like to thank Sunder Sahayanathan from the Bhabha Atomic Research Center, Mumbai, for helpful discussions and comments. This research has made use of data, software, and/or web tools obtained from NASAs High Energy Astrophysics Science Archive Research Center (HEASARC), a service of Goddard Space Flight Center and the Smithsonian Astrophysical Observatory. Part of this work is based on archival data, software, or online services provided by the ASI Science Data Center (ASDC). This research has made use of the XRT Data Analysis Software (XRTDAS) developed under the responsibility of the ASI Science Data Center (ASDC), Italy, and the NuSTAR Data Analysis Software (NuSTARDAS) jointly developed by the ASI Science Data Center (ASDC, Italy) and the California Institute of Technology (Caltech, USA). Data from the Steward Observatory spectropolarimetric monitoring project are used. This programme is supported by Fermi Guest Investigator grants NNX08AW56G, NNX09AU10G, and NNX12AO93G. The OVRO 40 M Telescope Fermi Blazar Monitoring Program is supported by NASA under awards NNX08AW31G and NNX11A043G, and by the NSF under awards AST-0808050 and AST-1109911.

References

  1. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2011, ApJ, 736, 131 [NASA ADS] [CrossRef] [Google Scholar]
  2. Acciari, V. A., Aliu, E., Aune, T., et al. 2009, ApJ, 703, 169 [NASA ADS] [CrossRef] [Google Scholar]
  3. Acero, F., Ackermann, M., Ajello, M., et al. 2015, ApJS, 218, 23 [Google Scholar]
  4. Albert, J., Aliu, E., Anderhub, H., et al. 2007, ApJ, 663, 125 [NASA ADS] [CrossRef] [Google Scholar]
  5. Aleksić, J., Anderhub, H., Antonelli, L. A., et al. 2010, A&A, 519, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Aleksić, J., Alvarez, E. A., Antonelli, L. A., et al. 2012, A&A, 542, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Aleksić, J., Ansoldi, S., Antonelli, L. A., et al. 2015, A&A, 578, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Alexander, T. 1997, in Astronomical Time Series, eds. D. Maoz, A. Sternberg, & E. M. Leibowitz, Astrophys. Space Sci. Libr., 218, 163 [Google Scholar]
  9. Archambault, S., Archer, A., Beilicke, M., et al. 2015, ApJ, 808, 110 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bartoli, B., Bernardini, P., Bi, X. J., et al. 2016, ApJS, 222, 6 [NASA ADS] [CrossRef] [Google Scholar]
  11. Błażejowski, M., Blaylock, G., Bond, I. H., et al. 2005, ApJ, 630, 130 [NASA ADS] [CrossRef] [Google Scholar]
  12. Böttcher, M. 2007, Ap&SS, 307, 69 [NASA ADS] [CrossRef] [Google Scholar]
  13. Breeveld, A. A., Landsman, W., Holland, S. T., et al. 2011, in AIP Conf. Ser. 1358, eds. J. E. McEnery, J. L. Racusin, & N. Gehrels, 373 [Google Scholar]
  14. Brinkmann, W., Papadakis, I. E., den Herder, J. W. A., & Haberl, F. 2003, A&A, 402, 929 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [NASA ADS] [CrossRef] [Google Scholar]
  16. Chevalier, J., Kastendieck, M. A., Rieger, F., et al. 2015, ArXiv e-prints [arXiv:1509.03104] [Google Scholar]
  17. Chitnis, V. R., Pendharkar, J. K., Bose, D., et al. 2009, ApJ, 698, 1207 [NASA ADS] [CrossRef] [Google Scholar]
  18. Chitnis, V. R., Acharya, B. S., Anupama, G. C., et al. 2011, Proc. 32nd International Cosmic Ray Conference held at Beiging, China, 9, 166 [Google Scholar]
  19. Donnarumma, I., Vittorini, V., Vercellone, S., et al. 2009, ApJ, 691, L13 [NASA ADS] [CrossRef] [Google Scholar]
  20. Fossati, G., Buckley, J. H., Bond, I. H., et al. 2008, ApJ, 677, 906 [NASA ADS] [CrossRef] [Google Scholar]
  21. Franceschini, A., Rodighiero, G., & Vaccari, M. 2008, A&A, 487, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Ghisellini, G., Padovani, P., Celotti, A., & Maraschi, L. 1993, ApJ, 407, 65 [Google Scholar]
  23. Ghisellini, G., Maraschi, L., & Dondi, L. 1996, A&AS, 120, C503 [NASA ADS] [Google Scholar]
  24. Giebels, B., & Degrange, B. 2009, A&A, 503, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Gothe, K. S., Prabhu, T. P., Vishwanath, P. R., et al. 2013, Exp. Astron., 35, 489 [NASA ADS] [CrossRef] [Google Scholar]
  26. Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [NASA ADS] [CrossRef] [Google Scholar]
  27. Horan, D., Acciari, V. A., Bradbury, S. M., et al. 2009, ApJ, 695, 596 [NASA ADS] [CrossRef] [Google Scholar]
  28. Isobe, N., Sugimori, K., Kawai, N., et al. 2010, PASJ, 62, L55 [NASA ADS] [Google Scholar]
  29. jie Qian, S., zhen Zhang, X., Witzel, A., et al. 1998, Chin. Astron. Astrophys., 22, 155 [NASA ADS] [CrossRef] [Google Scholar]
  30. Katarzynski, K., Ghisellini, G., Tavecchio, F., et al. 2005, A&A, 433, 479 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Koul, R., Rannot, R. C., & Mitra, A. 2011, Proc. 32nd International Cosmic Ray Conference held at Beiging, China, 9, 107 [Google Scholar]
  33. Krawczynski, H., Sambruna, R., Kohnle, A., et al. 2001, ApJ, 559, 187 [NASA ADS] [CrossRef] [Google Scholar]
  34. Krawczynski, H., Hughes, S. B., Horan, D., et al. 2004, ApJ, 601, 151 [NASA ADS] [CrossRef] [Google Scholar]
  35. Li, B., Zhang, H., Zhang, X., et al. 2013, Ap&SS, 347, 349 [NASA ADS] [CrossRef] [Google Scholar]
  36. Lichti, G. G., Bottacini, E., Ajello, M., et al. 2008, A&A, 486, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Liu, F. K., Liu, B. F., & Xie, G. Z. 1997, A&AS, 123, 569 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Malkov, M. A., & Drury, L. O. 2001, Rep. Prog. Phys., 64, 429 [NASA ADS] [CrossRef] [Google Scholar]
  39. Mankuzhiyil, N., Ansoldi, S., Persic, M., et al. 2012, ApJ, 753, 154 [NASA ADS] [CrossRef] [Google Scholar]
  40. Matsuoka, M., Kawasaki, K., Ueno, S., et al. 2009, PASJ, 61, 999 [NASA ADS] [CrossRef] [Google Scholar]
  41. Max-Moerbeck, W., Hovatta, T., Richards, J. L., et al. 2014, MNRAS, 445, 428 [NASA ADS] [CrossRef] [Google Scholar]
  42. McHardy, I. 2008, PoS(BLAZAR 2008)014 [Google Scholar]
  43. Mufakharov, T., Mingaliev, M., Sotnikova, Y., Naiden, Y., & Erkenov, A. 2015, MNRAS, 450, 2658 [NASA ADS] [CrossRef] [Google Scholar]
  44. Padovani, P., & Giommi, P. 1995, ApJ, 444, 567 [NASA ADS] [CrossRef] [Google Scholar]
  45. Paliya, V. S., Bottcher, M., Diltz, C., et al. 2015, ApJ, 811, 143 [NASA ADS] [CrossRef] [Google Scholar]
  46. Pian, E., Türler, M., Fiocchi, M., et al. 2014, A&A, 570, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Punch, M., Akerlof, C. W., Cawley, M. F., et al. 1992, Nature, 358, 477 [NASA ADS] [CrossRef] [Google Scholar]
  48. Pushkarev, A. B., Kovalev, Y. Y., & Lister, M. L. 2010, ApJ, 722, L7 [NASA ADS] [CrossRef] [Google Scholar]
  49. Ramakrishnan, V., Hovatta, T., Nieppola, E., et al. 2015, MNRAS, 452, 1280 [CrossRef] [Google Scholar]
  50. Richards, J. L., Max-Moerbeck, W., Pavlidou, V., et al. 2011, ApJS, 194, 29 [NASA ADS] [CrossRef] [Google Scholar]
  51. Romano, P., Campana, S., Chincarini, G., et al. 2006, A&A, 456, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Roming, P. W. A., Kennedy, T. E., Mason, K. O., et al. 2005, Space Sci. Rev., 120, 95 [NASA ADS] [CrossRef] [Google Scholar]
  53. Saha, L., & Bhattacharjee, P. 2015, J. High Energy Astrophys., 56, 9 [NASA ADS] [CrossRef] [Google Scholar]
  54. Saha, L., Chitnis, V. R., Vishwanath, P. R., et al. 2013, Astropart. Phys., 42, 33 [NASA ADS] [CrossRef] [Google Scholar]
  55. Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
  56. Shukla, A., Chitnis, V. R., Vishwanath, P. R., et al. 2012, A&A, 541, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Sinha, A., Shukla, A., Misra, R., et al. 2015, A&A, 580, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Smith, P. S., Montiel, E., Rightley, S., et al. 2009, ArXiv e-prints [arXiv:0912.3621] [Google Scholar]
  59. Tavecchio, F., Maraschi, L., & Ghisellini, G. 1998, ApJ, 509, 608 [NASA ADS] [CrossRef] [Google Scholar]
  60. Tluczykont, M., Bernardini, E., Satalecka, K., et al. 2010, A&A, 524, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Tramacere, A., Giommi, P., Perri, M., Verrecchia, F., & Tosti, G. 2009, A&A, 501, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
  63. Ushio, M., Tanaka, T., Madejski, G., et al. 2009, ApJ, 699, 1964 [NASA ADS] [CrossRef] [Google Scholar]
  64. Uttley, P., & McHardy, I. M. 2001, MNRAS, 323, L26 [NASA ADS] [CrossRef] [Google Scholar]
  65. Vainio, R., Pohl, M., & Schlickeiser, R. 2004, A&A, 414, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Vaughan, S., Edelson, R., Warwick, R. S., & Uttley, P. 2003, MNRAS, 345, 1271 [NASA ADS] [CrossRef] [Google Scholar]
  67. Wu, D.-X., Fan, J.-H., Liu, Y., et al. 2014, PASJ, 66, 117 [NASA ADS] [Google Scholar]
  68. Zhang, F. J., & Bååth, L. B. 1996, Ap&SS, 235, 195 [NASA ADS] [CrossRef] [Google Scholar]
  69. Zhang, F. J., & Baath, L. B. 1991, MNRAS, 248, 566 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

The 21 states contemporaneous with HAGAR time periods for which SED has been constructed.

In the text
Table 2

Fractional variability (Fvar) in different wavebands with different time binnings.

In the text
Table 3

Lognormal trends in the different wavebands.

In the text
Table 4

Fit parameters for the different SED states with R = 6.0 × 1016 cm, δ = 21, γmin = 1000, and γmax = 10γb.

In the text

All Figures

thumbnail Fig. 1

Schematic of the HAGAR telescope array. The hexagonal array has a radius of 50 m, and each telescope has seven PMTs in a hexagonal array.
In the text
thumbnail Fig. 2

Multiwavelength light curve of Mkn 421 from 2009−2015 showing in panel 1): radio fluxes at 15 GHz from the OVRO; panel 2): optical V-band flux from the CCD-SPOL; panel 3): degree and angle of the optical polarization using data from CCD-SPOL; and panel 4): UV flux in the Swift-UVOT UW2 band. Fluxes in the UW1 and WM2 bands follow a similar trend, and thus only one band has been plotted to avoid cluttering. Panel 5): Swift-XRT count rates; panel 6): MAXI count rate (averaged over 10 days); panel 7): Swift-BAT count rates (10 days averaged); panel 8): Fermi-LAT flux in 10-7 ph/cm2/ s averaged over ten days; and panel 9): HAGAR counts/min, averaged over each observation season. The black dotted line denotes the Crab count rate.
In the text
thumbnail Fig. 3

Fractional variability Fvar as a function of frequency.
In the text
thumbnail Fig. 4

Hardness ratio in the X-ray(Swift-XRT) band and GeV (Fermi-LAT) bands. While the trend of spectral hardening with flux is clear in the X-ray band, no such trend is seen in the GeV band.
In the text
thumbnail Fig. 5

z-DCF between the various wavebands. A positive lag indicates the lower energy flare leads the high-energy flare.
In the text
thumbnail Fig. 6

Histograms of the fluxes (shown in black) at different wavebands. In all of the cases, a lognormal distribution (blue line) fits better than the Gaussian distribution (red line). The reduced chi-squares are given in Table 3.
In the text
thumbnail Fig. 7

Excess variance vs. the mean flux for the different wavebands. The black lines show the best-fit linear regression line.
In the text
thumbnail Fig. 8

Model SEDs during the 21 states fit with a one-zone SSC, along with the model SED during the February 2010 flare (Shukla et al. (2012), plotted in thick black line for reference).
In the text
thumbnail Fig. 9

Cross plot of the fit parameters for the one-zone SSC. The black dotted line in the first panel corresponds to the relation p2 = p1 + 1, which is what would have been expected from a synchrotron cooling break. The second panel shows the variation of the synchrotron peak frequency with the total bolometric luminosity. A strong correlation is clearly observed.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.