| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | A8 | |
| Number of page(s) | 23 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201628221 | |
| Published online | 28 April 2016 | |
Protostars: Forges of cosmic rays?
1
Laboratoire Univers et Particules de Montpellier, UMR 5299 du CNRS,
Université de Montpellier,
place E. Bataillon, cc072,
34095
Montpellier,
France
e-mail: Marco.Padovani@umontpellier.fr; Alexandre.Marcowith@umontpellier.fr
2
INAF–Osservatorio Astrofisico di Arcetri, Largo E. Fermi
5, 50125
Firenze,
Italy
3
CEA, IRFU, SAp, Centre de Saclay, 91191
Gif-Sur-Yvette,
France
e-mail:
patrick.hennebelle@cea.fr
4
IRAP, Université de Toulouse, CNRS, 9 avenue du Colonel Roche, BP 44346, 31028
Toulouse Cedex 4,
France
Received: 29 January 2016
Accepted: 24 February 2016
Context. Galactic cosmic rays are particles presumably accelerated in supernova remnant shocks that propagate in the interstellar medium up to the densest parts of molecular clouds, losing energy and their ionisation efficiency because of the presence of magnetic fields and collisions with molecular hydrogen. Recent observations hint at high levels of ionisation and at the presence of synchrotron emission in protostellar systems, which leads to an apparent contradiction.
Aims. We want to explain the origin of these cosmic rays accelerated within young protostars as suggested by observations.
Methods. Our modelling consists of a set of conditions that has to be satisfied in order to have an efficient cosmic-ray acceleration through diffusive shock acceleration. We analyse three main acceleration sites (shocks in accretion flows, along the jets, and on protostellar surfaces), then we follow the propagation of these particles through the protostellar system up to the hot spot region.
Results. We find that jet shocks can be strong accelerators of cosmic-ray protons, which can be boosted up to relativistic energies. Other promising acceleration sites are protostellar surfaces, where shocks caused by impacting material during the collapse phase are strong enough to accelerate cosmic-ray protons. In contrast, accretion flow shocks are too weak to efficiently accelerate cosmic rays. Though cosmic-ray electrons are weakly accelerated, they can gain a strong boost to relativistic energies through re-acceleration in successive shocks.
Conclusions. We suggest a mechanism able to accelerate both cosmic-ray protons and electrons through the diffusive shock acceleration mechanism, which can be used to explain the high ionisation rate and the synchrotron emission observed towards protostellar sources. The existence of an internal source of energetic particles can have a strong and unforeseen impact on the ionisation of the protostellar disc, on the star and planet formation processes, and on the formation of pre-biotic molecules.
Key words: cosmic rays / ISM: jets and outflows / stars: protostars
© ESO, 2016
1. Introduction
Cosmic rays (CRs), ordinary matter, and magnetic fields represent the fundamental elements of the Galaxy; they have comparable pressures and are coupled together by electromagnetic forces (Ferrière 2001). The interaction between CRs and the interstellar matter lays the foundation for the rich chemistry that is observed in molecular clouds. In fact, as soon as the UV interstellar radiation field is absorbed, at about 4 mag of visual extinction (McKee 1989) and far from the X-ray flux produced by embedded protostars (Krolik & Kallman 1983; Silk & Norman 1983), CRs are the main ionising agents of molecular hydrogen, the most abundant component of molecular clouds. From this process, increasingly complex species are produced, allowing the characterisation of the physical and chemical properties of protostellar sources.
The key parameter in the calculation of molecular abundances from observations and from chemical models is the CR ionisation rate, ζ. Determining the value of ζ is not straightforward since the propagation of CRs inside a cloud has to be accurately described and a number of processes taken into account: energy losses (Padovani et al. 2009), magnetic field effects (Cesarsky & Völk 1978; Chandran 2000; Padovani & Galli 2011, 2013; Padovani et al. 2013), and screening due to self-generated Alfvén waves in the plasma (Skilling & Strong 1976; Cesarsky & Völk 1978; Hartquist et al. 1978; Rimmer et al. 2012; Morlino & Gabici 2015).
In addition to the chemistry, CRs play another important role in regulating the formation of protostellar discs. A magnetic field entrained in a collapsing cloud brakes the rotational motions as long as the field is frozen in the gas (see e.g. Galli et al. 2006; Mellon & Li 2008; Hennebelle & Fromang 2008). One of the speculated mechanisms that mitigates the magnetic braking effect relies on non-ideal magnetohydrodynamic effects, namely ambipolar diffusion, Hall, and Ohmic diffusion (Shu et al. 2006; Dapp & Basu 2010; Krasnopolsky et al. 2011; Braiding & Wardle 2012a,b; Masson et al. 2016; Tomida et al. 2015). The associated diffusion coefficients depend on the abundance of the charged species, which in turn is predicted by the CR ionisation rate. Padovani et al. (2013; 2014) showed that, at least in the formation process of low-mass protostellar discs, a proper treatment of CR propagation can lead to very low values of ζ. As a consequence, in the central region of a collapsing cloud the coupling between gas and magnetic field is weaker than usually assumed, flux freezing is no longer valid, and the influence of the magnetic field on the collapse is reduced.
Cleeves et al. (2013) studied the inhibition of CR propagation in protoplanetary discs of Class II protostars as a result of magnetised stellar winds. They found that, in addition to X-ray ionisation from the central star, ζ is set by short-lived radionuclides and it is of the order of 10-19 s-1. On the other hand, Ceccarelli et al. (2014) and Podio et al. (2014) found very high values of ζ towards two protostars (OMC-2 FIR 4 and L1157-B1). These high values of ζ cannot be due to the interstellar CR flux since the column density is too high, which damps the propagation of interstellar CRs (Padovani et al. 2013). Following the same reasoning, the interstellar electron flux cannot explain the synchrotron emission observed towards the bow shock of DG Tau by Ainsworth et al. (2014).
The purpose of this paper is to investigate the possibility of accelerating particles, i.e. of generating local CRs, inside or in the immediate vicinity of a protostar. Our investigation is justified by simple arguments on the energetics of the system. The gravitational luminosity of an accretion shock on the surface of a protostar reads 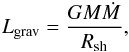 (1)where G is the gravitational constant, M is the protostellar mass, Ṁ is the accretion rate, and Rsh is the shock radius. If we consider the gravitational collapse of an early Class 0 protostar with M = 0.1 M⊙, Ṁ = 10-5M⊙ yr-1 (e.g. Shu et al. 1987; Belloche et al. 2002), Rsh = 2 × 10-2 AU (Masunaga & Inutsuka 2000), then Lgrav = 3 × 1034 erg s-1. The luminosity of the interstellar CRs impinging on a molecular cloud core can be estimated by
(1)where G is the gravitational constant, M is the protostellar mass, Ṁ is the accretion rate, and Rsh is the shock radius. If we consider the gravitational collapse of an early Class 0 protostar with M = 0.1 M⊙, Ṁ = 10-5M⊙ yr-1 (e.g. Shu et al. 1987; Belloche et al. 2002), Rsh = 2 × 10-2 AU (Masunaga & Inutsuka 2000), then Lgrav = 3 × 1034 erg s-1. The luminosity of the interstellar CRs impinging on a molecular cloud core can be estimated by 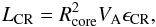 (2)where Rcore is the core radius, VA is the Alfvén speed in the surrounding medium, supposed to be the warm neutral medium, and ϵCR is the energy density of the interstellar CRs based on the latest Voyager 1 observations (Stone et al. 2013; Ivlev et al. 2015). Here we adopt Rcore = 0.1 pc, VA = 9.3 × 105 cm s-1 (based on nH = 0.5 cm-3 and B = 3 μG; Ferrière 2001), and ϵCR = 1.3 × 10-12 erg cm-3, then LCR = 1.2 × 1029 erg s-1 ≪ Lgrav. In previous studies we demonstrated that the interstellar CR flux is strongly attenuated at high column densities (Padovani et al. 2009, 2013), and so we expect ϵCR at the protostellar surface to be much lower than its interstellar value and, a fortiori, LCR ⋘ Lgrav close to the protostar. Thus, if a small fraction of the gravitational energy can be used to produce local CRs, they could easily be dominant over the ISM ones. For a massive star the gravitational energy available to generate high-energy CRs is even higher since Ṁ could be as high as 10-3M⊙ yr-1 and in principle their γ emission can be observed (see e.g. Araudo et al. 2007; Bosch-Ramon et al. 2010; Munar-Adrover et al. 2011).
(2)where Rcore is the core radius, VA is the Alfvén speed in the surrounding medium, supposed to be the warm neutral medium, and ϵCR is the energy density of the interstellar CRs based on the latest Voyager 1 observations (Stone et al. 2013; Ivlev et al. 2015). Here we adopt Rcore = 0.1 pc, VA = 9.3 × 105 cm s-1 (based on nH = 0.5 cm-3 and B = 3 μG; Ferrière 2001), and ϵCR = 1.3 × 10-12 erg cm-3, then LCR = 1.2 × 1029 erg s-1 ≪ Lgrav. In previous studies we demonstrated that the interstellar CR flux is strongly attenuated at high column densities (Padovani et al. 2009, 2013), and so we expect ϵCR at the protostellar surface to be much lower than its interstellar value and, a fortiori, LCR ⋘ Lgrav close to the protostar. Thus, if a small fraction of the gravitational energy can be used to produce local CRs, they could easily be dominant over the ISM ones. For a massive star the gravitational energy available to generate high-energy CRs is even higher since Ṁ could be as high as 10-3M⊙ yr-1 and in principle their γ emission can be observed (see e.g. Araudo et al. 2007; Bosch-Ramon et al. 2010; Munar-Adrover et al. 2011).
The organisation of the paper is the following. In Sect. 2 we examine the acceleration processes that can take place in protostellar shocks, carefully analysing the conditions leading to particle acceleration (see also Padovani et al. 2015), and in Sect. 3 we evaluate the pressure of accelerated CRs. In Sect. 4 we verify in what part of the protostar these conditions are fulfilled, and in Sect. 5 we evaluate the maximum energy that can be reached and the emerging spectrum at the shock surface. In Sect. 6 we describe the propagation mechanism of local CRs, how they can be re-accelerated at the reverse bow shock of a jet, and how they propagate in the hot spot region. In Sect. 7 we derive the CR ionisation rate along the jet and the temperature profile of the protostellar disc. In Sect. 8 we use our modelling to explain observational results, and in Sect. 9 we summarise our conclusions. Finally, in the appendices we give more details on alternative acceleration sites and mechanisms (Appendix A), the damping of turbulence in a jet (Appendix B), the collisional character of the shocks and the thermal equilibration (Appendix C), the calculation of the ion-neutral damping condition (Appendix D), and the relevance of using a steady-state model (Appendix E).
2. Cosmic-ray acceleration in protostellar shocks
Protostars are classified as a function of their spectral energy distribution in the near- and mid-infrared domain (Adams et al. 1987; André et al. 1994). These protostars are surrounded by dusty envelopes that absorb and re-emit at infrared wavelengths the energy irradiated by the central forming star, and this envelope becomes increasingly optically thin during the evolutionary sequence. The most embedded objects are named Class 0; they have a very weak emission at infrared wavelengths with relevant emission in the submillimetre spectral range. At this stage the envelope has already started its gravitational collapse and collimated polar outflows and jets can be observed, but the envelope mass is still much larger than the central condensation. Class I objects represent the following step in the evolution of prestellar cores where the envelope progressively dissolves through accretion processes onto the central object together with ejecta in the form of outflows and jets. These objects are detectable in the infrared, but not at optical wavelengths. Finally, Class II and Class III objects are pre-main sequence stars, which are the most evolved stages of a protostar. These objects can be observed at both optical and infrared wavelengths. Class II sources present an optically thick circumstellar disc, while in Class III the disc is optically thin, but both are lacking a circumstellar envelope.
In the following we identify a number of possible particle acceleration sites in protostars. Some of them are peculiar in the first stages of protostar collapse (mainly Class 0), such as accretion flows in the protostellar envelope; others, such as jets, are common to Class 0 and the more evolved protostar classes. This work focuses on shock acceleration, but alternative processes are discussed in Appendix A.
2.1. Diffusive shock acceleration
Also known as first-order Fermi acceleration, diffusive shock acceleration (DSA) is a process where charged particles systematically gain energy while crossing a shock front. Multiple shock crossings allow the particle energy to rapidly increase and to reach the relativistic domain. The motion of particles back and forth from upstream to downstream requires the presence of magnetic fluctuations that produce a scattering of the pitch angle, which is the angle between the particle’s velocity and the mean magnetic field. As a consequence, the distribution in momentum space of the emerging accelerated particles is set by the ratio of the relative energy gain in an acceleration (or Fermi) cycle to the probability of being advected with the scattering centres downstream. In the limit of strong shocks, when the magnetic field is not dynamically dominant, this ratio only depends on the shock compression ratio r (see Eq. (7)), and once r is fixed the shock distribution is a power law. This process is described in several reviews (e.g. Drury 1983; Kirk 1994). In the following subsections we describe in greater detail the conditions (summarised in Padovani et al. 2015) that have to be satisfied in order to effectively accelerate particles through the DSA mechanism: criteria that need to be fulfilled regardless of the origin of the magnetic disturbances causing the particle scatterings (Sects. 2.2 and 2.3), those associated with the shock age and geometry (Sect. 2.5), and with magnetic field fluctuations that are self-generated by the particles themselves (Sects. 2.4 and 3).
All the conditions limiting the maximum energy of the accelerated particles are written as functions of the upstream flow velocity in the shock reference frame 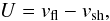 (3)where vfl and vsh are the flow and shock velocities, respectively, both taken in the observer reference frame. We note that vfl will later be equated to vacc or vjet depending on the acceleration site.
(3)where vfl and vsh are the flow and shock velocities, respectively, both taken in the observer reference frame. We note that vfl will later be equated to vacc or vjet depending on the acceleration site.
Figure 1 outlines the configuration of a protostar used for our modelling. The shock in the accretion flow is assumed to be stationary (vsh = 0). Shocks inside jets move more slowly than the flow (see Sect. 4.2) so that the upstream region is close to the protostar. The reverse bow shock (also known as Mach disc) and the bow shock, when observed, usually move slowly or are stationary as well (Caratti o Garatti & Eislöffel 2009). After passing through the jet shock, the gas flow spreads out until it yields a bow shock with its reverse bow shock. In the intershock region, known as the working surface, the pressure gradient forces perpendicular to the jet are so high that the gas is ejected radially and propagates into the surrounding region, called the hot spot region (e.g. Stahler & Palla 2005), through the bow wings. Multiple shocks are observed, and so throughout the paper we only account for the presence of a single jet shock.
We briefly discuss the consequences of recurring acceleration processes in Sect. 9, and in Appendix A we describe alternative mechanisms that may provide efficient CR acceleration in addition to DSA.
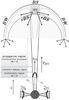 |
Fig. 1 Sketch of the protostar configuration employed in the paper. Accretion flow, jet, and shock velocities (vacc, vjet, and vsh, respectively) are in the observer reference frame. Shock and transverse radii are labelled Rsh and R⊥, respectively. Bow shock, reverse bow shock, bow wings, and working surface are labelled BS, rBS, BW, and ws, respectively. The shaded areas show the regions where CR acceleration takes place (Sect. 2.1) and where turbulence is damped and particle propagation occurs (Sect. 6). The dot-filled region corresponds to the hot spot region (Sect. 6.2). |
2.2. Condition on shock velocity
In order to have efficient particle acceleration, the flow has to be supersonic and super-Alfvénic. These two conditions are combined into the relation ![\begin{eqnarray} \label{Uhighercsva} \frac{U}{10^{2}~\mathrm{km~s^{-1}}}>&&\max\left\{9.1\times10^{-2}\left[\gamma_{\rm ad} (1+x) \left(\frac{T}{10^{4}~\mathrm{K}}\right)\right]^{0.5},\right.\\\nonumber &&\left.2.2\times10^{-4}\left(\frac{n_{\rm H}}{10^{6}~\mathrm{cm^{-3}}}\right)^{-0.5}\left(\frac{B}{10~\mathrm{\mu G}}\right)\right\}, \end{eqnarray}](/articles/aa/full_html/2016/06/aa28221-16/aa28221-16-eq36.png) (4)where γad is the adiabatic index, T the upstream temperature, nH the total number density of hydrogen, x the ionisation fraction, and B the magnetic field strength. The two terms inside the braces on the right-hand side of Eq. (4) are the ambient (or upstream) sound speed, cs, and Alfvén speed, VA, respectively, of the total gas, i.e. when ions and neutrals are coupled, in units of 102 km s-1. The contribution of helium and heavier species in the background plasma is neglected.
(4)where γad is the adiabatic index, T the upstream temperature, nH the total number density of hydrogen, x the ionisation fraction, and B the magnetic field strength. The two terms inside the braces on the right-hand side of Eq. (4) are the ambient (or upstream) sound speed, cs, and Alfvén speed, VA, respectively, of the total gas, i.e. when ions and neutrals are coupled, in units of 102 km s-1. The contribution of helium and heavier species in the background plasma is neglected.
The electron temperature, Te, can be estimated by observations, and downstream of a shock any temperature difference is rapidly thermalised so that the proton temperature, Tp, can be safely assumed to be equal to Te. In fact, even if in the presence of collisionless shocks, such that the passage of the shock creates a gradient between the temperatures of the two species (mpTe ≃ meTp), it is possible to demonstrate that the time needed to reach temperature equilibrium is shorter than the time between two consecutive shocks (see Appendix C).
2.3. Condition on low-energy cosmic-ray acceleration: collisional losses
We are interested in the acceleration of low-energy (≲100 MeV−1 GeV) CRs since they are responsible for the bulk of the ionisation. We have to verify that the shock acceleration rate is higher than the collisional loss rate, 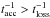 . Adapting Drury et al. (1996) to account for both parallel and perpendicular shock configurations1, the acceleration rate is given by
. Adapting Drury et al. (1996) to account for both parallel and perpendicular shock configurations1, the acceleration rate is given by ![\begin{eqnarray} \label{nuacc} t^{-1}_{\rm acc}~&=&~\frac{1.1\times10^{-8}}{\gamma-1}\frac{k_{\rm u}^{\alpha}(r-1)}{r[1+r(k_{\rm d}/k_{\rm u})^{\alpha}]} \tilde\mu^{-1}\\\nonumber &&\times\left(\frac{U}{\mathrm{10^{2}~km~s^{-1}}}\right)^{2} \left(\frac{B}{\mathrm{10~\mu G}}\right)~\mathrm{s^{-1}}, \end{eqnarray}](/articles/aa/full_html/2016/06/aa28221-16/aa28221-16-eq50.png) (5)where
(5)where 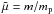 is the particle mass normalised to the proton mass, ku and kd are the diffusion coefficient in the upstream and downstream media, respectively, defined by
is the particle mass normalised to the proton mass, ku and kd are the diffusion coefficient in the upstream and downstream media, respectively, defined by 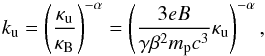 (6)with κB the Bohm diffusion coefficient, e the elementary charge, γ the Lorentz factor, and
(6)with κB the Bohm diffusion coefficient, e the elementary charge, γ the Lorentz factor, and 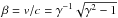 (v and c are the speed of the particle and the speed of light, respectively), and they can possibly be dependent on the particle momentum (Jokipii 1987). For a parallel shock α = −1 and ku = kd, while for a perpendicular shock α = 1 and, since the magnetic field is compressed by a factor r, ku = rkd (Priest 1994). The shock compression ratio, r, is given by
(v and c are the speed of the particle and the speed of light, respectively), and they can possibly be dependent on the particle momentum (Jokipii 1987). For a parallel shock α = −1 and ku = kd, while for a perpendicular shock α = 1 and, since the magnetic field is compressed by a factor r, ku = rkd (Priest 1994). The shock compression ratio, r, is given by 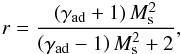 (7)where
(7)where 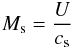 (8)is the sonic Mach number and in the following the adiabatic index is set to γad = 5/3. Obviously, Eq. (7) supposes that the shock is adiabatic, an assumption that might not always be satisfied. Owing to the dynamical nature of protostars, shocks might sometimes be radiative, in which case the DSA scenario should be modified as, for instance, injection from the thermal pool might not work. In this case, alternative acceleration mechanisms should be considered (see Appendix A). In addition, Eq. (7) is obtained in hydrodynamics, whereas DSA requires the presence of a magnetic field. Here we verified that magnetic pressure on each side of the shock front is much lower than the ram pressure of the flow so that the magnetic field is dynamically negligible and Eq. (7) remains valid. However, the magnetic field is relevant for particle scattering.
(8)is the sonic Mach number and in the following the adiabatic index is set to γad = 5/3. Obviously, Eq. (7) supposes that the shock is adiabatic, an assumption that might not always be satisfied. Owing to the dynamical nature of protostars, shocks might sometimes be radiative, in which case the DSA scenario should be modified as, for instance, injection from the thermal pool might not work. In this case, alternative acceleration mechanisms should be considered (see Appendix A). In addition, Eq. (7) is obtained in hydrodynamics, whereas DSA requires the presence of a magnetic field. Here we verified that magnetic pressure on each side of the shock front is much lower than the ram pressure of the flow so that the magnetic field is dynamically negligible and Eq. (7) remains valid. However, the magnetic field is relevant for particle scattering.
The collisional energy loss rate is given by ![\begin{equation} \label{nuloss} t^{-1}_{\rm loss}=3.2\times10^{-9}\frac{\beta}{\gamma-1}\tilde\mu^{-1} \left(\frac{n_{\rm H}}{\mathrm{10^{6}~cm^{-3}}}\right) \left[\frac{L(E)}{\mathrm{10^{-25}~GeV~cm^{2}}}\right]~\mathrm{s^{-1}}, \end{equation}](/articles/aa/full_html/2016/06/aa28221-16/aa28221-16-eq67.png) (9)where L(E) is the energy loss function (Padovani et al. 2009), which was extended to lower energies to include Coulomb losses. These functions are given for protons by Mannheim & Schlickeiser (1994),
(9)where L(E) is the energy loss function (Padovani et al. 2009), which was extended to lower energies to include Coulomb losses. These functions are given for protons by Mannheim & Schlickeiser (1994), 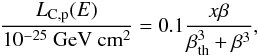 (10)where βth = 2 × 10-3(T/ 104 K)0.5. For electron Coulomb losses, we use the analytic fit by Swartz et al. (1971),
(10)where βth = 2 × 10-3(T/ 104 K)0.5. For electron Coulomb losses, we use the analytic fit by Swartz et al. (1971), 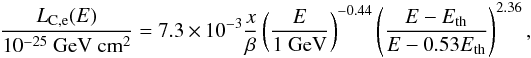 (11)where Eth is the electron thermal energy. Synchrotron losses, LS,e, were included in the energy loss function for electrons and they read (Schlickeiser 2002)
(11)where Eth is the electron thermal energy. Synchrotron losses, LS,e, were included in the energy loss function for electrons and they read (Schlickeiser 2002) 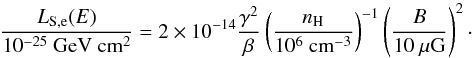 (12)The maximum energy of accelerated particles set by energy losses, Eloss, is found when
(12)The maximum energy of accelerated particles set by energy losses, Eloss, is found when 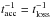 , leading to
, leading to ![\begin{eqnarray} \label{FEloss} \,\beta\left[\frac{L(E)}{\mathrm{10^{-25}~GeV~cm^{2}}}\right]\,&=&\,3.4\frac{k_{\rm u}^{\alpha}(r-1)}{r[1+r(k_{\rm d}/k_{\rm u})^{\alpha}]} \\\nonumber &&\times\left(\frac{U}{10^{2}~\mathrm{km~s^{-1}}}\right)^{2} \left(\frac{n_{\rm H}}{10^{6}~\mathrm{cm^{-3}}}\right)^{-1} \left(\frac{B}{10~\mu\mathrm{G}}\right)\cdot \end{eqnarray}](/articles/aa/full_html/2016/06/aa28221-16/aa28221-16-eq77.png) (13)
(13)
2.4. Condition on CR acceleration: ion-neutral friction
In this work we assume that CR scattering occurs in the so-called quasi-linear regime. This assumes that the level of magnetic fluctuations produced by the CRs themselves or by the background turbulence is lower than the background large-scale magnetic field or at most equal to it. In that regime the CR’s pitch angle is only slightly deflected during an interaction with a magnetic perturbation so that the gyromotion around the background magnetic field can be retained as a good approximation of the trajectory (Schlickeiser 2002).
The main limit on the possibility of CR acceleration is given by the presence of an incompletely ionised medium. The collision rate between ions and neutrals can actually be high enough to decrease the effectiveness of DSA. The presence of neutrals damps the CR self-generated fluctuations that allow the CRs to move back and forth across the shock multiple times. Ions and neutrals are effectively decoupled if the wave frequency is higher than the ion-neutral collision frequency, otherwise neutrals take part in the coherent oscillations between ions and Alfvén waves. Here we consider resonant waves whose pulsation satisfies the condition ω ~ VA/rg, where the gyroradius is 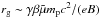 . Following Eq. (11) in Drury et al. (1996) and accounting for the fact that CRs are not fully relativistic, we find that the critical energy separating these two regimes, Ecoup, is derived by solving the following relation:
. Following Eq. (11) in Drury et al. (1996) and accounting for the fact that CRs are not fully relativistic, we find that the critical energy separating these two regimes, Ecoup, is derived by solving the following relation: 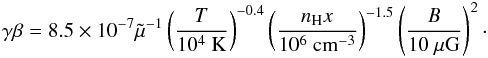 (14)If the CR energy is higher than Ecoup, ions and neutrals are coupled.
(14)If the CR energy is higher than Ecoup, ions and neutrals are coupled.
The upper cut-off energy due to wave damping, Edamp, is set by requiring that the flux of locally accelerated CRs advected downstream by the flow be equal to the flux of CRs lost upstream because of the lack of waves (due to wave damping) to confine the CRs. Following Drury et al. (1996), using their exact equation for the wave damping rate, accounting for departures from fully relativistic behaviour, and assuming U to be much higher than the Alfvén speed, Edamp follows from2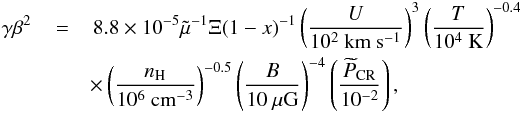 (15)where
(15)where 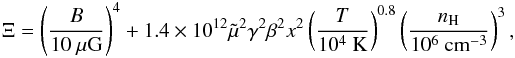 (16)and
(16)and 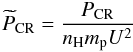 (17)is the fraction of the shock ram pressure going into CR acceleration (see also Sect. 3).
(17)is the fraction of the shock ram pressure going into CR acceleration (see also Sect. 3).
The normalisation is taken with respect to the proton mass since the contribution of electrons to the total CR pressure is negligible. Both Eqs. (14) and (15) are valid for T ∈ [ 102,105 ] K.
If Edamp>Ecoup, then Edamp is in the coupled regime, i.e. neutrals coherently move with ions and ion-generated waves are weakly damped. The condition Edamp>Ecoup can be written by combining Eqs. (14) and (15) as 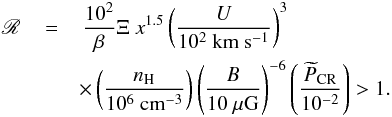 (18)In the following sections we consider shocks in three types of environments: in jets, in accretion flows in the collapsing envelopes, and on the surfaces of protostars. Using the range of parameters in Table 1, we find R≪ 1 in protostellar envelopes (see Sect. 4.1). Therefore, the following two conditions on shock age and geometry (Sect. 2.5) are uniquely discussed with reference to shocks in jets and on protostellar surfaces.
(18)In the following sections we consider shocks in three types of environments: in jets, in accretion flows in the collapsing envelopes, and on the surfaces of protostars. Using the range of parameters in Table 1, we find R≪ 1 in protostellar envelopes (see Sect. 4.1). Therefore, the following two conditions on shock age and geometry (Sect. 2.5) are uniquely discussed with reference to shocks in jets and on protostellar surfaces.
2.5. Conditions arising from shock age and geometry
The limit on the maximum energy determined by the age of the shock, Eage, is found when the acceleration time, given by the inverse of Eq. (5), is equal to the age of the shock, tage. The latter can be assumed to be of the order of the dynamical time of the jet (≳103 yr, de Gouveia Dal Pino 1995) or equal to the accretion time in the case of a surface shock, i.e. the time needed for a mass element in the envelope to reach the central protostar (~105 yr, Masunaga & Inutsuka 2000). Then, Eage is computed from ![\begin{eqnarray} \label{Eage} \gamma-1\,&=&\,3.2\times10^{2}\frac{k_{\rm u}^{\alpha}(r-1)}{r[1+r(k_{\rm d}/k_{\rm u})^{\alpha}]}\tilde\mu^{-1}\\\nonumber &&\times\left(\frac{U}{10^{2}~\mathrm{km~s^{-1}}}\right)^{2} \left(\frac{B}{10~\mathrm{\mu G}}\right) \left(\frac{t_{\rm age}}{10^{3}~\mathrm{yr}}\right)\cdot \end{eqnarray}](/articles/aa/full_html/2016/06/aa28221-16/aa28221-16-eq97.png) (19)When R> 1, the most stringent constraint is given by the geometry of the shock. In particular, the upstream diffusion length, λu = κu/U, has to be at most a given fraction ϵ< 1 of the shock radius, namely the distance from the source, Rsh. For a Class 0 protostar, we assume the accretion on the protostellar surface to be still spherical and not driven by accretion columns from the inner disc. We also assume the shock to be planar since the CR’s mean free path around the shock is smaller than the transverse size of the jet, R⊥. Because of the spherical geometry, no transverse escape either upstream or downstream is expected. In contrast, in the jet configuration CRs may also escape in the transverse direction. The maximum energy due to upstream escape losses, Eesc,u, follows from
(19)When R> 1, the most stringent constraint is given by the geometry of the shock. In particular, the upstream diffusion length, λu = κu/U, has to be at most a given fraction ϵ< 1 of the shock radius, namely the distance from the source, Rsh. For a Class 0 protostar, we assume the accretion on the protostellar surface to be still spherical and not driven by accretion columns from the inner disc. We also assume the shock to be planar since the CR’s mean free path around the shock is smaller than the transverse size of the jet, R⊥. Because of the spherical geometry, no transverse escape either upstream or downstream is expected. In contrast, in the jet configuration CRs may also escape in the transverse direction. The maximum energy due to upstream escape losses, Eesc,u, follows from 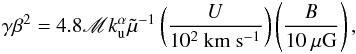 (20)where
(20)where 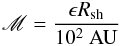 (21)or
(21)or ![\begin{eqnarray} \mathscr{M}=\min\left[\frac{\epsilon R_{\rm sh}}{10^{2}~\mathrm{AU}}, \frac{R_{\perp}}{10^{2}~\mathrm{AU}}\right] \end{eqnarray}](/articles/aa/full_html/2016/06/aa28221-16/aa28221-16-eq104.png) (22)for a shock on the protostellar surface or in the jet, respectively. In the following we assume ϵ = 0.1 (Berezhko et al. 1996).
(22)for a shock on the protostellar surface or in the jet, respectively. In the following we assume ϵ = 0.1 (Berezhko et al. 1996).
Since jet shocks have a small transverse dimension, there is a further condition for the escape of CRs downstream: the maximum energy due to downstream escape losses, Eesc,d, is found when the acceleration time, the inverse of Eq. (5), is equal to the downstream diffusion time, tdiff,d, which is given by3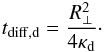 (23)Then, Eesc,d follows from
(23)Then, Eesc,d follows from ![\begin{eqnarray} \label{FEescd} \gamma\beta^{2}(\gamma-1)\,&=&\,2.1\mathscr{C}\frac{(k_{\rm u}k_{\rm d})^{\alpha}(r-1)}{r[1+r(k_{\rm d}/k_{\rm u})^{\alpha}]}\tilde\mu^{-1}\\\nonumber &&\times\left(\frac{U}{10^{2}~\mathrm{km~s^{-1}}}\right)^{2} \left(\frac{B}{10~\mathrm{\mu G}}\right)^{2} \left(\frac{R_{\perp}}{10^{2}~\mathrm{AU}}\right)^{2}, \end{eqnarray}](/articles/aa/full_html/2016/06/aa28221-16/aa28221-16-eq109.png) (24)with C= 1 or r2 for a parallel or a perpendicular shock, respectively.
(24)with C= 1 or r2 for a parallel or a perpendicular shock, respectively.
Finally, if the shock is supersonic and super-Alfvénic (Eq. (4)) and if R> 1 (Eq. (18)), the maximum energy reached by a particle is ![\begin{eqnarray} \label{Emax} E_{\rm max}=\min[E_{\rm loss},E_{\rm damp},E_{\rm age},E_{\rm esc,u},E_{\rm esc,d}], \end{eqnarray}](/articles/aa/full_html/2016/06/aa28221-16/aa28221-16-eq112.png) (25)where Eloss, Edamp, Eage, Eesc,u, and Eesc,d are given by Eqs. (13), (15), (19), (20), and (24), respectively.
(25)where Eloss, Edamp, Eage, Eesc,u, and Eesc,d are given by Eqs. (13), (15), (19), (20), and (24), respectively.
3. Pressure of accelerated CRs
The value of the maximum energy is constrained by the fraction of the shock ram pressure that is channelled to CR pressure (see Eqs. (15) and (17)). We predict both non-relativistic and mildly relativistic CRs and we checked a posteriori that there is no strong back-reaction. This means that the upstream medium is not warned by these CRs that a shock is coming and we can safely assume that the shock and the DSA process are unmodified. For this reason, we can describe the CR momentum distribution function at the shock surface in the test-particle regime with a power law of momentum 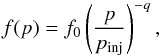 (26)with f0 normalisation constant; pinj<p<pmax, where pinj is the injection momentum (Eq. (32)) and pmax is the maximum momentum (given by Eq. (25)); and q = 3r/ (r − 1) is the CR distribution index in the test-particle limit, with r the compression ratio at the shock surface (Eq. (7)). By definition, f(p) is related to the CR density per unit volume, nCR, by
(26)with f0 normalisation constant; pinj<p<pmax, where pinj is the injection momentum (Eq. (32)) and pmax is the maximum momentum (given by Eq. (25)); and q = 3r/ (r − 1) is the CR distribution index in the test-particle limit, with r the compression ratio at the shock surface (Eq. (7)). By definition, f(p) is related to the CR density per unit volume, nCR, by 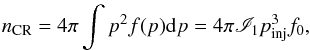 (27)where
(27)where ![\begin{eqnarray} \label{I1} {\mathscr I}_{1}=\frac{1}{q-3}\left[1-\left(\frac{p_{\rm max}}{p_{\rm inj}}\right)^{3-q}\right]\cdot \end{eqnarray}](/articles/aa/full_html/2016/06/aa28221-16/aa28221-16-eq122.png) (28)Assuming an efficient pitch-angle scattering and hence an isotropic CR distribution, the CR pressure reads
(28)Assuming an efficient pitch-angle scattering and hence an isotropic CR distribution, the CR pressure reads 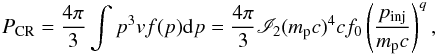 (29)where v is the CR velocity with
(29)where v is the CR velocity with 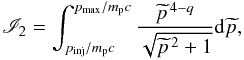 (30)where
(30)where 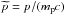 .
.
Berezhko & Ellison (1999) give the expressions for the normalised CR pressure in non-relativistic and relativistic regimes and also in the transition region. Eliminating f0 by equating Eqs. (27) and (29), the sum of these pressures gives 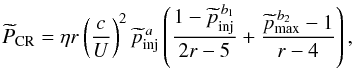 (31)where a = 3/(r − 1), b1 = (2r − 5)/(r − 1), and b2 = (r − 4)/(r − 1). The parameter η ∈ [ 10-6,10-3 ] (Berezhko & Ellison 1999) is the shock efficiency, which represents the fraction of particles extracted from the thermal plasma and injected into the acceleration process by a shock. In the context of supernova remnants at relativistic energies, it is assumed that at least 10% of the shock ram pressure goes into CR acceleration (Berezhko & Ellison 1999). In contrast, protostellar shocks are expected to be much less energetic events, with
(31)where a = 3/(r − 1), b1 = (2r − 5)/(r − 1), and b2 = (r − 4)/(r − 1). The parameter η ∈ [ 10-6,10-3 ] (Berezhko & Ellison 1999) is the shock efficiency, which represents the fraction of particles extracted from the thermal plasma and injected into the acceleration process by a shock. In the context of supernova remnants at relativistic energies, it is assumed that at least 10% of the shock ram pressure goes into CR acceleration (Berezhko & Ellison 1999). In contrast, protostellar shocks are expected to be much less energetic events, with 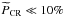 ; accordingly, in the following we assume η ∈ [ 10-6,10-5 ]. Following Blasi et al. (2005), the minimum (or injection) momentum, pinj, of a particle able to cross the shock that enters the acceleration process is related to the thermal particle momentum, pth, through
; accordingly, in the following we assume η ∈ [ 10-6,10-5 ]. Following Blasi et al. (2005), the minimum (or injection) momentum, pinj, of a particle able to cross the shock that enters the acceleration process is related to the thermal particle momentum, pth, through 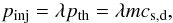 (32)where cs,d is the sound speed in the downstream region in the strong shock limit given by (Berezhko & Ellison 1999)
(32)where cs,d is the sound speed in the downstream region in the strong shock limit given by (Berezhko & Ellison 1999) 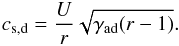 (33)This is a good approximation in our case since both the sonic and the Alfvénic Mach numbers (Eqs. (8) and (A.4), respectively) are greater than 1. The value of the parameter λ depends on the shock efficiency η and it reads
(33)This is a good approximation in our case since both the sonic and the Alfvénic Mach numbers (Eqs. (8) and (A.4), respectively) are greater than 1. The value of the parameter λ depends on the shock efficiency η and it reads 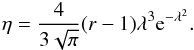 (34)Equations (27)–(30) are general and can be adapted to any acceleration scenario presented in Sect. 2.
(34)Equations (27)–(30) are general and can be adapted to any acceleration scenario presented in Sect. 2.
4. Potential CR acceleration sites
In this section, we identify and characterise possible sites of CR acceleration in protostars. In particular, we consider accretion flows in the envelope, the protostellar surface of Class 0 objects, and also jets in more evolved sources.
4.1. Accretion flows in collapsing envelopes
A number of Class 0 collapsing envelopes have been observed and their density and temperature profiles have been modelled (e.g. Ceccarelli et al. 2000; Crimier et al. 2009). Assuming a spherical collapse, U ≃ 1−10 km s-1 at 100 AU. If B = 10 μG in the initial (pre-collapse) volume of radius 0.1 pc and assuming field freezing, the magnetic field strength in the final (post-collapse) volume of radius 100 AU is about 400 mG. This naive estimate is comparable within a factor of 2 with the value found by Alves et al. (2012) who estimate B ≈ 200 mG from observations of shock-induced H2O masers. This is an averaged quantity, but Imai et al. (2007) computed the position of the H2O masers, and found the farther one to be at about 110 AU. Finally, the ionisation fraction has to be of the order of 10-4 to 10-5 in order to justify the presence of maser pumping (Strelnitskij 1984; Wootten 1989). Masers arise in the presence of shocks and they are usually associated with jet activity rather than accretion flows; in other words, the values for both magnetic field strength and ionisation fraction have to be regarded as upper limits in our estimates. We check all the conditions in Sect. 2.1 and make a parameter study using the ranges of values shown in the first row of Table 1 verifying that Eq. (18) is not fulfilled in accretion flows (R≪ 1). The ionisation fraction and the shock velocity are too small and they quench the CR acceleration, and the magnetic field strength is also high enough to produce a sub-Alfvénic shock. This means that we can rule out accretion flows as possible CR acceleration sites.
Ranges of values of the parameters described in the text.
4.2. Jets
Jets are observed at all stages during the evolution of a protostar, from the main infall phase of Class 0 objects (e.g. HH 212, McCaughrean et al. 2002) to evolved Class I protostars (e.g. HH 111, Reipurth et al. 1997) and to Class II sources (e.g. HH 30, Watson & Stapelfeldt 2004). Jet speeds, vjet, are similar for different classes, between about 60 and 300 km s-1 with shock velocities, vsh, of the order of 20−140 km s-1 (Raga et al. 2002; 2011; Hartigan & Morse 2007; Agra-Amboage et al. 2011). In the equations of Sect. 2.1, U is the upstream flow velocity in the shock reference frame (see Eq. (3) with vfl = vjet). Taking the extreme values of vjet and vsh, we assume U to be in the range 40−160 km s-1. A stationary shock is seen at 20 AU in Class I and II protostars, while for the time being the resolution is too low for Class 0 objects. There are also moving internal shocks, spaced each other by about 100 AU.
The total hydrogen density is between 103 and 107 cm-3 (Lefloch et al. 2012; Gómez-Ruiz et al. 2012) with temperatures from about 104 K up to about 106 K (Frank et al. 2014). Thus far there are no measurements of magnetic field strengths. The only theoretical estimate has been carried out by Teşileanu et al. (2009; 2012) who have found B ~ 300−500 μG for Class II sources. The transverse radius of a jet is about 10 AU and 50 AU at a distance of 100 AU and 1000 AU from the source, respectively, and the opening angle spans from about 4° for RW Aur to about 15° for DG Tau (Cabrit et al. 2007). Hartigan et al. (2004) give estimates closer to the source: about 5 AU of transverse radius at a distance of about 15 AU from the central object for the two Classical T Tauri stars HN Tau and UZ Tau E.
The ionisation fraction in Class II objects for the atomic gas can be as high as 0.94, decreasing towards the source as a result of recombination processes due to higher densities (Maurri et al. 2014). The ionisation fraction in Class I objects is similar to that in Class II objects, x ~ 0.05−0.9, but with higher electron and total densities (Nisini et al. 2005; Antoniucci et al. 2008; Garcia López et al. 2008; Frank et al. 2014). Conversely, Class 0 jets are mainly molecular, allowing for a rapid dissociative recombination that acts to dramatically decrease the ionisation fraction. For instance in the Class 0 HH 211, nH ~ 105 cm-3 with x ~ (1.6−5) × 10-3 at about 1000 AU from the source (Dionatos et al. 2010). The second row of Table 1 summarises the range of parameter values.
4.3. Protostellar surfaces
In order to study the efficiency of CR acceleration on protostellar surfaces, we used the computational results of Masunaga & Inutsuka (2000) for the Class 0 protostellar collapse of an initially homogeneous cloud core. Their simulation describes the phase of main accretion when the protostar mass grows because of the steady accretion from the infalling envelope. They give the temporal evolution of temperature, density, and flow velocity in the observer reference frame, which – assuming a stationary shock – is equal to the upstream flow velocity in the shock reference frame. Considering the shock to be stationary, the downstream region is close to the protostar and the upstream region towards the envelope, namely the opposite configuration with respect to the jet shock case. The radius of the protostar is set to 2 × 10-2 AU and we find that only the last time step of the simulation, corresponding to the end of the main accretion phase, leads to a strong proton acceleration. The ranges of parameter values are listed in the third row of Table 1.
5. Spectrum of accelerated CRs at the shock surface
For jet and protostellar surface shocks we perform a parametric study using the values in the second and third rows of Table 1. In order to calculate 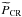 , we fix η = 10-5 in Eq. (31) and we omit the contribution of the last term, which contains
, we fix η = 10-5 in Eq. (31) and we omit the contribution of the last term, which contains 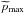 . To be consistent, Emax should be recursively computed and then Eq. (31) solved, but we verified that the variation in
. To be consistent, Emax should be recursively computed and then Eq. (31) solved, but we verified that the variation in 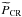 is lower than a factor of about 3. With this assumption,
is lower than a factor of about 3. With this assumption, 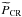 only depends on the shock velocity with respect to the upstream flow and the ionisation fraction, spanning from 2 × 10-3 (U = 40 km s-1, x = 0.9) to 5 × 10-2 (U = 160 km s-1, x = 0.01).
only depends on the shock velocity with respect to the upstream flow and the ionisation fraction, spanning from 2 × 10-3 (U = 40 km s-1, x = 0.9) to 5 × 10-2 (U = 160 km s-1, x = 0.01).
We study the case of a Bohm-type diffusion shock (ku = 1, see Eq. (6)) since this is the most favourable circumstance for accelerating CRs in the case of self-generated waves (see also Sect. 5.4.1). In fact, the upstream diffusion coefficient can be written as a function of the magnetic field strength and of its turbulent component, δB (see Drury 1983): 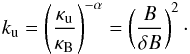 (35)If ku = 1, then δB = B, i.e. the magnetic fluctuations responsible for pitch angle scattering are large enough to cause DSA to be effective at its maximum degree (see also Sect. 2.1). To justify this assumption, we compute ku following Pelletier et al. (2006) for the case of a parallel shock (α = −1)
(35)If ku = 1, then δB = B, i.e. the magnetic fluctuations responsible for pitch angle scattering are large enough to cause DSA to be effective at its maximum degree (see also Sect. 2.1). To justify this assumption, we compute ku following Pelletier et al. (2006) for the case of a parallel shock (α = −1) 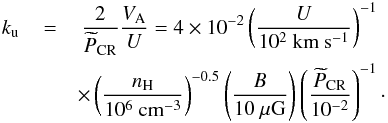 (36)With the values in the second and third rows of Table 1, ku is found to be about 1.
(36)With the values in the second and third rows of Table 1, ku is found to be about 1.
5.1. Maximum CR energy at the jet shock surface
For jet shocks, we set the temperature at T = 104 K, and consider magnetic field strengths between 50 μG and 1 mG as well as shock velocities between 40 and 160 km s-1, then we study the parameter space of hydrogen density, nH ∈ [ 103,107 ] cm-3, and ionisation fraction, x ∈ [ 0.01,0.9 ], for a shock at a distance Rsh = 100 AU from the protostar and a transverse radius R⊥ = 10 AU.
We first consider the case of a parallel shock. Figure 2 shows the maximum energy that a shock-accelerated proton can reach in the case of a parallel shock. We find that for low shock velocities with respect to the upstream flow (U = 40 km s-1) the acceleration process is efficient only for low values of B (for B> 100 μG, Emax is lower than 1−10 keV). By increasing both U and B, the maximum energy attains higher values (from about 100 MeV to about 13 GeV). It is interesting to note that once the combination of parameters satisfies the condition R> 1 (see Eq. (18)), Emax rapidly reaches a constant value, encompassed by the cyan contours in each subplot. In fact, the maximum energy is generally controlled by downstream escape (Eq. (24)), which is independent of both nH and x. The number in each subplot shows the maximum value of Emax in GeV that can be attained for given values of the shock velocity and the magnetic field strength.
Electrons can be accelerated as well, but generally Emax for electrons is much lower than Emax for protons because of wave damping and stronger energy losses. For instance, for U = 160 km s-1 and B = 1 mG, Emax ~ 300 MeV for a narrow range of density and ionisation fractions (nH ≳ 3 × 106 cm-3, x ≳ 0.6). For lower values of B and U, Emax ≲ 50 MeV.
Supposing the magnetic field to have a strong toroidal component, we repeat the calculation for the case of a perpendicular shock. We find that Emax increases by a factor of 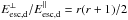 , where superscripts ⊥ and ∥ refer to a perpendicular and parallel shock, respectively.
, where superscripts ⊥ and ∥ refer to a perpendicular and parallel shock, respectively.
For the sake of completeness, we show in Sect. 5.4.3, Fig. 7, the results for a higher temperature, T = 105 K.
 |
Fig. 2 Case of a parallel shock in jets: ionisation fraction, x, versus total hydrogen density, nH, for different combinations of initial parameters. The magnetic field strength varies from 50 μG to 1 mG (from left to right), while the shock velocity varies from 40 to 160 km s-1 (from top to bottom). The temperature is assumed equal to 104 K and the shock distance from the protostar and its transverse radius are Rsh = 100 AU and R⊥ = 10 AU, respectively. The colour map shows the values of Emax in the case of a parallel shock when the conditions imposed by Eqs. (4) and (18) are simultaneously satisfied. Cyan contours delimit the regions where Emax reaches its maximum asymptotic value shown in GeV in each subplot. Vertically hatched regions refer to combinations of parameters corresponding to strong wave damping (R< 1). The two solid white stars in the upper left and lower right plots show the values of nH and x considered for the evaluation of the emerging spectra (models |
5.2. Accelerated CR spectrum at the protostellar shock
For protostellar surfaces, we study the parameter space of magnetic field strength and ionisation fraction using ϵ = 0.1 (Eq. (20)), η = 10-5 (Eq. (31)), and ku = 1 (Eq. (35)) for both a parallel and a perpendicular shock. Figure 3 shows that at the protostellar surface accelerated CR protons can reach Emax ≈ 26 GeV and Emax ≈ 37 GeV in the case of a parallel and a perpendicular shock, respectively. The values of the magnetic field where CR acceleration is possible, B ~ 3−10 G, are compatible with those computed by e.g. Garcia et al. (2001). Because of high temperatures, Coulomb losses are dominant and Emax is constrained by Eloss. Thus, for a perpendicular shock Emax increases by a factor of 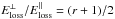 .
.
 |
Fig. 3 Case of parallel (left) and perpendicular (right) shocks on protostellar surfaces: ionisation fraction, x, versus magnetic field strength, B, for the parameters specified in the third line of Table 1 (Rsh = 2 × 10-2 AU). The colour map shows the values of Emax when the conditions imposed by Eqs. (4) and (18) are simultaneously verified. The cyan contour delimits the region where Emax gets its maximum asymptotic value shown in GeV in each subplot. Vertically hatched regions refer to combinations of parameters corresponding to strong wave damping (R< 1). The solid white star in the left panel shows the values of B and x considered for the evaluation of the emerging spectrum (models |
The maximum energy can be even higher in the case of massive protostars where shocks are much stronger because the mass is higher. It is important to bear in mind that, in principle, CRs accelerated at the protostellar surface shock could also be re-accelerated in jet shocks.
5.3. Emerging CR spectrum at the shock surface
The solution given by Eq. (26) is used to compute the emerging CR spectrum at the shock surface. The energy distribution function of shock-accelerated CRs reads 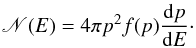 (37)Then, the CR flux emerging from the shock surface, j(E), namely the number of particles per unit energy, time, area, and solid angle reads
(37)Then, the CR flux emerging from the shock surface, j(E), namely the number of particles per unit energy, time, area, and solid angle reads 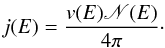 (38)We compute the emerging CR proton spectrum in the case of a parallel shock both in a jet (for two opposite and extreme cases: a weak and a strong shock, labelled
(38)We compute the emerging CR proton spectrum in the case of a parallel shock both in a jet (for two opposite and extreme cases: a weak and a strong shock, labelled 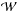 and
and  , respectively) and on a protostellar surface, labelled
, respectively) and on a protostellar surface, labelled 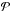 . The relevant parameters are shown in Table 2 and by the white stars in Figs. 2 and 3. We note that when assuming η = 10-5, the normalised CR pressure (Eq. (17)) for all three models is lower than 10%, as predicted in Sect. 3.
. The relevant parameters are shown in Table 2 and by the white stars in Figs. 2 and 3. We note that when assuming η = 10-5, the normalised CR pressure (Eq. (17)) for all three models is lower than 10%, as predicted in Sect. 3.
Parameters to calculate the particle distribution f(p) in the case of parallel shocks for κu = κB and η = 10-5.
Figure 4 displays the above shock-accelerated proton spectra together with their corresponding Maxwellian distributions of thermal protons.
 |
Fig. 4 Emerging spectra of the shock-accelerated protons (solid lines) for the models described in the text. The dashed lines represent the corresponding Maxwellian distributions of the thermal protons. |
5.4. Effect of specific parameters on Emax
There are a number of mechanisms that can dramatically attenuate the emerging CR spectrum at the shock surface such as variations in diffusion coefficient (Sect. 5.4.1), in CR pressure (Sect. 5.4.2), and in temperature (Sect. 5.4.3).
5.4.1. Upstream diffusion coefficient
A variation of the diffusion coefficient can strongly modify the CR flux. In our derivation, we assume Bohm-like diffusion (κu = κB), but – since κu = κB(B/δB)− 2α (Eq. (35)) – for a parallel shock κu ≥ κB, while for a perpendicular shock κu ≤ κB. In the case of parallel shocks, an increase in κu corresponds to a reduction in δB, the turbulence produced by the accelerated CRs that is responsible for DSA (see Sect. 2.1), resulting in a decrease in the shock acceleration efficiency. As shown in Fig. 5, considering for instance κu = 30 κB for a parallel shock, the shock velocity has to be higher than at least 80 km s-1 and the magnetic field greater than 50 μG to accelerate CR protons above 100 MeV.
In order to assess how much the upstream diffusion coefficient affects Emax, we compute the relation between these two quantities for a parallel shock, assuming U = 160 km s-1, nH = 6 × 105 cm-3, and x = 0.6, such as in model 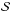 . As shown in Fig. 6, the values of ku = (B/δB)2 at which Emax drops below the threshold for efficient acceleration are about 2, 20, and 40 for B = 50 μG, 500 μG, and 1 mG, respectively.
. As shown in Fig. 6, the values of ku = (B/δB)2 at which Emax drops below the threshold for efficient acceleration are about 2, 20, and 40 for B = 50 μG, 500 μG, and 1 mG, respectively.
 |
Fig. 6 Maximum energy of accelerated protons as a function of (B/δB)2 in the case of parallel shocks for U = 160 km s-1, nH = 6 × 105 cm-3, and x = 0.6 with B = 50 μG (dotted line), 500 μG (dashed line), and 1 mG (solid line). |
In the case of perpendicular shocks, if κu decreases, then δB also decreases. However, as pointed out by Jokipii (1987), in this case Emax increases by a factor of kukd = (B/δB)4/r (see also Eq. (24)). In this configuration particles drift along the shock face colliding with it several times in a single scattering mean free path. In other words, since the magnetic field turbulence decreases as does the particle-wave scattering, particles are more easily caught by the shock, the acceleration time is reduced, and then Emax increases. Nevertheless, two effects limit the increase in Emax. First, the perpendicular transport is usually controlled by magnetic field line wandering (Kirk et al. 1996), and it is enhanced with respect to the solution obtained from pure scattering, and the expected Emax is reduced. Second, to avoid any anisotropy in the particle distribution, in order for DSA to take place at the injection momentum, pinj (Eq. (32)), particles must be scattered in the time required to drift through the shock (Jokipii 1987). This gives a constraint to the maximum value of ku, ku,max, which in turn defines Emax, 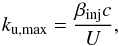 (39)where βinj is related to pinj. Once the temperature is fixed, the injection momentum only depends on the shock velocity with respect to the upstream flow, then ku is uniquely a function of U. For instance, using the range of U for jets (see Sect. 4.2), ku,max is limited between 2.44 (U = 40 km s-1) and 2.29 (U = 160 km s-1). This means that for a perpendicular shock, DSA is efficient in a narrow range of ku, but particles can still be injected in the acceleration process by means of other mechanisms (see Appendix A). However, for U = 160 km s-1, assuming ku = ku,max = 2.29, Emax is about 100 GeV for a shock at Rsh = 100 AU from the propostar. This means that for perpendicular shocks at larger Rsh, where the transverse radius, R⊥, is also larger, CRs can reach TeV energies and their γ emission could be a target for Cherenkov telescopes (a work is in preparation to quantify this aspect).
(39)where βinj is related to pinj. Once the temperature is fixed, the injection momentum only depends on the shock velocity with respect to the upstream flow, then ku is uniquely a function of U. For instance, using the range of U for jets (see Sect. 4.2), ku,max is limited between 2.44 (U = 40 km s-1) and 2.29 (U = 160 km s-1). This means that for a perpendicular shock, DSA is efficient in a narrow range of ku, but particles can still be injected in the acceleration process by means of other mechanisms (see Appendix A). However, for U = 160 km s-1, assuming ku = ku,max = 2.29, Emax is about 100 GeV for a shock at Rsh = 100 AU from the propostar. This means that for perpendicular shocks at larger Rsh, where the transverse radius, R⊥, is also larger, CRs can reach TeV energies and their γ emission could be a target for Cherenkov telescopes (a work is in preparation to quantify this aspect).
5.4.2. CR pressure
The accelerated CR spectrum at the shock surface can also be attenuated if the CR pressure decreases. In fact, the normalisation constant f0 (Eq. (29)) is directly proportional to PCR, which in turn depends on the parameter η (Eq. (31)). In addition, CR pressure controls Emax through Edamp (Eq. (15)). For instance, if in model  we decrease η by a factor of 10, then Emax decreases by a factor of about 500. This translates into a lower number of high-energy CRs available to “refill” the low-energy part of the spectrum during propagation, so that thermalisation occurs at a lower column density and the ionisation rate decreases.
we decrease η by a factor of 10, then Emax decreases by a factor of about 500. This translates into a lower number of high-energy CRs available to “refill” the low-energy part of the spectrum during propagation, so that thermalisation occurs at a lower column density and the ionisation rate decreases.
5.4.3. Temperature
An increase in temperature of one order of magnitude from 104 K to 105 K results in an almost negligible increase in the maximum energy achieved (see Fig. 7) because Emax is set by Eesc,d (Eq. (24)) or Eloss (Eq. (13)) for a jet shock or a protostellar surface shock, respectively. Both Eesc,d and Eloss, for parallel shocks, are proportional to (r−1)/ [ r(r + 1) ] and the compression ratio r depends on the temperature (see lower panel of Fig. 8). In addition, the space of solutions narrows and there are no combinations of total hydrogen density and ionisation fraction allowing the particle acceleration for U = 40 km s-1. In fact, the condition R> 1 (Eq. (18)) is never satisfied because of the temperature dependence in the factor Ξ (Eq. (16)). The higher the temperature, the lower both the sonic Mach number and the particle pressure (see Fig. 8). Then, for increasing temperatures the shock enters the subsonic regime, the condition in Eq. (4) is no longer fulfilled, and the acceleration process becomes ineffective. However, even when Ms> 1, 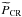 can be so low that particle acceleration is damped (R< 1).
can be so low that particle acceleration is damped (R< 1).
 |
Fig. 8 Sonic Mach number (upper panel), normalised CR pressure (middle panel), compression ratio and factor proportional both to Eesc,d and Eloss for parallel shocks (grey and black lines, respectively, in lower panel) as a function of the temperature for x = 0.3, η = 10-5; U = 40 km s-1 (solid lines), U = 80 km s-1 (dashed lines), U = 120 km s-1 (dotted lines), and U = 160 km s-1 (dash-dotted lines). |
6. Propagation of accelerated CRs in the jet
As shown in Fig. 1, CRs are accelerated downstream of the shock surface (acceleration zone). Here the turbulence produced by CRs (δB ≲ B) triggers the acceleration process. So far, B and δB have not been determined by observations, except for two sources where we have some information on the magnetic field morphology and magnitude (Carrasco-González et al. 2010; Lee et al. 2014).
Moving farther and farther away from the shock, δB decreases (turbulence damping zone) unless there are other turbulence sources. In a partially ionised medium such as in a jet, damping occurs through ion-neutral collisions for waves generated by particles with energies above a few MeV and through resonant interaction with the background plasma, i.e. linear Landau damping, for waves generated by particles with energies below a few MeV (see Appendix B). It is found that the resonant self-generated waves produced at the shock front are damped over length scales much shorter than the distance between the inner shock in the jet and the termination shock.
Entering the propagation zone, we assume that the turbulence created at the jet-outflow interface discussed in Appendix A is negligible. In this case, CR propagation in the jet is dominated by energy losses and can be treated using the continuous slowing-down approximation (Takayanagi 1973; Padovani et al. 2009). Neglecting magnetic turbulence, we can imagine that CRs propagate by gyrating around magnetic field lines, losing energy because of collisions with hydrogen atoms or molecules5. We compute the attenuation of accelerated CR protons at the jet shock surface shown in Fig. 4, along the jet and towards the termination shock, using the method developed in Padovani et al. (2009). The two upper panels of Fig. 9 show the results for both models 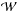 and
and  (see Table 2 for more details). The accelerated CR protons soon start to lose energy with increasing column density and their flux is attenuated; the most energetic CRs are slowed down to 0.1–100 MeV, contributing to the bulk of the ionisation. We note that even if CR electrons are not efficiently accelerated in the jet (see Sect. 2.4), they are created as the product of hydrogen ionisation due to CR protons (See Appendix B in Ivlev et al. 2015 for the calculation of the secondary electron spectrum).
(see Table 2 for more details). The accelerated CR protons soon start to lose energy with increasing column density and their flux is attenuated; the most energetic CRs are slowed down to 0.1–100 MeV, contributing to the bulk of the ionisation. We note that even if CR electrons are not efficiently accelerated in the jet (see Sect. 2.4), they are created as the product of hydrogen ionisation due to CR protons (See Appendix B in Ivlev et al. 2015 for the calculation of the secondary electron spectrum).
 |
Fig. 9 Propagated spectra in the absence of magnetic turbulence for models |
It is evident that the CR spectrum related to model 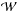 is attenuated faster with column density than the spectrum related to model
is attenuated faster with column density than the spectrum related to model  . This happens because Emax for model
. This happens because Emax for model 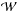 is about 100 MeV, while for model
is about 100 MeV, while for model  it is about 13 GeV (see Table 2), so that the latter model has a larger “reservoir” of high-energy CR protons, which gradually populate the low-energy part of the spectrum. We also note that if Emax ≲ 105 eV, the spectrum is completely thermalised as soon as the column density is of the order of 1019 cm-2. This is to say that CR protons are not sufficiently accelerated to take part in the ionisation process and this happens irrespective of the shape of the spectrum at low energies.
it is about 13 GeV (see Table 2), so that the latter model has a larger “reservoir” of high-energy CR protons, which gradually populate the low-energy part of the spectrum. We also note that if Emax ≲ 105 eV, the spectrum is completely thermalised as soon as the column density is of the order of 1019 cm-2. This is to say that CR protons are not sufficiently accelerated to take part in the ionisation process and this happens irrespective of the shape of the spectrum at low energies.
Nevertheless, these CR spectra have to be regarded as upper limits. In fact, Padovani & Galli (2011) and Padovani et al. (2013) demonstrated how the calculation of the ionisation rate cannot be carried out without accounting for gyromotion effects due to the presence of magnetic fields. Since CRs perform helicoidal motion around field lines, the effective column density that they pass through, Neff, is higher than the column density along the line of sight, Nlos. Currently there is no observational estimate of the magnetic field strength and of its configuration in protostellar jets, but it is possible to conjecture about the presence of a strong toroidal component such as that depicted by Teşileanu et al. (2014). Furthermore, the angle between magnetic field lines and the disc surface has to be lower than 60° in order to have a successful jet launching (Blandford & Payne 1982). Using Eqs. (19)–(24) from Padovani et al. (2013) and assuming that the toroidal field component is larger than about 50% of the total field, we estimate that Neff can be a factor of about 100−300 higher than Nlos. Because of this increase in column density, the CR proton flux of both models is more rapidly thermalised at ~5 × 1022 cm-2 and ~8 × 1023 cm-2 for models 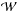 and
and  respectively (see lower panels of Fig. 9).
respectively (see lower panels of Fig. 9).
6.1. (Re-)acceleration at the reverse bow shock
The jet morphology is far from being universally defined. Jet lengths spread over orders of magnitude and usually there is not just a single final bow shock, but the innermost knots are all resolved into bow shocks due to a time-variable jet emitting dense-gas bullets (e.g. McCaughrean et al. 2002). The situation is further complicated by jet angle variations due to precession (e.g. Devine et al. 1997) or orbital motion (e.g. Noriega-Crespo et al. 2011). For the sake of simplicity, we account for a single shock at 100 AU from the protostar (see Sect. 4.2), following CR propagation up to the reverse bow shock (rBS). Once the accelerated CRs reach the rBS, they are subjected to further acceleration before entering the hot spot region (see Sect. 6.2 and Fig. 1). In Sect. 9 we will briefly discuss the dependence of Emax on Rsh and on multiple shocks.
We suppose that two processes take place at the rBS: the acceleration of thermal protons (electrons are not efficiently accelerated, see Sect. 5.1) and the re-acceleration of CRs propagated from the jet shock. Finally, we expect the bow shock to be much weaker than the rBS because of the interaction with the surrounding material and we neglect any further CR acceleration.
Shocks developed along a jet can also re-accelerate a pre-existing population of accelerated CRs. Following Melrose & Pope (1993), if the momentum distribution function of the CRs accelerated at the jet shock and propagated upstream of the rBS is fJS, prop(p), the distribution function of the re-accelerated CRs, fJS, reacc(p), reads 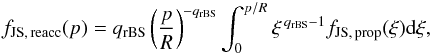 (40)where qrBS = 3rrBS/ (rrBS − 1) is the shock index, rrBS is the compression ratio at the rBS, and R3 = rJS accounts for adiabatic losses because of the decompression that develops behind the rBS. It is important to note that re-acceleration at the rBS also involves the secondary CR electrons produced during primary ionisation. These CR electrons are boosted up to relativistic energies and in Sect. 8.1 we will show their relevance to explaining synchrotron emission.
(40)where qrBS = 3rrBS/ (rrBS − 1) is the shock index, rrBS is the compression ratio at the rBS, and R3 = rJS accounts for adiabatic losses because of the decompression that develops behind the rBS. It is important to note that re-acceleration at the rBS also involves the secondary CR electrons produced during primary ionisation. These CR electrons are boosted up to relativistic energies and in Sect. 8.1 we will show their relevance to explaining synchrotron emission.
The total CR distribution function at the reverse bow shock surface, frBS(p), is given by 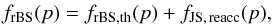 (41)where frBS, th is the distribution function of thermal protons accelerated at the rBS surface and fJS, reacc is given by Eq. (40). In order to compare the contribution of the re-accelerated CRs with the more freshly accelerated component of thermal protons at the rBS, we consider for instance both models
(41)where frBS, th is the distribution function of thermal protons accelerated at the rBS surface and fJS, reacc is given by Eq. (40). In order to compare the contribution of the re-accelerated CRs with the more freshly accelerated component of thermal protons at the rBS, we consider for instance both models 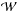 and
and  and a distance for the rBS, DrBS = 1.8 × 103 AU, corresponding to the position of the bow shock in DG Tau (knot C; Eislöffel & Mundt 1998). Assuming a constant total hydrogen density of 105 cm-3 and 6 × 105 cm-3 for model
and a distance for the rBS, DrBS = 1.8 × 103 AU, corresponding to the position of the bow shock in DG Tau (knot C; Eislöffel & Mundt 1998). Assuming a constant total hydrogen density of 105 cm-3 and 6 × 105 cm-3 for model 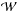 and
and  , respectively (see Table 2), the accelerated CRs pass through a line-of-sight column density of 2.7 × 1021 cm-2 and 1.6 × 1022 cm-2, respectively. The propagated CR proton and electron spectra, including gyromotion effects (see Sect. 6), from the jet shock surface are labelled “JS, prop” in Fig. 10. The decrease at low energies is due to energy losses during the propagation (see also Fig. 9). Using these spectra as input to the integral of Eq. (40), we compute the re-accelerated CR spectra at the rBS surface (“JS, reacc” in Fig. 10), making use of Eqs. (37) and (38).
, respectively (see Table 2), the accelerated CRs pass through a line-of-sight column density of 2.7 × 1021 cm-2 and 1.6 × 1022 cm-2, respectively. The propagated CR proton and electron spectra, including gyromotion effects (see Sect. 6), from the jet shock surface are labelled “JS, prop” in Fig. 10. The decrease at low energies is due to energy losses during the propagation (see also Fig. 9). Using these spectra as input to the integral of Eq. (40), we compute the re-accelerated CR spectra at the rBS surface (“JS, reacc” in Fig. 10), making use of Eqs. (37) and (38).
We evaluate the CR proton spectrum drawn from the thermal pool at the rBS (labelled “rBS, th” in Fig. 10) following Sect. 5 and assuming the same values for the shock velocity, ionisation fraction, total hydrogen density, magnetic field strength, and temperature as for the shock at 100 AU. However, the considered transverse radius, R⊥, which enters the evaluation of the maximum energy through the condition on shock geometry (see Eqs. (20) and (24)), is larger by about two orders of magnitude than R⊥ computed at 10 AU, and for DG Tau it is about 1.3 × 103 AU6. As a consequence, Emax can increase to TeV energies, being mainly constrained by downstream escape losses (see Sect. 4.2).
6.2. Solution in the hot spot region
After the rBS, in the hot spot region the flow is expected to be turbulent. The turbulence is likely connected with flow-ambient medium interactions. Cunningham et al. (2009, see references therein) considered the propagation of stellar jets in a turbulent medium that may be associated with a molecular cloud disrupted through thermal or Vishniac instability. Other fluid instabilities that can lead to turbulent motions are also expected while the jet propagates in the interstellar medium. Hence we account for the possibility that the downstream hot spot flow is turbulent, computing the CR distribution in the downstream medium using a two-zone model. This approximation is strictly valid if the length scales over which the escape and loss processes occur are longer than the scale of the region under consideration. This allows us to use space-average diffusion and loss terms.
The particle energy distribution function in the downstream jet medium, N(E,t), evolves following ![\begin{equation} \label{Nevolve} \frac{\partial}{\partial t}{\mathscr N}(E,t)= -\frac{\partial}{\partial E}\left[\frac{\ud E}{\ud t}{\mathscr N}(E,t)\right] -\frac{{\mathscr N(E,t)}}{t_{\rm esc,d}}+Q(E), \end{equation}](/articles/aa/full_html/2016/06/aa28221-16/aa28221-16-eq290.png) (42)where Q(E) is the injection rate at the shock front (see Eq. (50)) and tesc,d accounts for downstream losses due to both advection, which is produced by the downstream flow carrying the scattering centres of CRs, and diffusion. It can be written as
(42)where Q(E) is the injection rate at the shock front (see Eq. (50)) and tesc,d accounts for downstream losses due to both advection, which is produced by the downstream flow carrying the scattering centres of CRs, and diffusion. It can be written as 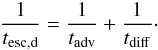 (43)The advection time is given by
(43)The advection time is given by 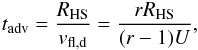 (44)with vfl,d the downstream flow velocity in the observer reference frame and RHS the radius of the hot spot region. The downstream diffusion time reads
(44)with vfl,d the downstream flow velocity in the observer reference frame and RHS the radius of the hot spot region. The downstream diffusion time reads 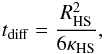 (45)where the factor 6 accounts for three-dimensional diffusion. The diffusion coefficient in the hot spot region, κHS, reads
(45)where the factor 6 accounts for three-dimensional diffusion. The diffusion coefficient in the hot spot region, κHS, reads 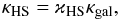 (46)which we assume is proportional to the local galactic diffusion coefficient, κgal, since we suppose that the turbulence self-generated at the shock surface has damped at large distances from the shock front. From radio galactic emission observations and secondary-to-primary CR ratios, κgal deduced for the propagation in the local ISM reads
(46)which we assume is proportional to the local galactic diffusion coefficient, κgal, since we suppose that the turbulence self-generated at the shock surface has damped at large distances from the shock front. From radio galactic emission observations and secondary-to-primary CR ratios, κgal deduced for the propagation in the local ISM reads 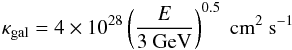 (47)for E ≥ 3 GeV (Berezinskii et al. 1990). For lower energies, κgal is not well constrained and we assume κgal = 4 × 1028 cm2 s-1. Some recent estimates using Voyager 1 data (Herbst et al. 2012) give κgal ≃ 1026−1027 cm2 s-1, so we adopt ϰHS = 0.01−1 to account for possible turbulence enhancement with respect to the local value.
(47)for E ≥ 3 GeV (Berezinskii et al. 1990). For lower energies, κgal is not well constrained and we assume κgal = 4 × 1028 cm2 s-1. Some recent estimates using Voyager 1 data (Herbst et al. 2012) give κgal ≃ 1026−1027 cm2 s-1, so we adopt ϰHS = 0.01−1 to account for possible turbulence enhancement with respect to the local value.
The energy loss per unit time is described by ![\begin{eqnarray} \label{dotE} \left|\frac{\ud E}{\ud t}\right|=\frac{E}{t_{\rm ad}} +3\beta\left(\frac{n_{\rm H}}{10^{6}~\mathrm{cm^{-3}}}\right)\left[\frac{L(E)}{10^{-25}~\mathrm{GeV~cm^{2}}}\right] ~\mathrm{GeV~s^{-1}}, \end{eqnarray}](/articles/aa/full_html/2016/06/aa28221-16/aa28221-16-eq306.png) (48)where L(E) is the energy loss function described in Sect. 2.3. The adiabatic time, tad, accounts for the fact that behind the bow shock there is a re-expansion of the flow so that CRs adiabatically lose energy; it is given by
(48)where L(E) is the energy loss function described in Sect. 2.3. The adiabatic time, tad, accounts for the fact that behind the bow shock there is a re-expansion of the flow so that CRs adiabatically lose energy; it is given by 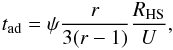 (49)where ψ is equal to 1.5 or 3 for non-relativistic or relativistic particles, respectively (see e.g. Lerche & Schlickeiser 1982).
(49)where ψ is equal to 1.5 or 3 for non-relativistic or relativistic particles, respectively (see e.g. Lerche & Schlickeiser 1982).
The injection rate at the shock front, Q(E), which we assume to be time-independent, reads 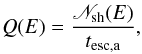 (50)where Nsh(E) is given by Eq. (37) and tesc,a is the escaping time from the acceleration zone. Following Moraitis & Mastichiadis (2007), we can write
(50)where Nsh(E) is given by Eq. (37) and tesc,a is the escaping time from the acceleration zone. Following Moraitis & Mastichiadis (2007), we can write 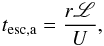 (51)where
(51)where ![\hbox{${\mathscr L}=k_{\rm u}^{-\alpha}\kappa_{\rm B}U^{-1}[1+r(k_{\rm d}/k_{\rm u})^{\alpha}]$}](/articles/aa/full_html/2016/06/aa28221-16/aa28221-16-eq314.png) is the size of the region around the shock where the acceleration takes place. For electrons, Eq. (51) should include a term in the denominator for radiative losses, but it is negligible for energies lower than TeV and a magnetic field strength lower than 1 mG.
is the size of the region around the shock where the acceleration takes place. For electrons, Eq. (51) should include a term in the denominator for radiative losses, but it is negligible for energies lower than TeV and a magnetic field strength lower than 1 mG.
In general, we can assume particles to be in a steady state since the lifetime, given by 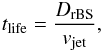 (52)where DrBS is the distance of the reverse bow shock, is much longer than the escape time downstream (see Appendix E) and this allows us to put ∂N(E,t) /∂t = 0 in Eq. (42). Ginzburg & Syrovatskii (1964) give the analytical solution of Eq. (42) in the steady-state case,
(52)where DrBS is the distance of the reverse bow shock, is much longer than the escape time downstream (see Appendix E) and this allows us to put ∂N(E,t) /∂t = 0 in Eq. (42). Ginzburg & Syrovatskii (1964) give the analytical solution of Eq. (42) in the steady-state case, ![\begin{eqnarray} \label{Nprop} {\mathscr N}(E)=\left(\frac{\ud E}{\ud t}\right)^{-1}\int_{E}^{E_{\rm max}}Q(E^{\prime})\exp\left[-\frac{\tau(E,E^{\prime})}{t_{\rm esc,d}}\right]\ud E^{\prime}, \end{eqnarray}](/articles/aa/full_html/2016/06/aa28221-16/aa28221-16-eq318.png) (53)where
(53)where 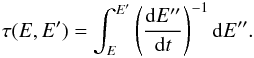 (54)Finally, the solution of Eq. (53) allows us to derive the particle spectra in the hot spot region, jHS, which reads
(54)Finally, the solution of Eq. (53) allows us to derive the particle spectra in the hot spot region, jHS, which reads 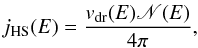 (55)where
(55)where 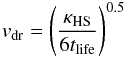 (56)is the drift velocity of the particles in the turbulent hot spot region (Skilling 1975). The resulting CR spectra in the hot spot region, labelled “HS” in Fig. 10, are encompassed by a shaded region; the upper and lower limits are obtained by assuming ϰHS equal to 1 and 0.01, respectively.
(56)is the drift velocity of the particles in the turbulent hot spot region (Skilling 1975). The resulting CR spectra in the hot spot region, labelled “HS” in Fig. 10, are encompassed by a shaded region; the upper and lower limits are obtained by assuming ϰHS equal to 1 and 0.01, respectively.
We note that Ptuskin et al. (2006) compute different trends for κgal at low energies. Therefore we also calculate the emerging spectra in the hot spot region by considering an increasing and a decreasing diffusion coefficient at non-relativistic energies, namely accounting for the plain diffusion model (hereafter PD), κgal ∝ β-2, and the diffusive re-acceleration model (hereafter DR), κgal ∝ β(γ2−1)0.17, respectively. The resulting CR spectra, jHS, both for CR protons and electrons at most increase or decrease by one order of magnitude in the non-relativistic energy range, using the PD or the DR model, respectively (we note that 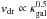 ).
).
Finally, Fig. 10 also displays the expected CR proton and electron spectra propagating into the hot spot region after the rBS acceleration (see Sect. 6.2) and the interstellar CR spectra constrained by the most recent observations of the Alpha Magnetic Spectrometer (Aguilar et al. 2014; 2015), while at low energies we used the results of Stone et al. (2013) based on Voyager observations (see also Ivlev et al. 2015). A comparison between the hot spot and the interstellar CR spectra confirms that effects such as synchrotron emission for a shock such as model  (Sect. 8.1) and high ionisation rates (Sect. 8.2 and 8.3) cannot be due to the interstellar CR flux, but could be explained by a source of accelerated particles in jet shocks.
(Sect. 8.1) and high ionisation rates (Sect. 8.2 and 8.3) cannot be due to the interstellar CR flux, but could be explained by a source of accelerated particles in jet shocks.
 |
Fig. 10 Spectra of accelerated protons (blue) and secondary electrons (red) for model |
7. Cosmic-ray ionisation rate
In the next subsections we examine the range of values of the ionisation rate expected inside a jet accounting for the different effects described in Sects. 5.4.1, 5.4.2, and 6 (diffusion coefficient, shock CR pressure, and gyromotion, respectively). Then we investigate the impact on the heating of the protostellar disc due to these locally accelerated CRs.
7.1. Ionisation rate along the jet
We use the emerging CR spectra of the jet shock-accelerated protons (models  and
and  ) shown in Fig. 4 to compute the CR ionisation rate, ζ, which reads
) shown in Fig. 4 to compute the CR ionisation rate, ζ, which reads 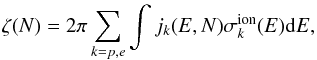 (57)where jk is the spectrum of the accelerated CR protons or secondary electrons (see Eq. (38) and Sect. 6). We apply the modelling described in Padovani et al. (2009) to study the variation of ζ with increasing column density, i.e. while CR protons propagate inside the jet. With respect to Padovani et al. (2009), cross sections,
(57)where jk is the spectrum of the accelerated CR protons or secondary electrons (see Eq. (38) and Sect. 6). We apply the modelling described in Padovani et al. (2009) to study the variation of ζ with increasing column density, i.e. while CR protons propagate inside the jet. With respect to Padovani et al. (2009), cross sections, 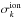 , were modified to include the effect of relativistic protons and electrons (see Krause et al. 2015). This does not invalidate the previous results since the spectra used in Padovani et al. (2009) have a negligible high-energy component, so that any former conclusion remains accurate. The resulting ionisation rates at the shock surface show values between 3 × 10-10 s-1 (model
, were modified to include the effect of relativistic protons and electrons (see Krause et al. 2015). This does not invalidate the previous results since the spectra used in Padovani et al. (2009) have a negligible high-energy component, so that any former conclusion remains accurate. The resulting ionisation rates at the shock surface show values between 3 × 10-10 s-1 (model 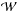 ) and 5 × 10-9 s-1 (model
) and 5 × 10-9 s-1 (model  ).
).
Because of the strong toroidal magnetic field configuration expected in jets (Blandford & Payne 1982), we assume that the transverse diffusion is negligible so that the accelerated CRs are confined to the jet. Figure 11 displays the total ionisation rate (primary protons plus secondary electrons) for increasing column density along the line of sight for the two models 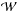 and
and  , hereafter labelled
, hereafter labelled 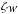 and
and 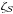 , respectively.
, respectively.
Without including gyromotion effects, 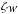 is about one order of magnitude lower than
is about one order of magnitude lower than 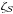 at low column densities, N ≲ 1022 cm-2. Then, around N = 1023 cm-2
at low column densities, N ≲ 1022 cm-2. Then, around N = 1023 cm-2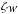 decreases ever more rapidly until CRs are completely thermalised around 3 × 1024 cm-2. Conversely, model
decreases ever more rapidly until CRs are completely thermalised around 3 × 1024 cm-2. Conversely, model  is not strongly attenuated, not even at N = 1026 cm-2, because of the larger reservoir of high-energy CRs that gives an efficient ionisation at higher column densities (see also Sect. 6). If we account for the impact of gyromotion, both
is not strongly attenuated, not even at N = 1026 cm-2, because of the larger reservoir of high-energy CRs that gives an efficient ionisation at higher column densities (see also Sect. 6). If we account for the impact of gyromotion, both 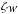 and
and 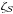 decrease by about one order of magnitude at low column densities, but then CRs are more rapidly thermalised at about 2 × 1022 cm-2 and about 4 × 1023 cm-2 for model
decrease by about one order of magnitude at low column densities, but then CRs are more rapidly thermalised at about 2 × 1022 cm-2 and about 4 × 1023 cm-2 for model 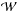 and
and  , respectively.
, respectively.
 |
Fig. 11 Ionisation rate at the shock surface in a jet as a function of the molecular hydrogen column density for models |
Figure 11 also shows the dependence of ζ on column density with an upstream diffusion coefficient κu = 30 κB. As explained in Sect. 5.4.1 (see also Figs. 5 and 6), Emax decreases for increasing values of κu, and accelerated CRs are thermalised at a lower column density (N ≃ 1025 cm-2).
We finally evaluate the trend of the ionisation rate for model  assuming a shock efficiency η = 1.5 × 10-6 (Eq. (34)), which is about one order of magnitude lower than the value used in the previous sections. The drop in ζ is due to fact that when η decreases, then Emax is fixed by Edamp (Eq. (15)). In this case the accelerated CR protons are thermalised at a column density more than three orders of magnitude lower (N ≃ 7 × 1022 cm-2) than in the case of η = 10-5.
assuming a shock efficiency η = 1.5 × 10-6 (Eq. (34)), which is about one order of magnitude lower than the value used in the previous sections. The drop in ζ is due to fact that when η decreases, then Emax is fixed by Edamp (Eq. (15)). In this case the accelerated CR protons are thermalised at a column density more than three orders of magnitude lower (N ≃ 7 × 1022 cm-2) than in the case of η = 10-5.
Even if the knowledge of some parameters constraining our modelling is still missing (e.g. shock efficiency, magnetic field strength and configuration, turbulent magnetic field component), we can imagine that the accelerated CR flux and the corresponding ionisation rate could be even markedly modified by the mechanisms discussed in this paper. Whatever the involved processes, the ionisation rate due to the shock particle acceleration may be higher than the typical values of 10-17−10-18 s-1 estimated for dense cores and protostellar discs due to the interstellar cosmic-ray flux, at least in a region close to the acceleration site.
7.2. Ionisation and heating rates in a protostellar disc
In order to quantify the variation of the ionisation degree in a protostellar disc due to accelerated CRs propagating from the hot spot region, we use the two-dimensional disc density profile described in Andrews et al. (2011) and Cleeves et al. (2013). We propagate the hot spot CR proton and electron spectra computed for both models  and
and  (see Fig. 10) accounting for a dilution factor d-2, where d is the distance from the hot spot, and we consider the distance of the hot spot region equal to 1.8 × 103 AU as in DG Tau (Sect. 6.2). Figure 12 shows the expected ionisation rate in the disc: while for model
(see Fig. 10) accounting for a dilution factor d-2, where d is the distance from the hot spot, and we consider the distance of the hot spot region equal to 1.8 × 103 AU as in DG Tau (Sect. 6.2). Figure 12 shows the expected ionisation rate in the disc: while for model 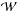 the ionisation rate is comparable to that due to the interstellar CR flux, for model
the ionisation rate is comparable to that due to the interstellar CR flux, for model 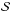 the value of ζ increases up to about 10-14 s-1 in the upper layers of the protostellar disc.
the value of ζ increases up to about 10-14 s-1 in the upper layers of the protostellar disc.
In order to check that ζ ≈ 10-14 s-1 does not give a gas temperature, Tg, that is higher than the observed values, we follow the approach outlined by Goldsmith (2001) and Galli et al. (2002) used to compute Tg by balancing the heating by the locally accelerated CRs and the cooling due to molecular and atomic transitions and collisions with dust grains. In the approximation where the dust temperature, Td, is independent of interaction with the gas, the thermal balance equation is given by 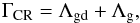 (58)where Λgd is the gas-dust energy transfer rate, given by Burke & Hollenbach (1983) and is given by
(58)where Λgd is the gas-dust energy transfer rate, given by Burke & Hollenbach (1983) and is given by 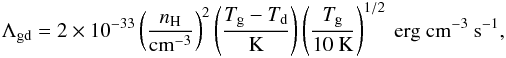 (59)while Λg is the gas cooling rate by molecular and atomic transitions, given by Goldsmith (2001)
(59)while Λg is the gas cooling rate by molecular and atomic transitions, given by Goldsmith (2001) 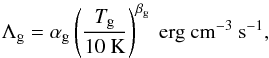 (60)where αg and βg are parameters that depend on the total hydrogen density and the molecular depletion factor, fd. We adopt a dependence of fd on nH given by fd = exp(nH/ndep) or fd = fd,max for nH ≤ ndeplog (fd,max) or nH>ndeplog (fd,max), respectively. The critical density for CO depletion is taken to be ndep = 5.5 × 104 cm-3 and the maximum depletion factor is fd,max = 100. The CR heating rate reads
(60)where αg and βg are parameters that depend on the total hydrogen density and the molecular depletion factor, fd. We adopt a dependence of fd on nH given by fd = exp(nH/ndep) or fd = fd,max for nH ≤ ndeplog (fd,max) or nH>ndeplog (fd,max), respectively. The critical density for CO depletion is taken to be ndep = 5.5 × 104 cm-3 and the maximum depletion factor is fd,max = 100. The CR heating rate reads 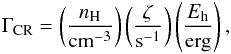 (61)where Eh is the mean heat input per ionisation (Glassgold et al. 2012). Neglecting the UV heating by the interstellar radiation field, we can estimate the net effect of locally accelerated CRs on the gas temperature. We consider two positions in the disc upper layers at a radius R = 50 AU (nH = 7 × 105 cm-3, Td = 100 K) and R = 200 AU (nH = 8 × 104 cm-3, Td = 30 K), e.g. Cleeves et al. (2013). Assuming that the column density passed through the accelerated CRs coming from the hot spot is 1019 cm-2 and ζ = 10-14 s-1, we find Tg = 130 K and 108 K at R = 50 AU and 200 AU, respectively. These values of Tg are comparable with those estimated by Cleeves (2013).
(61)where Eh is the mean heat input per ionisation (Glassgold et al. 2012). Neglecting the UV heating by the interstellar radiation field, we can estimate the net effect of locally accelerated CRs on the gas temperature. We consider two positions in the disc upper layers at a radius R = 50 AU (nH = 7 × 105 cm-3, Td = 100 K) and R = 200 AU (nH = 8 × 104 cm-3, Td = 30 K), e.g. Cleeves et al. (2013). Assuming that the column density passed through the accelerated CRs coming from the hot spot is 1019 cm-2 and ζ = 10-14 s-1, we find Tg = 130 K and 108 K at R = 50 AU and 200 AU, respectively. These values of Tg are comparable with those estimated by Cleeves (2013).
 |
Fig. 12 CR ionisation rate profile in a protostellar disc according to model |
8. Comparison with observations
In the following subsections we describe a number of examples where we adopt our modelling as a theoretical support for observations.
8.1. Synchrotron emission in DG Tau
Ainsworth et al. (2014) detected synchrotron emission towards the low-mass T Tauri star DG Tau through observations at low frequencies (325 and 610 MHz) speculating that this could be due to relativistic electrons accelerated in the interaction between the jet and the ambient medium. This emission is associated with a bow shock at a distance of about 1800 AU, 13′′ from the central source, which is moving at about 100 km s-1 (knot C in Eislöffel & Mundt 1998). The minimum magnetic field strength and particle energy that can explain the synchrotron emission is Bmin ≈ 110 μG and Etot ≈ 2.5 × 1052 eV (Ainsworth et al. 2014).
The jet structure of DG Tau is well studied down to subarcsecond scales (Maurri et al. 2014) where other knots and inner bow shocks were discovered in addition to the arcsecond-scale knots (Eislöffel & Mundt 1998). Moreover, McGroarty et al. (2009) and Oh et al. (2015) computed kinematic and physical properties along the jet. Even if we are aware of this complex structure, we show that the synchrotron emission seen towards DG Tau can be explained by the acceleration of secondary CR electrons in the jet-hot spot system. According to our model constraints (Sect. 2), it is not possible to have an efficient acceleration of thermal electrons, although secondary CR electrons produced in a previous shock can be re-accelerated (see Sect. 6.1). Through this mechanism CR electrons gain a noticeable boost at relativistic energies at the rBS surface.
For this reason, we suppose that a first acceleration takes place at the shock surface of an inner knot (knot B in Eislöffel & Mundt 1998), computing the emerging CR spectrum according to Sect. 5, and we follow the propagation of the accelerated CR protons and secondary electrons up to knot C (as in Sect. 6) accounting for gyromotion effects. Then we consider re-acceleration at the rBS (Sect. 6.1) and diffusion in the hot spot region (Sect. 6.2). Finally, following Longair (2011), assuming an isotropic distribution of re-accelerated secondary electrons in the hot spot region with Lorentz factors in the range [ γmin,γmax ], we estimate their synchrotron emissivity, εν, which is given by 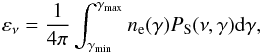 (62)where PS(ν,γ) is the power emitted at frequency ν by a single electron with Lorentz factor γ averaged over all possible directions, which reads
(62)where PS(ν,γ) is the power emitted at frequency ν by a single electron with Lorentz factor γ averaged over all possible directions, which reads 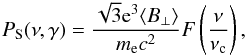 (63)with
(63)with 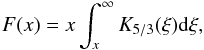 (64)where x = ν/νc, K5/3 is the modified Bessel function of order 5/3, and
(64)where x = ν/νc, K5/3 is the modified Bessel function of order 5/3, and 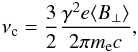 (65)where ⟨ B⊥ ⟩ is the average value of the perpendicular component of the magnetic field, which is equal to πB/ 4 for an isotropic electron population. The electron density per unit volume, ne(γ), is given by
(65)where ⟨ B⊥ ⟩ is the average value of the perpendicular component of the magnetic field, which is equal to πB/ 4 for an isotropic electron population. The electron density per unit volume, ne(γ), is given by 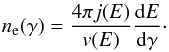 (66)The synchrotron emissivity has to be converted into spectral energy flux density, Sν, so as to compare the model to Giant Metrewave Radio Telescope (GMRT) and Expanded Very Large Array (EVLA) observations of DG Tau (Ainsworth et al. 2014; and Lynch et al. 2013, respectively). Assuming a Gaussian beam profile, Sν reads
(66)The synchrotron emissivity has to be converted into spectral energy flux density, Sν, so as to compare the model to Giant Metrewave Radio Telescope (GMRT) and Expanded Very Large Array (EVLA) observations of DG Tau (Ainsworth et al. 2014; and Lynch et al. 2013, respectively). Assuming a Gaussian beam profile, Sν reads 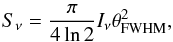 (67)where θFWHM is the synthesised beam size in radians. The specific intensity, Iν, is given by
(67)where θFWHM is the synthesised beam size in radians. The specific intensity, Iν, is given by 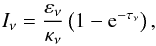 (68)where τν = Rκν is the optical depth and R is the radius of the emitting region. Finally, the specific absorption coefficient, κν, reads
(68)where τν = Rκν is the optical depth and R is the radius of the emitting region. Finally, the specific absorption coefficient, κν, reads ![\begin{eqnarray} \kappa_{\nu}=\frac{1}{8\pi m_{\rm e}\nu^{2}}\int_{\gamma_{\rm min}}^{\gamma_{\rm max}}\gamma^{2}P_{\rm S}(\nu,\gamma)\frac{\ud}{\ud\gamma} \left[\frac{n_{\rm e}(\gamma)}{\gamma^{2}}\right]\ud\gamma. \end{eqnarray}](/articles/aa/full_html/2016/06/aa28221-16/aa28221-16-eq402.png) (69)Relying on the above equations, we compute the expected synchrotron emission spectrum. We assume a constant magnetic field strength of 300 μG for both knots B and C, R of the order of 1300 AU (Ainsworth et al. 2014), and we compute the expected synchrotron emission for two values of the shock velocity with respect to the upstream flow (U = 100 km s-1 and 200 km s-1) because of the uncertainty in its value. We also adopt an error of 30% in the emitting region radius. As shown by Fig. 13, we find a synchrotron spectral index of −1.01, which is close to the value inferred from observations (−0.89 ± 0.07, Ainsworth et al. 2014), and we are able to explain the observations with U = 100 km s-1. It is important to note that the synchrotron emission would be inefficient if secondary CR electrons were not re-accelerated in subsequent shocks: this is the key process to accelerate CR electrons in the synchrotron energy domain (see Fig. 10). Finally, we also show in Fig. 13 the frequency range that was observed by LOFAR, which can give a further constraint to our model.
(69)Relying on the above equations, we compute the expected synchrotron emission spectrum. We assume a constant magnetic field strength of 300 μG for both knots B and C, R of the order of 1300 AU (Ainsworth et al. 2014), and we compute the expected synchrotron emission for two values of the shock velocity with respect to the upstream flow (U = 100 km s-1 and 200 km s-1) because of the uncertainty in its value. We also adopt an error of 30% in the emitting region radius. As shown by Fig. 13, we find a synchrotron spectral index of −1.01, which is close to the value inferred from observations (−0.89 ± 0.07, Ainsworth et al. 2014), and we are able to explain the observations with U = 100 km s-1. It is important to note that the synchrotron emission would be inefficient if secondary CR electrons were not re-accelerated in subsequent shocks: this is the key process to accelerate CR electrons in the synchrotron energy domain (see Fig. 10). Finally, we also show in Fig. 13 the frequency range that was observed by LOFAR, which can give a further constraint to our model.
 |
Fig. 13 Spectral energy flux density as a function of the frequency. GMRT and EVLA observations (yellow solid circles) from Ainsworth et al. (2014) and Lynch et al. (2013), respectively, are shown together with their fit (yellow dashed line) predicting a synchrotron spectral index of −0.89 ± 0.07 (Ainsworth et al. 2014). The two black shaded regions show the result of our modelling using two different shock velocities with respect to the upstream flow (U = 100 km s-1 and 200 km s-1) and their widths refer to an assumed error of 30% on the value of the hot spot radius, the central value (RHS = 1300 AU, Ainsworth et al. 2014) pinpointed by the white dotted lines. The green shaded areas show the two LOFAR bands (LBA=low band antenna; HBA = high band antenna), and their lower boundary in Sν corresponds to the sensitivity limit using its most extended configuration (van Haarlem et al. 2013). |
8.2. High ionisation rate in L1157-B1
Another case of remarkably high level of ionisation was measured by Podio et al. (2014) in the bow shock of L1157 known as B1. They found that the observed abundances of the HCO+ and N2H+ ions, which are usually employed such as probes of the ionisation rate, can be simultaneously reproduced only by assuming ζ = 3 × 10-16 s-1. The youngest knot, termed B0, lies at about 1.2 × 104 AU, while B1 is at 1.7 × 104 AU with a hot spot cavity radius of about 1.2 × 103 AU (Lefloch et al. 2012), assuming a source distance of 250 pc (Looney et al. 2007). The jet velocity is of the order of 100 km s-1 with shock velocities between 20 and 40 km s-1 (Bachiller et al. 2001; Tafalla et al. 2015). The total hydrogen density is of the order of 105−106 cm-3 (e.g. Gómez-Ruiz et al. 2015). Podio et al. 2014 traced the cold gas with temperatures of 60−200 K and there are hints of a warm gas component with a temperature of at least 103 K that can explain the water lines (Busquet et al. 2014).
Our modelling can explain the high ionisation rate in B1 if we assume that thermal protons are accelerated in B0 and, once they reach B1, that they undergo a further acceleration without any additional thermal proton acceleration. This situation can take place supposing that 1) the shock velocity with respect to the upstream flow and/or the shock efficiency is too low at the bow-shock surface B1 or 2) the upstream diffusion coefficient is too large to have an efficient acceleration of thermal particles.
We follow the steps described in Sects. 5 and 6 (calculation of the emerging CR spectrum at B0, its propagation up to B1, its re-acceleration at B1, and the hot spot region diffusion), assuming U = 60 km s-1 and U = 40 km s-1 in B0 and B1, respectively, Neff/Nlos = 2 × 102 (see Sect. 6), B ≲ 100 μG, x = 0.2−0.4, T = 103 K, nH = 105 cm-3, ku = 1, and η = 5 × 10-6 in both B0 and B1. We obtain proton and secondary electron spectra leading to a total ionisation rate ζ = 6.1 × 10-16 s-1, consistent within a factor of about 2 with the value estimated from observations.
The values of U, B, T, x, nH, ku, and η can vary along the shock surfaces B0 and B1, which is why our result has to be interpreted as a proof of concept. Further observations could give better constraints on the above parameters to test the validity of our hypothesis.
Figure 14 shows the comparison between the ionisation rate due to the local CRs accelerated in the hot spot, ζHS, and the value due to the interstellar CRs assuming a spectrum similar to that from Voyager 1, ζISM (Stone et al. 2013; Ivlev et al. 2015). We conclude that the high value of ζ observed in L1157 and explained by our modelling may not be due to interstellar CRs. In fact, at the hot spot (R = 1.7 × 104 AU), ζHS is about a factor of 10 higher than ζISM. Then, entering the envelope towards the protostar, the contribution of the hot spot CR flux to the total ionisation rate becomes negligible at R ≲ 5 × 103 AU because of the geometric dilution factor, d-2, where d is the distance from the hot spot.
Following Sect. 7.2, we compute the gas temperature in the envelope of L1157 only accounting for the heating due to both interstellar and locally accelerated CRs. The dust temperature profile is given by T(r) = 300(R/ AU)-0.41 K (Chiang et al. 2010; 2012). Neglecting the UV heating by the interstellar radiation field, for R ≲ 300 AU gas and dust are coupled, while for larger radii, at first Tg decreases because the heating by the interstellar CRs is too weak, then CRs at the hot spot cause a slight increase in Tg with respect to Td, up to 30 K.
 |
Fig. 14 Dust and gas temperature (solid and dashed red lines, respectively) as a function of the distance from the protostar L1157. The plot also shows the ionisation rate of interstellar CRs (dash-dotted green line), of CRs coming from the hot spot (dashed green line), and the total value (solid green line). |
8.3. High ionisation rate in OMC-2 FIR 4
Ceccarelli et al. (2014) observed one of the closest known intermediate-mass protostars in Orion, OMC-2 FIR 4, via Herschel observations of HCO+ and N2H+. The abundance of these molecular ions were used to estimate the ionisation rate which reaches values of the order of 1.5 × 10-12 and 4 × 10-14 s-1 at 1600 AU and 3700 AU from the source centre, respectively. Actually, the structure of this protostar is highly complex since it contains a cluster of a few embedded intermediate- and low-mass protostars (Shimajiri et al. 2008; López-Sepulcre et al. 2013). It is also worth noting that Shimajiri et al. (2008) found the presence of a shock region produced by the interaction of an external bipolar outflow driven by the nearby OMC-2 FIR 3 region, lying to the north-east of OMC-2 FIR 4 (see also López-Sepulcre et al. 2013). This shock appears to be responsible for the high degree of fragmentation observed in OMC-2 FIR 4.
Thus far no jet activity has been observed in OMC-2 FIR 4. Nevertheless, in order to justify the extremely high values of ζ, the presence of a mechanism able to accelerate particles inside the source must be postulated since at a radius of the order of thousands of AU the interstellar CR flux is strongly attenuated (Padovani et al. 2013). Assuming that no jet is present and that the accretion on the protostellar surface is still spherical, we can recover an efficient proton acceleration at the protostellar surface (Sect. 4.3). For instance, following Sect. 2 we compute the emerging proton spectrum by considering U = 260 km s-1, T = 9.4 × 105 K, nH = 1.9 × 1012 cm-3, B = 5 G, x = 0.3, ku = 1, and η = 10-5 at Rsh = 2 × 10-2 AU as in the model by Masunaga & Inutsuka (2000). The maximum energy of the accelerated CRs is Emax = 11.4 GeV. Then, neglecting magnetic turbulence (see Sect. 6), we propagate the proton and secondary electron fluxes up to the two positions where the ionisation rate in OMC-2 FIR 4 was estimated, 1600 AU and 3700 AU. Combining the density profiles in Masunaga & Inutuska (2000) and Crimier et al. (2009), we find that the accelerated particles go through a column density of about 1.8 × 1024 cm-2. Accounting for a geometrical dilution factor of (Rsh/R)2, with R = 1600 AU and 3700 AU, we obtain ζ = 3 × 10-15 s-1 and 6 × 10-16 s-1, respectively. However, including gyromotion effects would increase the effective column density (Sect. 6), causing a further reduction in the ionisation rate.
It is important to emphasise that the above result is obtained by neglecting any diffusion process. Since it is difficult to describe turbulence in the envelope, we briefly discuss the effects of diffusion here. If the accelerated CRs undergo diffusion during propagation from the shock surface, the CR energy distribution function at a distance R from the shock and at a time t in the case of continuous CR injection from a point source reads 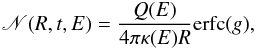 (70)where κ(E) is the diffusion coefficient,
(70)where κ(E) is the diffusion coefficient, 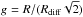 , and
, and 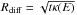 is the diffusion length (Aharonian 2004). If R ≫ Rdiff, then
is the diffusion length (Aharonian 2004). If R ≫ Rdiff, then 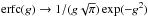 and the propagated spectrum is attenuated as
and the propagated spectrum is attenuated as ![\hbox{$R^{-2}\exp[-R^{2}/(2R_{\rm diff}^{2})]$}](/articles/aa/full_html/2016/06/aa28221-16/aa28221-16-eq449.png) , i.e. much faster than in the free-streaming case. In contrast, if R ≪ Rdiff, then erfc(g) → 1 and the propagated spectrum is attenuated as R-1, as opposed to R-2 in the free-streaming case, and ζ would be much higher: ζ = 3 × 10-10 s-1 and ζ = 1 × 10-10 s-1 at R = 1600 AU and R = 3700 AU, respectively.
, i.e. much faster than in the free-streaming case. In contrast, if R ≪ Rdiff, then erfc(g) → 1 and the propagated spectrum is attenuated as R-1, as opposed to R-2 in the free-streaming case, and ζ would be much higher: ζ = 3 × 10-10 s-1 and ζ = 1 × 10-10 s-1 at R = 1600 AU and R = 3700 AU, respectively.
As shown in Fig. 15, the values of ζ computed from observations lie between the two extreme cases of free streaming and pure diffusion with R ≪ Rdiff7. However, after performing a check on gas temperature (as outlined in Sect. 7.2), the attenuation of the spectrum with a factor R-1 corresponds to higher values of Tg than those determined by Ceccarelli et al. (2014) from a large-velocity gradient analysis. We can conclude that the propagation mechanism is probably neither purely diffusive nor free streaming. A better knowledge of the magnetic field configuration close to the protostar and of its turbulence degree is needed for a more careful description of CR propagation from the protostellar surface to the envelope.
 |
Fig. 15 Ionisation rate (upper panel) and temperatures of gas and dust (lower panel) as a function of the distance from the protostar OMC-2 FIR 4. Observational estimates of ζ and Tg (black solid circles and squares, respectively; Ceccarelli et al. 2014) are compared to the results from the modelling described in Sect. 8.3 (green and red solid lines). The green and red shaded areas encompass the range of ζ and Tg by assuming a dilution factor R-1 (purely diffusive propagation) and R-2 (free-streaming propagation). The green dash-dotted and dashed lines show the interstellar CR ionisation rate assuming a spectrum similar to that from Voyager 1 (Stone et al. 2013) and an enhanced CR proton flux (see model H in Ivlev et al. 2015). The red dashed line shows the trend of the dust temperature (Masunaga & Inutsuka 2000; Crimier et al. 2009). |
8.4. 10Be enrichment in meteorites
Ceccarelli et al. (2014) argued that the accelerated proton flux causing the high ionisation rate could also be responsible for the formation of short-lived radionuclei, such as 10Be, contained in the calcium-aluminium-rich inclusions (CAIs) of carbonaceous meteorites. In fact, the measured abundance of 10Be in meteorites is higher than that found in the ISM and this should be due to spallation reactions between the accelerated CRs and the thermal gas that took place during the earliest phases of the protosolar nebula.
To test the consequences of our modelling, we use the emerging spectrum at the protostellar surface (Sect. 8.3) scaled at 1 AU, taking into account the geometric dilution of R-1 or R-2, appropriate for the purely diffusive or free-streaming case, respectively. We calculate the fluence per unit time, Ft, which reads 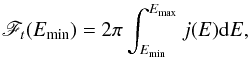 (71)where Emin ≃ 50 MeV is the energy threshold for the spallation reaction p + 16O → 10Be + ... (Gounelle et al. 2006) and Emax = 11.4 GeV (Sect. 8.3). We find Ft = 2 × 1017 and 8 × 1018 protons cm-2 yr-1 at 1 AU, for the purely diffusive and free-streaming cases, respectively. This means that an irradiation time of a few tens of years can explain the values of the fluence derived by Gounelle et al. (2013) equal to 1019−1020 protons cm-2, in agreement with the estimates by Ceccarelli et al. (2014). This result is also consistent with the X-wind model predictions (Shu et al. 1997), according to which a proto-CAI of radius RCAI spends a time t ~ 20(RCAI/ 1 cm) yr in the reconnection ring. Nevertheless, it is important to note that the model by Gounelle et al. (2013) predicts too much heating (Tatischeff et al. 2014). If diffusion is present, the particle flux in Eq. (71) is higher and the fluence computed by Gounelle et al. (2013) would be even more easily recovered.
(71)where Emin ≃ 50 MeV is the energy threshold for the spallation reaction p + 16O → 10Be + ... (Gounelle et al. 2006) and Emax = 11.4 GeV (Sect. 8.3). We find Ft = 2 × 1017 and 8 × 1018 protons cm-2 yr-1 at 1 AU, for the purely diffusive and free-streaming cases, respectively. This means that an irradiation time of a few tens of years can explain the values of the fluence derived by Gounelle et al. (2013) equal to 1019−1020 protons cm-2, in agreement with the estimates by Ceccarelli et al. (2014). This result is also consistent with the X-wind model predictions (Shu et al. 1997), according to which a proto-CAI of radius RCAI spends a time t ~ 20(RCAI/ 1 cm) yr in the reconnection ring. Nevertheless, it is important to note that the model by Gounelle et al. (2013) predicts too much heating (Tatischeff et al. 2014). If diffusion is present, the particle flux in Eq. (71) is higher and the fluence computed by Gounelle et al. (2013) would be even more easily recovered.
9. Conclusions
In this paper we investigated the possibility of accelerating CRs within a protostellar source by means of shock processes. Diffusive shock acceleration (DSA) is the main process leading to CR acceleration: a CR gains energy up to the relativistic domain by multiple back-and-forth shock crossings. A number of conditions have to be satisfied in order for DSA to be effective, some of them related to magnetic fluctuations (determining pitch-angle scattering), others associated with cooling processes and also shock velocity, age, and geometry constraints. We focused our attention on the effectiveness of shocks in accretion flows, in jets, and on protostellar surfaces. Our main conclusions are the following:
-
1.
At jet shocks, CR protons can be effectively extracted from the thermal plasma and accelerated up to relativistic energies, while CR electrons can only reach energies of about 300 MeV because of wave damping and energy losses.
-
2.
In accretion flows, the ionisation fraction is too small and the shock velocity too low, which prevents any CR acceleration. Furthermore, the high magnetic field strength implies sub-Alfvénic flow speeds.
-
3.
On protostellar surfaces, shocks caused by impacting material during the collapse phase are strong enough to boost CR protons, but not electrons.
The set of conditions that has to be fulfilled is highly non-linear: small variations in one or more parameters (magnetic field strength, ionisation fraction, total hydrogen density, temperature, flow velocity, upstream diffusion coefficient, and shock efficiency) can make the acceleration process inefficient. As a consequence, since a protostar is a highly dynamic system, CR acceleration can be a very intermittent process; for instance, a locally enhanced ionisation rate caused by the accelerated particles could modify the local ionisation fraction and then the efficiency of this acceleration mechanism. The intrinsic limit of our modelling lies in the observational uncertainties of these parameters. High-resolution observations carried out for example with ALMA will help to have better constraints, with special consideration for the magnetic field configuration. In addition, the parameters listed above are not constant all along the shock surface so that the efficiency of the acceleration can be reduced. However, while we only accounted for acceleration at the surface of a single inner jet shock at 100 AU plus re-acceleration at the final reverse bow shock, jets usually show multiple inner shocks, which makes it possible to recover the acceleration efficiency of our modelling.
After demonstrating the possibility of accelerating CR protons in a jet shock, we described their propagation in the jet, also accounting for secondary CR electrons produced by the ionisation process. Once the reverse bow shock is reached, CR protons and electrons are re-accelerated together with a local component of thermal protons before streaming in the hot spot region. A number of observations can be explained by our modelling. In particular:
-
1.
The synchrotron emission seen in the bow shock of DG Tau can be explained by the presence of high-energy CR electrons. Using the available parameter values for DG Tau, we succeeded in reproducing the synchrotron index estimated by observations. The most important conclusion is that the electrons responsible for synchrotron emission are the secondary CR electrons re-accelerated at the bow shock.
-
2.
The high ionisation seen towards the bow shock B1 in L1157 can be reproduced if we assume that the first acceleration of thermal protons takes place in the shock B0 and that the further acceleration of thermal particles in B1 is inefficient (e.g. because of low flow velocity and shock efficiency, or high upstream diffusion coefficient).
-
3.
We attempted to describe the high ionisation towards OMC-2 FIR 4. So far no jet activity has been observed, which is why we explained the observed ionisation rate and the 10Be abundance assuming that CR acceleration takes place directly on the protostellar surface. However, it is important to remember that this source shows hints of fragmentation so that our modelling may not be directly applied.
The most limiting condition for the maximum energy reached by a CR proton is due to the geometry of the jet. In fact, the jet transverse radius increases with the distance of the shock from the source and CRs are confined in the jet for a longer time since their possibility of escaping in the perpendicular direction decreases. In this way they can reach higher energies. Thus, if DSA takes place in a jet shock far from a protostar, it is possible to accelerate CR protons up to 1−10 TeV energies and in principle their γ emission could be observed with the next generation of ground-based telescopes such as CTA.
In closing, it is important to note that D’Alessio et al. (1998) found that in the disc region between 0.2 AU and 4 AU the ionisation fraction is smaller than the minimum value required to have magnetorotational instability operating near the disc midplane. The acceleration of CRs inside protostars predicted by our modelling would cause an increase in the number of electrons. As a consequence, the extension of the so called “dead zone” (Gammie 1996) could be modified together with the planetesimal formation efficiency.
See Appendix D for details on the derivation of Edamp.
The factor 4 in the denominator of Eq. (23) comes from the fact that the diffusion process in the perpendicular direction is in two dimensions.
R⊥ at the bow shock of DG Tau has been estimated from the value of the volume of the emitting region evaluated by Ainsworth et al. (2014).
Acknowledgments
The authors thank Cecilia Ceccarelli, Daniele Galli, and Vincent Tatischeff for valuable discussions. We acknowledge the financial support of the Agence National pour la Recherche (ANR) through the COSMIS project. This work has been carried out thanks to the support of the OCEVU Labex (ANR-11-LABX-0060) and the A*MIDEX project (ANR-11-IDEX-0001-02) funded by the “Investissements d’Avenir” French government programme managed by the ANR. M.P. and A.M. also acknowledge the support of the CNRS-INAF PICS project “Pulsar wind nebulae, supernova remnants and the origin of cosmic rays”.
References
- Adams, F. C., Lada, C. J., & Shu, F. H. 1987, ApJ, 312, 788 [NASA ADS] [CrossRef] [Google Scholar]
- Agra-Amboage, V., Dougados, C., Cabrit, S., & Reunanen, J. 2011, A&A, 532, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aguilar, M., Aisa, D., Alpat, B., et al. 2014, Phys. Rev. Lett., 113, 221102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aguilar, M., Aisa, D., Alpat, B., et al. 2015, Phys. Rev. Lett., 144, 171103 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F. A. 2004, Very High Energy Cosmic Gamma Radiation (River Edge, NJ: World Scientific Publishing) [Google Scholar]
- Ainsworth, R. E., Scaife, A. M. M., Ray, T. P., et al. 2014, ApJ, 792, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Alves, F. O., Vlemmings, W. H. T., Girart, J. M., & Torrelles, J. M. 2012, A&A, 542, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., & Montmerle, T. 1994, ApJ, 420, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Espaillat, C., et al. 2011, ApJ, 732, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Antoniucci, S., Nisini, B., Giannini, T., & Lorenzetti, D. 2008, A&A, 479, 503 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Araudo, A. T., Romero, G. E., Bosch-Ramon, V., & Paredes, J. M. 2007, A&A, 476, 1289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bachiller, R., Pérez Gutiérrez, M., Kumar, M. S. N., & Tafalla, M. 2001, A&A, 372, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., André, P., Despois, D., & Blinder, S. 2002, A&A, 393, 927 [Google Scholar]
- Berezhko, E. G. 1996, Astropart. Phys., 5, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Berezhko, E. G., & Ellison, D. C. 1999, ApJ, 526, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Berezinskii, V. S., Bulanov, S. V., Dogiel, V. A., & Ptuskin, V. S. 1990, Astrophysics of Cosmic Rays (Amsterdam: North holland) [Google Scholar]
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Blasi, P., Gabici, S., & Vannoni, G. 2005, MNRAS, 361, 907 [NASA ADS] [CrossRef] [Google Scholar]
- Bosch-Ramon, V., Romero, G. E., Araudo, A. T., & Paredes, J. M. 2010, A&A, 511, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Braiding, C. R., & Wardle, M. 2012a, MNRAS, 422, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Braiding, C. R., & Wardle, M. 2012b, MNRAS, 427, 3188 [NASA ADS] [CrossRef] [Google Scholar]
- Burke, J. R., & Hollenbach, D. J. 1983, ApJ, 265, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Busquet, G., Lefloch, B., Benedettini, M., et al. 2014, A&A, 561, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cabrit, S., Codella, C., Gueth, F., et al. 2007, A&A, 468, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caratti o Garatti, A., & Eislöffel, J. 2009, in Astrophys. Space Sci. Proc., Protostellar Jets in Context, eds. K. Tsinganos, et al., 329 [Google Scholar]
- Carrasco-González, C., Rodríguez, L. F., Anglada, G., et al. 2010, Science, 330, 1209 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ceccarelli, C., Castets, A., Caux, E., et al. 2000, A&A, 355, 1129 [NASA ADS] [Google Scholar]
- Ceccarelli, C., Dominik, C., López-Sepulcre, A., et al. 2014, ApJ, 790, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Cesarsky, C. J., & Völk, H. J. 1978, A&A, 70, 367 [NASA ADS] [Google Scholar]
- Chandran, B. D. G. 2000, ApJ, 529, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, H.-F., Looney, L. W., Tobin, J. J., & Hartmann, L. 2010, ApJ, 709, 470 [Google Scholar]
- Chiang, H.-F., Looney, L. W., & Tobin, J. J. 2012, ApJ, 756, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Cleeves, L. I., Adams, F. C., & Bergin, E. A. 2013, ApJ, 772, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Crimier, N., Ceccarelli, C., Lefloch, B., & Faure, A. 2009, A&A, 506, 1229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cunningham, A., Krumholz, M. R., Klein, R. I., & McKee, C. F. 2009, in AAS Meet. Abstr., 214, 604.05 [Google Scholar]
- D’Alessio, P., Cantó Jorge, Calvet, N., & Lizano, S. 1998, ApJ, 500, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Dapp, W. B., & Basu, S. 2010, A&A, 521, L56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Gouveia Dal Pino, E. M. 1995, AIP Conf. Proc., 345, 427 [NASA ADS] [CrossRef] [Google Scholar]
- de Gouveia Dal Pino, E. M., & Lazarian, A. 2005, A&A, 441, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Gouveia Dal Pino, E. M., Kowal, G., & Lazarian, A. 2014, 8th Int. Conf. Numerical Modeling of Space Plasma Flows, ASTRONUM 2013, ASP Conf. Ser., 488, 8 [NASA ADS] [Google Scholar]
- Devine, D., Bally, J., Reipurth, B., & Heathcote, S. 1997, AJ, 114, 2095 [NASA ADS] [CrossRef] [Google Scholar]
- Dionatos, O., Nisini, B., Cabrit, S., Kristensen, L., & Pineau Des Forêts, G. 2010, A&A, 521, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dougados, C., Cabrit, S., Lavalley, C., & Ménard, F. 2000, A&A, 357, L61 [NASA ADS] [Google Scholar]
- Drury, L. O’C. 1983, Ref. Prog. Phys., 46, 973 [Google Scholar]
- Drury, L. O’C., Duffy, P., & Kirk, J. G. 1996, A&A, 309, 1002 [NASA ADS] [Google Scholar]
- Earl, J. A., Jokipii, J. R., & Morfill, G. 1988, ApJ, 331, 91 [Google Scholar]
- Eislöffel, J., & Mundt, R. 1998, AJ, 115, 1554 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrière, K. 2001, Rev. Mod. Phys., 73, 1031 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, A., Ray, T. P., Cabrit, S., et al. 2014, Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 451 [Google Scholar]
- Galli, D., Walmsley, M. C., & Gonçalves, J. 2002, A&A, 394, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galli, D., Lizano, S., Shu, F. H., & Allen, A. 2006, ApJ, 647, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Gammie, C. F. 1996, ApJ, 457, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia, P. J. V., Ferreira, J., Cabrit, S., & Binette, L. 2001, A&A, 377, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GarciaLópez, R., Nisini, B., Giannini, T., et al. 2008, A&A, 487, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giacalone, J., & Jokipii, J. R. 2007, ApJ, 663, 41 [Google Scholar]
- Ginzburg, V. L., & Syrovatskii, S. I. 1964, The Origin of Cosmic Rays (Oxford: Pergamon) [Google Scholar]
- Glassgold, A. E., Galli, D., & Padovani, M. 2012, ApJ, 756, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P. F. 2001, ApJ, 557, 736 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Gómez-Ruiz, A. I., Gusdorf, A., Leurini, S., et al. 2012, A&A, 542, A9 [Google Scholar]
- Gómez-Ruiz, A. I., Codella, C., Lefloch, B., et al. 2015, MNRAS, 446, 3346 [NASA ADS] [CrossRef] [Google Scholar]
- Gounelle, M., Shu, F. H., Shang, H., et al. 2006, ApJ, 640, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Gounelle, M., Chaussidon, M., & Rollion-Bard, C. 2013, ApJ, 763, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Hartigan, P., & Morse, J. 2007, ApJ, 660, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Hartigan, P., Morse, J. A., & Raymond, J. 1994, ApJ, 436, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Hartigan, P., Edwards, S., & Pierson, R. 2004, ApJ, 609, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Hartquist, T. W., Doyle, H. T., & Dalgarno, A. 1978, A&A, 68, 65 [NASA ADS] [Google Scholar]
- Hawley, J. F. 2000, ApJ, 528, 46 [Google Scholar]
- Hennebelle, P., & Fromang, S. 2008, A&A, 477, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herbst, K., Heber, B., Kopp, A., Sternal, O., & Steinhilber, F. 2012, ApJ, 761, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Imai, H., Nakashima, K., Bushimata, T., et al. 2007, PASJ, 59, 1007 [CrossRef] [Google Scholar]
- Ivlev, A., Padovani, M., Galli, D., & Caselli, P. 2015, ApJ, 812, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Jean, P., Gillard, W., Marcowith, A., & Ferrière, K. 2009, A&A, 508, 1099 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jokipii, J. R. 1987, ApJ, 313, 842 [Google Scholar]
- Kirk, J. G. 1994, in Plasma Astrophysics, eds. A. O. Benz, & T. J.-L. Courvoisier (Berlin: Springer Verlag), 225 [Google Scholar]
- Kirk, J. G., Duffy, P., Gallant, Y. A. 1996, A&A, 314, 1010 [NASA ADS] [Google Scholar]
- Krause, J., Morlino, G., & Gabici, S. 2015, The 34th International Cosmic Ray Conference [arXiv:1507.05127] [Google Scholar]
- Krolik, J. H., & Kallman, T. R. 1983, ApJ, 267, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Krasnopolsky, R., Li, Z.-Y., & Shang, H. 2011, ApJ, 733, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Kulsrud, R., & Cesarsky, C. J. 1971, ApL, 8, 189 [Google Scholar]
- Lee, C.-F., Rao, R., Ching, T.-C., Lai, S.-P., & Hirano, N. 2014, ApJ, 797, 9 [Google Scholar]
- Lefloch, B., Cabrit, S., Busquet, G., et al. 2012, ApJ, 757, 25 [Google Scholar]
- Lerche, I., & Schlickeiser, R. 1982, A&A, 107, 148 [NASA ADS] [Google Scholar]
- Longair, M. S. 2011, High Energy Astrophysics (Cambridge: Cambridge University Press) [Google Scholar]
- Looney, L. W., Tobin, J. J., & Kwon, W. 2007, ApJ, 670, L131 [NASA ADS] [CrossRef] [Google Scholar]
- López-Sepulcre, A., Taquet, V., Sánchez-Monge, Á., et al. 2013, A&A, 556, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lynch, C., Mutel, R. L., Güdel, M., Ray, T., Skinner, S. L. et al. 2013, ApJ, 766, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Mannheim, K., & Schlickeiser, R. 1994, A&A, 286, 983 [NASA ADS] [Google Scholar]
- Masson, J., Chabrier, G., Hennebelle, P., Vaytet, N., & Commerçon, B. 2016, A&A, 587, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masunaga, H., & Inutsuka, S. 2000, ApJ, 531, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Maurri, L., Bacciotti, F., Podio, L., et al. 2014, A&A, 565, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McCaughrean, M., Zinnecker, H., Andersen, M., Meeus, G., & Lodieu, N. 2002, The Messenger, 109, 28 [NASA ADS] [Google Scholar]
- McGroarty, F., Podio, L., Bacciotti, F., & Ray, T. 2009, in Astrophys. Space Sci. Proc., Protostellar Jets in Context, eds. K. Tsinganos, et al., 577 [Google Scholar]
- McKee, C. F. 1989, ApJ, 345, 782 [NASA ADS] [CrossRef] [Google Scholar]
- Mellon, R. R., & Li, Z.-H. 2008, ApJ, 681, 1356 [NASA ADS] [CrossRef] [Google Scholar]
- Melrose, D. B., & Pope, M. H. 1993, PASA, 10, 222 [Google Scholar]
- Moraitis, K., & Mastichiadis, A. 2007, A&A, 462, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morlino, G., & Gabici, S. 2015, MNRAS, 451, 100 [Google Scholar]
- Morse, J. A., Heathcote, S., Cecil, G., Hartigan, P., & Raymond, J. C. 1993, ApJ, 410, 764 [NASA ADS] [CrossRef] [Google Scholar]
- Munar-Adrover, P., Paredes, J. M., & Romero, G. E. 2011, A&A, 530, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noriega-Crespo, A., Raga, A. C., Lora, V., Stapelfeldt, K. R., & Carey, S. J. 2011, ApJ, 723, 16 [Google Scholar]
- Nisini, B., Bacciotti, F., Giannini, T., et al. 2005, A&A, 441, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oh, H., Pyo, T.-S., Yuk, I.-S., & Park, B.-G. 2015, J. Korean Astron. Soc., 48, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, M., & Galli, D. 2011, A&A, 530, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Padovani, M., & Galli, D. 2013, in Advances in Solid State Physics, Cosmic Rays in Star-Forming Environments, eds. D. F. Torres, & O. Reimer, 34, 61 [Google Scholar]
- Padovani, M., Galli, D., & Glassgold, A. E. 2009, A&A, 501, 619 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Padovani, M., Hennebelle, P., & Galli, D. 2013, A&A, 560, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Padovani, M., Galli, D., Hennebelle, P., Commerçon, B., & Joos, M. 2014, A&A, 571, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Padovani, M., Hennebelle, P., Marcowith, A., & Ferrière, K. 2015, A&A, 582, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pelletier, G., Lemoine, M., & Marcowith, A. 2006, A&A, 453, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrosian, V., & Bykov, A. M. 2008, Space Sci. Rev., 134, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Podio, L., Lefloch, B., Ceccarelli, C., Codella, C., & Bachiller, R. 2014, A&A, 556, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prantzos, N., Boehm, C., Bykov, A. M., et al. 2011, Rev. Mod. Phys., 83, 1001 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R. 1994, in Plasma Astrophysics, eds. A. O. Benz, & T., J.-L. Courvoisier (Berlin: Springer Verlag) [Google Scholar]
- Ptuskin, V. S., Moskalenko, I. V., Jones, F. C., Strong, A. W., & Zirakashvili, V. N. 2006, ApJ, 642, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Raga, A. C., Velázquez, P. F., Cantó, J., & Masciadri, E. 2002, A&A, 395, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raga, A. C., Noriega-Crespo, A., Lora, V., Stapelfeldt, K. R., & Carey, S. J. 2011, ApJ, 730, 17 [Google Scholar]
- Reipurth, B., Hartigan, P., Heathcote, S., Morse, J. A., & Bally, J. 1997, AJ, 114, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Rieger, F. M., & Duffy, P. 2006, ApJ, 652, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Rimmer, P. B., Herbst, E., Morata, O., & Roueff, E. 2012, A&A, 537, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlickeiser, R. 2002, Cosmic Ray Astrophysics (Berlin, Heidelberg: Springer-Verlag) [Google Scholar]
- Shimajiri, Y., Takahashi, S., Takakuwa, S., Saito, M., & Kawabe, R. 2008, ApJ, 683, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H., Adams, F. C., & Lizano, S. 1987, ARA&A, 25, 23 [Google Scholar]
- Shu, F., Shang, H., Glassgold, A. E., & Lee, T. 1997, Science, 277, 1475 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H., Galli, D., Lizano, S., & Cai, M. 2006, ApJ, 647, 382 [NASA ADS] [CrossRef] [Google Scholar]
- Skilling, J. 1975, MNRAS, 172, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Skilling, J., & Strong, A. W. 1976, A&A, 53, 253 [NASA ADS] [Google Scholar]
- Silk, J., & Norman, C. 1983, ApJ, 272, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Stahler, S. W., & Palla, F. 2005, in The Formation of Stars (Wiley-VCH), 475 [Google Scholar]
- Stone, E. C., Cummings, A. C., McDonald, F. B., et al. 2013, Science, 341, 150 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Strelnitskij, V. S. 1984, MNRAS, 207, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Swartz, W. E., Nisbet, J. S., & Green, A. E. S. 1971, J. Geophys. Res., 76, 8425 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Bachiller, R., Lefloch, B., et al. 2015, A&A, 573, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takayanagi, M. 1973, PASJ, 25, 327 [NASA ADS] [Google Scholar]
- Tatischeff, V., Duprat, J., & de Séréville, N. 2014, ApJ, 796, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Teşileanu, O., Massaglia, S., Mignone, A., Bodo, G., & Bacciotti, F. 2009, A&A, 507, 581 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teşileanu, O., Mignone, A., Massaglia, S., & Bacciotti, F. 2012, ApJ, 746, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Teşileanu, O., Matsakos, T., Massaglia, S., et al. 2014, A&A, 562, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tomida, M., Okuzumi, S., & Machida, M. N. 2015, ApJ, 801, 117 [NASA ADS] [CrossRef] [Google Scholar]
- van Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watson, A. M., & Stapelfeldt, K. R. 2004, ApJ, 602, 860 [NASA ADS] [CrossRef] [Google Scholar]
- Wootten, A. 1989, ApJ, 337, 858 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, H., & Lazarian, A. 2004, ApJ, 614, 757 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Alternative acceleration mechanisms
A.1. Shear acceleration at the jet-outflow interface
At the interface between the jet and the outflow, particles see two fluids moving at different velocities and they can gain energy by being scattered by magnetic field turbulence in the same manner as in the DSA process except that the up- and downstream media are replaced by the outer and inner shear flows. In order to establish which of these two mechanisms prevails, we compare the acceleration timescale due to DSA, tacc, given by the inverse of Eq. (5), and that due to shear acceleration, tshear. Following Rieger & Duffy (2006), tshear reads 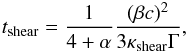 (A.1)where κshear = kshearκgal, with kshear = 0.01−1. The shear flow coefficient, Γ, reads (Earl et al. 1988)
(A.1)where κshear = kshearκgal, with kshear = 0.01−1. The shear flow coefficient, Γ, reads (Earl et al. 1988) 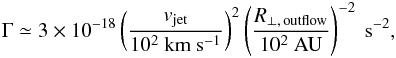 (A.2)where we assumed vjet ≫ voutflow and R⊥ , jet ≪ R⊥ , outflow. The parameter α comes from the assumption of momentum-dependent scattering time τ ∝ pα (Rieger & Duffy 2006). Using the three different trends for κgal described in Sect. 6.2, we find α = −2 for a constant diffusion coefficient at non-relativistic energies, α = −1 for the DR model, and α = −4 for the PD model. We note that in this last case, tshear → ∞ and the shear acceleration does not occur. We compute tacc for model
(A.2)where we assumed vjet ≫ voutflow and R⊥ , jet ≪ R⊥ , outflow. The parameter α comes from the assumption of momentum-dependent scattering time τ ∝ pα (Rieger & Duffy 2006). Using the three different trends for κgal described in Sect. 6.2, we find α = −2 for a constant diffusion coefficient at non-relativistic energies, α = −1 for the DR model, and α = −4 for the PD model. We note that in this last case, tshear → ∞ and the shear acceleration does not occur. We compute tacc for model  minimising tshear (by taking kshear = 1, vjet = 300 km s-1, and R⊥ , outflow = 103 AU), and we find tacc<tshear when E ≲ 100 GeV. At a greater distance from the protostar, DSA is even more favoured since
minimising tshear (by taking kshear = 1, vjet = 300 km s-1, and R⊥ , outflow = 103 AU), and we find tacc<tshear when E ≲ 100 GeV. At a greater distance from the protostar, DSA is even more favoured since 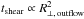 . However, in terms of geometrical efficiency, shear acceleration could be more efficient than DSA since, in principle, the former process can occur all along the jet-outflow contact surface while DSA takes place only at a shock surface.
. However, in terms of geometrical efficiency, shear acceleration could be more efficient than DSA since, in principle, the former process can occur all along the jet-outflow contact surface while DSA takes place only at a shock surface.
A.2. Acceleration by shocked background turbulence
The basic requirement for the acceleration mechanism described thus far assumes that the waves providing the scattering of the energetic particles are self-generated by the particles themselves. However, turbulence in protostars can be injected by other means since jets propagate into a turbulent environment (Giacalone & Jokipii 2007) and because the magneto-rotational instability in the accretion process induces turbulent motions (Hawley 2000). The level of background turbulence is poorly known, but it could overcome the turbulent fluctuations generated by any CR accelerated at a shock front. Finally, it might even be that background turbulence is required to trigger CR acceleration, which, if efficient enough, could enter the self-generated regime.
Background turbulence prevails over self-generated turbulence if 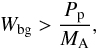 (A.3)where
(A.3)where 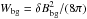 is the background magnetic pressure; Pp ∝ p4vf(p) is the particle pressure at momentum p, where p is related to the wavenumber k through the resonance condition k ∝ 1 /rL, rL being the Larmor radius (e.g. Drury et al. 1996); and
is the background magnetic pressure; Pp ∝ p4vf(p) is the particle pressure at momentum p, where p is related to the wavenumber k through the resonance condition k ∝ 1 /rL, rL being the Larmor radius (e.g. Drury et al. 1996); and 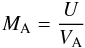 (A.4)is the Alfvénic Mach number. If a background CR distribution is present, then the condition becomes
(A.4)is the Alfvénic Mach number. If a background CR distribution is present, then the condition becomes ![\appendix \setcounter{section}{1} \begin{eqnarray} W_{\rm bg} > \frac{P_{\rm p}}{M_{\rm A}}\left[1-\frac{f_{\rm bg}(p)}{f(p)}\right]\cdot \end{eqnarray}](/articles/aa/full_html/2016/06/aa28221-16/aa28221-16-eq497.png) (A.5)If the above condition is fulfilled, DSA theory has to be applied with diffusion coefficients controlled by background turbulence, i.e. diffusion coefficients that deviate from the Bohm scaling given by Eq. (6).
(A.5)If the above condition is fulfilled, DSA theory has to be applied with diffusion coefficients controlled by background turbulence, i.e. diffusion coefficients that deviate from the Bohm scaling given by Eq. (6).
A.3. Turbulent second-order Fermi acceleration
Low-energy particles, in the non- or mildly-relativistic regime, can be subject to stochastic acceleration by the turbulence generated around the shock. The relative importance of stochastic acceleration and pitch-angle scattering is given by the ratio of the two corresponding timescales (Petrosian & Bykov 2008), namely 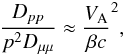 (A.6)where Dpp and Dμμ are the Fokker-Planck coefficients, μ being the cosine of the pitch angle. As discussed in Prantzos et al. (2011), stochastic acceleration is important only if it can overcome the particle losses given by Eq. (9). Second-order Fermi acceleration becomes important when β ~ VA/c, but for typical ranges of total hydrogen, ionisation fraction, and magnetic field strength in a protostar (Sect. 4), this acceleration mechanism turns out to be negligible.
(A.6)where Dpp and Dμμ are the Fokker-Planck coefficients, μ being the cosine of the pitch angle. As discussed in Prantzos et al. (2011), stochastic acceleration is important only if it can overcome the particle losses given by Eq. (9). Second-order Fermi acceleration becomes important when β ~ VA/c, but for typical ranges of total hydrogen, ionisation fraction, and magnetic field strength in a protostar (Sect. 4), this acceleration mechanism turns out to be negligible.
A.4. Magnetic reconnection
In more evolved protostars, magnetic reconnection is expected in coronal winds above the accretion disc and in accretion columns from the inner disc region to the central source. De Gouveia Dal Pino & Lazarian (2005) proposed that an acceleration mechanism similar to DSA takes place in reconnection sites. In fact, particles are expected to gain energy bouncing between converging flux tubes with oppositely directed magnetic fields. Through 3D magnetohydrodynamic numerical simulations, de Gouveia Dal Pino et al. (2014) found the formation of a hard proton power spectrum (∝E-1) for proton energies between about 10 GeV and 1 TeV.
Appendix B: Turbulent damping in jets
In a plasma, turbulent perturbations can either be damped by collisional or collisionless processes depending on the ratio between the wavelength of the perturbations to the proton mean free path due to collisions (see Yan & Lazarian 2004). Here, the resonant waves have a wavelength, λ, given by 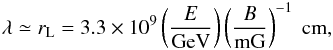 (B.1)while the proton mean free path, ℓmfp, reads
(B.1)while the proton mean free path, ℓmfp, reads 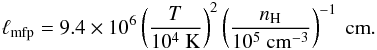 (B.2)The damping is in the collisional regime if λ>ℓmfp otherwise it is in the collisionless regime. In the conditions prevailing in stellar jets, particles with energies higher than a few MeV generate waves that are damped in the collisional regime. The dominant collisional damping process is due to ion-neutral collisions and the damping rate is given by Eq. (D.2). If E> 1 GeV, then Γ ≈ ωn(ω/ωi)2, while if E ∈ [ 3 × 10-3,1 ] GeV, we have Γ ≈ ωn. The damping scale is
(B.2)The damping is in the collisional regime if λ>ℓmfp otherwise it is in the collisionless regime. In the conditions prevailing in stellar jets, particles with energies higher than a few MeV generate waves that are damped in the collisional regime. The dominant collisional damping process is due to ion-neutral collisions and the damping rate is given by Eq. (D.2). If E> 1 GeV, then Γ ≈ ωn(ω/ωi)2, while if E ∈ [ 3 × 10-3,1 ] GeV, we have Γ ≈ ωn. The damping scale is 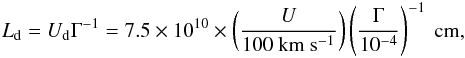 (B.3)where Ud is the downstream flow velocity. If we assume Γ = ωn, we obtain Ld ~ 4 × 10-4 AU, which is very small with respect to the distance between the internal shock in the jet and the termination shock. At high energies, although the damping is weaker and scales as (E/ GeV)-2, the damping scale is always much smaller than 1 AU, since the typical maximum energy found is of the order of 10 GeV.
(B.3)where Ud is the downstream flow velocity. If we assume Γ = ωn, we obtain Ld ~ 4 × 10-4 AU, which is very small with respect to the distance between the internal shock in the jet and the termination shock. At high energies, although the damping is weaker and scales as (E/ GeV)-2, the damping scale is always much smaller than 1 AU, since the typical maximum energy found is of the order of 10 GeV.
At low energies, the damping corresponds to very short wavelengths and occurs in the collisionless regime. The appropriate damping rate is given by Eq. (A.13) in Jean et al. (2009). It corresponds to the linear Landau damping rate, ΓLD, which is the resonant interaction of the waves with the background thermal plasma. The difficulty here is fixing a value of the wave pitch-angle Θ (the angle between the wave number and the magnetic field direction). Downstream of the shock, accounting for the magnetic field compression at the shock, this angle is likely large, close to 90°, and causes the damping to vanish. However, one can argue that the magnetic field keeps some obliquity downstream. For instance, starting with an upstream pitch angle of 45°, a compression of the transversal magnetic component produces a downstream pitch angle Θ = 63°, leading to ΓLD ≈ 30F(Θ) [ 5.4 × 10-4 + 0.8G(Θ) ] s-1, with F(Θ) ≈ 0.17 and G(Θ) ≈ 1.17, respectively. It follows that the damping length is very small as before, but it increases rapidly for Θ → 90° or 0°. Nevertheless, these cases are likely marginal for our modelling and we assume that waves are also rapidly damped behind the shock in the collisionless regime.
Appendix C: Collisionless character of the shocks and thermal equilibration
The collision time between protons and electrons and the gyro-period have to be compared in order to determine whether a shock is collisional or collisionless. Equivalently, the proton-electron collision length (λc) can be compared with the Larmor radius (rL,th) of a thermal particle. If λc>rL,th, then the shock is collisionless and it is mediated by magnetic field rather than by collisions. In this case the shock can accelerate thermal plasma particles. Conversely, if λc<rL,th, then the shock is collisional and it can accelerate particles only if these are already accelerated in the pre-shocked medium and if magnetic fields are also involved.
The proton-electron collision length reads 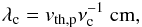 (C.1)where vth,p is the proton thermal speed and νc the proton-electron collision frequency. These quantities are given by
(C.1)where vth,p is the proton thermal speed and νc the proton-electron collision frequency. These quantities are given by 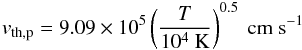 (C.2)and
(C.2)and 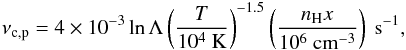 (C.3)where lnΛ ~ 20 is the Coulomb logarithm. The Larmor radius for a proton reads
(C.3)where lnΛ ~ 20 is the Coulomb logarithm. The Larmor radius for a proton reads 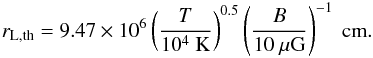 (C.4)Then a shock is collisional if
(C.4)Then a shock is collisional if 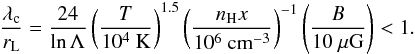 (C.5)Using the values in Table 1, it is possible to verify that shocks both in accretion flows and jets are collisionless.
(C.5)Using the values in Table 1, it is possible to verify that shocks both in accretion flows and jets are collisionless.
Because collisionless shocks are present, we have to justify the assumption of equal temperature downstream in our calculation (Tp,d = Te,d = T). In fact, since recurrent shocks spaced of about 100 AU are observed along the jets, the temperature T entering the equations in Sect. 2.2 is the upstream temperature during the passage of the first shock, and the downstream temperature for the following shocks.
The temperature of a species s is proportional to its mass and downstream reads 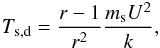 (C.6)where k is the Boltzmann constant and s = p,e. The thermal equilibrium between protons and electrons that have different downstream temperatures is reached after a time teq given by
(C.6)where k is the Boltzmann constant and s = p,e. The thermal equilibrium between protons and electrons that have different downstream temperatures is reached after a time teq given by 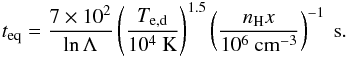 (C.7)This is the time needed to balance Te and Tp and it has to be compared with the time between the passage of two consecutive shocks, Δtsh, which reads
(C.7)This is the time needed to balance Te and Tp and it has to be compared with the time between the passage of two consecutive shocks, Δtsh, which reads 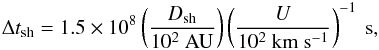 (C.8)Dsh being the distance between two successive shocks. If teq< Δtsh, then protons and electrons reach the same temperature before another shock arrives. It is straightforward to verify that the last inequality is always verified for the values in Table 1 assuming that shocks in jets are separated by about 100 AU. This confirms the correctness of our hypothesis, and so we can keep using the same temperature for protons and electrons for any shock, the latter being observable.
(C.8)Dsh being the distance between two successive shocks. If teq< Δtsh, then protons and electrons reach the same temperature before another shock arrives. It is straightforward to verify that the last inequality is always verified for the values in Table 1 assuming that shocks in jets are separated by about 100 AU. This confirms the correctness of our hypothesis, and so we can keep using the same temperature for protons and electrons for any shock, the latter being observable.
Appendix D: Evaluation of Edamp
Equation (29) in Drury et al. (1996), assuming the shock velocity to be much higher than the Alfvén speed, gives 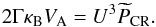 (D.1)The wave damping rate, Γ, reads (Drury et al. 1996)
(D.1)The wave damping rate, Γ, reads (Drury et al. 1996) 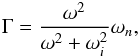 (D.2)with ωn = nH(1−x) ⟨ σv ⟩ and ωi = nHx ⟨ σv ⟩. The average value of the product between the charge exchange cross section and the collision velocity, ⟨ σv ⟩, is given by Kulsrud & Cesarsky (1971)
(D.2)with ωn = nH(1−x) ⟨ σv ⟩ and ωi = nHx ⟨ σv ⟩. The average value of the product between the charge exchange cross section and the collision velocity, ⟨ σv ⟩, is given by Kulsrud & Cesarsky (1971) 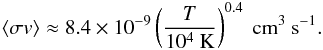 (D.3)For resonant waves, ω is given by the ratio between the Alfvén speed and the particle’s gyrofrequency
(D.3)For resonant waves, ω is given by the ratio between the Alfvén speed and the particle’s gyrofrequency 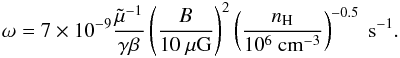 (D.4)Equation (15) is found by substituting Eqs. (D.2)–(D.4) in Eq. (D.1).
(D.4)Equation (15) is found by substituting Eqs. (D.2)–(D.4) in Eq. (D.1).
Appendix E: Justification for the steady-state model
In order to justify the steady-state hypothesis in Sect. 6.2, we have to verify whether tesc,d (Eq. (43)) is lower than the lifetime tlife (Eq. (52)) of a bow shock. Here we consider two sources with differing distances of the reverse bow-shock, DrBS: HH 111 and DG Tau with DrBS = 7 × 104 AU and DrBS = 1.8 × 103 AU, respectively.
E.1. HH 111
Morse et al. (1993) states that the upper limit to the shock velocity at the apex of the bow shock V in HH 111 is vsh = 100 km s-1, while the jet velocity is vjet = 400 km s-1. Then, the shock velocity in the shock reference frame is U = 300 km s-1 and tlife ≃ 835 yr. We assume the hot spot radius to be of the order of the transverse radius of knot V, which is about 2 × 103 AU (Reipurth et al. 1997), then tadv (Eq. (44)) is about 40 yr. Since tdiff ≪ tadv at any energy, then tesc,d ≃ tdiff ≪ tlife and we can use the steady-state approximation.
E.2. DG Tau
Eislöffel & Mundt (1998) estimates that knot C, which corresponds to the bow shock, was ejected in 1936, so tlife ≃ 80 yr. In the same paper they compute vjet ≃ 200 km s-1. Hartigan et al. (1994) calculate vsh ≃ 100 km s-1, then U ≃ 100 km s-1. The hot spot radius is about 1300 AU (Ainsworth et al. 2014) and tadv ≃ tlife. As for HH 111, tdiff ≪ tadv, the steady-state approximation is still marginally valid for this source.
All Tables
Parameters to calculate the particle distribution f(p) in the case of parallel shocks for κu = κB and η = 10-5.
All Figures
 |
Fig. 1 Sketch of the protostar configuration employed in the paper. Accretion flow, jet, and shock velocities (vacc, vjet, and vsh, respectively) are in the observer reference frame. Shock and transverse radii are labelled Rsh and R⊥, respectively. Bow shock, reverse bow shock, bow wings, and working surface are labelled BS, rBS, BW, and ws, respectively. The shaded areas show the regions where CR acceleration takes place (Sect. 2.1) and where turbulence is damped and particle propagation occurs (Sect. 6). The dot-filled region corresponds to the hot spot region (Sect. 6.2). |
| In the text | |
 |
Fig. 2 Case of a parallel shock in jets: ionisation fraction, x, versus total hydrogen density, nH, for different combinations of initial parameters. The magnetic field strength varies from 50 μG to 1 mG (from left to right), while the shock velocity varies from 40 to 160 km s-1 (from top to bottom). The temperature is assumed equal to 104 K and the shock distance from the protostar and its transverse radius are Rsh = 100 AU and R⊥ = 10 AU, respectively. The colour map shows the values of Emax in the case of a parallel shock when the conditions imposed by Eqs. (4) and (18) are simultaneously satisfied. Cyan contours delimit the regions where Emax reaches its maximum asymptotic value shown in GeV in each subplot. Vertically hatched regions refer to combinations of parameters corresponding to strong wave damping (R< 1). The two solid white stars in the upper left and lower right plots show the values of nH and x considered for the evaluation of the emerging spectra (models |
| In the text | |
 |
Fig. 3 Case of parallel (left) and perpendicular (right) shocks on protostellar surfaces: ionisation fraction, x, versus magnetic field strength, B, for the parameters specified in the third line of Table 1 (Rsh = 2 × 10-2 AU). The colour map shows the values of Emax when the conditions imposed by Eqs. (4) and (18) are simultaneously verified. The cyan contour delimits the region where Emax gets its maximum asymptotic value shown in GeV in each subplot. Vertically hatched regions refer to combinations of parameters corresponding to strong wave damping (R< 1). The solid white star in the left panel shows the values of B and x considered for the evaluation of the emerging spectrum (models |
| In the text | |
 |
Fig. 4 Emerging spectra of the shock-accelerated protons (solid lines) for the models described in the text. The dashed lines represent the corresponding Maxwellian distributions of the thermal protons. |
| In the text | |
 |
Fig. 5 Same as Fig. 2, but for an upstream diffusion coefficient κu = 30 κB for a parallel shock. |
| In the text | |
 |
Fig. 6 Maximum energy of accelerated protons as a function of (B/δB)2 in the case of parallel shocks for U = 160 km s-1, nH = 6 × 105 cm-3, and x = 0.6 with B = 50 μG (dotted line), 500 μG (dashed line), and 1 mG (solid line). |
| In the text | |
 |
Fig. 7 Same as Fig. 2, but for a temperature of 105 K. |
| In the text | |
 |
Fig. 8 Sonic Mach number (upper panel), normalised CR pressure (middle panel), compression ratio and factor proportional both to Eesc,d and Eloss for parallel shocks (grey and black lines, respectively, in lower panel) as a function of the temperature for x = 0.3, η = 10-5; U = 40 km s-1 (solid lines), U = 80 km s-1 (dashed lines), U = 120 km s-1 (dotted lines), and U = 160 km s-1 (dash-dotted lines). |
| In the text | |
 |
Fig. 9 Propagated spectra in the absence of magnetic turbulence for models |
| In the text | |
 |
Fig. 10 Spectra of accelerated protons (blue) and secondary electrons (red) for model |
| In the text | |
 |
Fig. 11 Ionisation rate at the shock surface in a jet as a function of the molecular hydrogen column density for models |
| In the text | |
 |
Fig. 12 CR ionisation rate profile in a protostellar disc according to model |
| In the text | |
 |
Fig. 13 Spectral energy flux density as a function of the frequency. GMRT and EVLA observations (yellow solid circles) from Ainsworth et al. (2014) and Lynch et al. (2013), respectively, are shown together with their fit (yellow dashed line) predicting a synchrotron spectral index of −0.89 ± 0.07 (Ainsworth et al. 2014). The two black shaded regions show the result of our modelling using two different shock velocities with respect to the upstream flow (U = 100 km s-1 and 200 km s-1) and their widths refer to an assumed error of 30% on the value of the hot spot radius, the central value (RHS = 1300 AU, Ainsworth et al. 2014) pinpointed by the white dotted lines. The green shaded areas show the two LOFAR bands (LBA=low band antenna; HBA = high band antenna), and their lower boundary in Sν corresponds to the sensitivity limit using its most extended configuration (van Haarlem et al. 2013). |
| In the text | |
 |
Fig. 14 Dust and gas temperature (solid and dashed red lines, respectively) as a function of the distance from the protostar L1157. The plot also shows the ionisation rate of interstellar CRs (dash-dotted green line), of CRs coming from the hot spot (dashed green line), and the total value (solid green line). |
| In the text | |
 |
Fig. 15 Ionisation rate (upper panel) and temperatures of gas and dust (lower panel) as a function of the distance from the protostar OMC-2 FIR 4. Observational estimates of ζ and Tg (black solid circles and squares, respectively; Ceccarelli et al. 2014) are compared to the results from the modelling described in Sect. 8.3 (green and red solid lines). The green and red shaded areas encompass the range of ζ and Tg by assuming a dilution factor R-1 (purely diffusive propagation) and R-2 (free-streaming propagation). The green dash-dotted and dashed lines show the interstellar CR ionisation rate assuming a spectrum similar to that from Voyager 1 (Stone et al. 2013) and an enhanced CR proton flux (see model H in Ivlev et al. 2015). The red dashed line shows the trend of the dust temperature (Masunaga & Inutsuka 2000; Crimier et al. 2009). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


