| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 27 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201527685 | |
| Published online | 10 May 2016 | |
Interstellar fullerene compounds and diffuse interstellar bands
1
UPMC Univ. Paris 06, UMR 7095, Institut d’Astrophysique de
Paris,
75014
Paris,
France
e-mail: omont@iap.fr
2
CNRS, UMR 7095, Institut d’Astrophysique de Paris,
75014
Paris,
France
Received:
3
November
2015
Accepted:
24
February
2016
Recently, the presence of fullerenes in the interstellar medium (ISM) has been confirmed and new findings suggest that these fullerenes may possibly form from polycyclic aromatic hydrocarbons (PAHs) in the ISM. Moreover, the first confirmed identification of two strong diffuse interstellar bands (DIBs) with the fullerene, C60+, connects the long standing suggestion that various fullerenes could be DIB carriers. These new discoveries justify reassessing the overall importance of interstellar fullerene compounds, including fullerenes of various sizes with endohedral or exohedral inclusions and heterofullerenes (EEHFs). The phenomenology of fullerene compounds is complex. In addition to fullerene formation in grain shattering, fullerene formation from fully dehydrogenated PAHs in diffuse interstellar clouds could perhaps transform a significant percentage of the tail of low-mass PAH distribution into fullerenes including EEHFs. But many uncertain processes make it extremely difficult to assess their expected abundance, composition and size distribution, except for the substantial abundance measured for C60+. EEHFs share many properties with pure fullerenes, such as C60, as regards stability, formation/destruction and chemical processes, as well as many basic spectral features. Because DIBs are ubiquitous in all lines of sight in the ISM, we address several questions about the interstellar importance of various EEHFs, especially as possible carriers of diffuse interstellar bands. Specifically, we discuss basic interstellar properties and the likely contributions of fullerenes of various sizes and their charged counterparts such as C60+, and then in turn: 1) metallofullerenes; 2) heterofullerenes; 3) fulleranes; 4) fullerene-PAH compounds; 5) H2@C60. From this reassessment of the literature and from combining it with known DIB line identifications, we conclude that the general landscape of interstellar fullerene compounds is probably much richer than heretofore realized. EEHFs, together with pure fullerenes of various sizes, have many properties necessary to be suitably carriers of DIBs: carbonaceous nature; stability and resilience in the harsh conditions of the ISM; existing with various heteroatoms and ionization states; relatively easy formation; few stable isomers; spectral lines in the right spectral range; various and complex energy internal conversion; rich Jahn-Teller fine structure. This is supported by the first identification of a DIB carrier as C60+. Unfortunately, the lack of any precise information about the complex optical spectra of EEHFs and most pure fullerenes other than C60 and about their interstellar abundances still precludes definitive assessment of the importance of fullerene compounds as DIB carriers. Their compounds could significantly contribute to DIBs, but it still seems difficult that they are the only important DIB carriers. Regardless, DIBs appear as the most promising way of tracing the interstellar abundances of various fullerene compounds if the breakthrough in identifying C60+ as a DIB carrier can be extended to more spectral features through systematic studies of their laboratory gas-phase spectroscopy.
Key words: astrochemistry / ISM: molecules / ISM: lines and bands / dust, extinction / line: identification / line: profiles
© ESO, 2016
1. Introduction
Since the initial observation of the diffuse interstellar bands (DIBs; Heger 1922) with their confirmation and the early guesses as to their origin (Merrill 1934, 1936; see e.g. Herbig 1975; Snow 2014, for the history of DIB studies), identification of their carriers has remained one of the most puzzling problems in astrophysics (see e.g. extensive reviews by Herbig 1995; Jenniskens & Desert 1994; Snow & McCall 2006; Cox 2006, 2011, 2015; Sarre 2006, 2008; Snow 2014, and the proceedings of two whole symposia devoted to DIBs: Tielens & Snow 1995; and especially Cami & Cox 2014). The strongest bands are amazingly conspicuous, absorbing up to 10−30% of the interstellar radiation at their central wavelengths in sight lines with high extinction (Fig. 3.2a). They are ubiquitous, not only along lines of sight in the Galactic disk, but also at surprisingly high galactic latitude and in other galaxies. With the current survey sensitivity, the number of bands confirmed as DIBs has now increased to about 500 (see e.g. Hobbs et al. 2009, 2008 and Fig. 6). This sensitivity, reaching absorption depths of less than one percent, approaches the confusion limit in the most crowded spectral regions.
Among the most recent developments, note: 1) the extension of DIB detection to the near-infrared (Joblin et al. 1990; Geballe et al. 2011, 2014; Cox et al. 2014; Rawlings et al. 2014; Hamano et al. 2015; Zasowski et al. 2015); 2) the detection of DIBs along millions of line of sight in sky surveys (e.g. Munari et al. 2008; Yuan & Liu 2012; Kos et al. 2013, 2014; Lan et al. 2015a,b; Zasowski et al. 2015; Baron et al. 2015a,b; Puspitarini et al. 2015); 3) the multiplication of extragalactic DIB detections (see e.g. Cordiner 2014; Welty et al. 2014, and references therein); and 4) the confirmation of the first DIB-carrier identification as C (Campbell et al. 2015; Walker et al. 2015).
(Campbell et al. 2015; Walker et al. 2015).
There is more or less general agreement that DIB carriers are suspected of being large carbon-based molecules (with ≳10−100 atoms) in the gas phase, although other possibilities remain open (see e.g. Snow 1995, 2014). In addition, the absence of perfect intensity correlation between the strongest DIBs means that most of them need independent carriers (e.g. Herbig 1995; Cami et al. 1997; Snow 2001, 2014; Tielens 2014). The three different allotropic forms of known interstellar carbonaceous particles are thus the most popular candidates for DIB carriers.
-
1)
Linear carbon chains, which are known in dense molecular clouds with Cn skeleton and n ≲ 10, have been repeatedly proposed as DIB carriers (see e.g. Thaddeus 1995; Snow 1995; Maier et al. 2004; Zack & Maier 2014); for example, C
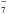 was proposed as the carrier of several DIBs by Tulej et al. (1998), but rejected by McCall et al. (2001). Their stability is well confirmed (see e.g. Jin et al.
2009). However, one may raise questions
about the survival for long of small carbon chains against photo-dissociation in the
diffuse medium (see e.g. Tielens 2014).
Nevertheless, long chains remain key candidates for DIB carriers. Although no
completely convincing mechanism has been proposed for their gas phase synthesis in
diffuse clouds and they do not form efficiently in graphite laser ablation
experiments, they could be formed as fragmentation products of photo-processed grain
mantles after high energy cosmic ray bombardment or grain collisions.
was proposed as the carrier of several DIBs by Tulej et al. (1998), but rejected by McCall et al. (2001). Their stability is well confirmed (see e.g. Jin et al.
2009). However, one may raise questions
about the survival for long of small carbon chains against photo-dissociation in the
diffuse medium (see e.g. Tielens 2014).
Nevertheless, long chains remain key candidates for DIB carriers. Although no
completely convincing mechanism has been proposed for their gas phase synthesis in
diffuse clouds and they do not form efficiently in graphite laser ablation
experiments, they could be formed as fragmentation products of photo-processed grain
mantles after high energy cosmic ray bombardment or grain collisions. -
2)
Graphenic compounds of various size contain a substantial part of interstellar carbon. Besides larger graphitic dust grains, polycyclic aromatic hydrocarbons (PAHs) appear as the dominant carbonaceous particles, with NC ~ 20 − 100. This is evidenced by their strong 6−12 μm IR emission bands which require up to ~10% of interstellar carbon. They have been proposed as the best potential carriers for DIBs (Van der Zwet & Allamandola 1985; Léger & d’Hendecourt 1985; Crawford et al. 1985 and e.g. Salama 1996, 2011; Salama & Ehrenfreund 2014); better than their slightly larger avatars of PAH-clusters (see e.g. Montillaud & Joblin 2014) or flakes of hydrogenated amorphous carbon (HAC; e.g. Jones 2014, 2015). But all attempts to identify a single DIB with a known band of a defined PAH have failed up to now (see e.g. Salama et al. 2011; Steglich et al. 2011; Salama & Ehrenfreund 2014). However, the variety of their possible ionized and dehydrogenated forms is far from being fully explored experimentally or theoretically. The likelihood of PAHs as carriers of major DIBs also suffers from the very large variety of their possible sizes, shapes and isomers (see e.g. Gredel et al. 2011), lacking the general specificity of DIBs. However, this large variety could be mitigated by the trend of interstellar PAHs to naturally evolve toward a few most stable forms (Tielens 2005, 2014; Andrews et al. 2015).
-
3)
Fullerenes, since their discovery, have also been advocated as very attractive candidates for DIB carriers (e.g. Kroto 1988, 1989; Léger et al. 1988b; Kroto & Jura 1992). The identification proposed by Foing & Ehrenfreund (1994, 1997) of two strong DIBs with the near-IR doublet of the spectrum of C
 measured by Fulara et al. (1993a; see also Kato
et al. 1991; Gasyna et al. 1992; Fig. 3), seemed to confirm this suggestion.
Although the impact of such a breakthrough had been tempered until very recently by
the absence of gas-phase spectroscopy of C
measured by Fulara et al. (1993a; see also Kato
et al. 1991; Gasyna et al. 1992; Fig. 3), seemed to confirm this suggestion.
Although the impact of such a breakthrough had been tempered until very recently by
the absence of gas-phase spectroscopy of C ,
it is now fully confirmed by the brilliant experiment of Campbell et al. (2015). With this first identification of a DIB
carrier, fullerene compounds clearly appear as viable candidates for carriers of other
DIBs. However, despite their many attractive features, such as stability, spectral
specificity, various forms (size, ionization state, heteroatoms, endohedral and
exohedral compounds), the low abundance of C60 made it difficult for various fullerenes to
produce strong enough DIBs (e.g. Cami 2014;
Sect. 8.2).
,
it is now fully confirmed by the brilliant experiment of Campbell et al. (2015). With this first identification of a DIB
carrier, fullerene compounds clearly appear as viable candidates for carriers of other
DIBs. However, despite their many attractive features, such as stability, spectral
specificity, various forms (size, ionization state, heteroatoms, endohedral and
exohedral compounds), the low abundance of C60 made it difficult for various fullerenes to
produce strong enough DIBs (e.g. Cami 2014;
Sect. 8.2).
 in interstellar diffuse clouds (Sect. 2.4) justify a general reappraisal of various fullerene compounds as DIB-carrier candidates. In addition to the strength of the above arguments favouring fullerenes, this is further supported by several recent results including: models and laboratory demonstration of C60 formation from dehydrogenated PAHs (Zhen et al. 2014; Berné et al. 2015a); and experiments confirming the easy formation of C60 endometals (Dunk et al. 2013, 2014) and of PAH-fullerene dyads (Dunk et al. 2013).
in interstellar diffuse clouds (Sect. 2.4) justify a general reappraisal of various fullerene compounds as DIB-carrier candidates. In addition to the strength of the above arguments favouring fullerenes, this is further supported by several recent results including: models and laboratory demonstration of C60 formation from dehydrogenated PAHs (Zhen et al. 2014; Berné et al. 2015a); and experiments confirming the easy formation of C60 endometals (Dunk et al. 2013, 2014) and of PAH-fullerene dyads (Dunk et al. 2013).
The paper is organized as follows. We first briefly review the main properties of pure fullerenes relevant for their interstellar behaviour and DIBs. Five other main classes of fullerene compounds are then discussed: 1) metallofullerenes, especially endohedral ones M@C60; 2) heterofullerenes (mostly C59N and C59Si); 3) fulleranes; 4) PAH-fullerene associations and 5) H2@C60. Finally we reconsider the idea that fullerene compounds might be carriers of some DIBs.
 |
Fig. 1 a) Adapted from Fig. 5 of Pennington & Stenger (1996). Schematic diagram of basic electronic shells of C60 in Hückel approximation and resulting first excited states of C60 (E< ~ 3 eV), singlet (see e.g. Sassara et al. 1997, 2001) and triplet. b) From Table 6 of Bendale et al. (1992). Schematic diagram of the first electronic levels of C |
2. Facts and questions about interstellar fullerenes
2.1. Energy levels and optical properties of C60 and its ions
2.1.1. C60
The electronic level structure of the 60 π electrons of C60 in the icosahedral symmetry Ih (see e.g. Dresselhaus et al. 1996) is schematized in Fig. 1. With its highest occupied molecular orbital, HOMO, made of closed shells (...4g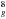 7h
7h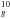 4h
4h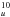 ), the ground state is spin singlet S0. There is a significant gap between the energies of the first triplet and singlet excited states, ~1.6 and ~1.9 eV, respectively (e.g. Cavar et al. 2005). All optical transitions from the ground state to triplet states are forbidden, as well as to the first five singlet excited states for symmetry reasons. It also occurs that the first allowed transitions at 4024 Å and 3980 Å are somewhat weak (f ~ 0.015), so that all strong transitions are located in the UV (Sassara et al. 2001; Leach et al. 1992). The strength of most electronic transitions of fullerenes are drastically reduced by screening by the π electron shell of the cage (Westin & Rosén 1993; Dresselhaus et al. 1996).
), the ground state is spin singlet S0. There is a significant gap between the energies of the first triplet and singlet excited states, ~1.6 and ~1.9 eV, respectively (e.g. Cavar et al. 2005). All optical transitions from the ground state to triplet states are forbidden, as well as to the first five singlet excited states for symmetry reasons. It also occurs that the first allowed transitions at 4024 Å and 3980 Å are somewhat weak (f ~ 0.015), so that all strong transitions are located in the UV (Sassara et al. 2001; Leach et al. 1992). The strength of most electronic transitions of fullerenes are drastically reduced by screening by the π electron shell of the cage (Westin & Rosén 1993; Dresselhaus et al. 1996).
 |
Fig. 2 Adapted from Fig. 5 of Stepanov (2002). Flow chart of the energy internal conversion in C60 with the characteristic timescales and rates: τ1< ~ 20 ps is the time to reach the S1,2,3 states from the initially excited state Sn, by electronic to vibrational internal energy conversion; τ2 ≈ 1 ns reflects the intersystem crossing time; k3 ≈ 0.3−1 μs-1 is the slow decay rate through fluorescence directly to the ground state S0; τ4 ≈ 100 μs to 1 ms or shorter is the radiationless decay from the lowest triplet state to the ground state; kPF is the rate of Poincaré fluorescence from the triplet state discussed in Appendix G; and τ5, possibly >~100 s, is the very slow decay of vibrational excitation through infrared emission. Of course, as long as there is no emission of visible or infrared photons, the total energy, E(Sn), is conserved; when the excitation is transferred to the electronic state i, the energy difference E(Sn) − Ei appears as vibrational energy. |
However, Herzberg-Teller coupling with vibrational states (plus complex Jahn-Teller effect, Chancey & O’Brien 1997) allows spectacular weak absorption and fluorescence emission in the forbidden transitions from the first singlet excited states; however, its very rich energy structure is extremely difficult to disentangle (Sassara et al. 1997; Orlandi & Negri 2002; Cavar et al. 2005), see Appendix E.
The wave functions of most of all these electronic orbitals are highly concentrated in a thin shell about the cage, as well accounted for in the “jellium” model, for example, where the π electrons are confined in a deep potential well (e.g. Rüdel et al. 2002; Chakraborty et al. 2008). However, close to the ionization limit, there is a series of additional more extended diffuse states studied using scanning tunnelling spectroscopy by Feng et al. (2008) and multi-photon photoionization by Johansson & Campbell (2013). They are similar to, but somewhat different from atomic Rydberg states, corresponding to an ionized cage such as C with one orbiting electron. Most of them have the classical binding energy close to 13.6/n2 eV with n ≥ 3, but the most interesting ones, the lowest s and p states, have an energy significantly lower by ~1 eV (e.g. Feng et al. 2008; Johansson & Campbell 2013). They are often called SAMOs (superatom molecular orbitals). For pure fullerenes, their energy is too high to exhibit absorption at visible wavelengths.
with one orbiting electron. Most of them have the classical binding energy close to 13.6/n2 eV with n ≥ 3, but the most interesting ones, the lowest s and p states, have an energy significantly lower by ~1 eV (e.g. Feng et al. 2008; Johansson & Campbell 2013). They are often called SAMOs (superatom molecular orbitals). For pure fullerenes, their energy is too high to exhibit absorption at visible wavelengths.
C60 has a large number (174) of vibrational modes. Most of them are highly degenerate, leaving only 46 different frequencies. Only four transitions are infrared active with t1u symmetry and wavelengths equal to 7.0, 8.5, 17.4 and 18.9 μm (Krätschmer et al. 1990).
The fluorescence and phosphorescence of C60 have been extensively studied and are well understood (e.g. Dresselhaus et al. 1996; Weisman 1999; Sassara et al. 1997; Salazar et al. 1997; Stepanov et al. 2002; Heden et al. 2003; Echt et al. 2005; Cavar et al. 2005; and Appendix G). The corresponding steps of internal energy conversion following the absorption of a UV photon are schematized in Fig. 2: 1) a very fast (≤20 ps) transfer first to adjacent electronic levels and then cascade to the lowest electronic excited singlets S1, S2, S3..., by internal conversion from electronic to vibration energy (IEC); 2) very low yield (a few 10-4) of radiative fluorescence from S123 to S0, but fast (nanosecond), almost complete IEC transfer to the triplet state; long lifetime of this triplet state; followed mainly by radiationless transfer to the ground state S0 with IEC conversion of the triplet electronic energy to vibrations. 3) Besides negligible phosphorescence, a significant decay mode of the triplet state should be delayed fluorescence (“Poincaré fluorescence”; Léger et al. 1988a) with thermal return from T1 to S123 electronic states. This is discussed in Appendix G for various fullerene compounds. It seems that the precise contribution of the Poincaré fluorescence to the cooling of C60 compounds remains somewhat uncertain, albeit significant, in interstellar conditions. 4) Finally, in isolated molecules, the rest of the vibrational energy should be emitted in the C60 infrared modes. However, because of the total transition weakness of these modes, the overall time constant τIR for such infrared gas-phase cooling should be two orders of magnitude longer than the time given by Léger et al. (1989) for typical PAHs (Sect. 6.2) and thus possibly exceed 100 s.
2.1.2. C60 ions
The excited level structure of the C60 ions, such as C (and C
(and C , see Appendix F), is substantially different because their ground state is not a closed shell. Because of this, they have more allowed transitions in the visible and even near-infrared range. However, their excited states remain more undetermined than those of C60, especially because of the Jahn-Teller effect.
, see Appendix F), is substantially different because their ground state is not a closed shell. Because of this, they have more allowed transitions in the visible and even near-infrared range. However, their excited states remain more undetermined than those of C60, especially because of the Jahn-Teller effect.
Good-quality optical-near-IR absorption spectra of C and C
and C in neon matrices were first obtained and disentangled by Fulara et al. (1993a) (see also Kato et al. 1991; Gasyna et al. 1992; Kern et al. 2014). Both ions show strong features around 1 μm. Recently, the sophisticated experiment of Campbell et al. (2015) has provided accurate data, devoid of matrix effects, for the prominent double band at 9577.56 and 9632.76 Å of C
in neon matrices were first obtained and disentangled by Fulara et al. (1993a) (see also Kato et al. 1991; Gasyna et al. 1992; Kern et al. 2014). Both ions show strong features around 1 μm. Recently, the sophisticated experiment of Campbell et al. (2015) has provided accurate data, devoid of matrix effects, for the prominent double band at 9577.56 and 9632.76 Å of C and its vibronic satellites (Fig. 3). While Campbell et al. cannot measure accurate band strengths, improved f-values, for the corresponding bands in an Ne matrix, are provided by Strelnikov et al. (2015), namely f = 0.015 ± 0.005 for the 966 nm absorption and f = 0.01 ± 0.003 for the 958 nm absorption. However, matrix effects could substantially affect line strengths, as possibly seen from the large difference between the line ratios measured by Strelnikov et al. in matrix and Campbell et al. in free C
and its vibronic satellites (Fig. 3). While Campbell et al. cannot measure accurate band strengths, improved f-values, for the corresponding bands in an Ne matrix, are provided by Strelnikov et al. (2015), namely f = 0.015 ± 0.005 for the 966 nm absorption and f = 0.01 ± 0.003 for the 958 nm absorption. However, matrix effects could substantially affect line strengths, as possibly seen from the large difference between the line ratios measured by Strelnikov et al. in matrix and Campbell et al. in free C molecules, and we note that Walker et al. (2015) favour twice higher f-values.
molecules, and we note that Walker et al. (2015) favour twice higher f-values.
The electronic energy levels and the visible spectrum of C were theoretically analyzed by Bendale et al. (1992) (see Fig. 1). They found that the ground state of the ion distorts from Ih symmetry preferentially to D5d symmetry (see Campbell et al. 2015) (however, the energy of the ground level of the isomer with D3d symmetry is only slightly higher). Bendale et al. identified the strong ~1 μm transition as connecting the ground state 2A1u, corresponding to the state 7h
were theoretically analyzed by Bendale et al. (1992) (see Fig. 1). They found that the ground state of the ion distorts from Ih symmetry preferentially to D5d symmetry (see Campbell et al. 2015) (however, the energy of the ground level of the isomer with D3d symmetry is only slightly higher). Bendale et al. identified the strong ~1 μm transition as connecting the ground state 2A1u, corresponding to the state 7h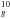 4h
4h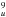 in the Ih symmetry, to one 2E1g excited state corresponding to the Ih state 7h
in the Ih symmetry, to one 2E1g excited state corresponding to the Ih state 7h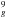 4h
4h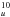 (Fig. 1). It is possible that the splitting of 60 cm-1 between the 9577 and 9633 Å components is due to the Jahn-Teller effect, but it does not seem to have been determined yet. All other visible features derived in Table 6 of Bendale et al. (1992; Fig. 1) are significantly weaker, in agreement with the absorption spectrum of Fulara et al. (1993a). The SAMO states of C
(Fig. 1). It is possible that the splitting of 60 cm-1 between the 9577 and 9633 Å components is due to the Jahn-Teller effect, but it does not seem to have been determined yet. All other visible features derived in Table 6 of Bendale et al. (1992; Fig. 1) are significantly weaker, in agreement with the absorption spectrum of Fulara et al. (1993a). The SAMO states of C do not seem to have been studied yet. However, they should not appear in the visible range.
do not seem to have been studied yet. However, they should not appear in the visible range.
Most vibrational frequencies of C and C
and C remain close to, but often significantly different from those of C60. However, Jahn-Teller effect may break degeneracies and introduce new active vibration modes (see e.g. Kern et al. 2013; Berné et al. 2013).
remain close to, but often significantly different from those of C60. However, Jahn-Teller effect may break degeneracies and introduce new active vibration modes (see e.g. Kern et al. 2013; Berné et al. 2013).
Only a few low doublets of C are connected to the ground doublet by an allowed transition (Table 6 of Bendale et al. 1992). In the whole near-infrared and visible range, the strongest transition by far from the ground level corresponds to the bands at 9577/9633 Å towards the low lying excited doublet 2E1g. This level could perhaps carry a marginal (Poincaré) fluorescence (Appendix G).
are connected to the ground doublet by an allowed transition (Table 6 of Bendale et al. 1992). In the whole near-infrared and visible range, the strongest transition by far from the ground level corresponds to the bands at 9577/9633 Å towards the low lying excited doublet 2E1g. This level could perhaps carry a marginal (Poincaré) fluorescence (Appendix G).
 |
Fig. 3 Successive key steps in identification of strong diffuse interstellar bands of C |
2.2. C70 and other fullerenes
Basing the analysis of the optical properties of fullerenes on those of C60 may be misleading because its high symmetry relative to other fullerenes makes its spectrum somewhat unique. The next most stable fullerene, C70, with a lower symmetry, represents a more realistic model for the intricate details of the electronic spectroscopy. While its strongest absorption transitions are also located in the UV, it shows a significantly stronger absorption in the visible than C60. It seems that only a part of its rich visible absorption is identified well, except in the red where a weak allowed transition coexists with Herzberg-Teller bands (Orlandi & Negri 2002; Scuseria 1991).
From the original discovery experiment (Kroto et al. 1985), it is well known that a whole series of fullerene cages C2n generally form together with C60 in various experiments producing fullerenes (see e.g. Dunk et al. 2012; and Zhang et al. 2013, for updated references). The general prominence of even numbers of carbon atoms, NC, and the more or less specific prominence of C60, C70, and then other “magic” numbers, such as C50 and C32, are explained by stability arguments, especially by minimizing the number of adjacent pentagons in the cage structure (see e.g. Díaz-Tendero et al. 2006). However, all cages with even NC, from ~28 to well above 70, share a similar basic stability, since differences in the energy required for C2 loss remain relatively small (e.g. Díaz-Tendero et al. 2006; Berné et al. 2015a, and references therein). This should be kept in mind for interstellar fullerenes by considering all such values of NC, since it is possible that the prominence of C60 abundance might remain relatively limited in astrophysical contexts (Sects. 2.2 and 2.3.4).
Such a similarity of various cages is reflected in the values of their first and second ionization potentials (IP; e.g. in Fig. 2 of Díaz-Tendero et al. 2006). Compared to the value for C60 (7.6 eV), the IPs of other fullerenes are smaller by typically only 0.5−1.0 eV, while the C70 IP is practically the same as C60. One can expect similar resemblances in electron affinities, bond strengths, vibration frequencies, chemical properties, etc., for the whole family of fullerene cages. However, the lower symmetry may have various consequences including increasing chemical activity and the number of active IR modes and shortening the time constant for IR energy emission.
More importantly, variations in the electron number with NC introduces basic differences in filling the HOMO shell and thus in the actual properties of the ground state and the optical spectra of various pure fullerenes. This might be important when considering DIB carriers, since they might have smaller LUMO-HOMO gaps and richer optical spectra than C60. But their known optical absorption spectra generally do not display prominent features in the visible range (Koponen et al. 2008; Lan et al. 2015a,b). Such calculated data seem to still be lacking for most of their cations. But for C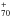 , Fulara et al. (1993b) observed a relatively weak absorption system in the range of 7000−8000 Å with vibrational structure. At shorter visible wavelengths, it remains difficult to infer the actual gas-phase spectrum of C
, Fulara et al. (1993b) observed a relatively weak absorption system in the range of 7000−8000 Å with vibrational structure. At shorter visible wavelengths, it remains difficult to infer the actual gas-phase spectrum of C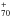 either from the spectrum studied in an oleum solvent (Cataldo et al. 2012, 2013) or from CNDO/S calculations (Kato et al. 1991).
either from the spectrum studied in an oleum solvent (Cataldo et al. 2012, 2013) or from CNDO/S calculations (Kato et al. 1991).
The very long triplet lifetime of C70 makes its cooling dominated by Poincaré fluorescence (Appendix G). It is not impossible that the situation be the same for other cages.
SAMO states of fullerenes other than C60 do not seem to have been addressed yet. However, one may infer that they should be similar to those of C60 and its ions and not contribute to the visible absorption of neutrals and cations. Anions might be considered in a similar way to C (Appendix F).
(Appendix F).
For each value of NC, fullerene cages may exist in an impressive number of different isomers. However, activation barriers for transformations to the most stable forms – albeit substantial, 7.14 ev for C60 (e.g. Dunk et al. 2012) – remain about twice smaller than the activation energies to degrade fullerene cages by C2 ejection (Sect. 2.3.5). One may therefore expect that interstellar fullerene cages reorganize into their most stable isomer, for instance by simultaneous absorption of two UV photons (Sect. 2.3.4), on time scales much shorter than the fullerene lifetime. In addition, accretion of C+ should lower the reorganization activation barriers (Dunk et al. 2012, and Sect. 2.3.4, Note 2).
2.3. Fullerene physics and chemistry in interstellar conditions
One key property of fullerenes is the exceptional stability of their carbon cage. Once formed, it is difficult to destroy the cage or to even modify it by, for example, subtracting or adding a C2 molecule or introducing heteroatoms in the cage network or inside. On the other hand, minor modifications that preserve the cage size and composition are much easier, such as ionization, isomerization, exohedral addition of atoms and other chemical reactions including association with PAHs. Therefore, it is clear that the total abundance of a fullerene, such as C60 in its different ionization or chemical states, makes much more sense than its abundance in a given state.
2.3.1. Ionization state
In interstellar conditions ionization and recombination processes for fullerenes are likely to be similar to those of PAHs (e.g. Tielens 2005, 2013). Both the UV absorption cross-section per carbon atom and the photoionization yield should be comparable for PAHs and fullerenes (Verstraete & Léger 1992; Berkowitz 1999). A broad picture of the state of ionization of interstellar C60 is thus provided by that of, say, C54H18 PAHs (e.g. by Fig. 6.7 of Tielens 2005). However, the value of the electron recombination rate remains uncertain for both PAHs (see e.g. Montillaud et al. 2013) and fullerenes. As for small PAHs, in the normal diffuse interstellar medium (ISM), the most frequent charge states of fullerenes should be singly ionized (cations) and then neutral (see e.g. Le Page et al. 2003; Tielens 2005; Montillaud et al. 2013). This is consistent with the detection of C there (Sect. 2.4). However, anions should not be overlooked, as for PAHs (e.g. Salama et al. 1996), and dications may also be rarely present.
there (Sect. 2.4). However, anions should not be overlooked, as for PAHs (e.g. Salama et al. 1996), and dications may also be rarely present.
The electron attachment energy to fullerenes is substantial, EA = 2.666 ± 0.001 eV for C60 (Stochkel & Andersen 2013; see also Huang et al. 2014). Despite contradictory early estimates, it is now confirmed that the rate of electron attachment to fullerenes is high (e.g. Viggiano et al. 2010, and references therein). Therefore, despite their large photo-detachment cross-section, the abundance of fullerene anions, especially C , may be substantial in regions that are well shielded from UV radiation, as with PAHs (e.g. Omont 1986; Salama et al. 1996).
, may be substantial in regions that are well shielded from UV radiation, as with PAHs (e.g. Omont 1986; Salama et al. 1996).
The ionization potential of C is only 11.5 eV (Dresselhaus et al. 1996). C
is only 11.5 eV (Dresselhaus et al. 1996). C may thus be converted into C
may thus be converted into C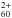 by interstellar far-UV photons just below 13.6 eV. However, efficient internal energy conversion between electronic levels, including super-excited auto-ionizing states, implies relatively small cross-sections for photo-ionization close to threshold. It results in very low values for the photoionization yield, which often reaches unity only ~9 eV above threshold (see e.g. Jochims et al. 1996). Nevertheless, the photo-ionization is more efficient than photo-destruction by C2 ejection (e.g. Leach 2001), so that the abundance of C
by interstellar far-UV photons just below 13.6 eV. However, efficient internal energy conversion between electronic levels, including super-excited auto-ionizing states, implies relatively small cross-sections for photo-ionization close to threshold. It results in very low values for the photoionization yield, which often reaches unity only ~9 eV above threshold (see e.g. Jochims et al. 1996). Nevertheless, the photo-ionization is more efficient than photo-destruction by C2 ejection (e.g. Leach 2001), so that the abundance of C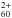 might be significant in regions with very strong UV radiation. We note, nevertheless, that the C
might be significant in regions with very strong UV radiation. We note, nevertheless, that the C has been found substantial even, for example, in Orion sight lines when the UV photon intensity is high (Galazutdinov et al. 2000; Misawa et al. 2009; and Fig. 4). This puts limits on a very easy formation of C
has been found substantial even, for example, in Orion sight lines when the UV photon intensity is high (Galazutdinov et al. 2000; Misawa et al. 2009; and Fig. 4). This puts limits on a very easy formation of C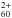 .
.
2.3.2. Chemistry – Preliminary remarks
Despite their overall chemical stability, fullerenes are also known to be fairly reactive. Chemical processes mostly imply addition reactions that may be seen in a simplistic way as breaking one of their double C=C bonds (located only on the hexagons). Fullerenes should thus react with various atoms, radicals, ions, or other reactive molecular species found in the ISM. However, in most cases it is probable that the adducts thus formed would rapidly return to the initial, more stable state mostly under the action of UV photolysis. In addition to the possible durable association of some strongly bound heteroatoms discussed in Sects. 3 and 4, it seems that at least three classes of chemical processes with abundant species might play a significant role in the overall balance of fullerene interstellar compounds: hydrogenation; accretion of C+, and chemical association of fullerenes with PAHs (Sect. 6.1). Chemical reactions with other species are generally less important. But notable exceptions include destruction of fullerenes in reactions with energetic ions such as He+ (Sect. 2.3.5), possible formation of some EEHFs (Sects. 3 and 4) and perhaps reaction with atomic oxygen.
Because of its overwhelming abundance reactions with highly reactive atomic hydrogen are by far the most frequent. They lead mostly to H accretion and to the formation of hydrogenated fullerenes (fulleranes). The physics and potential interstellar properties of these key compounds are discussed in Sect. 5.
Accretion of C+ might be thought of as a key starting point for the transformation of interstellar fullerene compounds. Its importance is discussed in Appendix A and Sect. 2.3.4. It seems that the reaction C+ + C60→ C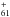 might proceed without an activation barrier at a rate close to the Langevin rate. However, it is probable that the binding energy of C+ to C60 remains modest, which should make C
might proceed without an activation barrier at a rate close to the Langevin rate. However, it is probable that the binding energy of C+ to C60 remains modest, which should make C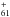 relatively easy to destroy by UV photolysis. However, C61H
relatively easy to destroy by UV photolysis. However, C61H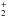 might be more stable. Also note that small carbon chains attached to fullerenes seem to be pretty stable in laboratory conditions of fullerene formation (Pellarin et al. 2002; Shvartsburg et al. 2000), while C+ accretion might efficiently grow such chains in interstellar conditions.
might be more stable. Also note that small carbon chains attached to fullerenes seem to be pretty stable in laboratory conditions of fullerene formation (Pellarin et al. 2002; Shvartsburg et al. 2000), while C+ accretion might efficiently grow such chains in interstellar conditions.
One may also wonder about the possible importance of fullerenes for interstellar chemical composition and processes (see e.g. Millar 1992; Petrie & Bohme 2000) and about whether they might play a significant role in interstellar chemistry like PAHs (see e.g. Lepp et al. 1988). But, despite their reactivity, it is not expected that fullerenes play as important a role because of their much smaller abundance than PAHs. This is certainly true for gas-phase fullerenes with the modest abundance found for C (Sect. 2.4). It might perhaps be less obvious for fullerenes bound to PAHs if their abundance were much larger (Sect. 6).
(Sect. 2.4). It might perhaps be less obvious for fullerenes bound to PAHs if their abundance were much larger (Sect. 6).
2.3.3. Formation
Possible modes of formation of astrophysical fullerenes have been discussed by various authors (see e.g. Tielens 2008; Chuvilin et al. 2010; Cami et al. 2011; Berné & Tielens 2012; Cami 2014, and references therein; Zhen et al. 2014; Berné et al. 2015a). The two most likely processes now seem to be either 1) degradation of PAHs or carbon grains under the violent action of UV radiation, especially dehydrogenation of PAHs (see e.g. Montillaud et al. 2013; Zhen et al. 2014; Berné et al. 2015a) or of other hydrogenated carbonaceous particles (see e.g. Duley & Williams 2011; Micelotta et al. 2012); or 2) shattering in carbon grain collisions in shocks.
The physical conditions in carbon vaporization from grain shattering might be more or less roughly similar to classical “bottom-up” formation of fullerenes in the laboratory (Smalley 1992; Dunk et al. 2012; Krätschmer et al. 1990), such as by laser ablation of graphite, laser ablation of HAC (Scott et al. 1997), and arc discharge with graphite electrodes, or in nature (Rietmeijer 2006).
Very recent studies that demonstrate the easy formation of C60 from fast electron irradiation of graphene (Chuvilin et al. 2010) or large PAHs (Zhen et al. 2014) or that model the folding of PAHs into fullerene cages (Berné et al. 2015a), strongly support relatively easy “top-down” formation of fullerenes in a variety of interstellar and circumstellar environments. The size distribution of interstellar fullerenes is of course a key question. There is currently evidence for the existence only of C60 and C in the ISM (and C70 in one source) (Sect. 2.4). This is not surprising given their well-known higher stability compared to other fullerenes. The detailed model of Berné et al. (2015a) confirms this trend in the conditions of strong UV radiation of reflection nebulae. There, about 60−70 C atoms is the typical expected size of dominant dehydrogenated PAHs.
in the ISM (and C70 in one source) (Sect. 2.4). This is not surprising given their well-known higher stability compared to other fullerenes. The detailed model of Berné et al. (2015a) confirms this trend in the conditions of strong UV radiation of reflection nebulae. There, about 60−70 C atoms is the typical expected size of dominant dehydrogenated PAHs.
However, in weaker UV radiation, the transition to fully dehydrogenated PAHs occurs for NC< 60 (e.g. Montillaud et al. 2013; Le Page et al. 2003; Berné & Tielens 2012). Such graphene fragments should be as unstable as larger ones discussed by Berné et al. (2015a) or Pietrucci & Andreoni (2014), among others. In interstellar conditions1, they should likewise quickly fold and transform into fullerene cages, with small activation energies, only a few eV. One may thus imagine that interstellar PAHs might give birth to a whole series of fullerene cages of various sizes.
2.3.4. Cage growth and decay
As Berné et al. (2015a) have recalled, fullerene cages with arbitrary even number of carbon atoms NC should be fairly stable against abstraction or adjunction of C2 particles (see e.g. their Table 3 giving values of the internal energy, Ei ~ 25−40 eV, needed for C2 abstraction from C58 to C66). Dissociation energies for C2 ejection from fullerene cages are not significantly less for NC ~ 40−60 than for NC ~ 60−70 (except for C60 and C70; see e.g. Gluch et al. 2004; Díaz-Tendero et al. 2006). Nevertheless, the internal energy Ei needed to eject C2 should decrease for smaller NC. The value of Ei is thus expected to be significantly lower for NC ~ 25−40 than for NC ≳ 60. However, even for Ei ≈ 15−25 eV as expected for NC ~ 30−40, C2 UV abstraction still needs the simultaneous absorption of at least two hard-UV photons. Therefore such a process must be relatively rare, not more often than about once every 106 yr for NC ~ 30−50 in standard diffuse clouds (Sect. 2.3.4). But such rates could be enough to perhaps stand as a dominant destruction process of such cages. One may even expect a more rapid cage destruction for NC< 25. This contrasts with the likelihood that UV sputtering is negligible for NC ≳ 60 in diffuse clouds, as may be inferred from Berné et al. (2013).
Of course, one should compare these rates with possible competing growth by C+ accretion resulting from the very rapid accretion rate given by Eq. (A.1), ~10-4 yr-1. The relatively weak binding of the external C could make C -C unstable2 for a redistributed intramolecular vibrational energy ≳10 eV (Sect. 2.2), i.e. even perhaps by the absorption of a single hard-UV photon, with a very uncertain photolysis rate. One may therefore expect that the rate of growth of the cage by C+ accretion is also relatively slow. However, the comparison of various uncertain rates – UV C2-decay of C2n cages, C+ accretion by C2n, and UV photolysis of C2n-C, C2n-CH2 and their cations (Appendix A) – makes it very difficult to predict whether a slow growth or decay of the cages will take over as a function of their size and the UV intensity. Therefore, the resulting size distribution of fullerenes in diffuse clouds remains unclear. Detailed modelling is mandatory to try to predict its behaviour even approximately.
-C unstable2 for a redistributed intramolecular vibrational energy ≳10 eV (Sect. 2.2), i.e. even perhaps by the absorption of a single hard-UV photon, with a very uncertain photolysis rate. One may therefore expect that the rate of growth of the cage by C+ accretion is also relatively slow. However, the comparison of various uncertain rates – UV C2-decay of C2n cages, C+ accretion by C2n, and UV photolysis of C2n-C, C2n-CH2 and their cations (Appendix A) – makes it very difficult to predict whether a slow growth or decay of the cages will take over as a function of their size and the UV intensity. Therefore, the resulting size distribution of fullerenes in diffuse clouds remains unclear. Detailed modelling is mandatory to try to predict its behaviour even approximately.
It seems, however, unavoidable that a significant part of the tail of the distribution of PAHs that are small enough to be fully dehydrogenated will eventually transform into fullerenes. Of course the rates at which the low-mass tail of PAH distribution is destroyed and repopulated are highly uncertain. Many intricate processes should be considered, including UV C2/C2H2 abstraction, C+ accretion, and even sputtering by reaction with atomic oxygen. However, since fullerenes are significantly more stable than PAHs (Sect. 2.3.5), it seems reasonable to surmise that the total amount of fullerenes could perhaps reach several percent of that of PAHs, i.e. up to 10-3 at least of total interstellar carbon (see also Sect. 6). Also, a significant amount of small fullerenes or PAHs could also be produced in grain shattering (e.g. Scott et al. 1997). But all these processes are so uncertain that the conjecture of a substantial abundance of small fullerenes remains somewhat hypothetical, although it is now confirmed that gas-phase C alone contributes several 10-4 of interstellar carbon (Sect. 2.4).
alone contributes several 10-4 of interstellar carbon (Sect. 2.4).
2.3.5. Destruction
Fullerene cages are known to be very resistant to various destruction processes (e.g. Lifshitz 2000; Cataldo et al. 2009). Even in the harsh conditions of the ISM, it is believed that fullerenes could be very resilient to the most frequent potentially destructive processes such as very intense UV fields, shocks, PAH collisions, X rays, or chemical reactions such as oxidation. Even if the cage is substantially disrupted, it is possible that it might still have a high probability of eventually returning quickly to some highly stable fullerene compound of the same or different form.
All in all, despite curvature constraints, the fullerenes should be more stable than PAHs with a comparable number of atoms, because they lack fragile C-H bonds and dangling C atoms. As discussed above, the most efficient violent destruction process, loss of a C2 molecule, has a high dissociation energy, ~11 eV, in C60, ~8–9 eV for other cages, which requires a very high total internal energy, ~25−40 eV, to achieve actual dissociation (Tables 2 and 3 of Berné et al. 2015a). The UV photo-destruction of C2n thus implies repeated simultaneous absorptions of several UV photons. It is practically excluded in the normal ISM for 2n ≳ 50 (however, see Sect. 2.3.4 for smaller cages), but it can be achieved in exceptional conditions close to a star with strong UV emission (Berné et al. 2015a). On the other hand, as seen above, repeated shrinking by UV C2 loss could eventually destroy the smallest cages.
However, fullerenes will be eventually destroyed by the same processes as PAHs, although less easily, mostly by successive impact knockouts of C atoms or C2 molecules. Micelotta et al. (2014) estimate that the ejection of C from C60 requires an energy transferred during the collision that is twice as large as for PAHs. Such dominant processes might include: 1) mostly moderate shocks in the diffuse ISM; 2) cosmic rays especially in denser clouds; and 3) sputtering by electrons in the hot gas (see e.g. Micelotta et al. 2010a,b, 2011, 2014; Dunk et al. 2012). Large fullerenes should thus have lifetimes that are at least comparable to or longer than the estimate for PAHs of a few 108 yr by Micelotta et al. (2010a).
Indeed, because of their stability, one of the most important sinks of fullerene molecules of the interstellar gas could be their eventual accretion onto dust grains. On the one hand, sticking C60 and other fullerenes on pure graphenic surfaces, such as PAHs or even possibly graphite, might seem difficult because of the spherical shape which may prevent van der Waals binding energies as high as for PAHs which are flat, although charged particles may provide more significant binding energies (e.g. Petrie & Bohme 2000). But on the other hand, fullerenes display a much higher reactivity and may efficiently bind to carbonaceous grain surfaces similar to their addition reactions to PAHs (Sect. 6.1). In addition, previous strong binding of fullerenes to PAHs or PAH clusters might also mediate the incorporation of fullerenes into dust grains. Such fullerene molecules deposited on grains may eventually be returned to the gas phase by rare violent desorption processes, such as grain-grain collisions, exposure to cosmic rays, X rays, or strong UV (e.g. Léger et al. 1985). But it seems at least equally probable that they are rather partially altered and more or less definitely incorporated into larger carbon cluster structures in the grain.
Such physical and chemical properties of fullerenes in the ISM have been repeatedly advocated since their discovery in 1985 to predict their significant presence in the ISM (see e.g. Kroto 1988, 1989; Léger et al. 1988b; Kroto & Jura 1992; Leach 2006; Cami 2014 and references therein). This presence is now definitely proved by the astrophysical detection of C60, and C in various sources3.
in various sources3.
2.4. Interstellar abundances
Long after the initial proposed identification of C in the ISM by Foing & Ehrenfreud (1994) taking advantage of the laboratory spectrum of Fulara et al. (1993a), the presence of C60+ has been recently confirmed in diffuse interstellar clouds (Campbell et al. 2015) and the presence of C60 previously in various environments as described by Cami (2014) and Berné et al. (2015b), among others: various types of carbon-rich planetary nebulae (Cami et al. 2010; García-Hernández et al. 2010, 2011a,b, 2012; Gielen et al. 2011, Otsuka et al. 2013); a single pre-planetary nebula (Zhang & Kwok 2011); various interstellar environments (Rubin et al. 2011; Peeters et al. 2012; Boersma et al. 2012), including reflection nebulae such as NGC 7023 (Sellgren et al. 2007, 2010; Berné & Tielens 2012) and young stellar objects (Roberts et al. 2012).
in the ISM by Foing & Ehrenfreud (1994) taking advantage of the laboratory spectrum of Fulara et al. (1993a), the presence of C60+ has been recently confirmed in diffuse interstellar clouds (Campbell et al. 2015) and the presence of C60 previously in various environments as described by Cami (2014) and Berné et al. (2015b), among others: various types of carbon-rich planetary nebulae (Cami et al. 2010; García-Hernández et al. 2010, 2011a,b, 2012; Gielen et al. 2011, Otsuka et al. 2013); a single pre-planetary nebula (Zhang & Kwok 2011); various interstellar environments (Rubin et al. 2011; Peeters et al. 2012; Boersma et al. 2012), including reflection nebulae such as NGC 7023 (Sellgren et al. 2007, 2010; Berné & Tielens 2012) and young stellar objects (Roberts et al. 2012).
Except for the two strong DIBs close to 9600 Å of C (Foing & Ehrenfreud 1994; Campbell et al. 2015; and their vibronic satellites detected by Walker et al. 2015; Fig. 3), all these fullerene identifications are based on mid-IR spectral bands measured with the infrared spectrometer (IRS) of Spitzer Space Observatory. Amongst the four IR active bands of C60, those at 17.4 μm and 18.9 μm are easier to disentangle from stronger PAH bands than those at 8.5 and 7.0 μm. The identification of C
(Foing & Ehrenfreud 1994; Campbell et al. 2015; and their vibronic satellites detected by Walker et al. 2015; Fig. 3), all these fullerene identifications are based on mid-IR spectral bands measured with the infrared spectrometer (IRS) of Spitzer Space Observatory. Amongst the four IR active bands of C60, those at 17.4 μm and 18.9 μm are easier to disentangle from stronger PAH bands than those at 8.5 and 7.0 μm. The identification of C was also similarly achieved in the mid-infrared (Berné et al. 2013).
was also similarly achieved in the mid-infrared (Berné et al. 2013).
 |
Fig. 4 Correlation between the sum of the equivalent widths, EW9600, of the two DIBs at 9577 Å and 9633 Å of C |
With the confirmation of the C DIB identification and the new f-value provided in Ne matrix by Strelnikov et al. (2015), the abundance of C
DIB identification and the new f-value provided in Ne matrix by Strelnikov et al. (2015), the abundance of C can now be relatively accurately estimated in interstellar diffuse clouds. We have used for that 13 typical sight lines of diffuse clouds where these DIBs have been detected well (Galazutdinov et al. 2000; Cox et al. 2014; see Fig. 4, excluding peculiar sight lines). The ratio of the sum of the equivalent widths of the two C
can now be relatively accurately estimated in interstellar diffuse clouds. We have used for that 13 typical sight lines of diffuse clouds where these DIBs have been detected well (Galazutdinov et al. 2000; Cox et al. 2014; see Fig. 4, excluding peculiar sight lines). The ratio of the sum of the equivalent widths of the two C DIBs to reddening, EW9600 /E(B − V), ranges from 210 mÅ/mag (HD 186745) to 400 mÅ/mag (HD 183143) with an average value of 300 mÅ/mag. This is substantially lower than the value for HD 183143, 1060 mÅ/mag, initially quoted by Foing & Ehrenfreund (1994), but very close to the more precise value, 451 mÅ/mag, given by Foing & Ehrenfreund (1997).
DIBs to reddening, EW9600 /E(B − V), ranges from 210 mÅ/mag (HD 186745) to 400 mÅ/mag (HD 183143) with an average value of 300 mÅ/mag. This is substantially lower than the value for HD 183143, 1060 mÅ/mag, initially quoted by Foing & Ehrenfreund (1994), but very close to the more precise value, 451 mÅ/mag, given by Foing & Ehrenfreund (1997).
From Eq. (2), the average abundance of C (fraction of total interstellar carbon including dust, in gas-phase C
(fraction of total interstellar carbon including dust, in gas-phase C ) can be estimated as
) can be estimated as 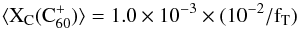 (1)where fT is the sum of the oscillator strengths of the two bands of C
(1)where fT is the sum of the oscillator strengths of the two bands of C . The new f-values measured in an Ne matrix by Strelnikov et al. (2015) (see Sect. 2.1.2), yield fT = 0.025 ± 0.008, hence
. The new f-values measured in an Ne matrix by Strelnikov et al. (2015) (see Sect. 2.1.2), yield fT = 0.025 ± 0.008, hence 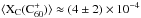 , if any matrix effect on fT is negligible in this4.
, if any matrix effect on fT is negligible in this4.
In the two dozen PNe where the C60 mid-IR emission bands are detected, its abundance is estimated in the range 0.05 × 10-4–10-2 of the available carbon (Cami et al. 2010, 2011; García-Hernández et al. 2010, 2011a,b, 2012; etc.). However, these values might be affected by the assumptions about the strength and the excitation of the infrared vibration modes (see e.g. Bernard-Salas et al. 2012). It should also be stressed that only ~3% of all PNe observed in the Milky Way with Spitzer-IRS show evidence of the C60 mid-IR bands (Otsuka et al. 2014). The abundance of both C60 and C seems significantly smaller in reflection nebulae such as NGC 7023 (Berné & Tielens 2012; Sellgren et al. 2010; Berné et al. 2013).
seems significantly smaller in reflection nebulae such as NGC 7023 (Berné & Tielens 2012; Sellgren et al. 2010; Berné et al. 2013).
The weakness or the absence of observed DIBs at the wavelength of a number of weak forbidden visible transitions of C60, as well as of the two broad allowed bands at 3980 and 4024 Å, seems to put roughly similar constraints, ~10-4 of interstellar carbon, on the abundance of neutral C60 in diffuse clouds (see Appendix E). This is consistent with the C abundance quoted above, since a significantly larger abundance of C
abundance quoted above, since a significantly larger abundance of C than C60 is expected in regions with strong UV, as for PAH cations (e.g. Montillaud et al. 2013; Tielens 2005, 2008).
than C60 is expected in regions with strong UV, as for PAH cations (e.g. Montillaud et al. 2013; Tielens 2005, 2008).
C70 has been identified in one of the many sources where C60 has been found, the planetary nebula Tc 1. Its abundance there has been estimated to be comparable to C60 (Cami et al. 2010). However, the predominance of cooling by Poincaré fluorescence in C70 (Appendix G) may have led to underestimating its abundance in all sources. Although Poincaré fluorescence is less important for C60, its possible influence should also be carefully addressed for abundance determinations from IR line intensity and the interpretation of IR-line ratios.
2.5. Outline of endohedral/exohedral fullerenes and heterofullerenes of possible interstellar interest
Fullerenes are known to form a rich variety of compounds by association with many atoms that may be bound to the carbon cage in three main ways. In endofullerenes the atoms (or molecules) are locked inside the cage; such a configuration is specific to fullerenes when compared to PAHs, and it is remarkably stable. In addition, fullerenes share two other modes of binding to heteroatoms with other carbon clusters, especially PAHs: exohedral adsorption on the outer surface, and incorporation as heteroatoms in the carbon network, replacing a C atom. Many exohedral atoms only have a limited activation energy for desorption, at most a few eV. Their expected interstellar stability is thus much less than for endofullerenes, with a few exceptions (Sect. 3.3). Heterofullerenes display higher stabilities, albeit variously (Sect. 4).
All these compounds, endohedral exohedral heterofullerenes (EEHFs), display the basic cage structure of fullerenes and most of its electronic level structure. Generally little is changed in the vibrational modes and the cage stability. But the presence of the heteroatom may bring fundamental changes in chemical properties and spectra, and in the ionization potential, owing to the addition of electrons to the cage by charge transfer (see e.g. Jura & Kroto 1992; Shinohara 2000; Dunk et al. 2014). In addition, covalent bonding with the cage may strongly perturb and hybridize the orbitals, lowering the symmetry and strengthening forbidden transitions of pure fullerenes.
More specifically, charge exchange with associated atoms may add one or several electrons in the LUMO orbital; as analyzed e.g. by Leach (2004), bonding to adducts may take one or two π electrons out of the HOMO orbital, as also in C , without changing much the remaining electronic structure of the cage. Such an unfilled HOMO shell allows new transitions from lower shells. Both cases open the way to new optical or IR transitions absent in C60. Associated metals also introduce additional levels in the DIB energy range, corresponding to their own energy levels.
, without changing much the remaining electronic structure of the cage. Such an unfilled HOMO shell allows new transitions from lower shells. Both cases open the way to new optical or IR transitions absent in C60. Associated metals also introduce additional levels in the DIB energy range, corresponding to their own energy levels.
As discussed in detail below, interstellar formation of EEHFs is often not obvious. However, EEHFs might perhaps form somewhat normally in the same interstellar processes together with pure fullerenes as long as heteroatoms are present to take part in the formation process. Interstellar cages of EEHFs are probably as resilient as those of pure fullerenes. Extraction of endohedral atoms also proves very difficult, but there are a few exceptions. But most exohedral compounds should be fragile to UV photolysis.
The next five sections summarize the most relevant basic properties of potential interstellar EEHFs for those that may be relevant in the ISM.
 |
Fig. 5 Adapted from Supplementary Fig. 5 of Dunk et al. (2014). Behaviour of the chemical elements for the formation of mono-atom endohedral compounds with C60: grey-blue squares, elements that form mono-metallofullerenes in laser graphite ablation; full yellow squares, elements that do not form confirmed mono-atom endohedral compounds; light blue squares, rare gases that form mono-atom endohedral compounds; yellow squares with grey-blue thick borders, other non metals that form mono-atom endohedral compounds. In addition, a few abundant cosmic elements that do not form confirmed mono-atom endohedral compounds in laser graphite ablation, are indicated by yellow squares with red thick borders. |
3. Potential interstellar metallofullerenes
3.1. Basic properties of endofullerenes
The ability to stably encapsulate various atoms and even molecules inside a carbon cage was immediately recognized as an essential property of fullerenes, with possible astrophysical implications (e.g. Kroto & Jura 1992). Long after that, endohedral compounds (endofullerenes, EF), especially with metals (metallofullerenes) are still a key component of the fullerene landscape (e.g. Dresselhaus 1996; Shinohara 2000; Eletskii 2000; Akasak & Nagase 2001; Guha & Nakamoto 2005; Lu et al. 2012; Popov et al. 2013; Cong et al. 2013; Dunk et al. 2013, 2014). Mono-atom endohedral fullerenes are known for a substantial number of the elements, as seen in Fig. 5 and Table B.1. Confirmed configurations include mainly metals, especially alkalis and some alkaline earths, but also non-metals such as N, P and rare gases.
But such endofullerenes have not been substantiated for most d-transition metals and a few other cosmically abundant elements (Mg, Si, Al), as well as the oxygen family. Indeed, as described by Shinohara (2000) and Dunk et al. (2014), for metals, the existence and properties of endohedral compounds are closely related to the possibility of charge transfer between the metal and the cage (Sect. 3.1.1).
Most EFs of this confirmed list are formed relatively easily in the various classical processes of formation of fullerenes, such as laser graphite ablation or arc discharge, by mixing some compound of the considered element with graphite (see e.g. a summary of these methods by Lu et al. 2012; Cong et al. 2013; Eletskii et al. 2000; Dunk et al. 2013, 2014). In addition, in many cases, EFs may be formed in small quantities just by bombarding fullerenes with atomic ions of moderate energy (a few tens of eV). Such EF synthesis has been achieved for rare gases (He, Ne, Ar), alkalis (Li, Na, K), Ca, etc. The threshold collisional energy of implantation increases from ~6 eV for He+ (Campbell et al. 1998) to ~50 eV for Ar+ or K+ (Deng et al. 2003).
There are various indications that most EFs might resist destruction practically as might empty fullerenes. One clue is precisely the high value of the energy of maximum efficiency for ion implantation, proving that below this value the probability of cage destruction or opening remains low. Another proof is the evidence that delayed laser photoemission of electrons is similar for endohedral and empty fullerenes, showing that both are capable of storing large amounts of internal energy without dissociation (Beck et al. 1996; Clipston et al. 2000). Except for very small atoms and their ions (H and He, but also N), opening the cage enough to allow the atom or its ion to escape requires injecting a lot of energy, typically a few tens of eV (see e.g. Wan et al. 1992; Campbell & Rohmund 2000), which is not very different from what is needed to extract a C2 molecule from the cage (discussed in Sect. 2.3.5).
3.1.1. Charge distribution and structure of endofullerenes
Electron charge transfer from the atom to the cage is general for confirmed endometals whose formation is favoured by it (Dunk et al. 2014). It typically implies one to three electrons depending on the metal valence: one for alkalis; two for alkaline earths like Ca, Ba; three for La (e.g. Shinohara 2000; Dunk et al. 2014; but see below for Ca and Mg). On the other hand, charge transfer is practically non-existent for rare gases and N (e.g. Eletskii et al. 2000). It is a key factor for the various properties of EFs: atom position, bonding to the cage, internal motions, ionization potential, the structure of excited electronic levels, the optical spectrum (Sect. 3.1.2), electron and nuclear spin resonance; superconductivity, etc.
Charge transfer obviously depends mainly on the ionization potential of the metal (IP) being small enough; e.g., very roughly, IP1 − e2/rF ≲ EA, where IP1 is the first IP, rF the radius of the fullerene cage and EA the electron attachment energy to the cage. For rF ≈ 3.5 Å and EA ≈ 2.7 eV, it requires IP1 ≲ 6.8 eV. This immediately shows (see e.g. Table B.1) that charge transfer is not possible for Mg, as well as for Fe and other d-transition metals. It may thus explain why these metals do not (easily) form endohedral compounds.
When charge transfer fully operates for n electrons, neutral metallofullerenes with alkalis and alkaline earths have thus a structure close to Mn+@C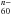 . But, as noted, this is not the case for Mg. Even for Ca, if the transfer of the first 4s electron proves complete, the case does not seem as clear for the second one because the energies of the systems Ca+@C
. But, as noted, this is not the case for Mg. Even for Ca, if the transfer of the first 4s electron proves complete, the case does not seem as clear for the second one because the energies of the systems Ca+@C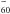 and Ca2+@C
and Ca2+@C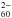 are close, therefore the ground state is instead a hybrid state (e.g. Stener et al. 2002), even if the transfer of two electrons dominates (Wang et al. 1993).
are close, therefore the ground state is instead a hybrid state (e.g. Stener et al. 2002), even if the transfer of two electrons dominates (Wang et al. 1993).
Because the extra-electrons occupy the LUMO orbital of the empty fullerene, their ionization energy is reduced compared to the latter by an amount of the order of the LUMO-HOMO gap. For example, the ionization potential (IP) of M@C60 is lowered with respect to C60 from 7.6 eV to typically ~6.0−6.4 eV for alkalis and ~6−7 eV for Ca@C60 (Broclawik & Eiles 1998; Stener et al. 1999, 2002). On the other hand, the second IP, i.e. the IP of (M@C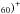 , does not seem much smaller than that of C
, does not seem much smaller than that of C (11.5 eV).
(11.5 eV).
Charge transfer induces a strong electrostatic interaction between the positive ion and the negatively charged cage. This implies that the most stable position for the metal ion is generally, but not always, not the centre of the cage, but a position closer to the cage, with some chemical bonding. However, for C60 the possible position is always multiple with energy degeneracy due to the initial high symmetry. Such a configuration breaks the original symmetry and opens complex possibilities for splitting the energy levels and for the internal motion of the encapsulated ion (e.g. Hernández-Rojas et al. 1996; Zhang et al. 2008).
3.1.2. Electronic energy levels of endofullerenes
Endohedral fullerenes, like other EEHFs, are interesting candidates for DIB carriers because they may have relatively strong electronic transitions in the visible range thus differing from C60 and other pure fullerenes. But this is probably not the case for non-metal atoms located in the centre of a C60 cage such as He and Ne, as well as for H2@C60 (Sect. 7).
On the other hand, in metallofullerenes the optical spectrum may be completely modified by charge exchange. In addition, the outer orbitals of the endohedral atom or ion are strongly perturbed by the strong attractive potential of the cage (e.g. Connerade et al. 2000; Xu et al. 1996; Hasoglu et al. 2013). They may also be transformed by entering chemical bonding between the metal and the cage, and eventually hybridize with fullerene SAMO orbitals (Sect. 2.1.1).
As quoted, charge transfer may add n electrons to the cage CNC giving the same electronic structure as C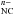 . One may thus expect, e.g. for Na@C60, a spectrum similar to C
. One may thus expect, e.g. for Na@C60, a spectrum similar to C for the lower electronic transitions, especially in the infrared, but one should find a richer spectrum at shorter wavelengths since the ionization potential (IP) of Na@C60 (~6-7 eV) is much higher than the attachment energy of C
for the lower electronic transitions, especially in the infrared, but one should find a richer spectrum at shorter wavelengths since the ionization potential (IP) of Na@C60 (~6-7 eV) is much higher than the attachment energy of C (2.7 eV). This allows the presence of additional bound electronic levels, including SAMO ones. In the same way, the spectrum of metallofullerene cations, (M@C60)+, for metals of valence n, is similar to C
(2.7 eV). This allows the presence of additional bound electronic levels, including SAMO ones. In the same way, the spectrum of metallofullerene cations, (M@C60)+, for metals of valence n, is similar to C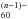 – e.g., C60 for alkalis, and again C
– e.g., C60 for alkalis, and again C for alkaline earths such as (Ca@C60)+, i.e. Ca2+@C
for alkaline earths such as (Ca@C60)+, i.e. Ca2+@C .
.
Analysis of the optical spectra of metallofullerenes thus presents the same difficulties as do C60 or C . It is therefore not surprising that even theoretical studies of their energy levels and excitation are lacking, incomplete or ambiguous, and we are still waiting for laboratory spectra. The accuracies of wavelength determinations are still far from being useful in constraining possible associations of visible DIB features with metallofullerenes. Estimates of line strengths are practically always lacking.
. It is therefore not surprising that even theoretical studies of their energy levels and excitation are lacking, incomplete or ambiguous, and we are still waiting for laboratory spectra. The accuracies of wavelength determinations are still far from being useful in constraining possible associations of visible DIB features with metallofullerenes. Estimates of line strengths are practically always lacking.
The simplest cases, such as K@C60 and Ca@C60 and their cations provide a good illustration of this situation (see Appendix C, where various calculations about Mg@C60 are also reviewed despite the absence of confirmed experimental evidence).
The situation is more confused for several other cosmically important elements, such as Si, Fe, and other d-transition metals for which the existence and a fortiori the structure of endohedral compounds are not established (see e.g. Cong et al. 2013; Dunk et al. 2014). However, there is evidence that at least Si may have stable heterocompounds (Sect. 4.3). The case of endohedral Fe is, of course, especially tantalizing because of the large Fe abundance and the richness of its visible spectra (e.g. Simon & Joblin 2009; Tang et al. 2006). But Fe@C60 does not seem to have been isolated in the laboratory (see e.g. Basir & Anderson 1999), while various forms of exohedral Fe are known as discussed below (Sect. 3.3.1).
3.2. Possible interstellar formation of metallofullerenes
As quoted above, some metals easily form endohedral compounds when they are present in fullerene formation processes (Dunk et al. 2013, 2014). Therefore, metals such as Na, K, Ca, which display significant abundances (see Table B1), should be first candidates for interstellar endometals. This is especially true for possible fullerene formation in interstellar grain collisions, whose carbon-vaporization physics might be somewhat similar to laser ablation.
But one should keep in mind that the possible interstellar “top-down” fullerene formation from PAHs (Sect. 2.3.3) is completely different from “bottom-up” cage formation in laboratory. We therefore keep considering the possibility that other most abundant metals such as Fe, Mg, Si, Al, and Ni, might give interstellar endofullerenes while they are known not to normally do in laboratory conditions (Dunk et al. 2014 and Table B.1). The only possibility for ensuring this seems to be with a metal atom tightly bound to the edge of highly dehydrogenated PAHs (dPAHs) when they begin the folding process to form the cage. However, evaluating the order of magnitude of the actual rates of endohedral formation appears as a difficult task by implying two key steps in the modelling: metal attachment to the PAH, and non-ejection of the attached metal in the final outcome of the folding process. Both processes are very uncertain but may be roughly addressed as follows.
It seems that most metal ions could efficiently attach to more or less dehydrogenated neutral dPAHs. For order-of-magnitude estimates, we may tentatively assume a rate up to 10-9cm-3s-1, although it is a significant fraction of the Langevin rate. Assuming nH = 50 cm-3 and a total interstellar abundance of metals in the gas phase of 2 × 10-6 yields that a dPAH frequently attaches a metal about every 3 × 105 yr or so. However, the duration of the time the metal remains stuck to the PAH skeleton crucially depends on the nature of its binding to the PAH. Only the dangling bonds at the periphery of dPAHs should open the possibility of tight bonding, with binding energies possibly higher than the strongest hydrogen bonding to PAHs (~4.8 eV, e.g. Montillaud et al. 2013). The actual existence of such strong metal-dPAH binding is not warranted. It needs to be explored further. Nevertheless, a significant probability of finding some metals that are strongly bound to dPAHs, such as Fe, Ni, or Si, seems possible since they are known to form strong bonding with carbon shell structures (see e.g. Lee et al. 1997 for binding of Ni to the edge of carbon nanotubes and Sects. 4.3 and 3.3.1 for strongly bound incorporation of Si and Fe into fullerene shells, respectively). But the question remains more uncertain for metals such as Mg, Ca, and Al, and a fortiori alkalis.
An additional difficulty is keeping the metal atom attached to the carbon shell, possibly inside, when the latter finally folds into a stable fullerene cage. This seems possible since the folding activation energy to be overcome by UV heating impulse is estimated to be only ~4 eV for NC ~ 66 by Berné et al. (2015a). When an endofullerene is eventually formed, one may expect that it remains stable in the last steps when the cage reorganizes with eventual C2 ejections. The same could be true for hetero Si (Sect. 4.3).
But there is no need to say that all these processes, hence their outcome, are extremely uncertain. Nevertheless it would be very useful to explore them with the power of modern simulations.
3.3. Strongly bound exohedral fullerenes
3.3.1. Fe and other metals
As usual the case of iron fullerene compounds is complicated because of the propensity of iron to form complex bonding, especially with carbonaceous surfaces. Anyway, independently of the uncertain existence and properties of Fe@C60, iron reacts efficiently with the outer surface of fullerenes to form two main compounds, as for other d-transition metals (Basir & Anderson 1999).
One of this compounds is an exohedral coordination complex weakly bound (1−3 eV) to the surface. It forms with no activation barrier at low collision energy between Fe+ and C60. It seems similar to Fe binding to PAHs with binding energy 0.6−2.5 eV, as calculated by Simon & Joblin (2007). However, such weakly bound Fe or Fe+ cannot survive long on free fullerenes to interstellar UV photolysis.
The other complex, C60Fe, or rather C Fe, is observed in C60+Fe+ collisions at energies ≳10 eV. It thus has a substantial activation barrier to formation, ~8−10 eV, is chemically bound and remains stable for injected energy up to ~20 eV. Basir & Anderson (1999) have proposed that this complex is a network-bound structure, with the metal atom probably sitting above the fullerene surface, chemically bound to two or more carbon atoms. Not much more information seems available about such C60Fe+ or C60Fe compounds, which might be stable in interstellar conditions, but should probably not form easily there. Nothing seems to be known either about their electronic levels and optical spectrum. One may expect that the strong binding with Fe and the distortion of the cage significantly modify the C60 electronic level structure. More importantly, the large number of low excited levels of Fe and Fe+ in the range ~2–3 eV must add a number of visible transitions with significant oscillator strengths, as found by Simon & Joblin (2009) for Fe-PAH+ weakly bound complexes.
Fe, is observed in C60+Fe+ collisions at energies ≳10 eV. It thus has a substantial activation barrier to formation, ~8−10 eV, is chemically bound and remains stable for injected energy up to ~20 eV. Basir & Anderson (1999) have proposed that this complex is a network-bound structure, with the metal atom probably sitting above the fullerene surface, chemically bound to two or more carbon atoms. Not much more information seems available about such C60Fe+ or C60Fe compounds, which might be stable in interstellar conditions, but should probably not form easily there. Nothing seems to be known either about their electronic levels and optical spectrum. One may expect that the strong binding with Fe and the distortion of the cage significantly modify the C60 electronic level structure. More importantly, the large number of low excited levels of Fe and Fe+ in the range ~2–3 eV must add a number of visible transitions with significant oscillator strengths, as found by Simon & Joblin (2009) for Fe-PAH+ weakly bound complexes.
Either way, when discussing possible structures for interstellar Fe bound to carbonaceous particles, one should keep in mind the strong catalysis power of Fe in forming complex particles (see e.g. Zhou et al. 2006), although significantly abundant carbon nanotubes seem excluded in the ISM. As stated above, the case of fullerene compounds with other less cosmically abundant d-transition metals seems very similar to Fe compounds (Basir & Anderson 1999); e.g., various compounds of Ni have been recently theoretically addressed by Neyts et al. (2011).
3.3.2. Oxygen compounds
Oxygen is known to react efficiently with fullerenes; even atmospheric O2 is the main cause of their decomposition in normal conditions. Oxygen may thus form a long list of oxides with C60, including hetero C59O, possibly O@C60, and many somewhat unstable exohedral mono- or poly-oxides (see e.g. Heymann & Weisman 2006).
Christian et al. (1992a) have reported that C59O+ significantly forms in collisions of O+ with C60 and is amazingly stable for collision energies up to at least ~30 eV. They suggest two possible structures for C59O+: either hetero inclusion of trivalent O+ in the carbon cage network or endohedral CO@C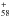 . However, the DFT theory of Jiao et al. (2002) has found that the most stable shape of C59O should be an open fullerene cage, but C59O seems to have never been synthesized (Vostrowsky & Hirsch 2006). Therefore, the question of its long survival in the ISM remains open.
. However, the DFT theory of Jiao et al. (2002) has found that the most stable shape of C59O should be an open fullerene cage, but C59O seems to have never been synthesized (Vostrowsky & Hirsch 2006). Therefore, the question of its long survival in the ISM remains open.
The most stable exohedral oxide is the epoxy C60O with a bridging bond of O on one double bond C=C of C60 (Heymann & Weisman 2006); however, it is very unstable (Christian et al. 1992a). It should therefore be rapidly photolyzed by the interstellar UV radiation.
Sulphur fullerene compounds present some similarities with oxygen (e.g. Jiao et al. 2002; Ren et al. 2004). It is even more difficult to assess their eventual interstellar importance.
4. Potential interstellar azafullerenes, silafullerenes and other heterofullerenes
As reviewed by Vostrowsky & Hirsch (2006), many heteroelements are able to enter the carbon network of fullerene cages, replacing a carbon atom. Besides the most studied C59N and other azafullerenes, the synthesis of C59X has been reported for X = B, P, Si, O, Ni and other d-transition metals, and many calculations have addressed them. We stress the possible interstellar interest of C59Si and other silafullerenes. For transition metals, O and S we refer to Sect. 3.3.2.
4.1. C59N, C59HN and other azafullerenes in the laboratory and models
Nitrogen heterofullerenes (azafullerenes) are among the best-studied fullerene derivatives as a result of the propensity of N to easily replace C atoms in carbon compounds. C59N (or rather its dimer (C59N)2) and its derivatives stand as the most studied heterofullerenes. The high reactivity of this radical may generate a variety of stable azafullerenes including C59HN and C59N-PAH dyads.
All such species keep most properties of pure fullerenes, but besides enhancing the chemical activity, the presence of the additional N electron on the cage, may significantly alter the electronic structure and its energy levels. Compared to C60, the ionization potential is significantly decreased (from 7.6 eV for C60 to about 6 eV for C59N, see Xie et al. 2003), but the electron affinity remains similar.
As reviewed by Vostrowsky & Hirsch (2006), although it is hard to produce in graphite laser ablation, C59N forms more or less easily in a variety of processes – mostly concerning exohedral nitrogen derivatives of fullerenes, but also gas discharge, ion implantation, etc. The stability of its cage proves comparable to, albeit slightly less than C60 (Clipston 2000 from delayed photoionization, Christian et al. 1992b from ion collisions, etc). However, its destruction begins by losing a CN molecule rather than C2. The radical reactivity of C59N is such that only its dimer, (C59N)2, is stable in laboratory conditions and most experimental information about C59N indeed comes from dimer studies.
In addition to (C59N)2, many adducts of C59N are known. However, despite the rich chemistry of azafullerenes it seems that, as for C60, the only adducts that have a chance to reach significant interstellar abundances, are with hydrogen, carbon or PAHs. C59HN is well studied both experimentally (e.g. Keshavarz-K et al. 1996; Buchachenko & Breslavskaya 2005) and theoretically (e.g. Andreoni et al. 1996). The binding energy of H to C59N and the ionization potential are estimated to be ~3.4 eV (Buchachenko & Brestlavskaya 2005) and ~6.1 eV (Andreoni et al.), respectively. The binding energy of many other C59N adducts is probably similar. This includes C59N–PAH dyads and their cations. Such dyads of C59N bound to coronene, coranulene, etc. can be easily synthesized as shown by Hauke et al. (2004).
As the cage properties are mostly preserved, the vibrational modes of azafullerenes do not prove very different from the corresponding fullerenes. A number of theoretical studies have provided models for the electronic energy levels of basic azafullerenes, corroborated by spectral measurements. All optical transitions of C59N+ remain very weak with f-values staying below a few 10-3 (Xie et al. 2004). There is a significant increase in the case of C59N with theoretical f-values reaching ~10-2 in several bands in the range 4000–8000 Å (Ren et al. 2000). Band intensities prove even larger for C59N adducts with a strong broad feature about 4400 Å (Hauke et al. 2006). This includes C59HN and (C59N)2 (see Fig. 3a of Keshavarz-K et al. 1996; and f-values estimates by Ren et al. 2000).
4.2. Interstellar C59N and other azafullerenes
C59N and other derived azafullerenes appear to be interesting candidates for interstellar fullerenes because of the extraordinary stability of the C59N cage and the related propensity of N atoms to replace C in carbon networks. It has been repeatedly suggested that interstellar PAHs could contain significant amounts of nitrogen in their graphene network, at the level of possibly ~1−2%, in order to explain the properties of their 6.2 μm feature (Hudgins et al. 2005; Tielens 2008) (although this interpretation has been contested by Pino et al. 2008). If this is confirmed for PAHs, there is a possibility of finding a similar situation for interstellar fullerenes. Even only 1% of randomly distributed N-atoms would mean that there is one N-atom in 33% of the 60-atom cages, to be compared with 55% and 10% for 0 and 2 N atoms, respectively. But a high abundance of azafullerenes, similar to nitrogen-substituted PAHs, is not warranted in the most likely formation processes of interstellar fullerenes (Sect. 2.3.3). N atoms migh tend to be ejected in the formation process of fullerenes from PAH because their binding is weaker than for carbon atoms. Despite the nitrogen presence expected in carbon grains (e.g. Jones 2013), azafullerene formation in grain-grain shattering might be inefficient because of the expected similarities of this process with graphite laser ablation, which produces little C59N. One very hypothetical way of forming C59N could perhaps be UV-processing of exohedral nitrogen derivatives of fullerenes bound to PAHs or grains, if any.
In C59HN the binding energy of H to the cage in the vicinity of N, ~3.4 eV, is significantly higher than the direct binding energy of H to a C60 cage, ~2.7 eV (Sect. 2.3.1). One may infer that the ratio n(C59HN+)/n(C59N+) is probably greater than n(C60H+)/n(C ); it could thus be significant. One might therefore expect a significant abundance of C59HN+ if C59N+ was abundant enough.
); it could thus be significant. One might therefore expect a significant abundance of C59HN+ if C59N+ was abundant enough.
4.3. C59Si and other silafullerenes
Besides azafullerenes, silicon heterofullerenes (silafullerenes) seem by far the most attractive case because of their stability that results from the similarity of binding properties of Si and C and of the large abundance of silicon. Fullerene cages may thus amazingly support the stable replacement of up to ~20 C atoms by Si (Ray et al. 1998; Vostrowsky & Hirsch 2006). However, in the ISM we will only consider C59Si here (and possibly C58Si2).
The high stability of silafullerenes is amazing. Although the binding energy of Si is computed to be much smaller than that of C (Billas et al. 1999; Marcos et al. 2003), silafullerenes resist temperatures up to ~4000 K before dissociating, and the first dissociation product is generally C2, seldom SiC. This behaviour is explained well by molecular dynamics simulations (Marcos et al. 2003).
The computed electronic level structure of C59Si and other silafullerenes is substantially different from C60. The LUMO-HOMO gaps are smaller. The first visible allowed optical transitions appear then at longer wavelength; however, they remain relatively weak (Koponen et al. 2008; Lan et al. 2015a,b) and no results seem available for cations. Similarly, the ionization potentials decrease by about 0.5−0.7 eV per Si atom (Tenorio & Robles 2000).
Substantial abundances of silafullerenes in the ISM are not excluded. Since grain shattering could create physical conditions similar to graphite laser vaporization and Si is abundant in carbon grains, shattering could efficiently produce C2n−1Si and C2nSi2 with various n, like laser ablation of mixtures of graphite with a small Si proportion (e.g. Pellarin et al. 1997, 1999). Si atoms could also strongly bound to dehydrogenated PAHs and survive their folding into fullerene cages (Sect. 3.2)5.
5. Interstellar fulleranes
5.1. Fulleranes in the laboratory and models
Hydrogen may be bound in large quantities on the outer surface of fullerenes by opening their numerous double bonds (30 in C60) to form strong CH alkane bonds. This sort of more or less hydrogenated fullerenes, fulleranes, up to highly hydrogenated compounds, such as C60H18 and C60H36, have long been recognized as major members of the fullerene family. Their cosmic importance has also been discussed for a long time (Webster 1992; Iglesias-Groth 2006, and references therein). Their presence has been claimed in meteorites (Becker & Bunch 1997), but this experimental evidence has been contested (Hammond & Zare 2008).
The energetics of the binding of H atoms to a fullerene cage is known rather precisely both experimentally and theoretically (see e.g. Bettinger et al. 2002 and also Vehvilainen et al. 2011; Okamoto 2001). It is summarized in Table 1. The H binding energies for larger even or odd numbers of H atoms seem comparable to C60H2 and C60H, respectively, probably up to about C60H36. The situation is similar for cations with significantly stronger binding – 2.9 eV for H on C (Petrie et al. 1995).
(Petrie et al. 1995).
The visible spectrum of C60H2 was measured by Bensasson et al. (1995), together with that of C60H4. Both spectra display a relatively strong feature near 4350 Å, similarly to most other C60 adducts (e.g. Smith et al. 1995; Kordatos et al. 2003; Wang et al. 2012). Not much seems known about the optical spectra of C60H, C60H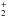 and C60H+.
and C60H+.
Infrared, visible and UV spectroscopy studies of highly hydrogenated fulleranes were performed in matrix, mostly for astrophysical implications, by Cataldo & Iglesias-Groth (2009), Cataldo et al. (2014), Iglesias-Groth et al. (2012), and references therein. The main findings are strong characteristic bands due to C–H stretching close to 3.5 μm and the washing out most of the optical and near-UV bands of C60.
The variable large number of H atoms in fulleranes destroys the unique symmetry properties of C60. This might diminish their interest for DIBs, except light fulleranes, such as C60H, C60H2, and their ions.
5.2. Interstellar fulleranes
Fulleranes should form efficiently in the ISM by H accretion, especially onto ionized fullerenes (Appendix D). Although the activation energies needed to extract H or H2 from fulleranes are significant (~1.9−3.3 eV for neutrals, Table 1), their values remain significantly smaller than in PAHs (4.8 eV). One therefore expects that fulleranes lose more easily their H atoms by UV photolysis than PAHs for similar numbers of carbon atoms NC. However, PAHs are known to remain practically completely hydrogenated for NC ~ 60 in standard interstellar UV (e.g. Fig. 10 of Montillaud et al. 2013 and Fig. 10 of Le Page et al. 2001). As a result, the interstellar dissociation of fulleranes is not straightforward. It is qualitatively discussed in Appendix D.
The question is made difficult for various reasons including the need of an elaborate thermodynamic treatment of H-photolysis by a single hard-UV photon, the uncertainty about internal energy conversion, the various H binding modes, the possible role of specific reactions of fulleranes with H, forming H2 (#4 in Table 1). Although there is no doubt that UV photolysis should be very efficient for the first H atom of fulleranes with an odd number of H atoms, such as C60H, the outcome is less clear for even H numbers, such as C60H2. Although an efficient dehydrogenation of C60 fulleranes in diffuse clouds does not seem impossible, it is concluded in Appendix D that the question should be considered as unsettled until an elaborate treatment is provided, similar to the methods used for PAHs, as in Le Page et al. (2001, 2003) or Montillaud et al. (2013). Therefore, the ratio of the abundances of fulleranes to fullerenes, such as C60H2/C60 remains uncertain. However, the rate of UV H photolysis is obviously reduced when the number of H atoms is large, for larger fullerenes including C70, in UV-shielded regions, and even more for fullerenes attached to PAHs or dust grains. It is on the other hand increased for smaller cages than C60.
There are many other fullerene hydrocarbons, such as C61H and C61H2, longer chains, and their cations. But, as discussed in Sect. 2.3.2, the UV photolysis of C61 might be too fast to allow significant abundances, unless C61H2 (methanofullerene) is more stable. Note that C61H2 has a characteristic spectral feature at 432 nm (Anthony et al. 2003 and Sect. 5.1) while the optical spectra of C61H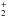 seems unknown.
seems unknown.
6. Associations of interstellar fullerenes with PAHs
As pointed out in Sect. 1, fullerenes are known to form somewhat stable associations with PAHs. They deserve special consideration because of the large interstellar abundance of PAHs. Such associations could be frequent, and fullerenes might keep some of their specific properties when engaged in them and more or less easily episodically return to the gas phase.
6.1. Formation, destruction and abundance
Orders of magnitude of the percentage of interstellar fullerenes bound in such associations might be tentatively estimated when building on the work carried out for modelling PAH clustering (e.g. Montillaud & Joblin 2014). However, as noted, the most stable and important fullerene-PAH associations are likely to be chemically bound because of the fullerene reactivity, while slightly weaker van der Waals interactions probably dominate the binding of clusters of larger PAHs. As shown, for instance, by Dunk et al. (2013; see also García-Hernández et al. 2013), fullerene-PAH dyads form easily in the laboratory in reactions of PAHs such as coronene with C60 (and C70) in energetic conditions. Coronene then loses one or two H atoms and is bound to C60 by one or two C-C bonds (see Fig. 2 of Dunk et al.). C60 easily reacts with linear PAHs (e.g. Petrie & Bohm 2000; García-Hernández et al. 2013), but not or with difficulty with fully hydrogenated non-linear PAHs such as coronene (Petrie & Bohm 2000; Dunk et al. 2013). As expected, Dunk et al. find that partially dehydrogenated coronene shows a higher reactivity. In interstellar conditions, we may thus expect that similar dyads form easily in reactions of fullerenes with dehydrogenated PAHs, but more rarely with fully hydrogenated PAHs. The following simple considerations show that it is not impossible that such associations might constitute an important reservoir for interstellar fullerene compounds.
The frequency of close collisions between fullerenes and PAHs depends a lot on the charge state of the two particles. It is clear that it is negligible when the two particles have a charge with the same sign. One of the most favourable cases is a collision between a cation and a neutral particle. These collisions should occur close to the Langevin rate, ~10-9 cm3 s-1, in both cases not depending on which is the cation. The rate of close collisions when both PAH and fullerene are neutral is significantly smaller by a factor ~3−5.
It is proven that there is a sharp transition between almost full hydrogenation and dehydrogenation of interstellar PAHs depending on their number of carbon atoms NC and the interstellar UV radiation field (ISRF). In the model of Montillaud et al. (2013) their Fig. 10 shows that, for NC~ 60, this transition occurs for typical values ~3–20 G0 (where G0 is the Habing intensity, see Note 7).
For crude estimates, we assume that PAHs contain 10% of interstellar carbon in PAHs and that they are half ionized with NC = 80. This yields 3 × 106 yr for the order of magnitude of the interval between close collisions of C60 or C with PAHs in diffuse clouds. It is likely that there is on average a low but significant probability of cycloaddition reactions in such close collisions. It is thus possible that the rate of formation of fullerene-PAH dyads be faster than the rate of destruction of fullerenes – about every 109 yr from Micelotta et al. (2010a, 2014), see Sect. 2.3.5.
with PAHs in diffuse clouds. It is likely that there is on average a low but significant probability of cycloaddition reactions in such close collisions. It is thus possible that the rate of formation of fullerene-PAH dyads be faster than the rate of destruction of fullerenes – about every 109 yr from Micelotta et al. (2010a, 2014), see Sect. 2.3.5.
However, such dyads are certainly more fragile than fullerenes themselves, by just breaking their double C-C bridging bond. The exact binding energy seems unknown, but it should be slightly higher than for the C60 or C dimers. If one adopts the DFT theoretical estimate, 0.6−1 eV, of Bihlmeier et al. (2005) and Wang et al. (2014) for these dimers, a best guess for the binding energy of C60 to a PAH could be ~2−3 eV, but this value is highly uncertain. The activation energy is even more uncertain.
dimers. If one adopts the DFT theoretical estimate, 0.6−1 eV, of Bihlmeier et al. (2005) and Wang et al. (2014) for these dimers, a best guess for the binding energy of C60 to a PAH could be ~2−3 eV, but this value is highly uncertain. The activation energy is even more uncertain.
If one tries to compare the rate of dissociation in the interstellar UV of such dyads with H atoms in PAHs, it is possible that the much larger number of carbon atoms compensates for the weaker bond, ~3 eV vs. 4.8 eV. Therefore, it is possible that such dyads of fullerenes with heavy PAHs might survive fairly long.
On the other hand, as discussed in Sect. 2.3.3, fully dehydrogenated PAHs should be highly unstable and they possibly very quickly fold and transform into fullerene cages with NC ~ 30−50. Information is lacking for estimating the reactivity of such unstable smaller fullerenes cages with larger PAHs and with various fullerenes.
All in all, it is possible that such PAH-fullerene dyads and associations of fullerenes with PAH clusters contain a significant fraction of interstellar fullerenes (the associations to carbonaceous grains should also be considered as Cami et al. 2010 suggested). But the importance of such dyads still has to be confirmed.
6.2. Properties
A key question about such fullerene association with carbonaceous particles is whether the engaged fullerene might keep most of its main properties. In such dyads, the structure of the cage should not be much affected together with its electronic levels, and also its vibration modes (García-Hernández et al. 2013). However, one may expect the appearance of a few additional modes linked to the PAH-C60 bond, some mixing of the vibration modes of the C60 and PAH moities, the significant modification of the IR spectrum, and the slight but significant changes of the wavelengths of electronic fullerene transitions. On the other hand, one needs to consider the possibility of exchanging energy and charge with the PAH moiety and the modification of statistical properties related to the total number of C atoms NC. As discussed below, hydrogenation and the stability of other adducts could be deeply modified, the fullerene ionization made more difficult and most of the IR emission transferred to the PAH bands.
As is obvious from the discussion above, the stability of PAH hydrogenation against photolysis should be enormously improved with the large increase in NC and the high energy of the PAH C-H bonds (assuming that the intramolecular vibrational redistribution is effective), so that the PAH should recover its total hydrogenation immediately after the dyad formation. However, even if the H-photolysis of fulleranes bound to PAHs is probably inefficient, one should perhaps also consider reactions of atomic H with fulleranes bound to the PAH forming H2 (such as reaction #4 of Table 1). If their very low activation energy (~0.1 eV) could be overcome, their rate can be comparable to the rate of accretion of H onto fullerenes or fulleranes, possibly reducing the average number of H atoms on the PAH-bound fullerene. This question should be carefully addressed.
As the ionization potential of C60 is significantly higher (7.6 eV) than for relatively large PAHs (e.g. 6.36 eV for ovalene, C36H16), one may expect that the ionization mostly stays on the PAH moiety in ionized C60-PAH associations while the C60 moiety remains practically neutral. This is obviously capital for the expected fullerene optical spectrum. It may also significantly bear on its infrared emission since the vibrational energy conversion between the two moieties is certainly fast and the infrared bands of PAHs are much stronger than those of C60. Adopting the values from Choi et al. (2000) for the IR band strengths of C60 yields a total strength for its four IR bands of 58 km/mol. In comparison, from models of Langhoff (1996), the total strengths of the infrared bands of ovalene (C32H14), neutral and cation, are 772 and 1629 km/mol, respectively. It turns out that only a small fraction of the UV energy absorbed by a C60-PAH dyad should be emitted in the IR bands of C60. As C60 contributes about half the dyad UV absorption, one might underestimate the abundance of fullerenes locked in such dyads by an order of magnitude when applying the usual assumption of complete conversion of the UV energy that it absorbs, into its IR emission bands.
As other (6, 6) adducts, C60-PAH dyads are expected to display universal characteristic optical features absent in C60 (Sect. 5.1): a relatively strong, sharp band close to 4330−4350 Å, and a broader feature close to 7000 Å. This is confirmed for neutral Diels-Alder adducts such as C60-anthracene (Udvardi et al. 1995). But no precise information seems to exist for the corresponding cation spectra.
C59N and other azafullerenes form single-bond adducts easily with many compounds, including PAHs (Sect. 4.2). Because it is likely that reaction rates and dissociation energies are similar to those of fullerenes with PAHs, the above discussion of various PAH-fullerene dyads should also roughly apply to such PAH-azafullerene dyads.
7. Interstellar H2@C60?
It has long been recognized that space inside fullerene cages is large enough to contain molecules. We limit our interstellar discussion to H2@C60.
7.1. Properties of H2@C60
7.1.1. H@C60?
H-atoms and protons are certainly among the atomic particles that can most easily go through the cage surface of fullerenes in both directions. The most recent theoretical discussion of the interaction energy between H and C60 seems to be that of Vehvilainen et al. (2011), who summarizes previous works. The lowest value of the energy barrier preventing H atoms entering or getting out the cage is found to be only about 2.5−3 eV. Bound states may exist on both sides of this barrier. While H may chemisorb on the outer surface of the cage with a substantial binding energy, ~2 eV (Sect. 5), the binding energy at the centre of the cage seems practically zero. Endohedral H@C60 should thus have H confined by a relatively high energy barrier. However, H@C60 seems to have never been confirmed in the laboratory. This looks consistent with its expected instability at room temperature.
Similarly, H@C does not seem to have been formally identified either. All the positive charge should stay on the cage, again with a neutral H atom inside, a binding energy close to zero at the centre of the cage, and a significant lowering of the energy barrier with respect to H@C60 (Ramachandran et al. 2008). The last point should make H@C
does not seem to have been formally identified either. All the positive charge should stay on the cage, again with a neutral H atom inside, a binding energy close to zero at the centre of the cage, and a significant lowering of the energy barrier with respect to H@C60 (Ramachandran et al. 2008). The last point should make H@C even easier to form and dissociate than H@C60.
even easier to form and dissociate than H@C60.
7.1.2. H2@C60 in the laboratory
Unlike elusive H@C60, H2@C60 is a well-established stable endofullerene. Its formation proves to not be easy, however (Komatsu et al. 2005), confirming the impenetrability of the fullerene cage to easy H2 crossing. Such an efficient confinement warrants the stability of H2@C60 (Murata et al. 2006), which might compare to C60.
Detailed studies illustrate the spectacular consequences of the confinement of the H2 molecule (see e.g. the review by Vehvilainen et al. 2011), including, for example, infrared spectroscopy (Mamone et al. 2009, 2011; Ge et al. 2011), inelastic neutron scattering (Vehvilainen et al. 2011), and NMR studies (Murata et al. 2006; Turro et al. 2010).
The 2 μm absorption spectroscopy of solid films of H2@C60 has fully confirmed theoretical predictions for its fine structure. The classical rotation structure of H2 is replaced by a completely different set of quantum levels resulting from the coupled translational and rotational motion of the H2 quantum rotor in the C60 cage.
In addition, confinement strongly enhances the intensity of the forbidden IR transitions similarly to the effect observed for H2 confined in a gas at high pressure (e.g. Frommhold 1993).
7.2. Is there a possibility of finding interstellar H2@C60?
H2@C60 could have an ISM lifetime that is not so much shorter than fullerene cages themselves because it is hard to imagine a way to take H2 out of the cage without destroying the cage. Given the cosmic abundance of hydrogen, H2@C60 might be one of the fullerene compounds to be considered in the ISM. However, forming H2@C60 in interstellar conditions does not seem straightforward since there is no hope of directly injecting an H2 molecule into the cage. One may nevertheless try to imagine a few processes that are eventually able to form it.
As stated in Sect. 7.1.1, it seems easy to inject a proton H+ into the cage, where it must immediately stabilize into H by charge exchange with the cage. This accretion rate could equal a small but significant fraction η of the large Langevin rate (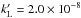 cm3 s-1), because of the small size of H+ and the likely absence of a high activation barrier (Ramachandran et al. 2008). For n(H) = 50 cm-3 and a proton abundance of 3 × 10-4, the rate of forming H@C
cm3 s-1), because of the small size of H+ and the likely absence of a high activation barrier (Ramachandran et al. 2008). For n(H) = 50 cm-3 and a proton abundance of 3 × 10-4, the rate of forming H@C from C60 + H+ could reach η × 10-2 yr-1. Similar to photolysis discussions (Appendix D), it seems that, with an activation energy as low as ~2.5 eV, H@C60 can hardly survive any absorption of a hard-UV photon. The latter occurs every few years with standard UV radiation (Note 7). This does not leave much time for the arrival of a second H+, forming H2@C60 at the rate η′ × 10-2 yr-1.
from C60 + H+ could reach η × 10-2 yr-1. Similar to photolysis discussions (Appendix D), it seems that, with an activation energy as low as ~2.5 eV, H@C60 can hardly survive any absorption of a hard-UV photon. The latter occurs every few years with standard UV radiation (Note 7). This does not leave much time for the arrival of a second H+, forming H2@C60 at the rate η′ × 10-2 yr-1.
All in all, this would yield a global formation rate of H2@C60 that is lower than ηη′ × 10-4 yr-1, i.e. perhaps ~10-8–10-9 yr-1 in such very uncertain assumed conditions. This could be just enough to yield that a certain number of C60 cages could contain an H2 molecule at the end of their lifetime estimated to be ≳a few 108 yr (Sect. 2.3.5). But this result remains extremely fragile because of the many uncertainties of the various parameters.
An alternativ and even more tentative less documented process to form H2@C60 might perhaps be violent perturbations of the cage, e.g. in shocks, in presence of a large amount of hydrogen bound to the outer surface. As seen in laser formation of H2@C60 (Oksengorn 2003) or in simulations (e.g. Long et al. 2013 for a breathing-trap mechanism for H-encapsulation), such violent perturbations may temporarily distort or open the cage, with or without loss of C2 molecules, eventually allowing exohedral H2 to enter it. Appealing cases for such a process could be H-saturated fulleranes bound to PAHs (Sect. 6.2) or grains, or perhaps free fulleranes.
It seems that the presence of endohedral H2 would not change the basic properties of interstellar fullerenes much, making it difficult to reveal its presence, except thanks to specific spectroscopic features. However, even if it were significant, the presence of endohedral H2 should be difficult to confirm because the abundance of H2@C , for instance, could hardly be expected to exceed or even reach 10-9. There is thus practically no chance to ever detect its near-IR H2 2 μm absorption. UV spectroscopy is more sensitive by orders of magnitude than absorption of weak IR lines. It can detect H2 column densities lower than ~1014 cm-2 (e.g. Gillmon et al. 2006). But even so, the UV detection of H2@C60 seems out of reach.
, for instance, could hardly be expected to exceed or even reach 10-9. There is thus practically no chance to ever detect its near-IR H2 2 μm absorption. UV spectroscopy is more sensitive by orders of magnitude than absorption of weak IR lines. It can detect H2 column densities lower than ~1014 cm-2 (e.g. Gillmon et al. 2006). But even so, the UV detection of H2@C60 seems out of reach.
The presence of endohedral H2, if any, in fullerene DIB carriers should, however, cause a very small wavelength shift of the DIB itself with respect to a H2-less fullerene. One might thus expect weak satellites to fullerene DIBs. This could be the best way to confirm or deny the existence of significant amounts of endohedral H2. The expected value of such shifts should be addressed theoretically. A very rough idea of their expected order of magnitude might be obtained by considering the average polarizability per unit volume corresponding to an H2 molecule within a C60 fullerene cage. Using the shift value measured for C60 visible forbidden bands by Sassara et al. (1997), ~35 cm-1, in a Ne matrix, for example, one may infer a rough order of magnitude of 9 cm-1 for the endohedral-H2 shift by scaling from the polarizability per unit volume of Ne. There is no hint of such weak satellites in the observed spectra of the 9600 Å C DIBs. It thus appears that the presence of endohedral H2 cannot exceed a few percent of the C
DIBs. It thus appears that the presence of endohedral H2 cannot exceed a few percent of the C cages. But high telluric noise in this spectral range still restricts the sensitivity of this limit value.
cages. But high telluric noise in this spectral range still restricts the sensitivity of this limit value.
8. Fullerene compounds and DIBs
In spite of so many question marks, such an inventory of potential properties of various interstellar fullerene compounds allows us to briefly discuss the possibility further that they could significantly be carriers of DIBs. Even after the first success of the recent confirmation of the C DIBs, the two main obvious difficulties for this purpose remain the uncertainties about the wavelengths and strengths of visible (and near-IR) bands of other fullerene compounds, and about their interstellar abundances.
DIBs, the two main obvious difficulties for this purpose remain the uncertainties about the wavelengths and strengths of visible (and near-IR) bands of other fullerene compounds, and about their interstellar abundances.
8.1. Line strengths, abundances and DIB strengths
It is useful to recall the general relation between the expected equivalent width of a DIB, the abundance of its carrier M and the band oscillator strength f. It may write (see e.g. Cami 2014) 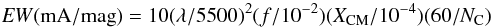 (2)where EW(mA/mag) is the equivalent width expressed in mÅ for 1 mag of interstellar reddening E(B − V), and XCM denotes the fraction of interstellar carbon locked up in the considered type M of “CNC” molecules (e.g. Ca@C60 or C59N). Note that XCM in Eq. (2) refers to the total carbon abundance in the ISM assumed to be χC = NC/NH = 3.9 × 10-4, while Cami (2014) refers to NC/NH = 1.4 × 10-4, i.e. the carbon abundance in the interstellar gas. Our convention yields that the abundance of molecules M relative to H is χM = NM/NH = 0.65 × 10-5 XCM × (60 /NC).
(2)where EW(mA/mag) is the equivalent width expressed in mÅ for 1 mag of interstellar reddening E(B − V), and XCM denotes the fraction of interstellar carbon locked up in the considered type M of “CNC” molecules (e.g. Ca@C60 or C59N). Note that XCM in Eq. (2) refers to the total carbon abundance in the ISM assumed to be χC = NC/NH = 3.9 × 10-4, while Cami (2014) refers to NC/NH = 1.4 × 10-4, i.e. the carbon abundance in the interstellar gas. Our convention yields that the abundance of molecules M relative to H is χM = NM/NH = 0.65 × 10-5 XCM × (60 /NC).
Therefore, typical weak DIBs with EW ~ 10 mÅ/mag might be explained with a modest but significant oscillator strength f ~ 10-2, and a carbon fraction XCM ~ 10-4, comparable to standard abundances reported for interstellar C60 and ~4 times smaller than the average abundance found for C in diffuse clouds (Sect. 2.4).
in diffuse clouds (Sect. 2.4).
Note that for such low values of XCM ~ 10-4 (and NC = 60), the abundances of endo- or heterofullerenes M remain very small, χM ~ 10-9. When the fullerene compound includes a heteroatom, this abundance is also the abundance of the heteroatom locked up in M. Such low abundances are always smaller than cosmic abundances of all important elements (Table B.1). They are even smaller than depleted abundances in the cold diffuse ISM (Savage & Sembach 1996 and Table B.1) for most interesting elements such as Fe, Mg, Si, Na, K, Ca, etc. discussed in Sects. 3 and 4. Therefore, the limitation for EEHFs reaching an abundance large enough to be considered as carriers of DIBs will practically always come from the total number of fullerene cages available, not from limited interstellar abundance of their associated heteroatom.
 |
Fig. 6 Distribution of the equivalent widths per unit reddening, EW/EB − V, of 489 diffuse interstellar bands observed in the line of sight of HD 183143 with EB − V = 1.27, by Hobbs et al. (2009). |
8.2. Which fullerene compounds could be carriers of strong DIBs?
It is well known that the vast majority of the ~500 DIBs are relatively weak with EW/E(B − V) < 50 mÅ, see e.g. Fig. 6 for the best studied line of sight, HD 183143, from Hobbs et al. (2009). For this star with E(B − V) = 1.27, apart from four very strong DIBs whose EW/E(B − V) spreads out between 350 and 4000 mA/mag, there are 22 strong bands with EW/E(B − V) between 100 and 300 mA/mag and 19 slightly weaker ones between 50 and 100 mA/mag – i.e. the total approaches 50 as noted by Salama et al. (1996). The strategy for identifying the DIB carriers should first address these strong bands, but a proper assessment and understanding of the weak DIBs might also be fundamental (see Sect. 8.3).
It is obvious from Eq. (3) that targeting strong DIBs with EW ~ 100–300 mA/mag would imply values of f or XCM significantly larger than standard values of Eq. (3), i.e. 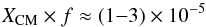 (3)with e.g. f ~ 0.05–0.1 and XCM ~ (2−3) × 10-4. As discussed in Sects. 3−6, it seems difficult to get oscillator strengths f that are much greater than 10-2 for visible transitions connected to pure levels of the “C60” cage. However, f ≳ 0.1 does not seem completely impossible for a very few strong lines in the case of heteroatoms or adducts, but the difficulty should be to keep the carbon abundance XCM ~ 10-4 or more for such compounds (Sects. 3 and 4).
(3)with e.g. f ~ 0.05–0.1 and XCM ~ (2−3) × 10-4. As discussed in Sects. 3−6, it seems difficult to get oscillator strengths f that are much greater than 10-2 for visible transitions connected to pure levels of the “C60” cage. However, f ≳ 0.1 does not seem completely impossible for a very few strong lines in the case of heteroatoms or adducts, but the difficulty should be to keep the carbon abundance XCM ~ 10-4 or more for such compounds (Sects. 3 and 4).
Therefore, with pure carbon C60–C70 compounds, it seems impossible to meet the requirement of Eq. (3) for strong DIBs except in a few exceptional cases. The C DIBs at 9577 and 9633 Å are the most obvious examples. The search for other cases should focus on cations of other pure fullerenes and a few heteroatoms and adducts.
DIBs at 9577 and 9633 Å are the most obvious examples. The search for other cases should focus on cations of other pure fullerenes and a few heteroatoms and adducts.
Azafullerenes do not seem very promising because of their lack of strong transitions and their questionable abundances. The case of fulleranes seems more interesting, especially in molecular diffuse clouds and even perhaps as cations in typical atomic diffuse clouds (see Sect. 5.2 and Appendix D). As quoted in Sect. 3.1.2, alkali endofullerenes should have a few strong allowed transitions from the ground state in the optical range. But the possibility that these endometals might be DIB carriers relies entirely on their abundance being large enough as the result of an extremely efficient formation (Dunk et al. 2013). Their formation from PAH folding does not look very promising. Grain shattering could be more efficient, but the required abundances for strong DIBs seem difficult to reach.
Similar considerations apply to other C60–C70 EEHFs that are much more poorly known and more or less hypothetical, but perhaps they are more promising for a few of them. C60Fe+ and C59Si+ should be considered first. The optical spectrum of C59Si (and C58Si2) display a few significantly strong visible transitions (Sect. 4.3) and it is possible that some abundances of silafullerenes approach those of pure fullerenes. The visible spectrum of C60Fe+ and other fullerene-Fe compounds should be richer (Sect. 3.3.1), but the possibility that they could eventually carry strong DIBs remains highly hypothetical because of the required abundances.
Besides the most stable fullerenes C60–C70, it might remain attractive to explore the field of smaller fullerene compounds (mostly cations), since folding dehydrogenated PAHs with NC< 60 appears as the most promising way of forming interstellar fullerene cages (Sects. 2.3.3 and 2.3.4). One should similarly explore the case of carbon chains or rings attached to fullerenes if they could prove abundant enough in the ISM, since they might combine the stability of fullerenes with the large f-values of carbon chains.
We finally recall that the 4430 Å DIB is stronger by an order of magnitude than most of the other strong DIBs that we have considered, and that the abundance-strength constraint for its carrier increases in proportion. It seems practically excluded that we can meet this constraint by any of the single fullerene compounds we have reviewed. One possibility with fullerenes could be to involve a whole family of compounds if they could meet the tough constraints on wavelength, band strength, and abundance.
8.3. Fullerene compounds and weak DIBs
Now that the detection of the C strong DIBs at ~9600 Å is confirmed, it is clear that a number of weaker DIBs – with EW ~ 5–30 mA/mag – could have some C60 compound as carrier. This first includes a few weaker C
strong DIBs at ~9600 Å is confirmed, it is clear that a number of weaker DIBs – with EW ~ 5–30 mA/mag – could have some C60 compound as carrier. This first includes a few weaker C allowed bands, as estimated in Table 6 of Bendale et al. (1992). Their uncertain values yield expected equivalent widths for those bands that are smaller than the observed sum of the ~9600 Å DIBs by factors 5 to 40. But the strength they computed for the ~9600 Å DIBs is around five times larger than the actual strength of these bands.
allowed bands, as estimated in Table 6 of Bendale et al. (1992). Their uncertain values yield expected equivalent widths for those bands that are smaller than the observed sum of the ~9600 Å DIBs by factors 5 to 40. But the strength they computed for the ~9600 Å DIBs is around five times larger than the actual strength of these bands.
Of course, first-priority efforts must further address the 3980 Å and 4024 Å broad bands of C60, which could have been tentatively detected (see Sassara et al. 2001). One may also expect more weak bands of other C60–C70 compounds, including C70 and C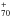 , and some weak vibronic lines of C60 – EW ~ 5–10 mA/mag – as addressed by Herbig (2000) and discussed in Appendix E. Similarly, more weak forbidden vibronic bands of C
, and some weak vibronic lines of C60 – EW ~ 5–10 mA/mag – as addressed by Herbig (2000) and discussed in Appendix E. Similarly, more weak forbidden vibronic bands of C could be present.
could be present.
Even C and anions of other abundant fullerene compounds might be considered as possible carriers of “C2” DIBs in UV shielded clouds (Sect. 2.3.1 and Appendix F).
and anions of other abundant fullerene compounds might be considered as possible carriers of “C2” DIBs in UV shielded clouds (Sect. 2.3.1 and Appendix F).
8.4. Interstellar environment, DIBs and fullerenes
Of course the properties of DIBs in some way reflect the physical conditions and abundances of the interstellar environment where they form, which influence DIB carriers. Correlations among DIBs themselves allow the definition of DIB families whose members behave similarly with respect to the environment. It is well established that the UV interstellar radiation field seems to be the main factor intervening in the differentiation of the main DIB families. They are traditionally named “σ” and “ζ” (discussed in many works: Krelowski & Walker 1987; Krelowski et al. 1992; Krelowski 2014; and, e.g., Vos et al. 2011; Kos et al. 2013; Herbig 1993, 1995; Cami et al. 1997; Tielens 2013; Sonnentrucker 2014; Lan et al. 2015a,b; Bailey et al. 2015a,b) and “C2” (Thorburn et al. 2003; Kaźmierczak et al. 2010, 2014); and they correspond to UV non-shielded, partially-shielded and very-shielded sight lines, respectively.
The most important effects of the radiation field on DIB carriers obviously concern their ionization state, although it may also induce photo-dissociation. The ionization (and perhaps hydrogenation) properties of various fullerenes might fit well with these characteristics. It seems especially likely that cations should be associated with “σ” DIBs such as 5780 Å (e.g. Cami et al. 1997; Friedman et al. 2011; Vos et al. 2011; Farhang et al. 2015), including C .
.
Fullerene (or PAH) anions could be good candidates as carriers of “C2” DIBs (Appendix F), but the lack of gas-phase laboratory spectra still precludes checking this conjecture.
One may also look for DIBs especially strong in regions with strong UV and low density, which might perhaps be carried by dications. From the high latitude study of Lan et al. (2015a,b), corroborated by Maíz-Apellániz et al. (2015), a possibly intriguing case seems the DIB at about 4885 Å. The average value given by Lan et al. for EW/EB − V of this DIB is three times larger than for the classical sightline HD 183143 (Hobbs et al. 2009); however, the reported band width is also much broader, which makes its strength more uncertain. In contrast, most other DIBs have a ratio of the high-latitude value to the HD 183143 value comprised between 0.7 and 1.4. Figures 13, 12 and 8 of Lan et al. confirm that this 4885 Å DIB displays a strong anti-correlation with H2 and a pronounced saturation at high extinction.
The extension of DIB studies to a large number of sight lines from massive surveys at high Galactic latitude (van Loon et al. 2013; Kos et al. 2014; Lan et al. 2015a,b; Baron et al. 2015a,b) confirms the general resilience of DIBs at high latitude, amazingly even at latitudes higher than dust for DIBs such as 8120 Å (Kos et al. 2014). It might also show a possible peculiar behaviour of the prominent strongest 4430 Å DIB, in spite of the difficulty of accurately measuring its strength because of its large width; for example, Lan et al. (2015a,b), as well as Maíz-Apellániz et al. (2015), found an average value for EW/EB − V of this DIB that is more than three times less than for the HD 183143 sight line (Hobbs et al. 2009). This could confirm that its ratio to “σ” 5780 Å and even “ζ” 5797 Å DIBs might decrease at high Galactic latitude, as reported earlier by McIntosh & Webster (1993), while it seems to be a well confirmed “σ” DIB (see e.g. Fig. 13 of Lan et al.). One might thus infer a special fragility of its likely cation carriers. This could be confirmed by its early destruction in SN 2012ap (Milisavljevic et al. 2014). We also note the extreme behaviour of the 5797 Å DIB in the sight line of SN 2014J in M82 (Welty et al. 2014).
DIB studies now extend well into the near-infrared range up to 1.8 μm (Geballe et al. 2011; Zasowski et al. 2015; Cox et al. 2014). Correlations have already been found with visible DIBs. It would be interesting to improve these correlations since it is possible to have a better chance there to find “perfect” correlation between two DIBs with the same carrier, one in the visible and the other in the infrared. EEHFs should be good candidates for such correlations since many of them are expected to have strong near-infrared transitions.
8.5. Emission bands
The amazing appearance in the Red Rectangle (RR) nebula of sharp emission features coinciding with four major DIBs (Schmidt et al. 1980) has always been recognized as a key clue for identifying of DIB carriers (see e.g. van Winckel et al. 2002; Sarre et al. 2006; van Winckel 2014). It is especially striking that these four DIBs (5797 Å, 5850 Å, 6379 Å and 6614 Å) are exactly the prominent members of the best defined “DIB family” (“ζ”) whose carriers have a positive correlation with H2 (Sect. 8.4 and e.g. Fig. 13 of Lan et al. 2015a,b) and are thus enhanced in UV-shielded interstellar “ζ” lines of sight (see e.g. Vos et al. 2011). This might be consistent with milder UV conditions in the RR nebula than in the diffuse ISM, as also shown by the good correlation of the spatial emission of these bands with neutral Na (Kerr et al. 1999). Such conditions might be expected, but would need to be confirmed from models similar to that of Men’shchikov et al. (2002), yielding a lack of ionizing far-UV photons resulting from the reddened F-type stellar spectrum and the absence of an additional ionizing source, together with a high gas density n ≳ 104 cm-3. But building such models would be difficult because of the complexity of the far-UV spectrum of the RR (Sitko et al. 2008).
The nature of the carriers of these bands stil need to be elucidated: why they are so uniquely important in the RR6 and what the emission mechanism is. Fullerene compounds may appear as good candidates, for the same arguments as given before for DIBs in general (but PAHs and other carbonaceous particles cannot be excluded). However, the origin of their abundance there should not be obvious. The peculiar abundances of the RR photosphere, devoid of refractory elements (Waelkens et al. 1992 and Table B.1), could point to the absence of these elements (such as Fe, Ca, Mg, etc.) in these emission DIB carriers.
The most promising emission mechanism of these RR bands could be some fluorescence process as advocated by Witt (2014, and references therein). However, the fluorescence yield must be high, which implies tight conditions for the internal energy conversion. Either the spontaneous emission from the upper state U of the DIB to the ground state of the same multiplicity (typical lifetime ~10-6 s for f ~ a few 10-2) is faster than internal conversion to other metastable states M, which finally leads to vibrational excitation and IR emission. Or the energy may be returned from M to U through thermodynamic equilibrium, if the difference in energy between U and M is small enough (delayed or Poincaré fluorescence (PF), Léger et al. 1998a, see Appendix G). As pointed out by Witt (2014), such an efficient delayed fluorescence should be easier to achieve with small particles such as C20. But it does not seem impossible for fullerenes if their level structure and internal conversion could meet these conditions (Sect. 2.1.1). As discussed in Appendix G, PF appears specially favourable for C70 compounds; it could also operate for other cages, even perhaps for C60 compounds. The case of peculiar fullerene orbitals, such as those of endohedral atoms, adducts, or SAMOs, should be specially addressed. Since, the interaction of these orbitals with the bath of regular cage orbitals should be much weaker than for cage orbitals, one may expect that internal conversion is slowed down.
8.6. Matching band profiles and other DIB properties?
Following Snow (2014), among others, DIB carriers must comply with an impressive list of requirements (see Sect. 1). As regards fullerene compounds as candidates, we have already addressed a number of these requirements, such as size, stability, carbonaceous nature, ionization states, interstellar formation, required abundance, and line strengths. It is easily seen that additional properties shared with PAHs, such as strong dependence on metallicity or absence of polarization (see e.g. Cox et al. 2007, 2011), are also easily met by fullerene compounds.
Key information about DIB carriers is also clearly embodied in their wavelength distribution and band profiles (e.g. Sarre 2014). The wavelength domain where DIBs show up has always been recognized as highly characteristic (see e.g. Fig. 1 of Witt 2014) – concentration in the visible range, and more specifically high density in the range 5500−6500 Å, low density at ~4000−5000 Å and absence in the UV (but see Bhatt & Cami 2015). As for PAHs (and other carbonaceous particles), such a distribution is well accounted for if the DIBs correspond to the first allowed transitions of fullerenes between the highly symmetric ground state and the first singlet (or doublet for ions) excited state accessible through an electric dipole transition.
Such a situation also fits well with the widths observed for DIBs. Their full width at half maximum (FWHM) ranges from ~0.5 to 2 Å (~1−5 cm-1) for most of them, with an extension to ~4 to 20 Å (~10−100 cm-1) for the broadest ones (~5% of them at the most; see e.g. Hobbs et al. 2009; but see York et al. 2014 for confirmed ones). The short lifetime of the excited state and rotational broadening have long been proposed as the main causes susceptible to explain such line widths.
The Lorentz width connected to a lifetime τ may be written 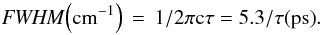 (4)The width of the broadest DIBs (~10−100 cm-1) might thus be explained by ultrafast sub-picosecond internal conversion (IC) of fullerenes (Sect. 2.1.1) or other carbonaceous particles such as PAHs (see e.g. Marciniak et al. 2015; Reddy et al. 2010). The 4430 Å DIB, however, seems the only one strong enough to allow the verification that the profile actually seems Lorentzian, as shown for this band by Snow et al. (2002). The width they report, 17 Å (~90 cm-1) yields τ ~ 0.06 ps. Although very short, this is still within the expected order of magnitude for the IC lifetime of the main singlet levels of fullerenes such as C60 (e.g. Stepanov et al. 2002, see Sect. 2.1.1 and Fig. 2).
(4)The width of the broadest DIBs (~10−100 cm-1) might thus be explained by ultrafast sub-picosecond internal conversion (IC) of fullerenes (Sect. 2.1.1) or other carbonaceous particles such as PAHs (see e.g. Marciniak et al. 2015; Reddy et al. 2010). The 4430 Å DIB, however, seems the only one strong enough to allow the verification that the profile actually seems Lorentzian, as shown for this band by Snow et al. (2002). The width they report, 17 Å (~90 cm-1) yields τ ~ 0.06 ps. Although very short, this is still within the expected order of magnitude for the IC lifetime of the main singlet levels of fullerenes such as C60 (e.g. Stepanov et al. 2002, see Sect. 2.1.1 and Fig. 2).
The rare confirmed very broad DIBs (York et al. 2014) might be explained in this way. (Weak broad DIBs could be much more numerous but are not detectable, and other large molecules, such as PAHs, have similar IC features). The large width of UV bands, close to 10 Å (or more, Sassara et al. 2001) on top of a crowded absorption background, could be the main reason for the quasi absence of strong UV DIBs (Bhatt & Cami 2015).
On the other hand, one has to explain why the majority of DIBs are too narrow to allow internal conversion times faster than ~1 ps. This might point to more peculiar transitions that are not as well coupled to the main phonon bath of large molecules, i.e. to cage vibrations for fullerene compounds. Such a slower IC might be expected with the lowest excited levels of most fullerene compounds or with SAMO states or with transitions of EEHFs connected with their heteroatoms (Sects. 3 and 4) or adducts.
The 9577/9633 Å bands give tight constraints on IC in C . Their intrinsic FWHM, 2.4−2.7 ± 0.2 cm-1, measured at 5.8 K in the laboratory by Campbell et al. (2015), is interpreted as mainly due to internal conversion, indicating a lifetime of ~2 ps for the excited electronic state. The slightly larger width measured for the DIBs (3.05 ± 0.05 cm-1 towards HD 183143, Foing & Ehrenfreund 1997) might include a small contribution from rotational broadening, but smaller than expected from the modelling of Edwards & Leach (1993) and Foing & Ehrenfreund (1997). Therefore, this result seems to point out to low rotational excitation in diffuse clouds, perhaps similar to the conclusions by Cami et al. (2004) for the 6614 Å DIB.
. Their intrinsic FWHM, 2.4−2.7 ± 0.2 cm-1, measured at 5.8 K in the laboratory by Campbell et al. (2015), is interpreted as mainly due to internal conversion, indicating a lifetime of ~2 ps for the excited electronic state. The slightly larger width measured for the DIBs (3.05 ± 0.05 cm-1 towards HD 183143, Foing & Ehrenfreund 1997) might include a small contribution from rotational broadening, but smaller than expected from the modelling of Edwards & Leach (1993) and Foing & Ehrenfreund (1997). Therefore, this result seems to point out to low rotational excitation in diffuse clouds, perhaps similar to the conclusions by Cami et al. (2004) for the 6614 Å DIB.
The width of C DIBs is close to the median (in cm-1) of the distribution of DIB widths. These C
DIBs is close to the median (in cm-1) of the distribution of DIB widths. These C data strengthen previous conclusions that there is no problem for explaining DIB widths with a combination of IC and rotational broadening for fullerene carriers.
data strengthen previous conclusions that there is no problem for explaining DIB widths with a combination of IC and rotational broadening for fullerene carriers.
On the other hand, the most extreme broadening observed for some DIBs especially in the line of sight of He-36 (Dahlstrom et al. 2013) seems to require larger rotation constants that implies molecules smaller than ~20 atoms (Oka et al. 2014). This seems to exclude fullerenes as carriers of these bands, unless perhaps one considers the very smallest cages or some other peculiar fine structure of fullerene lines.
A few DIBs, such as 6614 Å, display a clear multicomponent structure that could contain crucial information on their carrier (see e.g. Sarre 2014 and references therein). The case of the 6614 Å DIB analyzed by Cami et al. (2004), might be hardly compatible with spherical tops such as fullerenes. Various possible reasons for the structure of this DIB have been recently discussed by Marshall et al. (2015).
9. Conclusion
Despite the difficulties assessing the actual importance of fullerene compounds, one may confirm that they display an impressive panel of attractive features as DIB carriers. Many of these compounds should be practically as stable in interstellar conditions as pure fullerenes such as C60. They therefore stand among the most stable interstellar compounds. Easy interstellar formation of cages of various sizes from dehydrogenated PAHs seems now likely, while other formation modes, such as grain shattering, are possible. The properties of their excited electronic levels and fast internal conversion may explain the gross features of the DIB wavelength distribution. When combining a variety of all factors, their rich diversity of forms compare well with the number of weak DIBs. Compared to PAHs, their high symmetry, especially for C60 compounds, the well-defined hierarchy of cage and isomer stability, and the diversity of sizes, adducts, and heteroatom abundances and properties could be able to produce the observed pattern of DIB strengths. The comparison of interstellar and laboratory gas-phase widths of 9600 Å bands of C strengthens the propositions that other observed DIB widths and profiles might be eventually accounted for by the combination of fast internal conversion, rotation levels and fine Jahn-Teller structure of fullerene compounds. But it is possible that the extreme and variable broadening observed for some DIBs in peculiar sight lines, such as He-36, be incompatible with fullerene carriers.
strengthens the propositions that other observed DIB widths and profiles might be eventually accounted for by the combination of fast internal conversion, rotation levels and fine Jahn-Teller structure of fullerene compounds. But it is possible that the extreme and variable broadening observed for some DIBs in peculiar sight lines, such as He-36, be incompatible with fullerene carriers.
As for C60, fullerene compounds should exist in various ionization states, cations being dominant in standard diffuse interstellar clouds. These ionization properties, as well as those of PAHs, might eventually nicely explain the behaviour of the different DIB “families” in various UV environments. But this is still unclear. The same might be true for the strong emission DIBs of the Red Rectangle (which are major members of the “ζ” low-UV family of classical absorption DIBs). One might imagine that this emission might be explained by some special properties of internal conversion and fluorescence such as Poincaré fluorescence.
At any rate, two major drawbacks affect fullerene compounds as DIB candidates. To start with, many varieties completely lack precise laboratory data, especially gas-phase visible spectra, which are mandatory for carrier identification. More fundamentally, practically all known cases seem to fail at the requirement for strong DIBs in the product of the oscillator strength and the carbon fraction in the DIB carrier, f × XCM> 10-5 (Eq. (3)). Visible transitions with f larger than a few 10-2 seem extremely rare in all fullerene compounds with known spectra because of selection rules and screening by cage π electrons. Fullerenes are less abundant than PAHs by one or two orders of magnitude, holding probably less than a few 10-3 of interstellar carbon in total. It thus seems unlikely that the abundance of many individual fullerene molecules may exceed XCM = 10-4 of interstellar carbon. Identification of strong DIB carriers with fullerenes should thus eventually rely on exceptional cases, which remain mostly hypothetical.
The recently confirmed near-IR double DIB of C at 9577/9633 Å might be considered as the first outstanding example. Despite their peculiar wavelength range, these DIBs display all the standard properties of the “σ” DIB family, strengthening the proposition that the “σ” carriers should be cations. The substantial, but modest, abundance of C
at 9577/9633 Å might be considered as the first outstanding example. Despite their peculiar wavelength range, these DIBs display all the standard properties of the “σ” DIB family, strengthening the proposition that the “σ” carriers should be cations. The substantial, but modest, abundance of C , 4 ± 2 × 10-4 of interstellar carbon, provides a good scale for the abundances of other fullerene compounds, since there are good arguments that they could only be smaller than or comparable to that of C
, 4 ± 2 × 10-4 of interstellar carbon, provides a good scale for the abundances of other fullerene compounds, since there are good arguments that they could only be smaller than or comparable to that of C at best.
at best.
However, even if eventually other fullerene compounds reached high abundances, XCM ~ (1−3) × 10-4, this would leave serious difficulties for allowing them to be the carriers of twenty or so strongest DIBs (Sect. 8.2), since it implies f ≳ 0.05−0.1 for these DIBs (Eq. (3)). Such f-values are practically absent in our survey of important fullerene compounds with known or estimated visual spectra (except perhaps a few endohedral metallofullerenes, and carbon-chain adducts). However, the possible existence of transitions approaching these values might not be totally excluded in fullerene and fullerane cations with unknown spectra, such as C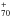 , C
, C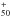 , silafullerenes, C60Fe+ and smaller analogues. Azafullerene cations, as well as other very stable fullerene compounds of transition metals or Mg, if any, might also be tentatively considered for weaker DIBs. But it is unlikely that the abundances of these more or less hypothetical compounds may approach that of C
, silafullerenes, C60Fe+ and smaller analogues. Azafullerene cations, as well as other very stable fullerene compounds of transition metals or Mg, if any, might also be tentatively considered for weaker DIBs. But it is unlikely that the abundances of these more or less hypothetical compounds may approach that of C .
.
On the other hand, now that the detection of the 9600 Å C strong DIBs is confirmed, it is clear that a number of weaker DIBs – with EW ~ 5−30 mA/mag – could have some fullerene compound as carrier. This should include: 1) A few weaker visible allowed bands of C
strong DIBs is confirmed, it is clear that a number of weaker DIBs – with EW ~ 5−30 mA/mag – could have some fullerene compound as carrier. This should include: 1) A few weaker visible allowed bands of C ; 2) Some of the many identified weak forbidden vibronic lines of C60 that should give DIBs with EW ~ 5–10 mA/mag, as well as weak vibronic bands of C
; 2) Some of the many identified weak forbidden vibronic lines of C60 that should give DIBs with EW ~ 5–10 mA/mag, as well as weak vibronic bands of C to be identified; 3) In the same strength range, similar bands of various other fullerene compounds (see Sect. 8.3), but their number could be limited and remains very uncertain because the abundances and many f-values are unknown. 4) Even C
to be identified; 3) In the same strength range, similar bands of various other fullerene compounds (see Sect. 8.3), but their number could be limited and remains very uncertain because the abundances and many f-values are unknown. 4) Even C and other anions, as possible carriers of “C2” DIBs. However, the crowding of such weak DIBs and the complexity of matrix distortion of fullerene spectra make gas-phase spectroscopy mandatory for identifying these fullerene DIBs. A few fullerene dications could also be considered (Sect. 8.4).
and other anions, as possible carriers of “C2” DIBs. However, the crowding of such weak DIBs and the complexity of matrix distortion of fullerene spectra make gas-phase spectroscopy mandatory for identifying these fullerene DIBs. A few fullerene dications could also be considered (Sect. 8.4).
To summarize, the confirmation of the 9600 Å C strong DIBs strengthens the importance of interstellar fullerenes in two main ways:
strong DIBs strengthens the importance of interstellar fullerenes in two main ways:
-
1)
The substantial abundance of C
 in diffuse clouds shows that fullerenes are significant compounds of the ISM (but much
less abundant than PAHs). From this abundance, one may expect that a number of other
fullerenes (with different sizes and various atoms in hetero, endohedral or exohedral
compounds) might eventually prove significantly abundant. But identifying their
importance and estimating their abundance remain awfully difficult because of the
complexity of their physics and of interstellar processes and of the lack of
spectroscopic data for their identification.
in diffuse clouds shows that fullerenes are significant compounds of the ISM (but much
less abundant than PAHs). From this abundance, one may expect that a number of other
fullerenes (with different sizes and various atoms in hetero, endohedral or exohedral
compounds) might eventually prove significantly abundant. But identifying their
importance and estimating their abundance remain awfully difficult because of the
complexity of their physics and of interstellar processes and of the lack of
spectroscopic data for their identification. -
2)
This confirmation of the first DIB identification also strengthens the attraction of various fullerene compounds as DIB carrier candidates. One might expect that many weak fullerene DIBs will be identified as soon as sensitive gas-phase spectroscopy is available for major fullerene compounds, such as C60 and C70 and their ions. But the possibility that other fullerene compounds are the carriers of other strongest DIBs remains subject to very constraining conditions about their abundance, which should approach that of C
 ,
and large strengths of their visible bands, which seem rare among known compounds.
Fullerenes remain key DIB candidates, but it is also possible that other carriers,
such as PAHs or carbon chains, ares dominant.
,
and large strengths of their visible bands, which seem rare among known compounds.
Fullerenes remain key DIB candidates, but it is also possible that other carriers,
such as PAHs or carbon chains, ares dominant.
 DIBs, may seem frustrating. However, it is just an illustration of the enormous complexity of the issue of the DIB carriers and the fact that solving this problem will require long-term collective organized efforts and the close cooperation of astronomers, molecular physicists, astrochemists, and spectroscopists, as mentioned by Tielens (2014) and Cox & Cami (2014), among others.
DIBs, may seem frustrating. However, it is just an illustration of the enormous complexity of the issue of the DIB carriers and the fact that solving this problem will require long-term collective organized efforts and the close cooperation of astronomers, molecular physicists, astrochemists, and spectroscopists, as mentioned by Tielens (2014) and Cox & Cami (2014), among others.
Identification of DIBs, even if weak, appears the best way to trace interstellar fullerene compounds and their abundances. More generally, the importance of interstellar fullerenes obviously justifies major efforts for improving the knowledge of their properties that are relevant to interstellar conditions. Refined quantum calculations of various compounds remain essential for disentangling complex structures and their energy levels and tracing possible strong transitions in the visible or near-infrared range. They should be extended to simulate the formation, destruction, and evolution of these compounds in interstellar conditions. However, once key compounds and transitions have been identified, the most crucial step is accurate laboratory spectroscopy. Matrix spectroscopy may remain useful, but gas-phase spectroscopy appears to be ultimately mandatory. The tour-de-force experiment of Campbell et al. (2015) shows the level of experimental complexity required. Although it should be difficult to extend to neutral fullerenes, it should open the way to systematic studies of the most important ionized interstellar fullerene compounds.
As suggested e.g. by Duley & Williams (2011) and Micelotta et al. (2012), similar processes could form fullerenes especially in planetary nebulae from carbonaceous nanoparticles that are more aliphatic than pure PAHs, resulting from the decomposition of hydrogenated amorphous carbon (HAC; see also Merino et al. 2014).
Similar to the accretion of a carbon atom (Dunk et al. 2012), the accretion of C+ should substantially lower the activation barriers for isomer reorganization of fullerene cages, possibly to values as low as ~2.5 eV. It is therefore possible that C+ accretion, even of short duration, favours isomer stabilization by soft-UV photon absorption.
Walker et al. (2015) favour a value of
fT twice larger which would yield
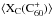 twice smaller.
twice smaller.
The detection of a similar weak emission in the 6614 Å DIB from the ISM of our Galaxy has very recently been announced by Burton Williams et al. (2015).
From e.g. Fig. 21 of Vos et al. (2011), it is seen that most DIBs form in diffuse clouds with UV energy density ~1−10 G0, where G0 = 1 habing = 5.29 × 10-14 erg cm-3 = 0.59 “Draine field”.
Acknowledgments
I thank Christine Joblin and Olivier Berné for numerous comments and discussions and for
sharing insights and unpublished work. I am very deeply indebted to Sydney Leach for many
discussions and for sharing his interest and insights in fullerene physics, for careful
reading and improving the manuscript, and for also sharing unpublished work. I am indebted
to Matt Lehnert for his detailed, careful reading and for improving the manuscript. I
especially thank Dmitry Strelnikov for his careful reading of the manuscript, important
comments and suggestions, and for providing me in advance with their unpublished data on
C spectroscopy. I would like to thank Giacomo Mulas, Elisabetta Micelottta, Roland Gredel,
Fernand Spiegelman, Aude Simon, Nick Cox, Jose Cernicharo, Jeronimo Bernard-Salas, Steven
Federman, Patrick Boissé, Françoise Remacle, Benoit Mignolet, Michel Broyer, Thomas Pino,
Adolf Witt, Brice Ménard, Ting-wen Lan, Chao Liu and Xiaowei Liu for many discussions and
comments on various aspects of the manusript, as well as Chentao Yang for his nice help. I
especially thank Madeleine Roux-Merlin for her precious help in finding many references. I
thank Joli Adams for her many and detailed suggestions for correcting the english. I thank
the anonymous referee very much for the very helpful suggestions for shortening and
improving the manuscript.
spectroscopy. I would like to thank Giacomo Mulas, Elisabetta Micelottta, Roland Gredel,
Fernand Spiegelman, Aude Simon, Nick Cox, Jose Cernicharo, Jeronimo Bernard-Salas, Steven
Federman, Patrick Boissé, Françoise Remacle, Benoit Mignolet, Michel Broyer, Thomas Pino,
Adolf Witt, Brice Ménard, Ting-wen Lan, Chao Liu and Xiaowei Liu for many discussions and
comments on various aspects of the manusript, as well as Chentao Yang for his nice help. I
especially thank Madeleine Roux-Merlin for her precious help in finding many references. I
thank Joli Adams for her many and detailed suggestions for correcting the english. I thank
the anonymous referee very much for the very helpful suggestions for shortening and
improving the manuscript.
References
- Agúndez, M., Fonfría, J. P., Cernicharo, J., et al. 2012, A&A, 543, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Akasak, T., & Nakase, 2001, Endofullerenes: A New Family of Carbon Clusters, eds. T. Akasak, & S. Nagase (Dordrecht, Netherlands: Kluwer Academic) [Google Scholar]
- Andersen, J. U., Brink, C., Hvelplund, P., et al. 1996, Phys. Rev. Lett., 77, 3991 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Andersen, J. U., Gottrup, C., Hansen, K., Hvelplund, P., & Larsson, M. O. 2001, Eur. Phys. J. D, 17, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreoni, W., Curioni, A., Holczer, K., et al. 1996, J. Am. Chem. Soc., 118, 11335 [CrossRef] [Google Scholar]
- Andrews, H., Boersma, C., Werner, M. W., et al. 2015, ApJ, 807, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Anthony, S. M., Bachilo, S. M., & Weisman, R. B. 2003, J. Phys. Chem. A, 107, 10674 [CrossRef] [Google Scholar]
- Bachilo, S. M., Benedetto, A. F., Weisman, R. B., et al. 2000, J. Phys. Chem. A, 104, 11265 [CrossRef] [Google Scholar]
- Bailey, M., van Loon, J. T., Sarre, P. J., & Beckman, J. E. 2015a, MNRAS, 454, 4013 [NASA ADS] [CrossRef] [Google Scholar]
- Bailey, M., van Loon, J. T., Farhang, A., et al. 2015b, A&A, 585, A12 [Google Scholar]
- Baleizão, C., & Berberan-Santos, M. N. 2007, J. Chem. Phys., 126, 204510 [NASA ADS] [CrossRef] [Google Scholar]
- Baleizão, C., & Berberan-Santos, M. N. 2011, Chem. Phys. Chem., 12, 1247 [CrossRef] [Google Scholar]
- Baron, D., Poznanski, D., Watson, D., Yao, Y., & Prochaska, J. X. 2015a, MNRAS, 447, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Baron, D., Poznanski, D., Watson, D., et al. 2015b, MNRAS, 451, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Basir, Y. S., & Anderson, S. L. 1999, Int. J. Mass Spectr., 185, 603 [CrossRef] [Google Scholar]
- Beck, R. D., Weis, P., Rockenberger, J., & Kappes, M. M. 1996, Surf. Rev. Lett., 3, 771 [CrossRef] [Google Scholar]
- Becker, L., & Bunch, T. E. 1997, Met. Planet. Sci., 32, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Berkowitz, J. 1999, Chem. Phys., 111, 1446 [NASA ADS] [CrossRef] [Google Scholar]
- Bendale, R. D., Stanton, J. F., & Zerner, M. C. 1992, Chem. Phys. Lett., 194, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Bensasson, R. V., Bienvenue, E., Janot, J.-M. et al. 1995, Chem. Phys. Lett., 245, 566 [NASA ADS] [CrossRef] [Google Scholar]
- Bernard-Salas, J., Cami, J., Peeters, E., et al. 2012, ApJ, 757, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Berné, O., & Tielens, A. G. G. M. 2012, Proc. Nat. Acad. Sci., 109, 401 [Google Scholar]
- Berné, O., Mulas, G., & Joblin, C. 2013, A&A, 550, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berné, O., Montillaud, J., & Joblin, C. 2015a, A&A, 577, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berné, O., Montillaud, J., Mulas, G., & Joblin, C. 2015b, SF2A-2015: Proc. Annual meeting of the French Society of Astronomy and Astrophysics, eds. F. Martins, S. Boissier, V. Buat, L. Cambrésy, & P. Petit, 65 [Google Scholar]
- Bettinger, H. F., Rabuck, A. D., Scuseria, G. E., et al. 2002, Chem. Phys. Lett., 360, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Bhatt, N. H., & Cami, J. 2015, ApJS, 216, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Bihlmeier, A., Samson, C. C. M., & Klopper, W. 2005, Chem. Phys. Chem., 6, 2625 [CrossRef] [Google Scholar]
- Billas, I. M. L., Massobrio, C., Boero, M., et al. 1999, J. Chem. Phys., 111, 6787 [NASA ADS] [CrossRef] [Google Scholar]
- Boersma, C., Rubin, R. H., & Allamandola, L. J. 2012, ApJ, 753, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Bolskar, R. D., Gallagher, S. H., Armstrong, R. S., Lay, P. A., & Reed, C. A. 1995, Chem. Phys. Lett., 247, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Broclawik, E., & Eilmes, A. 1998, J. Chem. Phys., 108, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Buchachenko, A. L., & Breslavskaya, N. N. 2005, Russ. Chem. Bull., 54, 51 [CrossRef] [Google Scholar]
- Burton Williams, T., Sarre, P., Marshall, C., Spekkens, K., & Kuzio de Naray, R. 2015, IAU General Assembly, Meeting 29, 2255619 [Google Scholar]
- Cami, J. 2014, IAU Symp., 297, 370 [NASA ADS] [Google Scholar]
- Cami, J., & Cox, N. L. J. 2014, IAU Symp., 297 [Google Scholar]
- Cami, J., Sonnentrucker, P., Ehrenfreund, P., & Foing, B. H. 1997, A&A, 326, 822 [NASA ADS] [Google Scholar]
- Cami, J., Salama, F., Jiménez-Vicente, J., Galazutdinov, G. A., & Krełowski, J. 2004, ApJ, 611, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Cami, J., Bernard-Salas, J., Peeters, E., & Malek, S. E. 2010, Science, 329, 1180 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cami, J., Bernard-Salas, J., Peeters, E., & Malek, S. E. 2011, IAU Symp., 280, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell, E. E. B., & Rohmund, F. 2000, Rep. Prog. Phys., 63, 1061 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell, E. E. B., Ehlich, R., Heusler, G., et al. 1998, Chem. Phys., 239, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell, E. K., Holz, M., Gerlich, D., & Maier, J. P. 2015, Nature, 523, 322 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cataldo, F., & Iglesias-Groth, S. 2009, MNRAS, 400, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Cataldo, F., Strazzulla, G., & Iglesias-Groth, S. 2009, MNRAS, 394, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Cataldo, F., Iglesias-Groth, S., & Manchado, A. 2012, Fullerenes Nanotubes and Carbon Nanostructures, 20, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Cataldo, F., Iglesias-Groth, S., & Hafez, Y. 2013, Eur. Chem. Bull., 2, 1013 [Google Scholar]
- Cataldo, F., García-Hernández, D. A., Manchado, A., & Iglesias-Groth, S. 2014, IAU Symp., 297, 294 [NASA ADS] [Google Scholar]
- Cavar, E., Blüm, M.-C., Pivetta, M., et al. 2005, Phys. Rev. Lett., 95, 196102 [NASA ADS] [CrossRef] [Google Scholar]
- Chakraborty, H. S., Madjet, M. E., Rost, J.-M., & Manson, S. T. 2008, Phys. Rev. A, 78, 013201 [NASA ADS] [CrossRef] [Google Scholar]
- Chancey, C. C., & O’Brien, C. M. 1997. The Jahn-Teller effect in C60 and other icosahedral complexes (Princeton University Press) [Google Scholar]
- Chang, A. H. H., Ermler, W. C., & Pitzer, R. M. 1991, J. Chem. Phys., 94, 5004 [NASA ADS] [CrossRef] [Google Scholar]
- Chergui, M. 2000, Low Temperature Physics, 26, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, C., Kertesz, M., & Mihaly, L. 2000, J. Phys. Chem. A, 104, 102 [CrossRef] [Google Scholar]
- Christian, J. F., Wan, Z., Anderson, S. L. 1992a, Chem. Phys. Lett., 199, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Christian, J. F., Wan, Z., & Anderson, S. L. 1992b, J. Phys. Chem., 96, 10597 [CrossRef] [Google Scholar]
- Christian, J. F., Wan, Z., & Anderson, S. L. 1992c, J. Phys. Chem., 96, 3574 [CrossRef] [Google Scholar]
- Chuvilin, A., Kaiser, U., Bichoutskaia, E., Besley, N. A., & Khlobystov, A. N. 2010, Nature Chem., 2, 450 [CrossRef] [Google Scholar]
- Clipston, N. L. 2000, J. Phys. Chem. A, 104, 9171 [CrossRef] [Google Scholar]
- Close, J. D., Federmann, F., Hoffmann, K., & Quaas, N. 1997, Chem. Phys. Lett., 276, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Cong, H., Bing, Y., Takeshi, A., & Xing, L. 2013, Coordination Chem. Rev., 257, 2880 [CrossRef] [Google Scholar]
- Connerade, J. P., & Solovyov, A. V. 2005, J. Phys. B, 38, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Connerade, J. P., Dolmatov, V. K., & Lakshmi, P. A. 2000, J. Phys. B, 33, 251 [Google Scholar]
- Cordiner, M. A. 2014, IAU Symp., 297, 41 [NASA ADS] [Google Scholar]
- Cox, N. L. J. 2006, Ph.D. Thesis, Amsterdam University [Google Scholar]
- Cox, N. L. J. 2011, in PAHs and the Universe: A Symposium to Celebrate the 25th Anniversary of the PAH Hypothesis, eds. C. Joblin, & A. G. G. M. Tielens, EAS Pub. Ser., 46, 349 [Google Scholar]
- Cox, N. L. J. 2015, ArXiv e-prints [arXiv:1504.03281] [Google Scholar]
- Cox, N. L. J., & Cami, J. 2014, IAU Symp., 297, 412 [NASA ADS] [Google Scholar]
- Cox, N. L. J., Kaper, L., Foing, B. H., & Ehrenfreund, P. 2005, A&A, 438, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, N. L. J., Boudin, N., Foing, B. H., et al. 2007, A&A, 465, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, N. L. J., Ehrenfreund, P., Foing, B. H., et al. 2011, A&A, 531, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, N. L. J., Cami, J., Kaper, L., et al. 2014, A&A, 569, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crawford, M. K., Tielens, A. G. G. M., & Allamandola, L. J. 1985, ApJ, 293, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Dahlstrom, J., York, D. G., Welty, D. E., et al. 2013, ApJ, 773, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Deng, R., Clegg, A., & Echt, O. 2003, Int. J. Mass Spectr., 223, 695 [CrossRef] [Google Scholar]
- Díaz-Tendero, S., Sánchez, G., Alcamí, M., & Martín, F. 2006, Int. J. Mass Spectr., 252, 133 [CrossRef] [Google Scholar]
- Dresselhaus, M. S., Dresselhaus, G., & Eklund, P. C. 1996, Science of Fullerenes and Carbon Nanotubes (San Diego: Academic Press) [Google Scholar]
- Duley, W. W., & Williams, D. A. 2011, ApJ, 737, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Dunbar, R. C., Uechi, G. T., Asamoto, B., et al. 1994, J. Am. Chem. Soc., 116, 2466 [CrossRef] [Google Scholar]
- Dunk, P. W., Kaiser, N. K., Hendrickson, C. L., et al. 2012, Nature Commun., 3, 855 [NASA ADS] [CrossRef] [Google Scholar]
- Dunk, P. W., Adjizian, J.-J., Kaiser, N. K., et al. 2013, Proc. Nat. Acad. Sci., 110, 18081 [Google Scholar]
- Dunk, P. W., Mulet-Gas, M., Nakanishi, Y., et al. 2014, Nature Commun., 5, 5844 [NASA ADS] [CrossRef] [Google Scholar]
- Echt, O., Yao, S., Deng, R., & Hansen, K. 2005, J. Phys. Chem. A, 108, 6944 [CrossRef] [Google Scholar]
- Edwards, S. A., & Leach, S. 1993, A&A, 272, 533 [NASA ADS] [Google Scholar]
- Ehrenfreund, P., & Foing, B. H. 1995, Planet. Space Sci., 43, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Ehrenfreund, P., & Foing, B. H. 2010, Science, 329, 1159 [NASA ADS] [CrossRef] [Google Scholar]
- Ehrenfreund, P., & Foing, B. 2015, Nature, 523, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Erhler, O. T., Yang, J. P., Hättig, C., et al. 2006, J. Chem. Phys., 125, 074312 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Etheridge, H. T., Averitt, R. D., Halas, N. J., & Weisman, R. B. 1995, J. Phys. Chem., 99, 11306 [CrossRef] [Google Scholar]
- Farhang, A., Khosroshahi, H. G., Javadi, A., et al. 2015, ApJ, 800, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, M., Zhao, J., & Petek, H. 2008, Science, New Series, 320, 359 [Google Scholar]
- Foing, B. H., & Ehrenfreund, P. 1994, Nature, 369, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Foing, B. H., & Ehrenfreund, P. 1997, A&A, 317, L59 [NASA ADS] [Google Scholar]
- Frommhold, L. 1993, Collisison-Induced Absorption in Gases, Cambridge Monographs on Atomic, Molecular, and Chemical Physics (Cambridge, England: Cambridge University Press), 2 [Google Scholar]
- Fulara, J., Lessen, D., Freivogel, P., & Maier, J. P. 1993a, Nature, 366, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Fulara, J., Jakobi, M., & Maier, J. P. 1993b, Chem. Phys. Lett., 206, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Galazutdinov, G. A., Krełowski, J., Musaev, F. A., Ehrenfreund, P., & Foing, B. H. 2000, MNRAS, 317, 750 [NASA ADS] [CrossRef] [Google Scholar]
- García-Hernández, D. A., Manchado, A., García-Lario, P., et al. 2010, ApJ, 724, L39 [NASA ADS] [CrossRef] [Google Scholar]
- García-Hernández, D. A., Kameswara Rao, N., & Lambert, D. L. 2011a, ApJ, 729, 126 [NASA ADS] [CrossRef] [Google Scholar]
- García-Hernández, D. A., Iglesias-Groth, S., Acosta-Pulido, J. A., et al. 2011b, ApJ, 737, L30 [NASA ADS] [CrossRef] [Google Scholar]
- García-Hernández, D. A., Kameswara Rao, N., & Lambert, D. L. 2012, ApJ, 759, L21 [NASA ADS] [CrossRef] [Google Scholar]
- García-Hernández, D. A., Cataldo, F., & Manchado, A. 2013, MNRAS, 434, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Gasyna, Z., Andrews, L., & Schatz, P. N. 1992, J. Phys. Chem., 96, 1525 [CrossRef] [Google Scholar]
- Ge, M., Nagel, U., Hüvonen, D., et al. 2011, J. Chem. Phys., 134, 054507 [NASA ADS] [CrossRef] [Google Scholar]
- Geballe, T. R., Najarro, F., Figer, D. F., Schlegelmilch, B. W., & de La Fuente, D. 2011, Nature, 479, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Geballe, T. R., Najarro, F., de la Fuente, D., et al. 2014, IAU Symp., 303, 75 [NASA ADS] [Google Scholar]
- Gielen, C., Cami, J., Bouwman, J., Peeters, E., & Min, M. 2011, A&A, 536, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillmon, K., Shull, J. M., Tumlinson, J., & Danforth, C. 2006, ApJ, 636, 891 [NASA ADS] [CrossRef] [Google Scholar]
- Gluch, K., Matt-Leubner, S., Echt, O., et al. 2004, J. Chem. Phys., 121, 2137 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gredel, R., Carpentier, Y., Rouillé, G., et al. 2011, A&A, 530, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guha, S., & Nakamoto, K. 2005, Coordination Chem. Rev., 249, 1111 [CrossRef] [Google Scholar]
- Hamano, S., Kobayashi, N., Kondo, S., et al. 2015, ApJ, 800, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Hammond, M. R., & Zare, R. N. 2008, Geochim. Cosmochim. Acta, 72, 5521 [NASA ADS] [CrossRef] [Google Scholar]
- Hands, I. D., Dunn, J. L., Bates, C. A., et al. 2008, Phys. Rev. B, 77, 5445 [CrossRef] [Google Scholar]
- Hansen, K., Müller, R., Brockhaus, P., et al. 1997, Z. Phys. D, 42, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Hasoglu, M. F., Zhou, H.-L., Gorczyca, T. W., & Manson, S. T. 2013, Phys. Rev. A, 87, 3409 [NASA ADS] [CrossRef] [Google Scholar]
- Haufler, R. E., Chai, Y., Chibante, L. P. F., et al. 1991, J. Chem. Phys., 95, 2197 [NASA ADS] [CrossRef] [Google Scholar]
- Hauke, F., et al. 2004, Chem. Comm., 766 [Google Scholar]
- Hauke, F., et al. 2006, Chem. Eur. J., 12, 4813 [CrossRef] [Google Scholar]
- Hedén, M., Bulgakov, A. V., Mehlig, K., & Campbell, E. E. B. 2003, J. Chem. Phys., 118, 7161 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, M. L. 1922, Lick Observatory Bulletin, 10, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Herbig, G. H. 1975, ApJ, 196, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Herbig, G. H. 1993, ApJ, 407, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Herbig, G. H. 1995, ARA&A, 33, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Herbig, G. H. 2000, ApJ, 542, 334 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hernández-Rojas, J., Bretón, J., & Gomez Llorente, J. M. 1996, J. Chem. Phys., 104, 1179 [NASA ADS] [CrossRef] [Google Scholar]
- Heymann, D., & Weisman, R. W. 2006, C. R. Chimie, 9, 1107 [CrossRef] [Google Scholar]
- Hobbs, L. M., York, D. G., Snow, T. P., et al. 2008, ApJ, 680, 1256 [NASA ADS] [CrossRef] [Google Scholar]
- Hobbs, L. M., York, D. G., Thorburn, J. A., et al. 2009, ApJ, 705, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, D. L., Dau, P. D., Liu, H.-T., & Wang, L.-S. 2014, J. Chem. Phys., 140, 224315 [NASA ADS] [CrossRef] [Google Scholar]
- Hudgins, D. M., Bauschlicher, C. W., Jr., & Allamandola, L. J. 2005, ApJ, 632, 316 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iglesias-Groth, S. 2006, MNRAS, 368, 1925 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias-Groth, S., & Esposito, M. 2013, ApJ, 776, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias-Groth, S., García-Hernández, D. A., Cataldo, F., & Manchado, A. 2012, MNRAS, 423, 2868 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, E. B. 2009, ApJ, 700, 1299 [NASA ADS] [CrossRef] [Google Scholar]
- Jenniskens, P., & Desert, F.-X. 1994, A&AS, 106, 39 [NASA ADS] [Google Scholar]
- Jiao, H., Chen, Z., Hirsch, A., & Thiel, W. 2002, Phys. Chem. Chem. Phys., 4, 4916 [CrossRef] [Google Scholar]
- Jin, C., Lan, H., Peng, L., Suenaga, K., & Iijima, S. 2009, Phys. Rev. Lett., 102, 205501 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Joalland, B., Simon, A., Marsden, C. J., & Joblin, C. 2009, A&A, 494, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joblin, C., D’Hendecourt, L., Leger, A., & Maillard, J. P. 1990, Nature, 346, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Jochims, H. W., Baumgaertel, H., & Leach, S. 1996, A&A, 314, 1003 [NASA ADS] [Google Scholar]
- Johansson, J.O., & Campbell, E. E. B. 2013, Chem. Soc. Rev., 42, 5661 [CrossRef] [Google Scholar]
- Jones, A. P. 2013, A&A, 555, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P. 2014, Planet. Space Sci., 100, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. 2015, Highlights of Astronomy, 16, 707 [NASA ADS] [Google Scholar]
- Kato, T., Kodama, T., Shida, T., et al. 1991, Chem. Phys. Lett., 180, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Kaźmierczak, M., Schmidt, M. R., Bondar, A., & Krełowski, J. 2010, MNRAS, 402, 2548 [NASA ADS] [CrossRef] [Google Scholar]
- Kaźmierczak, M., Schmidt, M., Weselak, T., Galazutdinov, G., & Krełowski, J. 2014, IAU Symp., 297, 121 [NASA ADS] [Google Scholar]
- Kern, B., Strelnikov, D., Weis, P., Böttcher, A., & Kappes, M. M. 2013, J. Phys. Chem. A, 117, 8251 [CrossRef] [Google Scholar]
- Kern, B., Strelnikov, D., Weis, P., Böttcher, A., & Kappes, M. M. 2014, J. Phys. Chem. Lett., 5, 457 [CrossRef] [Google Scholar]
- Kerr, T. H., Hurst, M. E., Miles, J. R., & Sarre, P. J. 1999, MNRAS, 303, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Keshavarz-K, M., González, R., Hicks, R. G., et al. 1996, Nature, 383, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Klaiman, S., Gromov, E. V., & Cederbaum, L. S. 2013, J. Phys. Chem. Lett., 4, 3319 [CrossRef] [Google Scholar]
- Klaiman, S., Gromov, E. V., & Cederbaum, L. S. 2014, Phys. Chem. Chem. Phys., 16, 13287 [CrossRef] [Google Scholar]
- Komatsu, K., Murata, M., & Murata, Y. 2005, Science, 307, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Koponen, L., Puska, M. J., & Nieminen, R. M. 2008, J. Chem. Phys., 128, 154307 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kordatos, K., DaRos, T., Prato, M., Bensasson, R. V., & Leach, S. 2003, Chem. Phys., 293, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Kos, J., Zwitter, T., Grebel, E. K., et al. 2013, ApJ, 778, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Kos, J., Zwitter, T., Wyse, R., et al. 2014, Science, 345, 791 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Krätschmer, W., Lamb, L. D., Fostiropoulos, K., & Huffman, D. R. 1990, Nature, 347, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Krełowski, J. 2014, IAU Symp., 297, 23 [NASA ADS] [Google Scholar]
- Krelowski, J., & Walker, G. A. H. 1987, ApJ, 312, 860 [NASA ADS] [CrossRef] [Google Scholar]
- Krełowski, J., Snow, T. P., Seab, C. G., & Papaj, J. 1992, MNRAS, 258, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Kroto, H. W. 1987, eds. A. Léger, et al., NATO Advanced Science Institutes (ASI) Series C, 191, 197 [Google Scholar]
- Kroto, H. 1988, Science, 242, 1139 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kroto, H. W. 1989, Ann. Phys., 14, 169 [CrossRef] [EDP Sciences] [Google Scholar]
- Kroto, H. W., & Jura, M. 1992, A&A, 263, 275 [NASA ADS] [Google Scholar]
- Kroto, H. W., Heath, J. R., Obrien, S. C., Curl, R. F., & Smalley, R. E. 1985, Nature, 318, 16 [Google Scholar]
- Lan, Y., Kang, H., & Niu, T. 2015a, Eur. Phys. J. D, 69, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lan, T.-W., Ménard, B., & Zhu, G. 2015b, MNRAS, 452, 3629 [Google Scholar]
- Langhoff, S. R. 1996, J. Phys. Chem., 100, 2819 [CrossRef] [Google Scholar]
- Leach, S. 2001, Can. J. Phys., 79, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Leach, S. 2004, Israel J. Chem., 44, 193 [CrossRef] [Google Scholar]
- Leach, S., Vervloet, M., Desprès, A., et al. 1992, Chem. Phys., 160, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, Y. H., Kim, S. G., & Tománek, D. 1997, Phys. Rev. Lettt., 78, 2393 [NASA ADS] [CrossRef] [Google Scholar]
- Léger, A., & D’Hendecourt, L. 1985, A&A, 146, L81 [NASA ADS] [Google Scholar]
- Léger, A., Jura, M., & Omont, A. 1985, A&A, 144, 147 [NASA ADS] [Google Scholar]
- Léger, A., D’Hendecourt, L., & Boissel, P. 1988a, Phys. Rev. Lett., 60, 921 [NASA ADS] [CrossRef] [Google Scholar]
- Léger, A., D’Hendecourt, L., Verstraete, L., & Schmidt, W. 1988b, A&A, 203, 145 [NASA ADS] [Google Scholar]
- Léger, A., D’Hendecourt, L., & Defourneau, D. 1989, A&A, 216, 148 [NASA ADS] [Google Scholar]
- Le Page, V., Snow, T. P., & Bierbaum, V. M. 2001, ApJS, 132, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Le Page, V., Snow, T. P., & Bierbaum, V. M. 2003, ApJ, 584, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Lepp, S., Dalgarno, A., van Dishoeck, E. F., & Black, J. H. 1988, ApJ, 329, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Lifshitz, C. 2000, Int. J. Mass Spectr., 198, 1 [CrossRef] [Google Scholar]
- Long, Z., Zhou, X., & Cai, H. 2013, Chem. Phys. Lett., 583, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, X., Feng, L., Akasaka, T., et al. 2012, Chem. Soc. Rev., 41, 7723 [CrossRef] [Google Scholar]
- Lyras, A., & Bachau, H. 2005, J. Phys. B: At. Mol. Opt. Phys., 38, 1119 [NASA ADS] [CrossRef] [Google Scholar]
- Maier, J. P. 1994, Nature, 370, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Maier, J. P., Walker, G. A. H., & Bohlender, D. A. 2004, ApJ, 602, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Maíz Apellániz, J., Barbá, R. H., Sota, A., & Simón-Díaz, S. 2015, A&A, 583, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mamone, S., Ge, M., Hüvonen, D., et al. 2009, J. Chem. Phys., 130, 081103 [NASA ADS] [CrossRef] [Google Scholar]
- Mamone, S., Chen, J. Y.-C., Bhattacharyya, R., et al. 2011, Co. Chem. Rev., 255, 938 [CrossRef] [Google Scholar]
- Marciniak, A., Despré, V., Barillot, T., et al. 2015, Nature Commun., 6, 7909 [NASA ADS] [CrossRef] [Google Scholar]
- Marcos, P. A., Alonso, J. A., Molina, L. M., et al. 2003, J. Chem. Phys., 119, 1127 [NASA ADS] [CrossRef] [Google Scholar]
- Marshall, C. C. M., Krełowski, J., & Sarre, P. J. 2015, MNRAS, 453, 3912 [NASA ADS] [CrossRef] [Google Scholar]
- McCall, B. J., Thorburn, J., Hobbs, L. M., Oka, T., & York, D. G. 2001, ApJ, 559, L49 [NASA ADS] [CrossRef] [Google Scholar]
- McIntosh, A., & Webster, A. 1993, MNRAS, 261, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Men’shchikov, A. B., Schertl, D., Tuthill, P. G., Weigelt, G., & Yungelson, L. R. 2002, A&A, 393, 867 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merino, P., Svec, M., Martinez, J. I., et al. 2014, Nature Commun., 5, 3054 [NASA ADS] [CrossRef] [Google Scholar]
- Merrill, P. W. 1934, PASP, 46, 206 [NASA ADS] [CrossRef] [Google Scholar]
- Merrill, P. W. 1936, PASP, 48, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Micelotta, E. R., Jones, A. P., & Tielens, A. G. G. M. 2010a, A&A, 510, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Micelotta, E. R., Jones, A. P., & Tielens, A. G. G. M. 2010b, A&A, 510, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Micelotta, E. R., Jones, A. P., & Tielens, A. G. G. M. 2011, A&A, 526, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Micelotta, E. R., Jones, A. P., Cami, J., et al. 2012, ApJ, 761, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Micelotta, E. R., Cami, J., Peeters, E., et al. 2014, IAU Symp., 297, 339 [NASA ADS] [Google Scholar]
- Milisavljevic, D., Margutti, R., Crabtree, K. N., et al. 2014, ApJ, 782, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Millar, T. J. 1992, MNRAS, 259, 35P [NASA ADS] [CrossRef] [Google Scholar]
- Misawa, T., Gandhi, P., Hida, A., Tamagawa, T., & Yamaguchi, T. 2009, ApJ, 700, 1988 [NASA ADS] [CrossRef] [Google Scholar]
- Montillaud, J., & Joblin, C. 2014, A&A, 567, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montillaud, J., Joblin, C., & Toublanc, D. 2013, A&A, 552, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Munari, U., Tomasella, L., Fiorucci, M., et al. 2008, A&A, 488, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murata, M. 2006, J. Am. Chem. Soc., 128, 8025 [CrossRef] [Google Scholar]
- Neyts, E., Maeyens, A., Pourtois, G., & Bogaerts, A. 2011, Carbon, 49, 1013 [CrossRef] [Google Scholar]
- Oka, T., Welty, D. E., Johnson, S., et al. 2013, ApJ, 773, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Oka, T., Welty, D. E., Johnson, S., et al. 2014, ApJ, 793, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Okamoto, Y. 2001, J. Phys. Chem. A 2001, 105, 7634 [Google Scholar]
- Oksengorn, B. 2003, C. R. Chimie, 6, 467 [CrossRef] [Google Scholar]
- Omont, A. 1986, A&A, 164, 159 [NASA ADS] [Google Scholar]
- Orlandi, G., & Negri, F. 2002, Photochem. Photobiol. Sci., 1, 289 [CrossRef] [Google Scholar]
- Otsuka, M., Kemper, F., Hyung, S., et al. 2013, ApJ, 764, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Otsuka, M., Kemper, F., Cami, J., Peeters, E., & Bernard-Salas, J. 2014, MNRAS, 437, 2577 [NASA ADS] [CrossRef] [Google Scholar]
- Peeters, E., Tielens, A. G. G. M., Allamandola, L. J., & Wolfire, M. G. 2012, ApJ, 747, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Pellarin, M., Ray, C., Mélinon, P., et al. 1997, Chem. Phys. Lett., 277, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Pellarin, M., Ray, C., Lermé, J., et al. 1999, Eur. Phys. J. D, 9, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Pellarin, M., Cottancin, E., Lerme, J., et al. 2002, J. Chem. Phys., 117, 3088 [NASA ADS] [CrossRef] [Google Scholar]
- Pennington, C. H., & Stenger, V. A. 1996, Rev. Mod. Phys., 68, 855 [NASA ADS] [CrossRef] [Google Scholar]
- Petrie, S., & Bohme, D. K. 2000, ApJ, 540, 869 [Google Scholar]
- Petrie, S., Becker, H., Baranov, V., & Bohme, D. K. 1995, Int. J. Mass Spectr. Ion Processes, 145, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrucci, F., & Andreoni, W. 2014, J. Chem. Theory Comput., 10, 913 [CrossRef] [Google Scholar]
- Pino, T., Dartois, E., Cao, A.-T., et al. 2008, A&A, 490, 665 [CrossRef] [EDP Sciences] [Google Scholar]
- Popov, A.A., Yang, S., & Dunsch, L. 2013, Chem. Rev., 113, 5989 [CrossRef] [PubMed] [Google Scholar]
- Puspitarini, L., Lallement, R., Babusiaux, C., et al. 2015, A&A, 573, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramachandran, C. N., et al. 2008, Chem. Phys. Lett., 461, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Rawlings, M. G., Adamson, A. J., & Kerr, T. H. 2014, ApJ, 796, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Ray, C., Pellarin, M., Lermé, J. L., et al. 1998, Phys. Rev. Lett., 80, 5365 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, V. S., Ghanta, S., & Mahapatra, S. 2010, Phys. Rev. Lett., 104, 111102 [NASA ADS] [CrossRef] [Google Scholar]
- Ren, A., Feng, J., Sun, X., et al. 2000, Int. J. Quant. Chem., 78, 422 [CrossRef] [Google Scholar]
- Ren, X., Hentges, R., Becker, U., et al. 2004, J. Mol. Struct., 686, 43 [CrossRef] [Google Scholar]
- Rietmeijer, F. J. M. 2006, Natural Fullerenes and Related Structures of Elemental Carbon (Springer) [Google Scholar]
- Roberts, K. R. G., Smith, K. T., & Sarre, P. J. 2012, MNRAS, 421, 3277 [NASA ADS] [CrossRef] [Google Scholar]
- Rubin, R. H., Simpson, J. P., O’Dell, C. R., et al. 2011, MNRAS, 410, 1320 [NASA ADS] [CrossRef] [Google Scholar]
- Rüdel, A., Fronzoni, G., Venuti, M., & Decleva, P. 2002, Phys. Rev. Lett., 89, 125503 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Salama, F., & Ehrenfreund, P. 2014, IAU Symp., 297, 364 [NASA ADS] [Google Scholar]
- Salama, F., Bakes, E. L. O., Allamandola, L. J., & Tielens, A. G. G. M. 1996, ApJ, 458, 621 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Salama, F., Galazutdinov, G. A., Krełowski, J., et al. 2011, ApJ, 728, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Salazar, F. A., Fedorov, A., & Berberan-Santos, M. N. 1997, Chem. Phys. Lett., 271, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Sarre, P. J. 2006, J. Mol. Spectrosc., 238, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Sarre, P. J. 2008, IAU Symp., 251, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Sarre, P. J. 2014, IAU Symp., 297, 34 [NASA ADS] [Google Scholar]
- Sassara, A., Zerza, G., & Chergui, M. 1996a, J. Phys. B: At. Mol. Opt. Phys., 29, 4997 [NASA ADS] [CrossRef] [Google Scholar]
- Sassara, A., Zerza, G., & Chergui, M. 1996b, Chem. Phys. Lett., 261, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Sassara, A., Zerza, G., Chergui, M., Negri, F., & Orlandi, G. 1997, J. Chem. Phys., 107, 8731 [NASA ADS] [CrossRef] [Google Scholar]
- Sassara, A., Zerza, G., Chergui, M., & Leach, S. 2001, ApJS, 135, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Savage, B. D., & Sembach, K. R. 1996, ARA&A, 34, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, G. D., Cohen, M., & Margon, B. 1980, ApJ, 239, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, A., Duley, W. W., & Pinho, G. P. 1997, ApJ, 489, L193 [NASA ADS] [CrossRef] [Google Scholar]
- Scuseria, G. E. 1991, Chem. Phys. Lett., 180, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Sellgren, K., Uchida, K. I., & Werner, M. W. 2007, ApJ, 659, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Sellgren, K., Werner, M. W., Ingalls, J. G., et al. 2010, ApJ, 722, L54 [NASA ADS] [CrossRef] [Google Scholar]
- Shinohara, H. 2000, Rep. Prog. Phys., 63, 843 [NASA ADS] [CrossRef] [Google Scholar]
- Shvartsburg, A. A., Hudgins, R. R., Dugourd, P., et al. 2000, Phys. Rev. Lett., 84, 2421 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Simon, A., & Joblin, C. 2007, J. Phys. Chem. A, 111, 9745 [CrossRef] [PubMed] [Google Scholar]
- Simon, A., & Joblin, C. 2009, J. Phys. Chem. A, 113, 4878 [CrossRef] [PubMed] [Google Scholar]
- Sitko, M. L., Bernstein, L. S., & Glinski, R. J. 2008, ApJ, 680, 1426 [NASA ADS] [CrossRef] [Google Scholar]
- Slanina, Z., & Lee, S. L. 1994, J. Mol. Structure: Theochem, 304, 173 [CrossRef] [Google Scholar]
- Smalley, R. E. 1992, Acc. Chem. Res., 25, 98 [CrossRef] [Google Scholar]
- Smith, A. B. III, Strongin, R. M., Brard, L., et al. 1995, J. Am. Chem. Soc., 117, 5492 [CrossRef] [Google Scholar]
- Snow, T. P. 1995, in The Diffuse Interstellar Bands, eds. A. G. G. M. Tielens, & T. P. Snow (Kluwer), Astrophys. Space Sci. Libr., 202 [Google Scholar]
- Snow, T. P. 2001, Spectrochim. Acta, 57, 615 [Google Scholar]
- Snow, T. P. 2014, IAU Symp., 297, 3 [NASA ADS] [Google Scholar]
- Snow, T. P., & McCall, B. J. 2006, ARA&A, 44, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Snow, T. P., Zukowski, D., & Massey, P. 2002, ApJ, 578, 877 [NASA ADS] [CrossRef] [Google Scholar]
- Sonnentrucker, P. 2014, IAU Symp., 297, 13 [NASA ADS] [Google Scholar]
- Steglich, M., Bouwman, J., Huisken, F., & Henning, T. 2011, ApJ, 742, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Stener, M., Fronzoni, G., Toffoli, D., et al. 1999, Chem. Phys. Lett., 309, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Stener, M., Deng, K.-M., Yang, J.-L., & X. Wang, X. 2002, J. Phys. B: At. Mol. Opt. Phys., 35, 1421 [NASA ADS] [CrossRef] [Google Scholar]
- Stepanov, A. G., Portella-Oberli, M. T., Sassara, A., & Chergui, M. 2002, Chem. Phys. Lett., 358, 516 [NASA ADS] [CrossRef] [Google Scholar]
- Stochkel, K., & Andersen, J. U. 2013, J. Chem. Phys., 139, 164304 [NASA ADS] [CrossRef] [Google Scholar]
- Strelnikov, D., & Krätschmer, W. 2010, Carbon, 48, 1702 [CrossRef] [Google Scholar]
- Strelnikov, D., Kern, B., & Kappes, M. M. 2015, A&A, 584, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tang, C., Chen, J. Y.-C., Sartori, E., et al. 2006, Chin. J. Chem., 24, 1133 [CrossRef] [Google Scholar]
- Tenorio, F., & Robles 2000, J. Int. J. Quant. Chem., 80, 220 [CrossRef] [Google Scholar]
- Thaddeus, P. 1995, in The Diffuse Interstellar Bands, eds. A. G. G. M. Tielens, & T. P. Snow (Kluwer), Astrophys. Space Sci. Lib., 202, 369 [Google Scholar]
- Thorburn, J. A., Hobbs, L. M., McCall, B. J., et al. 2003, ApJ, 584, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M. 2005, The Physics and Chemistry of the Interstellar Medium (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Tielens, A. G. G. M. 2008, ARA&A, 46, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tielens, A. G. G. M. 2013, Rev. Mod. Phys., 85, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M. 2014, IAU Symp., 297, 399 [NASA ADS] [Google Scholar]
- Tielens, A. G. G. M., & Snow, T. P. 1995, The Diffuse Interstellar Bands (Kluwer), Astrophys. Space Sci. Lib., 202 [Google Scholar]
- Tomita, S., et al. 2005, Phys. Rev. Lett., 94, 053002 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tulej, M., Kirkwood, D. A., Pachkov, M., & Maier, J. P. 1998, ApJ, 506, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Turro, N. J., Ganchenkova, M. G., Oikkonen, L. E., & Nieminen, R. M. 2010, Acc. Chem. Res., 43, 335 [CrossRef] [Google Scholar]
- Udvardi, L., Surja, P. R., Kfirti, J., & Pekker, S. 1995, Synthetic Metals, 70, 1377 [CrossRef] [Google Scholar]
- Van der Zwet, G. P., & Allamandola, L. J. 1985, A&A, 146, 76 [NASA ADS] [Google Scholar]
- van Loon, J. T., Bailey, M., Tatton, B. L., et al. 2013, A&A, 550, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Winckel, H. 2014, IAU Symp., 297, 180 [NASA ADS] [Google Scholar]
- Van Winckel, H., Cohen, M., & Gull, T. R. 2002, A&A, 390, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vehvilainen, T. T., Friedman, J. F., Shuman, N. S., et al. 2011, Phys. Rev. B, 84, 085447 [NASA ADS] [CrossRef] [Google Scholar]
- Verstraete, L., & Léger, A. 1992, A&A, 266, 513 [NASA ADS] [Google Scholar]
- Viggiano, A. A., Cederbaum, L. S., & Jordan, K. D. 2010, J. Chem. Phys., 132, 194307 [NASA ADS] [CrossRef] [Google Scholar]
- Voora, D. K., Alford, J. M., Chai, Y., et al. 2013, J. Phys. Chem. Lett., 2013, 849 [CrossRef] [Google Scholar]
- Vos, D. A. I., Cox, N. L. J., Kaper, L., Spaans, M., & Ehrenfreund, P. 2011, A&A, 533, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vostrowsky, O., & Hirsch, A. 2006, Chem. Rev., 106, 5191 [CrossRef] [Google Scholar]
- Waelkens, C., Van Winckel, H., Trams, N. R., & Waters, L. B. F. M. 1992, A&A, 256, L15 [NASA ADS] [Google Scholar]
- Walker, G., Bohlender, D., Maier, J., & Campbell, E. 2015, ApJ, 812, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Wan, Z., Christian, J. F., & Anderson, S. L. 1992, Phys. Rev. Lett., 69, 1352 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wang, L. S., He, Y., Li, Y., & Su, H. 1993, Chem. Phys. Lett., 207, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, H., Harding, L. B., Gray, S. K., & Rice, S. A. 2012, J. Phys. Chem. A, 116, 255 [CrossRef] [Google Scholar]
- Wang, Y., Zettergren, H., Rousseau, P., et al. 2014, Phys. Rev. A, 89, 062708 [NASA ADS] [CrossRef] [Google Scholar]
- Webster, A. 1992, MNRAS, 257, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Welty, D. E., Ritchey, A. M., Dahlstrom, J. A., & York, D. G. 2014, ApJ, 792, 106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Westin, E., & Rosén 1993, Z. Phys. D, 26, S276 [Google Scholar]
- Weisman, R. B. 1999, in Optical and Electronic Properties of Fullerenes and Fullerene-Based Materials, eds. J. Shinar, et al. (New York: Marcel Dekker), 83 [Google Scholar]
- Witt, A. N. 2014, IAU Symp., 297, 173 [NASA ADS] [Google Scholar]
- Xie, R. 2003, Phys. Rev. Lett., 90, 206602 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Xie, R. 2004, J. Chem. Phys., 120, 5133 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Xu, Y. B., Tan, M. Q., & Becker, U. 1996, Phys. Rev. Lett., 76, 3538 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- York, B., Sonnentrucker, P., Hobbs, L. M., et al. 2014, IAU Symp., 297, 138 [NASA ADS] [Google Scholar]
- Yuan, H. B., & Liu, X. W. 2012, MNRAS, 425, 1763 [NASA ADS] [CrossRef] [Google Scholar]
- Zack, L. N., & Maier, J. P. 2014, in The Diffuse Interstellar Bands, Proc. IAU Symp., 297, 237 [NASA ADS] [Google Scholar]
- Zasowski, G., Ménard, B., Bizyaev, D., et al. 2015, ApJ, 798, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y., & Kwok, S. 2011, ApJ, 730, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, M., Harding, L. B., Gray, S. K., et al. 2008, J. Phys. Chem. A, 112, 5478 [CrossRef] [Google Scholar]
- Zhang, J., Bowles, F. L., Bearden, D. W., et al. 2013, Nat. Chem., 5, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Zhen, J., Castellanos, P., Paardekooper, D. M., Linnartz, H., & Tielens, A. G. G. M. 2014, ApJ, 797, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, Z., Sfeir, M. Y., Zhang, L., et al. 2006, ApJ, 638, L105 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Interstellar accretion of C+ to C60
From their measurement of the C+ + C60→ C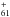 accretion process, Christian et al. (1992c)
suggested that there is no activation energy, though they cannot exclude a small
(<0.5 eV) barrier. Indeed, a reaction barrier
seems unlikely since, e.g., no reaction barrier was found by Strelnikov &
Krätschmer (2010) for C3 reacting with C60, and C and C+ should be even more reactive
than C3. However,
as quoted by Berné et al. (2015a), the actual rate
of C+ accretion,
kC
+, is apparently unknown. A possible guess is that it equals a
significant fraction η of the Langevin rate kL, with perhaps
η at least
~0.1. For a reduced mass
m (reduced
atomic mass μ) and a particle of polarizability α, kL = 2πe
(α/m)0.5 = 2.34 ×
10-9 [ α(Å3)
/μ ] 0.5. Therefore, for
C+ and the
polarizability of C60, α ≈ 80 × Å3, kL = 6 ×
10-9 cm3 s-1. This yields, for the rate of C+ accretion,
accretion process, Christian et al. (1992c)
suggested that there is no activation energy, though they cannot exclude a small
(<0.5 eV) barrier. Indeed, a reaction barrier
seems unlikely since, e.g., no reaction barrier was found by Strelnikov &
Krätschmer (2010) for C3 reacting with C60, and C and C+ should be even more reactive
than C3. However,
as quoted by Berné et al. (2015a), the actual rate
of C+ accretion,
kC
+, is apparently unknown. A possible guess is that it equals a
significant fraction η of the Langevin rate kL, with perhaps
η at least
~0.1. For a reduced mass
m (reduced
atomic mass μ) and a particle of polarizability α, kL = 2πe
(α/m)0.5 = 2.34 ×
10-9 [ α(Å3)
/μ ] 0.5. Therefore, for
C+ and the
polarizability of C60, α ≈ 80 × Å3, kL = 6 ×
10-9 cm3 s-1. This yields, for the rate of C+ accretion,
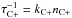 ,
,
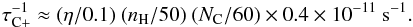 (A.1)Although
fullerenes with unpaired numbers of C are much less stable than C2n, the binding energy of
C60-C remains
substantial, possibly ~4 eV,
as Slanina & Lee 1994 found using the AM1
quantum-chemical method, or ~4.9 eV found from DFT by Pellarin et al. (2002). It could even be smaller (~3 eV, Mulas, priv. comm.) or larger
(Strelnikov, priv. comm.). A low value, ~3 eV, is consistent with the finding by Christian et al. (1992c) that the formation of
C
(A.1)Although
fullerenes with unpaired numbers of C are much less stable than C2n, the binding energy of
C60-C remains
substantial, possibly ~4 eV,
as Slanina & Lee 1994 found using the AM1
quantum-chemical method, or ~4.9 eV found from DFT by Pellarin et al. (2002). It could even be smaller (~3 eV, Mulas, priv. comm.) or larger
(Strelnikov, priv. comm.). A low value, ~3 eV, is consistent with the finding by Christian et al. (1992c) that the formation of
C in collisions of C+
with C60 is
efficient up to a collision energy approaching 10 eV, but that
C
in collisions of C+
with C60 is
efficient up to a collision energy approaching 10 eV, but that
C is negated when it exceeds 10 eV.
is negated when it exceeds 10 eV.
Such a mild binding should make C60–C+ (and perhaps C60–C) relatively easy to destroy by UV photolysis as in the case of smaller-PAH hydrogenation, if their internal conversion of energy is comparable to PAHs. However, it is not clear whether this photolysis should prevent some cage or adduct growth by further C+ accretion, or reactions of C60–C+ with H (Sect. 2.3.4).
Molecules, such as C60–C+, C60–C and their possible derivatives, should be much more stable if C60 is bound to a PAH (Sect. 6.2).
Appendix B: Abundances of interstellar elements
See Table B.1.
Abundances for elements of interest for endohedral fullerenes and heterofullerenes.
Appendix C: Energy levels of C60 endo alkalis and alkaline earths
A complete computation of the first excited levels of K@C60 and Ca@C60 and their cations was
performed by Chang et al. (1991). It should provide
reasonable patterns of the level structure, but, as noted by Broklawik & Eilmes
(1998), such Hartree-Fock calculations, which neglect electron correlations, greatly
underestimate ionization potentials (often by ~2 eV). Similarly, they cannot be trusted for the energy of excited
states either. Nevertheless, from the values computed by Chang et al., one may infer that
each EF among K@C60, Ca@C60, and Ca@C should have at least one allowed absorption transition in the visible or near-infrared
range.
should have at least one allowed absorption transition in the visible or near-infrared
range.
It is important to compute the oscillator strengths of these transitions. Most of them
are between cage levels. The strength of corresponding transitions of
C ,
which are weak (Appendix F), could probably provide a guess of their order of magnitude
for the first transitions close to 1 μm, but this is questionable at shorter
wavelengths. For the transitions related to the atomic levels, one should remember that
the fullerene cage is a practically perfect Faraday cage for its interior (e.g. Connerade
& Solovyov 2005), which may considerably
reduce their line strengths.
,
which are weak (Appendix F), could probably provide a guess of their order of magnitude
for the first transitions close to 1 μm, but this is questionable at shorter
wavelengths. For the transitions related to the atomic levels, one should remember that
the fullerene cage is a practically perfect Faraday cage for its interior (e.g. Connerade
& Solovyov 2005), which may considerably
reduce their line strengths.
As quoted, the impossibility of charge transfer may explain the difficulty of forming Mg@C60, contrary to Ca@C60. Nevertheless, the case of Mg@C60 has been taken as an example by several theoretical studies (e.g. Broclawik & Eiles 1998; Stener et al. 2002; Lyras & Bachau 2005). Indeed the possibility that it could form in the peculiar interstellar conditions cannot be excluded. The results of these studies seem to show that Mg@C60 might display several transitions in the visible, including between atomic levels. However, it is probable that the latter are substantially quenched by cage screening.
Appendix D: Interstellar dehydrogenation of fulleranes
The leading processes determining the abundance ratio of interstellar fulleranes to their parent fullerene (e.g. C60) obviously are hydrogen photolysis by typical interstellar UV field7 and the reactions listed in Table 1 with hydrogen or the reverse reactions (Bettinger et al. 2002), or rather the reactions of H with the same fullerene compounds but ionized.
The rate of formation of C60H+ from C through the reaction C
through the reaction C + H exceeds 5 ×
10-9{n(H)/50 cm-3}s-1 (Petrie et al. 1995). Due to its small activation energy, ≲2 eV (Table 1), C60H should be dissociated in
practically every absorption of a hard UV photon (see e.g. Fig. 10 of Le Page et al. 2001 for PAHH+ with similar H-binding energy),
i.e. with a rate ~1 yr-1 = 3 ×
10-8s-1 (see e.g. Tielens 2005). Assuming that the abundance ratios C60H/C60 or C60H+/C
+ H exceeds 5 ×
10-9{n(H)/50 cm-3}s-1 (Petrie et al. 1995). Due to its small activation energy, ≲2 eV (Table 1), C60H should be dissociated in
practically every absorption of a hard UV photon (see e.g. Fig. 10 of Le Page et al. 2001 for PAHH+ with similar H-binding energy),
i.e. with a rate ~1 yr-1 = 3 ×
10-8s-1 (see e.g. Tielens 2005). Assuming that the abundance ratios C60H/C60 or C60H+/C roughly equal the ratio of these two rates, both ratios might thus be ~0.1−0.2, with a large uncertainty.
roughly equal the ratio of these two rates, both ratios might thus be ~0.1−0.2, with a large uncertainty.
The case of C60H2 and other even-H fulleranes seems more uncertain since their photo-dissociation is much more difficult because of their higher H binding and activation energies, ≳3.3 eV (Table 1). Because of the high rate expected for the accretion of H onto C60H+ (and even onto C60H), two-photon dissociation processes may be neglected (Sect. 2.3.4), and the photo-dissociation must be achieved by the absorption of a single hard UV-photon. As for PAHs, an elaborate modelling is needed to estimate the photo-dissociation rate of C60H2 rate even qualitatively.
However, one could try to explore this photolysis by scaling from the modelling of PAH dehydrogenation in diffuse clouds (e.g. Le Page et al. 2001, 2003; Berné & Tielens 2012; Montillaud et al. 2013, and references therein). For PAHs in diffuse clouds, all authors agree that the limit for full dehydrogenation lies for a number of C atom NC ~ 30−40, but with a substantial uncertainty of several orders of magnitude for the average photo-dissociation rate (see e.g. Fig. 3 of Montillaud et al. 2013); for example, Fig. 10 of Le Page et al. (2001) shows that in their model the dehydrogenation limit is NC ≈ 30 for PAHs (activation energy Eac = 4.8 eV) and NC ≈ 80 for a PAHH+ with Eac = 2.9 eV. It is thus expected that this limit for Eac = 3.3 eV lies just about NC ≈ 60. Even if other models could push this limit above NC = 60, several additional specific factors may contribute to make this dehydrogenation limit even more uncertain for fulleranes than for PAHs. The internal energy conversion may indeed proceed differently. Several key rates and activation energies are unknown for the reactions of Table 1 and for their reverses, implying various neutral and ionized fullerene compounds. The additional destruction of C60H2 in the reaction C60H2 + H → C60H + H2 could be non-negligible in some circumstances despite the non-zero activation energy (~0.1 eV).
We also stress that the degree of hydrogenation of interstellar fullerenes should critically depend on the UV intensity, the density of atomic hydrogen, and the size of the fullerene cage. The photo-dissociation rates are also expected to significantly depend on the number of H atoms of the fullerane for a given NC. Therefore, although an efficient dehydrogenation of C60-fulleranes in diffuse clouds does not appear to be impossible, the question should be considered as unsettled until an elaborate treatment is provided.
However, the likelihood of finding fulleranes should be increased in UV-shielded molecular diffuse clouds, as well as in fullerenes attached to PAHs or carbon grains.
Appendix E: DIBs and forbidden transitions of C60
Surprisingly, the richest optical spectra of fullerenes have been obtained in the laboratory for forbidden transitions of C60 that cover a good part of the visible range. Various techniques have been used, including absorption spectroscopy in cold molecular beams (Haufler et al. 1991; Hansen et al. 1997) or He droplets (Close et al. 1997), combined absorption and fluorescence spectroscopy in rare gas matrices (Sassara et al. 1996a, 1997; Chergui 2000), phosphorescence (Sassara et al. 1996b), fluorescence and phosphorescence from individual C60 molecules excited by local electron tunneling (Cavar et al. 2005).
For identifying weak DIBs, the most interesting laboratory data are obviously absorption
spectroscopy of Haufler et al. (1991), Hansen et
al. (1997), Close et al. (1997), and Sassara et al. (1996a). Herzberg-Teller coupling with vibration states allows weak absorption in
the forbidden transitions from the ground state h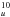 1Ag to the first
singlet excited states h
1Ag to the first
singlet excited states h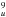 t1u1T1g,
1T2g, and
1Gg. However, the
very rich vibronic structure is difficult to disentangle because these electronic excited
levels are almost completely degenerate within ~100 cm-1 (~0.01 eV) and eventually mixed by the coupling with the rare-gas
matrix (Sassara et al. 1997; Chergui 2000; Orlandi & Negri 2002; Cavar et al. 2005).
Significant f-values have been computed by Sassara et al. (1997) for these transitions. Half a dozen of them
approach 0.01, and a similar number lie in the range 0.001−0.003.
t1u1T1g,
1T2g, and
1Gg. However, the
very rich vibronic structure is difficult to disentangle because these electronic excited
levels are almost completely degenerate within ~100 cm-1 (~0.01 eV) and eventually mixed by the coupling with the rare-gas
matrix (Sassara et al. 1997; Chergui 2000; Orlandi & Negri 2002; Cavar et al. 2005).
Significant f-values have been computed by Sassara et al. (1997) for these transitions. Half a dozen of them
approach 0.01, and a similar number lie in the range 0.001−0.003.
As the abundance of C60, XC60, is expected to be a factor of a
few units lower than that of C in diffuse clouds (Sect. 2.4), it should be close to 10-4 of interstellar carbon.
Therefore, the expected equivalent width of the corresponding DIBs (Eq. (5)) may approach
~10 mÅ/mag for the strongest
ones, while others, which are two or three times weaker, should be barely detectable.
in diffuse clouds (Sect. 2.4), it should be close to 10-4 of interstellar carbon.
Therefore, the expected equivalent width of the corresponding DIBs (Eq. (5)) may approach
~10 mÅ/mag for the strongest
ones, while others, which are two or three times weaker, should be barely detectable.
Of course, securely identifying weak DIBs at this level, close to the confusion limit, is
a real challenge, which requires perfect spectroscopic data. But, despite the beautiful
work performed in the past 25 yrs for the sophisticated spectroscopy of visible forbidden
bands of C60, it
seems that it has not yet fully reached the demanding requirements for definitely
identifying them as DIBs, for various reasons. The most detailed and complete work was
carried out by Sassara et al. (1996a, 1997) for their measurement in absorption and
fluorescence, while further vibronic assignments and strength theoretical estimates are
discussed by Orlandi & Negri (2002). But
these results are plagued by intricate matrix effects. The case of the strong DIBs of
C has shown how such effects may be difficult to predict (Campbell et al. 2015; Strelnikov et al. 2015). The situation is expected to be even more complicated for the
first excited levels of C60 because of the quasi-degeneracy of these levels,
1T1g,
1T2g, and
1Gg. Checks with
gas phase data are thus mandatory. But they are available only for a limited wavelength
range, 5900−6300 Å (Haufler et
al. 1991; Hansen et al. 1997) (as well as the He droplet data of Close et al. 1997).
has shown how such effects may be difficult to predict (Campbell et al. 2015; Strelnikov et al. 2015). The situation is expected to be even more complicated for the
first excited levels of C60 because of the quasi-degeneracy of these levels,
1T1g,
1T2g, and
1Gg. Checks with
gas phase data are thus mandatory. But they are available only for a limited wavelength
range, 5900−6300 Å (Haufler et
al. 1991; Hansen et al. 1997) (as well as the He droplet data of Close et al. 1997).
On this basis, Herbig (2000) was nevertheless able to tentatively identify a possible match of the strongest C60 feature of Haufler et al. with a well-confirmed DIB at 6071.2 Å. However, as quoted by Herbig, this identification cannot be considered as secure, especially for such a weak DIB (EW = 6.9 mÅ/mag in HD 183143, Hobbs et al. 2009). In addition, both Close et al. (1997) and Hansen et al. (1997) have said that there could be a problem in the wavelength recording of the preliminary spectrum shown in their Fig. 2 by Haufler et al. The main problem seems to be in the blue part of the spectrum. However, even for the central, strongest feature close to 6070 Å, Hansen et al. report a wavelength blue-shifted by ~2 Å. Such a shift is enough to jeopardize identification with the DIB at 6071.7 Å. But it could make the association plausible with another nearby stronger, broad DIB at 6068.4 Å (EW = 13 mÅ/mag in HD 183143). It is difficult to say which association, if any, has the best chance of being real. However, both DIBs would yield about 10-4 of interstellar carbon for the order of magnitude of the C60 abundance, if the f-value approaches 10-2.
To summarize, current molecular-beam data of C60 are compatible with at least a match of the strongest band at 6070−6071 Å with a confirmed DIB of ~10 mÅ/mag. This would yield an abundance of C60~10-4 of interstellar carbon in the sight line of HD 183143, which seems consistent with the abundance of ~ 5 × 10-4 for C60 (Sect. 2.4). But it is obvious that such a detection of a single band of C60 cannot be considered as secure by any means.
Appendix F: Could C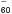 be carrier of “C2”
DIBs?
be carrier of “C2”
DIBs?
As quoted in Sect. 2.3.1, the C anion may include a significant percentage of C60 cages in UV-shielded regions. It might thus be a good
candidate for weak DIBs in such sight lines, such as the so-called ‘C2’ DIBs. Indeed, two of the three
excited electronic energy levels of C
anion may include a significant percentage of C60 cages in UV-shielded regions. It might thus be a good
candidate for weak DIBs in such sight lines, such as the so-called ‘C2’ DIBs. Indeed, two of the three
excited electronic energy levels of C ,
2T1g and
2Ag, are connected
to the ground level 2T1u by “allowed” optical transitions
(Klaiman et al. 2013, 2014).
,
2T1g and
2Ag, are connected
to the ground level 2T1u by “allowed” optical transitions
(Klaiman et al. 2013, 2014).
The first corresponds to a well-documented band in the very near infrared close to
1 μm (Kato
et al. 1991; Fulara et al. 1993a; Bolskar et al. 1995;
Tomita et al. 2005; Hands et al. 2008; Strelnikov et al. 2015; and references therein). While most of these experiments were
performed with C in Ne matrix or in solution, the 300 K storage ring spectrum of Tomita et al. provides an
accurate value of the wavelength of the main band at 10 659 Å. Its strength is very
comparable to the nearby band of C
in Ne matrix or in solution, the 300 K storage ring spectrum of Tomita et al. provides an
accurate value of the wavelength of the main band at 10 659 Å. Its strength is very
comparable to the nearby band of C with an oscillator strength of 0.022 ±
0.005 (Strelnikov et al. 2015).
This wavelength does not correspond to any of the NIR DIBs known in this wavelength range
(Hamano et al. 2015; Cox et al. 2014). Indeed, most of the observed sight lines have
“σ”
characteristics with strong UV radiation where C
with an oscillator strength of 0.022 ±
0.005 (Strelnikov et al. 2015).
This wavelength does not correspond to any of the NIR DIBs known in this wavelength range
(Hamano et al. 2015; Cox et al. 2014). Indeed, most of the observed sight lines have
“σ”
characteristics with strong UV radiation where C is not expected to be present. But no hint of absorption is even seen in the very reddened
“ζ” line of
sight of 4U 1907+19 with the very good sensitivity of Cox et al. (see their Fig. 6). One may infer the rough limit EW<
10 mÅ/mag, and Eq. (2) yields XC(C
is not expected to be present. But no hint of absorption is even seen in the very reddened
“ζ” line of
sight of 4U 1907+19 with the very good sensitivity of Cox et al. (see their Fig. 6). One may infer the rough limit EW<
10 mÅ/mag, and Eq. (2) yields XC(C ) < 0.5 × 10-4 in this sight line,
and significantly lower values in other (σ-type) sight lines, such as HD 183143.
) < 0.5 × 10-4 in this sight line,
and significantly lower values in other (σ-type) sight lines, such as HD 183143.
The other allowed transition, 2Ag–2T1u, of
C is expected in a very different (blue) spectral range. While the three other electronic
levels of C
is expected in a very different (blue) spectral range. While the three other electronic
levels of C may be interpreted as the adjunction of one electron on the cage in one of the available
first excited states of C60, the Ag level is very different. The wave
function of the additional electron is very diffuse with a large extension far outside the
central C60 core.
According to various estimates (Klaiman et al. 2013, 2014; Voora et al. 2013), its energy is very close to but below the
electron detachment limit (within ~100−150 meV). Together with the accurately determined value of the electron
attachment energy, EA = 2.666 ± 0.001 eV (Stochkel
& Andersen 2013), this yields the range
~2.5−2.9 eV for the energy of the transition
2Ag-2T1u, i.e.
~4300−5000 Å for its wavelength. This is the
range where about half of all known “C2” DIBs are concentrated (Thorburn et al. 2003). The oscillator strength of this 2Ag-2T1u transition,
if real, seems unknown. However, even a modest f-value of a few 10-2 might be enough to account for
observed “C2” DIBs,
as in the case of 4U 1907+19; considering one of the strongest “C2” DIBs, at 4964.0 Å, the
detection of which is clear (but not reported) in the spectrum of Fig. 1 of Cox et al. (2005), one may infer an equivalent width EW ~ 10 mÅ/mag. The limit
derived above for the abundance of C
may be interpreted as the adjunction of one electron on the cage in one of the available
first excited states of C60, the Ag level is very different. The wave
function of the additional electron is very diffuse with a large extension far outside the
central C60 core.
According to various estimates (Klaiman et al. 2013, 2014; Voora et al. 2013), its energy is very close to but below the
electron detachment limit (within ~100−150 meV). Together with the accurately determined value of the electron
attachment energy, EA = 2.666 ± 0.001 eV (Stochkel
& Andersen 2013), this yields the range
~2.5−2.9 eV for the energy of the transition
2Ag-2T1u, i.e.
~4300−5000 Å for its wavelength. This is the
range where about half of all known “C2” DIBs are concentrated (Thorburn et al. 2003). The oscillator strength of this 2Ag-2T1u transition,
if real, seems unknown. However, even a modest f-value of a few 10-2 might be enough to account for
observed “C2” DIBs,
as in the case of 4U 1907+19; considering one of the strongest “C2” DIBs, at 4964.0 Å, the
detection of which is clear (but not reported) in the spectrum of Fig. 1 of Cox et al. (2005), one may infer an equivalent width EW ~ 10 mÅ/mag. The limit
derived above for the abundance of C on this sight line, XC(C
on this sight line, XC(C ) < 0.5 × 10-4 of interstellar
carbon, and Eq. (5) would then yield f> 2 × 10-2 if
this DIB was due to C
) < 0.5 × 10-4 of interstellar
carbon, and Eq. (5) would then yield f> 2 × 10-2 if
this DIB was due to C .
Of course, the half dozen confirmed “C2” DIBs in this range may have completely different
origin than C
.
Of course, the half dozen confirmed “C2” DIBs in this range may have completely different
origin than C .
However, one may also consider that more than one DIB might thus be explained if the
C
.
However, one may also consider that more than one DIB might thus be explained if the
C band was split by some fine structure in the excited (or even the ground) level, and other
fullerene anions might also contribute if abundant enough.
band was split by some fine structure in the excited (or even the ground) level, and other
fullerene anions might also contribute if abundant enough.
Appendix G: Delayed (Poincaré) fluorescence in fullerenes
Delayed fluorescence (or more precisely thermally activated delayed fluorescence, TADF) is a well-known cooling process for large molecules by evacuating the (vibration) energy of a state m with slow cooling through radiation from an upper electronic level e. Its rate remains generally low because of the factor exp(− ΔE/kTv), where ΔE ≫ kTv is the difference between e and m energies, and Tv is the inner (vibration) temperature of the molecule. Its possible importance in the case of PAHs was stressed by Léger et al. (1988a) under the name of “Poincaré fluorescence” (PF).
Its properties are significantly different for neutrals and ions. Neutral molecules, or more precisely those with an even number of electrons, often have a spin-singlet ground state, whereas most excited states exist in both forms, singlet and triplet. As shown e.g. by Salazar et al. (1997), Bachilo et al. (2000), Baleizão & Berberan-Santos (2007), and references therein, several reasons may contribute to the importance of PF in fullerenes: 1) very efficient intersystem conversion (ISC) channelling 100% of the energy of absorbed UV photons into the lowest triplet level T1 (Fig. 2); 2) the very long lifetime of this level; 3) small energy splitting, ΔEST = ES1 − ET1, typically ~0.3 eV for C60 or C70 compounds.
PF dominates the cooling of C70 even for very low Tv and vibration energy Ev (250−300 K, a few eV) because of the very long triplet lifetime – tens of ms – (e.g. Bachilo et al. 2000; Baleizão et al. 2011). C70 derivatives, such as C70H2, also display PF, but at lower rates. PF is even significantly modified in the 13C isotopologue of C70, confirming that key energy conversion rates may be extremely sensitive to actual energy-level patterns.
PF has similarly been demonstrated for C60 and derivatives, such as C61H2, but with lower rates because of the shorter triplet lifetime (e.g. Salazar et al. 1997; Anthony et al. 2003; Baleizão et al. 2011, and references therein). Its very well-behaved properties allow its use e.g. for accurate determination of the ΔEST gap of C61H2 (Anthony et al. 2003). It is also probably involved in the observed exponential variation in the triplet lifetime with
larger Ev following the absorption of UV photons (Etheridge et al. 1995; Heden et al. 2003; Deng et al. 2003; Etch et al. 2005).
All in all, it seems obvious that PF should be considered as potentially important in the energy conversion processes of interstellar fullerenes. It may have led to underestimate the abundance of C70 (Sect. 2.4). It should be eventually considered for the PF process proposed to explain emission DIBs (Witt 2014 and Sect. 8.5).
However, the actual importance of PF in the cooling of interstellar C60 remains less obvious because of the more efficient IEC from the triplet to the ground state. If PF probably dominates at high Ev ≳ 5–7 eV, the case should be investigated in detail at lower energy, which corresponds to the bulk of the cooling.
On the other hand, in the case of singly ionized fullerenes, the internal energy
conversion (IEC) and radiative cooling may be deeply modified by the presence of a low
doublet (although it is possible that higher metastable quadruplets play a similar role to
triplets of neutrals). For example, both C or C
or C exhibit a doublet D1 about 1 eV above the ground doublet D0, with an allowed
D1-D0 transition. The existence of this doublet may accelerate
the IEC down to D0,
as proved for C
exhibit a doublet D1 about 1 eV above the ground doublet D0, with an allowed
D1-D0 transition. The existence of this doublet may accelerate
the IEC down to D0,
as proved for C (Erhler et al. 2006; Andersen et al. 2001). It would leave all the energy stored in
vibrations for a very long time – up to ~10−100 s
if IR cooling played alone, Sect. 2.1.1. But PF could be much faster as proved in the case
of C
(Erhler et al. 2006; Andersen et al. 2001). It would leave all the energy stored in
vibrations for a very long time – up to ~10−100 s
if IR cooling played alone, Sect. 2.1.1. But PF could be much faster as proved in the case
of C for Tv ~ 1000 −
1500 K (Andersen et al. 1996,
2001). For lower typical values of Tv ~ 500–1000 K
(Ev ≳ 3 −
10 eV) following the absorption of a single UV photon, the transition
between IR and PF cooling may arise in the range of Ev ~ 3−7 eV,
depending on the exact value of the energy of D1. PF should thus be important for interstellar
C
for Tv ~ 1000 −
1500 K (Andersen et al. 1996,
2001). For lower typical values of Tv ~ 500–1000 K
(Ev ≳ 3 −
10 eV) following the absorption of a single UV photon, the transition
between IR and PF cooling may arise in the range of Ev ~ 3−7 eV,
depending on the exact value of the energy of D1. PF should thus be important for interstellar
C and might even be significant for C
and might even be significant for C .
.
All Tables
Abundances for elements of interest for endohedral fullerenes and heterofullerenes.
All Figures
 |
Fig. 1 a) Adapted from Fig. 5 of Pennington & Stenger (1996). Schematic diagram of basic electronic shells of C60 in Hückel approximation and resulting first excited states of C60 (E< ~ 3 eV), singlet (see e.g. Sassara et al. 1997, 2001) and triplet. b) From Table 6 of Bendale et al. (1992). Schematic diagram of the first electronic levels of C |
| In the text | |
 |
Fig. 2 Adapted from Fig. 5 of Stepanov (2002). Flow chart of the energy internal conversion in C60 with the characteristic timescales and rates: τ1< ~ 20 ps is the time to reach the S1,2,3 states from the initially excited state Sn, by electronic to vibrational internal energy conversion; τ2 ≈ 1 ns reflects the intersystem crossing time; k3 ≈ 0.3−1 μs-1 is the slow decay rate through fluorescence directly to the ground state S0; τ4 ≈ 100 μs to 1 ms or shorter is the radiationless decay from the lowest triplet state to the ground state; kPF is the rate of Poincaré fluorescence from the triplet state discussed in Appendix G; and τ5, possibly >~100 s, is the very slow decay of vibrational excitation through infrared emission. Of course, as long as there is no emission of visible or infrared photons, the total energy, E(Sn), is conserved; when the excitation is transferred to the electronic state i, the energy difference E(Sn) − Ei appears as vibrational energy. |
| In the text | |
 |
Fig. 3 Successive key steps in identification of strong diffuse interstellar bands of C |
| In the text | |
 |
Fig. 4 Correlation between the sum of the equivalent widths, EW9600, of the two DIBs at 9577 Å and 9633 Å of C |
| In the text | |
 |
Fig. 5 Adapted from Supplementary Fig. 5 of Dunk et al. (2014). Behaviour of the chemical elements for the formation of mono-atom endohedral compounds with C60: grey-blue squares, elements that form mono-metallofullerenes in laser graphite ablation; full yellow squares, elements that do not form confirmed mono-atom endohedral compounds; light blue squares, rare gases that form mono-atom endohedral compounds; yellow squares with grey-blue thick borders, other non metals that form mono-atom endohedral compounds. In addition, a few abundant cosmic elements that do not form confirmed mono-atom endohedral compounds in laser graphite ablation, are indicated by yellow squares with red thick borders. |
| In the text | |
 |
Fig. 6 Distribution of the equivalent widths per unit reddening, EW/EB − V, of 489 diffuse interstellar bands observed in the line of sight of HD 183143 with EB − V = 1.27, by Hobbs et al. (2009). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


