| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | A71 | |
| Number of page(s) | 10 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201527278 | |
| Published online | 12 May 2016 | |
Constraints on the presence of a 3.5 keV dark matter emission line from Chandra observations of the Galactic centre
1
Institute of Theoretical Astrophysics, University of
Oslo, PO 1029
Blindern, 0315
Oslo,
Norway
e-mail:
signe.riemer-sorensen@astro.uio.no
2
ARC Centre of Excellence for All-sky Astrophysics
(CAASTRO), NSW,
2016,
Australia
Received: 31 August 2015
Accepted: 7 April 2016
Context. Recent findings of line emission at 3.5 keV in both individual and stacked X-ray spectra of galaxy clusters have been speculated to have dark matter origin.
Aims. If the origin is indeed dark matter, the emission line is expected to be detectable from the Milky Way dark matter halo.
Methods. We perform a line search in public Chandra X-ray observations of the region near Sgr A*. We derive upper limits on the line emission flux for the 2.0−9.0 keV energy interval and discuss their potential physical interpretations including various scenarios of decaying and annihilating dark matter.
Results. While we find no clear evidence for its presence, the upper flux limits are not inconsistent with the recent detections for conservative mass profiles of the Milky Way.
Conclusions. The results depend mildly on the spectral modelling, and strongly on the choice of dark matter profile.
Key words: dark matter / line: identification / Galaxy: center / X-rays: galaxies
© ESO, 2016
1. Introduction
Recent results by Bulbul et al. (2014) and Boyarsky et al. (2014) show a narrow excess of emission around 3.5 keV in both individual and stacked X-ray spectra of galaxy clusters. The spectral shape is consistent with mono-energetic line emission. There are no obvious astrophysical origins and alternative options such as dark matter have been considered (Bulbul et al. 2014; Boyarsky et al. 2014; Iakubovskyi 2015, and references therein). If this is the case, the line should also be detectable from other dark matter dominated objects, in particular when stacking spectra from many different observations. Such dedicated line searches were performed in individual galaxy clusters (Urban et al. 2015; Iakubovskyi et al. 2015), individual galaxies (Anderson et al. 2015; Boyarsky et al. 2014), as well as stacked spectra of galaxies (Anderson et al. 2015) and dwarf galaxies (Malyshev et al. 2014). With some searches providing low-significance confirmation of the stacked galaxy cluster signal at 3.5 keV, and some providing strong upper limits on the dark matter line emission flux (Iakubovskyi 2015, gives a detailed list of all searches), the discussion is still ongoing. The nearest object that should provide detectable line emission if the origin is indeed dark matter, is the Milky Way halo, providing a nearby consistency check. In this paper we analyse stacked X-ray spectra towards the Milky Way Centre to look for such a line, but find no clear evidence for its existence.
2. Data
We use a number of publicly available1Chandra X-ray observations of the region within 20′ of Sgr A* located at (RA, Dec) = (17h45m40.0409s, −29°0′28.118′′) corresponding to galactic coordinates (l,b) = (359.944°, −0.04605°). The observation identification numbers (Obs ID) and exposure times are listed inTable 1. All the selected exposures are observed with the ACIS I0-I3 chips and consequently the total field of view is a square of 16.8′ × 16.8′. The raw data were processed chip-by-chip using the software package, ciao version 4.6 with caldb 4.6.12, following the ACIS data analysis guide3. In brief, the steps are:
Reprocessing: the files are reprocessed with ciao to ensure the application of the most up-to-date calibration database and to set the observation-specific bad pixel file so cosmic rays etc. are excluded from the analysis. All observations were taken in faint mode, which uses a 3 × 3 pixel island to grade the events for bad pixel exclusion.
Source region selection: in order to minimise calibration uncertainties we avoid the edges of each chip by cutting a square of 8′ × 8′ (Chandra X-ray Center 2014). We also exclude a circle with radius of 2.5′around Sgr A* as illustrated inFig. 1.
Point source removal and deflaring: point sources were removed from the images using the wavdetect4 routine in ciao with the standard threshold value of 10-6 allowing for up to two spurious source detections per field. The detected sources are given inFig. 1 where the ellipses have axes of 2–16′′ and a total area corresponding to less than 1% of the chip area. Likewise we iteratively removed periods with flaring activity where the flux exceeded ±3σ of the mean, using the lc_sigma_clipping5 routine. The light curves were visually inspected during the process and none of them contained strong flares extending over several bins.
Background selection: we did not remove any background from the observations. Rather we added the line emission visible in observations taken with the telescope in the stowed position (“lid on”)6 to the model later. These are denoted “instrumental lines” inTable 3 (Chandra X-ray Center 2014; Bartalucci et al. 2014). Figure 1 clearly shows pockets of extended diffuse emission, on scales smaller than expected for dark matter emission from the halo. While exclusion of these regions would improve the expected dark matter signal to noise, they would also decrease the observed field of view significantly and with the danger of removing underlying halo substructure.
Public Chandra observations used in the analysis.
 |
Fig. 1 Fluxed image of the observations inTable 1 showing the positions of each 8′ × 8′ chip for each observation (magenta squares) and the regions removed as point sources (small green ellipses, <1% of the total area) and Sgr A (white circle). The data have been smoothed with a five-pixel Gaussian for visualisation purposes. |
Spectrum extraction: the spectra for the source regions described above were extracted using specextract7 with the default settings apart from the rebinning, which was set to at least 15 counts per bin. The redistribution matrix files (RMFs) and the ancillary response files (ARFs) were also computed. They contain the necessary information to perform the analysis in physical units and to compensate for a non-uniform effective collecting area on the detector.
Stacking: the spectra and response files are weighted and stacked using the combine_spectra routine in ciao providing a summed source spectrum, an exposure-weighted source ARF, a source RMF weighted by exposure time and ARF, and an area- and exposure-weighted background spectrum. The resulting stacked spectrum of all observations is shown inFig. 2.
 |
Fig. 2 Left: the stacked spectrum and best-fit base model (without any additional line emission) in normalised counts keV-1 s-1, and χ residuals below for the 2.0−9.0 keV. No significant emission line excess is seen around 3.5 keV. Right: same for the 3.0−6.0 keV interval. The red curve shows the model including the mass-scaled expected signal from Bulbul et al. (2014) and residuals under the assumption of a Navarro-Frenk-White (NFW) profile for the Milky Way dark matter halo. |
3. Spectrum modelling
Modelling the astrophysical X-ray emission of the Milky Way centre is notoriously difficult because there are many contributing sources with a range of different signatures (e.g. Revnivtsev et al. 2007) that may hide the line we are looking for. However, since we are not interested in the physical properties of the unresolved sources contributing to the broad features of the background emission, we do not require the model to represent the underlying physics, allowing us to chose the simplest possible model that provides a good fit to the data.
3.1. Energy intervals
We use the Xspec 12.8 fitting package for analysing the spectra8. We consider two energy intervals for the base model fit, namely the broad interval of 2.0−9.0 keV, and the narrower interval of 3.0−6.0 keV. Below 2 keV the spectrum is dominated by astrophysical emission lines that cannot be individually resolved. Above 9 keV there is a wide complex of instrumental Au lines. Similarly to Bulbul et al. (2014) we examine the 3−6 keV interval thoroughly due to the possible excess around 3.5 keV. This interval is chosen to be wide enough to measure the continuum accurately and avoiding the strong S and Si lines below 3 keV and Fe lines above 6 keV.
3.2. Base model
The base for our explorations is a line-free apec model (i.e. with the abundance parameter fixed to zero, Smith et al. 2001) combined with a power law and eight Gaussians to mimic residual detector background (Bartalucci et al. 2014) and a photo-electric absorption model (wabs) to account for galactic absorption. Following Muno et al. (2004) we assume a fixed absorption with an average equivalent hydrogen column density of 6 × 1022 atoms cm-2. If we fit the 2.0−9.0 keV interval for the absorption we obtain a value of 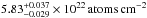 , consistent with the fixed value. The line-free model is pre-fitted to intervals that appear line-free (3.4−3.6 keV and 4.3−5.2 keV), before we add the known instrumental lines from Bartalucci et al. (2014) and atomic emission lines (all listed inTable 3).
, consistent with the fixed value. The line-free model is pre-fitted to intervals that appear line-free (3.4−3.6 keV and 4.3−5.2 keV), before we add the known instrumental lines from Bartalucci et al. (2014) and atomic emission lines (all listed inTable 3).
The parameters of the apec and power law models are somewhat degenerate leading to large uncertainties. However, even the extreme case of removing one or the other from the base model leads to very similar flux constraints, and we take the sum of the two to be robustly determined. The best fit normalisations of the instrumental lines are of the same order of magnitude as those given in the literature for blank sky spectra (Bartalucci et al. 2014; Chandra X-ray Center 2014).
For the atomic lines we include all lines with emissivities larger than 5 × 10-19 photons cm-3 s-1 for a plasma temperature of 2 keV, as listed inTable 3 (this corresponds to the atomic lines used in Bulbul et al. 2014). The central values of the lines are allowed to “budge” by 0.01 keV in the fit to account for uncertainties and mis-calibrations in the spectra. The widths are assumed to be unresolved, but we also checked that fit quality was not improved by allowing for broadening up to 0.1 keV. The normalisations are free to vary and we do not make any assumptions about their internal relations. Atomic lines that do not change the best fit χ2 are removed from the final model (marked inTable 3).
Since atomic emissivities depend on the plasma temperature, which is more complicated towards the centre of the Milky Way than in galaxy clusters, the list in Bulbul et al. (2014) may not be sufficient here. To account for this as well as possible instrumental artefacts, a number of extra lines are added to the fit with the central energies and normalisations as free parameters while fitting the base model. They do not correspond to any known atomic transitions but are simply a parameterisation of our ignorance. Only the broad interval fit is improved by such additional lines at the best fit energies of 4.84 keV and 9.01 keV (listed inTable 3). The origins of the additional lines are unknown and could potentially be due to non-astrophysical processes such as decaying dark matter. The normalisations of the lines are similar to the upper limits on line emission at other energies, and we leave the interpretation of the lines to the reader, but note that the upper flux limits presented in Sects. 5 and 6 remain valid even at those energies because we do not remove their contribution from the flux constraints but rather include them in the total flux.
Line free base model and instrumental lines.
Emission lines included in the base model.
The final base model with best fit with χ2/ d.o.f. = 621.9 / 406 = 1.53 and 172.02 / 172 = 1.00 for the broad and narrow intervals respectively is shown inFig. 3. The fit quality is somewhat worse for the broad interval due to the large number of S and Si lines below 3 keV and the Fe lines at 6−8 keV despite our attempt to include all the lines in the model. The residuals inFig. 3 are random, with no significant structures at the scale of the instrumental resolution. Where overlapping, the results from the two intervals are consistent.
 |
Fig. 3 Left: the best fit incident model spectrum of the base model showing contributions of the individual additive model components for the 2.0−9.0 keV interval. Right: as left, for the 3.0−6.0 keV interval. |
3.3. Additional line
On top of the best fit base model we add an unresolved Gaussian to account for non-astrophysical line emission. The galactic absorption is also applied to the additional line so the entire model consists of 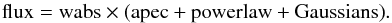 (1)We fit the model to the stacked spectrum for each central energy, in 0.05 keV steps, and then increase the normalisation of the additional Gaussian and refit all free parameters until
(1)We fit the model to the stacked spectrum for each central energy, in 0.05 keV steps, and then increase the normalisation of the additional Gaussian and refit all free parameters until 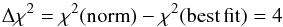 (2)corresponding to the upper 95% confidence level for one degree of freedom (the normalisation) marginalised over all other parameters9. The line flux is calculated in bins of full width half max (FWHM) of the spectral resolution around the central value approximated by (Chandra X-ray Center 2014)
(2)corresponding to the upper 95% confidence level for one degree of freedom (the normalisation) marginalised over all other parameters9. The line flux is calculated in bins of full width half max (FWHM) of the spectral resolution around the central value approximated by (Chandra X-ray Center 2014) 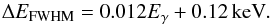 (3)For each energy we regard the entire flux in all Gaussians including atomic lines, instrumental lines, and the additional lines as an upper limit on the possible emission from dark matter. Only the smooth component is subtracted from the model, resulting in a very conservative limit as the line flux can have astrophysical origin, but the method takes into account the risk of a non-astrophysical line hiding under an astrophysical emission line. We also present the results produced by subtracting the instrumental features that have widths much wider than the instrumental resolution (1.12, 1.49, 1.81, 9.71 keV). This mainly affects energies above 4 keV.
(3)For each energy we regard the entire flux in all Gaussians including atomic lines, instrumental lines, and the additional lines as an upper limit on the possible emission from dark matter. Only the smooth component is subtracted from the model, resulting in a very conservative limit as the line flux can have astrophysical origin, but the method takes into account the risk of a non-astrophysical line hiding under an astrophysical emission line. We also present the results produced by subtracting the instrumental features that have widths much wider than the instrumental resolution (1.12, 1.49, 1.81, 9.71 keV). This mainly affects energies above 4 keV.
Bulbul et al. (2014) estimate the maximum contribution from atomic lines around 3.5 keV by using the ratios of different species. Because of the dependence on the assumed plasma conditions (e.g. temperature, Jeltema & Profumo 2015, 2014), the method cannot easily be transferred to the Milky Way, and is not applied here. The resulting flux limits are shown inFig. 4.
 |
Fig. 4 Constraints on line emission flux in the stacked spectrum (95% confidence). The cyan lines represent the entire 2–9 keV interval model, and purple lines the 3–6 keV interval. Solid lines represent the total flux in line emission (including instrumental and astrophysical lines) and for dotted lines the broad instrumental lines have been subtracted. |
4. Mass within field of view
The dark matter emission scales with the amount of dark matter within the observed field of view. The emission is directly proportional to density for decaying dark matter, whereas for annihilating dark matter it scales with density squared. We calculate the mass within the field of view as the integral along the line of sight of a 16′ × 16′ square, assuming the density variation over this region to be negligible10. We subtract the area of a circle with radius of 2.5′to account for the removed region around Sgr A* (7%, taking the gaps between the chips into account changes this by <1%) and an additional 1% to account for the removed point sources. The total area of the field of view becomes 16′ × 16′ × 0.92−2π(2.5′)2 = 196.25′2. The uncertainty on the final mass within the field of view arising from the choice of mass profile is much larger than any uncertainty on the area being covered by the observations.
For the dark matter density profile as a function of radius (r), we consider various profiles. The Einasto profile (Einasto & Haud 1989) is based on observed stellar density profiles, ![\begin{equation} \rho_\mathrm{DM}(r) = \rho_\odot\exp{\left[ -\frac{2}{\alpha} \left( \left(\frac{r}{r_\mathrm{s}} \right)^\alpha -\left(\frac{r_\odot}{r_\mathrm{s}} \right)^\alpha \right) \right]} , \end{equation}](/articles/aa/full_html/2016/06/aa27278-15/aa27278-15-eq73.png) (4)where rs is the scale radius, ρ⊙ is the density at solar radius r⊙ from the galactic centre, and α is a constant. The parameter values and the results of integrating over density and density squared are given inTable 4. The main uncertainty is on the α parameter. Simulations show that α can vary quite significantly (Dutton & Macciò 2014). We adopt a default value of α = 0.17 (Dutton & Macciò 2014) as well as the larger value of 0.20 (Tissera et al. 2010) representing a more cored profile and leading to ~40% uncertainty on the density integral and a factor of two for the squared integral.
(4)where rs is the scale radius, ρ⊙ is the density at solar radius r⊙ from the galactic centre, and α is a constant. The parameter values and the results of integrating over density and density squared are given inTable 4. The main uncertainty is on the α parameter. Simulations show that α can vary quite significantly (Dutton & Macciò 2014). We adopt a default value of α = 0.17 (Dutton & Macciò 2014) as well as the larger value of 0.20 (Tissera et al. 2010) representing a more cored profile and leading to ~40% uncertainty on the density integral and a factor of two for the squared integral.
Simulations indicate that the dark matter profiles may be steeper than the Einasto profile for cold dark matter e.g. following the Navarro-Frenk-White (NFW) profile Navarro et al. (1997) and flatter for warm dark matter (e.g. isothermal profile) (Weber & de Boer 2010) or when including baryons (Dutton & Macciò 2014). Both cases can be described by the generalised profile 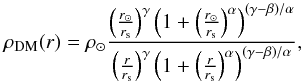 (5)with α = γ = 1 and β = 3 for the NFW profile, and α = β = 2 and γ = 0 for an isothermal profile.
(5)with α = γ = 1 and β = 3 for the NFW profile, and α = β = 2 and γ = 0 for an isothermal profile.
For the NFW profile, the observed parameter range given inTable 4 leads to uncertainty of a factor of two on the density integral and an order of magnitude on the density squared. For the isothermal profile the integrated mass is smaller than the NFW profile by a factor of 20 when using the parameters from Sofue et al. (2010), but their value of the local dark matter density is somewhat smaller than recent dynamical constraints (Pato et al. 2015), which we will adopt here. The squared integral is smaller by three orders of magnitude.
The differences between the various profiles are much larger than the uncertainties resulting from parameter uncertainties. For the sterile neutrinos that will be discussed inSect. 6, their behaviour and expected dark matter profiles depend on the production mechanism, but resonant production leads to cold dark-matter-like structures. Consequently, we adopt the NFW profile which also lies in the middle of the range of values inTable 4. We also show the effect of using the isothermal profile with the same local dark matter density (Sofue et al. 2010; Pato et al. 2015). The uncertainty of mass profile selection can be avoided by looking at the outskirts of dark matter halos rather than the centres, but the expected signal will also be weaker.
Density profiles and masses within field of view.
 |
Fig. 5 A selection of density profiles and parameter ranges fromTable 4 as a function of radius from the galactic centre (solid line) and along the line of sight towards Sgr A* (dashed line). The vertical black line indicates the solar radius, and the dotted vertical lines are the mass-weighted average distances for each of the profiles. |
5. General constraints
InFig. 4 we present the general flux constraints on line emission near Sgr A*. In the shaded regions line emission is excluded at 95% confidence based on all line emission in the model. These constraints apply to all dark matter candidates with mono-energetic photon emission proportional to the density, whether from decays or other processes. For decays, the probability is proportional to density while for annihilation-like processes the interaction requires two particles and the probability is proportional to density squared. This includes scattering processes.
5.1. Decay-like dark matter
The allowed decay rate leading to photon emission is shown inFig. 6 (left) for one photon per decay. For two-photon interactions, the constraints are a factor of two stronger. There is also a factor of two difference depending on whether the particles are of Majorana or Dirac type (because the decay probability is linear in number density). Here we assume the particles to be of Majorana type (their own anti-particles). If they instead are Dirac particles, the constraints are weakened by a factor of two.
These constraints are relevant to, for example, models where the dark matter decays to axions that are then converted to photons in magnetic fields (e.g. Cicoli et al. 2014; Conlon & Day 2014). This can explain a signal from galaxy clusters, which would be absent in the Milky Way because the axion-photon conversion depends on the magnetic field strength (e.g. Conlon & Day 2014; Alvarez et al. 2015).
5.2. Annihilation-like dark matter
For annihilating dark matter, the local flux is given by 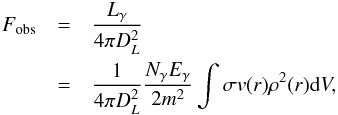 (6)where m is the particle mass, Nγ is the number of photons per interaction, Eγ is the photon energy, σ is the interaction cross section, v(r) is the velocity distribution of the dark matter as a function of radius and the integral is over the observed volume. For a back-of-the-envelope calculation we assume two photons with Eγ = m per annihilation and that ⟨σv⟩ is independent of radius. Reordering and converting units we get
(6)where m is the particle mass, Nγ is the number of photons per interaction, Eγ is the photon energy, σ is the interaction cross section, v(r) is the velocity distribution of the dark matter as a function of radius and the integral is over the observed volume. For a back-of-the-envelope calculation we assume two photons with Eγ = m per annihilation and that ⟨σv⟩ is independent of radius. Reordering and converting units we get ![\begin{eqnarray} \left<\sigma v \right> [\!\cm^{-3}\,{\rm s}^{-1}] &=& 1.74\times10^{-11} \cm^{-3}\,{\rm s}^{-1}\\[3mm] \nonumber &&\times F_\mathrm{obs}[\!\erg\cm^{-2}\,{\rm s}^{-1}] \\[3mm] \nonumber &&\times \frac{D_L^2[\!\kpc^2]}{\int \rho^2(r) \mathrm{d} V[M_\odot^2\kpc^{-3}]} \frac{m^2[\!\keV^2]}{E_\gamma[\!\keV]} \cdot \end{eqnarray}](/articles/aa/full_html/2016/06/aa27278-15/aa27278-15-eq132.png) (7)The resulting constraint is plotted inFig. 6 (right). The integral over density squared is very sensitive to the choice of dark matter profile with a span of three orders of magnitude between the extremes inTable 4. For the weakest constraints ⟨σv⟩ ≳ 10-34 cm3 s-1 (e.g. Cline & Frey 2014; Finkbeiner & Weiner 2014) is allowed for all energies (masses), but for any other density profile, it is ruled out. The situation is similar for directly annihilating dark matter (e.g. Dudas et al. 2014; Frandsen et al. 2014; Baek & Okada 2014) since they are all designed to produce the stacked cluster signal.
(7)The resulting constraint is plotted inFig. 6 (right). The integral over density squared is very sensitive to the choice of dark matter profile with a span of three orders of magnitude between the extremes inTable 4. For the weakest constraints ⟨σv⟩ ≳ 10-34 cm3 s-1 (e.g. Cline & Frey 2014; Finkbeiner & Weiner 2014) is allowed for all energies (masses), but for any other density profile, it is ruled out. The situation is similar for directly annihilating dark matter (e.g. Dudas et al. 2014; Frandsen et al. 2014; Baek & Okada 2014) since they are all designed to produce the stacked cluster signal.
 |
Fig. 6 Left: general constraints on the interaction rate with one-photon emission proportional to matter density (95% confidence) for an isothermal (dashed lines) and NFW profile (solid lines). The grey lines show the combination of previous constraints (Lattanzi et al. 2013, and references therein). The cyan lines are for the entire 2–9 keV interval model, and the purple lines are for the 3–6 keV interval. Right: constraints on the velocity-averaged cross-section for models with two-photon emission from dark matter annihilating into two photons from the total line emission flux for an isothermal (dashed lines) and NFW dark matter profile (solid lines). |
6. Constraints on sterile neutrinos
Bulbul et al. (2014) and Boyarsky et al. (2014) interpreted the detected line emission excess in the context of sterile neutrinos. In this section we introduce the sterile neutrino and discuss the Milky Way non-detection in this context. The sterile neutrino is a strong particle candidate for the dark matter, viable with or without super symmetry or universal extra dimensions. With just three sterile neutrinos (gauge singlets), one can obtain the correct abundance of dark matter, a very simple explanation for the observed flavour oscillations and mass splittings of the active neutrinos, and a natural explanation for the baryon asymmetry (Dodelson & Widrow 1994; Shi & Fuller 1999; Dolgov & Hansen 2002; Abazajian et al. 2001a; Asaka et al. 2005; Asaka & Shaposhnikov 2005; Canetti et al. 2013b). The underlying particle model, called the νMSM, is described in detail in a number of papers (Asaka et al. 2005, 2007; Asaka & Shaposhnikov 2005; Shaposhnikov & Tkachev 2006; Shaposhnikov 2008; Gorbunov & Shaposhnikov 2007; Laine & Shaposhnikov 2008; Canetti et al. 2013a), and recent reviews (Boyarsky et al. 2009b; Kusenko 2009; Drewes 2013). Additionally, the sterile neutrino may have interesting effects on a range of astrophysical objects, for example as an explanation for pulsar kick velocities, facilitating core collapse supernova explosions, affecting early star formation, reionization and structure formation, or assisting inflation (Kusenko & Segrè 1997; Kusenko et al. 2008; Hansen & Haiman 2004; Fryer & Kusenko 2006; Hidaka & Fuller 2006; Biermann & Kusenko 2006; Mapelli et al. 2006; Shaposhnikov & Tkachev 2006; Bezrukov & Shaposhnikov 2008; Petraki & Kusenko 2008; Petraki 2008; Boyanovsky 2008; Gorbunov et al. 2008). The lightest of the three sterile neutrinos provides an attractive dark matter candidate. The two free parameters of mass, ms, and mixing angle with the active neutrinos, sin2(2θ), are unconstrained from particle physics, but as seen inFig. 7 various observations have already excluded large parts of this parameter space (Laine & Shaposhnikov 2008; Canetti et al. 2013b; Boyarsky et al. 2008a; Riemer-Sørensen & Hansen 2009; Boyarsky et al. 2006a; Horiuchi et al. 2014).
The mass is firmly bound from below through the phase space density of nearby dwarf galaxies. This so-called Tremaine-Gunn bound (Tremaine & Gunn 1979) gives a model-independent boundary of roughly ms> 0.4 keV (Boyarsky et al. 2008b). The limit can be increased if the production method is known, for example, for resonant production the boundary is approximately 1 keV (Boyarsky et al. 2008b).
Observations of small scale structure from the Lyman α forest can provide limits on the mass if the velocity distribution is known (Hansen et al. 2002; Viel et al. 2005, 2006; Seljak et al. 2006). The velocity distribution of the sterile neutrinos depends on their production mechanism in the early Universe, and while the originally proposed non-resonant production (Dodelson & Widrow 1994) is ruled out, in general masses above 2 keV are allowed (Boyarsky et al. 2009a; Horiuchi et al. 2014). A plausible mechanism is via resonant production (Shi & Fuller 1999), which requires a large initial lepton asymmetry (Serpico & Raffelt 2005; Dolgov & Hansen 2002). However, the lepton asymmetry cannot be so large that it violates big bang nucleosynthesis, and consequently there is a strong lower limit on the mixing angle to produce enough sterile neutrinos to account for the observed dark matter density (Laine & Shaposhnikov 2008). With a reasonable choice of parameter values, the resonant production provides sterile neutrinos with clustering properties similar to cold dark matter despite the keV mass (Boyarsky et al. 2009a). Consequently dark matter simulations indicate an NFW profile for Milky Way sized halos, which may be flattened by the inclusion of baryons (Navarro et al. 1997; Kuhlen et al. 2013; Dutton & Macciò 2014). The sterile neutrinos can also be produced at the electro-weak scale by decays of a gauge singlet Higgs boson (Kusenko 2009), or from their couplings to, for example, the inflaton (Shaposhnikov & Tkachev 2006).
 |
Fig. 7 Mass-mixing angle constraints on sterile neutrino like dark matter candidates. Above/below the dashed black lines the sterile neutrinos will be over/under produced relative to the observed dark matter density (Laine & Shaposhnikov 2008; Canetti et al. 2013b). The grey shaded regions are X-ray exclusion lines from XMM-Newton and Chandra observations (Boyarsky et al. 2008a, 2006a; Riemer-Sørensen & Hansen 2009) with the Boyarsky et al. (2008a) constraints rescaled by a factor of two due to mass estimate uncertainties as recommended in Boyarsky et al. (2009b). The cyan and purple regions are the parameter space ruled out by the present Sgr* analysis assuming an NFW profile for the Milky Way halo. The cyan lines are for the case where the entire 2–9 keV interval is modelled, and the purple lines are for the 3–6 keV interval. The dashed lines are for the isothermal profile where the constraints are weakened by an order of magnitude. The dotted grey line show the constraints from Horiuchi et al. (2014) for which the model contains some lines of astrophysical origin. The green error bar is the signal from Boyarsky et al. (2014), and the blue error bars represent the signal from Bulbul et al. (2014) with the small range indicating the best fit to the entire stack of spectra. The larger bars indicate the range of results from their different analyses. All the inferred signals are ruled out at 95% confidence under the NFW assumption. |
The sterile neutrinos can decay via a one-loop diagram to an active neutrino and a photon. Since the two-body decay takes place almost at rest (v/c ≈ 10-3 for galaxies), the decay line is very narrow and easily searched for in X-ray and soft gamma-ray observations. The fluxes are converted to constraints in the ms−sin2(2θ) parameter space for sterile neutrinos of the Majorana type, assuming the sterile neutrinos to account for all of the dark matter in the observed field of view (Abazajian et al. 2001b; Riemer-Sørensen et al. 2006; Boyarsky et al. 2007): ![\begin{equation} \label{eq-massmixing} \sin^2(2\theta) \leq 10^{18} \left(\frac{F_\mathrm{obs}}{\erg\cm^{-2}\,{\rm s}^{-1}}\right) \left( \frac{m_{\rm s}}{\keV}\right) \left[ \frac{(M_\mathrm{fov}/\Ms)}{(D_L/\Mpc)^2} \right] , \end{equation}](/articles/aa/full_html/2016/06/aa27278-15/aa27278-15-eq143.png) (8)where Fobs is the observed flux limit, Mfov is the total dark matter mass within the field of view, and DL,i is the luminosity distance.
(8)where Fobs is the observed flux limit, Mfov is the total dark matter mass within the field of view, and DL,i is the luminosity distance.
The Eγ = 0.3−12 keV range is constrained from various objects observed with the Chandra and XMM-Newton X-ray telescopes (Boyarsky et al. 2006a,b; Riemer-Sørensen et al. 2006; Abazajian & Koushiappas 2006; Boyarsky et al. 2007, 2008b,a; Riemer-Sorensen et al. 2007; Riemer-Sørensen & Hansen 2009; Loewenstein et al. 2009; Loewenstein & Kusenko 2010, 2012). InFig. 7 we show a selection of the strongest robust constraints (Boyarsky et al. 2008a; Riemer-Sørensen & Hansen 2009; Horiuchi et al. 2014). Some analyses have claimed stronger constraints, but were later found to be too optimistic (Abazajian & Koushiappas 2006; Boyarsky et al. 2006b, 2008b,a; Abazajian et al. 2001b; Watson et al. 2006, 2012; Yüksel et al. 2008). The higher energy range of 3−48 keV has been constrained from the diffuse X-ray background observed with the High Energy Astronomy Observatory (HEAO; Boyarsky et al. 2006a) and the 3−80 keV with NuSTAR (Riemer-Sørensen et al. 2015). The emission-line constraints depend only on the amount and current properties of observed dark matter and are thus independent of the production mechanism.
Another potential signal from sterile neutrinos has been suggested at 8.7 keV (Prokhorov & Silk 2010; Koyama et al. 2007) from Suzaku observations towards the Milky Way centre. A sterile neutrino origin of this signal would require a mixing angle of sin2(2θ) = 4.4 ± 2.2 × 10-12, which is clearly ruled out by the present analysis (magenta error bars inFig. 7).
7. The 3.5 keV line discussed
Apart from the original detection in stacked galaxy-cluster spectra from XMM-Newton and individual clusters observed with Chandra and XMM-Newton (>3σ in various subsamples of the data, Bulbul et al. 2014; Boyarsky et al. 2014), Iakubovskyi et al. (2015) detected the line at 2σ significance in a range of XMM-Newton observations of individual clusters. Urban et al. (2015) also detected the line in Suzaku observations of the Perseus cluster, but not from other clusters. With detections from several different telescopes, an instrumental origin is unlikely for the Perseus signal. In order to pin down the origin of the line we need observations of several types of objects with different properties such as dark matter profiles and astrophysical background. However, searches in galaxies, dwarf galaxies and the Milky Way have been less conclusive and some even contradicting. Already the pre-Bulbul et al. (2014) analysis of M 31 Chandra observations by Horiuchi et al. (2014) was in conflict with the stacked cluster signal at the 95% confidence level if assuming a decaying dark matter origin. The same is the case for stacked XMM-Newton spectra of dwarf spheroidal galaxies (Malyshev et al. 2014) and stacked spectra of galaxies from both XMM-Newton and Chandra (Anderson et al. 2015, rule out the signal at 7.8σ), and one analysis of deep XMM-Newton observations of the Draco dwarf galaxy (Jeltema & Profumo 2016, more than 99% confidence). However, Ruchayskiy et al. (2015) do detect a line signal at 2.3σ from a part of the same XMM-Newton observation, while the full data set is inconsistent with the signal predicted from Perseus. This perfectly illustrates the complexity of the on-going discussion. A number of searches do not find any evidence for line emission, but do not rule out a dark matter origin of the Perseus signal either, for example Jeltema & Profumo (2015, analysing XMM-Newton , Tamura et al. (2015, Suzaku , Sekiya et al. (2016, Suzaku , and Figueroa-Feliciano et al. (2015, sounding rocket microcalorimeter data).
Decaying dark matter cannot explain all the observations directly (assuming it is single-type), but as already mentioned inSect. 5, more complicated models can explain the line presence in galaxy clusters but not in smaller objects. For example, axion to photon conversion depends on the magnetic field strength and length scale and consequently provide different flux predictions for different objects (e.g. Cicoli et al. 2014; Conlon & Day 2014). Also, atomic transitions have been considered as the origin of the line with the Kxviii transition able to account for all of the galaxy-cluster line excess (Jeltema & Profumo 2015; Phillips et al. 2015) or high-n Sxvi transitions populated by charge transfer processes to the ground state (Gu et al. 2015). Better energy resolution is needed to confirm or reject these scenarios.
Assuming an NFW profile for the Milky Way, the constraints presented here are similar to those of Horiuchi et al. (2014) for sterile neutrino masses near 7 keV, and up to an order of magnitude better than previous constraints at higher energies. If we instead assume a cored profile like the isothermal profile inTable 4, the constraints weaken by up to a factor of 20. Consequently, the constraining power of the Sgr A* observations depends on the assumptions about the dark matter profile, and while we do not see any evidence for line emission from the galactic centre, we cannot rule out the existence for the flattest density profiles.
Boyarsky et al. (2015) analysed XMM-Newton data of the galactic centre and found a 2.0−5.7σ evidence for line emission around 3.5 keV. However, the line emission in Boyarsky et al. (2015) is only consistent with non-detection in blank sky data (Boyarsky et al. 2006a; Riemer-Sørensen et al. 2006) for steeper than cored dark matter profiles such as Einasto or NFW, for which there is a tension with the results presented here. This discrepancy can neither confirm nor rule out a dark matter origin of the line emission, but calls for further investigation with better resolution of the atomic lines and independent measurements of the element abundances and total mass profile near the galactic centre.
8. Future improvements
Several factors play a role when deciding where to look for decaying dark matter. First of all the signal strength is determined by the mass within the field of view and average distance. Remarkably, the line of sight integral for various astrophysical objects from cosmological background to clusters of galaxies to dwarf satellites is very similar, and consequently the expected signal is very similar (Boyarsky et al. 2006b), but the mass profile uncertainty has to be taken into account. The second factor is the expected background level from astrophysical sources. Here dwarf galaxies have an advantage (Loewenstein et al. 2009; Riemer-Sørensen & Hansen 2009). The real advantage of the Milky Way centre is its proximity and the large amount of data available, which can be directly compared to the “other” directions in the Milky Way via the blank sky data (Boyarsky et al. 2006b; Riemer-Sørensen et al. 2006). Unfortunately the prospects for improving the constraints using the galactic centre are not very optimistic since the main uncertainty lies with the inner slope of the dark matter halo profile. This can be partly mitigated by looking off-centre, which will also reduce the astrophysical background emission. Moving the field of view just 1deg above or below the galactic plane reduces the differences between the integrated line of sights to <10% for the considered profiles. However, it also reduces the mass within the field of view by roughly an order of magnitude and consequently we would need to increase the observation time by two orders of magnitude to compensate statistically. At the moment, less than 100 ks of Chandra with an offset of ≈1deg spectra exist. Instead future improvements will come from increased spectral resolution of, for example, Astro-H and Micro-X microcalorimeters (Mitsuda et al. 2014; Figueroa-Feliciano et al. 2015), and mapping of the spatial morphology of the emission with existing instruments (XMM-Newton, Chandra, Suzaku).
9. Conclusions
The Milky Way data does not clearly show the emission line detected in stacked galaxy cluster spectra. The constraints on the allowed X-ray line emission flux are sensitive to the predicted amount of dark matter in the field of view. For an NFW profile the new constraints are up to an order of magnitude stronger than previous constraints, in particular for photon energies above 4.0 keV. For a cored isothermal profile the decaying dark matter constraints weaken by a factor of 20 and are thus weaker than previous constraints, but provide a cross-check based on a different object. Despite the improved constraints, the non-detection of line emission near Sgr A* is not inconsistent with the cluster line detection for the most conservative choice of dark matter profiles for the Milky Way.
Acknowledgments
Thanks to Steen H. Hansen, Yassaman Farzan and Neal Weiner for inspiring discussions and to the anonymous referees for constructive comments. S.R.S. would like to thank NORDITA for hosting the News in Neutrino Physics 2014 workshop during which most of the analysis was carried out. Parts of this research were conducted by the Australian Research Council Centre of Excellence for All-sky Astrophysics (CAASTRO), through project No. CE110001020.
References
- Abazajian, K., & Koushiappas, S. M. 2006, Phys. Rev. D, 74, 023527 [NASA ADS] [CrossRef] [Google Scholar]
- Abazajian, K., Fuller, G. M., & Patel, M. 2001a, Phys. Rev. D, 64, 023501 [NASA ADS] [CrossRef] [Google Scholar]
- Abazajian, K., Fuller, G. M., & Tucker, W. H. 2001b, ApJ, 562, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Alvarez, P. D., Conlon, J. P., Day, F. V., Marsh, M. C. D., & Rummel, M. 2015, J. Cosmol. Astropart. Phys., 4, 013 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, M. E., Churazov, E., & Bregman, J. N. 2015, MNRAS, 452, 3905 [NASA ADS] [CrossRef] [Google Scholar]
- Asaka, T., & Shaposhnikov, M. 2005, Phys. Lett. B, 620, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Asaka, T., Blanchet, S., & Shaposhnikov, M. 2005, Phys. Lett. B, 631, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Asaka, T., Shaposhnikov, M., & Laine, M. 2007, JHEP, 1, 91 [Google Scholar]
- Baek, S., & Okada, H. 2014, ArXiv e-prints [arXiv:1403.1710] [Google Scholar]
- Bartalucci, I., Mazzotta, P., Bourdin, H., & Vikhlinin, A. 2014, A&A, 566, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernal, N., & Palomares-Ruiz, S. 2012, J. Cosmol. Astropart. Phys., 1, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Bezrukov, F., & Shaposhnikov, M. 2008, Phys. Lett. B, 659, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Biermann, P. L., & Kusenko, A. 2006, Phys. Rev. Lett., 96, 091301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Boyanovsky, D. 2008, Phys. Rev. D, 78, 103505 [NASA ADS] [CrossRef] [Google Scholar]
- Boyarsky, A., Neronov, A., Ruchayskiy, O., & Shaposhnikov, M. 2006a, MNRAS, 370, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Boyarsky, A., Neronov, A., Ruchayskiy, O., Shaposhnikov, M., & Tkachev, I. 2006b, Phys. Rev. Lett., 97, 261302 [NASA ADS] [CrossRef] [Google Scholar]
- Boyarsky, A., Nevalainen, J., & Ruchayskiy, O. 2007, A&A, 471, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boyarsky, A., Iakubovskyi, D., Ruchayskiy, O., & Savchenko, V. 2008a, MNRAS, 387, 1361 [NASA ADS] [CrossRef] [Google Scholar]
- Boyarsky, A., Malyshev, D., Neronov, A., & Ruchayskiy, O. 2008b, MNRAS, 387, 1345 [NASA ADS] [CrossRef] [Google Scholar]
- Boyarsky, A., Lesgourgues, J., Ruchayskiy, O., & Viel, M. 2009a, Phys. Rev. Lett., 102, 201304 [NASA ADS] [CrossRef] [Google Scholar]
- Boyarsky, A., Ruchayskiy, O., & Shaposhnikov, M. 2009b, Ann. Rev. Nucl. Part. Sci., 59, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Boyarsky, A., Ruchayskiy, O., Iakubovskyi, D., & Franse, J. 2014, Phys. Rev. Lett., 113, 251301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Boyarsky, A., Franse, J., Iakubovskyi, D., & Ruchayskiy, O. 2015, Phys. Rev. Lett., 115, 161301 [NASA ADS] [CrossRef] [Google Scholar]
- Bulbul, E., Markevitch, M., Foster, A., et al. 2014, ApJ, 789, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Canetti, L., Drewes, M., Frossard, T., & Shaposhnikov, M. 2013a, Phys. Rev. D, 87, 093006 [NASA ADS] [CrossRef] [Google Scholar]
- Canetti, L., Drewes, M., & Shaposhnikov, M. 2013b, Phys. Rev. Lett., 110, 061801 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Chandra X-ray Center 2014, Proposer’s Observatory Guide [Google Scholar]
- Cicoli, M., Conlon, J. P., Marsh, M. C. D., & Rummel, M. 2014, Phys. Rev. D, 90, 023540 [NASA ADS] [CrossRef] [Google Scholar]
- Cline, J. M., & Frey, A. R. 2014, J. Cosmol. Astropart. Phys., 10, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Conlon, J. P., & Day, F. V. 2014, J. Cosmol. Astropart. Phys., 11, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Dodelson, S., & Widrow, L. M. 1994, Phys. Rev. Lett., 72, 17 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dolgov, A. D., & Hansen, S. H. 2002, Astropart. Phys., 16, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Drewes, M. 2013, Int. J. Mod. Phys. E, 22, 1330019 [NASA ADS] [CrossRef] [Google Scholar]
- Dudas, E., Heurtier, L., & Mambrini, Y. 2014, Phys. Rev. D, 90, 035002 [NASA ADS] [CrossRef] [Google Scholar]
- Dutton, A. A., & Macciò, A. V. 2014, MNRAS, 441, 3359 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, J., & Haud, U. 1989, A&A, 223, 89 [NASA ADS] [Google Scholar]
- Figueroa-Feliciano, E., Anderson, A. J., Castro, D., et al. 2015, ApJ, 814, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P., & Weiner, N. 2014, ArXiv e-prints [arXiv:1402.6671] [Google Scholar]
- Frandsen, M. T., Sannino, F., Shoemaker, I. M., & Svendsen, O. 2014, J. Cosmol. Astropart. Phys., 5, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Fryer, C. L., & Kusenko, A. 2006, ApJS, 163, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Gorbunov, D., & Shaposhnikov, M. 2007, JHEP, 10, 15 [Google Scholar]
- Gorbunov, D., Khmelnitsky, A., & Rubakov, V. 2008, J. Cosmol. Astropart. Phys., 10, 41 [Google Scholar]
- Gu, L., Kaastra, J., Raassen, A. J. J., et al. 2015, A&A, 584, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hansen, S. H., & Haiman, Z. 2004, ApJ, 600, 26 [Google Scholar]
- Hansen, S. H., Lesgourgues, J., Pastor, S., & Silk, J. 2002, MNRAS, 333, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Hidaka, J., & Fuller, G. M. 2006, Phys. Rev. D, 74, 125015 [NASA ADS] [CrossRef] [Google Scholar]
- Horiuchi, S., Humphrey, P. J., Oñorbe, J., et al. 2014, Phys. Rev. D, 89, 025017 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Iakubovskyi, D. 2015, ArXiv e-prints [arXiv:1510.00358] [Google Scholar]
- Iakubovskyi, D., Bulbul, E., Foster, A. R., Savchenko, D., & Sadova, V. 2015, ArXiv e-prints [arXiv:1508.05186] [Google Scholar]
- Jeltema, T., & Profumo, S. 2014, ArXiv e-prints [arXiv:1411.1759] [Google Scholar]
- Jeltema, T., & Profumo, S. 2015, MNRAS, 450, 2143 [NASA ADS] [CrossRef] [Google Scholar]
- Jeltema, T. E., & Profumo, S. 2016, MNRAS, 458, 3592 [NASA ADS] [CrossRef] [Google Scholar]
- Koyama, K., Uchiyama, H., Hyodo, Y., et al. 2007, PASJ, 59, 237 [NASA ADS] [Google Scholar]
- Kuhlen, M., Guedes, J., Pillepich, A., Madau, P., & Mayer, L. 2013, ApJ, 765, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Kusenko, A. 2009, Phys. Rep., 481, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kusenko, A., & Segrè, G. 1997, Phys. Lett. B, 396, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Kusenko, A., Mandal, B. P., & Mukherjee, A. 2008, Phys. Rev. D, 77, 123009 [NASA ADS] [CrossRef] [Google Scholar]
- Laine, M., & Shaposhnikov, M. 2008, J. Cosmol. Astropart. Phys., 6, 31 [Google Scholar]
- Lattanzi, M., Riemer-Sørensen, S., Tórtola, M., & Valle, J. W. F. 2013, Phys. Rev. D, 88, 063528 [NASA ADS] [CrossRef] [Google Scholar]
- Loewenstein, M., & Kusenko, A. 2010, ApJ, 714, 652 [NASA ADS] [CrossRef] [Google Scholar]
- Loewenstein, M., & Kusenko, A. 2012, ApJ, 751, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Loewenstein, M., Kusenko, A., & Biermann, P. L. 2009, ApJ, 700, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Malyshev, D., Neronov, A., & Eckert, D. 2014, Phys. Rev. D, 90, 103506 [NASA ADS] [CrossRef] [Google Scholar]
- Mapelli, M., Ferrara, A., & Pierpaoli, E. 2006, MNRAS, 369, 1719 [NASA ADS] [CrossRef] [Google Scholar]
- Mitsuda, K., Kelley, R. L., Akamatsu, H., et al. 2014, in SPIE Proc. Future Missions III: ASTRO-H, 9144, 91442 [Google Scholar]
- Muno, M. P., Arabadjis, J. S., Baganoff, F. K., et al. 2004, ApJ, 613, 1179 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Nesti, F., & Salucci, P. 2013, J. Cosmol. Astropart. Phys., 7, 16 [Google Scholar]
- Pato, M., Iocco, F., & Bertone, G. 2015, J. Cosmol. Astropart. Phys., 12, 001 [NASA ADS] [CrossRef] [Google Scholar]
- Petraki, K. 2008, Phys. Rev. D, 77, 105004 [NASA ADS] [CrossRef] [Google Scholar]
- Petraki, K., & Kusenko, A. 2008, Phys. Rev. D, 77, 065014 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, K. J. H., Sylwester, B., & Sylwester, J. 2015, ApJ, 809, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Prokhorov, D., & Silk, J. 2010, ApJ, 725, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Read, J. I. 2014, J. Phys. G Nucl. Phys., 41, 063101 [NASA ADS] [CrossRef] [Google Scholar]
- Revnivtsev, M., Vikhlinin, A., & Sazonov, S. 2007, A&A, 473, 857 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riemer-Sørensen, S., & Hansen, S. H. 2009, A&A, 500, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riemer-Sørensen, S., Hansen, S. H., & Pedersen, K. 2006, ApJ, 644, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Riemer-Sorensen, S., Pedersen, K., Hansen, S. H., & Dahle, H. 2007, Phys. Rev. D, 76, 043524 [NASA ADS] [CrossRef] [Google Scholar]
- Riemer-Sørensen, S., Wik, D., Madejski, G., et al. 2015, ApJ, 810, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Ruchayskiy, O., Boyarsky, A., Iakubovskyi, D., et al. 2015, ArXiv e-prints [arXiv:1512.07217] [Google Scholar]
- Sekiya, N., Yamasaki, N. Y., & Mitsuda, K. 2016, PASJ, in press, DOI: 10.1093/pasj/psv081 [Google Scholar]
- Seljak, U., Makarov, A., McDonald, P., & Trac, H. 2006, Phys. Rev. Lett., 97, 191303 [NASA ADS] [CrossRef] [Google Scholar]
- Serpico, P. D., & Raffelt, G. G. 2005, Phys. Rev. D, 71, 127301 [NASA ADS] [CrossRef] [Google Scholar]
- Shaposhnikov, M. 2008, JHEP, 8, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Shaposhnikov, M., & Tkachev, I. 2006, Phys. Lett. B, 639, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, X., & Fuller, G. M. 1999, Phys. Rev. Lett., 82, 2832 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. K., Brickhouse, N. S., Liedahl, D. A., & Raymond, J. C. 2001, ApJ, 556, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Sofue, Y., Honma, M., & Omodaka, T. 2009, PASJ, 61, 227 [NASA ADS] [Google Scholar]
- Sofue, Y., Honma, M., & Omodaka, T. 2010, PASJ, 62, 1367 [NASA ADS] [CrossRef] [Google Scholar]
- Tamura, T., Iizuka, R., Maeda, Y., Mitsuda, K., & Yamasaki, N. Y. 2015, PASJ, 67, 23 [NASA ADS] [Google Scholar]
- Tissera, P. B., White, S. D. M., Pedrosa, S., & Scannapieco, C. 2010, MNRAS, 406, 922 [NASA ADS] [Google Scholar]
- Tremaine, S., & Gunn, J. E. 1979, Phys. Rev. Lett., 42, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Urban, O., Werner, N., Allen, S. W., et al. 2015, MNRAS, 451, 2447 [NASA ADS] [CrossRef] [Google Scholar]
- Viel, M., Lesgourgues, J., Haehnelt, M. G., Matarrese, S., & Riotto, A. 2005, Phys. Rev. D, 71, 063534 [NASA ADS] [CrossRef] [Google Scholar]
- Viel, M., Lesgourgues, J., Haehnelt, M. G., Matarrese, S., & Riotto, A. 2006, Phys. Rev. Lett., 97, 071301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Watson, C. R., Beacom, J. F., Yüksel, H., & Walker, T. P. 2006, Phys. Rev. D, 74, 033009 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, C. R., Li, Z., & Polley, N. K. 2012, J. Cosmol. Astropart. Phys., 3, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, M., & de Boer, W. 2010, A&A, 509, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xue, X. X., Rix, H. W., Zhao, G., et al. 2008, ApJ, 684, 1143 [NASA ADS] [CrossRef] [Google Scholar]
- Yüksel, H., Beacom, J. F., & Watson, C. R. 2008, Phys. Rev. Lett., 101, 121301 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Fluxed image of the observations inTable 1 showing the positions of each 8′ × 8′ chip for each observation (magenta squares) and the regions removed as point sources (small green ellipses, <1% of the total area) and Sgr A (white circle). The data have been smoothed with a five-pixel Gaussian for visualisation purposes. |
| In the text | |
 |
Fig. 2 Left: the stacked spectrum and best-fit base model (without any additional line emission) in normalised counts keV-1 s-1, and χ residuals below for the 2.0−9.0 keV. No significant emission line excess is seen around 3.5 keV. Right: same for the 3.0−6.0 keV interval. The red curve shows the model including the mass-scaled expected signal from Bulbul et al. (2014) and residuals under the assumption of a Navarro-Frenk-White (NFW) profile for the Milky Way dark matter halo. |
| In the text | |
 |
Fig. 3 Left: the best fit incident model spectrum of the base model showing contributions of the individual additive model components for the 2.0−9.0 keV interval. Right: as left, for the 3.0−6.0 keV interval. |
| In the text | |
 |
Fig. 4 Constraints on line emission flux in the stacked spectrum (95% confidence). The cyan lines represent the entire 2–9 keV interval model, and purple lines the 3–6 keV interval. Solid lines represent the total flux in line emission (including instrumental and astrophysical lines) and for dotted lines the broad instrumental lines have been subtracted. |
| In the text | |
 |
Fig. 5 A selection of density profiles and parameter ranges fromTable 4 as a function of radius from the galactic centre (solid line) and along the line of sight towards Sgr A* (dashed line). The vertical black line indicates the solar radius, and the dotted vertical lines are the mass-weighted average distances for each of the profiles. |
| In the text | |
 |
Fig. 6 Left: general constraints on the interaction rate with one-photon emission proportional to matter density (95% confidence) for an isothermal (dashed lines) and NFW profile (solid lines). The grey lines show the combination of previous constraints (Lattanzi et al. 2013, and references therein). The cyan lines are for the entire 2–9 keV interval model, and the purple lines are for the 3–6 keV interval. Right: constraints on the velocity-averaged cross-section for models with two-photon emission from dark matter annihilating into two photons from the total line emission flux for an isothermal (dashed lines) and NFW dark matter profile (solid lines). |
| In the text | |
 |
Fig. 7 Mass-mixing angle constraints on sterile neutrino like dark matter candidates. Above/below the dashed black lines the sterile neutrinos will be over/under produced relative to the observed dark matter density (Laine & Shaposhnikov 2008; Canetti et al. 2013b). The grey shaded regions are X-ray exclusion lines from XMM-Newton and Chandra observations (Boyarsky et al. 2008a, 2006a; Riemer-Sørensen & Hansen 2009) with the Boyarsky et al. (2008a) constraints rescaled by a factor of two due to mass estimate uncertainties as recommended in Boyarsky et al. (2009b). The cyan and purple regions are the parameter space ruled out by the present Sgr* analysis assuming an NFW profile for the Milky Way halo. The cyan lines are for the case where the entire 2–9 keV interval is modelled, and the purple lines are for the 3–6 keV interval. The dashed lines are for the isothermal profile where the constraints are weakened by an order of magnitude. The dotted grey line show the constraints from Horiuchi et al. (2014) for which the model contains some lines of astrophysical origin. The green error bar is the signal from Boyarsky et al. (2014), and the blue error bars represent the signal from Bulbul et al. (2014) with the small range indicating the best fit to the entire stack of spectra. The larger bars indicate the range of results from their different analyses. All the inferred signals are ruled out at 95% confidence under the NFW assumption. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


