| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 16 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201527013 | |
| Published online | 16 May 2016 | |
The 2–10 keV unabsorbed luminosity function of AGN from the LSS, CDFS, and COSMOS surveys⋆,⋆⋆
1
Institute for Astronomy, Astrophysics, Space Applications and
Remote Sensing (IAASARS), National Observatory of Athens, 15236
Penteli,
Greece
2
INAF–Osservatorio Astronomico di Bologna, via Ranzani
1, 40127
Bologna,
Italy
3
Lund Observatory, Department of Astronomy and Theoretical Physics,
Lund University, Box
43, 22100
Lund,
Sweden
e-mail:
piero@astro.lu.se
4
Service d’astrophysique, IRFU, CEA Saclay,
91191
Gif-sur-Yvette,
France
5
Geneva Observatory, University of Geneva,
ch. des Maillettes 51,
1290
Versoix,
Switzerland
6
Max-Planck-Institut für extraterrestrische Physick,
85478
Garching,
Germany
7
Department of Physics, Yale University,
PO Box 208121, New Haven, CT
06520,
USA
8
Instituto de Física de Cantabria (CSIC-UC),
39005
Santander,
Spain
9
INAF–IASF Milano, via Bassini 15, 20133
Milano,
Italy
10
ICREA and Institut de Ciències del Cosmos (ICC), Universitat de
Barcelona (IEEC-UB), Martí y
Franquès 1, 08028
Barcelona,
Spain
11
Argelander Institute for Astronomy, Bonn University,
53121
Bonn,
Germany
12
Physics Department, Aristotle University of
Thessaloniki, 54124
Thessaloniki,
Greece
13
Università di Bologna, Dipartimento di Fisica e
Astronomia, via Berti Pichat
6/2, 40127
Bologna,
Italy
Received: 20 July 2015
Accepted: 16 December 2015
The XMM-Large scale structure (XMM-LSS), XMM-Cosmological evolution survey (XMM-COSMOS), and XMM-Chandra deep field south (XMM-CDFS) surveys are complementary in terms of sky coverage and depth. Together, they form a clean sample with the least possible variance in instrument effective areas and point spread function. Therefore this is one of the best samples available to determine the 2–10 keV luminosity function of active galactic nuclei (AGN) and their evolution. The samples and the relevant corrections for incompleteness are described. A total of 2887 AGN is used to build the LF in the luminosity interval 1042–1046 erg s-1 and in the redshift interval 0.001–4. A new method to correct for absorption by considering the probability distribution for the column density conditioned on the hardness ratio is presented. The binned luminosity function and its evolution is determined with a variant of the Page-Carrera method, which is improved to include corrections for absorption and to account for the full probability distribution of photometric redshifts. Parametric models, namely a double power law with luminosity and density evolution (LADE) or luminosity-dependent density evolution (LDDE), are explored using Bayesian inference. We introduce the Watanabe-Akaike information criterion (WAIC) to compare the models and estimate their predictive power. Our data are best described by the LADE model, as hinted by the WAIC indicator. We also explore the recently proposed 15-parameter extended LDDE model and find that this extension is not supported by our data. The strength of our method is that it provides unabsorbed, non-parametric estimates, credible intervals for luminosity function parameters, and a model choice based on predictive power for future data.
Key words: surveys / galaxies: active / X-rays: general / methods: statistical
Based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA member states and NASA.
Tables with the samples of the posterior probability distributions are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/590/A80
© ESO, 2016
1. Introduction
An accurate census of active galactic nuclei (AGN) is a central element in understanding the cosmic history of accretion onto supermassive black holes (BH). Black hole growth is in turn closely connected to star formation. Scaling relations exist between the masses of the BH and of the bulge of the host galaxies (Magorrian et al. 1998; Ferrarese & Merritt 2000; Gebhardt et al. 2000; Marconi & Hunt 2003; Häring & Rix 2004; Hopkins et al. 2007; Kormendy & Bender 2009; Gültekin et al. 2009; Zubovas & King 2012). On a larger scale, it has been recognised that BHs and their hosts have been growing together for a large part of cosmic time (Marconi et al. 2004; Alexander & Hickox 2012) and that they exhibit a similar downsizing trend, i.e. that more massive systems were formed earlier than lower mass systems (Cowie et al. 1996; Ueda et al. 2003; Kodama et al. 2004; Hasinger et al. 2005; Fontanot et al. 2009; Santini et al. 2009).
Active galactic nuclei are the principal constituent of the extragalactic X-ray sky, and their integrated contribution essentially builds up the X-ray cosmic background (Setti & Woltjer 1989; Comastri et al. 1995). Modelling the X-ray background requires knowledge of the X-ray luminosity function (LF) of AGN, their evolution, and the distribution of the column density of the absorbing medium. The fraction of Compton-thick AGN with column densities NH ≳ 1024 cm-2 have especially notable uncertainties (Gilli et al. 2007; Treister et al. 2009; Akylas et al. 2012).
X-ray LFs started to be estimated as soon as AGN samples became available (Maccacaro et al. 1983, 1984) and progressed with Einstein and ROSAT surveys (Maccacaro et al. 1991; Boyle et al. 1993, 1994; Page et al. 1996). Among the recent estimates in the 2–10 keV band, we mention Ueda et al. (2003), La Franca et al. (2005), Barger et al. (2005), Silverman et al. (2008), Ebrero et al. (2009), Yencho et al. (2009), Aird et al. (2010, hereafter A10), Ueda et al. (2014, hereafter U14), Miyaji et al. (2015, hereafter M15), Vito et al. (2014), Buchner et al. (2015) and Aird et al. (2015, hereafter A15). Several methods and models have been explored over the years; the remaining uncertainties regard the evolution of the LF at high redshift and the (redshift-dependent) amount of obscuration. Further progress in such studies requires large samples containing a sizeable number of AGN at redshift ≳3 and depends on knowledge of the joint (NH, z) distribution (U14; M15).
A common approach to the most recent estimates of the AGN LF (e.g. A10; U14; M15) is to amass a very large number of AGN from different surveys made with different instruments, ranging from all-sky and shallow to pencil-beam and deep. Two possible pitfalls with that approach are that different instruments have i) different energy responses, which sometimes, do not even overlap, as in the case of Swift/BAT vs. Chandra and XMM-Newton; and ii) different point spread functions (PSF). In case i), biases may arise if the LFs in different bands are different (e.g. because the amount of obscuration may evolve with redshift). In case ii), large PSFs in medium-deep surveys (e.g. the ASCA surveys, used by A10; U14; M15) may conceal close pairs of AGN. Furthermore, using data from very different energy bands requires detailed spectral modelling (as done by U14) that may introduce more uncertainties.
We adopt a different approach. We build a sample with a selection as clean and well defined as possible. We limit ourselves to XMM-Newton surveys in the 2–10 keV band so that we have the same energy response and consistent PSFs. We focus on three surveys at different levels of depth and area; ordered from the widest and shallowest to the narrowest and deepest, we choose the XMM-Large scale structure survey (XMM-LSS; Chiappetti et al. 2013), the XMM-Cosmological evolution survey (XMM-COSMOS; Cappelluti et al. 2009), and the XMM-Chandra deep field survey (XMM-CDFS; Ranalli et al. 2013). Together, these surveys provide ~3000 objects.
Our approach to absorption corrections is to use the Swift/BAT spectral atlas of local AGN (Burlon et al. 2011), and the 0.5–2/2–10 keV flux ratio and the redshift of the objects from which we build the LF. With this information, we derive a conditioned probability distribution for the amount of absorption for each AGN. We regard this as an improvement over A10, who did not correct for absorption; over U14, who derived the (NH, z) distribution from a small subset of their sample; and over M15, who took the (NH, z) distribution from U14. Our approach to absorption corrections naturally accounts for the possible increase in the fraction of absorbed AGN from z = 0 to ~2 that has been proposed (La Franca et al. 2005; Ballantyne et al. 2006; Treister & Urry 2006; Hasinger 2008; Hiroi et al. 2012; Iwasawa et al. 2012). Moreover, by integrating the absorption distributions over the flux ratio, we are able to test whether our data are compatible with the (NH, z) distributions obtained by U14 and by Hasinger (2008).
The most recent papers (U14; M15) estimate the LFs as parametric fits with the maximum likelihood (ML) method. We instead use two different methods: binned estimates and Bayesian inference. The former provides a non-parametric representation of the LF, which is very useful to investigate whether there is any feature of the data that is not reproduced by the parametric models. Bayesian inference builds on the same likelihood function of the ML method, but provides a more accurate ascertainment of the allowed parameter space along with theoretically sound methods to evaluate and compare models. Bayesian inference has already been used to estimate LFs by A10 and Fotopoulou et al. (2016). We take this method a step further: We use Bayesian methods to investigate whether the models correctly reproduce the data features and the predictive accuracy of our LF estimate.
We release1 the code we developed for the analysis we describe in the form of the package LFTools, which includes programmes for absorption corrections, binned estimates, maximum-likelihood estimates, and Bayesian inference.
In Sect. 2, we present the samples and surveys from which they are drawn. In Sect. 3, we introduce our method to correct luminosities for the amount of absorption. In Sect. 4, we derive binned estimates of the LF. In Sect. 5, we introduce parametric forms for the LF, and present methods and results from Bayesian inference. In Sect. 6 we introduce the concept of posterior predictive power, and estimate this power using the Watanabe-Akaike information criterion. In Sect. 7 we consider a proposed extension to the LDDE model. In Sect. 8 we discuss our results. Finally in Sect. 9 we present our conclusions.
Throughout this paper, we assume a flat ΛCDM cosmology with H0 = 70, ΩM = 0.3, and ΩΛ = 0.7. We also assume, for K corrections, a power-law spectrum with photon index Γ = 1.7 (Ranalli et al. 2015). The “log” and “ln” symbols designate the base-10 and natural logarithm, respectively.
 |
Fig. 1 Areas covered by the XMM-LSS (black solid curve), XMM-CDFS (red long-dashed curve), and XMM-COSMOS (green short-dashed curve) surveys, vs. 2–10 keV flux. Although the nominal depth of LSS is 10 ks, it also includes the Subaru Deep Field (Ueda et al. 2008) whose exposure is 100 ks. The blue dotted curve shows the LSS coverage after including selection effects (availability of redshifts and reliability of the optical counterpart identification; i.e. Ω(f) from Eq. (1); see Sect. 2.4). The CDFS and COSMOS have nearly complete redshift availability (either spectroscopic of photometric) so selection effects can be ignored. |
 |
Fig. 2 Luminosity-redshift diagram for the XMM-LSS, XMM-CDFS, and XMM-COSMOS surveys. The contours are logarithmically scaled and show the fraction of objects with z and L inside the contour (levels at 97%, 94.8%, 90%, 83%, 70%, and 48% from outermost to innermost). The data points show the objects outside the lowest contour. At z> 0.5, the XMM-CDFS systematically probes AGN that are fainter by up to one order of magnitude. Observed luminosities, corrected only for Galactic absorption, are shown. |
2. Samples
The coverage curves for the XMM-LSS, XMM-COSMOS, and XMM-CDFS surveys are shown in Fig. 1. Two curves are shown for XMM-LSS: the nominal coverage and a corrected coverage accounting for redshift incompleteness (see Sect. 2.4).
The distribution in the luminosity-redshift plane of the AGN in the XMM-LSS, XMM-COSMOS, and XMM-CDFS survey is shown in Fig. 2. The peaks of the distributions occur all around z ~ 1.1–1.2, but at three distinct luminosities: L ~ 1.7 × 1044, 4.8 × 1043, and 2.0 × 1043 erg s-1 for XMM-LSS, XMM-COSMOS, and XMM-CDFS, respectively. The XMM-CDFS probes a complementary part of the luminosity-redshift plane with respect to the other two surveys, allowing one to reach luminosities which, redshifts being equal, are one order of magnitude fainter.
2.1. X-ray selected AGN from the XMM-LSS
The XMM-LSS catalogue (Chiappetti et al. 2013) contains 2573 objects with a hard X-ray detection and with point-like morphology. Of these, 459 have a spectroscopic redshift determination, while 1846 (among which all the 459 are included) have a photometric redshift. The remaining have either no optical counterpart or no photometric redshift; this is mostly due to non-uniform optical coverage of the field.
The X-ray catalogue contains matches to optical sources obtained with the likelihood ratio technique, which provides a probability value for the X-ray/optical match given by considering the sky coordinates and their uncertainties. In this work, we only consider sources with match probability larger than 95%, so that our LSS sample consists of 1520 objects. Histograms of the fluxes of the objects in the two samples are presented in Fig. 3. The fraction of objects used for this paper is therefore 1520/2573 ~ 59%.
Photometric redshifts
Photometric redshifts (photo-z in the following) for LSS (Melnyk et al. 2013) were recomputed using the LePhare SED fitting code (Ilbert et al. 2006; Arnouts et al. 1999), with a flat prior on the redshift distribution, in order to obtain the photo-z probability distributions. We stress that we do not use photo-z at their nominal value; we rather consider for each source its own entire probability density (see Sects. 4 and 5.4).
2.2. X-ray selected AGN from the XMM-CDFS
The redshift information is almost complete (95.3%, or 323 objects out of 339) so no correction for incompleteness is needed.
Photometric redshifts
The XMM-CDFS catalogue (Ranalli et al. 2013) contains photometric redshifts from different published sources available at the time it was compiled. Probability distributions were however not available. Therefore, we use photometric redshifts from Hsu et al. (2014), so that the full probability distributions can be included.
2.3. XMM-COSMOS
The XMM-COSMOS catalogue (Cappelluti et al. 2009) contains 1079 sources with detection in the 2–10 keV band; 1044 of these have a redshift. Since the redshift completeness is 97%, completeness corrections are not necessary.
Photometric redshifts
Probability distributions for photometric redshift are taken from from Salvato et al. (2011), which is an update over Salvato et al. (2009).
2.4. Corrections for incompleteness of redshift and match
The coverage should be corrected to reflect the above selection; we define the corrected coverage Ω(f) at flux f as 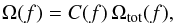 (1)where C(f) is the correction to be made at flux f, and Ωtot is the uncorrected coverage. We use a simple model in which C(f) only depends on the X-ray flux
(1)where C(f) is the correction to be made at flux f, and Ωtot is the uncorrected coverage. We use a simple model in which C(f) only depends on the X-ray flux 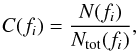 (2)where the correction C(fi) is assumed equal to the ratio of the number of selected objects (N) over the total number of objects (Ntot) in a flux bin with centre fi and width Δ Logf = 0.1 (Fig. 3). The quantities Ωtot and Ω from Eq. (1) are shown in Fig. 1 as the black solid and blue dotted curve, respectively. When needed, C(f) is interpolated over the C(fi). The same method has been used by M15.
(2)where the correction C(fi) is assumed equal to the ratio of the number of selected objects (N) over the total number of objects (Ntot) in a flux bin with centre fi and width Δ Logf = 0.1 (Fig. 3). The quantities Ωtot and Ω from Eq. (1) are shown in Fig. 1 as the black solid and blue dotted curve, respectively. When needed, C(f) is interpolated over the C(fi). The same method has been used by M15.
 |
Fig. 3 Normalised histograms of LSS fluxes. The blue histogram shows the full sample of 2573 objects, the red histogram shows the sample we used that contains 1520 objects with a redshift and an optical counterpart match probability of >95%. |
The above method implicitly assumes that, in each flux bin, the objects available for the LF (i.e. those with a reliable optical counterpart and redshift) have the same characteristics as the objects that are not available for the LF. This assumption could be violated in some cases; we illustrate this with an example. We consider the LF of the objects with only a spectroscopic redshift. There is a selection effect that spectroscopic objects have on average lower redshifts than objects with photometry alone. This is due to i) brighter objects that make spectroscopy feasible or less expensive; and ii) more spectral lines that are available at optical wavelengths for low-redshift objects, while high-redshift objects often need infrared spectroscopy, which is more demanding in terms of instrument availability. Thus, the spectroscopic-only LF should be a little higher at low redshifts and a little lower at high redshifts than the spectroscopic+photometric LF. This effect can actually be seen in our data. We found that the spectroscopic-only LF lies a factor ~1.5 above the spectroscopic+photometric LF at z ≲ 1, and that this behaviour is reversed at z ≳ 1. This threshold at z ~ 1 is coherent with the redshift distribution, which indicates that the spectroscopic z is the majority at z ≲ 1 and the photometric z prevails at values ≳1. We stress, however, that such a factor 1.5 is still within the 1σ uncertainty of the binned LF presented in Sect. 4. We consider our simple method to be appropriate for the present data; we caution that a more articulated treatment may be needed in case of severely incomplete, or biased, samples.
3. Probability distributions for absorption corrections
 |
Fig. 4 Probability distribution of the unabsorbed/absorbed flux ratio in the 2–10 keV, as a function of the measured 0.5–2/2–10 keV flux ratio, for the Burlon sample, at redshift zero. The x-axis shows Log(SH), therefore hard sources are on the left and soft sources are on the right. The y-axis shows Log(U), therefore no correction is at the bottom and large corrections are at the top. The colour scale goes from white (low probability) to black (high probability). |
The fluxes quoted in both the LSS and CDFS catalogues are not corrected for intrinsic absorption. However, the LF should be computed with intrinsic luminosities, i.e. corrected for absorption. Ideally, corrections should be made by determining the column density of every source by means of spectral fits, but this may not be feasible for faint sources and/or for large samples. Instead, here we apply a statistical correction based on the band ratio SH between the fluxes in the 0.5–2 and 2–10 keV bands 2.
The band ratio is chosen over the hardness ratio, which would convey the same information, because fluxes are more readily available than counts in the LSS catalogue, and because the band ratio does not depend on the instrument (while the hardness ratio does) so that this method can also be applied to surveys with future instruments.
Let U be the ratio between the 2–10 keV unabsorbed and absorbed fluxes. Different combinations of column densities, spectral slope, and redshift may lead to similar values of SH (or U), but there is no one-to-one correspondence between SH and U. At any redshift, we consider the conditional probability P(U | SH), which is the probability of each possible correction U for a source with a given SH. Following the definition of conditional probabilities we can express it in terms of the joint probability of U and SH, normalised by P(SH), 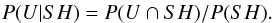 (3)To calculate the above distributions, we consider a simple spectral model consisting of an absorbed power law, and a grid of values for its parameters: column density NH, photon index Γ, and redshift z. We obtain U and SH from the model for all of the points in the grid.
(3)To calculate the above distributions, we consider a simple spectral model consisting of an absorbed power law, and a grid of values for its parameters: column density NH, photon index Γ, and redshift z. We obtain U and SH from the model for all of the points in the grid.
An estimate of the distributions of U and SH at a given z can therefore be obtained by considering the joint distribution of (NH, Γ) at that z. For simplicity, we assume the distribution P(NH,Γ) to be independent from z. In the following, we take the P(NH,Γ) distribution from the complete sample of AGN detected by Swift/BAT and collected by Burlon et al. (2011; hereafter “Burlon sample”). The Burlon sample offers good-quality spectra for a volume-limited set of AGN. This sample has been selected in a harder energy band than the 2–10 keV of this work, so this ensures that the sample is much less biased against absorbed sources, than if we used a spectral atlas selected in the 2–10 keV band. There are several estimates of the fraction of absorbed AGN in the literature, which we review in Sect. 3.1.
With regard to the absorption correction, the main feature is the presence of heavily-obscured objects, which produces a very wide distribution of U for sources with no 0.5–2 keV detection (leftmost column in Fig. 4); see discussion in Sect. 3.1.
 |
Fig. 5 Medians of the absorption correction U for the objects in the XMM-LSS, XMM-CDFS, and XMM-COSMOS surveys, over a grid of redshift and observed luminosity. Probability distributions for photometric redshifts have been included. The corrections are mostly significant for objects in the faint tail of the luminosity function (i.e. L ≲ 43–44.5, depending on z), or for z ≳ 3. The correction U (Sect. 3) is logarithmic, hence U = 0.5 corresponds to the luminosity being corrected by a factor of 2. The colour scale goes from black (median correction is 0) to bright yellow (median correction is 0.6). White areas are not populated. |
To smooth the distribution, we consider the parameters both at their face values, and after adding Gaussian random errors with standard deviations equal to those resulting from the spectral fits.
The P(U | SH) distributions at z = 0, resulting from the Burlon sample, are plotted in Fig. 4. The main features are:
-
as expected, softer sources are on average less absorbed and need fewer corrections;
-
sources without a detection in the 0.5–2 keV band (i.e. with SH = 0) may potentially need large corrections; their P(U) is considerably broader than that of sources with SH> 0. This however depends on whether a hard Γ or a large NH is preferred when fitting sources with low-quality spectra.
In Fig. 5, we show the median correction U, which resulted from applying our method to the surveys described in this paper. The objects were grouped according to their redshift and observed luminosity (considering probability distributions of photometric redshift). For z ≲ 3, corrections are small for objects in the bright tail of the LF, and larger for objects in the faint tail. At z ≳ 3, larger corrections also appear for high-luminosity objects (L> 1044.5).
3.1. Fraction of heavily obscured AGN
In this Sect., we compare several estimates of the fraction of obscured (NH> 2 × 1022 cm-2) and Compton-thick (NH> 1 × 1024 cm-2; hereafter CT) AGN in the literature. Our aim is to check that our use of the Burlon et al. (2011) sample is consistent with current knowledge.
Burlon et al. (2011) analysed a sample of 199 spectra of AGN selected in the 15–200 keV band with Swift/BAT, finding that 53% were obscured and 5.5% CT3. They also claim that after correcting for the observational bias, which makes CT sources difficult to detect, the CT fraction could rise to 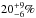 . Similar fractions, of 7% CT and 43% obscured AGN, have been found by Malizia et al. (2009) in an INTEGRAL-selected complete sample.
. Similar fractions, of 7% CT and 43% obscured AGN, have been found by Malizia et al. (2009) in an INTEGRAL-selected complete sample.
At lower energies, Brightman & Ueda (2012) reanalysed Chandra spectra in the CDFS using models accounting for Compton scattering and the geometry of circumnuclear material, finding a fraction of 5.5% CT objects. These authors estimate that after accounting for the observational bias, this fraction should rise to ~20% in the local Universe, and to ~40% at z = 1–4. In a sample of galaxies selected in the infrared with magnitude K< 22 and with 1.4 <z< 2.5, Daddi et al. (2007) found a fraction of 20% CT.
From fits to the cosmic X-ray background, Akylas et al. (2012) found that a fraction of 5–50% is allowed. Fractions of the order of 10% are also reported in Treister et al. (2009) and in the models by Hopkins et al. (2006) and Gilli et al. (2007). At high redshift and for intermediate luminosities, Hasinger (2008) reports that there is “convincing evidence” that there is no large change in the relative numbers of Compton-thin and -thick AGN with respect to the local Universe.
Our use of the Burlon et al. (2011) sample to derive the absorption correction is therefore supported by the available literature. If the larger fractions of CT AGN obtained after correcting for the observational bias were held true, then our corrections could be regarded as very conservative.
3.2. High-redshift evolution of the absorbed fraction
The fraction of absorbed AGN seems to be larger at high redshift than in the local Universe (La Franca et al. 2005; Ballantyne et al. 2006; Treister & Urry 2006). Hasinger (2008) found an increase that could be modelled as (1 + z)0.62 ± 0.11 for 0 <z< 2, saturating at z ~ 2. This is approximately a factor of 2 at z ~ 2. Ueda et al. (2014) found an increase by a factor of ~1.5 between the redshift intervals 0.1 <z< 1 and 1 <z< 3.
The Burlon et al. (2011) sample consists of objects at z ~ 0, so one could ask if the absorption evolution could have any effect on our method. We never use the marginal distribution P(NH) from Burlon et al. (2011); instead in Eq. (3), we use the (NH,Γ) joint distribution to obtain the conditioned probability of the needed correction, given the observed soft/hard flux ratio. The absorption correction mostly depends on NH, thus P(U | SH) is essentially analogous to P(NH | SH). The evolution of absorption is reflected in an evolution of the flux ratio SH, therefore our method naturally accounts for the evolution of absorption.
One possibility is that the Burlon et al. (2011) sample is still missing some kind of (NH,Γ) combination, which is rare in the local Universe but becomes abundant at high redshift (or, conversely, something that is abundant becomes rare). For example, if Compton-thick AGN, were more abundant at high redshift, then our corrections would err on the conservative side (less correction than needed). We prefer not to speculate on how the Compton-thick population (or that of any other kind of AGN) changes with redshift. However, we stress that i) the Burlon et al. (2011) sample contains 11 Compton-thick AGN (6% of total) so our corrections are not over-influenced by just one or a few objects; and ii) the fraction of Compton-thick AGN does not seem to vary much with redshift (see Sect. 3.1).
 |
Fig. 6 Luminosity function, from combined XMM-LSS, CDFS, and COSMOS data, with binned estimates (black data points with 1σ error bars) and Bayesian highest posterior densities (HPD) under the LDDE (blue area) and LADE (red area) models. For both models, the darker areas show the 68.3% HPD intervals, while the lighter areas show the 99.7% HPD intervals. |
 |
Fig. 7 Luminosity function, from XMM-LSS, CDFS, and COSMOS data, with binned estimates from all surveys together (black data points) and Bayesian highest posterior densities (68.3% HPD interval) for individual surveys under the LDDE model (red: LSS; yellow: CDFS; green: COSMOS). |
4. Binned luminosity function
The differential luminosity function Φ is defined as the number of objects N per comoving volume V and per unabsorbed luminosity L as follows: 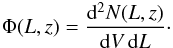 (4)A few variants of the original 1 /Vmax method (Schmidt 1968) have been proposed with the aim of refining the method; examples are Page & Carrera (2000), La Franca & Cristiani (1997), Miyaji et al. (2001). Here we build on Page & Carrera (2000) and include absorption corrections and probability distributions for photometric redshift in the method.
(4)A few variants of the original 1 /Vmax method (Schmidt 1968) have been proposed with the aim of refining the method; examples are Page & Carrera (2000), La Franca & Cristiani (1997), Miyaji et al. (2001). Here we build on Page & Carrera (2000) and include absorption corrections and probability distributions for photometric redshift in the method.
The LF in a bin with luminosity and redshift boundaries Lmin, Lmax and zmin, zmax, respectively, and containing N objects, is approximated by 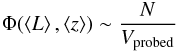 (5)with
(5)with 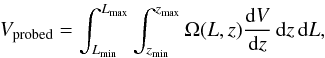 (6)where ⟨L⟩ and ⟨z⟩ are the log-average luminosity and average redshift of the bin, respectively; Ω(L,z) is the survey coverage at the flux that an object of luminosity L would have if placed at redshift z; and dV/ dz is the comoving volume.
(6)where ⟨L⟩ and ⟨z⟩ are the log-average luminosity and average redshift of the bin, respectively; Ω(L,z) is the survey coverage at the flux that an object of luminosity L would have if placed at redshift z; and dV/ dz is the comoving volume.
For each source i, the unabsorbed 2–10 keV luminosity Li is obtained from the observed 2–10 keV flux fi and the 0.5–2/2–10 keV flux ratio SHi, considering the following redshift and absorption probability distributions (Sect. 3): 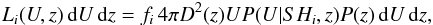 (7)where D(z) is the luminosity distance. Therefore we replace N in Eq. (5) with
(7)where D(z) is the luminosity distance. Therefore we replace N in Eq. (5) with 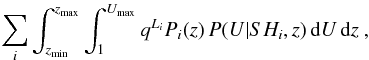 (8)where qLi is 1 if Lmin ≤ Li(U,z) <Lmax, and is 0 otherwise. For sources with photo-z, Pi(z) is the probability density obtained from the template fitting, while for sources with spectroscopic redshift, we use Dirac’s δ, Pi(z) = δ(zspec). Errors on N are estimated assuming Gaussianity (for N ≥ 50) or by interpolating the tables in Gehrels (1986) (for N< 50).
(8)where qLi is 1 if Lmin ≤ Li(U,z) <Lmax, and is 0 otherwise. For sources with photo-z, Pi(z) is the probability density obtained from the template fitting, while for sources with spectroscopic redshift, we use Dirac’s δ, Pi(z) = δ(zspec). Errors on N are estimated assuming Gaussianity (for N ≥ 50) or by interpolating the tables in Gehrels (1986) (for N< 50).
As for Vprobed (Eq. (6)), the integrals should run on the unabsorbed luminosities, while the coverage Ω(L,z) should refer to the observed (i.e. absorbed) fluxes. Therefore we replace Eq. (6) with 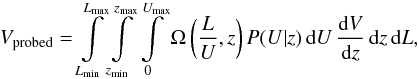 (9)where L/U is therefore the absorbed luminosity, and P(U | z) is the marginal probability of an absorption correction U, conditioned only by the redshift z.
(9)where L/U is therefore the absorbed luminosity, and P(U | z) is the marginal probability of an absorption correction U, conditioned only by the redshift z.
 |
Fig. 8 Luminosity function, from XMM-LSS, CDFS, and COSMOS data, with binned estimates from all surveys together (black data points) and Bayesian highest posterior densities (68.3% HPD interval) for individual surveys under the LADE model. Colours as in Fig. 7. |
The binned LF is shown in Fig. 6 (and also, for comparison, in Figs. 7 and 8).
5. Bayesian inference
Bayesian inference relies on a different interpretation of what a probability is with respect to the classical (frequentist) interpretation. In the Bayesian framework, probability measures our degree of belief about a proposition; a probability can be assigned to the parameters subject of inference or to abstract ideas such as models. We will not go over the theory details here; a nice introduction can be found in Trotta (2008) or in the book by Gregory (2005). Advanced methods can be found in Gelman et al. (2013). Example applications pertaining to astronomical catalogues, source detection, flux estimate, etc. can be found in Andreon (2012) and Andreon & Hurn (2013).
The outcome of Bayesian inference is a posterior probability distribution that yields the probability P(θ) for a vector of parameters θ. There are some similarities with maximum-likelihood (ML) methods: for example, the same likelihood function is used. However, while ML aims to find just the best-fit values for θ (with confidence intervals derived by asymptotic theory), Bayesian inference aims to obtain P(θ) for all possible or reasonable values of θ, and therefore offers a more accurate description of how the model fits the data.
Exploring the parameter space becomes computationally intensive as soon as the dimensionality of the parameters θ becomes larger than a few; the models considered in this paper have either eight (LADE) or nine (LDDE) dimensions. Effective methods are therefore valuable. Nested sampling has been proposed as a particularly powerful method (Skilling 2004, 2006), and has already been used for LF estimates by A10. The most popular implementation is the MultiNest library (Feroz & Hobson 2008; Feroz et al. 2009, 2013), which we used to derive the posterior distributions for the LF parameters.
In this section, we first describe the ingredients needed for Bayesian inference: parametric models of LF with redshift evolution and the likelihood function. Next, we present our results.
5.1. Parametric form for the luminosity function
A broken power-law form has been suggested for the z ~ 0 AGN luminosity function since early works (Maccacaro et al. 1983, 1984) as follows: ![\begin{eqnarray} \label{eq:doublepow} \frac{{\rm d} \Phi (L)}{{\rm d} \mbox{Log}\, L} = A \left[ \left( \frac{L}{L_*} \right)^{\gamma_1} + \left( \frac{L}{L_*} \right)^{\gamma_2} \right]^{-1} , \end{eqnarray}](/articles/aa/full_html/2016/06/aa27013-15/aa27013-15-eq112.png) (10)where A is the normalisation, L∗ is the knee luminosity, and γ1 and γ2 are the slopes of the power law below and above L∗.
(10)where A is the normalisation, L∗ is the knee luminosity, and γ1 and γ2 are the slopes of the power law below and above L∗.
The LF parameters however evolve with redshift (Boyle et al. 1994; Page et al. 1996; Jones et al. 1997). Two simple and alternative forms for evolution are pure luminosity evolution (PLE; Mathez 1978; Braccesi et al. 1980) and pure density evolution (PDE; Schmidt 1968; Schmidt & Green 1983). The basic ideas of these forms are that L∗ is brighter at higher z (PLE) or A is larger at higher z (PDE). Several models have been proposed in the literature that bridge between these two possibilities and provide reasonable descriptions of the data. We focus on the two models that are currently most commonly used. Their complex functional forms are justified by the necessity to allow the bright end of the LF to move at larger luminosity at increasing z (to the right, in any panel of Fig. 6), while at the same time having the faint end of the LF move at lower number densities (to the bottom, in the same figure). Thus they can model the AGN downsizing: moving from the high-redshift Universe to present, the more luminous AGN have became much fainter and the less luminous AGNs have become more common.
5.2. Luminosity and density evolution
The luminosity and density evolution model (LADE; Ueda et al. 2003, A10) joins both kinds of evolution, and also enables a change in the pace of luminosity evolution after a critical redshift zc. Following A10, we use a double power law for the luminosity evolution 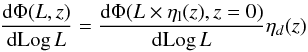 (11)with
(11)with ![\begin{eqnarray} \label{eq:lade2} \eta_{\rm l}(z) = \frac{1}{k} \left[ \left( \frac{1+z_{\rm c}}{1+z} \right) ^{p_1} + \left( \frac{1+z_{\rm c}}{1+z} \right) ^{p_2} \right], \end{eqnarray}](/articles/aa/full_html/2016/06/aa27013-15/aa27013-15-eq119.png) (12)
(12)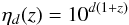 (13)
(13)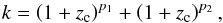 (14)where the evolution parameters are the critical redshift zc, the luminosity evolution exponents p1 and p2, and the density evolution exponent d. In particular, d is assumed to be negative to allow the faint end of the LF to decrease at larger z.
(14)where the evolution parameters are the critical redshift zc, the luminosity evolution exponents p1 and p2, and the density evolution exponent d. In particular, d is assumed to be negative to allow the faint end of the LF to decrease at larger z.
Following Fotopoulou et al. (2016) and at variance with A10, we have normalised the LADE model so that at z = 0, ηl = 1, and Eq. (11) reduces to the local LF.
5.3. Luminosity-dependent density evolution
Luminosity-dependent density evolution (LDDE), in the formalism introduced by Ueda et al. (2003), can be expressed as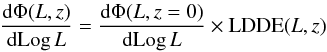 (15)with
(15)with 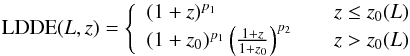 (16)and
(16)and 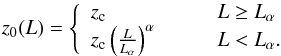 (17)The evolution parameters are the critical redshift zc, the evolution exponents p1 and p2, and two parameters (α and Lα) that give a luminosity dependence to zc. Although the functional form is different, the main features are the same as for LADE. The main difference is that, for increasing z, the slope of the faint end of the LF stays constant in LADE, while it changes (it flattens) in LDDE.
(17)The evolution parameters are the critical redshift zc, the evolution exponents p1 and p2, and two parameters (α and Lα) that give a luminosity dependence to zc. Although the functional form is different, the main features are the same as for LADE. The main difference is that, for increasing z, the slope of the faint end of the LF stays constant in LADE, while it changes (it flattens) in LDDE.
In U14, this model is further extended to include a luminosity dependence on p1 and a second break at a redshift z>z0, adding six more parameters (with a total of 15 parameters, we refer to this extension as LDDE15). Several parameters in U14 are fixed at values, which make the LF decline faster beyond z ~ 3, reproducing the results by Fiore et al. (2012). In the following, we initially consider the nine-parameter LDDE and compare it to LADE, deferring our treatment of LDDE15 to Sect. 7.
5.4. Likelihood function
The likelihood function can be obtained, following Marshall et al. (1983) (see also Loredo 2004), by considering a Poissonian distribution for the probability of detecting a number yi of AGN of given luminosity Li and redshift zi, 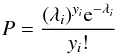 (18)with
(18)with 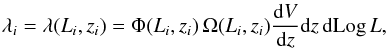 (19)where λ is the expected number of AGN with given Li and zi; and Φ is the LF evaluated at the source luminosity and redshift.
(19)where λ is the expected number of AGN with given Li and zi; and Φ is the LF evaluated at the source luminosity and redshift.
The likelihood ℒ is then defined as the product of the probability of detecting every source i in the catalogue times the probability of not detecting any AGN in the remaining parameter space Lj, zj, i.e., 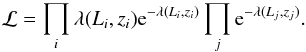 (20)The product of the exponential terms is actually extended over the entire parameter space. Therefore, the log-likelihood S = ln ℒ may be written as
(20)The product of the exponential terms is actually extended over the entire parameter space. Therefore, the log-likelihood S = ln ℒ may be written as 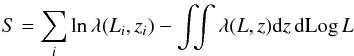 (21)so that S may considered as the sum of a “source term” (the left term, which is a sum over all sources) and a “coverage term” (the right term, i.e. the integral of λ). The integrals extend over the 0.0001–4 and 1041–1046 erg s-1 ranges in redshift and luminosity, respectively. Also, only the sources falling in these ranges are considered.
(21)so that S may considered as the sum of a “source term” (the left term, which is a sum over all sources) and a “coverage term” (the right term, i.e. the integral of λ). The integrals extend over the 0.0001–4 and 1041–1046 erg s-1 ranges in redshift and luminosity, respectively. Also, only the sources falling in these ranges are considered.
Marshall et al. (1983) drop the coverage and comoving volume from the sums in the first term of Eq. (21) because they do not depend on the fit parameters and can be treated as constants. Therefore, these authors obtain the same expression found by Loredo (2004) using a more correct approach. Here, consistent with Loredo (2004), we drop only the coverage and keep the comoving volume because we need to consider the dependence of λ on the redshift (whenever the source has a photo-z) and on the absorption. Therefore we rewrite Eq. (21) as 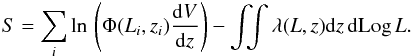 (22)For each source, Φi is averaged over the redshift and absorption distributions
(22)For each source, Φi is averaged over the redshift and absorption distributions 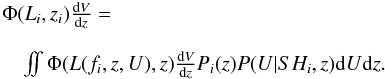 (23)For sources with a spectroscopic redshift, P(z) may be interpreted as a δ distribution as carried out for the binned LF.
(23)For sources with a spectroscopic redshift, P(z) may be interpreted as a δ distribution as carried out for the binned LF.
As noticed for the binned LF, the survey coverage should refer to observed, i.e. absorbed, fluxes. Therefore in the coverage term in Eq. (22), λ should be (compare with Eqs. (9) and (19)) 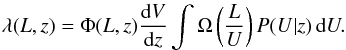 (24)Selection effects can be included in the likelihood function (Eq. (22)) following A10. If the expected number of objects λ is reduced by the factor C(L,z) defined in Eq. (2) as
(24)Selection effects can be included in the likelihood function (Eq. (22)) following A10. If the expected number of objects λ is reduced by the factor C(L,z) defined in Eq. (2) as 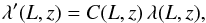 (25)then λ in Eq. (22) has to be replaced by λ′. In practice, this amounts to the reduction of the coverage function introduced in Eq. (1).
(25)then λ in Eq. (22) has to be replaced by λ′. In practice, this amounts to the reduction of the coverage function introduced in Eq. (1).
5.5. Results
Mode and 68.3% highest posterior density interval for the parameters under the LADE model.
We used the nested sampling method, together with the likelihood function and the parametric form described above, to compute the posterior probability distribution (hereafter just posterior) for the LF parameters. We repeated the computation for four combinations of data (all surveys together, and each survey individually) and models (LADE and LDDE). The result of each computation is a set of ~7000–8000 draws from the posterior; the exact number depends on the individual run, and on when the MultiNest algorithm attains convergence. These are available at the CDS. In Tables 1 and 2 we summarise the content of the draws: for each parameter, we report the mode4 and the 68.3% (“1σ”) highest posterior density (HPD) interval5. The HPD is the interval containing a given fraction of the posterior density, such that the posterior density inside the HPD is always larger than outside.
From the same sets of draws discussed above we produced the following plots of the LF. In Fig. 6 we plot the 68.3% and 99.7% (“3σ”) pointwise HPD intervals of the LF derived from all surveys together under either the LADE or the LDDE model. A comparison with the binned estimate reveals that the LADE and LDDE modes offer a largely overlapping description of the LF at z ≳ 1.
Some differences appear at low redshift (z ≲ 1) where LADE and LDDE appear to under-predict the LF at L ≳ 1044 and L ≳ 1045 erg s-1, respectively. A least-squares fit to the LF bins at luminosities brighter than the LF knee (Table 3) shows a progressive steepening of the bright tail of the LF. The same effect is seen also in M15, albeit not as clearly as here. The LADE model (Eqs. (11)–(14)) does not allow the double power-law slopes to change with redshift; the LDDE model (Eqs. (15)–(17)) allows some change but which in practice looks insufficient to follow the present data; therefore LADE has the largest deviations. The bright tail slope is determined by the sources with z> 1, which are the majority at bright luminosities (see Fig. 2), so the behaviour of the tail slope at lower redshifts is only loosely constrained by our data (for this reason, LADE nonetheless provides a better description of our data; see Sect. 8.1).
Mode and 68.3% highest posterior density interval for the parameters under the LDDE model.
Some discrepancies also appear in some redshift bins at the lowest luminosities. The large error bars on the binned LF show that the number of objects in these bins is limited; any discrepancy is contained within 2σ anyway.
The posterior densities for the double power-law parameters (A, γ1, γ2, and L∗) from all surveys together under the LADE or LDDE model are plotted as histograms in Fig. 9. The two models yield differences in A and L∗ of 2 and 1 order of magnitudes, respectively. This may be explained by noting that the double power-law parameters are coupled: a larger L∗ needs a smaller A and a steeper slope at L<L∗, which is indicated by the difference between LADE and LDDE for the left peaks of γ1 and γ2.
The parameters γ1 and γ2 have identical, double-peaked posteriors because they can be exchanged in Eq. (10) with no effect on the LF. The LDDE and LADE fully agree on the slope at L>L∗, whose average and 1σ dispersion are γ = 2.50 ± 0.13 and 2.50 ± 0.09 for LDDE and LADE, respectively. This value is slightly less steep than that quoted by A10 for their colour pre-selected sample (γ2 = 2.80 ± 0.12), but it is within the 1σ uncertainty for the X-ray-only sample of A10 (γ2 = 2.36 ± 0.15) under the LDDE model. Both U14 and M15 quote steeper slopes (U14: γ2 = 2.71 ± 0.09; M15: γ2 = 2.77 ± 0.12). A less steep slope at L>L∗ may result from the absorption corrections, if a larger fraction of heavily-absorbed objects is allowed.
So far we have commented qualitatively on the LF features; further quantitative evaluation of the differences among the models and surveys is presented in Sect. 6.
 |
Fig. 9 Posterior probability densities for double power-law parameters for all surveys combined, under the LDDE (blue) and LADE (red) models. The plotted variables are identified in the top right corner of each panel. The normalisation A is in Mpc-3, the knee luminosity L∗ is in erg s-1. The histograms are normalised hence the vertical scales are arbitrary. |
 |
Fig. 10 Posterior probability densities for double power-law and evolution parameters for individual surveys under the LDDE model; colours as in Fig. 7. For comparison, we also plot (blue histogram) the probability density for all surveys together under the same model. The plotted variables are identified in the top right corner of each panel. The normalisation A is in Mpc-3, the luminosities L∗ and Lα are in erg s-1. The histograms are normalised hence the vertical scales are arbitrary. |
 |
Fig. 11 Posterior probability densities for double power-law parameters for individual surveys under the LADE model; colours as in Fig. 7. For comparison, we also plot (blue histogram) the probability density for all surveys together under the same model. The plotted variables are identified in the top right corner of each panel. The normalisation A is in Mpc-3, the knee luminosity L∗ is in erg s-1. The histograms are normalised hence the vertical scales are arbitrary. |
5.6. Differences among individual surveys
The different surveys may exhibit some variance in the LF parameters. Possible reasons include, for example, the presence of large-scale structures (or voids) in the surveyed volume, small number effects at the edges of the luminosity and redshift intervals, residual effects of data reduction and source detection. In Figs. 7 and 8 we plot the 68.3% HPD intervals under the LDDE and LADE models, respectively, for each individual survey. The largest discrepancies appear at the edges of the luminosity and redshift bins where differences of up to one order of magnitude are present. The knee region is, apart from the lowest redshift panel, the area where the different surveys agree best. There seems to be more variance under the LADE model, where the XMM-LSS is consistently steeper at L ≳ L∗.
The areas where some discrepancies appear are subject to larger errors because of the low number of objects in the relevant ranges of luminosities and redshift: namely, the very low- and very high-luminosity bins at all redshifts. The XMM-CDFS LF seems to be less steep than the two others at L ≳ L∗, which is probably because of larger amounts of obscured objects.; this is illustrated in Figs. 10 and 11, where the posterior densities for all parameters are plotted, under the LDDE and LADE models, respectively. The XMM-CDFS also requires a lower L∗, by a factor 3–10, than the two other surveys; this probably reflects the better sampling of intrinsically fainter objects by the XMM-CDFS. The critical redshift zc at which the rate of evolution changes is found to be in the 1.5–2.5 interval for LDDE; it is less well constrained for LADE. The XMM-COSMOS data do not seem to require a decrease in the LF after zc, as hinted by the LADE d and LDDE p2 parameters, which are both consistent with zero.
6. Model comparison
An important reason why Bayesian inference enables a powerful model comparison is that it naturally includes the idea of Occam’s razor, which is that among competing models predicting a similar outcome, one should choose that with the fewest assumptions. Several metrics for model comparison have been devised in the literature, which contain integrals over the parameter volume (either prior, or posterior). A model with fewer parameters than another also has a smaller parameter volume; and a model whose parameters are all well-constrained occupies a smaller volume than a model with unconstrained parameters. It is in this way that Occam’s razor is incorporated.
Bayesian evidence, also called marginal likelihood, is the integral of the data likelihood over the prior volume. Bayesian evidence was used by A10 to estimate that LDDE was performing slightly better than LADE, and by A15 to reckon that LADE was not only significantly better than LDDE, but also that LDDE15 (see Sect. 7) was preferred over LADE.
Evidence is an effective metric when the priors can be easily defined, especially in their tails (Trotta 2008). For LF, however, the prior choices are still somewhat subjective. For example, the question arises as to which interval should be permitted for L∗ in the case of flat priors; log-normal, Cauchy, or exponential priors could be equally or more justified and effective, but it is difficult to tune their parameters in an objective manner. Therefore, in the following we prefer to focus on metrics that are based on the data likelihood given the posterior distribution.
We introduce the Watanabe-Akaike information criterion (WAIC; Watanabe 2010). It is one of a family of criteria that estimate the predictive power of a model, i.e. how a model can anticipate new data, can be extrapolated into unobserved regions of the luminosity-redshift space, or suggest future observations to improve the model weaknesses. A comprehensive review of the Bayesian methods is in Gelman et al. (2013, Chap. 7) (see also Gelman et al. 2014); an application of two of such methods to the problem of LF fitting is in Fotopoulou et al. (2016). The underlying idea is to compute the data likelihood under more than one model and compare these likelihoods after accounting for the different number of parameters6. The “information criterion” part of the name comes from the following reasoning: since every model is only an approximation of reality, then different models can cause different losses of information with respect to reality. Therefore, one should choose the model that preserves most information. This is the same concept as having more predictive power.
The WAIC method takes advantage of the fact that our data are naturally partitioned with each survey representing one partition. The starting point is the data log-likelihood, averaged over the posterior distribution of the parameters θ of model M. For consistency with Gelman et al. (2013), we call it “log pointwise predictive density” (lppd), defined as 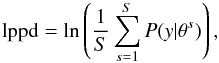 (26)where each θs is a sample from the posterior distribution of the parameters, S is the number of posterior samples, y is the observed data, and P(y | θs) is the data likelihood given the parameters θs. We can rewrite lppd after partitioning the data
(26)where each θs is a sample from the posterior distribution of the parameters, S is the number of posterior samples, y is the observed data, and P(y | θs) is the data likelihood given the parameters θs. We can rewrite lppd after partitioning the data 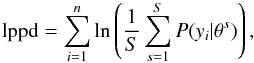 (27)which highlights the contribution from each survey i of n = 3 considered here, whose data are represented by yi. We obtain S = 1000 and use the same posterior draws from which Figs. 7–11 are plotted.
(27)which highlights the contribution from each survey i of n = 3 considered here, whose data are represented by yi. We obtain S = 1000 and use the same posterior draws from which Figs. 7–11 are plotted.
Differences between the values of the Watanabe-Akaike information criterion, for all surveys together under the LADE, LDDE, and LDDE15 models.
The WAIC operates by adding a correction pWAIC to lppd to further adjust for the number of parameters. The correction is the variance of lppd among the different surveys as follows: 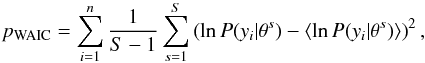 (28)where the angular brackets ⟨⟩ indicate that the average over s should be taken.
(28)where the angular brackets ⟨⟩ indicate that the average over s should be taken.
The WAIC is finally defined as 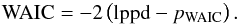 (29)Absolute WAIC values are not relevant since they are dominated by the sample size; only the differences carry statistical meaning. The ΔWAIC values for the LDDE and LADE models are shown in Table 4. The lower the WAIC, the more predictive power the model has. A difference of 27 can be observed between LDDE and LADE, leading to a preference for LADE. Table 4 also shows LDDE15, which is discussed in the next Section.
(29)Absolute WAIC values are not relevant since they are dominated by the sample size; only the differences carry statistical meaning. The ΔWAIC values for the LDDE and LADE models are shown in Table 4. The lower the WAIC, the more predictive power the model has. A difference of 27 can be observed between LDDE and LADE, leading to a preference for LADE. Table 4 also shows LDDE15, which is discussed in the next Section.
7. On a proposed extension to LDDE
In U14, we present an extension to the LDDE model. The main difference is the inclusion of a second break at a redshift z>z0. This adds six more parameters, making a total of 15 parameters for the double power law plus evolution. This model, which we call here LDDE15, takes the following functional form7 (compare with Eqs. (16), (17)): 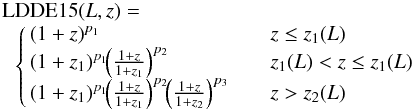 (30)with
(30)with 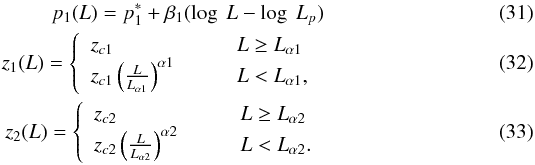 In U14, p3, zc2, α2, and Lα2 were fixed at values that make the LF decline faster beyond z ~ 3, reproducing the results by (Fiore et al. 2012). A15 considered this model and used Bayesian methods to check whether all parameters could be constrained by the data, finding reasonably tight dispersions around the means for most of the parameters. Parameters Lp and p3 seem to have looser constraints.
In U14, p3, zc2, α2, and Lα2 were fixed at values that make the LF decline faster beyond z ~ 3, reproducing the results by (Fiore et al. 2012). A15 considered this model and used Bayesian methods to check whether all parameters could be constrained by the data, finding reasonably tight dispersions around the means for most of the parameters. Parameters Lp and p3 seem to have looser constraints.
We have also used Bayesian inference with the LDDE15 model, using the same priors of A15. These priors are slightly more informative than what used in Sect. 5; the main difference is that γ1 and γ2 are no longer bimodal and that the allowed intervals for p1, p2, and p3, and for zc1 and zc2, are not overlapping.
Mode and 68.3% highest posterior density interval for the parameters under the LDDE15 model.
The mode and HPD intervals of our posterior densities for all parameters are shown in Table 5. In Fig. 12 we plot the histograms of the posterior densities; for the parameters in common with LDDE we also plot the LDDE histograms for comparison. Most of the parameters in common have similar (within a few full width half maximums) posterior densities. The role of LDDE’s α and Lα (shaping the luminosity-dependent decrease of the LF at high redshift) is taken by α2 and Lα2 in LDDE15, which assume similar values. We find 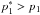 , and 0 ≲ β1 ≲ 1, but Lp cannot be constrained. The second critical redshift (zc2) can be constrained in the 2.6–3.7 interval (to be compared with 2.1 ≲ zc1 ≲ 2.2). The other parameters (Lp, p2, p3, α1, and Lα1) could either not be constrained at all, or only mildly constrained (p3, whose posterior is very skewed towards the boundary).
, and 0 ≲ β1 ≲ 1, but Lp cannot be constrained. The second critical redshift (zc2) can be constrained in the 2.6–3.7 interval (to be compared with 2.1 ≲ zc1 ≲ 2.2). The other parameters (Lp, p2, p3, α1, and Lα1) could either not be constrained at all, or only mildly constrained (p3, whose posterior is very skewed towards the boundary).
 |
Fig. 12 Posterior probability densities for double power-law and evolution parameters for all surveys together under the LDDE (blue) and LDDE15 (orange) model. |
In summary, of 15 parameters in the LDDE15 model, only ten could be fully constrained, and another is skewed towards its boundary. Also, the WAIC for the LDDE15 model is larger (Table 4). This is due to the presence in LDDE15 of parameters with unconstrained posterior densities, which enlarge the parameter volume. Our interpretation is that the data discussed in this paper do not support this particular extension of the LDDE model.
8. Discussion
8.1. LDDE vs. LADE
Our findings appear to be at odds with A15 found (U14 did not compare LDDE with LDDE15). It is unclear what is causing this difference. A15 probably has a somewhat better sampling of the LF in the 3 <z< 4 redshift interval (from their Fig. 3 we count ~140 objects, compared with 97 in our samples), but the difference in the number of objects looks too small to justify the different results. Photometric redshifts were computed by A15 using templates and codes that are different from what we used. Most notably, the photometric redshifts used here are tuned for X-ray sources in that they include a bias towards AGN rather than galaxies; while A15 uses a more general set of templates that may give less accurate redshifts and a larger outlier rate (see their Sect. 2.6). The possibility of cosmic variance explaining the different results seems unlikely, given that some fields (CDFS and COSMOS) are common between A15 and this work.
However, A15 also attempt to build a nested model for LF evolution (flexible double power law). The underlying idea of this model is closer to LADE than LDDE: a polynomial characterisation on z is put on each of the four double power-law parameters. This allows these authors to investigate up to what orders the polynomial coefficients can be constrained. They find a maximum of ten parameters (ten is the sum of the orders of all four polynomials). Constraining at most ten parameters looks closer to our results.
It is possible that future larger surveys, most notably the XXL, or an increase in the number of spectroscopic redshifts might yield different results. In the meantime, non-parametric methods, such as our formulation in Sect. 4 or the interesting Bayesian adaptation by Buchner et al. (2015), will continue to play an important role in understanding how future models should be shaped.
 |
Fig. 13 Redshift distribution for all surveys combined, in four different bins of luminosity (the average Log L of the bin shown in each panel). The distribution peaks at increasing redshift for higher luminosities, illustrating the downsizing of black hole accretion during the lifetime of the Universe. |
8.2. Redshift distribution
The LF can be plotted in terms of redshift to show the luminosity-dependent redshift distribution (RD). In Fig. 13, we present the binned RD from all surveys combined in four bins of luminosity (42 ≤ Log L< 43, 43 ≤ Log L< 44, 44 ≤ Log L< 45, and 45 ≤ Log L< 46). The peak of the RD depends on the luminosity bin; at increasing luminosities, the peak is found at higher redshift. Our data clearly show the downsizing of BH growth, i.e. the idea that accretion was happening on more massive scales at larger redshift (Cowie et al. 1996; Ueda et al. 2003; Hasinger et al. 2005). For the highest luminosity bin that we considered (average Log L = 45.5), the peak of accretion happens between z ~ 2.0 and 2.5. For the lowest luminosity bin (average Log L = 42.5), an upper limit to the peak could be put at z ≲ 0.5. The data are overall consistent, within errors, with other determinations (e.g. U14, M15).
9. Conclusions
We have presented the luminosity function (LF) estimated from the XMM-LSS, XMM-COSMOS, and XMM-CDFS surveys, and from their combination. A total of 2887 AGN is used to build the LF in the luminosity interval 1042–1046 erg s-1 and in the redshift interval 0.001-4.
We presented a method to account for absorption statistically, based on the probability distribution of the absorber column density conditioned on the soft/hard flux ratio. We apply this method both to non-parametric estimates, modifying the (Page & Carrera 2000) method, and to parametric estimates, introducing the corrections in the likelihood formula.
We presented both non-parametric and parametric estimates of the LF. The parametric form is a double power law with either LADE or LDDE evolution. Bayesian inference methods allow us to obtain a full and reliable characterisation of the allowed parameter space. The full posterior probability density for both the LF and the LF parameters is shown for both the LADE and LDDE models. The results are consistent, within errors, with previous literature. A comparison between the non-parametric and parametric estimates reveals that the LADE and LDDE modes offer a largely overlapping description of the LF at z ≳ 1. Some differences appear at low redshift (z ≲ 0.5), where LADE appears to under-predict the LF at L ≳ 1044 erg s-1. Difference also exist in each redshift bin at the lowest luminosities, however, where the number of objects in the lower luminosity bin is small so uncertainties are large.
We introduced the use of the fully Bayesian, Watanabe-Akaike information criterion (WAIC) to compare the predictive power of different models. The LADE model is found to have more predictive power than the LDDE model. The difference in WAIC values between the two models can be interpreted as a measure of how better one model can describe future and/or out-of-sample data. We have investigated the 15-parameter extended LDDE model (LDDE15), finding that our data do not support this extension. Among the possible explanation for this discrepancy between our results and Ueda et al. (2014), we mention a different approach in computing photometric redshift, and the different sample sizes in the 3 <z< 4 redshift range. The binned LF, plotted as a redshift distribution, clearly illustrates the downsizing of black hole accretion, which is in agreement with previous studies.
On the author’s website: http://www.astro.lu.se/~piero/LFtools/index.html and on the source code repository: https://github.com/piero-ranalli/LFtools
Burlon et al. (2011) report a fraction of 4.6% but they define CT as having NH> 1.5 × 1024 cm-2.
Formally, the mode is ill-defined for a sample of floating point numbers. In practice, the location of the peak of a histogram of the drawn values gives the most probable value; this is what we report. The mode of the posterior is usually suggested as a Bayesian analogue to the best-fit value in frequentist statistics.
The main difference between the WAIC and the better known, similarly named Akaike information criterion (AIC; Akaike 1973) used in Fotopoulou et al. (2016), is that the WAIC averages over the posterior distribution of the parameters, while AIC uses the maximum-likelihood estimate.
A similar extension is considered in M15, where p2 also has a dependence on L (like Eq. (31), but with its own exponent β2), but where α2 and Lα2 are missing. In M15, as in U14, some parameters are fixed in the fit.
Acknowledgments
We thank an anonymous referee whose comments have contributed to improving the presentation of this paper. P.R. acknowledges a grant from the Greek General Secretariat of Research and Technology in the framework of the programme Support of Postdoctoral Researchers. F.J.C. acknowledges support by the Spanish ministry of Economy and Competitiveness through the grant AYA2012-31447.
References
- Aird, J., Nandra, K., Laird, E. S., et al. 2010, MNRAS, 401, 2531 [NASA ADS] [CrossRef] [Google Scholar]
- Aird, J., Coil, A. L., Georgakakis, A., et al. 2015, MNRAS, 451, 1892 [NASA ADS] [CrossRef] [Google Scholar]
- Akaike, H. 1973, in 2nd International Symposium on Information Theory, Academiai Kiado, reprinted in Selected Papers of Hirotugu Akaike (Springer 1998), 199 [Google Scholar]
- Akylas, A., Georgakakis, A., Georgantopoulos, I., Brightman, M., & Nandra, K. 2012, A&A, 546, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alexander, D. M., & Hickox, R. C. 2012, New A Rev., 56, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S. 2012, in Astrostatistical Challenges for the New Astronomy, ed. J. Hilbe (Springer), 41 [Google Scholar]
- Andreon, S., & Hurn, M. 2013, Statistical Analysis and Data Mining, 6, 15 [Google Scholar]
- Arnouts, S., Cristiani, S., Moscardini, L., et al. 1999, MNRAS, 310, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Ballantyne, D. R., Everett, J. E., & Murray, N. 2006, ApJ, 639, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Barger, A. J., Cowie, L. L., Mushotzky, R. F., et al. 2005, AJ, 129, 578 [NASA ADS] [CrossRef] [Google Scholar]
- Boyle, B. J., Griffiths, R. E., Shanks, T., Stewart, G. C., & Georgantopoulos, I. 1993, MNRAS, 260, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Boyle, B. J., Shanks, T., Georgantopoulos, I., Stewart, G. C., & Griffiths, R. E. 1994, MNRAS, 271, 639 [NASA ADS] [CrossRef] [Google Scholar]
- Braccesi, A., Zitelli, V., Bonoli, F., & Formiggini, L. 1980, A&A, 85, 80 [NASA ADS] [Google Scholar]
- Brightman, M., & Ueda, Y. 2012, MNRAS, 423, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Buchner, J., Georgakakis, A., Nandra, K., et al. 2015, ApJ, 802, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Burlon, D., Ajello, M., Greiner, J., et al. 2011, ApJ, 728, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Cappelluti, N., Brusa, M., Hasinger, G., et al. 2009, A&A, 497, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiappetti, L., Clerc, N., Pacaud, F., et al. 2013, MNRAS, 429, 1652 [NASA ADS] [CrossRef] [Google Scholar]
- Comastri, A., Setti, G., Zamorani, G., & Hasinger, G. 1995, A&A, 296, 1 [NASA ADS] [Google Scholar]
- Cowie, L. L., Songaila, A., Hu, E. M., & Cohen, J. G. 1996, AJ, 112, 839 [Google Scholar]
- Daddi, E., Alexander, D. M., Dickinson, M., et al. 2007, ApJ, 670, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Ebrero, J., Carrera, F. J., Page, M. J., et al. 2009, A&A, 493, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feroz, F., & Hobson, M. P. 2008, MNRAS, 384, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Feroz, F., Hobson, M. P., & Bridges, M. 2009, MNRAS, 398, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Feroz, F., Hobson, M. P., Cameron, E., & Pettitt, A. N. 2013, ArXiv e-prints [arXiv:1306.2144] [Google Scholar]
- Ferrarese, L., & Merritt, D. 2000, ApJ, 539, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Fiore, F., Puccetti, S., Grazian, A., et al. 2012, A&A, 537, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontanot, F., De Lucia, G., Monaco, P., Somerville, R. S., & Santini, P. 2009, MNRAS, 397, 1776 [NASA ADS] [CrossRef] [Google Scholar]
- Fotopoulou, S., Georgantopoulos, I., Hasinger, G., et al. 2016, A&A, 587, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gebhardt, K., Bender, R., Bower, G., et al. 2000, ApJ, 539, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N. 1986, ApJ, 303, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Gelman, A., Carlin, J., Stern, H., et al. 2013, Bayesian Data Analysis, Third Edition, Chapman & Hall/CRC Texts in Statistical Science (Taylor & Francis) [Google Scholar]
- Gelman, A., Hwang, J., & Vehtari, A. 2014, Statistics and Computing, 24, 997 [Google Scholar]
- Gilli, R., Comastri, A., & Hasinger, G. 2007, A&A, 463, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gregory, P. 2005, Bayesian Logical Data Analysis for the Physical Sciences: A Comparative Approach with ‘Mathematica’ Support (Cambridge University Press) [Google Scholar]
- Gültekin, K., Richstone, D. O., Gebhardt, K., et al. 2009, ApJ, 698, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Häring, N., & Rix, H.-W. 2004, ApJ, 604, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Hasinger, G. 2008, A&A, 490, 905 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hasinger, G., Miyaji, T., & Schmidt, M. 2005, A&A, 441, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hiroi, K., Ueda, Y., Akiyama, M., & Watson, M. G. 2012, ApJ, 758, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., et al. 2006, ApJS, 163, 1 [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., Robertson, B., & Krause, E. 2007, ApJ, 669, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Hsu, L.-T., Salvato, M., Nandra, K., et al. 2014, ApJ, 796, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iwasawa, K., Gilli, R., Vignali, C., et al. 2012, A&A, 546, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, L. R., McHardy, I. M., Merrifield, M. R., et al. 1997, MNRAS, 285, 547 [Google Scholar]
- Kodama, T., Yamada, T., Akiyama, M., et al. 2004, MNRAS, 350, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Bender, R. 2009, ApJ, 691, L142 [NASA ADS] [CrossRef] [Google Scholar]
- La Franca, F., & Cristiani, S. 1997, AJ, 113, 1517 [NASA ADS] [CrossRef] [Google Scholar]
- La Franca, F., Fiore, F., Comastri, A., et al. 2005, ApJ, 635, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Loredo, T. J. 2004, in AIP Conf. Ser. 735, eds. R. Fischer, R. Preuss, & U. V. Toussaint, 195 [Google Scholar]
- Maccacaro, T., Gioia, I. M., Avni, Y., et al. 1983, ApJ, 266, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Maccacaro, T., Gioia, I. M., & Stocke, J. T. 1984, ApJ, 283, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Maccacaro, T., della Ceca, R., Gioia, I. M., et al. 1991, ApJ, 374, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, AJ, 115, 2285 [NASA ADS] [CrossRef] [Google Scholar]
- Malizia, A., Stephen, J. B., Bassani, L., et al. 2009, MNRAS, 399, 944 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, A., & Hunt, L. K. 2003, ApJ, 589, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, A., Risaliti, G., Gilli, R., et al. 2004, MNRAS, 351, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Marshall, H. L., Tananbaum, H., Avni, Y., & Zamorani, G. 1983, ApJ, 269, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Mathez, G. 1978, A&A, 68, 17 [NASA ADS] [Google Scholar]
- Melnyk, O., Plionis, M., Elyiv, A., et al. 2013, A&A, 557, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miyaji, T., Hasinger, G., & Schmidt, M. 2001, A&A, 369, 49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miyaji, T., Hasinger, G., Salvato, M., et al. 2015, ApJ, 804, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Page, M. J., & Carrera, F. J. 2000, MNRAS, 311, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Page, M. J., Carrera, F. J., Hasinger, G., et al. 1996, MNRAS, 281, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Ranalli, P., Comastri, A., Vignali, C., et al. 2013, A&A, 555, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ranalli, P., Georgantopoulos, I., Corral, A., et al. 2015, A&A, 577, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salvato, M., Hasinger, G., Ilbert, O., et al. 2009, ApJ, 690, 1250 [CrossRef] [Google Scholar]
- Salvato, M., Ilbert, O., Hasinger, G., et al. 2011, ApJ, 742, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Santini, P., Fontana, A., Grazian, A., et al. 2009, A&A, 504, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmidt, M. 1968, ApJ, 151, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, M., & Green, R. F. 1983, ApJ, 269, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Setti, G., & Woltjer, L. 1989, A&A, 224, L21 [NASA ADS] [Google Scholar]
- Silverman, J. D., Green, P. J., Barkhouse, W. A., et al. 2008, ApJ, 679, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Skilling, J. 2004, in Bayesian inference and maximum entropy methods in sci- ence and engineering, AIP Conf. Proc., 735, 395 [Google Scholar]
- Skilling, J. 2006, Bayesian Analysis, 1, 833 [Google Scholar]
- Treister, E., & Urry, C. M. 2006, ApJ, 652, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Treister, E., Urry, C. M., & Virani, S. 2009, ApJ, 696, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Trotta, R. 2008, Contemporary Physics, 49, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Ueda, Y., Akiyama, M., Ohta, K., & Miyaji, T. 2003, ApJ, 598, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Ueda, Y., Watson, M. G., Stewart, I. M., et al. 2008, ApJS, 179, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Ueda, Y., Akiyama, M., Hasinger, G., Miyaji, T., & Watson, M. G. 2014, ApJ, 786, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Vito, F., Gilli, R., Vignali, C., et al. 2014, MNRAS, 445, 3557 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, S. 2010, J. Machine Learning Res., 11, 3571 [Google Scholar]
- Yencho, B., Barger, A. J., Trouille, L., & Winter, L. M. 2009, ApJ, 698, 380 [NASA ADS] [CrossRef] [Google Scholar]
- Zubovas, K., & King, A. R. 2012, MNRAS, 426, 2751 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Mode and 68.3% highest posterior density interval for the parameters under the LADE model.
Mode and 68.3% highest posterior density interval for the parameters under the LDDE model.
Differences between the values of the Watanabe-Akaike information criterion, for all surveys together under the LADE, LDDE, and LDDE15 models.
Mode and 68.3% highest posterior density interval for the parameters under the LDDE15 model.
All Figures
 |
Fig. 1 Areas covered by the XMM-LSS (black solid curve), XMM-CDFS (red long-dashed curve), and XMM-COSMOS (green short-dashed curve) surveys, vs. 2–10 keV flux. Although the nominal depth of LSS is 10 ks, it also includes the Subaru Deep Field (Ueda et al. 2008) whose exposure is 100 ks. The blue dotted curve shows the LSS coverage after including selection effects (availability of redshifts and reliability of the optical counterpart identification; i.e. Ω(f) from Eq. (1); see Sect. 2.4). The CDFS and COSMOS have nearly complete redshift availability (either spectroscopic of photometric) so selection effects can be ignored. |
| In the text | |
 |
Fig. 2 Luminosity-redshift diagram for the XMM-LSS, XMM-CDFS, and XMM-COSMOS surveys. The contours are logarithmically scaled and show the fraction of objects with z and L inside the contour (levels at 97%, 94.8%, 90%, 83%, 70%, and 48% from outermost to innermost). The data points show the objects outside the lowest contour. At z> 0.5, the XMM-CDFS systematically probes AGN that are fainter by up to one order of magnitude. Observed luminosities, corrected only for Galactic absorption, are shown. |
| In the text | |
 |
Fig. 3 Normalised histograms of LSS fluxes. The blue histogram shows the full sample of 2573 objects, the red histogram shows the sample we used that contains 1520 objects with a redshift and an optical counterpart match probability of >95%. |
| In the text | |
 |
Fig. 4 Probability distribution of the unabsorbed/absorbed flux ratio in the 2–10 keV, as a function of the measured 0.5–2/2–10 keV flux ratio, for the Burlon sample, at redshift zero. The x-axis shows Log(SH), therefore hard sources are on the left and soft sources are on the right. The y-axis shows Log(U), therefore no correction is at the bottom and large corrections are at the top. The colour scale goes from white (low probability) to black (high probability). |
| In the text | |
 |
Fig. 5 Medians of the absorption correction U for the objects in the XMM-LSS, XMM-CDFS, and XMM-COSMOS surveys, over a grid of redshift and observed luminosity. Probability distributions for photometric redshifts have been included. The corrections are mostly significant for objects in the faint tail of the luminosity function (i.e. L ≲ 43–44.5, depending on z), or for z ≳ 3. The correction U (Sect. 3) is logarithmic, hence U = 0.5 corresponds to the luminosity being corrected by a factor of 2. The colour scale goes from black (median correction is 0) to bright yellow (median correction is 0.6). White areas are not populated. |
| In the text | |
 |
Fig. 6 Luminosity function, from combined XMM-LSS, CDFS, and COSMOS data, with binned estimates (black data points with 1σ error bars) and Bayesian highest posterior densities (HPD) under the LDDE (blue area) and LADE (red area) models. For both models, the darker areas show the 68.3% HPD intervals, while the lighter areas show the 99.7% HPD intervals. |
| In the text | |
 |
Fig. 7 Luminosity function, from XMM-LSS, CDFS, and COSMOS data, with binned estimates from all surveys together (black data points) and Bayesian highest posterior densities (68.3% HPD interval) for individual surveys under the LDDE model (red: LSS; yellow: CDFS; green: COSMOS). |
| In the text | |
 |
Fig. 8 Luminosity function, from XMM-LSS, CDFS, and COSMOS data, with binned estimates from all surveys together (black data points) and Bayesian highest posterior densities (68.3% HPD interval) for individual surveys under the LADE model. Colours as in Fig. 7. |
| In the text | |
 |
Fig. 9 Posterior probability densities for double power-law parameters for all surveys combined, under the LDDE (blue) and LADE (red) models. The plotted variables are identified in the top right corner of each panel. The normalisation A is in Mpc-3, the knee luminosity L∗ is in erg s-1. The histograms are normalised hence the vertical scales are arbitrary. |
| In the text | |
 |
Fig. 10 Posterior probability densities for double power-law and evolution parameters for individual surveys under the LDDE model; colours as in Fig. 7. For comparison, we also plot (blue histogram) the probability density for all surveys together under the same model. The plotted variables are identified in the top right corner of each panel. The normalisation A is in Mpc-3, the luminosities L∗ and Lα are in erg s-1. The histograms are normalised hence the vertical scales are arbitrary. |
| In the text | |
 |
Fig. 11 Posterior probability densities for double power-law parameters for individual surveys under the LADE model; colours as in Fig. 7. For comparison, we also plot (blue histogram) the probability density for all surveys together under the same model. The plotted variables are identified in the top right corner of each panel. The normalisation A is in Mpc-3, the knee luminosity L∗ is in erg s-1. The histograms are normalised hence the vertical scales are arbitrary. |
| In the text | |
 |
Fig. 12 Posterior probability densities for double power-law and evolution parameters for all surveys together under the LDDE (blue) and LDDE15 (orange) model. |
| In the text | |
 |
Fig. 13 Redshift distribution for all surveys combined, in four different bins of luminosity (the average Log L of the bin shown in each panel). The distribution peaks at increasing redshift for higher luminosities, illustrating the downsizing of black hole accretion during the lifetime of the Universe. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


