| Issue |
A&A
Volume 589, May 2016
|
|
|---|---|---|
| Article Number | A87 | |
| Number of page(s) | 17 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201527874 | |
| Published online | 18 April 2016 | |
Self-organisation in protoplanetary discs
Global, non-stratified Hall-MHD simulations
1
Univ. Grenoble Alpes, IPAG,
38000
Grenoble,
France
e-mail:
william.bethune@univ-grenoble-alpes.fr
2
CNRS, IPAG, 38000
Grenoble,
France
Received: 1 December 2015
Accepted: 7 March 2016
Context. Recent observations have revealed organised structures in protoplanetary discs, such as axisymmetric rings or horseshoe concentrations, evocative of large-scale vortices. These structures are often interpreted as the result of planet-disc interactions. However, these discs are also known to be unstable to the magneto-rotational instability (MRI) which is believed to be one of the dominant angular momentum transport mechanism in these objects. It is therefore natural to ask whether the MRI itself could produce these structures without invoking planets.
Aims. The nonlinear evolution of the MRI is strongly affected by the low ionisation fraction in protoplanetary discs. The Hall effect in particular, which is dominant in dense and weakly ionised parts of these objects, has been shown to spontaneously drive self-organising flows in local, shearing box simulations. Here, we investigate the behaviour of global MRI-unstable disc models dominated by the Hall effect and characterise their dynamics.
Methods. We validated our implementation of the Hall effect into the PLUTO code with predictions from a spectral method in cylindrical geometry. We then performed 3D unstratified Hall-MHD simulations of Keplerian discs for a broad range of Hall, Ohmic, and ambipolar Elsasser numbers.
Results. We confirm the transition from a turbulent to an organised state as the intensity of the Hall effect is increased. We observe the formation of zonal flows, their number depending on the available magnetic flux and on the intensity of the Hall effect. For intermediate Hall intensity, the flow self-organises into long-lived magnetised vortices. Neither the addition of a toroidal field nor Ohmic or ambipolar diffusion change this picture drastically in the range of parameters we have explored.
Conclusions. Self-organisation by the Hall effect is a robust phenomenon in global non-stratified simulations. It is able to quench turbulent transport and spontaneously produce axisymmetric rings or sustained vortices. The ability of these structures to trap dust particles in this configuration is demonstrated. We conclude that Hall-MRI driven organisation is a plausible scenario that could explain some of the structures found in recent observations.
Key words: accretion, accretion disks / magnetohydrodynamics (MHD) / protoplanetary disks / stars: formation / turbulence
© ESO, 2016
1. Introduction
Protoplanetary discs are the birthplace of planets. There are now many observations available, from millimetre wavelengths (Brogan et al. 2015) to the infrared (Benisty et al. 2015). Surprisingly, these observations indicate that protoplanetary discs have complex internal structures, with features like spiral arms (Muto et al. 2012; Benisty et al. 2015), asymmetric traps (van der Marel et al. 2013) and rings (Brogan et al. 2015).
The origin of these structures is largely unknown. Most of the theoretical models developed to date involve at least one planet carving a gap (van der Marel et al. 2013; Dipierro et al. 2015) or exciting spiral density waves (Benisty et al. 2015). For this reason, structures are usually seen as a consequence of planet formation. However, the presence of Jupiter mass planets in very young discs such as HL Tau is questionable since it implies a very fast formation scenario. It is therefore natural to ask whether these structures could appear without planets and even be one of the driving mechanisms behind planet formation. To answer this question, one has to focus on the dynamics of a planet-free disc, a long-standing problem in theoretical astrophysics.
Accretion discs are believed to be subject to the magnetorotational instability (MRI), a magnetohydrodynamic (MHD) instability appearing spontaneously in magnetised discs in Keplerian rotation (Balbus & Hawley 1991). The relevance of this instability in the context of protoplanetary disc is, however, being debated (Turner et al. 2014). In particular, these objects are so cold that they cannot maintain a high ionisation fraction (Gammie 1996). This has led to the concept of magnetically “dead” zones where the ionisation fraction of the disc is so low that the standard MHD approach breaks down and the MRI potentially vanishes.
A strong effort has recently been devoted to the study of these weakly ionised regions, typically located at radii larger than one astronomical unit (au), and they are precisely the regions we are now capable of resolving observationally. It has been shown that in this regime, three “non-ideal” effects have to be taken into account in the MHD framework (Balbus & Terquem 2001; Kunz & Balbus 2004): Ohmic diffusion, ambipolar diffusion, and the Hall drift. It is well known that both Ohmic and ambipolar diffusion act to damp and potentially eliminate the MRI by decoupling the flow from magnetic field lines (Blaes & Balbus 1994; Jin 1996; Papaloizou & Terquem 1997), hence the historical denomination of dead zones. On the other hand, the Hall effect leads to new branches of instabilities (Wardle 1999; Balbus & Terquem 2001; Kunz 2008) because of its dispersive nature.
The saturation of the MRI and the outcome of a disc subject to these non-ideal effects is still the subject of intense debate. Stratified models including Ohmic and ambipolar diffusion only have shown that the disc could become essentially laminar (i.e. not turbulent) in the midplane, with a strong magnetically driven jet at the disc surface (Bai & Stone 2013; Simon et al. 2013; Gressel et al. 2015). For radii1 between 1 and 10 au (where Hall effect dominates diffusive processes) a large-scale midplane stress is found by adding the Hall effect, with a strong field polarity dependence and no turbulence (Lesur et al. 2014; Bai 2014), whereas the outer disc is found to be essentially insensitive to the Hall effect (Bai 2015), though some polarity dependence could persist (Simon et al. 2015).
The results of Lesur et al. (2014) and Bai (2014) and, in particular, the presence of a large-scale “laminar” stress are both important and potentially problematic results. In effect, these simulations were done in the stratified shearing box framework (Hawley et al. 1995) with a very limited radial extension (typically a few scale heights), so the Lesur et al. (2014) and Bai (2014) results indicate that the MRI is indeed active in these simulations, but it tends to produce structures that are larger than the simulation box. As a matter of fact, unstratified shearing box models have already indicated that the Hall-dominated MRI is prone to produce large-scale structures, such as zonal fields and flows (Kunz & Lesur 2013, hereafter KL13) in wide enough boxes. All of these elements tend to point toward the fact that the Hall effect could be an efficient mechanism for triggering self-organisation in protoplanetary discs.
In this paper, we explore this hypothesis using full 3D cylindrical models of accretion discs dominated by the Hall effect. Our aim is not to reproduce the exact structure of a disc with its detailed ionisation equilibrium but to test the hypothesis of self-organisation in a global model, free of the artefacts found in local, i.e. shearing-box simulations. We start by describing the physical framework in detail and giving and some remarkable facts concerning Hall dynamics. We then depict our numerical model and present the tests performed to validate it along with a reproduction and discussion of the multifluid models of O’Keeffe & Downes (2014). Next, we move to the core of the paper with the presentation and characterisation of several Hall-dominated models, putting emphasis on the physical mechanisms driving self-organisation. We then explore some potential treats to these mechanisms such as diffusive effects and more complex field configurations. We conclude by discussing the link between these results and recent observations along with extensions of this work to more realistic numerical setups.
2. Framework
2.1. Physical model
We want to model a thin disc of partially ionised gas orbiting a central mass and threaded by a weak magnetic field. On the scales considered, our problem fits in the non-ideal magnetohydrodynamic (MHD) framework. In this attempt to study the Hall effect in global disc simulations, we wish to concentrate on the midplane dynamics, thereby neglecting vertical stratification effects. Using cylindrical coordinates (r,ϕ,z), we take the gravitational force as being oriented radially and assume periodicity in the vertical direction on a scale h. Radial stratification is eliminated by using an isothermal disc model with a flat density distribution and by taking the initial magnetic field to be constant and uniformly vertical over the whole domain.
The relevant equations for our model are those of inviscid, compressible non-ideal MHD. We denote by ρ the bulk density, v the bulk velocity, 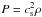 the pressure with an isothermal sound speed cs, and J = ∇ × B the electric current deduced from the magnetic field B = | B | eb. Gravity is oriented along the cylindrical radius as g = −(1 /r2)er. The three relevant non-ideal MHD effects, namely Ohmic dissipation, the Hall effect, and ambipolar diffusion, are characterised by their diffusivities ηO, ηH, and ηA, respectively (e.g. Wardle 2007). With these definitions, the dynamical equations read as
the pressure with an isothermal sound speed cs, and J = ∇ × B the electric current deduced from the magnetic field B = | B | eb. Gravity is oriented along the cylindrical radius as g = −(1 /r2)er. The three relevant non-ideal MHD effects, namely Ohmic dissipation, the Hall effect, and ambipolar diffusion, are characterised by their diffusivities ηO, ηH, and ηA, respectively (e.g. Wardle 2007). With these definitions, the dynamical equations read as ![\begin{eqnarray} \label{eqn:dyn-rho} &&\partial_t \rho = - \bm{\nabla \cdot} \left[ \rho \bm{v} \right], \\ \label{eqn:dyn-v} &&\partial_t \left[ \rho \bm{v} \right] = - \bm{\nabla \cdot} \left[ \rho \bm{v \otimes v} \right] - \bnab P + \bm{J \times B} + \rho\bm{g}, \\ \label{eqn:dyn-b} &&\partial_t \bm{B} = \bm{\nabla \times} \left[ \bm{v \times B} - \eta_{\mathrm{O}} \bm{J} - \eta_{\mathrm{H}} \bm{J \times e_{\it b}} + \eta_{\mathrm{A}} \bm{J} \times {\bm e}_{\it b} \times \bm{e}_{\it b} \right]. \end{eqnarray}](/articles/aa/full_html/2016/05/aa27874-15/aa27874-15-eq13.png) To characterise the intensity of the Hall induction term, we use the Alfvén velocity vA = B/
To characterise the intensity of the Hall induction term, we use the Alfvén velocity vA = B/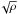 and introduce the dimensionless parameter
and introduce the dimensionless parameter 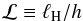 (4)ratio of the Hall length ℓH ≡ ηH/vA as defined in KL13 and the geometric scale height of the disc. The Hall length is very convenient since it only depends on the microphysical properties of the plasma and not on the field strength. In a plasma made of electrons, singly charged ions and neutrals, the Hall length is given by
(4)ratio of the Hall length ℓH ≡ ηH/vA as defined in KL13 and the geometric scale height of the disc. The Hall length is very convenient since it only depends on the microphysical properties of the plasma and not on the field strength. In a plasma made of electrons, singly charged ions and neutrals, the Hall length is given by 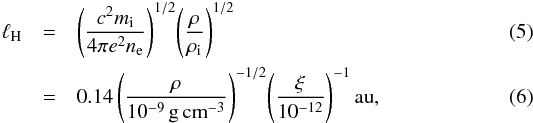 where mi is the ion mass, ne the electron number density, and ρi is the ion density. The numerical value has been obtained assuming a plasma made of electrons, heavy ions, and neutral molecules (mean molecular mass μ = 2.34 mH) with an ionisation fraction ξ. The precise calculation of the Hall length involves solving a complex chemical network and depends on the presence and size distribution of grains, which is beyond the scope of this paper. We note, however, that typical values for ℒ range from ℒ ~ 100 at 5 au down to ℒ ~ 10-2 at 100 au for 1 μm size grains (e.g. Simon et al. 2015), smaller grains leading to higher values of ℒ. Because the Hall effect is a dispersive term, it induces a strong Courant-Friedrichs-Lewy (CFL) constraint on the timestep of our explicit scheme. For this reason, we restrict ourselves to simulations with ℒ ≤ 10 to keep computation times within reasonable bounds.
where mi is the ion mass, ne the electron number density, and ρi is the ion density. The numerical value has been obtained assuming a plasma made of electrons, heavy ions, and neutral molecules (mean molecular mass μ = 2.34 mH) with an ionisation fraction ξ. The precise calculation of the Hall length involves solving a complex chemical network and depends on the presence and size distribution of grains, which is beyond the scope of this paper. We note, however, that typical values for ℒ range from ℒ ~ 100 at 5 au down to ℒ ~ 10-2 at 100 au for 1 μm size grains (e.g. Simon et al. 2015), smaller grains leading to higher values of ℒ. Because the Hall effect is a dispersive term, it induces a strong Courant-Friedrichs-Lewy (CFL) constraint on the timestep of our explicit scheme. For this reason, we restrict ourselves to simulations with ℒ ≤ 10 to keep computation times within reasonable bounds.
Most of our simulations neglect Ohmic and ambipolar diffusion to focus on Hall-MHD. We do, however, briefly explore the impact of these diffusion terms on our results in Sect. 6. It is customary to quantify the importance of diffusion terms via the Lundquist and Elsasser numbers defined by 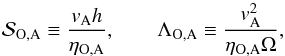 (7)respectively, where the index stands for Ohmic or ambipolar diffusion. When setting the value of these parameters, it will be with respect to the initial Alfvén velocity B0/
(7)respectively, where the index stands for Ohmic or ambipolar diffusion. When setting the value of these parameters, it will be with respect to the initial Alfvén velocity B0/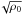 .
.
We wish to exclude most stratification effects. Since we do not solve for the chemistry of the disc, fixing a constant ℓH gives a natural extension of the local simulations of KL13. We choose to set ηO constant so that 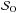 describes a disc that is either entirely stable or unstable to the MRI (Jin 1996). Most previous studies on ambipolar diffusion were conducted at a given ΛA, but with a constant Alfvén velocity, this corresponds to a disc that is gradually stabilised by the diffusivity ηA ∝ r3 / 2. We choose instead to use a constant ion-neutral coupling time τA so that ηA(r,t) = τAvA(r,t)2 everywhere and at all times. With an initially constant Alfvén velocity, the initial
describes a disc that is either entirely stable or unstable to the MRI (Jin 1996). Most previous studies on ambipolar diffusion were conducted at a given ΛA, but with a constant Alfvén velocity, this corresponds to a disc that is gradually stabilised by the diffusivity ηA ∝ r3 / 2. We choose instead to use a constant ion-neutral coupling time τA so that ηA(r,t) = τAvA(r,t)2 everywhere and at all times. With an initially constant Alfvén velocity, the initial 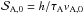 is constant, too, making the disc entirely unstable and facilitating comparison with the Ohmic case.
is constant, too, making the disc entirely unstable and facilitating comparison with the Ohmic case.
2.2. Simplified model of Hall dynamics
We point out some properties derived from the dynamical Eq. (3)here and refer the reader to the Sect. 4 of KL13 for a discussion about the following model.
After we discard the ambipolar and Ohmic terms, and assuming a constant Hall length, the induction equation of Hall MHD reads as ![\begin{eqnarray} \nonumber \partial_t \bm{B} &=& \bm{\nabla \times} \left[ \bm{v\times B}-\lH \bm{J \times B}\right] \\ \label{eqn:induc_easy}& =&\bm{\nabla \times} \left[ \bm{v\times B}\right]- \lH \bm{\nabla \times} \left[ \bm{\nabla \cdot} \left(\bm{B \otimes B} \right) \right]. \end{eqnarray}](/articles/aa/full_html/2016/05/aa27874-15/aa27874-15-eq40.png) (8)For illustrative purposes we use the shearing box model to remove curvature terms; we can then average over the periodic vertical and azimuthal directions and obtain the simplified equation
(8)For illustrative purposes we use the shearing box model to remove curvature terms; we can then average over the periodic vertical and azimuthal directions and obtain the simplified equation ![\begin{eqnarray} \partial_t \brac{\bm{B}_z}_{yz} &=& \brac{\bm{\nabla \times} \left[\bm{v \times B}\right]_z} - \lH \brac{\bm{\nabla \times} \left[ \bm{\nabla \cdot} \left(\bm{B \otimes B} \right) \right]_z} \nonumber\\ \label{eq:inucinde} &&\simeq \eta_t \frac{\partial^2}{\partial x^2} \brac{B_z} - \lH \frac{\partial}{\partial x^2} \brac{B_xB_y} \end{eqnarray}](/articles/aa/full_html/2016/05/aa27874-15/aa27874-15-eq41.png) (9)where we approximated the ideal MHD term by a turbulent resistivity (Lesur & Longaretti 2009). This expression shows that in the presence of the Hall effect, the horizontal Maxwell stress appears explicitly in the induction equation. Since this component of the stress also drives the transport of angular momentum (Balbus & Papaloizou 1999), this expression implies a tight connection between the transport of angular momentum and that of vertical magnetic flux tubes. These relations will prove useful in understanding our results.
(9)where we approximated the ideal MHD term by a turbulent resistivity (Lesur & Longaretti 2009). This expression shows that in the presence of the Hall effect, the horizontal Maxwell stress appears explicitly in the induction equation. Since this component of the stress also drives the transport of angular momentum (Balbus & Papaloizou 1999), this expression implies a tight connection between the transport of angular momentum and that of vertical magnetic flux tubes. These relations will prove useful in understanding our results.
2.3. Linear stability
We recall that in Hall MHD, differentially rotating flows embedded in a magnetic field can be subject to the Hall-shear instability (HSI), different in essence from the magneto-rotational instability (Kunz 2008). Indeed, angular-momentum conservation is central to the MRI mechanism, whereas the HSI only relies on electric currents and needs not disturb the bulk of the flow. One other fundamental difference is the dependence of the HSI on the orientation of the magnetic field with respect to the rotation axis. In the case favorable to instability (Ω·B> 0), it can be shown (Simon et al. 2015) that the HSI develops when the local shear frequency is higher than the whistler frequency at the considered wavenumber k, that is, 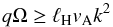 (10)with q ≡ | dlog Ω / dlog r | = 3 / 2 in our non-stratified Keplerian case. Given a constant ℓH, we see that the flow will be Hall-shear stable for all wave numbers down to the minimal k0 = 2π/h for Alfvén velocities above the critical value
(10)with q ≡ | dlog Ω / dlog r | = 3 / 2 in our non-stratified Keplerian case. Given a constant ℓH, we see that the flow will be Hall-shear stable for all wave numbers down to the minimal k0 = 2π/h for Alfvén velocities above the critical value 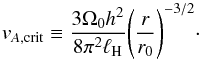 (11)
(11)
2.4. Diagnostics
We use brackets to denote space averaging, with subscript indicating the coordinate over which a function is integrated:
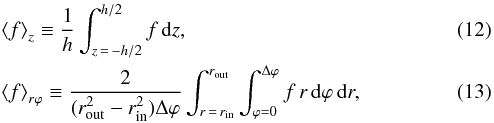 where rin and rout delimit the active computational domain, and Δϕ is the angular extent of the disc. Subscripts will be omitted when obvious from the context. We use an overline for the time averaging of an already volume-averaged quantity:
where rin and rout delimit the active computational domain, and Δϕ is the angular extent of the disc. Subscripts will be omitted when obvious from the context. We use an overline for the time averaging of an already volume-averaged quantity: 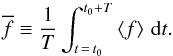 (14)As a characterisation of the spatial coherence of the flow, we use the auto-correlation function
(14)As a characterisation of the spatial coherence of the flow, we use the auto-correlation function  \equiv \frac{\int f(t,y,z) f(t+x,y,z) \, \dd t}{\int f(t,y,z)^2\,\dd t} \end{eqnarray}](/articles/aa/full_html/2016/05/aa27874-15/aa27874-15-eq53.png) (15)and define a normalised correlation factor
(15)and define a normalised correlation factor  \equiv \frac{1}{h} \int_{z \,=\, -h/2}^{h/2} \mathcal{A}_{r,\varphi}[f](z)\, \dd z \end{equation}](/articles/aa/full_html/2016/05/aa27874-15/aa27874-15-eq54.png) (16)equal to unity where the correlation length is equal to the height h. We also use
(16)equal to unity where the correlation length is equal to the height h. We also use $}](/articles/aa/full_html/2016/05/aa27874-15/aa27874-15-eq55.png) defined by substituting ϕ and z and replacing h by the angular extent Δϕ.
defined by substituting ϕ and z and replacing h by the angular extent Δϕ.
Following Balbus & Papaloizou (1999), the turbulent Reynolds stress tensor is defined with the velocity fluctuations about the density-weighted averaged flow: 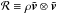 where
where 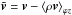 /⟨ρ⟩ϕz. The Maxwell stress tensor is simply defined as ℳ ≡ −B ⊗ B. We introduce two dimensionless measures of turbulent stress, and the first one is the usual α parameter of Shakura & Sunyaev (1973):
/⟨ρ⟩ϕz. The Maxwell stress tensor is simply defined as ℳ ≡ −B ⊗ B. We introduce two dimensionless measures of turbulent stress, and the first one is the usual α parameter of Shakura & Sunyaev (1973): 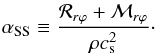 (17)Since we work in a cylindrical setup, an alternative definition for α is possible using Ω and the characteristic length h. We thus define
(17)Since we work in a cylindrical setup, an alternative definition for α is possible using Ω and the characteristic length h. We thus define 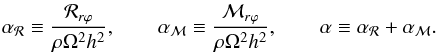 (18)It should be emphasised again that in a disc in true hydrostatic equilibrium,
(18)It should be emphasised again that in a disc in true hydrostatic equilibrium, 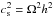 , so that αSS = α. In a cylindrical system such as ours, this equality does not hold anymore, and one has to pick Eq. (17)or (18). In the following, we use Eq. (18)as our main diagnostic since the fluctuations are essentially incompressible, making the sound speed less relevant physically than the geometrical velocity Ωh.
, so that αSS = α. In a cylindrical system such as ours, this equality does not hold anymore, and one has to pick Eq. (17)or (18). In the following, we use Eq. (18)as our main diagnostic since the fluctuations are essentially incompressible, making the sound speed less relevant physically than the geometrical velocity Ωh.
2.5. Units
We take the inner radius r0 and the Keplerian velocity at the inner radius v0 as distance and velocity units, resulting in a natural frequency unit Ω0 ≡ v0/r0. Time is expressed relative to the orbital period at the inner radius T0 ≡ 2π/ Ω0 and density relative to the initial constant density ρ0. Magnetic field strength is expressed as an Alfvén velocity B/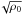 , and the initial vertical magnetic field is always denoted B0. We also use the initial thermal pressure
, and the initial vertical magnetic field is always denoted B0. We also use the initial thermal pressure 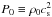 .
.
3. Method and validation
3.1. Description
3.1.1. Numerical scheme
The dynamical Eqs. (1)−(3)are explicitly integrated in time with a modified version of the finite volume code PLUTO (Mignone et al. 2007) in 3D cylindrical geometry. The magnetic field is evolved with the constrained transport method (Evans & Hawley 1988), preserving ∇·B = 0 to machine precision.
Our implementation of the Hall effect is the same as what is described in Appendix A of Lesur et al. (2014): the Hall induction flux is incorporated in a conservative manner within a modified HLL Riemann solver. Since the Hall effect introduces dispersive waves, the whistler speed required when computing Godunov fluxes is truncated on the grid scale in the direction under consideration. The face-centred electric currents must be provided to this solver as an external parameter. These are computed by finite difference of either the volume-averaged or the face-centred magnetic field of neighbouring cells, according to the cylindrical expression for the curl operator.
We use a second-order accurate Runge-Kutta time-integration scheme, a piecewise linear space reconstruction of the fields within each cell, and the Van Leer slope limiter. The FARGO module (Mignone et al. 2012) is employed to substantially increase the initial timesteps and reduce the numerical diffusivity due to the advection by the mean Keplerian flow.
3.1.2. Grid and boundary conditions
Our computational domain is cylindrical, truncated in the azimuthal direction to quarter discs Δϕ = π/ 2 for all runs except one 2π full disc, saving computational time while revealing global effects already. The ratio of the cylinder height h to its inner radius r0 is fixed to 1 / 4 for all simulations, consistently with our thin disc assumption. We set the outer radius at 5r0, giving an aspect ratio of 16. The sound speed is fixed to 10% of the Keplerian velocity at the inner radius, so that our geometrical scale height h resembles the hydrostatic pressure scale height cs/ Ω in the computational domain, which is equal at r ≃ 1.8r0. This domain is meshed with 32 grid cells in the vertical direction, 512 uniformly distributed cells in the radial and azimuthal directions (2048 azimuthal cells for the 2π run), giving a square mesh in the 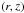 plane and an almost cubic grid at r ≈ 2.5r0.
plane and an almost cubic grid at r ≈ 2.5r0.
All runs are initialised with a density ρ = ρ0 on the whole domain, a Keplerian azimuthal velocity field vϕ = r− 1 / 2, and uniform Bz = B0. The vertical and azimuthal boundary conditions are periodic. Special care was taken with the radial boundary conditions, for they can drastically affect the physics in the computational domain. The same type of conditions is imposed at the two radial boundaries. Unless otherwise stated, they are as follows: the radial and vertical velocities vanish as do the radial derivative of the density; the azimuthal velocity is set to its initial Keplerian value; the azimuthal component of the magnetic field is forced to zero; the vertical component is set to B0; the radial component follows from the divergence free condition.
Boundary conditions alone allow the development of large-scale quasi-steady spiral waves within the domain in a purely hydrodynamical setup. These undesirable effects appeared for a variety of boundary conditions, so we chose to add damping buffer zones to smooth the transition from the active domain to the boundaries and smooth these structures out. The buffers span a radial extent h from both radial boundaries, where all hydrodynamical fields are linearly relaxed over time. They are excluded from all subsequent space averagings.
In the half of the buffer closest to the boundary, all velocity components are brought back to their initial value with an exponential relaxation of v → v − S1(r)(v − v0)δt/τ, with a characteristic time scale of τ = 0.125 / Ω(r) and with a linear modulation S1(r) such that the relaxation is fully active at the boundary and vanishes at the middle of the buffer.
In the whole buffer, the density is relaxed in the following manner. First, the average radial density distribution ⟨ρ⟩ϕz(r) is computed. Let rb be the radius of the edge of the current buffer. In each cell the density is relaxed exponentially in time to the arithmetic mean between the local average density and the average at the edge of the buffer: ![\begin{equation} \rho(r,\varphi,z) \mapsto \rho(r,\varphi,z) - S_2(r) \left[\brac{\rho}(r)-\brac{\rho}(r_{\rm b})\right] \frac{\delta t}{2\tau}, \end{equation}](/articles/aa/full_html/2016/05/aa27874-15/aa27874-15-eq96.png) (19)where S2(r) is again a linear modulation equal to one at the boundary and zero at rb.
(19)where S2(r) is again a linear modulation equal to one at the boundary and zero at rb.
This separation into two sub-buffers helps to prevent an accumulation of mass between the buffer and the active domain, avoiding the formation of a local minimum of potential vorticity and keeping the flow Rossby stable (Lovelace et al. 1999). Also, relaxing the density to its average value from the active domain mimics outflow conditions and allows long time behaviour such as a density drop by accretion, to take place.
We impose a constant resistivity ηb = 4 × 10-4 in the buffers, stabilizing the MRI for typical magnetic field intensities without affecting the CFL condition. Moreover, in Hall MHD simulations we linearly decrease the Hall length from the active domain and make it vanish at the boundaries, avoiding unnecessary Hall drift waves at the interface.
Finally, after a first round of simulations, we found that magnetic flux losses were sometimes too large to maintain a near statistically steady system. This prevented us from computing proper time averages and comparing our results with previous works. Part of this monotonic decrease in net flux comes from turbulent accretion or excretion of mass out of the computational domain, but it is amplified by the Hall term 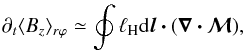 (20)which is always negative since we damp the Maxwell stress in the buffers with Ohmic diffusion. This term inputs negative flux from the boundaries, which spreads to the active domain and progressively stabilises the flow.We thus renormalise the total vertical magnetic flux at each timestep in the active domain Bz(r,ϕ,z) → Bz(r,ϕ,z) − ⟨Bz⟩ + ⟨B0⟩. This way, we obtain quasi-steady states in all of our regimes. In the ideal-MHD case, the amount of magnetic flux thus added varies between 10% and 30% of the initial magnetic flux over 200T0, the larger flux losses corresponding to the higher transport rates, which occurs for higher initial net flux. In the strong-Hall regime, less than 5% of the total flux is lost from 50T0 to 200T0 in the organised phase. These flux losses are small on a dynamical time scale, and we verified that the maximal turbulent stress attained in time were the same with and without this procedure. The qualitative level of self-organisation was also consistent between runs with and without the flux renormalisation.
(20)which is always negative since we damp the Maxwell stress in the buffers with Ohmic diffusion. This term inputs negative flux from the boundaries, which spreads to the active domain and progressively stabilises the flow.We thus renormalise the total vertical magnetic flux at each timestep in the active domain Bz(r,ϕ,z) → Bz(r,ϕ,z) − ⟨Bz⟩ + ⟨B0⟩. This way, we obtain quasi-steady states in all of our regimes. In the ideal-MHD case, the amount of magnetic flux thus added varies between 10% and 30% of the initial magnetic flux over 200T0, the larger flux losses corresponding to the higher transport rates, which occurs for higher initial net flux. In the strong-Hall regime, less than 5% of the total flux is lost from 50T0 to 200T0 in the organised phase. These flux losses are small on a dynamical time scale, and we verified that the maximal turbulent stress attained in time were the same with and without this procedure. The qualitative level of self-organisation was also consistent between runs with and without the flux renormalisation.
One caveat of this method is that mass losses should enhance the turbulent stress in time as the relative importance of magnetic to thermal pressure increases (Hawley et al. 1995).
3.2. Validation
We developed a Chebyshev pseudo-spectral method to compute the MRI eigenmodes in axisymmetric cylindrical coordinates, described in Appendix A. It includes viscosity and all three non-ideal MHD effects, and was tested in ideal, Ohmic, Hall, and Ohmic plus Hall configurations.
The method returns the axisymmetric eigenmodes of the non-ideal MHD equations, linearised about a stationary Keplerian flow with uniform vertical magnetic field. In this section, we take the computational domain to be the unit square (r,z) ∈ [1,2]2. The boundary conditions are periodic in z, with vanishing vr, vϕ, and Bϕ, ∂rvz and ∂rBz at the radial boundaries.
We compared the profiles predicted with a resolution of 256 spectral modes to the result of direct numerical simulations (DNS) on a 2562 grid. The initial and boundary conditions implemented in PLUTO are the same as those of the spectral method, with a white noise of amplitude δv/cs< 10-10 seeded in the vr and vz fields. The fastest growing MRI mode rapidly dominates, and the growth is slow enough that we can extract the radial profiles at a given height, normalise them so that they have the same amplitude, and compare them to linear predictions.
We show in Fig. 1 a comparison of the MRI linear modes including both Ohmic diffusion and the Hall effect. This setup has B0 = 2 × 10-3, ηO = 3 × 10-3, and ℓH = 1.0 and would be linearly stable in the absence of the Hall effect because of Ohmic damping with 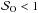 (Jin 1996). Five of these normalised radial profiles are drawn in Fig. 1. These profiles show that our DNS implementation accurately reproduces the spectral predictions, with an average error of the order of 10-3.
(Jin 1996). Five of these normalised radial profiles are drawn in Fig. 1. These profiles show that our DNS implementation accurately reproduces the spectral predictions, with an average error of the order of 10-3.
 |
Fig. 1 Radial profiles of the fastest growing cylindrical MRI eigenmode for B0 = 2 × 10-3, ηO = 3 × 10-3, and ℓH = 1.0; comparison between the predictions (solid lines) and DNS (squares). |
For this particular setup, the measured growth rate γ = 0.0988 matches the predicted rate γ0 = 0.0989 (see Fig. 2). In all our tests, the relative error between predicted and measured growth rates was less than 10-3. The same linear analysis was performed in 3D cylindrical coordinates with only one computational grid cell in the azimuthal direction, so that we preserved the axisymmetric conditions while testing the 3D implementation of the code. Finally, we ensured that the 2D and 3D implementations gave similar results in the non-linear phase for similar initial conditions.
 |
Fig. 2 Exponential growth of the perturbed magnetic field Br. |
3.3. Comparison with previous works
The only global simulations that include the Hall effect published to date are those of O’Keeffe & Downes (2014). Since their setup is similar to ours, it it is natural to begin our report with a comparative study. We wish to reproduce their highest resolution simulations for the two orientations of the initially axial magnetic field with respect to the rotation axis: Up for aligned (corresponding to run “res4-mf”) and Down for oppositely directed (corresponding to their run “480-mf-minusbz”).
We first converted their units into ours and get the following values (see Appendix B): the computational domain is (r,ϕ,z) ∈ [1,5.2] × [0,π/ 2] × [0,0.39], meshed with a grid 480 × 480 × 36. The isothermal sound speed is fixed to cs = 4.35 × 10-2, the initial magnetic field is B0 = 2.2 × 10-3, and the Hall length is ℓH = 5.5 × 10-3. We integrated the dynamical equations on a longer time interval of 130 inner orbits in order to see if the total magnetic energy grows exponentially as seen by O’Keeffe & Downes (2014) in their Fig. 13. They also report the appearance of transient waves exciting resonant modes from the radial boundaries, motivating the inclusion of damping buffer zones. We used similar buffers of width 0.2r0 where the hydrodynamical variables ρ and v are relaxed to their initial values on a characteristic time of one local orbital period. In addition, we chose to maintain the total vertical magnetic flux and mass constant within the active domain, using the procedure described in Sect. 3.1.2 for both Bz and ρ. This modification of the original setup was necessary in order to keep a quasi-steady turbulent state and measure a statistically meaningful difference between the two runs; otherwise, mass and flux losses were about twice larger in the first stage of run Up compared to run Down, after which both runs had a compatible level of turbulent stress slowly decreasing with time.
 |
Fig. 3 Space-averaged αSS parameter (upper panel) and total magnetic energy (lower panel) over time, in the active domain for the two comparison runs Up (solid red) and Down (dashed blue). |
We show in Fig. 3 the evolution in time of the space-averaged ⟨αSS⟩ and the total magnetic energy for the two runs, corresponding to the Figs. 12 and 13 from O’Keeffe & Downes (2014).
We find a slightly lower linear growth rate in run Down, in agreement with the fact that axisymmetric configurations are stabilised by the Hall effect when the magnetic field is anti-aligned with respect to the rotation axis (Balbus & Terquem 2001). During the steady turbulent phase from 60T0 to 130T0, we measure 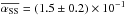 in run Up and
in run Up and 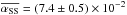 in run Down, greater than the results of O’Keeffe & Downes (2014) by a factor 2 for run Up and a factor 8 for run Down. However, we can compare these values with the local Hall-MHD simulations Z2L and Z4L of Sano & Stone (2002), where they used similar input parameters in extended shearing boxes: B0 = ± 2.5 × 10-3, ℓH ≃ vA/ Ω ≈ 5.5 × 10-3 at radius 1.8r0, plus an additional resistivity such that ΛO = 100, so high enough to affect the saturation level of the turbulence only in a minor way. These two runs yielded
in run Down, greater than the results of O’Keeffe & Downes (2014) by a factor 2 for run Up and a factor 8 for run Down. However, we can compare these values with the local Hall-MHD simulations Z2L and Z4L of Sano & Stone (2002), where they used similar input parameters in extended shearing boxes: B0 = ± 2.5 × 10-3, ℓH ≃ vA/ Ω ≈ 5.5 × 10-3 at radius 1.8r0, plus an additional resistivity such that ΛO = 100, so high enough to affect the saturation level of the turbulence only in a minor way. These two runs yielded 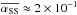 in Z2L (Up case) and
in Z2L (Up case) and 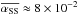 in Z4L (Down case), similar to our results both in magnitude and ratio.
in Z4L (Down case), similar to our results both in magnitude and ratio.
Concerning the total magnetic energy, we do not observe a long-term growth as reported by O’Keeffe & Downes (2014). The total magnetic energy is about twice more in run Up compared to run Down, scaling as the ratio of stresses in accordance with previous studies of MRI-induced turbulence in local ideal MHD simulations (see e.g. Minoshima et al. 2015, Fig. 2). The mean magnetic energy density is 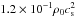 in run Down, comparable again to run Z4 of Sano & Stone (2002) (see their Fig. 1). It is possible that the long-term exponential growth found by O’Keeffe & Downes (2014) both in turbulent stress and in magnetic energy (their Figs. 12 to 15) reflects a state that is not converged yet, whence our higher values for αSS.
in run Down, comparable again to run Z4 of Sano & Stone (2002) (see their Fig. 1). It is possible that the long-term exponential growth found by O’Keeffe & Downes (2014) both in turbulent stress and in magnetic energy (their Figs. 12 to 15) reflects a state that is not converged yet, whence our higher values for αSS.
We do observe the formation of structures such as gaps close to the inner and outer boundaries, but we attribute them to the damping buffer zones for the density accumulates precisely at the edge between the the inner buffer and the active domain. This is the kind of density structures we want to avoid when implementing our own buffers, as described in Sect. 3.1.2. Finally, we note that the strong turbulent activity (αSS ~ 10-1) is due to the large geometrical thickness of the disc compared to its pressure scale height near the inner boundary (Ωh ≫ cs). For this reason, turbulence becomes transonic and strong density waves develop. This unrealistic feature is absent from our other 3D runs, for which we enforce Ωh ≲ cs.
4. Results
4.1. Numerical protocol
All of the global simulations to date have been computed in the weak Hall regime (ℓH/h ≪ 1), which only moderately affect the dynamics of the system. However, discs are known to exhibit regions with a much stronger Hall effect, in particular in the so-called dead zone between 1 and 10 au (Lesur et al. 2014). In these regions, we expect ℓH/h to be of the order of 10 in the disc midplane. In this section we focus on this regime and on its impact on the overall disc dynamics.
The integration time varied from one run to the next depending on the steadiness of the flow, with a default lower bound of 200 inner orbits, which is about 18 orbits at the outer radius. The boundary conditions are those described in Sect. 3.1.2. We ensured that the purely hydrodynamic case was stable, with only faint spiral waves coming from the inner boundary (δvr/cs ~ δρ/ρ0 ≲ 10-4).
Since we are mostly interested in the non-linear evolution of the system, we initialised the flow in a specific way. We started from a Keplerian flow in ideal MHD, threaded by a constant vertical magnetic field B0 = 10-3. Perturbations were added to the three components of the velocity field with a large amplitude δv/cs = 10%, so that MRI modes rapidly develop on the entire domain. After t ≈ 30T0, the MRI saturates, and we stop the simulation at t = 50T0 in a fully turbulent configuration, as illustrated in Fig. 4. Only 3% of the total mass has left the box at that moment, equally from the inner and outer radial boundaries. The radial profile of ⟨ρ⟩ϕz is decreased by about 10% close to the radial boundaries, and density waves create fluctuations of about 0.1ρ0 in the active domain. The turbulent state thus obtained is not subject to a radial density stratification.
 |
Fig. 4 Vertical magnetic field in the turbulent flow when switching on the Hall effect, at t = 50T0. |
All subsequent runs are launched from this configuration, with non-ideal effects switched on and with the net magnetic flux fixed to the desired value. Apart from saving 50T0 of computational time, this method allows us to have the same initial conditions for all runs, and to have initial conditions that are turbulent over the whole domain so that self-organisation processes cannot be attributed to an excessively symmetric initial state. The parameters used in the following 3D Hall MHD runs are listed in Table 1.
We have not systematically explored negative mean field configurations B0·Ω< 0. In effect, the Hall effect is known to be sensitive to the field polarity. In particular, the vertical field configuration we present is known to be stable for negative weak field strengths (Balbus & Terquem 2001): 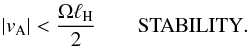 (21)This implies that sub-equipartition magnetic fields are necessarily stable in the negative polarity configuration when ℒ = O(1). We have checked successfully that it was the case in our numerical simulations, so we do not discuss this case any further. Configurations with a strong mean toroidal field, however, can still become unstable, as demonstrated by Simon et al. (2015).
(21)This implies that sub-equipartition magnetic fields are necessarily stable in the negative polarity configuration when ℒ = O(1). We have checked successfully that it was the case in our numerical simulations, so we do not discuss this case any further. Configurations with a strong mean toroidal field, however, can still become unstable, as demonstrated by Simon et al. (2015).
Simulations with net vertical magnetic flux.
4.2. Turbulence
Our study starts by sampling ℒ for different values of the large-scale magnetic flux. We wish to find whether the transition from high to low transport states found in KL13 still occurs in cylindrical geometry, and how it depends on the available net flux, and to characterise these states in terms of turbulent stress and critical ℒ.
Figure 5 presents the profiles of normalised Reynolds and Maxwell stress for the ideal-MHD run B3L0 and the Hall MHD run B3L3. Since we kill the MRI within the buffer zones, the stress has to vanish at the boundaries of the active domain, attaining its maximum near 3.5r0. We note a local increase in Reynolds stress near the outer boundary, possibly due to a characteristic damping time that is too long in the outer buffer. The profile of Maxwell stress is essentially shifted by a factor two higher by the Hall effect; the Reynolds stress does not increase as much, but we show in the lower panel that the ratio of Maxwell to Reynolds stress profiles roughly remains constant with radius in both runs with a value ℳ / ℛ ≈ 2 in ideal MHD and 3 in Hall-MHD, comparable to previous shearing-box simulations (see e.g. Hawley et al. 1995).
 |
Fig. 5 Upper panel: radial profiles of the magnetic (red) and kinetic (blue) contribution to α in runs B3L3 (solid line) and B3L0 (dashed line); lower panel: ratio of Maxwell to Reynolds stress in the same runs. The time averaging is performed between 100T0 and 200T0. |
For all the runs with ℒ ∈ [0,1], we approximately reached a statistically steady state at the end of the simulation, and averaged the total turbulent stress in time over at least 50T0 (100T0 in most cases). These values of  are presented in Fig. 6 against the corresponding value of ℒ. We find a good qualitative agreement with Fig. 11 of KL13: the turbulent activity is enhanced for small ℒ (orange region in Fig. 6), reaching its peak value for ℒ ≈ 0.1 at all B0, beyond which the system forks to a low-transport state with a mean stress that is significantly lower than in the ideal MHD case. We also find that the stress increases with B0 for ℒ < 0.1 in accordance with previous ideal-MHD local simulations (e.g. Sano & Stone 2002).
are presented in Fig. 6 against the corresponding value of ℒ. We find a good qualitative agreement with Fig. 11 of KL13: the turbulent activity is enhanced for small ℒ (orange region in Fig. 6), reaching its peak value for ℒ ≈ 0.1 at all B0, beyond which the system forks to a low-transport state with a mean stress that is significantly lower than in the ideal MHD case. We also find that the stress increases with B0 for ℒ < 0.1 in accordance with previous ideal-MHD local simulations (e.g. Sano & Stone 2002).
 |
Fig. 6 Time-averaged total turbulent stress |
A significant fraction of mass is lost in these simulations: up to 50% in run B3L3. The ratio of accreted to excreted mass is approximately 1 in runs B3L0 to B3L2, increases to 1.8 in B3L3, 1.5 in B3L4, and decreases to 0.8 in B3L5 and only 25% in B3L6. In this last run, the excreted mass is transported by spiral density waves propagating through the entire domain, whereas turbulent accretion is totally suppressed. The same general trend is observed for all values of B0. Despite this significant amount of mass lost, imposing a constant mean magnetic field made it possible to reach quasi-steady states over several hundred inner orbits.
4.3. Zonal flows
4.3.1. Characterisation
We move our attention to the structural properties of the system, starting with Hall-induced zonal flows. As indicated in Table 1, we find that the flow self-organises to long-lived axisymmetric structures whenever ℒ ≳ 1 (blue region in Fig. 6). At a given ℒ, the number of bands depends on the initially available magnetic flux, more flux producing a larger number of bands. Reciprocally, at a given B0 the number of bands is found to increase with ℒ, the exception being run B5L7, where the flow instantaneously crystalised into three positive and negative magnetic field bands.
 |
Fig. 7 Vertical magnetic field in the run B3L6 at t = 300T0. |
We show in Fig. 7 the state of run B3L6 at time 300T0. The vertical magnetic field appears to be organised in four axisymmetric bands, with little to no apparent vertical structure, leaving the rest of the domain almost field-free.
4.3.2. Physical origin
The dynamics of these zonal fields or bands have been explored by KL13, and we recover here a similar qualitative picture. We first emphasise that the zonal field regions are dynamically stable. As demonstrated in Fig. 8, the vertical field strength in each band is so strong that it quenches the linear HSI. This explains why a stronger mean initial vertical flux leads to more bands of similar width. That being said, since the bands have a limited radial extent, they should smear out radially because of diffusion (either numerical, physical, or turbulent), reducing the field strength in the band and ultimately making the whole band HSI unstable again. This is not observed in our simulations, and instead we find a confinement effect that calls for a proper explanation.
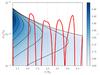 |
Fig. 8 HSI linear growth rates for the mode with vertical wave vector kz = 2π/h (blue color + contour lines), and local vertical Alfvén velocity (red) in run B3L6 averaged from 200T0 to 300T0. |
The zonal field confinement takes its roots in the HSI at the boundary of each bands: the vertical flux is weaker but non-zero, allowing localised HSI modes to develop. This leads to the generation of a localised Maxwell stress at the border of each band, as illustrated in Fig. 9. However, in Hall-MHD, the Maxwell stress appears explicitly in the induction Eq. (9)through the Hall term. This equation predicts that a local maximum of the Maxwell stress pushes away positive vertical flux tubes. As a result, the growth of HSI modes at the border of each band pushes the vertical magnetic flux back in the band, thereby confining the flux in the HSI-stable region. This confinement mechanism by the Maxwell stress is sketched in Fig. 10 and explains the global organisation observed in these simulations.
The bifurcation to such a self-organised state from a fully turbulent state occurs when confinement overcomes diffusion. KL13 show from Eq. (9)that the transition happens near a critical ℒ0 that depends on the stabilising Alfvén velocity (11)and on the turbulent magnetic Prandtl number 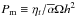 via
via 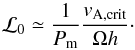 (22)Using Pm ≈ 2 as measured in local simulations (Lesur & Longaretti 2009), they deduce ℒ0 ≈ 0.2. The same argument holds in our case, and the fact that the transition still happens near this critical value translates into a turbulent magnetic Prandtl number of order unity again in a global, non-stratified setup.
(22)Using Pm ≈ 2 as measured in local simulations (Lesur & Longaretti 2009), they deduce ℒ0 ≈ 0.2. The same argument holds in our case, and the fact that the transition still happens near this critical value translates into a turbulent magnetic Prandtl number of order unity again in a global, non-stratified setup.
 |
Fig. 9 Radial profiles of Bz (filled red), 107 × ℳrϕ (dashed, filled blue) and 106×ℛrϕ (solid green) in run B3L6, averaged in time between 160T0 and 230T0. |
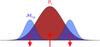 |
Fig. 10 Bz confinement mechanism by belts of Maxwell stress ℳrϕ: the magnetic field decreases in regions of negative second derivative of ℳ, and increases where the curvature of ℳ is positive. |
Looking at the Reynolds component of the stress, we show in Fig. 9 that it is the dominant component of the total stress in this organised configuration, by a factor ten above the Maxwell stress. The physical origin of this stress resides in large-scale spiral waves, unaffected by the presence of zonal fields. We found a plateau of total stress when increasing ℒ beyond unity although the Maxwell stress kept decreasing below 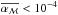 near the end of the simulation. After ruling out a possible defect of our inner damping regions, we think these waves may be excited by residual turbulence and local minima of potential vorticity near the zonal flows.
near the end of the simulation. After ruling out a possible defect of our inner damping regions, we think these waves may be excited by residual turbulence and local minima of potential vorticity near the zonal flows.
4.4. Vortices
4.4.1. Characterisation
For intermediate Hall strengths, the level of turbulent stress remains quite high but the aspect of the turbulent structures gets more clumpier as ℒ is increased (red region in Fig. 6). We quantify this structural transition in Fig. 11, with the median value (over the radial extent of the disc) of the normalised correlation lengths of δBz ≡ Bz − B0 in the vertical and azimuthal directions. The change from small to large-scale fluctuations occurs rapidly for ℒ ≳ 0.2, and when ℒ ≥ 1, the correlation factor is stalled near unity.
 |
Fig. 11 Median value of the vertical (upper panel) and azimuthal (lower panel) auto-correlation profiles of the vertical magnetic field δBz, measured at the end of the quarter-disc runs B3 (red plus), B4 (green cross) and B5 (blue circles); the orange, red and blue regions correspond respectively to a turbulent, vortex and zonal flow final state. |
 |
Fig. 12 Vertical magnetic field in run 2πL5 at time 300T0. |
During the transition ℒ ≈ 0.4, the turbulent fluctuations merge to form a sustained patch of magnetic field in runs B4L5 and B5L5. One band was formed in run B3L5 with the same ℒ; Fig. 6 shows that it is affected by large fluctuations in stress over time, indicating that the structure is not steady. To test its stability, we ran the full-disc simulation 2πL5 and found that the band would actually break and instead form a large patch as illustrated in Fig. 12. In this run the average vertical field is Bz ≈ 8 × 10-3 inside the patch. Similar to the zonal flows of Sect. 4.3, this region displays no structure in the vertical direction. We verified that these magnetic islands were not a mere product of the large-scale flux adjustment procedure (see Sect. 3.1.2). These large scale patches have not been observed in KL13 local simulations probably because their horizontal extension covers several geometrical scale heights h in radius and azimuth. For larger ℒ ≳ 1, the bands are stable in the full-disc configuration as confirmed in run 2πL6. The formation of a band in run B3L5 is facilitated by the smaller angular extent of the domain, and therefore accidental. We also confirm with run 2πL4 that lower values for ℒ ≲ 0.2 keep the flow turbulent in 2π disc simulations.
 |
Fig. 13 Vertical vorticity fluctuation δωz in the (ϕ,r) plane of run 2πL5, centred on the vortex, averaged in the vertical direction and in time with five snapshots between 250T0 and 290T0. The vertical axis δr/r0 is the radial distance to the measured centre of the vortex. |
In the limit of incompressible Hall-MHD, the canonical vorticity 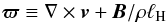 (23)is a conserved quantity (see equation 7 of KL13). An increase in magnetic flux therefore comes with a decrease in vorticity flux. We show in Fig. 13 the vertical component of the vorticity fluctuation from the initial Keplerian flow: δω ≡ ∇ × (v − r− 1 / 2eϕ), averaged in time over 40 inner orbits for better discernibility. We observe that the accumulation of magnetic flux is indeed balanced by a decrease in vorticity flux: δωz ≃ −δBz/ρℓH ≈ 3 × 10-2, making this patch a true vortex and attesting to the role of the Hall effect in its formation. Its centre is localised near 3.8r0, and the ratio of its major to minor axis is χ ≈ 5.2; the corresponding proper rotation period is
(23)is a conserved quantity (see equation 7 of KL13). An increase in magnetic flux therefore comes with a decrease in vorticity flux. We show in Fig. 13 the vertical component of the vorticity fluctuation from the initial Keplerian flow: δω ≡ ∇ × (v − r− 1 / 2eϕ), averaged in time over 40 inner orbits for better discernibility. We observe that the accumulation of magnetic flux is indeed balanced by a decrease in vorticity flux: δωz ≃ −δBz/ρℓH ≈ 3 × 10-2, making this patch a true vortex and attesting to the role of the Hall effect in its formation. Its centre is localised near 3.8r0, and the ratio of its major to minor axis is χ ≈ 5.2; the corresponding proper rotation period is 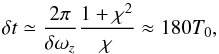 (24)or approximately 25 local orbits. This turn-over time is longer than the local dynamical time scale, which is why our time averages suffer from random fluctuations.
(24)or approximately 25 local orbits. This turn-over time is longer than the local dynamical time scale, which is why our time averages suffer from random fluctuations.
4.4.2. Confinement mechanism
The radial confinement of the vortex obeys the same mechanism as for the zonal flows; we can address it with a one-dimensional approach similar to the axisymmetric model of Sect. 2.2. In the case of zonal flows, a band of magnetic field is pushed from both its inner and outer sides by the (r,ϕ) component of the Maxwell stress ℳrϕ, which is the product of the magnetic field component along the streamlines Bϕ with the component perpendicular to the streamlines −Br. A vortex is defined by closed streamlines, dragging and wrapping the horizontal magnetic field around. In a frame following the vortex at its local Keplerian velocity, one can use the magnetic field components along (B∥) and perpendicular (−B⊥) to the velocity streamlines. The product of these components defines a projected Maxwell stress ℳ⊥∥; this stress appears at the boundary of the magnetic patch and pushes magnetic flux in the perpendicular direction −e⊥, thus confining the vortex from all directions.
 |
Fig. 14 Projected stress in the (ϕ,r) plane of run 2πL5, centered on the vortex, averaged in the vertical direction and in time with five snapshots between 250T0 and 290T0; the vertical axis δr/r0 is the radial distance to the measured centre of the vortex. |
We confirm this picture by showing the averaged map of projected Maxwell stress ℳ⊥∥ of run 2πL5 in Fig. 14. We find that it is negligibly small inside the vortex, attesting to the MHD stability of this region, while the overall positive stress around the vortex provides the required confinement.
5. Dust trapping
An important question is the ability of the previous structures to accumulate dust particles in the process of planetary formation. It is known that aerodynamic drag make dust grains migrate outwards in super-Keplerian regions and migrate inwards in sub-Keplerian regions (Weidenschilling 1977). A disc region trapped between a super-Keplerian part at its inner side and a sub-Keplerian part at its outer side therefore constitute a dust trap2 where dust grains accumulate.
In the incompressible Hall-MHD limit, an increase in magnetic flux should come with a decrease in vorticity flux, so that the flux of canonical vorticity defined by Eq. (23)is conserved. This is equivalent to a velocity profile steepened in regions of accumulated magnetic field and flattened outside, making both zonal flows and vortices potential dust traps.
5.1. Capture by zonal flows
To see how the conservation of the canonical vorticity flux is altered in our compressible case, we draw in Fig. 15 the deviation from a Keplerian rotation profile in run B3L6. We observe a transition from super to sub-Keplerian rotation speed only in the first two bands. In the outer half, the initially turbulent state plus the steady mass excretion by spiral waves have reduced the average density to about 10% of its initial value and slightly increased it in the centre of the radial domain. This global density (and therefore pressure) gradient is sufficient to maintain a sub-Keplerian flow in the outer part of the disc, preventing dust trapping in the last two bands.
 |
Fig. 15 Relative fluctuations of angular velocity (solid blue) and vertical magnetic field (dashed red) in run B3L6, averaged in time between 260T0 and 300T0. The arrows indicate regions of favoured dust accumulation. |
In general, protoplanetary discs are expected to be globally sub-Keplerian thanks to a mean negative pressure gradient3. This deviation from Keplerian rotation can be computed by considering the radial equilibrium 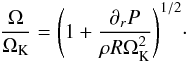 (25)The average pressure gradient entering this equation can be estimated from the aspect ratio of the disc ε = cs/RΩK so that one expects
(25)The average pressure gradient entering this equation can be estimated from the aspect ratio of the disc ε = cs/RΩK so that one expects 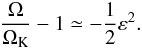 (26)Assuming a typical value of ε = 0.1, we find that the deviations to Keplerian rotation driven by our zonal flows in Fig. 15 are marginally sufficient to create super-Keplerian regions (and thus dust traps) when this mean pressure gradient is included. For this reason, we expect that only a few of these zonal flows (the strongest ones) can trap dust in models including a realistic mean pressure gradient.
(26)Assuming a typical value of ε = 0.1, we find that the deviations to Keplerian rotation driven by our zonal flows in Fig. 15 are marginally sufficient to create super-Keplerian regions (and thus dust traps) when this mean pressure gradient is included. For this reason, we expect that only a few of these zonal flows (the strongest ones) can trap dust in models including a realistic mean pressure gradient.
5.2. Capture by vortices
The possible role of hydrodynamic vortices as dust traps in protoplanetary discs was highlighted by Barge & Sommeria (1995) and Tanga et al. (1996), and has now received both analytical and numerical investigations (e.g. Johansen et al. 2004; Chavanis2000). We focus on the necessary condition for a vortex to be a dust trap: that it is over-pressured with respect to the surrounding flow (see footnote 2). In our globally isothermal simulations, this translates into an over-density in the vortex.
 |
Fig. 16 Density distribution in run 2πL5 at time 300T0. |
We show in Fig. 16 a snapshot of the density distribution in run 2πL5 at time 300T0. Comparing with Fig. 12, there is clearly an over-density at the location of the vortex, with mean value 1.5ρ0 inside at 300T0, so this vortex would be able to trap dust particles.
6. Threats to self-organisation
The simulations presented so far were done in the Hall MHD regime with an imposed mean vertical magnetic field. However, stratified shearing box models (e.g. Lesur et al. 2014) also indicate that the magnetic field could be essentially toroidal in the midplane of protoplanetary discs, which could in turn affect the formation and stability of zonal flows. Besides, ionisation models (e.g. Simon et al. 2015) suggest that the Hall effect is only dominant in the intermediate regions (1 au ≲ r ≲ 30 au) of protoplanetary discs, the inner and outer regions being dominated by Ohmic and ambipolar diffusion, respectively (Turner et al. 2014). These diffusive processes could prevent the formation of sharp magnetic accumulations. We investigate the robustness of our previous findings against these effects in the three next sections.
6.1. Toroidal field
6.1.1. Method
We ran eight simulations where both the vertical and azimuthal magnetic fluxes are imposed and adjusted at each timestep. As before, we let a disc evolve over 50T0 from a Keplerian flow with initial magnetic field B = B0ez + Bϕeϕ to a fully turbulent flow, where B0 = Bϕ = 10-3 is initially constant over the whole domain. This choice of initial conditions does not correspond to an MHD equilibrium, but the intensity of the magnetic field is weak enough to reach a steady turbulence in an overall Keplerian flow. We activated the Hall effect from this starting point in all eight runs and lowered the average vertical magnetic field to B0 = 10-4 for half of them, keeping Bϕ = 10-3. The stopping time is set to 300T0 for runs T3L3 and T4L2 and to 200T0 for the others. The parameters of these runs are given in Table 2.
6.1.2. Results
Simulations with net vertical and toroidal magnetic flux.
From the last column of Table 2, we notice minor differences in the final state of these simulation compared to the case of a purely vertical mean field: run T3L3 produced three bands instead of four, and run T4L2 did not produce a distinct vortex but only short-lived patchy magnetic islands.
We then compare the average stress in these toroidal runs with the previous vertical ones in Fig. 17. The addition of a toroidal magnetic field is seen to have no significant impact on the stress. In particular, the transition from high to low transport states near ℒ ≈ 0.1 is preserved. Only the run T4L3 shows a turbulent stress significantly higher than the analogue run with zero net toroidal flux. This stress comes essentially from the Reynolds component: in all the runs with ℒ = 1 the Maxwell stress kept decreasing below 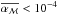 at the end of the simulation, but since the Reynolds stress was statistically steady at a much higher values we did not prolong these runs further.
at the end of the simulation, but since the Reynolds stress was statistically steady at a much higher values we did not prolong these runs further.
These differences attest to the presence of a slightly stronger turbulent activity that is able to weaken magnetic structuring but not drastically change the picture.
 |
Fig. 17 Time-averaged stress |
6.2. Ohmic diffusion
6.2.1. Linear stability
The presence of Ohmic resistivity narrows the range of accessible HSI modes. In the strong Hall limit, the marginal stability of axisymmetric Hall-shear modes with wave vector k in a background vertical field requires (Balbus & Terquem 2001): 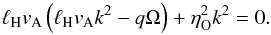 (27)The addition of resistivity affects the two bounds between which instability occurs:
(27)The addition of resistivity affects the two bounds between which instability occurs: 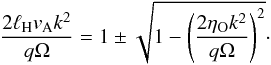 (28)To study self-organisation, the system must initially be between these two bounds. A minimum magnetic field intensity is necessary for linear instability and the possibility of sustaining turbulence. In the other limit, the field intensity required to damp the largest scales k0 = 2π/h is lowered by diffusivity, which may help the formation of Hall-shear stable regions and favour self-organisation. We tune this range of unstable magnetic fields with the magnetic Reynolds number
(28)To study self-organisation, the system must initially be between these two bounds. A minimum magnetic field intensity is necessary for linear instability and the possibility of sustaining turbulence. In the other limit, the field intensity required to damp the largest scales k0 = 2π/h is lowered by diffusivity, which may help the formation of Hall-shear stable regions and favour self-organisation. We tune this range of unstable magnetic fields with the magnetic Reynolds number 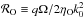 .
.
6.2.2. Method
The numerical setup used in this section is the same as in Sect. 4, but with a constant resistivity ηO in the active domain (and always the resistivity ηb in the damping buffer zones). We sampled two values of magnetic Lundquist numbers 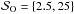 , and the magnetic Reynolds number ℛO is appreciably close to unity only in the small
, and the magnetic Reynolds number ℛO is appreciably close to unity only in the small 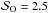 case. These values should be low enough to produce observable effects in our runs, but not prevent self-organisation by immediately damping any perturbation. All four runs are integrated in time from 50T0 to 200T0.
case. These values should be low enough to produce observable effects in our runs, but not prevent self-organisation by immediately damping any perturbation. All four runs are integrated in time from 50T0 to 200T0.
6.2.3. Results
Simulations with Ohmic diffusion.
We see in Table 3 that resistivity does affect the number of zonal flows produced in our simulations: two in O3N1 and one in O3N2, instead of four in the ηO = 0 case of run B3L6. However, the outcome of runs O3N0 and O4N1 is the same as their non-resistive versions: a vortex in the former case and one band in the latter.
It is worth noting that from run O3N1 to O3N2, increasing the resistivity by a factor ten resulted in an increase in Maxwell stress by a factor two. Similarly, the total stress is twice higher in O4N3 than in the non-resistive equivalent scenario B4L6. This behaviour comes from the diffusive broadening of the bands, leaving a wider region linearly unstable at their edges and maintaining a larger fraction of the domain unstable to the MRI.
We thus find that for magnetic Lundquist numbers 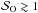 , Ohmic diffusion can reduce the number of zonal flows, but the system keeps self-organising. A similar final state is obtained when resuming the organised run B3L6 with resistivity: diffusion overcomes concentration between the bands and allows them to merge. That a band remains at the end of the simulation suggests that this merging process is halted once the bands are too far to share magnetic flux. At this point, Ohmic diffusion adds to turbulent diffusion in Eq. (9), balancing the confinement by Maxwell stress.
, Ohmic diffusion can reduce the number of zonal flows, but the system keeps self-organising. A similar final state is obtained when resuming the organised run B3L6 with resistivity: diffusion overcomes concentration between the bands and allows them to merge. That a band remains at the end of the simulation suggests that this merging process is halted once the bands are too far to share magnetic flux. At this point, Ohmic diffusion adds to turbulent diffusion in Eq. (9), balancing the confinement by Maxwell stress.
6.3. Ambipolar diffusion
We finally look at the impact of ambipolar diffusion on self-organisation. With its non-linear dependence on B, this effect may lead to more complex behaviours than Ohmic diffusion. The region of protoplanetary discs dynamically affected by ambipolar diffusion is expected to overlap the Hall-dominated region, with typical ambipolar Elsasser numbers ΛA below unity (Simon et al. 2015). We first test the robustness of Hall self-organisation against ambipolar diffusion, then turn our attention to a configuration in which Bai & Stone (2014) report self-organisation without the Hall effect, and finally compare it to our Hall-dominated simulations.
As previously, we activate ambipolar diffusion and the Hall effect simultaneously at 50T0 and integrate until 200T0 with various values for the large-scale magnetic flux, the ambipolar Lundquist number 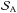 via the ratio
via the ratio 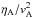 , and the Hall parameter. The ambipolar Lundquist numbers are similar to the Ohmic Lundquist numbers of the previous section, and the corresponding Elsasser numbers range from 0.01 to 1.
, and the Hall parameter. The ambipolar Lundquist numbers are similar to the Ohmic Lundquist numbers of the previous section, and the corresponding Elsasser numbers range from 0.01 to 1.
6.3.1. Hall+Ambipolar MHD
Simulations with ambipolar diffusion.
We see in Table 4 that the total turbulent stress is not significantly affected by ambipolar diffusion in the low-transport state, since the magnetic contribution is still negligibly small. Compared to the non-diffusive case, we find a smaller number of zonal flows with ambipolar diffusion in runs A3N0 to A3N2, but it is larger than the case of an equivalent Ohmic Lundquist number (see Table 3). An inefficient merging of magnetic bands may be explained by the fact that ambipolar diffusion has little influence on the field-free region between the bands.
When lowering the average magnetic flux in run A4N5, we obtain a disc filled with large-scale channel modes and no zonal field. Since the average magnetic field is far below the threshold for HSI stabilisation, linear modes develop until the ambipolar diffusive damping rate, of order ηA/h2, balances their growth rate. The resulting stress has an almost flat radial profile, providing no confinement at the scale of our computational domain. Run A4N6 proves that when increasing ℒ at the same field intensity, the Hall effect becomes competitive again, and we recover several zonal fields.
 |
Fig. 18 Radial profiles in run A3N4, averaged in the vertical and azimuthal directions, and in time between 150T0 and 250T0. Upper panel: vertical magnetic field (solid red) and Maxwell stress (dashed blue); lower panel: contributions of the Hall (solid black) and ambipolar (dashed green) drifts to the induction of vertical magnetic field ∂tBz. |
A new feature is the possibility of forming zonal fields at lower ℒ < 1, as demonstrated by runs A3N3 and A3N4. We show in Fig. 18 the radial profile of vertical magnetic field in run A3N4 and the contributions of both non-ideal effects to the induction Eq. (3)in the vertical direction. The variations in Bz have a much smaller amplitude than in Hall-only runs (see Fig. 9), but they still show a clear anti-correlation with the variations in Maxwell stress. As previously, we find that the Hall effect tries to increase Bz in the bands and decrease it between. The ambipolar drift does precisely the opposite: it tries to smooth out the profile of Bz, and both contributions appear to cancel out on average.
Since the Hall effect now balances ambipolar rather than turbulent diffusion, the self-organisation threshold given by Eq. (22)no longer needs to hold. Ambipolar diffusion acts to damp fluctuations in magnetic field, so the turbulent diffusivity ηt entering Eq. (9)must eventually decrease when the ambipolar diffusivity is increased. In the limit of strong ambipolar diffusion, the bifurcation to a self-organised state should depend on ηA alone. That we observe two bands at ℒ = 0.2 may result from an effective diffusivity ηt + ηA that is less than in the Hall-only case, due to the decrease in ηt as a function of ηA.
We conclude that self-organisation holds for ambipolar Elsasser numbers down to ΛA = 0.01 and that ambipolar diffusion can enable the formation of zonal flows for ℒ as low as 0.2.
6.3.2. Self-organisation with only ambipolar diffusion
Magnetic self-organisation was also reported by Bai & Stone (2014) in local simulations of MRI turbulent flows without the Hall effect. Since ambipolar diffusion was found to enhance magnetic flux concentration, we only included this non-ideal effect and tried to reproduce the physical conditions of their run AD-4-64 within our global setup in run ABS. The initial magnetic field is set to 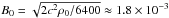 , and the ambipolar Elsasser number ΛA = 1 is constant throughout the computational domain, so that both setups should match at the inner boundary. Considering the narrowness of the magnetic structures observed by Bai & Stone (2014), we used the HLLD approximate Riemann solver to reduce numerical diffusivity in this run alone.
, and the ambipolar Elsasser number ΛA = 1 is constant throughout the computational domain, so that both setups should match at the inner boundary. Considering the narrowness of the magnetic structures observed by Bai & Stone (2014), we used the HLLD approximate Riemann solver to reduce numerical diffusivity in this run alone.
 |
Fig. 19 Normalised vertical magnetic field ⟨Bz⟩ /B0 in run ABS. |
In comparison to their Fig. 7, we confirm in our Fig. 19 that the vertical magnetic flux does concentrate into bands. They are most clearly visible in the inner half of the disc, where they live a few tens of orbits before being disrupted and formed again in the turbulent flow. Averaging this profile in time, we find mean fluctuations of about 0.3B0 revealing five bands at radii 1.5, 1.9, 2.2, 2.6, and 3.2r0. We note a broadening of these bands with radius, suggesting some self-similar scaling 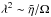 of the characteristic concentration length scale λ with the local time scale for some effective anti-diffusivity
of the characteristic concentration length scale λ with the local time scale for some effective anti-diffusivity 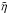 , and not a constant concentration length of order h as for the Hall effect.
, and not a constant concentration length of order h as for the Hall effect.
We show in Fig. 20 the correlation profiles of δBz in run ABS at time 200T0. The median values are 0.3 and 0.08 for the vertical and azimuthal correlation lengths, respectively, with peak values up to 0.5 in azimuthal correlation at the location of each spotted band. These median values are consistent with those from a fully turbulent state (see Fig. 11). In particular there is no strong vertical coherence in the bands, confirming that these magnetic concentrations can never stabilise the flow in the full height of the disc. In comparison, the zonal fields produced by the Hall effect are always Hall-shear stable with vertical correlation factors close to unity.
We conclude that the self-organisation process observed by Bai & Stone (2014) is fundamentally different from the Hall-induced self-organisation mechanism presented in this paper.
 |
Fig. 20 Radial profiles of averaged vertical (solid red) and azimuthal (dashed blue) correlations lengths for the fluctuation in vertical magnetic field δBz in run ABS at time 200T0. |
7. Summary and discussion
We have presented a number of non-ideal MHD simulations dedicated to the Hall-dominated regions of protoplanetary discs. We employed a global non-stratified model designed to naturally extend results from local shearing box simulations. For this purpose, we have extended the PLUTO code to include the Hall effect in cylindrical geometry and validated our implementation in the linear regime of the resistive MRI. We then performed a series of global Hall-MHD simulations, focusing on the different stages of self-organisation found as the intensity of the Hall effect is increased. Finally, we addressed the consequences of a net toroidal magnetic flux, as well as Ohmic or ambipolar diffusion, in this picture of Hall-induced self-organisation.
We can summarise our main findings as follows:
-
1.
We confirmed the transition from enhanced to low-ered turbulent transport states when increasing the in-tensity of the Hall effect; the turning point is found atℒ ≈ 0.1, comparable to the estimate of KL13.
-
2.
In the strong Hall limit ℒ ≳ 1, self-organisation leads to the formation of stationary zonal flows in cylindrical geometry; as the Hall length or the available magnetic flux is increased, so does the number of zonal flows, until the computational domain is filled with bands of accumulated magnetic field with typical width h.
-
3.
When increasing ℒ from zero, the transition from a small-scale turbulence to axisymmetric zonal flows is accompanied by the formation of large-scale magnetised vortices, a feature barely accessible in local simulations for it requires a large aspect ratio in the radial over vertical directions.
-
4.
Both the vortices and the zonal flows caused by the Hall effect may play a role in the process of planetary formation, since they can affect the rotation profile of the gas sufficiently to trap dust particles.
-
5.
The self-organisation mechanism described in this paper holds when including a net toroidal field, Ohmic, or ambipolar diffusion; both diffusive effects cause the magnetic structures to merge over time, but do not change the total torque exerted on the disc significantly; ambipolar diffusion is found to enable self-organisation at lower Hall parameter ℒ.
These results demonstrate that Hall-MRI is a very promising mechanism through which large-scale structures can form and be observed. One should, however, keep in mind that these simulations are still very simplified and leave many questions open. First, we neglected vertical stratification entirely and simplified the radial structure to keep relatively constant diffusion parameters. Vertical stratification can be very important because it drives surface winds and accretion thanks to magnetic torques. Stratified shearing box models including the Hall effect have not shown any obvious self-organisation, but this is likely due to the limited radial extension of these boxes. The mechanism we propose for the self organisation is relatively simple and robust as it only relies on three hypotheses: 1- the disc is ionised sufficiently to be MRI/HSI unstable; 2- the r − φ component of the Maxwell stress vanishes for strong enough field strengths; and 3- the Hall length scale is close to the disc scale height. Hypotheses 1 and 3 are usually satisfied in the midplane of stratified models. However, hypothesis 2 can be violated when a strong large-scale wind is present, as the Maxwell stress is not only due to local physics but also to the global wind dynamics. Testing self-organisation in global stratified models is therefore essential to confirm this picture.
It is also worth pointing out that several of our simulations exhibit stable magnetised vortices. This might look surprising since vortices are known to be strongly unstable in magnetised discs due to magneto-elliptic instabilities (Mizerski & Bajer 2009). We have not investigated the stability of these objects extensively, but the presence of a strong field in the vortex core is most certainly the key to their stability, because this tends to rigidify flow motions and prevent fluid particles from entering into a resonance with the vortex turnover frequency.
Whether the structures produced in our simulations can be observed is yet another open question. It is clear that some of these structures are dust traps, so should accumulate millimetre-sized dust particles. However, this dust might also react on the flow and even affect the ionisation structure, thereby changing the dynamics. This complex interplay between MHD, dust, and chemistry has not been included in our models so as not to complicate them too much, but this step will be required if one is to predict the dust-density contrast in rings and vortices and predict observational properties of these features.
These radii have been computed assuming a minimum mass solar nebula (MMSN, Hayashi 1981) for the disc density and temperature structure. Real discs are likely to deviate significantly from this model, so these radii should be taken with care when comparing to specific astrophysical objects.
These regions are sometimes refered to as pressure bumps. As a result of the radial geostrophic equilibrium, the trap we describe necessarily corresponds to a pressure bump, but we prefer avoiding this terminology since dust grains are only sensitive to the gas velocity and not to the gas pressure.
Acknowledgments
We thank Mario Flock for helping us with the initial setup of our simulations and Matthew Kunz for useful discussions. This work was granted access to the HPC resources of IDRIS under the allocation 2015-042231 made by GENCI. Some of the computations presented in this paper were performed using the Froggy platform of the CIMENT infrastructure (https://ciment.ujf-grenoble.fr), which is supported by the Rhône-Alpes region (GRANT CPER07_13 CIRA), the OSUG@2020 labex (reference ANR10 LABX56) and the Equip@Meso project (reference ANR-10-EQPX-29-01) of the programme Investissements d’Avenir supervised by the Agence Nationale pour la Recherche.
References
- Bai, X.-N. 2014, ApJ, 791, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, X.-N. 2015, ApJ, 798, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, X.-N., & Stone, J. M. 2013, ApJ, 769, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, X.-N., & Stone, J. M. 2014, ApJ, 796, 31 [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., & Papaloizou, J. C. B. 1999, ApJ, 521, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., & Terquem, C. 2001, ApJ, 552, 235 [Google Scholar]
- Barge, P., & Sommeria, J. 1995, A&A, 295, L1 [NASA ADS] [Google Scholar]
- Benisty, M., Juhász, A., Boccaletti, A., et al. 2015, A&A, 578, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blaes, O. M., & Balbus, S. A. 1994, ApJ, 421, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Brogan, C. L., Perez, L. M., ALMA Partnership, et al. 2015, ApJ, 808, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Chavanis, P. H. 2000, A&A, 356, 1089 [NASA ADS] [Google Scholar]
- Dipierro, G., Price, D., Laibe, G., et al. 2015, MNRAS, 453, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, C. R., & Hawley, J. F. 1988, ApJ, 332, 659 [Google Scholar]
- Gammie, C. F. 1996, ApJ, 457, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Gressel, O., Turner, N. J., Nelson, R. P., & McNally, C. P. 2015, ApJ, 801, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1995, ApJ, 440, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, C. 1981, Progr. Theor. Phys. Suppl., 70, 35 [Google Scholar]
- Jin, L. 1996, ApJ, 457, 798 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., Andersen, A. C., & Brandenburg, A. 2004, A&A, 417, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kersalé, E., Hughes, D. W., Ogilvie, G. I., Tobias, S. M., & Weiss, N. O. 2004, ApJ, 602, 892 [NASA ADS] [CrossRef] [Google Scholar]
- Kunz, M. W. 2008, MNRAS, 385, 1494 [NASA ADS] [CrossRef] [Google Scholar]
- Kunz, M. W., & Balbus, S. A. 2004, MNRAS, 348, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Kunz, M. W., & Lesur, G. 2013, MNRAS, 434, 2295 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G., & Longaretti, P.-Y. 2009, A&A, 504, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lesur, G., Kunz, M. W., & Fromang, S. 2014, A&A, 566, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lovelace, R. V. E., Li, H., Colgate, S. A., & Nelson, A. F. 1999, ApJ, 513, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Mignone, A., Flock, M., Stute, M., Kolb, S. M., & Muscianisi, G. 2012, A&A, 545, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minoshima, T., Hirose, S., & Sano, T. 2015, ApJ, 808, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Mizerski, K. A., & Bajer, K. 2009, J. Fluid Mech., 632, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Muto, T., Grady, C. A., Hashimoto, J., et al. 2012, ApJ, 748, L22 [NASA ADS] [CrossRef] [Google Scholar]
- O’Keefe, W. 2013, Ph.D. Thesis, Dublin City University [Google Scholar]
- O’Keeffe, W., & Downes, T. P. 2014, MNRAS, 441, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Papaloizou, J. C. B., & Terquem, C. 1997, MNRAS, 287, 771 [NASA ADS] [CrossRef] [Google Scholar]
- Sano, T., & Stone, J. M. 2002, ApJ, 577, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Simon, J. B., Bai, X.-N., Armitage, P. J., Stone, J. M., & Beckwith, K. 2013, ApJ, 775, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J. B., Lesur, G., Kunz, M. W., & Armitage, P. J. 2015, MNRAS, 454, 1117 [NASA ADS] [CrossRef] [Google Scholar]
- Tanga, P., Babiano, A., Dubrulle, B., & Provenzale, A. 1996, Icarus, 121, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, N. J., Fromang, S., Gammie, C., et al. 2014, Protostars and Planets VI, 411 [Google Scholar]
- van der Marel, N., van Dishoeck, E. F., Bruderer, S., et al. 2013, Science, 340, 1199 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wardle, M. 1999, MNRAS, 307, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Wardle, M. 2007, Ap&SS, 311, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Spectral method for linear non-ideal MHD in axisymmetric configuration
We start with the full set of equations describing a magnetised fluid in non-ideal compressible magnetohydrodynamics:
![\appendix \setcounter{section}{1} \begin{eqnarray} &&\partial_t \rho + \bm{\nabla \cdot} \left[ \rho \bm{v}\right] = 0 \label{eqn:} \\ &&\rho \left(\partial_t \bm{v} + \bm{v \cdot\nabla v}\right) = - \bnab P + \bm{J \times B} + \upsilon \bm{\Delta} \bm{v} - \rho\bnab\Phi \label{eqn:} \\ &&\!\begin{split} \partial_t \bm{B}=& \bm{\nabla \times} \left[ \bm{v \times B} - \eta \bm{\nabla\times B} \right.\\ &\left.\,\,\,\,- \lH \left( \bm{\nabla\times B} \right) \bm{\times B} + \gamma \left(\left(\bm{\nabla\times B}\right) \bm{\times B} \right) \bm{\times B} \right] \label{eqn:} \end{split} \end{eqnarray}](/articles/aa/full_html/2016/05/aa27874-15/aa27874-15-eq343.png) completed by the closures J = ∇ × B and
completed by the closures J = ∇ × B and 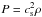 where ρ is the fluid density, v is its velocity, B the magnetic field, P the pressure, J the electric current density, η the Ohmic diffusivity, υ the kinematic viscosity, ℓH the Hall length, and γ the ambipolar diffusion coefficient. Here, Φ is a gravitational potential ∝r-1 in cylindrical coordinates (r,ϕ,z).
where ρ is the fluid density, v is its velocity, B the magnetic field, P the pressure, J the electric current density, η the Ohmic diffusivity, υ the kinematic viscosity, ℓH the Hall length, and γ the ambipolar diffusion coefficient. Here, Φ is a gravitational potential ∝r-1 in cylindrical coordinates (r,ϕ,z).
These equations are linearised about the stationary solution 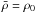 ,
, 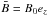 ,
, 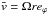 where Ω(r) ∝ rq and q = −3 / 2 in the Keplerian case. We restrict ourselves to axisymmetric perturbations: ∂ϕ = 0. Defining
where Ω(r) ∝ rq and q = −3 / 2 in the Keplerian case. We restrict ourselves to axisymmetric perturbations: ∂ϕ = 0. Defining 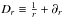 , the equation for the perturbed density reads as
, the equation for the perturbed density reads as 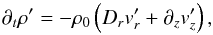 (A.4)and the perturbed velocity as
(A.4)and the perturbed velocity as ![\appendix \setcounter{section}{1} \begin{eqnarray} \partial_t v'_{\it r} &=& - \frac{c_{\rm s}^2}{\rho_0} \partial_{\it r} \rho' + \upsilon \left( \partial_{\it r}^2 + \frac{1}{r}\partial_{\it r} \right) \left[ v'_{\it r} \right] \nonumber\\ &&\quad + 2\Omega v'_{\varphi} + \frac{B_0}{\rho_0}\left( \partial_z B'_{\it r} - \partial_{\it r} B'_z \right)\\ \partial_t v'_{\varphi} &=& - \left(2+q\right) \Omega v'_{\it r} + \frac{B_0}{\rho_0}\partial_z B'_{\varphi} \\ \partial_t v'_z &=& -\frac{c_{\rm s}^2}{\rho_0}\partial_z \rho' + \upsilon \partial_z^2 v'_z. \end{eqnarray}](/articles/aa/full_html/2016/05/aa27874-15/aa27874-15-eq362.png) Finally for the perturbed magnetic field,
Finally for the perturbed magnetic field, ![\appendix \setcounter{section}{1} \begin{eqnarray} \begin{split} \partial_t \bm{B'} &=& \bm{\nabla \times} \left[ \Omega r \bm{e}_{\varphi} \times \bm{B'} - B_0 \bm{e}_{\it z} \times \bm{v'} - \eta \bm{\nabla \times B'} \right. \\[2mm] +&&\left. \lH B_0 \bm{e}_{\it z} \times \left( \bm{\nabla \times B'} \right) + \gamma B_0^2 \bm{e}_{\it z} \times \bm{e}_{\it z} \times \left( \bm{\nabla \times B'} \right)\right] . \end{split} \end{eqnarray}](/articles/aa/full_html/2016/05/aa27874-15/aa27874-15-eq363.png) (A.8)Since we look for axisymmetric configurations, we can reduce the number of variables and naturally ensure the ∇·B = 0 condition using the vector potential Aϕ such that Br = −∂zAϕ and Bz = DrAϕ. The linearised induction equations become
(A.8)Since we look for axisymmetric configurations, we can reduce the number of variables and naturally ensure the ∇·B = 0 condition using the vector potential Aϕ such that Br = −∂zAϕ and Bz = DrAϕ. The linearised induction equations become
![\appendix \setcounter{section}{1} \begin{eqnarray} &&\partial_t B'_{\varphi}= B_0 \partial_z v'_{\varphi} + \sigma \partial_z^2 B'_{\varphi} \notag\\ &&\qquad\qquad + \lH B_0 \partial_z \left( \partial_z^2 - \partial_{\it r} D_{\it r} - \partial_{\it r}\left[\Omega r \right] \right) \left[ A'_{\varphi} \right]\notag \\ &&\qquad \qquad + \eta \left(\partial_{\it r}^2 + \frac{1}{r}\partial_{\it r} - \frac{1}{r^2} \right) \left[ B'_{\varphi}\right]\notag\\ &&\partial_t \left[-\partial_z A'_{\varphi}\right] = B_0 \partial_z v'_{\it r} - \sigma\partial_z\left( \partial_z^2 + \partial_{\it r} D_{\it r} \right) \left[ A'_{\varphi}\right] + \lH B_0 \partial_z B'_{\varphi} \end{eqnarray}](/articles/aa/full_html/2016/05/aa27874-15/aa27874-15-eq368.png) (A.9)with
(A.9)with  . At this stage, we have a linear system of partial differential equations for the the six fields
. At this stage, we have a linear system of partial differential equations for the the six fields 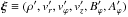 , which we can write as ∂tξ = Δ·ξ. Noticing that the periodic z coordinate appears only in derivatives, we can replace it by a parameter ikz and reduce the problem to a system of one-dimensional equations. Expanding over a finite set of Chebyshev polynomials, the extraction of eigenmodes amounts to solving the generalised eigenvalue problem Δ·ξk = ωkΓ·ξk, where Γ is almost the identity matrix, in which a few lines are used to implement boundary conditions.
, which we can write as ∂tξ = Δ·ξ. Noticing that the periodic z coordinate appears only in derivatives, we can replace it by a parameter ikz and reduce the problem to a system of one-dimensional equations. Expanding over a finite set of Chebyshev polynomials, the extraction of eigenmodes amounts to solving the generalised eigenvalue problem Δ·ξk = ωkΓ·ξk, where Γ is almost the identity matrix, in which a few lines are used to implement boundary conditions.
 |
Fig. A.1 Stability map with the parameters from Kersalé et al. (2004). Our maximum growth rate is indicated with a black dot, theirs with a red cross. |
To test this method, we tried to reproduce the stability map from Fig. 3a of Kersalé et al. (2004). The setup is the same as the one described in Sect. 3.2, including viscosity and Ohmic resistivity with diffusivities ν = η = 0.003 and no Hall effect. The maximum growth rate is computed for different values of the background magnetic field B0 and vertical wave number kz of the eigenmode. The spectral resolution used for this map is set to 32 modes after checking on several points that resolutions of 256, 64, or even 16 spectral modes gave the same eigenvalue to better than 10-4 relative accuracy.
The resulting map is shown in Fig. A.1. Our unstable domain is geometrically very similar to the one of Kersalé et al. (2004), but extends over a larger portion of the (kz,B0) plane and displays higher growth rates. This comes from our different choice of boundary conditions for vϕ and Bϕ. Our maximum growth rate γM ≈ 0.266Ω0 at 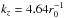 , B0 = 0.10 is nevertheless very close to the one they found in this plane.
, B0 = 0.10 is nevertheless very close to the one they found in this plane.
Appendix B: Numerical setup of O’Keeffe & Downes (2014)
We present here the numerical setup of O’Keeffe & Downes (2014) and make the connection of their parameters real units to our dimensionless parameters.
O’Keeffe & Downes (2014) use a cubic box of size Lx = Ly = 2.6 and Lz = 0.195. The setup is a quarter disc with rint = 0.5 and rext = 2.58. The units are such that 1 numerical length unit corresponds to 5.2 au (O’Keefe 2013, p. 80). This means that the disc extends from r0 = 2.6 au to r1 = 13.4 au.
This cylindrical disc is filled with a flow of uniform initial density with ρ = 1.17 × 10-11 g cm-3 and a mean molecular mass mn = mH that gives a number density n = 7 × 1012 cm-3. The ionisation fraction is assumed to be 4 × 10-11, which implies a electron density of ne = 2.82 × 102 cm-3.
The initial field strength is chosen to be 50 mG, so that the Alfvén speed is 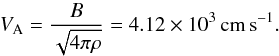 (B.1)The sound speed is not mentioned in O’Keeffe & Downes (2014) but may be found in O’Keefe (2013), p. 81: cs = 8.04 × 104 cm s-1. This sound speed is coherent with a gas made of H2 at T = 130 K.
(B.1)The sound speed is not mentioned in O’Keeffe & Downes (2014) but may be found in O’Keefe (2013), p. 81: cs = 8.04 × 104 cm s-1. This sound speed is coherent with a gas made of H2 at T = 130 K.
With the values quoted above, we get the following dimensionless parameters 
The surprisingly low relative strength of the Hall effect (ℓH/h = 1.4 × 10-2 ≪ 1) comes from the high ionisation fraction and the low midplane density compared to other models (e.g. Wardle 2007) and the large geometrical thickness compared to the pressure scale height (hΩ0/cs = 9).
All Tables
All Figures
 |
Fig. 1 Radial profiles of the fastest growing cylindrical MRI eigenmode for B0 = 2 × 10-3, ηO = 3 × 10-3, and ℓH = 1.0; comparison between the predictions (solid lines) and DNS (squares). |
| In the text | |
 |
Fig. 2 Exponential growth of the perturbed magnetic field Br. |
| In the text | |
 |
Fig. 3 Space-averaged αSS parameter (upper panel) and total magnetic energy (lower panel) over time, in the active domain for the two comparison runs Up (solid red) and Down (dashed blue). |
| In the text | |
 |
Fig. 4 Vertical magnetic field in the turbulent flow when switching on the Hall effect, at t = 50T0. |
| In the text | |
 |
Fig. 5 Upper panel: radial profiles of the magnetic (red) and kinetic (blue) contribution to α in runs B3L3 (solid line) and B3L0 (dashed line); lower panel: ratio of Maxwell to Reynolds stress in the same runs. The time averaging is performed between 100T0 and 200T0. |
| In the text | |
 |
Fig. 6 Time-averaged total turbulent stress |
| In the text | |
 |
Fig. 7 Vertical magnetic field in the run B3L6 at t = 300T0. |
| In the text | |
 |
Fig. 8 HSI linear growth rates for the mode with vertical wave vector kz = 2π/h (blue color + contour lines), and local vertical Alfvén velocity (red) in run B3L6 averaged from 200T0 to 300T0. |
| In the text | |
 |
Fig. 9 Radial profiles of Bz (filled red), 107 × ℳrϕ (dashed, filled blue) and 106×ℛrϕ (solid green) in run B3L6, averaged in time between 160T0 and 230T0. |
| In the text | |
 |
Fig. 10 Bz confinement mechanism by belts of Maxwell stress ℳrϕ: the magnetic field decreases in regions of negative second derivative of ℳ, and increases where the curvature of ℳ is positive. |
| In the text | |
 |
Fig. 11 Median value of the vertical (upper panel) and azimuthal (lower panel) auto-correlation profiles of the vertical magnetic field δBz, measured at the end of the quarter-disc runs B3 (red plus), B4 (green cross) and B5 (blue circles); the orange, red and blue regions correspond respectively to a turbulent, vortex and zonal flow final state. |
| In the text | |
 |
Fig. 12 Vertical magnetic field in run 2πL5 at time 300T0. |
| In the text | |
 |
Fig. 13 Vertical vorticity fluctuation δωz in the (ϕ,r) plane of run 2πL5, centred on the vortex, averaged in the vertical direction and in time with five snapshots between 250T0 and 290T0. The vertical axis δr/r0 is the radial distance to the measured centre of the vortex. |
| In the text | |
 |
Fig. 14 Projected stress in the (ϕ,r) plane of run 2πL5, centered on the vortex, averaged in the vertical direction and in time with five snapshots between 250T0 and 290T0; the vertical axis δr/r0 is the radial distance to the measured centre of the vortex. |
| In the text | |
 |
Fig. 15 Relative fluctuations of angular velocity (solid blue) and vertical magnetic field (dashed red) in run B3L6, averaged in time between 260T0 and 300T0. The arrows indicate regions of favoured dust accumulation. |
| In the text | |
 |
Fig. 16 Density distribution in run 2πL5 at time 300T0. |
| In the text | |
 |
Fig. 17 Time-averaged stress |
| In the text | |
 |
Fig. 18 Radial profiles in run A3N4, averaged in the vertical and azimuthal directions, and in time between 150T0 and 250T0. Upper panel: vertical magnetic field (solid red) and Maxwell stress (dashed blue); lower panel: contributions of the Hall (solid black) and ambipolar (dashed green) drifts to the induction of vertical magnetic field ∂tBz. |
| In the text | |
 |
Fig. 19 Normalised vertical magnetic field ⟨Bz⟩ /B0 in run ABS. |
| In the text | |
 |
Fig. 20 Radial profiles of averaged vertical (solid red) and azimuthal (dashed blue) correlations lengths for the fluctuation in vertical magnetic field δBz in run ABS at time 200T0. |
| In the text | |
 |
Fig. A.1 Stability map with the parameters from Kersalé et al. (2004). Our maximum growth rate is indicated with a black dot, theirs with a red cross. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.