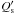| Issue |
A&A
Volume 589, May 2016
|
|
|---|---|---|
| Article Number | A55 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201527100 | |
| Published online | 13 April 2016 | |
Can brown dwarfs survive on close orbits around convective stars?
1
Université Paris-Sud, CNRS, Institut d’Astrophysique Spatiale,
UMR8617,
91405
Orsay Cedex,
France
e-mail:
cilia.damiani@ias.u-psud.fr
2
Observatoire astronomique de l’Université de Genève,
51 ch. des Maillettes,
1290
Versoix,
Switzerland
e-mail:
rodrigo.diaz@unige.ch
Received: 1 August 2015
Accepted: 23 February 2016
Context. The mass range of brown dwarfs extends across the planetary domain to stellar objects. There is a relative paucity of brown dwarfs companions around FGKM-type stars compared to exoplanets for orbital periods of less than a few years, but most of the short-period brown dwarf companions that are fully characterised by transits and radial velocities are found around F-type stars.
Aims. We examine the hypothesis that brown dwarf companions could not survive on close orbit around stars with important convective envelopes because the tides and angular momentum loss, the result of magnetic braking, would lead to a rapid orbital decay with the companion being quickly engulfed.
Methods. We use a classical Skumanich-type braking law and constant time-lag tidal theory to assess the characteristic timescale for orbital decay for the brown dwarf mass range as a function of the host properties.
Results. We find that F-type stars may host massive companions for a significantly longer time than G-type stars for a given orbital period, which may explain the paucity of G-type hosts for brown dwarfs with an orbital period less than five days. On the other hand, we show that the small radius of early M-type stars contributes to orbital decay timescales that are only half those of F-type stars, despite their more efficient tidal dissipation and magnetic braking. For fully convective later type M-dwarfs, orbital decay timescales could be orders of magnitude greater than for F-type stars. Moreover, we find that, for a wide range of values of tidal dissipation efficiency and magnetic braking, it is safe to assume that orbital decay for massive companions can be neglected for orbital periods greater than ten days.
Conclusions. For orbital periods greater than ten days, brown dwarf occurrence should largely be unaffected by tidal decay, whatever the mass of the host. On closer orbital periods, the rapid engulfment of massive companions could explain the lack of G and K-type hosts in the sample of known systems with transiting brown dwarfs. However, the paucity of M-type hosts cannot be an effect of tidal decay alone, but may be the result of a selection effect in the sample and/or the formation mechanism.
Key words: binaries: close / brown dwarfs / stars: rotation / planet-star interactions
© ESO, 2016
1. Introduction
Brown dwarfs are sub-stellar objects that occupy the mass range between the heaviest gas giants planets and the lowest mass stars, usually considered to be between 13 and 80 Jupiter masses. The higher end of this mass interval can be well defined by a relevant physical phenomenon, namely having insufficient mass to sustain hydrogen fusion reactions in their core. This clearly distinguishes two different kinds of objects: those that are able to be in nuclear equilibrium for most of their lifetime, defined as stars, and those that lack significant support against gravitational contraction, defined as brown dwarfs (Burrows et al. 1997). The lower bound mass for the definition of a brown dwarf has often been taken to be the deuterium-burning limit, but such a distinction is currently debated, since deuterium-burning has a negligible impact on stellar structure and evolution (Chabrier & Baraffe 2000). Based on observations, it may be more relevant to distinguish brown dwarfs and giant planets based on their dominant formation mechanisms, which allows a mass overlap between these two populations (Luhman 2012; Chabrier et al. 2014). Of course, such a definition is not without its challenges, since it is not straightforward to infer the formation of a particular object based on its observable properties. Moreover, it is not yet clear whether brown dwarfs form like stars or whether they are the result of a different formation scenario, that may or may not share common properties with the formation of planets (Chabrier et al. 2014).
The statistics of brown dwarf and giant planet companions to stars potentially bears important information on the formation of this objects. In particular, an important result of the radial velocity surveys has been the identification of the so-called brown dwarf desert, i.e., a lack of companions with a mass between 10 and 100 MJ relative to planetary or stellar companions within 3 AU around main-sequence FGKM-type stars (Marcy & Butler 2000; Grether & Lineweaver 2006; Sahlmann et al. 2011). The frequency of companions decreases with increasing mass before the desert, but increases for heavier masses towards the stellar companion range. This may stem from qualitatively and quantitatively different formation mechanisms and help to distinguish brown dwarfs and giant planets (Ma & Ge 2014; Chabrier et al. 2014).
The results of transit surveys shed a different light on the brown dwarf desert. However, transit surveys that are capable of detecting brown dwarf companion to main-sequence stars are mainly focused on exoplanets detection and characterisation. Nevertheless, close-in giant planets and brown dwarfs have approximately the same radius, therefore one could assume that they have the same transit detection bias. Recently, Csizmadia et al. (2015) computed the relative frequency of brown dwarfs and hot Jupiters based on CoRoT (Baglin et al. 2006) data and found a brown dwarf/hot Jupiter occurrence ratio of ≈14%. They note that it is inconsistent with the results of ground-based transit surveys, for which they estimate an occurrence ratio of 0.05%.They reckon that a major factor for explaining the discrepancy may be that ground-based surveys are biased in their detection of transits smaller than 1%. Likewise, Santerne et al. (2016) conducted a systematic survey of Kepler (Borucki et al. 2010) planetary candidates, using radial velocities to determine their masses. They were able to derive the occurrence rate of brown dwarfs and giant planets on orbital periods up to 400 days. They find an occurrence rate of 0.29 ± 0.17% for brown dwarfs, which is 15 times smaller than the value of 4.6 ± 0.6% that they derive for giant planets. They conclude that their values are in agreement with the brown dwarf/hot Jupiter occurrence ratio derived by Csizmadia et al. (2015), but they note that the brown dwarfs detected by CoRoT have orbital periods of less than 10 days, while in the Kepler sample, they have periods between 10 and 170 days. We also note that their sample selects candidates with a transit depth that is less than 3%, which by construction rejects massive companions orbiting M stars. Therefore, even now, no definitive companion census has been measured by transit surveys that extends to the brown dwarf regime, but it appears that the occurrence rate of close-in brown dwarfs is smaller than that of close-in giant planets and, possibly, that the brown dwarf frequency decreases for shorter periods. This could either be the consequence of their formation mechanism or the result of strong tidal interactions that lead to the faster engulfment of more massive companions.
Even at the time of the first detection of a very massive transiting companion with a short orbital period (Deleuil et al. 2008), there was observational evidence that close-orbiting companions to F-type stars could be more massive than companions to lower mass hosts. A few years later, Bouchy et al. (2011) discussed this trend again and also put forward an interesting proposition to try and explain the prevalence of F-type hosts amongst the transiting systems with a massive companion. They commented that tidal interactions alone do not necessarily result in the engulfment of the companion, because companions that are massive enough can, instead, reach a state of tidal equilibrium with synchronous orbital mean motion and stellar spin. But even in that case, magnetic braking in the central star would lead to a loss of angular momentum that is transferred to the orbit of the companion through tides and lead to orbital decay. It is known that early- and mid-F-type dwarfs are typically rapid rotators, independent of their age, as a consequence of a small outer convective zone, weak stellar winds, and smaller losses of angular momentum. Thus Bouchy et al. (2011) proposed that close-in massive planets and brown dwarfs could survive tidally induced orbital decay when orbiting early or mid F-type dwarfs, but be engulfed by G and late F-type dwarfs owing to their more efficient magnetic braking.
Using a numerical model that includes tidal interactions, stellar evolution, magnetic braking and a consistent calculation of tidal dissipation Q′ by gravity waves, Guillot et al. (2014) have computed the survival time of companions to stars in the mass range 0.8 to 1.4 M⊙, and with masses between 0.2 and 200 MJ on an initial orbital period of three days. They conclude that massive close-in planets and brown dwarfs are engulfed preferentially around G-dwarfs, but they also note that observations show an even stronger deficit of massive companions around G-dwarfs than found by their model. Recently, Mathis (2015b) computed the frequency-averaged tidal dissipation in the convective envelope of low-mass stars and found that it is very sensitive to the mass and aspect ratio of the radiative core. They estimated that, at a given stellar rotation rate, the frequency-averaged tidal dissipation efficiency in the convective envelope decreases with increasing mass on the main sequence for masses between 0.5 and 1.4 M⊙. Adding the tidal dissipation in the convective envelope to the one in the radiative zone treated by Guillot et al. (2014) could reconcile their results to observations. The quantitative effects of the evolution of the rotation of the star on the dissipation in the convective envelope, however, still remains to be investigated.
In this paper, we put Bouchy et al.’s hypothesis to the test and compare the dynamical evolution of massive companions around stars F and G stars, but we also extend the comparison to K and M hosts. We produce a general analytic formulation of the characteristic timescale for orbital decay while accounting for the combined effects of tides and magnetic braking. In Sect. 2, we recall how the inclusion of magnetic braking changes the configurations of tidal equilibrium, which is now a dynamical equilibrium state that evolves in time. In Sect. 3 we use the equilibrium tide theory and a classical Skumanich-type braking law to evaluate the ranges of orbital periods and rotation periods that correspond to different orbital decay regimes, depending on the distance to the dynamical equilibrium state. We also provide quantitative estimates for the survival time of a massive companion around dwarfs with an outer convective envelope that surrounds a radiative zone. In Sect. 4, we discuss the resulting observable effects on the relative frequency of massive companions around different types of host. Finally in Sect. 5, we provide our conclusions.
2. Tidal pseudo-equilibrium
We consider a system composed of a star and a gravitationally bound companion of masses M⋆ and Mc, respectively, and radii R⋆ and Rc. They are considered as rigid bodies with moments of inertia about their rotation axis that are noted C⋆ and Cc, respectively. Both those moments can be written as C = M(rgR)2, where rg is the non-dimensional radius of gyration. The periodically varying potential experienced by both objects generates a tidal disturbance in the fluid. Regardless of the mechanism, dissipation of the tides is directly associated with the secular transfer of angular momentum between the spin and the orbit, as well as a loss of energy from the system. In a closed system, the system evolves towards a minimum of energy while the total angular momentum L remains constant. But the open lines of the magnetic field of the host can support a magnetised wind that efficiently extracts angular momentum from the star with a very low mass loss rate. In this case, where neither the total energy nor the total angular momentum is conserved, the configuration corresponding to the minimum of energy evolves with time. Previous studies have shown the importance of magnetic braking for the dynamics of exoplanetary systems (Bolmont et al. 2012; Ferraz-Mello et al. 2015). But even without a detailed knowledge of the tidal dissipation mechanism or wind-braking efficiency and by reasoning only on the extrema of the total energy of the system as a function of the orbital elements, the outcome of tidal evolution under the constraint of angular momentum loss can be assessed. Following Hut (1980), Damiani & Lanza (2015) have shown that the system evolves towards a minimum of energy that it is characterised by a circular and aligned orbit, as in the case of conserved angular momentum, but the synchronisation condition becomes  where ω and Ω are the angular velocity of the companion and the star respectively, n is the mean orbital motion and β(t) is a function of time defined as
where ω and Ω are the angular velocity of the companion and the star respectively, n is the mean orbital motion and β(t) is a function of time defined as 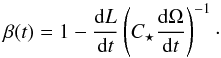 (3)The parameter β(t) can be seen as the ratio of the tidal torque to the total torque acting on the star. A value β(t) ~ 1 corresponds to the case where the total angular momentum of the system is approximately conserved and is equivalent to the case where magnetic braking is neglected. A value β(t) ~ 0 corresponds to the case where the total angular momentum loss of the system is the angular momentum loss of the star through its wind, while the tidal torque acting on the star is negligible. The tidal torque can only spin up the star when Ω <n. As shown in Damiani & Lanza (2015), the dynamical equilibrium state is possible only when Ω <n. Provided that β< 1, at a given time t, Damiani & Lanza (2015) show that the dynamical equilibrium can be reached only if the total angular momentum exceeds a critical value Lcrit(t) given by
(3)The parameter β(t) can be seen as the ratio of the tidal torque to the total torque acting on the star. A value β(t) ~ 1 corresponds to the case where the total angular momentum of the system is approximately conserved and is equivalent to the case where magnetic braking is neglected. A value β(t) ~ 0 corresponds to the case where the total angular momentum loss of the system is the angular momentum loss of the star through its wind, while the tidal torque acting on the star is negligible. The tidal torque can only spin up the star when Ω <n. As shown in Damiani & Lanza (2015), the dynamical equilibrium state is possible only when Ω <n. Provided that β< 1, at a given time t, Damiani & Lanza (2015) show that the dynamical equilibrium can be reached only if the total angular momentum exceeds a critical value Lcrit(t) given by 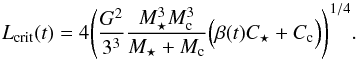 (4)This value depends on β(t), which is time dependent, and it requires Ω <n. Thus, as the system evolves, the conditions for the existence of equilibrium also change, but the dynamical equilibrium state can be reached when 0 <β(t) < 1 and L(t) >Lcrit(t). In other words, the orbital decay is significantly affected by magnetic braking as long as the system can maintain L(t) >Lcrit(t) and enter into the pseudo-equilibrium state. This stationary state could be stable or unstable depending on the sign of the second partial derivative of the energy in this state. It can be shown that the equilibrium will be stable if the orbital angular momentum h satisfies
(4)This value depends on β(t), which is time dependent, and it requires Ω <n. Thus, as the system evolves, the conditions for the existence of equilibrium also change, but the dynamical equilibrium state can be reached when 0 <β(t) < 1 and L(t) >Lcrit(t). In other words, the orbital decay is significantly affected by magnetic braking as long as the system can maintain L(t) >Lcrit(t) and enter into the pseudo-equilibrium state. This stationary state could be stable or unstable depending on the sign of the second partial derivative of the energy in this state. It can be shown that the equilibrium will be stable if the orbital angular momentum h satisfies 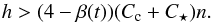 (5)If we consider the critical angular momentum in the absence of magnetic braking, i.e. when β = 1, this is expressed as
(5)If we consider the critical angular momentum in the absence of magnetic braking, i.e. when β = 1, this is expressed as 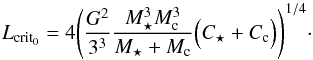 (6)At L = Lcrit0, the unique mean motion that corresponds to co-rotation is
(6)At L = Lcrit0, the unique mean motion that corresponds to co-rotation is 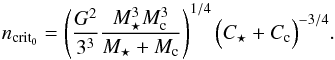 (7)The values of Lcrit0 and ncrit0 only depend on the masses and radii of the star and the companion, and there is no need to know the value of β to compute them. Moreover, in the case where magnetic braking is present, it can be shown that ns(t), defined as the maximum orbital frequency allowing the existence of a pseudo-stable state is given by
(7)The values of Lcrit0 and ncrit0 only depend on the masses and radii of the star and the companion, and there is no need to know the value of β to compute them. Moreover, in the case where magnetic braking is present, it can be shown that ns(t), defined as the maximum orbital frequency allowing the existence of a pseudo-stable state is given by 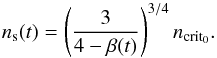 (8)Since the equilibrium state can be reached only if 0 <β(t) < 1, ns(t) always verifies
(8)Since the equilibrium state can be reached only if 0 <β(t) < 1, ns(t) always verifies 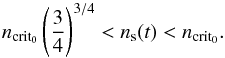 (9)Similarly, it can be shown that the corresponding condition for the existence of a pseudo-stable state in terms of total angular momentum satisfies Lcrit(t) <Ls(t) <Lcrit0. Thus as long as the orbital mean motion n ≲ 0.8 ncrit0 and L>Lcrit0, the system can reach a pseudo-stable equilibrium. In this way, provided that the orbital motion is prograde, the companion may not be directly engulfed into the star as long as Porb ≳ 1.25Pcrit0, where Pcrit0 = 2π/ncrit0. Since Pcrit0 only depends on the masses and radii of the star and the companion, the closest orbital period allowed, purely based on stability principles, can be computed, even without a detail knowledge of the tidal dissipation efficiency or the wind braking. We give this quantity as a function of the companion in Fig. 1 for different host masses. The properties of the host stars are given in Table 1. The Roche limit, where we suppose that the companion may be disrupted by tides, is also plotted in this figure by computing the orbital period that corresponds to the semi-major axis aR defined as:
(9)Similarly, it can be shown that the corresponding condition for the existence of a pseudo-stable state in terms of total angular momentum satisfies Lcrit(t) <Ls(t) <Lcrit0. Thus as long as the orbital mean motion n ≲ 0.8 ncrit0 and L>Lcrit0, the system can reach a pseudo-stable equilibrium. In this way, provided that the orbital motion is prograde, the companion may not be directly engulfed into the star as long as Porb ≳ 1.25Pcrit0, where Pcrit0 = 2π/ncrit0. Since Pcrit0 only depends on the masses and radii of the star and the companion, the closest orbital period allowed, purely based on stability principles, can be computed, even without a detail knowledge of the tidal dissipation efficiency or the wind braking. We give this quantity as a function of the companion in Fig. 1 for different host masses. The properties of the host stars are given in Table 1. The Roche limit, where we suppose that the companion may be disrupted by tides, is also plotted in this figure by computing the orbital period that corresponds to the semi-major axis aR defined as: 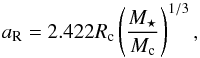 (10)taking Rc = 1.2RJ for the whole mass range.
(10)taking Rc = 1.2RJ for the whole mass range.
 |
Fig. 1 Upper bound on the closest orbital period allowing the existence of a pseudo-stable equilibrium state (provided that Ω <n) as a function of the mass of the companion for different hosts (solid lines). The colour of the line corresponds to the spectral type of the host, as indicated on the plot. The orbital period corresponding to the Roche limit is given as a dashed-line, with the same colour convention. |
Firstly, we see that the Roche limit is closer to the star than the closest stable orbit. Thus the survival of the companion is not threatened by tidal disruption before it can enter the stationary state. Secondly, we see that, for a given companion mass, the closest stable orbit gets closer with decreasing stellar mass. Thus a convective star should be able to retain a massive companion on closer orbit than the more massive hosts. Thirdly, for a given host mass, the closest stable orbit gets closer to the host with increasing companion mass. Thus more massive companions should be able to survive on orbits where planets are found. The critical factor that differentiate massive companions and Jupiter-like planets will be the characteristic timescale of orbital decay through the interplay between tidal interaction and magnetic braking. For a given host mass, rotation frequency and orbital period, more massive companions have greater total angular momentum. Through Eq. (4), this makes them more likely to enter the stationary state. But the value of their tidal torque will also be greater than for less massive planets, which increases the value of β and, through Eq. (5), sets a higher value on the required ratio of angular momentum to ensure their stability. It is thus necessary to describe more accurately the evolution of the tidal torque and the wind torque in time, and the resulting evolution of the orbital parameters.
3. Interplay between the tidal torque and the wind torque
By examining the total mechanical energy of the system as a function of the orbital elements, we have characterised the orbital configuration that corresponds to the minimum of energy. The mechanical energy of the system is not conserved because dissipative fluid processes convert the mechanical energy of the tidal torque into heat, but also because the stellar wind removes kinetic energy from the system. To assess the rate of change of the orbital elements, we must assume some form of tidal dissipation and magnetic braking. Following Damiani & Lanza (2015), we use a formulation based on Barker & Ogilvie (2009), obtained in the framework of the equilibrium tide assuming a constant Q′. Adopting a constant Q′ implies that the time lag between the maximum of the tidal potential and the tidal bulge in each body scales with the orbital period and that the relevant tidal frequency is the orbital frequency. This may not give identical numerical factors as other formulations of tidal friction but, given our lack of knowledge of the actual values of Q′ and its dependence on tidal frequency, this approximation remains reasonable (see Mathis & Remus 2013; Ogilvie 2014 for detailed reviews on tidal dissipation). We use a Skumanich-type law for magnetic braking with a torque of magnitude Γmb = −αmbC⋆Ω3, where the value of αmb is estimated from observed rotation periods of stars of different ages. This formulation overlooks the complex physics of stellar winds (Matt et al. 2012; Réville et al. 2015) but, for the sake of generality, we assume that magnetic braking depends only on the mass, radius, and rotation rate of the star (as in Kawaler 1988). Following Dobbs-Dixon et al. (2004), we take αmb = 1.5 × 10-14γ yr where γ = 0.1 for F stars and γ = 1.0 for latter type stars. To account for a possible relationship between the tidal dissipation efficiency and the extent of the convective envelope, we use a value of Q′ = 108 for F stars, Q′ = 106 for latter type stars (Mathis 2015b,a; Ogilvie & Lin 2007). Those values are somewhat arbitrary, but we do not attempt to precisely estimate an absolute time for the survival of a companion on close orbit, but instead we aim to compare the survival time of companions of different mass around different kind of stars. This qualitative parametrisation should be realistic for stars with an outer convective envelope surrounding a radiative zone, because we expect their dynamos and tidal dissipation mechanisms to be similar. We assume that the companion is quickly synchronised with the orbit, so that the evolution of the system only depends on the tides raised in the star and its magnetic braking.
The temporal evolution of the stellar spin frequency and the orbital mean motion follows the following set of dimensionless equations: 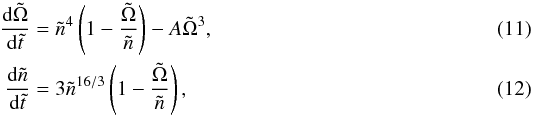 where
where 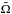 and
and 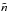 are dimensionless variables that are related to the ones previously defined by the following relationships:
are dimensionless variables that are related to the ones previously defined by the following relationships: 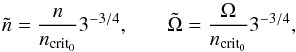 (13)and A is a non-dimensional constant defined as
(13)and A is a non-dimensional constant defined as 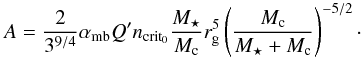 (14)The stationary state, i.e. when the torque exerted on the star by the wind is balanced by the tidal torque, is equivalent to
(14)The stationary state, i.e. when the torque exerted on the star by the wind is balanced by the tidal torque, is equivalent to 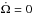 . According to Eq. (11), this means
. According to Eq. (11), this means 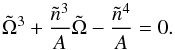 (15)The discriminant of this cubic equation in
(15)The discriminant of this cubic equation in 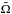 is always negative when
is always negative when 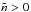 , thus for each positive
, thus for each positive 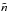 there is one real value
there is one real value 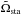 that corresponds to the torque balance. Using Cardano’s method, the real root of Eq. (15) can be written as
that corresponds to the torque balance. Using Cardano’s method, the real root of Eq. (15) can be written as ![\begin{equation} \label{eqstat} \tilde{\Omega}_{\rm sta} = \tilde{n} \, \sqrt[3]{\frac{\tilde{n}}{2A}} \left(\sqrt[3]{1+\sqrt{1+\frac{4\tilde{n}}{27A}}} +\sqrt[3]{1-\sqrt{1+\frac{4\tilde{n}}{27A}} }\right)\cdot \end{equation}](/articles/aa/full_html/2016/05/aa27100-15/aa27100-15-eq73.png) (16)The corresponding stationary period Psta is shown in Fig. 2 as a function of the orbital period for several masses of host and companion.
(16)The corresponding stationary period Psta is shown in Fig. 2 as a function of the orbital period for several masses of host and companion.
 |
Fig. 2 Stellar rotation period corresponding to torque balance as a function of the orbital period in days for companions of masses Mc = 13 (top) and 80 (bottom) Jupiter masses and hosts of different masses (see Table 1) shown in different colours, as indicated on the plots. The solid portion of the lines correspond to orbits where the stationary state is stable, and the dotted portion shows the unstable stationary state (when Porb ≲ 1.25Pcrit0). The solid black line on each plot represents the synchronisation between the orbital period and the stellar spin period. |
We note that when the system has a spin period Pspin, such as Pspin<Porb, both the tidal torque and the wind torque act to spin down the star and the tides push the companion outward. In this case, tidal interaction does not threaten the survival of the companion. But, as the star keeps loosing angular momentum, it will eventually reach a state where Pspin ≥ Porb and tidal evolution may lead to orbital decay and threaten the survival of the companion. We focus our study on this kind of orbital configuration.
3.1. Timescales of evolution
For a circular and aligned system, and assuming that the companion is synchronised with the orbit, the rate of variation of the total angular momentum of the system is 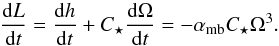 (17)When the wind torque is much smaller than the tidal torque acting on the star (i.e. when Pspin>Psta, see Fig. 2), we can assume that the total angular momentum of the system is approximately conserved so that
(17)When the wind torque is much smaller than the tidal torque acting on the star (i.e. when Pspin>Psta, see Fig. 2), we can assume that the total angular momentum of the system is approximately conserved so that 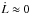 and the in-spiral time of the orbit τa can be written (Barker & Ogilvie 2009)
and the in-spiral time of the orbit τa can be written (Barker & Ogilvie 2009) 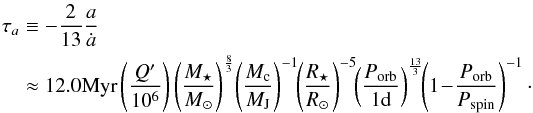 (18)If the orbit is inside co-rotation, angular momentum is transferred from the orbit to the spin of the star at a rate that is set by the tidal torque alone. The spin-up time of the star is then
(18)If the orbit is inside co-rotation, angular momentum is transferred from the orbit to the spin of the star at a rate that is set by the tidal torque alone. The spin-up time of the star is then 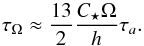 (19)On the other hand, when the wind torque is much stronger than the tidal torque acting on the star (i.e. when Porb ≤ Pspin ≤ Psta), we can assume that
(19)On the other hand, when the wind torque is much stronger than the tidal torque acting on the star (i.e. when Porb ≤ Pspin ≤ Psta), we can assume that 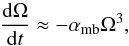 (20)and the spin-down of the star takes place on the characteristic time of the magnetic braking
(20)and the spin-down of the star takes place on the characteristic time of the magnetic braking 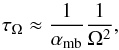 (21)then by Eq. (17)we have
(21)then by Eq. (17)we have 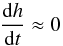 (22)so we can assume that h ≈ const., so that for a circular orbit, the orbital period remains constant.
(22)so we can assume that h ≈ const., so that for a circular orbit, the orbital period remains constant.
When the system is close to the pseudo-stable stationary state, where the wind torque is opposite in sign and equal in magnitude to the tidal torque (i.e when Pspin ~ Psta), we have 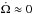 and Ω ≈ Ωsta. From Eq. (17)we get
and Ω ≈ Ωsta. From Eq. (17)we get 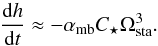 (23)Since the orbital angular momentum is given by
(23)Since the orbital angular momentum is given by 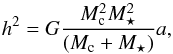 (24)we have
(24)we have 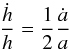 (25)so that
(25)so that 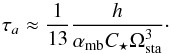 (26)In this way we see that when the system is close to the pseudo-stable stationary state, the rate of orbital decay depends explicitly on magnetic braking, but it has also a non-linear dependance with the efficiency of tidal friction through the value of Ωsta.
(26)In this way we see that when the system is close to the pseudo-stable stationary state, the rate of orbital decay depends explicitly on magnetic braking, but it has also a non-linear dependance with the efficiency of tidal friction through the value of Ωsta.
As the tides transfer angular momentum from the orbit to the star, any system that would enter the pseudo-stable stationary state would, eventually, become unstable by exhaustion of orbital angular momentum. Whenever Porb ≲ Pcrit0, the stationary state is unstable and the in-spiral characteristic time is not given by Eq. (26)because the system moves away from the torque balance as soon as it reaches it, and 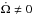 . In this case, the relevant timescale for orbital decay is given by Eq. (18). It is easy to show then that τΩ ≥ τa, which neglects the spin-down effects of magnetic braking. Indeed, by Eq. (5), we get that, for unstable systems, the orbital angular momentum is at most four times the total spin angular momentum. The moment of inertia of the companion being small compared to the host, it is safe to consider that when the stationary state is unstable, the ratio of stellar spin to orbital angular momentum is large enough to let the tidal spin-up time of the star be larger than the in-spiral time by Eq. (19). Thus, even for rapidly rotating hosts, when the stationary state is unstable, the relevant timescale for orbital decay is given by Eq. (18). Close to the stationary state, the characteristic timescale for orbital decay is thus different whether the stationary state is pseudo-stable or not. The former depends non-linearly on magnetic braking and tidal dissipation efficiency, and the later is a linear function of tidal dissipation efficiency alone.
. In this case, the relevant timescale for orbital decay is given by Eq. (18). It is easy to show then that τΩ ≥ τa, which neglects the spin-down effects of magnetic braking. Indeed, by Eq. (5), we get that, for unstable systems, the orbital angular momentum is at most four times the total spin angular momentum. The moment of inertia of the companion being small compared to the host, it is safe to consider that when the stationary state is unstable, the ratio of stellar spin to orbital angular momentum is large enough to let the tidal spin-up time of the star be larger than the in-spiral time by Eq. (19). Thus, even for rapidly rotating hosts, when the stationary state is unstable, the relevant timescale for orbital decay is given by Eq. (18). Close to the stationary state, the characteristic timescale for orbital decay is thus different whether the stationary state is pseudo-stable or not. The former depends non-linearly on magnetic braking and tidal dissipation efficiency, and the later is a linear function of tidal dissipation efficiency alone.
In Fig. 3, we give characteristic in-spiral times as a function of the orbital period for different host and companion masses. When the pseudo-stable stationary state is stable, τa is computed with Eq. (26)taking Pspin = Psta. When Porb<Pc0, the stationary state can no longer be stable. Therefore, we compute τa using Eq. (18). We must assume a different value for the spin of the star, since the system is no longer in the stationary state. As discussed above, in this case the evolution proceeds as if the total angular momentum were conserved (the characteristic timescale for the spin-down of the star is much slower than the tidal spin-up). The rotation period of the star is a function of the (conserved) total angular momentum and the orbital period only. To illustrate the transition between the two regimes, we have set the value of the total angular momentum in the unstable state to the one it has at the end of the pseudo-stable stationary state. The transition between the two regimes is materialised by a cross symbol in the curves. There, the stationary state can no longer be stable and the in-spiral time stops being set by the magnetic braking of the star.
 |
Fig. 3 Typical timescale for tidal decay τa as a function of the orbital period for different masses of host and companion as indicated on the figure. The cross symbol outlines the transition where the stationary state can no longer be stable and the in-spiral time stops being set by the magnetic braking of the star. See text for details. |
We see that, whatever the orbital period, the in-spiral time of companions that are more massive than 13 MJup, is about one order of magnitude greater around F-type stars than around G and K-type stars. This provides a quantitative measure of the difference between G-K and F-type stars that was first evoked by Bouchy et al. (2011), and agrees with the sophisticated simulations of Guillot et al. (2014). For early M-type stars, the in-spiral time is about half that of F-type stars, despite their being almost entirely convective. Indeed, the moment of inertia of an F-type star is typically two orders of magnitude greater than that of an M-type star, mainly because of their difference in radius. On the other hand the orbital angular momentum scales as the inverse square root of the host mass. Thus, for given companion mass and orbital distance, the orbital angular momentum around F-type star is just a few times greater than when orbiting an M-type star. The ratio of orbital to spin angular momentum can thus be one to two orders of magnitude greater for an F-type star than for an M-type star. As can be seen form Eq. (26), this partly compensates for the difference in their magnetic braking efficiency.
 |
Fig. 4 Mass versus period of well-characterised transiting companions with Mc ≥ 0.1 and Porb ≤ 40 days. The colour of the symbol is blue if the host star has Teff ≥ 6200 K, red if Teff ≤ 3300 K, and black otherwise. The detection limit well within the reach of typical radial velocity surveys capabilities is given by a dotted line. |
 |
Fig. 5 Contours of the minimum orbital period of an 80 Jupiter mass companion for which τa ≥ 5 Gyr as a function of the tidal quality factor in the star |
4. Discussion
Assuming that the values we chose for the tidal dissipation and magnetic braking are reasonable, we find that for massive companions around G and K stars, the characteristic timescale for orbital decay is only shorter than ~10 Gyr for orbital periods closer than about five days. On the other hand, they can survive over the same timescale down to orbital periods of about three days when orbiting an F-type star, and about four days for early M-type host. As conjectured by Bouchy et al., this would indeed explain the prevalence of F-type hosts amongst the transiting systems with a massive companion on a very close orbit. Besides, based on the same reasoning, massive companions are expected to survive on closer orbits around M-stars than around G-stars.
In Fig. 4, we present the mass as a function of the orbital periods up to 40 days for systems with measured radial velocities and detected transits. Out of the 11 well-characterised transiting companions that are more massive than ~13 MJ, six are orbiting stars with Teff ≥ 6200 K. This number becomes to five out of seven if we consider companions with orbital periods shorter than 10 days, and five out of six for orbital periods shorter than 5 days. The number of BD companions is small and robust statistics are difficult to establish, but it appears that observations are consistent with the idea that the combined effect of tidal dissipation and magnetic braking shape the distribution of massive companions on very short orbits, in agreement with Bouchy et al.’s hypothesis.
They only discussed the qualitative difference in tidal effects expected between early or mid F-type on the one hand and G and late F-type stars on the other hand. We have shown here that massive companions could also survive on a close-in orbit for a long time around early M-dwarfs, despite their efficient dissipation and braking. And indeed, we see that for masses greater than about 10 MJ and orbital periods shorter than five days, all the systems discovered so far are found exclusively around F or M stars. The large preponderance of F-type hosts compared to M-type hosts may be readily attributed to observational biases against M-type hosts in the sample. First these stars are faint and difficult to follow up with ground-based radial velocities, and they also have a deeper transit that excludes them from exoplanet search programs, which is the main focus of short-period transit surveys. A systematic survey of the transiting short-period companions to M-type stars, whatever their mass range, could easily validate our theory.
Our estimation of the characteristic timescale for orbital decay as a function of the orbital period is sensitive to the choice of parameters. Indeed, studies attempting to calibrate the stellar modified tidal quality factor Q′ with the observed distribution of orbital periods of exoplanets find a value that is somewhat greater than that considered here (Jackson et al. 2009; Hansen 2010). However, they generally neglect the effect of magnetic braking and seem to be inconsistent with the circularisation of stellar binaries (Ogilvie & Lin 2007). We cannot exclude that the actual value of tidal dissipation is very different from what has been assumed here. Moreover, our approach can also be extended to the case of fully convective late-type M dwarfs, with some words of caution. First, it is expected that, because they are fully convective, tidal dissipation in those stars should be weak (Wu 2005; Mathis 2015b). Second, the absence of a tachoclyne may also affect how the magnetic field is generated in these stars, which could imply a braking law that is not Skumanich-like. Tying age to rotation for late-type M dwarfs is very challenging because both their age and rotation period are difficult to measure, but there is observational evidence that older stars are generally slow rotators for both early-type and late-type M dwarfs (West et al. 2015). Leaving aside the complexity of the saturated regime for fast rotators, the magnetic braking law that we used here could also apply to late-type M dwarfs, using an appropriate value of αmb (Reiners & Mohanty 2012).
The orbital and rotation periods that correspond to the stationary state are dependant on the value of the assumed Q′ and αmb. The lower the Q′, the lower the star’s stationary spin period and, therefore, the faster the loss of angular momentum and orbital decay of the planet in the stationary state. But, whereas τa is directly proportional to Q′ when the stationary state is unstable, it does not decrease as fast with decreasing Q′ when the stationary state is stable. In the same way, τa in the stable stationary state does not scale as αmb, because the stationary spin has a non-linear dependance with this parameter through Eq. (16). This is illustrated in Fig. 5, which shows the value of the minimum orbital period that allows τa ≥ 5 Gyrs for a 80 MJup companion orbiting either an F5, G5, or M5-type star, as a function of Q′ and γ = αmb/ 1.5 × 10-14 yr.
Given the wide range of possible values for αmb and Q′ considered here, we can safely conclude that orbital decay for massive companions can be neglected for orbital periods greater than ten days.
We also see that, if Q′ ≲ 107 and γ ≳ 0.6 for G-type stars, and if Q′ ≳ 4 × 107 and γ ≲ 0.4 for F-type stars, the lack of massive companions on orbital periods shorter than five days around G-type stars compared to F-type stars could, indeed, result from the combined effect of tidal interaction and magnetic braking. This is consistent with the fact that stars with a more extended convective zone would have a greater tidal dissipation efficiency and stronger magnetic braking, as stated in Bouchy et al. (2011). Owing to the strong dependance of the tidal torque with the stellar radius, massive companions can also survive on very close orbits around late M-type stars, even if their magnetic braking is efficient.
5. Conclusions
We have shown that M-type stars, either fully convective or not, are capable of harbouring massive companions on close orbits for extended periods of time. The lack of detection of massive companions orbiting convective stars on short orbit can not only be due to the combined effect of tidal dissipation and magnetic braking on the orbital decay. However, for massive companions on orbital periods shorter than five days, these effects may very well explain the lack of systems detected around a G-type host, in agreement with Bouchy et al. (2011) and Guillot et al. (2014). Nevertheless, assuming reasonable values for the magnetic braking and tidal dissipation factors, we would not expect these effects to produce a difference in the proportion of G- and F-type hosts on orbital periods greater than ~6 days. Extending the range of values for these parameters, we show that tidal decay can be safely neglected for massive companions on an orbit greater than ~10 days. Unfortunately, the small number of transiting BD does not provide us with reliable statistics yet. Moreover, caution must be taken, since we cannot rule out the effect of selection biases that may give a lesser priority to the full characterisation of systems that display rather deep transits. In the near future, the estimation of the completeness and observational biases of CoRoT and Kepler down to very low-mass host stars will be available. This will establish the actual relative frequency of BD around F- and later-type stars. If there is a lack of close-in BD around late M-type stars compared to F-type stars, this could be the signature of an inefficient formation process and would help to constrain formation and evolution theories of brown dwarfs and massive extrasolar planets.
Acknowledgments
The authors are grateful to the referee, S. Mathis, for valuable comments that improved the manuscript. C.D. wishes to thank J. P. Marques and F. Baudin for helpful discussions and for providing the CESAM evolutionary tracks. R.F.D. carried out this work within the frame of the National Center for Competence in Research “PlanetS” supported by the Swiss National Science Foundation (SNSF). C.D. acknowledges funding from the ANR (Agence Nationale de la Recherche, France) program IDEE (ANR-12-BS05-0008) “Interaction Des Étoiles et des Exoplanètes”.
References
- Baglin, A., Auvergne, M., Boisnard, L., et al. 2006, in 36th COSPAR Scientific Assembly, COSPAR Meeting, 36, 3749 [NASA ADS] [Google Scholar]
- Barker, A. J., & Ogilvie, G. I. 2009, MNRAS, 395, 2268 [NASA ADS] [CrossRef] [Google Scholar]
- Bolmont, E., Raymond, S. N., Leconte, J., & Matt, S. P. 2012, A&A, 544, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bouchy, F., Deleuil, M., Guillot, T., et al. 2011, A&A, 525, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burrows, A., Marley, M., Hubbard, W. B., et al. 1997, ApJ, 491, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., & Baraffe, I. 2000, ARA&A, 38, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., Johansen, A., Janson, M., & Rafikov, R. 2014, Protostars and Planets VI, 619 [Google Scholar]
- Cox, A. N. 2000, Allen’s astrophysical quantities (New York: AIP Press, Springer) [Google Scholar]
- Csizmadia, S., Hatzes, A., Gandolfi, D., et al. 2015, A&A, 584, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Damiani, C., & Lanza, A. F. 2015, A&A, 574, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deleuil, M., Deeg, H. J., Alonso, R., et al. 2008, A&A, 491, 889 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dobbs-Dixon, I., Lin, D. N. C., & Mardling, R. A. 2004, ApJ, 610, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraz-Mello, S., Tadeu dos Santos, M., Folonier, H., et al. 2015, ApJ, 807, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Grether, D., & Lineweaver, C. H. 2006, ApJ, 640, 1051 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T., Lin, D. N. C., Morel, P., Havel, M., & Parmentier, V. 2014, in EAS Pub. Ser., 65, 327 [Google Scholar]
- Hansen, B. M. S. 2010, ApJ, 723, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Hut, P. 1980, A&A, 92, 167 [NASA ADS] [Google Scholar]
- Jackson, B., Barnes, R., & Greenberg, R. 2009, ApJ, 698, 1357 [NASA ADS] [CrossRef] [Google Scholar]
- Kawaler, S. D. 1988, ApJ, 333, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L. 2012, ARA&A, 50, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, B., & Ge, J. 2014, MNRAS, 439, 2781 [NASA ADS] [CrossRef] [Google Scholar]
- Marcy, G. W., & Butler, R. P. 2000, PASP, 112, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, S. 2015a, in SF2A-2015: Proc. Annual meeting of the French Society of Astronomy and Astrophysics, eds. F. Martins, S. Boissier, V. Buat, L. Cambrésy, & P. Petit, 401 [Google Scholar]
- Mathis, S. 2015b, A&A, 580, L3 [Google Scholar]
- Mathis, S., & Remus, F. 2013, in Lect. Notes Phys. 857, eds. J.-P. Rozelot, & C. Neiner (Berlin: Springer Verlag), 111 [Google Scholar]
- Matt, S. P., MacGregor, K. B., Pinsonneault, M. H., & Greene, T. P. 2012, ApJ, 754, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Morel, P. 1997, A&AS, 124, 597 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Morel, P., & Lebreton, Y. 2008, Ap&SS, 316, 61 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ogilvie, G. I. 2014, ARA&A, 52, 171 [Google Scholar]
- Ogilvie, G. I., & Lin, D. N. C. 2007, ApJ, 661, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., & Mohanty, S. 2012, ApJ, 746, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Réville, V., Brun, A. S., Matt, S. P., Strugarek, A., & Pinto, R. F. 2015, ApJ, 798, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Sahlmann, J., Ségransan, D., Queloz, D., et al. 2011, A&A, 525, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santerne, A., Moutou, C., Tsantaki, M., et al. 2016, A&A, 587, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- West, A. A., Weisenburger, K. L., Irwin, J., et al. 2015, ApJ, 812, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y. 2005, ApJ, 635, 688 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Upper bound on the closest orbital period allowing the existence of a pseudo-stable equilibrium state (provided that Ω <n) as a function of the mass of the companion for different hosts (solid lines). The colour of the line corresponds to the spectral type of the host, as indicated on the plot. The orbital period corresponding to the Roche limit is given as a dashed-line, with the same colour convention. |
| In the text | |
 |
Fig. 2 Stellar rotation period corresponding to torque balance as a function of the orbital period in days for companions of masses Mc = 13 (top) and 80 (bottom) Jupiter masses and hosts of different masses (see Table 1) shown in different colours, as indicated on the plots. The solid portion of the lines correspond to orbits where the stationary state is stable, and the dotted portion shows the unstable stationary state (when Porb ≲ 1.25Pcrit0). The solid black line on each plot represents the synchronisation between the orbital period and the stellar spin period. |
| In the text | |
 |
Fig. 3 Typical timescale for tidal decay τa as a function of the orbital period for different masses of host and companion as indicated on the figure. The cross symbol outlines the transition where the stationary state can no longer be stable and the in-spiral time stops being set by the magnetic braking of the star. See text for details. |
| In the text | |
 |
Fig. 4 Mass versus period of well-characterised transiting companions with Mc ≥ 0.1 and Porb ≤ 40 days. The colour of the symbol is blue if the host star has Teff ≥ 6200 K, red if Teff ≤ 3300 K, and black otherwise. The detection limit well within the reach of typical radial velocity surveys capabilities is given by a dotted line. |
| In the text | |
 |
Fig. 5 Contours of the minimum orbital period of an 80 Jupiter mass companion for which τa ≥ 5 Gyr as a function of the tidal quality factor in the star |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.