| Issue |
A&A
Volume 556, August 2013
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201321870 | |
| Published online | 02 August 2013 | |
Close-binary evolution
I. Tidally induced shear mixing in rotating binaries
1
College of Science, Guizhou University,
Guiyang, 550025
Guizhou Province
PR China
e-mail: songhanfeng@163.com; sci.hfsong@gzu.edu.cn
2
Geneva Observatory, Geneva University,
1290
Sauverny,
Switzerland
3
National Astronomical Observatories/Yunnan Observatory, the
Chinese Academy of Sciences, Kunming, 650011
Yunnan Province, PR
China
4
Key Laboratory for the Structure and Evolution of Celestial
Objects, Chinese Academy of Sciences, 650011
Kunming, PR
China
Received:
10
May
2013
Accepted:
27
June
2013
Context. Tides are known to play an important role in binary evolution, leading in particular to synchronization of axial and orbital rotations and to binary mass transfer.
Aims. We study how tides in a binary system induce some specific internal shear mixing that can substantially modify the evolution of close binaries prior to mass transfer.
Methods. We constructed numerical models accounting for tidal interactions, meridional circulation, transport of angular momentum, shears and horizontal turbulence. Furthermore, we considered a variety of orbital periods and initial rotation velocities.
Results. Depending on orbital periods and rotation velocities, tidal effects may spin down (spin-down case) or spin up (spin-up case) the axial rotation. In both cases, tides may induce a high internal differential rotation. The resulting tidally induced shear mixing is so efficient that the internal distributions of angular velocity and chemical elements are highly influenced. The evolutionary tracks are modified, and in for spin down as well as for spin up, large amounts of nitrogen can be transported to the stellar surfaces before any binary mass transfer. Meridional circulation, when properly treated as a advection, always tends to counteract the tidal interaction, tending to spin up the surface when it is braked down and vice versa. As a consequence, the times needed for the axial angular velocity to become equal to the orbital angular velocity may be longer than given by typical synchronization timescales. Moreover, because of the meridional circulation some differential rotation remains in tidally locked binary systems.
Key words: binaries: close / stars: rotation / stars: abundances / stars: evolution
© ESO, 2013
1. Introduction
Rotation is an important factor to be considered in the evolution of massive stars (Kippenhahn & Thomas 1970; Endal & Sofia 1976; Meynet & Maeder 1997; Langer 1998). The centrifugal force not only gives the star an oblate shape, but it also induces many instabilities, leading to the mixing of chemical elements in the stellar interiors (Maeder & Meynet 2000; Heger et al. 2000a; Huang 2004a,b). In addition to convection and semi-convection, there are several processes that may contribute to the mixing of the chemical elements in stellar interiors, such as shears generated by internal differential rotation, meridional circulation, magnetic instabilities, and magnetic braking at the surface of the star, which favors high shears (Chaboyer & Zahn 1992; Zahn 1992; Maeder & Meynet 2001, 2005; Meynet et al. 2011; Mathis et al. 2004a,b). These physical processes are active in both single and binary stars. They may have important consequences on observable properties (Langer & Maeder 1995; Heger & Langer 2000b; Song et al. 2009, 2011). They can mix the material of the core and envelope, leading, among other consequences, to nitrogen enrichment at the stellar surface. Many B- and O-type stars show nitrogen excesses (Walborn 1976; Heap et al. 2006; Hunter et al. 2009; Przybilla et al. 2010) and the mentioned instabilities may play a role in this.
Recent results suggest that half of the massive stars in the Tarentula region may exchange mass with a binary companion, which potentially strongly affects the course of stellar evolution through tides, mass transfer and mergers (Sana et al. 2013; de Mink et al. 2013). The fraction of binary systems and the fraction of short-period O-type stars vary considerably in different clusters (Mahy et al. 2009); the binary properties are possibly related to the density of the clusters.
Many physical effects studied in the context of single-star evolution need also to be considered in the framework of binary evolution. Here we concentrate on the interaction of some effects of rotation, such as meridional circulation, shears, and horizontal turbulence, with binary evolution. In particular, the tidally induced shear mixing (TISM) may be important in binary evolution. The tidal interactions produce braking, particularly in the outer stellar layers, and thus may enhance the internal differential rotation. The instabilities associated to high shears result in a significant transport of the chemical elements. In the present work we aim to investigate how the tidal braking and its related effects, in particular TISM, can affect the evolution of close binaries.
On top of that, meridional circulation, when correctly treated as a circulation and not as a diffusion, often reacts in a interesting way, by even being able to transport angular momentum from regions with low rotation to regions where rotation is fast (Maeder 2009). Thus, by studying TISM in the framework of models where meridional circulation is consistently treated, we may see the reactions of the star to the interaction of meridional circulation and tidal braking. These effects, which were not predicted, appear to play a significant role in binary evolution.
The paper is organized as follows: the tidal braking is presented in Sect. 2. The equations expressing internal transport of chemical elements and angular momentum are presented in Sect. 3. In Sect. 4, the results of numerical calculation are described and discussed in detail. Finally, conclusions are drawn in Sect. 5.
2. Tidal interactions in rotating binaries
One may distinguish the equilibrium and dynamical tides (Zahn 1966, 1975). For not yet synchronized systems that are subject to the
effects of dynamical tides, the dissipation mechanisms play a major role. These are
typically the viscous effect of turbulence in stars with a convective envelope and the
radiative damping for stars with a radiative envelope (Zahn 1977). A new expression for the tidal synchronization timescale due to a turbulent
medium has been proposed by Toledano et al. (2007),
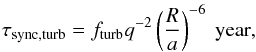 (1)where
a is the separation between the two components in a binary system,
fturb ~ 1 depends on the structure of the star. Equation (1)
can be applied to stars with an envelope hosting a strong turbulence due to convection and,
maybe, due to rotational instabilities, such as the horizontal turbulence proposed by Zahn
(1992). However, the adequation of this expression
to this last case is still under question, since the viscous effect of horizontal turbulence
is about eight orders of magnitude smaller than the viscosity of classical convection in
massive stars.
(1)where
a is the separation between the two components in a binary system,
fturb ~ 1 depends on the structure of the star. Equation (1)
can be applied to stars with an envelope hosting a strong turbulence due to convection and,
maybe, due to rotational instabilities, such as the horizontal turbulence proposed by Zahn
(1992). However, the adequation of this expression
to this last case is still under question, since the viscous effect of horizontal turbulence
is about eight orders of magnitude smaller than the viscosity of classical convection in
massive stars.
The dynamical synchronization timescale due to radiative damping for stars with a radiative
envelope, without the contribution of the equilibrium tide, has been given by (Zahn 1977),
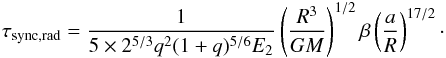 (2)Here,
q = M′/M
is the mass ratio, M′ is the mass of the companion star,
R and M are the radius and mass of the primary star
considered here, G is the gravity constant,
β = Ie/MR2
is the so-called gyration radius, Ie is the moment of inertia of
the external layers where tidal energy is dissipated, and E2 is
the tidal coefficient, which is sensitive to the structure of the star, in particular to the
size of the convective core. It can be expressed by (Yoon et al. 2010)
(2)Here,
q = M′/M
is the mass ratio, M′ is the mass of the companion star,
R and M are the radius and mass of the primary star
considered here, G is the gravity constant,
β = Ie/MR2
is the so-called gyration radius, Ie is the moment of inertia of
the external layers where tidal energy is dissipated, and E2 is
the tidal coefficient, which is sensitive to the structure of the star, in particular to the
size of the convective core. It can be expressed by (Yoon et al. 2010) 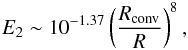 (3)where
Rconv is the convective-core radius.
(3)where
Rconv is the convective-core radius.
A comparison of the above two dissipation timescales (Eqs. (1) and (2)) for the turbulent and radiative cases has been performed by de Mink et al. (2009).
In the present work, the change of the spin angular momentum due to tidal interaction is
computed using Eq. (5.6) from Zahn (1977):
![\begin{eqnarray} \frac{{\rm d}I_{\rm e}\Omega}{{\rm d}t}=-3MR^{2}\Bigg(\Omega-\omega_{\rm{orb}}\Bigg)\Bigg(\frac{GM}{R^{3}}\Bigg)^{1/2}\Bigg[q^{2}\Bigg(\frac{R}{a}\Bigg)^{6}\Bigg]E_{2}s_{22}^{5/3}, \end{eqnarray}](/articles/aa/full_html/2013/08/aa21870-13/aa21870-13-eq15.png) (4)where
IeΩ is the angular momentum of the external layers where tidal
energy is dissipated, and Ω and ωorb are the angular velocity of
axial and orbital rotation, respectively. Tidal interactions spin the star down when
Ω > ωorb and up when
Ω < ωorb.
(4)where
IeΩ is the angular momentum of the external layers where tidal
energy is dissipated, and Ω and ωorb are the angular velocity of
axial and orbital rotation, respectively. Tidal interactions spin the star down when
Ω > ωorb and up when
Ω < ωorb.
Strictly speaking, the effect of tidal braking should be applied to the whole radiative envelope. Because some differential rotation is generally present, there may be some deviations from the above current expressions for tidal braking. However, some approximations are justified. In our current models, we treat a limited fraction of the outer layers (about 3% of the total mass) with the assumptions of constant chemical abundances Xi = const., constant luminosity L = const., and angular velocity Ω = const. These homogeneous outer layers of small-mass content may encompass about 30% of the total radius, which implies that about 92% of the total tidal effect (going like R6) is deposited in these layers (for a value of 20% of the radius, the deposited fraction would be 79%). This means that most of the energy dissipated by the tidal torque is deposited in the outer layers, where the angular velocity is taken as a constant. Therefore, the various approximations made in the models are internally consistent.
Assuming Ie and ωorb are constant
in Eq. (4), we can obtain, trot, the typical timescale for a
decrease by a factor e of the difference between Ω and ω,
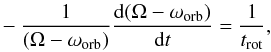 (5)with
(5)with
![\begin{eqnarray} \frac{1}{t_{\rm rot}}=3 \left(\frac{GM}{R^{3}}\right)^{1/2}\frac{MR^{2}}{I_{\rm e}}E_{2} \left[ q^{2} \left(\frac{R}{a}\right)^{6}\right]s_{22}^{5/3}. \end{eqnarray}](/articles/aa/full_html/2013/08/aa21870-13/aa21870-13-eq31.png) (6)The
synchronization rate
(6)The
synchronization rate 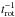 is a function of both the strength of the perturbing potential as measured by the quantity
in brackets
is a function of both the strength of the perturbing potential as measured by the quantity
in brackets ![\hbox{$[q^{2}(\frac{R}{a})^{6}]$}](/articles/aa/full_html/2013/08/aa21870-13/aa21870-13-eq33.png) , and of the tidal frequency
, and of the tidal frequency
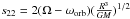 .
.
In the remainder of the paper, we shall trot, the synchronization timescale (implicitly estimated on the zero age main-sequence, ZAMS), while the time, given by our evolutionary models, in which Ω = ωorb is named the effective synchronization time. The two times may be quite different because they do not encompass the same physics: trot only accounts for the change of Ω due to the tidal interaction and is estimated for initial values on the ZAMS, while the synchronization time accounts for the changes with time of Ω − ωorb and for the evolutions with time of all the quantities involved in the expressions of trot, as well as for all the other processes (in addition to tidal interactions) that modify the surface angular velocity of the star (changes of the radius of the star and all the processes redistributing the angular momentum inside the star).
For a circular orbit, the orbital angular momentum of a binary with an orbital separation
a is given by ![\begin{eqnarray} J_{\rm{orb}}= M_{1}M_{2}\left[\frac{Ga}{M_{1}+M_{2}}\right]^{1/2}, \end{eqnarray}](/articles/aa/full_html/2013/08/aa21870-13/aa21870-13-eq37.png) (7)so
that
(7)so
that 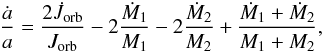 (8)where
a dot indicates time derivation.
(8)where
a dot indicates time derivation.
3. Internal transport of chemical elements and of angular momentum
3.1. Equation for angular momentum transport
The transport of angular momentum inside a star is implemented following the prescription
of Zahn (1992). This prescription was complemented
by Talon & Zahn (1997) and Maeder &
Zahn (1998). In the radial direction, it obeys the equation
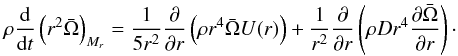 (9)The
first term on the right-hand side of this equation is the divergence of the advected flux
of angular momentum, while the second term is the divergence of the diffused flux.
D is the total diffusion coefficient in the vertical direction, taking
into account the various instabilities that transport angular momentum. The effects of
expansion or contraction are automatically included in a Lagrangian treatment. During the
evolution, central density increases and the core spins faster, the second term allows,
for example, the transport of angular momentum from the core to the surface. It will also
transmit the external braking to the interior of the star. The meridional circulation is
most efficient for such transports, its velocity was determined by Zahn (1992) and Maeder & Zahn (1998),
(9)The
first term on the right-hand side of this equation is the divergence of the advected flux
of angular momentum, while the second term is the divergence of the diffused flux.
D is the total diffusion coefficient in the vertical direction, taking
into account the various instabilities that transport angular momentum. The effects of
expansion or contraction are automatically included in a Lagrangian treatment. During the
evolution, central density increases and the core spins faster, the second term allows,
for example, the transport of angular momentum from the core to the surface. It will also
transmit the external braking to the interior of the star. The meridional circulation is
most efficient for such transports, its velocity was determined by Zahn (1992) and Maeder & Zahn (1998), ![\begin{eqnarray} U(r)&=& \frac{P}{\bar{\rho g} C_{\rm P} \bar{T}} \frac{1}{\left[ \nabla_{\rm{ad}} - \nabla_{\rm{rad}} + (\varphi/\delta) \nabla_\mu \right]}\nonumber\\ &&\times \left[ \frac{L(r)}{M_\star(r)} \left( E_\Omega^\star+ E_\mu \right) + \frac{C_{\rm P}}{\delta}\frac{\partial \Theta}{\partial t}\right], \end{eqnarray}](/articles/aa/full_html/2013/08/aa21870-13/aa21870-13-eq41.png) (10)where
CP is the specific heat at constant pressure,
(10)where
CP is the specific heat at constant pressure,
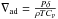 is the adiabatic gradient,
is the adiabatic gradient, 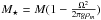 , and
, and
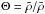 is the ratio of the variation
of the density to the average density on an equipotential. Both ϕ and
δ arise from the equation of state in the form
is the ratio of the variation
of the density to the average density on an equipotential. Both ϕ and
δ arise from the equation of state in the form
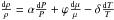 , and
EΩ and Eμ are
terms that depend on the Ω- and μ-distributions, respectively. The
quantities
, and
EΩ and Eμ are
terms that depend on the Ω- and μ-distributions, respectively. The
quantities 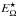 and
Eμ are given by (Maeder 2009)
and
Eμ are given by (Maeder 2009)
![\begin{eqnarray} E_\Omega^\star &=& 2 \Bigg[ 1-\frac{\bar{\Omega^{2}}}{2\pi G\bar{\rho}} - \frac{\bar{\epsilon}+\bar{\epsilon}_{\rm{grav}}}{\varepsilon_{m}}\Bigg] \frac{\tilde{g}}{\bar{g}}-\frac{\rho_{m}}{\bar{\rho}} \Bigg\{ \frac{r}{3} \frac{{\rm d}}{{\rm d}r}\Bigg[H_{\rm T}\frac{\rm d}{{\rm d}r}\Bigg(\frac{\Theta}{\delta}\Bigg) \nonumber\\ &&-\chi_{\rm T} \Theta + \Bigg(1-\frac{1}{\delta}\Bigg) \Theta \Bigg]-\frac{2H_{\rm T}}{r} \Bigg(\frac{\Theta}{\delta}\Bigg) + \frac{2}{3}\Theta \Bigg\} \nonumber \\ &&-\frac{\bar{\epsilon}+\bar{\epsilon}_{\rm{grav}}}{\epsilon_{m}} \Bigg[H_{\rm T}\frac{{\rm d}}{{\rm d}r}\Bigg(\frac{\Theta}{\delta}\Bigg)+\Bigg(f_{\epsilon}\epsilon_{\rm T}-\chi_{\rm T}\Bigg) \Bigg(\frac{\Theta}{\delta}\Bigg) \\\nonumber & &+\left(2-f_{\epsilon}-\frac{1}{\delta}\right)\Theta\Bigg], \end{eqnarray}](/articles/aa/full_html/2013/08/aa21870-13/aa21870-13-eq54.png) (11)with
(11)with
![\begin{eqnarray} E_{\mu}&=&\frac{\rho_{m}}{\bar{\rho}} \Bigg\{\frac{r}{3} \frac{\rm d}{{\rm d}r}\Bigg[H_{\rm T}\frac{\rm d}{{\rm d}r}(\frac{\varphi}{\delta}\Lambda)-\Bigg(\chi_{\mu}+\frac{\varphi}{\delta}\chi_{\rm T} +\frac{\varphi}{\delta}\Bigg)\Bigg] \Lambda \nonumber\\ &&-\frac{2H_{\rm T}}{r} \frac{\varphi}{\delta}\Lambda\Bigg\}+\frac{\bar{\epsilon}+\bar{\epsilon}_{\rm{grav}}}{\epsilon_{m}}\Bigg[H_{\rm T}\frac{\rm d}{{\rm d}r}\Bigg(\frac{\varphi}{\delta}\Lambda\Bigg)\nonumber\\ && +\Bigg(f_{\epsilon}\epsilon_{\mu}+f_{\epsilon}\frac{\varphi}{\delta}\epsilon_{\rm T}-\chi_{\mu}-\frac{\varphi}{\delta}\chi_{\rm T}-\frac{\varphi}{\delta}\Bigg) \Lambda\Bigg], \end{eqnarray}](/articles/aa/full_html/2013/08/aa21870-13/aa21870-13-eq55.png) (12)where
the quantities have the same significations as in Maeder & Zahn (1998). We have taken the same boundary conditions as
Talon et al. (1997; see also Denissenkov et al.
1999; Meynet & Maeder 2000).
(12)where
the quantities have the same significations as in Maeder & Zahn (1998). We have taken the same boundary conditions as
Talon et al. (1997; see also Denissenkov et al.
1999; Meynet & Maeder 2000).
3.2. Equation for the transport of chemical species
The horizontal turbulence competes efficiently with the advective term of meridional
circulation for transporting the chemical species (Chaboyer & Zahn 1992). The horizontal flow tends to homogenize the
layers in such a way that the resulting transport of chemical species by both meridional
circulation and horizontal turbulence can be computed as a diffusive process with the
coefficient Deff. The change of the abundance for a given
chemical element i in the shell with coordinate r is
thus (Zahn 1992)
![\begin{eqnarray} \rho \frac{{\rm d} X_i}{{\rm d} t} = \frac{1}{r^2} \frac{\partial}{\partial r} \Bigg[ \rho r^2 ( D + D_{\rm{eff}}) \frac{\partial X_i}{\partial r}\Bigg] + \Bigg( \frac{{\rm d} X_i}{{\rm d} t}\Bigg)_{\rm{nucl}}, \end{eqnarray}](/articles/aa/full_html/2013/08/aa21870-13/aa21870-13-eq59.png) (13)where
D is the same as in Eq. (9) and is the total diffusion coefficient in
the vertical direction, taking into account the instabilities that transport the chemical
elements. The last term accounts for the change in abundances produced by nuclear
reactions. We can then define an effective diffusion coefficient,
Deff that combines the effects of horizontal diffusion and
of the meridional circulation (Chaboyer & Zahn 1992),
(13)where
D is the same as in Eq. (9) and is the total diffusion coefficient in
the vertical direction, taking into account the instabilities that transport the chemical
elements. The last term accounts for the change in abundances produced by nuclear
reactions. We can then define an effective diffusion coefficient,
Deff that combines the effects of horizontal diffusion and
of the meridional circulation (Chaboyer & Zahn 1992), 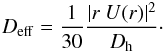 (14)We
have applied the shellular-rotation hypothesis, which postulates that in differentially
rotating stars the angular velocity Ω is constant on isobars. This results from the strong
horizontal turbulence, which is expected because there is no restoring force in the
horizontal (isobaric) direction, as the buoyancy force (the restoring force of the density
gradient) acts in the vertical direction. Zahn (1992) related the diffusion coefficient to the viscosity caused by horizontal
turbulence
(14)We
have applied the shellular-rotation hypothesis, which postulates that in differentially
rotating stars the angular velocity Ω is constant on isobars. This results from the strong
horizontal turbulence, which is expected because there is no restoring force in the
horizontal (isobaric) direction, as the buoyancy force (the restoring force of the density
gradient) acts in the vertical direction. Zahn (1992) related the diffusion coefficient to the viscosity caused by horizontal
turbulence 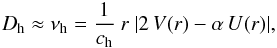 (15)where
ch is a constant on the order of 1,
V(r) is the horizontal component of the meridional
circulation velocity, U(r) its vertical component (see
Eq. (9)), and in this expression
(15)where
ch is a constant on the order of 1,
V(r) is the horizontal component of the meridional
circulation velocity, U(r) its vertical component (see
Eq. (9)), and in this expression 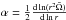 .
.
Differential rotation induces shear turbulence at the interface of layers that have
different rotational velocities. A layer remains stable if the excess of kinetic energy
due to differential rotation is inferior to the energy needed to overcome the stabilizing
density gradient in radiative zones (this is expressed by the Richardson
criterion). The effects of thermal dissipation, which reduce the buoyancy
force, are accounted for. The coefficient of diffusion by shear turbulence was determined
by Maeder (1997)
![\begin{eqnarray} D_{\rm{shear}} =f_{\rm{energ}} \frac{H_{\rm P}}{g\delta} \frac{K}{\Bigg[\frac{\varphi}{\delta}\nabla_\mu+ \Bigg( \nabla_{\rm{ad}} - \nabla_{\rm{rad}} \Bigg)\Bigg]} \Bigg(\frac{9\pi}{32}\ \Omega\ \frac{{\rm d} \ln \Omega}{{\rm d} \ln r} \Bigg)^2, \end{eqnarray}](/articles/aa/full_html/2013/08/aa21870-13/aa21870-13-eq66.png) (16)where
(16)where
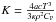 is the thermal diffusivity, and with fenergy ≈ 1, and
is the thermal diffusivity, and with fenergy ≈ 1, and
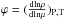 .
.
4. Physical ingredients of the models
The treatment of rotation was developed in a series of papers published previously by the Geneva group (Maeder 1999, 1997; Maeder & Meynet 2000; Maeder & Zahn 1998; Meynet & Maeder 1997, 2000; see also the recent review by Maeder & Meynet 2012).
The initial abundances of H, He, and metals were set to X = 0.720,
Y = 0.266, and Z = 0.014. The mixture of heavy elements
was that by Asplund et al. (2005) except for the Ne
abundance, which was taken from Cunha et al. (2006).
The nuclear reaction rates were generated with the NetGen tool1. They originate mainly from the Nacre database (Angulo et al. 1999), although some have been redetermined more recently
and have been updated (see Ekstr m
et al. 2012, for more details). The convective zones
were determined with the Schwarzschild criterion. For the H- and He-burning phases, the
convective core was extended by overshooting over a distance
dover = 0.10Hp, with
Hp the local pressure scale height.
m
et al. 2012, for more details). The convective zones
were determined with the Schwarzschild criterion. For the H- and He-burning phases, the
convective core was extended by overshooting over a distance
dover = 0.10Hp, with
Hp the local pressure scale height.
The evolution of a binary system consisting of a 15 and a 10 M⊙
star is investigated in this paper. We assumed that the orbit is circular and that the spin
axis of the model stars is perpendicular to the orbital plane. We focused on the evolution
of the primary star. From Eq. (8), assuming that the mass loss by stellar winds is
negligible before any mass transfer, one has for the cases considered here that
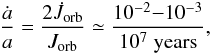 (17)therefore
the variation of the orbital separation between the two components is negligible and was
assumed to keep a constant value during the evolution of the binary system.
(17)therefore
the variation of the orbital separation between the two components is negligible and was
assumed to keep a constant value during the evolution of the binary system.
The evolution is followed from the onset of central H burning to the moment of Roche lobe overflow (RLOF). Starting from an initial solid-body rotation, we then calculated the evolution of the angular velocity inside the model, consistently accounting for the various transport mechanisms presented in Sect. 3 and for the tidal interactions between the two stars.
Unlike stellar winds, the tidal braking does not only spin down the star, but it may also spin it up. We modeled the tidal mixing in two series of evolutionary sequences:
-
Spin-down case: the orbital periods and the initial rota-tion velocities were chosen so that tidal interaction spinsthe primary down. The initial velocity was chosen asυini/υcrit = 0.6, υini is the equatorial surface velocity on the ZAMS and υcrit is the critical velocity at the same stage (the critical velocity is defined as the equatorial velocity such that the centrifugal acceleration exactly balances the gravity at the equator). The consequences of tidal braking were explored for different initial orbital periods ranging from 1.1 to 1.8 days. For comparison, a model starting with υini/υcrit = 0.6 on the ZAMS that does not account for tidal braking, was also computed.
-
Spin-up case: the orbital periods and the initial rotation velocities were chosen so that tidal interaction spins the primary up. The initial velocity was taken as υini/υcrit = 0.2. The initial orbital periods were chosen between 0.9 and 1.4 days. A model without tidal interaction with υini/υcrit = 0.2 was also computed.
5. Spin-down case: tidal braking
5.1. Impact on rotation
 |
Fig. 1 Evolution as a function of time of the surface equatorial velocity for a 15 M⊙ star with υini = 0.6υcrit and a 10 M⊙ companion for different initial orbital periods. The case without any tidal interaction is also shown. |
 |
Fig. 2 Variation of the angular velocity as a function of the radius in solar units. The continuous lines refer to the spin-down case with an orbital period equal to 1.8 days. The dashed curves correspond to the spin-down case with an orbital period equal to 1.1 days. Different ages are plotted with different colors as indicated in the inset, for both the continuous and dashed lines. The curve corresponding to an age of 119 000 years is the same for the model in the system with an orbital period P of 1.1 days and in the one with an orbital period of 1.8 days. |
The time evolution of the surface velocity is plotted for various orbital periods in Fig. 1. We see the rapid decrease of the velocities due to tidal braking. Synchronization is realized near the minimum of the curves. After that point, the angular velocity Ω at the surface is maintained approximately at the value imposed by the orbital angular velocity and thus remains constant. Because during the main-sequence phase the radii of the star progressively increase, the surface velocities also slightly increase after synchronization. From Fig. 1, we also see that
-
The surface velocity of tidally braked stars is much lower at a given age than the surface velocity of an isolated star starting its evolution on the ZAMS with the same initial velocity. This illustrates the well-known fact that for these orbital periods, the tidal interactions are very strong.
-
Synchronization timescales are shorter in orbital systems with shorter periods, because tidal torques are stronger.
-
At the time of synchronization, lower surface velocities are evidently obtained in systems with longer orbital periods.
The evolution of the angular velocity inside models of different ages and in systems with
various orbital periods is shown in Fig. 2 up to
4 × 106 yr. We can see in the model with an orbital period,
Porb = 1.1 days how tidal braking imposes an angular
velocity at the surface converging around 6.6 × 10-5 s
(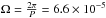 s) after about 1 million years. The same kind of convergence occurs in the various models,
but at later times. Clearly, the angular velocity is decreased everywhere in the interior
of the star by tidal braking, not only at the surface (compare the continuous and dashed
curves in Fig. 2, which show the differences due to different tidal torques; when the
braking is stronger, the core is also more strongly slowed down). This comes from the
coupling due mainly to meridional currents. Most interestingly, some gradient of Ω is
maintained in the star at the time of synchronization as a result of meridional
circulation, as discussed below.
s) after about 1 million years. The same kind of convergence occurs in the various models,
but at later times. Clearly, the angular velocity is decreased everywhere in the interior
of the star by tidal braking, not only at the surface (compare the continuous and dashed
curves in Fig. 2, which show the differences due to different tidal torques; when the
braking is stronger, the core is also more strongly slowed down). This comes from the
coupling due mainly to meridional currents. Most interestingly, some gradient of Ω is
maintained in the star at the time of synchronization as a result of meridional
circulation, as discussed below.
We may also compare the gradients of Ω in the models with and without tidal interactions (see Figs. 3 and 4). First, we note from Fig. 4 that at the beginning of the braking, the gradients of Ω are stronger in the tidally braked models. This will imply stronger mixing of the chemical elements before synchronization. Second, we see that after synchronization (after about 3.0 × 106 years), the gradients of Ω are shallower in the tidal braked models.
This last situation results from the interplay of many physical processes. Indeed, there is an impressive number of effects influencing Ω inside the models: the structural changes, the convective transport, the shear turbulence that tends to erode the Ω-gradients, the meridional circulation that can smooth or build the Ω-gradients up, the tidal effects that can remove or bring angular momentum. Mass loss can also remove angular momentum, especially when a magnetic field is present in outer layers. One of these effects may be dominant at a given moment at some point inside the star, while part of these effects or all can interact in other periods/regions of the star, so it is very difficult to identify a clear-cut cause for the shallower Ω-gradients in post-synchronized systems.
 |
Fig. 3 Variation of the angular velocity ([s-1]) as a function of the radius and age inside a 15 M⊙ model with υini/υcrit= 0.6 computed without tidal interaction. |
 |
Fig. 4 Same as Fig. 3 for a 15 M⊙ model with tidal braking. The companion is a 10 M⊙ star and the orbital period is 1.4 days. Note that the maximum radius is not coinciding with the total radius of the star, only a portion of the interior is represented. |
 |
Fig. 5 Amplitude of the vertical component of the meridional circulation velocity in cm per second in a 15 M⊙ model at various stages. The dashed lines correspond to a rotating model with υini = 0.6 υcrit and are computed without tidal interaction. The continuous lines show the situation when tidal interactions are accounted for, assuming a close companion of 10 M⊙ orbiting the primary with an initial period of 1.4 days. Different ages are plotted with different colors as indicated in the inset, for both the continuous and dashed lines. The different colors have the same meaning as in Fig. 2. |
We carefully examined the effects and behavior of the meridional circulation in relation with tidal effects. In Fig. 5, the variation as a function of the Lagrangian mass of U22 is shown for the spin-down Case with an initial orbital period of 1.4 days (the continuous lines). A negative value of U2(r) corresponds to a net transport of angular momentum from the core to the envelope. A positive value corresponds to the reverse situation, i.e., to a net transport of angular momentum from the envelope to the core. We see that at the beginning of evolution (curves for the ages 1 and 3 × 106 years in Fig. 5), the meridional circulation transports angular momentum from the core to the envelope. Thus, while tidal braking slows down the envelope, circulation tends to counteract this effect by accelerating it. After about 5 × 106 years, meridional circulation changes sign and the transport of angular momentum is from the envelope to the core, favoring the increase of the ratio between Ω in the core and that in the envelope at a time where synchronization tends to homogenize the internal rotation.
Comparing the variation of U2 in the models with and without tidal interaction, one sees important differences. In the model without tidal interaction, U2 is always very negative for the range of ages considered thus there is a net transport of angular momentum from the rapidly spinning core to the slowly rotating envelope. This process acts in the same direction as a diffusive process. In the model with tidal interactions, meridional circulation transports angular momentum from the core to the envelope in a first period until ~5 × 106 years, as in the model without tidal interaction, but with much higher negative velocities, as can be seen in Fig. 5. Then, as the circulation changes sign, the transport of angular momentum goes from the envelope to the core. This last process can no longer be modeled through a diffusive process. Thus, it is essential to describe circulation currents as an advective process.
This redistribution of the angular momentum inside the star by meridional circulation has consequences for the synchronization time. Since circulation tends to counteract the braking of the surface by the tidal torque, it increases the time needed for achieving synchronization. In Table 1, two times are indicated. In the second column trot is given for the various initial orbital periods and for ZAMS values. The third column shows the effective time at which Ω = ωorb as given by our evolutionary stellar models.
The values of trot are extremely short, much shorter than 1% of the main-sequence lifetime of a 15 M⊙ star. This is quite consistent with the very short timescales obtained by de Mink et al. (2009) and also with the very rapid decrease of the surface velocity shown in our models (see Fig. 1).
The effective time at which Ω = ωorb is much longer than trot by large factors greater than 70. The main reason for this is the outward transport of angular momentum by circulation, which counteracts tidal braking. It must be noted, however, that looking at Fig. 1, the decrease of the equatorial surface velocity is quite fast, and from an observational point of view the star may be considered as synchronized well before the time at which one has a strict equality Ω = ωorb. Thus, our results do not contradict the observed fact that all binaries of the sample of B-type stars observed by Abt et al. (2002) with periods shorter than 2.4 days (18 stars) are synchronized.
The main consequences of these findings are that
-
tidal braking has a strong impact on meridional currents, which inturn redistribute the angular momentum inside the star;
-
trot as defined above greatly underestimates the time needed for Ω to become equal to ωorb;
-
the gradient of Ω is not flat when synchronization is achieved.
Synchronization timescales, trot, as given by Eq. (6) for ZAMS values and using the moment of inertia of the whole star and time at which Ω = ωorb from the numerical models for 15 M⊙ starting with an initial equatorial velocity on the ZAMS equal to 390 km s-1.
 |
Fig. 6 Variation as a function of the Lagrangian mass coordinate of the shear diffusion coefficient in the radiative envelope of our 15 M⊙ model. The continuous lines refer to the spin down case with an initial orbital period of 1.8 days. The dashed lines show the case when the initial orbital period is equal to 1.1 days. The curves for the periods equal to 1.1 and 1.8 days, corresponding to an age of 119 000 years, are the same and thus are superposed. The different colors has the same significations as in Fig. 2. |
 |
Fig. 7 Variation as a function of time of the ratio in number at the surface of nitrogen to hydrogen for 15 M⊙ stellar models with (spin-down case) and without tidal interactions. The curves are labeled with the values of the initial orbital period. |
5.2. Impact on the chemical composition and evolutionary tracks
Vertical shear turbulence is the main driver for chemical mixing. We now consider see how the shear diffusion coefficient varies as a function of the Lagrangian mass coordinate in models with different tidal interactions (Fig. 6). At the beginning, the diffusion is quite low since the Ω-gradients are very faint. Then the braking produces a strong shear and the diffusion increases. One notes that after about 0.2 Myr, the shear diffusion coefficient is slightly higher in the model with the longer orbital period, indicating that stronger Ω-gradients are produced by tidal interactions in these systems. This probably comes from the fact that torques in longer-period systems are active over longer durations than in shorter-period systems.
As a result of the Ω-gradients induced by the tidal interactions, the surface becomes enriched in nitrogen (see Fig. 7). In stars with tidal braking a given enrichment is reached for higher values of the surface gravity than in single stars starting with the same initial rotation, indicating a much more efficient mixing. Interestingly enough, these models produce relatively high nitrogen abundances for high log g values, but low surface velocities (see Fig. 1). Thus, tidal mixing strongly changes the correlation between surface velocity, nitrogen abundance and surface gravity with respect to the correlations obtained in models without tidal mixing.
 |
Fig. 8 Variation as a function of time of the surface helium mass fraction for 15 M⊙ with (spin-down case) and without tidal interactions. The curves are labeled with the values of the initial orbital period. |
 |
Fig. 9 Variation as a function of the Lagrangian mass coordinate of the mass fraction of hydrogen in 15 M⊙ models with (spin-down case) and without tidal interaction at the same age during the main-sequence phase. Curves for different initial orbital periods are shown. |
 |
Fig. 10 Evolutionary tracks for 15 M⊙ models with (spin-down case) and without tidal interaction. Curves for different initial orbital periods are shown. For close binaries, only the part of the track corresponding to the period before the Roche lobe overflow is plotted. |
In Fig. 8, the analog of Fig. 7 is shown but for the surface enrichments in helium. One sees the same qualitative behavior as for nitrogen, but with smaller amplitudes that are likely not observable.
The different mixings undergone by the stars produce internal compositions that greatly differ at a given age. This can be seen in Fig. 9 where the variations of the mass fraction of hydrogen in our 15 M⊙ are shown at a given age for various efficiencies of the tidal braking. We see that in short-period systems, the hydrogen profiles is less affected than in longer period systems. This directly results from the point raised above, indicating that shear mixing is more efficient in longer-period systems.
The consequences of these various hydrogen compositions on the evolutionary tracks in the HR diagram can be seen in Fig. 10. All tracks with tidal interactions are shifted to the blue with respect to the track without tidal interaction. The longer the initial period, the greater the blueshift, consistent with stronger mixing in longer-period systems. The mass-age-luminosity relation is significantly influenced by tidal mixing, in the sense of an overluminosity for a given mass in the case of tidal braking.
6. Spin-up case: tidal acceleration
6.1. Impact on rotation
 |
Fig. 11 Evolution as a function of time of the surface equatorial velocity for a 15 M⊙ star with υini = 0.2υcrit and a 10 M⊙ companion for different initial orbital periods. The case without any tidal interaction is also shown. |
 |
Fig. 12 Variation of the angular velocity as a function of the radius in solar units. The continuous lines refer to the spin-up case with an orbital period equal to 1.4 days. The dashed curves correspond to the spin-up case with an orbital period equal to 1.0 days. Different ages are plotted with different colors as indicated in the inset, for both the continuous and dashed lines. The curves for the periods equal to 1.0 and 1.4 days, corresponding to an age of 113 000 years, are the same and thus are superposed. |
 |
Fig. 13 Same as Fig. 1 for a 15 M⊙ model with υini = 0.2 υcrit. The continuous lines show the situation when tidal interactions are accounted for assuming, a close companion of 10 M⊙ orbiting the primary with an initial period of 1.4 days. The dashed lines correspond to a rotating model computed without tidal interaction. The different colors have the same meaning as in Fig. 2. |
Now we discuss situations when the primary is spun up by tidal interactions. Figure 11 shows how the surface velocity varies as a function of time for tidal spin up. The models with tidal interactions rapidly become fast rotators under the influence of their companions. As expected, when the orbital period is short, the surface velocity increases very rapidly and reaches a high value.
The evolution of Ω inside different tidally spin-up models are shown in Fig. 12. We can see how tidal interaction forces the surface angular velocity to approach the value of the orbital velocity which is 7.26 × 10-6 s-1 for the system with an orbital period of 1.0 days, and 5.19 × 10-6 s-1, for the system with an orbital period of 1.4 days. These systems even reach Roche lobe overflow before they are synchronized.
We see that the gradient of Ω eventually increases slightly.
In Fig. 13, the radial component of the vertical velocity of meridional circulation is shown. During the whole period considered, circulation transports angular momentum from the envelope to the core. Thus, we obtain the same kind of general behavior for tidal spin up as for tidal spin down: meridional circulation counteracts the effect of the tidal interaction. When the surface is spun down, circulation tends to accelerate it, and when the surface is spun up, it tends to slow it down. Thus, for both tidal spin up and down, the synchronization times are increased due to the redistribution of the angular momentum inside the star by meridional circulation.
From Table 2, we see that the synchronization timescale trot is much shorter than the time at which the RLOF occurs. On the other hand, the RLOF occurs before the effective time when Ω = ωorb. That means that the values shown in the third column of Table 2 are a lower limit for the times t(Ω = ωorb). Thus we have a very similar situation as for spin down, where trot is much shorter than the time at which Ω = ωorb. In contrast, however, with the spin down case, here we cannot say that Ω converges very rapidly toward values near ωorb. It does therefore appear more difficult to reach synchronization in tidally spin-up systems.
The reason is likely that following ones an inward transport of a given mass carries more angular momentum than an outward transport of the same mass, because the specific angular momentum increases as a function of the distance to the center. Thus, it is easier for the circulation to slow down the surface when it is accelerated by the tidal interaction than for the opposite situation in the case of spin down.
Synchronization timescales trot as given by Eq. (6) for ZAMS values and using the moment of inertia of the whole star and time at which a RLOF occurs for 15 M⊙ starting with an initial equatorial velocity on the ZAMS equal to 130 km s-1.
 |
Fig. 14 Variation as a function of the Lagrangian mass coordinate of the shear diffusion coefficient in the radiative envelope of our 15 M⊙ model. The continuous lines refer to the spin-up case with an initial orbital period of 1.4 days. The dashed lines show the case when the initial orbital period is equal to 1.0 days. The curves for the periods equal to 1.0 and 1.4 days, corresponding to an age of 113 000 years, are the same and thus are superposed. The different colors have the same meaning as in Fig. 2. |
For of tidal spin-up, we also see that a proper advective treatment of meridional circulation is needed for the whole period. A diffusive treatment would not account for the direction of the transport of angular momentum at any moment and thus would even produce effects with the wrong sign. Incidentally, Fig. 13 also shows that the velocity of the circulation currents tends to decrease with time. This reflects the fact that the gradient of Ω eventually increases slightly (see Fig. 12).
 |
Fig. 15 Variation as a function of time of the ratio, in number, of nitrogen to hydrogen at the surface of a 15 M⊙ stellar model with (spin-up case) and without tidal interactions. The curves are labeled with the values of the initial orbital period. |
6.2. Impact on the chemical composition
Tidal acceleration boosts the shear diffusion and the surface nitrogen enrichments, as can be seen in Figs. 14 and 15. From Fig. 14, one sees that the shear diffusion coefficient is higher in shorter-period systems. This is the reverse of what is obtained in systems that are tidally spun down. In spin-down system, we had larger Dshear in longer-period systems as a result of a weaker, but longer active torque acting on the surface. In spin-up systems, we have higher Dshear in shorter-period systems as a result of a shorter active, but stronger torque acting on the surface.
As a consequence of the shears in tidally interacting systems, strong surface enrichments in nitrogen result, as can be seen in Fig. 15. A given nitrogen enhancement is obtained earlier, i.e., for lower surface gravity values in shorter-period systems. The surface helium enrichments reflect the same trend, but with limited amplitudes (see Fig. 16). The variations of the mass fraction of hydrogen are shown in Fig. 17. Consistently with other results, we see that for shorter initial periods, the effects of the tidal spinning up are stronger, again due the higher Ω-gradients.
The impact on the evolutionary tracks can be seen in Fig. 18. There is a shift of tidally accelerated models toward redder positions than for the model without tidal interaction for periods shorter than about 1.2–1.3 days. This is because globally the stars are rapidly spun up and the centrifugal acceleration becomes considerable. The centrifugal acceleration balances the gravity. This tends to make the star to follow an evolution corresponding to a lower initial mass, thus with a lower luminosity and a higher redshift. For the period 1.4 days, one sees that the track is only very slightly overluminous with respect to the track without tidal interaction. In that case, the hydrostatic effects and those of chemical mixing are more or less compensating for each other. This produces a track not far from the one computed without tidal interaction.
 |
Fig. 16 Variation as a function of time of the surface helium mass fraction for 15 M⊙ with (spin-up case) and without tidal interactions. The curves are labeled with the values of the initial orbital period. |
 |
Fig. 17 Variation as a function of the Lagrangian mass coordinate of the mass fraction of hydrogen in 15 M⊙ models with (spin-up case) and without tidal interaction at the same age during the main-sequence phase. Curves for different initial orbital periods are shown. |
 |
Fig. 18 Evolutionary tracks for 15 M⊙ models with (spin up case) and without tidal interaction. Curves for different initial orbital periods are shown. For close binaries, only the part of the track corresponding to the period before the Roche Lobe Overflow is plotted. |
7. Conclusions and observable consequences
From the above results, we can deduce some interesting general trends and consequences:
-
1)
At least up to the RLOF, the direction of the meridionalcirculation is always in a sense that counteracts the effects of thetidal interaction. Meridional currents are spinning up the surfacewhen it is braked down (spin-down case), and are braking it downwhen it is accelerated (spin-up case). This illustrates howcirculation is driven by what happens at the surface, tending torestore previous equilibrium. These trends seem to be a generalproperty of meridional circulation.
-
2)
To correctly model the effects of tidal interactions, a proper account of the transport of angular momentum by advection through meridional currents is essential.
-
3)
The effective time for obtaining Ω = ωorb may extend over periods that cover a significant fraction of the main-sequence lifetime.
-
4)
Whatever tides brake down the surface or spin it up, they boost the shear diffusion coefficient and the surface nitrogen enrichments.
-
5)
How these effects vary as a function of the initial period depends on whether tidal interactions brake down or spin up the star. For braking down, the effects obtained at the end of synchronization on the surface enrichments are enlarged when the initial period increases. The contrary occurs for tidal spin up.
From the point of view of possible interesting observable consequences of tidal interactions, we can note that
-
1)
Spin-up systems studied here encounter RLOF before they aresynchronized.
-
2)
The possibility through asteroseismology to probe the internal rotation rate of stars during their synchronization period or after synchronization (but before any RLOF) would provide extremely interesting constraints on the present models.
-
3)
Tidal braking produces stars that are strongly nitrogen-rich, rotate slowly and present a high surface gravity. This braking can be invoked to explain some slow, non-evolved rotators with strong nitrogen enrichment.
-
4)
Tidal spinning up may produce fast rotators before the RLOF episode. After RLOF, the loss of the envelope will probably slow down the star considerably. Thus it will be likely not possible to produce fast rotators after a homogeneous evolution through tidal interaction. The process can be initiated by tidal spin up but, at a given point, RLOF will stop it.
-
5)
In tidal spin up, part of the angular momentum acquired by the primary will be locked into the core due to the redistribution of the angular momentum. Is there any link with gamma-Ray bursts? This has to be studied in more detail in forthcoming works.
We note that the results would be very different if some process would force the star to rotate as a solid body in its interior (this might be caused for instance by a strong internal magnetic field). We can suspect that the results would be qualitatively similar to those obtained when a magnetic braking is applied at the surface of a solid body rotating star (Meynet et al. 2011): a very fast change of the surface velocity (short time for obtaining Ω = ω) and no tidal mixing during the synchronization period. This will be studied in a forthcoming paper.
Acknowledgments
This work was sponsored by Key Laboratory for the Structure and Evolution of Celestial Objects, Chinese Academy of Sciences, (Grant No. OP201107), the Key Foundation at Guizhou education department (No. 2010002). We thank Patrick Eggenberger for having made available his routine for the change of angular momentum in the outer layers and for very useful remarks helping to improve this paper. We are very grateful to Jean-Paul Zahn (referee) for his valuable suggestions and insightful remarks, which have improved this paper greatly.
References
- Abt, H. A., Levato, H., & Grosso, M. 2002, ApJ, 573, A359 [NASA ADS] [CrossRef] [Google Scholar]
- Angulo, C., & Descouvemont, P. 2001, Nucl. Phys. A, 690, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. T. G. Barnes, III, & F. N. Bash (San Francisco: ASP), ASPC, 336, 25 [Google Scholar]
- Chaboyer, B., & Zahn, J.-P. 1992, A&A, 253, 173 [NASA ADS] [Google Scholar]
- Cunha, K., Hubeny, I., & Lanz, T. 2006, ApJ, 647, L143 [NASA ADS] [CrossRef] [Google Scholar]
- de Jager, C., Nieuwenhuijzen, H., & van der Hucht, K. A. 1988, A&AS, 72, 259 [NASA ADS] [Google Scholar]
- Denissenkov, P. A., Ivanova, N. S., & Weiss, A. 1999, A&A, 341, 181 [NASA ADS] [Google Scholar]
- de Mink, S. E., Cantiello, M., Langer, N., et al. 2009, A&A, 497, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Mink, S. E., Langer, N., Izzard, R. G., et al. 2013, ApJ, 764, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Endal, A. S., & Sofia, S. 1976, ApJ, 210, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heap, S. R., Lanz, T., & Hubeny, I. 2006, ApJ, 638, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., & Langer, N. 2000, ApJ, 544, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., Langer, N., & Woosley, S. E. 2000, ApJ, 528, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, R. Q. 2004a, A&A, 422, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huang, R. Q. 2004b, A&A, 425, 591 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, I., Brott, I., Langer, N., et al. 2009, A&A, 496, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kippenhahn, R., & Thomas, H.-C. 1970, Stellar Rotation, Proc. IAU Colloq. 4, held at the Ohio State University, Columbus, Ohio, 8–11 September, 1969, ed. A. Slettebak (Gordon and Breach Science Publishers), 20 [Google Scholar]
- Langer, N. 1998, A&A, 329, 551 [NASA ADS] [Google Scholar]
- Langer, N., & Maeder, A. 1995, A&A, 295, 685 [NASA ADS] [Google Scholar]
- Maeder, A. 1997, A&A, 321, 134 [NASA ADS] [Google Scholar]
- Maeder, A. 1999, A&A, 347, 185 [NASA ADS] [Google Scholar]
- Maeder, A. 2003, A&A, 399, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars (Berlin, Heidelberg: Springer Verlag) [Google Scholar]
- Maeder, A., & Meynet, G. 2000, ARA&A, 38, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., & Meynet, G. 2001, A&A, 373, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maeder, A., & Meynet, G. 2005, A&A, 440, 1041 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maeder, A., & Meynet, G. 2012, Rev. Mod. Phys., 84, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., & Zahn, J.-P. 1998, A&A, 334, 1000 [NASA ADS] [Google Scholar]
- Mahy, L., Nazé, Y., Rauw, G., et al. 2009, A&A, 502, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., & Zahn, J.-P. 2004, A&A, 425, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., Palacios, A., & Zahn, J.-P. 2004, A&A, 425, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., & Maeder, A. 1997, A&A, 321, 465 [NASA ADS] [Google Scholar]
- Meynet, G., & Maeder, A. 2000, A&A, 361, 101 [NASA ADS] [Google Scholar]
- Meynet, G., Eggenberger, P., & Maeder, A. 2011, A&A, 525, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Przybilla, N., Firnstein, M., Nieva, M. F., Meynet, G., & Maeder, A. 2010, A&A, 517, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sana, H., de Koter, A., de Mink, S. E., et al. 2013, A&A, 550, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269 [Google Scholar]
- Song, H. F., Zhong, Z., & Lu, Y. 2009, A&A, 504, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Song, H. F., Lu, Y., & Wang, J. Z. 2011, PASJ, 63, 835 [NASA ADS] [Google Scholar]
- Talon, S., & Zahn, J.-P. 1997, A&A, 317, 749 [Google Scholar]
- Toledano, O., Moreno, E., Koenigsberger, G., Detmers, R., & Langer, N. 2007, A&A, 461, 1057 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walborn, N. R. 1976, IAUS, 72, 153 [NASA ADS] [Google Scholar]
- Yoon, S.-C., Woosley, S. E., & Langer, N. 2010, ApJ, 725, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J.-P. 1966, AnAp, 29, 489 [Google Scholar]
- Zahn, J.-P. 1975, A&A, 41, 329 [NASA ADS] [Google Scholar]
- Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS] [Google Scholar]
- Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
All Tables
Synchronization timescales, trot, as given by Eq. (6) for ZAMS values and using the moment of inertia of the whole star and time at which Ω = ωorb from the numerical models for 15 M⊙ starting with an initial equatorial velocity on the ZAMS equal to 390 km s-1.
Synchronization timescales trot as given by Eq. (6) for ZAMS values and using the moment of inertia of the whole star and time at which a RLOF occurs for 15 M⊙ starting with an initial equatorial velocity on the ZAMS equal to 130 km s-1.
All Figures
 |
Fig. 1 Evolution as a function of time of the surface equatorial velocity for a 15 M⊙ star with υini = 0.6υcrit and a 10 M⊙ companion for different initial orbital periods. The case without any tidal interaction is also shown. |
| In the text | |
 |
Fig. 2 Variation of the angular velocity as a function of the radius in solar units. The continuous lines refer to the spin-down case with an orbital period equal to 1.8 days. The dashed curves correspond to the spin-down case with an orbital period equal to 1.1 days. Different ages are plotted with different colors as indicated in the inset, for both the continuous and dashed lines. The curve corresponding to an age of 119 000 years is the same for the model in the system with an orbital period P of 1.1 days and in the one with an orbital period of 1.8 days. |
| In the text | |
 |
Fig. 3 Variation of the angular velocity ([s-1]) as a function of the radius and age inside a 15 M⊙ model with υini/υcrit= 0.6 computed without tidal interaction. |
| In the text | |
 |
Fig. 4 Same as Fig. 3 for a 15 M⊙ model with tidal braking. The companion is a 10 M⊙ star and the orbital period is 1.4 days. Note that the maximum radius is not coinciding with the total radius of the star, only a portion of the interior is represented. |
| In the text | |
 |
Fig. 5 Amplitude of the vertical component of the meridional circulation velocity in cm per second in a 15 M⊙ model at various stages. The dashed lines correspond to a rotating model with υini = 0.6 υcrit and are computed without tidal interaction. The continuous lines show the situation when tidal interactions are accounted for, assuming a close companion of 10 M⊙ orbiting the primary with an initial period of 1.4 days. Different ages are plotted with different colors as indicated in the inset, for both the continuous and dashed lines. The different colors have the same meaning as in Fig. 2. |
| In the text | |
 |
Fig. 6 Variation as a function of the Lagrangian mass coordinate of the shear diffusion coefficient in the radiative envelope of our 15 M⊙ model. The continuous lines refer to the spin down case with an initial orbital period of 1.8 days. The dashed lines show the case when the initial orbital period is equal to 1.1 days. The curves for the periods equal to 1.1 and 1.8 days, corresponding to an age of 119 000 years, are the same and thus are superposed. The different colors has the same significations as in Fig. 2. |
| In the text | |
 |
Fig. 7 Variation as a function of time of the ratio in number at the surface of nitrogen to hydrogen for 15 M⊙ stellar models with (spin-down case) and without tidal interactions. The curves are labeled with the values of the initial orbital period. |
| In the text | |
 |
Fig. 8 Variation as a function of time of the surface helium mass fraction for 15 M⊙ with (spin-down case) and without tidal interactions. The curves are labeled with the values of the initial orbital period. |
| In the text | |
 |
Fig. 9 Variation as a function of the Lagrangian mass coordinate of the mass fraction of hydrogen in 15 M⊙ models with (spin-down case) and without tidal interaction at the same age during the main-sequence phase. Curves for different initial orbital periods are shown. |
| In the text | |
 |
Fig. 10 Evolutionary tracks for 15 M⊙ models with (spin-down case) and without tidal interaction. Curves for different initial orbital periods are shown. For close binaries, only the part of the track corresponding to the period before the Roche lobe overflow is plotted. |
| In the text | |
 |
Fig. 11 Evolution as a function of time of the surface equatorial velocity for a 15 M⊙ star with υini = 0.2υcrit and a 10 M⊙ companion for different initial orbital periods. The case without any tidal interaction is also shown. |
| In the text | |
 |
Fig. 12 Variation of the angular velocity as a function of the radius in solar units. The continuous lines refer to the spin-up case with an orbital period equal to 1.4 days. The dashed curves correspond to the spin-up case with an orbital period equal to 1.0 days. Different ages are plotted with different colors as indicated in the inset, for both the continuous and dashed lines. The curves for the periods equal to 1.0 and 1.4 days, corresponding to an age of 113 000 years, are the same and thus are superposed. |
| In the text | |
 |
Fig. 13 Same as Fig. 1 for a 15 M⊙ model with υini = 0.2 υcrit. The continuous lines show the situation when tidal interactions are accounted for assuming, a close companion of 10 M⊙ orbiting the primary with an initial period of 1.4 days. The dashed lines correspond to a rotating model computed without tidal interaction. The different colors have the same meaning as in Fig. 2. |
| In the text | |
 |
Fig. 14 Variation as a function of the Lagrangian mass coordinate of the shear diffusion coefficient in the radiative envelope of our 15 M⊙ model. The continuous lines refer to the spin-up case with an initial orbital period of 1.4 days. The dashed lines show the case when the initial orbital period is equal to 1.0 days. The curves for the periods equal to 1.0 and 1.4 days, corresponding to an age of 113 000 years, are the same and thus are superposed. The different colors have the same meaning as in Fig. 2. |
| In the text | |
 |
Fig. 15 Variation as a function of time of the ratio, in number, of nitrogen to hydrogen at the surface of a 15 M⊙ stellar model with (spin-up case) and without tidal interactions. The curves are labeled with the values of the initial orbital period. |
| In the text | |
 |
Fig. 16 Variation as a function of time of the surface helium mass fraction for 15 M⊙ with (spin-up case) and without tidal interactions. The curves are labeled with the values of the initial orbital period. |
| In the text | |
 |
Fig. 17 Variation as a function of the Lagrangian mass coordinate of the mass fraction of hydrogen in 15 M⊙ models with (spin-up case) and without tidal interaction at the same age during the main-sequence phase. Curves for different initial orbital periods are shown. |
| In the text | |
 |
Fig. 18 Evolutionary tracks for 15 M⊙ models with (spin up case) and without tidal interaction. Curves for different initial orbital periods are shown. For close binaries, only the part of the track corresponding to the period before the Roche Lobe Overflow is plotted. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


