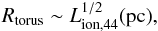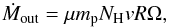| Issue |
A&A
Volume 587, March 2016
|
|
|---|---|---|
| Article Number | A129 | |
| Number of page(s) | 20 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201527808 | |
| Published online | 02 March 2016 | |
Anatomy of the AGN in NGC 5548
VI. Long-term variability of the warm absorber
1
XMM-Newton Science
Operations Centre, ESAC, Camino Bajo del Castillo s/n, Urb. Villafranca del Castillo,
28692 Villanueva de la Cañada, Madrid, Spain
e-mail:
jebrero@sciops.esa.int
2
SRON Netherlands Institute for Space Research,
Sorbonnelaan 2, 3584 CA
Utrecht, The
Netherlands
3
Leiden Observatory, Leiden University,
PO Box 9513, 2300 RA
Leiden, The
Netherlands
4
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD
21218,
USA
5
Department of Physics and Astronomy, The Johns Hopkins
University, Baltimore, MD
21218,
USA
6
Dipartimento di Matematica e Fisica, Università degli Studi Roma
Tre, via della Vasca Navale
84, 00146
Roma,
Italy
7
INAF–IASF Bologna, via Gobetti 101, 40129
Bologna,
Italy
8
Department of Astronomy, University of Geneva,
16 Ch. d’Ecogia, 1290
Versoix,
Switzerland
9
Mullard Space Science Laboratory, University College
London, Holmbury St. Mary,
Dorking, Surrey,
RH5 6NT,
UK
10
University Grenoble Alpes, IPAG, 38000
Grenoble,
France
11
CNRS, IPAG, 38000
Grenoble,
France
12
Max-Planck-Institut für Extraterretrische Physik,
Giessenbachstrasse,
85748
Garching,
Germany
13
Astronomisches Institut, Ruhr-Universität Bochum,
Universitätstrasse 150, 44801
Bochum,
Germany
14
Department of Physics, 192-0397 Tokyo Metropolitan
University, 1-1 Minami-Osawa,
Hachioji, 192-0397
Tokyo,
Japan
15
Instituto de Astronomía, Universidad Católica del
Norte, Avenida Angamos 0610,
Casilla 1280, Antofagasta, Chile
Received: 23 November 2015
Accepted: 5 January 2016
Context. We observed the archetypal Seyfert 1 galaxy NGC 5548 in 2013−2014 in the context of an extensive multiwavelength campaign involving several satellites, which revealed the source to be in an extraordinary state of persistent heavy obscuration.
Aims. We re-analyzed the archival grating spectra obtained by XMM-Newton and Chandra between 1999 and 2007 in order to characterize the classic warm absorber (WA) using consistent models and up-to-date photoionization codes and atomic physics databases and to construct a baseline model that can be used as a template for the physical state of the WA in the 2013 observations.
Methods. We used the latest version of the photoionization code CLOUDY and the SPEX fitting package to model the X-ray grating spectra of the different archival observations of NGC 5548.
Results. We find that the WA in NGC 5548 is composed of six distinct ionization phases outflowing in four kinematic regimes. The components seem to be in the form of a stratified wind with several layers intersected by our line of sight. Assuming that the changes in the WA are solely due to ionization or recombination processes in response to variations in the ionizing flux among the different observations, we are able to estimate lower limits on the density of the absorbing gas, finding that the farthest components are less dense and have a lower ionization. These limits are used to put stringent upper limits on the distance of the WA components from the central ionizing source, with the lowest ionization phases at several pc distances (<50, <20, and <5 pc, respectively), while the intermediately ionized components lie at pc-scale distances from the center (<3.6 and <2.2 pc, respectively). The highest ionization component is located at ~0.6 pc or closer to the AGN central engine. The mass outflow rate summed over all WA components is ~0.3 M⊙ yr-1, about six times the nominal accretion rate of the source. The total kinetic luminosity injected into the surrounding medium is a small fraction (~0.03%) of the bolometric luminosity of the source. After adding the contribution of the UV absorbers, this value augments to ~0.2% of the bolometric luminosity, well below the minimum amount of energy required by current feedback models to regulate galaxy evolution.
Key words: X-rays: galaxies / galaxies: active / galaxies: Seyfert / galaxies: individual: NGC 5548 / techniques: spectroscopic
© ESO, 2016
1. Introduction
Active galactic nuclei (AGN) are powered by gravitational accretion of matter on to the central supermassive black hole (SMBH) that resides in their center (Rees 1984), emitting vast amounts of energy across the spectrum. X-ray emission is a characteristic feature of AGN spectra and finds its origin in the inverse Compton scattering of lower energy photons in a hot corona in the vicinity of the SMBH (e.g., Sunyaev & Titarchuk 1980; Haardt & Maraschi 1993). With the advent of medium- and high-resolution X-ray spectroscopy, it was discovered that absorption lines of photoionized species blueshifted with respect to the systemic velocity of the host galaxies (Kaastra et al. 2000), were present in the soft X-ray spectra of more than 50% of nearby Seyfert 1 galaxies (Reynolds 1997; George et al. 1998). This so-called warm absorber (WA) typically shows multiple ionization phases with temperatures ~104−106 K, column densities ranging from 1020−1024 cm-2, and outflow velocities of a few hundred to thousands of km s-1 (e.g., Blustin et al. 2005).
While their ubiquity suggests that WA are an important structural feature in AGN, their contribution as sources of cosmic feedback (the relation between the SMBH growth and star formation in the host galaxy) has been a matter of debate for many years. Recent studies seem to indicate that the contribution of WA with low-to-moderate velocities is negligible in terms of feedback, with the exception of the so-called ultra-fast outflows (UFOs), which would be able to carry enough momentum to be a significant source of feedback (see Tombesi et al. 2013, and references therein). Current models show that kinetic luminosities (kinetic energy carried by the outflow per unit time) ranging between 0.5% and 5% of the bolometric luminosity (Di Matteo et al. 2005; Hopkins & Elvis 2010) must be fed back in order to significantly affect the interstellar medium (ISM) of the galaxy and reproduce the observed M − σ relation (Ferrarese & Merritt 2000; Gebhardt et al. 2000).
A key parameter for reliably estimating the mass outflow rate (hence the kinetic luminosity injected into the ISM) is the actual location of the WA. Current scenarios for the origin of these ionized outflows are: (i) disk-driven winds, which are launched within hundreds of gravitational radii (Murray & Chiang 1995; Elvis 2000); and (ii) thermal winds evaporating from an irradiated dusty torus that surrounds the AGN engine, which lie at pc-scale distances (Krolik & Kriss 2001). Ideally, tight limits can be put on the distance by measuring variability on the ionization properties of the WA in response to changes in the incident ionizing flux (e.g., Detmers et al. 2008; Longinotti et al. 2010; Kaastra et al. 2012). High-density gas will ionize/recombine faster than low-density gas, allowing us to determine reliable lower limits to the density and hence strict upper limits on the distance where this gas crosses our line of sight. This is, however, very challenging because the observations of a given object are often sparse, washing out the possible effects of variability, and lacking the signal-to-noise ratio required to significantly measure the expected changes.
NGC 5548 is an archetypal Seyfert-1 galaxy (MBH = 3.24 × 107M⊙, Pancoast et al. 2014), the first in which narrow absorption lines in the X-rays were detected (Kaastra et al. 2000). Since then, its ionized outflow has been widely studied, both in the X-rays (Kaastra et al. 2002; Steenbrugge et al. 2005, 2003, 2005; Detmers et al. 2008, 2009; Krongold et al. 2010; Andrade-Velázquez et al. 2010) and in the ultraviolet (Crenshaw & Kraemer 1999; Brotherton et al. 2002; Arav et al. 2002; Crenshaw et al. 2003, 2009).
Following the success of the multiwavelength campaign on Mrk 509 (introduced in Kaastra et al. 2011), NGC 5548 was observed extensively in 2013−2014 in the context of a large dedicated multiwavelength campaign led by XMM-Newton, comprising also observations with Chandra, NuSTAR, INTEGRAL, HST-COS, and including Swift monitoring, with the objective of characterizing the properties of the WA with unprecedented detail. An overview of the campaign can be found in Mehdipour et al. (2015; Paper I). Interestingly, the soft X-ray flux of NGC 5548 during the campaign was remarkably low, about 25 times lower than the median flux of the source in previous observations. Our analysis suggests that this is caused by a long-lasting stream of obscuring material situated at light-day distances, partially covering the X-ray source and the broad line region (BLR), as reported in Kaastra et al. (2014).
This paper is organized as follows. In Sect. 2 we briefly summarize the motivation for the re-analysis of the grating X-ray spectra of NGC 5548, and the observations used in this paper. In Sect. 3 we describe the analysis of the data, while in Sect. 4 we discuss the results. Our conclusions are reported in Sect. 5. Throughout this paper we assume a cosmological framework with H0 = 70 km s-1 Mpc-1, ΩM = 0.3, and ΩΛ = 0.7. The quoted errors refer to 68.3% confidence level (ΔC = 1 for one parameter of interest) unless otherwise stated.
2. NGC 5548 revisited
2.1. Motivation
The reasons to carry out a comprehensive re-analysis of the archival high-resolution grating spectra of NGC 5548 are two-fold. The main consequence of the extraordinary obscuration observed during the 2013 campaign (Kaastra et al. 2014) is the depression of the soft X-ray continuum, which makes the detection of WA features very challenging, although it gives us an excellent opportunity to study the X-ray emission of the narrow line region (NLR) of a Seyfert 1 galaxy with unprecedented detail (Whewell et al. 2015). The depressed X-ray flux is not intrinsically low, since the hard X-ray continuum is comparable to the historical fluxes of NGC 5548 in that energy band, but it is caused by the presence of obscuring material crossing our line of sight. Moreover, according to Swift monitoring, this obscuration has lasted since at least February 2012 (Mehdipour et al. 2016). An analysis of the data from our multiwavelength campaign reveals that the obscurer, possibly in the form of a clumpy stream of gas, is located within a few light days of the central SMBH, extending to outside of the BLR but closer in than the expected location of the WA (Kaastra et al. 2014). The ionizing photons that reach the WA are therefore severely diminished.
By comparing the properties of the WA with those measured earlier, we can take advantage of this unexpected situation to measure the response of the ionized gas, giving us an opportunity to constrain the location of the WA components with unprecedented accuracy. This, however, poses an important problem as very few counts are left in the soft X-ray spectrum (where the bulk of the WA features lie) in spite of the large exposure time (~660 ks with XMM-Newton RGS at the core of the campaign). Our strategy to model the WA during 2013 relied on the assumption that most of the parameters of the classic persistent WA outflow will remain the same with respect to the archival observations, at least the number of components, their outflow velocity, broadening of the lines and, possibly, their column density. If one gets an accurate characterization of the WA from past observations, this baseline model can then be applied to the obscured spectrum of NGC 5548, dramatically decreasing that number of free parameters that would prevent a spectral analysis otherwise.
NGC 5548 archival observations log.
 |
Fig. 1 Stability curves obtained with different versions of XSTAR and CLOUDY (black solid line, CLOUDY v13; black dot-dashed line, CLOUDY v98; red dashed line, XSTAR v1; red dotted line, XSTAR v2.2.1bk) for the same input spectral energy distribution. The solid dots represent the WA components of Steenbrugge et al. (2005). |
Our second motivation stems from the fact that different atomic physics codes were used to derive the WA properties reported in the literature. The ionization state of the WA components is usually computed using a photoionization code that calculates the transmission through a slab of material where all ionic column densities are linked through a photoionization balance model. Previous modeling of the NGC 5548 WA made use of XSTAR1 (Kallman & Krolik 1999) or CLOUDY2 (Ferland et al. 2013), which use slightly different atomic physics databases. Furthermore, since past observations of NGC 5548 span many years, the published WA parameters are computed using different versions of these codes, which evolve and are updated with time.
Differences between photoionization codes and versions of codes are not negligible. To illustrate this, in Fig. 1 we show four stability curves obtained from the output ionization balance provided by different versions of XSTAR and CLOUDY. In all cases the input spectral energy distribution (SED) was that of NGC 5548 reported by Steenbrugge et al. (2005). While the four lines agree reasonably well at low ionization values, the differences between them are dramatic for higher values of the ionization parameter ξ. In particular, the ionization balance used by Steenbrugge et al. (2005), computed with XSTAR v1, lacks several unstable areas (the branches with negative slope) and the Compton shoulder at high temperatures. Even the more recent versions of CLOUDY and XSTAR (v13 and v2.2.1, respectively), although they reproduce the same overall shape reasonably well, show strong deviations with respect to each other. The solid dots overplotted on top of the curves represent the positions where the WA components detected by Steenbrugge et al. (2005) fall, showing that a fit to the same spectrum with such different ionization balances provide significantly different ionization parameter ξ values.
Therefore, in order to obtain a comprehensive picture of the WA properties that can be used as a template for the 2013−2014 campaign as well as consistent parameter values, it is essential to re-analyze the archival grating spectra of NGC 5548 using the same, and most up-to-date, photoionization code for all of them.
2.2. Archival data
We used a total of 12 Chandra and XMM-Newton individual archival observations in this paper. In some cases, the observations were taken in consecutive orbits and with the same instrumental configuration, allowing us to co-add the spectra in order to obtain a better signal-to-noise ratio. Below we briefly describe each of the observations. The observations log is shown in Table 1.
Prior to the 2013 campaign, NGC 5548 was observed three times by XMM-Newton, once in 2000 (ObsID 0109960101) for 26.1 ks, and twice in 2001 (ObsIDs 0089960301 and 0089960401) for ~96 and 36 ks, respectively. In this paper we used solely the Reflection Grating Spectrometer (RGS, den Herder et al. 2001) data, that were processed using the XMM-Newton Science Analysis System (SAS) v13.5 (Gabriel et al. 2004). The data were rebinned by a factor of 3 to avoid oversampling. In what follows, the RGS spectra will be identified in the paper as R00x, R01y, and R01z, respectively.
There are nine archival observations of NGC 5548 taken with the gratings onboard Chandra, seven with the Low Energy Transmission Grating Spectrometer (LETGS, Brinkman et al. 2000) and two with the High Energy Grating Spectrometer (HETGS, Canizares et al. 2005). The HETGS/ACIS-S spectra were extracted from the TGCat archive3. The data were binned by a factor of two, and the Gehrels-statistic used by default in HETGS data was replaced by the true Poissonian error. In order to obtain consistent results for the MEG and HEG gratings, the MEG fluxes were scaled by a factor of 0.954 relative to the HEG fluxes. The observations were performed in 2000, with an exposure of 82 ks, and in 2002 as part of an UV/X-ray campaign with an exposure of 153 ks (Steenbrugge et al. 2005). Throughout this paper these observations will be identified as H00 and H02, respectively.
The LETGS/HRC-S spectra were reduced using the Chandra Interactive Analysis of Observations software (CIAO, Fruscione et al. 2006) v4.5, until the level 1.5 event files were created. The rest of the procedure, until the creation of the final level 2 event files, was performed following an independent method first reported in Kaastra et al. (2002). This results in an improved wavelength accuracy determination and effective area generation. NGC 5548 was observed with Chandra LETGS once in 1999 for 86 ks (labeled as L99 hereafter), and twice in 2002, 2005, and 2007. In the latter three cases the observations were taken in consecutive orbits, allowing us to co-add the two spectra to obtain a higher signal-to-noise. Therefore, we ended up with a ~340 ks spectrum in 2002, ~141 ks in 2005, and ~138 ks in 2007, that are labeled throughout the paper as L02, L05, and L07, respectively.
3. Data analysis
3.1. Strategy
The archival observations of NGC 5548 sum up to ~1.1 Ms of exposure time of grating spectra, although with great disparity in data quality among the different datasets. A modeling strategy that makes the most of this large amount of data is therefore required in order to maximize the scientific return. On one hand, fits to the individual observations in which all the parameters are left free would lead to too large error bars for most of the relevant parameters, or in those observations with a low S/N in completely unconstrained values. On the other hand, a joint fit of all the spectra together (3 RGS, 2 HETGS, and 4 LETGS) is not feasible, as it requires a prohibitive amount of computing time due to the large number of data channels and models that need to be evaluated together.
We therefore adopted a mixed approach for modeling these data. Since the 2002 data constitute the bulk of the archival data (~500 ks taking the L02 and H02 observations together), and they are dominant in terms of S/N contribution, we used them to create a model template for the rest of the archival observations. We first obtained a best-fit model for the 2002 data, including the continuum, broad and narrow emission lines, radiative recombination continua (RRCs), and absorption troughs produced by the WA (see the detailed modeling in Sect. 3.2). This best-fit model was then used as a starting point to analyze the rest of the archival spectra, leaving as free parameters only those of the continuum, the flux of the O vii forbidden line, and the ionization parameter log ξ of each WA component. The O vii forbidden line flux was set free since it is known to vary (Detmers et al. 2009), whereas the rest of the lines are too weak to measure significant changes or are not even significantly detected (partially due to the wavenlength coverage, partially due to the lower S/N). Therefore, all other parameters describing the emission lines as well as the absorption lines (NH, outflow velocity, velocity broadening) are kept frozen.
With this strategy we aim at determining the most relevant parameters that are known to vary between observations, such as the spectral shape of the continuum and the WA ionization parameter. The dynamics of the persistent outflows in NGC 5548 have barely changed over ~20 years, i.e. the different kinematic components can be easily cross-identified between the different observations, but their ionization state can be substantially different. We therefore assume that the observed variations in the WA are mainly due to ionization changes rather than being caused by the dissapearance of any of these outflows, or the appearance of newer ones.
3.2. Modeling
The archival grating spectra of NGC 5548 were analyzed using the SPEX fitting package4 version 2.05 (Kaastra et al. 1996). The fitting method was C-statistics (Cash 1979). The adopted cosmological redshift for NGC 5548 was z = 0.017175 (de Vaucouleurs et al. 1991). The foreground Galactic column density was set to NH = 1.45 × 1020 cm-2 (Wakker et al. 2011) using the hot model in SPEX, with the temperature fixed to 0.5 eV to mimic a neutral gas. Throughout the analysis we assumed proto-Solar abundances of Lodders & Palme (2009).
3.2.1. The Chandra 2002 spectra
As mentioned in Sect. 3.1, we modeled the L02 and H02 datasets in order to obtain a baseline model template that could be used as a starting point to analyze the remaining archival spectra. The methodology reported below was firstly described in the supplementary material of Kaastra et al. (2014). The fits were carried out in the 2−60 Å range for the LETGS spectrum, and in the 1.55−15.5 Å and 2.5−26 Å range for the HEG and MEG spectra, respectively. The continuum was modeled with a power law plus a modified black body (mbb model in SPEX), which considers modifications of a simple black body model by coherent Compton scattering based on the calculations of Kaastra & Barr (1989).
Superimposed to the continuum we added four broad emission lines, modeled with Gaussians, representing the 1s−2p and 1s−3p transitions of O vii, and the 1s−2p transition of O viii and C vi. Their parameter values were taken from the previous analysis of these datasets by Steenbrugge et al. (2005). In addition to them we included a set of narrow emission lines, namely the He-like triplets of Ne ix, O vii, and N vi, the forbidden line of the He-like C v, and the 1s−2p transitions of Ne x and N vii, as well as radiative recombination continua (RRCs). With the exception of the forbidden lines of O vii and C v, these lines are difficult to detect in the L02 and H02 spectra. Therefore we fixed their normalization to the values obtained in the 2013 campaign (Whewell et al. 2015), where the lines are clearly visible against the strongly obscured continuum. The narrow lines and RRCs are convolved with a velocity dispersion of σv = 463 km s-1 (see the supplementary material in Kaastra et al. 2014). For further information we point the reader to Whewell et al. (2015), who present a detailed analysis of the narrow lines and RRCs in NGC 5548.
 |
Fig. 2 Spectral energy distribution of NGC 5548. Data points are those of Steenbrugge et al. (2005). |
Continuum best-fit parameters of the 2002 observations.
The WA was modeled using the xabs model in SPEX, which calculates the transmission of a slab of material where all the ionic column densities are linked through a photoionization balance model. As shown in Sect. 2.1, the choice of the photoionization code that computes this model is critical. Here we used CLOUDY version 13.01, and we provided as input the spectral energy distribution (SED) of Steenbrugge et al. (2005; see Fig. 2). The output photoionization balance was provided to SPEX to fit the absorption troughs caused by an intervening WA. Since Steenbrugge et al. (2005) used an older version of their photoionization code, we looked for further WA components that might have remained undetected in their analysis.
We started from the four WA components reported in Steenbrugge et al. (2005), and added additional xabs components on a one-by-one basis until the fit no longer improved. The xabs free parameters were the ionization parameter log ξ, the hydrogen column density NH, the outflow velocity vout, and the Gaussian turbulent velocity σv, while the covering factor was fixed to unity. The ionization parameter ξ is a measure of the ionization state of the gas, and it is defined as
where L is the ionizing luminosity in the 1−1000 Ryd range, n is the hydrogen density of the gas, and R is the distance of the gas to the ionizing source.
The L02 and H02 spectra were fit simultaneously, but we allowed the power law and modified black body parameters to be different for each dataset (to account for continuum variability), as well as the ionization parameters log ξ of the WA (to account for possible short-term variations, as the observations were taken 3.5 days apart). The rest of the parameters were coupled so that they had the same values for both datasets. We assumed that the WA components absorb the continuum and the broad emission lines, but not the narrow emission lines and RRCs.
We found that the WA in NGC 5548 is composed of six distinct ionization phases, labeled from A to F in order of increasing ionization. The final C-stat/d.o.f. was 2402/2090 for L02, and 2890/2560 for H02. The best-fit values of the joint L02 and H02 analysis are reported in Tables 2−4. The log ξ values of these observations presented here differ from those shown in Table S2 in the supplementary material of Kaastra et al. (2014) by ~0.25 dex due to a bug in CLOUDY, which caused the ionizing flux to be calculated in the 1−∞ range instead of the conventional range of 1−1000 Ryd. The L02 spectrum together with the best-fit model are shown in Fig. 3.
Emission features best-fit parameters of the 2002 observations.
Warm absorber best-fit parameters of the 2002 observations.
3.2.2. The remaining archival spectra
 |
Fig. 3 Chandra LETGS spectrum of NGC 5548 in 2002 (L02). The solid red line represents our best-fit model. Some relevant WA absorption features have been labeled. |
After obtaining a best-fit model for the 2002 Chandra spectra, we used it as a template for modeling the remaining archival datasets. As we mentioned in Sect. 3.1, we left as free parameters in the fits only the continuum parameters (power law and modified black body emission), the flux of the narrow O vii forbidden emission line, and the ionization parameter of each WA component. The remaining parameters were kept fixed to those obtained in the joint fit of the L02 and H02 datasets. In modeling the WA, the ionization balance used as input by xabs was based on the SED of Steenbrugge et al. (2005), because it is the one with a wider contemporaneous frequency coverage. We therefore adopted it as a template SED for the rest of the archival observations. We note that, although ideally one would need to derive a SED for each of the individual observations, the assumption of a template SED will not significantly affect the xabs parameters determination. In the absence of huge spectral changes (such as those originated by obscuration events), the different SEDs may change their normalization due to the intrinsic variability of the source but not their shape, which is the key factor in computing the xabs parameters. The best-fit results are shown in Table 5.
The ionization structure of the WA in NGC 5548 depicted in the 2002 Chandra observations, showing six distinct ionization components, is also seen in the rest of the archival datasets. In some cases, some of the components are either not detected or are blended with other components due to a poor signal-to-noise ratio of the spectrum. This is the case for R00x (very short exposure, ~26 ks) or L07 (very low intrinsic flux). A more detailed view of the parameter variability between the different archival observations is discussed in Sect. 4.
Best-fit parameters of the remaining archival observations.
4. Discussion
4.1. Spectral properties
The archival observations of NGC 5548 span almost 8 years, with the bulk of the datasets taken in the period 1999−2002. In Fig. 4 we show the evolution in time of the overall 0.2−10 keV flux of the source to provide a reference on the flux state of the source at the epoch of each observation, along with the soft (0.2−2 keV) and hard (2−10 keV) fluxes, and their hardness ratios (HR = (H − S) / (H + S)).
In the 1999−2002 period, NGC 5548 experienced a maximum flux variability of a factor of ~2, with a median flux of ~5 × 10-11 erg cm-2 s-1. In 2005, the overall flux decreased by almost a factor of 3 with respect to the L02 observation, and even further in 2007 when it reached a minimum of ~10-11 erg cm-2 s-1. The behavior of the soft (0.2−2 keV) and hard (2−10 keV) X-ray fluxes is very similar, following the same trends as the overall X-ray flux over the years. This suggests that the source variability is due to intrinsic changes rather than obscuration processes such as the one reported in Kaastra et al. (2014). During the obscuration event the hard X-ray flux stayed at the historical values while the soft X-ray flux decreased dramatically. Furthermore, this supports our approach of using the 2002 SED for the WA analysis of all the archival observations, as the variations only involved the normalization but did not significantly changed the shape of the SED. More detailed studies of the broadband continuum of NGC 5548 is reported in Mehdipour et al. (2015; Paper I) and Ursini et al. (2015; Paper III). An in-depth discussion on the origin and variability of the soft excess in NGC 5548 is also reported in Papers I and VII (Mehdipour et al. 2015, 2016).
 |
Fig. 4 Fluxes in the 0.2−10 keV, 0.2−2 keV, and 2−10 keV bands, and hardness ratios (HR = (H − S) / (H + S)) as a function of time in days since the first observation (L99) for all of the observations used in this paper. |
4.2. Thermal stability of the warm absorber
 |
Fig. 5 Thermal stability curves of the NGC 5548 archival observations (L99 and H00 in the top panels; R00x and R01y in the middle panels; R01z and H02 in the bottom panels) showing the pressure ionization parameter as a function of the electron temperature (solid line). The curves have been computed from the SED of Steenbrugge et al. (2005). The X-ray WA components in each observation are represented as solid squares (A to F). For comparison, the dashed horizontal lines represent in each panel the location of the WA components in the L02 observation. |
 |
Fig. 6 Thermal stability curves of the NGC 5548 archival observations (L02 and L05 in the top panels; L07 in the bottom panel) showing the pressure ionization parameter as a function of the electron temperature (solid line). The curves have been computed from the SED of Steenbrugge et al. (2005). The X-ray WA components in each observation are represented as solid squares (A to F). For comparison, the dashed horizontal lines represent in each panel the location of the WA components in the L02 observation. |
Some clues on the structure of the X-ray WA can be drawn from the thermal stability curves of the photoionized gas. These curves, also known as cooling curves, are determined by the ionizing SED that illuminates the gas. They are typically represented as plots of the pressure ionization parameter Ξ as a function of the electron temperature T. The pressure ionization parameter Ξ (Krolik et al. 1981) is defined as
where ξ is the ionization parameter defined in Eq. (1), c is the speed of light, k is the constant of Boltzmann, and T is the electron temperature. The different values of Ξ were computed using CLOUDY version 13.01, which provided a grid of ionization parameters ξ and their corresponding electron temperatures T for a thin layer of gas irradiated by the ionizing continuum. For consistency with the analysis we performed in Sect. 3.2, we used as input SED that of Steenbrugge et al. (2005) for all of the archival observations, and assumed the proto-Solar abundances of Lodders & Palme (2009).
The curve thus generated divides the Ξ −T plane in two regions: below the curve heating dominates cooling, whereas above the curve cooling dominates heating. In the points on the curve, the heating rate equals the cooling rate so that the gas is in thermal equilibrium. The branches of the curve with negative derivative dT/ dΞ < 0 (those where the curve turns backwards) are unstable against isobaric thermal perturbations (e.g., vertical displacements from the curve). This means that for a photoionized gas in an unstable branch, if it is subject to a small positive temperature perturbation its temperature will keep increasing until it reaches a stable branch of the curve (those with positive derivative dT/ dΞ > 0). Conversely, a small negative temperature perturbation will cause the gas temperature to decrease until it falls in a stable region of the Ξ−T plane. Moreover, gas components sharing the same Ξ value are nominally in pressure equilibrium with each other, and therefore they are likely part of the same long-lived structure.
In Figs. 5 and 6 we show the thermal stability curves of the archival observations of NGC 5548 analyzed in this paper. The curves are the same in all of the observations since the same input SED was used to generate the curve. Overplotted on the curves are the different WA components detected in each archival observation. While in most of the cases the WA components B to F seem to be in pressure equilibrium, the extent of the uncertainties makes the opposite equally likely, and therefore there are no grounds to claim pressure equilibrium. The large error bars associated with most of the observations are mainly due to the uncertainties in the determination of ξ. It is possible that some of the components might be truly in pressure equilibrium, but their different outflow velocities and turbulence suggest that they likely originate from different spatial regions.
On the other hand, we can examine the evolution of the WA components as they move along the curve between the different epochs of the archival observations. Since the uncertainty of the WA components in the vertical axis is much smaller than in the horizontal axis, it is possible to examine vertical displacements along the curve. For this reason, for comparison among the different datasets, we also show as horizontal dashed lines in Figs. 5 and 6 the location of the WA components in observation L02, the one with the best determined WA parameters. In the first grating observation (L99) the flux of the source was slightly higher than in L02. The WA components are higher on the curve than at the L02 epoch except for components C and E, which were in a similar ionization state. In H00, an observation taken almost 2 months later, the overall flux decreased by a factor of 2 but all the WA components were in a higher ionization state. Component C “jumped” the unstable branch that was just above its position in the L99 curve, almost blending with component D. Similar jumps happen for components E and F. In this case, the drop in flux between L99 and H00 could have happened shortly before the observation, not giving the gas enough time to respond to this change. In support of this argument, R00x was observed almost 11 months after H00, maintaining a similar flux level, but with all components significantly less ionized. The uncertainties in this observation, however, are quite large due to the short exposure (only 26 ks). R01y, observed ~200 days later, has a flux higher by a factor of ~2 compared to R00x, and it has all six components in an ionization state fully consistent with L02. Similarly for R01z, observed two days later. H02, taken six months later with a flux half of that in R01z, shows little change in the WA components, except for D and F which climbed in the curve toward the unstable branches above them. Again, we lack here information about the flux history of the source in the days or weeks prior to this observation, which could provide a hint on what initiated this change. Interestingly, when the L02 observation was taken 4 days later these components had returned to their positions in the stable branches of the curve, which tells us something about the time scales at which they respond (but see the discussion in Sect. 4.3). Finally, on much longer time scales, L05 was observed ~3 years later when the source had a flux level ~3 times lower than in the L02 epoch. Even though the error bars are rather large, one can see a dramatic change in the location of the WA components on the curve, all of them moving toward lower positions in the curve. The last observation in 2007 has the lowest overall flux, several times lower than that of L02, and the associated error bars are so large that no useful conclusion can be extracted from it other than the WA components seem to be located at similar positions as in 2005.
It is worth noting again that each observation is just a snapshot of a dynamical picture in which each gas component is reacting differently to changes in the ionizing flux over the years, a picture that is incomplete since we do not have a continuous monitoring of the flux history of the source between observations. However, this provides support for the fact that the response to flux variations on different time scales is motivated by the different densities of the absorbing gas components. If their densities could be constrained through their variability, we would have a powerful tool to also constrain their location with respect to the central ionizing source.
4.3. Warm absorber variability
 |
Fig. 7 Ionization parameter ξ against the ionizing luminosity L in units of the luminosity of the L02 observation L0 for components A and B (top panels), C and D (middle panels), and E and F (bottom panels). Black filled circles represent the LETGS observations, red crosses the HETGS observations, and green filled triangles the RGS observations. The dotted horizontal line indicates no response to continuum changes, while the dashed diagonal shows ξ proportional to L and indicates instantaneous response to variations in the ionizing flux. |
 |
Fig. 8 Variation in the ionization parameter Δlog ξ on different time scales (in days) for components A and B (top panels), C and D (middle panels), and E and F (bottom panels). The dashed line represents no variability. |
Motivated by the behavior of the WA components along the stability curves shown in Sect. 4.2, we looked for additional signatures of variability that would help to constrain the typical time scales at which each component responds to flux changes. In Fig. 7 we show the values of the ionization parameter ξ plotted against the ionizing luminosity L for each component and archival observation using the L02 parameters as reference values. We chose to use L02 for its quality and because the WA parameters were best determined for this observation. For each component the dotted horizontal line indicates that the WA did not respond to variations in flux with respect to that of L02 (i.e. the ionization parameter ξ is the same as that of L02 for each component). A dashed diagonal line shows ξ proportional to L, and marks the trend that the WA would follow if the material responds instantaneously to continuum changes.
The lowest flux observations, L05 and L07, have typically large uncertainties in the ionization parameter ξ for all the WA components. Overall they seem to be consistent with an immediate response for components A to C, while components D to F could be consistent with any trend at the 2σ confidence level. All the WA components of H00 are systematically more ionized that those of L02, even though the ionizing luminosity at the H00 epoch was ~20% lower than that of L02. Similarly most components are more highly ionized in H02, which has an ionizing flux close to that of L02. The exceptions are components A and E, which are inconsistent at only the 2σ level. A similar behavior is seen for the WA in R00x (ionizing flux comparable to L02) but with systematically lower ionized components, with the exception of components D and F. The observations with higher ionizing luminosity, the RGS observations in 2001 and L99, show different trends. In general, both R01y and R01z are closer to the no response trend (i.e. their WA components have a ξ value close to those of L02). However, for components A and B the errors are large enough that they are within 2σ also consistent with an immediate response trend. On the other hand, the WA components in L99 show a variety of behaviors: A and B are significantly more ionized than in L02, D and F are consistent with the gas responding immediately, while C and E would be closer to a no response scenario.
It is clear that, in spite of the large uncertainties associated with the determination of ξ, the WA components show some kind of variability as seen in Figs. 5−7, and in the values listed in Table 5. If these changes are due to photoionization or recombination of the ionized gas in response to continuum changes, it is then possible to estimate a lower limit on the density of the absorbing gas via the following equation (Bottorff et al. 2000):
where trec(Xi) is the recombination time scale of the ion Xi, αr(Xi) is the recombination rate from ion Xi − 1 to ion Xi, and f(Xi) is the fraction of element X at the ionization level i. The recombination rates αr are known from atomic physics and the fractions f can be determined from the ionization balance of the source. Therefore, for a given ion Xi it is possible to obtain a lower limit on the density n if an upper limit on the recombination time trec is known, since trec ∝ 1 /n.
The archival observations of NGC 5548 allow us to probe variability on time scales that range from two days to almost a decade. In Fig. 8 we show the measured variations in the ionization parameter ξ between each individual observation (e.g., the first observation is compared with the rest, then the second is compared with the rest, and so on). This enables us to estimate the typical time scale at which the different WA components begin to vary, which can be used as a proxy for the recombination time of the gas. In this sense, we will adopt the first point where significant changes can be seen as trec for a given WA component. For component A there are no signatures of variability in ξ below ~500 days, and similarly for component B although there are marginal hints of variability at 4 and ~60 days. Components C and D start showing marginal evidence for variability at 4 days, becoming more significant on time scales of 60 days. Component E also begins to significantly vary at ~60 days, while component F does so at 4 days.
Another variable in Eq. (3) that needs to be determined is the fraction of a given element X in an ionization state i. This can be done by means of the ionization balance of NGC 5548 that provides the ionic column densities of all the ions, which can be divided by the total hydrogen column density to obtain f(Xi). We looked for the ions that contribute substantially to the fit for each WA component (i.e. the ones that because of their column density, oscillator strengths, and signal-to-noise of their features in the spectrum, are driving the fit), so that they can be used as a proxy for that component. We used the ionic column densities of these ions to feed the SPEX auxiliary program rec_time, which delivers as output the product ntrec. The ions used for each component and their corresponding ntrec product are listed in Appendix B. Using the averaged ⟨ ntrec ⟩ values, and the variability time scales described above as upper limits for trec, we obtained lower limits to the density of the absorbing gas n for each WA component. We find that the WA components with the lowest density are components A and B (of the order of a few thousands of cm-3 or higher), while the higher ionization components C to F have densities of the order of tens of thousands of cm-3. These values are listed in Table 6.
4.4. Location of the warm absorbers
From the definition of the ionization parameter (Eq. (1)) it follows immediately that we can use the lower limit on the density n calculated in Sect. 4.3 to constrain the location of the WA with respect to the central ionizing source: 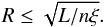 (4)The ionizing luminosity was calculated by integrating the template SED shown in Fig. 2 in the 1−1000 Ryd range, obtaining L = 1.97 × 1044 erg s-1. With this value and those of ξ for the L02 dataset, which are representative of the flux state and the ionization state of the WA, we obtained upper limits on the distance of the WA components that are listed in the last column of Table 6. We conclude that the WA in NGC 5548 has a stratified structure, where the lowest ionization components A and B are the farthest, at ≲50 and ≲20 pc from the central source, respectively. Components C and D lie at the order of ~4 pc or less, whereas components E and F are located at pc and sub-pc distances, respectively.
(4)The ionizing luminosity was calculated by integrating the template SED shown in Fig. 2 in the 1−1000 Ryd range, obtaining L = 1.97 × 1044 erg s-1. With this value and those of ξ for the L02 dataset, which are representative of the flux state and the ionization state of the WA, we obtained upper limits on the distance of the WA components that are listed in the last column of Table 6. We conclude that the WA in NGC 5548 has a stratified structure, where the lowest ionization components A and B are the farthest, at ≲50 and ≲20 pc from the central source, respectively. Components C and D lie at the order of ~4 pc or less, whereas components E and F are located at pc and sub-pc distances, respectively.
The determination of the density lower limits described above allows for much better constrained distances compared to other distance estimations. Some of them, such as the one described in Blustin et al. (2005), involve assumptions on the conservation of momentum, which are only valid for radiatively-driven winds. Since there is increasing evidence that AGN ionized winds can also be launched by other mechanisms (shocks, thermal instabilities, magnetic fields) or a combination of them, these assumptions need to be handled with caution. The most basic approach to estimate the distance of the intervening gas used in the literature (e.g., Blustin et al. 2005) is by assuming that the bulk of the WA mass is concentrated in a layer with thickness Δr that needs to be less than or equal to the distance to the central source R so that Δr/R ≤ 1. Together with the approximation NH ≈ nΔr, it follows that R ≤ L/NHξ. Applying this method to NGC 5548 we derive distance constraints that are at least one order of magnitude higher that those obtained from Eq. (4).
Variability time scales, density, and location of the WA components in NGC 5548.
Furthermore, we can use a similar argument based on the non-detection of variability on smaller time scales to set upper limits on the density of the absorbing gas, and hence lower limits on their possible location. Following this, we see that components A and B have lower limits on R of the order of ~30 and ~10 pc, while the highest ionization components, C to F, are at sub-pc scales or further from the black hole (see Table 6).
The scenario depicted by these distance estimations, where high-density highly ionized gas is located much closer to the central SMBH than the less dense lowly ionized absorber, is consistent with the picture sketched in Kazanas et al. (2012). In this work, a line of sight at a given inclination angle intersects several layers of a stratified wind, each of them with different ξ and density such as the ones seen in NGC 5548. WA components with a variety of ionization phases are thus originally launched from different parts of the disk, most likely due to the combined effect of magnetic and radiation pressure (Fukumura et al. 2010).
In the context of the unification models of AGN, these ionized winds are much farther from the SMBH than the broad line region (BLR), which is located at a few light-days distance (Pancoast et al. 2014; Kaastra et al. 2014). For comparison, the inner edge of the torus can be estimated from the approximate relation for the dust sublimation radius (Krolik & Kriss 2001)
where Lion,44 is the ionizing luminosity in units of 1044 erg s-1, obtaining a distance of ~1.4 pc. The most ionized WA component F is thus generated closer to the disk than the inner edge of the torus, in agreement with the scenario discussed in Kazanas et al. (2012). According to their lower limits on R, components C to E, all of them with log ξ> 2, may also extend down to distances comparable to the torus inner edge.
With respect to the location of the narrow line region (NLR) in NGC 5548, Detmers et al. (2009) constrained it to a cone extending between 1 and 15 pc from the central black hole, depending on its exact geometry. More recently, Peterson et al. (2013) used [O iii] variability to estimate the size of the NLR in NGC 5548. They found it to be compact (RNLR ~ 1−3 pc) although its actual extent is possibly larger if it is elongated toward the line of sight. In this respect, the analysis of the narrow emission lines in the stacked RGS spectrum of NGC 5548 during the 2013−2014 campaign, renders a location for the NLR of rmin = 13.9 ± 0.6 pc from the nucleus (Whewell et al. 2015). This analysis also shows the narrow emission lines to be absorbed by WA component B, located at 13 <R< 20 pc, a range consistent with the location of the NLR estimated by Whewell et al. (2015), although no conclusions can be firmly drawn on the possible connection between the absorbers along our line of sight and the emitting clouds that extend over a much larger region.
4.5. Energetics of the warm absorbers
With the distance constraints for the WA derived in Sect. 4.4 we can estimate the amount of mass carried by the outflows into the ISM of NGC 5548. For an outflow in the form of a partial thin spherical shell at a distance R from the central source and moving radially at constant speed v, the mass outflow rate is:
where μ = 1.4 is the mean atomic mass per proton, mp is the proton mass, and Ω is the solid angle subtended by the outflow, which ranges between 0 and 4π sr. The main source of uncertainty in this equation is introduced by the parameter Ω, which depends on the geometry of the WA outflow and is usually unknown. Typically, Ω = π/ 2 sr is assumed, as inferred from the observed type-1/type-2 ratio in nearby Seyfert galaxies (Maiolino & Rieke 1995), and the fact that ionized outflows are detected in approximately half of the observed Seyfert 1 galaxies (Dunn et al. 2007). This value is only an estimate, and we note that it will not hold if the outflows are bent because of gravitational and/or magnetic processes.
Since Ṁout scales with the distance R, the farthest components will carry considerably more mass per unit time than the inner ones, even if the former are much less dense than the latter; and similarly for the fastest winds with respect to the slower velocity winds. Indeed we calculate that for components A, B, and C, located at pc-scale distances, their mass outflow rates are of the order of Ṁout ≃ 0.05ΩM⊙ yr-1. These values are almost a factor of two higher than those of components E and F, with mass outflow rates of Ṁout ≃ 0.03ΩM⊙ yr-1. We have expressed all these Ṁout values as a function of Ω to reflect the uncertainty associated with this parameter.
Assuming that the absorbers subtend a solid angle of Ω = π/ 2 sr, the mass outflow rates for components A to C are in the range of Ṁout ~ 0.06−0.09M⊙ yr-1, while those of components E to F are of the order of ~0.04−0.05M⊙ yr-1. Component D contributes much less with Ṁout ~ 0.01M⊙ yr-1. The Ṁout values for all WA components are reported in Table 7. In general, these values are similar or slightly higher than the mass accretion rate of the source, Ṁacc ≡ Lbol/ηc2 = 0.05M⊙ yr-1 (assuming a nominal accretion efficiency of η = 0.1, and a bolometric luminosity of Lbol = 2.82 × 1044 erg cm-1). The sum of the mass conveyed per unit time by all of the X-ray WA components is ~0.3 M⊙ yr-1, about six times the nominal mass accretion rate in NGC 5548. For comparison, these values are of the same order of magnitude as those measured in other active galaxies (e.g., Costantini 2010; Crenshaw & Kraemer 2012), and they are typically almost one order of magnitude lower than the mass outflow rates measured in powerful starburst galaxies (e.g., Veilleux et al. 2005).
Energetics of the X-ray WA components.
The kinetic energy per unit time carried by the outflows is defined as 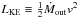 . The WA components have values of LKE of the order of a few times 1039−40 erg s-1 for the opening angle assumed above (see Table 7). The total kinetic luminosity injected into the medium by the sum of all the components, LKE ~ 7.8 × 1040 erg s-1, constitute a small fraction of the bolometric luminosity of the source, LKE/Lbol ~ 0.03%. This value, even if we assume the extreme case of an opening angle of 4π, is well below the range of 0.5−5% of the bolometric luminosity typically assumed by feedback models as the minimum amount required to reproduce the observed M − σ relation (Hopkins & Elvis 2010 and references therein).
. The WA components have values of LKE of the order of a few times 1039−40 erg s-1 for the opening angle assumed above (see Table 7). The total kinetic luminosity injected into the medium by the sum of all the components, LKE ~ 7.8 × 1040 erg s-1, constitute a small fraction of the bolometric luminosity of the source, LKE/Lbol ~ 0.03%. This value, even if we assume the extreme case of an opening angle of 4π, is well below the range of 0.5−5% of the bolometric luminosity typically assumed by feedback models as the minimum amount required to reproduce the observed M − σ relation (Hopkins & Elvis 2010 and references therein).
However, this picture is incomplete if we only focus on the X-ray WA, without taking the effect of the UV absorbers into account. The latter are typically located further away than the X-ray WA, and carry large amounts of matter, which may have a measurable effect in the energy budget of the AGN. In general, a direct comparison between the X-ray and UV absorbers in AGN is difficult because of the higher parameter uncertainties of the former with respect to the latter, especially those regarding spectral resolution. However, in those cases where simultaneous X-ray and UV observations are taken, there is increasing evidence that some of the low ionization X-ray WA components may originate in the same gas responsible for the absorption in the UV band (e.g., Mrk 279, Costantini et al. 2007; Mrk 509, Ebrero et al. 2011; NGC 4593, Ebrero et al. 2013). An extensive discussion on the possible relation between the X-ray and UV absorbers in NGC 5548 can be found in Arav et al. (2015). Here we will assume that the UV absorbers of NGC 5548 contribute to the mass-energy budget as an independent component. Arav et al. (2015) provide column densities and distance estimates for three of the six UV components. These parameters are well determined for UV component 1 (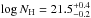 cm-2, and
cm-2, and 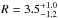 pc), but less constrained for the UV components 3 and 5 (R in the 5−15 pc range, and log NH< 21.5 and <20.7 cm-2, respectively). These values predict outflow mass rates Ṁout, assuming also a solid angle of Ω = π/ 2 sr, of ~0.23M⊙ yr-1, ~0.55 M⊙ yr-1, and ~0.04 M⊙ yr-1, respectively. These values combined translate into a kinetic luminosity of LKE,UV/Lbol ~ 0.17%, almost five times higher than that of the X-ray WA. However, even after summing the X-ray and UV contributions, the total amount energy fed back into the medium is ~0.2% or less (since part of the contribution of the UV absorbers may overlap with that of the lowest ionization X-ray WA). This is still below the minimum amount required to produce a significant effect in terms of feedback.
pc), but less constrained for the UV components 3 and 5 (R in the 5−15 pc range, and log NH< 21.5 and <20.7 cm-2, respectively). These values predict outflow mass rates Ṁout, assuming also a solid angle of Ω = π/ 2 sr, of ~0.23M⊙ yr-1, ~0.55 M⊙ yr-1, and ~0.04 M⊙ yr-1, respectively. These values combined translate into a kinetic luminosity of LKE,UV/Lbol ~ 0.17%, almost five times higher than that of the X-ray WA. However, even after summing the X-ray and UV contributions, the total amount energy fed back into the medium is ~0.2% or less (since part of the contribution of the UV absorbers may overlap with that of the lowest ionization X-ray WA). This is still below the minimum amount required to produce a significant effect in terms of feedback.
If these winds are not transient and are continuously launched from the inner regions of the AGN throughout its activity lifetime (t ~ 108 yr), the total kinetic energy deposited into the surroundings, EK = LKEt, is of the order of a few times 1055 erg. This is almost two orders of magnitude lower than the energy required to terminate or even regulate star-forming episodes in the host galaxy, which is estimated to be ~1057 erg (Krongold et al. 2010). It is also negligible compared to the binding energy of massive galactic bulges (E ~ 1060 erg), a value required by quasar feedback simulations to effectively regulate structure formation in the inter-galactic medium (e.g., Scannapieco & Oh 2004; Hopkins et al. 2005).
5. Conclusions
We have re-analyzed the archival observations of NGC 5548 taken with the grating spectrometers onboard XMM-Newton (RGS) and Chandra (LETGS and HETGS) between 1999 and 2007. The motivations behind this exercise were twofold. In the first place we aimed at characterizing the variability of the ionized absorption features in the spectra of the source through a systematic analysis using up-to-date photoionized codes and atomic physics, since different versions of the codes provide significantly different ionization balances (see Sect. 2.1). Secondly, we built a fully characterized and accurate model of the X-ray WA to be used to model the WA in the 2013−2014 RGS data. These data were obtained when the source was heavily obscured in the soft X-rays, imposing severe limitations on our ability to characterize and fit the WA in those spectra (Kaastra et al. 2014; Di Gesu et al. 2015).
Using as a baseline the longest archival observation (the combined HETGS+LETGS spectra of 2002), we found that the WA in NGC 5548 is composed of six distinct ionization phases with increasing column densities NH as the ionization parameter ξ increases, moving outwards in four kinematic regimes (vout ~−250, ~−550, ~−800, ~−1200 km s-1). Assuming that the changes in the WA between the different archival observations occur only due to ionization/recombination processes (i.e. outflow velocity and column density remain the same), we detect significant variations in ionization of the WA components in response to the changes in the intrinsic flux level of the source. Using the ions that contribute the most to each WA component fit and the variations in their ionic column densities among the observations, we are able to estimate lower limits on the density of the gas, observing that the lowest ionization components are less dense than the higher ionization components.
Lower limits on the density can be used to estimate a stringent upper limit on the location of the various WA components, thus revealing a stratified structure in the absorbing gas. The lower ionization phases are located at distances of the order of pc to tens of pc, whereas the intermediate components lie at pc to sub-pc distances. The highest ionization WA component is located between ~0.4 and ~0.6 pc from the central ionizing source. This scenario is consistent with the WA components being launched from different regions close to the accretion disk, possibly due to a combination of magnetic and radiative processes, forming a stratified wind composed of multiple layers that are crossed by our line of sight (Kazanas et al. 2012).
The mass outflow rate summed over all X-ray WA components detected in NGC 5548 is Ṁout ~ 0.3 M⊙ yr-1, about six times the nominal accretion rate of the black hole. The kinetic luminosity injected into the surroundings of the central SMBH by the WA is however still a small fraction (~0.03%) of the bolometric luminosity of NGC 5548. Even adding the contribution of the UV absorbers, the total kinetic luminosity (LKE/Lbol ~ 0.2%) is not enough to affect the ISM of the host galaxy as invoked by current feedback models, which require that between 0.5% and 5% of the bolometric luminosity of the AGN must be fed back to the medium. The total kinetic energy deposited into the medium throughout the average lifetime of the AGN (t ~ 108 yr), assuming a constant level of activity, is two orders of magnitude lower than that required to quench star formation and affect the evolution of the host galaxy.
Acknowledgments
This work is based on observations obtained by XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA member states and the USA (NASA). The scientific results reported in this article are based on observations made by the Chandra X-ray observatory. We thank the International Space Science Institute (ISSI) in Bern for support and hospitality. SRON is supported financially by NWO, the Netherlands Organization for Scientific Research. This work was supported by NASA through grants for HST program number 13184 from the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Incorporated, under NASA contract NAS5-26555. M.M. acknowledges support from NWO and the UK STFC. M.C. acknowledges financial support from contracts ASI/INAF n.l/037/12/0 and PRIN INAF 2011 and 2012. P-O.P. acknowledges financial support from the CNES and from the CNRS/PICS. S.B. acknowledges INAF/PICS for financial support. G.P. acknowledges support of the Bundesministerium für Wirtschaft und Technologie/Deutsches Zentrum für Luft- und Raumfahrt (BMWI/DLR, FKZ 50 OR 1408). H.S. was supported by Grant-in-Aid for JSPS Fellows, 15J02737. M.W. acknowledges the support of a Ph.D. studentship awarded by the UK STFC. We thank the anonymous referee for his/her constructive comments.
References
- Andrade-Velázquez, M., Krongold, Y., Elvis, M., et al. 2010, ApJ, 711, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Arav, N., Chamberlain, C., Kriss, G. A., et al. 2015, A&A, 577, A37 (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arav, N., Korista, K. T., & de Kool, M. 2002, ApJ, 566, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Blustin, A. J., Page, M. J., Fuerst, S. V. et al. 2005, A&A, 431, 111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bottorff, M. C., Korista, K. T., & Shlosman, I. 2000, ApJ, 537, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Brinkman, A. C., Gunsing, C. J. T., Kaastra, J. S. 2000, SPIE, 4012, 81 [Google Scholar]
- Brotherton, M. S., Green, R. F., Kriss, G. A., et al. 2002, ApJ, 565, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Canizares, C. R., Davis, J. E., Dewey, D., et al. 2005, PASP, 117, 1144 [NASA ADS] [CrossRef] [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Costantini, E., Space Sci. Rev., 157, 265 [Google Scholar]
- Costantini, E., Kaastra, J. S., Arav, N., et al. 2007, A&A, 461, 121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crenshaw, D. M., & Kraemer, S. B. 1999, ApJ, 521, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Crenshaw, D. M., & Kraemer, S. B. 2012, ApJ, 753, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Crenshaw, D. M., Kraemer, S. B., Gabel, J. R., et al. 2003, ApJ, 594, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Crenshaw, D. M., Kraemer, S. B., Schmitt, H. R., et al. 2009, ApJ, 698, 281 [NASA ADS] [CrossRef] [Google Scholar]
- den Herder, J.-W., Brinkman, A. C., Kahn, S. M., et al. 2001, A&A, 365, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin Jr., H. G., et al. 1991, Third Reference Catalogue of Bright Galaxies, Version 3.9 [Google Scholar]
- Detmers, R. G., Kaastra, J. S., Costantini, E., et al., 2008, A&A, 488, 67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Detmers, R. G., Kaastra, J. S., & McHardy, I. M. 2009, A&A, 504, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Gesu, L., Costantini, E., Ebrero, J., et al. 2015, A&A, 579, A42 (Paper IV) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Matteo, T., Springel, V., & Hernquist, L. 2005, Nature, 433, 604 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dunn, J. P., Crenshaw, D. M., Kraemer, S. B., et al. 2007, AJ, 134, 1061 [NASA ADS] [CrossRef] [Google Scholar]
- Ebrero, J., Kriss, G. A., Kaastra, J. S., et al. 2011, A&A, 534, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ebrero, J., Kaastra, J. S., Kriss, G. A., et al. 2013, MNRAS, 435, 3028 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M. 2000, ApJ, 545, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Porter, R. L., van Hoof, P. A. M., et al. 2013, Rev. Mex. Astron. Astrofis., 49, 137 [Google Scholar]
- Ferrarese, L., & Merritt, D. 2000, ApJ, 539, 9 [Google Scholar]
- Fruscione, A., McDowell, J. C., Allen, G. E., et al., 2006, SPIE, 6270, 1 [Google Scholar]
- Fukumura, K., Kazanas, D., Contopoulos, I., et al. 2010, ApJ, 715, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Gabriel, C., Denby, M., Fyfe, D. J., et al. 2004, ASP Conf. Proc., 314, 759 [Google Scholar]
- Gebhardt, K., Bender, R., Bower, G., et al. 2000, ApJ, 539, 13 [Google Scholar]
- George, I. M., Turner, T. J., Netzer, H., et al. 1998, ApJS, 114, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Maraschi, L. 1993, ApJ, 413, 507 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hopkins, P. F., & Elvis, M. 2010, MNRAS, 401, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., et al. 2005, ApJ, 630, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Kaastra, J. S., & Barr, P. 1989, A&A, 226, 59 [NASA ADS] [Google Scholar]
- Kaastra, J. S., Mewe, R., & Nieuwenhuizen, H. 1996, 11th Colloq. on UV and X-ray Spectroscopy of Astrophysical and Laboratory Plasmas, 411 [Google Scholar]
- Kaastra, J. S., Mewe, R., Liedahl, D. A., et al. 2000, A&A, 354, L83 [NASA ADS] [Google Scholar]
- Kaastra, J. S., Steenbrugge, K. C., Raassen, A. J. J., et al. 2002, A&A, 386, 427 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaastra, J. S., Petrucci, P.-O., Cappi, M., et al. 2011, A&A, 534, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaastra, J. S., Detmers, R. G., Mehdipour, M., et al. 2012, A&A, 539, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaastra, J. S., Kriss, G. A., Cappi, M., et al. 2014, Science, 345, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Kallman, T. R., & Krolik, J. H. 1999, XSTAR photoionization code, http://heasarc.gsfc.nasa.gov/xstar/xstar.html [Google Scholar]
- Kazanas, D., Fukumura, K., Behar, E., et al. 2012, Astron. Rev., 7, 92 [CrossRef] [Google Scholar]
- Krolik, J. H., & Kriss, G. A. 2001, ApJ, 561, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Krolik, J. H., McKee, C. F., & Tarter, C. B. 1981, ApJ, 249, 422 [NASA ADS] [CrossRef] [Google Scholar]
- Krongold, Y., Elvis, M., Andrade-Velázquez, M., et al. 2010, ApJ, 710, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K., & Palme, H. 2009, Meteorit. Planet. Sci. Suppl., 72, 5154 [NASA ADS] [Google Scholar]
- Longinotti, A. L., Costantini, E., Petrucci, P.-O., et al. 2010, A&A, 510, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maiolino, R., & Rieke, G. H. 1995, ApJ, 454, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Mehdipour, M., Kaastra, J. S., Kriss, G. A., et al. 2015, A&A, 575, A22 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mehdipour, M., Kaastra, J. S., Kriss, G. A., et al. 2016, A&A, in press, DOI: 10.1051/0004-6361/201527729 (Paper VII) [Google Scholar]
- Murray, N., Chiang, J. 1995, ApJ, 454, 105 [Google Scholar]
- Pancoast, A., Brewer, B. J., Treu, T., et al. 2014, MNRAS, 445, 3073 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., Denney, K. D., De Rosa, G., et al. 2013, ApJ, 779, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Rees, M. J. 1984, ARA&A, 22, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, C. S. 1997, MNRAS, 286, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Scannapieco, E., & Oh, S. P. 2004, ApJ, 608, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Steenbrugge, K. C., Kaastra, J. S., de Vries, C. P., & Edelson, R. 2003, A&A, 402, 477 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steenbrugge, K. C., Kaastra, J. S., Crenshaw, D. M., et al. 2005, A&A, 434, 569 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sunyaev, R. A., & Titarchuk, L. G. 1980, A&A, 86, 121 [NASA ADS] [Google Scholar]
- Tombesi, F., Cappi, M., Reeves, J. N., et al. 2013, MNRAS, 430, 1102 [Google Scholar]
- Ursini, F., Boissay, R., Petrucci, P.-O., et al. 2015, A&A, 577, A38 (Paper III) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Veilleux, S., Cecil, G., & Bland-Hawthorne, J. 2005, ARA&A, 43, 769 [Google Scholar]
- Wakker, B. P., Lockman, F. J., & Brown, J. M. 2011, ApJ, 728, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Whewell, M., Branduardi-Raymont, G., Kaastra, J. S., et al. 2015, A&A, 581, A79 (Paper V) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: NGC 5548 archival spectra
In this appendix we show some of the NGC 5548 archival spectra used in this work, together with their best fit models: L99
(see Fig. A.1); R00x, R01y, and R01z (see Fig. A.2); L05 (see Fig. A.3), and L07 (see Fig. A.4).
 |
Fig. A.1 Chandra LETGS spectrum of NGC 5548 in 1999 (L99). The solid line represents our best-fit model. Some relevant WA absorption features have been labeled. |
 |
Fig. A.2 XMM-Newton RGS spectra of NGC 5548 in 2000 (R00x; top panels), and in 2001 (R01y, middle panels; R01z, bottom panels). The solid line represents our best-fit model. Some relevant WA absorption features have been labeled. |
 |
Fig. A.3 Chandra LETGS spectra of NGC 5548 in 2005 (L05). The solid line represents our best-fit model. Some relevant WA absorption features have been labeled. The spectrum has been rebinned for clarity. |
 |
Fig. A.4 Chandra LETGS spectra of NGC 5548 in 2007 (L07). The solid line represents our best-fit model. Some relevant WA absorption features have been labeled. The spectrum has been rebinned for clarity. |
Appendix B: Ionic species for variabilitycalculations
In Tables B.1 to B.6 we list the ions that were used in Sect. 4.3 as a proxy for each WA component, together with their corresponding product ntrec as provided by the SPEX auxiliary program rec_time.
List of ions used a proxy for the WA component A.
List of ions used a proxy for the WA component B.
List of ions used a proxy for the WA component C.
List of ions used a proxy for the WA component D.
List of ions used a proxy for the WA component E.
List of ions used a proxy for the WA component F.
All Tables
All Figures
 |
Fig. 1 Stability curves obtained with different versions of XSTAR and CLOUDY (black solid line, CLOUDY v13; black dot-dashed line, CLOUDY v98; red dashed line, XSTAR v1; red dotted line, XSTAR v2.2.1bk) for the same input spectral energy distribution. The solid dots represent the WA components of Steenbrugge et al. (2005). |
| In the text | |
 |
Fig. 2 Spectral energy distribution of NGC 5548. Data points are those of Steenbrugge et al. (2005). |
| In the text | |
 |
Fig. 3 Chandra LETGS spectrum of NGC 5548 in 2002 (L02). The solid red line represents our best-fit model. Some relevant WA absorption features have been labeled. |
| In the text | |
 |
Fig. 4 Fluxes in the 0.2−10 keV, 0.2−2 keV, and 2−10 keV bands, and hardness ratios (HR = (H − S) / (H + S)) as a function of time in days since the first observation (L99) for all of the observations used in this paper. |
| In the text | |
 |
Fig. 5 Thermal stability curves of the NGC 5548 archival observations (L99 and H00 in the top panels; R00x and R01y in the middle panels; R01z and H02 in the bottom panels) showing the pressure ionization parameter as a function of the electron temperature (solid line). The curves have been computed from the SED of Steenbrugge et al. (2005). The X-ray WA components in each observation are represented as solid squares (A to F). For comparison, the dashed horizontal lines represent in each panel the location of the WA components in the L02 observation. |
| In the text | |
 |
Fig. 6 Thermal stability curves of the NGC 5548 archival observations (L02 and L05 in the top panels; L07 in the bottom panel) showing the pressure ionization parameter as a function of the electron temperature (solid line). The curves have been computed from the SED of Steenbrugge et al. (2005). The X-ray WA components in each observation are represented as solid squares (A to F). For comparison, the dashed horizontal lines represent in each panel the location of the WA components in the L02 observation. |
| In the text | |
 |
Fig. 7 Ionization parameter ξ against the ionizing luminosity L in units of the luminosity of the L02 observation L0 for components A and B (top panels), C and D (middle panels), and E and F (bottom panels). Black filled circles represent the LETGS observations, red crosses the HETGS observations, and green filled triangles the RGS observations. The dotted horizontal line indicates no response to continuum changes, while the dashed diagonal shows ξ proportional to L and indicates instantaneous response to variations in the ionizing flux. |
| In the text | |
 |
Fig. 8 Variation in the ionization parameter Δlog ξ on different time scales (in days) for components A and B (top panels), C and D (middle panels), and E and F (bottom panels). The dashed line represents no variability. |
| In the text | |
 |
Fig. A.1 Chandra LETGS spectrum of NGC 5548 in 1999 (L99). The solid line represents our best-fit model. Some relevant WA absorption features have been labeled. |
| In the text | |
 |
Fig. A.2 XMM-Newton RGS spectra of NGC 5548 in 2000 (R00x; top panels), and in 2001 (R01y, middle panels; R01z, bottom panels). The solid line represents our best-fit model. Some relevant WA absorption features have been labeled. |
| In the text | |
 |
Fig. A.3 Chandra LETGS spectra of NGC 5548 in 2005 (L05). The solid line represents our best-fit model. Some relevant WA absorption features have been labeled. The spectrum has been rebinned for clarity. |
| In the text | |
 |
Fig. A.4 Chandra LETGS spectra of NGC 5548 in 2007 (L07). The solid line represents our best-fit model. Some relevant WA absorption features have been labeled. The spectrum has been rebinned for clarity. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



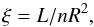
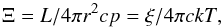
![\begin{equation} \label{trec} t_{\rm rec}(X_i)=\left(\alpha_{\rm r}(X_i)n\left[\frac{f(X_{i+1})}{f(X_i)}-\frac{\alpha_{\rm r}(X_{i-1})}{\alpha_{\rm r}(X_i)}\right]\right)^{-1}, \end{equation}](/articles/aa/full_html/2016/03/aa27808-15/aa27808-15-eq250.png)