| Issue |
A&A
Volume 587, March 2016
|
|
|---|---|---|
| Article Number | A8 | |
| Number of page(s) | 16 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201527679 | |
| Published online | 11 February 2016 | |
Testing the blazar sequence with the least luminous BL Lacertae objects
INAF–Osservatorio Astrofisico di Torino, via Osservatorio 20,
10025
Pino Torinese,
Italy
e-mail:
raiteri@oato.inaf.it
Received: 2 November 2015
Accepted: 10 December 2015
In a previous paper, we proposed a new method to select low-power BL Lacs (LPBLs) based on mid-infrared emission and flux contrast through the Ca II spectral break; that study led to the selection of a complete sample formed by 34 LPBLs with 0.05 <z ≤ 0.15 and radio luminosities spanning the range log Lr = 39.2–41.5 [erg s-1]. We now assemble the broadband spectral energy distributions (SEDs) of these sources to investigate their nature and compare them with brighter BL Lacs. We find that the ratios between the X-ray and radio luminosities range from ~20 to ~30 000 and that the synchrotron peak frequencies span a wide energy interval, from log νpeak ~ 13.5 to ~20 [Hz]. This indicates a broad variety of SED shapes and a mixture of BL Lac flavors. Indeed, although the majority of our LPBLs are high-energy peaked BL Lacs (HBLs), we find that a quarter of them are low-energy peaked BL Lacs (LBLs), despite the fact that the sample is biased against the selection of LBLs. The analysis of the median LPBL SED confirms disagreement with the blazar sequence at low radio luminosities. Furthermore, if we limit the sample to the LBLs subsample, we find that their median SED shape is essentially indistinguishable from that of the most luminous BL Lacs. We conclude that the observed radio power is not the main driving parameter of the multiwavelength properties of BL Lacs.
Key words: galaxies: active / BL Lacertae objects: general / galaxies: jets
© ESO, 2016
1. Introduction
Blazars are active galactic nuclei (AGNs) showing extreme properties. Their flux variability at all wavelengths, high and variable polarization, apparent superluminal motion of the radio knots, and high brightness temperatures are all signatures of relativistic motion in a plasma jet that is oriented at a small angle with respect to the line of sight. The consequent Doppler beaming of the nonthermal jet emission usually makes this emission dominate over the thermal emission from both the AGN nucleus (accretion disk, broad and narrow line regions, dusty torus) and the host galaxy. Therefore, the study of blazar emission is the most efficient tool to unveil the nature of extragalactic jets.
Blazars include flat-spectrum radio quasars (FSRQs) and BL Lac objects. The classical distinction between them is based on the strength of the emission lines, whose rest-frame equivalent width (EW) must be smaller than 5 Å to define a BL Lac (Stickel et al. 1991). Another quantity used to identify blazars is the value of the flux density contrast across the Ca II spectral break (Stocke et al. 1991), which is reduced with respect to that of quiescent galaxies in case of a nonthermal contribution.
BL Lacs were further divided into radio-selected BL Lacs (RBL) and X-ray selected BL Lacs (XBL) until Padovani & Giommi (1995) proposed a more physical classification into high-energy cutoff BL Lacs (HBL) and low-energy cutoff BL Lacs (LBL), setting the dividing line between the two classes at Fx/Fr ~ 200, where Fx is the 0.3–3.5 keV flux and Fr = νFν at 5 GHz. In the usual log νFν versus log ν representation, the blazar spectral energy distribution (SED) shows two main bumps corresponding to the synchrotron (from radio to UV or X-rays) and inverse-Compton (from X to γ rays) jet emission contributions. In the LBL SED, the synchrotron peak falls in the infrared–optical band, while it is in the UV-X-rays in HBL1. The operation of new TeV Telescopes, such as the Major Atmospheric Gamma Imaging Cherenkov Telescopes (MAGIC), the High Energy Stereoscopic System (H.E.S.S.) and the Very Energetic Radiation Imaging Telescope Array System (VERITAS), and the planning of more sophisticated TeV instruments, such as the Cherenkov Telescope Array (CTA; Acharya et al. 2013) has called attention to the extremely high-energy peaked BL Lacs (EHBL). Following Bonnoli et al. (2015), they are characterized by Fx/Fr ≳ 104, where Fx is the X-ray flux in the 0.1–2.4 keV band, and Fr = νFν at 1.4 GHz.
Fossati et al. (1998; hereafter F98) proposed a unifying view of the blazar SED behavior. These authors suggested that when the radio power decreases the synchrotron peak frequency shifts to higher energies and the Compton dominance, i.e., the ratio between the inverse-Compton and synchrotron peak luminosities, decreases. In this way, FSRQs, LBLs, and HBLs form a continuous spectral sequence, which is the so-called “blazar sequence”. This picture was subsequently confirmed by Donato et al. (2001), who also included hard X-ray data in the analysis. However, some authors have criticized this view. On one side, the existence of high-power HBL has been claimed (see, e.g., Padovani et al. 2003; Giommi et al. 2012). On the other side, LBL of low power have been found in deeper radio-selected samples (Padovani et al. 2003; Caccianiga & Marchã 2004; Antón & Browne 2005). These authors argued that the blazar sequence of F98 may be the result of selection biases because the high-power sources were mostly radio-selected objects, while the low-power sources were mainly X-ray selected objects (see also Landt & Bignall 2008). Moreover, Nieppola et al. (2008) suggested that the anticorrelation between synchrotron peak frequency and luminosity disappears when correcting for the relativistic Doppler boosting effect. The blazar sequence has then been revisited by Ghisellini & Tavecchio (2008), who substituted the dependence of the jet emission properties on the jet power alone with a dependence on two parameters, namely the black hole mass and accretion rate. The accretion rate has also been invoked by Meyer et al. (2011) as a second parameter needed to define the SED features.
The least luminous blazars are extremely interesting because they enable us to explore the behavior of the blazars properties at very low radio power and they probe the jet formation and emission processes at the lowest levels of accretion. These sources allow us to test the low-power end of the blazar sequence, which predicts that they are all HBLs. A major difficulty in finding low-luminosity BL Lacs comes from the dilution of the jet emission by the host starlight in the optical and near-IR bands. In Capetti & Raiteri (2015, hereafter Paper I), we proposed a new method to select low-power BL Lacs (LPBLs) based on a new diagnostic plane that includes the W2−W3 color from the Wide-Field Infrared Survey Explorer (WISE) all-sky survey (AllWISE) and the Dn(4000) index derived from the Digital Sky Survey (SDSS). We isolated 36 LPBLs candidates up to redshift 0.15. Their radio luminosity at 1.4 GHz goes from log Lr = 39.2 to 41.5 [erg s-1]. By carefully considering the completeness of our sample, we analyzed the BL Lac radio luminosity function (RLF), finding a dramatic paucity of LPBLs with respect to the extrapolation of the RLF toward low power. We thus suggested that a sharp break is present in their RLF, located at log Lr ~ 41 [erg s-1]. This implies that the LPBLs we consider represent the very end of the luminosity function of this class of objects and, therefore, they represent the ideal test bed for a better understanding of the nature of relativistic jets at low power.
In this paper, we analyze the LPBLs of Paper I in detail to explore their nature. In Sects. 2 and 3, we present the LPBLs sample and the collected multiwavelength data. These are used in Sect. 4 to estimate their broadband spectral indices and to build their SEDs. The SED properties are analyzed in the context of the blazar sequence in Sect. 5, while in Sect. 6 we discuss the effect of Doppler beaming. Our summary and conclusions are given in Sect. 7.
Throughout the paper we adopt a cosmology with H0 = 70 km s-1 Mpc-1, ΩM = 0.29, and ΩΛ = 0.71. When we speak of luminosities Lb in a given band b (where b = r,i,o,x, γ for radio, infrared, optical, X-ray, and γ-ray, respectively) we mean Lb = 4 πD2νFν, where D is the luminosity distance and Fν the flux density at the frequency ν, corrected for the Galactic absorption, when necessary, and k-corrected. The parameter Fν is assumed to have a power-law dependence on frequency, Fν ~ ν−α, where α is the energy spectral index. This is linked to the photon spectral index Γ through Γ = α + 1. We also use the term “color” to indicate a broadband spectral index.
2. The LPBLs sample
In Paper I we selected LPBLs according to a new diagnostic plane that includes the W2−W3 color from AllWISE and the Dn(4000) index2 derived from the SDSS. In this plane, LPBLs populate the so-called forbidden zone, a region that is scarcely populated by other sources; see Fig. 1. The forbidden zone is circumscribed, on the one hand, by a limit on the Dn(4000) and is obtained by requiring that the ratio f between the nonthermal jet flux to the host galaxy flux at 3900 Å is at least 1/3, and, on the other hand, by the Dn(4000) versus W2−W3 relationship that holds for a sample of 21 065 bright nearby galaxies. Starting from the radio-selected sample by Best & Heckman (2012) and filtering objects with small emission line EW (≲5 Å in the rest frame), we isolated 36 LPBL candidates up to redshift 0.15. Their radio luminosity at 1.4 GHz spans the range log Lr = 39.2–41.5 [erg s-1].
 |
Fig. 1 LPBLs identified in Paper I (blue circles). They lie in the “forbidden zone” of the Dn(4000) versus the W2–W3 diagram, which is defined by the Dn(4000) limit obtained by requiring that the nonthermal jet contribution is at least 1/3 of the host galaxy one at 3900 Å, and by the 1-sigma lower limit to the average relation holding for the 21 065 bright nearby galaxies (black dots; see Paper I for details). |
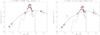 |
Fig. 2 Examples of the SED of two LPBLs, namely ID=786 and ID=1845. We show data analyzed by us (colored symbols) as well as data downloaded from the ASDC (grey dots); see Fig. A.1 for a full description. The near-IR, optical, and X-ray data have been corrected for Galactic absorption. We overplot the logarithmic parabolic fit through the data points at 1.4 GHz, 12 μm, rest-frame 3900 Å, and 1 keV (black empty circles), where the infrared and optical fluxes have been corrected for the host galaxy contribution. The grey line represents an elliptical galaxy template normalized to the W2 flux density. |
The name itself, forbidden zone, was conceived to mean that we are not expecting a significant number of contaminants there. Indeed, in Paper I, we were able to identify just one class of contaminants, the E+A galaxies, which we discarded by looking at their Hδ absorption. The further selection of BL Lac candidates based on small EW also excludes possible contaminants from most of the AGN classes. A preliminary analysis of the selected LPBLs properties gave strength to the idea that they are genuine BL Lacs. All but one3 LPBL are hosted in massive elliptical galaxies with stellar velocity dispersion σ> 160 km s-1, leading to black hole masses log (MBH/M⊙) > 7.8 (Tremaine et al. 2002), i.e., above the threshold to produce a radio-loud AGN (Chiaberge & Marconi 2011). Moreover, all LPBLs have radio morphologies dominated by a compact core in the FIRST images, and in some cases they also show a one-sided jet or a halo. All these properties are typical of BL Lacs. Furthermore, the values of their radio-optical spectral index overlap with those characterizing BL Lacs.
Among the 36 LPBLs identified in Paper I, 35 objects are in the redshift range 0.05 <z ≤ 0.15 and, as discussed in that paper, form a complete sample. Among them, we realized that in the object with ID=9591 the radio source is actually not associated with the optical galaxy. Indeed, the offset between the radio and optical sources is 4 8. In all other objects the offset is significantly smaller with a distribution having a median value of only 0
8. In all other objects the offset is significantly smaller with a distribution having a median value of only 0 3. We then remove it from the sample. Therefore, we are left with 34 objects, which are listed in Table 1.
3. We then remove it from the sample. Therefore, we are left with 34 objects, which are listed in Table 1.
3. Data selection
In our search for multiwavelength data for our 34 LPBLs, we focused on those bands that are more suitable to study the jet emission and on those catalogs/archives that are able to provide the largest coverage of our sample. The resulting broadband SEDs are shown in the appendix and two examples are shown in Fig. 2. Data downloaded from the Asi Science Data Center4 (ASDC) are added “in background” for completeness. From inspection of the SEDs it is clear that because of the host contamination, the spectral bands in which we can measure the jet emission are significantly less in LPBLs than in brighter blazars. Indeed, the host represents the bulk of the emission in the region spanning from the mid-infrared to the optical. As described in more detail below, the method used for our BL Lac selection enables us to isolate the jet emission in two bands located at the boundaries of this region. In the following, we discuss the data used to analyze the jet emission in the various bands.
The 34 BL Lac objects identified by Capetti & Raiteri (2015) and their k-corrected luminosities in the various bands.
3.1. Radio
Our 34 LPBLs were selected from the sample of 18286 radio sources built by Best & Heckman (2012). We use radio data from the Faint Images of the Radio Sky at Twenty-cm (FIRST) survey. Therefore, our reference radio frequency is 1.4 GHz.
In general, there are many data available in the radio band. In particular, for 22 LPBLs the Green Bank survey (Gregory & Condon 1991) provides information at 4.8 GHz. The average radio spectral index between 1.4 and 4.8 GHz is 0.02 with a standard deviation of 0.07. This confirms that we are dealing with objects with flat radio spectra, as expected for BL Lacs. The scatter of radio data for the same source is likely due to the jet emission variability and to different spatial resolution. Only a few objects have millimeter observations and these are not further considered.
3.2. Infrared
In the infrared we use the all-sky survey made by the WISE satellite (Wright et al. 2010), which provides magnitudes in the four filters W1 (3.4 μm), W2 (4.6 μm), W3 (12 μm), and W4 (22 μm). Cross-match with the AllWISE catalog5 was performed with a 3 arcsec radius (see Paper I).
We choose 12 μm as the reference wavelength in the infrared to reduce the strong contamination by the host galaxy light and, at the same time, have accurate data. We calculate the host contribution at the W3 wavelength by normalizing the SWIRE template of a 13 Gyr old elliptical galaxy6 (Polletta et al. 2007) to the W2 value (see Fig. 2). This contribution is then subtracted to the AllWISE W3 flux density to get the jet emission at that wavelength. This correction is likely overestimated, since it assumes that the whole emission in W2 is from the host galaxy; however, it has a negligible effect on the W3 value because of the steep fall of the galaxy emission going toward the far infrared. Indeed, the host contribution in W3 is only about 1% of the jet contribution.
3.3. Optical
We calculate the jet flux density Fo at 3900 Å rest frame from the Dn(4000) values derived from the SDSS spectra by the group from the Max Planck Institute for Astrophysics and Johns Hopkins University7 (Brinchmann et al. 2004; Tremonti et al. 2004),
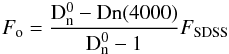 where FSDSS is the SDSS flux density at 3900 Å (reddening-corrected), and
where FSDSS is the SDSS flux density at 3900 Å (reddening-corrected), and 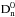 is the Dn(4000) value for quiescent galaxies, which slightly changes with redshift (see Paper I).
is the Dn(4000) value for quiescent galaxies, which slightly changes with redshift (see Paper I).
3.4. X-rays
Most of our sources have X-ray flux measurements. In principle, these could also be affected by the emission from the host hot coronae. However, the LPBL X-ray luminosity usually exceeds those measured from the galactic components, which are generally smaller than 1042erg s-1 (Fabbiano et al. 1992).
Flux densities at 1 keV were derived from the ROSAT All Sky Survey (RASS), which provides the source count rate in the 0.1–2.4 keV energy range. Counts-to-flux conversion factors are given for three possible photon spectral indices Γx = 1,2,3. Adopting a search radius of 30 arcsec, we found seven sources in the RASS Faint Source Catalog8 and 17 in the Bright Source catalog9 (Voges et al. 1999). Since in general we do not know the spectral slope of each source, we consider all the three possibilities and correct for Galactic absorption using WebPIMMS10. Figure 3 shows the ROSAT count rates corresponding to an un-absorbed flux of 10-11 erg cm-2 s-1 as a function of NH for the three spectral indices. The spread of the count rate due to different slopes is minimum for log NH = 20.2–20.3 [cm-2], and grows for both increasing and decreasing Galactic absorption. We fit the three relationships with fourth-order polynomial curves and apply them to find the de-absorbed flux corresponding to our LPBLs count rates.
For the following analysis, we use the 1 keV de-absorbed flux densities obtained with Γx = 2. However, given the distribution of column densities for our LPBLs, since all but one (ID=1103) of them is 20.0 ≲ log NH ≲ 20.7 [cm-2], the flux measurements obtained by adopting Γx = 1 or 3 differ by at most 40% from the adopted values.
 |
Fig. 3 ROSAT count rate corresponding to an unabsorbed flux of 10-11 erg cm-2 s-1 versus the Galactic hydrogen column density NH for the three values of the X-ray photon spectral index Γx = 1 (blue), 2 (red), and 3 (green). Plus signs indicate the values derived with WebPIMMS, and solid curves represent polynomial fits through them. Open circles correspond to the NH values of our LPBLs. |
For the ten sources lacking RASS data, we searched for observations with other X-ray satellites. We derive 1 keV flux densities of ID=3591 from the seven-year Swift-XRT point source catalog (1SWXRT; D’Elia et al. 2013). In the case of ID=7186, we use the 3XMM-DR5 catalog11, containing source detections drawn from 13 yr of XMM-Newton observations (Rosen et al. 2015). We use Chandra data reported by the ASDC for ID=1087.
Taking into account that the faintest LPBL in the RASS has a count rate of 0.025 counts/s, we assume an upper limit of 0.02 counts/s for the remaining seven sources without X-ray detection. This corresponds to a flux of 1.12 × 10-13 erg cm-2 s-1 for a Γx = 2 spectral index, and implies 6–10 counts for typical exposure times of 300–500 s. The actual flux upper limits are obtained by correcting the limit to the count rate for Galactic absorption toward each individual source.
3.5. γ-rays
The Fermi Large Area Telescope Third Source Catalog (3FGL; Acero et al. 2015) includes the first four years of data from the mission. We found 13 Fermi counterparts to our objects, up to a maximum distance of ~400 arcsec. In the catalog, the spectra of all these objects have been fitted with a power law, which is plotted in the SEDs reported in the appendix with its uncertainties on both the flux and spectral index (giving rise to a “butterfly”). According to the 3FGL, only one object, ID=3403, has a possible association with a TeV source.
Classification of the LPBLs into the various BL Lacs groups based on the ratio between X-ray to radio luminosities or, equivalently, to the radio-X-ray spectral index.
In summary, to analyze the jet emission in LPBLs, we can rely on data in the radio, mid-infrared, optical, X rays (for most of them), and γ rays (for some of them).
Even if all objects span a small range of redshift, we need to perform k-correction to derive rest-frame luminosities (see Table 1) and colors. When k-correcting (or transforming flux densities from one frequency to another inside the same band), we need spectral indices. In the radio we assume αr = 0, while at γ rays we use the specific index of each source. In more detail, to calculate the rest-frame 1 GeV luminosity Lγ reported in Table 1, we transformed the flux density at the pivot energy (energy at which the error is minimum) into flux density at 1 GeV and then k-corrected, in both cases, with the specific spectral index of each source given in the 3FGL. For the other bands we follow F98. Since we do not know a priori what type of BL Lac objects we are dealing with, we use average values between those corresponding to the Slew and 1 Jy samples, namely, αi = 0.70, αo = 0.94, αx = 1.325. We stress that because of the limited range of redshift of the LPBLs sample, the corrections are very small and the precise values adopted do not affect significantly our analysis.
4. The nature of LPBLs
One useful quantity to establish the flavor of BL Lacs is the ratio of the X-ray to radio fluxes. As mentioned in the Introduction, according to Padovani & Giommi (1995) and Bonnoli et al. (2015), this ratio should be greater than 200 and 10000 to define an HBL and EHBL, respectively. Equivalently, F98 defined HBL as those objects with αrx ≲ 0.75, while LBL have αrx ≳ 0.75.
 |
Fig. 4 Broadband spectral indices for the objects in our LPBL sample, separating LBL (red circles) from HBL (blue diamonds) and EHBL (green squares). |
 |
Fig. 5 Upper panel: radio-to-γ-ray SEDs for the 34 objects analyzed in this paper (colored dots). Solid lines represent parabolic fits to the radio-X-ray data. Vertical dotted lines identify the parabola apices, which give an indication of the synchrotron peak position. For the objects without X-ray detection, the peak location should be considered an upper limit. Lower panels: luminosities versus the synchrotron peak frequency. Blue dots, red diamonds, green squares, and pink asterisks refer to radio, infrared, optical, and X-ray bands, respectively. In all panels, upper limits due to the lack of detection in the X-ray band are indicated with arrows. |
 |
Fig. 6 γ-ray photon spectral index Γγ versus the radio-X-ray energy spectral index αrx. Red dots represent LBL, blue diamonds HBL, and green squares EHBL. |
We calculate broadband spectral indices for our LPBLs after dereddening and k-correction. To ease the comparison with previous results, radio fluxes were converted from 1.4 to 5 GHz and optical fluxes from 3900 to 5500 Å.
In Table 2 we list the ratio of the X-ray to the radio luminosity and the radio-X-ray spectral index. Based on these parameters, which give the same indication, seven objects are LBL, 19 are HBL, and four are EHBL. For the remaining four objects, all without an X-ray detection, the resulting lower limit on αrx does not lead to a secure classification.
As mentioned in the Introduction, we are dealing with sources whose flux is variable at all wavelengths with timescales ranging from minutes to months. We are using catalog data, which are not taken simultaneously, and this may cause some distortion of the SED. However, while the individual classifications must be taken with some caution, we do not expect that variability can alter the conclusions drawn from a sizeable sample of objects.
In Fig. 4 we show the optical-X-ray versus radio-X-ray and the radio-optical versus optical-X-ray spectral indices for the three BL Lac classes. They are in good agreement with the results obtained by Donato et al. (2001), because the different BL Lac classes cover the same range of values. The positive dependence of αox on αrx is a signature of the SED curvature that increases from EHBL toward LBL. This effect can be studied in a more quantitative way by reproducing the SEDs with a log-parabolic model.
In Fig. 5 we show the radio, infrared, optical, X-ray, and γ-ray luminosities of our LPBLs (see Table 1). The radio–X-ray SEDs are fitted with a log-parabolic curve, whose apex roughly represents the synchrotron peak. Although in principle this should be determined through a synchrotron emission model, the uncertainty derived from the choice of the model parameters makes a simple parabolic fit equally valid for our purposes. In the lower panel, luminosities in the various bands are plotted as a function of the synchrotron peak frequency νpeak. There is no significant trend of νpeak with Lr, Li, or Lo. Conversely, νpeak clearly increases with Lx. This is the natural consequence of the large spread in the X-ray luminosities of the various BL Lac classes.
 |
Fig. 7 Examples of the SED of two LPBLs, namely ID=2440 and ID=2061. The solid line represents a logarithmic parabolic fit, including the radio, infrared, optical, and X-ray data points, which does not match the infrared and optical data. These are instead well reproduced by a three-point fit excluding the X-ray datum (dot-dashed line). The case shown in the left panel indicates that the X-ray emission is likely dominated by the inverse-Compton component; that in the right panel highlights how the upper limit to the X-ray flux leads to a large overestimate of the synchrotron peak frequency. The grey line represents an elliptical galaxy template normalized in W2 and the grey dots show data collected from the ASDC. |
Our estimate of the synchrotron peak frequency ranges from log ν = 14.3 to 20.8 (see Table 2), i.e., from the infrared to hard X-rays, confirming that the sample includes both LBL as well as HBL and EHBL. For the sources not detected in X-rays, the peak location must be considered as an upper limit. By adopting log νpeak = 15 as a dividing value between LBL and HBL, overall we recover a classification in concordance with that based on the X-rays/radio comparison. There are only three exceptions (indicated with an asterisk in Table 2). For these objects we look for further data that can constrain their nature. The X-ray spectrum of ID=3591 is soft (XRT data from the ASDC) and this would define it as an HBL. We have γ-ray information from Fermi for the other two objects. In Fig. 6 we plot Γγ versus αrx, highlighting the various BL Lac classes. As expected, Γγ increases with αrx and all HBL have Γγ< 2 but one, ID=10537, whose nature thus remains unclear. The LBL definition of ID=2440 is instead confirmed by its very soft γ-ray spectrum. Furthermore, for two LPBLs not classified with the X-rays/radio method, the peak location suggests a definition as LBL (these objects are denoted as “LBL?” in Table 2).
However, in LBLs the X-ray emission is generally dominated by the inverse-Compton contribution. Therefore, a fit to the synchrotron bump including the X-ray emission overestimates νpeak. We tested the relevance of this effect by fitting the radio-to-optical SED of our sources, and indeed we found that in some cases the three-point fit gives a νpeak that is significantly lower than the four-point fit, and as low as log νpeak ~ 13.5 (see Fig. 7)12. In particular, the νpeak shift is significant for most objects without an X-ray detection and, in general, means that the four-point fit overestimates the synchrotron contribution to the X-ray flux.
At the opposite end of the νpeak distribution, we obtained formal values as high as 1020.8 Hz for the EHBLs, which are not well constrained by the available measurements, however. In two of such sources the SED shown in the appendix suggests a peak location between 1018–1019 Hz.
BL Lacs drawn from flux limited radio samples are known to include mostly LBL (e.g., Padovani et al. 2003). Conversely, the LPBL sample considered here, although initially selected in the radio band, is biased against the selection of LBL. Indeed, one of the requirements is a significant dilution of the host emission by the nonthermal emission across the Ca II break; sources peaking at low energies, well before the optical band, are less likely to be selected. Indeed, as shown by Fig. 15 in Paper I, the selection function of LPBL has a cut-off at a luminosity that shifts toward a higher power when αro increases, thus disfavoring the detection of LBL with respect to HBL.
In summary, our classification of LPBLs in their different flavors shows that while the bulk of our LPBL sample is formed by HBLs (or EHBLs), despite the negative bias in our sample about one quarter of them are LBLs.
According to F98, all the sources with log Lr< 42 at 5 GHz have log νpeak> 15.5. When correcting for the difference in cosmology, the above luminosity limit translates into log Lr< 41.2 at 1.4 GHz. All our LPBLs but two fulfill this requirement, but they are characterized by peak frequencies that, for the objects that lack an X-ray detection, may reach log νpeak ~ 13.5. We recall that Padovani et al. (2003) found six BL Lacs under the above luminosity limit with peak frequencies extending down to ~1013 Hz and seven were found by Antón & Browne (2005) down to ~1014 Hz. In both cases, the minimum 1.4 GHz luminosity of the objects is log Lr ~ 40.2, so our analysis confirms and extends the results of these previous studies to lower luminosities.
5. The blazar sequence
As mentioned in the Introduction, F98 identified a continuous trend of the blazar SEDs, where BL Lacs of lower radio power exhibit higher synchrotron and inverse-Compton peak frequencies and lower Compton dominance with respect to the higher power objects. In their work, the faintest SED has a median 5 GHz luminosity13 of log Lr = 40.97, and according to their model the peak synchrotron frequency is around log ν = 16.5 [Hz]. Subsequently, Donato et al. (2001) added a hard X-ray point to the F98 SEDs and slightly modified the model, so that the peak frequency of the faintest SED shifted to log ν ~ 16. If instead we fit their radio-to-hard-X points with a simple log-parabolic curve, we get a peak frequency of log ν = 16.2. The data points of the faintest three SED in these works are plotted in Fig. 8 and some of their properties are reported in Table 3.
 |
Fig. 8 Median SED for the 34 objects analyzed in this paper (black dots). The red and blue dots represent the SEDs obtained by splitting the sample into two groups of increasing radio luminosities (see text and Table 3). Gray symbols refer to the SEDs of the three faintest subsamples in the F98 work, complemented by the hard X-ray data points from Donato et al. (2001). The curves are log-parabolic fits to the radio-to-X-ray median luminosities with the peak indicated with vertical lines. |
Properties of the median BL Lacs SED.
Following F98 we consider the median luminosities in the various bands of all 34 LPBLs, obtaining the values tabulated in Table 3 and plotted in Fig. 8. Building median SEDs has the advantage of reducing the effects of variability when nonsimultaneous data are used.
The presence of upper limits to the X-ray fluxes does not affect the estimate of the median luminosity in this band because they are all located within the faintest half of the distribution. For this reason, the median is well defined14. The radio luminosity of the faintest median SED in F98 and Donato et al. (2001) is similar to that of our sample of LPBLs. However, the two SEDs diverge at increasing frequencies, reaching a difference of a factor ~40 at 1 keV. Indeed, a log-parabolic fit gives a peak frequency at log ν = 15.3 for the LPBLs, which is substantially lower than that found by F98 and Donato et al. This highlights that our sample is very different from that of the faintest objects analyzed by F98 because it includes a much higher fraction of LBLs.
We can further split our sample into groups of radio luminosity. We define two subsamples of equal size. The median luminosities are reported in Table 3 and shown in Fig. 8. The median γ-ray luminosity is only defined for the brighter sample. There are no significant differences in both shape and peak frequency between these two SEDs, despite the difference in radio luminosity. Moreover, the corresponding νpeak lies in between the peaks of the two least luminous groups considered by F98. Apparently, the trend of increasing νpeak at decreasing log Lr does not apply to the least luminous BL Lacs.
 |
Fig. 9 Same as Fig. 8, but now different colors refer to the three flavors of BL Lac objects (red=LBL, blue=HBL, green=EHBL). |
Because of the different flavor of BL Lacs in our sample, the above described median SEDs are the result of a mixture of sources with different properties. Therefore, we calculate the median SEDs for LBL, HBL, and EHBL separately. The result is shown in Fig. 9, where the parabolic fits are made through the radio-to-X-ray data for the HBL and EHBL cases, while for the LBL we do not consider the X-ray point for the above discussed reasons. Aside from the obvious shift of νpeak, there are two notable features. The first is the small difference in radio luminosity among the three classes, where LBL (EHBL) are only a factor of two brighter (fainter) than HBL. The second is the similarity of our LBL SED shape with that of the LBL in F98, which have radio luminosities 30–600 times higher.
6. The beaming effect
Up to now we have not considered the fact that blazars are beamed sources with their luminosities enhanced by relativistic Doppler boosting, which also blueshifts the synchrotron peak frequency. The relationship between the emitted luminosities L′ and their beamed counterparts is L = δ4L′, where δ is the Doppler factor15. Analogously, the frequencies transform as ν = δν′.
Nieppola et al. (2008) considered Doppler factors derived from the study of the total flux density variability and found that they anticorrelate with the peak frequency. These authors suggested that the anticorrelation between Lr and νpeak becomes a positive correlation when correcting for beaming. Nieppola et al. (2008) used Doppler factors inferred from the analysis of radio data. However, the jet radiation at different frequencies is likely emitted from different regions along the jet, each with its own Doppler factor. Indeed, the usually long (weeks to months) delay of the radio variations after the higher energy variations (in particular optical and γ-ray), and the longer radio variability timescales (e.g., Raiteri et al. 2008; Villata et al. 2009) suggest that the radio emission comes from a more external and extended jet zone than that producing the high-frequency synchrotron radiation. Taking into account that the Doppler factor δ depends on both the bulk Lorentz factor and the viewing angle, accelerating/decelerating processes and/or bends in the jet structure (e.g., Lister 2001; Lister et al. 2013) would cause a spread of δ values within the same source in different bands. In turn, this would produce a distortion of the observed SED shape with respect to the intrinsic SED shape.
7. Summary and conclusions
We explored the properties of the SED of a complete sample of 34 BL Lacs of low power. These objects have been selected in the redshift range 0.05 <z< 0.15 in Paper I based on a new diagnostic plane that includes the W2−W3 color from WISE and the Dn(4000) index derived from the SDSS.
We collected multiwavelength data focusing on those bands that allow us to study the jet emission. We have a complete coverage at the frequencies used for the sample selection (1.4 GHz, 12 μm, and rest-frame 3900 Å). X-ray fluxes are available for most of the sources (27 out of 34), while only 13 of them are detected at γ-rays.
We classified the LPBL based on the ratio between radio and X-rays luminosities or, equivalently, on the radio-X-ray spectral index, finding that seven of them are LBL, 19 are HBL, and four are EHBL. The lack of X-rays data prevent us from obtaining a robust classification for the last four objects.
We derived an estimate of the synchrotron peak frequency from each SED through a log-parabolic fit to the k-corrected jet luminosities. Overall, the mix of BL Lac types is confirmed by the location of the peak frequency, ranging from log ν = 14.3 to 20.8, i.e., from the infrared to the hard X-rays. However, the SEDs of some LPBLs are better described by a three-point fit (excluding the X-ray data). For these sources, the peak frequency shifts at much lower energies, as low as log νpeak ~ 13.5, which implies that the X-ray emission also receives a contribution from the inverse-Compton process, as expected in LBLs. LPBLs with synchrotron peaks located at even lower energies would be very difficult to find with our method. Indeed, the nonthermal contribution to the optical flux might be insufficient to lower the Dn(4000) and the lines EW might not be significantly reduced with respect to the parent population.
We estimated the median SED for the sample as a whole and for two subsamples based on different thresholds of radio luminosity. The advantage of this approach is to mitigate the effects of variability when nonsimultaneous data are used, as in our case. We found that the peak frequencies obtained with such an analysis all fall at log νpeak ~ 15.5 Hz. These values are lower than that characterizing the least luminous group of BL Lacs considered by F98 that have similar radio luminosity of our LPBLs. In our sample, the sources classified as LBL, HBL, or EHBL do not differ significantly in radio luminosity. The peak frequency of the median SED of LBLs is located at log νpeak ~ 14.6, consistent with the value derived by F98 for much more luminous BL Lacs.
Apparently, there is no clear connection between the SED shape and the radio power within the LPBL sample. At least at low luminosity, BL Lacs do not populate any preferred region in the log Lr versus νpeak plane and the trend of increasing νpeak at decreasing Lr does not extend to the least luminous BL Lacs. The reason is the presence of a significant fraction of LBL objects. This is remarkable when considering that our LPBL sample is biased against the selection of LBLs.
Furthermore, the SED of the LBLs included in our sample is very similar to that of radio-selected BL Lacs that are up to two-three orders of magnitude more luminous. These results cast serious doubts on the idea that the radio luminosity is the main driving parameter of the multiwavelength properties of BL Lacs.
In contrast, there is a clear positive dependence of νpeak on log Lx. This implies that X-ray flux-limited samples necessarily lead to the selection of objects with synchrotron peaks at higher energies. Previous works had already suggested that the blazar sequence is an artifact due to biases in the samples used by F98. The present analysis confirms this result with a much larger sample of LPBLs reaching luminosities one order of magnitude lower.
Finally, the shape of the intrinsic SED can be distorted by relativistic beaming in case there are accelerating/decelerating processes in the jet and/or bends in the jet structure. This suggests caution in interpreting the observed spread in the spectral behavior of BL Lacs.
An alternative definition names low-, intermediate-, and high-synchrotron peaked (LSP, ISP, and HSP) BL Lacs as those sources with the synchrotron peak frequency < 1014, between 1014 and 1015, and > 1015 Hz, respectively (Abdo et al. 2010).
The Dn(4000) index represents the ratio between the flux densities on the red (4000–4100 Å) and blue (3850–3950 Å) side of the Ca II spectral break (Balogh et al. 1999).
To make a comparison with the SEDs in the appendix easier, here the SEDs are plotted in the observed log νFν diagram. As a consequence, their νpeak, even when corrected for redshift, may be slightly different from the values reported in Table 2.
We have lowered by a factor 1.85 and 1.76 the points of F98 and Donato et al. (2001), respectively, to account for the differences in the choice of cosmological parameters.
Acknowledgments
Part of this work is based on archival data, software, or online services provided by the ASI Science Data Center (ASDC). This research has made use of data obtained from the 3XMM XMM-Newton serendipitous source catalog compiled by the ten institutes of the XMM-Newton Survey Science Centre selected by ESA. Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the US Department of Energy Office of Science. The SDSS-III website is http://www.sdss3.org/. SDSS-III is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS-III Collaboration, including the University of Arizona, the Brazilian Participation Group, Brookhaven National Laboratory, University of Cambridge, Carnegie Mellon University, University of Florida, the French Participation Group, the German Participation Group, Harvard University, the Instituto de Astrofisica de Canarias, the Michigan State/Notre Dame/JINA Participation Group, Johns Hopkins University, Lawrence Berkeley National Laboratory, Max Planck Institute for Astrophysics, Max Planck Institute for Extraterrestrial Physics, New Mexico State University, New York University, Ohio State University, Pennsylvania State University, University of Portsmouth, Princeton University, the Spanish Participation Group, University of Tokyo, University of Utah, Vanderbilt University, University of Virginia, University of Washington, and Yale University. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, ApJ, 708, 1310 [NASA ADS] [CrossRef] [Google Scholar]
- Acero, F., Ackermann, M., Ajello, M., et al. 2015, ApJS, 218, 23 [Google Scholar]
- Acharya, B. S., Actis, M., Aghajani, T., et al. 2013, Astropart. Phys., 43, 3 [Google Scholar]
- Antón, S., & Browne, I. W. A. 2005, MNRAS, 356, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Balogh, M. L., Morris, S. L., Yee, H. K. C., Carlberg, R. G., & Ellingson, E. 1999, ApJ, 527, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Best, P. N., & Heckman, T. M. 2012, MNRAS, 421, 1569 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnoli, G., Tavecchio, F., Ghisellini, G., & Sbarrato, T. 2015, MNRAS, 451, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Caccianiga, A., & Marchã, M. J. M. 2004, MNRAS, 348, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Capetti, A., & Raiteri, C. M. 2015, A&A, 580, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiaberge, M., & Marconi, A. 2011, MNRAS, 416, 917 [NASA ADS] [CrossRef] [Google Scholar]
- D’Elia, V., Perri, M., Puccetti, S., et al. 2013, A&A, 551, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donato, D., Ghisellini, G., Tagliaferri, G., & Fossati, G. 2001, A&A, 375, 739 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabbiano, G., Kim, D.-W., & Trinchieri, G. 1992, ApJS, 80, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fossati, G., Maraschi, L., Celotti, A., Comastri, A., & Ghisellini, G. 1998, MNRAS, 299, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., & Tavecchio, F. 2008, MNRAS, 387, 1669 [NASA ADS] [CrossRef] [Google Scholar]
- Giommi, P., Padovani, P., Polenta, G., et al. 2012, MNRAS, 420, 2899 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, P. C., & Condon, J. J. 1991, ApJS, 75, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Landt, H., & Bignall, H. E. 2008, MNRAS, 391, 967 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L. 2001, ApJ, 562, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., Aller, M. F., Aller, H. D., et al. 2013, AJ, 146, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, E. T., Fossati, G., Georganopoulos, M., & Lister, M. L. 2011, ApJ, 740, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Nieppola, E., Valtaoja, E., Tornikoski, M., Hovatta, T., & Kotiranta, M. 2008, A&A, 488, 867 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Padovani, P., & Giommi, P. 1995, ApJ, 444, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, P., Perlman, E. S., Landt, H., Giommi, P., & Perri, M. 2003, ApJ, 588, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Polletta, M., Tajer, M., Maraschi, L., et al. 2007, ApJ, 663, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Raiteri, C. M., Villata, M., Larionov, V. M., et al. 2008, A&A, 480, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosen, S. R., Webb, N. A., Watson, M. G., et al. 2015, A&A, accepted [arXiv:1504.07051] [Google Scholar]
- Stickel, M., Fried, J. W., Kuehr, H., Padovani, P., & Urry, C. M. 1991, ApJ, 374, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Stocke, J. T., Morris, S. L., Gioia, I. M., et al. 1991, ApJS, 76, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Tremaine, S., Gebhardt, K., Bender, R., et al. 2002, ApJ, 574, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Villata, M., Raiteri, C. M., Larionov, V. M., et al. 2009, A&A, 501, 455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voges, W., Aschenbach, B., Boller, T., et al. 1999, A&A, 349, 389 [NASA ADS] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Spectral energy distributions
In Fig. A.1, we show the broadband SEDs of our sources. They contain the FIRST as well as other radio data (NVSS; Green Bank, VLBI); the AllWISE flux densities in the W1, W2, W3, and W4 bands, the J,H,K flux densities from the 2MASS; the SDSS spectrum; the RASS and 3XMM X-ray data, and the 3FGL γ-ray fluxes. The near-infrared, optical, and X-ray data have been corrected for Galactic absorption.
The RASS 0.1–2.4 fluxes have been converted into 1 keV flux densities with all the three possible spectral indices Γx = 1,2,3 to quantify the uncertainties. At γ rays, we show the 3FGL data for the various energy bins, the flux density at the pivot energy, and the butterfly resulting from the power-law spectral fit.
 |
Fig. A.1 Broadband SEDs of the 34 LPBLs analysed in this paper. Red dots represent flux densities derived from the FIRST, AllWISE, 2MASS, RASS, 3XMM, and 3FGL catalogs. Blue plus signs show other radio data and the γ-ray flux density at the pivot energy; the black crosses represent the 1.4 GHz FIRST data converted into 5 GHz ones with αr = 0. The SDSS spectrum and the Fermi power-law fit butterfly are plotted in blue. Near-infrared, optical, and X-ray data have been corrected for Galactic absorption. The black circles highlight the reference radio (1.4 GHz), infrared (W3 band), optical (3900 Å rest-frame), X-ray (1 keV), and γ-ray (1 GeV) jet flux densities. In the W3 band, the jet flux density has been corrected for the host contamination estimated from an elliptical galaxy template (grey line) normalized in the W2 band. In the optical, the jet contribution has been derived from the Dn(4000). Grey dots show data downloaded from the ASDC. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
We also highlight the reference radio (1.4 GHz), infrared (W3 band), optical (3900 Å rest-frame), X-ray (1 keV), and γ-ray (1 GeV) jet flux densities (see Sect. 3). In the W3 band, the jet flux has been corrected for the host contamination estimated from an elliptical galaxy template normalized in the W2 band. The optical jet emission has been derived from the Dn(4000). For the sources for which no RASS detection was available, we give upper limits obtained by assuming a ROSAT count rate of 0.02 counts/s. The 1 GeV flux density was obtained from the flux density at the pivot energy. We also plot data downloaded from the ASDC.
Appendix A.1: Notes on individual sources
-
ID=507
The soft X-ray spectrum from XMM-Newton confirmsits HBL nature.
-
ID=786
Its HBL flavor is verified by the soft X-ray and hard γ-ray spectra.
-
ID=1103
The soft X-ray and mildly hard γ-ray spectra agree with an HBL classification.
-
ID=1315
Its HBL nature is confirmed by the soft X-ray and hard γ-ray spectra.
-
ID=1845
Its HBL flavor is verified by the soft X-ray and hard γ-ray spectra.
-
ID=1906
Its HBL nature is confirmed by the soft X-ray and hard γ-ray spectra.
-
ID=2061
LBL with no detection in X-rays. With respect to the four-point fit to the SED, the three-point fit shifts log νpeak from <14.5 to 13.7.
-
ID=2281
LBL with no detection in X-rays; log νpeak decreases from <14.9 to 14.1, changing the SED fit from four to three points.
-
ID=2440
Its LBL definition is confirmed by its hard X-ray and soft γ-ray spectra, which also suggests a Compton dominance. Indeed, log νpeak goes from <15.1 in the four-point fit to the SED to 14.0 in the three-point fit.
-
ID=3091
We classified it as HBL, however, log νpeak shifts from 15.1 in a four-point to 13.7 in a three-point SED fit. It may be that the SDSS spectrum met the source in a particularly low optical state.
-
ID=3403
This is the famous EHBL 1ES 1426+426, which has been extensively studied in X-rays. Indeed, its SED reveals an extremely bright X-ray flux and an exceptionally hard γ-ray spectrum, clearly identifying the source as an EHBL. The value log νpeak = 20.8 we found is clearly overestimated; the XMM-Newton and ASDC data allow us to position it at log νpeak ~ 17–18.
-
ID=3591
Its LBL classification based on the radio and X-ray brightness is contradicted by the high synchrotron peak frequency as well as a soft X-ray (XRT) and a flat UV (UVOT+GALEX) spectrum (ASDC data). The 5 GHz flux density calculated from its 1.4 GHz FIRST value adopting αr = 0 is much higher than the other radio data, so that the wrong LBL definition is likely due to an underestimate of its Lx/Lr and overestimate of its αrx.
-
ID=4022
Its HBL nature is confirmed by the high X-ray flux with a soft X-ray and a hard γ-ray spectrum.
-
ID=4156
LBL without X-ray detection with log νpeak shifting from <14.7 in a four-point to 14.1 in a three-point SED fit.
-
ID=4601
LBL without X-ray detection, with log νpeak decreasing from <14.9 to 14.4 when changing the SED fit from four to three points.
-
ID=4756
The soft X-ray spectrum from XMM-Newton agrees with its HBL classification.
-
ID=5076
Its LBL flavor is confirmed by the low X-ray flux compared to the infrared and optical fluxes and by its soft γ-ray spectrum.
-
ID=6428
EHBL with a clearly overestimated log νpeak = 20.4. The ASDC data show that its X-ray flux is extremely variable and that ROSAT found the source in a very bright state. Nonetheless, when considering the other X-ray data also, the source still appears as an HBL, which is proved by the mildly hard γ-ray spectrum.
-
ID=6943
EHBL with a clearly overestimated log νpeak = 20.8. The XMM-Newton data confirm the X-ray brightness given by the RASS and add spectral information in favor of its EHBL nature, suggesting a log νpeak of 17–18.
-
ID=7186
Its HBL classification is strengthened by the soft XMM-Newton X-ray spectrum.
-
ID=9640
A high X-ray state compared to the infrared and optical states, coupled with the hard X-ray spectrum detected by XMM-Newton, confirm its EHBL nature and suggest that the synchrotron peak falls at log ν> 18.
-
ID=10537
The flavor of this BL Lac is difficult to assess. Both the four-point and three-point SED fits fail to give a satisfactory reproduction of the data. The high optical flux suggests an HBL classification, which is supported by a possible soft X-ray spectrum, but contradicted by the mildly soft γ-ray spectrum.
All Tables
The 34 BL Lac objects identified by Capetti & Raiteri (2015) and their k-corrected luminosities in the various bands.
Classification of the LPBLs into the various BL Lacs groups based on the ratio between X-ray to radio luminosities or, equivalently, to the radio-X-ray spectral index.
All Figures
 |
Fig. 1 LPBLs identified in Paper I (blue circles). They lie in the “forbidden zone” of the Dn(4000) versus the W2–W3 diagram, which is defined by the Dn(4000) limit obtained by requiring that the nonthermal jet contribution is at least 1/3 of the host galaxy one at 3900 Å, and by the 1-sigma lower limit to the average relation holding for the 21 065 bright nearby galaxies (black dots; see Paper I for details). |
| In the text | |
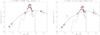 |
Fig. 2 Examples of the SED of two LPBLs, namely ID=786 and ID=1845. We show data analyzed by us (colored symbols) as well as data downloaded from the ASDC (grey dots); see Fig. A.1 for a full description. The near-IR, optical, and X-ray data have been corrected for Galactic absorption. We overplot the logarithmic parabolic fit through the data points at 1.4 GHz, 12 μm, rest-frame 3900 Å, and 1 keV (black empty circles), where the infrared and optical fluxes have been corrected for the host galaxy contribution. The grey line represents an elliptical galaxy template normalized to the W2 flux density. |
| In the text | |
 |
Fig. 3 ROSAT count rate corresponding to an unabsorbed flux of 10-11 erg cm-2 s-1 versus the Galactic hydrogen column density NH for the three values of the X-ray photon spectral index Γx = 1 (blue), 2 (red), and 3 (green). Plus signs indicate the values derived with WebPIMMS, and solid curves represent polynomial fits through them. Open circles correspond to the NH values of our LPBLs. |
| In the text | |
 |
Fig. 4 Broadband spectral indices for the objects in our LPBL sample, separating LBL (red circles) from HBL (blue diamonds) and EHBL (green squares). |
| In the text | |
 |
Fig. 5 Upper panel: radio-to-γ-ray SEDs for the 34 objects analyzed in this paper (colored dots). Solid lines represent parabolic fits to the radio-X-ray data. Vertical dotted lines identify the parabola apices, which give an indication of the synchrotron peak position. For the objects without X-ray detection, the peak location should be considered an upper limit. Lower panels: luminosities versus the synchrotron peak frequency. Blue dots, red diamonds, green squares, and pink asterisks refer to radio, infrared, optical, and X-ray bands, respectively. In all panels, upper limits due to the lack of detection in the X-ray band are indicated with arrows. |
| In the text | |
 |
Fig. 6 γ-ray photon spectral index Γγ versus the radio-X-ray energy spectral index αrx. Red dots represent LBL, blue diamonds HBL, and green squares EHBL. |
| In the text | |
 |
Fig. 7 Examples of the SED of two LPBLs, namely ID=2440 and ID=2061. The solid line represents a logarithmic parabolic fit, including the radio, infrared, optical, and X-ray data points, which does not match the infrared and optical data. These are instead well reproduced by a three-point fit excluding the X-ray datum (dot-dashed line). The case shown in the left panel indicates that the X-ray emission is likely dominated by the inverse-Compton component; that in the right panel highlights how the upper limit to the X-ray flux leads to a large overestimate of the synchrotron peak frequency. The grey line represents an elliptical galaxy template normalized in W2 and the grey dots show data collected from the ASDC. |
| In the text | |
 |
Fig. 8 Median SED for the 34 objects analyzed in this paper (black dots). The red and blue dots represent the SEDs obtained by splitting the sample into two groups of increasing radio luminosities (see text and Table 3). Gray symbols refer to the SEDs of the three faintest subsamples in the F98 work, complemented by the hard X-ray data points from Donato et al. (2001). The curves are log-parabolic fits to the radio-to-X-ray median luminosities with the peak indicated with vertical lines. |
| In the text | |
 |
Fig. 9 Same as Fig. 8, but now different colors refer to the three flavors of BL Lac objects (red=LBL, blue=HBL, green=EHBL). |
| In the text | |
 |
Fig. A.1 Broadband SEDs of the 34 LPBLs analysed in this paper. Red dots represent flux densities derived from the FIRST, AllWISE, 2MASS, RASS, 3XMM, and 3FGL catalogs. Blue plus signs show other radio data and the γ-ray flux density at the pivot energy; the black crosses represent the 1.4 GHz FIRST data converted into 5 GHz ones with αr = 0. The SDSS spectrum and the Fermi power-law fit butterfly are plotted in blue. Near-infrared, optical, and X-ray data have been corrected for Galactic absorption. The black circles highlight the reference radio (1.4 GHz), infrared (W3 band), optical (3900 Å rest-frame), X-ray (1 keV), and γ-ray (1 GeV) jet flux densities. In the W3 band, the jet flux density has been corrected for the host contamination estimated from an elliptical galaxy template (grey line) normalized in the W2 band. In the optical, the jet contribution has been derived from the Dn(4000). Grey dots show data downloaded from the ASDC. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


