EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 586 (February 2016) A&A, 586 (2016) A54 Full HTML
Free Access
Issue
A&A
Volume 586, February 2016
Article Number A54
Number of page(s) 19
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201424020
Published online 26 January 2016

© ESO, 2016

1. Introduction

In recent years, a growing number of protoplanetary disks have been found to have a gap region between the inner near-infrared-emitting region and the outer disk (e.g., Espaillat et al. 2008; Benisty et al. 2010; Mulders et al. 2011; Honda et al. 2012; Maaskant et al. 2013; Matter et al. 2014). The mechanisms possibly involved in the formation of a gap include dynamical clearing by a giant planet, grain growth, and photoevaporation (Williams & Cieza 2011). These pre-transitional disks are likely in the intermediate evolutionary stage between an early-stage disk that is optically thick from the dust sublimation radius to the outer edge and a transitional disk, whose inner region is already cleared. Studies of pre-transitional disks are important to improve our understanding of disk evolution and planet formation.

Table 1

Observation log of our VLTI/AMBER observation of HD 144432.

HD 144432 is an isolated Herbig Ae star with spectral type A9/F0, and is likely a member of the star association SCO-B 2-2 at a distance of 145 ± 20 pc (Pérez et al. 2004, see also the discussion therein about the distance). The strong near-infrared (NIR) excess of this Herbig Ae star is a clear signature of hot dust.

In our previous simple temperature-gradient model of HD 144432 derived from infrared (IR) interferometric observations (Chen et al. 2012), the disk consists of two components. The inner region of the model disk is a narrow ring with an inner radius of ~0.21 AU, and an inner temperature of ~1600 K. The outer disk region extends from ~1 AU to ~10 AU with an inner-edge temperature of ~400 K. The lack of IR emission in the region from ~0.23 AU to ~1 AU is possibly a signature of a discontinuity in the dust distribution, and therefore a signature of the pre-transitional nature of the disk. However, there is an alternative interpretation of the emission-free region, which is that dust exists in this region but is shadowed by a puffed-up rim (Dullemond et al. 2001) so that it is too cold to emit effectively at IR wavelengths. In our previous work, we also found that an extended component that scatters stellar light is needed to account for the fact that even at short interferometric baselines (~9–20 m), the NIR visibilities are lower than one. Plausible origins of this scattering material include an infalling remnant envelope, dust entrained in the stellar wind/outflow (Monnier et al. 2006), or a flaring outer disk (Pinte et al. 2008). To obtain a more detailed modeling than in our previous paper of all available interferometric data, we performed radiative transfer modeling and present this in the present paper.

In this paper, we compare two-dimensional radiative transfer (RT) models with all available interferometric observations of HD 144432 to study the dust distribution around the object. We describe the data set in Sect. 2. The modeling process and model results are presented in Sect. 3. We discuss the results in Sect. 4 and present the conclusions in Sect. 5.

2. Observations and data reduction

We observed HD 144432 on 2009 Apr. 18 and 2010 Apr. 18 with the VLTI/AMBER instrument (see Table 1). The AMBER instrument is a near-infrared beam combiner that records three-beam interferograms (Petrov et al. 2007). The instrument was operated in the low spectral resolution mode (R = 35) and recorded fringes in the H and K bands simultaneously. The fringe tracker FINITO was not used. The observations of HD 144432 were conducted using the linear baseline configuration E0-G0-H0 1 and the triangle configuration D0-H0-G1 of the 1.8 m auxiliary telescopes (ATs). For data processing, we used the AMBER data reduction package amdlib 3.0 2. We selected 30% of the target and calibrator frames with the highest fringe signal-to-noise-ratio (SNR) to improve the visibility SNR (Tatulli et al. 2007) of each target and calibrator data set. Furthermore, we applied a method that equalizes the histograms of the optical path differences of the target and calibrator interferograms (Kreplin et al. 2012) to improve the calibration of the visibilities. On both nights we used the calibrator star HD 142669, which has a uniform disk diameter of dUD = 0.27 ± 0.05 mas3.

We complemented our data with existing data from the literature, including the K-band observation with KI (Monnier et al. 2005; Eisner et al. 2009), the H-band observation with IOTA (Monnier et al. 2006), the mid-infrared (MIR) interferometry with VLTI/MIDI (Leinert et al. 2004), as well as the spectral energy distribution (SED; Leinert et al. 2004).

3. Modeling

To interpret all the interferometric data, we employ Monte-Carlo radiative transfer (MCRT) modeling using the code RADMC-3D 4, which is the follow-up version of RADMC (Dullemond & Dominik 2004). The code RADMC has been intensively used in modeling circumstellar disks (e.g., Dominik et al. 2003; Pontoppidan et al. 2007; Kreplin et al. 2013). Both RADMC and RADMC-3D use the instant-re-emission method (Lucy 1999) and the immediate temperature correction method (Bjorkman & Wood 2001).

In the modeling process, we assume a distance of 145 pc and a stellar luminosity of 7.6 L⊙ (Pérez et al. 2004). For the star SED, we adopt the same Kurucz model as in our previous paper (Chen et al. 2012). The dust consists of astronomical silicate (Draine & Lee 1984) and amorphous carbon (Jager et al. 1998). We assume a grain size distribution with n(a) ∝ a-3.5 with small grains (amin = 0.01 μm, amax = 1.0 μm) and large grains (amin = 1.0 μm, amax = 1000 μm). 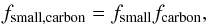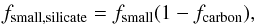We use the parameters fsmall and fcarbon to control the dust composition, so that the fractions of mass in small carbonaceous grains, small silicate grains, large carbonaceous grains, and large silicate grains are fsmall,carbon=fsmallfcarbon,\begin{eqnarray} f_\mathrm{small,carbon} = f_\mathrm{small} f_\mathrm{carbon} , \end{eqnarray}(1)fsmall,silicate=fsmall(1−fcarbon),\begin{eqnarray} f_\mathrm{small,silicate} = f_\mathrm{small} (1-f_\mathrm{carbon}) , \end{eqnarray}(2)flarge,carbon=(1−fsmall)fcarbon,\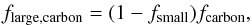begin{eqnarray} f_\mathrm{large,carbon} = (1-f_\mathrm{small}) f_\mathrm{carbon} , \end{eqnarray}(3)and flarge,silicate=(1−fsmall)(1−fcarbon),\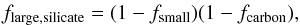begin{eqnarray} f_\mathrm{large,silicate} = (1-f_\mathrm{small}) (1-f_\mathrm{carbon}) , \end{eqnarray}(4)respectively. We assume thermal coupling between the disk species. In the calculation of each visibility, we take into account the field-of-view (FOV) effect of the interferometer used by multiplying the predicted brightness distribution with a mask with a diameter of the interferometer FOV (VLTI/AMBER: 0.25′′; KI: 0.05′′; IOTA/IONIC3: 0.8′′; VLTI/MIDI: 0.52′′).

Our previous temperature-gradient modeling (Chen et al. 2012) suggests that the disk is oriented roughly face-on, with the inclination of ~10° and a position angle (PA) of the major disk axis of ~30°. In the following, we adopt this inclination angle and PA of our previous best-fit temperature-gradient model.

Our disk models and results are presented below. We first try to find models that can roughly reproduce the visibilities and the SED at λ < 15 μm. This subset of data (hereafter “data set 1”) is chosen because it is sensitive to a relatively small parameter set and the computational cost of the parameter-space scanning can therefore be reduced. We only further refine the model to fit the full data set (hereafter “data set 0”), including the SED data at λ > 15 μm, when the fitting of data set 1 is sucessful. 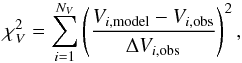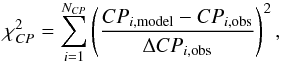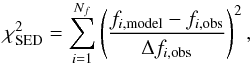To quantitatively measure the deviation of the model predictions from a given data set, we define χV2=∑i=1NV(Vi,model−Vi,obsΔVi,obs)2,\begin{eqnarray} \chi^2_V = \ChiSquareDef{V} , \end{eqnarray}(5)χCP2=∑i=1NCP(CPi,model−CPi,obsΔCPi,obs)2,\begin{eqnarray} \chi^2_{CP} = \ChiSquareDef{CP} , \end{eqnarray}(6)χSED2=∑i=1Nf(fi,model−fi,obsΔfi,obs)2,\begin{eqnarray} \chi^2_\mathrm{SED} = \ChiSquareDef{f} , \end{eqnarray}(7)and χred2=χV2+χCP2+χSED2NV+NCP+Nf−Np,\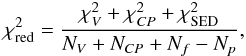begin{eqnarray} \chi^2_{\mathrm{red}} = \frac { \chi^2_V + \chi^2_{CP} + \chi^2_\mathrm{SED} } { N_V + N_{CP} + N_{f} - N_{p} } , \end{eqnarray}(8)in which V, CP, and f denote visibilty, closure phase, and flux, respectively, and NV, NCP, Nf are the numbers of observational points shown in the figures. The parameter Np is the number of free parameters in a model setting.

We use spherical coordinates (r,θ,ϕ) throughout the paper.

thumbnail Fig. 1

Model scanning run A (simple one-component disks), and the model parameters of the best model A1 with minimum χ1,red2\hbox{$\chi^2_\mathrm{1,red}$}, which is calculated by comparing each model with data set 1. a: parameter ranges of model scanning run A, number of tested parameter values (steps) per parameter, and parameters of the best model A1. The listed parameters are: Rin = inner radius of the disk, Rout = outer radius of the disk, hin = scale height at inner radius, ph = scale-height power-law index, pΣ = surface-density power-law index, τ(2 μm) = midplane optical depth at 2 μm, fsmall = fraction of small grains in the dust, fcarbon = fraction of carbon in the dust. b: χ1,red2\hbox{$\chi^2_\mathrm{1,red}$} maps of Model run A. For each subset of parameters, the χ1,red2\hbox{$\chi^2_\mathrm{1,red}$} shown is the lowest value for all combinations with other parameters. For example, for each pair of (Rin, Rout) values, the χ1,red2\hbox{$\chi^2_\mathrm{1,red}$} values for all possible (hin, ph) combinations within the described ranges were compared and the minimum value found is plotted into the map at left panel. c: the dust density distribution of the model, in units of g cm-3. d: K- (left) and N-band (right) model images A1, in units of erg cm-2 s-1 Hz-1. e: NIR and MIR visibilities, and closure phases CP (red dots: observations; black lines: model). The VLTI data are our own data. The data sets 2004 IOTA, 2003 KI, 2007 KI, and 2003 MIDI mentioned in the panels are taken from Monnier et al. (2006, 2005), Eisner et al. (2009), and Leinert et al. (2004), respectively. f: SED (from Leinert et al. 2004). The lines denote the model contributions from different radial regions. The red dots are the observations.

3.1. Simple power-law disk with vertical rim (Model A1)

We start with a simple disk model in which the surface density of the disk obeys the power-law distribution 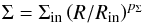Σ=Σin(R/Rin)pΣ\begin{eqnarray} \Sigma= \Sigma_{\mathrm{in}} \left( {R}/{R_\mathrm{in}} \right)^{\pSigma} \end{eqnarray}(9)for 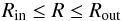Rin≤R≤Rout\begin{eqnarray} R_{\mathrm{in}}\leq R \leq R_{\mathrm{out}} \end{eqnarray}(10).For the vertical distribution of the gas, we assume the Gaussian function ρgas(R,θ)=Σ(R)12πHexp[−R2(π2−θ)22H2]\hbox{$\rho_\mathrm{gas}(R,\theta) = \Sigma(R) \frac{1}{\sqrt{2\pi}H} \exp\left[ -\frac{R^2(\frac\pi2-\theta)^2}{2H^2} \right]$}.For the scale height H, we assume the power-law distribution h≡HR=hin(R/Rin)ph\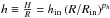hbox{$ h\equiv \frac{H}{R} = h_{\mathrm{in}} \left( {R}/{R_\mathrm{in}} \right) ^{p_h} $}. Therefore, the free parameters involved here are the inner and outer radii Rin and Rout, the power-law indices pΣ and ph, the dimensionless scale height hin at the inner radius, the parameters fsmall and fcarbon to control the dust composition, and the mass scaling factor Σin, or equivalently, the total dust mass, or the mid-plane optical depth τ(2 μm). The mid-plane optical depth is calculated as 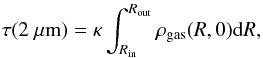τ(2μm)=κ∫RinRoutρgas(R,0)dR,\begin{eqnarray} \TauMidPlane = \kappa \int_{R_\mathrm{in}}^{R_\mathrm{out}} \rho_\mathrm{gas}(R,0) {\rm d} R, \end{eqnarray}(11)where κ is the absorption coefficient of the dust at 2 μm. We tested a large number of RT models (see Fig. 1a) and calculated the reduced chi-square 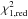χ1,red2\hbox{$\chi^2_\mathrm{1,red}$} for each model by comparing the model predictions with data set 1. We find that 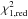χ1,red2\hbox{$\chi^2_\mathrm{1,red}$} mainly depends on the four parameters Rin, Rout, hin, and ph, while it shows only weak dependence on other parameters (for τ(2 μm) ≫ 1; see Appendix A for more details). Therefore, in our model scanning run A, we computed models on a grid of these four parameters, with five to ten different parameter values (steps) per parameter and a total model number of 7 × 5 × 10 × 9 = 3150. The ranges of the scanned parameter and the best model are presented in Fig. 1. None of these models is able to approximately reproduce data set 1. For the best model A1 (see table in Fig. 1a), the 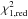χ1,red2\hbox{$\chi^2_\mathrm{1,red}$} is 8.56, and the individual contributions to χ2 from each data subset are 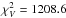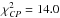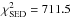χV2=1208.6\hbox{$\chi^2_V=1208.6$}, χCP2=14.0\hbox{$\chi^2_{CP}=14.0$}, χSED2=711.5\hbox{$\chi^2_\mathrm{SED}=711.5$}, respectively.

3.2. Disk with curved inner disk rim (Model B1)

Because of the density dependency of the sublimation temperature and the dust settling effect, the inner disk rim is predicted to be curved (Isella & Natta 2005; Tannirkulam et al. 2007). Therefore, we also tested models with a curved rim to investigate whether the rim curvature improves the model fitting. We add the curvature to the rim in a parameterized way. The inner radius of the disk is assumed to increase with height Rin(θ)=Rin(0)[1+fcurv(π2−θ)2],\hbox{$ R_\mathrm{in} (\theta) = R_\mathrm{in} (0) \left[ 1+f_\mathrm{curv}\left(\frac\pi2-\theta\right)^2 \right] ,$} where fcurv is a free parameter to control how curved the rim is. The curvature is implemented as a cut through the density profile prior to the RT calculations. Near the mid-plane and Rin, our parameterized curvature rim has roughly a parabolic profile, which is similar to those found in Isella & Natta (2005). For instance, when the parameter fcurv is set to 10, the inner radius at 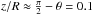z/R≈π2−θ=0.1\hbox{$z/R\approx \frac\pi2-\theta =0.1$} is 10% larger than Rin(0). This curvature is comparable with the self-consistent solution in Isella & Natta (2005; see Fig. 2 therein).

In our model scanning run B, we computed models on a grid of five parameters, with a total model number of 5 × 3 × 6 × 7 × 4 = 2520. The scanned parameter ranges and the best model are presented in Fig C.1. None of these models is able to approximately reproduce data set 1. The best model B1 has a 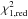χ1,red2\hbox{$\chi^2_\mathrm{1,red}$} of 8.94.

3.3. Self-shadowed disk (Model C1)

We decided to test disk models with a shadowed region behind an optically thick puffed-up inner rim because single-component disk models were unable to reproduce data set 1. We set the scale height of such a disk as 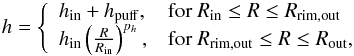h={hin+hpuff,forRin≤R≤Rrim,outhin(RRin)ph,forRrim,out≤R≤Rout,\begin{equation} h=\left\{ \begin{array}{ll} h_\mathrm{in}+h_\mathrm{puff} , & \textrm{for}~ R_{\mathrm{in}}\leq R \leq R_{\mathrm{rim,out}} \\ h_\mathrm{in} \left( {R} \over {R_\mathrm{in}} \right) ^{p_h} , & \textrm{for}~ R_{\mathrm{rim,out}}\leq R \leq R_{\mathrm{out}} , \end{array} \right. \end{equation}(12)where Rrim,out = Rin(1 + Wrim). Therefore, the additional parameters of this model are the relative width Wrim and the additional scale height hpuff of the puffed-up rim.

In our model scanning run C, we computed models on a grid of five parameters with a total model number of 5 × 3 × 5 × 10 × 7 = 5250. The scanned parameter ranges and the best model are presented in Fig. C.2. None of these models is able to approximately reproduce data set 1. The best model C1 has a 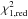χ1,red2\hbox{$\chi^2_\mathrm{1,red}$} of 7.23.

3.4. Two-component disk Model D1

The failure of all our disk models consisting of a homogeneous, optically thick disk (models A1 and B1) or a disk consisting of a narrow inner rim, a shadowed region, and an outer disk region (all of these components are optically thick; model C1), suggests that another disk structure is needed to reproduce the data. In particular, all these models with an optically-thick inner rim are unable to reproduce the NIR SED and visibilities (see also the additional studies in Appendix B). On the other hand, we found that with an optically thin dust (τ < 1 at 2 μm) located in the sub-AU region, it is possible to roughly reproduce the NIR observations (Appendix B.4). Therefore, we additionally tested models with an inner optically thin component and an outer optically thick component. In our model scanning run D, we computed models on a grid of five parameters, with a total model number of 5 × 5 × 5 × 5 × 5 = 3125. The parameter ranges and results (model D1) are shown in Fig. C.3. We found that, with this class of models, the 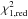χ1,red2\hbox{$\chi^2_\mathrm{1,red}$} can be reduced to 2.55, much lower than in any of the previous models. In model D1, the computed NIR excess consists of thermal emission from the inner disk, scattered stellar light from the inner disk, and scattered light from the outer disk. The mass of the optically thin inner disk is 1.3 × 10-12M⊙.

3.5. Two-component disk Model DA0

A problem of the models in run D is that, with the carbon/silicate ratio of 1:1, they cannot reproduce the strong 10 μm silicate feature in the SED. Therefore, we also tested models with different carbon/silicate ratio. In our model scanning run DA, we set carbon/silicate = 1:9. We also added large grains into the model so that the SED data at λ > 15 μm can also be reproduced. The parameter ranges and results are shown in Fig. C.4. The model DA0 approximately reproduced the whole data set 0, including the silicate feature and the SED data at λ > 15 μm. In model DA0, similar to model D1, the computed NIR excess consists of thermal emission from the inner disk, scattered stellar light from the inner disk, and scattered light from the outer disk. The mass of the optically thin inner disk is 1.8 × 10-11M⊙.

3.6. Three-component disk Model E0

The purpose of parameter scanning run E is to test the possibility of modeling the data with a two-component inner disk consisting of both an optically thin and an optically thick component in addition to an optically thick outer disk. The goal of this study is to investigate whether we can really discriminate in our study between (i) an inner optically thin disk and (ii) an inner optically thin disk with an additional optically thick core. The parameter ranges and results are shown in Fig. C.5. The model E0 roughly reproduced data set 0, with a 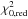χ0,red2\hbox{$\chi^2_\mathrm{0,red}$} (2.93) only slightly higher than that of model DA0 (2.50). This small χ2 difference is probably too small to reliably discriminate between these two models.

4. Discussion

4.1. Optical depth and composition of the inner NIR-emitting dust

In our modeling we found that an optically thin dust located at the sub-AU region is needed to reproduce the NIR SED and visibilities. In our previous temperature-gradient modeling (Chen et al. 2012), a blackbody emission with T ~ 1600 K at ~ 0.2 AU from the central star was needed to reproduce the NIR SED and visibilities. Our RT modeling presented here suggests that this kind of hot emission at this location requires an optically thin dust composed of small grains. All the models tested with an optically thick rim at ~ 0.2 AU, on the other hand, predict a temperature that is too low, and therefore, a red SED. In other words, the SEDs they predict are flatter in 2–7 μm than the observed SED. Therefore, they either underestimate the flux at ~ 2 μm (as in model A1, B1, and C1), or overestimate both the flux at ~ 7 μm and the MIR visibilities (as in model A2, B2, and C2 shown in Appendix B).

The temperature of a passively heated dust depends on both its optical depth and the wavelength dependency of its optical properties (e.g., Dullemond & Monnier 2010). If an optically thin gray dust lies at 0.2 AU from a central heating source of L∗ = 7.6 L⊙, its radiative-equilibrium temperature would be 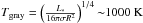Tgray=L∗16πσR2)(1/4~1000K\hbox{$T_\mathrm{gray}= \left( \frac{L_*}{16\pi\sigma{R^2}} \right)^{1/4} {\sim}1000~\Kelvin$}. However, astronomical dust is non-gray, typically with an opacity lower in the IR than in the UV/optical, and therefore with a cooling parameter ϵ< 1 (for definition of this parameter see Eq. 10 in Dullemond & Monnier 2010). This kind of non-gray dust will be overheated to 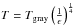T=Tgray1ϵ)(14\hbox{$T=T_\mathrm{gray}\left(\frac1\epsilon\right)^{\frac14}$} (see, e.g., Eq. (9) in Dullemond & Monnier 2010). Therefore, by choosing dust with ϵ ≪ 1 (corresponding to small grain size), it is possible to reproduce the observed blue NIR emission.

The situation for optically thick dust is different. Within optically thick dust with ϵ ≪ 1, only a thin surface layer is subject to the overheating effect. The inner parts are much cooler (see, e.g., Eq. (11) and Fig. 9 in Dullemond & Monnier 2010). The overall emission of this kind of dust is a mixture of the blue emission from the surface layer and the redder emission from the inner body. Therefore, the overall color of the emission is not substantially bluer than that from an optically thick gray dust. This insensitivity of the NIR SED to the ϵ parameter has been confirmed by our parameter scanning run AS (see Appendix A), which covers a wide range of ϵ by choosing different dust compositions.

Therefore, we conclude that the hot NIR emission is likely dominated by an optically thin component. However, it cannot be excluded that an optically thick component may coexist in the sub-AU region (e.g., model E0). This component likely has low scale height (<0.01), so that it intersects only a small fraction of stellar light and the NIR emission is still dominated by the optically thin component.

4.2. Overall structure of the CS disk

We compared several kinds of MCRT models with the observations. We found that all the models with the NIR emission dominated by an optically thick inner rim, without an optically thin component, are unable to reproduce the observations (see Sects. 3.1, 3.2 and 3.3 for the model scanning). The best model that we found (model D0) consists of an inner optically thin component and an outer optically thick component. However, we cannot exclude the alternative model with an inner sub-AU region consisting of both optically thin and optically thick components (model E0). The additional optically thick component in this model has a low scale height and the NIR emission is still dominated by the optically thin component.

? classified the Herbig Ae/Be stars into two groups, based on the shape of their SED. The SEDs of group I objects can be fitted with a power law and a blackbody and the SEDs of group II objects can be fitted with merely a power law. The different spectral shapes have been interpreted in the following way: group I objects have flaring disks and group II objects have self-shadowed disks (Dullemond & Dominik 2004). In recent years, evidence of disk gaps has been found in a growing number of group I objects (e.g., Benisty et al. 2010; Mulders et al. 2011; Honda et al. 2012; Maaskant et al. 2013; Matter et al. 2014). Therefore, it has been suggested that the gap region is a common feature of most group I Herbig stars, and the blackbody part of a SED of that type is created by the illuminated inner wall of the outer disk (Honda et al. 2012; Maaskant et al. 2013). Recent studies of group II objects with high spatial resolution provide evidence that some of them also contain gaps. For example, Schegerer et al. (2013) fitted the observation of the group IIa object HD 142666 with a RT model with a disk gap from 0.35 AU to 0.8 AU. Menu et al. (2015) found that a population of group II disks have large MIR half-light radii, which are more consistent with gapped disks rather than continuous disks.Taking advantage of high-resolution infrared interferometry and MCRT modeling, we find evidence of a gap region in the group II object HD 144432. This result reinforced the aforementioned suggestion by Menu et al. (2015).The gap in our model of HD 144432 has an outer radius of only ~ 1.4 AU, while the reported gap outer radii of group I objects range from 5.6 AU to 63 AU.

The disk gap in our model is possibly a signature of planet formation in the disk (Bryden et al. 1999; Zhu et al. 2011; Kley & Nelson 2012; ALMA Partnership et al. 2015). Grain growth of dust is another mechanism that is able to create disk cavities. However, numerical simulations of grain growth (Birnstiel et al. 2012) predict inside-out growth of dust and smooth radial distribution of dust size , which seems to be inconsistent with the dust distributions in our models. Therefore, grain growth is unlikely to be the only mechanism to explain the dust distribution found in our modeling. Furthermore, photoevaporation clearing is another possible mechanism that is able to create the gap in the disk of HD 144432. According to numerical simulations of the photoevaporation clearing process (Alexander et al. 2006; Alexander & Armitage 2007; Owen et al. 2010), the first step of disk clearing is the opening of a gap at ~ 1 AU, which prevents the inner disk from being replenished. Consequently, the inner disk is quickly drained into the center, and then the inner edge of outer disk starts to move outward. The gap in HD 144432 has a small outer radius of ~ 1.4 AU, comparable with a newly opened photoevaporative gap. Therefore, the disk might be observed in the photoevaporation-starved accretion phase.This scenario is consistent with the fact that the object is still accreting ( Ṁ ≈ 8.5 × 10-8M⊙ yr-1, Garcia Lopez et al. 2006).However, with the current data set, we cannot distinguish between the various gap-opening mechanisms because, unfortunately, the uv coverage of our data set is poor, the baseline lengths are too short to fully resolve the inner disk region, and image reconstruction is not possible with this type of uv coverage. We also cannot exclude the possibility that more than one mechanism is responsible for the disk evolution (e.g., Rosotti et al. 2013; Alexander & Armitage 2009).

The inner radii of the inner disk components of the two best models DA0 (Fig. 5) and E0 (Fig. 6) are approximately 0.21 and 0.15 AU. These radii are similar to the dust sublimation radius of 0.13 AU suggested by the size-luminosity relation reported by Monnier et al. (2005) for a dust sublimation temperature of 1500 K and a luminosity of 7.6 L⊙. To our knowledge, there is no radial velocity measurement indicating a close binary in this object. Therefore, it is likely that the inner radius of the inner disk of HD 144432 is indeed defined by dust sublimation.

For some pre-transitional disks, the innermost NIR-emitting regions inside the gaps are suggested to be optically thin (Mulders et al. 2010; Benisty et al. 2010; Espaillat et al. 2010; Maaskant et al. 2013; Matter et al. 2014). The origin of such optically thin dust with large scale height remains unclear. Krijt & Dominik (2011) proposed that an optically thin halo can arise from the destructive collision between planetesimals on highly-inclined orbits. Bans & Königl (2012) proposed that a centrifugally-driven dusty disk wind can arise from the disk close to the dust sublimation radius. Our model E0 seems to be compatible with this scenario.

5. Summary and conclusions

We computed two-dimensional RT models for the Herbig Ae star HD 144432. The following results were obtained.

All computed models with only optically thick components cannot reproduce the observations. One main problem of such models is that the NIR excess in the SED of this object cannot be reproduced with an inner optically thick disk rim, when the constraints on the size of the NIR-emitting region imposed by the NIR interferometric observations are taken into account. The best model that we found consists of an inner optically thin component at 0.21–0.32 AU and an optically thick outer disk at 1.4–10 AU. In an alternative model with similar quality, the inner sub-AU region consists of an optically thin and an optically thick component. In each of the above models, there exists a gap region, and the NIR emission is dominated by the inner optically thin component. Therefore, our modeling suggests that the dust distribution in the protoplanetary disk of HD 144432 differs from the dust distribution of an early-stage disk, which is optically thick from the dust sublimation radius to the outer edge.

3

Taken from the Catalogue of Stellar Diameters (CADARS; Pasinetti Fracassini et al. 2001).

5

Exceptions to such an insensitivity are discussed below. 1) For the models with a low τ(2 μm) and a steep surface density profile (bottom left region in the left χ2 panel of Fig. A.1b) the outer parts of the disk become optically thin, so that the fluxes at long wavelengths are reduced. However, the NIR SED stays approximately the same. 2) For the models with only large grains (fsmall = 0, bottom region in the right panel of Fig. A.1b), the disk emits more at long wavelengths and less at NIR, in comparison with the models with small grains. However, the slope of the NIR SED does not change. Therefore, in these regions of parameter space, the model still predicts a red NIR SED. Therefore, the main problem of models with optically thick inner rim, that is, too red NIR SED, cannot be solved by altering these four parameters.

Acknowledgments

We thank our ESO colleagues for their excellent support during the observations. The comments and suggestions from an anonymous referee helped to improve the quality of the paper.

References

  1. Alexander, R. D., & Armitage, P. J. 2007, MNRAS, 375, 500 [NASA ADS] [CrossRef] [Google Scholar]
  2. Alexander, R. D., & Armitage, P. J. 2009, ApJ, 704, 989 [NASA ADS] [CrossRef] [Google Scholar]
  3. Alexander, R. D., Clarke, C. J., & Pringle, J. E. 2006, MNRAS, 369, 229 [NASA ADS] [CrossRef] [Google Scholar]
  4. ALMA Partnership, Brogan, C. L., Pérez, L. M., et al. 2015, ApJ, 808, L3 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bans, A., & Königl, A. 2012, ApJ, 758, 100 [NASA ADS] [CrossRef] [Google Scholar]
  6. Benisty, M., Tatulli, E., Ménard, F., & Swain, M. R. 2010, A&A, 511, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Birnstiel, T., Andrews, S. M., & Ercolano, B. 2012, A&A, 544, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Bjorkman, J. E., & Wood, K. 2001, ApJ, 554, 615 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bryden, G., Chen, X., Lin, D. N. C., Nelson, R. P., & Papaloizou, J. C. B. 1999, ApJ, 514, 344 [NASA ADS] [CrossRef] [Google Scholar]
  10. Chen, L., Kreplin, A., Wang, Y., et al. 2012, A&A, 541, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Dominik, C., Dullemond, C. P., Waters, L. B. F. M., & Walch, S. 2003, A&A, 398, 607 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [Google Scholar]
  13. Dullemond, C. P., & Dominik, C. 2004, A&A, 417, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Dullemond, C. P., & Monnier, J. D. 2010, ARA&A, 48, 205 [NASA ADS] [CrossRef] [Google Scholar]
  15. Dullemond, C. P., Dominik, C., & Natta, A. 2001, ApJ, 560, 957 [NASA ADS] [CrossRef] [Google Scholar]
  16. Eisner, J. A., Graham, J. R., Akeson, R. L., & Najita, J. 2009, ApJ, 692, 309 [NASA ADS] [CrossRef] [Google Scholar]
  17. Espaillat, C., Calvet, N., Luhman, K. L., Muzerolle, J., & D’Alessio, P. 2008, ApJ, 682, L125 [NASA ADS] [CrossRef] [Google Scholar]
  18. Espaillat, C., D’Alessio, P., Hernández, J., et al. 2010, ApJ, 717, 441 [NASA ADS] [CrossRef] [Google Scholar]
  19. Garcia Lopez, R., Natta, A., Testi, L., & Habart, E. 2006, A&A, 459, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Honda, M., Maaskant, K., Okamoto, Y. K., et al. 2012, ApJ, 752, 143 [NASA ADS] [CrossRef] [Google Scholar]
  21. Isella, A., & Natta, A. 2005, A&A, 438, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Jager, C., Mutschke, H., & Henning, T. 1998, A&A, 332, 291 [NASA ADS] [Google Scholar]
  23. Kley, W., & Nelson, R. P. 2012, ARA&A, 50, 211 [NASA ADS] [CrossRef] [Google Scholar]
  24. Kreplin, A., Kraus, S., Hofmann, K.-H., et al. 2012, A&A, 537, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Kreplin, A., Weigelt, G., Kraus, S., et al. 2013, A&A, 551, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Krijt, S., & Dominik, C. 2011, A&A, 531, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Leinert, C., van Boekel, R., Waters, L. B. F. M., et al. 2004, A&A, 423, 537 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Lucy, L. B. 1999, A&A, 344, 282 [NASA ADS] [Google Scholar]
  29. Maaskant, K. M., Honda, M., Waters, L. B. F. M., et al. 2013, A&A, 555, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Matter, A., Labadie, L., Kreplin, A., et al. 2014, A&A, 561, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Meeus, G., Waters, L. B. F. M., Bouwman, J., et al. 2001, A&A, 365, 476 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Menu, J., van Boekel, R., Henning, T., et al. 2015, A&A, 581, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Monnier, J. D., Millan-Gabet, R., Billmeier, R., et al. 2005, ApJ, 624, 832 [NASA ADS] [CrossRef] [Google Scholar]
  34. Monnier, J. D., Berger, J.-P., Millan-Gabet, R., et al. 2006, ApJ, 647, 444 [NASA ADS] [CrossRef] [Google Scholar]
  35. Mulders, G. D., Dominik, C., & Min, M. 2010, A&A, 512, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Mulders, G. D., Waters, L. B. F. M., Dominik, C., et al. 2011, A&A, 531, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Owen, J. E., Ercolano, B., Clarke, C. J., & Alexander, R. D. 2010, MNRAS, 401, 1415 [NASA ADS] [CrossRef] [Google Scholar]
  38. Pasinetti Fracassini, L. E., Pastori, L., Covino, S., & Pozzi, A. 2001, A&A, 367, 521 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Pérez, M. R., van den Ancker, M. E., de Winter, D., & Bopp, B. W. 2004, A&A, 416, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Petrov, R. G., Malbet, F., Weigelt, G., et al. 2007, A&A, 464, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Pinte, C., Ménard, F., Berger, J. P., Benisty, M., & Malbet, F. 2008, ApJ, 673, L63 [NASA ADS] [CrossRef] [Google Scholar]
  42. Pontoppidan, K. M., Dullemond, C. P., Blake, G. A., et al. 2007, ApJ, 656, 980 [NASA ADS] [CrossRef] [Google Scholar]
  43. Rosotti, G. P., Ercolano, B., Owen, J. E., & Armitage, P. J. 2013, MNRAS, 430, 1392 [NASA ADS] [CrossRef] [Google Scholar]
  44. Schegerer, A. A., Ratzka, T., Schuller, P. A., et al. 2013, A&A, 555, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Tannirkulam, A., Harries, T. J., & Monnier, J. D. 2007, ApJ, 661, 374 [NASA ADS] [CrossRef] [Google Scholar]
  46. Tatulli, E., Millour, F., Chelli, A., et al. 2007, A&A, 464, 29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Williams, J. P., & Cieza, L. A. 2011, ARA&A, 49, 67 [NASA ADS] [CrossRef] [Google Scholar]
  48. Zhu, Z., Nelson, R. P., Hartmann, L., Espaillat, C., & Calvet, N. 2011, ApJ, 729, 47 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Additional parameter study for the simple one-component disk (model type A; Sect. 3.1)

In our additional model scanning run AS presented in Fig. A.1, we kept the parameters Rin, Rout, hin fixed and computed models on a grid of the four parameters pΣ, τ(2 μm), fcarbon, and fsmall, with a total model number of 5 × 6 × 6 × 5 = 900. The parameter ranges and results are shown in Fig. A.1. The results show that 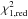χ1,red2\hbox{$\chi^2_\mathrm{1,red}$} is almost insensitive to the above free parameters 5. This supports our decision to keep these parameters constant in most of our parameter-scanning runs.

thumbnail Fig. A.1

Same as Fig. 1, except for model run AS and compared with data set 1. Model AS1 is the model with minimum χ1,red2\hbox{$\chi^2_\mathrm{1,red}$}.

Appendix B: Comparing scanned models with data set 2

In the model scanning runs A, B, and C, we notice that all these models cannot reproduce the NIR emission. To investigate this deviation of the models from the observations, we compare the model results with data set 2, which is composed of the following data:

  • all the SED data with wavelengths <7 μm;

  • all NIR visibilities with baseline length >30 m; and

  • all NIR closure phases.

In the following sections, we want to investigate whether optically thick one-component models of type A, B, or C (see Sect. 3.1–3.3) are at least able to reproduce the NIR observations (ignoring the long-wavelength data).

thumbnail Fig. B.1

Same as Fig. 1, except for model run A and compared with data set 2. Model A2 is the model with minimum χ2,red2\hbox{$\chi^2_\mathrm{2,red}$}.

Appendix B.1: Model A2

For this goal, we compared the models in the parameter scanning run A with data set 2. The parameter ranges and results are shown in Fig. B.1. The 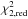χ2,red2\hbox{$\chi^2_\mathrm{2,red}$} of the best model A2 is 4.01. The high 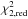χ2,red2\hbox{$\chi^2_\mathrm{2,red}$} value of model A2 indicates that it cannot reproduce the NIR SED and visibilities.

thumbnail Fig. B.2

Same as Fig. 1, except for model run B and compared with data set 2. Model B2 is the model with minimum χ2,red2\hbox{$\chi^2_\mathrm{2,red}$}.

Appendix B.2: Model B2

We compared the models in the parameter scanning run B with data set 2. The parameter ranges and results are shown in Fig. B.2. The 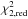χ2,red2\hbox{$\chi^2_\mathrm{2,red}$} of the best model B2 is 4.18. The high 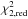χ2,red2\hbox{$\chi^2_\mathrm{2,red}$} value of model B2 indicates that it cannot reproduce the NIR SED and visibilities.

thumbnail Fig. B.3

Same as Fig. 1, except for model run C and compared with data set 2. Model C2 is the model with minimum χ2,red2\hbox{$\chi^2_\mathrm{2,red}$}.

Appendix B.3: Model C2

We compared the models in the parameter scanning run C with data set 2. The parameter ranges and results are shown in Fig. B.3. The 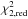χ2,red2\hbox{$\chi^2_\mathrm{2,red}$} of the best model C2 is 3.67. The high 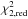χ2,red2\hbox{$\chi^2_\mathrm{2,red}$} value of model C2 indicates that it cannot reproduce the NIR SED and visibilities.

thumbnail Fig. B.4

Same as Fig. 1, except for model run F and compared with data set 2. Model F2 is the model with minimum χ2,red2\hbox{$\chi^2_\mathrm{2,red}$}.

Appendix B.4: Model F2

The purpose of parameter scanning run F is to test whether data set 2 can be reproduced by an NIR-emitting optically thin dust model with only an optically thin dust component located at sub-AU distance from the star. The parameter ranges and results are shown in Fig. B.4. The model E2 can approximately reproduce data set 2, with 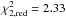χ2,red2=2.33\hbox{$\chi^2_\mathrm{2,red}=2.33$}. In run E, we fix the Wring of the optically thin ring to 50%. This is justified by the degeneracy between Wring and Rin, which is illustrated in the next section. Similarly, there is a degeneracy between h and τ (see Sect. B.6), and we therefore fix h to 0.5.

thumbnail Fig. B.5

Same as Fig. 1, except for model run FA and compared with data set 2. Model FA2 is the model with minimum χ2,red2\hbox{$\chi^2_\mathrm{2,red}$}.

Appendix B.5: Model scanning FA

The purpose of parameter scanning run FA is to explore the effect of changing Wring and Rin. The parameter ranges and results are shown in Fig. B.5. There is a degeneracy between Wring and Rin.

thumbnail Fig. B.6

Same as Fig. 1, except for model run FB and compared with data set 2. Model FB2 is the model with minimum χ2,red2\hbox{$\chi^2_\mathrm{2,red}$}.

Appendix B.6: Model scanning FB

The purpose of parameter scanning run FB is to explore the effect of changing h and τ. The parameter ranges and results are shown in Fig. B.6. There is a degeneracy between h and τ.

Appendix C: Additional figures

thumbnail Fig. C.1

Same as Fig. 1, except for model run B and compared with data set 1. Model B1 is the model with minimum χ1,red2\hbox{$\chi^2_\mathrm{1,red}$}. The listed parameters are: fcurve = curvatureoftheinnerrim, other parameters are same as in Fig. 1.

thumbnail Fig. C.2

Same as Fig. 1, except for model run C and compared with data set 1. Model C1 is the model with minimum χ1,red2\hbox{$\chi^2_\mathrm{1,red}$}. The listed parameters are: Wrim = non - dimensionalwidthoftheinnerrim, hpuff = additionalscaleheightoftherim, other parameters are same as in Fig. 1.

thumbnail Fig. C.3

Same as Fig. 1, except for model run D and compared with data set 1. Model D1 is the model with minimum χ1,red2\hbox{$\chi^2_\mathrm{1,red}$}. The listed parameters are: Wring,1 = (Rout,1−Rin,1) /Rin,1 (relative radial width of the inner component), Wgap = Rin,2−Rout,1 (radial width of the gap), Rin,i = inner radius of component i, Rout,i = outer radius of component i, hin,i = scale height of component i at its inner radius, ph,i = scale-height power-law index of component i, pΣ,i = surface-density power-law index of component i, τi = midplane optical depth of component i at 2 μm, Mdust,i = dust mass of component i.

thumbnail Fig. C.4

Same as Fig. 1, except for model run DA and compared with data set 0. Model DA0 is the model with minimum χ0,red2\hbox{$\chi^2_\mathrm{0,red}$}. The listed parameters are similar to those in Fig. C.3.

thumbnail Fig. C.5

Same as Fig. 1, except for model run E and compared with data set 0. Model E0 is the model with minimum χ0,red2\hbox{$\chi^2_\mathrm{0,red}$}. The listed parameters are similar to those in Fig. C.3.

All Tables

Table 1

Observation log of our VLTI/AMBER observation of HD 144432.

In the text

All Figures

thumbnail Fig. 1

Model scanning run A (simple one-component disks), and the model parameters of the best model A1 with minimum χ1,red2\hbox{$\chi^2_\mathrm{1,red}$}, which is calculated by comparing each model with data set 1. a: parameter ranges of model scanning run A, number of tested parameter values (steps) per parameter, and parameters of the best model A1. The listed parameters are: Rin = inner radius of the disk, Rout = outer radius of the disk, hin = scale height at inner radius, ph = scale-height power-law index, pΣ = surface-density power-law index, τ(2 μm) = midplane optical depth at 2 μm, fsmall = fraction of small grains in the dust, fcarbon = fraction of carbon in the dust. b: χ1,red2\hbox{$\chi^2_\mathrm{1,red}$} maps of Model run A. For each subset of parameters, the χ1,red2\hbox{$\chi^2_\mathrm{1,red}$} shown is the lowest value for all combinations with other parameters. For example, for each pair of (Rin, Rout) values, the χ1,red2\hbox{$\chi^2_\mathrm{1,red}$} values for all possible (hin, ph) combinations within the described ranges were compared and the minimum value found is plotted into the map at left panel. c: the dust density distribution of the model, in units of g cm-3. d: K- (left) and N-band (right) model images A1, in units of erg cm-2 s-1 Hz-1. e: NIR and MIR visibilities, and closure phases CP (red dots: observations; black lines: model). The VLTI data are our own data. The data sets 2004 IOTA, 2003 KI, 2007 KI, and 2003 MIDI mentioned in the panels are taken from Monnier et al. (2006, 2005), Eisner et al. (2009), and Leinert et al. (2004), respectively. f: SED (from Leinert et al. 2004). The lines denote the model contributions from different radial regions. The red dots are the observations.
In the text
thumbnail Fig. A.1

Same as Fig. 1, except for model run AS and compared with data set 1. Model AS1 is the model with minimum χ1,red2\hbox{$\chi^2_\mathrm{1,red}$}.
In the text
thumbnail Fig. B.1

Same as Fig. 1, except for model run A and compared with data set 2. Model A2 is the model with minimum χ2,red2\hbox{$\chi^2_\mathrm{2,red}$}.
In the text
thumbnail Fig. B.2

Same as Fig. 1, except for model run B and compared with data set 2. Model B2 is the model with minimum χ2,red2\hbox{$\chi^2_\mathrm{2,red}$}.
In the text
thumbnail Fig. B.3

Same as Fig. 1, except for model run C and compared with data set 2. Model C2 is the model with minimum χ2,red2\hbox{$\chi^2_\mathrm{2,red}$}.
In the text
thumbnail Fig. B.4

Same as Fig. 1, except for model run F and compared with data set 2. Model F2 is the model with minimum χ2,red2\hbox{$\chi^2_\mathrm{2,red}$}.
In the text
thumbnail Fig. B.5

Same as Fig. 1, except for model run FA and compared with data set 2. Model FA2 is the model with minimum χ2,red2\hbox{$\chi^2_\mathrm{2,red}$}.
In the text
thumbnail Fig. B.6

Same as Fig. 1, except for model run FB and compared with data set 2. Model FB2 is the model with minimum χ2,red2\hbox{$\chi^2_\mathrm{2,red}$}.
In the text
thumbnail Fig. C.1

Same as Fig. 1, except for model run B and compared with data set 1. Model B1 is the model with minimum χ1,red2\hbox{$\chi^2_\mathrm{1,red}$}. The listed parameters are: fcurve = curvatureoftheinnerrim, other parameters are same as in Fig. 1.
In the text
thumbnail Fig. C.2

Same as Fig. 1, except for model run C and compared with data set 1. Model C1 is the model with minimum χ1,red2\hbox{$\chi^2_\mathrm{1,red}$}. The listed parameters are: Wrim = non - dimensionalwidthoftheinnerrim, hpuff = additionalscaleheightoftherim, other parameters are same as in Fig. 1.
In the text
thumbnail Fig. C.3

Same as Fig. 1, except for model run D and compared with data set 1. Model D1 is the model with minimum χ1,red2\hbox{$\chi^2_\mathrm{1,red}$}. The listed parameters are: Wring,1 = (Rout,1−Rin,1) /Rin,1 (relative radial width of the inner component), Wgap = Rin,2−Rout,1 (radial width of the gap), Rin,i = inner radius of component i, Rout,i = outer radius of component i, hin,i = scale height of component i at its inner radius, ph,i = scale-height power-law index of component i, pΣ,i = surface-density power-law index of component i, τi = midplane optical depth of component i at 2 μm, Mdust,i = dust mass of component i.
In the text
thumbnail Fig. C.4

Same as Fig. 1, except for model run DA and compared with data set 0. Model DA0 is the model with minimum χ0,red2\hbox{$\chi^2_\mathrm{0,red}$}. The listed parameters are similar to those in Fig. C.3.
In the text
thumbnail Fig. C.5

Same as Fig. 1, except for model run E and compared with data set 0. Model E0 is the model with minimum χ0,red2\hbox{$\chi^2_\mathrm{0,red}$}. The listed parameters are similar to those in Fig. C.3.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.