| Issue |
A&A
Volume 585, January 2016
|
|
|---|---|---|
| Article Number | A151 | |
| Number of page(s) | 12 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201527266 | |
| Published online | 14 January 2016 | |
Magnetic fields in primordial accretion disks
1 Sorbonne Universités, UPMC Univ. Paris 06, UMR 7095, Institut d’Astrophysique de Paris, 75014 Paris, France
e-mail: latif@iap.fr
2 CNRS, UMR 7095, Institut d’Astrophysique de Paris, 75014 Paris, France
3 Departamento de Astronomía, Facultad Ciencias Físicas y Matemáticas, Universidad de Concepción, Av. Esteban Iturra s/n Barrio Universitario, Casilla 160-C, Chile
Received: 28 August 2015
Accepted: 3 November 2015
Magnetic fields are considered a vital ingredient of contemporary star formation and may have been important during the formation of the first stars in the presence of an efficient amplification mechanism. Initial seed fields are provided via plasma fluctuations and are subsequently amplified by the small-scale dynamo, leading to a strong, tangled magnetic field. We explore how the magnetic field provided by the small-scale dynamo is further amplified via the α–Ω dynamo in a protostellar disk and assess its implications. For this purpose, we consider two characteristic cases, a typical Pop. III star with 10M⊙ and an accretion rate of 10-3M⊙ yr-1, and a supermassive star with 105M⊙ and an accretion rate of 10-1M⊙ yr-1. For the 10M⊙ Pop. III star, we find that coherent magnetic fields can be produced on scales of at least 100 AU, which are sufficient to drive a jet with a luminosity of 100L⊙ and a mass outflow rate of 10-3.7M⊙ yr-1. For the supermassive star, the dynamical timescales in its environment are even shorter, implying smaller orbital timescales and an efficient magnetization out to at least 1000 AU. The jet luminosity corresponds to ~106.0L⊙ and a mass outflow rate of 10-2.1M⊙ yr-1. We expect that the feedback from the supermassive star can have a relevant impact on its host galaxy.
Key words: methods: analytical / cosmology: theory / early Universe / dark ages, reionization, first stars / black hole physics / stars: Population III
© ESO, 2016
1. Introduction
Magnetic fields play an important role in contemporary star formation. They strongly contribute to the transfer of angular momentum (Hawley & Balbus 1991; Fromang et al. 2004; Shu et al. 2007; Hennebelle & Fromang 2008), launch collimated jets and outflows (Shu et al. 1995; Banerjee & Pudritz 2006; Fendt 2009; Wang et al. 2010), stabilize the accretion disk, and help in suppressing fragmentation (Hennebelle & Teyssier 2008; Banerjee et al. 2009; Price & Bate 2008).
In studies of primordial star formation, it was originally less clear whether the role of magnetic fields has been significant, as the initial magnetic field strength was very uncertain within the framework of ΛCDM (see e.g. Grasso & Rubinstein 2001; Kulsrud & Zweibel 2008; Ryu et al. 2012; Widrow et al. 2012). The first cosmological simulations had shown that primordial stars form in dark matter halos with 105−106M⊙ at z ~ 20 (Abel et al. 2002; Bromm et al. 2002) or even earlier (Reed et al. 2005; Gao et al. 2010). Subsequently, significant efforts were dedicated to a more realistic modelling and to investigate the longer-term evolution of these systems. Yoshida et al. (2008) performed the first simulations revealing the formation of a self-gravitating disk from cosmological initial conditions, while Clark et al. (2011) and Greif et al. (2012) explored the fragmentation of the resulting disks. These predominantly Lagrangian-type simulations were complemented with grid-based simulations using the adaptive mesh refinement (AMR) technique, confirming the formation of disks and the potential fragmentation (Latif et al. 2013c; Bovino et al. 2014). Inayoshi & Haiman (2014), Tanaka & Omukai (2014), and Latif & Schleicher (2015a,b) employed analytical models to further investigate the long-term evolution of clumps forming as a consequence of disk fragmentation. These studies suggest that the clumps move inwards because of the short migration timescale and merge with the central object.
As we discuss below, magnetic fields may have played a relevant role during primordial star formation because of the efficient amplification of magnetic fields. Observationally, there is no evidence that magnetic fields were present during Pop. III star formation, but there are a number of independent observations suggesting the existence of magnetic fields at rather early stages in the Universe. The far-infrared – radio correlation, a correlation between star formation activity and synchrotron emission due to magnetic fields (Yun et al. 2001), has been demonstrated to hold at least until z ~ 2 via Herschel results (Ivison et al. 2010; Magnelli et al. 2015), implying strong magnetic fields at a time when the Universe was about 3 billion years old. Similarly, investigations exploring the correlation between quasar rotation measures and the number of normal galaxies along the line of sight have indicated that Milky-Way-type magnetic fields are present in galaxies at z ~ 2 (Kronberg et al. 2008; Bernet et al. 2008). In quasars, strong rotation measures have been observed even at z = 5, showing that strong magnetic fields can build up at early stages in the central regions of active galactic nuclei (Hammond et al. 2012). Even in the intergalactic medium, blazar observations point at a minimum magnetic field strength of ≳10-18 G (Dermer et al. 2011; Tavecchio et al. 2011; Dolag et al. 2011; Arlen et al. 2014).
While the strength of a primordial field is very uncertain, astrophysical mechanisms suggest an initial field strength of ~10-20 G. The Biermann battery operates on kpc scales under favourable conditions (Biermann 1950), while both the Weibel instability (Weibel 1959) and the generation of spontaneously emitted magnetic fields occurs on much smaller scales, comparable to a few Debye lengths. Recent calculations by Schlickeiser (2012) suggest the production of ~10-10 G magnetic fields in protogalaxies due to plasma fluctuations (Yoon et al. 2014). So, both the Weibel instability and plasma fluctuations can produce a magnetic field on small scales. The small-scale dynamo (Kazantsev 1968) can enhance the magnetic field strength via turbulence (Brandenburg & Subramanian 2005; Schober et al. 2012b) and lead to the rapid production of a strong, tangled magnetic field. After saturation on small scales, the dynamo enters the non-linear regime, and larger scales are magnetised on their respective eddy-turnover timescales (Schekochihin et al. 2002; Schleicher et al. 2013b). The conditions for the dynamo to operate require turbulence and a critical magnetic Reynolds number Rmcrit = vℓ/η, where v and ℓ are the characteristic turbulent velocity and length scales and η the turbulent diffusivity. The minimum magnetic Reynolds number for the dynamo to operate is about Rmcrit ~ 100; for details see Brandenburg & Subramanian (2005) and Schober et al. (2012b). Both the Ohmic and ambi-polar resistivity during primordial star formation are found to be sufficiently low to stop efficient magnetic field amplification (Schober et al. 2012a). The amplification time corresponds to the timescale of turbulent fluctuations, and is therefore much shorter than the evolutionary timescale of the system.
Cosmological simulations show that turbulence is driven by gravitational instabilites during the gravitational collapse in primordial halos forming at z = 15−30 (Turk et al. 2012; Latif et al. 2013b,e), as also expected from analytical considerations (Elmegreen & Burkert 2010; Klessen & Hennebelle 2010). Continuous infall and accretion onto the primordial disk further helps to drive turbulence even in the absence of other mechanisms like the magneto-rotational instability (Hawley & Balbus 1991; Balbus & Hawley 1998). The other requirement for the small-scale dynamo to operate is the coupling between the gas and the magnetic field. Magnetic dissipiative processes, such as Ohmic dissipation and ambi-polar diffusion, are less effective in primordial gas because of the higher temperatures and a larger ionization degree. Maki & Susa (2004, 2007) and Susa et al. (2015) have investigated the dissipation of magnetic fields in primordial gas clouds and found that the resistivity is a few orders of magnitude lower than in present-day star-forming clouds and the efficient coupling of magnetic fields with the gas ensures an important pre-condition for the operation of the dynamo. Similar results for the ionization degree have been obtained in an independent study by Glover & Savin (2009).
Analytical studies suggest that the small-scale dynamo operates soon after virialization of the halo and leads to a strong magnetic field in approximate equipartition with turbulent energy (de Souza & Opher 2010; Schleicher et al. 2010; Schober et al. 2012a). The equipartition field strength is rather independent of the initial seed field, as the initial amplification occurs on particularly small scales with rapid amplification. While it is difficult to resolve the dynamo process in numerical simulations during gravitational collapse, requiring a typical resolution of at least 64 cells per Jeans length, this has been achieved in a number of studies during the past years (Sur et al. 2010, 2012; Federrath et al. 2011b; Peters et al. 2012; Turk et al. 2012; Latif et al. 2013d). Turk et al. (2012) and Latif et al. (2013d) performed cosmological magneto-hydrodynamical simulations and confirmed that the small-scale dynamo is operational during the formation of protogalaxies, and the operation of the small-scale dynamo has been confirmed even for turbulence driven by supernova explosions (Balsara et al. 2004; Balsara & Kim 2005). Furthermore, substantial progress has been made in the theoretical understanding of the dynamo, including the regime at high Mach numbers, different types of turbulence, and a large range of magnetic Prandtl numbers (Federrath et al. 2011a, 2014; Schober et al. 2012b; Bovino et al. 2013; Schleicher et al. 2013a).
While the fields produced by the small-scale dynamo are strongly tangled, observations show coherent fields even on galactic scales, even though perturbations may be significant (e.g. Beck et al. 1996). A large-scale field can be generated via the α–Ω dynamo in differentially rotating disks (Steenbeck et al. 1966; Vainshtein & Ruzmaikin 1971; Parker 1971; Brandenburg & Subramanian 2005). Simulations of isolated disk galaxies have shown that the α–Ω dynamo efficiently amplifies magnetic fields on their orbital timescale and the magnetic field strength reaches equipartition value (Gressel et al. 2008; Wang & Abel 2009; Pakmor & Springel 2013). They even become dynamically important, launch outflows, and constrain the star formation efficiency. Various studies (Ruzmaikin et al. 1988; Schmitt 1990; Kulsrud 1999; Moss et al. 2012, 2013) suggest that the large-scale dynamo is essential to generate ordered magnetic fields observed in spiral galaxies. We therefore emphasize that such dynamo processes have not only been confirmed in idealized scenarios, but in simulations of real astrophysical systems.
The turbulent amplification of magnetic fields in primordial disks has been studied by Pudritz & Silk (1989) and Tan & Blackman (2004). They suggested the formation of coherent fields in high-redshift protogalactic disks via the α–Ω dynamo, while Silk & Langer (2006) explored the implications of the magneto-rotational instability as a potential magnetization mechanism. The formation of jets has been explored in simulations by Machida et al. (2006, 2008) and Machida & Doi (2013) starting from an initially coherent field. These studies typically explored the early phases of protostar formation and could not follow the evolution at later times, where the impact of magnetic fields is potentially more significant. Performing cosmological simulations, which self-consistently include all physical processes, still appears to exceed current computational capabilities, in particular, for studies aiming to investigate long-term evolution. It is therefore necessary to employ analytical models incorporating the most relevant processes, which have been tested with individual simulations, such as the small-scale dynamo and the α–Ω dynamo in the context of present work.
In this paper, we explore the formation of a large-scale magnetic field in the protostellar disk during the formation of a Pop III star as well as a supermassive star and study its implications. For this purpose, we combine the α–Ω dynamo model of magnetic field amplification with recently developed disk models for the environment of Pop. III stars and supermassive stars by Latif & Schleicher (2015b,a). Assuming that the initial magnetization is provided by the small-scale dynamo, we calculate the required number of e-folding times to reach saturation with the α–Ω dynamo. We further employ the resulting model of the magnetic field structure to estimate the luminosity and mass outflow rate of a jet, and discuss its implications for early structure formation.
This article is structured as follows: in Sect. 2, we present the general disk model and lay out the adopted framework to model magnetic field amplification and the potential of the field to drive a jet. In Sect. 3, we apply the disk model both to a 10M⊙ Pop. III star as well as a supermassive star, explore the resulting strength of the magnetic field, and the potential power of the jet. We discuss our results and conclusions in Sect. 4.
2. Disk structure and magnetic fields
2.1. Generic disk model
To compute the properties of a self-gravitating accretion disk formed in a primordial halo at z ~ 20, we employ the analytical framework described by Latif & Schleicher (2015a). The formation of this kind of disk is a consequence of angular momentum conservation in the aftermath of halo collapse, which occurs in about a free-fall time (Clark et al. 2011; Greif et al. 2012; Latif et al. 2013c; Latif & Volonteri 2015). We presume that the disk is in an approximate steady-state and is marginally stable as a result of self-regulation (e.g. Lodato 2007). The disk stability is described via the Toomre criterion (Toomre 1964), given as 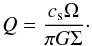 (1)Here Ω and cs are the orbital frequency and the sound speed of the disk, G is the gravitational constant, and Σ is the surface density of the disk. Under stationary conditions, Σ follows from the accretion rate Ṁtot and the disk viscosity ν via
(1)Here Ω and cs are the orbital frequency and the sound speed of the disk, G is the gravitational constant, and Σ is the surface density of the disk. Under stationary conditions, Σ follows from the accretion rate Ṁtot and the disk viscosity ν via 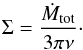 (2)The disk scale height can be estimated as
(2)The disk scale height can be estimated as 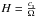 , assuming hydrostatic equilibrium in the vertical direction. This assumption is accurate for Q ≥ 1, while modifications are necessary once self-gravity becomes important in the vertical direction (Lodato 2007).
, assuming hydrostatic equilibrium in the vertical direction. This assumption is accurate for Q ≥ 1, while modifications are necessary once self-gravity becomes important in the vertical direction (Lodato 2007).
Assuming thermal equilibrium, the temperature of the disk is determined from the balance of heating and cooling. The viscous heating rate for a self-gravitating disk can be estimated by solving Eq. (50) given in Lodato (2007). The heating rate per surface area is Q+ = νΣ(RΩ′)2. In the case of Keplerian rotation, we have 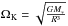 . We assume here that the disk is not fully Keplerian, as it should be partly supported by turbulent and thermal pressure. Therefore, we consider an efficiency parameter ϵK = Ω/ΩK ~ 0.5, where Ω is the angular velocity of the disk. We here assume that the turbulent velocity is 0.5 times the sound speed, which implies that the turbulent support is a fixed fraction of the thermal support. As the velocity profile approximately follows a Keplerian relation even though it has a slightly different slope and a potentially lower normalization, we expect an approximate scaling of ϵK as R− 1/2. As we show below, the main contribution to jet formation results from the inner parts of the disk, and neglecting this dependence is thus not too relevant.
. We assume here that the disk is not fully Keplerian, as it should be partly supported by turbulent and thermal pressure. Therefore, we consider an efficiency parameter ϵK = Ω/ΩK ~ 0.5, where Ω is the angular velocity of the disk. We here assume that the turbulent velocity is 0.5 times the sound speed, which implies that the turbulent support is a fixed fraction of the thermal support. As the velocity profile approximately follows a Keplerian relation even though it has a slightly different slope and a potentially lower normalization, we expect an approximate scaling of ϵK as R− 1/2. As we show below, the main contribution to jet formation results from the inner parts of the disk, and neglecting this dependence is thus not too relevant.
The viscous heating rate for this kind of disk is given as 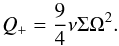 (3)The cooling rate per surface area of the disk can be computed as follows:
(3)The cooling rate per surface area of the disk can be computed as follows: 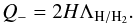 (4)Depending on the regime under consideration, ΛH/H2 denotes the atomic or molecular cooling rate in units of erg/cm3/ s. For a disk around a typical Pop. III star, the cooling on larger scales is driven by molecular hydrogen line cooling, while it is dominated by collisionally-induced emission (CIE) of molecular hydrogen in the interior. The detailed expressions for the cooling rates, including approximations employed for the optical depth, are given by Latif & Schleicher (2015a). In fact, the model was further extended by Latif & Schleicher (2015b) for the disks of supermassive stars exposed to larger accretion rates, as the disks on large radii cool via molecular hydrogen line cooling, while the interior is dominated by atomic hydrogen line cooling as a result of the viscous heating.
(4)Depending on the regime under consideration, ΛH/H2 denotes the atomic or molecular cooling rate in units of erg/cm3/ s. For a disk around a typical Pop. III star, the cooling on larger scales is driven by molecular hydrogen line cooling, while it is dominated by collisionally-induced emission (CIE) of molecular hydrogen in the interior. The detailed expressions for the cooling rates, including approximations employed for the optical depth, are given by Latif & Schleicher (2015a). In fact, the model was further extended by Latif & Schleicher (2015b) for the disks of supermassive stars exposed to larger accretion rates, as the disks on large radii cool via molecular hydrogen line cooling, while the interior is dominated by atomic hydrogen line cooling as a result of the viscous heating.
The disk viscosity is parametrized via the α-formalism of Shakura & Sunyaev (1973) as 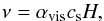 (5)where αvis is the viscous parameter. For Q = 1, αvis can be determined using the above equations as
(5)where αvis is the viscous parameter. For Q = 1, αvis can be determined using the above equations as 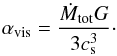 (6)In the same way, the surface density of the disk follows as
(6)In the same way, the surface density of the disk follows as 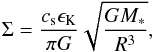 (7)and the number density inside the disk is approximated as
(7)and the number density inside the disk is approximated as 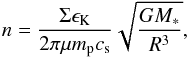 (8)with μ the mean molecular weight. We adopt μ ~ 2 for the molecular gas and μ ~ 1.2 in the atomic cooling regime.
(8)with μ the mean molecular weight. We adopt μ ~ 2 for the molecular gas and μ ~ 1.2 in the atomic cooling regime.
2.2. From small-scale to large-scale magnetic fields
In the following, we consider the evolution of magnetic fields for the disk model given above. For this purpose, we employ the dynamo model of Arshakian et al. (2009) for disk galaxies, where the initial magnetization is provided via the small-scale dynamo and the α–Ω dynamo subsequently produces an ordered magnetic field. The main parameters for the dynamo are the angular velocity Ω, the disk height H, the disk radius R, and the mass density ρ, which are determined by the model above. The large-scale magnetic field component is defined via a volume integration over a characteristic scale λav ~ 2R based on the Reynolds averaging procedure (Krause & Raedler 1980). The small-scale component then describes the deviation from the Reynolds average. For the largest eddies, we expect a characteristic scale comparable to the disk height H. For primordial disks with H/R ~ 0.1−0.5, which implies a characteristic ratio of λav/H ~ 4−20. For very thick disks, the assumption of scale separation may then only hold at an approximate level. In the presence of central massive objects, however, we expect a relevant flattening to occur because of the gravity of the central source.
We assume here that well before the formation of the disk, a seed magnetic field has been generated, for instance, by the Biermann battery (Biermann 1950) or as a result of plasma fluctuations (Schlickeiser 2012), which was subsequently amplified via the small-scale dynamo (Kazantsev 1968). The small-scale dynamo starts in the kinematic phase, where amplification occurs on the viscous length scale lν, with a characteristic timescale corresponding to the eddy-turnover time on that scale. Once the magnetic field has saturated on the viscous scale lν, amplification continues on larger scales, leading to a linear growth in this regime. On the driving scale of turbulence, the magnetic field is then saturated after a few eddy-turnover times (Schekochihin et al. 2002; Beresnyak 2012; Schleicher et al. 2013b). The equipartition field strength B∗ is defined as 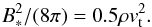 (9)Owing to the short timescales involved, we expect this process to be completed when the disk has formed. We then estimate the magnetic field strength Bss produced by the small-scale dynamo as
(9)Owing to the short timescales involved, we expect this process to be completed when the disk has formed. We then estimate the magnetic field strength Bss produced by the small-scale dynamo as 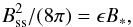 (10)where ϵ is the saturation fraction and vt the turbulent velocity. We adopt a characteristic value of ϵ ~ 0.3, which is consistent with turbulence in the subsonic to trans-sonic regime (Federrath et al. 2011a). Indeed, the turbulent velocity in the disk is typically of the order of the sound speed, so we adopt vt ~ 0.5cs (Clark et al. 2011; Greif et al. 2012; Latif et al. 2013a, 2014b). We assume here that the turbulence is predominantly driven by infall and accretion onto the disk accompanied by gravitational instabilities (cf. Elmegreen & Burkert 2010; Klessen & Hennebelle 2010), but additional contributions may come from the magneto-rotational instability. The largest eddies within the disk have a maximum size lt given by the disk height H, which therefore defines the characteristic length scale of the magnetic field. Further, a small-scale random field on the scales of the disk height is expected to induce a weak large-scale component. The strength of this component scales as N− 1/2, where
(10)where ϵ is the saturation fraction and vt the turbulent velocity. We adopt a characteristic value of ϵ ~ 0.3, which is consistent with turbulence in the subsonic to trans-sonic regime (Federrath et al. 2011a). Indeed, the turbulent velocity in the disk is typically of the order of the sound speed, so we adopt vt ~ 0.5cs (Clark et al. 2011; Greif et al. 2012; Latif et al. 2013a, 2014b). We assume here that the turbulence is predominantly driven by infall and accretion onto the disk accompanied by gravitational instabilities (cf. Elmegreen & Burkert 2010; Klessen & Hennebelle 2010), but additional contributions may come from the magneto-rotational instability. The largest eddies within the disk have a maximum size lt given by the disk height H, which therefore defines the characteristic length scale of the magnetic field. Further, a small-scale random field on the scales of the disk height is expected to induce a weak large-scale component. The strength of this component scales as N− 1/2, where 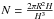 is the number of turbulent cells in the disk (Hogan 1983; Ruzmaikin et al. 1988; Arshakian et al. 2009). Therefore, we expect an initial field strength of
is the number of turbulent cells in the disk (Hogan 1983; Ruzmaikin et al. 1988; Arshakian et al. 2009). Therefore, we expect an initial field strength of 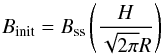 (11)on large scales. The initial magnetic field strength is subsequently amplified via the α–Ω dynamo. To model the α effect, we adopt the parametrization given in Eq. (9.60) of Krause & Raedler (1980). The helicity defining α is considered an average over the disk height H, corresponding to the maximum scale of turbulent fluctuations. Thus,
(11)on large scales. The initial magnetic field strength is subsequently amplified via the α–Ω dynamo. To model the α effect, we adopt the parametrization given in Eq. (9.60) of Krause & Raedler (1980). The helicity defining α is considered an average over the disk height H, corresponding to the maximum scale of turbulent fluctuations. Thus, 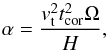 (12)where tcor is the correlation timescale defined as
(12)where tcor is the correlation timescale defined as 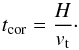 (13)Combining the above equations, α can be computed as
(13)Combining the above equations, α can be computed as 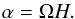 (14)The turbulent diffusivity is calculated based on mixing length theory as
(14)The turbulent diffusivity is calculated based on mixing length theory as 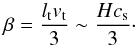 (15)The joint action of both α and β can be described by the so-called dynamo number given as
(15)The joint action of both α and β can be described by the so-called dynamo number given as 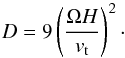 (16)The value of D needs to be larger than a critical value Dc = 7 for the dynamo to operate, as found from numerical simulations of galactic dynamos (Ruzmaikin et al. 1988; Arshakian et al. 2009). The critical value Dc given here depends on the overall thickness of the disk, and this estimate has been determined from thin galactic disks, while for primordial accretion disks we expect H/R ~ 0.1−0.5. With a dynamo number D ~ 40, an enhancement by a factor of 5 in Dc can be accommodated. The precise value of Dc should, however, be checked using numerical simulations. The growth rate for the dynamo is computed as
(16)The value of D needs to be larger than a critical value Dc = 7 for the dynamo to operate, as found from numerical simulations of galactic dynamos (Ruzmaikin et al. 1988; Arshakian et al. 2009). The critical value Dc given here depends on the overall thickness of the disk, and this estimate has been determined from thin galactic disks, while for primordial accretion disks we expect H/R ~ 0.1−0.5. With a dynamo number D ~ 40, an enhancement by a factor of 5 in Dc can be accommodated. The precise value of Dc should, however, be checked using numerical simulations. The growth rate for the dynamo is computed as 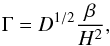 (17)and the amplification timescale is (Arshakian et al. 2009)
(17)and the amplification timescale is (Arshakian et al. 2009) 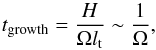 (18)implying that tgrowth ~ torb/ (2π), with torb the orbital timescale of the disk. The final field strength due to the α–Ω effect is related to the equipartition field strength B∗. The final field strength is then computed via the expression
(18)implying that tgrowth ~ torb/ (2π), with torb the orbital timescale of the disk. The final field strength due to the α–Ω effect is related to the equipartition field strength B∗. The final field strength is then computed via the expression 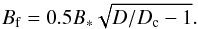 (19)The ratio of Bf/Bini yields the number of e-folding times required to reach the final field strength.
(19)The ratio of Bf/Bini yields the number of e-folding times required to reach the final field strength.
While the amplification occurs on the timescale tgrowth defined in Eq. (18), the resulting magnetic field is initially ordered only on scales corresponding to the half-thickness of the disk. Full ordering over the entire disk radius occurs then on the ordering timescale given as (Moss et al. 1998) 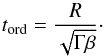 (20)Combining the assumptions above, one can show that tord ~ 3R/ (D1/4vt), which is about three times longer than the growth time tgrowth as the disk is rather thick in our case with H/R ~ 0.1−0.5 (Latif & Volonteri 2015).
(20)Combining the assumptions above, one can show that tord ~ 3R/ (D1/4vt), which is about three times longer than the growth time tgrowth as the disk is rather thick in our case with H/R ~ 0.1−0.5 (Latif & Volonteri 2015).
2.3. Jet formation
The presence of a coherent magnetic field in the disk can lead to the formation of magnetic jets and outflows. Our jet formation model is based on the framework of Tan & Blackman (2004). We consider the toroidal component Bφ,s to be the final field strength produced by the α–Ω dynamo as defined in Eq. (19). The toroidal component Bφ is larger than the poloidal magnetic field Br, as it is amplified by the shear. The ratio of the poloidal magnetic field Br,s to the toroidal field Bφ,s can be evaluated based on the timescales of buoyancy and convection given as 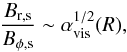 (21)where αvis is the previously introduced disk viscosity parameter. Requiring that ∇·B = 0, one can show that
(21)where αvis is the previously introduced disk viscosity parameter. Requiring that ∇·B = 0, one can show that 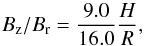 (22)where Bz,s is the vertical field inside the disk. Under the assumption of momentum conservation, the magnetic Poynting flux is transferred into mechanical energy during the propagation to larger scales. Considering that at a larger distance from the star, the energy of the outflow is dominated by the kinetic energy of the matter, we can express the outflow luminosity as
(22)where Bz,s is the vertical field inside the disk. Under the assumption of momentum conservation, the magnetic Poynting flux is transferred into mechanical energy during the propagation to larger scales. Considering that at a larger distance from the star, the energy of the outflow is dominated by the kinetic energy of the matter, we can express the outflow luminosity as 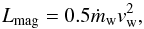 (23)where vw is the terminal velocity of the outflow and ṁw is the mass outflow rate. According to theoretical models for the magnetically driven outflows, vw can be estimated from the escape velocity vesc as (Shu et al. 2000; Konigl & Pudritz 2000)
(23)where vw is the terminal velocity of the outflow and ṁw is the mass outflow rate. According to theoretical models for the magnetically driven outflows, vw can be estimated from the escape velocity vesc as (Shu et al. 2000; Konigl & Pudritz 2000) 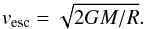 (24)In the following, we adopt a differential formulation by considering the vertical Poynting flux through a disk annulus with radius R and thickness dR. Its contribution to the jet luminosity is thus given as (Lovelace et al. 2002)
(24)In the following, we adopt a differential formulation by considering the vertical Poynting flux through a disk annulus with radius R and thickness dR. Its contribution to the jet luminosity is thus given as (Lovelace et al. 2002) 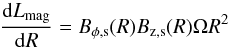 (25)for quasi-static conditions. The differential magnetic luminosity of the annulus dLmag drives a differential outflow rate dṁw, which is related via
(25)for quasi-static conditions. The differential magnetic luminosity of the annulus dLmag drives a differential outflow rate dṁw, which is related via 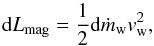 (26)where the terminal velocity vw is given as the escape velocity at radius R. Integrating the expressions for dLmag and dṁw yields the magnetic luminosity and mass outflow rate within radius R. In particular, we define
(26)where the terminal velocity vw is given as the escape velocity at radius R. Integrating the expressions for dLmag and dṁw yields the magnetic luminosity and mass outflow rate within radius R. In particular, we define 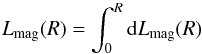 (27)and
(27)and 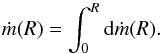 (28)
(28)
3. Results
In the following, we employ the model outlined above to explore the disk properties and their impact on magnetic field amplification and jet formation for two characteristic cases, a Pop. III star and a supermassive star. In the first case, we consider a typical mode of Pop. III star formation, with cooling driven by molecular hydrogen and moderate accretion rates of ~10-3M⊙ yr-1 (e.g. Abel et al. 2002; Bromm et al. 2002; Yoshida et al. 2008). As a typical mass, we adopt ~10M⊙ during the protostellar accretion phase (see e.g. Latif et al. 2013c), which may increase to >100M⊙ until the star reaches the main sequence.
We compare this scenario with the accretion disk surrounding a supermassive protostar of ~105M⊙, which is expected to form in more massive primordial halos in the presence of strong UV backgrounds (Hosokawa et al. 2013; Latif et al. 2013e, 2014a; Schleicher et al. 2013a; Regan et al. 2014; Ferrara et al. 2014). In this regime, simulations have derived characteristic accretion rates of 10-1M⊙ yr-1. Here, we aim to quantify the characteristic magnetic field strength, jet luminosities, and mass outflow rates in both cases. The mass out flow rate and jet power can be particularly valuable to determine the strength of protostellar feedback from such protostars.
3.1. Pop. III star
In the case of a Pop. III star with moderate accretion rates, the cooling on larger scales is due to molecular hydrogen line cooling, while at smaller scales and for densities above ~1014 cm-3, the cooling is driven via CIE of molecular hydrogen. In the following, we describe the disk structure obtained in both regimes, employing the cooling rates as described by Latif & Schleicher (2015a). For the protostar, we adopt a generic mass of 10M⊙ with an accretion rate of ~10-3M⊙ yr-1, as found in numerical simulations by Latif et al. (2013c). The disk structure obtained with our model is given in Fig. 1, where we show the density and temperature structure both in the molecular cooling and the CIE cooling regime.
 |
Fig. 1 Surface density (top panel), gas mid-plane density (middle panel), and the gas temperature (bottom panel) of the disk for a 10 M⊙ central star with an accretion rate of 10-3M⊙ yr-1. The left panels represent the CIE cooling regime, while the right panels show the regime of H2 line cooling. |
The surface density of the disk increases from ~30 g cm-2 at 300 AU to ~5 × 105 g cm-2 at 1 AU, and follows Σ ∝ R-1.5. The mid-plane density of the disk at 300 AU is 1010 cm-3, which increases to ~1017 cm-3 at 1 AU. The temperature increases in the H2 cooling regime towards smaller scales until it reaches ~2000 K, where CIE cooling sets in on scales of ~10 AU. From that point, the temperature remains approximately constant, with a minor decrease towards 1 AU.
The magnetic field strength obtained in this kind of disk via the dynamo process is shown in Fig. 2, and includes the coherent magnetic field component produced by the small-scale dynamo (Binit) as well as the final field strength obtained via the α–Ω dynamo. From the small-scale dynamo, we obtain a characteristic field strength Binit of 10-3−100.2 G on scales ranging from 300 AU down to 1 AU. The higher Binit is due to high gas densities of at least 109 cm-3 as well as high temperatures in the gas reflected by an amount of turbulent energy, which is about 50% of the thermal energy and consistent with estimates from numerical simulations (Greif et al. 2012; Latif et al. 2013c). The magnetic field strength is further enhanced by the α–Ω dynamo, with a final field strength Bf of 10-1.8−10+ 2.4 G.
 |
Fig. 2 Initial magnetic field strength Binit generated by the small-scale dynamo (the top panel) and the final magnetic field strength Bf generated by the α−Ω dynamo (middle panel) for a 10 M⊙ central star with an accretion rate of 10-3M⊙ yr-1. In the bottom panel, we show the orbital timescale, the growth time of the α–Ω dynamo, and the ordering timescale. The left panels represent the CIE cooling regime, while the right panels show the regime of H2 line cooling. |
We further show the orbital timescale, the growth time and ordering timescale within the same figure. As mentioned in Sect. 2.2, the growth time corresponds to about 1/(2π) of the orbital time. Depending on the scale, the ratio between the initial and final magnetic field strength varies between ~50 on scales of 1 AU and ~5 on scales of 300 AU, corresponding to 2.7−5 e-folding times until saturation. The ordering timescale may add a few more e-folds. Considering the characteristic timescale for accretion, tacc = M∗/Ṁ ~ 104 yr, we find that the timescale to reach saturation becomes comparable to the accretion time on scales of ~300 AU and is considerably shorter on smaller scales. As a result, our assumption of saturation is justified at least until scales of 100 AU.
The resulting properties of the magnetic outflow are given in Fig. 3, showing the magnetic luminosity and mass outflow rate within a given radius R both in the CIE cooling and the molecular cooling regime. It is clearly noticeable that both quantities are dominated by contributions from the inner 10 AU, where the disk structure is determined by CIE cooling. The magnetic power to drive the outflow reaches up to 100L⊙ at 10 AU, corresponding to a mass outflow of 10-3.7M⊙ yr-1. While the mass loss from the outflow corresponds to a minor reduction of the mass reaching the central object, it provides a relevant feedback mechanism towards larger scales with a characteristic velocity of ~60 km s-1, which can drive the magnetization on larger scales with a more coherent magnetic field.
 |
Fig. 3 Expected properties of the magnetic outflow for a 10M⊙ star with an accretion rate of 10-3M⊙ yr-1. The magnetic luminosity is depicted in the top panel, while the bottom panel shows the mass outflow rate within a given radius R. The left panels represent the CIE cooling regime, while the right panels show the regime of H2 line cooling. |
3.2. Supermassive star
Now we consider the accretion disk surrounding a supermassive star with 105M⊙ and an accretion rate of 0.1M⊙ yr-1, as motivated via numerical simulations (Latif et al. 2013e, 2014a; Regan et al. 2014). The thermal properties of the disk structure were previously explored by Latif & Schleicher (2015b). They found that the disk is dominated by molecular cooling at large radii, while a transition to the atomic cooling regime may occur on scales of ~300 AU as a result of viscous heating and the collisional dissociation of atomic hydrogen.
The resulting disk structure in terms of density and temperature is plotted in Fig. 4. Because of the high accretion rates, the disk is considerably denser in this case with the surface density ranging from 103.2 g cm-2 at 1000 AU to 105.5 g cm-2 at 30 AU. Similarly, the gas mid-plane density ranges from ~1012 cm-3 on large radii to 1016 cm-3 in the interior parts of the disk. In the molecular cooling regime, the temperature of the disk increases towards smaller scales as a result of viscous heating, leading to temperatures of ~4000 K where molecular hydrogen is efficiently dissociated. Within the central 300 AU, the gas temperature is almost constant with a very minor decrease towards higher densities.
 |
Fig. 4 Surface density (top panel), gas mid-plane density (middle panel) and the gas temperature (bottom panel) of the disk are shown for 105M⊙ central star with an accretion rate of 10-1M⊙ yr-1. The left panels show the atomic cooling regime in the inner parts of the disk, while the right panels show the H2 cooling regime on larger scales. |
The expected magnetic field strengths produced by the dynamo processes in the disk are then given in Fig. 5. On scales corresponding to the disk radius, the small-scale dynamo contributes an initial field strength Binit ranging from 10-2.5 G at R = 1000 AU up to 10-0.8 G at R ~ 39 AU. The field strength is further enhanced via the α–Ω dynamo, leading to a final field strength Bf of 1−200 G. The ratio between the initial and final field strength thus varies between ~1000 on large radii and ~1260 on smaller scales, corresponding to ~7 e-folding times. As a result of the considerably larger mass of the central object, the characteristic timescales are significantly reduced compared to the previous scenario, with a growth time of ~30 yr on scales of 300 AU. The growth time is significantly smaller than the characteristic timescale for accretion, tacc = M∗/Ṁ ~ 106 yr, so one can assume that saturation has occurred on scales of at least 1000 AU.
 |
Fig. 5 Initial magnetic field strength Binit generated by the small-scale dynamo (top panel) and the final magnetic field strength Bf generated by the α–Ω dynamo (middle panel) for a 105M⊙ star with an accretion rate of 10-1M⊙ yr-1. In the bottom panel, we show the orbital timescale, the growth time of the α–Ω dynamo, and the ordering timescale. The left panels show the atomic cooling regime in the inner parts of the disk, while the right panels show the H2 cooling regime on larger scales. |
The resulting properties of the magnetic outflow are finally shown in Fig. 6. Both the magnetic luminosity and mass outflow rate are dominated by the inner parts of the disk, in this case corresponding to the inner 400 AU where the gas is atomic. The outflow luminosity at that point corresponds to roughly 106.0L⊙, and the mass outflow rate to 10-2.1M⊙ yr-1. The outflow therefore does not strongly reduce the accretion onto the central object, but provides a potentially strong and powerful feedback mechanism towards larger scales with a characteristic velocity of ~1200 km s-1. Especially as the radiative feedback resulting from rapidly accreting supermassive stars is considered to be weak due to their large extended atmospheres (Hosokawa et al. 2013; Schleicher et al. 2013a), the magnetic outflow can provide a relevant mechanism for feedback on larger scales, including the magnetization of the interstellar and intergalactic medium.
 |
Fig. 6 Expected properties of the magnetic outflow for a 105M⊙ star with an accretion rate of 10-1M⊙ yr-1. The magnetic luminosity is depicted in the top panel, while the bottom panel shows the mass outflow rate within a given radius R. The left panels represent the atomic cooling regime, while the right panels show the regime of H2 line cooling. |
The typical lifetime of a supermassive star is about 1 Myr and is much longer than all other times scales shown in Fig. 5. The jet is expected to reach a steady state in a few disk rotation timescales, i.e. ~100 yr (Kudoh et al. 2003). The expected jet velocity is about 1200 km s-1, for which the jet can travel about 1.2 kpc within the star’s life. We therefore expect that the jet can have a significant impact on the centre of the host galaxy and may affect the subsequent accretion onto the resulting black hole.
4. Discussion and conclusions
In this paper, we have considered the evolution of magnetic fields after the formation of a self-gravitating primordial disk around the central protostar. While previous studies have shown that a strong, tangled magnetic field can be produced via the small-scale dynamo (e.g. Schleicher et al. 2010; Sur et al. 2010; Schober et al. 2012a; Turk et al. 2012; Latif et al. 2013d), we have explored how the resulting magnetic field can subsequently grow via the α–Ω dynamo in a self-gravitating accretion disk (Inayoshi & Haiman 2014; Latif & Schleicher 2015a). Using the resulting magnetic field structure, we estimated the expected jet properties and calculated the magnetic luminosity as well as the mass outflow rate. We applied our model to two characteristic cases: a conventional 10M⊙ Pop. III star with a typical accretion rate of 10-3M⊙ yr-1 and a 105M⊙ supermassive star with an accretion rate of 10-1M⊙ yr-1.
For the conventional Pop. III star, our results show that the α–Ω dynamo produces coherent magnetic fields within the protostellar disk at least out to radii of 100 AU. The resulting strength of the coherent field ranges from ~0.1 G on this particular scale up to ~250 G on a scale of 1 AU. The predominant contribution to the jet comes from the central 10 AU, producing a jet luminosity of ~100L⊙ and a mass outflow rate of 10-3.7M⊙ yr-1, implying a negligible mass loss compared to the accretion rate of 10-3M⊙ yr-1.
However, while such Pop. III stars are expected to form in minihalos with characteristic masses of 106M⊙ and typical escape velocities of ~10 km s-1 (Abel et al. 2002; Bromm et al. 2002; Yoshida et al. 2008), the characteristic velocity of the jet is about ~60 km s-1, implying that the jet can potentially escape. We estimate that typical timescales for the jet to leave the halo correspond to about 5 million years. During that time, the jet can provide relevant feedback onto the halo itself and contribute to the magnetization of the surrounding environment. Particularly, in dense cosmological environments consisting of several minihalos, the jet may contribute to the magnetization of the intergalactic material.
For the supermassive star, the dynamo amplification is even more efficient owing to shorter characteristic timescales in the stellar environment, implying an efficient magnetization of the disk at least out to radii of 1000 AU. The resulting magnetic field strengths range from ~1 G on that scale up to 200 G on scales of 39 AU. The outflow is predominantly driven within the central 300 AU, with a jet luminosity of about 106.0L⊙ and a mass outflow rate of 10-2.1M⊙ yr-1. Also, in this case the outflow is negligible compared to the accretion rate, but can provide a strong mechanical feedback onto the surrounding gas. Previous studies indicated that the radiative feedback of rapidly accreting supermassive stars is rather weak (Hosokawa et al. 2013; Schleicher et al. 2013a). Therefore, it is particularly relevant if feedback occurs in the form of jets and outflows which provides a mechanism to connect the central object with the evolution on larger scales already during the early stages of AGN formation. The expected outflow velocity is of the order 1200 km s-1, and therefore considerably larger than the escape velocity of the dark matter halo. Within the lifetime of the star, the jet can therefore propagate over a distance of 1.2 kpc and significantly affect the central region of the host galaxy as well as subsequent accretion onto the central black hole. However, the formation sites of supermassive stars are expected to be very rare, as they require rather special conditions to form. The estimates of the number density of supermassive stars suggest that a few of these objects are expected to form per Gpc-3 (Dijkstra et al. 2014; Habouzit et al. 2015).
Our results show that magnetic feedback has already occurred during the formation of the first generations of stars with typical mass outflow rates between 1−10% of the mass accretion rate. We expect similar results to hold not only in the primordial case, but even after metal enrichment, for instance, in protostellar disk where dust cooling is significant (Tanaka & Omukai 2014). As recently shown by Susa et al. (2015), the coupling between the magnetic field and the gas is rather efficient for a large range of metallicities and densities, and we expect the dynamo mechanism to operate independently of the metallicity of the forming object. However, in the case of low-mass objects, the characteristic orbital and dynamo timescales are becoming longer. At the same time, it is also expected that the accretion rate decreases with increasing metallicity, also implying that more time is available for the dynamo to operate. The interplay between such a dynamo operation, metal cooling, and gas accretion should therefore be studied in greater detail. As a general result, it appears plausible, however, that magnetized jets and outflows can already be expected from the first generations of protostars, which may act as relevant sources of turbulence at low metallicity in a very similar fashion as in the present-day interstellar medium (e.g. Wang et al. 2010).
Beyond the general population of high-redshift stars, it is of particular interest to explore the consequence of magnetic feedback resulting from supermassive stars, which have been predicted to form in a number of cosmological simulations (Latif et al. 2013e, 2014a; Regan et al. 2014). The jets from such supermassive stars provide strong feedback and can therefore have a substantial influence on the evolution of their host galaxy. Similar to the feedback from supermassive black holes, such jets can potentially suppress star formation in part of the halo (Maiolino et al. 2012) or temporarily enhance star formation by compressing the pre-existing clumps (Silk 2013). We therefore propose that the resulting feedback mechanism should be included in future simulations studying the formation of the first active galactic nuclei.
We have assumed here that turbulence is mainly driven by gravitational instabilities as shown by high-resolution cosmological simulations (Turk et al. 2012; Latif et al. 2013d). We emphasize that numerical simulations often underestimate the amount of turbulence during gravitational collapse, as turbulent eddies need to be resolved with at least 32−64 cells depending on the magneto-hydrodynamical scheme (Sur et al. 2010; Federrath et al. 2011b; Turk et al. 2012; Latif et al. 2013d). Results from these studies therefore need to be regarded as a lower limit. The presence of the MRI may further help to drive turbulence, and it is even conceivable that both instabilities are operational at the same time (Fromang et al. 2004).
Our model combines various astrophysical processes such as the amplification of magnetic seed fields via the small-scale dynamo and the α−Ω mechanism. We assume that the α−Ω dynamo provides a large-scale component of the magnetic field and that the available Poynting flux drives a magnetic outflow, as is well known in the context of protostars and black holes. A complete modelling of all relevant processes is still difficult under primordial conditions, as the formation of primordial protostellar accretion disks can only be modelled since a few years (see e.g. Clark et al. 2011; Greif et al. 2012). However, the presence of the small-scale dynamo during gravitational collapse has already been confirmed by numerical simulations (Sur et al. 2010; Federrath et al. 2011b; Turk et al. 2012; Latif et al. 2013d), and subsequent studies may now address further evolution after the formation of a disk in greater detail.
The assumption of an initially turbulent magnetic field has been motivated by the efficient amplification of magnetic fields via the small-scale dynamo, which does not require the existence of a disk. The magneto-rotational instability (MRI) may become operational in the protostellar disks forming around Pop III and supermassive stars, where it can contribute to the generation of turbulence and amplification of magnetic fields (Silk & Langer 2006).
Acknowledgments
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No. 656428. We thank the anonymous referee for his/her feedback, which helped us to improve the manuscript.
References
- Abel, T., Bryan, G. L., & Norman, M. L. 2002, Science, 295, 93 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Arlen, T. C., Vassilev, V. V., Weisgarber, T., Wakely, S. P., & Yusef Shafi, S. 2014, ApJ, 796, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Arshakian, T. G., Beck, R., Krause, M., & Sokoloff, D. 2009, A&A, 494, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1998, Rev. Mod. Phys., 70, 1 [Google Scholar]
- Balsara, D. S., & Kim, J. 2005, ApJ, 634, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Balsara, D. S., Kim, J., Mac Low, M.-M., & Mathews, G. J. 2004, ApJ, 617, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Banerjee, R., & Pudritz, R. E. 2006, ApJ, 641, 949 [NASA ADS] [CrossRef] [Google Scholar]
- Banerjee, R., Vázquez-Semadeni, E., Hennebelle, P., & Klessen, R. S. 2009, MNRAS, 398, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., Brandenburg, A., Moss, D., Shukurov, A., & Sokoloff, D. 1996, ARA&A, 34, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Beresnyak, A. 2012, Phys. Rev. Lett., 108, 035002 [NASA ADS] [CrossRef] [Google Scholar]
- Bernet, M. L., Miniati, F., Lilly, S. J., Kronberg, P. P., & Dessauges-Zavadsky, M. 2008, Nature, 454, 302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Biermann, L. 1950, Z. Naturforsch. Teil A, 5, 65 [Google Scholar]
- Bovino, S., Schleicher, D. R. G., & Schober, J. 2013, New J. Phys., 15, 013055 [NASA ADS] [CrossRef] [Google Scholar]
- Bovino, S., Latif, M. A., Grassi, T., & Schleicher, D. R. G. 2014, MNRAS, 441, 2181 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., & Subramanian, K. 2005, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bromm, V., Coppi, P. S., & Larson, R. B. 2002, ApJ, 564, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, P. C., Glover, S. C. O., Smith, R. J., et al. 2011, Science, 331, 1040 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- de Souza, R. S., & Opher, R. 2010, Phys. Rev. D, 81, 067301 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dermer, C. D., Cavadini, M., Razzaque, S., et al. 2011, ApJ, 733, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Dijkstra, M., Ferrara, A., & Mesinger, A. 2014, MNRAS, 442, 2036 [NASA ADS] [CrossRef] [Google Scholar]
- Dolag, K., Kachelriess, M., Ostapchenko, S., & Tomàs, R. 2011, ApJ, 727, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., & Burkert, A. 2010, ApJ, 712, 294 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Chabrier, G., Schober, J., et al. 2011a, Phys. Rev. Lett., 107, 114504 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Sur, S., Schleicher, D. R. G., Banerjee, R., & Klessen, R. S. 2011b, ApJ, 731, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Schober, J., Bovino, S., & Schleicher, D. R. G. 2014, ApJ, 797, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Fendt, C. 2009, ApJ, 692, 346 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrara, A., Salvadori, S., Yue, B., & Schleicher, D. 2014, MNRAS, 443, 2410 [NASA ADS] [CrossRef] [Google Scholar]
- Fromang, S., Balbus, S. A., Terquem, C., & De Villiers, J.-P. 2004, ApJ, 616, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, L., Theuns, T., Frenk, C. S., et al. 2010, MNRAS, 403, 1283 [NASA ADS] [CrossRef] [Google Scholar]
- Glover, S. C. O., & Savin, D. W. 2009, MNRAS, 393, 911 [NASA ADS] [CrossRef] [Google Scholar]
- Grasso, D., & Rubinstein, H. R. 2001, Phys. Rep., 348, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Greif, T. H., Bromm, V., Clark, P. C., et al. 2012, MNRAS, 424, 399 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Gressel, O., Elstner, D., Ziegler, U., & Rüdiger, G. 2008, A&A, 486, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habouzit, M., Volonteri, M., Latif, M., et al. 2015, MNRAS, submitted [arXiv:1507.05971] [Google Scholar]
- Hammond, A. M., Robishaw, T., & Gaensler, B. M. 2012, ArXiv e-prints [arXiv:1209.1438] [Google Scholar]
- Hawley, J. F., & Balbus, S. A. 1991, ApJ, 376, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., & Fromang, S. 2008, A&A, 477, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., & Teyssier, R. 2008, A&A, 477, 25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hogan, C. J. 1983, Phys. Rev. Lett., 51, 1488 [Google Scholar]
- Hosokawa, T., Yorke, H. W., Inayoshi, K., Omukai, K., & Yoshida, N. 2013, ApJ, 778, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Inayoshi, K., & Haiman, Z. 2014, MNRAS, 445, 1549 [NASA ADS] [CrossRef] [Google Scholar]
- Ivison, R. J., Margnelli, B., Ibar, E., et al. 2010, A&A, 518, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kazantsev, A. P. 1968, Sov. J. Exper. Theor. Phys., 26, 1031 [Google Scholar]
- Klessen, R. S., & Hennebelle, P. 2010, A&A, 520, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Konigl, A., & Pudritz, R. E. 2000, Protostars and Planets IV, 759 [Google Scholar]
- Krause, F., & Raedler, K. H. 1980, Mean-field magnetohydrodynamics and dynamo theory (Oxford: Pergamon Press) [Google Scholar]
- Kronberg, P. P., Bernet, M. L., Miniati, F., et al. 2008, ApJ, 676, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Kudoh, T., Matsumoto, R., & Shibata, K. 2003, Ap&SS, 287, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Kulsrud, R. M. 1999, ARA&A, 37, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Kulsrud, R. M., & Zweibel, E. G. 2008, Rep. Progr. Phys., 71, 046901 [Google Scholar]
- Latif, M. A., & Schleicher, D. R. G. 2015a, MNRAS, 449, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Latif, M. A., & Schleicher, D. R. G. 2015b, A&A, 578, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Latif, M. A., & Volonteri, M. 2015, MNRAS, 452, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Latif, M. A., Schleicher, D. R. G., Schmidt, W., & Niemeyer, J. 2013a, MNRAS, 433, 1607 [NASA ADS] [CrossRef] [Google Scholar]
- Latif, M. A., Schleicher, D. R. G., Schmidt, W., & Niemeyer, J. 2013b, MNRAS, 430, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Latif, M. A., Schleicher, D. R. G., Schmidt, W., & Niemeyer, J. 2013c, ApJ, 772, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Latif, M. A., Schleicher, D. R. G., Schmidt, W., & Niemeyer, J. 2013d, MNRAS, 432, 668 [NASA ADS] [CrossRef] [Google Scholar]
- Latif, M. A., Schleicher, D. R. G., Schmidt, W., & Niemeyer, J. C. 2013e, MNRAS, 436, 2989 [NASA ADS] [CrossRef] [Google Scholar]
- Latif, M. A., Schleicher, D. R. G., Bovino, S., Grassi, T., & Spaans, M. 2014a, ApJ, 792, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Latif, M. A., Schleicher, D. R. G., & Schmidt, W. 2014b, MNRAS, 440, 1551 [NASA ADS] [CrossRef] [Google Scholar]
- Lodato, G. 2007, Nuovo Cimento Rivista Serie, 30, 293 [Google Scholar]
- Lovelace, R. V. E., Li, H., Koldoba, A. V., Ustyugova, G. V., & Romanova, M. M. 2002, ApJ, 572, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Machida, M. N., & Doi, K. 2013, MNRAS, 435, 3283 [NASA ADS] [CrossRef] [Google Scholar]
- Machida, M. N., Omukai, K., Matsumoto, T., & Inutsuka, S.-I. 2006, ApJ, 647, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Machida, M. N., Matsumoto, T., & Inutsuka, S.-I. 2008, ApJ, 685, 690 [NASA ADS] [CrossRef] [Google Scholar]
- Magnelli, B., Ivison, R. J., Lutz, D., et al. 2015, A&A, 573, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maiolino, R., Gallerani, S., Neri, R., et al. 2012, MNRAS, 425, L66 [NASA ADS] [CrossRef] [Google Scholar]
- Maki, H., & Susa, H. 2004, ApJ, 609, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Maki, H., & Susa, H. 2007, PASJ, 59, 787 [NASA ADS] [Google Scholar]
- Moss, D., Shukurov, A., & Sokoloff, D. 1998, Geophys. Astrophys. Fluid Dyn., 89, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Moss, D., Stepanov, R., Arshakian, T. G., et al. 2012, A&A, 537, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moss, D., Beck, R., Sokoloff, D., et al. 2013, A&A, 556, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pakmor, R., & Springel, V. 2013, MNRAS, 432, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1971, ApJ, 163, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, T., Schleicher, D. R. G., Klessen, R. S., et al. 2012, ApJ, 760, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D. J., & Bate, M. R. 2008, MNRAS, 385, 1820 [NASA ADS] [CrossRef] [Google Scholar]
- Pudritz, R. E., & Silk, J. 1989, ApJ, 342, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, D. S., Bower, R., Frenk, C. S., et al. 2005, MNRAS, 363, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Regan, J. A., Johansson, P. H., & Haehnelt, M. G. 2014, MNRAS, 439, 1160 [NASA ADS] [CrossRef] [Google Scholar]
- Ruzmaikin, A. A., Sokolov, D. D., & Shukurov, A. M. 1988, Magnetic fields of galaxies Astrophys. Space Sci. Lib., 133 [Google Scholar]
- Ryu, D., Schleicher, D. R. G., Treumann, R. A., Tsagas, C. G., & Widrow, L. M. 2012, Space Sci. Rev., 166, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Schekochihin, A. A., Cowley, S. C., Hammett, G. W., Maron, J. L., & McWilliams, J. C. 2002, New J. Phys., 4, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Schleicher, D. R. G., Banerjee, R., Sur, S., et al. 2010, A&A, 522, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schleicher, D. R. G., Palla, F., Ferrara, A., Galli, D., & Latif, M. 2013a, A&A, 558, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schleicher, D. R. G., Schober, J., Federrath, C., Bovino, S., & Schmidt, W. 2013b, New J. Phys., 15, 023017 [NASA ADS] [CrossRef] [Google Scholar]
- Schlickeiser, R. 2012, Phys. Rev. Lett., 109, 261101 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitt, D. 1990, in Rev. Modern Astron. 3, ed. G. Klare, 86 [Google Scholar]
- Schober, J., Schleicher, D., Federrath, C., et al. 2012a, ApJ, 754, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Schober, J., Schleicher, D., Federrath, C., Klessen, R., & Banerjee, R. 2012b, Phys. Rev. E, 85, 026303 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shu, F. H., Najita, J., Ostriker, E. C., & Shang, H. 1995, ApJ, 455, L155 [Google Scholar]
- Shu, F. H., Najita, J. R., Shang, H., & Li, Z.-Y. 2000, Protostars and Planets IV, 789 [Google Scholar]
- Shu, F. H., Galli, D., Lizano, S., Glassgold, A. E., & Diamond, P. H. 2007, ApJ, 665, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Silk, J. 2013, ApJ, 772, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Silk, J., & Langer, M. 2006, MNRAS, 371, 444 [NASA ADS] [CrossRef] [Google Scholar]
- Steenbeck, M., Krause, F., & Rädler, K.-H. 1966, Z. Naturforsch. Teil A, 21, 369 [Google Scholar]
- Sur, S., Schleicher, D. R. G., Banerjee, R., Federrath, C., & Klessen, R. S. 2010, ApJ, 721, L134 [NASA ADS] [CrossRef] [Google Scholar]
- Sur, S., Federrath, C., Schleicher, D. R. G., Banerjee, R., & Klessen, R. S. 2012, MNRAS, 423, 3148 [NASA ADS] [CrossRef] [Google Scholar]
- Susa, H., Doi, K., & Omukai, K. 2015, ApJ, 801, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, J. C., & Blackman, E. G. 2004, ApJ, 603, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, K. E. I., & Omukai, K. 2014, MNRAS, 439, 1884 [NASA ADS] [CrossRef] [Google Scholar]
- Tavecchio, F., Ghisellini, G., Bonnoli, G., & Foschini, L. 2011, MNRAS, 414, 3566 [NASA ADS] [CrossRef] [Google Scholar]
- Toomre, A. 1964, ApJ, 139, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Turk, M. J., Oishi, J. S., Abel, T., & Bryan, G. L. 2012, ApJ, 745, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Vainshtein, S. I., & Ruzmaikin, A. A. 1971, AZh, 48, 902 [NASA ADS] [Google Scholar]
- Wang, P., & Abel, T. 2009, ApJ, 696, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, P., Li, Z.-Y., Abel, T., & Nakamura, F. 2010, ApJ, 709, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Weibel, E. S. 1959, Phys. Rev. Lett., 2, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Widrow, L. M., Ryu, D., Schleicher, D. R. G., et al. 2012, Space Sci. Rev., 166, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, P. H., Schlickeiser, R., & Kolberg, U. 2014, Phys. Plasmas, 21, 032109 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshida, N., Omukai, K., & Hernquist, L. 2008, Science, 321, 669 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Yun, M. S., Reddy, N. A., & Condon, J. J. 2001, ApJ, 554, 803 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Surface density (top panel), gas mid-plane density (middle panel), and the gas temperature (bottom panel) of the disk for a 10 M⊙ central star with an accretion rate of 10-3M⊙ yr-1. The left panels represent the CIE cooling regime, while the right panels show the regime of H2 line cooling. |
| In the text | |
 |
Fig. 2 Initial magnetic field strength Binit generated by the small-scale dynamo (the top panel) and the final magnetic field strength Bf generated by the α−Ω dynamo (middle panel) for a 10 M⊙ central star with an accretion rate of 10-3M⊙ yr-1. In the bottom panel, we show the orbital timescale, the growth time of the α–Ω dynamo, and the ordering timescale. The left panels represent the CIE cooling regime, while the right panels show the regime of H2 line cooling. |
| In the text | |
 |
Fig. 3 Expected properties of the magnetic outflow for a 10M⊙ star with an accretion rate of 10-3M⊙ yr-1. The magnetic luminosity is depicted in the top panel, while the bottom panel shows the mass outflow rate within a given radius R. The left panels represent the CIE cooling regime, while the right panels show the regime of H2 line cooling. |
| In the text | |
 |
Fig. 4 Surface density (top panel), gas mid-plane density (middle panel) and the gas temperature (bottom panel) of the disk are shown for 105M⊙ central star with an accretion rate of 10-1M⊙ yr-1. The left panels show the atomic cooling regime in the inner parts of the disk, while the right panels show the H2 cooling regime on larger scales. |
| In the text | |
 |
Fig. 5 Initial magnetic field strength Binit generated by the small-scale dynamo (top panel) and the final magnetic field strength Bf generated by the α–Ω dynamo (middle panel) for a 105M⊙ star with an accretion rate of 10-1M⊙ yr-1. In the bottom panel, we show the orbital timescale, the growth time of the α–Ω dynamo, and the ordering timescale. The left panels show the atomic cooling regime in the inner parts of the disk, while the right panels show the H2 cooling regime on larger scales. |
| In the text | |
 |
Fig. 6 Expected properties of the magnetic outflow for a 105M⊙ star with an accretion rate of 10-1M⊙ yr-1. The magnetic luminosity is depicted in the top panel, while the bottom panel shows the mass outflow rate within a given radius R. The left panels represent the atomic cooling regime, while the right panels show the regime of H2 line cooling. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


