| Issue |
A&A
Volume 585, January 2016
|
|
|---|---|---|
| Article Number | A22 | |
| Number of page(s) | 14 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201526300 | |
| Published online | 09 December 2015 | |
Amplitude and frequency variations of oscillation modes in the pulsating DB white dwarf star KIC 08626021
The likely signature of nonlinear resonant mode coupling
1 Université de Toulouse, UPS-OMP, IRAP, 31400 Toulouse, France
e-mail: weikai.zong@irap.omp.eu
2 CNRS, IRAP, 14 avenue Édouard Belin, 31400 Toulouse, France
3 Département de Physique, Université de Montréal, CP 6128, Succursale Centre-Ville, Montréal, QC H3C 3J7, Canada
4 Institut d’Astrophysique et de Géophysique, Quartier Agora, Allée du 6 Août 19c, 4000 Liège, Belgium
Received: 12 April 2015
Accepted: 22 October 2015
Context. The signatures of nonlinear effects affecting stellar oscillations are difficult to observe from ground observatories because of the lack of continuous high-precision photometric data spanning extended enough time baselines. The unprecedented photometric quality and coverage provided by the Kepler spacecraft offers new opportunities to search for these phenomena.
Aims. We use the Kepler data accumulated on the pulsating DB white dwarf KIC 08626021 to explore in detail the stability of its oscillation modes, searching, in particular, for evidence of nonlinear behaviors.
Methods. We analyze nearly two years of uninterrupted short-cadence data, concentrating on identified triplets that are caused by stellar rotation and that show intriguing behaviors during the course of the observations.
Results. We find clear signatures of nonlinear effects that could be attributed to resonant mode coupling mechanisms. These couplings occur between the components of the triplets and can induce different types of behaviors. We first notice that a structure at 3681 μHz, identified as a triplet in previous published studies, is in fact forming a doublet, with the third component being an independent mode. We find that a triplet at 4310 μHz and this doublet at 3681 μHz (most likely the two visible components of an incomplete triplet) have clear periodic frequency and amplitude modulations, which are typical of the so-called intermediate regime of the resonance, with timescales consistent with theoretical expectations. Another triplet at 5073 μHz is likely in a narrow transitory regime in which the amplitudes are modulated while the frequencies are locked. Using nonadiabatic pulsation calculations, based on a model representative of KIC 08626021 to evaluate the linear growth rates of the modes in the triplets, we also provide quantitative information that could be useful for future comparisons with numerical solutions of the amplitude equations.
Conclusions. The observed modulations are the clearest hints of nonlinear resonant couplings occurring in white dwarf stars identified so far. These should resonate as a warning to projects that aim at measuring the evolutionary cooling rate of KIC 08626021, and of white dwarf stars in general. Nonlinear modulations of the frequencies can potentially jeopardize any attempt to measure such rates reliably, unless they can be corrected beforehand. These results should motivate further theoretical work to develop the nonlinear stellar pulsation theory.
Key words: white dwarfs / stars: individual: KIC 08626021 / techniques: photometric
© ESO, 2015
1. Introduction
The temporal variations of the amplitude and frequency of oscillation modes often seen, or suspected, in pulsating stars cannot be explained by the linear nonradial stellar oscillation theory (Unno et al. 1989) and must be interpreted in the framework of a nonlinear theory. It is believed that nonlinear mechanisms, such as resonant mode couplings, could generate such modulations, as, e.g., in the helium dominated atmosphere (DB) white dwarf star GD 358 (Goupil et al. 1998). Resonant couplings are, for instance, predicted to occur when slow stellar rotation produces triplet structures whose component frequencies satisfy the relation ν+ + ν− ~ 2ν0, where ν0 is the frequency of the central m = 0 mode. The theoretical exploration of these mechanisms was extensively developed in Buchler et al. (1995, 1997), but was almost interrupted more than a decade ago because of the lack of clear observational evidence of such phenomena, as a result of the difficulty in capturing amplitude or frequency variations that occur on timescales of months to years from ground-based observatories. Nevertheless, the presence of resonant couplings within rotationally split mode triplets was proposed for the first time as the explanation for the frequency and amplitude of long-term variations observed in the GW Vir pulsator PG 0122+200 (Vauclair et al. 2011) from successive campaigns on this object. This suggests that pulsating white dwarfs could be among the best candidates to detect and test the nonlinear resonant coupling theory.
White dwarfs constitute the ultimate evolutionary fate expected for ~98% of the stars in our Galaxy. While cooling down, they cross several instability strips in which they develop observable nonradial g-mode oscillations. Among these, the helium atmosphere DB white dwarfs which represent ~20% of all white dwarfs, are found to pulsate in the effective temperature range of 21 000 K to 28 000 K (Beauchamp et al. 1999; Fontaine & Brassard 2008; Winget & Kepler 2008). All classes of pulsating white dwarfs are particularly valuable for probing their interior with asteroseismology, but it has also been proposed that hot DB pulsators with apparently stable modes could be used to measure their cooling rate, which is dominated by neutrino emission (Winget et al. 2004). The secular rates of change for the pulsation periods in hot DB pulsators is expected to be ~10-13 ss-1, corresponding to a timescale of 3 × 105 years. However, this possibility could be seriously impaired by other phenomena affecting the pulsation frequencies on shorter timescales. Such variations in amplitude and frequency have indeed been suspected in several white dwarf stars (e.g., PG 0122+200, Vauclair et al. 2011; WD 0111+0018, Hermes et al. 2013; HS 0507+0434B, Fu et al. 2013), as stellar evolution theory cannot explain the variations with estimated timescales at least two orders of magnitude shorter than the expected cooling rates. Nonlinear effects on stellar pulsations, including resonant mode coupling mechanisms could induce such modulations and need to be considered carefully (Vauclair 2013).
In this context, observations from space of a multitude of pulsating stars, including white dwarfs, has open up new horizons. The Kepler spacecraft monitored a 105 deg2 field in the Cygnus-Lyrae region for nearly four years without interruption, obtaining unprecedented high quality photometric data for asteroseismology (Gilliland et al. 2010). These uninterrupted data are particularly suited to searching for long-term temporal frequency and amplitude modulations of the oscillation modes.
Among the six pulsating white dwarfs discovered in the Kepler field, KIC 08626021 (aka WD J1929+4447 or GALEX J192904.6+444708) is the only identified DB pulsator (Østensen et al. 2011). Based on the first month of short cadence (SC) Kepler data, Østensen et al. (2011) estimated that this star has an average rotation period Prot ~ 1.7 days, derived from the observed frequency spacings of three groups of g-modes that has been interpreted as triplets due to rotation. Subsequent independent efforts to isolate a seismic model for KIC 08626021 from Bischoff-Kim & Østensen (2011) and Córsico et al. (2012) both suggest that the effective temperature of the star is significantly hotter than the value determined from the survey spectroscopy. However, the masses determined from these two models are not consistent with each other. More recently, a new asteroseismic analysis based on the full Kepler data set provided by Bischoff-Kim et al. (2014), confirmed the former results found by Bischoff-Kim & Østensen (2011). We point out that a new asteroseismic analysis of KIC 08626021 is discussed in Giammichele et al. (in prep.).
KIC 08626021 has been observed by Kepler for nearly two years in short cadence mode without interruption since the quarter Q10. Thus, it is a suitable candidate to investigate the long-term amplitude and frequency modulations of the oscillation modes occurring in this star. In this paper, we present a new thorough analysis of the Kepler light curve obtained on the DB pulsator KIC 08626021, that emphasizes, in particular, the time dependence of the amplitudes and frequencies of the modes associated with rotationally split triplets (Sect. 2). We provide arguments that link the uncovered amplitude and frequency modulations with the nonlinear mode coupling mechanisms (Sect. 3), before summarizing and concluding (Sect. 4).
2. The frequency content of KIC 08626021 revisited
The pulsating white dwarf star KIC 08626021 has been continuously observed by Kepler in short cadence (SC) mode from quarter Q10.1 to Q17.2 (when the second inertial wheel of the satellite failed). A light curve from Q7.2, well disconnected from the main campaign, is also available for that star. Some analysis of these data have already been reported in the literature (Østensen et al. 2011; Córsico et al. 2012), including most recently the asteroseismic study of Bischoff-Kim et al. (2014, hereafter BK14) which was based on the full Q10.1 – Q17.2 data set. We initially considered using these published results as the starting point of our present study, but we realized that important details were lacking for our specific purposes. Consequently, we detail below, as a necessary step, our own thorough analysis of the frequency content of KIC 08626021.
2.1. The Kepler photometry
All the data gathered by Kepler for that star are now in the public domain. We obtained the light curves from the Mikulski Archive for Space Telescopes (MAST)1. As is standard, these data were processed through the Kepler Science Processing Pipeline (Jenkins et al 2010). In the following, we concentrate on the consecutive data that covers Q10.1 to Q17.2, without considering Q7.2 that would introduce a large time gap in the assembled light curve. With this restriction, we are left with a mere 23 months of high precision photometric data starting from BJD 2 455 740 and ending on BJD 2 456 424 (~684 days) with a duty cycle of ~87%.
We constructed the full light curve from each quarter corrected light curves, which most notably include a correction for the amplitude due to the contamination of the star by a closeby object (this correction consider that only ~47.3% of the light comes from the DB white dwarf). Tests indicate that the main differences between these corrected data and the raw data set used by BK14 occur in the measured amplitudes of the light variations, but has otherwise no noticeable incidence on the extracted frequencies. Each quarter light curve was then individually corrected to remove long-term residual trends (using sixth-order polynomial fits) and data points that differ significantly from the local standard deviation of the light curve were removed by applying a running 3σ clipping filter. The later operation just very slightly decreases the overall noise level.
 |
Fig. 1 Top panel: condensed representation of the full Kepler light curve (Amplitude is the residual relative to the mean brightness intensity of the star vs. time in Barycentric Julian Date) covering from Q10.1 to Q17.2 (~684 days) of KIC 08626021. Between quarters, scatter sometime changes due to different levels of noise in the data (all quarters are not equivalent in photometric quality). Bottom panel: close-up view showing one day of the Kepler light curve by slices of 0.1 days. At this scale, the oscillations are clearly apparent. |
 |
Fig. 2 Lomb-Scargle periodogram (LSP; amplitude in % of the mean brightness vs. frequency in μHz) of the Kepler light curve. The represented range covers the frequency region where the pulsation modes are detected (no significant signal is found outside these limits). Note that some well known Kepler instrumental artefacts are within this frequency range but can easily be recognized. |
The resulting ligth curve is shown in Fig. 1 and the corresponding Lomb-Scargle periodogram (LSP; Scargle 1982) is given in Fig. 2. The low-amplitude multi-periodic modulations are clearly seen with dominant periodicities of the order of a few minutes, typical of g-mode oscillations observed in pulsating DB white dwarfs. The formal frequency resolution in the LSP (defined as the inverse of the total time base line of the observations) reaches ~0.017 μHz.
2.2. Defining a secure detection threshold
Before proceeding with the extraction of the frequencies, a brief discussion of the criterion that is used to define the confidence level of the detections is necessary. With ground-based observations of pulsating compact stars, a widely used rule of thumb was to consider the limit of 4σ (4 times the average local noise in the Fourier Transform) as the threshold above which a signal could safely be considered as real. However, with space observations, in particular with Kepler, it became increasingly clear that this rule underestimates the risks of false detections resulting from statistical noise fluctuations. The reason lies most probably in the very large number of data points collected during months (or years) of observations with a sampling time of only 58 s in SC mode. In particular, more than half a million frequency bins are necessary to represent the LSP of the 684 days Kepler photometric data of KIC 08626021 and noise fluctuations are very likely to occur at least one time (and more) above a standard 4σ threshold. For this reason, the trend has been to increase the threshold to higher signal-to-noise (S/N) values in somewhat arbitrary ways to avoid false detections (e.g., BK14 just assumes that the acceptable limit is 5σ).
 |
Fig. 3 False alarm probability Pn of having at least n peaks caused by noise above a given S/N threshold in the LSP of KIC 08626021 (see text for details). In each panel, the three vertical lines indicate, from left to right, the S/N value corresponding to Pn = 0.1, 0.01, and 0.0001, respectively. The limit P1 = 0.0001, meaning that the risk of having a false detection above that threshold is reduced to less than 1 chance over 10 000, defines our adopted criterion. It corresponds to the limit of 5.6σ. |
Instead of adopting an arbitrary value, we quantitatively estimate what should be an acceptable threshold with the following procedure. Using the same time sampling as the observations, we randomly build 10 000 artificial light curves just containing white gaussian noise (a random normal deviate is calculated at each time point). The LSPs of these artificial light curves are then calculated, as well as the median values of the noise in each resulting LSPs. For any given S/N threshold (xσ defined as x times the median noise level) we then find the number of times that at least n peaks in the LSP (which by definition are just noise structures) happen to be above the chosen limit. Then, dividing by the number of tests (10 000 here), we obtain the false alarm probability Pn(x) that at least n peaks above a given S/N threshold of xσ is due to noise.
Figure 3 shows the results of this procedure for the probabilities P1 to P5 as functions of the S/N threshold. The most interesting case is P1 (the probability that at least 1 peak due to noise is above the threshold). We clearly see here that at the usual 4σ limit, the probability to have at least one false detection is close to 1 (and ~0.5 to have at least 5 false detections according to P5), confirming that this threshold is particularly unsafe in our case. However, P1 eventually decreases with increasing S/N to reach 0.1 (10% chance) at S/N ~ 4.58, 0.01 (1% chance) at S/N ~ 4.92 (approximately the detection threshold chosen by BK14), and less than 1 chance out of 10 000 at S/N = 5.56 (this is the limit above which not a single peak due to noise has been found among the 10 000 randomly generated light curves).
Based on these calculations, we adopt, in the following, the conservative 5.6σ threshold as our limit of detection.
List of frequencies detected in KIC 08626021.
2.3. Extraction of the frequencies
We used a dedicated software, Felix (Frequency Extraction for LIghtcurve eXploitation) that was developed by one of us (S.C.), to first extract the frequency content of KIC 08626021 down to our adopted detection threshold of 5.6σ (we, in practice, pushed down the limit to ~5σ; see below). The method used is based on the standard prewhithening and nonlinear least square fitting techniques (Deeming 1975) that works with no difficulty in the present case. The code Felix greatly eases and accelerates the application of this procedure, especially for long and consecutive time series photometry obtained from spacecrafts like CoRoT and Kepler (Charpinet et al. 2010, 2011).
The list of extracted periodic signals is provided in Table 1 which gives their fitted attributes (frequency in μHz, period in seconds, amplitude in % of the mean brightness, phase relative to a reference t0 time, and S/N above the local median noise level) along with their respective error estimates (σf, σP, σA, and σPh). Figures 4–6 show zoomed-in views of all the identified peaks in the LSP.
 |
Fig. 4 Lomb-Scargle periodogram of the triplets at 4310 μHz (top panel) and 5073 μHz (bottom panel) after nearly two years of Kepler photometry gathered on KIC 08626021. The nearly equal frequency spacings are marked in the two panels. The dashed red horizontal line refers to the 5.6σ detection threshold of local noise level. |
 |
Fig. 5 Lomb-Scargle periodogram in the 3677−3686 μHz frequency range where a doublet and an independent frequency are above the 5.6σ detection threshold of local noise level. The bold black vertical segment and vertical dashed line indicate the position of one possible third component for the doublet, as shown in the bottom panel. The two top panels are the expanded view of the two components as indicated by the vertical arrows in the bottom panel. Both the fine structures of the two components show well-resolved closed peaks and have the same frequency separation of 0.044 μHz. |
 |
Fig. 6 Lomb-Scargle periodogram of 8 frequencies after nearly two years of Kepler photometry gathered on KIC 08626021. The two frequencies f11 and f12 are with 5.0−5.5σ of local noise level. Frequency f8 and f10 are linear combination frequencies. |
We find 13 very clear independent frequencies that come out well above the detection threshold. Two additional lower amplitude peaks (f8 and f10) appear as significant but are linked to other frequencies through linear combinations and are therefore likely not independent pulsation modes. Two more frequencies (f11 and f12) can be identified above 5σ but below 5.6σ which we mention for completeness, but that cannot be considered as secured detections. A comparison with the completely independent analysis of BK14 shows that we agree on all the relevant, well secured frequencies (i.e, with a sufficiently high S/N). We point out, however, that some additional features of the frequency spectrum are not discussed in BK14 and we differ in how to interpret some of the mode associations (see below).
As reported in BK14, six of the extracted frequencies (f1 and f2) form two very well defined, nearly symmetric triplets with a frequency spacing of ~3.392 μHz and ~3.206 μHz (Fig. 4). These are readily interpreted as rotationally split triplets, thus giving an average rotation period of ~1.75 days for the star. However, we argue that the three frequencies shown in Fig. 5 cannot correspond to the components of a triplet, as BK14 suggest. These frequencies form a clearly asymmetric structure with the left component (f7) being significantly more distant than the right component (f3, +) from the central peak (f3,0). We note in this context that the frequency separation between f3,0 and f3, + (3.208μHz) is similar or very close to the frequency splitting characterizing the f2 and f1 triplets. Our interpretation is therefore that the middle (f3,0) and right (f3, +) peaks are two components of a triplet whose third component is undetected, while the left peak (f7) is a completely independent mode. This has some implications in finding an asteroseismic solution for KIC 08626021 as attempted by BK14, since eight independent periods should be considered and not seven (see Giammichele et al., in prep.).
Furthermore, not reported in BK14, we show in Fig. 5 that the two components of the incomplete triplet are in fact surrounded by additional structures (not tabulated in Table 1). The central peak (f3,0) appears to have two resolved symmetric sidelobes that are located 0.044 μHz away, while the right peak (f3, +) shows a sidelobe also separated by 0.044 μHz. These intriguing hyperfine structures cannot be associated with rotation since a much larger rotational splitting signature has already been found. Moreover, the very small frequency separation involved would indicate a modulating phenomenon that occurs on a very long timescale of ~263 days.
This finding brings us to the main subject of the present paper, which is to show that this hyperfine structure, along with other behaviors that we discuss below, can be linked to long-term amplitude and frequency modulations that are generated by nonlinear resonant coupling mechanisms between the components of rotationally split triplets.
 |
Fig. 7 Frequency and amplitude modulations in the f1 triplet at 4310 μHz. The top panel shows the sLSP (giving the amplitude in % as a function of frequency in μHz and time in days) of the triplet as a whole. The middle and bottom left panels show increasingly expanded views around the average frequency (the solid vertical lines) of each component, with the bottom left panel obtained from prewhitening subsets of the data, thus measuring precisely the frequencies, as a function of time. The lower right panel provides the measured amplitudes as a function of time obtained for each subset of data (see text for details). |
2.4. Amplitude and frequency modulations
From now on, we mainly focus our discussions on the two well defined triplets f1 and f2, and on the doublet f3 (i.e., the two visible components of an incomplete triplet). In order to analyze the temporal variability of these modes and their relationship, we used our software Felix to compute the sliding Lomb-Scargle periodogram (sLSP) of the data set. This technique consists of building time-frequency diagrams by filtering in only parts of the data as a function of time. In the present case, we chose a filter window that is 180-day wide sled along the entire light curve by time steps of 7 days. This ensures a good compromise, for our purposes, between time resolution, frequency resolution (to resolve close structures in each LSP), and S/N. The sLSP gives an overall view of the amplitude and frequency variability that could occur for a given mode (see, e.g., the top left panel of Fig. 7). We acknowledge that BK14 also provide a similar analysis, but they chose a sliding window that is only 14-day wide, hence providing a much lower resolution in frequency. This has strong consequences on the interpretation of these data that will become obvious below. As a complementary (and more precise) method, we also extracted the frequencies (through prewithening and nonlinear least square fitting techniques) in various parts of the light curve, i.e., the 23-month light curve of KIC 08626021 was divided into 20 time intervals, each containing six months of data (for precision in the measurements) except for the last three intervals at the end of the observations. This second approach provides a measure of the (averaged) frequencies and amplitudes at a given time, along with the associated errors (see, e.g., the bottom left panel of Fig. 7).
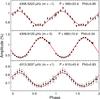 |
Fig. 8 Amplitude modulations observed in the f1 triplet presented in phase diagrams with a folding period of 580 and 610 days for the two side components, and 680 days for the central component. These periods, and their associated formal errors, were estimated by fitting a sine wave (red curve) to the amplitude variations. |
2.4.1. The f1 triplet
Figure 7 shows the amplitude and frequency modulations observed for the three components that form the f1 triplet near 4310 μHz. In this plot, views of the frequency variations with time are illustrated from top to bottom-left panels. The top panel first shows the sLSP of the triplet as a whole (similar to Fig. 2 of BK14) where the signal appears, at this scale, stable in frequency but varying in amplitude for at least the central component. Then we provide increasingly expanded views (from middle-left to bottom-left panel) around the average frequency of each component. In addition, the bottom right panel shows how the amplitude of each component varies with time.
It is mentionned in BK14 that the modes, and these three components in particular, are stable in frequency over the 2-year duration of the observations. We clearly demonstrate here that this is not the case. Their statement is based on a time-frequency analysis involving a sliding Fourier Transform (sFT) that only uses a 14-day-wide window, which clearly does not permit a sufficient frequency resolution to uncover the modulations that we report here. We find that both the amplitudes and frequencies show very suggestive signatures of quasi-periodic modulations with an average timescale that we can roughly estimate to ~620 days. Figures 8 and 9 illustrate further this periodicity in phase diagrams. Although very similar, we find that the modulation period associated with the side components of the triplets (~600 d) could be slightly shorter than the modulation period of the central component (~680 d). Note that the modulating periods in this triplet were obtained by searching for the best fit of a pure sine wave function to the amplitude variations. The zero phase is relative to the time of the first data point (BJD = 2 455 739.836). The same procedure was not applied to the frequency modulations since the patterns are clearly more complex than a pure sine wave function. However, since Fig. 7 suggests a cyclic behavior with roughly the same timescale, the folding periods used to construct Fig. 9 were chosen to be those derived for the amplitude modulations. This allows us to check that indeed at least two of the components (the m = + 1 and m = −1 modes) accomodate rather well these periodicities, as the curves connect near phase 12. For the central (m = 0) component, a slightly longer estimated periodicity does not permit to cover entirely the suspected modulation cycle with the data, leaving a gap between phase 0.9 and 1 where the behavior is not monitored. We cannot say in that case whether this curve would eventually connect smoothly at phase 1 or if a discontinuity exists, suggesting that either the chosen folding period is not appropriate or an additional trend is affecting the frequency of this mode.
In addition, we note that the frequency and amplitude modulations show obvious correlations, as both evolve in phase with the same period (with period of ~600 days and zero phase of ~0.84), for the side components, and are somewhat antiphased with the central component (with zero phase of 0.34), as shown in Figs. 8 and 9. We quantitatively checked this fact by computing the correlation coefficients between, e.g., the amplitudes of the m = + 1 and m = −1 components (ρA+,A− = + 0.93; i.e., indicative of a strong correlation) and the amplitudes of the m = + 1 and m = 0 components (ρA+,A0 = −0.82; i.e., indicative of a strong anti-correlation). Such correlated behavior suggests that the modes involved are somehow connected, either through a common cause that affects their amplitudes and frequencies similarly or through direct interactions that occur between the components of the triplet. This will be discussed further in Sect. 3.
2.4.2. The f2 triplet
Figure 10 shows the modulations observed in the other triplet, f2, at 5073 μHz. The frequencies in this triplet appear to be stable during the nearly two years of Kepler observations, while the amplitudes show clear modulations. Note that the amplitude of the m = + 1 component went down at some point below a signal-to-noise ratio of 4σ and was essentially lost in the noise during a portion of the last half of the observations. Four measurements could not be obtained because of this and when it was still possible to spot this component, the errors remained large.
Again in this case, the amplitudes of the two side components seem to evolve nearly in phase with a quasi-periodic behavior on a timescale that is probably slightly larger than the duration of the observations and close to a timescale of ~700 days. However, contrary to the previous case, a connection with the central component is less clear. The later seems to follow a variation pattern possibly occurring on a longer timescale. Therefore, f2 behaves somewhat differently from f1, a feature that we will discuss more in the next section.
 |
Fig. 9 Same as Fig. 8 but for the frequency modulations observed in the f1 triplet. Note that the adopted folding periods are the values derived for the corresponding amplitude modulations. |
 |
Fig. 10 Same as Fig. 7 but for the f2 triplet at 5073 μHz. Note that the component at 5076 μHz has a very low amplitude and plunges below the 4σ detection threshold during the second half of the observations, making it difficult to follow (hence the 4 missing data points). |
 |
Fig. 11 Same as Fig. 7 but for the doublet f3 at 3682 μHz and the nearby independent frequency f7 at 3678 μHz. |
 |
Fig. 12 Frequency and amplitude modulations of the components that form the linear combination f1, − + f4 = f8. The panels are similar to those described in Fig. 7. The three components show clear periodic modulations evolving in phase. In each bottom left subpanels, a segment indicates the 0.01 μHz scale. |
2.4.3. The f3 doublet
The 3677−3686 μHz frequency range is shown in Fig. 11 and contains the independent frequency (f7) and the two visible components of the incomplete triplet f3 (thus forming a doublet).
Each component of this doublet shows clear signatures of correlated variations for both amplitudes and frequencies. We note in particular a periodic modulation that occurs on a somewhat shorter timescale than for the two previous cases. A very quick look at Fig. 11 indicates a period of roughly 280 days for the amplitude variations of both modes as well as for the frequency modulation of f3,0, which in fact can readily be connected to the hyperfine-structure sidelobes discussed in Sect. 2.3 and illustrated in Fig. 5. The frequency of f3, +, for its part, seems to also follow a periodic trend but, quite interestingly, on a timescale that could be around twice (~550 days) the period of the other components.
It appears now clearly that a periodic frequency and amplitude modulation process is responsible for the equidistant peaks surrounding f3,0 and f3, +. In this context, the frequency separation of 0.044 μHz should provide a more precise estimate of the period of this modulation, which is ~263 days. Note that the other two triplets discussed previously do not show similar hyperfine splitting structures around their components simply because the period of their modulations appear to be slightly longer than the observational time baseline and those structures cannot be resolved. In the case of f3, the observations are long enough to resolve the modulation. We further note that the amplitudes of the two components of f3 evolves in antiphase while the frequencies are in phase during the first half of the run but then evolve in antiphase during the last part of the observations, which reflects the fact that the frequency variation of f3, + has approximately twice the period of the modulation seen in the frequency of f3,0.
In contrast, the mode f7 shows a totally different behavior as both its frequency and amplitude appear stable throughout the observing run. This could further support, if need be, the interpretation that f7 and the f3 complex are not part of a same triplet structure (as assumed by BK14). We indeed note that the theoretical framework in which these modulations can possibly be understood (nonlinear resonant couplings, as discussed in Sect. 3) forbids the possibility that the components of a triplet behave in different regimes.
2.4.4. Other correlated modulations
For completeness, we also illustrate the interesting behavior of three frequencies that are related by a linear combination. Figure 12 shows the amplitude and frequency modulations of f1, −, f4 and f8, that satisfy almost exactly (within 2σ of the formal measurement errors) the relation f8 = f1, − + f4 (see Table 1).
 |
Fig. 13 Top panel: comparison between the measured amplitude A8 of f8 and 60 × A1, −·A4 (where A1, − and A4 are the amplitudes of f1, − and f4, respectively) at each time segment (see text). Bottom panel: same as top panel but for a comparison between the measured frequency f8 and sum of the frequencies f1, − + f4. In both cases, the relationship is exactly statisfied along the plain diagonal line. All the measurements are found to be within 2σ of this line. |
It is striking to see how the three components follow nearly exactly the same trends in both frequency and amplitude. These modulations could be related to the so-called parents/child mode nonlinear interactions discussed by Breger & Montgomery (2014) or to other nonlinearities encountered in white dwarfs (e.g., Brassard et al. 1995; Wu 2001). In this context, we note, again according to the values given in Table 1, that the mean relative amplitude of f8 (A8 = 0.00121) is ~60 times larger than the product of the relative amplitudes of f1, − (A1, − = 0.00867) and f4 (A4 = 0.00233) whose value is 0.000020. Figure 13 shows that these relationships also hold (within 2σ), both for frequencies and amplitudes, for each individual measurement done as a function of time illustrated in Fig. 12. Interestingly, if this combination were to be related to the mechanism of Wu (2001), the factor of 60 connecting A8 to A1, −·A4 would possibly imply that the inclination angle of the star should be 50°<i< 60° (following Eq. (20) in Wu 2001). Alternately, f8 could result from a resonant mode coupling phenomenon where f8 is a true eigenmode of the star (possibly of higher degree ℓ) whose amplitude is boosted above the detection limit by the resonance following Eq. (5) of Breger & Montgomery (2014, see also Dziembowski 1982. We indeed find that our results, instead of using phase (we here use frequency), are similar to the linear combination frequency families that are described in Breger & Montgomery (2014, e.g., comparing their Figs. 4, 5 to our Fig. 13. However, at this stage, we cannot decipher which of these potential mechanisms could explain the details of this combination of frequencies because of the lack of further independent constraints (such as the inclination angle of KIC 08626021). Finally, we point out that one of the frequencies involved in this relation, f1, −, is also involved as one of the components of the f1 triplet discussed in Sect. 2.4.1 (and illustrated in Fig. 7).
Another similar linear combination has also been identified, involving f1, +, f9 and f10, but the low amplitudes of f9 and f10 have prevented us from analyzing its frequency and amplitude modulations. In the following, we concentrate on a possible theoretical interpretation of the frequency and amplitude modulations observed in the triplets, and we do not discuss further the properties of linear combination frequencies.
3. Links with nonlinear resonant couplings
The frequency and amplitude modulations that are observed in the two triplets and the doublet of KIC 08626021 cannot be related to any evolutionary effect, such as neutrino cooling, because the timescale involved is several orders of magnitude shorter than the cooling rate of DB white dwarfs (Winget et al. 2004). The signature of orbiting companions around the star is also ruled out by the fact that the variations occurring in different frequencies are not correlated in phase and do not have the same amplitude modulations (Silvotti et al. 2007). We also considered possibilities that instrumental modulations could occur, e.g., on a per quarter basis, such as a slightly varying contamination from the nearby star that could modulate the amplitude of the modes, but then all modes should be affected similarly, which is not what is observed. Finally, the possibility was raised that changes in the background state of the star, such as those induced by magnetic cycles or through an hypothetical angular momentum redistribution mechanism, could be responsible for the observed modulations. It is indeed well known that magnetic cycles have an impact on the frequencies of the p-modes observed in the Sun, which lead to small frequency drifts that correlate well in time with tracers of the solar surface activity (see, e.g., Salabert et al. 2015 and references therein). One could imagine that such mechanisms may exist in white dwarfs as well. We think, however, that such effects would be hardly compatible with how the modes in KIC 08626021 are found to vary. In the Sun, all the modes appear to be globally affected following the same trends to some various extent, while in our case we see, for instance, a triplet f1 that shows correlated changes in frequency, and at the same time another triplet f2 whose frequencies appear to be constant. We find a mode f7 that also does not change while the two visible components of the doublet f3 nearby show correlated variations in frequency. This makes it difficult to connect these behaviors to a common global cause (i.e., small changes of the stellar structure). A cyclic redistribution of angular momentum, for its part, would affect the frequencies of the m = + 1 and m = −1 components with an anti-correlation, while the central m = 0 component should not be affected (and it is found to vary in f1). All triplets should be affected nearly the same way, but f2, showing constant frequencies, clearly is not and somewhat rules out this possibility.
Instead, we prefer to fall back to a simpler possibility. We develop in this section arguments that nonlinear resonant mode coupling mechanisms, by which both the amplitudes and frequencies of oscillation modes can be modulated on timescales of weeks, months, and even years, appears as a natural explanation for some of the observed behaviors.
3.1. The amplitude equations formalism
The amplitude equations (AEs) formalism is, to our knowledge, the only existing theoretical tool to investigate mode couplings for nonradial oscillation modes in pulsating stars. AEs in the stellar context have been extensively studied since the 1980’s for different types of couplings (Dziembowski 1982; Buchler & Goupil 1984; Moskalik 1985; Dziembowski & Goode 1992; Goupil & Buchler 1994; van Hoolst 1994; Buchler et al. 1995; Goupil et al. 1998; Wu 2001; Wu & Goldreich 2001).
In the present context, we limit ourselves to the type of resonances that is discussed in Buchler et al. (1995, 1997) and Goupil et al. (1998), which involves linear frequency combinations such that ν1 + ν2 ~ 2 ν0, and, more specifically, a particular case in which a ℓ = 1 mode is split by slow rotation and form a nearly symmetric triplet. This choice is obviously driven by the specific configuration of the modes studied in KIC 08626021, which, we recall, are all identified as ℓ = 1 rotationally split g-mode triplets.
To clarify this further, we do not consider here other potential coupling mechanisms described, e.g., in Wu & Goldreich (2001) because they address a different problem, namely the problem of mode amplitude saturation through a proposed mechanism that indeed involves a nonlinear resonant mode coupling, but with one parent mode that is overstable (thus gaining energy) and two independent child modes that are damped (thus dissipating the energy). In our case, we observe and focus on a different nonlinear resonant coupling that occurs within triplets of ℓ = 1g-modes which result from the slow rotation of the star. The three modes in the triplets are overstable and nonlinearly interact with each other because slow rotation induces a near resonance relation between their frequencies (see below). Wu & Goldreich (2001), Wu (2001), Montgomery (2005), and other related studies do not treat this case and therefore cannot be helpful to describe and interpret what is occurring inside a rotationally split triplet. The only available framework for this is the Buchler et al. (1995, 1997) and Goupil et al. (1998) papers that explicitely developed a theory to describe this kind of interaction and that should not be confused with various other works on nonlinear interactions between modes. We point out that it does not mean that the Wu & Goldreich (2001) mechanism cannot also occur in KIC 08626021, but considering the linear growth rates expected for the observed modes (see Sect. 3.3 and Table 2), eventual limit cycles that lead to cyclic amplitude variations would have timescales much longer (~1000 yrs) than what is seen. This could hardly be connected to the observed features and would most likely not be noticeable in the available data that only cover a time baseline of two years.
Mode identification and linear nonadiabatic growth rates, κ0, from the best seismic model of KIC 08626021.
Going back to the configuration of interest involving rotationally split triplets, rotation when treated to first order approximation would lead to a strictly symmetric triplet that exactly satisfies the above mentionned relationship. However, terms of higher order are never exactly zero and a small asymmetry, dominated by the second order term, always exists. This asymmetry is, in fact, essential for driving the various resonant coupling behaviors. The second order effect of rotational splitting, δνt, that matters can be estimated following the equation given in Goupil et al. (1998): 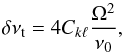 (1)where Ckℓ is the first order Ledoux constant (~0.5 for dipole g-modes) and Ω = 1 /Prot is the rotation frequency of the star. Prot is estimated from the first order average separation, Δν, between the components of the triplets and its value is ~1.75 days for KIC 08626021 (see Sect. 2). An asymmetry can also be evaluated directly from the measured frequencies of each triplet component, simply from the relation
(1)where Ckℓ is the first order Ledoux constant (~0.5 for dipole g-modes) and Ω = 1 /Prot is the rotation frequency of the star. Prot is estimated from the first order average separation, Δν, between the components of the triplets and its value is ~1.75 days for KIC 08626021 (see Sect. 2). An asymmetry can also be evaluated directly from the measured frequencies of each triplet component, simply from the relation 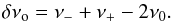 (2)According to the resonant AEs from Buchler et al. (1995) in which they ignored the slight interactions between modes with different ℓ and k, for the components in the ℓ = 1 triplet with frequencies ν−, ν0 and ν+, the corresponding amplitudes A−, A0 and A+ and phases φ−, φ0 and φ+ should obey the following relations
(2)According to the resonant AEs from Buchler et al. (1995) in which they ignored the slight interactions between modes with different ℓ and k, for the components in the ℓ = 1 triplet with frequencies ν−, ν0 and ν+, the corresponding amplitudes A−, A0 and A+ and phases φ−, φ0 and φ+ should obey the following relations  where R− ,0, + and q[(1,2,3)(1,2,3)] are the nonlinear coupling coefficients associated with each component. Their values depend on complex integrals of the eigenfunctions of the modes involved in the coupling. The quantities κ−, κ0, and κ+ are the linear growth rates of the m = −1,0, + 1 components, respectively.
where R− ,0, + and q[(1,2,3)(1,2,3)] are the nonlinear coupling coefficients associated with each component. Their values depend on complex integrals of the eigenfunctions of the modes involved in the coupling. The quantities κ−, κ0, and κ+ are the linear growth rates of the m = −1,0, + 1 components, respectively.
The numerical solutions of the AEs associated with this resonance identify three distinct regimes (see the example provided in Buchler et al. 1997). In order of magnitude, the occurrence of these three regimes can be roughly quantified by a parameter, D, defined as 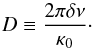 (4)But the ranges for this parameter that defines the boundaries of the various regimes depends somewhat on the values of the nonlinear coefficients in the real star.
(4)But the ranges for this parameter that defines the boundaries of the various regimes depends somewhat on the values of the nonlinear coefficients in the real star.
The first predicted situation is the nonlinear frequency lock regime in which the observed frequencies appear in exact resonance (δν = 0) and the amplitudes are constant. In the case of the DB white dwarf star GD 358, numerical solutions of the AEs indicated that the range of the D parameter that corresponds to this regime was between 0 and 20 (Goupil et al. 1998). However, these values are probably not universal and depend on the specific properties of the mode being considered, in particular on the value of the linear growth rate, κ0, of the central component of the considered triplet.
When the triplet components move away from the resonance center (δν ≠ 0), they enter the so-called intermediate regime where their amplitudes and frequencies are no longer stable and modulations can appear in the pulsations. In this regime, periodic variations can be expected with a timescale of 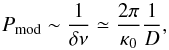 (5)i.e., roughly the timescale that is derived from the inverse of the frequency asymmetry of the triplet (dominated by the second order effect of stellar rotation), which is connected to the inverse of the growth rate of the pulsating mode by the D parameter (Goupil et al. 1998).
(5)i.e., roughly the timescale that is derived from the inverse of the frequency asymmetry of the triplet (dominated by the second order effect of stellar rotation), which is connected to the inverse of the growth rate of the pulsating mode by the D parameter (Goupil et al. 1998).
Far from the resonance condition, the modes recover the regime of steady pulsations with nonresonant frequencies. In the nonresonant regime, the nonlinear frequency shifts become very small and the frequencies are close to the linear ones.
We finally point out that, in addition to the above three regimes, there exits a narrow hysteresis (transitory) regime between the frequency lock and intermediate regimes where the frequencies can be locked while the amplitudes still follow a modulated behavior.
3.2. Connection with the observed triplets
In light of the theoretical framework summarized above, we point out that some of the behaviors observed in the two triplets f1 and f2 and in the doublet f3 (an incomplete triplet) can be quite clearly connected to nonlinear resonant couplings that occur in different regimes. We discuss each case below, but since the linear growth rate of the modes is an important ingredient to these resonance mechanism, we provide first some results of linear nonadiabatic pulsation calculations specifically tuned for a model representing best the DBV star KIC 08626021.
3.2.1. Nonadiabatic properties of the observed modes
Following our re-analysis of the data obtained for KIC 08626021 with Kepler, the recognition that eight independent periods have to be considered for a detailed asteroseismic study (and not only seven as used in BK14) coupled with our present need for a realistic seismic model representation of the star to carry out a nonadiabatic study of the mode properties led us to attempt a new asteroseismic analysis for this object. The details of this seismic study – a subject by its own that deserves a specific attention – are fully reported in Giammichele et al. (in prep.). The seismic solution that is obtained by Giammichele et al. (in prep.) for KIC 08626021 constitutes a major improvement over any of the fits proposed so far for this star, considering that it reproduces the eight independent periodicities to the actual precision of the Kepler observations. It is, therefore, an excellent reference for our purposes.
We used this specific seismic model to estimate the theoretical linear growth rates of the fitted pulsations modes. These computations were done by using two different nonadiabatic pulsation codes, one still working in the frozen convection (FC) approximation (Brassard et al. 1992; Fontaine et al. 1994; Brassard & Fontaine 1997) and the other implementing a more realistic time-dependent convection (TDC) treatement (Dupret 2001; Grigahcène et al. 2005). In DA and DB white dwarf pulsators, the superficial convection layer has an important contribution to the driving of modes (through the sometimes called convective driving mechanism). The positions of the theoretical instability strips, in particular the blue edges, are particularly sensitive to the adopted treatment (TDC vs. FC) and to the efficiency of convection itself that controls the depths of the convection zone (the α parameter in the Mixing Length Theory; see Van Grootel et al. 2012). These can also affect the growth rate of each individual mode. Unfortunately, the oscillation periods have essentially no sensitivity to the α parameter, which is therefore not constrained by seismology. In this context, we explored various combinations of α values for the two different nonadiabatic treatments of the convection perturbation to estimate the typical range of values one would expect for the growth rate of the modes.
The results of these nonadiabatic calculations are summarized in Table 2 for the triplet (and doublet) components f1, f2, f3, and, to be complete, for the other fitted frequencies as well. All these modes can effectively be driven in this star and the value of the growth rate κ0 mostly depends on the radial order of the mode, strongly increasing when k increases. For the modes of interest, we find that κ0 lies in the ranges 2 × 10-13−7 × 10-12, 2 × 10-12−4 × 10-11, and 1 × 10-11−2 × 10-10 for f2, f1, f3, which, from the seismic solution of Giammichele et al. (in prep.), are successive dipole modes of radial order k = 3, 4, and 5, respectively.
3.2.2. Triplets in the intermediate regime
The periodic amplitude and frequency modulations that are observed in the triplet at 4310 μHz (f1) immediately suggest that this triplet is in the intermediate regime of the resonance (see Fig. 7 again). Both the prograde and retrograde components show a modulation of frequency and amplitude with a period of ~600 d. The central (m = 0) component of f1 has a frequency and amplitude modulation that is perhaps slightly longer (~680 d; precision is low here as this is about the same timescale as the duration of the observing campaign), but remains of the same order. For comparison purposes, we provide in Table 2 the modulation timescale Pm(th) ~ 1 /δνt (Eq. (5)) expected from the asymmetry, δνt, that is caused by the second order correction to the rotational splitting. The latter is computed with the Ckℓ value obtained from the reference model and the value Prot = 1.75 days for the rotation period of the star. With Pm(th) ≃ 620 days, the value obtained is sufficiently consistent with the observed modulation period to support the idea that we have indeed uncovered the right explanation for the behavior of the components in this triplet. Interestingly, the asymmetry can also be derived directly from the measured frequencies. Using directly the values given in Table 1, the quantity δνo represents the asymmetry for the frequencies averaged over the observation time baseline. We find it to be very small, i.e., much smaller than δνt, suggesting that even in this intermediate regime the nonlinear interactions may already have forced the frequencies of the triplet components to a locked position (where δν → 0), on average (since the frequencies are still varying with time, oscillating around their mean value).
According to the nonlinear resonant coupling theory, all the three components in a triplet should have the same modulations, both in amplitude and frequency. The slight difference between the side components and the central component in terms of the modulation period might be that the interaction of the modes in the DBV star is more complex than the idealized case described by the theory. It might also be a suggestion that the growth rates for each component of the triplet are not similar (as is assumed in this theoretical framework). The shape of the amplitude modulations of the retrograde component f1, − is not as smooth as the other two components. This might be caused by the additional coupling of the mode with f4 at 2659 μHz (see Sect. 2.4.4 and Fig. 12). Such a coupling that occurs outside the triplet is not considered by Buchler et al. (1995) who neglects other interactions with independent modes (i.e, the triplet is considered as an isolated system).
The second structure that can also be associated with the intermediate regime is the doublet f3. We recall that the best interpretation for this doublet is that it belongs to a ℓ = 1 triplet with one of the side components (the low frequency one, f3, −) missing, most likely because its amplitude is below the detection threshold. The two remaining components show clear periodic modulations of both frequencies and amplitudes. All variations occur on a somewhat shorter timescale of Pm(obs) ~ 263 days (which means that they are fully resolved in our data set, contrary to the modulations of f1; see Sect. 2.4.3 and Fig. 11), except for the frequency of the f3, − component whose modulation period appear to be approximately twice that value (Pm(obs) ~ 550 days). For this f3 mode, the second order rotational splitting correction δνt also suggests a shorter modulation timescale of Pm(th) ~ 518 days, which is comparable but not strictly identical. It is not possible in this case to evaluate δνo because of the missing third component.
3.2.3. A triplet in the transitory hysteresis regime
The case of the f2 triplet at 5073 μHz (see Sect. 2.4.2 and Fig. 10) is slightly different in that the frequencies are clearly stabilized while the amplitudes are modulated. This suggests that f2 is in another configuration, in between the frequency lock regime (where both amplitudes and frequencies are locked and therefore non-variable) and the intermediate regime. This configuration could be linked to the narrow transitory hysteresis regime briefly mentionned in Sect. 3.1. This finding shows that two neighbor triplets can belong to different resonant regimes (frequency lock, narrow transition, intermediate or nonresonant), as it was also noticed for the white dwarf star GD 358 (Goupil et al. 1998).
3.3. Linear growth rates and the D parameter
Table 2 also provides the estimated values for the parameter D derived from Eq. (4) and from the values of δνt (Eq. (1)) and κ0 (obtained from the seismic model of KIC 08626021; see Sect. 3.2.1). We find that D lies in the ranges 3 × 103−6 × 104, 1 × 104−5 × 105 and 7 × 102−1 × 104 for the triplet f1, f2 and f3, respectively. These values are at least one order of magnitude larger than the range given in Goupil et al. (1998) for the intermediate regime (D ~ 9−25 for the white dwarf star GD 358). This large difference is clearly caused by the linear growth rates (κ0) adopted for the modes. Our values come from a detailed linear nonadiabatic calculation based on the seismic model. Since the three triplets are fitted to low radial order consecutive modes (k = 3, 4, and 5), their corresponding linear growth rates are generally small and differ substantially from one mode to the other (κ0 increases rapidly with k). In contrast, Goupil et al. (1998) roughly scaled the growth rate of the modes according to the relationship 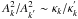 , assuming that all the coupling coefficients qR are of the same order of magnitude, leading to estimated values of κ0 ~ 10-8. Values comparable to Goupil et al. (1998) for the growth rate could be obtained only if the three triplets were assigned to higher radial orders (k between 10 and 15 instead of 3 to 5). This would require a huge shift compared to the current seismic solution which is clearly not permitted on the seismic modeling side.
, assuming that all the coupling coefficients qR are of the same order of magnitude, leading to estimated values of κ0 ~ 10-8. Values comparable to Goupil et al. (1998) for the growth rate could be obtained only if the three triplets were assigned to higher radial orders (k between 10 and 15 instead of 3 to 5). This would require a huge shift compared to the current seismic solution which is clearly not permitted on the seismic modeling side.
In the AEs formalism of Buchler et al. (1997), the solutions admit three distinct regimes and one narrow transitory regime. Those regimes are related to the distance from the resonance center (i.e., δν = 0). The parameter D in this transitory regime should be slightly smaller than in the intermediate regime, as this transitory regime is closer to the resonance center. This means that D should be smaller for f2, which is in this transitory regime, compared to f1 and f3 that are in the intermediate regime. The ranges given for the D values in Table 2 still permit this constraint to be roughly satisfied, but the overall larger D values for f2 could also lead to a contradiction here.
We think, at this stage, that further quantitative comparisons between theoretical considerations and the observed properties of the modulations would require to solve the amplitude equations specifically for this case. This is however beyond the scope of this paper, as no specific modeling tools for these nonlinear effects is available to us at present. We emphasize that with a detailed numerical solution of the nonlinear amplitude equations, the unknown coupling coefficients could, in principle, be determined from fitting the observed frequency and amplitude modulations. These coefficients, if known, would then allow us to derive the D parameter which is strongly related to the different regimes of the nonlinear resonances. With the determination of this parameter, a measurement of the growth rate of the oscillation modes would then possibly follow, leading for the first time to an independent estimation of the linear nonadiabatic growth rates of the modes and a direct test of the nonadiabatic pulsation calculations.
4. Summary and conclusion
Frequency and amplitude modulations of oscillation modes have been found in several rotationally split triplets that are detected in the DB pulsator KIC 08626021, thanks to the high-quality and long-duration photometric data obtained with the Kepler spacecraft. These modulations show signatures that point toward nonlinear resonant coupling mechanisms which occur between the triplet components. This is the first time that such signatures are identified so clearly in white dwarf pulsating stars, although hints of such effects had already been found from ground-based campaigns in the past (e.g., Vauclair et al. 2011).
Reanalysing in detail the nearly two years of Kepler photometry obtained for this star, we have detected 13 very clear independent frequencies above our estimated secure detection threshold (5.6σ; see Sect. 2.2 and Table 1), two frequencies that appear to be linear combinations of other independent modes, and two additional, but significantly less secured, frequencies emerging just above 5σ the mean noise level. Overall, we find that our secured frequencies are consistent with those reported in BK14, but we somewhat differ in the interpretation of some structures in the frequency spectrum.
Most notably, we find that three frequencies in the 3677−3686 μHz range, formerly identified as the components of a single triplet by BK14, cannot be interpreted like this. We conclude instead that one of the frequencies (f7 in Table 1) is an independent mode while the other two (f3,0 and f3, +) form the visible components of an incomplete triplet whose third component is not seen. This has some implications for the seismic modeling which should in fact include eight independent frequencies and not only seven as in BK14. A new detailed seismic analysis of KIC 08626021 based on these eight modes is provided by Giammichele et al. (in prep.). The frequency spacings (observed between the two components of f3 and the components of other two well identified triplets, f1 and f2) indicate an average rotation period of ~1.75 days for KIC 08626021, i.e., in agreement with the value given by BK14.
Also differing from BK14, we find that the two components of the f3 doublet have a hyperfine structure with sidelobes separated by 0.044 μHz, which indicates a modulating phenomenon that occurs on a long timescale of ~263 days. In addition, the components that form triplets show long-term and quasi-periodic frequency and/or amplitude modulations which appear to be correlated, as they evolve either in phase or antiphase. The triplet at 4310 μHz (f1) show signs of periodic modulation of both the frequencies and amplitudes with a timescale of roughly 600 days with the side components evolving in phase, while the central mode is in antiphase. The timescale appears somewhat shorter (263 days) for the f3 doublet while the triplet f2 shows only modulations in amplitudes (the frequencies appear stable during the observations) with a probable timescale of ~700 days.
We show that these behaviors can be related to the so-called nonlinear resonant coupling mechanisms that is expected to occur within rotationnally split triplets. The amplitude equations (Buchler et al. 1997; Goupil et al. 1998) predict three main regimes in which the triplet components may behave differently. It appears that f1 and f3 can be linked to the so-called intermediate regime of the resonance where both the amplitude and frequency of the modes should experience a periodic modulation. We find that the timescales expected from the theory are quite consistent with the observed periodicities of the modulations. The triplet f2 shows a different behavior that can be associated with a narrow transitory hysteresis regime between the intermediate regime and the frequency locked regime in which locked frequencies and modulated amplitude solutions can coexist.
We also found correlated frequency and amplitude modulations in a linear combination of frequencies which involves the modes f1, − and f4, and the frequency f8. This configuration may be related to parents/child mode interactions in pulsating stars, f8 being either a combination frequency resulting from strong nonlinearities or, because the amplitude ratio is large, an eigenmode whose amplitude has been significantly enhanced by a resonant coupling phenomenon (see Breger & Montgomery 2014). Further investigations need to be carried out to evaluate which explanation is the most plausible.
As an additional step toward comparing more quantitatively observations to the theoretical expectations, we estimated theoretical linear growth rates (see Table 2) of the triplet central components using the seismic model provided by Giammichele et al. (in prep.). We used two different nonadiabatic pulsation codes for these computations: one working in the frozen convection approximation (Brassard et al. 1992; Fontaine et al. 1994; Brassard & Fontaine 1997) and the other implementing a time-dependent convection treatement (Dupret 2001; Grigahcène et al. 2005). The modes of interest f2, f1 and f3 have growth rates that are in the ranges 2 × 10-13−7 × 10-12, 2 × 10-12−4 × 10-11, and 1 × 10-11−2 × 10-10, respectively. With these values, we finally estimate the parameter D (a key parameter that measures how far away is the mode from the resonance center) which is found in the range 3 × 103−6 × 104, 1 × 104−5 × 105 and 7 × 102−1 × 104 for the mode triplet f1, f2 and f3, respectively. These values are significantly larger than those estimated in Goupil et al. (1998) and need further investigation, but going beyond this would require to solve the amplitude equations for the specific case of KIC 08626021, which is currently not possible.
We also want to emphasize the fact that the uncovered frequency modulations, which are related to nonlinear coupling mechanisms and that occur on timesscales long enough to be difficult to detect but short compared to the secular evolution timescale, can potentially impair any attempt to measure reliably the effects of the cooling of the white dwarf on the pulsation periods. Measuring the changing rate of the pulsation periods in white dwarf stars could indeed offer an opportunity to constrain the neutrino emission physics (Winget et al. 2004; Sullivan et al. 2008). However, one should be extremely careful of the potential contamination of nonlinear effects, which may need to be corrected first. Some independent modes in KIC 08626021 that seem to be stable in frequency over much longer timescales and that do not apparently couple with other modes could be good candidates for measuring period rates of change. But nonlinear interactions could still be affecting them on longer timescales that we cannot detect with Kepler.
Finally, the observed periodic frequency and amplitude modulations that occur in the intermediate regime of the resonance may allow for new asteroseismic diagnostics, providing in particular a way to measure for the first time linear growth rates of pulsation modes in white dwarf stars. This prospect should motivate further theoretical work on nonlinear resonant mode coupling physics and revive interest in nonlinear stellar pulsation theory in general.
Note that the two last data points with larger error bars are less secure measurements due to the fact that the sliding Fourier transform reaches the end of the data set and incorporates shorter portions of the light curve. This affects the frequency resolution and consequently the precision of the measurements.
Acknowledgments
Funding for the Kepler mission is provided by NASA’s Science Mission Directorate. We greatfully acknowledge the Kepler Science Team and all those who have contributed to making the Kepler mission possible. W.K.Z. acknowledges the financial support from the China Scholarship Council. V. Van Grootel is an F.R.S-FNRS Research Associate. This work was supported in part by the Programme National de Physique Stellaire (PNPS, CNRS/INSU, France) and the Centre National d’Études Spatiales (CNES, France).
References
- Beauchamp, A., Wesemael, F., Bergeron, P., et al. 1999, ApJ, 516, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Bischoff-Kim, A., & Østensen, R. H. 2011, ApJ, 742, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Bischoff-Kim, A., Østensen, R. H., Hermes, J. J., & Provencal, J. 2014, ApJ, 794, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Brassard, P., & Fontaine, G. 1997, White dwarfs, 214, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Brassard, P., Pelletier, C., Fontaine, G., & Wesemael, F. 1992, ApJS, 80, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Brassard, P., Fontaine, G., & Wesemael, F. 1995, ApJS, 96, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Breger, M., & Montgomery, M. H. 2014, ApJ, 783, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Buchler, J. R., & Goupil, M.-J. 1984, ApJ, 279, 394 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Buchler, J. R., Goupil, M.-J., & Serre, T. 1995, A&A, 296, 405 [NASA ADS] [Google Scholar]
- Buchler, J. R., Goupil, M.-J., & Hansen, C. J. 1997, A&A, 321, 159 [NASA ADS] [Google Scholar]
- Charpinet, S., Green, E. M., Baglin, A., et al. 2010, A&A, 516, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charpinet, S., Van Grootel, V., Fontaine, G., et al. 2011, A&A, 530, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H, Althaus, L. G., Miller Bertolami, M. M., & Bischoff-Kim, A. 2012, A&A, 541, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deeming, T. J. 1975, Ap&SS, 36, 137 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dupret, M. A. 2001, A&A, 366, 166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dziembowski, W. A. 1982, Acta Astron., 32, 147 [NASA ADS] [Google Scholar]
- Dziembowski, W. A., & Goode, P. R. 1992, ApJ, 394, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Fontaine, G., & Brassard, P. 2008, PASP, 120, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Fontaine, G., Brassard, P., Wesemael, F., & Tassoul, M. 1994, ApJ, 428, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Fu, J.-N., Dolez, N., Vauclair, G., et al. 2013, MNRAS, 429, 1585 [NASA ADS] [CrossRef] [Google Scholar]
- Gilliland, R. L., Timothy, M., Christensen-Dalsgaard, J., et al. 2010, PASP, 122, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Goupil, M.-J., & Buchler, J. R. 1994, ApJ, 279, 394 [Google Scholar]
- Goupil, M. J., Dziembowski, W. A., & Fontaine, G. 1998, Balt. Astron., 7, 21 [Google Scholar]
- Grigahcène, A., Dupret, M.-A., Gabriel, M., Garrido, R., & Scuflaire, R. 2005, A&A, 434, 1055 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hermes, J. J., Montgomery, M. H., Mullally, F., et al. 2013, ApJ, 766, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, J. M., Caldwell, D. A., Chandrasekaran, H., et al. 2010, ApJ, 713, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Montgomery, M. H. 2005, ApJ, 633, 1152 [Google Scholar]
- Moskalik, P. 1985, Acta Astron., 35, 229 [NASA ADS] [Google Scholar]
- Østensen, R. H. 2013, ASP Conf. Ser., 469, 3 [NASA ADS] [Google Scholar]
- Østensen, R. H., Bloemen, S., Vučković, M., et al. 2011, ApJ, 736, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Salabert, D., García, R. A., & Turck-Chièze, S. 2015, A&A, 578, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Silvotti, R., Schuh, S., Janulis, R., et al. 2007, Nature, 449, 189 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sullivan, D. J., Metcalfe, T. S., O’Donoghue, D., et al. 2008, MNRAS, 387, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H. 1989, Nonradial oscillations of stars (Tokyo: University of Tokyo Press), 2nd edn. [Google Scholar]
- Van Hoolst, T. 1994, A&A, 292, 183 [Google Scholar]
- Van Grootel, V., Dupret, M.-A., Fontaine, G., et al. 2012, A&A, 539, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vauclair, G. 2013, ASP Conf. Ser., 479, 223 [NASA ADS] [Google Scholar]
- Vauclair, G., Fu, J.-N., Solheim, J.-E., et al. 2011, A&A, 528, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winget, D. E., & Kepler, S. O. 2008, ARA&A, 46, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winget, D. E., Sullivan, D. J., Metcalfe, T. S., et al. 2004, ApJ, 602, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y. 2001, MNRAS, 323, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., & Goldreich, P. 2001, ApJ, 546, 469 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Mode identification and linear nonadiabatic growth rates, κ0, from the best seismic model of KIC 08626021.
All Figures
 |
Fig. 1 Top panel: condensed representation of the full Kepler light curve (Amplitude is the residual relative to the mean brightness intensity of the star vs. time in Barycentric Julian Date) covering from Q10.1 to Q17.2 (~684 days) of KIC 08626021. Between quarters, scatter sometime changes due to different levels of noise in the data (all quarters are not equivalent in photometric quality). Bottom panel: close-up view showing one day of the Kepler light curve by slices of 0.1 days. At this scale, the oscillations are clearly apparent. |
| In the text | |
 |
Fig. 2 Lomb-Scargle periodogram (LSP; amplitude in % of the mean brightness vs. frequency in μHz) of the Kepler light curve. The represented range covers the frequency region where the pulsation modes are detected (no significant signal is found outside these limits). Note that some well known Kepler instrumental artefacts are within this frequency range but can easily be recognized. |
| In the text | |
 |
Fig. 3 False alarm probability Pn of having at least n peaks caused by noise above a given S/N threshold in the LSP of KIC 08626021 (see text for details). In each panel, the three vertical lines indicate, from left to right, the S/N value corresponding to Pn = 0.1, 0.01, and 0.0001, respectively. The limit P1 = 0.0001, meaning that the risk of having a false detection above that threshold is reduced to less than 1 chance over 10 000, defines our adopted criterion. It corresponds to the limit of 5.6σ. |
| In the text | |
 |
Fig. 4 Lomb-Scargle periodogram of the triplets at 4310 μHz (top panel) and 5073 μHz (bottom panel) after nearly two years of Kepler photometry gathered on KIC 08626021. The nearly equal frequency spacings are marked in the two panels. The dashed red horizontal line refers to the 5.6σ detection threshold of local noise level. |
| In the text | |
 |
Fig. 5 Lomb-Scargle periodogram in the 3677−3686 μHz frequency range where a doublet and an independent frequency are above the 5.6σ detection threshold of local noise level. The bold black vertical segment and vertical dashed line indicate the position of one possible third component for the doublet, as shown in the bottom panel. The two top panels are the expanded view of the two components as indicated by the vertical arrows in the bottom panel. Both the fine structures of the two components show well-resolved closed peaks and have the same frequency separation of 0.044 μHz. |
| In the text | |
 |
Fig. 6 Lomb-Scargle periodogram of 8 frequencies after nearly two years of Kepler photometry gathered on KIC 08626021. The two frequencies f11 and f12 are with 5.0−5.5σ of local noise level. Frequency f8 and f10 are linear combination frequencies. |
| In the text | |
 |
Fig. 7 Frequency and amplitude modulations in the f1 triplet at 4310 μHz. The top panel shows the sLSP (giving the amplitude in % as a function of frequency in μHz and time in days) of the triplet as a whole. The middle and bottom left panels show increasingly expanded views around the average frequency (the solid vertical lines) of each component, with the bottom left panel obtained from prewhitening subsets of the data, thus measuring precisely the frequencies, as a function of time. The lower right panel provides the measured amplitudes as a function of time obtained for each subset of data (see text for details). |
| In the text | |
 |
Fig. 8 Amplitude modulations observed in the f1 triplet presented in phase diagrams with a folding period of 580 and 610 days for the two side components, and 680 days for the central component. These periods, and their associated formal errors, were estimated by fitting a sine wave (red curve) to the amplitude variations. |
| In the text | |
 |
Fig. 9 Same as Fig. 8 but for the frequency modulations observed in the f1 triplet. Note that the adopted folding periods are the values derived for the corresponding amplitude modulations. |
| In the text | |
 |
Fig. 10 Same as Fig. 7 but for the f2 triplet at 5073 μHz. Note that the component at 5076 μHz has a very low amplitude and plunges below the 4σ detection threshold during the second half of the observations, making it difficult to follow (hence the 4 missing data points). |
| In the text | |
 |
Fig. 11 Same as Fig. 7 but for the doublet f3 at 3682 μHz and the nearby independent frequency f7 at 3678 μHz. |
| In the text | |
 |
Fig. 12 Frequency and amplitude modulations of the components that form the linear combination f1, − + f4 = f8. The panels are similar to those described in Fig. 7. The three components show clear periodic modulations evolving in phase. In each bottom left subpanels, a segment indicates the 0.01 μHz scale. |
| In the text | |
 |
Fig. 13 Top panel: comparison between the measured amplitude A8 of f8 and 60 × A1, −·A4 (where A1, − and A4 are the amplitudes of f1, − and f4, respectively) at each time segment (see text). Bottom panel: same as top panel but for a comparison between the measured frequency f8 and sum of the frequencies f1, − + f4. In both cases, the relationship is exactly statisfied along the plain diagonal line. All the measurements are found to be within 2σ of this line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


