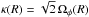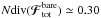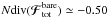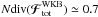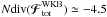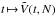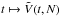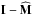| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A129 | |
| Number of page(s) | 21 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201527052 | |
| Published online | 08 December 2015 | |
Secular diffusion in discrete self-gravitating tepid discs II. Accounting for swing amplification via the matrix method⋆,⋆⋆
1
Institut d’Astrophysique de Paris and UPMC, CNRS (UMR 7095),
98bis Boulevard Arago,
75014
Paris,
France
e-mail:
fouvry@iap.fr
2
Institute of Astronomy & KICC, University of
Cambridge, Madingley
Road, Cambridge,
CB3 0HA,
UK
3
Rudolf Peierls Centre for Theoretical Physics, University of
Oxford, Keble Road,
Oxford
OX1 3RH,
UK
4
Laboratoire de Physique Théorique (IRSAMC), CNRS and UPS,
Univ. de Toulouse,
31062
Toulouse,
France
Received: 24 July 2015
Accepted: 25 August 2015
The secular evolution of an infinitely thin tepid isolated galactic disc made of a finite number of particles is investigated using the inhomogeneous Balescu-Lenard equation expressed in terms of angle-action variables. The matrix method is implemented numerically in order to model the induced gravitational polarisation. Special care is taken to account for the amplification of potential fluctuations of mutually resonant orbits and the unwinding of the induced swing amplified transients. Quantitative comparisons with N-body simulations yield consistent scalings with the number of particles and with the self-gravity of the disc: the fewer the particles and the colder the disc, the faster the secular evolution. Secular evolution is driven by resonances, but does not depend on the initial phases of the disc. For a Mestel disc with Q ~ 1.5, the polarisation cloud around each star boosts its secular effect by a factor of a thousand or more, accordingly promoting the dynamical relevance of self-induced collisional secular evolution. The position and shape of the induced resonant ridge are found to be in very good agreement with the prediction of the Balescu-Lenard equation, which scales with the square of the susceptibility of the disc. In astrophysics, the inhomogeneous Balescu-Lenard equation may describe the secular diffusion of giant molecular clouds in galactic discs, the secular migration and segregation of planetesimals in proto-planetary discs, or even the long-term evolution of population of stars within the Galactic centre. It could be used as a valuable check of the accuracy of N-body integrators on secular timescales.
Key words: galaxies: evolution / galaxies: kinematics and dynamics / galaxies: spiral / diffusion / gravitation
Appendices are available in electronic form at http://www.aanda.org
A copy of the linear matrix response code is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/584/A129
© ESO, 2015
1. Introduction
Because most of the stars are born in a stellar disc, galactic astronomy has striven to understand the dynamics and evolution of discs over cosmic time. Stars in cool discs are born on the almost closed orbits of their parent gas clouds, which means that they are confined to a very small volume of phase space. There is therefore a massive opportunity for increasing the entropy of the disc’s phase-space distribution by spreading stars orbits to a wider range of eccentricities and inclinations while conserving the system’s energy. Much empirical evidence of such heating has now been discovered: the random velocities of coeval cohorts of stars increases with the cohort’s age (Wielen 1977; Aumer & Binney 2009); the velocity distribution at the Sun contains streams of stars (Dehnen 1998); and the density of stars in phase space exhibits elongated features (resonance ridges) consistent with a resonant condition (Sellwood 2010; McMillan 2013).
Such long-term evolution of the system’s distribution function (DF) implies that the disc’s gravitational potential cannot have remained static and axisymmetric. Axisymmetric discs support spiral waves that can move through the disc; leading waves unwind into trailing waves and are amplified at corotation. Eventually each wave Landau damps by transferring its energy to stars that resonate with it: it heats the disc by increasing the eccentricity of resonating stars. In a disc made of a finite number of stars, shot noise is a natural excitation mechanism for launching such waves. When the disc is cool, fluctuations of the potential induced by these discrete encounters may be strongly amplified (Kalnajs 1972), so a weak stimulus can produce significant heat. Capturing this secular heating by shot noise requires an apparatus able to follow the dynamics of spiral waves from launch as leading waves through amplification and to thermalisation at resonances to determine their secular dynamical impact. In this paper we demonstrate how the Balescu-Lenard formalism provides an appropriate framework for taking such interactions into account.
The kinetic theory of stellar systems was initiated by Jeans (1929) and Chandrasekhar (1942) in the context of hot spherical stellar systems, such as elliptical galaxies and globular clusters for which the gravitational susceptibility can safely be neglected, as opposed to cold self-gravitating galactic discs. More generally, in astrophysics, the secular diffusion of giant molecular clouds in galactic discs, the secular migration and segregation of planetesimals in proto-planetary or debris discs, or even the long-term evolution of population of stars within the Galactic centre are all processes for which it is relevant to quantify the dynamical effect of gravitationally amplified potential fluctuations induced by the finite number of elements involved. More than 55 years ago, Balescu (1960) and Lenard (1960) developed a rigorous kinetic theory taking collective effects into account and obtained the corresponding kinetic equation for plasmas, the Balescu-Lenard equation. More recently Heyvaerts (2010) and Chavanis (2012) have transposed the corresponding non-linear kinetic equation to the angle-action variables that are the appropriate variables to describe spatially inhomogeneous multi-periodic systems. The corresponding inhomogeneous Balescu-Lenard equation accounts for self-driven orbital secular diffusion of a self-gravitating system induced by the intrinsic shot noise due to its discreteness. The formal transposition from position-velocity to angle-action implies that the secular interactions need not be local in space: they only need to correspond to gravitationally amplified long-range correlations and resonances, which are indeed the driving mechanism for the secular evolution of isolated astrophysical discs via angular momentum redistribution (Lynden-Bell & Kalnajs 1972).
The Balescu-Lenard equation is valid at the order 1 /N in an expansion of the dynamics in terms of this small parameter, where N ≫ 1 is the number of stars. Therefore, it takes finite-N effects into account and describes the evolution of the system on a timescale of about NtD, where tD is the dynamical time. For self-gravitating systems, the collective effects are responsible for an anti-shielding which tends to increase the effective mass of the stars, hence reducing the relaxation time. When the system is cold, each particle is dressed by the very strong gravitational polarisation it induces. Therefore secular effects can occur on much shorter timescales than one would naively expect, making the system behave as if it were made up of only Neff ~ N/10few particles. The purpose of this paper is to quantify this effect for stable but strongly susceptible galactic discs.
The Balescu-Lenard formalism has seldom been applied in its prime context, but only in various limits where it reduces to simpler kinetic equations (Landau 1936; Vlasov 1938; Chandrasekhar 1942; Rosenbluth et al. 1957). Weinberg (1993) presents an interesting first implementation, though in a somewhat over-simplified cartesian geometry. This formalism is quite unique in accounting for the non-linear evolution of discs and galaxies on secular timescales. While potentially probing similar processes, N-body simulations should be scrutinised carefully in this regime, as shadowing (Quinlan & Tremaine 1992) may, over many orbital times, impact resonant interactions. Nevertheless, N-body simulations have been shown to more or less reproduce growth rates of discs on dynamical timescales (see e.g. Sellwood & Evans 2001, and references therein, together with Appendix C); qualifying them quantitatively on secular timescales is now within reach of the Balescu-Lenard formalism.
A companion paper, (Fouvry et al. 2015a, hereafter Paper I) presented a simple and tractable quadrature for the Balescu-Lenard drift and diffusion coefficients under the assumption that the transient response of the disc can be described by tightly wound spirals via the WKB and epicyclic approximations. These simple expressions have provided insight into the physical processes at work during the secular diffusion of self-gravitating discrete discs. When applied to the secular evolution of an isolated stationary self-gravitating Mestel disc, it identified the importance of the corotation resonance in the inner regions of the disc leading to a regime with both radial migration and heating, in qualitative agreement with numerical simulations.
Yet, the tightly wound approximation is quantitatively questionable when transient spirals unwind. Indeed Paper I found a discrepancy between the predicted secular evolution timescale and the measured one, which might be driven by the incompleteness of the WKB basis, since such a basis can only correctly represent tightly wound spirals. It considered only resonances between orbits that are close to one another in position space, and did not allow remote orbits to resonate, nor wave packets to propagate between such non-local resonances. Yet, the seminal works from Goldreich & Lynden-Bell (1965), Julian & Toomre (1966), Toomre (1981) show that any leading spiral wave undergoes significant amplification during its unwinding to a trailing wave. Because it involves the unwinding of spirals this mechanism is not captured by the WKB formalism of Paper I.
In this paper, we avoid such approximations by using the matrix method (Kalnajs 1976) to estimate the gravitational amplification of the secular response and the role of non-local resonances. From this we compute numerically the drift and diffusion coefficients that appear in the Balescu-Lenard equation. We then compare those predictions to crafted sets of numerical experiments, allowing us to estimate ensemble averaged secular responses of a sizeable number of simulations as a function of the total number of particles N. Such ensemble averaging allows us to make robust predictions for the N-scaling of the secular response and its dependence on halo to disc mass fraction, hence probing the secular importance of gravitational polarisation.
The paper is organised as follows. Section 2 briefly presents the content of the inhomogeneous Balescu-Lenard equation. Section 3 presents our implementation of the matrix method to compute the diffusion equation for an isolated self-gravitating tapered Mestel disc. Section 4 computes numerically the exact drift and diffusion coefficient in action space for such a truncated Mestel disc, and compares the divergence of the corresponding flux density to the initial measured rate of change of the distribution function. Section 5 presents our N-body simulations and compares scaling of the flux with the number of particles and the fraction of mass in the disc. Finally, Sect. 6 wraps up. Appendix A presents the relevant bi-orthogonal basis function. Appendix C validates the response matrix method and the N-body integrator while matching growth rates and pattern speeds of unstable Mestel discs. Appendix D investigates the roles of self-gravity and basis completeness. Appendix E describes the sampling strategy for the initial distribution. Appendix G presents briefly the available online codes.
2. The inhomogeneous Balescu-Lenard equation
We intend to describe the long-term evolution of a system made of N particles. We assume that the gravitational background ψ0 of the system is stationary and integrable, and associated with the Hamiltonian H0. As a consequence, one can always remap the physical space-coordinates (x,v) to the angle-action coordinates (θ,J) (Goldstein 1950; Born 1960; Binney & Tremaine 2008). We define the intrinsic frequencies of motions along the action torus as 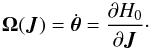 (1)Within these new coordinates, one has that along the unperturbed trajectories the angles θ are 2π-periodic, evolving with the frequencies Ω, whereas the actions J are conserved. We assume that the system is always in a virialised state, so that its distribution function (DF) can be written as a quasi-stationary DF of the form F = F(J,t), satisfying the normalisation constraint
(1)Within these new coordinates, one has that along the unperturbed trajectories the angles θ are 2π-periodic, evolving with the frequencies Ω, whereas the actions J are conserved. We assume that the system is always in a virialised state, so that its distribution function (DF) can be written as a quasi-stationary DF of the form F = F(J,t), satisfying the normalisation constraint 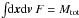 , where Mtot is the total mass of the system. On secular timescales, this isolated DF evolves under the effect of stellar “encounters” (finite-N effects). Such a collisional long-term evolution is descrided by the inhomogeneous Balescu-Lenard equation (Heyvaerts 2010; Chavanis 2012) which reads
, where Mtot is the total mass of the system. On secular timescales, this isolated DF evolves under the effect of stellar “encounters” (finite-N effects). Such a collisional long-term evolution is descrided by the inhomogeneous Balescu-Lenard equation (Heyvaerts 2010; Chavanis 2012) which reads ![\begin{eqnarray} \frac{\partial F}{\partial t} &=& \pi (2 \pi)^{d} \, \mu \, \frac{\partial}{\partial \bm{J}_{1}} \!\cdot\! \left[ \sum_{\bm{m}_{1} , \bm{m}_{2}} \!\! \bm{m}_{1} \!\! \int \!\! \mathrm{d} \bm{J}_{2} \, \frac{\delta_{\rm D} (\bm{m}_{1} \!\cdot\! \bm{\Omega}_{1} \!-\! \bm{m}_{2} \!\cdot\! \bm{\Omega}_{2})}{|\mathcal{D}_{\bm{m}_{1} , \bm{m}_{2}} (\bm{J}_{1} , \bm{J}_{2} , \bm{m}_{1} \!\cdot\! \bm{\Omega}_{1}) |^{2}} \right. \nonumber\\ && \left. \times \, \bigg( \bm{m}_{1} \!\cdot\! \frac{\partial }{\partial \bm{J}_{1}} \!-\! \bm{m}_{2} \!\cdot\! \frac{\partial }{\partial \bm{J}_{2}} \bigg) \, F (\bm{J}_{1} , t) \, F(\bm{J}_{2} , t) \right] , \label{definition_BL} \end{eqnarray}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq20.png) (2)where
(2)where 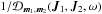 are the dressed susceptibility coefficients, d is the dimension of the physical space, μ = Mtot/N is the mass of the individual particles, and where we used the shortened notation Ωi = Ω(Ji,t). Since the r.h.s. is the divergence of a flux, this diffusion equation conserves the number of stars. One should also note the resonance condition encapsulated in the Dirac delta δD(m1·Ω1 − m2·Ω2), with the integration over the dummy variable J2 scanning for points where the resonance condition is satisfied. Note importantly right away that Eq. (2) scales like
are the dressed susceptibility coefficients, d is the dimension of the physical space, μ = Mtot/N is the mass of the individual particles, and where we used the shortened notation Ωi = Ω(Ji,t). Since the r.h.s. is the divergence of a flux, this diffusion equation conserves the number of stars. One should also note the resonance condition encapsulated in the Dirac delta δD(m1·Ω1 − m2·Ω2), with the integration over the dummy variable J2 scanning for points where the resonance condition is satisfied. Note importantly right away that Eq. (2) scales like 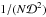 (since μ ∝ 1 /N), so that increasing N or increasing the heat content of the disc have the same effect. For a more detailed discussion on the content of the Balescu-Lenard equation, see Paper I.
(since μ ∝ 1 /N), so that increasing N or increasing the heat content of the disc have the same effect. For a more detailed discussion on the content of the Balescu-Lenard equation, see Paper I.
In order to solve the non-local Poisson equation, we follow Kalnajs’ matrix method (Kalnajs 1976), so that we introduce a complete biorthonormal basis of potentials and densities ψ(p)(x) and ρ(p)(x) such that ![\begin{equation} \Delta \psi^{(p)} \!= 4 \pi G \rho^{(p)} , \quad \int \!\! \mathrm{d} \bm{x} \, [ \psi^{(p)} (\bm{x}) ]^{*} \, \rho^{(q)} (\bm{x}) = - \, \delta_{p}^{q} . \label{definition_basis} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq31.png) (3)The dressed susceptibility coefficients appearing in Eq. (2) are then given by
(3)The dressed susceptibility coefficients appearing in Eq. (2) are then given by ![\begin{equation} \frac{1}{\mathcal{D}_{\bm{m}_{1} , \bm{m}_{2}} (\bm{J}_{1} , \bm{J}_{2} , \omega)} = \sum_{p , q} \psi_{\bm{m}_{1}}^{(p)} \!(\bm{J}_{1}) \, [ \mathbf{I} \!-\! \widehat{\mathbf{M}} (\omega) ]^{-1}_{p q} \, [ \psi_{\bm{m}_{2}}^{(q)} \!(\bm{J}_{2}) ]^{*} , \label{definition_1/D} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq32.png) (4)where I is the identity matrix and
(4)where I is the identity matrix and  is the response matrix defined as
is the response matrix defined as ![\begin{equation} \widehat{\mathbf{M}}_{pq} (\omega) = (2 \pi)^{d} \! \sum_{\bm{m}} \!\! \int \!\! \mathrm{d} \bm{J} \, \frac{\bm{m} \!\cdot\! \partial F / \partial \bm{J} }{\omega \!-\! \bm{m} \!\cdot\! \bm{\Omega}} \left[\psi_{\bm{m}}^{(p)} \!(\bm{J})\right]^{*} \psi_{\bm{m}}^{(q)} \!(\bm{J}) . \label{Fourier_M} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq35.png) (5)In the previous expression, we introduced as
(5)In the previous expression, we introduced as 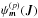 the Fourier transform in angles of the basis elements ψ(p)(x) using the convention that the Fourier transform of a function X(θ,J) is given by
the Fourier transform in angles of the basis elements ψ(p)(x) using the convention that the Fourier transform of a function X(θ,J) is given by 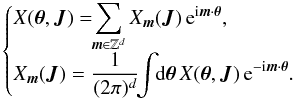 (6)In order to ease the understanding of the Balescu-Lenard Eq. (2), one may rewrite it as an anisotropic Fokker-Planck equation by introducing the relevant drift and diffusion coefficients. Indeed, Eq. (2) can be put into the form
(6)In order to ease the understanding of the Balescu-Lenard Eq. (2), one may rewrite it as an anisotropic Fokker-Planck equation by introducing the relevant drift and diffusion coefficients. Indeed, Eq. (2) can be put into the form ![\begin{equation} \frac{\partial F}{\partial t} = \sum_{\bm{m}_{1}} \frac{\partial }{\partial \bm{J}_{1}} \!\cdot\! \left[ \bm{m}_{1} \left( A_{\bm{m}_{1}} ( \bm{J}_{1} ) \, F ( \bm{J}_{1} ) + D_{\bm{m}_{1}} ( \bm{J}_{1} ) \, \bm{m}_{1} \!\cdot\! \frac{\partial F}{\partial \bm{J}_{1}} \right) \right] , \label{initial_BL_rewrite} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq39.png) (7)where Am1(J1) and Dm1(J1) are respectively the drift and diffusion coefficients associated with a given resonance m. We note that they both depend secularly on the DF F, but we omit this dependence to simplify our notations. The drift coefficients are given by
(7)where Am1(J1) and Dm1(J1) are respectively the drift and diffusion coefficients associated with a given resonance m. We note that they both depend secularly on the DF F, but we omit this dependence to simplify our notations. The drift coefficients are given by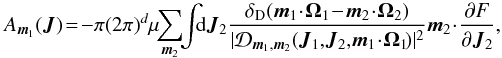 (8)and the diffusion coefficients are given by
(8)and the diffusion coefficients are given by 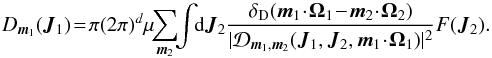 (9)One can also introduce the total flux of diffusion ℱtot as
(9)One can also introduce the total flux of diffusion ℱtot as 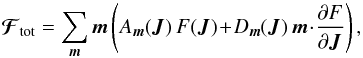 (10)so that the Balescu-Lenard equation from Eqs. (2) and (7) takes the explicitly conservative form
(10)so that the Balescu-Lenard equation from Eqs. (2) and (7) takes the explicitly conservative form 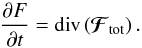 (11)
(11)
3. The Matrix diffusion equation
When computing the Balescu-Lenard diffusion and drift coefficients, three main difficulties have to be addressed. First, one must build the mapping (x,v) → (θ,J), because the drift and diffusion coefficients are associated with a diffusion in action space. The second difficulty follows from the non-locality of Poisson’s equation and the estimation of the response matrix  from Eq. (5). Indeed, as noted in Eq. (3), the matrix relies on potential basis elements ψ(p) which must be integrated over the whole action space with functions possessing a pole 1 / (ω − m·Ω). This cumbersome and difficult evaluation has to be performed numerically, along with the matrix inversion needed to estimate the susceptibility coefficients from Eq. (4). Finally, the third difficulty arises from the resonance condition δD(m1·Ω1 − m2·Ω2), which involves determining how orbits may resonate one with another. In Paper I we relied on the epicyclic approximation to build the angle-action mapping and on a WKB basis to treat gravity locally in order to solve these issues while obtaining tractable though approximate expressions.
from Eq. (5). Indeed, as noted in Eq. (3), the matrix relies on potential basis elements ψ(p) which must be integrated over the whole action space with functions possessing a pole 1 / (ω − m·Ω). This cumbersome and difficult evaluation has to be performed numerically, along with the matrix inversion needed to estimate the susceptibility coefficients from Eq. (4). Finally, the third difficulty arises from the resonance condition δD(m1·Ω1 − m2·Ω2), which involves determining how orbits may resonate one with another. In Paper I we relied on the epicyclic approximation to build the angle-action mapping and on a WKB basis to treat gravity locally in order to solve these issues while obtaining tractable though approximate expressions.
For a 2D axisymmetric potential, one can define explicitly the actions of the system. Following Lynden-Bell & Kalnajs (1972), Tremaine & Weinberg (1984), the two natural actions of the system are given by a quadrature and an identity 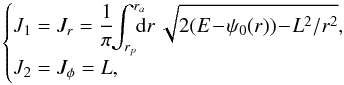 (12)where rp and ra are respectively the pericentre and the apocentre of the trajectory, while E and L are the energy and angular momentum of the star. The first action J1 encodes the amount of radial energy of the star, so that Jr = 0 corresponds to circular orbits. The second action J2 is the angular momentum L of the star. One can then define the two intrinsic frequencies of motion Ω1 = κ associated with the radial oscillations and Ω2 = Ωφ associated with the azimuthal oscillations. Indeed, one has
(12)where rp and ra are respectively the pericentre and the apocentre of the trajectory, while E and L are the energy and angular momentum of the star. The first action J1 encodes the amount of radial energy of the star, so that Jr = 0 corresponds to circular orbits. The second action J2 is the angular momentum L of the star. One can then define the two intrinsic frequencies of motion Ω1 = κ associated with the radial oscillations and Ω2 = Ωφ associated with the azimuthal oscillations. Indeed, one has 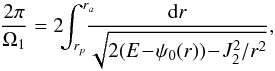 (13)while the azimuthal frequency Ω2 can then be determined via the relation
(13)while the azimuthal frequency Ω2 can then be determined via the relation 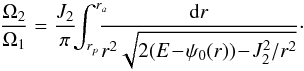 (14)At this stage, one should note that various coordinates can be used to represent the 2D action space. Indeed, once the background potential ψ0 is known, one has the bijections (rp,ra) ↔ (E,L) ↔ (Jr,Jφ). As a consequence, any orbit can equivalently be represented by the set of the pericentre and apocentre (rp,ra) or by its actions (J1,J2). However, determining the actions associated with one set (rp,ra) only requires the computation of a 1D integral as in Eq. (12), whereas determing the pericentre and apocentre associated with a set of actions (J1,J2) requires the inversion of the same non-trivial relation. Because the peri/apocentres are the two roots of the equation 2(E − ψ0(r)) − L2/r2 = 0, one also immediately obtains that for a given value of rp and ra, the energy E and the angular momentum L of the orbit are given by
(14)At this stage, one should note that various coordinates can be used to represent the 2D action space. Indeed, once the background potential ψ0 is known, one has the bijections (rp,ra) ↔ (E,L) ↔ (Jr,Jφ). As a consequence, any orbit can equivalently be represented by the set of the pericentre and apocentre (rp,ra) or by its actions (J1,J2). However, determining the actions associated with one set (rp,ra) only requires the computation of a 1D integral as in Eq. (12), whereas determing the pericentre and apocentre associated with a set of actions (J1,J2) requires the inversion of the same non-trivial relation. Because the peri/apocentres are the two roots of the equation 2(E − ψ0(r)) − L2/r2 = 0, one also immediately obtains that for a given value of rp and ra, the energy E and the angular momentum L of the orbit are given by 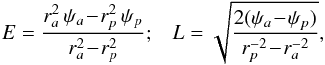 (15)where we used the shortening notations ψp/a = ψ0(rp/a). Therefore, in the upcoming calculations, we use (rp,ra) as the representative variables of the 2D action space.
(15)where we used the shortening notations ψp/a = ψ0(rp/a). Therefore, in the upcoming calculations, we use (rp,ra) as the representative variables of the 2D action space.
3.1. The basis elements
The expressions (4) and (5) of the susceptibility coefficients and the response matrix require the introduction of 2D potential-density basis elements. The 2D potential basis elements ψ(p) that we consider depend on two indices spanning the two degrees of freedom so that one has 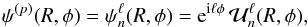 (16)where
(16)where 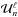 is a real radial function and (R,φ) are the usual polar coordinates. The associated surface densities elements are of the form
is a real radial function and (R,φ) are the usual polar coordinates. The associated surface densities elements are of the form 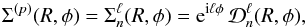 (17)where
(17)where 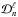 is a real radial function. The basis elements therefore depend on two indices ℓ ≥ 0 and n ≥ 0. In all the numerical calculations, we used the radial functions from Kalnajs (1976), which are recalled in Appendix A.
is a real radial function. The basis elements therefore depend on two indices ℓ ≥ 0 and n ≥ 0. In all the numerical calculations, we used the radial functions from Kalnajs (1976), which are recalled in Appendix A.
The next step is then to determine the Fourier transform with respect to the angles θ of the basis elements. Indeed, to compute the response matrix  from Eq. (5), one has to compute
from Eq. (5), one has to compute 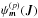 , where the resonance vector is given by m = (m1,m2). Following Eq. (6), it is given by
, where the resonance vector is given by m = (m1,m2). Following Eq. (6), it is given by 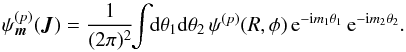 (18)From Lynden-Bell & Kalnajs (1972), the angles θ1 and θ2 associated with the actions from Eq. (12) are given by
(18)From Lynden-Bell & Kalnajs (1972), the angles θ1 and θ2 associated with the actions from Eq. (12) are given by 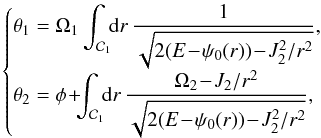 (19)where
(19)where 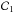 is a contour starting from the pericentre rp and going up to the current position r = r(θ1) along the radial oscillation. Following the notations from Tremaine & Weinberg (1984), one can straightforwardly show that Eq. (18) takes the form
is a contour starting from the pericentre rp and going up to the current position r = r(θ1) along the radial oscillation. Following the notations from Tremaine & Weinberg (1984), one can straightforwardly show that Eq. (18) takes the form 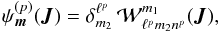 (20)where
(20)where 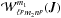 is given by
is given by ![\begin{equation} \mathcal{W}^{m_{1}}_{\ell^{p} m_{2} n^{p}} (\bm{J}) = \frac{1}{\pi} \!\! \int_{r_{p}}^{r_{a}} \!\!\!\!\!\! \mathrm{d} r \, \frac{\mathrm{d} \theta_{1}}{\mathrm{d} r} \mathcal{U}_{n^{p}}^{\ell^{p}} (r) \cos [ m_{1} \theta_{1} [r] \!+\! m_{2} (\theta_{2} \!-\! \phi) [r] ] . \label{expression_W} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq90.png) (21)In Eq. (21), the boundaries of the integral are given by the pericentre rp and apocentre ra associated with the action J. Such an expression underlines the reason why (rp,ra) appear naturally as good coordinates to describe the 2D action space. One can note that Eq. (21) involves an integral over r thanks to the change of variables θ1 → r, which satisfies
(21)In Eq. (21), the boundaries of the integral are given by the pericentre rp and apocentre ra associated with the action J. Such an expression underlines the reason why (rp,ra) appear naturally as good coordinates to describe the 2D action space. One can note that Eq. (21) involves an integral over r thanks to the change of variables θ1 → r, which satisfies 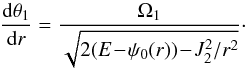 (22)In Eq. (21), θ1 [ r ] and (θ2 − φ) [ r ] only depend on r via the mappings from Eq. (19). Provided that
(22)In Eq. (21), θ1 [ r ] and (θ2 − φ) [ r ] only depend on r via the mappings from Eq. (19). Provided that 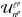 is a real function, the coefficients
is a real function, the coefficients 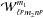 are always real. Because these coefficients involve two intricate integrals, they are numerically expensive to compute. However by parity, they obey
are always real. Because these coefficients involve two intricate integrals, they are numerically expensive to compute. However by parity, they obey 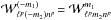 , which offers a significant reduction of the number of coefficients to compute.
, which offers a significant reduction of the number of coefficients to compute.
3.2. Computation of the response matrix
We now have all the elements required to compute the response matrix from Eq. (5). In its definition, one should note the presence of an integral over the dummy variable J, which, as discussed previously, is performed in the 2D (rp,ra)-space. The first step is to go from J = (J1,J2) to (E,L). The Jacobian of this transformation is given by 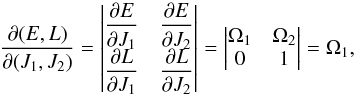 (23)so that one immediately has dJ1dJ2 = dEdL/Ω1. Given the expression (20) of the 2D Fourier transformed basis elements, the response matrix may be written as
(23)so that one immediately has dJ1dJ2 = dEdL/Ω1. Given the expression (20) of the 2D Fourier transformed basis elements, the response matrix may be written as 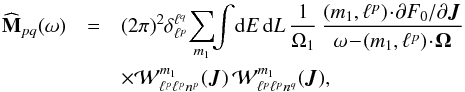 (24)where the sum on m2 has been executed using the Kronecker delta from Eq. (20). Moreover, we dropped the conjugate over
(24)where the sum on m2 has been executed using the Kronecker delta from Eq. (20). Moreover, we dropped the conjugate over 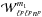 since the latter is always real. We may now perform the change of variables (E,L) → (rp,ra), so as to rewrite Eq. (24) as
since the latter is always real. We may now perform the change of variables (E,L) → (rp,ra), so as to rewrite Eq. (24) as 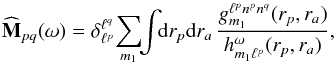 (25)where the functions
(25)where the functions 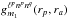 and
and 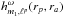 are respectively given by
are respectively given by ![\begin{eqnarray} g_{m_{1}}^{\ell^{p} n^{p} n^{q}} (r_{p} , r_{a})& = & \, (2 \pi)^{2} \bigg| \frac{\partial (E,L)}{\partial (r_{p} , r_{a})} \bigg| \, \frac{1}{\Omega_{1}} \bigg[ (m_{1} , \ell^{p}) \!\cdot\! \frac{\partial F_{0}}{\partial \bm{J}} \bigg] \nonumber \\ && \times \mathcal{W}^{m_{1}}_{\ell^{p} \ell^{p} n^{p}} (\bm{J}) \, \mathcal{W}^{m_{1}}_{\ell^{p} \ell^{p} n^{q}} (\bm{J}) , \label{definition_g} \end{eqnarray}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq112.png) (26)and
(26)and 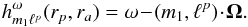 (27)It is important to note here that the response matrix is diagonal with respect to the ℓp and ℓq indices so that each ℓ may be treated independently. The definition of the function g from Eq. (26) involves the Jacobian ∂(E,L) /∂(rp,ra) of the transformation (E,L) → (rp,ra) which can be immediately computed from the expressions (15) of E = E(rp,ra) and L = L(rp,ra). Moreover, in some situations, the DF F = F(J), may also rather be defined as F = F(E,L). It is straightforward to show that one has
(27)It is important to note here that the response matrix is diagonal with respect to the ℓp and ℓq indices so that each ℓ may be treated independently. The definition of the function g from Eq. (26) involves the Jacobian ∂(E,L) /∂(rp,ra) of the transformation (E,L) → (rp,ra) which can be immediately computed from the expressions (15) of E = E(rp,ra) and L = L(rp,ra). Moreover, in some situations, the DF F = F(J), may also rather be defined as F = F(E,L). It is straightforward to show that one has ![\begin{equation} \bm{m} \!\cdot\! \frac{\partial F}{\partial \bm{J}} = m_{1} \Omega_{1} \bigg( \frac{\partial F}{\partial E} \bigg)_{L} \!+ m_{2} \left[ \Omega_{2} \bigg( \frac{\partial F}{\partial E} \bigg)_{L} \!+ \bigg( \frac{\partial F}{\partial L} \bigg)_{E} \right] \cdot \label{calculation_m.dF/dJ} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq123.png) (28)
(28)
3.3. Sub-region integration
The next step in the calculation is to perform the remaining integration over (rp,ra) from Eq. (25). Because of the presence of the resonant pole 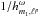 , such a numerical integration has to be performed carefully. We cut the integration domain (rp,ra) into various subregions indexed by i. The ith-region is centred around the position
, such a numerical integration has to be performed carefully. We cut the integration domain (rp,ra) into various subregions indexed by i. The ith-region is centred around the position 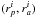 and corresponds to the square domain such that
and corresponds to the square domain such that ![\hbox{${r_{p} \!\in\! [r_{p}^{i} - \Delta r / 2 \,;\, r_{p}^{i} \!+\! \Delta r / 2 ]}$}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq127.png) and
and ![\hbox{$ r_{a} \!\in\! [r_{a}^{i} - \Delta r / 2;\, r_{a}^{i} \!+\! \Delta r / 2 ] $}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq128.png) , where Δr corresponds to the size of the subregions. The smaller Δr, the better the approximated estimations of the response matrix. Within the ith-region, one can write first-order Taylor expansions of the functions g and h from Eqs. (26) and (27) around the centre
, where Δr corresponds to the size of the subregions. The smaller Δr, the better the approximated estimations of the response matrix. Within the ith-region, one can write first-order Taylor expansions of the functions g and h from Eqs. (26) and (27) around the centre 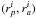 of the region such that
of the region such that 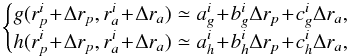 (29)where for convenience we shortened the index dependences from Eqs. (26) and (27). The coefficients
(29)where for convenience we shortened the index dependences from Eqs. (26) and (27). The coefficients 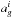 ,
, 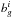 and
and 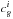 (similarly for h) are given by
(similarly for h) are given by 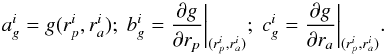 (30)In the numerical implementation, the coefficients involving partial derivatives are estimated by finite differences, so that one has for instance
(30)In the numerical implementation, the coefficients involving partial derivatives are estimated by finite differences, so that one has for instance 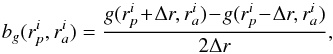 (31)which allows us to minimise the number of evaluations of g required. The approximated integration on each sub-region can then be performed and takes the form
(31)which allows us to minimise the number of evaluations of g required. The approximated integration on each sub-region can then be performed and takes the form 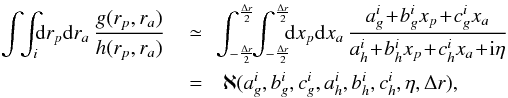 (32)where ℵ is an analytical function which only depends on the coefficients obtained in the limited developments from Eq. (29). In order to have a well-defined integral, we added an imaginary part η> 0 to the temporal frequency ω, so that ω = ω0 + iη. When looking for unstable modes in a disc, this imaginary part η corresponds to the growth rate of the mode. It is also crucial to note here that one always has
(32)where ℵ is an analytical function which only depends on the coefficients obtained in the limited developments from Eq. (29). In order to have a well-defined integral, we added an imaginary part η> 0 to the temporal frequency ω, so that ω = ω0 + iη. When looking for unstable modes in a disc, this imaginary part η corresponds to the growth rate of the mode. It is also crucial to note here that one always has 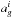 ,
, 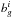 ,
, 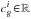 , and similarly
, and similarly 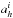 ,
, 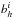 ,
, 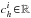 . The effective computation of the function ℵ is presented in Appendix B. Thanks to Eq. (32), the expression (25) becomes
. The effective computation of the function ℵ is presented in Appendix B. Thanks to Eq. (32), the expression (25) becomes 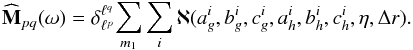 (33)In the previous expression, in order to effectively compute numerically the sum on m1, we introduce a bound
(33)In the previous expression, in order to effectively compute numerically the sum on m1, we introduce a bound 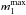 , so that the sum is only reduced to
, so that the sum is only reduced to 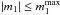 . Because of the requirement to truncate the action space in various subregions as in Eq. (33), the computation of the response matrix still remains a daunting task, to ensure appropriate numerical convergence. In Appendix C, we detail the validation of our implementation of the response matrix calculation by recovering known unstable modes of truncated Mestel discs (Zang 1976; Evans & Read 1998b; Sellwood & Evans 2001). Once the response matrix
. Because of the requirement to truncate the action space in various subregions as in Eq. (33), the computation of the response matrix still remains a daunting task, to ensure appropriate numerical convergence. In Appendix C, we detail the validation of our implementation of the response matrix calculation by recovering known unstable modes of truncated Mestel discs (Zang 1976; Evans & Read 1998b; Sellwood & Evans 2001). Once the response matrix  is known, the determination of the dressed susceptibility coefficients
is known, the determination of the dressed susceptibility coefficients 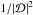 from Eq. (4) involves a straightforward summation1.
from Eq. (4) involves a straightforward summation1.
3.4. Critical resonant line
The resonance condition encapsulated in the Dirac delta δD(m1·Ω1 − m2·Ω2) generates an additional difficulty in the calculation of the Balescu-Lenard drift and diffusion coefficients from Eqs. (8) and (9). Recall the definition of the composition of a Dirac delta, and a function (Hörmander 2003), which in a d-dimensional setup takes the form 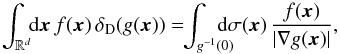 (34)where g-1(0) = {x | g(x) = 0 } is the hyper-surface of dimension (generically) (d − 1) defined by the constraint g(x) = 0, and dσ(x) is the surface measure on g-1(0). We have also naturally defined the euclidean norm of the gradient of g as
(34)where g-1(0) = {x | g(x) = 0 } is the hyper-surface of dimension (generically) (d − 1) defined by the constraint g(x) = 0, and dσ(x) is the surface measure on g-1(0). We have also naturally defined the euclidean norm of the gradient of g as  . Here we assumed that the resonance condition associated with the function g(J2) = m1·Ω1 − m2·Ω2 is non-degenerate, so that ∀x ∈ g-1(0), | ∇g(x) | > 0, which also ensures that the dimension of the set g-1(0) is (d − 1). One should note that this degeneracy condition is not satisfied by the Keplerian or harmonic potentials. Because we are considering an infinitely thin disc, the dimension of the physical space is given by d = 2, so that the set g-1(0) takes the form of a curve γ, that we call the critical resonant curve. Generically, it takes the form of an application of the type
. Here we assumed that the resonance condition associated with the function g(J2) = m1·Ω1 − m2·Ω2 is non-degenerate, so that ∀x ∈ g-1(0), | ∇g(x) | > 0, which also ensures that the dimension of the set g-1(0) is (d − 1). One should note that this degeneracy condition is not satisfied by the Keplerian or harmonic potentials. Because we are considering an infinitely thin disc, the dimension of the physical space is given by d = 2, so that the set g-1(0) takes the form of a curve γ, that we call the critical resonant curve. Generically, it takes the form of an application of the type 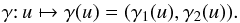 (35)One can then immediately compute the r.h.s. of Eq. (34) via
(35)One can then immediately compute the r.h.s. of Eq. (34) via 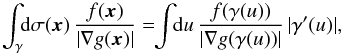 (36)where we have naturally defined
(36)where we have naturally defined 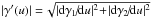 .
.
As noted in Eq. (15), using the pericentres and apocentres (rp,ra), given the Jacobian from Eq. (23) and proceeding in the same way as in Eq. (25) for the response matrix, one may rewrite the drift and diffusion coefficients from Eqs. (8) and (9) as 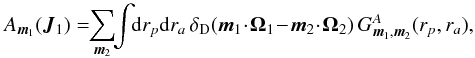 (37)and
(37)and 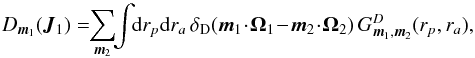 (38)where the functions
(38)where the functions 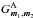 and
and 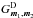 are respectively defined as
are respectively defined as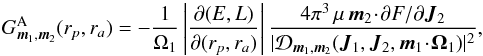 (39)and
(39)and 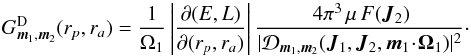 (40)For a given value of J1, m1 and m2, and introducing ω1 = m1·Ω1, we define the critical curve γm2(ω1) as
(40)For a given value of J1, m1 and m2, and introducing ω1 = m1·Ω1, we define the critical curve γm2(ω1) as 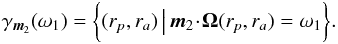 (41)The expressions (37) and (38) of the drift and diffusion coefficients immediately become
(41)The expressions (37) and (38) of the drift and diffusion coefficients immediately become 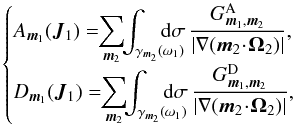 (42)where the resonant contribution | ∇(m2·Ω2) | is defined as
(42)where the resonant contribution | ∇(m2·Ω2) | is defined as ![\begin{equation} | \nabla (\bm{m}_{2} \!\cdot\! \bm{\Omega}_{2}) | = \sqrt{\bigg[ \bm{m}_{2} \!\cdot\! \frac{\partial \bm{\Omega}_{2}}{\partial r_{p}} \bigg]^{2} \!+\! \bigg[ \bm{m}_{2} \!\cdot\! \frac{\partial \bm{\Omega}_{2}}{\partial r_{a}} \bigg]^{2} } \cdot \label{definition_nabla_Omega} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq183.png) (43)The derivatives of the intrinsic frequencies with respect to rp and ra appearing in Eq. (43) are computed as in Eq. (31) using finite differences. Once the critical lines of resonances have been determined, the computation of the drift and diffusion coefficients from Eq. (42) is straightforward, so that the full secular diffusion flux ℱtot from Eq. (10) may be determined.
(43)The derivatives of the intrinsic frequencies with respect to rp and ra appearing in Eq. (43) are computed as in Eq. (31) using finite differences. Once the critical lines of resonances have been determined, the computation of the drift and diffusion coefficients from Eq. (42) is straightforward, so that the full secular diffusion flux ℱtot from Eq. (10) may be determined.
4. Balescu-Lenard flux divergences
We may now illustrate how the previous computations of the response matrix and the Balescu-Lenard drift and diffusion coefficients can be used to recover some results obtained in well-crafted numerical simulations of galactic discs. Indeed, Sellwood (2012; hereafter S12), studied the long-term evolution of an isolated stable truncated Mestel disc (Mestel 1963). After letting the disc evolve for hundreds of dynamical times, S12 observed a secular diffusion of the disc’s DF in action space, through the spontaneous generation of transient spiral waves. The most striking result of this evolution is given in Fig. 7 of S12, which exhibits the late time formation of a resonant ridge in action space along a specific resonant direction. Such diffusion features observed in the late evolution of an isolated, stable, and discrete system are thought to be signatures of a secular evolution induced by finite-N effects, as described by the Balescu-Lenard formalism. Because the system is made of a finite number N of pointwise particles, it undergoes (long-range) resonant encounters leading to an irreversible secular evolution. In order to investigate such a collisional evolution, Paper I applied the WKB limit of the Balescu-Lenard formalism to S12’s simulation. While most of the secular diffusion was qualitatively recovered, there remained a significant timescale discrepancy, since the typical timescale diffusion predicted by this approach was typically 103 times too slow compared to the observations made in S12. The use of a non-local basis such as Eq. (16) and the numerical computation of the response matrix from Eq. (24) allows us to incorporate in the present paper these previously ignored contributions from the WKB approach. In the upcoming sections, we therefore present briefly the disc considered by S12 and our determination of the secular diffusion flux predicted by the Balescu-Lenard formalism.
4.1. Initial setup
We consider the same disc as presented in Sellwood (2012). It is an infinitely thin Mestel disc for which the circular speed vφ is a constant V0 independent of the radius. The stationary background potential ψM and its associated surface density ΣM are given by ![\begin{equation} \psi_{\rm M} (R) = V_{0}^{2} \log \!\left[\! \frac{R}{R_{\rm max}} \!\right] ; \;\;\; \Sigma_{\rm M} (R) = \frac{V_{0}^{2}}{2 \pi G R}, \label{psi_Mestel_Sigma_Mestel} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq189.png) (44)where Rmax is a scale parameter of the disc. Following Toomre (1977), Binney & Tremaine (2008), a self-consistent DF for this system is given by
(44)where Rmax is a scale parameter of the disc. Following Toomre (1977), Binney & Tremaine (2008), a self-consistent DF for this system is given by ![\begin{equation} F_{\rm M} (E , J_{\phi}) = C_{\rm M} \, J_{\phi}^{q} \, \exp \left[ - E / \sigma_{r}^{2}\right] , \label{DF_Toomre} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq191.png) (45)where the exponent q is given by
(45)where the exponent q is given by 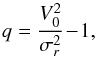 (46)with σr being the constant radial velocities spread within the disc. In Eq. (45), CM is a normalisation constant given by
(46)with σr being the constant radial velocities spread within the disc. In Eq. (45), CM is a normalisation constant given by ![\begin{equation} C_{\rm M} = \frac{V_{0}^{2}}{2^{1 + q/2} \, \pi^{3/2} \, G \, \sigma_{r}^{q+2} \, \Gamma \big[ \frac{1}{2} \!+\! \frac{q}{2} \big] \, R_{\rm max}^{q+1} } \cdot \label{definition_C_Toomre} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq196.png) (47)In order to deal with the central singularity of the Mestel disc along with its infinite extent, we introduce two tapering functions
(47)In order to deal with the central singularity of the Mestel disc along with its infinite extent, we introduce two tapering functions ![\begin{equation} \begin{cases} \displaystyle T_{\rm inner} (J_{\phi}) = \frac{J_{\phi}^{\nu_{\rm t}}}{(R_{\rm i} V_{0})^{\nu_{\rm t}} \!+\! J_{\phi}^{\nu_{\rm t}} } , \\ \displaystyle T_{\rm outer} (J_{\phi}) = \bigg[ 1 \!+\! \bigg[ \frac{J_{\phi}}{R_{0} V_{0}} \bigg]^{\mu_{\rm t}} \bigg]^{-1} , \end{cases} \label{definition_tapering} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq197.png) (48)where the indices νt and μt control the sharpness of the two tapers, while the radii Ri and R0 are two scale parameters. These tapers Tinner and Touter respectively represent the bulge and the outer truncation of the disc. In addition to these taperings, we also suppose that only a fraction ξ of the stellar disc is self-gravitating, with 0 ≤ ξ ≤ 1, while the rest of the gravitational potential is provided by the static halo. As a consequence, the active distribution function Fstar is given by
(48)where the indices νt and μt control the sharpness of the two tapers, while the radii Ri and R0 are two scale parameters. These tapers Tinner and Touter respectively represent the bulge and the outer truncation of the disc. In addition to these taperings, we also suppose that only a fraction ξ of the stellar disc is self-gravitating, with 0 ≤ ξ ≤ 1, while the rest of the gravitational potential is provided by the static halo. As a consequence, the active distribution function Fstar is given by 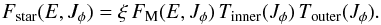 (49)We place ourselves in the same units system as in S12, so that we have V0 = G = Ri = 1. The other numerical factors are given by q = 11.4, νt = 4, μt = 5, ξ = 0.5, R0 = 11.5, and Rmax = 20. The contours of the tapered DF Fstar are illustrated in Fig. 1. At this stage, it is important to note that S12 restricted the perturbations forces to the harmonic sector mφ = 2, so that we may use the same restriction on the considered azimuthal number mφ. As a consequence, in the double resonance sum on m1 and m2 present in the Balescu-Lenard flux from Eq. (2), we assume that m1 and m2 belong to the restricted set {mr,mφ } ∈ {(−1,2),(0,2),(1,2) }, where (mr,mφ) = (−1,2) corresponds to the Inner Lindblad resonance (ILR), (mr,mφ) = (0,2) to the Corotation resonance (COR), and (mr,mφ) = (1,2) to the Outer Lindblad Resonance (OLR). All the upcoming calculations have also been performed while taking into account the contributions from the resonances associated with mr = ± 2, which were checked to be largely subdominant.
(49)We place ourselves in the same units system as in S12, so that we have V0 = G = Ri = 1. The other numerical factors are given by q = 11.4, νt = 4, μt = 5, ξ = 0.5, R0 = 11.5, and Rmax = 20. The contours of the tapered DF Fstar are illustrated in Fig. 1. At this stage, it is important to note that S12 restricted the perturbations forces to the harmonic sector mφ = 2, so that we may use the same restriction on the considered azimuthal number mφ. As a consequence, in the double resonance sum on m1 and m2 present in the Balescu-Lenard flux from Eq. (2), we assume that m1 and m2 belong to the restricted set {mr,mφ } ∈ {(−1,2),(0,2),(1,2) }, where (mr,mφ) = (−1,2) corresponds to the Inner Lindblad resonance (ILR), (mr,mφ) = (0,2) to the Corotation resonance (COR), and (mr,mφ) = (1,2) to the Outer Lindblad Resonance (OLR). All the upcoming calculations have also been performed while taking into account the contributions from the resonances associated with mr = ± 2, which were checked to be largely subdominant.
 |
Fig. 1 Contours of the initial distribution function Fstar from Eq. (49), in action space (Jφ,Jr). The contours are spaced linearly between 95% and 5% of the distribution function maximum. |
4.2. Initial drift and diffusion
As detailed in Eq. (33), the computation of the response matrix requires to consider a grid in the (rp,ra)-space. We considered a grid such that 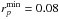 ,
, 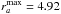 and Δr = 0.05. The sum on m1 appearing in Eq. (33) was reduced to
and Δr = 0.05. The sum on m1 appearing in Eq. (33) was reduced to 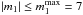 . The basis considered was Kalnajs 2D basis (Kalnajs 1976) with the parameters kKa = 7 and RKa = 5. One should note that despite having a disc which extends up to Rmax = 20, one can still consider a basis truncated at such a small RKa, so as to be able to efficiently capture the diffusion properties of the system in its inner regions, from where the secular diffusion is known to start. The radial basis elements were restricted to 0 ≤ n ≤ 8. When evaluating the response matrix, as in Eq. (32), one has to add a small imaginary part η to the frequency so as to regularise the resonant denominator. Throughout the calculations presented below, we considered η = 10-4 and checked that this choice had no impact on our results.
. The basis considered was Kalnajs 2D basis (Kalnajs 1976) with the parameters kKa = 7 and RKa = 5. One should note that despite having a disc which extends up to Rmax = 20, one can still consider a basis truncated at such a small RKa, so as to be able to efficiently capture the diffusion properties of the system in its inner regions, from where the secular diffusion is known to start. The radial basis elements were restricted to 0 ≤ n ≤ 8. When evaluating the response matrix, as in Eq. (32), one has to add a small imaginary part η to the frequency so as to regularise the resonant denominator. Throughout the calculations presented below, we considered η = 10-4 and checked that this choice had no impact on our results.
 |
Fig. 2 Illustration of 4 different critical resonant lines in the (rp,ra)-space. As defined in Eq. (41), a critical line is characterised by the resonant vectors m1, m2 and a location |
Since the total potential ψM is known via Eq. (44), the mapping to the angle-action coordinates is completely determined. The two intrinsic frequencies of the system can then be computed on the (rp,ra)-grid via Eqs. (13) and (14). Once these frequencies are known, the critical resonant lines introduced in Eq. (41) can be determined and are illustrated in Fig. 2. It is along these lines that one has to perform the integration present in the definitions of the drift and diffusion coefficients from Eq. (42).
Thanks to this expression, one can then compute the secular diffusion flux ℱtot defined in Eq. (11). Because the mass of the particles is given by μ = Mtot/N, it is natural to consider the quantity Nℱtot which is independent of N. The vector field −Nℱtot = −(NℱJφ,NℱJr), which represents the direction of diffusion of individual particles, is illustrated in Fig. 3. One can already note in Fig. 3 that the diffusion vector field is along a narrow resonant direction. Along this ridge, one typically has ℱJφ ≃ −2ℱJr, so the diffusion appears as aligned with the direction of the ILR resonance given by mILR = (2,−1).
 |
Fig. 3 Map of −Nℱtot, where the flux has been computed with m1,m2 ∈ {mILR,mCOR,mOLR}. Following Eq. (11), −Nℱtot corresponds to the direction of diffusion of individual particles in action-space. |
 |
Fig. 4 Left panel: map of Ndiv(ℱtot), where the total flux has been computed with m1,m2 ∈ {mILR,mCOR,mOLR}. Red contours, for which Ndiv(ℱtot) < 0 are associated with regions from which the orbits will be depleted, whereas blue contours, for which Ndiv(ℱtot) > 0 correspond to regions where the value of the DF will be increased during the secular diffusion. The contours are spaced linearly between the minimum and the maximum of Ndiv(ℱtot). The maximum value for the positive blue contours corresponds to Ndiv(ℱtot) ≃ 350, while the mininum value for the negative red contours is associated with Ndiv(ℱtot) ≃ −250. Right panel: from Sellwood (2012) – Fig. 7, contours of the change in the DF between the time tS12 = 1400 and tS12 = 0, for a run with 50M particles. Similarly to the left panel, red contours correspond to negative differences, i.e. regions emptied from their orbits, while blue contours correspond to positive differences, i.e. regions where the DF has increased during the diffusion. Both of these contours are aligned with the ILR direction of mILR = (2,−1) in the (Jφ,Jr)-plane, corresponding to the cyan line. |
Once the diffusion flux Nℱtot has been obtained, one can compute the divergence of this flux, to determine the regions for which the DF is expected to change during the secular diffusion. Figure 4 illustrates the contours of Ndiv(ℱtot). In Fig. 4, we obtained that the Balescu-Lenard formalism indubitably predicts the formation of a narrow resonant ridge aligned with the ILR-direction, as was observed in S12’s simulation. One also recovers that the stars which will populate the resonant ridge originate from the base of the ridge and diffuse along the direction associated with the ILR resonance. It is most likely that the slight shift in the position of the ridge is due to the fact that the Balescu-Lenard prediction was carried at t = 0+, while S12’s measurements are at t = 1400, so that we do not expect a perfect match. Other sources of discrepancies might be the use of a softening length in numerical simulations, which modifies the two-body interaction potential, or the difference between an ensemble average (as predicted by the secular formalism) and one specific realisation – our own simulations suggest that there is some variation in the position of the ridge between one run and another. Because we explicitly determined the value of Ndiv(ℱtot), we may now study the typical timescale of collisional relaxation predicted by this Balescu-Lenard estimation as detailed in Sect. 4.3. One may also investigate the respective roles of the self-gravitating amplification and the limitation to the tightly wound basis elements as presented in Appendices D.1 and D.2.
4.3. Timescale of diffusion
The most significant disagreement found in Paper I, while applying the WKB approximation of the Balescu-Lenard equation to S12’s simulation was a discrepancy between the time required to observe the resonant ridge in S12’s simulation and the collisional timescale for which the finite-N effects come into play. As already noted in Paper I, since the Balescu-Lenard Eq. (2) only depends on N through the mass of the individual particles μ = Mtot/N, we may rewrite it in the form ![\begin{equation} \frac{\partial F}{\partial t} = \frac{1}{N} C_{\rm BL} [F] , \label{BL_with_N} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq258.png) (50)where CBL [ F ] = Ndiv(ℱtot) is the N-independent Balescu-Lenard collisional operator, i.e. the r.h.s. of Eq. (2) multiplied by N = Mtot/μ. As expected, the larger the number of particles, the slower the secular evolution. This also illustrates the fact that the Balescu-Lenard equation comes from a kinetic Taylor expansion in the small parameter ε = 1 /N ≪ 1. We introduce the rescaled time τ = t/N, so that Eq. (50)reads
(50)where CBL [ F ] = Ndiv(ℱtot) is the N-independent Balescu-Lenard collisional operator, i.e. the r.h.s. of Eq. (2) multiplied by N = Mtot/μ. As expected, the larger the number of particles, the slower the secular evolution. This also illustrates the fact that the Balescu-Lenard equation comes from a kinetic Taylor expansion in the small parameter ε = 1 /N ≪ 1. We introduce the rescaled time τ = t/N, so that Eq. (50)reads ![\begin{equation} \frac{\partial F}{\partial \tau} = C_{\rm BL} [ F ] , \label{BL_with_tau} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq263.png) (51)letting us express the Balescu-Lenard equation without any explicit appearance of N. In Paper I, we estimated the time ΔτS12 required to observe the ridge as ΔτS12 ≃ 3 × 10-5. When performing the same measurement thanks to the contours of the diffusion flux div(ℱtot) computed within the WKB approximation, we obtained ΔτWKB ≃ 3 × 10-2, so that Paper I obtained the ratio ΔτS12/ ΔτWKB ≃ 10-3. This discrepancy was due to the limitation to tightly wound spirals. Because the estimation of the secular diffusion flux ℱtot presented in Fig. 4 was made using the matrix method (Kalnajs 1976) with a full basis, it captures the additional swing amplification. Indeed, given the map of Ndivℱtot obtained in Fig. 4, one may estimate the typical time ΔτBL required for such a flux to lead to the diffusion features observed in S12. The contours presented in Fig. 7 of S12 are separated by an increment equal to
(51)letting us express the Balescu-Lenard equation without any explicit appearance of N. In Paper I, we estimated the time ΔτS12 required to observe the ridge as ΔτS12 ≃ 3 × 10-5. When performing the same measurement thanks to the contours of the diffusion flux div(ℱtot) computed within the WKB approximation, we obtained ΔτWKB ≃ 3 × 10-2, so that Paper I obtained the ratio ΔτS12/ ΔτWKB ≃ 10-3. This discrepancy was due to the limitation to tightly wound spirals. Because the estimation of the secular diffusion flux ℱtot presented in Fig. 4 was made using the matrix method (Kalnajs 1976) with a full basis, it captures the additional swing amplification. Indeed, given the map of Ndivℱtot obtained in Fig. 4, one may estimate the typical time ΔτBL required for such a flux to lead to the diffusion features observed in S12. The contours presented in Fig. 7 of S12 are separated by an increment equal to 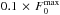 , where
, where 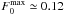 is the maximum of the normalised DF (via Eq. (49)). In order to observe the resonant ridge, the value of the DF should typically change by an amount of the order
is the maximum of the normalised DF (via Eq. (49)). In order to observe the resonant ridge, the value of the DF should typically change by an amount of the order 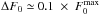 . From Fig. 4, one can note that the maximum of the divergence of the diffusion flux is given by | Ndiv(ℱtot) | max ≃ 350. Thanks to Eq. (11), one can immediately write the relation ΔF0 ≃ ΔτBL | Ndiv(ℱtot) | max, where ΔτBL is the time during which the Balescu-Lenard equation has to be evolved in order to develop a ridge. With the previous numerical values, one obtains ΔτBL ≃ 3 × 10-5. Comparing the numerically measured time ΔτS12 and the time ΔτBL predicted from the Balescu-Lenard equation, one obtains
. From Fig. 4, one can note that the maximum of the divergence of the diffusion flux is given by | Ndiv(ℱtot) | max ≃ 350. Thanks to Eq. (11), one can immediately write the relation ΔF0 ≃ ΔτBL | Ndiv(ℱtot) | max, where ΔτBL is the time during which the Balescu-Lenard equation has to be evolved in order to develop a ridge. With the previous numerical values, one obtains ΔτBL ≃ 3 × 10-5. Comparing the numerically measured time ΔτS12 and the time ΔτBL predicted from the Balescu-Lenard equation, one obtains 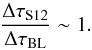 (52)As expected, the projection of the response over an unbiased basis leads to over a hundredfold increase of the susceptibility of the disc and therefore to a very significant acceleration of secular diffusion. Thanks to this mechanism, we now find a very good agreement between the diffusion timescales observed in numerical simulations and the predictions from the Balescu-Lenard formalism. This quantitative match is rewarding, both from the point of view of the accuracy of the integrator (symplecticity, timestep size, softening...), and from the relevance of the successive approximations underpinning the Balescu-Lenard formalism (timescale decoupling, truncation of the BBGKY hierarchy, neglect of the close encounter term ...).
(52)As expected, the projection of the response over an unbiased basis leads to over a hundredfold increase of the susceptibility of the disc and therefore to a very significant acceleration of secular diffusion. Thanks to this mechanism, we now find a very good agreement between the diffusion timescales observed in numerical simulations and the predictions from the Balescu-Lenard formalism. This quantitative match is rewarding, both from the point of view of the accuracy of the integrator (symplecticity, timestep size, softening...), and from the relevance of the successive approximations underpinning the Balescu-Lenard formalism (timescale decoupling, truncation of the BBGKY hierarchy, neglect of the close encounter term ...).
In Appendix D, we show that when considering either Fig. D.1, for which the self-gravity of the system has been turned off, or Fig. D.3 for which the loosely wound basis elements were not taken into account, one does not recover a narrow resonant ridge appearing on timescales compatible with S12’s simulations. Therefore, the main source of secular collisional diffusion oberved in S12 and recovered in Fig. 4 has to be the strong self-gravitating amplification of loosely wound perturbations, i.e. a sequence of uncorrelated swing amplified spirals sourced by finite-N effects is indeed the main driver of secular diffusion. The WKB formalism from Paper I identified correctly the family of orbits involved, but fell short in predicting how narrow the resonant ridge is and how strongly amplified the response is.
5. Comparison to N-body simulations
In Paper I, we relied on simulations presented in Sellwood (2012) to compare the divergence of the diffusion flux to the WKB prediction. In order to probe the expected scalings with the number of particles or with the active fraction of the disc, we now resort to our own N-body simulations.
5.1. N-body integration
The initial sampling of particles is critical when investigating the origin of secular evolution, as one must ensure that the disc is initially in a state of equilibrium. The sampling strategy we implemented is described in some detail in Appendix E.
Once sampled, we evolve the initial conditions using a straightforward particle-mesh N-body code with a single-timestep leapfrog integrator (e.g. Binney & Tremaine 2008, Sect. 3.4.1). We follow S12 and split the potential in which the particles move into two parts: (i) an axisymmetric contribution ψM from the unperturbed Mestel disc, as in Eq. (44), and (ii) a non-axisymmetric contribution ψ1(R,φ) that develops as perturbations grow in the disc. This splitting avoids difficulties in the treatment of the rigid component of the potential that is not included in the DF, due to the tapering functions and active fraction introduced in Eq. (49). We calculate ψ1 using cloud-in-cell interpolation (e.g. Binney & Tremaine 2008, Sect. 2.9.3) of the particles’ masses onto an Nmesh × Nmesh mesh of square cells spaced Δx apart, then filtering the resulting density field ρ(x,y) to isolate the disc response (see below), before applying the usual Fourier-space “doubling up” procedure to obtain the potential ψ1 at the cell vertices. The contribution of ψ1 to each particle’s acceleration is then obtained using the same cloud-in-cell interpolation scheme.
When computing the density mesh, we added a filtering scheme to include only the mφ = 2 disc response, similarly to what was considered in S12. We isolate this mφ = 2 mode by calculating 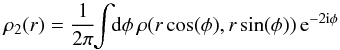 (53)immediately after the cloud-in-cell assignment of mass to the mesh at each timestep, then imposing the new mesh mass distribution
(53)immediately after the cloud-in-cell assignment of mass to the mesh at each timestep, then imposing the new mesh mass distribution 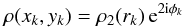 (54)with (rk,φk) chosen according to (xk,yk) = (rkcos(φk), rksin(φk)). To obtain ρ2(r) we use brute-force computation of Eq. (53) on a series of Nring radial rings with spacing Δr ≪ Δx, using the trapezium rule with Nφ = 720 points in φ for the angular integrals. These models are designed to reproduce as closely as possible the essential details of S12’s simulations. There are a couple of deliberate technical differences: S12 uses a polar mesh to obtain ψ1, whereas we use a cartesian mesh with a mφ = 2 prefiltering of the density field; S12 has a block timestep scheme instead of our simpler single-timestep one.
(54)with (rk,φk) chosen according to (xk,yk) = (rkcos(φk), rksin(φk)). To obtain ρ2(r) we use brute-force computation of Eq. (53) on a series of Nring radial rings with spacing Δr ≪ Δx, using the trapezium rule with Nφ = 720 points in φ for the angular integrals. These models are designed to reproduce as closely as possible the essential details of S12’s simulations. There are a couple of deliberate technical differences: S12 uses a polar mesh to obtain ψ1, whereas we use a cartesian mesh with a mφ = 2 prefiltering of the density field; S12 has a block timestep scheme instead of our simpler single-timestep one.
For the results presented here we used a timestep Δt = 10-3Ri/V0 on a mesh that extends to ± Rmax = 20 Ri with Nmesh = 120 cells, so that Δx = Ri/ 3. The filtering of the potential perturbations to the harmonic sector mφ = 2 was performed with Nring = 1000 radial rings, so that Δr = 2 Ri/ 100, and Nφ = 720 points in the azimuthal direction. Finally, the computation of the potential from the density via Fourier transform was performed with a softening length ε = Ri/ 6, comparable to the value used in Sellwood (2012), which considered a Plummer softening with ε = Ri/ 8. The results are not significantly changed when we halve the timestep or the mesh size. In Appendix C, we detail the validation of our N-body code by recovering known unstable modes of truncated Mestel discs (Zang 1976; Evans & Read 1998b; Sellwood & Evans 2001).
5.2. Scaling with N
In order to rid our measurements of individual fluctuations, we run multiple simulations for the same number of particles and perform an ensemble average of different evolution realisations for the same number of particles. This procedure allows us to estimate only the mean evolution, which is effectively what is described by the Balescu-Lenard formalism.
In order to study the scaling with N of these numerical simulations, one has to extract from the simulations a quantity on which to test this scaling and compare it with the predictions from the Balescu-Lenard formalism. The statistical nature of the initial sampling presents an additional difficulty. Indeed, because one only samples N stars as described in Appendix E, the initial effective DF fluctuates around the smooth background DF from Eq. (49) as a Poisson shot noise. These statistical fluctuations originate from the initial sampling and are not as such specific to the physical process captured by the Balescu-Lenard formalism, so that one should carefully disentangle these two contributions. Hence we introduce the function 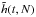 defined as
defined as 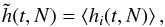 (55)where the operator ⟨·⟩ corresponds to the ensemble average, approximated here with the arithmetic average over the p = 32 different realisations of simulations for the same number of particles, indexed by i:
(55)where the operator ⟨·⟩ corresponds to the ensemble average, approximated here with the arithmetic average over the p = 32 different realisations of simulations for the same number of particles, indexed by i: 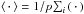 . In Eq. (55) the function hi(t,N) is a lag function which reads
. In Eq. (55) the function hi(t,N) is a lag function which reads ![\begin{equation} h_{i} (t ,N) = \!\! \int \!\! \mathrm{d} \bm{J} \, \left[ F_{i} (t ,\bm{J} , N) \!-\! \left\langle F (t = 0 , \bm{J} , N) \right\rangle\right]^{2} , \label{definition_hi_N} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq309.png) (56)where we defined as Fi(t,J,N) the normalised DF of the ith realisation for a number N of particles. Such a quantity is designed to quantify the “distance” between the initial mean DF ⟨F(t = 0)⟩ and the evolved DF Fi. We are interested in the early time behaviour of the lag function h from Eq. (55), so that we may perform its Taylor expansion
(56)where we defined as Fi(t,J,N) the normalised DF of the ith realisation for a number N of particles. Such a quantity is designed to quantify the “distance” between the initial mean DF ⟨F(t = 0)⟩ and the evolved DF Fi. We are interested in the early time behaviour of the lag function h from Eq. (55), so that we may perform its Taylor expansion 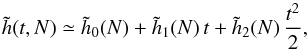 (57)where it is important to note that the coefficients
(57)where it is important to note that the coefficients 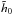 ,
, 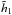 and
and 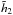 depend only on N. Let us now estimate each of these coefficients in turn. Thanks to Eq. (56), one can compute
depend only on N. Let us now estimate each of these coefficients in turn. Thanks to Eq. (56), one can compute 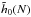 which reads
which reads ![\begin{equation} \tilde{h}_{0} (N) = \!\! \int \!\! \mathrm{d} \bm{J} \, \left\langle \left[ F \!-\! \left\langle F_{0} \right\rangle \right]^{2} \right\rangle , \label{calculation_h0} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq318.png) (58)where we used the shortened notations ⟨F0⟩ = ⟨F(t = 0,J,N)⟩ and F = F(t = 0,J,N). We note that this coefficient only depends on the properties of the initial sampling, and not on its dynamics. Because discrete sampling obeys Poisson statistics, one can write
(58)where we used the shortened notations ⟨F0⟩ = ⟨F(t = 0,J,N)⟩ and F = F(t = 0,J,N). We note that this coefficient only depends on the properties of the initial sampling, and not on its dynamics. Because discrete sampling obeys Poisson statistics, one can write 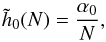 (59)where α0 is a constant independent of N. One may then compute
(59)where α0 is a constant independent of N. One may then compute 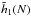 , which takes the form
, which takes the form ![\begin{equation} \tilde{h}_{1} (N) = 2 \!\! \int \!\! \mathrm{d} \bm{J} \, \left\langle \left[ F \!-\! \left\langle F_{0} \right\rangle \right] F' \right\rangle , \label{calculation_h1} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq324.png) (60)where we used the shortened notation F′ = [ ∂F/∂t ] (t = 0). One should note that the terms appearing in Eq. (60) have two different physical contents. Indeed, the term [F − ⟨F0⟩] involves the initial sampling, whereas F′ is driven by the dynamics of the system. If we assume that the sampling and the system’s dynamics are uncorrelated, one writes
(60)where we used the shortened notation F′ = [ ∂F/∂t ] (t = 0). One should note that the terms appearing in Eq. (60) have two different physical contents. Indeed, the term [F − ⟨F0⟩] involves the initial sampling, whereas F′ is driven by the dynamics of the system. If we assume that the sampling and the system’s dynamics are uncorrelated, one writes ![\begin{equation} \left\langle \left[ F \!-\! \left\langle F_{0} \right\rangle \right] F' \right\rangle = \left\langle F \!-\! \left\langle F_{0} \right\rangle \right\rangle \left\langle F' \right\rangle = 0 . \label{decorrelation_h1} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq328.png) (61)As a consequence, one immediately obtains from Eq. (60) that
(61)As a consequence, one immediately obtains from Eq. (60) that 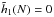 . One can finally compute the coefficient
. One can finally compute the coefficient 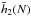 which reads
which reads ![\begin{equation} \tilde{h}_{2} (N) = 2 \!\! \int \!\! \mathrm{d} \bm{J} \, \left\langle \big[ F' \big]^{2} \!+\! \big[ F \!-\! \left\langle F_{0} \right\rangle \!\big] \, F '' \right\rangle , \label{calculation_h2} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq331.png) (62)where we used the shortened notation F′′ = [ ∂2F/∂t2 ] (t = 0). Using the same argument as in Eq. (61), we may get rid of the second term in the r.h.s. of Eq. (62). If we now also assume that the variance of [ F′ ] 2 is small compared to its expectation, one can write ⟨[ F′ ] 2⟩ = [⟨F′⟩]2, so that Eq. (62) becomes
(62)where we used the shortened notation F′′ = [ ∂2F/∂t2 ] (t = 0). Using the same argument as in Eq. (61), we may get rid of the second term in the r.h.s. of Eq. (62). If we now also assume that the variance of [ F′ ] 2 is small compared to its expectation, one can write ⟨[ F′ ] 2⟩ = [⟨F′⟩]2, so that Eq. (62) becomes ![\begin{equation} \tilde{h}_{2} (N) = 2 \!\! \int \!\! \mathrm{d} \bm{J} \, \left[ \left\langle F' \right\rangle \right]^{2} . \label{calculation_h2_II} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq335.png) (63)Now the dependence of the term ⟨F′⟩ with N follows from Eq. (50), so that one can write
(63)Now the dependence of the term ⟨F′⟩ with N follows from Eq. (50), so that one can write 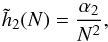 (64)where α2 is an amplitude independent of N. This scaling is a prediction from the Balescu-Lenard formalism. If the secular evolution observed in S12’s simulation was a Vlasov-only evolution, i.e. a collisionless evolution, one would expect a scaling of
(64)where α2 is an amplitude independent of N. This scaling is a prediction from the Balescu-Lenard formalism. If the secular evolution observed in S12’s simulation was a Vlasov-only evolution, i.e. a collisionless evolution, one would expect a scaling of 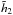 such that
such that 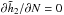 .
.
 |
Fig. 5 Illustration of the behaviour of the function |
 |
Fig. 6 Top panel: illustration of the behaviour of the function |
One may now compare these predictions to the scalings obtained from N-body runs. We considered number of particles given by N ∈ {8, 12, 16, 24, 32, 48, 64 } × 105, and for each of these values of N, we ran 32 different simulations with different initial conditions while using the N-body code described in Sect. 5.1. For each value of N, one may study the function 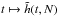 , as illustrated in Fig. 5. Once the behaviour of the function
, as illustrated in Fig. 5. Once the behaviour of the function 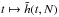 is known, one can fit these to parabolas as in Eq. (57), so as to determine the behaviour of the functions
is known, one can fit these to parabolas as in Eq. (57), so as to determine the behaviour of the functions 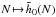 and
and 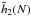 . The dependence with N of these coefficients is illustrated in Fig. 6. From the top panel of Fig. 6, we recover the scaling of
. The dependence with N of these coefficients is illustrated in Fig. 6. From the top panel of Fig. 6, we recover the scaling of 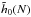 derived in Eq. (59) due to Poisson shot noise. The bottom panel of Fig. 6 displays the scaling
derived in Eq. (59) due to Poisson shot noise. The bottom panel of Fig. 6 displays the scaling 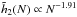 . Given the finite number of simulations considered and the uncertainties in the fits, this is in good agreement with the result presented in Eq. (64). This scaling of
. Given the finite number of simulations considered and the uncertainties in the fits, this is in good agreement with the result presented in Eq. (64). This scaling of 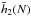 with N therefore confirms the relevance of the Balescu-Lenard formalism to describe the secular evolution of S12’s stable Mestel disc. Specifically, as explained below Eq. (64), if the features observed in S12’s simulation had only been the result of a collisionless mechanism, one would not have observed such a scaling of
with N therefore confirms the relevance of the Balescu-Lenard formalism to describe the secular evolution of S12’s stable Mestel disc. Specifically, as explained below Eq. (64), if the features observed in S12’s simulation had only been the result of a collisionless mechanism, one would not have observed such a scaling of 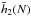 with N. This scaling confirms that the secular evolution of S12’s stable Mestel disc is the result of a collisional evolution seeded by the discrete nature of the system, and the effect of amplified distant resonant encounters. Another probe of the collisional scaling, which allows us to get rid of Poisson shot noise as present in Eq. (59), is described in Appendix F.
with N. This scaling confirms that the secular evolution of S12’s stable Mestel disc is the result of a collisional evolution seeded by the discrete nature of the system, and the effect of amplified distant resonant encounters. Another probe of the collisional scaling, which allows us to get rid of Poisson shot noise as present in Eq. (59), is described in Appendix F.
5.3. Scaling with ξ
Since the novelty of the Balescu-Lenard formalism is to capture the effect of gravitational polarisation, we now further compare qualitatively the prediction from Sect. 4 with the results obtained from numerical simulations, by studying the impact of the active fraction ξ of the disc on the observed properties of the secular diffusion. Indeed, as detailed in Sect. 4.1, the disc considered in S12 had an active fraction of ξ = 0.5, so only one half of the potential was due to the active component. If one increases the active fraction of the disc, one increases the strength of the self-gravitating amplification, and therefore accelerates the secular evolution of the disc, while still remaining in a regime of collisional evolution. Therefore the scaling of 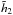 with N given by Eq. (64) remains the same, but the prefactor α2(ξ) increases because the secular evolution is amplified via a more efficient polarisation. The dependence of α2 with ξ can be both measured from N-body simulations but also predicted using the Balescu-Lenard formalism via the calculations presented in Sect. 4.2. Let us consider the same sets of simulations as in Sect. 5.2, so that the number of particles are given by N ∈ {8, 12, 16, 24, 32, 48, 64} × 105, and for each of these values of N, 32 different simulations with ξ = 0.6 are performed, in order to carry out ensemble averages.
with N given by Eq. (64) remains the same, but the prefactor α2(ξ) increases because the secular evolution is amplified via a more efficient polarisation. The dependence of α2 with ξ can be both measured from N-body simulations but also predicted using the Balescu-Lenard formalism via the calculations presented in Sect. 4.2. Let us consider the same sets of simulations as in Sect. 5.2, so that the number of particles are given by N ∈ {8, 12, 16, 24, 32, 48, 64} × 105, and for each of these values of N, 32 different simulations with ξ = 0.6 are performed, in order to carry out ensemble averages.
 |
Fig. 7 Top panel: illustration of the behaviour of the function |
The equivalent of Figs. 5 and 6 for ξ = 0.6 is illustrated in Fig. 7. Even for ξ = 0.6, one finds that the function 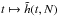 follows a parabola given by Eq. (57). One also recovers the predicted scalings with N of the functions
follows a parabola given by Eq. (57). One also recovers the predicted scalings with N of the functions 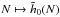 and
and 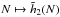 , respectively representing the initial Poisson shot noise of the sampling and the collisional scaling of the Balescu-Lenard secular evolution. As expected, when the active fraction of the disc is increased the secular evolution is accelerated. Thanks to these fits, one can study the dependence of the ratio α2(ξ = 0.6) /α2(ξ = 0.5), as defined in Eq. (64), both from numerical simulations as described in Figs. 6 and 7 and from the Balescu-Lenard equation using the matrix method described in Sect. 4.
, respectively representing the initial Poisson shot noise of the sampling and the collisional scaling of the Balescu-Lenard secular evolution. As expected, when the active fraction of the disc is increased the secular evolution is accelerated. Thanks to these fits, one can study the dependence of the ratio α2(ξ = 0.6) /α2(ξ = 0.5), as defined in Eq. (64), both from numerical simulations as described in Figs. 6 and 7 and from the Balescu-Lenard equation using the matrix method described in Sect. 4.
From the fits of 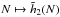 from Figs. 6 and 7, one can write
from Figs. 6 and 7, one can write 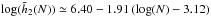 for ξ = 0.5 and
for ξ = 0.5 and 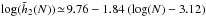 for ξ = 0.6, where we shifted the intercept of the fits to correspond to the centre of the considered region log (N) ∈ [ log (8) ;log (64) ]. One therefore obtains the ratio
for ξ = 0.6, where we shifted the intercept of the fits to correspond to the centre of the considered region log (N) ∈ [ log (8) ;log (64) ]. One therefore obtains the ratio ![\begin{equation} \frac{\alpha_{2} (0.6)}{\alpha_{2} (0.5)} \bigg|_{\rm NB} \simeq \exp \left[ 9.76 \!-\! 6.40 \right] \simeq 29 . \label{ratio_alpha2_NB} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq372.png) (65)One may now compare this N-body measurement to the same measurement performed via the Balescu-Lenard formalism. Following Eq. (63), one obtains that this ratio is given by
(65)One may now compare this N-body measurement to the same measurement performed via the Balescu-Lenard formalism. Following Eq. (63), one obtains that this ratio is given by ![\begin{equation} \frac{\alpha_{2} (\xi_{1})}{\alpha_{2} (\xi_{2})} = \frac{\displaystyle \int \!\! \mathrm{d} \bm{J} \, \big[ \text{div} (\bm{\mathcal{F}}_{\rm tot}^{\xi_{1}} ) \big]^{2} }{\displaystyle \int \!\! \mathrm{d} \bm{J} \, \big[ \text{div} (\bm{\mathcal{F}}_{\rm tot}^{\xi_{2}} ) \big]^{2}} , \label{ratio_alpha2_analytic} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq373.png) (66)where
(66)where 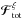 stands for the secular diffusion flux at t = 0+ with an active fraction ξ. The value of α2(ξ = 0.5) can be determined via Fig. 4, while the secular diffusion flux determined for ξ = 0.6 is illustrated in Fig. 8. Thanks to the contours presented in Figs. 4 and 8, one can perform the same estimation as in Eq. (65) starting from the Balescu-Lenard predictions. In order to focus on the contributions associated with the resonant ridge, the integrals on J in Eq. (66) were performed for Jφ ∈ [ 0.5; 1.2 ] and Jr ∈ [ 0.06; 0.15 ]. We measured
stands for the secular diffusion flux at t = 0+ with an active fraction ξ. The value of α2(ξ = 0.5) can be determined via Fig. 4, while the secular diffusion flux determined for ξ = 0.6 is illustrated in Fig. 8. Thanks to the contours presented in Figs. 4 and 8, one can perform the same estimation as in Eq. (65) starting from the Balescu-Lenard predictions. In order to focus on the contributions associated with the resonant ridge, the integrals on J in Eq. (66) were performed for Jφ ∈ [ 0.5; 1.2 ] and Jr ∈ [ 0.06; 0.15 ]. We measured 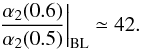 (67)Despite the difficulty of this measurement which required to consider a much more sensitive disc with ξ = 0.6, the ratios of α2 measured either via direct N-body simulations as in Eq. (65) or via application of the Balescu-Lenard formalism in Eq. (67) are within the same order of magnitude. As a consequence, one indeed checks that the Balescu-Lenard equation is able to correctly capture the relative effect of the disc’s susceptibility on the characteristics of the collisional secular diffusion. The strong consequence of modifying the active fraction, observed both in Eqs. (65) and (67), illustrates the relevance of the self-gravitating amplification in determining the typical timescale of secular diffusion of the system.
(67)Despite the difficulty of this measurement which required to consider a much more sensitive disc with ξ = 0.6, the ratios of α2 measured either via direct N-body simulations as in Eq. (65) or via application of the Balescu-Lenard formalism in Eq. (67) are within the same order of magnitude. As a consequence, one indeed checks that the Balescu-Lenard equation is able to correctly capture the relative effect of the disc’s susceptibility on the characteristics of the collisional secular diffusion. The strong consequence of modifying the active fraction, observed both in Eqs. (65) and (67), illustrates the relevance of the self-gravitating amplification in determining the typical timescale of secular diffusion of the system.
 |
Fig. 8 Map of Ndiv(ℱtot) with an active fraction ξ = 0.6 and using the same conventions as in Fig. 4. The contours are spaced linearly between the minimum and the maximum of Ndiv(ℱtot). The maximum value for the positive blue contours corresponds to Ndiv(ℱtot) ≃ 4200, while the minimum value for the negative red contours corresponds to Ndiv(ℱtot) ≃ −3200. As expected, one recovers that when the active fraction of the disc is increased, the susceptibility of the disc is increased, so that the norm of Ndiv(ℱtot) gets larger and the secular diffusion is fastened. |
5.4. Late-time evolution
The predictions of the Balescu-Lenard secular diffusion flux presented in Sect. 4 were only applied for the initial time of evolution, i.e. for the estimation of ℱtot(t = 0+). The N-body simulations presented in Sect. 5 allowed us to verify the appropriate scaling of the response of the system with the number of particles for the initial time of evolution as illustrated in Fig. 6. Using the Balescu-Lenard formalism to probe the late secular evolution of the system would require to evolve iteratively Eq. (2) over secular times. Such iterations are clearly beyond the scope of this first paper, however the use of N-body simulations allows us to start probing now such late times of evolution.
As discussed in Sect. 2, the Balescu-Lenard equation describes the long-term evolution of a discrete self-gravitating inhomogeneous system. Such a collisional evolution is only relevant for dynamically stable systems, i.e. systems assumed to be stable in the Vlasov sense, and remains valid as the system moves through a series of equlibria, while the drift and diffusion coefficients change with F. Because it has been obtained via a Taylor expansion of the dynamics at the order 1 /N in the number of particles, it remains valid only on secular timescales of the order NtD, with tD the dynamical time.
On such secular timescales, a Balescu-Lenard evolution can lead to two different outcomes. On the one hand, if the system remains stable during its entire evolution, the Balescu-Lenard equation will tend towards a 1 /N-stationary state2. Once such a stationary state of evolution has been reached, the dynamics is then governed by the next order kinetic effects in 1 /N2, which are not captured by the Balescu-Lenard equation. On the other hand, the Balescu-Lenard collisional evolution may also lead to a destabilisation of the system. Indeed, the long-term effects of the collisional diffusion, because they lead to an irreversible diffusion of the DF, may change its current state w.r.t. the collisionless (Vlasov) dynamics. After a slow and stable evolution sourced by collisional 1 /N effects, the system may then become dynamically unstable with respect to collisionless dynamics, which becomes the main driver of its later-time evolution, as was suggested by Sellwood (2012). S12 observes an out-of-equilibrium transition between the 1 /N Balescu-Lenard collisional evolution and the collisionless Vlasov evolution.
One can illustrate such a transition using the N-body simulations presented previously. In order to capture the change of regime of evolution within the disc (collisional vs. collisionless), for a given value of the number of particles, we define the quantity Σ2(t,N) as 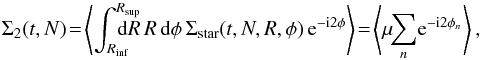 (68)where as in Eq. (55), the operator ⟨·⟩ corresponds to the ensemble average, approximated here with the arithmetic average over the p = 32 different realisations of simulations for the same number of particles N. The radii considered are restricted to the range R ∈ [ Rinf; Rsup ] = [ 1.2; 5 ], where the active surface density of the disc is little affected by the inner and outer tapers. Finally, to obtain the second equality in Eq. (68), as in Eq. (C.2), we replaced the active surface density of the disc by a discrete sum over all the particles of the system, where the sum on n is restricted to all the particle whose radius lies between Rinf and Rsup, while their azimuthal phase was written as φn. Such a quantity allows us to probe easily the presence of strong non-axisymmetric features within the disc. During the initial Balescu-Lenard collisional evolution of the system, one expects low values of Σ2. Indeed, during this evolution, one relies on the phase averaging approximation, which assumes that F = F(J,t), so that the DF of the system does not depend on the angles θ. During this collisional phase, Σ2 still remains non-zero because the system develops transient spiral waves, which sustain the secular evolution. On the long-term, this collisional evolution, through an irreversible diffusion of the DF, leads to a destabilisation of the system. Eventually, the dynamical drivers of evolution are no longer discrete resonant collisional effects but exponentially growing dynamical instabilities. In this regime of collisionless unstable evolution, one expects much larger values of Σ2, because of the appearance of strong non-axisymmetric bars within the disc. This bifurcation between these two regimes of diffusion is illustrated in Fig. 9, through the behaviour of the function
(68)where as in Eq. (55), the operator ⟨·⟩ corresponds to the ensemble average, approximated here with the arithmetic average over the p = 32 different realisations of simulations for the same number of particles N. The radii considered are restricted to the range R ∈ [ Rinf; Rsup ] = [ 1.2; 5 ], where the active surface density of the disc is little affected by the inner and outer tapers. Finally, to obtain the second equality in Eq. (68), as in Eq. (C.2), we replaced the active surface density of the disc by a discrete sum over all the particles of the system, where the sum on n is restricted to all the particle whose radius lies between Rinf and Rsup, while their azimuthal phase was written as φn. Such a quantity allows us to probe easily the presence of strong non-axisymmetric features within the disc. During the initial Balescu-Lenard collisional evolution of the system, one expects low values of Σ2. Indeed, during this evolution, one relies on the phase averaging approximation, which assumes that F = F(J,t), so that the DF of the system does not depend on the angles θ. During this collisional phase, Σ2 still remains non-zero because the system develops transient spiral waves, which sustain the secular evolution. On the long-term, this collisional evolution, through an irreversible diffusion of the DF, leads to a destabilisation of the system. Eventually, the dynamical drivers of evolution are no longer discrete resonant collisional effects but exponentially growing dynamical instabilities. In this regime of collisionless unstable evolution, one expects much larger values of Σ2, because of the appearance of strong non-axisymmetric bars within the disc. This bifurcation between these two regimes of diffusion is illustrated in Fig. 9, through the behaviour of the function 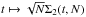 3. One can similarly observe this transition directly by looking at the active surface density Σt(R,φ,t) for these two different regimes. This is illustrated in Fig. 10, where one recovers that in the late time collisionless regime of evolution, the galaxy becomes strongly non-axisymmetric. S12 found that just after the disc becomes unstable, the pattern of the spiral response is consistent with the ILR frequency corresponding to the ridge4. Hence the phase transition observed in Fig. 10 is driven by all the free energy available in a cold disc, which via spiral transients secularly heats the disc, but only along a very tight resonant direction. This in turn leads the disc towards an orbital instability, transverse to the resonance (via the direct azimuthal analogue to the two stream instability in plasma physics, Lynden-Bell 1979; Pichon 1994). Qualitatively, one expects that the more massive and the narrower the ridge, the larger the number of orbits trapped in ILR resonance with little relative azimuthal dispersion, and the earlier the instability (Penrose 1960; Pichon & Lynden-Bell 1993).
3. One can similarly observe this transition directly by looking at the active surface density Σt(R,φ,t) for these two different regimes. This is illustrated in Fig. 10, where one recovers that in the late time collisionless regime of evolution, the galaxy becomes strongly non-axisymmetric. S12 found that just after the disc becomes unstable, the pattern of the spiral response is consistent with the ILR frequency corresponding to the ridge4. Hence the phase transition observed in Fig. 10 is driven by all the free energy available in a cold disc, which via spiral transients secularly heats the disc, but only along a very tight resonant direction. This in turn leads the disc towards an orbital instability, transverse to the resonance (via the direct azimuthal analogue to the two stream instability in plasma physics, Lynden-Bell 1979; Pichon 1994). Qualitatively, one expects that the more massive and the narrower the ridge, the larger the number of orbits trapped in ILR resonance with little relative azimuthal dispersion, and the earlier the instability (Penrose 1960; Pichon & Lynden-Bell 1993).
 |
Fig. 9 Behaviour of the function |
 |
Fig. 10 Illustration of the active surface density Σt for a N-body run with N = 8 × 105, restriced to the range R ≤ 6. Top panel: active surface density Σt at an early time t = 60, for which the galaxy remains globally axisymmetric. In this regime, the dynamics of the system is collisional and governed by the Balescu-Lenard Eq. (2). Bottom panel: active surface density Σt at a much later time t = 2400. The galaxy is then strongly non-axisymmetric. In this regime, the dynamics of the system is collisionless and governed by the Vlasov equation. |
In closing, it is quite striking that an isolated galactic disc, fully stable in the mean field sense, will, given time, drive itself through two-point resonant correlations towards instability, demonstrating the extent to which such cold systems are truly secularly metastable.
6. Conclusion
Most astrophysical discs formed through dissipative processes and have typically evolved over many dynamical times. Even in isolation, the long-range force of gravity allows their components to interact effectively through resonances, which given time may drive them secularly towards more likely equilibria. Such processes are captured by recent extensions of kinetic theories rewritten in angle-action variables (Heyvaerts 2010; Chavanis 2012). Solving these equations provide astronomers with a unique opportunity to quantify the induced secular angular momentum redistribution within these discs (Lynden-Bell & Kalnajs 1972) on cosmic timescales. While challenging, the numerical computation of the corresponding diffusion and drift coefficients is, as demonstrated, within reach of a relatively straightforward extension of the so-called matrix method (Kalnajs 1976), which computes the orbital response of self-gravitating discs using quadratures and linear algebra.
Paper I presented asymptotic expressions in the tightly wound limit and provided a qualitative insight into the physical processes at work during the secular diffusion of a self-gravitating discrete disc. Conversely, in this paper, we computed numerically the drift and diffusion coefficients of the inhomogeneous Balescu-Lenard equation for such infinitely thin stellar discs. The self-gravity of the disc was taken into account via the matrix method, validated on unstable Mestel discs. We computed the divergence of the flux density in action space, div(ℱtot). Swing amplification was shown to provide a significant boost for the diffusion timescale, which now matches the numerically measured one. These computations are the first exact calculation of the Balescu-Lenard diffusion and drift coefficients in the context of inhomogeneous multi-periodic systems. They capture the essence of self-induced evolution (nature), which should compete with environmentally induced evolution (nurture). We then compared these predictions to idealised numerical simulations of stable stationary and truncated Mestel discs sampled by pointwise particles, which were evolved for hundreds of dynamical times. Using ensemble averages of our N-body runs, we also identified a clear signature of the Balescu-Lenard process in the scaling of the diffusion features with N and ξ, the fraction of the mass within the disc. As originally identified by Goldreich & Lynden-Bell (1965), Julian & Toomre (1966) in the context of their linear response, the susceptibility of cold self-gravitating discs plays a critical role for their secular evolution as it is squared in the Balescu-Lenard equation, which boosts considerably the effect of discreteness. Indeed, both the numerical experiments and our computation of the fluxes show that Neff ~ N/104, which is consistent with the predicted rescaling in 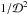 (it was shown forty years ago that for a Mestel disc
(it was shown forty years ago that for a Mestel disc 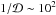 , depending on the exact temperature of the disc, Toomre 1981).
, depending on the exact temperature of the disc, Toomre 1981).
Jointly with Paper I we now have a qualitative and quantitative understanding of the initial secular orbital diffusion process induced by the discreteness of galactic discs. Our qualitative understanding allows us to identify the role played by the square susceptibility in boosting the diffusion. Our quantitative agreement in both amplitude, position, width and scaling of the induced orbital signatures strongly suggests that secular evolution is indeed driven by resonances as captured by the Balescu-Lenard formalism, and that it does not depend on the initial phases of the disc (since the matching Balescu-Lenard fluxes are phase averaged). It demonstrates that this equation initially reproduces the observed evolution of self-gravitating discs driven by resonant two-point correlations beyond the mean field approximation.
The next step will be to evolve iteratively Eq. (2) over a Hubble time, and compare with the result of N-body simulations. One should also model it jointly with an externally induced orbital diffusion (Fouvry et al. 2015b) arising from for example a (possibly anisotropic) cosmic environment (Codis et al. 2012, 2015) so as to assess which process dominates. At the technical level, the Balescu-Lenard formalism should be used to (in)validate N-body integrators accuracy on secular timescales. There are indeed very few analytical predictions on which to calibrate N-body experiments in this regime. Such an exploration would also allow us to get a better grasp of the impact of the numerical parameters used in the N-body integration (such as timestep, mesh size or softening length) on the long-term dynamics of the system.
Beyond the application described in this paper, the Balescu-Lenard formalism may in the future also be numerically implemented to describe for instance the secular diffusion of giant molecular clouds in galactic discs (which in turn could play a role in migration-driven metallicity gradients and disc thickening), the secular migration of planetesimals in partially self-gravitating proto-planetary debris discs, or even the long-term evolution of population of stars and gas blobs near the Galactic centre. In 3D, assuming spherical symmetry, its implementation could be useful to describe spherical systems dominated by radial orbits, or the secular evolution of tidal debris in our possibly flattened galactic halo using Stäckel potentials.
Online material
Appendix A: Kalnajs basis
We now detail the properties of the basis introduced in Kalnajs (1976) to describe 2D discs5. The basis depends on two parameters: an index kKa ∈N and a scale radius rKa ∈ R+. In all the upcoming formulae of this section, in order to shorten the notations, we write r for the dimensionless quantity r/rKa. As introduced previously in Eq. (16), the basis elements depend on two indices: the azimuthal number ℓ and the radial index n. One should note that we have ℓ ≥ 0 and n ≥ 0. The radial component of the potential elements are then of the form 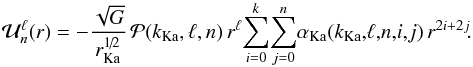 (A.1)The radial component of the density elements is given by
(A.1)The radial component of the density elements is given by 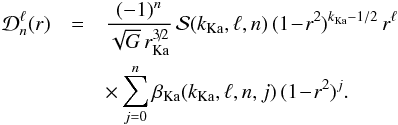 (A.2)In Eqs. (A.1) and (A.2), the coefficients
(A.2)In Eqs. (A.1) and (A.2), the coefficients 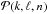 and
and 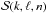 are defined by
are defined by ![\appendix \setcounter{section}{1} \begin{eqnarray} \mathcal{P} (k ,\ell , n)& = &\Bigg\{\! \frac{[2 k \!+\! \ell \!+\! 2 n \!+\! (1\!/2)] \Gamma [2 k \!+\! \ell \!+\! n \!+\! (1\!/2)]}{\Gamma [2 k \!+\! n \!+\! 1] \, \Gamma^{2} [\ell \!+\! 1] \, \Gamma[n \!+\! 1] } \nonumber \\ && \times \Gamma[\ell \!+\! n \!+\! (1\!/2)] \!\Bigg\}^{1\!/2} , \label{definition_P_Kalnajs} \end{eqnarray}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq419.png) (A.3)and
(A.3)and ![\appendix \setcounter{section}{1} \begin{eqnarray} \mathcal{S} (k , \ell , n) &= &\frac{\Gamma [k \!+\! 1]}{\pi \, \Gamma[2 k \!+\! 1] \, \Gamma [k \!+\! (1/2)]} \nonumber \\ && \times \Bigg\{\frac{[2k \!+\! \ell \!+\! 2 n \!+\! (1\!/2)] \, \Gamma [2 k \!+\! n \!+\! 1] \, \Gamma[2 k \!+\! \ell \!+\! n \!+\! (1\!/2)]}{\Gamma[\ell \!+\! n \!+\! (1/2)] \, \Gamma [n \!+\! 1]} \Bigg\}^{1/2} \cdot \label{definition_S_Kalnajs} \end{eqnarray}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq420.png) (A.4)Finally, in Eqs. (A.1) and (A.2), we have also introduced
(A.4)Finally, in Eqs. (A.1) and (A.2), we have also introduced ![\appendix \setcounter{section}{1} \begin{eqnarray} \alpha_{\rm Ka} (k , \ell , n , i , j) &= & \frac{[-k]_{i} \, [\ell \!+\! (1\!/2)]_{i} \, [2 k \!+\! \ell \!+\! n \!+\! (1/2)]_{j}}{[\ell \!+\! 1]_{i} \, [1]_{i} \, [\ell \!+\! i \!+\! 1]_{j} [\ell \!+\! (1\!/2)]_{j} [1]_{j}} \nonumber \\ && \times [i \!+\! \ell \!+\! (1\!/2)]_{j} \, [- n]_{j} , \label{definition_alpha_Kalnajs} \end{eqnarray}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq421.png) (A.5)and
(A.5)and ![\appendix \setcounter{section}{1} \begin{equation} \beta_{\rm Ka} (k , \ell , n , j) = \frac{[2 k \!+\! \ell \!+\! n \!+\! (1/2)]_{j} \, [k \!+\! 1]_{j} \, [- n]_{j}}{[2 k \!+\! 1]_{j} \, [k \!+\! (1/2)]_{j} \, [1]_{j} } \cdot \label{definition_beta_Kalnajs} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq422.png) (A.6)In the two previous expressions, we introduced the rising Pochhammer symbol [ a ] i defined as
(A.6)In the two previous expressions, we introduced the rising Pochhammer symbol [ a ] i defined as ![\appendix \setcounter{section}{1} \begin{eqnarray} [a]_{i} = \begin{cases} \begin{array}{ll} 1 & \text{if} \;\;\; i = 0 , \\ a \, (a \!+\! 1) \, ... \, (a \!+\! n \!-\! 1) & \text{if} \;\;\; i > 0 . \end{array} \label{definition_Pochhammer} \end{cases} \end{eqnarray}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq424.png) (A.7)
(A.7)
Appendix B: Calculation of ℵ
We now detail how the analytical function ℵ from Eq. (32) may be computed. In order to ease the implementation of its computation, we rewrite ℵ in an undimensionalised way as follows ![\appendix \setcounter{section}{2} \begin{eqnarray} \aleph (a_{g} , b_{g} , c_{g} , a_{h} , b_{h} , c_{h} , \eta , \Delta r) \, &=& \nonumber \\ && \!\! \int_{- \frac{\Delta r}{2}}^{\frac{\Delta r}{2}} \!\! \int_{- \frac{\Delta r}{2}}^{\frac{\Delta r}{2}} \!\! \mathrm{d} x_{p} \mathrm{d} x_{a} \, \frac{a_{g} \!+\! b_{g} x_{p} \!+\! c_{g} x_{a}}{a_{h} \!+\! b_{h} x_{p} \!+\! c_{h} x_{a} \!+\! {\rm i} \eta} \nonumber \\ & = &\frac{a_{g}}{a_{h}} (\Delta r)^{2} \!\! \int_{- \frac{1}{2}}^{\frac{1}{2}} \!\! \int_{- \frac{1}{2}}^{\frac{1}{2}} \!\! \mathrm{d} x \mathrm{d} y \, \frac{1 \!+\! \frac{b_{g} \Delta r}{a_{g}} x \!+\! \frac{c_{g} \Delta r}{a_{g}} y }{1 \!+\! \frac{b_{h} \Delta r}{a_{h}} x \!+\! \frac{c_{h} \Delta r}{a_{h}} y \!+\! i \frac{\eta}{a_{h}} } \nonumber \\ & = &\frac{a_{g}}{a_{h}} (\Delta r)^{2} \, \aleph_{\rm D} \left[ \frac{b_{g} \Delta r}{a_{g}} , \frac{c_{g} \Delta r}{a_{g}} , \frac{b_{h} \Delta r}{a_{h}} , \frac{c_{h} \Delta r}{a_{h}} , \frac{\eta}{a_{h}} \right] , \label{calculation_aleph} \end{eqnarray}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq425.png) (B.1)where we assumed that ag,ah ≠ 0 and used the change of variables x = xp/ Δr and y = xa/ Δr. We also defined the dimensionless function ℵD as
(B.1)where we assumed that ag,ah ≠ 0 and used the change of variables x = xp/ Δr and y = xa/ Δr. We also defined the dimensionless function ℵD as 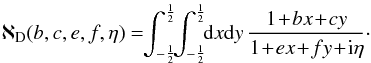 (B.2)To compute this integral, we may now exhibit a function G(x,y) such that
(B.2)To compute this integral, we may now exhibit a function G(x,y) such that 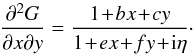 (B.3)One possible choice for G is given by
(B.3)One possible choice for G is given by ![\appendix \setcounter{section}{2} \begin{eqnarray} && G (x , y) = \frac{1}{4 e^2 f^2} \log \left[ e^2 x^2 \!+\! 2 e \left(f x y\!+\!x\right)\!+\!f^2 y^2\!+\!2 f y\!+\!\eta ^2\!+\!1 \right] \nonumber \\ && \times\bigg\{b f \left(e^2 x^2\!-\!\left(f y\!+\!{\rm i} \eta \!+\!1\right)^2 \right) \!+\!2 e f (e x\!+\!{\rm i} \eta \!+\!1) \!-\!c e \nonumber (e x\!+\!{\rm i} \eta \!+\!1)^2 \bigg\} \\ && \!+\!\frac{\rm i}{2 e^2 f^2} \bigg\{\frac{\pi }{2}\!-\!\tan ^{-1} \!\bigg[ \frac{e x\!+\!f y\!+\!1}{\eta } \bigg] \bigg\} \nonumber \\ && \times \bigg\{b f ( e^2 x^2\!-\!(f y\!+\!{\rm i} \eta \!+\!1)^2 ) \!+\! 2 e f (e x\!+\!{\rm i} \eta \!+\!1) \!-\!c e (e x\!+\!{\rm i} \eta \!+\!1)^2 \bigg\} \nonumber \\ & & \!+\!\frac{y}{4 e^2 f} \bigg\{f (\!-\!4 e\!+\!b (2 e x\!+\!f y\!+\!2 {\rm i} \eta \!+\!2)) \nonumber \\ & &\!+\!c e (2 e x\!-\!f y\!+\!2 {\rm i} \eta \!+\!2)\!+\!2 e f (c y\!+\!2) \log [e x\!+\!f y\!+\!{\rm i} \eta \!+\!1] \bigg\}. \label{choice_G} \end{eqnarray}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq434.png) (B.4)One should note in the previous expression the presence of a complex logarithm and a tan-1. However, because e,f,η ∈R and η ≠ 0, one can easily show that the arguments of both of these functions never cross the usual branch-cut of these functions {Im(z) = 0; Re(z) ≤ 0 }. As a consequence, the expression (B.2) can immediately be computed as
(B.4)One should note in the previous expression the presence of a complex logarithm and a tan-1. However, because e,f,η ∈R and η ≠ 0, one can easily show that the arguments of both of these functions never cross the usual branch-cut of these functions {Im(z) = 0; Re(z) ≤ 0 }. As a consequence, the expression (B.2) can immediately be computed as ![\appendix \setcounter{section}{2} \begin{equation} \aleph_{D} = G \left[ \tfrac{1}{2} , \tfrac{1}{2} \right] \!-\! G \left[ \tfrac{1}{2} , - \tfrac{1}{2} \right] \!-\! G \left[ - \tfrac{1}{2} , \tfrac{1}{2} \right] \!+\! G \left[ - \tfrac{1}{2} , - \tfrac{1}{2} \right] \cdot \label{computation_aleph_D} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq439.png) (B.5)
(B.5)
Appendix C: Response matrix and N-body validations
The computation of the response matrix as described in Sect. 3 was validated by recovering the results of the pioneer work of Zang (1976), extended in Evans & Read (1998a,b), and recovered numerically in Sellwood & Evans (2001). These papers predicted the precession rate ω0 = mφΩp and growth rate η = s of the unstable modes of a truncated Mestel disc similar to the stable one described in Sect. 4.1. To build up an unstable disc similar to the ones considered in these previous works, one has to consider a fully active disc, so that ξ = 1. So as to have Q = 1 (Toomre 1964), the velocity dispersion within the disc is given by q = 6, where the parameter q has been introduced in Eq. (46). Finally, a last parameter one can tune in order to modify the properties of the disc is the truncation index of the inner tapering νt defined in Eq. (48). While looking only for mφ = 2 modes, we considered three different truncations indices given by νt = 4, 6, 8. To compute the response matrix, we used the same numerical parameters as described in Sect. 4.2. Looking for unstable modes amounts to looking for complex frequencies ω = ω0 + iη such that the response matrix  from Eq. (24) possesses an eigenvalue equal to 1. Such a complex frequency is then associated with an unstable mode of pattern speed ω0 and growth rate η. To determine the growth rate and pattern speed of the unstable modes, we relied on Nyquist contours similarly to the technique presented in Pichon & Cannon (1997). For a fixed value of η, one can study the continuous complex curve
from Eq. (24) possesses an eigenvalue equal to 1. Such a complex frequency is then associated with an unstable mode of pattern speed ω0 and growth rate η. To determine the growth rate and pattern speed of the unstable modes, we relied on Nyquist contours similarly to the technique presented in Pichon & Cannon (1997). For a fixed value of η, one can study the continuous complex curve ![\hbox{${\omega_{0} \mapsto \det \big[ \mathbf{I} - \widehat{\mathbf{M}} (\omega_{0} , \eta) \big] }$}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq450.png) . Because for η → + ∞, one has
. Because for η → + ∞, one has  , the number of windings of this curve around the origin gives a lower bound on the number of unstable modes with a growth rate superior to η. By decreasing the value of η, one can then determine the largest value of η admitting an unstable mode, and therefore the most unstable mode of the disc. The Nyquist contours obtained for the truncation index νt = 6 are illustrated in Fig. C.1, while the measurements are gathered in Table C.1.
, the number of windings of this curve around the origin gives a lower bound on the number of unstable modes with a growth rate superior to η. By decreasing the value of η, one can then determine the largest value of η admitting an unstable mode, and therefore the most unstable mode of the disc. The Nyquist contours obtained for the truncation index νt = 6 are illustrated in Fig. C.1, while the measurements are gathered in Table C.1.
 |
Fig. C.1 Top panel: zoomed Nyquist contours in the complex plane of |
Once the characteristics (ω0,η) of the unstable modes have been determined, one can study in the physical space the shape of the mode. Indeed, for ω = ω0 + iη, one can compute  , and numerically diagonalise this matrix. One then considers its eigenvector Xmode (of size nmax, where nmax is the number of basis elements considered) associated with the eigenvalue almost equal to 1. The shape of the mode is then immediately given by
, and numerically diagonalise this matrix. One then considers its eigenvector Xmode (of size nmax, where nmax is the number of basis elements considered) associated with the eigenvalue almost equal to 1. The shape of the mode is then immediately given by ![\appendix \setcounter{section}{3} \begin{equation} \Sigma_{\rm mode} (R , \phi) = \text{Re} \left[ \sum_{p} \bm{X}_{\rm mode}^{p} \, \Sigma^{(p)} (R , \phi) \right] , \label{shape_mode_Matrix_Method} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq461.png) (C.1)where Σ(p) are the considered surface density basis elements. The shape of the recovered unstable mode for the truncated νt = 4 Mestel disc is illustrated in Fig. C.2.
(C.1)where Σ(p) are the considered surface density basis elements. The shape of the recovered unstable mode for the truncated νt = 4 Mestel disc is illustrated in Fig. C.2.
 |
Fig. C.2 Unstable mode for the truncated νt = 4 Mestel disc recovered via the matrix method presented in Sect. 3. Only positive contour levels are shown and are spaced linearly between 10% and 90% of the maximum norm. The radii associated with the resonances ILR, COR and OLR have been represented, as given by ω0 = m·Ω(Rm), where the intrinsic frequencies Ω(R) = (Ωφ(R),κ(R)) have to be computed within the epicyclic approximation. For a Mestel disc, they are given by Ωφ(R) = V0/R and |
 |
Fig. C.3 Measurement of the growth rate η and pattern speed ω0 of the mφ = 2 unstable modes of truncated Mestel discs with a random velocity given by q = 6 for various values of the truncation index νt = 6, 8. The basis coefficient plotted is associated with the basis element (ℓ,n) = (2,0), using the same basis elements as for the matrix method in Sect. 4.2. |
The same unstable modes were also used to validate the N-body code presented in Sect. 5. To run these simulations, we used the same sampling technique as described in Appendix E. In order not to be significantly impacted by the absence of a quiet start sampling (Sellwood 1983), for each value of νt, the measurements were performed with simulations of 20M particles. As observed in Sellwood & Evans (2001), the appropriate setting of the parameters of the N-body code are crucial to recover correctly the unstable modes of a disc. We considered a grid made with Nmesh = 120 grid cells, while using a softening length equal to ε = Ri/ 60. As described in Sect. 5, we similarly restricted the perturbing forces only to the harmonic sector mφ = 2, using Nring = 2400 radial rings, with Nφ = 720 azimuthal points. In order to extract the properties of the mode present within the disc, one may proceed as follows. For each simulation snapshot, one can estimate the active surface density within the disc via 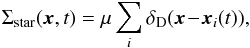 (C.2)where the sum on i is made on all the particles of the simulation and xi(t) is the position of the ith particle at time t. Such a surface density can be decomposed on the basis elements from Eq. (3) in the form
(C.2)where the sum on i is made on all the particles of the simulation and xi(t) is the position of the ith particle at time t. Such a surface density can be decomposed on the basis elements from Eq. (3) in the form 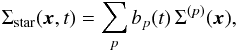 (C.3)where the sum on p is made on all the basis elements Σ(p) considered. The effective basis elements used during our measurements are the same as the ones used in the matrix method from Sect. 4.2. Thanks to the biorthogonality property from Eq. (3), the coefficients bp(t) can be immediately determined as
(C.3)where the sum on p is made on all the basis elements Σ(p) considered. The effective basis elements used during our measurements are the same as the ones used in the matrix method from Sect. 4.2. Thanks to the biorthogonality property from Eq. (3), the coefficients bp(t) can be immediately determined as 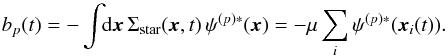 (C.4)As we are looking for unstable modes within the disc, we expect to have bp(t) ∝ exp [ −i(ω0 + iη)t ], where ω0 = mφΩp is the pattern speed of the mode and η = s its growth rate. As a consequence, one immediately obtains that
(C.4)As we are looking for unstable modes within the disc, we expect to have bp(t) ∝ exp [ −i(ω0 + iη)t ], where ω0 = mφΩp is the pattern speed of the mode and η = s its growth rate. As a consequence, one immediately obtains that 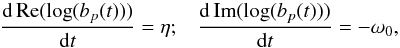 (C.5)if one is sufficently careful with the branch-cut of the complex logarithm. Such a linear scaling with t of Re(log (bp(t))) and Im(log (bp(t))) is therefeore the appropriate measurement procedure to use in order to estimate the growth rate and pattern speed of the unstable modes of these truncated Mestel discs. The measurements for the various values of the truncation index νt are illustrated in Fig. C.3. Once the basis coefficients bp(t) have been determined, one can study the shape of the recovered unstable modes in the physical space. Indeed, similarly to Eq. (C.1), the shape of the modes is given by
(C.5)if one is sufficently careful with the branch-cut of the complex logarithm. Such a linear scaling with t of Re(log (bp(t))) and Im(log (bp(t))) is therefeore the appropriate measurement procedure to use in order to estimate the growth rate and pattern speed of the unstable modes of these truncated Mestel discs. The measurements for the various values of the truncation index νt are illustrated in Fig. C.3. Once the basis coefficients bp(t) have been determined, one can study the shape of the recovered unstable modes in the physical space. Indeed, similarly to Eq. (C.1), the shape of the modes is given by ![\appendix \setcounter{section}{3} \begin{equation} \Sigma_{\rm mode} (R , \phi , t) = \text{Re} \left[ \sum_{p} b_{p} (t) \, \Sigma^{(p)} (R , \phi) \right] . \label{shape_mode_NB} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq486.png) (C.6)In analogy with Fig. C.2, for which the unstable modes have been obtained via the matrix method, Fig. C.4 illustrates the unstable mode of the same truncated νt = 4 Mestel disc.
(C.6)In analogy with Fig. C.2, for which the unstable modes have been obtained via the matrix method, Fig. C.4 illustrates the unstable mode of the same truncated νt = 4 Mestel disc.
 |
Fig. C.4 Unstable mode for the truncated νt = 4 Mestel disc recovered via direct N-body simulations as presented in Sect. 5. Only positive contour levels are shown and are spaced linearly between 20% and 80% of the maximum norm. Similarly to Fig. C.2, the radii associated with the resonances ILR, COR and OLR have been represented. |
Measurements of the pattern speed ω0 = mφΩp and growth rate η = s for unstable mφ = 2 modes of tapered Mestel discs.
As a conclusion, the growth rates and pattern speeds obtained either via the matrix method or direct N-body simulations are gathered in Table C.1. As observed in Sellwood & Evans (2001), the recovery of the unstable modes characteristics from direct N-body simulations when performed for truncated Mestel discs is a difficult task, for which convergence to the values predicted through linear theory may be difficult.
Appendix D: Why swing matters?
Let us investigate here briefly the importance of self-gravitation and the completeness of the projection basis in capturing the role of swing amplification.
 |
Fig. D.1 Map of |
Appendix D.1: Turning off the self-gravitating amplification
In order to investigate the role of the self-gravitating amplification, one may perform the same estimation as presented in Fig. 4, while neglecting collective effects. When neglecting collective effects, i.e. when assuming that 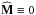 , one recovers the inhomogeneous Landau equation (Chavanis 2013) which reads
, one recovers the inhomogeneous Landau equation (Chavanis 2013) which reads ![\appendix \setcounter{section}{4} \begin{eqnarray} && \frac{\partial F}{\partial t} = \pi (2 \pi)^{d} \, \mu \, \frac{\partial}{\partial \bm{J}_{1}} \!\cdot\! \bigg[ \!\! \sum_{\bm{m}_{1} , \bm{m}_{2}} \!\! \bm{m}_{1} \!\! \int \!\! \mathrm{d} \bm{J}_{2} \, |A_{\bm{m}_{1} , \bm{m}_{2}} (\bm{J}_{1} , \bm{J}_{1})|^{2} \nonumber \\ && \,\times \delta_{\rm D} (\bm{m}_{1} \!\!\cdot\! \bm{\Omega}_{1} \!-\! \bm{m}_{2} \!\!\cdot\! \bm{\Omega}_{2}) \bigg(\! \bm{m}_{1} \!\!\cdot\! \frac{\partial }{\partial \bm{J}_{1}} \!-\! \bm{m}_{2} \!\!\cdot\! \frac{\partial }{\partial \bm{J}_{2}} \!\bigg) F (\bm{J}_{1} , t) F(\bm{J}_{2} , t) \bigg] .\! \label{definition_Landau} \end{eqnarray}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq497.png) (D.1)Equation (D.1) involves the bare susceptibility coefficients | Am1,m2(J1,J2) | 2, which can be equivalently defined (see Appendix B of Paper I) by
(D.1)Equation (D.1) involves the bare susceptibility coefficients | Am1,m2(J1,J2) | 2, which can be equivalently defined (see Appendix B of Paper I) by 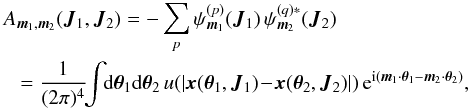 (D.2)where u(x) is the binary potential of interaction given by u(x) = −G/| x | for gravity. This estimation therefore does not require to estimate the response matrix from Eq. (24), but one still has to perform integrations along the resonant lines as in Eq. (42). Let us provide a first numerical implementation of this equation in the context of galactic dynamics. The contours of
(D.2)where u(x) is the binary potential of interaction given by u(x) = −G/| x | for gravity. This estimation therefore does not require to estimate the response matrix from Eq. (24), but one still has to perform integrations along the resonant lines as in Eq. (42). Let us provide a first numerical implementation of this equation in the context of galactic dynamics. The contours of 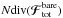 are illustrated in Fig. D.1. Comparing the maps of the dressed diffusion flux Ndiv(ℱtot) from Fig. 4 and the bare diffusion flux
are illustrated in Fig. D.1. Comparing the maps of the dressed diffusion flux Ndiv(ℱtot) from Fig. 4 and the bare diffusion flux 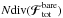 , allows us to assess the strength of the self-gravitating amplification. As expected, when turning off the self-gravity of the system, one reduces significantly the susceptibility of the system and therefore slows down its secular evolution by a factor of about 1000. One may also remark that while the secular appearance of a resonant ridge in the dressed diffusion from Fig. 4 was obvious, the shape of the contours obtained in the bare Fig. D.1 do not emphasise as clearly the appearance of such a narrow resonant ridge. One can still remark that the structure of the bare contours obtained in Fig. D.1 is similar to what was obtained in Fig. 9 of Paper I, through the WKB limit of the Balescu-Lenard equation. One can finally note that the amplitudes of the bare divergence contours obtained previously are similar to the WKB values obtained in Paper I. As a consequence, the comparison of Figs. 4 and D.1 emphasises that the strong self-gravitating amplification of loosely wound perturbations is indeed responsible for the appearance of a narrow ridge, while also ensuring that this appearance is sufficiently rapid, as observed in the diffusion timescales comparison from Eq. (52).
, allows us to assess the strength of the self-gravitating amplification. As expected, when turning off the self-gravity of the system, one reduces significantly the susceptibility of the system and therefore slows down its secular evolution by a factor of about 1000. One may also remark that while the secular appearance of a resonant ridge in the dressed diffusion from Fig. 4 was obvious, the shape of the contours obtained in the bare Fig. D.1 do not emphasise as clearly the appearance of such a narrow resonant ridge. One can still remark that the structure of the bare contours obtained in Fig. D.1 is similar to what was obtained in Fig. 9 of Paper I, through the WKB limit of the Balescu-Lenard equation. One can finally note that the amplitudes of the bare divergence contours obtained previously are similar to the WKB values obtained in Paper I. As a consequence, the comparison of Figs. 4 and D.1 emphasises that the strong self-gravitating amplification of loosely wound perturbations is indeed responsible for the appearance of a narrow ridge, while also ensuring that this appearance is sufficiently rapid, as observed in the diffusion timescales comparison from Eq. (52).
Appendix D.2: Turning off loosely-wound contributions
As emphasised in the Introduction, the WKB limit of the Balescu-Lenard equation presented in Fouvry et al. (2015a) was not able to capture the mechanism of swing amplification, which involves unwinding perturbations. By considering a complete and global basis as in Eq. (16), we have shown in Fig. 4 how the missing amplification from Fouvry et al. (2015a) could be recovered. Using the numerical method of estimation of the secular diffusion flux as presented in Sect. 3, one can try to recover the results obtained within the WKB formalism by carefully choosing the considered basis elements generically introduced in Eq. (16) and chosen to be Kalnajs basis elements as detailed in Appendix A. We recall that each basis element depends on two indices: an azimuthal index ℓ and a radial one n. Because in S12’s simulation perturbations were restricted to the harmonic sector mφ = 2, one only has to consider basis elements associated with ℓ = 2. Moreover, as illustrated in Fig. D.2, the larger n the radial index, the faster the radial variation of the basis elements and therefore the more tightly wound the basis elements. So as to get rid of the loosely-wound basis elements which are the ones which can get swing amplified, we perform a truncation of the radial indices considered. Therefore, we define the secular diffusion flux 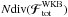 computed in the same way than Ndiv(ℱtot) as presented in Sect. 4.2, except that the basis elements are such that ncut ≤ n ≤ nmax, with ncut = 2 and nmax = 8. By keeping only the tightly wound basis elements, one can therefore consider the same contribution as the one considered in the WKB limit presented in Paper I. The contours of
computed in the same way than Ndiv(ℱtot) as presented in Sect. 4.2, except that the basis elements are such that ncut ≤ n ≤ nmax, with ncut = 2 and nmax = 8. By keeping only the tightly wound basis elements, one can therefore consider the same contribution as the one considered in the WKB limit presented in Paper I. The contours of 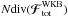 are illustrated in Fig. D.3. One can note that the values of the contours obtained in the map of
are illustrated in Fig. D.3. One can note that the values of the contours obtained in the map of 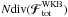 illustrated in Fig. D.3 are in the same order of magnitude as the ones which were presented in Fig. 9 of Paper I in the WKB limit. The presence of positive blue contours of
illustrated in Fig. D.3 are in the same order of magnitude as the ones which were presented in Fig. 9 of Paper I in the WKB limit. The presence of positive blue contours of 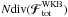 is also in agreement with a secular heating of the disc (i.e. an increase of Jr). However, these contours do not display a narrow resonant ridge as was observed in S12’s simulation or in Fig. 4.
is also in agreement with a secular heating of the disc (i.e. an increase of Jr). However, these contours do not display a narrow resonant ridge as was observed in S12’s simulation or in Fig. 4.
 |
Fig. D.2 Illustration of the radial basis elements of the ℓ = 2 Kalnajs basis elements for kKa = 7, defined in Appendix A, which were used in the estimation of the Balescu-Lenard diffusion flux in Sect. 4.2. As the radial index n increases, the basis elements get more and more wound. |
 |
Fig. D.3 Map of |
Appendix E: Sampling of the DF
In order to use the N-body integrator described in Sect. 5, one has to sample the particles according to the DF given by Eq. (49). We introduce the probability distribution function Fsp, normalised to 1 and thanks to which the sampling is performed. This probability DF Fsp is directly proportional to the active distribution function Fstar from Eq. (49), so that we may write ![\appendix \setcounter{section}{5} \begin{equation} F_{\rm sp} (E , L) = C_{\rm sp} \, L^{q} \exp [ -E / \sigma_{r}^{2} ] \, T_{\rm inner} (L) \, T_{\rm outer} (L) , \label{definition_F_sampling} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq520.png) (E.1)where Csp is a normalisation constant which is determined in the upcoming calculations. Because the mapping (E,L) → (Jr,Jφ) from Eq. (12) is not a trivial one, we do not perform the sampling of the stars in the action space (Jr,Jφ), but rather in the (E,L)-space. Moreover, one should pay attention to the fact that the DF Fsp from Eq. (E.1) is a probability distribution function in the (x,v)-space, so that d2xd2vFsp(x,v) is proportional to the number of particles in the infinitesimal volume d2xd2v around the position (x,v). As we want to sample the particles in the (E,L)-space, we introduce the function hsp(E,L) such that dEdLhsp(E,L) is proportional to the number of particles in the volume dEdL around the location (E,L). One can now determine hsp(E,L) as a function of F(E,L). Indeed, we have
(E.1)where Csp is a normalisation constant which is determined in the upcoming calculations. Because the mapping (E,L) → (Jr,Jφ) from Eq. (12) is not a trivial one, we do not perform the sampling of the stars in the action space (Jr,Jφ), but rather in the (E,L)-space. Moreover, one should pay attention to the fact that the DF Fsp from Eq. (E.1) is a probability distribution function in the (x,v)-space, so that d2xd2vFsp(x,v) is proportional to the number of particles in the infinitesimal volume d2xd2v around the position (x,v). As we want to sample the particles in the (E,L)-space, we introduce the function hsp(E,L) such that dEdLhsp(E,L) is proportional to the number of particles in the volume dEdL around the location (E,L). One can now determine hsp(E,L) as a function of F(E,L). Indeed, we have 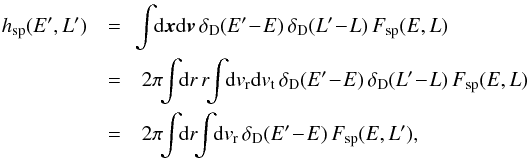 (E.2)using the fact that the tangential velocity satisfies vt = L/r. The last step is then to perform the change of variable vr → E. One has
(E.2)using the fact that the tangential velocity satisfies vt = L/r. The last step is then to perform the change of variable vr → E. One has 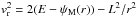 , so that
, so that 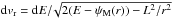 . Because the radial velocity can be both positive and negative, Eq. (E.2) takes the form
. Because the radial velocity can be both positive and negative, Eq. (E.2) takes the form 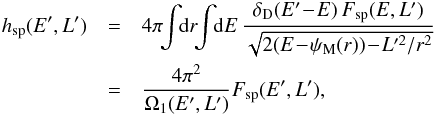 (E.3)where we used the definition (13) of the radial intrinsic frequency Ω1. One can then correctly normalise the probability distribution hsp and determine the value of the constant Csp from Eq. (E.1). One should pay attention to the fact that in addition to the tapering functions Tinner and Touter from Eqs. (48), we also assume that no stars have orbits that extend beyond Rmax. As a consequence, the allowed region in the (E,L)-space has to satisfy two constraints. First of all, the angular momentum Lstar has to satisfy
(E.3)where we used the definition (13) of the radial intrinsic frequency Ω1. One can then correctly normalise the probability distribution hsp and determine the value of the constant Csp from Eq. (E.1). One should pay attention to the fact that in addition to the tapering functions Tinner and Touter from Eqs. (48), we also assume that no stars have orbits that extend beyond Rmax. As a consequence, the allowed region in the (E,L)-space has to satisfy two constraints. First of all, the angular momentum Lstar has to satisfy 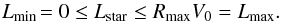 (E.4)Then, for a given value of Lstar, one can show that the energy of the star Estar must satisfy the constraint
(E.4)Then, for a given value of Lstar, one can show that the energy of the star Estar must satisfy the constraint ![\appendix \setcounter{section}{5} \begin{equation} E_{\rm min} (L_{\rm star}) = \psi_{\rm M} \bigg[ \frac{L_{\rm star}}{V_{0}} \bigg] \!+\! \frac{V_{0}^{2}}{2} \!\leq\! E_{\rm star} \!\leq\! \frac{L_{\rm star}^{2}}{2 R_{\rm max}^{2}} = E_{\rm max} (L_{\rm star}) . \label{constraint_Estar} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq547.png) (E.5)These two constraints allow us to completely characterise the (E,L)-space on which the sampling (E,L) has to be performed. One finally has to satisfy the constraint
(E.5)These two constraints allow us to completely characterise the (E,L)-space on which the sampling (E,L) has to be performed. One finally has to satisfy the constraint 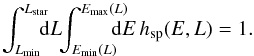 (E.6)Given the parameters presented after Eq. (49), one can numerically determine the value of the constant Csp which reads
(E.6)Given the parameters presented after Eq. (49), one can numerically determine the value of the constant Csp which reads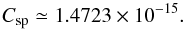 (E.7)We may now proceed to the sampling of the coordinates of the particles. Up to the sign of its radial velocity, one star is characterised by the set {Estar,Lstar,Rstar,φstar }. Given that the initial state is axisymmetric, the azimuthal angle of the star can be uniformly sampled between 0 and 2π. The next step is then to successively sample (Lstar,Estar) and finally Rstar, using successive rejection samplings as we now detail.
(E.7)We may now proceed to the sampling of the coordinates of the particles. Up to the sign of its radial velocity, one star is characterised by the set {Estar,Lstar,Rstar,φstar }. Given that the initial state is axisymmetric, the azimuthal angle of the star can be uniformly sampled between 0 and 2π. The next step is then to successively sample (Lstar,Estar) and finally Rstar, using successive rejection samplings as we now detail.
The heart of the rejection sampling is as follows. Let us assume that we want to generate sampling values from a function f(x), from which it is difficult to sample. However, we assume that we have at our disposal another distribution function g(x) from which the sampling is simple, and such that there exists a bound M> 1 satisfying f(x) <Mg(x). The smaller M, the more efficient the sampling. One then has to proceed as follows: sample both a proposal x from g and u uniformly between [ 0;1 ]. One then applies the selection ![\appendix \setcounter{section}{5} \begin{equation} \alpha = \frac{f (x)}{M g(x)} {:} \; \begin{cases} \displaystyle u < \alpha \; \Longrightarrow \; x \text{is kept.} \\[1mm] \displaystyle u \geq \alpha \; \Longrightarrow \; x \text{is rejected.} \end{cases} \label{presentation_rejection_sampling} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq563.png) (E.8)In order to have an efficient sampling, one should try to consider a function g close to f.
(E.8)In order to have an efficient sampling, one should try to consider a function g close to f.
We may now directly sample (E,L) thanks to this algorithm. The true sampling function is f(E,L) = hsp from Eq. (E.2). The simple sampling function is g(E,L) ∝ 1, defined on the domain characterised by the constraints from Eqs. (E.4) and (E.5). When performing a rejection sampling with such a uniform g(E,L), in order to determine the bound M(E,L), one only has to determine a uniform bound for f(E,L). With the numerical values introduced after Eq. (49), one can check that f(E,L) is such that 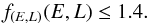 (E.9)The final element required to be able to perform the rejection sampling with f(E,L) is to be able to draw uniformly candidate (E,L) in the domains defined by the constraints from Eqs. (E.4) and (E.5), which is equivalent as sampling candidates (E,L) from the uniform probability distribution function g(E,L). To perform this uniform sampling, since the constraints from Eq. (E.5) are expressed for a given value of Lstar, it is more natural to first draw Lstar and then Estar. The probability distribution according to which Lstar has to be drawn is of the form fL(L) ∝ (Emax(L) − Emin(L)). When correctly normalised, it reads
(E.9)The final element required to be able to perform the rejection sampling with f(E,L) is to be able to draw uniformly candidate (E,L) in the domains defined by the constraints from Eqs. (E.4) and (E.5), which is equivalent as sampling candidates (E,L) from the uniform probability distribution function g(E,L). To perform this uniform sampling, since the constraints from Eq. (E.5) are expressed for a given value of Lstar, it is more natural to first draw Lstar and then Estar. The probability distribution according to which Lstar has to be drawn is of the form fL(L) ∝ (Emax(L) − Emin(L)). When correctly normalised, it reads ![\appendix \setcounter{section}{5} \begin{equation} f_{L} (L) = \frac{3}{2} \frac{1}{R_{\rm max} V_{0}} \left[ \frac{L^{2}}{2 R_{\rm max}^{2} V_{0}^{2}} \!-\! \frac{1}{2} \!-\! \log \left[ \frac{L}{R_{\rm max} V_{0}} \right] \right] \cdot \label{pdf_Lstar} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq573.png) (E.10)To sample L from fL, we use another rejection sampling by introducing the additional simple probability distribution function gL defined as
(E.10)To sample L from fL, we use another rejection sampling by introducing the additional simple probability distribution function gL defined as ![\appendix \setcounter{section}{5} \begin{equation} g_{L} (L) = - \frac{1}{R_{\rm max} V_{0}} \log \left[ \frac{L}{R_{\rm max} V_{0}} \right] \cdot \label{pdf_g_Lstar} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq576.png) (E.11)It is straightforward to check that fL< (3 / 2) gL, so that we may use the bound ML = 3 / 2 to perform the rejection sampling of Lstar. The final remark is to note that sampling L from gL is simple since its cumulative distribution function
(E.11)It is straightforward to check that fL< (3 / 2) gL, so that we may use the bound ML = 3 / 2 to perform the rejection sampling of Lstar. The final remark is to note that sampling L from gL is simple since its cumulative distribution function 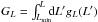 can be inverted so as to read
can be inverted so as to read ![\appendix \setcounter{section}{5} \begin{equation} G_{L}^{-1} (u) = R_{\rm max} V_{0} \exp \bigg[ 1 \!+\! W_{-1} \bigg(\! - \frac{u}{\text{e}} \bigg) \bigg] , \label{inverse_cumulative_g_Lstar} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq580.png) (E.12)where W-1 is the lower branch of the Lambert function W(x) for x ∈ [ −1 / e ;0 ]. With all these elements, the rejection sampling of Lstar following fL from Eq. (E.10) can be performed.
(E.12)where W-1 is the lower branch of the Lambert function W(x) for x ∈ [ −1 / e ;0 ]. With all these elements, the rejection sampling of Lstar following fL from Eq. (E.10) can be performed.
Once Lstar has been drawn, it only remains to sample uniformly Estar on the interval Estar ∈ [ Emin(Lstar) ;Emax(Lstar) ], as given by Eq. (E.4). Thanks to these uniformly drawn candidates (Estar,Lstar) and the uniform bound from Eq. (E.9), one can perform the rejection sampling from the probability distribution f(E,L).
For Estar and Lstar succesfully sampled, one may then sample the radius Rstar using a similar rejection sampling. The radius has to be sampled according to the probability distribution fR given by 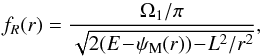 (E.13)so that one has fR ∝ vr. However, one should note that for r → rp/a, one has fR(r) → + ∞, so that the rejection sampling cannot be used without considering a probability DF g which also diverges for r → rp/a. In order to get rid of these divergences, instead of sampling the variable r, we sample the angle u ∈ [ −π/2 ;π/2 ], where we defined the mapping r → u(r) as
(E.13)so that one has fR ∝ vr. However, one should note that for r → rp/a, one has fR(r) → + ∞, so that the rejection sampling cannot be used without considering a probability DF g which also diverges for r → rp/a. In order to get rid of these divergences, instead of sampling the variable r, we sample the angle u ∈ [ −π/2 ;π/2 ], where we defined the mapping r → u(r) as 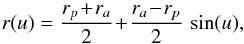 (E.14)so that one naturally has r(−π/2) = rp and r(π/2) = ra. The probability distribution function from which u has to be sampled is immediately given by
(E.14)so that one naturally has r(−π/2) = rp and r(π/2) = ra. The probability distribution function from which u has to be sampled is immediately given by 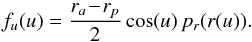 (E.15)Using the fact that the maximum of fu is reached for u = π/2, one can then sample u from fu using a rejection sampling with a uniform control probability distribution function gu(u) = 1 /π. Once u is known, it only remains to compute Rstar = r(ustar), so that the sampling of all the required quantities for one star has been performed.
(E.15)Using the fact that the maximum of fu is reached for u = π/2, one can then sample u from fu using a rejection sampling with a uniform control probability distribution function gu(u) = 1 /π. Once u is known, it only remains to compute Rstar = r(ustar), so that the sampling of all the required quantities for one star has been performed.
The final step of the sampling of the particles is to determine the physical coordinates of the particles (x,v) associated with the set {Estar,Lstar,Rstar,φstar }. These physical coordinates are the ones which are given to the N-body integrator. We draw uniformly the sign of the radial velocity εr ∈ {−1,1 }. Because we are considering a disc made only of prograde stars, one immediately obtains that the radial and tangential velocities vr and vt are given by 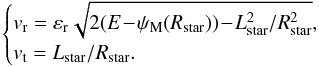 (E.16)The final step of the transformation to the (x,v)-coordinates is then straightforward, since one naturally has
(E.16)The final step of the transformation to the (x,v)-coordinates is then straightforward, since one naturally has 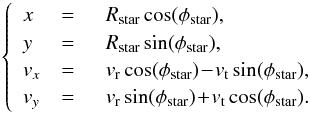 (E.17)One should note that the sampling procedure described previously does not correspond to a quiet start procedure (Sellwood 1983), which would lead to a reduction of the initial shot noise within the disc, as briefly discussed in Appendix C, with regard to the validation of the N-body code.
(E.17)One should note that the sampling procedure described previously does not correspond to a quiet start procedure (Sellwood 1983), which would lead to a reduction of the initial shot noise within the disc, as briefly discussed in Appendix C, with regard to the validation of the N-body code.
Appendix F: Another test of the scaling with N
One difficulty with the measurement of the scaling with N presented in Sect. 5.2 is that one has to disentangle the contributions from the initial sampling Poisson shot noise present through h0 from Eq. (59) and the effects due to the collisional Balescu-Lenard diffusion scaling through h2 from Eq. (64). Indeed, Poisson shot noise leads to fluctuations of the system DF about its mean value. In order not to be sensitive to such fluctuations, one could only consider fluctuations sufficiently large, i.e. fluctuations caused by an effective secular diffusion rather than caused by inevitable Poisson fluctuations. As a consequence, by restricting ourselves only to large fluctuations, we can get rid of Poisson’s effects. We therefore define the function 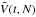 as
as ![\appendix \setcounter{section}{6} \begin{equation} \tilde{V} (t, N) = \!\! \int \!\! \mathrm{d} \bm{J} \, \chi \left[ \left\langle F (t , \bm{J} , N) \right\rangle \!-\! \left\langle F (t= 0 , \bm{J} , N) \right\rangle \!<\! C_{\tilde{V}} \right] , \label{definition_V} \end{equation}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq610.png) (F.1)where we introduced a threshold
(F.1)where we introduced a threshold 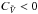 . Here χ [·] is a characteristic function equal to 1 if
. Here χ [·] is a characteristic function equal to 1 if 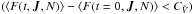 , and 0 otherwise. As a consequence,
, and 0 otherwise. As a consequence, 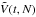 measures the volume in action space of the regions (depleted from particles, since
measures the volume in action space of the regions (depleted from particles, since 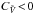 ) for which the mean DF has changed by more than
) for which the mean DF has changed by more than 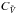 . For a sufficiently large value of the threshold
. For a sufficiently large value of the threshold 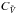 , such a construction allows us not to be polluted by Poisson sampling shot noise. For the initial times, as in Eq. (50), it is straightforward to study the scaling of
, such a construction allows us not to be polluted by Poisson sampling shot noise. For the initial times, as in Eq. (50), it is straightforward to study the scaling of 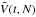 with t and N.
with t and N.
 |
Fig. F.1 Top panel: illustration of the behaviour of the function |
Indeed, one can write 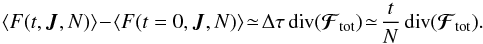 (F.2)\newpage
(F.2)\newpage
Introducing ![\hbox{${\tilde{V}_{0} = \int \! \mathrm{d} \bm{J} \, \chi \left[ \text{div} (\bm{\mathcal{F}}_{\rm tot}) \!<\! C_{\tilde{V}} \right] }$}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq626.png) , one can rewrite Eq. (F.2) as
, one can rewrite Eq. (F.2) as 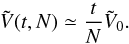 (F.3)Therefore, for a fixed value of N, one expects to observe a linear time dependence of the function
(F.3)Therefore, for a fixed value of N, one expects to observe a linear time dependence of the function 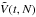 , as illustrated in Fig. F.1. In order to test the scaling of Eq. (F.3) with N, one may proceed as follows. Introducing a threshold value
, as illustrated in Fig. F.1. In order to test the scaling of Eq. (F.3) with N, one may proceed as follows. Introducing a threshold value  , for each value of N, we define the associated threshold time tthold(N) as
, for each value of N, we define the associated threshold time tthold(N) as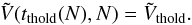 (F.4)Thanks to the scalings from Eq. (F.3), one immediately obtains that
(F.4)Thanks to the scalings from Eq. (F.3), one immediately obtains that 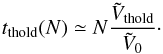 (F.5)Such a linear scaling of tthold(N) with N is a prediction from the Balescu-Lenard formalism and is nicely recovered in Fig. F.1.
(F.5)Such a linear scaling of tthold(N) with N is a prediction from the Balescu-Lenard formalism and is nicely recovered in Fig. F.1.
Appendix G: Distributed code description
For the sake of reproducibility, which has been lacking in the context of the linear response of stellar systems, we distribute the linear matrix response code we wrote for this paper both as a Mathematica package6, and a notebook7. The functions therein allow for:
-
The determination as a function of (rp,ra) of the orbits quantites: E, L, Jr, Ω1 and Ω2.
-
The construction of the 2D basis from Kalnajs (1976).
-
The computation of the Fourier transform w.r.t. the angles, i.e. the computation of
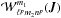 from Eq. (21).
from Eq. (21). -
The calculation of the 2D response matrix via Eq. (33).
It has been tested for the isochrone and the Mestel discs. A copy of the code is also available at the CDS.
A similar dynamical phase transition has been observed (Campa et al. 2008) in a toy model of systems with long-range interactions called the Hamiltonian Mean Field (HMF) model. During the slow collisional evolution, because of finite-N effects, the distribution function of the system changes with time. In certain cases, the system may become dynamically (Vlasov) unstable and undergo a rapid phase transition from a homogeneous phase to an inhomogeneous phase. This phase transition can be monitored by the magnetisation (see Fig. 1 of Campa et al. 2008) which is an order parameter playing a role similar to Σ2(t,N).
One could also check that the disc’s distribution function corresponds at that stage to an unstable configuration, using the matrix method described in Appendix C.
See also Earn & Sellwood (1995) for a similar rewriting of the basis normalisations.
Acknowledgments
We thank the referee, James Binney, for numerous valuable comments. J.B.F. thanks the Institute of Astronomy, Cambridge, for hospitality while this investigation was initiated. J.B.F. and C.P. also thank the theoretical physics sub-department, Oxford, for hospitality and the CNRS-Oxford exchange program for funding. J.B.F., C.P. and P.H.C. also thank the CNRS Inphyniti program for funding. C.P. thanks Clare and Churchill college, Cambridge, the French embassy and the community of http://mathematica.stackexchange.com for their help. J.M. thanks the Institut d’Astrophysique de Paris for their hospitality and the Ville de Paris for a “Research in Paris” award. We thank Donald Lynden-Bell, John Papaloizou, Walter Dehnen, Rebekka Bieri, Laura Monk, Gordon Ogilvie, Dmitry Pogosyan and Simon Prunet for stimulating discussions, and Eric Pharabod for his help with Fig. 4. Special thanks to Stephane Rouberol for customising the Horizon cluster for our purposes. This work is partially supported by the Spin(e) grants ANR-13-BS05-0005 of the French Agence Nationale de la Recherche (http://cosmicorigin.org) and by the LABEX Institut Lagrange de Paris (under reference ANR-10-LABX-63) which is funded by ANR-11-IDEX-0004-02.
References
- Aumer, M., & Binney, J. J. 2009, MNRAS, 397, 1286 [NASA ADS] [CrossRef] [Google Scholar]
- Balescu, R. 1960, Phys. Fluids, 3, 52 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics, 2nd edn., Princeton Series in Astrophysics (Princeton University Press) [Google Scholar]
- Born, M. 1960, The Mechanics of the Atom (F. Ungar Pub. Co.) [Google Scholar]
- Campa, A., Chavanis, P.-H., Giansanti, A., & Morelli, G. 2008, Phys. Rev. E, 78, 040102 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1942, Principles of Stellar Dynamics (University of Chicago Press) [Google Scholar]
- Chavanis, P.-H. 2012, Physica A, 391, 3680 [NASA ADS] [CrossRef] [Google Scholar]
- Chavanis, P.-H. 2013, A&A, 556, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Codis, S., Pichon, C., Devriendt, J., et al. 2012, MNRAS, 427, 3320 [NASA ADS] [CrossRef] [Google Scholar]
- Codis, S., Pichon, C., & Pogosyan, D. 2015, MNRAS, 452, 3369 [Google Scholar]
- Dehnen, W. 1998, AJ, 115, 2384 [NASA ADS] [CrossRef] [Google Scholar]
- Earn, D. J. D., & Sellwood, J. A. 1995, ApJ, 451, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, N. W., & Read, J. C. A. 1998a, MNRAS, 300, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, N. W., & Read, J. C. A. 1998b, MNRAS, 300, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Fouvry, J.-B., Pichon, C., & Chavanis, P.-H. 2015a, A&A, 581, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fouvry, J.-B., Pichon, C., & Prunet, S. 2015b, MNRAS, 449, 1967 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Lynden-Bell, D. 1965, MNRAS, 130, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Goldstein, H. 1950, Classical mechanics (Addison-Wesley) [Google Scholar]
- Heyvaerts, J. 2010, MNRAS, 407, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Hörmander, L. 2003, The analysis of linear partial differential operators. I, Classics in Mathematics (Springer-Verlag) [Google Scholar]
- Jeans, J. 1929, Astronomy and Cosmogony (Cambridge Univ. Press) [Google Scholar]
- Julian, W. H., & Toomre, A. 1966, ApJ, 146, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Kalnajs, A. J. 1972, in IAU Colloq. 10: Gravitational N-Body Problem, ed. M. Lecar, Astrophys. Space Sci. Lib., 31, 13 [Google Scholar]
- Kalnajs, A. J. 1976, ApJ, 205, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Landau, L. 1936, Phys. Z. Sowj. Union, 10, 154 [Google Scholar]
- Lenard, A. 1960, Annals of Physics, 10, 390 [Google Scholar]
- Lynden-Bell, D. 1979, MNRAS, 187, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D., & Kalnajs, A. J. 1972, MNRAS, 157, 1 [NASA ADS] [CrossRef] [Google Scholar]
- McMillan, P. J. 2013, MNRAS, 430, 3276 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Mestel, L. 1963, MNRAS, 126, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Penrose, O. 1960, Phys. Fluids, 3, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Pichon, C. 1994, Ph.D. Thesis, University of Cambridge [Google Scholar]
- Pichon, C., & Cannon, R. C. 1997, MNRAS, 291, 616 [NASA ADS] [CrossRef] [Google Scholar]
- Pichon, C., & Lynden-Bell, D. 1993, in Statistical Description of Transport in Plasma, Astro- and Nuclear Physics, eds. J. Misquich, G. Pelletier, & P. Schuck, 261 [Google Scholar]
- Quinlan, G. D., & Tremaine, S. 1992, MNRAS, 259, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenbluth, M., MacDonald, W., & Judd, D. 1957, Phys. Rev., 107, 1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Sellwood, J. A. 1983, J. Computat. Phys., 50, 337 [Google Scholar]
- Sellwood, J. A. 2010, MNRAS, 409, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A. 2012, ApJ, 751, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A., & Evans, N. W. 2001, ApJ, 546, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Toomre, A. 1964, ApJ, 139, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Toomre, A. 1977, ARA&A, 15, 437 [CrossRef] [Google Scholar]
- Toomre, A. 1981, in Structure and Evolution of Normal Galaxies, eds. S. M. Fall, & D. Lynden-Bell, 111 [Google Scholar]
- Tremaine, S., & Weinberg, M. D. 1984, MNRAS, 209, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Vlasov, A. 1938, Zh. Eksp. i Teor Fiz., 8, 291 [Google Scholar]
- Weinberg, M. D. 1993, ApJ, 410, 543 [Google Scholar]
- Wielen, R. 1977, A&A, 60, 263 [NASA ADS] [Google Scholar]
- Zang, T. A. 1976, Ph.D. Thesis, Massachusetts Institute of Technology [Google Scholar]
All Tables
Measurements of the pattern speed ω0 = mφΩp and growth rate η = s for unstable mφ = 2 modes of tapered Mestel discs.
All Figures
 |
Fig. 1 Contours of the initial distribution function Fstar from Eq. (49), in action space (Jφ,Jr). The contours are spaced linearly between 95% and 5% of the distribution function maximum. |
| In the text | |
 |
Fig. 2 Illustration of 4 different critical resonant lines in the (rp,ra)-space. As defined in Eq. (41), a critical line is characterised by the resonant vectors m1, m2 and a location |
| In the text | |
 |
Fig. 3 Map of −Nℱtot, where the flux has been computed with m1,m2 ∈ {mILR,mCOR,mOLR}. Following Eq. (11), −Nℱtot corresponds to the direction of diffusion of individual particles in action-space. |
| In the text | |
 |
Fig. 4 Left panel: map of Ndiv(ℱtot), where the total flux has been computed with m1,m2 ∈ {mILR,mCOR,mOLR}. Red contours, for which Ndiv(ℱtot) < 0 are associated with regions from which the orbits will be depleted, whereas blue contours, for which Ndiv(ℱtot) > 0 correspond to regions where the value of the DF will be increased during the secular diffusion. The contours are spaced linearly between the minimum and the maximum of Ndiv(ℱtot). The maximum value for the positive blue contours corresponds to Ndiv(ℱtot) ≃ 350, while the mininum value for the negative red contours is associated with Ndiv(ℱtot) ≃ −250. Right panel: from Sellwood (2012) – Fig. 7, contours of the change in the DF between the time tS12 = 1400 and tS12 = 0, for a run with 50M particles. Similarly to the left panel, red contours correspond to negative differences, i.e. regions emptied from their orbits, while blue contours correspond to positive differences, i.e. regions where the DF has increased during the diffusion. Both of these contours are aligned with the ILR direction of mILR = (2,−1) in the (Jφ,Jr)-plane, corresponding to the cyan line. |
| In the text | |
 |
Fig. 5 Illustration of the behaviour of the function |
| In the text | |
 |
Fig. 6 Top panel: illustration of the behaviour of the function |
| In the text | |
 |
Fig. 7 Top panel: illustration of the behaviour of the function |
| In the text | |
 |
Fig. 8 Map of Ndiv(ℱtot) with an active fraction ξ = 0.6 and using the same conventions as in Fig. 4. The contours are spaced linearly between the minimum and the maximum of Ndiv(ℱtot). The maximum value for the positive blue contours corresponds to Ndiv(ℱtot) ≃ 4200, while the minimum value for the negative red contours corresponds to Ndiv(ℱtot) ≃ −3200. As expected, one recovers that when the active fraction of the disc is increased, the susceptibility of the disc is increased, so that the norm of Ndiv(ℱtot) gets larger and the secular diffusion is fastened. |
| In the text | |
 |
Fig. 9 Behaviour of the function |
| In the text | |
 |
Fig. 10 Illustration of the active surface density Σt for a N-body run with N = 8 × 105, restriced to the range R ≤ 6. Top panel: active surface density Σt at an early time t = 60, for which the galaxy remains globally axisymmetric. In this regime, the dynamics of the system is collisional and governed by the Balescu-Lenard Eq. (2). Bottom panel: active surface density Σt at a much later time t = 2400. The galaxy is then strongly non-axisymmetric. In this regime, the dynamics of the system is collisionless and governed by the Vlasov equation. |
| In the text | |
 |
Fig. C.1 Top panel: zoomed Nyquist contours in the complex plane of |
| In the text | |
 |
Fig. C.2 Unstable mode for the truncated νt = 4 Mestel disc recovered via the matrix method presented in Sect. 3. Only positive contour levels are shown and are spaced linearly between 10% and 90% of the maximum norm. The radii associated with the resonances ILR, COR and OLR have been represented, as given by ω0 = m·Ω(Rm), where the intrinsic frequencies Ω(R) = (Ωφ(R),κ(R)) have to be computed within the epicyclic approximation. For a Mestel disc, they are given by Ωφ(R) = V0/R and |
| In the text | |
 |
Fig. C.3 Measurement of the growth rate η and pattern speed ω0 of the mφ = 2 unstable modes of truncated Mestel discs with a random velocity given by q = 6 for various values of the truncation index νt = 6, 8. The basis coefficient plotted is associated with the basis element (ℓ,n) = (2,0), using the same basis elements as for the matrix method in Sect. 4.2. |
| In the text | |
 |
Fig. C.4 Unstable mode for the truncated νt = 4 Mestel disc recovered via direct N-body simulations as presented in Sect. 5. Only positive contour levels are shown and are spaced linearly between 20% and 80% of the maximum norm. Similarly to Fig. C.2, the radii associated with the resonances ILR, COR and OLR have been represented. |
| In the text | |
 |
Fig. D.1 Map of |
| In the text | |
 |
Fig. D.2 Illustration of the radial basis elements of the ℓ = 2 Kalnajs basis elements for kKa = 7, defined in Appendix A, which were used in the estimation of the Balescu-Lenard diffusion flux in Sect. 4.2. As the radial index n increases, the basis elements get more and more wound. |
| In the text | |
 |
Fig. D.3 Map of |
| In the text | |
 |
Fig. F.1 Top panel: illustration of the behaviour of the function |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



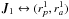
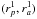
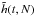
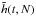
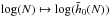
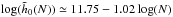
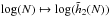
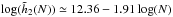
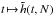
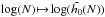
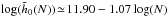
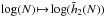
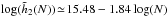
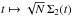
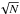
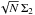
![\hbox{${\omega_{0} \mapsto \log \big| \! \det \big[ \mathbf{I} - \widehat{\mathbf{M}}(\omega_{0},\eta) \big] \big| }$}](/articles/aa/full_html/2015/12/aa27052-15/aa27052-15-eq456.png)