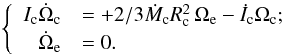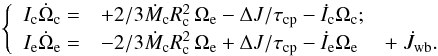| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A30 | |
| Number of page(s) | 16 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201526770 | |
| Published online | 17 November 2015 | |
Rotational evolution of slow-rotator sequence stars
1 Università di Catania, Dipartimento di Fisica e Astronomia, Sezione Astrofisica, via S. Sofia 78, 95123 Catania, Italy
e-mail: Alessandro.Lanzafame@oact.inaf.it
2 INAF–Osservatorio Astrofisico di Catania, via S. Sofia 78, 95123 Catania, Italy
3 Leibniz-Institut für Astrophysik Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
Received: 17 June 2015
Accepted: 16 September 2015
Context. The observed relationship between mass, age and rotation in open clusters shows the progressive development of a slow-rotator sequence among stars possessing a radiative interior and a convective envelope during their pre-main sequence and main-sequence evolution. After 0.6 Gyr, most cluster members of this type have settled on this sequence.
Aims. The observed clustering on this sequence suggests that it corresponds to some equilibrium or asymptotic condition that still lacks a complete theoretical interpretation, and which is crucial to our understanding of the stellar angular momentum evolution.
Methods. We couple a rotational evolution model, which takes internal differential rotation into account, with classical and new proposals for the wind braking law, and fit models to the data using a Monte Carlo Markov chain (MCMC) method tailored to the problem at hand. We explore to what extent these models are able to reproduce the mass and time dependence of the stellar rotational evolution on the slow-rotator sequence.
Results. The description of the evolution of the slow-rotator sequence requires taking the transfer of angular momentum from the radiative core to the convective envelope into account. We find that, in the mass range 0.85–1.10 M⊙, the core-envelope coupling timescale for stars in the slow-rotator sequence scales as M-7.28. Quasi-solid body rotation is achieved only after 1–2 Gyr, depending on stellar mass, which implies that observing small deviations from the Skumanich law ( ) would require period data of older open clusters than is available to date. The observed evolution in the 0.1–2.5 Gyr age range and in the 0.85–1.10 M⊙ mass range is best reproduced by assuming an empirical mass dependence of the wind angular momentum loss proportional to the convective turnover timescale and to the stellar moment of inertia. Period isochrones based on our MCMC fit provide a tool for inferring stellar ages of solar-like main-sequence stars from their mass and rotation period that is largely independent of the wind braking model adopted. These effectively represent gyro-chronology relationships that take the physics of the two-zone model for the stellar angular momentum evolution into account.
) would require period data of older open clusters than is available to date. The observed evolution in the 0.1–2.5 Gyr age range and in the 0.85–1.10 M⊙ mass range is best reproduced by assuming an empirical mass dependence of the wind angular momentum loss proportional to the convective turnover timescale and to the stellar moment of inertia. Period isochrones based on our MCMC fit provide a tool for inferring stellar ages of solar-like main-sequence stars from their mass and rotation period that is largely independent of the wind braking model adopted. These effectively represent gyro-chronology relationships that take the physics of the two-zone model for the stellar angular momentum evolution into account.
Key words: stars: rotation / stars: evolution / stars: late-type / open clusters and associations: general
© ESO, 2015
1. Introduction
In the past decade, stellar rotation has received a great deal of attention, both because of its promising potential as a precise stellar age estimator (Barnes 2007, 2010; Meibom et al. 2015) and the large amount of good quality data increasingly available, either as a byproduct of planetary transit searches or from dedicated stellar rotation observational programs (see, e.g. Herbst & Mundt 2005; Hodgkin et al. 2006; von Braun et al. 2005; Messina 2007; Messina et al. 2008, 2010). Rotation periods of young stars can in principle be derived with a precision of 10-4 using photometric monitoring, with surface differential rotation being probably the most important limiting factor for individual old stars (see, e.g. Epstein & Pinsonneault 2014).
Clusters data used in this work.
The realization by Barnes (2003) of the existence of a well-defined sequence of slowly rotating stars in the young open clusters color-period diagram has provided a criterion for establishing an empirical relationship between mass, age and rotation, which can be used to infer the age of stars that are sufficiently old to belong to that sequence. Barnes (2003) effectively disentangled the convergence of stellar periods towards a unique slow-rotator sequence, seen as a progressive reduction of the scatter that is due to the presence of fast rotators (from very young clusters to the Hyades), from the rotational evolution of stars in this sequence, which dominates the color-period diagram from the Hyades onwards. Subsequently, Barnes (2007) provided a calibration of his rotation-mass-age relationship using the observed rotation-mass distribution in open clusters and the solar age, rotation period and (B−V). More recently, Barnes & Kim (2010) provided evidence of a connection between the empirical rotation period functional dependence on (B−V) and the convective turnover timescale τ. Based on this, Barnes (2010) derived a nonlinear model formulated in terms of the Rossby number (Ro = P/τ) and two dimensionless empirical constants, which describes the rotational evolution towards the slow-rotator sequence.
In this work we focus on the rotational evolution of stars already on the slow-rotator sequence and study how well the current models are able to reproduce such evolution. We focus on the age interval between 0.1 and 2.5 Gyr, for which data with the richest details is available, providing strong constraints on the models. The observed clustering on this sequence in the mass-age-period space suggests that it corresponds to some equilibrium or asymptotic condition that still lacks a complete theoretical interpretation and may be crucial to our understanding of the stellar angular momentum evolution.
Data that has become available in recent years has revealed an evolutionary behavior of the slow-rotator sequence that seems difficult to reconcile with the original Barnes (2003) idea of a factorization of the time and mass dependence. Notably, in their study of rotation in M35 and M34, Meibom et al. (2009, 2011b) found that while G-type stars on the slow-rotator sequence spin down with a rate close to the Skumanich 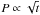 law, K-type stars spin down more slowly.
law, K-type stars spin down more slowly.
On the theoretical side, recent work concentrated on improving the description of the magnetic braking due to coupling between the stellar wind and magnetic fields generated by an internal stellar dynamo. Matt et al. (2012) performed two-dimensional axisymmetric magnetohydrodynamic simulations to compute steady-state solutions for solar-like stellar winds from rotating stars with dipolar magnetic fields, from which they derived a semi-analytic formulation for the external torque on the star. Gallet & Bouvier (2013) derived the angular momentum loss rate using the Matt et al. (2012) equation for the Alfvén radius together with a dynamo prescription that relates the stellar magnetic field to stellar rotation, as well as a wind prescription that relates the mass-loss rate to the stellar angular velocity, obtained from current theory and calibrated to the present-day Sun. Given the current uncertainties on the stellar magnetic fields and on the wind mass-loss, however, Matt et al. (2015) derived a scaling for the dependence of the stellar wind braking on Rossby number and an empirically derived scaling with stellar mass and radius.
In this work, we include these various wind braking laws in the classical two-zone description of the stellar rotational evolution and investigate to what extent they reproduce the slow-rotator sequence evolution. The models are fitted to the data by means of a Monte Carlo Markov chain (MCMC) method tailored to the case at hand. Using the parameters derived by the MCMC model fitting to the data, we derive period isochrones and tracks from 0.1 to 5 Gyr that are largely independent of the specific wind braking law adopted. These effectively represent gyro-chronology relationships that take the effects of differential rotation in the period evolution into account.
The paper is organized as follows. In Sect. 2 we discuss the data used in the present analysis. In Sect. 3 we present an empirical description of the slow-rotator sequence, which also illustrates the current state-of-the-art, together with a novel non-parametric empirical fit of its evolution. In Sect. 4 we present the MCMC fitting method of two-zone rotational evolution models with different wind braking prescriptions. In Sect. 5 the results of the MCMC fitting to the data are presented and discussed. The conclusions are in Sect. 6.
2. Data
For this work we use literature data of stars in open clusters that show a well-defined slow-rotator sequence, easily identifiable by eye as an over-density in the period-color diagram, also known in the literature as the “I-sequence” (Barnes 2003) or “ridge” (Kovacs 2015). The age at which this sequence begins to form is still rather undetermined, but it is evident that this is already well defined at the age of the Pleiades and present in all older open clusters. A summary is reported in Table 1. The data set includes clusters from 0.1 to 2.5 Gyr for which (B−V) measurements in the relevant range are readily available. The age interval is sampled in an optimal way, in the sense that data for open clusters not considered here would not improve the age sampling in a significant way. Since our method relies on an empirical fitting of the slow-rotator sequence to start with (see Sect. 3), data for field stars are not considered. Young loose stellar associations are also not considered in this work.
Rotation periods for the Pleiades are taken from Hartman et al. (2010). This data set includes 241 single stars in common with the compilation of probable Pleiades members by Stauffer et al. (2007), which provides near- and mid-infrared photometry together with a compilation of homogenised Johnson B and V magnitudes. For the Pleiades, following Stauffer et al. (1998) we adopt an age of 120 Myr.
Meibom et al. (2009) provide rotation periods and UBVRI photometry for 310 members of M35. The age of M35 has been estimated to 150 Myr (von Hippel et al. 2002), 175 Myr (Barrado y Navascués et al. 2001), and 180 Myr (Kalirai et al. 2003). Following Meibom et al. (2009), we adopt an age of 150 Myr.
Rotation periods and reddening corrected (B−V)0 for M34 are taken from Meibom et al. (2011b). The sample contains periods for 118 stars. From the rotation period of slow-rotator sequence stars, adopting the Skumanich law, Meibom et al. (2011b) estimated an age of 240 Myr, which we also adopt here.
Hartman et al. (2009) provide a clean sample of rotation periods for 372 stars in M37. Photometry for this cluster is from Kalirai et al. (2001). Following Hartman et al. (2008) we adopt an age of 550 Myr.
The rotation period data set of Delorme et al. (2011) includes 56 members of the Hyades and 35 members of Praesepe. They also provide BV photometry collected from the literature. Following the discussion in Delorme et al. (2011), we adopt an age of 600 Myr for both clusters.
Collier Cameron et al. (2009) present a photometric survey of rotation rates in the Coma Berenices cluster containing data for 27 members with available BV photometry. Following their discussion, we adopt an age for Coma Berenices equal to the Hyades and Praesepe age (600 Myr) within the uncertainties.
Meibom et al. (2011a) provide rotation periods for 71 cluster members of NGC6811. Photometry for this cluster is provided by Janes et al. (2013). Following Meibom et al. (2011a, and references we adopt an age of 1 Gyr.
Rotation periods and photometry for NGC6819 is taken from Meibom et al. (2015), who derived a gyro-age of 2.5 Gyr in agreement with the estimate by Jeffries et al. (2013).
It is worth noting that the cluster ages adopted here do not differ significantly from the isochrone ages adopted by Kovacs (2015). In the present work, isochrone and rotational ages are assumed to coincide.
3. Empirical description of the slow-rotator sequence evolution
3.1. Empirical models
The main assumption in Barnes (2003, 2007) is that rotation periods on the slow-rotator sequence can be represented empirically by a relationship of the form 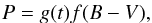 (1)where t is the stellar age and the color B−V is taken as a proxy of the stellar mass. Other authors fitted the function P = P(t,B−V) to different data sets (e.g. Meibom et al. 2009; Mamajek & Hillenbrand 2008), maintaining the same form and factorization as in Barnes (2007). Both Barnes (2007) and Mamajek & Hillenbrand (2008) derived their color-period relationship on a few well studied clusters (e.g. α Persei, Pleiades, Hyades) while the fit by Meibom et al. (2009) is based on a single cluster (M35).
(1)where t is the stellar age and the color B−V is taken as a proxy of the stellar mass. Other authors fitted the function P = P(t,B−V) to different data sets (e.g. Meibom et al. 2009; Mamajek & Hillenbrand 2008), maintaining the same form and factorization as in Barnes (2007). Both Barnes (2007) and Mamajek & Hillenbrand (2008) derived their color-period relationship on a few well studied clusters (e.g. α Persei, Pleiades, Hyades) while the fit by Meibom et al. (2009) is based on a single cluster (M35).
Barnes (2003) proposed that the mass dependence of the rotation periods in open clusters can be simply attributed to the moments of inertia of either the whole star or of the outer convection zone. This was later found inadequate by Barnes & Kim (2010), and led Barnes (2010) to the formulation of a different nonlinear empirical model, which provides the gyro-age of a star as 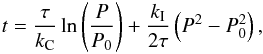 (2)where kC and kI are two dimensionless constants, constrained by the observations, and P0 is the initial rotation period, taken as the period on the zero-age main sequence. In the slow-rotator sequence limit we are concerned with, this semi-empirical formula gives
(2)where kC and kI are two dimensionless constants, constrained by the observations, and P0 is the initial rotation period, taken as the period on the zero-age main sequence. In the slow-rotator sequence limit we are concerned with, this semi-empirical formula gives 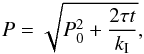 (3)which predicts that, asymptotically, P → g(t)f(B−V) with
(3)which predicts that, asymptotically, P → g(t)f(B−V) with 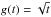 and
and 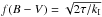 . The Barnes (2010) model gives a description of the mass-dependent evolution of fast-rotating stars to the slow-rotator sequence. An alternative description is the metastable dynamo model (MDM) of Brown (2014), which assumes a stochastic transition between two different dynamo regimes and is rooted in an original idea of Barnes (2003).
. The Barnes (2010) model gives a description of the mass-dependent evolution of fast-rotating stars to the slow-rotator sequence. An alternative description is the metastable dynamo model (MDM) of Brown (2014), which assumes a stochastic transition between two different dynamo regimes and is rooted in an original idea of Barnes (2003).
 |
Fig. 1 Rotation period scaled to the square root of age (in Myr) vs. (B−V). Periods of stars defining the slow-rotator sequence are represented with black dots, all others with gray dots. Our non-parametric fit of the slow-rotator sequence is shown as blue thick solid lines, with the Pleiades and M37 fits repeated in all panels as reference (black thin solid line and gray thick solid line respectively). The dotted line represent the f(B−V) function of Barnes (2007; B07), the dashed line that of Meibom et al. (2009; M09), the dot-dashed that of Mamajek & Hillenbrand (2008; M08), the dash-triple-dotted line the inverted Barnes (2010) relationship (Eq. (2), B10), the long-dashed line the Barnes (2010) asymptotic slow-rotator sequence limit (Eq. (3), B10a). |
The color-period diagrams for the clusters studied here are shown in Fig. 1. The stellar mass is estimated using the color-mass relationship of Barnes & Kim (2010), based on the effective temperature-color transformation of Lejeune et al. (1997, 1998). Periods are scaled to the square root of age (in Myr), so that data points would overlap in diagrams at different ages if the rotational evolution were exactly Skumanich-type. The slow-rotator sequence is easily identifiable in all clusters, with the only exception of the Pleiades and M35, for which some ambiguity may arise (see Sect. 3.2). From the comparison of the observed slow-rotator sequence at different ages it is evident that:
-
Stars withM < 1.0 M⊙ slow down at a slower rate than predicted by the Skumanich law until t ~ 0.55 Gyr.
-
From 0.55 to 2.5 Gyr, stars slow down at a faster rate than predicted by the Skumanich law, except for the NGC 6811 stars in the 0.8 ≤ M/M⊙ ≤ 0.9 mass range.
-
There is no evidence of stars of mass M < 0.8 M⊙ on the slow-rotator sequence at ages younger than 0.24 Gyr.
The current observed evolution of the slow-rotator sequence from 0.1 to 2.5 Gyr shows that the factorization expressed by Eq. (1) does not hold, at least before 0.55 Myr, because such a relationship would imply that the shape of the slow-rotator sequence is maintained throughout its evolution.
The data available contains periods for stars on the slow-rotator sequence with mass as low as M ≈ 0.5M⊙ for ages ≈0.6 Gyr, but no data for stars with M< 0.8 M⊙ is available at later ages.
In Fig. 1 we also report the f(B−V) empirical functions obtained by Barnes (2007), Meibom et al. (2009), and Mamajek & Hillenbrand (2008), as well as the inversion of Eq. (2) from Barnes (2010) and its asymptotic limit in Eq. (3). The comparison with observations shows that such relationships can describe the slow-rotator sequence only on limited age and mass ranges.
With the exception of stars of 0.8 ≤ M ≤ 0.9 M⊙ in NGC 6811, the slow-rotator sequence lies above the ≈0.55 Gyr sequence in the 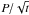 vs. (B−V) diagram. In the framework of the two-zone model (Sect. 4.1), this behavior could be attributed to the transport of angular momentum from the stellar core to the envelope in the earlier evolution after the ZAMS. We shall verify this in Sect. 4.
vs. (B−V) diagram. In the framework of the two-zone model (Sect. 4.1), this behavior could be attributed to the transport of angular momentum from the stellar core to the envelope in the earlier evolution after the ZAMS. We shall verify this in Sect. 4.
3.2. Non-parametric empirical fitting
 |
Fig. 2 Comparison of the empirical distribution function of the non-parametric fit residuals with the normal distribution function. Residuals are normalized to the standard deviation. |
In order to overcome the limitations of the empirical modeling discussed in Sect. 3.1, we perform a non-parametric fit to the slow-rotator sequence. To this end, we need a criterion for selecting the stars belonging to this sequence. For the older clusters, the selection is quite simple as only some outliers and a few remaining fast rotators need to be excluded. For the younger clusters, on the other hand, the slow-rotator sequence over-density is still easily identifiable in the color-period diagram, but the separation with stars approaching the slow-rotator sequence is somewhat arbitrary and prone to subjective choices. Slow-rotator sequence membership may become even more ill-defined if, following Barnes (2010), we consider the sequence as an asymptotic limit.
We note, however, that non-parametric fits to the older slow-rotator sequences produce residuals whose distribution can be approximated with a normal distribution. To trace back the sequence to the younger clusters with a criterion as homogeneous as possible, we set the width of the slow-rotator sequence as the maximum width that produces a distribution of residuals with a normality probability (see below) of at least 30% (see Fig. 2 and Table 2). We use the local polynomial regression fit (LOESS, Cleveland et al. 1992) with smoothing parameter between 0.8 and 1.0, and a Pearson normality test (Moore 1986; Thode Jr. 2002), as implemented in the statistical package R. In order to improve the fitting at the higher and lower end of the sequence, where the curvature is higher and a non-parametric fit would require a much denser data set, we use Eq. (3) as a normalization function, adjusting kI in order to mimic the slow-rotator sequence at ≈0.6 Gyr.
Our non-parametric fits are shown in Fig. 1, where the stars selected as members of the slow-rotator sequence are also highlighted. The non-parametric fit is used to derive periods for a grid of stellar masses, reported in Table 2 together with the standard deviation and the normality test probability. The comparisons of the empirical distribution functions of the residuals with normal distributions are shown in Fig. 2.
Our selection of stars belonging to the slow-rotator sequence in younger clusters is more restrictive than that adopted, for instance, by Barnes (2010). It should be considered, however, that the aim of the present work is to study in detail the rotational evolution of the slow-rotator sequence, under the assumption that this represents some equilibrium state or asymptotic behavior, deliberately ignoring fast rotators or stars still approaching the slow-rotator sequence. We also ignore periods much larger than the periods of the slow-rotator sequence, assuming that they are either incorrect or that these stars are not cluster members. In other words, we assume that the peak of the over-density of slow rotators in the color-period diagram corresponds to the maximum probability of having reached the equilibrium/asymptotic state and that stars in or near such a state have periods distributed normally around the peak. Such an approximation has the advantage of allowing a characterization of the width of the sequence using the standard deviation, which can then be used as input in our parametric fit described in Sect. 4. It turns out that such an approximation describes remarkably well the distribution in the older clusters, and that, by an appropriate selection, it can be extended to the younger clusters as well. For our purposes, it can safely be assumed that the standard deviation of the sequence includes both observational uncertainties and the intrinsic physical width due to the ongoing convergence onto the slow-rotator sequence.
4. Two-zone models Monte Carlo Markov chain fitting to the data
4.1. Two-zone rotational evolution models
Rotation periods from the non-parametric fit.
In our modeling of the rotational evolution of solar-like stars (whose structure is characterized by an inner radiative region, surrounded by a convective envelope), we adopt the theoretical framework of two-zone models (TZMs; see, e.g. MacGregor & Brenner 1991; Keppens et al. 1995; Allain 1998; Spada et al. 2011). The main assumption of the TZM is that the radiative interior and the convective envelope of the star rotate as rigid bodies, with angular velocities Ωc and Ωe, respectively; the rotational state of the whole star at a given time is thus completely specified by these two quantities.
During the pre-main sequence, the rotational evolution is dominated by evolutionary changes to the stellar structure (i.e., overall contraction, appearance and growth of a radiative core), and the interaction with the circumstellar disk. From the zero age main sequence onwards, the interior structure changes very little, and the rotational evolution essentially depends on the interplay between the angular momentum loss at the surface, due to the magnetized stellar wind, and the angular momentum exchange between core and envelope. These main physical ingredients are included in our models as follows:
-
The radiative core grows at the expenses of the sur-rounding envelope, thus subtracting from it the an-gular momentum (Allain 1998):
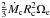 , where Mc and Rc are the mass and the radius of the core, respectively (in the following, we adopt the dot notation for derivatives with respect to time).
, where Mc and Rc are the mass and the radius of the core, respectively (in the following, we adopt the dot notation for derivatives with respect to time). -
The star-disk interaction is assumed to be very efficient, capable of keeping the surface angular velocity constant during the entire disk lifetime, τdisk (the so-called disk-locking approximation, see Koenigl 1991).
-
The rate of angular momentum loss from the surface due to the magnetized stellar wind is specified by the wind braking law
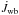 (see Sect. 4.2 for details).
(see Sect. 4.2 for details). -
Over the coupling timescale τcp, the amount of angular momentum
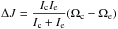 is transferred from the radiative interior to the convective envelope (see MacGregor & Brenner 1991).
is transferred from the radiative interior to the convective envelope (see MacGregor & Brenner 1991).
The TZM equations for Ωc and Ωe are therefore:
In the equations above, we have introduced the moments of inertia, Ic and Ie, of the radiative zone and of the convective envelope, respectively. Note the appearance of terms involving the time derivatives of the moments of inertia (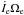 , etc.), as required by angular momentum conservation when significant structural changes take place.
, etc.), as required by angular momentum conservation when significant structural changes take place.
We begin the integration of Eqs. (4)and (5)when the star is still fully convective, when it is reasonable to assume that the star is rotating as a solid body. We thus set the initial conditions in terms of a single parameter, the initial period P0: 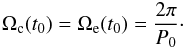 We extract the evolution of stellar structure quantities, Rc, Mc, etc., from stellar models of appropriate mass, calculated using the Yale Rotational stellar Evolution Code (YREC), in its non-rotational configuration (Demarque et al. 2008). The stellar models were calculated with initial composition and mixing length parameter αMLT calibrated on the Sun. Assuming the Grevesse & Sauval (1998) value of the solar metallicity, (Z/X)⊙ ,GS98 ≈ 0.0230, our solar calibration gives X0 = 0.7039, Y0 = 0.2773, Z0 = 0.0188, αMLT = 1.826.
We extract the evolution of stellar structure quantities, Rc, Mc, etc., from stellar models of appropriate mass, calculated using the Yale Rotational stellar Evolution Code (YREC), in its non-rotational configuration (Demarque et al. 2008). The stellar models were calculated with initial composition and mixing length parameter αMLT calibrated on the Sun. Assuming the Grevesse & Sauval (1998) value of the solar metallicity, (Z/X)⊙ ,GS98 ≈ 0.0230, our solar calibration gives X0 = 0.7039, Y0 = 0.2773, Z0 = 0.0188, αMLT = 1.826.
4.2. Wind braking laws
In our TZM framework, the wind braking law prescribes the dependence of 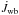 on the stellar mass (either directly or indirectly, i.e., through a dependence on other stellar structure variables), and on the surface angular velocity Ωe. In this work, we focus on the following wind braking laws:
on the stellar mass (either directly or indirectly, i.e., through a dependence on other stellar structure variables), and on the surface angular velocity Ωe. In this work, we focus on the following wind braking laws:
-
1.
The Kawaler (1988) law as modified byChaboyer et al. (1995):
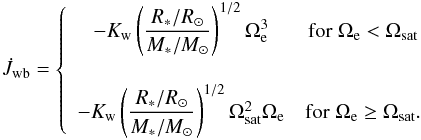 (6)Note that the dependence on
(6)Note that the dependence on 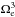 reproduces the empirical Skumanich law if the star rotates as a solid body. Our scaling of Kw requires that the numerical value given in Sect. 5 must be multiplied by 1.11 × 1047 g cm2 s to convert it into cgs units.
reproduces the empirical Skumanich law if the star rotates as a solid body. Our scaling of Kw requires that the numerical value given in Sect. 5 must be multiplied by 1.11 × 1047 g cm2 s to convert it into cgs units. -
2.
A hybrid braking law, which combines the classical Ωe dependence of Kawaler (1988) with the mass dependence suggested by Barnes & Kim (2010) and Barnes (2010) for the slow-rotator sequence:
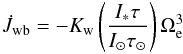 (7)where I∗ and I⊙ are the moment of inertia of the whole star and of the Sun, respectively, and Kw is an adjustable parameter with the same scaling as above.
(7)where I∗ and I⊙ are the moment of inertia of the whole star and of the Sun, respectively, and Kw is an adjustable parameter with the same scaling as above. -
3.
The braking law proposed by Gallet & Bouvier (2013). Their starting point is the very general expression
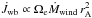 , where Ṁwind is the mass loss due to the stellar wind and rA is the Alfvèn radius, i.e., the radius of the (approximately) spherical region around the star where the wind is dominated by the magnetic field (Weber & Davis 1967). Gallet & Bouvier (2013) use an expression derived from the numerical simulation of Matt et al. (2012) to eliminate the Alfvèn radius from the braking law; their final result is
, where Ṁwind is the mass loss due to the stellar wind and rA is the Alfvèn radius, i.e., the radius of the (approximately) spherical region around the star where the wind is dominated by the magnetic field (Weber & Davis 1967). Gallet & Bouvier (2013) use an expression derived from the numerical simulation of Matt et al. (2012) to eliminate the Alfvèn radius from the braking law; their final result is ![\begin{eqnarray} \label{galletwb} \dot J_{\rm wb} = K_1^2 \, \Omega_{\rm e} \dot M_{\rm wind} \left[\frac{B_p^2R_*^2}{\dot M_{\rm wind}\sqrt{K_2^2 v_{\rm esc}^2 + \Omega_{\rm e}^2 R_*^2}} \right]^{2\,m} R_*^2 , \end{eqnarray}](/articles/aa/full_html/2015/12/aa26770-15/aa26770-15-eq83.png) (8)where
(8)where 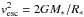 is the escape velocity at the stellar surface, Bp is the surface magnetic field and Ṁwind is the stellar mass loss rate due to the wind (see Sect. 3.3 of Gallet & Bouvier 2013, for details). In Eq. (8)the constants K1, K2, and m are fixed according to the numerical simulations of Matt et al. (2012); their values are: K1 = 1.30, K2 = 0.0506, m = 0.2177. The values of Bp and Ṁwind are calculated using the BOREAS subroutine (Cranmer & Saar 2011) with the filling factor slightly modified in order to reproduce the average filling factor of the present Sun as in Gallet & Bouvier (2013).
is the escape velocity at the stellar surface, Bp is the surface magnetic field and Ṁwind is the stellar mass loss rate due to the wind (see Sect. 3.3 of Gallet & Bouvier 2013, for details). In Eq. (8)the constants K1, K2, and m are fixed according to the numerical simulations of Matt et al. (2012); their values are: K1 = 1.30, K2 = 0.0506, m = 0.2177. The values of Bp and Ṁwind are calculated using the BOREAS subroutine (Cranmer & Saar 2011) with the filling factor slightly modified in order to reproduce the average filling factor of the present Sun as in Gallet & Bouvier (2013). -
4.
The braking law proposed by Matt et al. (2015). They derived a physically motivated scaling for the dependence of the wind braking law on Rossby number and adopted an empirical scaling with stellar mass and radius. For our purposes, the Matt et al. (2015) braking law can be recast in the form:
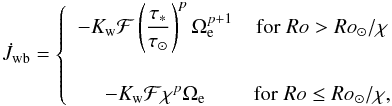 (9)with
(9)with 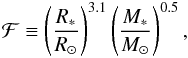 (10)and
(10)and 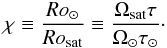 (11)Following Matt et al. (2015), we adopt p = 2, which implies that this model also reproduces the empirical Skumanich (1972) law in the solid-body rotation limit. The saturation regime is equivalent to that introduced by Krishnamurthi et al. (1997); here we adopt χ = 10 as in Matt et al. (2015) (see also Sect. 5).
(11)Following Matt et al. (2015), we adopt p = 2, which implies that this model also reproduces the empirical Skumanich (1972) law in the solid-body rotation limit. The saturation regime is equivalent to that introduced by Krishnamurthi et al. (1997); here we adopt χ = 10 as in Matt et al. (2015) (see also Sect. 5).
4.3. MCMC fitting of the TZM parameters
According to the TZM, the rotational evolution is completely determined by the stellar mass, which also selects the appropriate background stellar model, and by five parameters: the initial period P0, the disk lifetime τdisk, the coupling timescale τcp, and the two parameters contained in the wind braking laws (6)or (7). We use a MCMC approach to constrain the values of these parameters.
The MCMC method is a powerful technique to obtain quantitative inferences on a set of model parameters p from the observational data d (see, e.g. Appendix A of Tegmark et al. 2004 for a concise introduction). In the case at hand, the vector of model parameters for the TZM with, e.g, the braking law (6)is p ≡ (P0,τdisk,τcp,Kw,Ωsat), while for each mass listed in Table 2 the vector of data points contains the periods from the non-parametric fits at the various cluster ages. For the models with M∗ = 1.00 M⊙, we also consider the additional constraint based on the current solar rotation rate1: Ωe(t⊙) = 1.0 ± 0.1 Ω⊙.
Formally, Bayes’ Theorem relates the probability of the model, given the data, i.e., the posterior probability2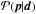 , to the compatibility of the data with the model, i.e., the likelihood
, to the compatibility of the data with the model, i.e., the likelihood 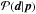 , and the intrinsic likeliness of the model (prior probability, or simply prior),
, and the intrinsic likeliness of the model (prior probability, or simply prior), 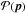 :
: 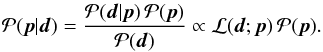 (12)In the following, we ignore the normalization
(12)In the following, we ignore the normalization 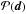 , which is a constant with respect to the models, and we use the notation ℒ(d;p) for the likelihood. In essence, the MCMC method consists of sampling the posterior probability by means of a quasi-random walk in the space of the parameters p, constructed as a chain of jumps guided by the values of the likelihood ℒ(d;p). Each step in the chain depends only on the previous one (Markov chain), and is partly stochastic (Monte Carlo). The steps are performed according to the following two-stage rule:
, which is a constant with respect to the models, and we use the notation ℒ(d;p) for the likelihood. In essence, the MCMC method consists of sampling the posterior probability by means of a quasi-random walk in the space of the parameters p, constructed as a chain of jumps guided by the values of the likelihood ℒ(d;p). Each step in the chain depends only on the previous one (Markov chain), and is partly stochastic (Monte Carlo). The steps are performed according to the following two-stage rule:
- 1.
Propose stage: pold → ptrial = pold + Δp, with Δp extracted from the jump function f(Δp).
- 2.
Acceptance/rejection stage: the probability to accept the jump is given by the Metropolis-Hastings rule (Metropolis et al. 1953; Hastings 1970):
![\begin{eqnarray} \label{methast} {\cal P}_{\rm accept} = \min \left[\dfrac{{\cal L}({\vec d};{\vec p}_{\rm trial})}{{\cal L}({\vec d};{\vec p}_{\rm old})}, 1 \right] . \end{eqnarray}](/articles/aa/full_html/2015/12/aa26770-15/aa26770-15-eq111.png) (13)
(13)
The Metropolis-Hastings rule ensures that a trial step increasing the likelihood is always accepted (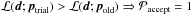 ), while at the same time even steps which reduce the likelihood retain a (proportionally small) non-zero probability to be accepted. This procedure is completely specified by the choice of the functions f(Δp) and ℒ(d;p).
), while at the same time even steps which reduce the likelihood retain a (proportionally small) non-zero probability to be accepted. This procedure is completely specified by the choice of the functions f(Δp) and ℒ(d;p).
We use a multi-dimensional Gaussian form for the jump function: 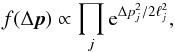 (14)where ℓj are the jump sizes and the index j (up to 5 in our case) runs over the elements of the parameter vector p. The jump function is critical to ensure that the steps in the chain are optimally correlated, providing a useful sampling of the posterior probability: the optimal regime is in between 100% step acceptance (i.e., a purely random walk) and 100% step rejection.
(14)where ℓj are the jump sizes and the index j (up to 5 in our case) runs over the elements of the parameter vector p. The jump function is critical to ensure that the steps in the chain are optimally correlated, providing a useful sampling of the posterior probability: the optimal regime is in between 100% step acceptance (i.e., a purely random walk) and 100% step rejection.
We define the likelihood in terms of the chi-square: 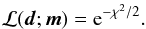 (15)The chi-square contains contributions from each cluster for which an estimate of the rotation period on the slow-rotator sequence at the mass considered is available:
(15)The chi-square contains contributions from each cluster for which an estimate of the rotation period on the slow-rotator sequence at the mass considered is available: ![\begin{eqnarray} \label{chisq} \chi^2 = \sum_{i\,=\,1}^n \left[\frac{ \Omega_{{\rm m},i} - \Omega_{{\rm o},i} }{\sigma_{\Omega,i} } \right]^2, \end{eqnarray}](/articles/aa/full_html/2015/12/aa26770-15/aa26770-15-eq119.png) (16)where Ωm,i ≡ Ωe(ti) is the angular velocity of the convective envelope calculated from a run of the TZM with the set of parameters p, while Ωo,i, σΩ,i are derived from Table 2 as follows:
(16)where Ωm,i ≡ Ωe(ti) is the angular velocity of the convective envelope calculated from a run of the TZM with the set of parameters p, while Ωo,i, σΩ,i are derived from Table 2 as follows: 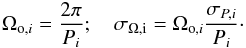 In practical applications, running the MCMC procedure at the optimal acceptance regime (~20% of attempted steps accepted), is often hindered by the existence of correlations in the way the parameters influence the model. In our case, for example, we can anticipate the existence of degenerate pairs of values of P0 and τdisk, i.e., a longer initial period and a shorter disk interaction, and vice versa, compensating each other to give a very similar evolution at sufficiently late times (say, a few hundred Myr onwards). Apart from computational efficiency, strong correlations can lead to oversampling of the degenerate regions of the parameter space, resulting in very biased, and practically useless, chains. We deal with this issue as recommended by Tegmark et al. (2004), by introducing a transformation from p to an uncorrelated vector u, and quantitatively checking the quality of the chain:
In practical applications, running the MCMC procedure at the optimal acceptance regime (~20% of attempted steps accepted), is often hindered by the existence of correlations in the way the parameters influence the model. In our case, for example, we can anticipate the existence of degenerate pairs of values of P0 and τdisk, i.e., a longer initial period and a shorter disk interaction, and vice versa, compensating each other to give a very similar evolution at sufficiently late times (say, a few hundred Myr onwards). Apart from computational efficiency, strong correlations can lead to oversampling of the degenerate regions of the parameter space, resulting in very biased, and practically useless, chains. We deal with this issue as recommended by Tegmark et al. (2004), by introducing a transformation from p to an uncorrelated vector u, and quantitatively checking the quality of the chain:
-
To transform to uncorrelated variables, we calculate thecorrelation matrix of the parameters
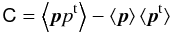 over a portion of the chain (typically, every 100 steps), then diagonalize it to obtain the matrices Λ and R:
over a portion of the chain (typically, every 100 steps), then diagonalize it to obtain the matrices Λ and R:  since C is by definition real and symmetric, the eigenvalues are real and the matrix R is orthogonal. The linear transformation
since C is by definition real and symmetric, the eigenvalues are real and the matrix R is orthogonal. The linear transformation ![\begin{eqnarray*} {\vec u} = \tens{\Lambda^{-1/2}} \tens{R^t} \left[{\vec p} - \left<{\vec p}\right> \right] \end{eqnarray*}](/articles/aa/full_html/2015/12/aa26770-15/aa26770-15-eq132.png) results in the very useful properties: ⟨u⟩ = 0, ⟨ uut ⟩ = 1, i.e., the variables ui are (linearly) uncorrelated and normalized to one. Operationally, the vector p is transformed into u before substitution into the jump function (14); the trial step is performed in the variables u, and then transformed back if the step is accepted. Since u is normalized to one, the choice of the jump sizes is particularly simple: ℓj = ℓ ≈ 1. The correlation matrix C is recalculated, and the matrices Λ and R are updated, every ~100 steps.
results in the very useful properties: ⟨u⟩ = 0, ⟨ uut ⟩ = 1, i.e., the variables ui are (linearly) uncorrelated and normalized to one. Operationally, the vector p is transformed into u before substitution into the jump function (14); the trial step is performed in the variables u, and then transformed back if the step is accepted. Since u is normalized to one, the choice of the jump sizes is particularly simple: ℓj = ℓ ≈ 1. The correlation matrix C is recalculated, and the matrices Λ and R are updated, every ~100 steps. -
To evaluate the quality of the chain, we calculate the autocorrelation of each parameter pj,
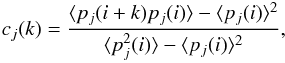 where pj(i), etc., is the value of pj at the step i of the chain. Typically, cj(k) decreases with k (its value at k = 1 being unity by definition): we define the correlation length of the chain as the value
where pj(i), etc., is the value of pj at the step i of the chain. Typically, cj(k) decreases with k (its value at k = 1 being unity by definition): we define the correlation length of the chain as the value 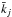 for which cj(k) drops below 0.5 for the first time. The effective length of the chain
for which cj(k) drops below 0.5 for the first time. The effective length of the chain 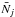 is thus the number of steps N divided by
is thus the number of steps N divided by 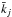 :
: 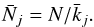 This is a measure of the number of independent points in the chain: if
This is a measure of the number of independent points in the chain: if 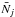 is sufficiently large, the average of pj over the chain, along with its standard deviation, can be considered representative of the best-fitting value of pj and its uncertainty, respectively. To ensure that we only use a portion of the chain sufficiently close to convergence, the first few hundred steps (burn-in phase) are discarded.
is sufficiently large, the average of pj over the chain, along with its standard deviation, can be considered representative of the best-fitting value of pj and its uncertainty, respectively. To ensure that we only use a portion of the chain sufficiently close to convergence, the first few hundred steps (burn-in phase) are discarded.
5. Results and discussion
The empirical description of Sect. 3 implies that, once a star settles on the slow-rotator sequence, it forgets most of its earlier rotational history. As suggested by Barnes (2003) or Brown (2014), fast rotators may have a different magnetic configuration than slow rotators and migrate to the slow-rotator sequence after a change in their magnetic configuration. This scenario, which still lacks clear observational support (but see Garraffo et al. 2015), implies that stars may settle on the slow-rotator sequence either after an initial rotational evolution like those described in Sects. 4.1 and 4.2, with parameters constant in time, or after an entirely different one, in which the parameters change with surface magnetic field configuration (e.g. Brown 2014). In the first case, convergence on the slow-rotator sequence would be just a consequence of the Ω dependence of the wind braking law, including the effects of the saturation regime, which is implicitly assumed in building our starting conditions. In the second case, both the overall scale factor and the exponent of Ω in the wind braking law may change at some stage of the evolution, which would require a different approach than that adopted here. In both cases, however, once on the slow-rotator sequence, the subsequent rotation period evolution is manifestly independent of the previous history, although the abundance of light elements may still depend on it (see, e.g. Bouvier 2008).
Our fitting, therefore, cannot constrain the stellar rotational history before settling on the slow-rotator sequence. In particular, it cannot constrain P0 and τdisk even if the earlier rotational history follows one of the models listed in Sects. 4.1 and 4.2 with parameters constant in time. Nevertheless, such parameters are necessary in our modeling for advancing the rotational evolution from the birth-line to the slow-rotator sequence. We therefore treat P0 and τdisk as nuisance parameters with reasonable priors and marginalize them out. The prior on P0 is uniformly distributed over the observed period range in the ONC (Rebull et al. 2004). The prior on τdisk is assumed to be an exponential decay with an e-folding time of ≈5 Myr (see, e.g. Fig. 11 in Hernández et al. 2008).
In our modeling, P0 and τdisk are degenerate with respect to the slow-rotator sequence evolution, in the sense that long P0 and short τdisk can lead to the same period at the age of the Pleiades as short P0 and long τdisk. Therefore, after checking compatibility by letting all parameters vary, we set τdisk = 3 Myr and marginalize P0 out for each mass and model. It is worth stressing that this is just a convenient way of setting the initial conditions for the slow-rotator sequence evolution and that no inference can be made on the actual distribution of P0 and τdisk.
The duration of the phase of the early stellar evolution that is affected by the saturation regime (Eq. (6) or (9)) depends on the assumptions made on the saturation threshold. As a consequence, the star may leave the saturation regime before or significantly after its settling on the slow-rotator sequence. In fact, if we consider the relationship proposed by Krishnamurthi et al. (1997): 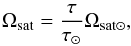 (17)with Ωsat ⊙ = 10 Ω⊙, or, equivalently, the saturation regime in the formulation of Matt et al. (2015) (see Sect. 4.2), stars of approximately solar mass will leave the saturation regime before settling on the slow-rotator sequence (starting from the Pleiades age in our modeling), but stars of lower mass will stay in the saturation regime for a significant part of their earlier evolution on the slow-rotator sequence. For this reasons, we adopt the strategy of testing different assumptions on Ωsat, rather than trying to fit it as a free parameter. We therefore consider Eq. (6)with:
(17)with Ωsat ⊙ = 10 Ω⊙, or, equivalently, the saturation regime in the formulation of Matt et al. (2015) (see Sect. 4.2), stars of approximately solar mass will leave the saturation regime before settling on the slow-rotator sequence (starting from the Pleiades age in our modeling), but stars of lower mass will stay in the saturation regime for a significant part of their earlier evolution on the slow-rotator sequence. For this reasons, we adopt the strategy of testing different assumptions on Ωsat, rather than trying to fit it as a free parameter. We therefore consider Eq. (6)with:
-
no saturation (model KA);
-
Ωsat = 10 Ω⊙ for all masses (model KS);
-
Ωsat as in Eq. (17)(model KK).
Note that an implicit mass dependence (through τ) enters both model KK, as a τ-dependent saturation threshold, and Eq. (7)(hereafter model KB), as a factor in the wind angular momentum loss. On the other hand, Eq. (9)(hereafter model MB) contains a complex mass dependence that is both explicit and implicit, through the dependence on τ and R∗, and the τ-dependence of the saturation threshold, respectively.
Slow-rotator sequence two-zone MCMC fitting results (see text for details on the different models).
The wind braking law (8)(model GB hereafter) contains, in principle, no adjustable parameters. However, in order to compare it with models derived from Eqs. (6)–(9), where Kw is treated as a free parameter, we assume K1 variable and check whether the fitted K1 shows some residual correlation with mass.
By fitting Kw or K1, we both test how well the models describe the mass dependence of the rotational evolution, and correct the mass dependence using the observational data.
After setting the initial conditions, we are left with two free parameters, p = (τcp,Kw) for the models KA, KS, KK, KB, and MB and p = (τcp,K1) for model GB. We fit these parameters using the MCMC method described in Sect. 4.3 and the data of Table 2. From this data set we exclude data for stellar mass <0.85 M⊙, since, for our purposes, the sampling in age in this mass range is still insufficient3. We also exclude the NGC 6811 periods, although we verify a posteriori (see below) the consistency of our results with the NGC 6811 data. The exclusion of the NGC 6811 periods is due to the irregular behavior in the empirical description of the evolution of the slow-rotator sequence of this cluster in comparison to the general trend. Indeed, Fig. 1 shows that the slow-rotator sequence of NGC 6811 tends to bend downwards between 0.8 and 0.9 M⊙, but this trend is not subsequently seen in the NGC 6819 periods (at the age of ≈2.5 Gyr). As this may outline some remaining problems with the NGC 6811 data, which might result in introducing biases in our results, we choose not to use the NGC 811 data in the fitting, but we verify a posteriori the compatibility of the final results with this data.
 |
Fig. 3 Correlation of the parameter Kw for models KA, KS, KK, KB, MB, and K1 for model GB with mass. The scaling factor of Kw is 1.11 × 1047 g cm2 s. The best linear fit is reported together with the uncertainties on the slope parameter. The linear Pearson correlation coefficient is given is each panel. |
The results of the fitting of the MCMC parameters are reported in Table 3, Fig. 3 and 5. Figure 3 shows that the Kw vs. M relation obtained for the KB models produces the lowest linear Pearson correlation coefficient, compatible, within the uncertainties, with no correlation. It is, indeed, remarkable that at t ≈ 0.55 Gyr the slow-rotator sequence follows the shape predicted by Barnes (2010) for the asymptotic slow-rotator sequence (Eq. (3)) with an appropriate rescaling of the free parameter kI. In a solid-body rotation regime, this shape comparison would manifestly imply the mass scaling proportional to I∗τ, implemented in model KB. Although stars at 0.55 Gyr have not yet reached this regime, our fit supports the validity of such mass scaling, at least in the mass range 0.85–1.1 M⊙. The confirmation of the general validity of such an empirical mass scaling awaits the acquisition of period data for M< 0.8 M⊙ at ages well beyond the current 0.6 Gyr limit.
Model MB also produces a significantly lower Kw vs. M correlation than the KA, KS, KK, and GB model. However, the Kw rise at M> 1.0 M⊙ indicates that the mass dependence of the MB wind braking law is less accurate than model KB at larger mass.
Model KA, i.e. the original Kawaler (1988) model with no saturation, tends to underestimate the wind braking at lower mass with respect to higher mass (or vice versa). Our fit compensates for this behavior with a systematic variation of Kw with mass. A saturation threshold constant in mass, as in model KS, helps to correct this behavior, but only by a negligible amount for M> 1 M⊙. A mass-dependent saturation threshold, as in Eq. (17), is somewhat more effective, but a clear Kw vs. M correlation remains.
The fitted values of K1 for model GB are very close to the one given in Gallet & Bouvier (2013), which derives from the original simulation of Matt et al. (2012), but show a clear correlation with M. A strong correlation of the fitted K1 with mass (using percentiles of the whole period sample) was also found by Gallet & Bouvier (2015), who interpreted it as due to a change in magnetic configuration with mass.
A comparison of the wind braking mass dependence of models KA, KB, and MB in the range 0.6 ≤ M/M⊙ ≤ 1.1 is shown in Fig. 4. Comparing the latter with Fig. 3, we deduce that the slope of the mass dependence of both models KB and MB is compatible with the observations in the range 0.85 ≤ M/M⊙ ≤ 1.0. For M> 1.0 M⊙, however, the slope of model MB is too steep and the observations favor a slope more similar to that of model KB. Note, furthermore, that the effective mass dependence of model MB depends on the saturation regime, although this has only a minor impact on the Kw fit, as in model KK.
 |
Fig. 4 Comparison of the mass dependence of models KA (solid black line), KB (red dashed line), and MB (blue dot-dashed line) at t = 0.55 Gyr. All quantities are in solar units. |
 |
Fig. 5 τcp vs. M for models KA (orange circle), KS (red pentagon), KK (plum diamond), MB (purple hexagon), KB (green square) and GB (blue triangle). Results from different models at the same mass are slightly shifted in abscissa for readability. The solid line represents the relation τcp ∝ M-7.28 obtained from model KB with an average ⟨ Kw ⟩ = 4.5. |
The resulting τcp is largely independent of the model adopted (Fig. 5). The largest difference is between model GB, which is the only one with a wind braking law not strictly proportional to Ω3, and all the others. Note that our τcp derived from model GB is very close to that derived by Gallet & Bouvier (2015) for the 90th percentile of the whole period distribution. As discussed below, a different Ω dependence results in a different angular momentum storage in the radiative interior, and therefore a different coupling timescale, but τcp remains a steep function of mass in all cases. Adopting model KB with an average ⟨ Kw ⟩ = 4.5, we obtain a τcp vs. M relationship which is well-represented by the power-law scaling: 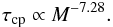 (18)In Fig. 5 this relationships is compared with the τcp obtained from each of the models tested in the MCMC fit.
(18)In Fig. 5 this relationships is compared with the τcp obtained from each of the models tested in the MCMC fit.
The evolution of the envelope and core angular velocities is plotted in Fig. 6. For clarity, only the results of models KB, MB, and GB are shown. Since the mass dependence has been corrected by the Kw fit, all models with a wind braking law proportional to Ω3 produce essentially the same Ωe and Ωc evolution.
In the 0.1–2.5 Gyr age range, the Ωe evolution deduced from model GB also overlaps with that deduced from all the other models. Differences with the other models become significant after 2.5 Gyr, but remain small even at the solar age (see Fig. 6). Model GB model predicts, however, a larger angular momentum storage in the core at early ages with respect to the other models.
The comparison of Figs. 1 and 6 explains the behavior of the slow-rotator sequence in the P/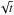 vs. (B−V) diagram. For M< 1.0 M⊙ at 0.1 Gyr, Ωe is well below the
vs. (B−V) diagram. For M< 1.0 M⊙ at 0.1 Gyr, Ωe is well below the 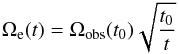 (19)relationship with t0 = 0.55 Gyr, and Ωobs the corresponding value from the non parametric fit (Sect. 3.2). The evolution proceeds by approaching such relationship until t = 0.55 Gyr, then Ωe decreases more steeply than Eq. (19). In the time-frames of Fig. 1, this corresponds to a slow-rotator sequence approaching the M37 sequence between 0.1 and 0.55 Gyr, then departing from it between 0.55 and 2.5 Gyr towards increasing P/
(19)relationship with t0 = 0.55 Gyr, and Ωobs the corresponding value from the non parametric fit (Sect. 3.2). The evolution proceeds by approaching such relationship until t = 0.55 Gyr, then Ωe decreases more steeply than Eq. (19). In the time-frames of Fig. 1, this corresponds to a slow-rotator sequence approaching the M37 sequence between 0.1 and 0.55 Gyr, then departing from it between 0.55 and 2.5 Gyr towards increasing P/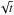 . The behavior for M ≥ 1 M⊙ is qualitatively similar, but, in this case, Ωe remains quite close to Eq. (19)until 0.55 Gyr, then decreases significantly faster than Eq. (19)afterwards. This explains why the slow-rotator sequence for M ≥ 1M⊙ remains close to the M37 sequence in the
. The behavior for M ≥ 1 M⊙ is qualitatively similar, but, in this case, Ωe remains quite close to Eq. (19)until 0.55 Gyr, then decreases significantly faster than Eq. (19)afterwards. This explains why the slow-rotator sequence for M ≥ 1M⊙ remains close to the M37 sequence in the 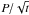 vs. (B−V) diagram until 0.55 Gyr, and then departs from it again from 0.55 to 2.5 Gyr toward higher
vs. (B−V) diagram until 0.55 Gyr, and then departs from it again from 0.55 to 2.5 Gyr toward higher 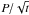 values.
values.
The comparison between Ωe and Ωc shows that a quasi-solid body rotation regime, and therefore a regime in which the wind braking dominates the rotational evolution, is achieved well after 1 Gyr. Furthermore, the comparison between Ωe and Eq. (19)with t0 = 2.5 Gyr shows that a quasi-Skumanich evolution is achieved well after 1 Gyr. This implies that in order to verify a departure from the Ω3 proportionality of the wind braking law, more data at ages well above 1 Gyr are needed.
Period isochrones in the period-color diagrams are calculated with model KB adopting ⟨ Kw ⟩ = 4.5 and correcting τcp for likely biases according to the power-law fitting shown in Fig. 5. These isochrones are essentially equivalent to those computed using any of the wind braking models tested after correcting the mass dependence through the fitted Kw and correcting τcp in the same way. The comparison with observations, shown in Fig. 7, outlines the observational origin of the small discrepancies found at the ages of the Pleiades and M35 for M ≥ 1.0 M⊙, where photometry and reddening uncertainties, particularly crucial for a cluster like M35, affect more significantly the results. Figure 7 also shows that our model reproduces satisfactorily the period distribution in NGC 6811 as well, even if it had been originally excluded from the MCMC fit. Even the reconstructed period at M = 0.85 M⊙, where the distribution apparently bends towards lower periods, lies on the upper envelope of the observed distribution and it is therefore compatible, in a statistical sense, with the observed distribution. Overall, however, the evolution of the slow-rotator sequence is reproduced with unprecedented accuracy.
Period isochrones recomputed for a logarithmically spaced age grid are reported in Table 4 and Fig. 8. Interpolation of Table 4 provides a tool for inferring stellar ages of solar-like main-sequence stars from their mass and rotation period, effectively representing an alternative gyro-chronology relationship that takes the physics of the two-zone model for the stellar angular momentum evolution into account.
6. Conclusions
Using a two-zone model MCMC fitting to the rotation periods vs color data from selected open clusters, we have compared new proposals for the wind braking law with the classical Kawaler (1988) one modified by Chaboyer et al. (1995). In our tests, we coupled the Kawaler (1988) braking law with different hypotheses regarding the saturation regime, including that of Krishnamurthi et al. (1997). The wind braking laws tested also included that of Gallet & Bouvier (2013), one derived from the work of Barnes & Kim (2010) and Barnes (2010), and the new proposal by Matt et al. (2015).
The MCMC fitting has been performed on the slow-rotator sequence between 0.1 and 2.5 Gyr. We propose a new quantitative criterion for identifying the slow-rotator sequence based on the symmetry of the data distribution around the density peak in the period-color diagram. Following this criterion, it is possible to assign a width of the period distribution around the density peak using the standard deviation. The value of the peak density as a function of colors (mass) is estimated using a non-parametric fit and, together with the standard deviation, constitute the data used in the MCMC fitting and in the definition of the likelihood function.
The main idea behind this work was to see how accurately a two-zone model with parameters constant in time can describe the rotational evolution on the slow-rotator sequence. In fact, it is evident that the slow-rotator sequence evolves in a regular and predictable way and it is then natural to explore the extent to which current models can reproduce this sort evolution.
We find that the difficulties in reconciling the observed behavior of the slow-rotator sequence evolution between 0.1 and 0.6 Gyr with the original Barnes (2003) idea of a factorization of time and mass dependence (Meibom et al. 2009, 2011b) can be simply attributed to a transfer of angular momentum from the radiative core to the convective envelope in the early slow-rotator sequence evolution. The two-zone model MCMC fitting leads to a robust (largely independent of the wind braking model adopted) estimate of the core-envelope coupling timescale τcp as a function of mass in the range 0.85 <M/M⊙< 1.10. In this mass range we find that τcp scales as M-7.28 on the slow-rotator sequence.
 |
Fig. 6 Comparison of the stellar envelope angular velocity evolution according to models KB (black solid line), MB (red dashed line), and GB (blue dot-dashed line) with observations. Mass scaling is corrected according to the MCMC fit for all models. The corresponding core angular velocity for each model is reported in gray with the same line style as for the envelope angular velocity. Dotted lines represent Eq. (19)(Skumanich law) with t0 = 0.55 and t0 = 2.50. |
 |
Fig. 7 Two-zone model MCMC fitting of the slow-rotator sequence (red diamonds) on the period-color diagram (black dots for the slow-rotator sequence, gray for others). Parameters from model KB are used, adopting ⟨ Kw ⟩ = 4.5 and correcting τcp for likely biases according to the power-law fitting shown in Fig. 5. |
 |
Fig. 8 Period evolutionary tracks calculated with model KB adopting ⟨ Kw ⟩ = 4.5 and correcting τcp for likely biases according to the power-law fitting shown in (Fig. 5). |
The importance of the core angular momentum storage and transfer to the convective envelope, in which enhanced viscosity that is due to (magneto-) hydrodynamical instabilities is expected to play an important role, has been outlined by many authors (see, e.g. references in Sect. 4.1). In this work we derive, for the first time, the empirical mass dependence of the core-envelope coupling timescale in the slow-rotator regime. Our empirical mass dependence of τcp represents a useful term of comparison for the theoretical description of angular momentum transport in stellar interiors. By focusing on the slow-rotator sequence, in which the TZM with constant parameters, as described in Sect. 4.1, is expected to capture the essential physics of the angular momentum evolution, we avoid the complications that arise in dealing with the fast-rotator regime, in which the TZM with constant parameters may break down (e.g. Brown 2014). The validity of the TZM for the slow-rotator regime is confirmed by the successful fit to the cluster data currently available. The wind braking law, for which the empirical dependence on stellar mass and angular velocity still gives better results than purely theoretical ones (see e.g. Matt et al. 2015), remains one of the critical aspects of this modeling.
Our results outline and explain the invalidity of a factorization like the one expressed by Eq. (1), on which most of the proposed gyro-chronology relationships are based, at least for the early (mass-dependent) evolution of the slow-rotator sequence. On the other hand, our results mean that the search for gyro-chronology relationships like the one recently proposed by Kovacs (2015), which is not based on known physics, are not justified. Kovacs (2015) proposal was motivated in fact by the disagreement between gyro-chronology relationships based on Eq. (1)and stellar evolution isochrone fitting, but the ages assumed for the clusters included in our analysis, which do not differ significantly from the isochrone ages assumed in Kovacs (2015), are fully compatible with our modeling of the rotational evolution of the slow-rotator sequence.
With a suitable choice of the free parameters, we tested the mass dependence of the models under scrutiny. We found that the mass scaling of the wind braking law implied by the models of Barnes (2010) and Barnes & Kim (2010) is the most consistent with the data, supporting the proposal that the convective turnover timescale τ is a key parameter in such a mass dependence. A definitive confirmation of the general validity of such mass dependence, however, would require period data of older cluster and lower stellar mass than is available to date. The mass scaling of the recent model by Matt et al. (2015) is found consistent with the data for 0.85 ≤ M ≤ 1.00 M⊙, but it decreases too steeply with mass for M> 1.00 M⊙. All the other models considered show a clear residual correlation with mass, indicating an incorrect mass scaling.
Small deviations from the Ω3 dependence of the wind braking law, such as those predicted by the Gallet & Bouvier (2013) model, are also compatible with observations in the 0.1–2.5 Gyr range. In fact, quasi-solid body rotation, the regime in which the wind braking dominates the angular momentum evolution, is achieved after 1–2 Gyr, depending on mass, so that small deviations from the Ω3 proportionality can be compensated for by a different angular momentum storage in the stellar core to produce, essentially, the same Ωe evolution. After correcting the mass scaling, differences between the Gallet & Bouvier (2013) model and models based on the Ω3 proportionality becomes not negligible after 2.5 Gyr, although they remain small even at the age of the Sun. A corollary of this is that verifying small deviations from the Ω3 proportionality would require data for clusters much older than 2.5 Gyr and that, in the 2–5 Gyr age range, deviations from the Skumanich law for M ≈ 1 M⊙ are expected to be small.
From our MCMC model fitting to the data, we derive period isochrones and tracks from 0.1 to 5.0 Gyr valid for stars with 0.85 ≤ M ≤ 1.10 M⊙. These are essentially independent of any assumption regarding the mass scaling of the wind braking law and compatible with small deviations from the Ω3 proportionality. By interpolating between the grid point, these tracks can be used to infer stellar ages from their mass and rotation period, providing alternative gyro-chronology relationships that take the physics of the two-zone model into account.
Acknowledgments
We are grateful to an anonymous referee, whose comments have contributed to improving the paper. A.C.L. thanks the Cosmic Magnetic Fields Branch of the Leibniz-Institut für Astrophysik Potsdam (AIP) for their kind hospitality. A.C.L. acknowledges the support received from the European Science Foundation (ESF) for the activity entitled “Gaia Research for European Astronomy Training”. F.S. acknowledges support from the Leibniz Institute for Astrophysics Potsdam (AIP) through the Karl Schwarzschild Postdoctoral Fellowship.
References
- Allain, S. 1998, A&A, 333, 629 [NASA ADS] [Google Scholar]
- Barnes, S. A. 2003, ApJ, 586, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, S. A. 2007, ApJ, 669, 1167 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, S. A. 2010, ApJ, 722, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, S. A., & Kim, Y.-C. 2010, ApJ, 721, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Barrado y Navascués, D., Deliyannis, C. P., & Stauffer, J. R. 2001, ApJ, 549, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Bouvier, J. 2008, A&A, 489, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, T. M. 2014, ApJ, 789, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Chaboyer, B., Demarque, P., & Pinsonneault, M. H. 1995, ApJ, 441, 876 [NASA ADS] [CrossRef] [Google Scholar]
- Cleveland, W. S., Grosse, E., & Shyu, W. M. 1992, Local regression models, Statistical Models in S (Wadsworth & Brooks/Cole) [Google Scholar]
- Collier Cameron, A., Davidson, V. A., Hebb, L., et al. 2009, MNRAS, 400, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Cranmer, S. R., & Saar, S. H. 2011, ApJ, 741, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Delorme, P., Collier Cameron, A., Hebb, L., et al. 2011, MNRAS, 413, 2218 [NASA ADS] [CrossRef] [Google Scholar]
- Demarque, P., Guenther, D. B., Li, L. H., Mazumdar, A., & Straka, C. W. 2008, Ap&SS, 316, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Epstein, C. R., & Pinsonneault, M. H. 2014, ApJ, 780, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Gallet, F., & Bouvier, J. 2013, A&A, 556, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallet, F., & Bouvier, J. 2015, A&A, 577, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garraffo, C., Drake, J. J., & Cohen, O. 2015, ApJ, 807, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. D., Gaudi, B. S., Holman, M. J., et al. 2008, ApJ, 675, 1233 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. D., Gaudi, B. S., Pinsonneault, M. H., et al. 2009, ApJ, 691, 342 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. D., Bakos, G. Á., Kovács, G., & Noyes, R. W. 2010, MNRAS, 408, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Hastings, W. K. 1970, Biometrika, 57, 97 [Google Scholar]
- Herbst, W., & Mundt, R. 2005, ApJ, 633, 967 [NASA ADS] [CrossRef] [Google Scholar]
- Hernández, J., Hartmann, L., Calvet, N., et al. 2008, ApJ, 686, 1195 [NASA ADS] [CrossRef] [Google Scholar]
- Hodgkin, S. T., Irwin, J. M., Aigrain, S., et al. 2006, Astron. Nachr., 327, 9 [Google Scholar]
- Janes, K., Barnes, S. A., Meibom, S., & Hoq, S. 2013, AJ, 145, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffries, Jr., M. W., Sandquist, E. L., Mathieu, R. D., et al. 2013, AJ, 146, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Kalirai, J. S., Ventura, P., Richer, H. B., et al. 2001, AJ, 122, 3239 [NASA ADS] [CrossRef] [Google Scholar]
- Kalirai, J. S., Fahlman, G. G., Richer, H. B., & Ventura, P. 2003, AJ, 126, 1402 [NASA ADS] [CrossRef] [Google Scholar]
- Kawaler, S. D. 1988, ApJ, 333, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Keppens, R., MacGregor, K. B., & Charbonneau, P. 1995, A&A, 294, 469 [NASA ADS] [Google Scholar]
- Koenigl, A. 1991, ApJ, 370, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Kovacs, G. 2015, A&A, 581, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krishnamurthi, A., Pinsonneault, M. H., Barnes, S., & Sofia, S. 1997, ApJ, 480, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Lejeune, T., Cuisinier, F., & Buser, R. 1997, A&AS, 125, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lejeune, T., Cuisinier, F., & Buser, R. 1998, A&AS, 130, 65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MacGregor, K. B., & Brenner, M. 1991, ApJ, 376, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, S. P., MacGregor, K. B., Pinsonneault, M. H., & Greene, T. P. 2012, ApJ, 754, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, S. P., Brun, A. S., Baraffe, I., Bouvier, J., & Chabrier, G. 2015, ApJ, 799, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Meibom, S., Mathieu, R. D., & Stassun, K. G. 2009, ApJ, 695, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Meibom, S., Barnes, S. A., Latham, D. W., et al. 2011a, ApJ, 733, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Meibom, S., Mathieu, R. D., Stassun, K. G., Liebesny, P., & Saar, S. H. 2011b, ApJ, 733, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Meibom, S., Barnes, S. A., Platais, I., et al. 2015, Nature, 517, 589 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Messina, S. 2007, Mem. Soc. Astron. Italiana, 78, 628 [Google Scholar]
- Messina, S., Distefano, E., Parihar, P., et al. 2008, A&A, 483, 253 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Messina, S., Parihar, P., Koo, J.-R., et al. 2010, A&A, 513, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., & Teller, E. 1953, J. Chem. Phys., 21, 1087 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, D. 1986, Tests of the chi-squared type. Goodness-of-Fit Techniques (New York: Marcel Dekker) [Google Scholar]
- Rebull, L. M., Wolff, S. C., & Strom, S. E. 2004, AJ, 127, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Skumanich, A. 1972, ApJ, 171, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Spada, F., Lanzafame, A. C., Lanza, A. F., Messina, S., & Collier Cameron, A. 2011, MNRAS, 416, 447 [NASA ADS] [Google Scholar]
- Stauffer, J. R., Schultz, G., & Kirkpatrick, J. D. 1998, ApJ, 499, L199 [NASA ADS] [CrossRef] [Google Scholar]
- Stauffer, J. R., Hartmann, L. W., Fazio, G. G., et al. 2007, ApJS, 172, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Tegmark, M., Strauss, M. A., Blanton, M. R., et al. 2004, Phys. Rev. D, 69, 103501 [CrossRef] [Google Scholar]
- Thode Jr., H. 2002, Testing for Normality (New York: Marcel Dekker) [Google Scholar]
- von Braun, K., Lee, B. L., Seager, S., et al. 2005, PASP, 117, 141 [NASA ADS] [CrossRef] [Google Scholar]
- von Hippel, T., Steinhauer, A., Sarajedini, A., & Deliyannis, C. P. 2002, AJ, 124, 1555 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, E. J., & Davis, Jr., L. 1967, ApJ, 148, 217 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Slow-rotator sequence two-zone MCMC fitting results (see text for details on the different models).
All Figures
 |
Fig. 1 Rotation period scaled to the square root of age (in Myr) vs. (B−V). Periods of stars defining the slow-rotator sequence are represented with black dots, all others with gray dots. Our non-parametric fit of the slow-rotator sequence is shown as blue thick solid lines, with the Pleiades and M37 fits repeated in all panels as reference (black thin solid line and gray thick solid line respectively). The dotted line represent the f(B−V) function of Barnes (2007; B07), the dashed line that of Meibom et al. (2009; M09), the dot-dashed that of Mamajek & Hillenbrand (2008; M08), the dash-triple-dotted line the inverted Barnes (2010) relationship (Eq. (2), B10), the long-dashed line the Barnes (2010) asymptotic slow-rotator sequence limit (Eq. (3), B10a). |
| In the text | |
 |
Fig. 2 Comparison of the empirical distribution function of the non-parametric fit residuals with the normal distribution function. Residuals are normalized to the standard deviation. |
| In the text | |
 |
Fig. 3 Correlation of the parameter Kw for models KA, KS, KK, KB, MB, and K1 for model GB with mass. The scaling factor of Kw is 1.11 × 1047 g cm2 s. The best linear fit is reported together with the uncertainties on the slope parameter. The linear Pearson correlation coefficient is given is each panel. |
| In the text | |
 |
Fig. 4 Comparison of the mass dependence of models KA (solid black line), KB (red dashed line), and MB (blue dot-dashed line) at t = 0.55 Gyr. All quantities are in solar units. |
| In the text | |
 |
Fig. 5 τcp vs. M for models KA (orange circle), KS (red pentagon), KK (plum diamond), MB (purple hexagon), KB (green square) and GB (blue triangle). Results from different models at the same mass are slightly shifted in abscissa for readability. The solid line represents the relation τcp ∝ M-7.28 obtained from model KB with an average ⟨ Kw ⟩ = 4.5. |
| In the text | |
 |
Fig. 6 Comparison of the stellar envelope angular velocity evolution according to models KB (black solid line), MB (red dashed line), and GB (blue dot-dashed line) with observations. Mass scaling is corrected according to the MCMC fit for all models. The corresponding core angular velocity for each model is reported in gray with the same line style as for the envelope angular velocity. Dotted lines represent Eq. (19)(Skumanich law) with t0 = 0.55 and t0 = 2.50. |
| In the text | |
 |
Fig. 7 Two-zone model MCMC fitting of the slow-rotator sequence (red diamonds) on the period-color diagram (black dots for the slow-rotator sequence, gray for others). Parameters from model KB are used, adopting ⟨ Kw ⟩ = 4.5 and correcting τcp for likely biases according to the power-law fitting shown in Fig. 5. |
| In the text | |
 |
Fig. 8 Period evolutionary tracks calculated with model KB adopting ⟨ Kw ⟩ = 4.5 and correcting τcp for likely biases according to the power-law fitting shown in (Fig. 5). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.