EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 584 (December 2015) A&A, 584 (2015) A16 Full HTML
Free Access
Issue
A&A
Volume 584, December 2015
Article Number A16
Number of page(s) 8
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201526655
Published online 13 November 2015

© ESO, 2015

1. Introduction

Recent observations of transition disks (disks with inner dust cavities) suggest that their structures may originate from particle trapping in pressure bumps (e.g. van der Marel et al. 2013; Zhang et al. 2014). Particle accumulation in pressure maxima has been suggested to solve the problem of rapid inwards drift of particles (e.g. Weidenschilling 1977; Brauer et al. 2008), implying that planetary embryos may form in localised environments (e.g. Klahr & Henning 1997; Johansen et al. 2007). Pressure bumps may occur because of the presence of one or multiple planets in the disk (e.g. Dodson-Robinson & Salyk 2011; Pinilla et al. 2012, 2015; Zhu et al. 2012), but other phenomena, such as dead zones may also create pressure traps and explain their structures (e.g. Regály et al. 2011; Flock et al. 2015). Observations of transition disks reveal that dust cavities appear to be smaller at shorter wavelengths (e.g. Dong et al. 2012; Garufi et al. 2013). This spatial segregation of small and mm-sized grains is a natural consequence of particle trapping in the planet-disk interaction scenario (e.g. Rice et al. 2006; de Juan Ovelar et al. 2013).

The spectral index αmm (Fν ∝ ναmm) provides information about the particle size in protoplanetary disks (see Testi et al. 2014, for a review). For (sub-) micron-sized dust, as found in the interstellar medium, αmm is expected to have values of ≳3.5–4.0 (e.g. Finkbeiner et al. 1999). When dust grows to millimetre sizes, αmm is expected to decrease (Draine 2006; Ricci et al. 2010). Radial increases in αmm (on 100 AU scales) have been found for individual disks without cavities (e.g. Guilloteau et al. 2011; Pérez et al. 2012), consistent with radial drift. In contrast, the inner region of transition disks is depleted of large grains, so that αmm would decrease with radius from the central star (Pinilla et al. 2014). However, these radial variations for αmm in transition disk have not been spatially resolved to date.

thumbnail Fig. 1

ALMA observations of dust continuum emission for SR 21 (top panels) and HD 135344B (bottom panels). The left columns show the Band 9 (689 GHz) and Band 7 (336 GHz) continuum, with the contour overlaid at 10, 20, ..., 90% of the peak. The third column shows the overlay of the contours with a step of 20% of the peak (black is Band 9, red is Band 7). The right column shows the resolved αmm in colour contours. The beam size is indicated in each plot.

In this paper, we combine observations from ALMA Cycle 0 at 689 GHz (~450 μm) and Cycle 1 at 336 GHz (~870 μm) of SR 21 and HD 135344B (also known as SAO 206462) to compare the morphological structures at the two frequencies and calculate αmm throughout the disk. In addition, we compare the results with a generic model of particle trapping and dust growth in a pressure bump induced by an embedded planet, and place the results in the context of other transition disks.

2. Targets and observations

SR 21 is a G3 star located in the Ophiuchus star-forming region at a distance of d = 120 pc (Loinard et al. 2008). The disk was identified as a transition disk by its mid-infrared SED, with a cavity radius of ~18 AU (Brown et al. 2007). Observations with the Submillimeter Array (SMA) at 850 μm confirmed a ~35 AU cavity and suggested an azimuthal disk asymmetry (Brown et al. 2009; Andrews et al. 2011), which was much more clearly seen with ALMA observations in Cycle 0 (Pérez et al. 2014). While 450 μm imaging with ALMA shows strong depletion of large mm-sized grains, by a factor of 103 or more in the inner region (van der Marel et al. 2015a), H-band scattered light imaging indicates that the small grains are much less depleted, perhaps by as little as a factor of 10 (Follette et al. 2013).

HD 135344B is an F4 star located in the Sco OB2-3 star-forming region at a distance of d = 140 pc (van Boekel et al. 2005). A cavity radius of ~45 AU was also identified by its SED (Brown et al. 2007) and confirmed by SMA observations (Brown et al. 2009). One of the most intriguing characteristics of this disk is its spiral arms observed in scattered light images (Muto et al. 2012; Garufi et al. 2013). The observations with VLT/NACO did not show signs of a gap in small dust grains down to 28 AU radius (Garufi et al. 2013).

Table 1

Observation properties.

thumbnail Fig. 2

Real part of the visibilities at 689 GHz (~450 μm, Band 9) and at 336 Gz (~870 μm, Band 7) for SR 21 (top panel) and HD 135344B (bottom panel). The plot includes error bars that are of the size of the plotting points. At both wavelengths, the models with the best-fit parameters are over-plotted (solid line), which is the ring model in the case of SR 21, and the vortex model for HD 135344B.

Our observations are from ALMA Cycle 0 program 2011.0.00724.S (P.I. Pérez) and Cycle 1 program 2012.1.00158.S (P.I. van Dishoeck), taken in Band 9 and Band 7, respectively. The details of the calibration are described in Pérez et al. (2014) and van der Marel et al. (2015c). For both observation sets, the images were obtained using Briggs weighting with a robust parameter of 0.5 and and the beam is set to be the same at both bands by the post-processing of the images, which is the best possible beam size corresponding to both the Band 7 and Band 9 observations (0.27′′). The details of the images are given in Table 1.

As the data are taken almost two years apart, the centre of the 2014 data was shifted before overlaying the images to compensate for the proper motion of the stars. The proper motion is −12, −24 mas yr-1 for SR 21 (Makarov 2007) and −20, −24 mas yr-1 for HD 135344B (Høg et al. 2000). Figure 1 shows the continuum maps and their overlay. The shape and contrast of the asymmetry look similar between Band 7 and 9 for HD 135344B. In contrast, SR 21 looks more symmetric in Band 7. There is an azimuthal shift in the continuum overlay for both sources. The position of the gain calibrator (the same for both observations) shifts ≲0.1 mas, meaning that the azimuthal shift is not due to calibration. With respect to the SMA images in 2006/2007 (Brown et al. 2009), the asymmetries are also shifted.

3. Data analysis

3.1. Visibilities and disk morphology

The real part of the visibilities at both frequencies is shown in Fig. 2. These are extracted from the continuum data and de-projected using i = 15° and position angle PA = 14° for SR 21, and i = 20° and PA = 63°, as derived in Pontoppidan et al. (2008) and van der Marel et al. (2015a). The data are binned by taking the mean of the available data points in bins of 20 kλ, with a minimum of five data points per bin. In Fig. 2, we show the real part of the visibilities for the two bands. The length of the projected baseline where the visibilities cross zero (the null) indicates the location inner edge of the cavity in a given bandpass (smaller values for the null mean that the cavity inner edge is further out for the same disk properties). The nulls for SR 21 are ~220 kλ at Band 9 and ~250 kλ at Band 7. For HD 135344B the null is almost at the same position at both wavelengths (~190 kλ). The imaginary part of the visibilities are presented in Appendix A.

To fit the visibility profiles and constrain the structure of both disks, we used the same morphological models described in Pérez et al. (2014). One model is a ring-like emission described by 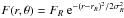, where rR is the location of the peak of the ring emission, FR the flux density at rR, and σR the ring width (ring model). The other model assumes a ring together with an azimuthal Gaussian profile to mimic a vortex structure (Lyra & Lin 2013). The vortex is described by 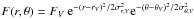, with rV and θV being the radius and PA at the peak of the vortex, FV the flux density at (rV,θV), and σθ,V,σr,V is the width of the vortex in the radial and azimuthal direction respectively (vortex model). The parameters of the best-fit model are found by minimising χ2 using the same Markov chain Monte Carlo (MCMC) approach implemented by Pérez et al. (2014). The results are summarised in Table 2. The errors from the MCMC calculations are much smaller than the spatial uncertainty from the observations, which is typically ~10% of the beam size (i.e. ~3 AU for SR 21 and ~4 for HD 135344B) for the high signal to noise of the data (Table 1). For the MCMC calculations, the inclination and PA are fixed to the values found by Pérez et al. (2014) for both disks. The model including a vortex did not converge to a physical solution for SR 21 in Band 7, because the azimuthal extension of the vortex covers more than 2π. In summary, the SR 21 data are best fit with a ring model, while the HD 135344B data are best fit with a vortex model (see Fig. 2). The residuals obtained by subtracting the best-fit model from the data in Band 7 are shown for both targets in Appendix B.

In the case of SR 21, the best-fit model indicates that larger grains, as traced at longer wavelengths by Band 7, are more spatially confined than the smaller grains traced at shorter wavelengths by Band 9 (σR ~ 12 AU at 870 μm vs. σR ~ 15 AU at 450 μm). Furthermore, the peak of emission in the ring is at larger radii in Band 7 than in Band 9 (rR ~ 41 AU at 870 μm vs. rR ~ 36 AU at 450 μm). The location of the inner edge of the cavity at the two frequencies varies from ~ 29 AU in Band 9 to ~ 35 AU in Band 7, which together with the wider ring, is consistent with the shift of the null of the visibilities (Fig. 2). For HD 135344B, the vortex model is consistently the best-fit model for both wavelengths. The inner edge of the cavity is almost constant in the two bands, as shown in the visibility nulls (Fig. 2). However, the width of the vortex in both the radial and azimuthal directions is significantly larger in Band 7, and its aspect ratio (σθ,V/σr,V) decreases from 7.1 in Band 9 to 3.3 in Band 7.

Table 2

Best-fit parameters the disk morphology models of ring or ring+vortex.

3.2. Spectral index

The position-dependent spectral index (right panels of Fig. 1) is calculated using both bands as 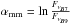/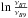. All data with F< 5σ are excluded. The dust emission within the cavity is detected at a high level of significance (S/N ~ 320σ and ~ 250σ in Band 7, and ~ 120σ and ~ 80σ in Band 9, for SR 21 and HD 135344B, respectively), so αmm can be accurately computed in the cavity separately from the dust ring. The uncertainty of αmm is calculated with error propagation from the observational uncertainty, which includes the calibration uncertainties (~20% and ~10% in Band 9 and 7, respectively) and the noise level or rms (σ) of the observations. With the high signal-to-noise of the data, the uncertainty in the spectral index σαmm at a given position is dominated by the calibration uncertainties and approximates to ≈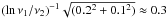, in both cases. However, for the relative spatial changes in αmm, the systematic calibration uncertainty does not contribute since it is constant across the field, and changes in αmm inside and outside the dust cavity have high significance with maximum values of σαmm of ≈0.01. SR 21 shows significant radial variations of αmm, with values of αmm ~ 3.8–4.2 within ~0.3′′ radius (~35 AU) and αmm ~ 2.6–3.0 outside (Δαmm ≳ 120σαmm). This implies a lack of mm-grains in the inner region (r ≲ 35 AU), and is consistent with accumulation of mm-grains in a localised region in the outer disk. For HD 135344B, no significant radial variations for αmm are found, and the values remain within a range of 2.6–3.2. Although Fig. 1 shows azimuthal variations of αmm for both sources, these depend considerably on how the two images are overlaid in the calculation of αmm (see Appendix C), and therefore any azimuthal variation within a range of αmm ≃ 2.6−3.2 remains uncertain.

4. Theoretical predictions of particle trapping

Dust trapping, in radial and azimuthal pressure bumps, depends on the coupling of the particles to the gas, pressure gradient, and disk turbulence. The dimensionless stopping time, Stokes number, quantifies the coupling of the particles and it is defined in the mid-plane (and assuming a Gaussian vertical profile for the gas density) as St = aρsπ/ 2Σg (with ρs being the volume density of a grain, with typical values of ~ 1g cm-3, Blum & Wurm 2008, and Σg the local gas surface density). Particles with St ~ 1 feel the strongest gas drag and therefore they move much faster to the regions of pressure maxima (e.g. Birnstiel et al. 2010; Pinilla et al. 2012). As the gas is turbulent, however, it is expected that the dust is turbulently mixed by the gas. The dust diffusion prevents the concentration of all the particles with St ~ 1 inside pressure traps. The drift of particles (and hence the trapping) is efficient for particles with St ≳ αvisc, where αvisc is a dimensionless number that quantifies the disk viscosity (Shakura & Sunyaev 1973). From the combination of radial drift and dust diffusion, it is expected that particles with St ~ 1 are more concentrated at the pressure maximum than St< 1. For example, the models of dust trapping by a vortex predict that larger grains would be more azimuthally concentrated in the centre of the vortex (Birnstiel et al. 2013; Lyra & Lin 2013), as observed in IRS 48 (van der Marel et al. 2015b) and HD 142527 (Casassus et al. 2015). Although turbulence can change the broadness of the dust concentration inside pressure bumps, it does not change the location of pressure maxima, i.e. the mean radial/azimuthal location of the dust concentration.

thumbnail Fig. 3

Dust density distribution when 1 MJup is embedded at 20 AU after 1 and 5 Myr of evolution (top and bottom panel respectively). The lines represent particle sizes with different Stokes numbers (St = [10-3,10-2,10-1,1]), which are proportional to the gas surface density profile.

Figure 3 shows the model predictions for particle trapping triggered by planet-disk interaction. The gas surface density is obtained from hydrodynamical simulations of a 1 MJup planet embedded in the disk at 20 AU distance from the star as in Pinilla et al. (2012). The initial gas surface density and temperature are assumed to be a power law, and the disk viscosity is taken to be αvisc = 10-3, as found for typical values of disk turbulence in simulations of MRI-active disks (e.g. Dzyurkevich et al. 2010). The dust density distributions are obtained from dust evolution models that include the dynamics and coagulation of dust particles Birnstiel et al. (2010). When a planet opens a gap in the disk, a pressure bump is formed at the outer edge of the gap, and large particles drift to the pressure maximum located in this case at ~30 AU. The particle sizes with different Stokes number (St = [10-3,10-2,10-1,1]) are shown to illustrate how the radial concentration becomes narrower for particles with higher St. The maximum grain size inside the trap is limited by dust fragmentation, which depends on αvisc (e.g. Birnstiel et al. 2010). For higher turbulence, the maximum grain size that particles can reach before fragmentation would be lower, causing the particles to easily escape from the bumps and then drift radially inwards. For more turbulent disks, a stronger pressure bump (with e.g. a more massive planet) would be required for trapping to occur (e.g. Pinilla et al. 2015). Figure 4 shows the intensity profile at 450 and 870 μm. The emission profile is only slightly narrower at 870 μm since the range of particles sizes that are traced is comparable. Both the dust density distributions and the intensity profiles become narrower at longer times of evolution.

Because of particle trapping, the region close to the planet is empty of mm/cm particles, and, therefore, αmm is expected to increase close to the location of the gap carved by the planet. Figure 4 also shows the expected radial profiles of αmm calculated from the models at 450 and 870 μm and convolved with a 2D Gaussian profile of 35 AU diameter. In the inner part (r ≲ 10 AU), αmm drops because of the presence of the mm-particles. Because there is no total filtration of particles at the outer edge of the gap, small grains still flow through the gap and grow again to mm-sizes in the inner region (r ≲ 10 AU). One way to prevent the presence of mm-grains is to increase the mass of the planet, and completely filter all particle sizes (Zhu et al. 2012; Pinilla et al. 2012, 2015).

At early times of dust evolution (~ 1 Myr), mm/cm grains are still distributed in the entire outer disk (r ≳ 30 AU) and radial variations of αmm are detected after convolution. This is not the case at 5 Myr, since the concentration of mm/cm particles becomes much narrower compared to the spatial resolution and hence the potential radial variation of αmm is smeared out and is not detected.

thumbnail Fig. 4

Top panel: intensity radial profiles at 450 and 870 μm obtained from the dust density distributions after 1 and 5 Myr of evolution. Bottom panel: radial profile of αmm calculated from the intensity profiles at 450 and 870 μm, which is convolved with 35 AU Gaussian beam.

5. Discussion

With the new ALMA observations of SR 21 and HD 135344B, it is possible to test whether radial/azimuthal trapping is the cause of disk structures (cavities and asymmetries). Observationally, radial trapping can be tested by analysing the location of the null in the real part of the visibilities at different wavelengths because, in the case of trapping, the mm-emission is expected to show a wider ring at shorter wavelengths. Thus, the inner edge of the ring (or dust cavity) should be located closer to the star at shorter wavelengths (Sect. 4). Additional insights can be gained by analysing the wavelength-dependent morphology and the position-dependent spectral index.

SR 21:

the current observations of SR 21 at 336 and 689 GHz suggest that the disk morphology at longer wavelengths is better described by a ring than by a vortex. From observations of 12CO, the disk mass of SR 21 has been inferred to be ~ 12 MJup, and the average value of the gas surface density close to the cavity is ~ 80 g cm-2 (van der Marel et al. 2015a). Analysis of recent observations of 13CO and C18O of this disk confirmed the disk mass (van der Marel et al. 2015c). Assuming that at each wavelength, particles with a maximum size of ≲3λ are traced (e.g. Draine 2006), observations at Band 7 and 9 traced particles with St ~ 2.5 × 10-3–5.0 × 10-3 close to the location of the cavity. These particles are still expected to be affected by radial drift and to move towards pressure maxima.

The fact that at a longer wavelength the morphology is better described by a ring than a vortex is in contradiction with model predictions of trapping by a vortex. Thus, the observed azimuthal structure is likely not caused by a vortex. Moreover, to sustain a long-lived vortex, the radial width of the vortex cannot be much higher than the disk scale height (≲2h, Barranco & Marcus 2005) and the fact that the radial width of the vortex in SR 21 is much larger that the disk scale height (~×5 hvan der Marel et al. 2015a), as found from the morphology fitting of the Band 9 data (Table 2), also disfavours the vortex scenario.

In the radial direction, larger grains traced at 870 μm are more narrowly concentrated than smaller grains traced at 450 μm in SR 21, as demonstrated in the shift of the nulls of the visibilities (see Fig. 2 and Table 2). The narrower concentration of larger grains is in agreement with particle trapping by a radial pressure bump. From measuring the broadness of the dust concentration inside the trap at different wavelengths, the disk turbulence could be estimated (broader implying higher turbulence) if the disk temperature and gas surface density profile are well constraint from observations. Further evidence that radial trapping occurs in SR 21 is given by the radial changes of the spectral index αmm, which increase outwards, as expected from radial trapping models (Fig. 4). The detection of radial variation of αmm with the current resolution suggests that particle trapping in SR 21 has occurred in ≲1 Myr because at longer times variations of αmm would not be detected (Fig. 4). The discrepancy between model predictions and observations for the values of αmm in the inner part of the disk come from the fact that we do not have total filtration of particles in the outer edge of the gap in our model.

Another potential explanation for variations of αmm is high optical depth, in which case the physical temperature is expected to be close to the brightness temperature. To reproduce the observed differences in αmm with optical depth effects alone, the emission must originate from a small surface area. Assuming that the emission is distributed in a homogeneous ring whose temperature is equal to the highest brightness temperature at the peak of emission obtained at the two frequencies (TB ≈ 32 K in Band 9 and ≈13 K in Band 7), the ring must be very narrow (≲3 AU in width). This contradicts the observed spatial extent of the emission in both bands (30–40 AU for SR 21 and 60–70 AU for HD 135344B, see Table 2). Thus, the radial variations of αmm cannot be due to optically thick emission alone. Pérez et al. (2014) demonstrated that the emission at Band 9 is marginally optically thick at the peak of emission, so it can only trace some of the mass surface density, and hence high angular resolution observations at longer wavelength are necessary to confirm our predictions at the location of the peak.

HD 135344B:

in this case, the model with the best-fit parameters for the disk morphology at the two wavelength is the vortex model (Table 2). The disk mass inferred from 12CO, 13CO, and C18O is ~ 20 MJup (van der Marel et al. 2015a,c) and the average value of the gas surface density at the location of the dust cavity is similar to that in SR 21 (~ 80 g cm-2). Therefore, the current observations trace particles with similar Stokes numbers as SR 21.

From the morphological models, the azimuthal width of the vortex increases at longer wavelengths in contradiction with predictions of particle trapping by vortices. Similar to SR 21, the radial width of the vortex is too large compared to the scale height of the disk. The origin of the azimuthal asymmetry is inconsistent with a vortex and may be related to the spiral arms observed at scattered light as also suggested by Pérez et al. (2014). In particular the bright spiral in the south coincides with the location of the asymmetry in the millimetre (Garufi et al. 2013; Quanz 2015, see also Appendix B). Indeed, the azimuthal shift of the peak (Fig. 1, also observed for SR 21) may be related to the physical rotation of spiral arms, but higher angular resolution observations are needed to confirm this prediction.

In contrast with SR 21, neither a shift of the null of the visibilities nor radial variations of αmm are detected for HD 135344B, but this does not exclude radial particle trapping. From the model predictions (Sect. 4), the dust density distribution of mm-grains is more narrowly concentrated at the pressure maximum after 5 Myr than at 1 Myr, and radial variations in αmm would not be detected with the current resolution (Fig. 4). Hence, the fact that radial changes in αmm are not detected for HD 135344B can be related to the fact that any instability (e.g. planet) responsible for the trapping formed earlier (~5 Myr ago) in HD 135344B than in SR 21 (~1 Myr ago). Another possibility is that trapping happens in more refined structures, such as spiral arms in gravitationally unstable disks, in which case any variations of αmm remains unresolved (Dipierro et al. 2015).

Besides longer evolution times, other disk and planet parameters, such as planet mass, turbulence, or disk temperature, can also affect the gap shape and thus the radial concentration of mm/cm-sized particles in pressure bumps, leading to a different spatial distribution of small and large grains. High contrast asymmetries have been observed in other transition disks and interpreted as vortices (e.g. Oph IRS 48, van der Marel et al. 2013). Detection of vortices in transition disks may be atypical because several parameters, such as strong turbulence or feedback from dust to the gas, can prevent a vortex from being long-lived (e.g. Ataiee et al. 2013; Zhu & Stone 2014; Raettig et al. 2015). Even in the case where a planet originally triggered the formation of the vortex, an eccentric orbit or the presence of addition planets can also lead to its rapid destruction (Ataiee & Pinilla 2015).

The current ALMA observations of SR 21 and HD 135344B suggest that anti-cyclonic vortices are not the origin of their low contrast azimuthal asymmetries. Observations at high angular resolution at longer, optically thin wavelengths, which provide information about the distribution of larger grains, will further constrain the origin of the observed dust structures in transition disks.

Online material

Appendix A: Imaginary part of the visibilities

Figure A.1 shows the imaginary part of the visibilities at 689 GHz (~450 μm, Band 9) and at 336 Gz (~870 μm, Band7) for SR 21 and HD 135344B. Non-zero imaginary visibilities indicate the presence of an azimuthal asymmetry (e.g. Isella et al. 2013). For HD 135344B, there are significant variations from zero at both frequencies. For SR 21, the non-zero values are marginal in Band 7, but are significant in Band 9 data.

thumbnail Fig. A.1

Imaginary part of the visibilities at 689 GHz (~450 μm, Band 9) and at 336 GHz (~870 μm, Band7) for SR 21 (top panel) and HD 135344B (bottom panel).

Appendix B: Residual maps

Figure B.1 illustrates the residual maps for both sources after subtracting the best-fit models (Table 2) to the Band 7 data (336 GHz). For SR 21 the best-fit is described by a ring model, whereas for HD 135344B it is a vortex model. The residuals for HD 135344B show a spiral structure, as also suggested by Pérez et al. (2014) in Band 9 (689 GHz).

thumbnail Fig. B.1

Residual maps after subtracting the best-fit models from Table 2, contours start at ± 3σ and space by 3σ steps.

Appendix C: Uncertainties in the azimuthal variations of the spectral index

thumbnail Fig. C.1

Calculated spectral index (αmm) assuming different alignments of the images for SR 21 (top panel) and HD 135344B (bottom panel).

The calculation of the spectral index (αmm) from the observations depends considerably on how the two images are

overlapped. To demonstrate that the apparent azimuthal variations remain uncertain, we shifted the alignment of the Band 7 and Band 9 images of SR21 and HD135344B by the positional uncertainty. Figure C.1 shows αmm by shifting 20 mas in both vertical and horizontal direction. The only reliable variation of αmm is in the radial direction for SR 21, which remains significant independent of the alignment. In HD 135344B, there is a hint of high values of αmm opposite to the azimuthal asymmetry, which also remains independent of the alignment.

Acknowledgments

We are thankful to the anonymous referee, who helped to improve the quality of this manuscript. We are grateful with M. Benisty and C. P. Dullemond for fruitful discussions. Astrochemistry in Leiden is supported by the Netherlands Research School for Astronomy (NOVA), by a Royal Netherlands Academy of Arts and Sciences (KNAW) professor prize, and by the European Union A-ERC grant 291141 CHEMPLAN. T.B. acknowledges support from NASA Origins of Solar Systems grant NNX12AJ04G. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2012.1.00158.S and #2011.0.00724.S. ALMA is a partnership of ESO (representing its member states), NSF (USA), and NINS (Japan), together with NRC (Canada) and NSC and ASIAA (Taiwan), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ.

References

  1. Andrews, S. M., Wilner, D. J., Espaillat, C., et al. 2011, ApJ, 732, 42 [NASA ADS] [CrossRef] [Google Scholar]
  2. Ataiee, S., Pinilla, P., Zsom, A., et al. 2013, A&A, 553, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Ataiee, S., & Pinilla, P. 2015, MNRAS, submitted [Google Scholar]
  4. Barranco, J. A., & Marcus, P. S. 2005, ApJ, 623, 1157 [NASA ADS] [CrossRef] [Google Scholar]
  5. Birnstiel, T., Dullemond, C. P., & Brauer, F. 2010, A&A, 513, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Birnstiel, T., Dullemond, C. P., & Pinilla, P. 2013, A&A, 550, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Blum, J., & Wurm, G. 2008, ARA&A, 46, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Brauer, F., Dullemond, C. P., & Henning, T. 2008, A&A, 480, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Brown, J. M., Blake, G. A., Dullemond, C. P., et al. 2007, ApJ, 664, L107 [NASA ADS] [CrossRef] [Google Scholar]
  10. Brown, J. M., Blake, G. A., Qi, C., et al. 2009, ApJ, 704, 496 [NASA ADS] [CrossRef] [Google Scholar]
  11. Casassus, S., Wright, C., Marino, S., et al. 2015, ApJ, 812, 126 [NASA ADS] [CrossRef] [Google Scholar]
  12. de Juan Ovelar, M., Min, M., Dominik, C., et al. 2013, A&A, 560, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Dipierro, G., Pinilla, P., Lodato, G., & Testi, L. 2015, MNRAS, 451, 5493 [Google Scholar]
  14. Dodson-Robinson, S. E., & Salyk, C. 2011, ApJ, 738, 131 [CrossRef] [Google Scholar]
  15. Dong, R., Rafikov, R., Zhu, Z., et al. 2012, ApJ, 750, 161 [NASA ADS] [CrossRef] [Google Scholar]
  16. Draine, B. T. 2006, ApJ, 636,1114 [NASA ADS] [CrossRef] [Google Scholar]
  17. Dzyurkevich, N., Flock, M., Turner, N. J., Klahr, H., & Henning, T. 2010, A&A, 515, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Finkbeiner, D. P., Davis, M., & Schlegel, D. J. 1999, ApJ, 524, 867 [NASA ADS] [CrossRef] [Google Scholar]
  19. Flock, M., Ruge, J. P., Dzyurkevich, N., et al. 2015, A&A, 574, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Follette, K. B., Tamura, M., Hashimoto, J., et al. 2013, ApJ, 767, 10 [NASA ADS] [CrossRef] [Google Scholar]
  21. Garufi, A., Quanz, S. P., Avenhaus, H., et al. 2013, A&A, 560, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Guilloteau, S., Dutrey, A., Piétu, V., & Boehler, Y. 2011, A&A, 529, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [NASA ADS] [Google Scholar]
  24. Isella, A., Pérez, L. M., Carpenter, J. M., et al. 2013, ApJ, 775, 30 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  25. Johansen, A., Oishi, J. S., Mac Low, M.-M., et al. 2007, Nature, 448, 1022 [Google Scholar]
  26. Klahr, H. H., & Henning, T. 1997, Icarus, 128, 213 [NASA ADS] [CrossRef] [Google Scholar]
  27. Loinard, L., Torres, R. M., Mioduszewski, A. J., & Rodríguez, L. F. 2008, ApJ, 675, L29 [NASA ADS] [CrossRef] [Google Scholar]
  28. Lyra, W., & Lin, M.-K. 2013, ApJ, 775, 17 [NASA ADS] [CrossRef] [Google Scholar]
  29. Makarov, V. V. 2007, ApJ, 670, 1225 [NASA ADS] [CrossRef] [Google Scholar]
  30. Muto, T., Grady, C. A., Hashimoto, J., et al. 2012, ApJ, 748, L22 [NASA ADS] [CrossRef] [Google Scholar]
  31. Pérez, L. M., Carpenter, J. M., Chandler, C. J., et al. 2012, ApJ, 760, L17 [NASA ADS] [CrossRef] [Google Scholar]
  32. Pérez, L. M., Isella, A., Carpenter, J. M., & Chandler, C. J. 2014, ApJ, 783, L13 [NASA ADS] [CrossRef] [Google Scholar]
  33. Pinilla, P., Benisty, M., & Birnstiel, T. 2012, A&A, 545, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Pinilla, P., Benisty, M., Birnstiel, T., et al. 2014, A&A, 564, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Pinilla, P., de Juan Ovelar, M., Ataiee, S., et al. 2015, A&A, 573, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Pontoppidan, K. M., Blake, G. A., van Dishoeck, E. F., et al. 2008, ApJ, 684, 1323 [NASA ADS] [CrossRef] [Google Scholar]
  37. Quanz, S. P. 2015, Ap&SS, 357, 148 [NASA ADS] [CrossRef] [Google Scholar]
  38. Raettig, N., Klahr, H., & Lyra, W. 2015, ApJ, 804, 35 [NASA ADS] [CrossRef] [Google Scholar]
  39. Regály, Z., Sándor, Z., Dullemond, C. P., & Kiss, L. L. 2011, A&A, 528, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Ricci, L., Testi, L., Natta, A., et al. 2010, A&A, 512, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Rice, W. K. M., Armitage, P. J., Wood, K., & Lodato, G. 2006, MNRAS, 373, 1619 [NASA ADS] [CrossRef] [Google Scholar]
  42. Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
  43. Testi, L., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. Klessen, C. Dullemond, & Th. Henning (Tucson: Univ. of Arizona Press) [Google Scholar]
  44. van Boekel, R., Dullemond, C. P., & Dominik, C. 2005, A&A, 441, 563 [Google Scholar]
  45. van der Marel, N., van Dishoeck, E. F., Bruderer, S., et al. 2013, Science, 340, 1199 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  46. van der Marel, N., van Dishoeck, E. F., Bruderer, S., Pérez, L., & Isella, A. 2015a, A&A, 579, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. van der Marel, N., Pinilla, P., Tobin, J., et al. 2015b, ApJ, 810, L7 [Google Scholar]
  48. van der Marel, N., et al. 2015c, A&A, submitted [Google Scholar]
  49. Weidenschilling, S. J. 1977, MNRAS, 180, 57 [NASA ADS] [CrossRef] [Google Scholar]
  50. Zhang, K., Isella, A., Carpenter, J. M., & Blake, G. A. 2014, ApJ, 791, 42 [NASA ADS] [CrossRef] [Google Scholar]
  51. Zhu, Z., & Stone, J. M. 2014, ApJ, 795, 53 [NASA ADS] [CrossRef] [Google Scholar]
  52. Zhu, Z., Nelson, R. P., Dong, R., Espaillat, C., & Hartmann, L. 2012, ApJ, 755, 6 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Observation properties.

In the text
Table 2

Best-fit parameters the disk morphology models of ring or ring+vortex.

In the text

All Figures

thumbnail Fig. 1

ALMA observations of dust continuum emission for SR 21 (top panels) and HD 135344B (bottom panels). The left columns show the Band 9 (689 GHz) and Band 7 (336 GHz) continuum, with the contour overlaid at 10, 20, ..., 90% of the peak. The third column shows the overlay of the contours with a step of 20% of the peak (black is Band 9, red is Band 7). The right column shows the resolved αmm in colour contours. The beam size is indicated in each plot.
In the text
thumbnail Fig. 2

Real part of the visibilities at 689 GHz (~450 μm, Band 9) and at 336 Gz (~870 μm, Band 7) for SR 21 (top panel) and HD 135344B (bottom panel). The plot includes error bars that are of the size of the plotting points. At both wavelengths, the models with the best-fit parameters are over-plotted (solid line), which is the ring model in the case of SR 21, and the vortex model for HD 135344B.

In the text
thumbnail Fig. 3

Dust density distribution when 1 MJup is embedded at 20 AU after 1 and 5 Myr of evolution (top and bottom panel respectively). The lines represent particle sizes with different Stokes numbers (St = [10-3,10-2,10-1,1]), which are proportional to the gas surface density profile.
In the text
thumbnail Fig. 4

Top panel: intensity radial profiles at 450 and 870 μm obtained from the dust density distributions after 1 and 5 Myr of evolution. Bottom panel: radial profile of αmm calculated from the intensity profiles at 450 and 870 μm, which is convolved with 35 AU Gaussian beam.
In the text
thumbnail Fig. A.1

Imaginary part of the visibilities at 689 GHz (~450 μm, Band 9) and at 336 GHz (~870 μm, Band7) for SR 21 (top panel) and HD 135344B (bottom panel).
In the text
thumbnail Fig. B.1

Residual maps after subtracting the best-fit models from Table 2, contours start at ± 3σ and space by 3σ steps.

In the text
thumbnail Fig. C.1

Calculated spectral index (αmm) assuming different alignments of the images for SR 21 (top panel) and HD 135344B (bottom panel).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.