| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A44 | |
| Number of page(s) | 17 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201525752 | |
| Published online | 18 November 2015 | |
Photometric classification of quasars from RCS-2 using Random Forest⋆
1 Instituto de Astrofísica, Pontificia Universidad Católica de Chile, 4860 Avenida Vicuña Mackenna, Santiago, Chile
e-mail: dcarrasco@student.unimelb.edu.au
2 School of Physics, University of Melbourne, Parkville, Victoria, VIC3010 Australia
3 Millennium Institute of Astrophysics, Chile
4 Departamento de Ciencia de la Computación, Pontificia Universidad Católica de Chile, 4860 Avenida Vicuña Mackenna, Santiago, Chile
5 Departamento de Ciencias Físicas, Universidad Andres Bello, 252 Avenida República, Santiago, Chile
6 South African Astronomical Observatory, PO Box 9, 7935 Observatory, South Africa
7 Kavli Institute for Cosmological Physics, University of Chicago, 5640 South Ellis Avenue, Chicago, IL 60637, USA
8 Department of Astronomy and Astrophysics, University of Chicago, 5640 South Ellis Avenue, Chicago, IL 60637, USA
9 Department of Astronomy and Astrophysics, University of Toronto, 60 St. George Street, Toronto, Ontario M5S 3H8, Canada
10 Institute of Astrophysics & Astronomy, Academia Sinica, 106 Taipei, Taiwan, R.O.C.
11 Departamento de Astronomía, Universidad de Chile, Casilla 36-D, Santiago, Chile
Received: 27 January 2015
Accepted: 24 August 2015
The classification and identification of quasars is fundamental to many astronomical research areas. Given the large volume of photometric survey data available in the near future, automated methods for doing so are required. In this article, we present a new quasar candidate catalog from the Red-Sequence Cluster Survey 2 (RCS-2), identified solely from photometric information using an automated algorithm suitable for large surveys. The algorithm performance is tested using a well-defined SDSS spectroscopic sample of quasars and stars. The Random Forest algorithm constructs the catalog from RCS-2 point sources using SDSS spectroscopically-confirmed stars and quasars. The algorithm identifies putative quasars from broadband magnitudes (g, r, i, z) and colors. Exploiting NUV GALEX measurements for a subset of the objects, we refine the classifier by adding new information. An additional subset of the data with WISE W1 and W2 bands is also studied. Upon analyzing 542 897 RCS-2 point sources, the algorithm identified 21 501 quasar candidates with a training-set-derived precision (the fraction of true positives within the group assigned quasar status) of 89.5% and recall (the fraction of true positives relative to all sources that actually are quasars) of 88.4%. These performance metrics improve for the GALEX subset: 6529 quasar candidates are identified from 16 898 sources, with a precision and recall of 97.0% and 97.5%, respectively. Algorithm performance is further improved when WISE data are included, with precision and recall increasing to 99.3% and 99.1%, respectively, for 21 834 quasar candidates from 242 902 sources. We compiled our final catalog (38 257) by merging these samples and removing duplicates. An observational follow up of 17 bright (r < 19) candidates with long-slit spectroscopy at DuPont telescope (LCO) yields 14 confirmed quasars. The results signal encouraging progress in the classification of point sources with Random Forest algorithms to search for quasars within current and future large-area photometric surveys.
Key words: techniques: photometric / quasars: general / surveys / catalogs
Full Tables 1−3 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/584/A44
© ESO, 2015
1. Introduction
Quasars are important astronomical targets, both individually as cosmic lighthouses and within well-defined quasar catalogs. As such, classifying and identifying them becomes an important, yet non-trivial task. Their significance in astronomy has led several groups to search and catalog them. These efforts include the Large Bright Quasar Survey (LBQS; e.g., Foltz et al. 1989; Hewett et al. 1995), the FIRST Bright Quasar Survey (FBQS; e.g., Gregg et al. 1996; White et al. 2000; Becker et al. 2001), the Palomar-Green survey of UV-excess objects (Green et al. 1986), and the FIRST-2MASS Red Quasar Survey (Glikman et al. 2007).
Among other applications, quasars can be used to study galaxy evolution (e.g., Hopkins et al. 2006), the intervening intergalactic gas (e.g., Lopez et al. 2008), cosmological evolution (e.g., Oguri et al. 2008), black hole physics (e.g., Portinari et al. 2012), and the analysis of individual galaxies and galaxy clusters due to gravitational lensing (e.g., Faure et al. 2009). The active nuclei of these galaxies produce high luminosities (typically ~1040 W) spanning a broad range of frequencies. This spectacular luminosity allows them to be observed at high redshifts, which provides insight into the distant Universe. Because of their large distances, most quasars are observed as point sources in optical surveys, meaning they can easily be misidentified as stellar sources when only photometric information is available. However, by sampling certain rest-frame wavelengths, one may distinguish between local and extragalactic sources through differing spectral characteristics.
The lack of a Balmer jump (at λrest = 3646 Å) in low-redshift (z ≲ 2.2) quasars separates them from the hot star population. The Lyα line emission and absorption characterized by the Lyα forest identified in high-redshift quasar spectra produce broadband colors that progressively redden with redshift (Richards et al. 2002). Owing to observational techniques, most quasar searches are based only on optical colors (e.g, Richards et al. 2001; Bovy et al. 2011), thus introducing a redshift-dependent bias. This arises from the distinctive strong line emission of quasars, affecting their broadband colors relative to the expected continuum flux. Particularly challenging is to select quasar targets at intermediate redshifts (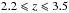 ), where classification is typically inefficient. Quasars with magnitudes brighter than ~21 are relatively rare, and it can be seen that the quasar and stellar loci cross in color space at z ~ 2.8 (e.g., Richards et al. 2002; Bovy et al. 2011).
), where classification is typically inefficient. Quasars with magnitudes brighter than ~21 are relatively rare, and it can be seen that the quasar and stellar loci cross in color space at z ~ 2.8 (e.g., Richards et al. 2002; Bovy et al. 2011).
Some previous studies have incorporated multiwavelength searches by combining different surveys. For example, Richards et al. (2006) combined magnitude measurements from different surveys to improve the performance of their quasar selection. Most of the previous work, however, has been based on color−color cuts. While effective, the selection and cut limits are both arbitrary and time-consuming, since all possibilities are explored by hand. By contrast, machine-learning algorithms have the advantage of adopting, in an automated way, the best criteria for choosing quasar candidates based on a sample of objects with predefined types. While the creation of such a so-called training set can be disadvantageous because it introduces biases or indeed because of the compilation of an adequately representative source catalog, this approach permits a fast, efficient classification of big data sets.
New methods and approaches in source classification are required to deal with the large volume of data, which are due to be taken over the coming years from next-generation sky surveys, such as ATLAS (Eales et al. 2010), LSST (LSST Science Collaboration et al. 2009), DES (The Dark Energy Survey Collaboration 2005), and Pan-STARRS (Kaiser et al. 2002). Efficient algorithms are vital in processing these forthcoming data to realize the science goals of these surveys. An automated methodology for bulk-classifying the source catalogs will be an essential ingredient in their success.
The main goal of this study is to use a machine-learning algorithm to construct a catalog of quasars selected from purely photometric information. Machine-learning algorithms have been used to classify objects for many years (e.g., Ball et al. 2006, 2007; Richards et al. 2011). The best known classification models are decision trees (Quinlan 1993), naive Bayes (Duda & Hart 1973), neural networks (Rumelhart et al. 1986), support vector machines (Cortes & Vapnik 1995), and Random Forest (Breiman 2001). As summarized by Ball & Brunner (2010), machine learning in astronomy has found a use in star-galaxy separation (e.g., Collister et al. 2007), classification of galaxy morphology (e.g., Huertas-Company et al. 2008), quasar/AGN classification (e.g., Pichara & Protopapas 2013; Pichara et al. 2012), galaxy photometric redshifts (e.g., Gerdes et al. 2010), and photometric redshift estimation of quasars (e.g., Wolf 2009).
Our approach to automated quasar identification from only photometric data is based on the Random Forest algorithm (Breiman 2001), which is a machine-learning algorithm based on multiple decision trees (Quinlan 1986). Applying Random Forests in astronomy is relatively novel, dating back only a few years (e.g., Dubath et al. 2011; Richards et al. 2011; Pichara et al. 2012). A key strength in the method is an efficient exploration of the spectrum of variable combinations, while avoiding arbitrary thresholding to define distinct object classes (such as stars, quasars). This approach has been used for the photometric redshift measurement of quasars (e.g., Carliles et al. 2010), while Carrasco Kind & Brunner (2013) extend this by also including prediction trees. These techniques are shown to be highly efficient and rapid, although training sets are integral to teaching the model which characteristics are more relevant to classify an object. Our work is the first to construct a catalog of quasar candidates with the Random Forest algorithm from purely photometric data spanning three different surveys over a wide wavelength range. This multi-wavelength approach has been shown to work well for quasar classification; for example, Richards et al. (2006) find that adding optical information to mid-infrared (MIR) data allows for a more efficient type 1 quasar selection. Gao et al. (2009) studied the distinction between quasars and stars with data from catalogs at different wavelengths, concluding that the Random Forest is an effective tool for object classification. Our search is founded primarily on broadband photometric data from the Red-Sequence Cluster Survey 2 (RCS-2) in addition to supplementary data from GALEX and WISE surveys. From these data, we constructed a catalog of point sources classified as quasars by the Random Forest algorithm. This classification prioritizes the precision over the completeness because our aim is to generate a catalog of reliable quasar candidates.
The article is organized as follows. In Sect. 2 we present the data used, including RCS-2, SDSS, WISE, and GALEX, in Sect. 3 we describe the Random Forest classifier, along with the training and testing sets used. Section 4 describes the results, and in Sect. 6 we present a discussion and summary of our findings. AB magnitudes are used unless otherwise noted.
2. Data
To construct a point-source training catalog, we cross-matched RCS-2 photometric sources with spectroscopically-confirmed stellar and quasars sources from SDSS. For subsets of this point-source catalog, we merged WISE and GALEX photometry. The search radius used in the cross-matching depends on the catalogs used. The source catalogs are described below.
2.1. RCS-2 data set
The second Red-Sequence Cluster Survey (RCS-2; Gilbank et al. 2011) is an optical imaging survey that aims to detect galaxy clusters in the 0.1 ≲ z ≲ 1.0 redshift range. It covers an area of ~1000 deg2. The data were taken at the CFHT telescope using the MegaCam square-degree imager. The survey was imaged in three filters: g′ (with a 5σ point source limiting AB magnitude of 24.4), r′ (limiting magnitude of 24.3), and z′ (limiting magnitude of 22.8). The median seeing in the r′ band is  . About 75% of the survey area is also observed in the i′ band (limiting magnitude of 23.7) as part of the Canada-France High-z quasar survey (Willott et al. 2005). Our point-source catalog uses all four bands, which means that the area of search is reduced to ~75% (~750 deg2).
. About 75% of the survey area is also observed in the i′ band (limiting magnitude of 23.7) as part of the Canada-France High-z quasar survey (Willott et al. 2005). Our point-source catalog uses all four bands, which means that the area of search is reduced to ~75% (~750 deg2).
Objects are classified according to their light distribution by comparing their curve of growth with a weighted average curve derived from a set of four to eight reference PSFs from nearby unsaturated stars. Each source is categorized by object type: 0-artifact/spurious object; 1 or 2-galaxy; 3-star; 4-saturated (Yee 1991; Yee et al. 1996). All point sources brighter than i< 17.5 are considered as saturated (Gilbank et al. 2011). In this study, we selected type-3 (point-source) objects.
2.2. SDSS data set
The Sloan Digital Sky Survey (SDSS; York et al. 2000) is an optical survey that covers ~10 000 deg2 of the sky. The data were obtained at the Apache Point Observatory with a dedicated 2.5 m telescope and imaged by a large-format mosaic CCD camera. The optical magnitudes of objects were measured through five optical broadband filters of u′, g′, r′, i′, and z′ (Fukugita et al. 1996) with limiting magnitudes of 22.3, 22.6, 22.7, 22.4, and 20.5, respectively, in the AB system. The SDSS PSF is typically ~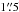 . We mainly used the data from the Data Release Nine (DR9; Ahn et al. 2012). It is important to clarify that we did not use SDSS magnitudes for the classification.
. We mainly used the data from the Data Release Nine (DR9; Ahn et al. 2012). It is important to clarify that we did not use SDSS magnitudes for the classification.
2.2.1. Quasars
Our source quasar catalog was derived predominantly from DR9. The DR9 Quasar Catalog contains 228 468 quasar spectra (Ahn et al. 2012). It is this quasar sample that we cross-matched with RCS-2 point sources to obtain a set of spectroscopically confirmed quasars with RCS-2 photometry.
2.2.2. Stars
Our catalog of stars stems mainly from spectroscopic confirmations of sources in SDSS Data Release 9. The catalog contains 668 054 confirmed stellar spectra (Ahn et al. 2012). We cross-matched this combined sample of stars to RCS-2 point source photometry to create a catalog of spectroscopically confirmed RCS-2 stars.
2.3. WISE data set
The Wide-Field Infrared Survey Explorer (WISE; Wright et al. 2010) is an infrared all sky survey. It has four MIR bands: W1 at 3.4 μm, W2 at 4.6 μm, W3 at 12 μm, and W4 at 22 μm with angular resolutions of 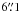 ,
, 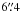 ,
, 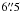 , and
, and 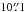 respectively. Limiting magnitudes (in Vega) are 16.5 for W1, 15.5 for W2, 11.2 for W3, and 7.9 for W4. In our study we used the W1 and W2 bands, following the approach by Stern et al. (2012), as mentioned in Sect. 3.1.3. For consistency, we convert these magnitudes to the AB system following Tokunaga & Vacca (2005) and Jarrett et al. (2011).
respectively. Limiting magnitudes (in Vega) are 16.5 for W1, 15.5 for W2, 11.2 for W3, and 7.9 for W4. In our study we used the W1 and W2 bands, following the approach by Stern et al. (2012), as mentioned in Sect. 3.1.3. For consistency, we convert these magnitudes to the AB system following Tokunaga & Vacca (2005) and Jarrett et al. (2011).
2.4. GALEX data set
The Galaxy Evolution Explorer (GALEX; Martin et al. 2005) is an orbital space telescope with a mission to compile an all-sky photometric map in the UV. The telescope images simultaneously with two bands: the far ultraviolet (FUV; effective wavelength 1528 Å with angular resolution 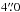 ) and the near ultraviolet (NUV; effective wavelength 2271 Å with angular resolution
) and the near ultraviolet (NUV; effective wavelength 2271 Å with angular resolution 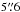 ). For the 26 000 deg2 All Sky-Imaging (AIS) catalog, 100-s exposures result in limiting (AB) magnitudes of 19.9 and 20.8 for the FUV and NUV, respectively. While there are other deeper GALEX catalogs targeting specific regions, we omit them in preference for a catalog of uniform depth. In this study, we have used the data from GR4/5.
). For the 26 000 deg2 All Sky-Imaging (AIS) catalog, 100-s exposures result in limiting (AB) magnitudes of 19.9 and 20.8 for the FUV and NUV, respectively. While there are other deeper GALEX catalogs targeting specific regions, we omit them in preference for a catalog of uniform depth. In this study, we have used the data from GR4/5.
Because reddening due to galactic dust becomes significant in the UV, we corrected each GALEX magnitude with the Schlegel et al. (1998) dust maps based on the extinction law from Cardelli et al. (1989).
3. Random Forest
The Random Forest algorithm (Breiman 2001) is a tree-based classification method that learns how to classify objects into different classes using a training set. In this context, a training set is a set of preclassified objects (their class is known); each object is characterized by a vector whose components are attribute values. To understand how Random Forest classifiers operate, we must first describe their fundamental components: decision trees. A decision tree (Quinlan 1986) is a graph theory structure where nodes represent attributes and edges are the possible values the attribute can take. For example, one node may represent the “(g−i) color” attribute, with two edges pointing out from the node representing two possible values, for example, “≤0.5” and “>0.5”. For a given object, depending on the value it has in the attribute “(g−i) color”, it will follow a path along one edge or the other from the node representing the attribute. At the end of the path (after following many other nodes that filter based on the values of the other potential attributes), the object will end up in a leaf. Leaves represent a class predicted from the tree: for example, a leaf may have a value “quasar” or “star”. Learning which paths are taken in a decision tree, using well-defined objects, provides us with an automated process of classifying unknown objects based on their attributes. The main challenge, therefore, is to build a suitable decision tree for a particular task, in our case, for the automatic classification of quasars and stars. Technical details about the building (training) process of a decision tree are beyond the scope of this paper, but they can be found in Quinlan (1986).
A Random Forest is an extension of decision trees, with stronger classification capabilities and better performance in many tasks. The core idea of a Random Forest model is to train several decision trees using samples (with replacement) from the training set, and subsequently use these decision trees to classify unknown objects.
This model is subsequently applied to a database containing many objects (with the same attributes) of unknown type in order to make a prediction of the class they belong to. For a training set of N objects described by F attributes, we define T as the number of trees in the Random Forest and M<F as the number of attributes used in each tree (T and M are model parameters). The training procedure is as follows:
-
Generate T data sets with N objects. Each data set is created by randomly sampling objects from the original training set with replacement. This means each of the T sets has the same number of elements as the training sets, but some objects are selected more than once.
-
From each of the T data sets, grow a full1 decision tree, but on each node select the best split from a set of F attributes selected randomly from the F initial attributes.
The creation of each decision tree is both independent and random, and it relies on two principles: the first is the diversity among individual classifiers arising from the training of individual trees on different samples. The second principle is that only a subset of randomly selected attributes are used to build each of the trees. As noted in Geurts et al. (2006), these help to find classification patterns in small subsets of attributes, each tree focusing on different subsets, thus improving the algorithm’s accuracy.
Every tree from the forest can assign a class to an object, based on the attribute values it has. The algorithm’s final predicted classification for a given object is the one selected by the majority of the T trees. Operating in this manner, the Random Forest algorithm runs efficiently on large databases and can handle F ~ 103 attributes.
To test the classifier we use a ten-fold cross-validation across the training set. This involves partitioning the training set into ten equal subsets. For a selected subset, we train the model with the other nine subsets and test the performance of the resultant classifications when applied to this selected subset. This procedure is carried out for each of the ten subsets. Results from each of these cross-validated runs are analyzed with performance metrics. To quantify the performance of the algorithm, for each class of object (i.e., stellar and QSO in this case) we use recall (r), precision (p), and F-Score (Fs) (Powers 2007), defined as
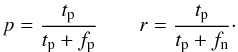 Here, tp, fp, and fn are the number of true positives, false positives, and false negatives, respectively.
Here, tp, fp, and fn are the number of true positives, false positives, and false negatives, respectively.
Recall therefore corresponds to the fraction of correctly classified objects of each class with respect to all objects genuinely belonging to that class. Precision is the fraction of correctly classified objects within each class compared to with respect to all objects classified by the algorithm as members of that class. Finally, F-score is the harmonic mean of precision and recall.
The program used for this implementation is the scikit-learn (Pedregosa et al. 2011) library for Python.
3.1. Training sets
Training sets are samples of objects for which the target class is known. In this study, the classes (stellar and QSO sources) are obtained by cross-identification of SDSS spectroscopically-confirmed targets to RCS-2 point sources, as discussed above in Sects. 2.2.1 and 2.2.2. A match between the two catalogs is obtained when their angular positions are separated by less than 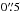 . The cross-matching is performed for both stellar and QSO sources, with 20 659 and 8762 matches made, respectively. From this preliminarily matched catalog we require RCS-2 targets to have measured flux in all four filters and photometric errors of less than 0.1 in each. Our catalogs consequently reduce in size to 4916 quasars and 10 595 stars. From these data, we create three different training sets summarised in Table 4. Each object within the training set is described by attributes of magnitude and color. We include all possible attributes to open the parameter space available for the algorithm to ensure an optimal classification.
. The cross-matching is performed for both stellar and QSO sources, with 20 659 and 8762 matches made, respectively. From this preliminarily matched catalog we require RCS-2 targets to have measured flux in all four filters and photometric errors of less than 0.1 in each. Our catalogs consequently reduce in size to 4916 quasars and 10 595 stars. From these data, we create three different training sets summarised in Table 4. Each object within the training set is described by attributes of magnitude and color. We include all possible attributes to open the parameter space available for the algorithm to ensure an optimal classification.
To create the cleanest possible QSO catalog from the Random Forest algorithm, we select the run with the highest precision. To find suitable parameters for the Random Forest, we perform a grid search within a limited discrete space over a set of possible values that will depend on each training set.
3.1.1. Training set 1 (TrS1)
 |
Fig. 1 Color−color diagrams of spectroscopically confirmed quasars (red) and stars (blue) in RCS-2. The upper diagram shows the colors g−r vs. r−i, and the bottom diagram shows the colors r−i vs. i−z. While it is possible to see a quasar clump and a stellar locus, in both cases there is no clean way to separate them. |
As discussed above, we created three training sets from the cross-matched catalog. The attributes used for the first training set are the colors g−r, g−i, g−z, r−i, r−z, and i−z, and the most relevant of these colors are g−r, r−i, and i−z. Following Richards et al. (2002), it is possible to separate quasars and stars without spectroscopic information by constructing color−color diagrams. In Fig. 1 we clearly see the characteristic stellar locus and a clump of quasars. For the algorithm, as we see below, it is possible also to use the magnitudes as attributes. We do not do it in this case because the information of the magnitudes is used in a previous step as we describe in Sect. 3.2.1.
Figure 2 shows the wide redshift range of QSOs from this sample in green: from 0 to 6 and peaking at z ~ 2.5. In color−color plots, the quasar population lying near this redshift peak can be contaminated with stars, making separation of the two populations more difficult (e.g., Fan 1999; Richards et al. 2002; Bovy et al. 2011).
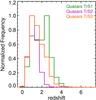 |
Fig. 2 Redshift distribution of quasars from the three training sets: TrS1 (green), TrS2 (magenta), and TrS3 (orange). The GALEX-based data (TrS2) do not probe as deep in redshift as the other two. While the sources with WISE fluxes (TrS3) appear to peak at a lower redshift, they nevertheless remain sensitive out to the redshifts explored by the optical-only data (TrS1). |
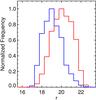 |
Fig. 3 Normalized distribution of r-band magnitudes from RCS-2 for quasars and stars listed in the TrS1 training set. We see that the peak of the stellar (blue) sources is approximately one magnitude brighter than for the quasars (red). |
It is important to analyze magnitude distributions because fluxes might be important attributes in distinguishing stars from quasars. Figure 3 therefore shows the magnitude distribution of stars (blue) and quasars (red), with the former peaking brighter than the latter. This means the training set is biased against faint objects. The number of quasars relative to the number of stars at faint magnitudes is higher; this arises because the fraction of stellar sources drops off faster than the fraction of QSOs toward fainter magnitudes. Moreover, the predominance of bright (r ≤ 22) objects within the training set introduces an observational bias that hinders accurate classification of faint objects (up to the catalog magnitude limit of r ~ 23). To address this excess of quasar classifications (leading to possible misidentification at faint magnitudes), our data set of objects to be classified that matches the magnitude distribution of the training set2. The data set is explained in more detail in Sect. 3.2.1.
Our training set TrS1 therefore comprises 4916 quasars and 10 595 stars.
3.1.2. Training set 2 (TrS2)
TrS2 is a subset of TrS1. We cross-identified all quasars and stars from TrS1 with GALEX objects detected in the NUV band and with a photometric error of 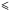 0.25 (consistent with magnitudes of ~22.5, around the limit magnitude in this band). The search radius used to match sources was
0.25 (consistent with magnitudes of ~22.5, around the limit magnitude in this band). The search radius used to match sources was 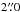 , based on the angular resolution of both surveys. Other studies use larger radii (Trammell et al. 2007; Worseck & Prochaska 2011; Agüeros et al. 2005), but for cross-matching SDSS and GALEX catalogs. It is important to note that while our objects were identified from SDSS, we used RCS-2 photometry featuring a better resolution, so that a smaller search radius is justified. Moreover, unlike the previous works cited before, we do not use the FUV band with a lower resolution. Our cross-matching yields a sample of 1228 quasars and 815 stars, and we note a significant decrease in the number of objects in the catalog, especially stars. We attribute this to both the lower angular resolution of GALEX with respect to SDSS/RCS-2 and to the redshift dependence of the UV emission from quasars: only QSOs with redshifts up to z ~ 2.0 should be detectable via observed-frame spectral attributes lying within the filter passband. Because stellar emission in the UV is typically low, there are considerably fewer stellar sources in this catalog. The stellar sources now present in this new sample will be predominantly blue stars.
, based on the angular resolution of both surveys. Other studies use larger radii (Trammell et al. 2007; Worseck & Prochaska 2011; Agüeros et al. 2005), but for cross-matching SDSS and GALEX catalogs. It is important to note that while our objects were identified from SDSS, we used RCS-2 photometry featuring a better resolution, so that a smaller search radius is justified. Moreover, unlike the previous works cited before, we do not use the FUV band with a lower resolution. Our cross-matching yields a sample of 1228 quasars and 815 stars, and we note a significant decrease in the number of objects in the catalog, especially stars. We attribute this to both the lower angular resolution of GALEX with respect to SDSS/RCS-2 and to the redshift dependence of the UV emission from quasars: only QSOs with redshifts up to z ~ 2.0 should be detectable via observed-frame spectral attributes lying within the filter passband. Because stellar emission in the UV is typically low, there are considerably fewer stellar sources in this catalog. The stellar sources now present in this new sample will be predominantly blue stars.
Including the GALEX NUV band is relevant because optical observations alone do not allow a clean separation between quasars and stars (See Fig. 1), especially at intermediate redshifts (2.2 ≲ z ≲ 3.5). UV flux data are very useful in quasar classification because stellar-QSO populations are well separated in UV-optical color space (Trammell et al. 2007). In Fig. 4 we can see the color−color diagrams of the quasars and stars with detections in the NUV band. Comparing the NUV-g vs. g−r plot to optical equivalents, we note the overlap between quasars and stars has almost disappeared.
There is a relation between the NUV detection of quasars and redshift. An important contribution to the bolometric flux is an intense, broad emission feature that dominates the spectral energy distribution (SED) at bluer wavelengths: the so-called big blue bump (Sanders et al. 1989). According to Trammell et al. (2007), NUV-band detections of quasars are almost complete up to z ~ 1.4 and are still well recovered at z ~ 1.7. However, by z ~ 2.0 the detection completeness declines to 50%. While it is not clear whether the FUV band or NUV band is best suited to quasar detection, we use just NUV owing to the small number (~10%) of NUV-detected sources having FUV fluxes as well. Moreover, the redshift range sampled by FUV sources appears smaller. Figure 2 shows that the TrS2 redshift coverage is complete only out to low redshifts compared to TrS1. Moreover, the limit of r-band magnitudes (Fig. 5) is much brighter than TrS1, suggesting that the lack of faint-magnitude stars is not a major problem in this training set.
 |
Fig. 4 Color−color diagrams of spectroscopically confirmed quasars (red) and stars (blue) in RCS-2. The upper diagrams show the optical g−r vs. r−i (left) and r−i vs. i−z (right) color plots. The bottom plot shows the NUV-g vs. g−i color space when including GALEX data. It can be seen that including the UV data provides a clearer separation between quasars and stars compared to solely optical data. |
For training set TrS2, the attributes used for Random Forest classification are the four magnitudes from RCS-2 bands: g, r, i, and z; the NUV band; and the colors: NUV-g, NUV-r, NUV-i, NUV-z, g−r, g−i, g−z, r−i, r−z, and i−z. As discussed in Sect. 3.1, all color combinations are added for analysis by the algorithm.
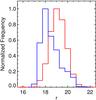 |
Fig. 5 Histogram of the normalized r-band magnitude distribution from cross-matched RCS-2 and GALEX data featured in the TrS2 data set. Quasars are shown in red, while stars are blue. According to the optical data presented in Fig. 3, stellar sources appear to have systematically brighter r-band magnitudes. |
3.1.3. Training set 3 (TrS3)
This training set is also a subset from TrS1 and is built by cross-identifying all quasars and stars from TrS1 with WISE sources detected in the W1 (3.4 μm) and W2 (4.6 μm) bands. The 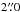 cross-matching search radius was chosen according to the angular resolution of both catalogs. As in the previous training set, we adopted a smaller matching radius compared to previous studies crossmatching SDSS with WISE sources (e.g., Wu et al. 2012; Lang et al. 2014). We used these bands following Stern et al. (2012), where they are used to select quasars from WISE. We additionally made a cut in the magnitude error corresponding to 0.2 in both bands, consistent with the magnitude limits of our sample. Following these selection criteria, we obtain a sample of 2748 quasars and 2679 stars. As can be seen in Fig. 6, using the WISE bands is useful because separation between quasars and stars in the color−color plots is cleaner than those using purely optical RCS-2 bands. We expect, therefore, that including these bands boosts the performance of the classifier.
cross-matching search radius was chosen according to the angular resolution of both catalogs. As in the previous training set, we adopted a smaller matching radius compared to previous studies crossmatching SDSS with WISE sources (e.g., Wu et al. 2012; Lang et al. 2014). We used these bands following Stern et al. (2012), where they are used to select quasars from WISE. We additionally made a cut in the magnitude error corresponding to 0.2 in both bands, consistent with the magnitude limits of our sample. Following these selection criteria, we obtain a sample of 2748 quasars and 2679 stars. As can be seen in Fig. 6, using the WISE bands is useful because separation between quasars and stars in the color−color plots is cleaner than those using purely optical RCS-2 bands. We expect, therefore, that including these bands boosts the performance of the classifier.
One additional advantage in using WISE bands, which is shared with TrS2, is the introduction of new bands (two in this case), resulting in higher quality classification. The advantages of TrS3 over TrS2 is the additional band available to the algorithm but also the wider redshift coverage, as seen in Fig. 2 (color orange): redshift coverage is complete up to z ~ 2, yet there are still detections up to z ~ 4. As such, we are able to classify objects to higher redshifts than in TrS2. More significantly, WISE detections cover the aforementioned midredshift range (2.2 ≲ z ≲ 3.5), where it is hard to separate quasars from stars. For putative QSOs in this redshift range, the algorithm used in conjunction with TrS3 will be very useful. Also, as seen in Fig. 7, the magnitude distribution of this sample is, on average, brighter than TrS1 (around 1 mag) but fainter than TrS2 (around 0.5 mag), allowing the classification of fainter objects with more information.
Attributes of the training set utilized by the algorithm are magnitudes in the four RCS2 bands: g, r, i, and z; W1 and W2 magnitudes from WISE; and the colors g−r, g−i, g−z, g-W1, g-W2, r−i, r−z, r-W1, r-W2, i−z, i-W1, i-W2, z-W1, z-W2, and W1-W2. As explained for the previous training sets, we make available all colors to the algorithm.
3.2. Data set
A data set is a sample of point sources for which the class is not known and where the trained classification model is applied. We have three data sets, one data set for each one of the training sets described above. They are all constructed with point sources from RCS-2 photometry with the same requirements as in the training sets.
 |
Fig. 6 Color−color diagrams of the spectroscopically confirmed quasars (red) and stars (blue) in RCS-2 with detection in the W1 and W2 bands from WISE. The upper left diagram shows the colors g−r vs. r−i, the upper right diagram shows the colors r−i vs. i−z, the bottom left diagram shows the colors i−z vs. z-W1, and the bottom left diagram shows the color z-W1 vs. W1-W2. |
3.2.1. Data set 1 (DS1)
This data set is classified using the algorithm trained on TrS1. It includes point sources from RCS-2 that meet the requirements described above. In total, 1 863 970 point sources define what we call data set DS0; however, for consistency we selected a subsample from these points matching the magnitude distribution of TrS1. Figure 8 shows the normalized r magnitude distribution of all the objects (stars and quasars) from TrS1. We took this distribution as the model for our data set. We matched the distribution by calculating the fraction of objects in each 0.5 mag bin and the number of objects in each bin from the DS0 point source data set. We calculated the number of objects corresponding to the fraction obtained from TrS1 in each bin, randomly selecting this quantity within the same magnitude range. We ultimately ended up with a sample of 542 895 photometric sources to be classified by the algorithm. Figure 9 shows these two distributions: the sample before the cut (DS0, in gray), and the sample after the cut (DS1, in magenta).
3.2.2. Data set 2 (DS2)
This data set has been classified using the algorithm trained on TrS2. It contains the point sources from DS0 that additionally have GALEX NUV-band detections. The cross-matching search radius and photometric error limits are the same as TrS2, as described in Sect. 3.1.2. Within this data set, there are 16 898 sources the algorithm must classify, of which 9242 sources are also in the DS1 data set.
3.2.3. Data set 3 (DS3)
This data set has been classified using the algorithm trained on TrS3. The point sources are those from DS0 with detection in the W1 and W2 bands from WISE. We applied the TrS3 criteria to the point source catalog for the cross-match and the limit in photometric errors. These constraints result in a data set of 242 902 point sources for classification. There are 138 658 objects in DS3 that form part of DS1.
In Fig. 10 we compare the r-band magnitude distribution of the three data sets. As expected, the faintest peak corresponds to DS1, while the brightest belongs to DS3.
4. Results
We trained the algorithm with the three training sets separately and then applied it to the corresponding data sets:
-
For TrS1, our grid search for M (the number of attributes) goes between three and six with a bin size of one, and we investigated values of T (the number of trees) between 10 and 150, in bins of ten. The optimal pair of parameters with an F score of 88.9% is M = 4 and T = 50. These return recall and precision values listed (for both stars and quasars) in the first column of Table 5. We subsequently applied this model to DS1 and obtained 21 501 quasars, which is 4.0% of the total number of sources. Figure 11 shows the r-band magnitude distribution of the two classifications. These distributions are similar to those seen in the TrS1 training set (Fig. 3). DS1 stellar classifications (blue) peak at magnitude 19 just as in TrS1, with a similar skew toward brighter magnitudes. The DS1 quasar classifications show a seemingly broader peak (at r ~ 20.25) than their TrS1 counterparts, with a slight skew toward fainter magnitudes. We also note that the percentages of objects classified as quasars is different between the DS1 candidates (4.0%) and verified objects from TrS1 (31.7%). This is in part due to our prioritization of the precision, but more importantly, it shows that even when the training sample is incomplete, the algorithm is capable of classifying objects that are not covered in the sample (in this case stars). Despite the low fraction of quasars in DS1 relative to TrS1, that their respective r-band distributions for both stellar and quasar classifications are similar is remarkable when merely considering colors are used as attributes for the classification.
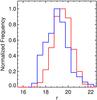
Fig. 7 Histogram of the normalized magnitude distributions in the RCS-2 r-band of quasars and stars from TrS3 (those sources with WISE photometry).
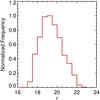
Fig. 8 Histogram of the normalized magnitude distribution in the r band of all the objects in TrS1.
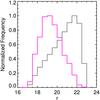
Fig. 9 Histogram of the normalized magnitude distribution in the r band of the point sources from RCS-2 (color gray) and the new data set DS1 that was obtained by matching its distribution with the distribution of TrS1.
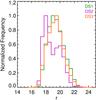
Fig. 10 Normalized r-band magnitude distribution in RCS-2 for each of our the three test data sets: DS1 (green), DS2 (magenta), and DS3 (orange). These data are the sources that the algorithm must classify.
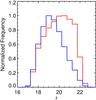
Fig. 11 Normalized r-band magnitude distributions of from quasar (red) and star (blue) candidates from DS1, as classified by the Random Forest algorithm. In parallel with the distribution of spectroscopically verified sources presented in Fig. 3, we note that stellar sources are generally brighter than quasars.
-
For TrS2, our search ranges between 3 and 15 with a bin size of 1 for M and 10 to 150 for T. We find that the optimal parameters for source classification are M = 5 and T = 150. The recall and precision resulting from these parameters are also shown in Table 5, and the F score is 97.2%. Classifying all sources from DS2, we obtain 6529 quasars, which corresponds to 38.6% of the objects. As with DS1, in Fig. 12 we show the r-band magnitude distribution for objects classified as stars and QSOs; it can be seen that the whole sample is brighter than the first one, as expected. Moreover, there is a notable similarity between this distribution and that of the TrS2 in Fig. 5.
-
For TrS3, our search ranges from 3 to 21 for M and from 10 to 150 for T. We find the best parameters to be M = 8 and T = 60. The results of recall and precision are shown in Table 5, and the F score is 99.2%. From the DS3 point sources 21 834 are classified as quasars, corresponding to 9.0% of the total. Figure 13 shows the r-band magnitude distribution of the classified objects, and as in the training sets, this sample reaches fainter magnitudes than DS2, but is brighter than the DS1.
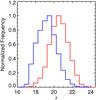
Fig. 13 Normalized r-band distributions of sources classified as quasars (red) and stars (blue) by the random forest algorithm when applied to the DS3 data set including WISE W1 and W2 photometry.
Figure 14 shows the r-band magnitude distribution of quasar candidates from each of the three data sets. The distributions are broadly similar; however, we note that quasars from DS1 and DS3 peak at a slightly fainter magnitude (r = 20.5), than DS2 (r = 20). This is in accordance to what we expect from the training sets. Furthermore, the DS1 magnitude distribution is broader, relative to TrS1. Quasars from the DS2 have the narrowest distribution of the three data sets, while DS3 has the lowest proportion of bright quasars.
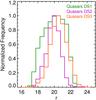 |
Fig. 14 The r-band magnitude distribution of quasars classified from the three data sets: DS1 (green), DS2 (magenta) and DS3 (orange). |
The total sample of point sources classified was 651 488. Of these 542 897 have detections only in the four optical RCS-2 bands, 16 898 also have GALEX NUV detections, and 242 902 have W1 and W2-band WISE detections within the stipulated magnitude error limits. We can assign some degree of confidence to these classifications contingent on how many surveys they have been selected in. Specifically, there are 1800 objects classified as quasars that are common to all three data sets. This low number is anticipated because few objects from the total sample are detected in the NUV band (the second training set is the smallest one), while even fewer sources have measurements in both WISE and GALEX. Nevertheless, for this same reason, these objects are very likely to be quasars; having been selected from three different training sets, the reliability of their classification is the strongest. Sources classified as quasars from two of the three data sets comprise 7514 distinct sources: 1821 from DS1 and DS2, 2788 from DS1 and DS3, and 2905 from DS2 and DS3). The remaining category of quasar classifications arise from selection in just one of the three data sets: these consist of 28 943 candidates, with 14 482 identified from DS1, 120 from DS2, and 14 341 from DS3. Combining these three groups of classifications, we arrive at 38 257 new quasar candidates from RCS-2. The majority of these arise via selection from DS1 and DS3 with only a small fraction from DS2. It is important to emphasize that objects only being classified as quasars in one of the data sets does not imply they are poor candidates, merely that they are not detected in GALEX or WISE, or potentially they are selected in just one data set. Including these extra bands for quasar classification serves the algorithm well and allows us to increase the overall recall statistic.
Example of the quasar candidates catalog from DS1.
Example of the quasar candidates catalog from DS2.
Example of the quasar candidates catalog from DS3.
For each data set, we constructed a catalog available at the CDS (table1.dat, table2.dat, table3.dat). In Tables 1−3 we show examples of the catalogs. Each contain the coordinates from the RCS-2 survey (in decimal hours), magnitudes in all the bands for which they have been detected (g, r, i, z, NUV, W1, and/or W2), and magnitude errors for these bands. The final two columns indicate whether they are classified as quasars in the other two data sets. As discussed in Sect. 4, we stress that candidates classified as quasars in only one of these sets does not necessarily signify a lower probability that they are quasars. Sources may be missed in the other surveys because of either the applied magnitude limit or the redshift of the putative quasar. Nevertheless, this indicator is useful in the case of an object classified as quasar in the three data sets when applying a “prioritization” for observational follow-up. For example, with spectroscopic confirmation of only a limited number of targets, those objects selected from all three surveys should be given priority, since they have been selected from three different training sets. In Tables 4 and 5 we summarize the results of the process.
In Fig. 15 we show the precision and recall for quasars within different magnitude bins, calculated for each of the three training sets with error bars corresponding to the standard error. As discussed previously, these sets have different magnitude limits, meaning there are fewer points sampling TrS3 and TrS2 compared to TrS1. As can be seen, the recall at brighter magnitudes in TrS1 is lower than in the other samples. We believe this arises from the relative magnitude distributions of stars and galaxies; there are many bright stars compared to quasars such that the algorithm recovers the majority of the stars, but a smaller fraction of quasars. Moreover, missing a few quasars in a small sample produces a higher percentage of missing objects. We attribute the TrS1 increment in the faintest magnitudes to a greater proportion of quasars as seen in Fig. 3. For the other cases, both precision and recall are stable with very small variations.
 |
Fig. 15 Precision (circles) and recall (triangles) for quasars as a function of the r magnitude for the three different training sets: TrS1 (green), TrS2 (magenta), and TrS3 (orange). |
4.1. Comparison with XDQSO
For illustrative purposes, we compare our classifications to a sample drawn from the SDSS DR8 XDQSO (Bovy et al. 2011) study. From this catalog we randomly selected a subsample of QSO or stellar sources with a minimum classification probability of 70%. We then matched this new sample to each of our independent data sets. The results are:
-
In DS1, we find 1450 XDQSO quasar candidates, 82.1% of whichare classified as quasars in our sample. For XDQSO stellarcandidates, there are 81 553 objects in our data set,2.5% of which are classified as quasars by our algorithm.
-
In DS2, the equivalent match yields 944 XDQSO quasar candidates, of which 97% are also classified as quasars by our algorithm. We find 1245 XDQSO star candidates, and 9.8% are classified as quasars in our sample.
-
In DS3, we find 2246 XDQSO candidates, with 99.6% of them among our quasar candidates. For the XDQSO star candidates, we have 34 509 in our data set. Three percent of them are classified as quasars in our catalog.
We would like to emphasize that these numbers are merely for reference, because they do not represent an estimation of the precision or recall of our samples, primarily because sources in the XDQSO catalog are also candidates lacking spectroscopic confirmation. We would need a complete spectroscopic sample of objects with which to compare in order to make a proper assessment. While our study uses a slightly newer release of the SDSS data (DR9 vs. DR8), there is little difference between them in the context of this work, save for some slight astrometric corrections. However, the degree of overlap between the two classification catalogs suggests our results are in good agreement with those drawn from Bovy et al. (2011).
5. Spectroscopic confirmation
An important step toward validating the putative quasar catalog described in Sect. 4 is through spectroscopic confirmation of our candidates. To painstakingly take spectra for all putative QSOs would be time-consuming and require a long-term observational program beyond the scope of the conceptual study we present here. Instead, we randomly sampled quasar candidates from the catalog with 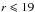 that were classified in at least two of the test sets. This bright magnitude limit was chosen so that with a modest telescope, observation of many targets was feasible. Our observations were carried out at the 2.5 m DuPont telescope at Las Campanas Observatory with the Boller & Chivens Spectrograph. We took long-slit spectra of 17 targets covering a wide wavelength range (6230 Å), which allowed coverage of the largest possible redshift interval given the instrumental constraints. While this is a small sample and thus insufficient for detailed statistical analysis, it provides an initial proof of concept of a Random Forest algorithm applied to the task of quasar classification. The results of our observations are shown in Table 6, and reduced spectra of the confirmed quasars and AGN are shown in Fig. 16.
that were classified in at least two of the test sets. This bright magnitude limit was chosen so that with a modest telescope, observation of many targets was feasible. Our observations were carried out at the 2.5 m DuPont telescope at Las Campanas Observatory with the Boller & Chivens Spectrograph. We took long-slit spectra of 17 targets covering a wide wavelength range (6230 Å), which allowed coverage of the largest possible redshift interval given the instrumental constraints. While this is a small sample and thus insufficient for detailed statistical analysis, it provides an initial proof of concept of a Random Forest algorithm applied to the task of quasar classification. The results of our observations are shown in Table 6, and reduced spectra of the confirmed quasars and AGN are shown in Fig. 16.
Number of spectroscopically confirmed sources in the TrS1, TrS2, and TrS3 training sets used by the Random Forest algorithm.
Results of the classification of RCS-2 point sources when processed by the Random Forest algorithm.
 |
Fig. 16 Reduced spectra of the confirmed quasars from Table 6, taken using the B and C long-slit spectrograph at the Du Pont 2.5 m telescope. |
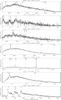 |
Fig. 16 continued. |
 |
Fig. 16 continued. |
Overview of our spectroscopic analysis of 17 quasar candidates selected by the Random Forest algorithm, and followed-up with long-slit spectroscopy at the Du Pont telescope.
We find 14 of the 17 candidates can be confirmed as quasars. Of the remaining three, one can also be considered an AGN with narrower emission lines. We note that AGN like this target are expected to have similar colors to those of quasars. It is significant that the two false positives were classified by the Random Forest algorithm based on RCS-2, NUV, and WISE data, further reinforcing that joint classification by these three datasets is not a “gold standard” for successful classification. Indeed, 5 of the 17 targets (or 36% of the quasars) did not fall in this category but were verified as quasars.
While our small sample size precludes detailed statistical insight, we nevertheless consider our results satisfactory. In the bright regime we sampled spectroscopically, there is a larger number of stars in the training sets. As we illustrate in Fig. 15, the precision in this region is characteristically lower compared to fainter magnitudes, therefore the algorithm performs very well under the conditions of a complete training set. We highlight the identification of three QSOs between 2.2 ≲ z ≲ 3.5: it is in this regime that stellar and quasar populations typically overlap in optical color−color space.
6. Summary and discussion
Based on a Random Forest algorithm, we built a catalog containing 38 257 new quasar candidates, with a precision over ~90%. A subset of these, 24% of the catalog, have photometric detections in GALEX and/or WISE) and accordingly achieve precisions of at least ~97%. The increase in precision with additional bands is anticipated, because the Random Forest algorithm performance improves when more information is provided. This is only significant, however, when that information assists in the separation of the object classes: the additional bands in this 24% subset greatly assist in separating quasars from stars in color−color space, as seen in Figs. 5 and 7). These results are comparable to those from different quasar candidate searches. For example, Richards et al. (2009) find an overall efficiency (similar to recall in our terms) of ~80%, rising to over 97% when UVX information is added.
Having been trained with a catalog of spectroscopically confirmed stars and quasars, the Random Forest algorithm is applied to RCS-2 point sources. We required that these point sources have measured magnitudes in each of the four RCS-2 bands with photometric errors below 0.1 mag. From these point sources, three data sets (DS1-3) were compiled. We first constructed a data set (DS0) with all point sources from RCS-2 with the aforementioned requirements. The first data set we used for classification (DS1) was a random subset of DS0 matching the r-band magnitude distribution of the training set (Fig. 8). The second (DS2), another subset of DS0, contains RCS-2 point sources with NUV-band GALEX detections. The third (DS3), also a subset of DS0, contains RCS-2 point sources with detections in the W1 and W2 WISE bands.
We constructed quasar candidate catalogs for each of these data sets. The first, with 21 501 quasar classifications from a total of 542 897 point sources, corresponds to 4.0% of the sample. DS2 has 6529 quasar candidates from 16 898 point sources (38.6% of the total sample), while DS3 selects 21 834 quasar candidates from 242 902 point sources (corresponding to 9.0% of the data set). Merging these quasar classifications and removing duplicates provided us with our final sample of 38 257 quasar candidates. This catalog is split into three (table1.dat, table2.dat, table3.dat), and is available at the CDS: they contain the coordinates from RCS-2 survey, magnitude in all detected bands (NUV, g, r, i, z, W1, W2), photometric errors of those magnitudes, and the data sets where they were classified as quasars.
The number of data sets within which a candidate was classified as a quasar does not indicate the reliability of the classification, merely that they (for example) have no WISE or GALEX data. Nevertheless, this is a useful indicator when seeking candidates that have the highest probability of being genuine quasars for the purposes of spectroscopic follow-ups.
We have obtained a reliable new sample of quasars candidates that can be used for a wide range of astronomical applications. From this sample, we obtained the spectra of 17 candidates with magnitudes r ~ 19, which were classified as quasars in at least two data sets. From this small sample, 14 were confirmed as quasars and 1 as an AGN. Even within this small sample, there is good agreement with our expectations.
The Random Forest algorithm works well in the classification of point sources into quasars and stars based on magnitude and color information. The algorithm is useful because it automatically chooses the attributes that optimally separate the two classes of object. The approach described here has broad applicability, permitting similar studies on future photometric surveys such as LSST, requiring only a training set and photometric information. The advantage of the Random Forest over many other approaches is its high level of automatization and suitability for processing large volumes of data. Training sets need be neither new nor large: our sample of spectroscopically confirmed SDSS sources, cross-matched with RCS-2 point sources, were entirely suitable for our purposes in this study. Extensions to the work we detail could entail including additional photometric information from other all-sky surveys, an application of the existing algorithm and training sets to new, larger photometric catalogs, and spectroscopic follow-up of Random Forest quasar candidates in order to gain insight into the performance of the technique beyond what is explored here.
We also approached this problem in a different way to find fainter candidates. The explanation and candidates are available in http://ph.unimelb.edu.au/~dcarrasco/html/files.html
Acknowledgments
We thank the referee for useful comments and suggestions. Support for L.F. Barrientos, K. Pichara, and T. Anguita is provided by the Ministry of Economy, Development, and Tourism’s Millennium Science Initiative through grant IC120009, awarded to The Millennium Institute of Astrophysics, MAS. We also acknowledge financial support from Proyecto Financiamiento Basal PFB06, Gemini Conicyt grant 32110010, Programa de Postgrado Instituto de Astrofísica and from BASAL PFB-06, and FONDEF D11I1060. L. F. Barrientos’ research is supported by proyecto FONDECYT 1120676. T. Anguita acknowledges support by proyecto FONDECYT 11130630. D.N.A Murphy acknowledges support through FONDECYT grant 3120214.
References
- Agüeros, M. A., Ivezić, Ž., Covey, K. R., et al. 2005, AJ, 130, 1022 [NASA ADS] [CrossRef] [Google Scholar]
- Ahn, C. P., Alexandroff, R., Allen de Prieto, C., et al. 2012, ApJS, 203, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Ball, N. M., & Brunner, R. J. 2010, Int. J. Mod. Phys. D, 19, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Ball, N. M., Brunner, R. J., Myers, A. D., & Tcheng, D. 2006, ApJ, 650, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Ball, N. M., Brunner, R. J., Myers, A. D., et al. 2007, ApJ, 663, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, R. H., White, R. L., Gregg, M. D., et al. 2001, ApJS, 135, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J., Hennawi, J. F., Hogg, D. W., et al. 2011, ApJ, 729, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Breiman, L. 2001, in Machine Learning, 5 [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Carliles, S., Budavári, T., Heinis, S., Priebe, C., & Szalay, A. S. 2010, ApJ, 712, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Carrasco Kind, M., & Brunner, R. J. 2013, MNRAS, 432, 1483 [NASA ADS] [CrossRef] [Google Scholar]
- Collister, A., Lahav, O., Blake, C., et al. 2007, MNRAS, 375, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Cortes, C., & Vapnik, V. 1995, in Machine Learning, 273 [Google Scholar]
- Dubath, P., Rimoldini, L., Süveges, M., et al. 2011, MNRAS, 414, 2602 [NASA ADS] [CrossRef] [Google Scholar]
- Duda, R. O., & Hart, P. E. 1973, Pattern classification and scene analysis (New York: Wiley) [Google Scholar]
- Eales, S., Dunne, L., Clements, D., et al. 2010, PASP, 122, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, X. 1999, AJ, 117, 2528 [NASA ADS] [CrossRef] [Google Scholar]
- Faure, C., Anguita, T., Eigenbrod, A., et al. 2009, A&A, 496, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foltz, C. B., Chaffee, F. H., Hewett, P. C., et al. 1989, AJ, 98, 1959 [NASA ADS] [CrossRef] [Google Scholar]
- Fukugita, M., Ichikawa, T., Gunn, J. E., et al. 1996, AJ, 111, 1748 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, D., Zhang, Y.-X., & Zhao, Y.-H. 2009, RA&A, 9, 220 [Google Scholar]
- Gerdes, D. W., Sypniewski, A. J., McKay, T. A., et al. 2010, ApJ, 715, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Geurts, P., Ernst, D., & Wehenkel, L. 2006, Machine Learning, 63, 3 [CrossRef] [Google Scholar]
- Gilbank, D. G., Gladders, M. D., Yee, H. K. C., & Hsieh, B. C. 2011, AJ, 141, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Glikman, E., Helfand, D. J., White, R. L., et al. 2007, ApJ, 667, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Green, R. F., Schmidt, M., & Liebert, J. 1986, ApJS, 61, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Gregg, M. D., Becker, R. H., White, R. L., et al. 1996, AJ, 112, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Hewett, P. C., Foltz, C. B., & Chaffee, F. H. 1995, AJ, 109, 1498 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., Robertson, B., & Springel, V. 2006, ApJS, 163, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Huertas-Company, M., Rouan, D., Tasca, L., Soucail, G., & Le Fèvre, O. 2008, A&A, 478, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jarrett, T. H., Cohen, M., Masci, F., et al. 2011, ApJ, 735, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N., Aussel, H., Burke, B. E., et al. 2002, in Survey and Other Telescope Technologies and Discoveries, eds. J. A. Tyson, & S. Wolff, SPIE Conf. Ser., 4836, 154 [Google Scholar]
- Lang, D., Hogg, D. W., & Schlegel, D. J. 2014, ArXiv e-prints [arXiv:1410.7397] [Google Scholar]
- Lopez, S., Barrientos, L. F., Lira, P., et al. 2008, ApJ, 679, 1144 [NASA ADS] [CrossRef] [Google Scholar]
- LSST Science Collaboration et al. 2009, ArXiv e-prints [arXiv:0912.0201] [Google Scholar]
- Martin, D. C., Fanson, J., Schiminovich, D., et al. 2005, ApJ, 619, L1 [Google Scholar]
- Oguri, M., Inada, N., Strauss, M. A., et al. 2008, AJ, 135, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
- Pichara, K., & Protopapas, P. 2013, ApJ, 777, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Pichara, K., Protopapas, P., Kim, D.-W., Marquette, J.-B., & Tisserand, P. 2012, MNRAS, 427, 1284 [NASA ADS] [CrossRef] [Google Scholar]
- Portinari, L., Kotilainen, J., Falomo, R., & Decarli, R. 2012, MNRAS, 420, 732 [NASA ADS] [CrossRef] [Google Scholar]
- Powers, D. M. W. 2007, Evaluation: From Precision, Recall and F-Factor to ROC, Informedness, Markedness and Correlation, Tech. Rep. SIE-07-001, School of Informatics and Engineering, Flinders University [Google Scholar]
- Quinlan, J. R. 1993, C 4.5: Programs for machine learning (Morgan Kaufmann Publishers) [Google Scholar]
- Quinlan, R. 1986, Machine Learning, 1, 81 [Google Scholar]
- Richards, G. T., Fan, X., Schneider, D. P., et al. 2001, AJ, 121, 2308 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T., Fan, X., Newberg, H. J., et al. 2002, AJ, 123, 2945 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T., Lacy, M., Storrie-Lombardi, L. J., et al. 2006, ApJS, 166, 470 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T., Myers, A. D., Gray, A. G., et al. 2009, ApJS, 180, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, J. W., Starr, D. L., Butler, N. R., et al. 2011, ApJ, 733, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Rumelhart, D. E., Hinton, G. E., & Williams, R. J. 1986, Nature, 323, 533 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sanders, D. B., Phinney, E. S., Neugebauer, G., Soifer, B. T., & Matthews, K. 1989, ApJ, 347, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Stern, D., Assef, R. J., Benford, D. J., et al. 2012, ApJ, 753, 30 [NASA ADS] [CrossRef] [Google Scholar]
- The Dark Energy Survey Collaboration. 2005, ArXiv e-prints [arXiv:astro-ph/0510346] [Google Scholar]
- Tokunaga, A. T., & Vacca, W. D. 2005, PASP, 117, 1459 [NASA ADS] [CrossRef] [Google Scholar]
- Trammell, G. B., Van den Berk, D. E., Schneider, D. P., et al. 2007, AJ, 133, 1780 [Google Scholar]
- White, R. L., Becker, R. H., Gregg, M. D., et al. 2000, ApJS, 126, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Willott, C. J., Delfosse, X., Forveille, T., Delorme, P., & Gwyn, S. D. J. 2005, ApJ, 633, 630 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, C. 2009, MNRAS, 397, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Worseck, G., & Prochaska, J. X. 2011, ApJ, 728, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, X.-B., Hao, G., Jia, Z., Zhang, Y., & Peng, N. 2012, AJ, 144, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Yee, H. K. C. 1991, PASP, 103, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Yee, H. K. C., Ellingson, E., & Carlberg, R. G. 1996, ApJS, 102, 269 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, Jr., J. E., et al. 2000, AJ, 120, 1579 [Google Scholar]
All Tables
Number of spectroscopically confirmed sources in the TrS1, TrS2, and TrS3 training sets used by the Random Forest algorithm.
Results of the classification of RCS-2 point sources when processed by the Random Forest algorithm.
Overview of our spectroscopic analysis of 17 quasar candidates selected by the Random Forest algorithm, and followed-up with long-slit spectroscopy at the Du Pont telescope.
All Figures
 |
Fig. 1 Color−color diagrams of spectroscopically confirmed quasars (red) and stars (blue) in RCS-2. The upper diagram shows the colors g−r vs. r−i, and the bottom diagram shows the colors r−i vs. i−z. While it is possible to see a quasar clump and a stellar locus, in both cases there is no clean way to separate them. |
| In the text | |
 |
Fig. 2 Redshift distribution of quasars from the three training sets: TrS1 (green), TrS2 (magenta), and TrS3 (orange). The GALEX-based data (TrS2) do not probe as deep in redshift as the other two. While the sources with WISE fluxes (TrS3) appear to peak at a lower redshift, they nevertheless remain sensitive out to the redshifts explored by the optical-only data (TrS1). |
| In the text | |
 |
Fig. 3 Normalized distribution of r-band magnitudes from RCS-2 for quasars and stars listed in the TrS1 training set. We see that the peak of the stellar (blue) sources is approximately one magnitude brighter than for the quasars (red). |
| In the text | |
 |
Fig. 4 Color−color diagrams of spectroscopically confirmed quasars (red) and stars (blue) in RCS-2. The upper diagrams show the optical g−r vs. r−i (left) and r−i vs. i−z (right) color plots. The bottom plot shows the NUV-g vs. g−i color space when including GALEX data. It can be seen that including the UV data provides a clearer separation between quasars and stars compared to solely optical data. |
| In the text | |
 |
Fig. 5 Histogram of the normalized r-band magnitude distribution from cross-matched RCS-2 and GALEX data featured in the TrS2 data set. Quasars are shown in red, while stars are blue. According to the optical data presented in Fig. 3, stellar sources appear to have systematically brighter r-band magnitudes. |
| In the text | |
 |
Fig. 6 Color−color diagrams of the spectroscopically confirmed quasars (red) and stars (blue) in RCS-2 with detection in the W1 and W2 bands from WISE. The upper left diagram shows the colors g−r vs. r−i, the upper right diagram shows the colors r−i vs. i−z, the bottom left diagram shows the colors i−z vs. z-W1, and the bottom left diagram shows the color z-W1 vs. W1-W2. |
| In the text | |
 |
Fig. 7 Histogram of the normalized magnitude distributions in the RCS-2 r-band of quasars and stars from TrS3 (those sources with WISE photometry). |
| In the text | |
 |
Fig. 8 Histogram of the normalized magnitude distribution in the r band of all the objects in TrS1. |
| In the text | |
 |
Fig. 9 Histogram of the normalized magnitude distribution in the r band of the point sources from RCS-2 (color gray) and the new data set DS1 that was obtained by matching its distribution with the distribution of TrS1. |
| In the text | |
 |
Fig. 10 Normalized r-band magnitude distribution in RCS-2 for each of our the three test data sets: DS1 (green), DS2 (magenta), and DS3 (orange). These data are the sources that the algorithm must classify. |
| In the text | |
 |
Fig. 11 Normalized r-band magnitude distributions of from quasar (red) and star (blue) candidates from DS1, as classified by the Random Forest algorithm. In parallel with the distribution of spectroscopically verified sources presented in Fig. 3, we note that stellar sources are generally brighter than quasars. |
| In the text | |
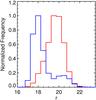 |
Fig. 12 Resulting normalized r-band distributions of sources classified in DS2 by the random forest algorithm, quasars (red) and stars (blue). The difference in these distributions mirrors those presented in the TrS2 training set data shown in Fig. 5. |
| In the text | |
 |
Fig. 13 Normalized r-band distributions of sources classified as quasars (red) and stars (blue) by the random forest algorithm when applied to the DS3 data set including WISE W1 and W2 photometry. |
| In the text | |
 |
Fig. 14 The r-band magnitude distribution of quasars classified from the three data sets: DS1 (green), DS2 (magenta) and DS3 (orange). |
| In the text | |
 |
Fig. 15 Precision (circles) and recall (triangles) for quasars as a function of the r magnitude for the three different training sets: TrS1 (green), TrS2 (magenta), and TrS3 (orange). |
| In the text | |
 |
Fig. 16 Reduced spectra of the confirmed quasars from Table 6, taken using the B and C long-slit spectrograph at the Du Pont 2.5 m telescope. |
| In the text | |
 |
Fig. 16 continued. |
| In the text | |
 |
Fig. 16 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



