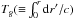| Issue |
A&A
Volume 583, November 2015
|
|
|---|---|---|
| Article Number | A112 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201526838 | |
| Published online | 03 November 2015 | |
Surface-effect corrections for solar-like oscillations using 3D hydrodynamical simulations
I. Adiabatic oscillations
1 LESIA, Observatoire de Paris, PSL Research University, CNRS, Université Pierre et Marie Curie, Université Denis Diderot, 92195 Meudon, France
e-mail: takafumi.sonoi@obspm.fr
2 Zentrum für Astronomie der Universität Heidelberg, Landessternwarte, Königstuhl 12, 69117 Heidelberg, Germany
3 GEPI, Observatoire de Paris, PSL Research University, CNRS, Université Denis Diderot, Sorbonne Paris Cité, 5 place Jules Janssen, 92195 Meudon, France
Received: 26 June 2015
Accepted: 14 September 2015
Context. The CoRoT and Kepler space-borne missions have provided us with a wealth of high-quality observational data that allows for seismic inferences of stellar interiors. This requires the computation of precise and accurate theoretical frequencies, but imperfect modeling of the uppermost stellar layers introduces systematic errors. To overcome this problem, an empirical correction has been introduced by Kjeldsen et al. (2008, ApJ, 683, L175) and is now commonly used for seismic inferences. Nevertheless, we still lack a physical justification allowing for the quantification of the surface-effect corrections.
Aims. Our aim is to constrain the surface-effect corrections across the Hertzsprung-Russell (HR) diagram using a set of 3D hydrodynamical simulations.
Methods. We used a grid of these simulations computed with the CO5BOLD code to model the outer layers of solar-like stars. Upper layers of the corresponding 1D standard models were then replaced by the layers obtained from the horizontally averaged 3D models. The frequency differences between these patched models and the 1D standard models were then calculated using the adiabatic approximation and allowed us to constrain the Kjeldsen et al. power law, as well as a Lorentzian formulation.
Results. We find that the surface effects on modal frequencies depend significantly on both the effective temperature and the surface gravity. We further provide the variation in the parameters related to the surface-effect corrections using their power law as well as a Lorentzian formulation. Scaling relations between these parameters and the elevation (related to the Mach number) is also provided. The Lorentzian formulation is shown to be more robust for the whole frequency spectrum, while the power law is not suitable for the frequency shifts in the frequency range above νmax. Finally, we show that, owing to turbulent pressure, the elevation of the uppermost layers modifies the location of the hydrogen ionization zone and consequently introduces glitches in the surface effects for models with high (low) effective temperature (surface gravity).
Conclusions. Surface-effect corrections vary significantly across the HR diagram. Therefore, empirical relations like those by Kjeldsen et al. must not be calibrated on the Sun but should instead be constrained using realistic physical modeling as provided by 3D hydrodynamical simulations.
Key words: asteroseismology / convection / stars: atmospheres / stars: low-mass / stars: oscillations / stars: solar-type
© ESO, 2015
1. Introduction
Our knowledge of solar-like oscillations has been recently improved thanks to the precise observations obtained with the CoRoT (Baglin et al. 2006a,b; Michel et al. 2008) and Kepler (Borucki et al. 2010) spacecrafts. Such oscillations are stochastically excited and damped by turbulent motions in the outermost layers of convective regions (for a review, see Samadi 2011). It is allowed to perform precise seismic determination of both the global stellar parameters and stellar interiors by the detection of a large number of consecutive radial orders and angular degrees, as well as mode identification (for a review, see Chaplin & Miglio 2013). A striking example is the ability of asteroseismology to improve the determination of stellar ages (e.g., Lebreton & Goupil 2014; Silva Aguirre et al. 2015).
However, asteroseimology still suffers from uncertainties that prevent us from making the best use of the precise seismic data. Indeed, precise and accurate determination of stellar interiors requires that we are able to model solar-like stars as realistically as possible. Although rotation and magnetic fields should affect properties of equilibrium structure and oscillation, we still do not have definitive methods of including them in the modeling. But, even if we neglect them, the deficient modeling of the uppermost layers of stars (hereafter surface effects) are already substantial obstacles to accurately determining oscillation frequencies.
For the Sun, a systematic discrepancy between observed and computed frequencies of the p modes has been emphasized (Christensen-Dalsgaard et al. 1988, 1996; Dziembowski et al. 1988; Christensen-Dalsgaard & Thompson 1997) and related to the poor modeling of the near-surface region. For instance, in classical standard models, the mixing-length theory is used to model convection, and this is only valid for efficient convection in deep interiors. However, convection becomes inefficient in the near-surface regions. Therefore, more complex physical processes need to be accounted for, such as compressible turbulence, which is neglected by the mixing-length theory.
For the Sun, there have been many attempts to analyze the surface effects, and they are based on a more sophisticated treatment of the surface convection than the mixing-length theory. Indeed, the frequencies of the high-order p-modes were found to be affected by the treatment of convection (e.g., Brown 1984; Zhugzhda & Stix 1994; Schlattl et al. 1997; Petrovay et al. 2007). Similar attempts have also been made with more realistic models constructed using 3D hydrodynamical simulations (Stein & Nordlund 1991; Rosenthal et al. 1999; Yang & Li 2007; Piau et al. 2014; Bhattacharya et al. 2015). It has been found that turbulent pressure (neglected in standard models) plays a major role in modifying the frequencies, since the induced elevation of the outer layer leads to the decrease in the frequencies. We also note that the thermal timescale is comparable to the oscillation periods in the near-surface regions. Consequently, one can expect that nonadiabatic effects on frequencies can have a non-negligible impact and should also be taken into account. This has been done partly by several authors (e.g., Houdek 2010; Grigahcène et al. 2013), but given the uncertainties related to the treatment of the convection-pulsation coupling, this would deserve being investigated more thoroughly.
In the absence of any definitive conclusions on the surface effects, Kjeldsen et al. (2008) have proposed an empirical power law to correct the theoretical frequency (see also Ball & Gizon 2014). They provide the value of the power index in the power law by analyzing the difference between the observed solar frequencies and the theoretical frequencies computed with Model S (Christensen-Dalsgaard et al. 1996). Since then, many authors have adopted the value to correct the computed frequencies for other stars than the Sun (e.g., Christensen-Dalsgaard et al. 2010; Doğan et al. 2010; Gruberbauer et al. 2013). Alternative strategies have been adopted to determine the value of the index (e.g., Gruberbauer et al. 2012; Lebreton & Goupil 2014), but still adopting the power-law function of Kjeldsen et al. (2008). Indeed, the correction is required since, without it, it is difficult to find a good model from comparison with the observations. At this stage, however, there is no physical justification for constraining the empirical surface-effect corrections.
In this article, we construct outer-layer models with 3D hydrodynamical simulations including non-local radiation transport for different types of solar-like stars (Sect. 2.1). The constructed 3D layers are patched to the standard interior model (Sect. 2.2). Then, the frequency differences with the standard models are evaluated (Sect. 2.3). We discuss the dependence on effective temperature and surface gravity when performing the functional fittings (Sect. 3). Discussion and conclusions are given in Sects. 4 and 5, respectively.
Characteristics of the 3D hydrodynamical models.
 |
Fig. 1 3D hydrodynamical models in the Teff−log g plane. The relative difference in the radius between PM and UPM is indicated by the color scale. |
2. Stellar patched models and related eigenfrequencies
We consider a set of 3D hydrodynamical models for which two types of corresponding 1D models were constructed, the patched models (PMs) and unpatched models (UPMs). Subsequently, the associated frequencies were computed in the framework of the adiabatic approximation.
2.1. Grid of 3D hydrodynamical models
We use the CO5BOLD code (Freytag et al. 2012) with the CIFIST grid (Ludwig et al. 2009). The adopted chemical mixture is similar to the solar abundances determined by Asplund et al. (2005). We considered ten models. The global characteristics of the models are summarized in Table 1 as well as the temperature at the bottom of the 3D models, Tb, and the frequency of the maximum mode height in the oscillation power spectrum, νmax, estimated by the scaling relation (e.g., Brown et al. 1991; Kjeldsen & Bedding 1995; Belkacem et al. 2011) 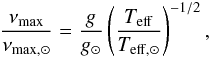 (1)which arises from the proportionality between νmax and the cut-off frequency. For solar values, we adopt νmax,⊙ = 3100 μHz, log g⊙ = 4.438, and Teff,⊙ = 5777 K. The location of the selected models in the Teff-log g plane is displayed in Fig. 1. We note that Model A corresponds to the Sun.
(1)which arises from the proportionality between νmax and the cut-off frequency. For solar values, we adopt νmax,⊙ = 3100 μHz, log g⊙ = 4.438, and Teff,⊙ = 5777 K. The location of the selected models in the Teff-log g plane is displayed in Fig. 1. We note that Model A corresponds to the Sun.
2.2. Computation of the patched models
Following Trampedach (1997) and Samadi et al. (2007, 2008), we construct a corresponding UPM and PM, for each 3D simulations. The UPMs were obtained using the CESTAM stellar evolution code (Marques et al. 2013) by matching the effective temperature, the gravity at the photosphere, and the temperature at the bottom of the 3D layers. The matching was performed through a Levenberg-Marquardt algorithm with three free parameters: the age, the total mass M, and the mixing length parameter αMLT. For post-main sequence stages (models H, I, and J), the central temperature rather than the age was considered as a free parameter because of their rapid evolution. Convection in the 1D models is treated using the standard mixing-length theory (Böhm-Vitense 1958) and thus does not include turbulent pressure. We also adopted the Eddington gray T−τ relation for the atmosphere of UPMs.
 |
Fig. 2 Comparison of the total pressure Ptot between PM and UPM of Model A. The abscissa is the radius divided by the solar radius, r/R⊙. The vertical arrow indicates the point of matching between the CESTAM model and the CO5BOLD model. Below the matching point, the profiles of PM and UPM are identical. |
Subsequently, the UPMs and corresponding 3D hydrodynamical models were matched to obtain the PMs. To this end, temporal and horizontal averages were performed at constant geometrical depth for the 3D models. Figure 2 compares the profiles of the total pressure in the PM and UPM of Model A. They are, by construction, identical below the matching point. Above, the pressure of the UPM is lower than of the PM at the same radius (which denotes the distance from the center). The difference in the pressure stratifications mainly depends on the effect of turbulent pressure in the PM. This additional source of pressure modifies the hydrostatic equilibrium so that, at the photosphere, the radii of the PM (RPM) and UPM (RUPM) are different. As summarized in Table 2, the relative difference RPM/RUPM−1 ranges between 0.01 and 0.2%. It increases with increasing effective temperature or with decreasing surface gravity (see Fig. 1). This can be explained as follows: with increasing effective temperature, the larger H− opacity requires a steeper temperature gradient for ensuring the required energy transfer. Therefore, the convective velocity increases. With decreasing surface gravity, the density in the near-surface region decreases. For ensuring the required convective transport, the convective velocity should be higher. In both cases, the contribution of turbulent pressure becomes prominent.
2.3. Computation of adiabatic oscillations
We computed adiabatic oscillations using the ADIPLS code (Christensen-Dalsgaard 2008) for both the PMs and UPMs. We considered only radial modes below the cut-off frequency. For the PMs, the main problem is to consider the turbulent pressure in computing the frequencies. A fully non-adiabatic oscillation code including a time-dependent treatment of convection is a natural way to account for the turbulent pressure and its perturbation. However, for the sake of simplicity, we adopted the adiabatic approach as proposed by Rosenthal et al. (1999), who considered two simplifying approximations that allow us to use a classical adiabatic oscillation code in a simple way:
-
the gas Γ1 approximation, for which the relative Lagrangian perturbation of turbulent pressure equals the Lagrangian perturbation of gas pressure,
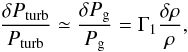 (2)where δ denotes the Lagrangian perturbation, Pturb the turbulent pressure, and Pg the gas pressure. Equation (2) permits us to express the perturbation of turbulent pressure as a function of the density perturbation.
(2)where δ denotes the Lagrangian perturbation, Pturb the turbulent pressure, and Pg the gas pressure. Equation (2) permits us to express the perturbation of turbulent pressure as a function of the density perturbation. the reduced Γ1 approximation, for which Γ1 is modified to become
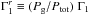 . It implies that the perturbation of turbulent pressure is neglected so that
. It implies that the perturbation of turbulent pressure is neglected so that  (3)
(3)
Characteristics of UPM and PM.
 |
Fig. 3 Frequency differences of radial modes between PM and UPM divided by νmax as a function of νPM/νmax (black solid line with dots). The green full line and the blue dashed line are least-square fittings with the Kjeldsen et al. (2008) power law, a(νPM/νmax)b in the range 0 <ν/νmax< 1.05 and in the whole range, respectively. The red line shows the modified Lorentzian, α [1−1/ { 1 + (νPM/νmax)β }]. |
Figure 3 shows the difference in radial-mode frequencies between the PM and UPM for Models A and B. The PM has a larger radius than the UPM due to the elevation by the turbulent pressure. The cavity where acoustic waves propagate then becomes larger, and the mode frequencies become lower for PM. As a consequence, the difference is negative for all of the models. We can also see that the difference becomes greater with increasing frequency. As the frequency becomes higher, the mode propagates farther in the outer region, so that it is affected by the surface effects more strongly.
For several models, the profiles of the frequency difference show oscillatory features as found in the bottom panel of Fig. 3. Actually, they are caused by the acoustic glitch in the hydrogen ionization zone and by the difference in the size of the acoustic cavity due to the turbulence elevation. This detail is discussed in Sect. 4.2.
3. Functional fittings to frequency difference
The power law proposed by Kjeldsen et al. (2008) is commonly used for correcting theoretical oscillation frequencies and for reproducing the observed frequencies. It is then worth discussing the validity of the fitting with the power law using the frequency difference between the PM and UPM. As mentioned below, however, the power law is not suitable at high frequency. We also propose a formulation based on a Lorentzian, which reduces to the power law in the low-frequency limit.
3.1. The Kjeldsen et al. (2008) power law
Since the PMs include realistic profiles of the upper stellar atmosphere, we considered their oscillation frequencies to be the observed ones. The correction proposed by Kjeldsen et al. (2008) thus becomes 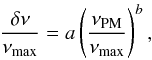 (4)where δν is correction of the frequency corresponding to νPM−νUPM, and the coefficients a and b are free parameters. Parameter a is, in the present study, non-dimensional. On the other hand, the parameter had a dimension in Kjeldsen et al. (2008), since the frequency correction δν on the lefthand side was not divided by νmax. By definition, a is thus the value of δν/νmax at νPM = νmax.
(4)where δν is correction of the frequency corresponding to νPM−νUPM, and the coefficients a and b are free parameters. Parameter a is, in the present study, non-dimensional. On the other hand, the parameter had a dimension in Kjeldsen et al. (2008), since the frequency correction δν on the lefthand side was not divided by νmax. By definition, a is thus the value of δν/νmax at νPM = νmax.
3.2. Parameter fitting
To determine the parameters a and b, we performed a least-square analysis. We fit Eq. (4) to the computed frequency difference so that the summation of the squared deviation, ![\begin{eqnarray} {\cal D}=\sum^{N}_{i}\left[\frac{\nu_{{\rm PM},i} - \nu_{{\rm UPM},i} - \delta\nu_i}{\nu_{\rm max}}\right]^{2}, \label{eq:D} \end{eqnarray}](/articles/aa/full_html/2015/11/aa26838-15/aa26838-15-eq67.png) (5)is minimized, where i denotes the label of the eigenmodes, and N is the number of the modes. Figure 3 shows the results for Models A and B They are determined in the range 0 <νPM/νmax< 1.05. Table 3 shows the reduced values of Eq. (5), i.e.,
(5)is minimized, where i denotes the label of the eigenmodes, and N is the number of the modes. Figure 3 shows the results for Models A and B They are determined in the range 0 <νPM/νmax< 1.05. Table 3 shows the reduced values of Eq. (5), i.e., 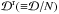 . For comparison, we also considered the deviation of the fit performed in the whole frequency range. The reduced values of the deviation in the whole range are significantly larger, which clearly shows that the power law is not suitable for the high frequency range (dashed blue curve in Fig. 3). However, the power law was originally used for fitting only intermediate-order modes of the Sun, and the high-frequency modes were not taken into account in Kjeldsen et al. (2008).
. For comparison, we also considered the deviation of the fit performed in the whole frequency range. The reduced values of the deviation in the whole range are significantly larger, which clearly shows that the power law is not suitable for the high frequency range (dashed blue curve in Fig. 3). However, the power law was originally used for fitting only intermediate-order modes of the Sun, and the high-frequency modes were not taken into account in Kjeldsen et al. (2008).
The values of a and b depend strongly on the choice of the fitting range. This point was also made by Kjeldsen et al. (2008) and is discussed in Sect. 4.3.
3.2.1. Parameters across the Teff–g plane
Regardless of the fitting range, we have found that the power index b certainly varies with models, as shown in Fig. 4 and Table 4. Kjeldsen et al. (2008) propose b = 4.90 in the case of the Sun, and many studies have adopted this value for other stars (e.g., Christensen-Dalsgaard et al. 2010; Doğan et al. 2010, 2013; Metcalfe et al. 2010; Tang & Gai 2011; Brandão et al. 2011; Van Eylen et al. 2012; Gilliland et al. 2013; Gruberbauer et al. 2013). When b is fixed, a simple fit provides the value of a (Kjeldsen et al. 2008).
Reduced values of the squared deviation, 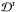 .
.
Then, a least-square fit provides the variation in a and b as a function of log Teff and log g, according to 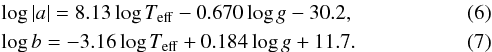 To measure the deviations of the computed coefficients from the above equations, we define
To measure the deviations of the computed coefficients from the above equations, we define 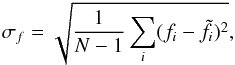 (8)where f corresponds to a or b (not log | a | or log b), i is a label indicating each model, N the number of the models, and
(8)where f corresponds to a or b (not log | a | or log b), i is a label indicating each model, N the number of the models, and 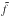 the value obtained by Eqs. (6) or (7). Here we have N = 10. We obtain σa = 4.6 × 10-4 and σb = 9.1 × 10-2, which means that the relative deviations are on the order of 10%.
the value obtained by Eqs. (6) or (7). Here we have N = 10. We obtain σa = 4.6 × 10-4 and σb = 9.1 × 10-2, which means that the relative deviations are on the order of 10%.
 |
Fig. 4 Values of log | a | (top) and b (bottom) obtained by the fitting with Eq. (4) in the range 0 <ν/νmax< 1.05 are indicated by colors on the Teff–log g plane. |
The trends of b and of the absolute value of a are the opposite. With increasing Teff or with decreasing g, b and | a | become smaller and larger, respectively. We recall that the coefficient a is the value of δν/νmax at ν = νmax by definition. Thus, it is the representative scale for δν/νmax. Rosenthal et al. (1999) suggested that this scale should be proportional to the elevation of the radius. Although their analysis was limited to the Sun, we confirm this tendency among the different models of stars. The trend of coefficient b is mainly determined by the low-order modes and we find that it also scales with the elevation. We discuss this issue in detail in Sect. 4.1.
3.3. Fitting a modified Lorentzian
As mentioned in Sect. 3.1, the power-law fitting does not work in the high-frequency range, since the gradient of the frequency difference becomes smaller. Ball & Gizon (2014) propose a correction functional with mode inertia and demonstrate that it can be well fit to the differences between the BiSON frequencies (Broomhall et al. 2009) and the standard model frequencies in the whole frequency range. For our models, we find that it works well in limited frequency ranges, but not in the whole range. Then, we alternatively propose a formulation based on a modified Lorentzian function, ![\begin{eqnarray} \frac{\delta\nu}{\nu_{\rm max}}=\alpha\left[1-\frac{1}{1+(\nu_{\rm PM}/\nu_{\rm max})^\beta}\right], \label{eq:Lorentzian} \end{eqnarray}](/articles/aa/full_html/2015/11/aa26838-15/aa26838-15-eq117.png) (9)where the first term in the brackets ensures that δν becomes zero when νPM = 0. By this definition, α/ 2 is the value of δν/νmax at νPM = νmax. As for a and b, the coefficients α and β are determined with a least-square analysis. The results are shown in Fig. 5 and Table 4.
(9)where the first term in the brackets ensures that δν becomes zero when νPM = 0. By this definition, α/ 2 is the value of δν/νmax at νPM = νmax. As for a and b, the coefficients α and β are determined with a least-square analysis. The results are shown in Fig. 5 and Table 4.
Coefficients of the Kjeldsen et al. (2008) and the Lorentzian fittings.
 |
Fig. 5 Values of log | α | (top) and β (bottom) obtained by the fitting with Eq. (9) are indicated by color on the Teff–log g plane. |
Figure 3 compares the fittings obtained using either Eqs. (4) or (9). The Lorentzian profile is found to fit the whole frequency range. We note that, as shown by Table 3, when we consider the frequency range 0 <ν/νmax< 1.05, both the power law and the Lorentzian profile provide us with the same magnitude for the error. Indeed, this is because Eq. (9) reduces to Eq. (4) in the low-frequency limit. In addition, it is worth mentioning that the parameters of the Lorentzian profile are weakly sensitive to the glitches in the intermediate frequency range. Indeed, they are mainly determined by the low- and high-frequency limits.
Similarly to the power-law fitting, we derive the variation in α and β with log Teff and log g, 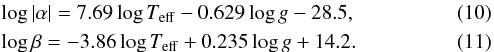 The deviations evaluated using Eq. (8) are σα = 5.0 × 10-2 and σβ = 3.1 × 10-2. The deviation of α is much larger compared to the case of a, while those of β and b are of the same order. By definition, the trends in a and α on log Teff and log g must be similar. The trend in β is also found to be similar to that in b.
The deviations evaluated using Eq. (8) are σα = 5.0 × 10-2 and σβ = 3.1 × 10-2. The deviation of α is much larger compared to the case of a, while those of β and b are of the same order. By definition, the trends in a and α on log Teff and log g must be similar. The trend in β is also found to be similar to that in b.
4. Discussion
4.1. Scalings with the atmosphere elevation
As discussed in Sect. 3, the absolute values of coefficients a and α increase with decreasing surface gravity or increasing effective temperature, while coefficients b and β show the opposite trends. Here, we show that these trends are related to the elevation of the outer layers because of the turbulent pressure in PM.
4.1.1. Coefficients a and α
According to Rosenthal et al. (1999), the frequency change between two similar models can be estimated as 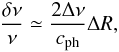 (12)where ΔR is the difference of radius between the two models, c the sound speed, and cph its value at the photosphere. Here, Δν is the asymptotic large separation,
(12)where ΔR is the difference of radius between the two models, c the sound speed, and cph its value at the photosphere. Here, Δν is the asymptotic large separation, 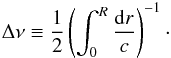 (13)Given that cph scales as
(13)Given that cph scales as 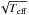 , we simplify the scaling relation of Eq. (12) as
, we simplify the scaling relation of Eq. (12) as 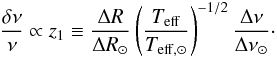 (14)Here, we consider ΔR as the difference of the radius between PM and UPM, RPM−RUPM. To derive a scale for the latter quantity, we start by dealing with the ratio of the turbulent pressure to the total pressure γ ≡ Pturb/Ptot. Hydrostatic equilibrium implies
(14)Here, we consider ΔR as the difference of the radius between PM and UPM, RPM−RUPM. To derive a scale for the latter quantity, we start by dealing with the ratio of the turbulent pressure to the total pressure γ ≡ Pturb/Ptot. Hydrostatic equilibrium implies 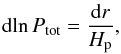 (15)where Hp = Ptot/ (ρg) is the pressure scale height. Assuming γ ≪ 1, ΔR = γHp, and since Hp scales as Teff/g, we finally derive
(15)where Hp = Ptot/ (ρg) is the pressure scale height. Assuming γ ≪ 1, ΔR = γHp, and since Hp scales as Teff/g, we finally derive 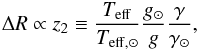 (16)where γ is evaluated at the photosphere.
(16)where γ is evaluated at the photosphere.
The ratio γ depends on the Mach number (defined as ℳa ≡ wrms/c, where wrms is the root mean square of the vertical component of the velocity) because by definition, 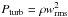 . Assuming a perfect gas, we obtain Pg ∝ ρT. Moreover,
. Assuming a perfect gas, we obtain Pg ∝ ρT. Moreover, 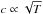 , so that Pturb/Pg ∝ ℳa. Finally, since γ ≪ 1, we establish the scaling relation
, so that Pturb/Pg ∝ ℳa. Finally, since γ ≪ 1, we establish the scaling relation 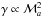 . As shown in Samadi et al. (2013), ℳa scales approximately as
. As shown in Samadi et al. (2013), ℳa scales approximately as 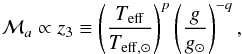 (17)where p = 2.35 and q = 0.152. Using this scaling relation, we finally have
(17)where p = 2.35 and q = 0.152. Using this scaling relation, we finally have 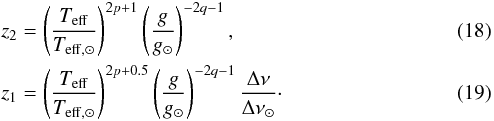 Figure 6 shows the value of a as a function of z1, which was evaluated with Eq. (19). For Δν, we used the average value of the large separation and adopted Δν⊙ = 134.9 μHz (Kjeldsen & Bedding 1995). We carried out a least-square fitting, fixing the power index of z1 to unity, or leaving it free. Although the analytical result gives | a | ∝ z1, we obtain
Figure 6 shows the value of a as a function of z1, which was evaluated with Eq. (19). For Δν, we used the average value of the large separation and adopted Δν⊙ = 134.9 μHz (Kjeldsen & Bedding 1995). We carried out a least-square fitting, fixing the power index of z1 to unity, or leaving it free. Although the analytical result gives | a | ∝ z1, we obtain 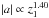 and
and 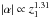 when the power index is free. The deviation from a linear scaling with z1 is likely due to the various simplifications adopted in the derivation of this scaling. As the alternative formulations for Eqs. (6) and (10), we finally have
when the power index is free. The deviation from a linear scaling with z1 is likely due to the various simplifications adopted in the derivation of this scaling. As the alternative formulations for Eqs. (6) and (10), we finally have ![\begin{eqnarray} && \log |a| = 7.28\log T_{\rm eff} - 1.83\log g \nonumber \\ &&\qquad\qquad + 1.40\log\Delta\nu [\mu {\rm Hz}] - 24.8, \\ && \log |\alpha|= 6.83\log T_{\rm eff} - 1.71\log g \nonumber \\ &&\qquad\qquad + 1.40\log\Delta\nu [\mu {\rm Hz}] - 23.5. \end{eqnarray}](/articles/aa/full_html/2015/11/aa26838-15/aa26838-15-eq180.png) The deviations defined by Eq. (8) are σa = 1.8 × 10-3 and σα = 3.0 × 10-3. Then, the above equations are less (more) suitable for a (α) than Eq. (6) (Eq. (10)). But they are at least based on physical considerations.
The deviations defined by Eq. (8) are σa = 1.8 × 10-3 and σα = 3.0 × 10-3. Then, the above equations are less (more) suitable for a (α) than Eq. (6) (Eq. (10)). But they are at least based on physical considerations.
 |
Fig. 6 Plots of the logarithm of | a | and the fitting line as a function of log z1. The black line is the result of the least-square fitting fixing the power-law index of z1 to unity, namely, corresponding to Eq. (19), | a | ∝ z1. For the red line, the power-law index is also set as the free parameter of the fitting. |
4.1.2. Power indices b and β
 |
Fig. 7 log b as a function of log z1 (top) or of log z3 (bottom). The black line is a result of a least-square fit. |
The trend of the coefficients b and β on the Teff–log g plane can be also explained in terms of the elevation due to the turbulent pressure. As shown in the top panel of Fig. 7, both coefficients decrease with increasing z1, although the dispersion is large (σb = 3.6 × 10-1, σβ = 4.9 × 10-1). As shown in the bottom panel of Fig. 7, the correlation is better with z3 for b and β (σb = 2.3 × 10-1, σβ = 3.2 × 10-1). Using the result of the fitting on the log z3−log b plane, we obtain the physically derived formulations for b and β,  although, in this case, the dispersion for both of them is greater than for Eqs. (7) and (11).
although, in this case, the dispersion for both of them is greater than for Eqs. (7) and (11).
The greater the elevation, the larger the difference in the structure of the convection zone between PM and UPM. Therefore, the low-order modes are more affected by surface effects (see Fig. 3). Consequently, the gradient of δν at intermediate frequencies becomes smaller and so do the power indices b and β.
To demonstrate that the elevation is responsible for the lower values of b and β, we performed a numerical experiment as follows: we took the mean of the quantity Vg (defined as Vg ≡ GMr/ (rc2), see Fig. 8 top panel) between PM and UPM and replace the original Vg with it in PM. This treatment reduces the difference in the structure, so that the situation becomes similar to the models with lower effective temperature or with higher surface gravity. Figure 9 shows the frequency difference between UPM and the modified PM. As we can see, the difference in the frequency of the low-order modes is reduced, and the profile is similar to Model A (see Fig. 3, top panel). The fit of the parameters indicates that the value of b is raised from 2.09 to 5.21 and that of β from 2.56 to 8.00.
Finally, we note that the entropy difference between the photosphere and the superadiabatic layer becomes larger with increasing effective temperature or decreasing surface gravity (e.g., Ludwig et al. 1999). The entropy difference should then correlate with the superadiabaticity, hence with the turbulent pressure. Then, it is natural that the trend of the entropy difference shown in Fig. 4 in their paper is similar to that of the coefficients, a, α, b, and β.
4.2. Oscillatory features in profiles of frequency difference
 |
Fig. 8 Vg (top) and sound speed c (bottom) in PM and UPM of Model B as a function of the acoustic radius, |
 |
Fig. 9 Frequency difference between PM and UPM as a function of the reduced frequency (the red curve with dots, same as the bottom panel of Fig. 3). For the blue one, the value of Vg is modified in PM as shown with the blue curve in the top panel of Fig. 8. The dashed black and magenta lines are fitting curves with Eqs. (4) and (9). The resulting coefficients are (a,b) = (−1.10 × 10-2,5.21) for Eq. (4) and (α/ 2,β) = (−1.21 × 10-2,8.00) for Eq. (9). |
As already mentioned, the Lorentzian formulation can reproduce the profiles of the frequency difference properly. However, for some models, oscillatory features are conspicuously close to νmax. They can lead to deviation from the Lorentzian curves. Here, we aim to interpret the oscillatory features.
A steep change in the structure or a discontinuity in stars, a so-called “acoustic glitch”, causes modulations in spacings of frequencies (e.g., Houdek & Gough 2007, 2011; Mazumdar et al. 2014). These modulations, then, may lead to modulations in the frequency difference. A useful diagnostic is the second difference with respect to the radial order n, defined by 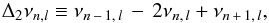 (24)where l is the angular degree. This second difference is less sensitive to the surface regions than the frequency ν itself and than the large separation Δν = νn,l−νn−1,l. Then, it is advantageous for extracting the effects of the glitches, located in the deeper interior.
(24)where l is the angular degree. This second difference is less sensitive to the surface regions than the frequency ν itself and than the large separation Δν = νn,l−νn−1,l. Then, it is advantageous for extracting the effects of the glitches, located in the deeper interior.
 |
Fig. 10 Profiles of the original PM and UPM for Model B. Panels a) and b) show Γ1 and Vg, respectively, as functions of the acoustic radius Tg. The dotted vertical lines indicate the locations of the Γ1 bumps due to the HeII and the H ionizations. Panels c) and d) show the second difference for ℓ = 0–2 and the frequency difference between PM and UPM for the radial modes, respectively, as functions of the frequency. |
 |
Fig. 11 Same as Fig. 10, but for the case where the Γ1 profiles are smoothed in both the H and the HeII bumps. In panels a) and b), the profiles of the original models are shown as dashed lines. Similarly, the frequency difference for the original models is plotted as a dashed line in panel d). |
Figure 10 shows the original properties of the PM and UPM for Model B. In panels (a) and (b), the Γ1 and Vg profiles of PM deviate from that of UPM above the matching point, respectively. The acoustic cavity of the PM is found to be larger due to turbulent elevation. Panel (c) shows the second difference of modes with l = 0–2. Both PM and UPM low-degree modes show modulation due to acoustic glitches. Furthermore, we can see a phase shift between them. This shift is responsible for modulating of the frequency difference.
Figure 11 shows the case where the Γ1 profiles are smoothed in both the HeII and the H bumps (panel a). Among the input variables for ADIPLS, Vg and A( ≡ dlnP/ dlnr/ Γ1−dlnρ/ dlnr) include Γ1. In this experiment, however, we only modify Γ1 in Vg, and not A to avoid changing the convective stability. Then, the curves of Vg form steeper walls and get closer in the upper part of the H bump (panel b). This reduces the difference in the acoustic cavities between PM and UPM, hence the difference in the locations of the glitches. Therefore, the phase shift in Δ2ν becomes smaller (panel d). In addition, this treatment results in the amplitude of the modulation in the second difference becoming smaller and similar between PM and UPM in the range 0.6 ≲ ν/νmax ≲ 1.2 (panel c). Consequently, the oscillatory features disappear in the frequency difference.
To check which bump mainly contributes to the oscillatory features, we also analyzed the case where either the HeII or the H bump is smoothed. When we smoothed the HeII bump, we found that the oscillatory features remain unchanged. Indeed, the HeII ionization zone is located below the matching point. Then, although the modulation amplitude of Δ2ν is certainly reduced, the smoothing does not have any influence on the phase shift. On the other hand, when we smooth the H bump, the curve of the frequency difference becomes almost identical to the one in the panel (d) of Fig. 11. The locations of the glitches in the H ionization zone are different between PM and UPM owing to the turbulent elevation. Then, the smoothing reduces the phase shift, as well as the modulation amplitude. Therefore, we conclude that the oscillatory features in the frequency difference are mainly produced by the H bump and the fact that the location of the H bump is different in the PM and UPM.
4.3. Dependence on the fitting range
Oscillation modes are observed in a limited range, so that the power-law correction has not been used over a wide range. Kjeldsen et al. (2008) suggest that the power-law index depends substantially on the frequency range considered. This means that the results of the coefficients used in the fit certainly can vary with the range.
To investigate this variation, we carried out a least-square fitting of the power law and the Lorentzian formulation by changing the fitting range. We fixed the width of the frequency range to 0.8 in unit of ν/νmax and tested with the ranges 0.0 to 0.8, 0.1 to 0.9, ..., and 0.8 to 1.6.
Figure 12 shows the case where the fitting is performed in the range 0.6 <ν/νmax< 1.4. We see that the Lorentzian formulation is found to be more robust than the power law even if we limit the fitting range. Figure 13 shows the reduced deviation 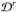 , defined in Sect. 3.2, of the fitting functions from the computed frequencies for Model A as a function of the fitting range. For this model, the Lorentzian formulation always has a smaller deviation. This conclusion is valid for the other models.
, defined in Sect. 3.2, of the fitting functions from the computed frequencies for Model A as a function of the fitting range. For this model, the Lorentzian formulation always has a smaller deviation. This conclusion is valid for the other models.
Figure 14 shows the coefficients of the power-law and the Lorentzian formulation as functions of the fitting range in the case of Model A. For most models, the coefficients a and α increase as the fitting range shifts to higher frequency, while b and β show the opposite trend. Then, the power indices b and β become higher in the lower frequency range. For Model A, we find that a (α) changes by a factor of 2.67 (1.51), with the change in the frequency range from 0.0–0.8 to 0.8–1.6, while b (β) by a factor of 4.50 (1.40). For all of the models, the coefficients of the Lorentzian formulation show less dependence on the frequency range. It implies that the Lorentzian formulation is more robust than the power law for modeling the surface frequency corrections.
 |
Fig. 12 Functional fittings with the power law (Eq. (4), the green curve) and the Lorentzian formulation (Eq. (9), the red curve) to the frequency difference of PM and UPM for Model A in the range 0.6 <ν/νmax< 1.4. |
 |
Fig. 13 Dependence of the deviation in the power law (Eq. (4)) and the Lorentzian formulation (Eq. (9)) on the fitting range for Model A. |
 |
Fig. 14 Dependence of the coefficients of the power law (Eq. (4)) and the Lorentzian formulation (Eq. (9)) on the fitting range for Model A. |
5. Conclusion
We analyzed frequency differences between standard models (unpatched models, UPMs) and patched models (UPMs). The latter were constructed using the CIFIST grid (Ludwig et al. 2009) of 3D hydrodynamical simulation computed with the CO5BOLD code (Freytag et al. 2012).
We addressed the variation in the free parameters introduced by the Kjeldsen et al. (2008) empirical surface-effect correction. We found that the coefficients vary significantly across the HR diagram. As a result of the functional fitting to the frequency difference, index b decreases with increasing effective temperature or with decreasing surface gravity, while coefficient a shows the opposite trend. These trends are caused by the elevation of the outer layers related to the modification of the hydrostatic equilibrium by the turbulent pressure. So far, b has been set to the solar-calibrated value in many applications, even for different stars, and a has been determined by using this value of b. The results of this study imply that such a treatment is not appropriate.
In addition, we confirm that the power-law function is not suitable for the high-frequency range, since the profile of the frequency difference becomes less steep as the frequency exceeds νmax. In general, solar-like oscillations are distributed symmetrically around νmax in the power spectra, and we cannot neglect the modes above νmax. Then, we propose a formulation based on a Lorentzian, which is found to successfully fit the profile of the frequency difference in the whole frequency range. The coefficients α and β have similar trends as a and b of the power law, respectively. Moreover, we show that the Lorentzian function is more robust against both the choice of the range of corrected frequencies and the glitches in the frequency differences induced by the difference in the location of the hydrogen ionization region between the PMs and UPMs.
In this paper, we limited ourselves to adiabatic oscillations as a first step. Therefore, the surface effects are mainly caused by the turbulent pressure in the equilibrium structure. Indeed, the turbulent pressure elevates the outer layers and eventually increases the stellar radius. It leads to an expansion of the acoustic cavity, and thus to the decrease in the frequencies.
However, the effect of both nonadiabaticity and time-dependent processes between convection and oscillation were not considered. The nonadiabaticity is also expected to play a non-negligible role in the near-surface regions, since the thermal timescale is comparable to or shorter than the oscillation periods. Moreover, convection can also affect oscillations through time-dependent processes. For instance, the perturbation of turbulent pressure and of the convective heat flux must be related to the nonadiabatic processes of the oscillations. Computing nonadiabatic oscillations using a time-dependent treatment of convection is thus a natural way to investigate these mechanisms. We will pursue these subjects in a subsequent paper.
Acknowledgments
The authors are grateful to M.-J. Goupil and M.-A. Dupret for their helpful comments. H.G.L. acknowledges financial support by the Sonderforschungsbereich SFB 881 “The Milky Way System” (subproject A4) of the German Research Foundation (DFG). T.S. has been supported by the ANR program IDEE “Interaction Des Étoiles et des Exoplanètes” (Agence Nationale de la Recherche, France).
References
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. T. G. Barnes, III, & F. N. Bash, ASP Conf. Ser., 336, 25 [Google Scholar]
- Baglin, A., Auvergne, M., Barge, P., et al. 2006a, in ESA SP, 1306, eds. M. Fridlund, A. Baglin, J. Lochard, & L. Conroy [Google Scholar]
- Baglin, A., Auvergne, M., Boisnard, L., et al. 2006b, in 36th COSPAR Scientific Assembly, COSPAR Meeting, 36, 3749 [NASA ADS] [Google Scholar]
- Ball, W. H., & Gizon, L. 2014, A&A, 568, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belkacem, K., Goupil, M. J., Dupret, M. A., et al. 2011, A&A, 530, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bhattacharya, J., Hanasoge, S. M., & Antia, H. M. 2015, ApJ, 806, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm-Vitense, E. 1958, Z. Astroph., 46, 108 [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Brandão, I. M., Doğan, G., Christensen-Dalsgaard, J., et al. 2011, A&A, 527, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Broomhall, A.-M., Chaplin, W. J., Davies, G. R., et al. 2009, MNRAS, 396, L100 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M. 1984, Science, 226, 687 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Brown, T. M., Gilliland, R. L., Noyes, R. W., & Ramsey, L. W. 1991, ApJ, 368, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Chaplin, W. J., & Miglio, A. 2013, ARA&A, 51, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J. 2008, Ap&SS, 316, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J., & Thompson, M. J. 1997, MNRAS, 284, 527 [NASA ADS] [Google Scholar]
- Christensen-Dalsgaard, J., Dappen, W., & Lebreton, Y. 1988, Nature, 336, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J., Dappen, W., Ajukov, S. V., et al. 1996, Science, 272, 1286 [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J., Kjeldsen, H., Brown, T. M., et al. 2010, ApJ, 713, L164 [NASA ADS] [CrossRef] [Google Scholar]
- Doğan, G., Brandão, I. M., Bedding, T. R., et al. 2010, Ap&SS, 328, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Doǧan, G., Metcalfe, T. S., Deheuvels, S., et al. 2013, ApJ, 763, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Dziembowski, W. A., Paterno, L., & Ventura, R. 1988, A&A, 200, 213 [NASA ADS] [Google Scholar]
- Freytag, B., Steffen, M., Ludwig, H.-G., et al. 2012, J. Comput. Phys., 231, 919 [Google Scholar]
- Gilliland, R. L., Marcy, G. W., Rowe, J. F., et al. 2013, ApJ, 766, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Grigahcène, A., Dupret, M.-A., Sousa, S. G., et al. 2013, in Stellar Pulsations: Impact of New Instrumentation and New Insights, eds. J. C. Suárez, R. Garrido, L. A. Balona, & J. Christensen-Dalsgaard, Astrophys. Space Sci. Proc., 31, 209 [Google Scholar]
- Gruberbauer, M., Guenther, D. B., & Kallinger, T. 2012, ApJ, 749, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Gruberbauer, M., Guenther, D. B., MacLeod, K., & Kallinger, T. 2013, MNRAS, 435, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Houdek, G. 2010, Astron. Nachr., 331, 998 [NASA ADS] [CrossRef] [Google Scholar]
- Houdek, G., & Gough, D. O. 2007, MNRAS, 375, 861 [NASA ADS] [CrossRef] [Google Scholar]
- Houdek, G., & Gough, D. O. 2011, MNRAS, 418, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] [Google Scholar]
- Kjeldsen, H., Bedding, T. R., & Christensen-Dalsgaard, J. 2008, ApJ, 683, L175 [NASA ADS] [CrossRef] [Google Scholar]
- Lebreton, Y., & Goupil, M. J. 2014, A&A, 569, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ludwig, H.-G., Freytag, B., & Steffen, M. 1999, A&A, 346, 111 [NASA ADS] [Google Scholar]
- Ludwig, H.-G., Caffau, E., Steffen, M., et al. 2009, Mem. Soc. Astron. Italiana, 80, 711 [Google Scholar]
- Marques, J. P., Goupil, M. J., Lebreton, Y., et al. 2013, A&A, 549, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mazumdar, A., Monteiro, M. J. P. F. G., Ballot, J., et al. 2014, ApJ, 782, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Metcalfe, T. S., Monteiro, M. J. P. F. G., Thompson, M. J., et al. 2010, ApJ, 723, 1583 [NASA ADS] [CrossRef] [Google Scholar]
- Michel, E., Baglin, A., Auvergne, M., et al. 2008, Science, 322, 558 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Petrovay, K., Erdélyi, R., & Thompson, M. J. 2007, Sol. Phys., 240, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Piau, L., Collet, R., Stein, R. F., et al. 2014, MNRAS, 437, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenthal, C. S., Christensen-Dalsgaard, J., Nordlund, Å., Stein, R. F., & Trampedach, R. 1999, A&A, 351, 689 [NASA ADS] [Google Scholar]
- Samadi, R. 2011, in Lect. Notes Phys. 305, eds. J.-P. Rozelot, & C. Neiner (Berlin Springer Verlag), 832 [Google Scholar]
- Samadi, R., Georgobiani, D., Trampedach, R., et al. 2007, A&A, 463, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Samadi, R., Belkacem, K., Goupil, M. J., Dupret, M.-A., & Kupka, F. 2008, A&A, 489, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Samadi, R., Belkacem, K., Ludwig, H.-G., et al. 2013, A&A, 559, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlattl, H., Weiss, A., & Ludwig, H.-G. 1997, A&A, 322, 646 [NASA ADS] [Google Scholar]
- Silva Aguirre, V., Davies, G. R., Basu, S., et al. 2015, MNRAS, 452, 2127 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, R. F., & Nordlund, Å 1991, in Challenges to Theories of the Structure of Moderate-Mass Stars, eds. D. Gough, & J. Toomre (Berlin: Springer Verlag), Lect. Notes Phys., 388, 195 [Google Scholar]
- Tang, Y. K., & Gai, N. 2011, A&A, 526, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trampedach, R. 1997, Master’s thesis, Aarhus University [Google Scholar]
- Van Eylen, V., Kjeldsen, H., Christensen-Dalsgaard, J., & Aerts, C. 2012, Astron. Nachr., 333, 1088 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, J. Y., & Li, Y. 2007, MNRAS, 375, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Zhugzhda, Y. D., & Stix, M. 1994, A&A, 291, 310 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 3D hydrodynamical models in the Teff−log g plane. The relative difference in the radius between PM and UPM is indicated by the color scale. |
| In the text | |
 |
Fig. 2 Comparison of the total pressure Ptot between PM and UPM of Model A. The abscissa is the radius divided by the solar radius, r/R⊙. The vertical arrow indicates the point of matching between the CESTAM model and the CO5BOLD model. Below the matching point, the profiles of PM and UPM are identical. |
| In the text | |
 |
Fig. 3 Frequency differences of radial modes between PM and UPM divided by νmax as a function of νPM/νmax (black solid line with dots). The green full line and the blue dashed line are least-square fittings with the Kjeldsen et al. (2008) power law, a(νPM/νmax)b in the range 0 <ν/νmax< 1.05 and in the whole range, respectively. The red line shows the modified Lorentzian, α [1−1/ { 1 + (νPM/νmax)β }]. |
| In the text | |
 |
Fig. 4 Values of log | a | (top) and b (bottom) obtained by the fitting with Eq. (4) in the range 0 <ν/νmax< 1.05 are indicated by colors on the Teff–log g plane. |
| In the text | |
 |
Fig. 5 Values of log | α | (top) and β (bottom) obtained by the fitting with Eq. (9) are indicated by color on the Teff–log g plane. |
| In the text | |
 |
Fig. 6 Plots of the logarithm of | a | and the fitting line as a function of log z1. The black line is the result of the least-square fitting fixing the power-law index of z1 to unity, namely, corresponding to Eq. (19), | a | ∝ z1. For the red line, the power-law index is also set as the free parameter of the fitting. |
| In the text | |
 |
Fig. 7 log b as a function of log z1 (top) or of log z3 (bottom). The black line is a result of a least-square fit. |
| In the text | |
 |
Fig. 8 Vg (top) and sound speed c (bottom) in PM and UPM of Model B as a function of the acoustic radius, |
| In the text | |
 |
Fig. 9 Frequency difference between PM and UPM as a function of the reduced frequency (the red curve with dots, same as the bottom panel of Fig. 3). For the blue one, the value of Vg is modified in PM as shown with the blue curve in the top panel of Fig. 8. The dashed black and magenta lines are fitting curves with Eqs. (4) and (9). The resulting coefficients are (a,b) = (−1.10 × 10-2,5.21) for Eq. (4) and (α/ 2,β) = (−1.21 × 10-2,8.00) for Eq. (9). |
| In the text | |
 |
Fig. 10 Profiles of the original PM and UPM for Model B. Panels a) and b) show Γ1 and Vg, respectively, as functions of the acoustic radius Tg. The dotted vertical lines indicate the locations of the Γ1 bumps due to the HeII and the H ionizations. Panels c) and d) show the second difference for ℓ = 0–2 and the frequency difference between PM and UPM for the radial modes, respectively, as functions of the frequency. |
| In the text | |
 |
Fig. 11 Same as Fig. 10, but for the case where the Γ1 profiles are smoothed in both the H and the HeII bumps. In panels a) and b), the profiles of the original models are shown as dashed lines. Similarly, the frequency difference for the original models is plotted as a dashed line in panel d). |
| In the text | |
 |
Fig. 12 Functional fittings with the power law (Eq. (4), the green curve) and the Lorentzian formulation (Eq. (9), the red curve) to the frequency difference of PM and UPM for Model A in the range 0.6 <ν/νmax< 1.4. |
| In the text | |
 |
Fig. 13 Dependence of the deviation in the power law (Eq. (4)) and the Lorentzian formulation (Eq. (9)) on the fitting range for Model A. |
| In the text | |
 |
Fig. 14 Dependence of the coefficients of the power law (Eq. (4)) and the Lorentzian formulation (Eq. (9)) on the fitting range for Model A. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.