| Issue |
A&A
Volume 583, November 2015
|
|
|---|---|---|
| Article Number | A77 | |
| Number of page(s) | 6 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201526690 | |
| Published online | 30 October 2015 | |
Research Note
Post-AGB stars in the Magellanic Clouds and neutron-capture processes in AGB stars
1
Konkoly Observatory, Research Centre for Astronomy and Earth Sciences,
Hungarian Academy of Sciences,
Konkoly Thege Miklós út 15–17,
1121
Budapest,
Hungary
e-mail: maria.lugaro@csfk.mta.hu
2
Monash Centre for Astrophysics (MoCA), Monash
University, 3800
Clayton, Victoria,
Australia
3
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741
Garching bei München,
Germany
4
Instituut voor Sterrenkunde, K.U. Leuven, Celestijnenlaan 200D bus
2401, 3001
Leuven,
Belgium
5
Research School of Astronomy and Astrophysics, Australian National
University, Canberra,
ACT
2611,
Australia
6
Karlsruhe Institute of Technology (KIT), Campus North, Institute
of Nuclear Physics, PO
Box 3640
Karlsruhe,
Germany
Received: 8 June 2015
Accepted: 8 September 2015
Aims. We explore modifications to the current scenario for the slow neutron-capture process (the s-process) in asymptotic giant branch (AGB) stars to account for the Pb deficiency observed in post-AGB stars of low metallicity ([Fe/H] ≃−1.2) and low initial mass (≃ 1−1.5 M⊙) in the Large and Small Magellanic Clouds.
Methods. We calculated the stellar evolution and nucleosynthesis for a 1.3 M⊙ star with [Fe/H] = −1.3 and tested different amounts and distributions of protons leading to the production of the main neutron source within the 13C-pocket and proton ingestion scenarios.
Results. No s-process models can fully reproduce the abundance patterns observed in the post-AGB stars. When the Pb production is lowered, the abundances of the elements between Eu and Pb, such as Er, Yb, W, and Hf, are also lowered to below those observed.
Conclusions. Neutron-capture processes with neutron densities intermediate between the s and the rapid neutron-capture processes may provide a solution to this problem and be a common occurrence in low-mass, low-metallicity AGB stars.
Key words: stars: abundances / stars: AGB and post-AGB
© ESO, 2015
1. Introduction
During the past decade, significant information has been gathered on the chemical compositions of post-asymptotic giant branch (AGB) stars in the Milky Way. This has led to the discovery of a class of post-AGB stars that have C/O > 1 and display extreme enrichment in the abundances of the elements heavier than Fe produced by slow neutron captures (the s-process, Van Winckel & Reyniers 2000; Reyniers & Van Winckel 2003; Reyniers et al. 2004). Since AGB stars can become C rich and have been confirmed both theoretically and observationally as the main stellar site for the s-process (see, e.g., Busso et al. 2001), it is natural to interpret these post-AGB observations as the signature of the nucleosynthesis and mixing events that occurred during the preceeding AGB phase. These events are currently identified as (i) the mixing of protons into the radiative He-rich intershell leading to the formation of a thin region rich in the main neutron source 13C (the 13C “pocket”); (ii) proton-ingestion episodes (PIEs) inside the convective thermal pulses (TPs); and (iii) the third dredge-up (TDU), which carries C and s-process elements from the He-rich intershell to the convective envelope and to the stellar surface. Since the details of all these processes are very uncertain (see discussion in, e.g., Busso et al. 1999; Herwig 2005; Campbell & Lattanzio 2008), observations of post-AGB stars provide strong constraints. Recent observations of the chemical composition of four low-metallicity ([Fe/H] from −1.15 to −1.34), s-process-rich, C-rich post-AGB stars in the Large (J050632, J052043, and J053250) and Small (J004441) Magellanic Clouds (LMC and SMC, respectively) have provided a challenge to AGB s-process models (De Smedt et al. 2012, 2014; van Aarle et al. 2013)1. Since we know the distance of these stars, it is possible to determine from the observed luminosity that their initial stellar mass was in the range 1–1.5 M⊙. Stellar AGB models in this range of mass and metallicity can produce the high observed abundances of the s-process elements, such as Zr and La (1 < [Zr/Fe] < 2 and 1 < [La/Fe] < 3), together with [Pb/La] ≃ 1, if a deep TDU is assumed after a last TP. Instead, negative [Pb/La] values are observed as upper limits (De Smedt et al. 2014). Here we test different possible modifications of the current AGB s-process scenario to explain the neutron-capture abundance pattern observed in the MC post-AGB stars.
Properties of the 13C-pocket models.
 |
Fig. 1 Hertzsprung-Russell diagram showing the evolution of our 1.3 M⊙, [Fe/H] = −1.3 model from the start of the main sequence to the white dwarf cooling track. The locations of the four post-AGB stars are represented by the red dots with error bars. The location of the third last thermal pulse (TP13) is also indicated. (The colour version of this figure is available in the online journal.) |
2. Stellar models
We have computed the structural evolution of a star of initial mass 1.3 M⊙ and [Fe/H] = −1.3 using the version of the Mt Stromlo/Monash evolutionary code updated by Campbell & Lattanzio (2008). In addition, low-temperature opacities were updated to those calculated by Lederer & Aringer (2009). Mass loss was included using the formula of Reimers (1975) during the RGB phase (with η = 0.4) and the formula of Vassiliadis & Wood (1993) during the AGB phase. Instantaneous mixing was used in convective zones, and the convective boundaries were defined using a search for convective neutrality (Frost & Lattanzio 1996). No overshoot was applied beyond this, which resulted in a small number of TDU episodes: five in total – from the 8th TP to the 12th TP – out of a total of 15 TPs, with the amount of mass carried to the envelope, MTDU, of the order of a few 10-3 M⊙. The last three TPs (13, 14, and 15) occurred after the star had left the AGB track (Fig. 1). During the 15th TP the post-AGB star became a born-again AGB star. This TP neither experienced the TDU nor the ingestion of the entire H-rich envelope of mass ~0.002 M⊙ in our model. The observed post-AGB stars did not experience this ingestion either since they are not H deficient.
We computed detailed nucleosynthesis models using a post-processing code (Cannon 1993) with a network of 320 nuclear species from neutrons to 210Po. Nuclear reaction rates were taken from the JINA database as of May 2012. The initial abundances in the nucleosynthesis models were taken from Asplund et al. (2009) scaled to the required [Fe/H], except for O, which was α-enhanced such that [O/Fe] = +0.4 both in the evolutionary and in the nucleosynthetic calculations. During the post-processing, we artificially introduced a given abundance Yp of protons at the deepest extent of each TDU episode, which led to the formation of the 13C pocket. Table 1 shows the main features of the 13C-pocket models where Yp is the proton abundance, MPMZ is the mass extent of the p-rich region, and 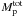 the total integrated mass of protons. We ran all of the models twice: with protons inserted after each of the five TDU episodes, and with protons inserted only after the last TDU episode (corresponding to the 12th TP), except for pocket_case2, which was run once, with protons inserted only after the last TDU episode. As done by De Smedt et al. (2012), we assumed an additional last TDU episode to artificially occur in all our models after the 13th TP (when the mass of the envelope is 0.033 M⊙). For this TDU episode we set MTDU to the values given in Table 1, such that the observed [La/Fe] was matched for each of the four stars. The TDU is very uncertain because it is affected by both physical and numerical choices (see, e.g., Frost & Lattanzio 1996; Mowlavi 1999), however, the amount of TDU does not affect the abundance patterns discussed below, it only alters the absolute abundances.
the total integrated mass of protons. We ran all of the models twice: with protons inserted after each of the five TDU episodes, and with protons inserted only after the last TDU episode (corresponding to the 12th TP), except for pocket_case2, which was run once, with protons inserted only after the last TDU episode. As done by De Smedt et al. (2012), we assumed an additional last TDU episode to artificially occur in all our models after the 13th TP (when the mass of the envelope is 0.033 M⊙). For this TDU episode we set MTDU to the values given in Table 1, such that the observed [La/Fe] was matched for each of the four stars. The TDU is very uncertain because it is affected by both physical and numerical choices (see, e.g., Frost & Lattanzio 1996; Mowlavi 1999), however, the amount of TDU does not affect the abundance patterns discussed below, it only alters the absolute abundances.
 |
Fig. 2 Proton abundance distribution artificially inserted during the post-processing in our models to simulate the formation of a 13C pocket after the 12th TP (left panel) and a PIE event during TP13 (right panel). Left panel: the thin line represents the standard exponentially decreasing proton distribution (pocket_case1) and the thick line the case where the proton abundance Yp is set to constantly equal 1.05 × 10-4 (pocket_case4). The dotted line represents the depth reached by the TDU. Right panel: the thin and thick lines represent two different proton distributions with a similar total amount of protons ingested: PIE_case1 (thin line) and PIE_case2 (thick line). The dotted line represents the maximum extension of the intershell convective region associated with TP13. The steep proton profile left over by the H-burning shell is also shown in the plot just above 0.638 M⊙. |
Properties of the PIE models.
The proton abundance distribution used in pocket_case1 (thin line of left panel in Fig. 2) is the same or very similar to the choice made in the models presented by De Smedt et al. (2012, 2014) and, as expected, produces the same results. According to our stellar evolution model, the 13C always burns completely before the onset of the following TP. In pocket_case2 we experimented with artificially keeping the temperature below 70 MK in the pocket, which is not enough to activate the 13C(α, n)16O reaction. A much lower value of the rate of this reaction is excluded since it is known within a factor of ~4 (Bisterzo et al. 2015), but it is possible that a TDU episode leading to the formation of the 13C pocket occurred in the earlier pulses, when the core mass and the temperature are lower. In fact, the core mass at which the TDU begins is uncertain and may be lower than in our model (Kamath et al. 2012). For example, if the first TDU episode occurred after the 2nd instead of the 8th TP, the temperature in the region of the 13C pocket would not have exceeed 70 MK before the development of the next TP. In this case the neutrons are released inside the following TP as the 13C is ingested. Next, we set the proton abundance Yp to be constant with values equal to 0.70 × 10-4 (pocket_case3) or 1.05 × 10-4 (pocket_case4, thick line of left panel of Fig. 2, and pocket_case5). Physically, this may correspond to efficient mixing inside the 13C pocket during the interpulse period induced by the difference in the angular momentum between the core and the envelope in a rotating AGB star. This mixing carries the neutron poison 14N into the 13C-rich layers (e.g., Piersanti et al. 2013), lowering the s-process efficiency. However, the actual effect is uncertain because magnetic fields can slow down the core by coupling it to the envelope and inhibit mixing. In the radiative 13C-pocket pocket_case4, the neutron flux lasts for roughly 30 000 yr, the total time-integrated neutron flux (neutron exposure) is ≃0.5 mbarn-1, and the neutron density reaches a maximum of 5.2 × 106 cm-3. In the case of the convective 13C pocket (pocket_case2), the neutron flux lasts for a much shorter time, of the order of 10 yr, and the neutron density reaches a much higher maximum of 2.5 × 1011 cm-3 for a similar neutron exposure as pocket_case4.
We also ran some preliminary tests to simulate a proton-ingestion episode (PIE) during the post-processing by inserting an artificial proton abundance distribution in the intershell before the convective zone of TP13 reaches its maximum extension. At this time the H shell is completely extinguished. These protons are ingested as the convective region extends outward. As in the 13C-pocket models, we artificially simulated a single last TDU event mixing the material from the He intershell into the envelope after TP13 had subsided, setting the amount of TDU mass to the value required to match the observed [La/Fe]. Table 2 shows the main features of the PIE models, where 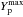 is the maximum proton abundance, Mext the mass extent of the p-rich region,
is the maximum proton abundance, Mext the mass extent of the p-rich region, 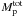 the total integrated mass of protons, and MTDU the TDU mass required to match each star. The MTDU required in the PIE models are typically lower than in the 13C-pocket models.
the total integrated mass of protons, and MTDU the TDU mass required to match each star. The MTDU required in the PIE models are typically lower than in the 13C-pocket models.
 |
Fig. 3 [X/Fe] ratios as a function of the atomic number Z predicted at the stellar surface by the models where one 13C pocket is introduced at the end of the TDU episode after the 12th TP as compared to the observations of each of the four post-AGB stars indicated in the panels. We normalise both model predictions and observations to meteoritic rather than photospheric solar abundances for the elements heavier than Fe (Asplund et al. 2009). Notably, this modifies the observed [Pb/Fe] upper limits reported by De Smedt et al. (2014) by −0.3 dex. The black line represents pocket_case1, which produces a similar pattern as that presented by De Smedt et al. (2014) with a high Pb abundance. Pocket_case2 is shown as a black dashed line. The coloured lines represent pocket_case3 (red) and pocket_case4 (blue). (The colour version of this figure is available in the online journal.) |
The proton abundance distribution is set to exponentially decrease with mass from a value 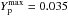 (PIE_case1, thin line of right panel of Fig. 2) or 0.007 (PIE_case2, thick line of right panel of Fig. 2, and PIE_case3) to a value of 10-4 over Mext. The protons are ingested in the convective region and captured by 12C, which results in the production of 13C. We ran a series of models varying the total mass of protons ingested
(PIE_case1, thin line of right panel of Fig. 2) or 0.007 (PIE_case2, thick line of right panel of Fig. 2, and PIE_case3) to a value of 10-4 over Mext. The protons are ingested in the convective region and captured by 12C, which results in the production of 13C. We ran a series of models varying the total mass of protons ingested 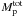 and found best solutions for
and found best solutions for 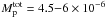 M⊙, that is, Mext = 0.8−4 × 10-3M⊙, depending on
M⊙, that is, Mext = 0.8−4 × 10-3M⊙, depending on 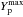 . This mass extent is relatively large: a more realistic profile to simulate overshoot of the convective intershell region into the proton tail left over by the H-burning shell would have a higher
. This mass extent is relatively large: a more realistic profile to simulate overshoot of the convective intershell region into the proton tail left over by the H-burning shell would have a higher 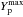 (e.g., ~0.2) and a much smaller Mext (~10-5M⊙, see Fig. 2). However, to set and follow such a profile appropriately requires very high temporal and spatial resolution, leading to extremely long running times with our computational tools. We leave this task to future work.
(e.g., ~0.2) and a much smaller Mext (~10-5M⊙, see Fig. 2). However, to set and follow such a profile appropriately requires very high temporal and spatial resolution, leading to extremely long running times with our computational tools. We leave this task to future work.
In comparison to the scenario of the 13C pocket, the neutron flux lasts for a very short time, of the order of 10-1 yr, five orders of magnitude shorter than in the radiative 13C pocket, while the neutron density reaches a maximum of 5 × 1013 cm-3 (e.g., in the PIE_case2 model), seven orders of magnitude higher than in the radiative 13C pocket. Even at this value of the neutron density, the neutron-capture path does not move farther away from the valley of β stability by more than two or three atomic mass numbers for each given element, and it still proceeds sequentially throughout each value of the proton number.
Finally, because the PIE was only included in the post-processing calculations, we cannot evaluate its feedback on the stellar structure and evolution. PIEs can lead to a splitting of the convective region, for example, as energy released by H burning creates a temperature inversion inside the convection zone. The amount of protons ingested in our model is small (up to 6 × 10-6M⊙), but in some PIE models this has been found to be enough to start the splitting of the convective zone (Miller Bertolami et al. 2006; Herwig et al. 2011). However, this effect is model dependent: the 3D PIE models of Stancliffe et al. (2011) did not find the split to occur even for larger amounts of protons, in contrast to the 3D PIE models of Woodward et al. (2015). The method we used to simulate a PIE is clearly artificial and preliminary, but any 1D model not considering hydrodynamics is necessarily inaccurate, and in addition, 3D PIE models do not agree with each other. Nevertheless, the usefulness of our approach lies in the opportunity of identifying major qualitative differences between the PIE and the 13C-pocket scenarios.
 |
Fig. 4 Same as Fig. 3, but for the PIE models. The black line represents PIE_case1 and the two coloured lines represent PIE_case2 (red) and PIE_case3 (blue). (The colour version of this figure is available in the online journal.) |
3. Results
If protons were introduced to produce a 13C pocket after each of the five TDU episodes computed by the stellar evolution code, it was not possible to find a solution for any of the four stars since the predicted [Pb/Fe] for the models that match [Zr/Fe] is always above the observed upper limit (by +0.2 dex for J050632 and by +0.6 for the other three stars). When we instead included only one 13C pocket, the production of Pb was lower and it was possible to find a case that simultaneously matched [Zr/Fe] and [Pb/Fe] (Fig. 3). The reason for this difference is that with more 13C pockets the material is recurrently exposed to several neutron fluxes, which pushes the abundance pattern towards Pb. In pocket_case2 MPMZ controls the total amount of 13C ingested and consequently the neutron exposure. The best fit to the observations was found using MPMZ = 10-3M⊙. A main difference in the results between the convective and the radiative models is that the [Rb/Fe] ratio (at Z = 37) is similar to [Zr/Fe] in the convective case while it is 1 dex lower than [Zr/Fe] in the radiative case. This is due to the higher neutron density, which favours the activation of the branching point at 86Rb producing the neutron magic 87Rb (van Raai et al. 2012; Karakas et al. 2012). The PIE model results are shown in Fig. 4. Because the general s-process elemental abundance pattern is a one-to-one function of the neutron exposure, it is possible to obtain very similar results in the PIE models to the 13C-pocket models by setting the amount of ingested protons to obtain a similar amount of free neutrons. As in the case of convective 13C pocket, [Rb/Fe] is close to [Zr/Fe] in the PIE cases due to the high neutron density. Observations of this element would be a powerful tool to distinguish between the different scenarios, but it is difficult to estimate its abundance in these stars because it presents only one very strong line, which is saturated.
The 13C-pocket models typically predict higher [C/Fe] ratios than observed, but this result depends on MPMZ. For example, in pocket_case5 we doubled MPMZ and matched the observed [C/Fe], within the error bars, for the three LMC stars. To match the [C/Fe] in J004441 instead requires a tenfold increase of the mass of the 13C pocket, which would cover the whole intershell. Extra-mixing phenomena at the base of the envelope during the red giant and AGB phases could remove C to produce N. Using the upper limit of the observed C abundance, the results for pocket_case5, and assuming that the excess C is converted into N via extra mixing, we expect [N/Fe] in J004441 to be greater than 2.5 dex. This is two orders of magnitude larger than the value of 0.61 ± 0.5 derived by De Smedt et al. (2014). The PIE models instead typically predict lower [C/Fe] ratios than observed, due to the lower MTDU. The O abundances are generally underestimated by all the models, which indicates that a higher O abundance must be present in the intershell and could be achieved if the timescale of He burning during the TPs was longer or if some mixing occurred between the base of the convective zone and the C-O core (Herwig 2000).
The four stars show positive [Y/Zr] while all the models predict negative values. We do not pursue this issue further because there may be a systematic error in the observations since the Y abundance is often based on a limited number of spectral lines. Another serious problem is that the models that produce [Pb/Fe] below the observational upper limits together with Y and Zr reasonably close to the observations underproduce the abundances of the elements between Eu and Pb, such as Eu, Dy, Er, Lu, Yb, Hf, and W. The number of lines used to determine the abundances of these elements are limited and often blended, but we cannot ascribe the mismatch to observational problems since all the four stars clearly show this problem for several of these elements.
4. Discussion and conclusions
It is not possible for the s-process to produce high abundances of the elements from Eu to W together with a Pb deficiency. This is because once the bottleneck at the nuclei with the magic number of neutrons 82 (138Ba and 139La) is bypassed, the neutron-capture flux proceeds through each isotope to 208Pb according to its neutron-capture cross section. In other words, the abundance pattern between the magic neutron numbers at Ba and Pb is almost completely determined by the neutron-capture cross sections of the isotopes involved. These are relatively well known (Bao et al. 2000), and that their values cannot be drastically changed is also demostrated by the fact that the s-process has no major problems (within 10−20%) in reproducing the solar system abundances of nuclei between Ba and Pb that are exclusively produced by the s-process. These are s-only nuclei such as 154Gd, 160Dy, and 170Yb, which typically contribute only a few percent to the total abundance of the element in the solar system (Arlandini et al. 1999; Bisterzo et al. 2011). Further observational constraints are available for a number of carbon-enhanced metal-poor (CEMP) stars, which have a metallicity roughly a factor of ten lower than the post-AGB stars considered here and are believed to have accreted s-process material from a more massive binary companion that evolved through the AGB phase. Bisterzo et al. (2012) compared CEMP-s stars (showing enhancements in the typical s-process element Ba) to AGB s-process models. They also included initial enhancements up to 2 dex in the rapid neutron-capture process (the r-process) elements to match the Eu abundances of CEMP-s/r stars (showing enhancements in both Ba and the typical r-process element Eu). The s-process models give a reasonable fit to the observations of all CEMP-s stars for which at least one element between Eu and Pb is observed (CS 22964-161, CS 22880-074, CS 29513-032, CS 22942-019, CS 30301-015, CS 30322-023, and HD 196944). Four out of nine CEMP-s/r stars with observations for the elements between Eu and Pb (CS 22898-027, CS 29497-030, HE 0338-3945, and HE 2148-1247) can also generally be matched by the models. The remaining five CEMP-s/r stars with observations for several elements between Dy and Pb (SDSS J1349-0229, CS 31062-050, LP 625-44, SDSS J0912+0216, and HD 209621) instead cannot be matched by the models because, as for the post-AGB stars discussed here, the observed abundances are too high even if the initial r-process abundances are enhanced.
As suggested for CEMP-s/r stars (Lugaro et al. 2012), an s/r neutron-capture process intermediate between the s and the r-process may have shaped the abundance pattern in the post-AGB stars. There are as yet no detailed models of this process for low-metallicity AGB stars, although PIE events have been identified as a a possible physical site (the i-process, Cowan & Rose 1977; Herwig et al. 2011). Overshoot leading to PIEs is uncertain, but known to be favoured in AGB stars of mass ~1 M⊙ and [Fe/H] < 2 (Fujimoto et al. 1990; Campbell & Lattanzio 2008; Cristallo et al. 2009; Lugaro et al. 2012) with recent 3D models supporting these results (Stancliffe et al. 2011; Herwig et al. 2014; Woodward et al. 2015). We stress that one-dimensional hydrostatic models of PIE events with artificial proton distributions like those presented here are not expected to describe the ingestion and the mixing correctly, and this may have a strong effect on the resulting abundance patterns. However, our 1D models are still informative. For example, we expect that the overabundance of Rb found in our PIE models may also be a prominent feature in more accurate PIE models, such as models in 3D (Herwig et al. 2011). Furthermore, the TDU mass that is required to match the observations cannot be substantially different from what we have found here; and to avoid overproduction of Pb, the amount of protons ingested during a PIE cannot be substantially different either. For example, taking J053250 and comparing it with the model predictions from the PIE model that ingested 6 × 10-6M⊙ of protons, we could match the observations by converting roughly two thirds of the predicted Pb abundance into abundances of the elements between Eu and Pb. In other words, a match to the observations would require the same amount of free neutrons that we have in our models, but distributed differently among the elements between Eu and Pb. This may be possible if the neutron density were a few orders of magnitude higher than in our models and the path of neutron captures were shifted farther away from the valley of β stability, as in the i-process.
The fact that all four post-AGB stars of low mass considered here show similar abundance patterns in the elements heavier than Fe suggests that the i-process may be a common occurrence in low-mass AGB stars up to [Fe/H] ~ −1. Since stars in this mass range are common, this would have important implications for the stellar yields that drive the chemical evolution of stellar clusters and galaxies. For example, these long-lived low-mass stars may be the i-process source required to match observations of [Ba/Fe] and [Ba/La] overabundances in open clusters (Mishenina et al. 2015). If the i-process is confirmed to be responsible for the abundances observed in CEMP-s/r and post-AGB stars, similarities and differences in the neutron-capture pattern of the two groups, which sample different metallicity ranges, will provide fundamental constraints to determine its metallicity dependence and its effect on the chemical evolution of stellar systems.
We do not discuss the composition of the mildly s-process-enhanced J053253 reported by van Aarle et al. (2013) because this star has recently been classified as a young stellar object candidate, indicating that its abundances more likely reflect the initial composition (Kamath et al. 2015).
Acknowledgments
We thank Marco Pignatari and Carolyn Doherty for discussion and suggestions and JINA for providing the online reaclib database. M.L. is a Momentum Project leader of the Hungarian Academy of Sciences. A.I.K. is an ARC Future Fellow (FT10100475). H.V.W. and K.D.S. acknowledge support of the KULeuven fund GOA/13/012. This research was supported under the Australian Research Councils Discovery Projects funding scheme (project numbers DP1095368 and DP120101815) and by the computational resources provided by the Monash e-Research Centre via the Australian Research Councils Future Fellowship funding scheme (FT100100305) and in part by the Australian Government through the National Computational Infrastructure under the National Computational Merit Allocation Scheme (projects g61 and ew6).
References
- Arlandini, C., Käppeler, F., Wisshak, K., et al. 1999, ApJ, 525, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bao, Z. Y., Beer, H., Käppeler, F., et al. 2000, Atomic Data and Nuclear Data Tables, 76, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Bisterzo, S., Gallino, R., Straniero, O., Cristallo, S., & Käppeler, F. 2011, MNRAS, 418, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Bisterzo, S., Gallino, R., Straniero, O., Cristallo, S., & Käppeler, F. 2012, MNRAS, 422, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Bisterzo, S., Gallino, R., Käppeler, F., et al. 2015, MNRAS, 449, 506 [NASA ADS] [CrossRef] [Google Scholar]
- Busso, M., Gallino, R., & Wasserburg, G. J. 1999, ARA&A, 37, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Busso, M., Gallino, R., Lambert, D. L., Travaglio, C., & Smith, V. V. 2001, ApJ, 557, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell, S. W., & Lattanzio, J. C. 2008, A&A, 490, 769 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cannon, R. C. 1993, MNRAS, 263, 817 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, J. J., & Rose, W. K. 1977, ApJ, 212, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Piersanti, L., Straniero, O., et al. 2009, PASA, 26, 139 [NASA ADS] [CrossRef] [Google Scholar]
- De Smedt, K., Van Winckel, H., Karakas, A. I., et al. 2012, A&A, 541, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Smedt, K., Van Winckel, H., Kamath, D., et al. 2014, A&A, 563, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frost, C. A., & Lattanzio, J. C. 1996, ApJ, 473, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Fujimoto, M. Y., Iben, I. J., & Hollowell, D. 1990, ApJ, 349, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F. 2000, A&A, 360, 952 [NASA ADS] [Google Scholar]
- Herwig, F. 2005, ARA&A, 43, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F., Pignatari, M., Woodward, P. R., et al. 2011, ApJ, 727, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F., Woodward, P. R., Lin, P.-H., Knox, M., & Fryer, C. 2014, ApJ, 792, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Kamath, D., Karakas, A. I., & Wood, P. R. 2012, ApJ, 746, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Kamath, D., Wood, P., & van Winckel, H. 2015, MNRAS, 454, 1468 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A. I., García-Hernández, D. A., & Lugaro, M. 2012, ApJ, 751, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Lederer, M. T., & Aringer, B. 2009, A&A, 494, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lugaro, M., Karakas, A. I., Stancliffe, R. J., & Rijs, C. 2012, ApJ, 747, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Miller Bertolami, M. M., Althaus, L. G., Serenelli, A. M., & Panei, J. A. 2006, A&A, 449, 313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mishenina, T., Pignatari, M., Carraro, G., et al. 2015, MNRAS, 446, 3651 [NASA ADS] [CrossRef] [Google Scholar]
- Mowlavi, N. 1999, A&A, 344, 617 [NASA ADS] [Google Scholar]
- Piersanti, L., Cristallo, S., & Straniero, O. 2013, ApJ, 774, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Reimers, D. 1975, Circumstellar envelopes and mass loss of red giant stars (New York: Springer-Verlag), 229 [Google Scholar]
- Reyniers, M., & Van Winckel, H. 2003, A&A, 408, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reyniers, M., Van Winckel, H., Gallino, R., & Straniero, O. 2004, A&A, 417, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stancliffe, R. J., Dearborn, D. S. P., Lattanzio, J. C., Heap, S. A., & Campbell, S. W. 2011, ApJ, 742, 121 [NASA ADS] [CrossRef] [Google Scholar]
- van Aarle, E., Van Winckel, H., De Smedt, K., Kamath, D., & Wood, P. R. 2013, A&A, 554, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Raai, M. A., Lugaro, M., Karakas, A. I., García-Hernández, D. A., & Yong, D. 2012, A&A, 540, A44 [Google Scholar]
- Van Winckel, H., & Reyniers, M. 2000, A&A, 354, 135 [NASA ADS] [Google Scholar]
- Vassiliadis, E., & Wood, P. R. 1993, ApJ, 413, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Woodward, P. R., Herwig, F., & Lin, P.-H. 2015, ApJ, 798, 49 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Hertzsprung-Russell diagram showing the evolution of our 1.3 M⊙, [Fe/H] = −1.3 model from the start of the main sequence to the white dwarf cooling track. The locations of the four post-AGB stars are represented by the red dots with error bars. The location of the third last thermal pulse (TP13) is also indicated. (The colour version of this figure is available in the online journal.) |
| In the text | |
 |
Fig. 2 Proton abundance distribution artificially inserted during the post-processing in our models to simulate the formation of a 13C pocket after the 12th TP (left panel) and a PIE event during TP13 (right panel). Left panel: the thin line represents the standard exponentially decreasing proton distribution (pocket_case1) and the thick line the case where the proton abundance Yp is set to constantly equal 1.05 × 10-4 (pocket_case4). The dotted line represents the depth reached by the TDU. Right panel: the thin and thick lines represent two different proton distributions with a similar total amount of protons ingested: PIE_case1 (thin line) and PIE_case2 (thick line). The dotted line represents the maximum extension of the intershell convective region associated with TP13. The steep proton profile left over by the H-burning shell is also shown in the plot just above 0.638 M⊙. |
| In the text | |
 |
Fig. 3 [X/Fe] ratios as a function of the atomic number Z predicted at the stellar surface by the models where one 13C pocket is introduced at the end of the TDU episode after the 12th TP as compared to the observations of each of the four post-AGB stars indicated in the panels. We normalise both model predictions and observations to meteoritic rather than photospheric solar abundances for the elements heavier than Fe (Asplund et al. 2009). Notably, this modifies the observed [Pb/Fe] upper limits reported by De Smedt et al. (2014) by −0.3 dex. The black line represents pocket_case1, which produces a similar pattern as that presented by De Smedt et al. (2014) with a high Pb abundance. Pocket_case2 is shown as a black dashed line. The coloured lines represent pocket_case3 (red) and pocket_case4 (blue). (The colour version of this figure is available in the online journal.) |
| In the text | |
 |
Fig. 4 Same as Fig. 3, but for the PIE models. The black line represents PIE_case1 and the two coloured lines represent PIE_case2 (red) and PIE_case3 (blue). (The colour version of this figure is available in the online journal.) |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


