| Issue |
A&A
Volume 583, November 2015
Rosetta mission results pre-perihelion
|
|
|---|---|---|
| Article Number | A6 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201526303 | |
| Published online | 30 October 2015 | |
First observations of H2O and CO2 vapor in comet 67P/Churyumov-Gerasimenko made by VIRTIS onboard Rosetta
1
LESIA, Observatoire de Paris, LESIA/CNRS, UPMC, Université
Paris-Diderot, 92195
Meudon, France
e-mail: dominique.bockelee@obspm.fr
2
INAF–IAPS, Istituto di Astrofisica e Planetologia Spaziali, via
del fosso del Cavaliere 100, 00133
Rome,
Italy
3
Space Physics Research Laboratory, University of
Michigan, Ann Arbor,
MI
48109,
USA
4
Institute for Planetary Research, Deutsches Zentrum für Luft- und
Raumfahrt (DLR), 12489
Berlin,
Germany
5
Université Grenoble Alpes, CNRS, Institut de Planétologie et
d’Astrophysique de Grenoble, 38026
Grenoble,
France
6
Department of Physics, Oxford University,
Oxford
OX1 3PU,
UK
7
Lunar Planetary Laboratory, University of Arizona,
Tucson, A2 85721-0092,
USA
8
INAF, Osservatorio Astrofisico di Arcetri,
Largo E. Fermi 5, 50125
Firenze,
Italy
9
National Central University, 320
Taipei,
Taiwan
10
Space Research Centre, Polish Academy of Sciences,
Bartycka 18a, 00-716
Warsaw,
Poland
Received: 13 April 2015
Accepted: 23 July 2015
Context. Outgassing from cometary nuclei involves complex surface and subsurface processes that need to be understood to investigate the composition of cometary ices from coma observations.
Aims. We investigate the production of water, carbon dioxide, and carbon monoxide from the nucleus of comet 67P/Churyumov-Gerasimenko (67P). These species have different volatility and are key species of cometary ices.
Methods. Using the high spectral-resolution channel of the Visible InfraRed Thermal Imaging Spectrometer (VIRTIS-H), we observed the ν3 vibrational bands of H2O and CO2 at 2.67 and 4.27 μm, respectively, from 24 November 2014 to 24 January 2015, when comet 67P was between 2.91 and 2.47 AU from the Sun. Observations were undertaken in limb-viewing geometry at distances from the surface of 0 to 1.5 km and with various line-of-sight (LOS) orientations in the body-fixed frame. A geometry tool was used to characterize the position of the LOS with respect to geomorphologic regions and the illumination properties of these regions.
Results. The water production of 67P did not increase much from 2.9 to 2.5 AU. High water column densities are observed for LOS above the neck regions, suggesting they are the most productive in water vapor. While water production is weak in regions with low solar illumination, CO2 is outgassing from both illuminated and non-illuminated regions, which indicates that CO2 sublimates at a depth that is below the diurnal skin depth. The CO2/H2O column density ratio varies from 2 to 60%. For regions that are in sunlight, mean values between 2 and 7% are measured. The lower bound value is likely representative of the CO2/H2O production rate ratio from the neck regions. For carbon monoxide, we derive column density ratios CO/H2O < 1.9% and CO/CO2< 80%. An illumination-driven model, with a uniformly active surface releasing water at a mean rate of 8 × 1025 s-1, provides an overall agreement to VIRTIS-H data, although some mismatches show local surface inhomogeneities in water production. Rotational temperatures of 90–100 K are derived from H2O and CO2 averaged spectra.
Key words: comets: general / comets: individual: 67P/Churyumov-Gerasimenko / infrared: planetary systems
© ESO, 2015
1. Introduction
Comets are among the most pristine bodies of the solar system and, as such, are expected to provide clues to the chemical and physical properties of the protosolar disk, 4.6 Gyr ago. More than two dozen molecular species have now been identified in cometary atmospheres, pointing to an interstellar-like chemistry (Bockelée-Morvan et al. 2000, 2004). However, questions arise as to the extent to which relative abundances measured in cometary atmospheres can be used to constrain chemical models of star-forming regions and protoplanetary disks, since they may not be representative of the nucleus’ initial composition. Outgassing from cometary nuclei involves complex surface and subsurface processes that depend on the physico-chemical properties of the cometary material and ice structure, as well as on current and past illumination conditions (Huebner et al. 2006; De Sanctis et al. 2010; Marboeuf & Schmitt 2014). In addition, compositional inhomogeneities and sublimation from icy grains may affect our understanding of coma composition.
The study of the development of cometary activity, with the goal of relating coma and nucleus chemical properties, is one of the main objectives of the Rosetta mission (Schulz 2012). Rosetta is a European Space Agency mission that encountered comet 67P/Churyumov-Gerasimenko (hereafter 67P) in August 2014 at rh = 3.5 AU from the Sun, and entered a 30 km bound orbit around the comet on 9 September 2014. It will accompany comet 67P on its journey toward perihelion (13 August 2015, q = 1.24 AU), with the nominal mission being completed at the end of 2015.
The Rosetta spacecraft (S/C) is carrying a suite of eleven instruments, among which is the Visible InfraRed Thermal Imaging Spectrometer (Coradini et al. 2007). VIRTIS is composed of two channels: VIRTIS-M, a spectro-imager operating both in the visible (0.25–1 μm) and infrared (1–5 μm) ranges at low spectral resolution (λ/Δλ = 70−380), and VIRTIS-H, a single-aperture infrared spectrometer (1.9–5.0 μm) with higher spectral resolution capabilities (λ/Δλ = 1300−3000).
The 2–5 μm range is rich in signatures of cometary molecules. The first cometary spectrum covering this range was acquired for comet 1P/Halley with the IKS instrument onboard the VEGA-1 S/C (Combes et al. 1988). More recently, 2−5 μm spectra have been acquired with the Deep Impact and EPOXI missions to 9P/Tempel 1 and 103P/Hartley 2 (A’Hearn et al. 2005, 2011; Feaga et al. 2007), and from the Infrared Space Observatory (ISO) and the AKARI space telescope (Crovisier et al. 1997; Ootsubo et al. 2012). Infrared surveys of cometary molecules in atmospheric windows are also ongoing from ground-based facilities, offering spectral resolutions >20 000 (e.g., Dello Russo et al. 2006).
The ν3 vibrational bands of water and carbon dioxide are the strongest vibrational bands that have been observed in cometary infrared spectra. Therefore, these two molecules were anticipated to be the first to be detected by VIRTIS. In this paper we focus on VIRTIS-H observations of H2O and CO2 acquired from 24 November 2014 to 24 January 2015. The observations are described in Sect. 2. In Sect. 3, H2O and CO2 column density and rotational temperature measurements are presented. Section 4 presents an upper limit on CO production. Observed H2O and CO2 column density variations with line-of-sight (LOS) orientation in the nucleus body frame and solar illumination are discussed in Sect. 5. Measurements are then compared to gas dynamics calculations of the inner coma of 67P (Sect. 6). A conclusion follows in Sect. 7.
2. Observations
2.1. VIRTIS-H
VIRTIS-H is a cross-dispersor spectrometer, working in the range 2−5 μm. Its design consists of a telescope, an entrance slit, followed by a collimator, and a prism separating eight orders of a grating (Drossart et al. 2000; Coradini et al. 2007). The spectral resolving power λ/Δλ varies between 1300 and 3000 within each order, where Δλ is the convolution of the channel spacing and grating resolution. The spectra are sampled on 3456 spectral elements, that is, 432 in each grating order. The spectral range covered by each order is given in Table 1.
As most remote-sensing Rosetta instruments, the LOS of VIRTIS is along the Z-axis of the S/C. The instantaneous field of view of the VIRTIS-H instrument is 0.58 × 1.74 mrad2 (the larger dimension being along the Y axis), which corresponds to 17 × 52 m on the comet for a S/C distance to the target of 30 km. The field of view (FOV) corresponds to a three-pixel-wide area on the focal plane array; in nominal mode, the summation of the signals received on each pixel is performed onboard.
The VIRTIS-H data are processed using the so-called CALIBROS pipeline (version 1.1). This pipeline subtracts dark images (acquired thanks to a shutter), corrects the instrumental and detector effects (odd/even pixels effects, despiking), calibrates the absolute flux of the spectra in radiance (W/m2/sr/μm), and saves the data in the format of the Planetary Data System.
The transfer function is derived from a dual approach using both on-ground and in-flight data. In a first step, the transfer function was derived from laboratory calibration measurements. Because spectral registration was found to be significantly modified after launch, consistency adjustments were made using observations of asteroid (21) Lutetia obtained during the Rosetta CRUISE phase in July 2010 (Coradini et al. 2011), yielding the current transfer function. This includes precise determination of the map of illuminated pixels, correction for stray light, and accurate dark-current interpolation in the flight configuration.
Throughout the paper, errors correspond to statistical noise. Biases remain in the calibration scheme, which causes systematic deviations that can be larger than the one-sigma statistical noise.
Hereafter, VIRTIS-H calibrated data are referred as to cubes because they are three-dimensional: intensity versus wavelength and acquisition number.
VIRTIS-H grating orders.
Log of the observations.
2.2. Data set
Rosetta observations of comet 67P are grouped in medium term planning periods (MTP), typically lasting one month, and short term planning periods (STP), lasting one week. The first dedicated coma observations of 67P with VIRTIS were obtained during MTP005 (28 July 2014, at 3.7 AU from the Sun). Observations carried out from August to September do not show any detection of molecular bands. Only marginal detections of H2O and CO2 were obtained in October 2014 (MTP008) before Philae-landing operations (MTP009). Therefore, we focus on coma observations undertaken between 24 November 2014 and 24 January 2015 (MTP010 to MTP012). Table 2 lists the VIRTIS-H data cubes analyzed in this paper, the observation dates, and geometric parameters. During this time frame, Rosetta was on a terminator orbit around the comet (phase angle in the range 80−100°) at distances between 18 and 30 km from the comet center. The heliocentric distance range was rh = 2.47−2.91 AU. The VIRTIS-M spectro-imaging channel was operated in parallel to VIRTIS-H for coma mapping (Capaccioni et al. 2015a). The analysis of the VIRTIS-M data will be the topic of a forthcoming paper.
VIRTIS-H observations were acquired with an acquisition time of 6 s, both on the source and on the dark background. A dark rate of 4 (i.e., one dark image every four acquisitions on-source) was determined to be optimum for signal-to-noise ratio (S/N) considerations. Some data were acquired with dark rates of 2, 8, and 16 to find this optimum. Because of data volume restrictions, on-board frame summing was occasionally performed.
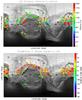 |
Fig. 1 Geometrical parameters of the VIRTIS-H LOS (LOS) from MTP010 to MTP012. A) Minimum distance of the LOS to the nucleus surface (in meters with the color scale given to the right); B) solar incidence angle (in degrees, with the color scale given to the right) of the closest point to the LOS. Each cross corresponds to a single 6 s acquisition. Only one in every four acquisitions is considered. The gray background represents the effective latitude based on the SHAP5 model composed of 300 000 facets to show the location of topographic features. |
2.3. Pointing geometry and limb distance
Requested limb distances (defined as the closest distance from the LOS to the nucleus) were typically 0.5–1 km. Pointing requests for these coma observations were designed so that the FOV would not intercept the nucleus, and therefore took into account expected uncertainties in the S/C pointing provided by the ESA Rosetta Science Ground Segment.
We only consider here observations with the FOV staring at a fixed position in inertial frame (in general limb offset in the solar direction) during cube acquisition. A few cubes during MTP011 were acquired with more complex pointing strategies and are not analyzed here. Neither did we consider cubes with the LOS in the nucleus shade, since low molecular signals are expected because of ineffective radiative IR pumping. Cube 00377746075 (STP035) is partly affected by shading (at the 20% level in number of acquisitions), however.
Because of S/C pointing errors, the LOS sometimes intercepted the nucleus during the observations. Table 2 provides for each cube the total number of acquisitions nacq, and the number of acquisitions ncoma not intercepting the nucleus. Throughout this paper we consider only acquisitions not intercepting the nucleus. The overall observing time (Δt) and the cumulated exposure time on the coma (Int.) are also provided in Table 2 for each data cube. Δt is two to three hours on average, that is less than one fourth of the nucleus rotation period of 12.40 h (Sierks et al. 2015).
The actual limb distance and orientation of the LOS in the comet inertial frame were determined using a digital shape model of the surface combined with S/C attitude data, and S/C and 67P trajectories. This was performed using the SPICE library (Acton 1996)1. The shape model was produced by the Optical, Spectroscopic, and Infrared Remote Imaging System (OSIRIS) imaging team for use within the Rosetta project (Sierks et al. 2015). The SHAP5 version (cg-spc-shap5-v0.1-esoc.bds) was used for our purpose. The shape model was also used to compute the solar illumination of the nucleus regions close to the LOS. This LOS characterization was performed using smoothed versions of SHAP5 (~6290 and 31 456 triangular facets instead of several millions), since a detailed description of the nucleus local topography would provide unnecessary precision.
 |
Fig. 2 LOS statistics from MTP010 to MTP012. A) Minimum distance of the LOS to the nucleus (in meter, bin size is 100 m); B) corresponding solar incidence angle (bin size is 10°). Only one in every four acquisitions have been considered. |
During data acquisition, the LOS moved with respect to the body-fixed frame, mainly because of nucleus rotation. Figure 1 displays the location of the closest point to the LOS in the (long, lat) 67P coordinates for single 6 s acquisitions and the local solar incidence angle at this point at the time of the observations. The minimum distance of the LOS to the surface varied from 10 m to ~1500 m (Fig. 2A). The distribution of the LOS minimum distances presents two maxima, resulting from the complex shape of the 67P nucleus (Fig. 2A). The solar incidence angle ranged from 0° to 180°, with most values within 0–50° since observations focused on the summer (northern) hemisphere in day time (Figs. 1 and 2B).
The nucleus of 67P has two lobes, referred to as the head and body, which are linked by the neck, in reference to the duck-like shape of the nucleus (Sierks et al. 2015). The central longitudes of the head and body are approximately 340° and 135°, respectively, in the SHAP5 coordinate system (Fig. 1). The orientations of the LOS in the body-fixed frame are discussed in detail in Sect. 5.
3. H2O and CO2 spectra, column densities, and rotational temperatures
The ν3 bands of H2O and CO2 at 2.67 and 4.27 μm, respectively, were the first vibrational bands expected to be detected by VIRTIS. H2O is the main molecule in cometary atmospheres and was first detected in 67P at 3.92 AU from the Sun (6 June 2014) by the Microwave Instrument of the Rosetta Orbiter (MIRO) with a total production rate estimated to be 1 × 1025 s-1 (Gulkis et al. 2014, 2015). CO2 was detected by the Rosetta Orbiter Spectrometer for Ion and Neutral Analysis (ROSINA) instrument onboard Rosetta (Hässig et al. 2015). Although CO2 is less abundant than H2O, the CO2 band is relatively easier to detect than the H2O band because its band strength is ten times higher. We considered only spectra acquired in orders 0 and 4 of VIRTIS-H (Table 1) for the analysis of the CO2 and H2O bands, respectively, as these bands are only partially covered in adjacent orders (order 1 for CO2 and orders 3 and 5 for H2O).
H2O and CO2 band intensities, column densities, and column density ratio.
 |
Fig. 3 VIRTIS-H average spectra of H2O and CO2 bands observed from 10 to 17 October 2014 (rh ~ 3.2 AU), in spectral orders 4 and 0, respectively. The continuum has been subtracted. Superimposed we show a model spectrum of the ro-vibrational structure of H2O (ν1 and ν3) and CO2ν3 bands. Derived CO2 and H2O column densities are ~1 × 1018 and 2 × 1019 m-2, respectively. |
The ν3 bands of both H2O and CO2 were first detected by VIRTIS-H at the beginning of October by averaging several data cubes2 (Fig. 3). During the time of December and January, both bands were detected with S/N on the band area reaching 40 on individual data cubes (Table 3). Figure 4 shows an average spectrum of H2O that was obtained by combining 35 data cubes acquired from 4 December 2014 to 24 January 2015. For this figure, we selected the data cubes with a S/N on the CO2 band area higher than 10. The S/N in the H2O average spectrum shown in Fig. 4 is 135. The CO2 spectrum obtained averaging the same 35 cubes is shown in Fig. 5 and has a S/N of 123.
 |
Fig. 4 VIRTIS-H spectrum of the 2.67 μm band of water. Average of 35 data cubes with most significant water and CO2 detections (those with S/N> 10). The continuum has been subtracted. Superimposed we show a model spectrum of H2O band (ν1 and ν3) for a rotational temperature Trot = 102 K (see text). The effective spectral resolution, derived from fitting, is Reff = 800. |
 |
Fig. 5 VIRTIS-H spectrum of CO2 band at 4.27 μm. Average of 35 data cubes with most significant water and CO2 detections (S/N> 10). The continuum has been subtracted. Superimposed we show a model spectrum of the ν3 CO2 band for Trot = 90 K. The effective spectral resolution, derived from fitting, is Reff = 869. |
At the spectral resolution of VIRTIS-H, the ro-vibrational structure of the H2O ν3 band is partly resolved (Figs. 3, 4), which provides information on the rotational temperature of water (Sect. 3.2). We note that the ten times weaker ν1 band partly lies in the spectral range of ν3 (Bockelée-Morvan & Crovisier 1989; Villanueva et al. 2012) and is considered in the synthetic H2O spectra shown in Figs. 3 and 4.
The P, R structure of the CO2ν3 band is resolved, but not the individual P and R ro-vibrational lines (Fig. 5).
The H2O and CO2 band intensities are given in Table 3. For H2O, they were derived by summing the radiances measured in wavelength intervals within 2.60–2.73 μm where significant water emission was expected. For CO2, the summation is made over 4.23–4.285 μm. A fourth-order polynomial baseline was subtracted from the spectra before the summation.
3.1. H2O and CO2 column densities
The main excitation mechanism for the H2O and CO2ν3 bands is expected to be fluorescence excited by solar infrared radiation (Crovisier 1987; Bockelée-Morvan 1987; Bockelée-Morvan et al. 2004). The determination of the H2O and CO2 column densities from the measured band intensities (Table 3) is then straightforward, providing optical depth effects are insignificant. Debout et al. (2015) performed radiative transfer modeling of the H2O and CO2ν3 bands for various production rates and heliocentric distances, from which it can be concluded that the band intensities measured by VIRTIS correspond to optically thin conditions.
The column density ⟨ N
⟩ (m-2) is related to the band intensity I (in W m-2 sr-1) through
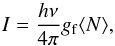 (1)where ν is the central frequency
of the band, and gf is the band emission rate (or
g-factor).
(1)where ν is the central frequency
of the band, and gf is the band emission rate (or
g-factor).
We assumed a g-factor gf = 3.349 × 10-4 s-1 and gf = 3.33 × 10-5 s-1 (at rh = 1 AU) for the H2O ν3 and ν1 bands, respectively (Villanueva et al. 2012). Ro-vibrational lines of the ν2+ν3–ν2 H2O band are present in the 2.6−2.73 μm range where the band intensity was calculated, but they do not contribute significantly to the observed emission (Bockelée-Morvan & Crovisier 1989; Villanueva et al. 2012). The 2.6–2.73 μm range covers 77% of the sum of the ν1 and ν3 band intensities at a rotational temperature Trot = 90 K, which approximates the excitation state of water observed by VIRTIS-H (Sect. 3.2). This factor was taken into account for the determination of the water column densities.
Turning to CO2, we used a g-factor at rh = 1 AU of 2.72 × 10-3 s-1 (Debout et al. 2015). The 4.23−4.285 μm range used for band intensity measurements covers 88.4% of the total ν3 band emission for Trot = 90 K, and this factor was applied to the measured intensity for the determination of the CO2 column density.
The derived column densities are given in Table 3
and are plotted as a function of time in Fig. 6
(left). A power-law fit to the values (not considering upper limits) leads to a
heliocentric variation in 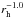 for water and in
for water and in
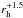 for CO2, suggesting a small increase of
67P water outgassing between 2.88 and 2.47 AU (15% on average), whereas the
CO2 production
slightly decreases. Admittedly, this study is biased by several effects (e.g., various
limb distances, LOS geometry, solar illumination conditions of the nucleus, uneven
distribution of data throughout the period), but it is worth recalling that Rosetta
remained on a terminator orbit during this time. Power-law fits to smaller data sets
(selecting LOS above regions of similar illumination conditions) lead to similar
conclusion, that is, that the activity of 67P did not increase significantly from 2.9 to
2.5 AU.
for CO2, suggesting a small increase of
67P water outgassing between 2.88 and 2.47 AU (15% on average), whereas the
CO2 production
slightly decreases. Admittedly, this study is biased by several effects (e.g., various
limb distances, LOS geometry, solar illumination conditions of the nucleus, uneven
distribution of data throughout the period), but it is worth recalling that Rosetta
remained on a terminator orbit during this time. Power-law fits to smaller data sets
(selecting LOS above regions of similar illumination conditions) lead to similar
conclusion, that is, that the activity of 67P did not increase significantly from 2.9 to
2.5 AU.
 |
Fig. 6 H2O and CO2 column densities A), and column density ratio ⟨ N(CO2)⟩/⟨ N(H2O)⟩B), as a function of time. The STP periods are indicated at the top, inside circles. |
3.2. Band fitting and rotational temperature
Model fitting of the H2O and CO2 bands was performed through χ2 minimization of fluorescence excitation models (Debout et al. 2015), with the rotational temperature Trot, the column density ⟨ N ⟩, and the effective spectral resolution Reff as free parameters.
For H2O, both the ν1 and ν3 bands were considered. These bands are mainly excited through direct infrared solar pumping from the ground vibrational state. However, for the ν1 band, spontaneous cascades from higher-energy excited vibrational states (mainly the combination band ν1+ν3) are significant, increasing by a factor of 2.0 the ν1g-factor (for emission) with respect to the resonant-fluorescence value (Bockelée-Morvan & Crovisier 1989; Villanueva et al. 2012). The fluorescence model used for fitting the VIRTIS-H water band does not consider combination bands and subsequent spontaneous decays, but assumes a relative ν1/ν3 emission rate of 0.10 given by full non-resonance fluorescence models (Villanueva et al. 2012). Since the contribution of the ν1 band to the fitted spectrum is weak (~3% times the intensity of ν3), this oversimplification should not affect the results significantly. Resonant fluorescence is assumed for CO2 (Debout et al. 2015). H2O and CO2ν3 ro-vibrational line strengths and frequencies were taken from the HITRAN data base (Rothman et al. 2009).
We assumed an ortho-to-para ratio (OPR) for water of 3. The data set acquired until the end of January 2015 does not provide a precise measurement of the OPR. OPRs measured so far in comets span between 2 and 3 (Bonev et al. 2007).
Synthetic VIRTIS-H spectra were obtained by convolving modeled ro-vibrational radiances at infinite resolution with a Gaussian profile of width Δλeff as a free parameter. The contribution of this convolved spectrum to each spectral channel was then computed taking into account their spectral response (FWHM of ~80% the channel spacing, e.g., FWHM ≃ 1.1 nm at 2.67 μm, Drossart et al. 2000). The derived effective spectral resolution Reff = λ/ Δλeff is ~900, that is, lower than the nominal spectral resolution. This is due to undersampling and some spectral broadening introduced by the current calibration scheme to correct for odd/even effects.
From the water and CO2 spectra shown in Figs. 4, 5 we derive Trot = 102 ± 4 K and 90 ± 3 K, respectively, pertaining to a mean distance to the surface of 800 m (additional errors on Trot can be caused by non-optimized baseline retrieval). Misfits for some water ro-vibrational lines show that the population distribution in the ground vibrational state cannot be described by a Boltzmann distribution, the reason being that the considered spectrum is an average of many spectra, and that even a single LOS is sampling molecules in various excitation states (because of variations of the kinetic temperature with position in the coma and expected non-LTE conditions in the more rarefied regions, e.g., Davidsson & Gutiérrez 2006). A feature longward of 2.79 μm is not reproduced by the model and might stem from the water ν1+ν3-ν1 hot band. There is also some unexplained discrepancy between the observed and modeled CO2 band shape (Fig. 5).
The moderate S/N makes it difficult to perform Trot retrievals from individual data cubes. However, from the cube 00380112315 (STP039), for which the S/N on the total H2O band area is 40 (Table 3), we derive Trot = 96 ± 4 K. During the acquisition of these data, the LOS remained above the neck region (Sect. 7), with a mean distance to the center of 67P of D = 2.73 km (as defined in Sect. 5.1), that is, at 730 m on average from the surface.
The measured rotational temperatures are indicative of the temperature of the gas sampled by the LOS. We calculated the population distribution of the H2O ground vibrational state taking into account both collisions and radiative decay (Zakharov et al. 2007), which show that the lowest ground-state rotational levels (up to J = 5) remain thermalized at the temperature of the gas for distances that exceed a few kilometers from the nucleus surface. For these calculations, we assumed isotropic water production rate at a rate of 1026 s-1 (Sect. 6). Moreover, the similarity of the rotational temperatures of H2O and CO2 is consistent with near-LTE conditions for both species. In a more rarefied coma, a higher Trot would have been measured for CO2 since rotational radiative decay is ineffective for this species.
The measured rotational temperatures are close to expected values for 67P at 2.5 AU from the Sun (Davidsson et al. 2010). In the Monte Carlo simulations presented in Sect. 6, which overall reproduce the measured column densities well, the gas temperatures on the day side are typically about 100 K at 500 m above the surface and about 75 K at 1500 m above the surface, with higher values above the neck regions. This is overall consistent with VIRTIS measurements, keeping in mind that the FOV of VIRTIS probes molecules at various distances from the nucleus.
4. CO v(1–0) band observations
Carbon monoxide has been identified as a significant molecule within the coma of 67P. A CO/CO2 ratio in number at the Rosetta S/C in the range ~0.25–5 has been measured in August–October 2014 (Hässig et al. 2015; Leroy et al. 2015). However, CO is more difficult to detect than CO2 with VIRTIS because its band strength is one order of magnitude lower than the CO2 band.
The v(1–0) band of CO at 4.67 μm lies in the spectral range of grating order 0 (Table 1). Using the HITRAN data base (Rothman et al. 2009) and the solar flux given by Labs & Neckel (1968), we derived a band g-factor gf = 2.51 × 10-4 s-1 at 1 AU from the Sun for a rotational temperature of 90 K (Debout et al. 2015). The VIRTIS-H spectrum obtained by averaging the 35 cubes where CO2 is detected with a S/N> 10 does not show significant CO emission. From this spectrum, we derive upper limits of 80% (3σ) for the ⟨ NCO ⟩/⟨ NCO2 ⟩ ratio, and of 1.9% (3σ) for the ⟨ NCO ⟩/⟨ NH2O ⟩ ratio, while the ⟨ NCO2 ⟩/⟨ NH2O ⟩ ratio is 2.5%.
Stastistics of the nucleus regions sampled by the LOS.
Large variations of the CO/CO2 number density ratio were observed by ROSINA in August-September 2014, with the highest values (up to ~5) observed in August, when the S/C Z axis was toward the northern (summer) hemisphere (Hässig et al. 2015), that is, at the latitudes sampled by VIRTIS. For October 2014, Leroy et al. (2015) reported CO/CO2 ratios of ~0.25 above the southern (winter) hemisphere, and of ~1 above the illuminated northern hemisphere. Therefore, the VIRTIS CO upper limit is altogether consistent with the ROSINA results.
5. H2O and CO2 production versus morphological regions and illumination
The large scatter in column densities and CO2/H2O column density ratio seen in Fig. 6 is related to the various LOS configurations in the nucleus-fixed frame, together with different illumination conditions of the nucleus of 67P. We characterized the mean LOS for each cube, using the morphological regions defined by Thomas et al. (2015). The nucleus of 67P nucleus is highly heterogeneous, and the northern hemisphere can be divided into nineteen geographical regions with specific morphological characteristics (Thomas et al. 2015). The regions are listed in Table 4 and are labeled from 1 to 22. The regions at the bottom of the body are Imhotep (13), Khepry (14), Aten (6), and part of Ash (5), with Ash, Aker (1), Anubis (2), Apis (4), Atum (8), Babi (9), and Seth (19) located in more central parts. The regions at the top of the head are Hatmehit (12), Maftet (16), Nut (17), and parts of Bastet (10) and Ma’at (15), with Ma’at, Hathor (7), Anuket (3), and Serqet (18) in central parts. The region in the neck is named Hapi (11). Un-named dark regions near the terminator are labeled 20 to 22. The location of the regions in 2D and 3D nucleus representations are shown in Fig. 7.
 |
Fig. 7 Geomorphological regions of 67P in 2D and 3D visualization (after Thomas et al. 2015). |
For each acquisition in the cubes, we computed the solid angle of each region, as seen from the closest point of the LOS to the comet center. This was done by determining the facets in the shape model belonging to each region and their solid angle. We then averaged the results obtained for all cube acquisitions to obtain the mean solid angle Ωm for the cube. Regions viewed with the largest solid angle (P1) from this point or in second rank (P2) are indicated in Table 3.
Table 4 lists the number of cubes where they are ranked P1 or P2 for each region. The nucleus obviously was not evenly covered (see also Fig.1), with only 14 regions appearing in P1 or P2. Some regions, such as Hapi, are often far in the classification because of their small surface area.
The mean illumination of the nucleus, as seen from this LOS location, is computed by weighting the illumination of each facet by their solid angle, with the illumination defined by the cosine of the solar incidence angle at the facets (set to 0 for solar incidence angles i> 90°). The arc cosine of this mean illumination defines the mean solar incidence angle at the nucleus (referred to below as solar incidence angle).
5.1. CO2 and H2O columns
 |
Fig. 8 Column densities as a function of mean nucleus solar insolation for regions populating the LOS. A) H2O, B) CO2. The color coding is that of Fig. 7 and corresponds to regions in P1. |
Column densities as a function of mean nucleus illumination as seen from the LOS are shown in Fig. 8. The highest values for H2O (those higher than 4 × 1019 m-2, so two to four times the average value of the remaining sample) are for LOS above Seth (red), Anuket (pale pink), and Hapi (light green), which means that they sample coma regions above the neck where strong dust activity has been observed with the OSIRIS cameras (Sierks et al. 2015).
In Fig. 9, we applied a factor to column densities to correct for both the distance of the LOS to the nucleus, and the nucleus cross-section S viewed from the closest LOS point to nucleus center. Here, we assumed that the column density scales as S/D, where D is the distance to the center of a sphere of radius rn = 2 km (the equivalent radius of the nucleus of 67P), sustaining the solid angle Ωm. This scaling is expected in the frame of the Haser model and assumes that the gas velocity is the same everywhere. The nucleus cross-section is given by S = Ωm × D2. The corrected water column density still shows excess above Seth, Anuket, and Hapi (Fig. 9A). This suggests that these regions are the most productive in water, in line with conclusions obtained from data acquired with MIRO (Biver et al. 2015; Lee et al. 2015; Gulkis et al. 2015) and consistent with the dust distribution around the nucleus (Sierks et al. 2015). On the other hand, the LOS above these regions does not exhibit CO2 excess (Fig. 9A). Hence, the lowest CO2/H2O column density ratios are observed for LOS above the neck regions (see Sect. 5.2).
The data set is too limited to investigate variations of gas production with local illumination in detail, except for the LOS above Imhotep and dark (un-named) regions that are observed with a solar incidence angle larger than 60°, on average. We can still report the following:
-
At large incidence angles, a low H2O column density is observed (Fig. 9A). Given the relatively high sublimation temperature of H2O together with the strong diurnal temperature variations of the surface of 67P (Capaccioni et al. 2015b; Tosi et al. 2015), we do not expect significant water outgassing in non-illuminated areas.
-
The corrected CO2 column density does not show significant trend with solar incidence (although a high value for Imhotep is observed, Fig. 9B), suggesting that CO2 is outgassing from both illuminated and non-illuminated areas. This indicates that CO2 sublimates from ice sources inside the nucleus at a depth that is below the diurnal skin depth. CO2 ice sources very close to the surface would imply a dependence of the flux on the illumination condition, as predicted by comet evolution models (de Sanctis et al. 2005; Marboeuf & Schmitt 2014). The diurnal skin depth has been estimated to ~1 cm from MIRO continuum measurements of the subsurface temperature (Schloerb et al. 2015). CO2 might be present beneath as pure ice or trapped in amorphous water ice or clathrate hydrates (de Sanctis et al. 2005; Marboeuf & Schmitt 2014).
The VIRTIS results are consistent with those of ROSINA, which observed distinct diurnal patterns for CO2 and H2O, with enhancements of CO2 when the S/C was in view of the poorly illuminated Imhotep region (Luspay-Kuti et al. 2015). The activity of 67P has some resemblance with that of 9P/Tempel 1. The CO2 and H2O maps of this comet obtained by the Deep Impact spacecraft show uncorrelated asymmetries, with water showing a profound enhancement in the sunward direction and CO2 presenting localized outgassing in less illuminated regions (Feaga et al. 2007).
 |
Fig. 9 Column densities corrected for LOS distance and nucleus cross-section as a function of solar incidence angle (see text). The color coding is that of Fig. 7 and corresponds to regions in P1. |
CO2/H2O column density ratio.
5.2. CO2/H2O column density ratio
Column density ratios as a function of solar incidence angle are displayed in Figs. 10A–F, using cubes for each plot for which a specific region appears in P1 or P2 (namely, Ash, Babi, Imhotep, Seth, Anuket, and Ma’at, which are the six regions that are the most frequently sampled by the data, see Table 4). An increase of the CO2/H2O column density ratio with decreasing illumination is observed for the bottom of the body of 67P (Imhotep and surroundings, Fig. 10C) and to some extent for regions in the central parts (Seth, Anuket and surroundings, Figs. 10D–E). For the LOS above Ma’at (head of 67P) there is a large scatter in the measured column density ratios (Fig. 10F).
Figure 11 shows the ⟨ N(CO2)⟩/⟨ N(H2O)⟩ column density ratio as a function of ⟨ N(H2O)⟩. There is a clear trend for high column density ratios when low H2O column densities are measured, whereas for water column densities higher than 4 × 1019 m-2, the CO2/H2O ratio stabilizes to a mean value of about 2%, with no significant differences observed between regions. This trend is also observed in specific regions such as Seth, Ash, and Ma’at (red, medium, and dark blue circles, respectively, in Fig. 11). Since the LOS above the regions Ash and Ma’at does not show a trend with solar illumination (e.g., Figs. 10A, F), the large scatter in the CO2/H2O column density ratios observed for these LOS possibly results from a significant (and variable) contribution of CO2 molecules outgassed from poorly illuminated regions at mid- or southern latitudes.
 |
Fig. 10 Column density ratio as a function of mean nucleus solar insolation for regions populating the LOS. Limb sounding above Ash A), Babi B), Imhotep C), Seth D), Anuket E), and Ma’at F). The labels given in the plots and titles are those of the regions in P1/P2 (see text). The color coding is that of Fig. 7 and corresponds to regions in P1. |
Table 5 shows the average CO2/H2O column density ratios for each region, obtained using cubes where the regions are in P1 or in P1 plus P2 classification. We only considered data with high solar illumination (i< 50°). Within uncertainties, the two options provide the same results. The column density ratio is typically within 0.02 to 0.05.
An important question is the extent to which the measured CO2/H2O column density ratios are representative of the production rate ratios, under the assumption that CO2 and H2O outflow at the same velocity (this is expected in inner collision-dominated cometary atmospheres). For the LOS probing the highly productive neck regions, the mean CO2/H2O ratio is 0.017 ± 0.004. However, the CO2/H2O production rate ratio from the neck could be slightly below this value since the LOS above the neck regions may also include a small contribution of CO2 molecules outgassed from poorly illuminated regions. For other regions, column density ratios may not directly translate into production rate ratios, since LOS might include molecules outgassed from other regions, especially CO2.
The similarity of the CO2/H2O column density ratio measured on the body (0.03 ± 0.02 for Ash) and the head (0.04 ± 0.02 on Ma’at) at similar latitudes might suggest that these two units of the nucleus are compositionally similar in terms of the CO2/H2O production rate ratio. However, the smaller lobe (head) undergoes daytime surface temperatures higher on average than the larger lobe (body), with the smooth plain Imhotep being even cooler due to the season (grazing sunlight for most of the daytime) (Tosi et al. 2015). Column density ratios may therefore not directly translate into abundance ratios inside the nucleus.
For regions sampled at high solar incidence angle (Imhotep region), the CO2/H2O column density ratio reaches values as high as 60%. These high values are lower limits to the CO2/H2O production rate ratio. Water molecules emitted from illuminated parts of the nucleus (e.g., Hapi) most likely contribute to the measured signal. High CO2/H2O number density ratios (reaching 200%) were also measured locally (30 km from the comet center) by the ROSINA experiment in September 2014, when the S/C pointed vertically toward the poorly illuminated Imhotep region (Hässig et al. 2015).
 |
Fig. 11 CO2/H2O column density ratio as a function of H2O column density. The color coding is that of Fig. 7. |
6. Comparison of water columns with gas-dynamics calculations
An interpretation of the retrieved column densities ⟨ N ⟩ by VIRTIS-H requires the use of a coma model. The relatively low gas production rates at the epoch of the observations imply that properly modeling the physics of the coma of comet 67P necessitates the use of a kinetic approach. The direct simulation Monte Carlo (DSMC) technique is the method of choice to solve the Boltzmann equation in the rarefied atmosphere of comets (Combi 1996).
The adaptive mesh particle simulator (AMPS) code has been extensively applied to the cometary coma (Tenishev et al. 2008, 2011; Combi et al. 2012; Fougere et al. 2013; Bieler et al. 2015) and has recently been extended to 3D with irregular nucleus shapes (Fougere 2014). In the context of this study, we used AMPS to model the H2O coma of comet 67P. Then, we performed calculations of modeled column densities to compare them with the VIRTIS-H measurements.
As described in detail by Tenishev et al. (2008), the simulations used surface boundary conditions derived from the thermophysical model of Davidsson & Gutiérrez (2006). The variation of water flux and sublimation temperature were determined by the local solar illumination taking into account the irregular shape of the nucleus (down-sampled version of SHAP5) and self-shadowing. Such a model driven solely by illumination reproduces the observations from the ROSINA Comet Pressure Sensor (COPS) to a large extent, as shown in Bieler et al. (2015). Hence, this model is a good way to compare the in situ data from ROSINA and the VIRTIS data that were obtained along the LOS.
Twelve different cases were studied, spanning the 12 h rotation period of the comet nucleus using the geometry on 23 August from 12:00 to 23:00 UT (one case every hour). Bieler et al. showed that after accounting for the spacecraft positioning over the next few months, the same model reasonably well reproduces the main aspects of the temporal variations of the ROSINA COPS data through December. The column densities were computed at the starting and ending observation times using the reference case with the closest Sun longitude angle to each VIRTIS-H observation time. As an example, Fig. 12 shows the modeled column densities for observation 00376211338 at its starting time. The VIRTIS-H FOV is shown at the center of VIRTIS-M FOV.
While the COPS data represent the total gas density, the signal is dominated by the most abundant species, water. Hässig et al. (2015) showed that even when the comet was at 3.5 AU, the coma of comet 67P in general mostly consisted of H2O. Hence, we multiplied all model column densities by a factor of 0.8 for comparison with the water column densities retrieved from VIRTIS-H. This is the typical water fraction in most comets (Bockelée-Morvan et al. 2004). This assumption ignores the compositional heterogeneities observed by Hässig et al. (2015), which would require a more advanced multispecies coma model.
The total water production rate in the model varies with time. The gas fluxes are based on the illumination, which varies with the Sun/nucleus geometry. In these simulations, the total water production rate ranges from 6.9 × 1025 to 8.7 × 1025 s-1 during the 12 h nucleus rotation.
 |
Fig. 12 Decimal log of the modeled water column density on 3 December 2014, 07:01:53 UT (starting time of VIRTIS-H cube 00376211338). The large rectangle is the VIRTIS-M FOV and the small square is VIRTIS-H FOV. The scale of the map is 5.7 × 5.7 km2. In the bottom left corner is shown the nucleus with the unilluminated bottom of the body (Imothep and Ash) in the foreground and the illuminated head in the background. The illuminated Seth and Hapi regions lie in between. |
Figure 13 shows the resulting H2O-averaged modeled column densities of the start and stop times compared with the VIRTIS-H column densities. The error bars for the model are derived from the values of the H2O column densities at the start and stop times, the differences of which can be large for the extended observations. The model and the data follow each other with a correlation equal to 0.6. In other words, an illumination-driven model with a uniformly active but highly irregular surface can reproduce both ROSINA-COPS and VIRTIS-H data, showing general agreement between the two instruments regarding both the level and distribution of water vapor in the coma. However, owing to the very large mean free paths for collisions between water molecules in the coma at these low gas production rates and the resulting molecular diffusion close to the nucleus surface and strong kinetic effects, the coma model based on matching the ROSINA-COPS data alone is not sensitive to patchy irregular active regions that are most likely distributed around the surface of the nucleus. In contrast, the VIRTIS-H limb measurements can be made as close as a few tens of meters from the nucleus surface, revealing these isolated activity regions. This effect may explain most of the differences between the model results and the VIRTIS-H data. Interestingly, the largest discrepancies are observed for high column density values, measured for LOS above Seth, Anuket, and Hapi (red, pale pink, and green symbols in Fig. 13B), that is, sampling the water jet above the neck regions. This strengthens the conclusion obtained in Sect. 5: these regions are more productive in water. An extended analysis of data from VIRTIS-H and other remote-sensing instruments will be necessary to obtain the details of these active regions and improve our understanding of the outgassing of comet 67P. The general agreement between DSMC calculations and VIRTIS data suggests a total water production rate of ~8 × 1025 s-1 for the period from November 2014 to January 2015.
 |
Fig. 13 Column densities from the DSMC model compared to VIRTIS-H column densities. A): model results (red) and measurements (black) are plotted as a function of time. B): model as a function of measurements, with the same color coding as in Fig. 7, corresponding to regions in P1. Modeled columns have been multiplied by a factor 0.8 to approximate the column density of H2O. The markers for the model are at the average point between the values found at the start and stop time of a given observation, which themselves give the error bars. The error bars for VIRTIS-H measurements are shown in Fig. 6. |
7. Conclusion
First observations of the near-nucleus coma of comet 67P/Churyumov-Gerasimenko with the VIRTIS instrument onboard Rosetta have provided interesting information on the distribution and levels of production of H2O, CO2, and CO at 2.5−2.9 AU from the Sun inbound.
-
The water production of 67P did not increase much from 2.9 to 2.5 AU.
-
High water column densities are observed for the LOS above neck regions, showing that these regions are the most productive in water vapor.
-
The CO2/H2O relative production rate from the highly productive neck regions is ~2%. A 3σ upper limit of 1.8% is measured for the CO/H2O column density ratio.
-
CO2 is outgassing from both illuminated and unilluminated regions, indicating that CO2 sublimates from ice sources inside the nucleus at a depth that is below the diurnal skin depth of ~1 cm (Schloerb et al. 2015).
-
Gas-dynamics calculations show general agreement between ROSINA and VIRTIS data regarding both the level and distribution of water vapor in the coma. The water production rate in this model ranges from 6.9 × 1025 to 8.7 × 1025 s-1 during comet rotation.
-
The average rotational temperatures of H2O and CO2 are similar (~90−100 K) and consistent with gas-dynamics calculations.
As the comet approaches the Sun, the signals will become stronger, allowing us to examine the outgassing of active regions and diurnal variations in great detail and to detect vibrational bands from minor organics species. We will also be able to monitor the changes of their production rates globally as 67P approaches perihelion and study this for different regions, in particular the southern hemisphere as it is progressively illuminated. This will provide important information to understand the source of the volatile molecules inside the nucleus and potentially retrieve their initial composition and possibly spatial heterogeneity.
Acknowledgments
The authors would like to thank the following institutions and agencies that supported this work: Italian Space Agency (ASI–Italy), Centre National d’Études Spatiales (CNES- France), Deutsches Zentrum fuer Luft- und Raumfahrt (DLR-Germany), National Aeronautic and Space Administration (NASA-USA). VIRTIS was built by a consortium from Italy, France and Germany, under the scientific responsibility of the Istituto di Astrofisica e Planetologia Spaziali of INAF, Rome (IT), which also leads the scientific operations. The VIRTIS instrument development for ESA has been funded and managed by ASI, with contributions from Observatoire de Meudon financed by CNES and from DLR. The instrument industrial prime contractor was former Officine Galileo, now Selex ES (Finmeccanica Group) in Campi Bisenzio, Florence, IT. The authors wish to thank the Rosetta Science Ground Segment and the Rosetta Mission Operations Centre for their fantastic support throughout the early phases of the mission. The VIRTIS calibrated data will be available through the ESA’s Planetary Science Archive (PSA) website. In fond memory of Angioletta Coradini, conceiver of the VIRTIS instrument, our leader and friend.
References
- Acton, C. H. 1996, Planet. Space Sci., 44, 65 [NASA ADS] [CrossRef] [Google Scholar]
- A’Hearn, M. F., Belton, M. J. S., Delamere, W. A., et al. 2005, Science, 310, 258 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- A’Hearn, M. F., Belton, M. J. S., Delamere, W. A., et al. 2011, Science, 332, 1396 [NASA ADS] [CrossRef] [Google Scholar]
- Bieler, A., Altwegg, K., Balsiger, H., et al. 2015, A&A, 583, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biver, N., Hofstadter, M., Gulkis, S., et al. 2015, A&A, 583, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bockelée-Morvan, D. 1987, A&A, 181, 169 [NASA ADS] [Google Scholar]
- Bockelée-Morvan, D., & Crovisier, J. 1989, A&A, 216, 278 [NASA ADS] [Google Scholar]
- Bockelée-Morvan, D., Lis, D. C., Wink, J. E., et al. 2000, A&A, 353, 1101 [NASA ADS] [Google Scholar]
- Bockelée-Morvan, D., Crovisier, J., Mumma, M. J., & Weaver, H. A. 2004, in Comets II, eds. M. C. Festou, H. U. Keller, & H. Weaver, 391 [Google Scholar]
- Bonev, B. P., Mumma, M. J., Villanueva, G. L., et al. 2007, ApJ, 661, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Capaccioni, F., Bockelée-Morvan, D., Filacchione, G., et al. 2015a, LPI Contribution No 1832, Lunar and Planet. Sci. Conf., 2494 [Google Scholar]
- Capaccioni, F., Coradini, A., Filacchione, G., et al. 2015b, Science, 347, aaa0628 [CrossRef] [Google Scholar]
- Combes, M., Moroz, V. I., Crovisier, J., et al. 1988, Icarus, 76, 404 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Combi, M. R. 1996, Icarus, 123, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Combi, M. R., Tenishev, V. M., Rubin, M., et al. 2012, ApJ, 749, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Coradini, A., Capaccioni, F., Drossart, P., et al. 2007, Space Sci. Rev., 128, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Coradini, A., Capaccioni, F., Erard, S., et al. 2011, Science, 334, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Crovisier, J. 1987, A&AS, 68, 223 [NASA ADS] [Google Scholar]
- Crovisier, J., Leech, K., Bockelée-Morvan, D., et al. 1997, Science, 275, 1904 [CrossRef] [Google Scholar]
- Davidsson, B., & Gutiérrez, P. J. 2006, Icarus, 180, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Davidsson, B. J. R., Gulkis, S., Alexander, C., et al. 2010, Icarus, 210, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Debout, V., Bockelée-Morvan, D., Zakharov, V. 2015, Icarus, in press [Google Scholar]
- DelloRusso, N., Mumma, M. J., DiSanti, M. A., et al. 2006, Icarus, 184, 255 [NASA ADS] [CrossRef] [Google Scholar]
- de Sanctis, M. C., Capria, M. T., & Coradini, A. 2005, A&A, 444, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Sanctis, M. C., Lasue, J., Capria, M. T., et al. 2010, Icarus, 207, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drossart, P., Semery, A., Bouye, M., et al. 2000, Proc. SPIE, 4131, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Feaga, L. M., A’Hearn, M. F., Sunshine, J. M., Groussin, O., & Farnham, T. L. 2007, Icarus, 190, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Fougere, N. 2014, Ph.D. Thesis, University of Michigan [Google Scholar]
- Fougere, N., Combi, M. R., Rubin, M., et al. 2013, Icarus, 225, 688 [NASA ADS] [CrossRef] [Google Scholar]
- Gulkis, S., and the MIRO Science team 2014, CBET No. 3912 [Google Scholar]
- Gulkis, S., Allen, M., von Allmen, P., et al. 2015, Science, 347, aaa0709 [CrossRef] [Google Scholar]
- Hässig, M., Altwegg, K., Balsiger, H., et al. 2015, Science, 347, aaa0276 [CrossRef] [Google Scholar]
- Huebner, W. F., Benkhoff, J., Capria, M.-T., et al. 2006, Heat and Gas Diffusion in Comet Nuclei (Noordwijk, The Netherlands: ESA Publications Division) [Google Scholar]
- Labs, D., & Neckel, H. 1968, Z. Astrophys., 69, 1 [NASA ADS] [Google Scholar]
- Lee, S., von Allmen, P., Allen, M., et al. 2015, A&A, 583, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Roy, L., Altwegg, K., Balsiger, H., et al. 2015, A&A, 583, A1 [Google Scholar]
- Luspay-Kuti, A., Hässig, M., Fuselier, S. A., et al. 2015, A&A, 583, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marboeuf, U., & Schmitt, B. 2014, Icarus, 242, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Ootsubo, T., Kawakita, H., Hamada, S., et al. 2012, ApJ, 752, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Rothman, L. S., Gordon, I. E., Barbe, A., et al. 2009, J. Quant. Spec. Radiat. Transf., 110, 533 [Google Scholar]
- Schloerb, F. P., Keihm, S., von Allmen, P., et al. 2015, A&A, 583, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schulz, R. 2012, Planet. Space Sci., 66, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Sierks, H., Barbieri, C., Lamy, P. L., et al. 2015, Science, 347, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Tenishev, V., Combi, M. R., & Davidsson, B. 2008, ApJ, 685, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Tenishev, V., Combi, M. R., & Davidsson, B. 2011, ApJ, 732, 104 [Google Scholar]
- Thomas, N., Sierks, H., Barbieri, C., et al. 2015, Science, 347, 0440 [CrossRef] [Google Scholar]
- Tosi, F., Capria, M. T., Capaccioni, F., et al. 2015, Lunar Planet. Sci. Conf., 46, 2156 [NASA ADS] [Google Scholar]
- Villanueva, G. L., Mumma, M. J., Bonev, B. P., et al. 2012, J. Quant. Spec. Radiat. Transf., 113, 202 [Google Scholar]
- Zakharov, V., Bockelée-Morvan, D., Biver, N., Crovisier, J., & Lecacheux, A. 2007, A&A, 473, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Geometrical parameters of the VIRTIS-H LOS (LOS) from MTP010 to MTP012. A) Minimum distance of the LOS to the nucleus surface (in meters with the color scale given to the right); B) solar incidence angle (in degrees, with the color scale given to the right) of the closest point to the LOS. Each cross corresponds to a single 6 s acquisition. Only one in every four acquisitions is considered. The gray background represents the effective latitude based on the SHAP5 model composed of 300 000 facets to show the location of topographic features. |
| In the text | |
 |
Fig. 2 LOS statistics from MTP010 to MTP012. A) Minimum distance of the LOS to the nucleus (in meter, bin size is 100 m); B) corresponding solar incidence angle (bin size is 10°). Only one in every four acquisitions have been considered. |
| In the text | |
 |
Fig. 3 VIRTIS-H average spectra of H2O and CO2 bands observed from 10 to 17 October 2014 (rh ~ 3.2 AU), in spectral orders 4 and 0, respectively. The continuum has been subtracted. Superimposed we show a model spectrum of the ro-vibrational structure of H2O (ν1 and ν3) and CO2ν3 bands. Derived CO2 and H2O column densities are ~1 × 1018 and 2 × 1019 m-2, respectively. |
| In the text | |
 |
Fig. 4 VIRTIS-H spectrum of the 2.67 μm band of water. Average of 35 data cubes with most significant water and CO2 detections (those with S/N> 10). The continuum has been subtracted. Superimposed we show a model spectrum of H2O band (ν1 and ν3) for a rotational temperature Trot = 102 K (see text). The effective spectral resolution, derived from fitting, is Reff = 800. |
| In the text | |
 |
Fig. 5 VIRTIS-H spectrum of CO2 band at 4.27 μm. Average of 35 data cubes with most significant water and CO2 detections (S/N> 10). The continuum has been subtracted. Superimposed we show a model spectrum of the ν3 CO2 band for Trot = 90 K. The effective spectral resolution, derived from fitting, is Reff = 869. |
| In the text | |
 |
Fig. 6 H2O and CO2 column densities A), and column density ratio ⟨ N(CO2)⟩/⟨ N(H2O)⟩B), as a function of time. The STP periods are indicated at the top, inside circles. |
| In the text | |
 |
Fig. 7 Geomorphological regions of 67P in 2D and 3D visualization (after Thomas et al. 2015). |
| In the text | |
 |
Fig. 8 Column densities as a function of mean nucleus solar insolation for regions populating the LOS. A) H2O, B) CO2. The color coding is that of Fig. 7 and corresponds to regions in P1. |
| In the text | |
 |
Fig. 9 Column densities corrected for LOS distance and nucleus cross-section as a function of solar incidence angle (see text). The color coding is that of Fig. 7 and corresponds to regions in P1. |
| In the text | |
 |
Fig. 10 Column density ratio as a function of mean nucleus solar insolation for regions populating the LOS. Limb sounding above Ash A), Babi B), Imhotep C), Seth D), Anuket E), and Ma’at F). The labels given in the plots and titles are those of the regions in P1/P2 (see text). The color coding is that of Fig. 7 and corresponds to regions in P1. |
| In the text | |
 |
Fig. 11 CO2/H2O column density ratio as a function of H2O column density. The color coding is that of Fig. 7. |
| In the text | |
 |
Fig. 12 Decimal log of the modeled water column density on 3 December 2014, 07:01:53 UT (starting time of VIRTIS-H cube 00376211338). The large rectangle is the VIRTIS-M FOV and the small square is VIRTIS-H FOV. The scale of the map is 5.7 × 5.7 km2. In the bottom left corner is shown the nucleus with the unilluminated bottom of the body (Imothep and Ash) in the foreground and the illuminated head in the background. The illuminated Seth and Hapi regions lie in between. |
| In the text | |
 |
Fig. 13 Column densities from the DSMC model compared to VIRTIS-H column densities. A): model results (red) and measurements (black) are plotted as a function of time. B): model as a function of measurements, with the same color coding as in Fig. 7, corresponding to regions in P1. Modeled columns have been multiplied by a factor 0.8 to approximate the column density of H2O. The markers for the model are at the average point between the values found at the start and stop time of a given observation, which themselves give the error bars. The error bars for VIRTIS-H measurements are shown in Fig. 6. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


