| Issue |
A&A
Volume 583, November 2015
Rosetta mission results pre-perihelion
|
|
|---|---|---|
| Article Number | A29 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201526152 | |
| Published online | 30 October 2015 | |
MIRO observations of subsurface temperatures of the nucleus of 67P/Churyumov-Gerasimenko
1
University of Massachusetts,
619 Lederle Graduate Research Tower,
Amherst,
MA
01003,
USA
e-mail:
schloerb@astro.umass.edu
2
JPL, California Institute of Technology,
4800 Oak Grove Drive,
Pasadena, CA
91109,
USA
3
LESIA-Observatoire de Paris, CNRS, UPMC, Université
Paris-Diderot, 5 place Jules
Janssen, 92195
Meudon,
France
4
LERMA, Observatoire de Paris, PSL Research University, CNRS, UMR
8112, UPMC,
75014
Paris,
France
5
Max-Planck-Institut für Sonnensystemforschung,
Justus-von-Liebig-Weg 3,
37077
Göttingen,
Germany
6
Planetary Science Institute, Tucson, AZ
85719,
USA
7
National Central University, Jhongli, 32001
Taoyuan City,
Taiwan
8
Aix Marseille Université, CNRS, Laboratoire d’Astrophysique de
Marseille, UMR 7326, 13388
Marseille,
France
9
Institut für Geophysik und extraterrestrische Physik, Technische
Universität Braunschweig, 38106
Braunschweig,
Germany
10
Deutsches Zentrum für Luft- und Raumfahrt, Institut für
Planetenforschung, 12489
Berlin,
Germany
Received: 21 March 2015
Accepted: 7 July 2015
Observations of the nucleus of 67P/Churyumov-Gerasimenko in the millimeter-wave continuum have been obtained by the Microwave Instrument for the Rosetta Orbiter (MIRO). We present data obtained at wavelengths of 0.5 mm and 1.6 mm during September 2014 when the nucleus was at heliocentric distances between 3.45 and 3.27 AU. The data are fit to simple models of the nucleus thermal emission in order to characterize the observed behavior and make quantitative estimates of important physical parameters, including thermal inertia and absorption properties at the MIRO wavelengths. MIRO brightness temperatures on the irregular surface of 67P are strongly affected by the local solar illumination conditions, and there is a strong latitudinal dependence of the mean brightness temperature as a result of the seasonal orientation of the comet’s rotation axis with respect to the Sun. The MIRO emission exhibits strong diurnal variations, which indicate that it arises from within the thermally varying layer in the upper centimeters of the surface. The data are quantitatively consistent with very low thermal inertia values, between 10–30 J K-1 m-2 s-1/2, with the 0.5 mm emission arising from 1 cm beneath the surface and the 1.6 mm emission from a depth of 4 cm. Although the data are generally consistent with simple, homogeneous models, it is difficult to match all of its features, suggesting that there may be some vertical structure within the upper few centimeters of the surface. The MIRO brightness temperatures at high northern latitudes are consistent with sublimation of ice playing an important role in setting the temperatures of these regions where, based on observations of gas and dust production, ice is known to be sublimating.
Key words: comets: general / comets: individual: 67P/Churyumov-Gerasimenko / radio continuum: planetary systems
© ESO, 2015
1. Introduction
Comets exhibit a remarkable range of phenomena that have captivated the imaginations of human observers for millenia. Today, we understand that the origin of this activity results from the process of sublimation of ices through the absorption of sunlight by a tiny cometary nucleus. The Microwave Instrument for the Rosetta Orbiter (MIRO) provides an opportunity to study the details of this process through measurements of the temperature of the nucleus of 67P/Churyumov-Gerasimenko (67P) in its near-surface layers.
Our first attempts to understand the MIRO continuum data consisted in viewing the observed brightness temperatures as a function of local solar time and “effective” latitude of the points on the surface (see Sect. 2.3 for the definition of these terms). As reported in MIRO’s initial publication (Gulkis et al. 2015), the observed brightness temperatures are a strong function of the effective latitude – a seasonal effect – and also exhibit diurnal variations indicating that the MIRO emission arises in the layers near the surface where the temperature varies diurnally. One of the points of the present paper is to follow up on these general statements with a more quantitative characterization of the emission and its dependence on solar illumination. Thus, we present a more detailed comparison of the data originally presented by Gulkis et al. (2015) to simple models of the thermal emission from the nucleus of 67P.
2. Observations
2.1. The MIRO instrument
The MIRO instrument is described in detail in Gulkis et al. (2007). For these observations, the relevant parts of the instrument are its two continuum channels for measurements at 0.533 mm and 1.594 mm wavelength. Important instrument parameters for continuum observations with these channels are summarized in Table 1.
The comet is observed using an off-axis parabolic antenna with a diameter of 30 cm. The low rms antenna surface errors (11 μm) and a large, 20 dB, Gaussian illumination taper are expected to lead to high main beam efficiencies greater than 93% for the SubMM (562 GHz) channel and greater than 99% for the MM (188 GHz) channel.
MIRO instrument parameters.
The MIRO instrument is calibrated by observing hot and cold blackbody calibration targets at typical temperatures of +18 °C and −47 °C respectively. The receiver output is proportional to the power that it receives from a source, and the blackbody targets provide a signal of known power, P, to the receiver that allows its calibration. Following the traditions of radio astronomy, the observed power is converted into an antenna temperature, TA = P/k, where k is Boltzmann’s constant. The targets and the signal from the antenna are observed as a part of the calibration sequence every 34 min, and this data is used to determine the TA values observed by the antenna. The observed antenna temperature, TA, may be used to derive a brightness temperature, TB, for the emission from a source. TB is defined to be the temperature of a blackbody filling the antenna beam pattern that is required to produce the observed power, TA. For MIRO we always employ the Planck function when computing the brightness temperature. Measurements of the signal on blank sky, corresponding to observation of the Cosmic Microwave Background, show that the receiver behaves very linearly over the range of powers observed between the calibration loads and the blank sky; the accuracy of the measurement is about 1 K absolute over most of this range.
2.2. Observation dates and geometry
All MIRO observations obtained during September 1–30 2014 have been included in this study. 67P was located between 3.45 and 3.27 AU from the Sun during this time period. For most of the observations, the Rosetta Spacecraft was located in a terminator orbit at a distance of approximately 30 km from the nucleus, resulting in the linear resolution noted in Table 1. Under these conditions, scanning motions of the spacecraft can lead to measurements of points on the surface of the comet corresponding to all local times of day. However, we note that observations from the terminator orbit tended to reduce the number of observations possible near local noon and local midnight.
Measurements of the diurnal variation of the MM and SubMM signals provide fundamental information on the thermophysical properties of the nucleus. Ideally, our experiment would have made observations of all points on the surface at all local solar times in order to measure the diurnal variation of the signal. During September 2014, the spacecraft conducted some special raster-scan mapping campaigns for MIRO to observe the nucleus in the continuum. However, the amount of time allocated and the available observing geometries did not allow fully sampled maps of the nucleus to be completed. Nevertheless, since the MIRO instrument is approximately co-boresighted with all other orbiter instruments and since MIRO acquires data at all times, it has been possible to collect data over much of the area of the nucleus covering a range of local solar times and latitudes. In all, approximately 200 000 observations for each MIRO channel intersected the nucleus at angles of incidence less than 60 degrees.
2.3. Nucleus shape model and insolation
The intersection points of the MM and SubMM beams on the comet nucleus were determined using a digital shape model of the surface. This model has been produced by the OSIRIS imaging team for use within the Rosetta project (Sierks et al. 2015), and in this work we employ the SHAP5 v0.1 model (Jorda et al. 2015). Intersection geometry has been computed using the SPICE software developed and supported by JPL (Acton 1996). The digital shape model and the SPICE system allow spacecraft and comet trajectory information to be combined with spacecraft attitude data to compute the location of the millimeter and submillimeter beams on the target.
We also employ the digital shape model to compute the solar illumination of our observation points. The irregular shape of the nucleus (Sierks et al. 2015) makes it important to account for the fact that the orientation of a specific point on the nucleus with respect to the Sun is not accurately derived from its latitude and longitude alone. We use the terms body latitude and body longitude to describe the location of a point on the surface of the nucleus based on the orientation of the radial vector to that point from the center-of-figure of the shape model. For solar insolation, however, we define an effective latitude and effective longitude based on the orientation of the local surface normal of a point on the surface with respect to the Sun. We use the term effective local solar time to indicate the solar phase with respect to the local surface normal.
The solar insolation varies significantly over the irregular 67P nucleus, owing to its shape and the orientation of its rotational axis. In mid-September, the subsolar latitude was approximately 43 degrees north, so that northern effective latitudes above 47 degrees were always in sunlight while southern effective latitudes below 47 degrees were always in darkness. Figure 1 presents a plot of the mean solar insolation, averaged over one rotation period in the middle of September, computed for each surface point on the digital shape model. It is clear that there are considerable variations in the amount of sunlight illuminating the surface from point to point on the nucleus.
 |
Fig. 1 Mean solar insolation on the surface of 67P during the month of September 2014. For each point on the surface, the mean value of the cosine of the angle of incidence during one rotation of the nucleus is computed for a date in mid-September using the SHAP5 digital shape model developed by the OSIRIS team. The effect of shadowing is considered in the calculation. It should be noted that the irregular shape of the comet results in some areas where the latitude and longitude refer to three surface points rather than one. For this figure, we have displayed the value for the outermost intersection point when this occurs. The region outlined with the solid white is that selected for fitting models of the diurnal brightness temperatures, as described in Sect. 3. The region outlined with the dotted line was used for fitting physical models, as described in Sect. 4. Most of the coverage used for model fitting lies in the Imhotep and Ash geomorphological regions defined by the OSIRIS team (Sierks et al. 2015). |
2.4. September 2014 dataset
For this paper we assembled a set of continuum measurements with an integration time of 1s for MIRO’s MM and SubMM channels. For each observation we computed the effective latitude and effective local solar time for 17 locations, representing equal area bins within the Gaussian main beam pattern, within the main beam’s intersection with the nucleus. This allows us to check the range of these properties within the beam and to create a beam averaged effective latitude and effective solar phase for each observation. We found that, although differences may be noted, they are typically not large and do not lead to very different results than would have been obtained using the geometry of the intersection point at the beam center alone.
3. Diurnal phase curves
 |
Fig. 2 Data obtained for the SubMM and MM channels in 4 degree wide bins of effective latitude are fit to a Fourier series. The SubMM and MM data for each bin are shown side-by-side; the effective latitude is shown in the lower right of each panel. Models that include both the first and second harmonics in the Fourier Series (solid) and models that only include the first harmonic terms (dashed) have been fit to each set of data. |
3.1. Background
The observation of diurnal variations from planetary surfaces is an old problem dating back to the initial microwave observations of the Moon. The basic behavior of the observed brightness temperature can be linked to the surface temperature of the body, the thermal properties of the surface materials, and the absorption coefficient of the surface materials at the wavelength of interest in a straightforward way. Following Muhleman (1972), we present a short review of the dependence of brightness temperature on physical parameters.
The temperature of the subsurface at depth x and time t, assuming uniform properties that do not depend on depth or temperature, and no internal sources of heat, is found by solving the heat equation 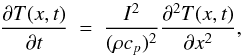 (1)where ρ is the density, cp is the specific heat, k is the thermal conductivity and I is the thermal inertia (
(1)where ρ is the density, cp is the specific heat, k is the thermal conductivity and I is the thermal inertia (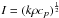 ). For the comet nucleus, the surface boundary condition for solution of the heat equation is
). For the comet nucleus, the surface boundary condition for solution of the heat equation is 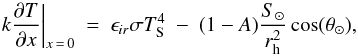 (2)where ϵir is the surface emissivity in the thermal infrared, σ is the Stefan-Bolzmann constant, A is the Bond Albedo, S⊙ is the Solar Constant, rh is the heliocentric distance, and θ⊙ is the angle of incidence of the Sun to the local surface. It can be shown (see e.g. Spencer et al. 1989) that the solution of the heat equation with this boundary condition and with the assumptions noted above yields a surface temperature that depends only on the thermal inertia, the Bond albedo and the infrared surface emissivity. In the derivation that follows, we show how the MIRO observations depend explicitly on the surface temperature variations, and therefore, make the case that our observations are sensitive to the thermal inertia parameter.
(2)where ϵir is the surface emissivity in the thermal infrared, σ is the Stefan-Bolzmann constant, A is the Bond Albedo, S⊙ is the Solar Constant, rh is the heliocentric distance, and θ⊙ is the angle of incidence of the Sun to the local surface. It can be shown (see e.g. Spencer et al. 1989) that the solution of the heat equation with this boundary condition and with the assumptions noted above yields a surface temperature that depends only on the thermal inertia, the Bond albedo and the infrared surface emissivity. In the derivation that follows, we show how the MIRO observations depend explicitly on the surface temperature variations, and therefore, make the case that our observations are sensitive to the thermal inertia parameter.
If we expand the temperature of the surface of the body (i.e. at x = 0) as a Fourier series, 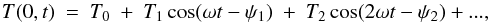 where ω = (2π) /P, P is the rotational period, and Tn and ψn are the amplitude and phase of the nth Fourier terms in the series, then the subsurface temperature may be derived through straightforward solution of the heat equation with the surface temperature as a boundary condition. This leads to the well known solution (Carslaw & Jaeger 1959)
where ω = (2π) /P, P is the rotational period, and Tn and ψn are the amplitude and phase of the nth Fourier terms in the series, then the subsurface temperature may be derived through straightforward solution of the heat equation with the surface temperature as a boundary condition. This leads to the well known solution (Carslaw & Jaeger 1959) 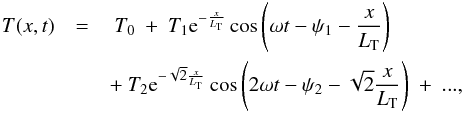 where LT is the thermal skin depth, which describes the attenuation of temperature waves that propagate into the surface. LT is related to the thermal parameters already defined according to
where LT is the thermal skin depth, which describes the attenuation of temperature waves that propagate into the surface. LT is related to the thermal parameters already defined according to 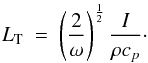 (3)The millimeter-wave brightness temperature observed by MIRO may be determined by solving the equation of radiative transfer, which involves an integration of the above temperature profile over depth into the surface. The most important parameter for this calculation is the absorption coefficient of the material at the wavelength of observation, αλ, and the emission from the subsurface is found to arise from a penetration depth
(3)The millimeter-wave brightness temperature observed by MIRO may be determined by solving the equation of radiative transfer, which involves an integration of the above temperature profile over depth into the surface. The most important parameter for this calculation is the absorption coefficient of the material at the wavelength of observation, αλ, and the emission from the subsurface is found to arise from a penetration depth 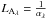 , which corresponds to optical depth unity in the material. We let ϵ be the emissivity of the surface at the MIRO wavelengths, then the result of the integration over the temperature profile, assuming nadir viewing, is
, which corresponds to optical depth unity in the material. We let ϵ be the emissivity of the surface at the MIRO wavelengths, then the result of the integration over the temperature profile, assuming nadir viewing, is 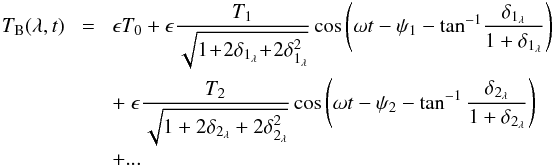 (4)where δλ is the ratio of the penetration depth at the wavelength of observation, LAλ to the thermal skin depth, LT
(4)where δλ is the ratio of the penetration depth at the wavelength of observation, LAλ to the thermal skin depth, LT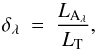 (5)and we have defined
(5)and we have defined 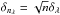 , where n is the order of the term in the Fourier series expansion.
, where n is the order of the term in the Fourier series expansion.
For observations with the MIRO instrument, therefore, we expect to see diurnal variations of the signal as long as the emission arises from a penetration depth that is comparable to the thermal skin depth (i.e. δλ is reasonably small). We note that the amplitude of the observed MIRO brightness temperature variations depends on the surface temperature variations, which in turn are controlled by the thermal inertia in a model with uniform, temperature independent thermal properties. Thus, the MIRO results may be used to constrain the thermal inertia of the model as well as the ratio of penetration depth to thermal skin depth. For common materials, including lunar soils (Gary & Keihm 1978), the penetration depth is expected to be approximately proportional to the wavelength. We therefore expect that δλ will increase between the SubMM channel and the MM channel. This implies that the diurnal variations seen in the MM channel will be smaller than those seen in the SubMM channel, and that the phase lag of the diurnal variations will be greater for the observation at the longer wavelength. This behavior is illustrated qualitatively in Gulkis et al. (2015).
A final point about observations of a rough, particulate surface at the MIRO wavelengths is that there is no strong dependence of the millimeter-wave emission on the orientation of the observer with respect to the solar illumination direction. The so-called “beaming” effect observed in the thermal infrared is certainly an important consideration in the interpretation of observations at those wavelengths. However, this effect is negligable for observations at millimeter wavelengths (Keihm et al. 2013; Müller 2002).
 |
Fig. 3 MIRO harmonic data fit results for the SubMM (open circles) and MM (filled circles) channels. The points are plotted with formal error bars shown as well. Often, since the formal errors are small, the errorbars do not extend beyond the point symbols. Panel a) shows the mean brightness temperature derived from the fits. Panel b) shows the first harmonic amplitude of the brightness temperature variation. Panel c) shows the phase of the first harmonic of the brightness temperature variation. |
 |
Fig. 4 MIRO harmonic data fits compared to the brightness temperature data. Panel a) shows the rms of the fits to each latitude bin. The MM rms is typically 2–3 K while the SubMM rms is typically 7–8 K. These values are significantly greater than would be expected from measurement errors alone, indicating some real, unmodeled, variations in the dataset. Panel b) shows all MM brightness temperatures compared to lines representing the mean model temperature plus the first harmonic amplitude and the mean minus the first harmonic amplitude. Panel c) shows the same information for the SubMM channel. |
3.2. Phase curve fitting
MIRO SubMM and MM continuum data have been used to construct fits of the diurnal brightness temperature variation. Observations are “binned” into 4 degree wide strips of effective latitude. In this study, we have limited the fitting to the bottom of the “body” lobe of the nucleus model, corresponding mainly to the Imhotep and Ash regions defined by the OSIRIS imaging team (Sierks et al. 2015). This is a region where the shape of the nucleus is not strongly curved and there are no large regions of shadows during the day, as occurs in the “neck” region of the nucleus. The region used for the selection of data was outlined in Fig. 1. The data were also filtered to exclude points that did not have the full main beam intersecting the nucleus and points observed with an emission angle from the surface greater than 30 degrees.
Our ability to derive accurate values for the harmonic coefficients of the diurnal phase curves is somewhat limited by poor phase coverage at some latitudes. Nonuniform sampling of the phase means that there is a possibility of aliasing power in the diurnal curve at higher harmonic orders into our fits to the low order coefficients. Fortunately, from the form of the expected variations in Eq. (4), higher order variations in the brightness temperature curves damp out more rapidly than the same terms in the surface temperature expansion, leading us to believe that this is not a strong effect. Nevertheless, we have made fits of both first and second order models to the data in order to assess the dependence of the amplitude and phase of the first harmonic on the order of the fitting function. Figure 2 shows a set of model fits, using Eq. (4) expanded to both first and second order, to the data in several effective latitude bins. The results of fits to the coefficients of the zeroth and first harmonics, which are used for our analysis described below, have been found to be consistent for the two fits.
As a final check for systematic errors in fitting the phase curves, we performed a simulation of the experiment using thermal models (described in Sect. 4) to provide simulated data. In this case, we found small bias errors between the parameters derived from a fit, using the actual phase coverage in the experiment, and the “true” value in the physical model. Biases exist because of the phase coverage and because the higher order terms are more important to the fit in some effective latitude bins than in others. To be conservative in our estimation of the likely errors, we have treated any systematic bias observed in the simulation experiment as a random error in calculating the error bars in figures presenting our results.
3.2.1. Fit results
Figure 3 shows the results of the Fourier model fits to the data. For each effective latitude bin, the mean brightness temperature, amplitude of the first harmonic of the brightness temperature, and phase of the first harmonic are shown. There are several obvious features in these results. First, as noted in Gulkis et al. (2015), the mean brightness temperature (Fig. 3a) is a strong function of the effective latitude. This seasonal effect follows simply from the fact that the mean solar insolation is also a strong function of the effective latitude. The second feature of the harmonic fits (Fig. 3b) is that the amplitude of the MM channel’s diurnal variation is smaller than that of the SubMM channel. This is the anticipated result of observing the damped thermal wave in the surface materials at a greater depth with the MM channel. Finally, the phase of the peak emission (Fig. 3c) observed by the MM channel falls later after noon local time than that observed for the SubMM channel. This is also the anticipated result of the propagation of the thermal wave into the surface of the nucleus.
The harmonic fits to the data have been illustrated in Fig. 2 for a few latitude bins. In Fig. 4 we present another view of the quality of the fits. Figure 4a shows the rms of the fit of each bin of effective latitude. The rms of the MM data is typically 2–3 K in each bin, whereas the rms of the SubMM data is usually worse, around 7–8 K. Both rms values exceed our expectation for measurement radiometric errors (see Table 1), which may be due in part to limiting the fits to the first two harmonic terms. However, since the higher order terms are expected to be small, this observation probably indicates real, underlying and unmodeled, physical effects in the data, although no correlations of the residuals with other likely parameters have been found as yet. Figures 4b and c show the brightness temperature measurements for the MM and SubMM channels respectively. Superimposed on these data are lines to represent the range of values from the model fit. The upper line shows the mean temperature plus the amplitude of the first harmonic, and the lower line shows the mean temperature minus the amplitude of the first harmonic. The model ranges show a good match to the range of the data, indicating that the mean and amplitudes derived in the model fit are a good match to the observations.
 |
Fig. 5 Ratio of the mean antenna temperature observed by the SubMM channel to that of the MM channel. This is a measure of the ratio of the power received by the MIRO instrument at the two wavelengths. The solid line on the figure shows the expected result for this ratio assuming that the SubMM brightness temperature is equal to the MM brightness temperature. |
3.2.2. Quantitative interpretation of fit results
As previously mentioned, the qualitative behavior of the amplitude and phase of the MM and SubMM diurnal variations are in agreement with general expectations. We now turn our attention to a quantitative comparison of the results. The first interesting comparison comes from consideration of the mean brightness temperatures derived for each effective latitude bin. As seen in Fig. 3a, the MM brightness temperatures are all greater than the SubMM values. This could be indicative of many things, including a real gradient in the diurnally averaged temperature in the upper few centimeters of the surface or some difference in the surface emissivity or volume scattering between the two wavelengths. However, there are also important instrumental effects which will be considered below.
To make a quantitative comparison, we consider the power received by the SubMM and MM channels, which is best expressed using the antenna temperature, TA values (see Sect. 2.1). Figure 5 shows the ratio of the antenna temperatures observed by the SubMM and MM receivers for each of the effective latitude bins. This ratio is plotted as a function of the antenna temperature (power) observed by the MM channel. For observations of a surface with the same brightness temperature at both wavelengths, the power ratio is expected to vary with the power received by the MM channel, owing to the nonlinear nature of the Planck function with wavelength. The solid line in the figure shows the expected ratio for observations of an object with the same brightness temperatures at the two wavelengths; other curves show the behavior when the power ratio is multiplied by a constant less than one. The observed values of the power ratio fall below the expectation for equal brightness temperature, and they are consistent with a value of approximately 0.94.
The value of 0.94 for the ratio of the powers is noteworthy because it is close to the expected ratio of the main beam efficiencies of the two wavelength channels. The comet nucleus extends over many beamwidths during these observations, and one might expect that the main beam efficiency would be a lower limit to what actually could actually be observed when the MIRO beam and sidelobes are convolved with a target the size of the nucleus. Preliminary modeling of the beam pattern, using data obtained during the instrument’s testing prior to delivery for integration with the spacecraft, shows that it is easy to account for half of the observed difference with this effect, and work is ongoing to try to determine whether the full difference can be accounted for by a difference in antenna efficiency between the two wavelengths. For this paper, we adopt the point of view that the measured ratio of 0.94 is the result of a difference in the beam efficiency between the two wavelengths. It is important to resolve this point, however, since a portion of the effect could be a real physical effect on the comet itself.
Following Sect. 3.1, the ratio of the amplitudes of the fits to the data in the two wavelength channels is expected to depend only on the values of δ for the two wavelengths. Similarly, the phase difference between the curves also depends on these values. Therefore, it is interesting to investigate whether the amplitude ratio and phase difference are consistent with a simple model with uniform properties.
From Eq. (4) we expect that the ratio of the amplitudes of the diurnal variation of the MM and SubMM channels will depend on the values of the δ parameter at the two wavelengths. Adopting δMM = 4 δSubMM, the approximate behavior of lunar soils at millimeter wavelengths (Gary & Keihm 1978), we may then compare the amplitude ratio to the expectations for different values of δSubMM. Figure 6 shows the ratios derived from the model fits shown in Fig. 3b compared to different values of δSubMM. For the specific assumption of a ratio consistent with lunar soils, we find that the best value for δSubMM is approximately 0.7, indicating that the SubMM penetration depth is about 0.7 times the thermal skin depth of the material. In this case, the MM emission would arise from about three thermal skin depths.
 |
Fig. 6 Ratio of the amplitude of the MM diurnal brightness temperature to the SubMM amplitude. The horizontal lines show expected ratio for different values of δSubMM under the assumption that δMM = 4δSubMM. |
 |
Fig. 7 Difference between the phase of the millimeter-wave diurnal brightness temperatures and the phase of the submillimeter-wave variations. The horizontal lines show the expectations for the same set of models that were compared to the amplitude ratio data in Fig. 6. The observed phase difference is too large to be explained by the simple model. |
Figure 7 shows the comparison of the phase difference between the MM and SubMM channels and the expectation from the same set of models shown in Fig. 6. In this case, we find that the observed phase difference in most cases cannot be explained by the simple model under consideration. Although the amplitude ratio and phase difference data could be brought into simultaneous agreement under some rather extreme assumptions for the δ values at the two wavelengths, δSubMM ~ 0.1 and δMM ~ 20 δSubMM, we believe that a more likely explanation of the disagreement with the expectations of the simple, homogeneous model is that the actual surface materials probed by MIRO may not be homogeneous with depth.
4. Comparison to simple thermophysical models
4.1. Model description
Fitting diurnal phase curves offers a way to characterize the data and look for trends and consistency within the dataset. However, to constrain thermophysical properties it is necessary to compare the data to physical models of the emission. Therefore, in this section, we conduct a comparison of the MIRO data to a simple model in which the physical properties are constant values for all depths and temperatures.
The model solution is found by solving the heat Eq. (1) under the boundary condition appropriate for absorption of solar radiation that heats the surface and emission of infrared radiation that cools the surface (Eq. (2)). For the models in this paper, we have explicitly not considered the effects of sublimation of ices in the surface material contributing to the energy balance and the final temperatures. Rather, our motivation has been to see whether models without this effect can provide a good representation of the observations.
Thermal model parameters.
In order to calculate temperatures from the thermal model, it is necessary to specify the values of several thermophysical parameters. Of all the thermal parameters in the model, the one with the greatest potential range of values is the thermal conductivity, which can change by orders of magnitude for small changes in other parameters like the material density. Therefore, in this study, we have adopted the strategy of setting a priori constraints on most parameters and then focussed on examining the behavior of the models as the thermal inertia, and hence the thermal conductivity, of the system is varied.
Our adopted values for thermal parameters are summarized in Table 2. We chose values of ρ = 470 kg m-3 based on the estimate of bulk density of 67P (Sierks et al. 2015); cp = 500 J kg-1 K-1 based on lunar soil sample measurements at 160 K (Hemingway et al. 1973); and ϵir = 0.95, consistent with measurements of lunar particulate soils (Birkebak 1972). The thermal conductivity and specific heat of materials on airless bodies are known to be dependent on the temperature of the material. For the thermal conductivity this effect is due to radiative transfer of energy between grains, but we note that this effect only becomes important at temperatures well above those observed on the nucleus at this heliocentric distance. The specific heat is also known to be variable, but sample calculations including this effect showed no change in the mean temperature achieved by the model and changes in the amplitude of the surface temperature variations of only a few percentage points over most of the region used to fit the thermal inertia. We therefore felt justified in using simple, temperature independent parameters for this analysis. Our adopted value of Bond Albedo, A = 0.01, is based on Spitzer Space Telescope observations (Lamy et al. 2008), and we note that measurements by the OSIRIS (Sierks et al. 2015) and VIRTIS (Capaccioni et al. 2015) instruments suggest values 50% larger might be appropriate. However, this small change in albedo has an insignificant effect on the thermal model results, and in general, plausible variations in all these parameters do not strongly affect the general conclusions of this work.
A wide range of thermal inertia values has been considered in this study, ranging from 5–120 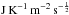 , corresponding to thermal conductivities of 1.06 × 10-4−6.13 × 10-1 J m-1 K-1 s-1 for the adopted ρ and cp values. The low end of the range (I = 5) corresponds to high porosity, fine grained material and is consistent with the low end of the range of values considered in the analysis of Spitzer Space Telescope observations of the 67P thermal flux (Lamy et al. 2008). The I = 120 value was an upper limit estimated by the Rosetta Project that could be representative of either a highly compact soil or a combination of millimeter-to-centimeter size rocks within a granular matrix.
, corresponding to thermal conductivities of 1.06 × 10-4−6.13 × 10-1 J m-1 K-1 s-1 for the adopted ρ and cp values. The low end of the range (I = 5) corresponds to high porosity, fine grained material and is consistent with the low end of the range of values considered in the analysis of Spitzer Space Telescope observations of the 67P thermal flux (Lamy et al. 2008). The I = 120 value was an upper limit estimated by the Rosetta Project that could be representative of either a highly compact soil or a combination of millimeter-to-centimeter size rocks within a granular matrix.
The thermal model was calculated for 35 values of the effective latitude, assuming no contribution of shadowing by the rough surface of the nucleus. For each effective latitude, Eq. (1) was solved numerically with Eq. (2) as the boundary condition for a set of eight thermal inertia values (I = 5, 8, 12, 22, 37, 60, 90, 120 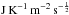 ). The thermal computations took into account the orbital elements, obliquity, and rotation period of 67P obtained from a fit to the JPL SPICE-based ephemeris. Seasonal effects were accounted for by running the thermal model calculations over a sufficient number of orbits that a periodic steady state was achieved. Computations were stopped at the September 2014 67P orbit position (heliocentric distance ~3.35 AU), and the resultant temperature profiles at 2 degree diurnal phase intervals were saved to files for each of the 35 latitudes and eight thermal inertia candidate values.
). The thermal computations took into account the orbital elements, obliquity, and rotation period of 67P obtained from a fit to the JPL SPICE-based ephemeris. Seasonal effects were accounted for by running the thermal model calculations over a sufficient number of orbits that a periodic steady state was achieved. Computations were stopped at the September 2014 67P orbit position (heliocentric distance ~3.35 AU), and the resultant temperature profiles at 2 degree diurnal phase intervals were saved to files for each of the 35 latitudes and eight thermal inertia candidate values.
The thermal model temperature profile outputs served as inputs to a radiative transfer program which computed model brightness temperatures for the two MIRO wavelengths. For each observation, the effective latitude and effective local solar time were determined from the digital shape model and the thermal model predictions were derived by interpolation of the model grid of solutions. The brightness temperature observed depends on the penetration depth for each of the MIRO wavelengths, LAλ. This parameter, like the thermal inertia, can also be quite variable depending on the composition and physical properties of the soil. Therefore, our approach has been to consider a wide range of values which include well-established values for the lunar soil (Gary & Keihm 1978) and recent laboratory measurements of 67P simulant materials (Heggy et al. 2012).
4.2. Fit to thermal inertia
For each MIRO observation, we computed a model brightness temperature for each of the 8 candidate thermal inertia values using a range of possible values of δλ, the ratio of the penetration depth, LAλ, to the thermal skin depth, LT. We have found that this ratio is very useful for model fitting, since the best solutions for this parameter at each thermal inertia do not vary strongly with the thermal inertia value. Comparisons of the model to the observed brightness temperatures for each wavelength were made for over 200 000 continuum measurements of the region outlined in Fig. 1. For the SubMM channel data, the brightness temperatures used in the fit were corrected for the 0.94 beam efficiency. This region lies on the body region of the nucleus and covers the Imhotep and Ash geomorphological regions identified by the OSIRIS team (Sierks et al. 2015). As was done for the diurnal curve fitting, this region was selected in order minimize strong shadowing of one body lobe on the other and possible self-heating effects of the more severe topography seen on the neck region of the nucleus. Data were restricted to include only emission angles of 60 degrees or less. The integration over the temperature profile took account of the angle of incidence of the receiver with the local surface; the surface emissivity at the MIRO wavelengths was assumed to be unity and not variable with angle of incidence.
For each candidate model, we make a direct comparison to the data for each point and compute χ2, the sum of the squares of the differences between model and data. The least squares solution for the best values of thermal inertia, I, and the ratio of the penetration depth, LAλ, to the thermal skin depth, LT, δλ, corresponds to a minumum in the surface defined by the grid of χ2 values. Near the minimum, the values of χ2 will follow a quadratic surface, and the shape of the surface can be used to define the best values for the parameters as well as an estimate for the errors using a procedure sometimes referred to as “brute force” least squares.
Figure 8 shows contours of the χ2 of the data compared to the model for all models in the grid.
 |
Fig. 8 Contour plots of χ2 of MIRO observations compared to models. The χ2 for the SubMM data is shown in the left-hand figure; the χ2 for the MM data is shown on the right. χ2 values have been normalized to the minimum value found in the fit, and the contours are shown for 1.1, 1.25, 1.5, 2, 3, and 4 times this minimum value. The scale for thermal inertia is logarithmic, but labeled with the values of the grid parameters. The LA/LT ratio models for the grid were computed on a linear scale. A (+) symbol is plotted at the location of the minimum value of χ2 derived from fitting the grid data near the minimum. The error ellipse, corresponding to an increase in χ2 of 5% above the minimum is shown. |
The χ2 values are normalized by the minimum value found by fitting a quadratic function to values in the grid, which corresponds to the reduced χ2 on the assumption that the expected variance of the data is best estimated by the scatter of the data points about the best fitting model. The contour levels shown correspond to 1.1, 1.25, 1.5, 2, 3, and 4 times the minimum value found for χ2. Ideally, in an experiment with 200 000 data points, a change in fitted parameters resulting in a 0.87% increase in χ2 above its minimum value would correspond to a 3σ event (99.7% probablility). However, in assessing the range of parameters that are compatible with our data, we think that it is prudent to be more conservative for a number of reasons. First, we are considering points from different locations on the surface of the nucleus, so the approximation that all locations can be described with the same model is probably an oversimplification. Second, the model does not include a number of likely physical effects, including local shadowing of points on the surface during the day. Third, the best fitting value of I is dependent on the selection of the 94% beam efficiency for the SubMM channel. Since this is an uncertain value it represents an additional error source to be considered. Fourth, the quadratic surface fit to the grid of solutions is not a perfect match to the actual values, and the rms of that fit to χ2 values in the grid is ~1% of the minimum χ2 value. Finally, we find that the choice of the actual grid points used to fit the quadratic surface can lead to changes in the best values for the parameters that exceed those likely based on random errors alone. For this reason, we have used a level of 5% above the χ2 minimum to indicate the range of parameter values at the ~99% confidence level. The error ellipse in the figure shows the range of values that are consistent with this level of confidence.
The fitted parameter values, and their associated errors, are presented in Table 2. The table is organized to present adopted parameters, used in the specific thermal model calculation and for derivation of other values, fitted parameters, which are derived from fits to the MIRO data, and derived parameters, which are computed from the adopted parameters and the fitted parameters. It is worth reiterating that the fitted values of thermal inertia, I, and the ratio of the penetration depth to thermal skin depth, δ, are independent of assumptions about the density and specific heat of the model. However, these parameters become important when the fitted parameters are used to derive other properties, such as the thermal skin depth of the model and the penetratration depth (LA). It is interesting to note that the derived I values are consistent for the two wavelengths and that the derived values for penetration depths are close to rather nominal values for the Moon (Gary & Keihm 1978). The derived penetration depths are not particularly well determined by the model, with errors of 50% for the SubMM channel, since they depend on uncertainties in the thermal skin depth as well as in the determination of the ratio of penetration depth to the thermal skin depth.
 |
Fig. 9 Comparison of MIRO harmonic data fit results for the submillimeter (open circles) and millimeter (filled circles) channels with thermal model closest to the best fitting thermal inertia (I = 22). Panel a) shows the mean temperature derived from the fits. Models for I = 12 and I = 37 are also shown for comparison. Panel b) shows the first harmonic amplitude. The SubMM channel model is shown as a solid black line, with dotted lines showing the range of values allowed by acceptable values of LA. The gray line shows the same results for the MM channel. Panel c) shows the phase of the first harmonic. The curves have the same meaning as in panel b). |
4.3. Comparison of thermal models to diurnal curves
One way to assess the quality of the fit of the thermal models to the MIRO data is to compare their predictions to the diurnal phase curve fits carried out in Sect. 3. In Fig. 9, we present a comparison of the thermal model closest to the best fit thermal inertia (I = 22), and assuming the best fitting value of LA for each wavelength, derived from the best ratio of LA/LT and the LT value for the best value of I. The range of acceptable LA values is rather large in the model fits, and so we have made our comparisons for both the nominal value and for values consistent with the acceptable range of this parameter.
It is notable that the behaviors observed for the mean temperature and the first harmonic parameters are generally in good agreement with the thermal model predictions in most cases. However, there are two possible discrepancies. First we note that the nominal thermal models tend to underpredict the amplitudes that are observed in the phase curve fits. The derived value of δ for the SubMM wavelength was 1 from the thermal model fits, whereas a value of ~0.7 was more consistent with the phase curve fits. Moreover, it is noteworthy that the phase difference in the thermal model predictions, seen in Fig. 9c, is not consistent with the phase curve result. At this time, these differences may just be the result of uncertainties in the derivation of the parameters, but in future work we hope to better understand how such a difference arose and whether it may be indicative of unmodeled features of the real nucleus surface.
A second important difference to point out is that the mean brightness temperature of the data and the model diverge significantly above 40 degrees effective latitude, with the model prediction heating to ~195 K close to 70 degrees, while the MIRO brightness temperatures level out at ~175 K at these effective latitudes. We think that an obvious reason for this deviation is that the thermal model does not include the effects of sublimation of the ices in places where the temperatures achieve a value that is capable of significant sublimation. Detailed thermal models that consider this effect are beyond the scope of this paper. However, we have calculated a simple thermal model, with sublimation treated simply as a part of the surface boundary condition. In this case, the boundary condition includes the cooling of the surface caused by the sublimation process in addition to heating by solar insolation and cooling by infrared radiation. This may be written 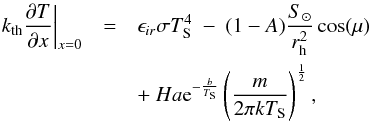 where TS is the surface temperature, H is the latent heat of sublimation (2.8345 × 106 J kg-1), m is the mass of the water molecule, and the constants a and b in the Clausius-Clapeyron equation have values 3.56 × 1012 Pa and 6141.667 K respectively (Fanale & Salvail 1984). A sublimation coefficient of 1 was assumed in view of the generally low temperatures of the nucleus (Kossacki & Markiewicz 2013). We find that the effect is to reduce the surface temperature at 70 degrees effective latitude by approximately 15 K compared to models with no sublimation, which is the approximate value observed by MIRO. The treatment of the effects of sublimation on the interpretation of the MIRO observations will be a subject of future work.
where TS is the surface temperature, H is the latent heat of sublimation (2.8345 × 106 J kg-1), m is the mass of the water molecule, and the constants a and b in the Clausius-Clapeyron equation have values 3.56 × 1012 Pa and 6141.667 K respectively (Fanale & Salvail 1984). A sublimation coefficient of 1 was assumed in view of the generally low temperatures of the nucleus (Kossacki & Markiewicz 2013). We find that the effect is to reduce the surface temperature at 70 degrees effective latitude by approximately 15 K compared to models with no sublimation, which is the approximate value observed by MIRO. The treatment of the effects of sublimation on the interpretation of the MIRO observations will be a subject of future work.
4.4. Deviations from the models
 |
Fig. 10 Residuals to best fitting model for the SubMM channel are overlaid on an image of the mean solar insolation for the nucleus. In this presentation, the comet is viewed from different directions and the image and contour maps are created in an orthographic projection. The contours of residuals are presented in units of brightness temperature (K); a color key for the contours is presented to the right of the contour maps. The viewing geometry is indicated on the top of each subfigure. |
If radiometric measurement and calibration uncertainies were the only error source in this investigation, then a good model of the MIRO data should fit the observations to about 1 K. However, there are certainly other sources of systematic errors that could be considered when assessing the quality of the fit. Indeed, given the existence of other possible systematic errors, and given the obvious complexity of the 67P surface, it should not be surprising that very simple models do not fit the data down to the radiometer errors. Some of the possible reasons for this are described below.
One consideration is that the temperature of a point on the surface is highly dependent on its orientation to the Sun. Given the large variation in mean brightness temperature with effective latitude, a relatively small error of 1 degree in the orientation of a surface normal in the digital shape model can lead to a 1 K difference in the brightness temperature. Moreover, the rough surface of the comet means that there are areas within the beam with different orientations. Finally, most places on the surface of the nucleus spend a portion of their day in shadow, and so the local illumination is more complex than can be accounted for in the simple models considered here.
Another consideration is that the nucleus may not have the same values of thermal properties or millimeter/submillimeter penetration depth at all points on the surface. If this is the case, then the best fit model will fail to reproduce the observations accurately and a large residual will appear. Therefore, we have made maps of the residuals to the best model in order to investigate possible variations over the surface. There are many real ways for the model not to match the data. First, we note that sublimation will tend to make negative residuals since this effect depresses the local temperature below what would be observed without the effect. We also note that one of the main results of an increase in thermal inertia over the model values is to increase the observed brightness temperature of the region at all times of day, which would lead to a positive residual. Finally, of course, points on the surface which have strong shadowing that is not in phase with the expectations of our simple treatment of effective latitude and longitude, as occurs in the neck region of the nucleus, would be expected to show residuals as well.
We have computed model residuals over the entire nucleus, not just the regions used for data fitting in this paper, in order to see whether the “local” results from the Imhotep region provide reasonable values for the rest of the surface. Figure 10 shows the residuals maps superimposed on images of the mean insolation as viewed towards the body, the head and the neck regions. Our fitting has been carried out using data from the body region, and it is notable that there are no large residuals over the Imhotep region which was the main region fit to the model. It is also apparent that the residuals on the head region of the nucleus are similarly small, indicating that the same model works reasonably well at that location. Large residuals are observed at many other places on the nucleus, however. At high body latitudes, where the mean insolation is also high, we note that the residuals tend to be negative and well correlated with the insolation map. This is perhaps best interpreted as the effect of sublimation from these locations depressing the temperatures observed by MIRO, as described in the previous section. Finally, there are significant residuals in the neck region of the nucleus. We caution that the effect of one lobe of the nucleus shadowing the other may lead to differences from our simple thermal model. However, it is interesting that the Hapi region has negative residuals which might be indicative of sublimation. The “walls” of the neck region, corresponding approximately to the Seth and Hathor regions, appear as positive residuals, which might indicate larger thermal inertia values in these areas. Detailed examination of the residuals maps shows correlations with many other surface features and will be the subject of a future paper.
5. Map of subsurface temperatures
The MIRO instrument offers a view below the surface of the nucleus which can be useful in the interpretation of outgassing results from the surface. Certain temperatures must be achieved in order to sublimate different ices, and our subsurface measurements of temperature may be useful in the identification of regions where some ices are sublimating and others are not. For example, the Rosina instrument has already found fluctuations of the composition of gas in the coma which may be related to diurnal or seasonal temperatures (Hässig et al. 2015). Therefore, it is useful to present maps of the likely temperatures within the surface that can guide further interpretations.
Given a thermal model that provides a reasonable fit to the observed MIRO brightness temperatures, it is possible to create a map of the physical temperatures that correspond to a particular depth below the surface. The MIRO emission arises from depths between approximately 1 cm and 4 cm. We adopt the thermal inertia model with a value of I = 22, corresponding to the best fitting values, and compute the model temperature, assuming the thermal parameters that have been adopted for this study, at a depth of 2 cm beneath the surface that would be implied by this value of the thermal inertia.
Figure 11 shows a predicted map of the diurnal maximum value of the temperature at a depth of 2 cm, according to the thermal model. Overall, there is a large variation of this quantity with latitude, but in detail the maximum temperature follows the solar insolation map in Fig. 1 very closely since, according to our results, the main determinant of the temperature in a particular region on the nucleus is expected to be its local orientation to the Sun.
 |
Fig. 11 Maximum temperature at a depth of 2 cm for the I = 22 thermal inertia model, which falls closest to our best fitting values. The thermal model does not include the effects of water ice sublimation and probably over estimates the temperatures in high latitude regions. |
6. Conclusions
Continuum observations of 67P were obtained by the MIRO instrument at MM (1.6 mm) and SubMM (0.5 mm) wavelengths. The observations are consistent with basic expectations for emission that arises from the diurnally varying subsurface of the comet nucleus, with the MM channel probing deeper than the SubMM channel. Quantitative fits of simple, homogeneous models favor low thermal inertia in the range I = 10–30 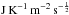 ; the thermal skin depth of this model is approximately 1 cm. The MM emission arises from a depth of approximately 4 cm, and the SubMM emission arises from a depth of approximately 1 cm, with uncertainties in these values of approximately 50%. These results are in good agreement with those of Choukroun et al. (2016) who studied the polar night temperatures of the nucleus with the MIRO instrument.
; the thermal skin depth of this model is approximately 1 cm. The MM emission arises from a depth of approximately 4 cm, and the SubMM emission arises from a depth of approximately 1 cm, with uncertainties in these values of approximately 50%. These results are in good agreement with those of Choukroun et al. (2016) who studied the polar night temperatures of the nucleus with the MIRO instrument.
Comparison of the mean MIRO brightness temperatures to the predictions of thermal models shows good agreement for most latitudes, but the data fall below the thermal model predictions at high latitudes where the temperatures should be the highest. This behavior is consistent with expectations of the sublimation of water ice at these locations where the surface is strongly heated by the sun. Moreover, we note that the temperatures seen by MIRO are consistent with the values required to explain the water gas production seen at this time from the active parts of the nucleus, as elaborated in the supplementary materials of Gulkis et al. (2015).
Simple homogenous models generally appear to give a consistent fit to both the MM and SubMM data, but there are some interesting inconsistencies as well. For example, the phase difference between MM and SubMM diurnal waves cannot be explained by a simple homogeneous model, and the best fitting homogeneous thermal model does not match all details of the observed phase curves. These differences may be a clue that there is vertical structure of the physical properties in the upper few centimeters of the surface materials. Such a depth variation would not be surprising in view of both laboratory simulations (e.g. Gruen et al. 1991,1993; Kossacki et al. 1997) and theoretical modeling (e.g. Prialnik & Mekler 1991; Espinasse et al. 1991; Steiner & Komle 1993; Benkhoff & Huebner 1995), which suggest that layers develop due to sublimation of and recondensation of ices. The possibility of directly probing these effects will be investigated in MIRO’s future work. Finally, comparison of the MIRO data to thermal model predictions show residuals that are correlated with surface features. This probably indicates regional differences in insolation, sublimation, and/or thermal properties and will be another topic for followup investigations.
Acknowledgments
The authors acknowledge support from their institutions and funding sources. A part of this work has been conducted at the Jet Propulsion Laboratory, California Institute of Technology, under contract to the National Aeronautics and Space Administration (NASA). Government sponsorship acknowledged. A part of the research was carried out at the Max-Planck Institut für Sonnensystemforschung with financial support from Deutsches Zentrum für Luft- und Raumfarht and Max-Planck Gesellschaft. Parts of the research were carried out by LESIA and LERMA, Observatoire de Paris, with financial support from CNES and CNRS/Institut des Sciences de l’Univers. A part of the research was carried out at the National Central University with funding from the Taiwanese National Science Counsel grant NSC 101-2111-M-008-016. A part of the research was carried out at the University of Massachusetts, Amherst, USA. The MIRO team acknowledges the OSIRIS team for providing pre-publication data and helpful discussions to support this analysis. Support from ESA’s Rosetta Mission Operations Control center and ESA’s Rosetta Science Ground Segment, for preparation and implementation of the observations, and communication of the acquired data, is gratefully acknowledged. We thank Y. Anderson, T. Koch, R. Nowicki, L. Pan and the late Dr. Lucas Kamp for their efforts in scheduling, operations, and support of the MIRO instrument.
References
- Acton, C. 1996, Planet. Space Sci., 44, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Benkhoff, J., & Huebner, W. F. 1995, Icarus, 114, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Birkebak, R. 1972, The Moon, 4, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Capaccioni, F., Coradini, A., Filacchione, G., et al. 2015, Science, 347, 628 [CrossRef] [Google Scholar]
- Carslaw, H., & Jaeger, J. 1959, Conduction of Heat in Solids (London: Oxford University Press) [Google Scholar]
- Choukroun, M., Keihm, S., Schloerb, F. P., et al. 2015, A&A, 583, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espinasse, S., Klinger, J., Ritz, C., & Schmitt, B. 1991, Icarus, 92, 350 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fanale, F., & Salvail, J. 1984, Icarus, 60, 476 [NASA ADS] [CrossRef] [Google Scholar]
- Gary, B. L., & Keihm, S. L. 1978, Proc. Lunar Planet. Sci. Conf. 9th, 2885 [Google Scholar]
- Gruen, E., Bar-Nun, A., Benkhoff, J., et al. 1991, in Comets in the post-Halley era, eds. R. L. Newburn, Jr., M. Neugebauer, & J. Rahe, IAU Colloq., 116, Astrophys. Space Sci. Lib., 167, 277 [Google Scholar]
- Gruen, E., Gebhard, J., Bar-Nun, A., et al. 1993, J. Geophys. Res., 98, 15091 [Google Scholar]
- Gulkis, S., Frerking, M., Crovisier, J., et al. 2007, Space Sci. Rev., 128, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Gulkis, S., Allen, M., von Allmen, P., et al. 2015, Science, 347, 0709 [Google Scholar]
- Hässig, M., Altwegg, K., Balsiger, H., et al. 2015, Science, 347, 0276 [CrossRef] [Google Scholar]
- Heggy, E., Palmer, E., Kofman, W., et al. 2012, Icarus, 221, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Hemingway, B., Robie, R., & Wilson, W. 1973, Proc. of the 4th Lun. Sci. Conf., 3, 2481 [Google Scholar]
- Jorda, L., Gaskell, R., Hviid, S. F., et al. 2015, NASA Planetary Data System and ESA Planetary Science Archive [Google Scholar]
- Keihm, S., Kamp, L., Gulkis, S., et al. 2013, Icarus, 226, 1086 [Google Scholar]
- Kossacki, K. J., & Markiewicz, W. 2013, Icarus, 224, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Kossacki, K. J., Kömle, N. I., Leliwa-Kopystyński, J., & Kargl, G. 1997, Icarus, 128, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Lamy, P., Toth, I., Groussin, O., et al. 2008, A&A, 489, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muhleman, D. 1972, Prog. Astronaut. Aeronaut, 28, 51 [NASA ADS] [Google Scholar]
- Müller, T. 2002, Meteor. Planet. Sci., 37, 1919 [Google Scholar]
- Prialnik, D., & Mekler, Y. 1991, ApJ, 366, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Sierks, H., Barbieri, C., Lamy, P., et al. 2015, Science, 347, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Spencer, J., Lebofsky, L., & Sykes, M. 1989, Icarus, 78, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, G., & Komle, N. I. 1993, J. Geophys. Res., 98, 9065 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Mean solar insolation on the surface of 67P during the month of September 2014. For each point on the surface, the mean value of the cosine of the angle of incidence during one rotation of the nucleus is computed for a date in mid-September using the SHAP5 digital shape model developed by the OSIRIS team. The effect of shadowing is considered in the calculation. It should be noted that the irregular shape of the comet results in some areas where the latitude and longitude refer to three surface points rather than one. For this figure, we have displayed the value for the outermost intersection point when this occurs. The region outlined with the solid white is that selected for fitting models of the diurnal brightness temperatures, as described in Sect. 3. The region outlined with the dotted line was used for fitting physical models, as described in Sect. 4. Most of the coverage used for model fitting lies in the Imhotep and Ash geomorphological regions defined by the OSIRIS team (Sierks et al. 2015). |
| In the text | |
 |
Fig. 2 Data obtained for the SubMM and MM channels in 4 degree wide bins of effective latitude are fit to a Fourier series. The SubMM and MM data for each bin are shown side-by-side; the effective latitude is shown in the lower right of each panel. Models that include both the first and second harmonics in the Fourier Series (solid) and models that only include the first harmonic terms (dashed) have been fit to each set of data. |
| In the text | |
 |
Fig. 3 MIRO harmonic data fit results for the SubMM (open circles) and MM (filled circles) channels. The points are plotted with formal error bars shown as well. Often, since the formal errors are small, the errorbars do not extend beyond the point symbols. Panel a) shows the mean brightness temperature derived from the fits. Panel b) shows the first harmonic amplitude of the brightness temperature variation. Panel c) shows the phase of the first harmonic of the brightness temperature variation. |
| In the text | |
 |
Fig. 4 MIRO harmonic data fits compared to the brightness temperature data. Panel a) shows the rms of the fits to each latitude bin. The MM rms is typically 2–3 K while the SubMM rms is typically 7–8 K. These values are significantly greater than would be expected from measurement errors alone, indicating some real, unmodeled, variations in the dataset. Panel b) shows all MM brightness temperatures compared to lines representing the mean model temperature plus the first harmonic amplitude and the mean minus the first harmonic amplitude. Panel c) shows the same information for the SubMM channel. |
| In the text | |
 |
Fig. 5 Ratio of the mean antenna temperature observed by the SubMM channel to that of the MM channel. This is a measure of the ratio of the power received by the MIRO instrument at the two wavelengths. The solid line on the figure shows the expected result for this ratio assuming that the SubMM brightness temperature is equal to the MM brightness temperature. |
| In the text | |
 |
Fig. 6 Ratio of the amplitude of the MM diurnal brightness temperature to the SubMM amplitude. The horizontal lines show expected ratio for different values of δSubMM under the assumption that δMM = 4δSubMM. |
| In the text | |
 |
Fig. 7 Difference between the phase of the millimeter-wave diurnal brightness temperatures and the phase of the submillimeter-wave variations. The horizontal lines show the expectations for the same set of models that were compared to the amplitude ratio data in Fig. 6. The observed phase difference is too large to be explained by the simple model. |
| In the text | |
 |
Fig. 8 Contour plots of χ2 of MIRO observations compared to models. The χ2 for the SubMM data is shown in the left-hand figure; the χ2 for the MM data is shown on the right. χ2 values have been normalized to the minimum value found in the fit, and the contours are shown for 1.1, 1.25, 1.5, 2, 3, and 4 times this minimum value. The scale for thermal inertia is logarithmic, but labeled with the values of the grid parameters. The LA/LT ratio models for the grid were computed on a linear scale. A (+) symbol is plotted at the location of the minimum value of χ2 derived from fitting the grid data near the minimum. The error ellipse, corresponding to an increase in χ2 of 5% above the minimum is shown. |
| In the text | |
 |
Fig. 9 Comparison of MIRO harmonic data fit results for the submillimeter (open circles) and millimeter (filled circles) channels with thermal model closest to the best fitting thermal inertia (I = 22). Panel a) shows the mean temperature derived from the fits. Models for I = 12 and I = 37 are also shown for comparison. Panel b) shows the first harmonic amplitude. The SubMM channel model is shown as a solid black line, with dotted lines showing the range of values allowed by acceptable values of LA. The gray line shows the same results for the MM channel. Panel c) shows the phase of the first harmonic. The curves have the same meaning as in panel b). |
| In the text | |
 |
Fig. 10 Residuals to best fitting model for the SubMM channel are overlaid on an image of the mean solar insolation for the nucleus. In this presentation, the comet is viewed from different directions and the image and contour maps are created in an orthographic projection. The contours of residuals are presented in units of brightness temperature (K); a color key for the contours is presented to the right of the contour maps. The viewing geometry is indicated on the top of each subfigure. |
| In the text | |
 |
Fig. 11 Maximum temperature at a depth of 2 cm for the I = 22 thermal inertia model, which falls closest to our best fitting values. The thermal model does not include the effects of water ice sublimation and probably over estimates the temperatures in high latitude regions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


