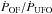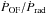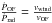| Issue |
A&A
Volume 583, November 2015
|
|
|---|---|---|
| Article Number | A99 | |
| Number of page(s) | 16 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201526020 | |
| Published online | 02 November 2015 | |
The multi-phase winds of Markarian 231: from the hot, nuclear, ultra-fast wind to the galaxy-scale, molecular outflow⋆
1
Scuola Normale Superiore, Piazza dei Cavalieri 7,
56126
Pisa,
Italy
e-mail:
chiara.feruglio@sns.it
2
IRAM–Institut de RadioAstronomie Millimétrique,
300 rue de la Piscine, 38406 Saint Martin
d’Hères,
France
3
INAF–Osservatorio Astronomico di Roma, via Frascati
33, 00040
Monteporzio Catone,
Italy
4
Dipartimento di Fisica e Astronomia, Universitá di
Firenze, via G. Sansone 1, 50019
Sesto Fiorentino, Firenze, Italy
5
Cavendish Laboratory, University of Cambridge,
19 J. J. Thomson Ave.,
Cambridge
CB3 0HE,
UK
6
Kavli Insitute for Cosmology, University of
Cambridge, Madingley
Road, Cambridge
CB3 0HA,
UK
7
ASDC-ASI, via del Politecnico, 00133
Roma,
Italy
8
Department of Astronomy and CRESST, University of
Maryland, College
Park, MD
20742,
USA
9
Joint Space Science Institute, University of
Maryland, College
Park, MD
20742,
USA
Received: 4 March 2015
Accepted: 25 August 2015
Mrk 231 is a nearby ultra-luminous IR galaxy exhibiting a kpc-scale, multi-phase AGN-driven outflow. This galaxy represents the best target to investigate in detail the morphology and energetics of powerful outflows, as well as their still poorly-understood expansion mechanism and impact on the host galaxy. In this work, we present the best sensitivity and angular resolution maps of the molecular disk and outflow of Mrk 231, as traced by CO(2−1) and (3−2) observations obtained with the IRAM/PdBI. In addition, we analyze archival deep Chandra and NuSTAR X-ray observations. We use this unprecedented combination of multi-wavelength data sets to constrain the physical properties of both the molecular disk and outflow, the presence of a highly-ionized ultra-fast nuclear wind, and their connection. The molecular CO(2−1) outflow has a size of ~1 kpc, and extends in all directions around the nucleus, being more prominent along the south-west to north-east direction, suggesting a wide-angle biconical geometry. The maximum projected velocity of the outflow is nearly constant out to ~1 kpc, thus implying that the density of the outflowing material must decrease from the nucleus outwards as ~r-2. This suggests that either a large part of the gas leaves the flow during its expansion or that the bulk of the outflow has not yet reached out to ~1 kpc, thus implying a limit on its age of ~1 Myr. Mapping the mass and energy rates of the molecular outflow yields 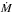 OF = [500−1000]
M⊙ yr-1 and
Ėkin,OF = [7−10] × 1043 erg s-1. The total kinetic energy of the outflow is Ekin,OF is of the same order of the total energy of the molecular disk, Edisk. Remarkably, our analysis of the X-ray data reveals a nuclear ultra-fast outflow (UFO) with velocity −20 000 km s-1,
OF = [500−1000]
M⊙ yr-1 and
Ėkin,OF = [7−10] × 1043 erg s-1. The total kinetic energy of the outflow is Ekin,OF is of the same order of the total energy of the molecular disk, Edisk. Remarkably, our analysis of the X-ray data reveals a nuclear ultra-fast outflow (UFO) with velocity −20 000 km s-1,
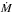 UFO = [0.3−2.1] M⊙ yr-1, and momentum load
UFO = [0.3−2.1] M⊙ yr-1, and momentum load
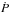 UFO/
UFO/
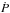 rad = [0.2−1.6]. We find
Ėkin,UFO ~
Ėkin,OF as predicted for outflows undergoing an energy conserving expansion. This suggests that most of the UFO kinetic energy is transferred to mechanical energy of the kpc-scale outflow, strongly supporting that the energy released during accretion of matter onto super-massive black holes is the ultimate driver of giant massive outflows. The momentum flux
rad = [0.2−1.6]. We find
Ėkin,UFO ~
Ėkin,OF as predicted for outflows undergoing an energy conserving expansion. This suggests that most of the UFO kinetic energy is transferred to mechanical energy of the kpc-scale outflow, strongly supporting that the energy released during accretion of matter onto super-massive black holes is the ultimate driver of giant massive outflows. The momentum flux
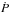 OF derived for the large scale outflows in Mrk 231 enables us to estimate a momentum boost
OF derived for the large scale outflows in Mrk 231 enables us to estimate a momentum boost
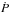 OF/
OF/
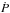 UFO ≈ [30−60]. The ratios Ėkin,UFO/Lbol,AGN = [1−5] % and Ėkin,OF/Lbol,AGN = [1−3] % agree with the requirements of the most popular models of AGN feedback.
UFO ≈ [30−60]. The ratios Ėkin,UFO/Lbol,AGN = [1−5] % and Ėkin,OF/Lbol,AGN = [1−3] % agree with the requirements of the most popular models of AGN feedback.
Key words: galaxies: individual: ... / galaxies: active / galaxies: evolution / galaxies: ISM / galaxies: kinematics and dynamics / quasars: general
© ESO, 2015
1. Introduction
Luminous AGN are likely to play a key role in the evolution of their host galaxies through powerful winds and outflows. In particular, during the earliest, dust obscured phase of AGN activity, characterized by a large amount of molecular gas available to fuel black hole accretion, the huge nuclear energy output enables the production of AGN-driven outflows. These can perturb and possibly expel most of the gas out of the host galaxy, therefore leading to the quenching of star-formation. Current theoretical models of galaxy evolution include AGN feedback to account for galaxy colours and the lack of a large population of local massive star forming galaxies (SFG, Granato et al. 2001, 2004; Di Matteo et al. 2005; Menci et al. 2006, 2008; Bower et al. 2006; Croton et al. 2006).
Observations across the electromagnetic spectrum reveal that AGN winds are widespread, suggesting that they cover large solid angles and an extremely broad range of gas ionization parameter (Elvis 2000 and references therein). In X-rays mildly ionized warm absorbers with velocities of ~500−1000 km s-1 are observed in more than half of AGN (Piconcelli et al. 2005; Blustin et al. 2005; McKernan et al. 2007). Furthermore, there is growing evidence for the existence of ultra-fast outflows (UFOs) via the detection of highly ionized Fe K-shell absorption arising from a gas moving at velocities up to 0.2–0.4c (Pounds et al. 2003; Reeves et al. 2009; Tombesi et al. 2011, 2015 and references therein). Optical/UV Broad Absorption Line (BAL) systems associated to ionized outflowing (−2000 ÷ −20 000 km s-1) gas has been observed in 20−40% of QSOs (Dai et al. 2008), with some remarkable examples reaching up to hundred of pc away from the nucleus (e.g., Borguet et al. 2013). Broad [OIII] emission lines with velocities up to a few thousands km s-1 are commonly found in AGN (Zhang et al. 2011; Shen & Ho, 2014), and ionized and neutral gas with similar velocities is found on galactic scale (1−30 kpc) in a few tens AGN from the local Universe up to z = 2−3 (Cano-Diaz et al. 2012; Rupke & Veilleux 2011, 2013; Harrison et al. 2014, 2012; Nesvadba et al. 2008; Genzel et al. 2014; Cresci et al. 2015). Radio observations have also detected many neutral atomic gas outflows with velocities up to 1500 km s-1 (Morganti et al. 2005; Teng et al. 2013). Finally, fast (up to 1000−2000 km s-1) molecular gas, extending on kpc scales is found in a few dozen, mostly highly obscured, AGN in dusty SFGs (Feruglio et al. 2010; Cicone et al. 2014; and Veilleux et al. 2013 for compilations of molecular outflows).
Two main scenarios for quasar-mode winds and feedback have been developed so far. The first is a two-stage mechanism (Lapi et al. 2005; Menci et al. 2008; Zubovas & King 2012; Faucher-Giguere & Quataert 2012), where a (semi)relativistic wind (such as the UFOs detected in the X-ray band), accelerated by the AGN radiation, shocks against the galaxy ISM. The shocked gas can reach temperatures of 107 K or larger. Hot gas extended on kpc scales has been detected in galaxies with galactic-scale outflows (Feruglio et al. 2013; Wang et al. 2014; Veilleux et al. 2014). If the cooling time of the post shock gas is smaller than the dynamical time, tcool<tdyn, then the gas can cool to ~104 K, emitting typical warm ionized gas lines ([OIII], Hα, etc). Further cooling leads to the formation of H2, which can further enhance the cooling rate, promptly leading to the formation of more complex molecules, and a multi-phase, galaxy-scale outflow with a momentum boost 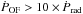 should develop. Simulations of AGN feedback triggered by cold precipitation produce indeed a multi-phase structure of the gas in the galaxy cores (Gaspari et al. 2013).
should develop. Simulations of AGN feedback triggered by cold precipitation produce indeed a multi-phase structure of the gas in the galaxy cores (Gaspari et al. 2013).
In the second scenario, outflows are radiatively accelerated by much slower, “gentle” winds, in which the momentum boost is at most 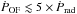 (Thompson et al. 2015). This may prevent gas clouds from escaping the halo gravitational potential, hence making them rain back onto the galaxy. Self-shielding of the galactic disk dusty clouds may further minimize AGN feedback.
(Thompson et al. 2015). This may prevent gas clouds from escaping the halo gravitational potential, hence making them rain back onto the galaxy. Self-shielding of the galactic disk dusty clouds may further minimize AGN feedback.
The geometry of quasar-driven outflows as well as their energy and momentum transport mechanisms are still poorly constrained by observations. This prevents both a clean discrimination between the two scenarios, and the development of detailed multi phase feedback models. This work aims at filling this gap by means of high spatial resolution CO mapping and deep X-ray spectroscopy of Mrk 231. Mrk 231 has been known for long as the closest ULIRG/QSO, with a total infrared luminosity of 3.6 × 1012L⊙ (Sanders et al. 2003), AGN bolometric luminosity of 5 × 1045 erg s-1, and a star formation rate of 140 M⊙ yr-1 (Veilleux et al. 2009). It is an iron low-ionization broad absorption-line quasars (FeLoBAL), and it displays nuclear neutral and ionized outflows in several optical and UV tracers (Lipari et al. 2009; Veilleux et al. 2014), and a powerful neutral outflow extended on at least 3 kpc (Rupke & Veilleux 2011). This is tracing a wide-angle conical outflow proceeding at an uniform speed of −1000 km s-1 along the minor axis of the molecular disk. The first prototypical massive molecular outflow, extended on kpc scale, was discovered in this galaxy (Feruglio et al. 2010; Fischer et al. 2010; Aalto et al. 2012; 2015; Gonzalez-Alfonso et al. 2014). These observations leave several questions open, i.e. (i) what are the size and the geometry of the molecular outflow; (ii) whether and how this outflow is associated with the atomic neutral and ionized ones; (iii) which is the momentum boost of the molecular outflow; (iv) is there evidence of any fast highly ionized nuclear wind in Mrk 231?
This work is a study of the multi-phase winds in Mrk 231 (z = 0.04217, DL = 187.6 Mpc, scale 0.837 kpc/′′). Specifically, Sect. 2 presents the (sub)millimeter observations of molecular gas traced by CO(2−1) and (3−2), obtained with the IRAM/PdBI. Section 3 presents an analysis of the kinematics of the nuclear region of Mrk 231, including the molecular disk and the outflow, and spatially resolved mass flow rates and outflow kinetic power. Section 4 presents an analysis of archival X-ray data from Chandra and NuSTAR, that led us to detect a nuclear, highly ionized UFO. In Sect. 5 the relation between the spatially-extended molecular outflow and the UFO is discussed in the framework of models for energy-conserving large-scale winds driven by AGN.
Plateau de Bure Interferometer observations of Mrk 231 used in this work.
2. (Sub)-Millimeter observations
We use three data sets obtained with the IRAM Plateau de Bure Interferometer (PdBI). The first data set (DS1) consists of observations carried out with the most extended (A) 6 antenna array configuration, which has a maximum baseline length of 760 m, at a frequency of 221.21 GHz, targeting the CO(2−1) line. Absolute flux calibration is based on the quasars 3C 84 (13.2 Jy) and 1150+497 (2.6 Jy), which also served as amplitude/phase calibrator. The accuracy of the absolute flux scale is of the order of 20%, while the relative flux calibration between the 4 available observations is better than 10%. The on source time of DS1 after calibration is 5.2 h. The synthesized beam is 0.48 by 0.36 arcsec, PA 73 deg (~400 pc at the redshift of the source z = 0.04217). The achieved visibility (thermal) noise is 1.3 mJy/beam in 20 MHz channels (corresponding to 27 km s-1). Natural weighting and a simple cleaning algorithm (hogbom) were used in order to minimize secondary lobes. The visibility tables and data cubes have been binned to a 20 MHz spectral resolution, which is our preferred trade-off between spectral sampling and sensitivity.
The second data set (DS2) has been obtained by merging the visibilities of DS1 with previous observations with short baselines reported in Cicone et al. (2012). The relative flux calibration of the short and long-baseline data is based on the quasar 3C84, which has varied from 7.7 Jy in 2010 to 13.2 Jy in 2013. Based on the light curve of 3C 84 around 220 GHz we can expect that the two data sets have consistent flux scales at the 20% level. DS2 has an on source time of 8.7 h, and 1σ sensitivity 0.8 mJy/beam in 20 MHz channels. Maps for DS2 were produced as detailed above, resulting in a clean beam of 0.9 by 0.8 arcsec, PA 57.
The third data set (DS3) consists of an observation of CO(3−2) at 331.8 GHz done in January 2012, using the compact (D) array configuration. The maximum phase rms during the observation was about 50 deg, water vapor around 1 mm, and system temperatures between 300 and 500 K. The quasar 1150 + 497 (0.96 Jy at 331.9 GHz) was used for phase/amplitude calibration. MWC349 was used for flux calibration and provides an accuracy of about 20% at this frequency. The synthesized beam is 1.5 by 1.3 arcsec, with a PA of 84 deg. The 1σ sensitivity is 8.0 mJy/beam per 20 MHz.
DS1 has the best angular resolution and will be used to locate and characterize the kinematics of the inner ~1 arcsec of the system. DS2 has the best sensitivity and will be used to map fainter and more diffuse emission. Table 1 summarizes the main parameters of the observations.
 |
Fig. 1 Continuum-subtracted spectra of CO(2−1) from DS1 (top panel) and of CO(3−2) (bottom panel). The plots display the full velocity range achieved by the observed bandwidth. Zoomed views are shown in the insets. |
2.1. 1.4 mm data
The 1.4 mm continuum was estimated by averaging the visibilities in two spectral regions free of lines in the range −3000 to −2000 km s-1, and 1500 to 1600 km s-1. We tested different channel ranges to average the continuum visibilities, mainly on the blue side (1500 to 3000 km s-1 negative velocities). The features seen at velocity −600 out to −1000 km s-1, and those out to +1000 km s-1, persist using different channel ranges to estimate the continuum. The significance of spectral features beyond these limits are more difficult to assess. In particular, on the red side, where the spectral range is limited to +1800 km s-1, the estimate of the continuum may be more uncertain, and features redder than +1000 km s-1 could be spurious. A point source fit to the visibilities averaged as explained above, gives a 1.4 mm continuum flux density of 43.8 ± 0.5 mJy (Table 2), in agreement both with the recent interferometric measurement of Aalto et al. (2015), done with similar baselines, and with Downes & Solomon (1998).
The continuum visibility table, derived as explained above, has been subtracted from the total uv data to produce the line table and the corresponding map. Figure 1, upper panel, shows the CO(2−1) spectrum, extracted in a circular region of diameter 1.5 arcsec centered on the emission peak on the map. The peak flux of CO(2−1) is 0.73 Jy, from a Gaussian fit of the spectral line, and agrees within the flux accuracy (± %20) with previous interferometric measurements of Cicone et al. (2012), Downes & Solomon (1998) (which had slightly larger beam), and with the flux measured with the IRAM 30 m dish (Solomon et al. 1997). This suggests that little emission is filtered out by long baselines and that most of the CO emission occurs within a 1.5 arcsec central region. The line profile is similar to that found in previous CO(1−0) and (2−1) observations (Feruglio et al. 2010; Cicone et al. 2012). CO(2−1) emission is detected out to about ± 1000 km s-1.
1.4 and 0.9 mm continua visibility fit parameters.
Figure 2 (upper panels) shows the channel contour maps of CO(2−1) emission integrated around the systemic velocity (± 300 km s-1), in the blue (–400 to –1000 km s-1), and red (400 to 1000 km s-1) sides of the line. Both the systemic and the red/blue shifted emission are more extended than the synthesized beam and have a size up to ~1.5 arcsec. We performed visibility fitting of these three CO(2−1) line components, systemic, blue and redshifted emission, after having averaged each visibility set in the corresponding spectral range (similarly to Cicone et al. 2012, and references therein). The positions, fluxes and sizes so derived are reported in Table 3 for each component, together with the respective spectral range and the adopted source model. The visibility fits are independent of the synthesized beam and of the CLEAN algorithm, and there is no need to deconvolve the apparent size on the map. The integrated fluxes agree within the errors with the measurements of Cicone et al. (2012). The FWHM size of the systemic gas component is 0.86 ± 0.01 arcsec, corresponding to a physical scale of ~700 pc. The bulk of the blue and red wing emission of CO(2−1) is compact, having FWHM sizes of about a beam by fitting a with Gaussian function. A fainter spatially extended structure is seen in the channel maps of the red and blue wings (Fig. 3), which can hardly be fitted by a simple Gaussian model, and, in the case of the receding component, is extended out to at least 1′′ (~1 kpc) north-east off the AGN. This component is also seen in HCN(1−0), on similar spatial scales and orientation (Aalto et al. 2012). The positions of both the systemic CO emission and of the 1.4 mm continuum are consistent with that of the 1.4 GHz radio continuum measured by the VLBI, which traces the AGN emission. The blue and the redshifted emissions are instead both offset from the AGN position in the south-western direction by (−0.2,−0.3) and (−0.2,−0.1) arcsec, respectively. These offsets are about ~10 larger than the position errors of our data, i.e., 0.02″ for the blue and 0.01″ for the red component, respectively (Table 3). The positions of the wing emission are consistent with those seen in HCN(1−0) (Aalto et al. 2012), and with those previously measured by Cicone et al. (2012)1.
 |
Fig. 2 Channel maps of CO(2−1) (DS1, upper panels) and CO(3−2) (lower panels) in three different velocity ranges (indicated by the labels). The contours start from 4σ and are in steps of 1σ for the blue and red wing maps (right and left panels for both CO transitions, respectively). Negative contours are shown by dotted lines, and are in steps of 1σ, starting at −1σ. In the systemic component map (middle panels), contours are in steps of 10σ starting from 10σ, for the sake of clarity. The synthesized beams are shown by hatched areas for each data set. 1σ = 0.14 Jy km s-1 for CO(2−1), = 0.72 Jy km s-1 for CO(3−2). The cross marks the position of the 1.4 GHz continuum as measured by the VLBI, α = 12:56:14.2339, δ = 56:52:25.237 (J2000, Ma et al. 1998). |
We discuss in the following the possibility that the spectral feature seen between −1000 and −700 km s-1 traces emission from a species different from CO. Specifically, this spectral feature peaks at a frequency of 221.864 (−860 km s-1), which corresponds to that expected for 13CS(5−4) (rest frame frequency 231.220 GHz). 13CS(5−4) was first detected in an extragalactic source in the 1 mm survey of Arp220 (Martin et al. 2011), and traces very dense gas. Its critical density is, in fact, of the order of 106 cm-3. The integrated emission is detected with an 8σ significance. Its FWHM is about 150 km s-1, and the zero spacing flux is 2.5 ± 0.3 mJy, by fitting an unresolved source. 12CS(5−4) is undetected in the IRAM 30 m spectrum down to a 1σ sensitivity of ~1 mK (8.7 mJy, Zhang, Ph.D. thesis). The isotopic ratio 12C /13C in Mrk 231 is about 40, based interferometric data of 12CO and 13CO J = 1−0 (Feruglio et al., in prep.), which agrees with the lower limit given by Glenn & Hunter (2001). Assuming that 13CO comes from approximately the same region as 12CO(1−0), we can apply this isotopic ratio to derive the expected strength of 13CS(5−4), which would be < 0.2 mJy. This suggests that the feature can hardly be identified with 13CS(5−4), and we conclude, therefore, that it is due to approaching CO(2−1).
2.2. 0.9 mm data
The 0.9 mm continuum has been estimated by fitting in the uv plane visibilities averaged in spectral windows. We have tested the continuum estimate and subtraction by using three different spectral windows for visibility averaging. In particular, averaging the spectral windows −1180 to −1000 km s-1, plus 1400 to 2000 km s-1 produces over-subtraction of the continuum red-wards of the line. We find that the best overall continuum subtraction results from using the spectral window 1400 to 2000 km s-1, which gives a continuum flux density of 72.0 ± 2.0 mJy (Table 2). This is our adopted best solution. The continuum visibility table, produced as explained above, has been subtracted from the total visibilities in order to produce the line emission visibility table, which has been used to map the CO(3−2) emission (Fig. 2, bottom panels).
 |
Fig. 3 Channel maps of CO(2−1) from DS1. Contours are in steps of 5σ, starting at 5σ. 1σ = 0.09 Jy km s-1. |
Visibility fits of the CO(2−1) and CO(3−2).
The CO(3−2) spectrum, extracted from a circular aperture of 3 arcsec diameter around the map peak, is shown in Fig. 1 (bottom panel). We measure a flux density of 658 ± 5 Jy km s-1 for the CO(3−2) systemic component. The single dish flux from Wilson et al. (2008), 480 ± 100 Jy km s-1, is slightly smaller than our estimate. A high velocity component is detected in CO(3−2) out to speeds of ± 1000 km s-1, similarly to CO(1−0) and (2−1). The CO(3−2) profile is similar to that of CO(2−1), (1−0), showing an enhanced red wing compared to the blue one. We acknowledge that the systematic uncertainty on the continuum measurement can affect the significance of the faint features seen at large velocities (in particular blue-wards of the line at velocity <−1000 km s-1), but features within ± 800 km s-1 from the line peak are persistent by adopting any of our tested spectral windows. The positions of the systemic, the red and blue-shifted components of CO(3−2) are consistent with those derived for CO(2−1), within the uncertainty associated to the larger beam and to the coarser uv coverage of DS3 (Table 3).
In the following we discuss the possible contribution of H13CN(4-3) emission to the red wing of CO(3−2). Sakamoto et al. (2009) found a ratio CO(3−2) /H13CN(4−3) = 10 in NGC 4418, which implies severe contamination of the CO(3−2) red wing for that source. A ratio of ~10 is excluded for Mrk 231 by the observed spectrum already (Fig. 1). Costagliola et al. (2011) measured for Mrk 231 a H13CN(1−0) = 1.7 Jy km s-1 at a 3σ level. From their spectrum, the line appears somewhat broader than the HCN(1−0), suggesting that it can be blended with some other nearby lines. Indeed, emission from SO (86.1 GHz), and SO2 (on the red side at 86.639 GHz) are expected within ± 300 MHz. These transitions are as bright as H13CN in the Orion and SgrB2 star forming regions (Turner et al. 1989), which can in principle also be the case in Mrk 231. Therefore the measure of Costagliola et al. (2011) must be considered as an upper limit. In fact, this would provide a ratio HCN/H13CN(1−0) ~ 8, based on the strength of HCN(1−0) measured by Aalto et al. (2012), i.e., a factor of five smaller than the isotopic 12C /13C ratio of 40 found by us. Adopting an isotopic ratio of 8 and HCN(4−3) = 65 ± 13 Jy km s-1 (Papadopoulos et al. 2007), we get H13CN(4−3) = 8 Jy km s-1, meaning that this would contribute 25% of the integrated flux in the red wing of CO(3−2). Adopting instead a ratio 13CO /12CO = 40, the contribution to the CO(3−2) red wing would be less than 5%.
 |
Fig. 4 Moment 1 map (left panel, levels are 20 km s-1 each) and Moment 2 map (right panel, levels are 25 km s-1 each) of the systemic component of CO(2−1). Cross: AGN position from Ma et al. (1998). |
The estimates given above assume that H13CN(4−3) is optically thick. Should this not be the case, its flux may be even smaller. Modeling with RADEX non-LTE radiative transport models (van der Tak et al. 2007) to reproduce flux of CO and HCN, suggests instead that H13CN(4−3) is optically thin. In fact, assuming Δv = 60 km s-1 and typical temperatures and column densities (Tkin = 60 K, NH = 1 × 1016 cm-2 for HCN and 1 × 1015 cm-2 for H13CN), we get τ ~ 1 × 10-2 for H13CN(4−3). In this case the flux of H13CN(4−3) would be very small and the contamination of the red wing of CO(3−2) negligible. The maps of the CO(3−2) give an observed temperature of T = 0.2 K in the red wing. The HCN(4−3) flux (65 Jy km s-1, Papadoupulos et al. 2007), implies 0.325 Jy for a line width of 200 km s-1. Ignoring the frequency difference between 340 and 330 GHz, than we would get 5.7 K/Jy for the PdBI data, thus T(HCN(4−3) = 1.85 K (i.e. 0.325 Jy). Modeling with RADEX, and assuming N(H13CN) ~ 1 × 1015 cm-2, n(H2) ~ 1 × 104 cm-3, and Tkin = 60 K, we get T(H13CN(4−3)) ~ 2.5 × 102 K, and S(H13CN(4−3)) = 4.4 mJy, which in turn would give 0.88 Jy km s-1 integrated intensity for a line width of 200 km s-1. In conclusion, a strong contamination from H13CN(4−3) is unlikely and most of the detected flux in the red wing of CO(3−2) is from high speed CO(3−2).
 |
Fig. 5 From left to right: model, model folded with the beam, observed distribution and residuals. Top panels: model of the molecular disk with an exponential disc function. Middle panels: model with two components, an outer ring and an inner exponential disk. Bottom panels: velocity dispersion of the two-component model. |
3. Results of (sub)-mm observations
3.1. Molecular disk
We built moment 1 and 2 maps of the CO(2−1) emission using DS1. The Moment 1 (velocity) map of CO(2−1) in Fig. 4, left panel, shows that rotation occurs in approximately the east-west direction, as previously measured by Downes & Solomon (1998), and the molecular disk extends out to a radius about 800 pc. The S-shaped pattern (Fig. 4) indicates that the kinematics in the inner disk deviates from a simple east-west rotation, and suggests the presence of an inner warped disk on scales of ≤ 0.2″, tilted with respect to the main rotation plane. The Moment 2 map (Fig. 4, right panel) is peaked close to the AGN, and shows branches of emission in the north, south and west directions, also indicating an additional kinematical component.
By fitting an exponential disk model to the visibilities in the velocity range −300 to 300 km s-1 (systemic component) we derive a similar size of the molecular disk of 720 pc FWHM (Table 4). The disk size derived from CO (3−2) is about 900 pc. To better constrain the properties of the molecular disk, we first fit the flux and velocity maps of the molecular disk (systemic component) using the kinematical disk model by Gnerucci et al. (2011a). We assumed that (i) the gas is circularly rotating in a thin disk; (ii) the gravitational potential depends only on the disk mass; and (iii) the disk surface mass density distribution is exponential, i.e. 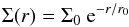 (1)where r is the distance from the center and r0 is the scale radius. Following Cresci et al. (2009), the adopted surface brightness profile for both components is exponential
(1)where r is the distance from the center and r0 is the scale radius. Following Cresci et al. (2009), the adopted surface brightness profile for both components is exponential 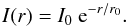 (2)The disk model and fit results are shown in Fig. 5, top panel. The model is then convolved with the beam of the data. The flux and velocity maps are fitted with a minimizing-χ2 method. Residuals due to the inner S-shaped feature are seen in the velocity map (Fig. 5, top right panel).
(2)The disk model and fit results are shown in Fig. 5, top panel. The model is then convolved with the beam of the data. The flux and velocity maps are fitted with a minimizing-χ2 method. Residuals due to the inner S-shaped feature are seen in the velocity map (Fig. 5, top right panel).
In order to account for the inner tilted disk we fit the velocity map with two components, i.e., an inner disk and an outer ring with the same exponential profile but different scale radii r0, and allowing for different inclinations (i) and position angles (PA). Position angles are measured in deg and are positive from east via north. This fit gives for the outer ring a scale radius of r0 = 0.24 arcsec, a PA of the line of nodes of −12deg, and inclination of i = 36 ± 10deg (including a dominant contribution from systematic uncertainties). For the inner disk, we find a scale radius of r0 = 0.12, a PA = 84deg, inclination = 58 ± 10deg (Table 4). The size (radius 200 pc), inclination and orientation of the velocity gradient (nearly north-south) of the inner warped disk of CO(2−1) match well those seen in the vibrationally excited transition HCN(3−2) v2 = 1 (Aalto et al. 2015), and that seen in the OH megamaser observation of Klockner et al. (2003).
Fit parameters derived for the molecular disk.
The dynamical mass enclosed within 400 pc from the AGN is  (with the errors dominated by the uncertainty on the inclination). Downes & Solomon (1998) found 1.27 × 1010M⊙ for an inclination of 10 deg (based on the ratio of the two semi-axis of the disk, and, therefore, probably affected by even larger uncertainties), with our best fit inclination of 36 deg it would be a factor of 10 smaller and, thus, in agreement with our measurements.
(with the errors dominated by the uncertainty on the inclination). Downes & Solomon (1998) found 1.27 × 1010M⊙ for an inclination of 10 deg (based on the ratio of the two semi-axis of the disk, and, therefore, probably affected by even larger uncertainties), with our best fit inclination of 36 deg it would be a factor of 10 smaller and, thus, in agreement with our measurements.
 |
Fig. 6 Position-velocity plots with east-west (left panel, left to right), south-north (middle panel, left to right) and PA −45 deg, south-west to north-east (right panel, left to right) cuts, through the CO(2−1) peak from DS1. Contours levels are 3 to 15σ, 1σ = 1.3 mJy/20 MHz. |
 |
Fig. 7 Position-velocity plots of CO(2−1) from DS2 along the same slices than in Fig. 6. Contours levels are 3 to 15σ, 1σ = 0.8 mJy/20 MHz. |
 |
Fig. 8 Position-velocity plots of CO(3−2) along the same slices than in Fig. 6. Contours levels are 3 to 15σ, 1σ = 0.8 mJy/20 MHz. |
3.2. Molecular outflow
Table 3 reports the results of the visibility fits of CO(2−1) and (3−2). The FWHM size of the high velocity wings of CO(2−1) is 0.35″ (0.3 kpc) and 0.44″ (0.4 kpc) for the red and blue components, respectively. In addition we detect lower surface brightness extended emission due to receding (redshifted) gas out to at least 1 kpc north-east off the AGN (Fig. 3). The CO(3−2) outflow component has a FWHM size of 0.6 (500 pc) and 0.8″ (700 pc) for the blue and red components, respectively.
Position-velocity plots along three different directions are shown in Figs. 6 to 8. For each data set, we extracted a horizontal (i.e. along the major axis of disk rotation, west-east cut), a vertical (south-north) and a −45 deg (south-west to north-east) cut. In all three data sets the rotation pattern of the outer disk is seen in the west-east cuts. Rotation is also visible along the other two directions in the high resolution data. Emission with velocity close to the systemic (± 300 km s-1/s) is extended out to about 1 arcsec from the nucleus.
The high velocity gas (v> 400 km s-1) is seen in all data sets, and along all the examined directions, suggesting that the velocity distribution is rather isotropic. However, both the high speed receding and approaching gas components extend southward of the nucleus, with the approaching one further elongated along the south-west direction (see middle and right panels of Fig. 6).
 |
Fig. 9 Velocity maps of the blue (left) and redshifted CO emission (right). The velocity (in km s-1 with respect to the systemic velocity, i.e. the CO(2−1) peak, is shown in the colour bars. The cross marks the AGN VLBI position. |
Figure 9 shows the Moment 1 maps of the red and blue CO(2−1) wings in the velocity ranges –500 to –1000 and 500 to 900 km s-1, respectively. In the blue component a velocity gradient is seen. The speed of the gas is ~− 900 km s-1 at the position of the nucleus, and decreases to −600 km s-1 at 0.4″ south-west of the nucleus. This is consistent with the position-velocity plot along the diagonal cut (Fig. 6, right panel). The bulk of the gas receding at velocities of 700−800 km s-1 is also located at ~0.3 arcsec south-west of the AGN (Fig. 9, right panel), and shows a milder velocity gradient along approximately the same axis as the approaching gas. Emission with velocity of about 700 to 800 km s-1 is also seen at (+0.8, +0.8″) offset from the phase center, along the same diagonal direction where the blueshifted velocity gradient is found. We cannot exclude that this feature is a residual side lobe, but the absence of the corresponding side lobe in the opposite direction, suggests that this feature might be real.
3.3. Mapping ṀOF and Ėkin,OF
We fitted the pixel-by-pixel spectra with three Gaussian functions, in order to simultaneously account for both low velocity (rotating disk) and high velocity gas (outflows). We define the maximum velocity, vmax, as the shift between the velocity peak of broad component and the systemic velocity plus 2σ, where σ is the velocity dispersion of the broad Gaussian component (vmax = velocityshiftbroad + 2σbroad, σbroad = FWHMbroad/ 2.35). The vmax map is show in Fig. 10. Based on these three component fits, we attempted to map the mass outflow rate and kinetic energy. In previous works (e.g. Feruglio et al. 2010) the mass outflow rate has been computed using the continuity fluid equation 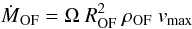 (3)where ρOF is the average mass density of the outflow, vmax is the maximum velocity of the outflowing gas, and ROF is the radius at which the outflow rate is computed, and Ω is the solid angle subtended by the outflow. Assuming a spherical sector,
(3)where ρOF is the average mass density of the outflow, vmax is the maximum velocity of the outflowing gas, and ROF is the radius at which the outflow rate is computed, and Ω is the solid angle subtended by the outflow. Assuming a spherical sector, 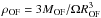 , then, ṀOF = 3 × vmax × MOF/ROF. In this formula, ROF is the distance from the nucleus (RA, Dec = 12:56:14.23, 56:52:25.20). Accordingly,
, then, ṀOF = 3 × vmax × MOF/ROF. In this formula, ROF is the distance from the nucleus (RA, Dec = 12:56:14.23, 56:52:25.20). Accordingly, 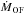 represents the instantaneous outflow rate of the material at the edge ROF (i.e., it is a local estimate) and it is three times larger than the total outflow mass divided by the time required to push this mass through a spherical surface of radius ROF. This estimator does not depend on the solid angle Ω subtended by the outflow. Figure 11 is the map of the outflow rate ṀOF derived by averaging the CO flux per beam of the broad Gaussian components in quadrants of increasing radii (south-west, south-east, north-east, north-west off the AGN), and by adopting αCO = 0.5 to convert from line luminosity to gas mass (Weiss et al. 2001).
represents the instantaneous outflow rate of the material at the edge ROF (i.e., it is a local estimate) and it is three times larger than the total outflow mass divided by the time required to push this mass through a spherical surface of radius ROF. This estimator does not depend on the solid angle Ω subtended by the outflow. Figure 11 is the map of the outflow rate ṀOF derived by averaging the CO flux per beam of the broad Gaussian components in quadrants of increasing radii (south-west, south-east, north-east, north-west off the AGN), and by adopting αCO = 0.5 to convert from line luminosity to gas mass (Weiss et al. 2001). 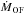 in Fig. 11, therefore, should not be considered a pixel by pixel estimator of the mass outflow rate, but rather the value in square sectors at increasing radii.
in Fig. 11, therefore, should not be considered a pixel by pixel estimator of the mass outflow rate, but rather the value in square sectors at increasing radii.
The outflow originates from the nucleus, and 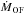 decreases in all directions with increasing distance from the nucleus. The outflow expands preferentially toward south-west, out to a distance of 0.4 arcsec from the nucleus.
decreases in all directions with increasing distance from the nucleus. The outflow expands preferentially toward south-west, out to a distance of 0.4 arcsec from the nucleus.
 |
Fig. 10 Maps of vmax = velocityshiftbroad + 2σbroad (colour scale in km s-1). The pixel size is 0.1 arcsec. The cross marks the AGN VLBI position. |
 |
Fig. 11 Map of |
3.4. ṀOF, Ėkin,OF and MOF/Mdisk radial profiles
In the following we study the mass outflow rate, kinetic power and MOF/Mdisk as a function of the distance from the nucleus. Since the outflow is located near the nucleus and rather symmetric, for the sake of simplicity we adopted an one dimensional average. We used DS1 to map the region at < 0.5 kpc with the best angular resolution, and DS2 to constrain any fainter high speed emitting gas further out from the nucleus. We extracted spectra from box regions centered on the nucleus and with increasing sides. We then fitted the spectra with three Gaussian functions (or four when the systemic line needs two components) to model both the rotating disk and the outflow components, and computed the mass outflow rate as detailed above. The gas masses of the disks (traced by the systemic CO line) and outflow (broad CO components) have been calculated by integrating the best fit models and by using αCO = 0.5.
Figure 12 compares the best fit CO(2−1) emission line profiles integrated in a square region around the nucleus (using DS1) with the integrated profiles from two adjacent square annuli at increasing distances from the nucleus (using DS3). The rms is ~1.3 × 10-3 Jy for all the spectra. For the receding gas, we detect high speed (800 km s-1) gas out to ≳ 1 kpc, and a deficit of gas with intermediate velocity (300−500 km s-1) at ≳0.5 kpc. For the approaching gas, this deficit is only seen at ≥0.9 kpc. The outflow mass rate 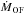 , the vmax, the kinetic energy rate
, the vmax, the kinetic energy rate 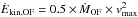 , and the ratio of outflow mass and molecular disk mass MOF/Mdisk are shown in Fig. 13 as a function of the distance from the nucleus (error-bars represent the statistical errors only). Specifically, the histograms represent integral quantities out to a given radius, while the points represent the local mass outflow rate in two annuli, computed by measuring the mass density and the outflow mass within the annuli. The integral mass outflow rate
, and the ratio of outflow mass and molecular disk mass MOF/Mdisk are shown in Fig. 13 as a function of the distance from the nucleus (error-bars represent the statistical errors only). Specifically, the histograms represent integral quantities out to a given radius, while the points represent the local mass outflow rate in two annuli, computed by measuring the mass density and the outflow mass within the annuli. The integral mass outflow rate 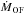 is ≈ 1000 M⊙ yr-1 within 400 pc from the nucleus, and 500−700 M⊙ yr-1 out to ~1 kpc. It is worth noting that the local mass outflow rate is about 500 M⊙ yr-1 within ~800 pc, while it drops to a few tens M⊙ yr-1 at ≳ 1 kpc. The vmax and the integral
is ≈ 1000 M⊙ yr-1 within 400 pc from the nucleus, and 500−700 M⊙ yr-1 out to ~1 kpc. It is worth noting that the local mass outflow rate is about 500 M⊙ yr-1 within ~800 pc, while it drops to a few tens M⊙ yr-1 at ≳ 1 kpc. The vmax and the integral 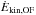 of the outflow remains nearly constant out to ~1 kpc, with
of the outflow remains nearly constant out to ~1 kpc, with 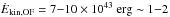 % of the AGN bolometric luminosity (Fig. 13, middle panel, see Sect. 5 for a detailed discussion). Finally, Fig. 13, right panel, shows that the outflow carries ~0.2−0.25 of the total disk mass out to ~1 kpc, while the outflow mass drops to less than 10% of the disk mass at ≳ 1 kpc.
% of the AGN bolometric luminosity (Fig. 13, middle panel, see Sect. 5 for a detailed discussion). Finally, Fig. 13, right panel, shows that the outflow carries ~0.2−0.25 of the total disk mass out to ~1 kpc, while the outflow mass drops to less than 10% of the disk mass at ≳ 1 kpc.
 |
Fig. 12 CO(2−1) emission line profiles extracted from square regions at different distances from the nucleus, as indicated by the colour-coded labels, and their multi-Gaussian best fit. |
 |
Fig. 13 Left panel: integral radial profiles (histogram) and profiles in annuli (points) of the outflow rate |
4. X-ray observations
4.1. X-ray data reduction
During the last three years Mrk 231 has been target of new, sensitive X-ray observations. Specifically, Chandra observed the galaxy for 400 ks in August 2012 (Veilleux et al. 2014), while NuSTAR has observed it twice, in August 2012 and May 2013 for a total of about 70 ks (Teng et al. 2014, T14 hereafter). These data have dramatically changed our understanding of the X-ray emission from Mrk 231. Previous broadband, non-focusing X-ray observations performed with BeppoSAX and Suzaku detected a ~3σ excess in the band above 10 keV which has been interpreted as evidence of nuclear continuum emerging after transmission through a Compton thick absorber (Braito et al. 2004), most likely with a variable covering factor (Piconcelli et al. 2013). This scenario has not been confirmed by the unprecedented angular resolution ultra-hard (>10 keV) X-ray NuSTAR observations presented by T14. They did not report any hard X-ray excess and revealed that Mrk 231 is therefore intrinsically X-ray weak, with a 2–10 keV luminosity of 4 × 1042 erg s-1. The best-fit model of the contemporaneous Chandra and NuSTAR spectrum consists of flat (Γ ≈ 1.4) power-law continuum emission modified by a patchy, Compton-thin absorber, plus a soft X-ray, starburst related, thermal emission. Furthermore, the deep Chandra observation has revealed the existence of a huge (~65 × 50 kpc) soft X-ray halo around the central AGN which can be accounted for by two thermal emission components with kT ~ 0.25 and 0.8 keV, respectively (Veilleux et al. 2014). Thanks to their high quality and sensitivity, these data sets also allow a detailed search for highly ionized fast or ultra-fast outflows seen in absorption against the nuclear X-ray emission.
Chandra data were taken from the CXC archive. Specifically, we combined the 2012 long (400 ks, Observation ID 13947, 13948, 13949) observation with those performed in 2000 and 2003 (153 ks in total, Observation ID 1031, 4028, 4029, 4030, Gallagher et al. 2005). The combined data set has a total exposure time on source of 553 ks. Data were reduced using CIAO 4.5. We extracted a spectrum from a circular region of 3 pixel radius (1.5 arcsec) centered on the nucleus using the tool dmextract. A background spectrum was extracted from an annulus with inner and outer radii 1 and 2 arcmin, respectively. In extracting the background, the regions of the front-illuminated detector have been masked. We verified that varying the background extraction regions, however, has little impact, because the background counts are a small fraction of the source counts in the spectral region of interest (a factor of ~1/500). Response matrices were computed using the tools mkwarf and mkrmf. The spectral analysis was performed in the 0.5−10 keV energy range. Given the large number of counts and the requirement to use the χ2 statistics in our modeling, we binned the spectrum with a minimum of 40 counts/channel.
The NuSTAR data were reduced with the pipeline NuSTARDAS version 0.11.1 and CALDB version 20130509 with the standard settings (see T14 for details). The background counts are a factor of ~1/10 those of the source. Spectra were extracted for each observation and for the two NuSTAR telescopes FPMA and FPMB, using a circular region of 1 arcmin radius. Spectra were binned with a minimum of 40 counts/channel as for the Chandra data set. Spectral bins between 3 and 79 keV were used in the fits. xspec 12.8.0 was used for the analysis.
 |
Fig. 14 The ratio between data the best model including two thermal components, a power law component and a narrow Gaussian emission line at 6.18 keV (6.44 keV rest frame, iron Kα). Black triangles = Chandra data; red dots = NuSTAR data. A strong excess around 6 keV and a deficit of counts around 7 keV are seen. Note that the NuSTAR data, even taking into account the lower spectral resolution, follow the Chandra data. |
4.2. Discovery of a nuclear ultra-fast wind
We exploited these data sets to constrain any nuclear wind. Based on T14 results, we first fitted the Chandra spectrum and the four NuSTAR spectra with a model including Galactic absorption along the line of sight, two thermal components, a power law component and a narrow emission line component, both reduced at low energies by photoelectric absorption (we used the xspec model zxipcf, i.e. a model including a partial covering and ionized absorber). The total χ2 of this fit is 498.9 for 468 deg of freedom (d.o.f.). Figure 14 shows the ratio between data and model. For plotting purposes the four NuSTAR spectra have been added together. Positive residuals are evident between 6 and 6.5 keV (6.2−6.7 keV rest frame, consistent with neutral Fe Kα emission) while negative residuals are seen around 7 keV. The feature resembles a P-Cygni profile, similar to that recently found by Nardini et al. (2015) in PDS456. In the latter case the emission line peaks however at ~7 keV rest frame, suggesting highly ionized Fe emission, unlike the case of Mrk 231. The deficit of counts around 7 keV is also very well visible in Figs. 4 and 5 of T14. We replaced the narrow emission line with a relativistic disk-line with inner and outer radii fixed at 10 and 1000 gravitational radii, and spectral index of the power emissivity law fixed at −2. The χ2 improves to 470.0 for 467 d.o.f. The equivalent width of the disk-line is 270 eV for the Chandra spectrum and around 130−140 eV for the four NuSTAR spectra. Residuals still show a deficit of counts around 7 keV.
 |
Fig. 15 67%, 90% and 99% iso-χ2 confidence levels derived from the fitting of the merged X-ray spectra for the absorption line normalization and energy (left panel), for the column density, NH, and redshift of the highly ionized absorber (middle panel), and for NH and ionization parameter, ξ, of the highly ionized absorber (right panel). |
We then added to the model a Gaussian absorption line, to account for this deficit of counts. The χ2 further improves to 452.45 for 464 dof when the normalization of the Gaussian absorption line is kept linked in the five spectra. The Δχ2 between the model without and with the Gaussian absorption line is 17.55 for three additional dof and no systematic residuals are seen in the iron line complex. Figure 15 shows the χ2 contours for the absorption line normalization and energy. The detection of the absorption line is significant at better than the 99.9% confidence level (or 3.5σ). To confirm the statistical significance of the absorption feature we run a Markov Chain Monte Carlo simulation by using the XSPEC chain command. This generates a chain of set of parameter values describing the parameter probability distribution. The chain is converted into probability distribution using the XSPEC margin command.
The Δχ2 between the models with and without the absorption line for the single Chandra spectrum is 11.6, while it is 7.3 between the two models for the four NuStAR spectra. The energy of the line is also similar in the two instruments, 7.1 ± 0.5 keV for the Chandra spectrum and 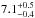 keV for the NuSTAR spectra. We conclude that the line is present with similar statistical significance in both instruments. The equivalent width of the absorption line is about twice in the NuSTAR spectra than in the Chandra spectrum. Fitting simultaneously the Chandra and NuSTAR spectra, but allowing the normalization of the absorption line to be different in the Chandra and NuStAR spectra, reduces the χ2 to 448.24, i.e. the Δχ2 is only 4.2. For the sake of simplicity, in the following analysis we keep the normalization of the absorption line linked between the Chandra and NuSTAR spectra.
keV for the NuSTAR spectra. We conclude that the line is present with similar statistical significance in both instruments. The equivalent width of the absorption line is about twice in the NuSTAR spectra than in the Chandra spectrum. Fitting simultaneously the Chandra and NuSTAR spectra, but allowing the normalization of the absorption line to be different in the Chandra and NuStAR spectra, reduces the χ2 to 448.24, i.e. the Δχ2 is only 4.2. For the sake of simplicity, in the following analysis we keep the normalization of the absorption line linked between the Chandra and NuSTAR spectra.
To further test the robustness of the detection of the absorption line at about 7.1 keV, we performed several additional spectral fits. First, we limited the band used to fit the NuSTAR data to 30−40 keV, up to which the source is detected with a signal to noise better than 3σ in bins smaller than 10 keV. The results were perfectly consistent with those obtained fitting the NuSTAR data in the full band, up to 79 keV. Second, we considered each single Chandra spectra (eight different observations) and fitted them simultaneously. The results were consistent with those obtained fitting the single Chandra spectrum obtained by adding together the eight observations. Third, we fit the Chandra and NuSTAR data with a model including an absorption edge at energy ≥ 7.1 keV, rest frame. The χ2 obtained linking the optical depth τ of the edge between the Chandra and NuSTAR data is 470.5 for 465 d.o.f., and the resulting τ is consistent with zero. Allowing the optical depth of the edge to be different in the Chandra and NuSTAR spectra produces a χ2 = 458.3 for 464 d.o.f., again much higher than the χ2 = 448.24 obtained using an absorption line.
We fitted the Chandra and NuSTAR spectra with a model including two thermal components (T1 and T2), a power law nuclear component (PL) and a disk line component. The latter two components are modified by two ionized absorbers (a low ionization absorber to account for the cold-warm gas along the line of sight, and a highly ionized absorber to account for the fast wind). The χ2 is again good, 452.4 for 463 d.o.f. The best fit parameters for all components are given in Table 5. Figure 15 shows the χ2 contours for the highly ionized absorber NH, ionization parameter and redshift. From the absorber redshift we derive a velocity of the absorbing gas of 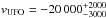 km s-1. The covering factor of the nuclear wind is consistent with being 1. The statistics only allows to obtain a lower limit of 0.7 at the 67% confidence level, as derived from the partial covering model (e.g. from the ratio of absorbed/unabsorbed power law, Table 5). In principle, the wind covering factor may be determined by a detailed analysis of the P-Cygni profile of the iron line feature, if the emission and the absorption come from the same expanding envelope (as in Nardini et al. 2015). Here we do not attempt such a detailed analysis, because the statistics does not allow us to distinguish between line emission from a wind and line emission from a relativistic accretion disk. We limit ourselves to note that a prominent P-Cygni profile (e.g. strong emission in addition to strong absorption, Fig. 14) points toward a large wind covering factor, provided that both features are produced by the same gas.
km s-1. The covering factor of the nuclear wind is consistent with being 1. The statistics only allows to obtain a lower limit of 0.7 at the 67% confidence level, as derived from the partial covering model (e.g. from the ratio of absorbed/unabsorbed power law, Table 5). In principle, the wind covering factor may be determined by a detailed analysis of the P-Cygni profile of the iron line feature, if the emission and the absorption come from the same expanding envelope (as in Nardini et al. 2015). Here we do not attempt such a detailed analysis, because the statistics does not allow us to distinguish between line emission from a wind and line emission from a relativistic accretion disk. We limit ourselves to note that a prominent P-Cygni profile (e.g. strong emission in addition to strong absorption, Fig. 14) points toward a large wind covering factor, provided that both features are produced by the same gas.
The comparison between our best fit model and the preferred model of T14 is not straightforward because we used a simpler ionized/partial covering absorber model for the nuclear obscuration, while they adopted the MYTORUS model. Furthermore, we used a two temperature MEKAL model for the starburst component, while T14 use two temperature MEKAL model plus a power law component and a 6.7 keV Fe line to account for contribution of a population of nuclear High Mass X-ray Binaries (HMXB). Finally, we used a disk Fe Kα line, while this component is automatically included in the MYTORUS model in T14. The best fit spectral index and luminosity of the nuclear X-ray component are similar in the two fits, Γ = 1.47 and L(2−10 keV) = 3 × 1042 ergs/s versus Γ = 1.4 and L(2−10 keV) ~ 4 × 1042 ergs/s. Our parametrization of the starburst component provides a warm component (T = 0.89 keV, similar to T14), plus a hot component (5.5 keV, which naturally accounts for the Fe 6.7 keV line). We tried to add a flat (Γ = 1.1) power law component to account for a HMXB population, but this does not improve significantly the χ2, and its normalization is < 30 times that of the AGN component (similarly to T14). We fit a Compton thin absorber with column density ~4 × 1022 cm-2, very low ionization parameter, uniformly covering the X-ray source, while T14 fit the data with two neutral absorber of similar total column densities. In conclusion, despite significant differences in the details of the adopted models, the broad band X-ray spectral reconstruction is quite similar, and characterized by a) a main AGN power law component with a rather flat spectral index; b) a Compton thin, moderately ionized absorber of ~4 × 1022 cm-2, uniformly covering the source; c) a warm thermal component and a hot component (or a flat power law plus a 6.7 Fe line) to account for the nuclear starburst. The detection of the absorption feature at about 7 keV is clearly not an artifact of the different spectral modeling, see discussion above, and it is well visible also in the residuals of Fig. 3 of T14.
Best fit model to the Chandra and NuSTAR merged X-ray spectra.
 |
Fig. 16 Left panel: the momentum boost |
The other outflow parameters can be computed from the best fit parameters as follows. The minimum distance of the outflowing gas can be estimated from the radius at which the observed velocity equals the escape velocity, 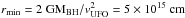 for a black hole mass of 8.7 × 107M⊙ (Kawakatu et al. 2007) and the lowest value of the outflow velocity. The maximum distance rmax of the outflowing gas can be computed from the definition of the ionization parameter
for a black hole mass of 8.7 × 107M⊙ (Kawakatu et al. 2007) and the lowest value of the outflow velocity. The maximum distance rmax of the outflowing gas can be computed from the definition of the ionization parameter 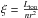 ,
, 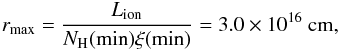 (4)where Lion ~ 1043 ergs/s is the luminosity integrated in the 13.6 eV−13.6 keV range. The mass outflow rate at rmin and rmax can then be estimated using:
(4)where Lion ~ 1043 ergs/s is the luminosity integrated in the 13.6 eV−13.6 keV range. The mass outflow rate at rmin and rmax can then be estimated using: 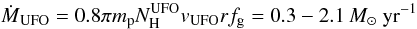 (5)where
(5)where 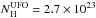 cm-2, and fg is a geometrical factor introduced by Krongold et al. (2007) and statistically estimated ~2 by Tombesi et al. (2010). Should the mass outflow rate be significantly larger than the value given above, a much deeper absorption line should be visible in the X-ray spectra (for reasonable values of ξ and vout). From the mass outflow rate and velocity we can estimate the momentum flux,
cm-2, and fg is a geometrical factor introduced by Krongold et al. (2007) and statistically estimated ~2 by Tombesi et al. (2010). Should the mass outflow rate be significantly larger than the value given above, a much deeper absorption line should be visible in the X-ray spectra (for reasonable values of ξ and vout). From the mass outflow rate and velocity we can estimate the momentum flux, 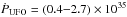 gr cm/s2, corresponding to a
gr cm/s2, corresponding to a 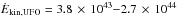 erg s-1. This can be compared with the radiation momentum flux
erg s-1. This can be compared with the radiation momentum flux 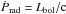 . The bolometric luminosity estimated by Lonsdale et al. (2003) and Farrah et al. (2003) is 5 × 1045 erg s-1. The momentum load is therefore
. The bolometric luminosity estimated by Lonsdale et al. (2003) and Farrah et al. (2003) is 5 × 1045 erg s-1. The momentum load is therefore 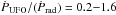 . Recently, Teng et al. (2014) measured an intrinsic X-ray luminosity in the range 0.5−30 keV of ~1043 erg s-1, about 10 times smaller than previous estimates. This would either imply an unusually large X-ray bolometric correction (≈ 1000) and hence a very large momentum load, or an overestimated AGN bolometric luminosity based on mid-infrared data.
. Recently, Teng et al. (2014) measured an intrinsic X-ray luminosity in the range 0.5−30 keV of ~1043 erg s-1, about 10 times smaller than previous estimates. This would either imply an unusually large X-ray bolometric correction (≈ 1000) and hence a very large momentum load, or an overestimated AGN bolometric luminosity based on mid-infrared data.
The detection of an UFO offers the unprecedented opportunity to directly compute the momentum load of the large scale, spatially resolved outflow with respect to that of the nuclear wind. The 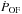 of the CO(2−1) outflow depends on velocity and is in the range 1.6−4 × 1036 erg cm-2 for v = 500 and 800 km s-1, respectively. Figure 16, left panel, shows the momentum load,
of the CO(2−1) outflow depends on velocity and is in the range 1.6−4 × 1036 erg cm-2 for v = 500 and 800 km s-1, respectively. Figure 16, left panel, shows the momentum load, 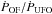 , versus the velocity of the molecular and atomic large scale outflows detected in Mrk 231 (references for the data are in the caption of the figure). The values of
, versus the velocity of the molecular and atomic large scale outflows detected in Mrk 231 (references for the data are in the caption of the figure). The values of 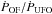 range from ≈ 20 to ≈ 100, i.e. strongly suggesting that the outflow does not conserve the momentum, if the UFO is identified with the inner semi-relativistic wind pushing the outer molecular outflow (Lapi et al. 2005; Zubovas & King 2012; Faucher-Giguere & Quataert 2012). Figure 16, right panel, shows the
range from ≈ 20 to ≈ 100, i.e. strongly suggesting that the outflow does not conserve the momentum, if the UFO is identified with the inner semi-relativistic wind pushing the outer molecular outflow (Lapi et al. 2005; Zubovas & King 2012; Faucher-Giguere & Quataert 2012). Figure 16, right panel, shows the 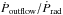 versus velocity of the outflows of Mrk 231 (red symbols). Black symbols are the results of Tombesi et al. (2015) for IRAS F11119+3257, a galaxy exhibiting both an X-ray UFO and an OH outflow, as revealed by Herschel spectroscopy (Veilleux et al. 2013). The solid lines represent the expectations for energy-conserving outflows with nuclear wind velocity vUFO ± 1σ and with covering factor f = 1 for both the nuclear winds and the molecular outflows.
versus velocity of the outflows of Mrk 231 (red symbols). Black symbols are the results of Tombesi et al. (2015) for IRAS F11119+3257, a galaxy exhibiting both an X-ray UFO and an OH outflow, as revealed by Herschel spectroscopy (Veilleux et al. 2013). The solid lines represent the expectations for energy-conserving outflows with nuclear wind velocity vUFO ± 1σ and with covering factor f = 1 for both the nuclear winds and the molecular outflows.
5. Discussion and conclusions
-
(i)
Molecular disk. We present the best spatial resolution and sensitivity CO map of the molecular disk of Mrk 231 obtained so far. In addition to the previously known main rotation of the disk, which occurs along nearly an east-west direction, we find evidence for a tilted inner nuclear disk on scales of 100 pc, more inclined on the line of sight. The CO gas distribution can be modeled by an outer exponential ring with radius 400 pc, PA = −12 deg, and inclination i = 36 ± 10 deg, plus an inner exponential disk with outer radius 200 pc, PA = 84 deg, and i = 58 deg on the line of sight. The inner, warped component matches the size, PA and inclination of the vibrationally excited HCN(3−2) v = 1, f (Aalto et al. 2015). The parameters of the inner tilted disk are also consistent with the OH mega-maser emission seen with the VLBI, which traces a disk with radius 30 to 200 pc, PA 56 deg and inclination 56 deg (Klockner et al. 2003). We can hardly estimate the mass of the inner tilted CO disk, but this detection shows that in addition to very dense gas traced by HCN(3−2) v2 = 1f, gas with density of the order 105 cm-3 is also present in the very inner regions. The existence of a warped inner disk with radius 170−250 pc was suggested also by Davies et al. (2004) based on stellar absorption studies. They pointed out that the warp should first occur in the gaseous phase and so be transferred to the stars formed in situ.
-
(ii)
Molecular outflow. The CO(2−1) high angular resolution data indicate that the molecular outflow has a size of at least 1 kpc. The bulk of both receding and approaching outflowing gas are located within ~400 pc from the nucleus, and peak ~0.2 arcsec south-west off the nucleus. Extended, redshifted emission with lower surface brightness is seen north-east off the nucleus out to ~1 kpc (see Fig. 3). The outflow is seen in all examined directions around the AGN (see Fig. 6). It is more prominent, however, along the south-west to north-east direction, suggesting a wide-angle likely biconical geometry. The approaching gas shows a gradient in projected velocity, with larger negative speed at the position of the AGN and decreasing velocity south-west off the nucleus. This allows to exclude a geometry where the approaching outflow expands with constant speed within an uniformly filled cone with axis located in the plane of the sky (as in this case no speed gradient would be observed) nor with axis parallel to our line of sight (in this case the maximum projected speed would be centered on the nucleus and decrease outwards symmetrically). An outflow expanding with uniform velocity between the observer and the molecular disc, in a cone with axis inclined with respect to our line of sight, would instead produce a velocity gradient as the observed one for the approaching gas, but it would also imply a similar gradient for the receding part, which instead is not observed. The projected velocities can be probably qualitatively be explained by an outflow with conical or lobe-like geometry with a slightly larger receding component (based in Figs. 2 and 3). However a firm and consistent picture explaining both velocity fields seen in Fig. 9 cannot be simply ascribed to orientation effects and probably inhomogeneities and asymmetries in the outflow can account for them. We also suggest that the redshifted emission seen north-east off the nucleus is tracing the receding part of the cone, which is located behind the molecular disk with respect to the observer. Interestingly, Krabbe et al. (1997) detected at approximately the same location a narrow Paα emission approaching with a speed of 1400 km s-1 with respect to the systemic one. The molecular outflow centroids, traced by the red and blueshifted wings of CO(2−1), are consistent with those seen in HCN (Aalto et al. 2015). We find that
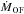 decreases with increasing distance from the nucleus in all directions (see Fig. 11), while the radially integrated vmax stays roughly constant out to ≳ 1 kpc. This implies, based on Eq. (3), that either the outflow average density, ρOF, or the outflow filling factor decrease from the nucleus outwards approximately as r-2 (or slightly steeper). This suggests different possible scenarios: (i) a large part of the gas with velocity of 300−600 km s-1 leaves the flow during its expansion. If the molecular clouds are pressure-confined, they will dissolve out in the wind, and CO may be efficiently photo dissociated by the UV radiation, since self shielding will be strongly reduced at low densities. Atomic carbon, either in neutral or ionized phase, can then, in principle, continue expanding out to larger distances at a constant velocity, as it is observed in SDSS J1148+5251, where most of the fast [CII] is located far from the AGN, and extended on scales of a few tens kpc (Cicone et al. 2015). Intriguingly, broad wings extending up to ± 1000 km s-1 can be seen in both [CII] 158 μm and [NII] 205 μm emission lines observed by Herschel in Mrk 231 (Fischer et al. 2010). Unfortunately, Herschel PACS does not provide sufficient angular resolution to assess whether the fast [CII] and [NII] gas are more extended than CO. A promising alternative would be to use the forbidden 3P fine structure line of atomic carbon ([CI] line at rest frame frequency 492.161 GHz), which is accessible by ALMA, on southern analogs of Mrk 231. (ii) The opening angle subtended by the paths of least resistance is relatively narrow; or (iii) only the highest velocity gas has been able to reach distances ≳ 1 kpc. The latter would imply an age of the outflow of ~1 Myr (assuming a constant expansion), which is 1−10% of a typical AGN duty cycle. The rate of kinetic energy carried by the outflow is ~1−2% of the AGN bolometric luminosity, and stays approximately constant out to 1 kpc. The decrease of the local
decreases with increasing distance from the nucleus in all directions (see Fig. 11), while the radially integrated vmax stays roughly constant out to ≳ 1 kpc. This implies, based on Eq. (3), that either the outflow average density, ρOF, or the outflow filling factor decrease from the nucleus outwards approximately as r-2 (or slightly steeper). This suggests different possible scenarios: (i) a large part of the gas with velocity of 300−600 km s-1 leaves the flow during its expansion. If the molecular clouds are pressure-confined, they will dissolve out in the wind, and CO may be efficiently photo dissociated by the UV radiation, since self shielding will be strongly reduced at low densities. Atomic carbon, either in neutral or ionized phase, can then, in principle, continue expanding out to larger distances at a constant velocity, as it is observed in SDSS J1148+5251, where most of the fast [CII] is located far from the AGN, and extended on scales of a few tens kpc (Cicone et al. 2015). Intriguingly, broad wings extending up to ± 1000 km s-1 can be seen in both [CII] 158 μm and [NII] 205 μm emission lines observed by Herschel in Mrk 231 (Fischer et al. 2010). Unfortunately, Herschel PACS does not provide sufficient angular resolution to assess whether the fast [CII] and [NII] gas are more extended than CO. A promising alternative would be to use the forbidden 3P fine structure line of atomic carbon ([CI] line at rest frame frequency 492.161 GHz), which is accessible by ALMA, on southern analogs of Mrk 231. (ii) The opening angle subtended by the paths of least resistance is relatively narrow; or (iii) only the highest velocity gas has been able to reach distances ≳ 1 kpc. The latter would imply an age of the outflow of ~1 Myr (assuming a constant expansion), which is 1−10% of a typical AGN duty cycle. The rate of kinetic energy carried by the outflow is ~1−2% of the AGN bolometric luminosity, and stays approximately constant out to 1 kpc. The decrease of the local 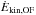 at larger radii can be explained as a consequence of decreasing
at larger radii can be explained as a consequence of decreasing 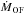 and constant vmax. A 3D rendering of the geometry of the molecular disk and outflow is shown in Fig. 17. The molecular disk consists of an inner tilted disk plus and outer component with approximately an east-west orientation. The observed direction of the rotation for these two rotating components is shown by the colour scale (red for the receding, blue for the approaching material). The molecular outflow is sketched out by a wide-angle biconical-like component plus a spherical one. The two cone-like components have been placed in order to match the south-west to north-east elongation seen in the CO(2−1) maps. The southern cone is located between the observer and the disk, inclined with respect to the line of sight, and shows an approaching and a brighter receding gas emission. The northern cone is located behind the molecular disc, and it is mainly receding, as testified by the redshifted velocities observed at this position. Since we cannot draw firm conclusions on the expansion velocity along the plane of the sky, we mention the possibility that the isotropic outflowing component can also be explained by receding and approaching outflows along the line of sight. It is worth noting that the neutral gas outflow reported by Rupke & Veilleux (2011) extends over a much larger region (~3 kpc) than that of the molecular gas traced by CO.
and constant vmax. A 3D rendering of the geometry of the molecular disk and outflow is shown in Fig. 17. The molecular disk consists of an inner tilted disk plus and outer component with approximately an east-west orientation. The observed direction of the rotation for these two rotating components is shown by the colour scale (red for the receding, blue for the approaching material). The molecular outflow is sketched out by a wide-angle biconical-like component plus a spherical one. The two cone-like components have been placed in order to match the south-west to north-east elongation seen in the CO(2−1) maps. The southern cone is located between the observer and the disk, inclined with respect to the line of sight, and shows an approaching and a brighter receding gas emission. The northern cone is located behind the molecular disc, and it is mainly receding, as testified by the redshifted velocities observed at this position. Since we cannot draw firm conclusions on the expansion velocity along the plane of the sky, we mention the possibility that the isotropic outflowing component can also be explained by receding and approaching outflows along the line of sight. It is worth noting that the neutral gas outflow reported by Rupke & Veilleux (2011) extends over a much larger region (~3 kpc) than that of the molecular gas traced by CO. 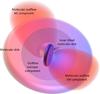
Fig. 17 3D cartoon of the molecular disk and outflow geometry in Mrk 231. The line of sight to the observer is perpendicular to the page. Red and blue colours represent the receding and approaching material for each component, respectively. The molecular disk consists of an inner disk, tilted by 58 deg on the line of sight, with a scale radius of 200 pc, plus and outer component with inclination 36 deg and scale radius 400 pc, with the line of nodes oriented in the east-west direction approximately. The molecular outflow is rendered by a wide-angle biconical-like component plus an isotropic one, represented here as a sphere for displaying purposes. For a detailed description of the cartoon see Sect. 5.
-
(iii)
Molecular outflow and disk global energetics. A complementary way to assess whether the outflow has a significant impact on the molecular disk is comparing their energetics, keeping in mind, however, that these energy estimates are affected by large uncertainties. The total energy of the molecular disk (quiescent component) is given by the sum of the gravitational potential energy, the rotational energy, the turbulent energy and the thermal one. The gravitational potential energy is Egrav = GMdynMgas/R, where Mdyn and Mgas are the dynamical and gas masses, G is the gravitational constant and R is the radius of the molecular disk (400 pc from our fit). The gas mass within this radius is Mgas = 1.8 × 109M⊙. The dynamical mass, modulus the inclination of the disk, is Mdynsin2(i) = 5.5 × 108M⊙, which gives Egravsin2(i) = 1.85 × 1056 erg. The rotational energy of the molecular disk is
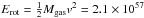 erg, where v = 345 km s-1 is the rotational velocity of the disk. The contribution of the turbulent energy is small and can be expressed as:
erg, where v = 345 km s-1 is the rotational velocity of the disk. The contribution of the turbulent energy is small and can be expressed as: 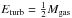 dv2 = 2.9 × 1055 erg, where dv is the turbulent velocity dispersion in the disk (which is likely of the order of ~40 km s-1). The thermal energy can be expressed as Etherm = nkTV = 1.2 × 1052 erg, assuming a temperature of the gas of T = 60 K based on CO(1−0) observations, an average gas density n = 3600 cm-3, and a disk with radius 400 pc and thickness 23 pc (Downes & Solomon 1998). The total energy budget of the molecular disk is therefore Edisk = 2.6−8.3 × 1057 erg, adopting a disk inclination of 36 and 10 deg, respectively. The kinetic energy of the outflow is given by its bulk motion. Based on the mass of the CO(2−1) outflow, we find Ekin,OF = 2.35 × 1057 erg, adopting an average velocity of 800 km s-1 and an outflow mass of 3.7 × 108M⊙ The turbulent contribution is negligible if we assume dvturb,OF = dvturb,disk ~ 40 km s-1. On the other hand if in the outflowing molecular clouds dvturb ~ 250 km s-1 (e.g. Williamson et al. 2014), the turbulent energy can contribute an additional ~10% to the outflow energy budget. Given all the uncertainties in these estimates, we conclude that the total energy of the outflow EOF is of the same order as Edisk.
dv2 = 2.9 × 1055 erg, where dv is the turbulent velocity dispersion in the disk (which is likely of the order of ~40 km s-1). The thermal energy can be expressed as Etherm = nkTV = 1.2 × 1052 erg, assuming a temperature of the gas of T = 60 K based on CO(1−0) observations, an average gas density n = 3600 cm-3, and a disk with radius 400 pc and thickness 23 pc (Downes & Solomon 1998). The total energy budget of the molecular disk is therefore Edisk = 2.6−8.3 × 1057 erg, adopting a disk inclination of 36 and 10 deg, respectively. The kinetic energy of the outflow is given by its bulk motion. Based on the mass of the CO(2−1) outflow, we find Ekin,OF = 2.35 × 1057 erg, adopting an average velocity of 800 km s-1 and an outflow mass of 3.7 × 108M⊙ The turbulent contribution is negligible if we assume dvturb,OF = dvturb,disk ~ 40 km s-1. On the other hand if in the outflowing molecular clouds dvturb ~ 250 km s-1 (e.g. Williamson et al. 2014), the turbulent energy can contribute an additional ~10% to the outflow energy budget. Given all the uncertainties in these estimates, we conclude that the total energy of the outflow EOF is of the same order as Edisk. -
(iv)
UFO and molecular outflow energy and momentum. We find a ratio
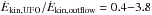 , suggesting that most of the nuclear wind kinetic energy is transferred to mechanical energy of the kpc scale outflow, which is thus undergoing an energy conserving expansion, as predicted by the most popular theoretical models (Faucher-Giguere & Quataert 2012; Zubovas & King 2012). In particular, the prediction of models for energy-conserving outflows is
, suggesting that most of the nuclear wind kinetic energy is transferred to mechanical energy of the kpc scale outflow, which is thus undergoing an energy conserving expansion, as predicted by the most popular theoretical models (Faucher-Giguere & Quataert 2012; Zubovas & King 2012). In particular, the prediction of models for energy-conserving outflows is 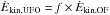 , where f is the fraction the nuclear wind energy that is deposited to the large scale outflow, and ranges from 0.5 to 1 in the models of Faucher-Giguere & Quataert (2012) and Zubovas & King (2012), respectively. We stress that our work does not make any assumption on f. In fact, we measure
, where f is the fraction the nuclear wind energy that is deposited to the large scale outflow, and ranges from 0.5 to 1 in the models of Faucher-Giguere & Quataert (2012) and Zubovas & King (2012), respectively. We stress that our work does not make any assumption on f. In fact, we measure 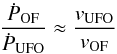 from which we derive f ~ 1 (see also Fig. 16). The mass loading factor, defined as
from which we derive f ~ 1 (see also Fig. 16). The mass loading factor, defined as 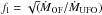 in Zubovas & King (2012), is ≈ 20 at the outer boundary of the molecular outflow (1 kpc), which also supports the two stage acceleration scenario. We find that
in Zubovas & King (2012), is ≈ 20 at the outer boundary of the molecular outflow (1 kpc), which also supports the two stage acceleration scenario. We find that 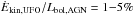 and
and 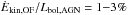 , in agreement with the requirements typically assumed by the most popular feedback models (Lapi et al. 2005; Menci et al. 2008; Di Matteo 2005; Gaspari et al. 2011, 2012).
, in agreement with the requirements typically assumed by the most popular feedback models (Lapi et al. 2005; Menci et al. 2008; Di Matteo 2005; Gaspari et al. 2011, 2012).
The momentum load of the nuclear wind, 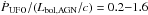 , agrees with the predictions for radiatively accelerated winds with scattering optical depth ~1 (King & Pounds 2003). These observations offered the first opportunity to compare the momentum boost of a spatially resolved outflow with respect to the nuclear wind. Specifically, we find
, agrees with the predictions for radiatively accelerated winds with scattering optical depth ~1 (King & Pounds 2003). These observations offered the first opportunity to compare the momentum boost of a spatially resolved outflow with respect to the nuclear wind. Specifically, we find ![\hbox{$\rm \dot {\it P}_{\rm OF}/\dot {\it P}_{UFO}=[16{-}113]$}](/articles/aa/full_html/2015/11/aa26020-15/aa26020-15-eq343.png) at 1 kpc based on CO(2−1), and in the range 8−100 for the outflows traced by HCN, OH and NaID, although with large uncertainties (Fig. 16). Accordingly, this result supports the two phase outflow acceleration mechanism scenario, whereby the momentum of the large scale outflow is boosted compared to that of the nuclear semi-relativistic wind. We remark that the nucleus of Mrk 231 is radiating close to the Eddington limit (Lbol,AGN/LEdd = 0.46 for a black hole mass of 8.7 × 107M⊙), matching again the requirements of models for driving massive outflows.
at 1 kpc based on CO(2−1), and in the range 8−100 for the outflows traced by HCN, OH and NaID, although with large uncertainties (Fig. 16). Accordingly, this result supports the two phase outflow acceleration mechanism scenario, whereby the momentum of the large scale outflow is boosted compared to that of the nuclear semi-relativistic wind. We remark that the nucleus of Mrk 231 is radiating close to the Eddington limit (Lbol,AGN/LEdd = 0.46 for a black hole mass of 8.7 × 107M⊙), matching again the requirements of models for driving massive outflows.
Tombesi et al. (2015) recently found a similar result for the galaxy IRAS F11119+3257, which hosts both an UFO and a massive molecular outflow detected through the OH absorption line by Herschel (Veilleux et al. 2013). They derived 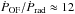 , estimating f = 0.2. It is worth noting that both Tombesi et al. (2015) and this work strengthen each other, supporting the AGN-driven energy-conserving outflows scenario and providing constraints to the models of AGN feedback.
, estimating f = 0.2. It is worth noting that both Tombesi et al. (2015) and this work strengthen each other, supporting the AGN-driven energy-conserving outflows scenario and providing constraints to the models of AGN feedback.
Sensitive and high angular resolution observations with ALMA and NOEMA are needed to further constrain the physics of quasar-driven outflows, and their impact in galaxy transformation. In particular, constraining any large-scale molecular outflow in quasars with well-studied UFO (e.g. PDS 456, PG 1211+143, Nardini et al. 2015, Pounds 2014) is a compelling experiment to be pursued with ALMA. On the other hand, understanding the impact of outflows on the cosmological evolution of galaxies requires a systematic approach, i.e. a search for nuclear molecular outflows out to z ~ 2 in unbiased, mass-selected samples.
Note that in Cicone et al. (2012) the phase reference center was wrongly quoted as the VLBI position, which produces an apparent discrepancy in the location of the outflow between that and this work.
Acknowledgments
C.F. thanks the IRAM staff for support in observations and data analysis, particularly Dennis Downes, Roberto Neri, Sergio Martin-Ruiz, Jan Martin Winters, Melanie Krips, and Sabine Koenig. We thank Susanne Aalto, Santiago Garcia-Burillo, and Andrea Ferrara for stimulating discussions. C.F. gratefully acknowledges financial support from PRIN MIUR 2010-2011, project “The Chemical and Dynamical Evolution of the Milky Way and Local Group Galaxies”, prot. 2010LY5N2T. C.F. and F.F. acknowledge financial support from INAF under the contract PRIN-INAF-2011. E.P. and A.B. acknowledge financial support from INAF under the contract PRIN-INAF-2012. S.V. acknowledges financial support from NASA grant G02-13129X. Data used in this work will be made available from http://cdsweb.u-strasbg.fr
References
- Aalto, S., Garcia-Burillo, S., Muller, S., et al. 2012, A&A, 537, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aalto, S., Garcia-Burillo, S., Muller, S., et al. 2015, A&A, 574, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blustin, A. J., Page, M. J., Fuerst, S. V., et al. 2005, A&A, 431, 111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borguet, B. C. J., Arav, N., Edmonds, D., et al. 2013, ApJ, 762, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Braito, V., Della ceca, R.,Piconcelli, E., et al. 2004, A&A, 420, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cano-Diaz, M., Maiolino, R., Marconi, A. et al. 2012, A&A, 537, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cicone, C., Feruglio, C., Maiolino, R., et al. 2012, A&A, 543, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cicone, C., Maiolino, R., Gallerani, S., et al. 2014, A&A, 562, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cresci, G., Hicks, E. K. S., Genzel, R., et al. 2009, ApJ, 697, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Cresci, G., Mainieri, V., Brusa, M., et al. 2015, ApJ, 799, 82 [Google Scholar]
- Croton, D. J., Springel, V., White, S. D. M., et al. 2006, MNRAS, 367, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, X., Shankar, F., & Sivakoff, G. R. 2008, ApJ, 672, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R., Tacconi, L. J., & Genzel, R., et al. 2004, ApJ, 613, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Di Matteo, T., Springel, V., & Hernquist, L., 2005, Nature, 433, 604 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Downes, D., & Solomon, P. M. 1998, ApJ, 507, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M. 2000, ApJ, 545, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Farrah, D., Afonso, J., Efstathiou, A., et al. 2003, MNRAS, 343, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Faucher-Giguere, C. A., & Quataert, E. 2012, MNRAS, 425, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Feruglio, C., Maiolino, R., Piconcelli, E., et al. 2010, A&A, 518, L155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feruglio, C., Fiore, F., Maiolino, R., et al. 2013, A&A, 549, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fischer, J., Sturm, E., Gonzalez-Alfonso, E., et al. 2010, A&A, 518, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallagher, S. C., Schmidt, G. D., Smith, P. S., et al. 2005, ApJ, 633, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Gaspari, M., Brighenti, F., D’Ercole, A., & Melioli, C. 2011, MNRAS, 415, 1549 [NASA ADS] [CrossRef] [Google Scholar]
- Gaspari, M., Brighenti, F., & Temi, P. 2012, MNRAS, 424, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Gaspari, M., Ruszkowski, M., & PengOh, S. 2013, MNRAS, 432, 3401 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Forter Schreiber, N. M., Rosario, D., et al. 2014, ApJ, 796, 7 [Google Scholar]
- Glenn, J., & Hunter, T. R. 2001, ApJS, 135, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Gnerucci, A., Marconi, A., Cresci, G., et al. 2011, A&A, 528, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez-Alfonso, E., Fischer, J., Gracia-Carpio, J., et al. 2014, A&A, 561, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harrison, C. M., Alexander, D. M., Swinbank, A. M., et al. 2012, MNRAS, 426, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, C. M., Alexander, D. M., Mullaney, J. R., & Swinbank, A. M. 2014, MNRAS, 441, 330 [Google Scholar]
- Kawakatu, N., Imanishi, M., & Nagao, T. 2007, ApJ, 661, 660 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. R. 2010, MNRAS, 402, 1516 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. R., & Pounds, K. A. 2003, MNRAS, 345, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Klockner, H., Baan, W. A., & Garret, M. A. 2003, Nature, 421, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Krabbe, A., Colina, L., Thatte, N., & Kroker, H. 1997, ApJ, 476, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Krongold, Y., Nicastro, F., Brickhouse, N. S., et al. 2007, ApJ, 659, 1022 [NASA ADS] [CrossRef] [Google Scholar]
- Lapi, A., Cavaliere, A., & Menci, N. 2005, ApJ, 619, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Lipari, S., Sanchez, S. F., Bergmann, M., et al. 2009, MNRAS, 392, 1295 [NASA ADS] [CrossRef] [Google Scholar]
- Lonsdale, C. J., Lonsdale, C. J., Smith, H. E., et al. 2003, ApJ, 592, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, C., Arias, E. F., Eubanks, T. M., et al. 1998, AJ, 116, 516 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Gallerani, S., Neri, R., et al. 2012, MNRAS, 425, 66 [Google Scholar]
- Martin, S., Krips, M., Martin-Pintado, J., et al. 2011, A&A, 527, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McKernan, B., Yaqoob, T., & Reynolds, C. S., et al. 2007, MNRAS, 379, 1359 [NASA ADS] [CrossRef] [Google Scholar]
- Menci, N., Fontana, A., Giallongo, E., et al. 2006, ApJ, 647, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Menci, N., Fiore, F., Puccetti, S., & Cavaliere, A. 2008, ApJ, 686, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Morganti, R., Tadhunter, C. N., & Oosterloo, T. A. 2005, A&A, 444, 9 [Google Scholar]
- Nardini, E., Reeves, J. N., Gofford, J., et al. 2015, Science, 347, 860 [Google Scholar]
- Nesvadba, N. P. H., Lehnert, M. D., De Breuck, C., et al. 2008, A&A, 491, 407 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papadopoulos, P., Isaak, K. G., & Van Der Werf, P. 2007, ApJ, 668, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Piconcelli, E., Jimenez-Bailon, E., Guainazzi, M., et al. 2005, A&A, 432, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piconcelli, E., Miniutti, G., Ranalli, P., et al. 2013, MNRAS, 428, 1185 [NASA ADS] [CrossRef] [Google Scholar]
- Pounds, K. A. 2014, MNRAS, 437, 3221 [NASA ADS] [CrossRef] [Google Scholar]
- Pounds, K. A., Reeves, J. N., King, A. R., et al. 2003a, MNRAS, 345, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Pounds, K. A., King, A. R., Page, K. L., & O’Brien, P. T. 2003b, MNRAS, 346, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Reeves, J. N., O’Brien, P. T., & Ward, M. J. 2003, ApJ, 593, 65 [Google Scholar]
- Rupke, D., & Veilleux, S. 2011, ApJ, 729, 27 [Google Scholar]
- Rupke, D., & Veilleux, S. 2013, ApJ, 768, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Sakamoto, K., Aalto, S., Costagliola, F., et al. 2013, ApJ, 764, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., & Ho, L. C. 2014, Nature, 513, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., Mazzarella, J. M., Kim, D. C., et al. 2003, AJ, 126, 1607 [Google Scholar]
- Solomon, P. M., Downes, D., Radford, S. J. E., & Barrett, J. W. 1997, ApJ, 478, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Teng, S. H., Veilleux, S., & Baker, A. J. 2013, ApJ, 765, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Teng, S. H., Brandt, W. N., Harrison, F. A., et al. 2014, ApJ, 758, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, A. R., Moran, J. M., & Swenson, Jr. G. W. 2001, eds. A. R. Thompson, J. M. Moran, & G. W. Swenson, 2nd edn. (New York: Wiley) [Google Scholar]
- Thompson, T. A., Fabian, A. C., Quataert, E., & Murray, N. 2015, MNRAS, 449, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Tombesi, F., Sambruna, R. M., Reeves, J. N., et al. 2010, ApJ, 719, 700 [NASA ADS] [CrossRef] [Google Scholar]
- Tombesi, F., Cappi, M., Reeves, J. N., et al. 2011, ApJ, 742, 44 [Google Scholar]
- Tombesi, F., Meléndez, M., Veilleux, S., et al. 2015, Nature, 519, 436 [Google Scholar]
- Turner, B. E. 1989, ApJS, 70, 539 [NASA ADS] [CrossRef] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schoier, F. L., et al. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Veilleux, S., Rupke, D. S. N., Kim, D.-C., et al. 2009, ApJS, 182, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., Melendez, M., Sturm, E., et al. 2013, ApJ, 776, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., Teng, S. H., Rupke, D. S. N., Maiolino, R., & Sturm, E. 2014, ApJ, 790, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J., Nardini, E., Fabbiano, G., et al. 2014, ApJ, 781, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, A., Neininger, N., Húttemeister, S., & Klein, U. 2001, A&A, 365, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Williamson, D. J., Thacker, R. J., Scannapieco, E., & Bruggen, M. 2014, MNRAS, 441, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, C. D., Petitpas, G. R., Iono, D., et al. 2008, ApJS, 178, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Kai, Dong, Xiao-Bo, Wang, Ting-Gui, & Gaskell, C. M. 2011, ApJ, 737, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Zubovas, K., & King, A. 2012, ApJ, 745, 34 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Continuum-subtracted spectra of CO(2−1) from DS1 (top panel) and of CO(3−2) (bottom panel). The plots display the full velocity range achieved by the observed bandwidth. Zoomed views are shown in the insets. |
| In the text | |
 |
Fig. 2 Channel maps of CO(2−1) (DS1, upper panels) and CO(3−2) (lower panels) in three different velocity ranges (indicated by the labels). The contours start from 4σ and are in steps of 1σ for the blue and red wing maps (right and left panels for both CO transitions, respectively). Negative contours are shown by dotted lines, and are in steps of 1σ, starting at −1σ. In the systemic component map (middle panels), contours are in steps of 10σ starting from 10σ, for the sake of clarity. The synthesized beams are shown by hatched areas for each data set. 1σ = 0.14 Jy km s-1 for CO(2−1), = 0.72 Jy km s-1 for CO(3−2). The cross marks the position of the 1.4 GHz continuum as measured by the VLBI, α = 12:56:14.2339, δ = 56:52:25.237 (J2000, Ma et al. 1998). |
| In the text | |
 |
Fig. 3 Channel maps of CO(2−1) from DS1. Contours are in steps of 5σ, starting at 5σ. 1σ = 0.09 Jy km s-1. |
| In the text | |
 |
Fig. 4 Moment 1 map (left panel, levels are 20 km s-1 each) and Moment 2 map (right panel, levels are 25 km s-1 each) of the systemic component of CO(2−1). Cross: AGN position from Ma et al. (1998). |
| In the text | |
 |
Fig. 5 From left to right: model, model folded with the beam, observed distribution and residuals. Top panels: model of the molecular disk with an exponential disc function. Middle panels: model with two components, an outer ring and an inner exponential disk. Bottom panels: velocity dispersion of the two-component model. |
| In the text | |
 |
Fig. 6 Position-velocity plots with east-west (left panel, left to right), south-north (middle panel, left to right) and PA −45 deg, south-west to north-east (right panel, left to right) cuts, through the CO(2−1) peak from DS1. Contours levels are 3 to 15σ, 1σ = 1.3 mJy/20 MHz. |
| In the text | |
 |
Fig. 7 Position-velocity plots of CO(2−1) from DS2 along the same slices than in Fig. 6. Contours levels are 3 to 15σ, 1σ = 0.8 mJy/20 MHz. |
| In the text | |
 |
Fig. 8 Position-velocity plots of CO(3−2) along the same slices than in Fig. 6. Contours levels are 3 to 15σ, 1σ = 0.8 mJy/20 MHz. |
| In the text | |
 |
Fig. 9 Velocity maps of the blue (left) and redshifted CO emission (right). The velocity (in km s-1 with respect to the systemic velocity, i.e. the CO(2−1) peak, is shown in the colour bars. The cross marks the AGN VLBI position. |
| In the text | |
 |
Fig. 10 Maps of vmax = velocityshiftbroad + 2σbroad (colour scale in km s-1). The pixel size is 0.1 arcsec. The cross marks the AGN VLBI position. |
| In the text | |
 |
Fig. 11 Map of |
| In the text | |
 |
Fig. 12 CO(2−1) emission line profiles extracted from square regions at different distances from the nucleus, as indicated by the colour-coded labels, and their multi-Gaussian best fit. |
| In the text | |
 |
Fig. 13 Left panel: integral radial profiles (histogram) and profiles in annuli (points) of the outflow rate |
| In the text | |
 |
Fig. 14 The ratio between data the best model including two thermal components, a power law component and a narrow Gaussian emission line at 6.18 keV (6.44 keV rest frame, iron Kα). Black triangles = Chandra data; red dots = NuSTAR data. A strong excess around 6 keV and a deficit of counts around 7 keV are seen. Note that the NuSTAR data, even taking into account the lower spectral resolution, follow the Chandra data. |
| In the text | |
 |
Fig. 15 67%, 90% and 99% iso-χ2 confidence levels derived from the fitting of the merged X-ray spectra for the absorption line normalization and energy (left panel), for the column density, NH, and redshift of the highly ionized absorber (middle panel), and for NH and ionization parameter, ξ, of the highly ionized absorber (right panel). |
| In the text | |
 |
Fig. 16 Left panel: the momentum boost |
| In the text | |
 |
Fig. 17 3D cartoon of the molecular disk and outflow geometry in Mrk 231. The line of sight to the observer is perpendicular to the page. Red and blue colours represent the receding and approaching material for each component, respectively. The molecular disk consists of an inner disk, tilted by 58 deg on the line of sight, with a scale radius of 200 pc, plus and outer component with inclination 36 deg and scale radius 400 pc, with the line of nodes oriented in the east-west direction approximately. The molecular outflow is rendered by a wide-angle biconical-like component plus an isotropic one, represented here as a sphere for displaying purposes. For a detailed description of the cartoon see Sect. 5. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.