| Issue |
A&A
Volume 582, October 2015
|
|
|---|---|---|
| Article Number | A51 | |
| Number of page(s) | 17 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201526386 | |
| Published online | 05 October 2015 | |
The center-to-limb variation across the Fraunhofer lines of HD 189733⋆
Sampling the stellar spectrum using a transiting planet
Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112, 21029 Hamburg, Germany
e-mail: stefan.czesla@hs.uni-hamburg.de
Received: 22 April 2015
Accepted: 30 July 2015
The center-to-limb variation (CLV) describes the brightness of the stellar disk as a function of the limb angle. Across strong absorption lines, the CLV can vary quite significantly. We obtained a densely sampled time series of high-resolution transit spectra of the active planet host star HD 189733 with UVES. Using the passing planetary disk of the hot Jupiter HD 189733 b as a probe, we study the CLV in the wings of the Ca ii H and K and Na i D1 and D2 Fraunhofer lines, which are not strongly affected by activity-induced variability. In agreement with model predictions, our analysis shows that the wings of the studied Fraunhofer lines are limb brightened with respect to the (quasi-)continuum. The strength of the CLV-induced effect can be on the same order as signals found for hot Jupiter atmospheres. Therefore, a careful treatment of the wavelength dependence of the stellar CLV in strong absorption lines is highly relevant in the interpretation of planetary transit spectroscopy.
Key words: planets and satellites: individual: HD 189733b / planets and satellites: atmospheres / stars: activity / stars: atmospheres
© ESO, 2015
1. Introduction
The discovery of the first transiting extrasolar planet HD 209458 b (Charbonneau et al. 2000) followed five years after the detection of the first extrasolar planet around a main-sequence star (51 Peg b, Mayor & Queloz 1995). Both 51 Peg b and HD 209458 b are Jovian planets orbiting their host stars at a distance of only a few hundredth of an AU, so-called hot Jupiters. At these distances, the atmospheres of the planets are exposed to strong stellar radiation fields. Unequaled in the solar system, the atmospheres of hot Jupiters can best be studied in transiting exoplanetary systems, where they can be observed in absorption against the bright background of the stellar disk.
In particular the stellar extreme ultraviolet and X-ray radiation efficiently deposit energy in the upper planetary atmosphere, where it is thought to derive a Parker-like planetary wind (e.g., Watson et al. 1981). The wind material reaches beyond the optical radius of the planet and effectively enlarges the radius of the disk, especially at wavelengths were the absorption and scattering cross section of the material is large, such as the hydrogen Lyman α line. Expanding planetary atmospheres like this have, indeed, been detected by means of ultraviolet transit spectroscopy, for instance, in the hot Jupiters HD 189733 b and HD 209458 b (Vidal-Madjar et al. 2003; Lecavelier Des Etangs et al. 2010). Further ultraviolet spectral features attributed to the upper planetary atmosphere have been found in HD 209458 b and WASP-12 b (e.g., Linsky et al. 2010; Fossati et al. 2010). Even an X-ray detection of the atmosphere of HD 189733 b has been reported (Poppenhaeger et al. 2013).
The planetary atmosphere can also be probed by in-transit excess absorption in the optical regime (e.g., Seager & Sasselov 2000; Brown 2001). Variations in the planetary radius due to the presence of an atmosphere can be probed, e.g., in the Fraunhofer Na i D1 and D2 lines at ≈5900 Å. In 2002, Charbonneau et al. announced the detection of in-transit excess absorption at a level of (2.32 ± 0.57) × 10-4 in the Na i D1 and D2 lines of HD 209458 observed with the Space Telescope Imaging Spectrograph (STIS) on board the Hubble Space Telescope (HST). While the first detection of atmospheric sodium was achieved with the HST, the visual regime is also accessible with ground-based instrumentation.
After its space-based discovery, the atmosphere of HD 209458 b was also the first to be detected with ground-based instrumentation. In a careful reanalysis of a data set earlier discussed by Narita et al. (2005), Snellen et al. (2008) found excess absorption in the Na i D1 and D2 lines of HD 209458 b at a level of (1.35 ± 0.17) × 10-3 in 0.75 Å wide spectral bands centered on the Na i D1 and D2 line cores. The signal is less pronounced when broader spectral bands are used. Today, ground-based transmission spectroscopy is regularly used to study planetary atmospheres; a number of successful detections of atmospheric sodium have been reported in the literature (see, e.g., Snellen et al. 2008; Wood et al. 2011; Sing et al. 2012; Zhou & Bayliss 2012; Burton et al. 2015).
The hot Jupiter HD 189733 b is one of the best-studied planets beyond the solar system to date. The planet orbits a K-type host star at a distance of ≈0.03 AU and transits the stellar disk every ≈2.2 d (Bouchy et al. 2005). In contrast to HD 209458, HD 189733 is a highly active star. The spectrum shows prominent chromospheric cores in the Ca ii H and K lines and, consequently, a large S-index of 0.525 (Wright et al. 2004; Knutson et al. 2010). This is consistent with rotational photometric variability on the level of a few percent? and an X-ray luminosity of 1.3 × 1028 erg s-1, which makes HD 189733 one of the most X-ray luminous K-type stars in the solar neighborhood, and certainly puts it among the most active planet host stars known to date (Schmitt et al. 1995; Croll et al. 2007; Poppenhaeger et al. 2013). Its distance of only 19.3 pc and resulting apparent brightness of V = 7.67 mag have made it a prime target for detailed follow-up campaigns at all wavelengths ranges.
HD 189733 was the target of an HST campaign carried out with the Advanced Camera for Surveys (ACS) presented by Pont et al. (2008). The authors find an almost featureless spectrum between 5500 and 10 500 Å. Later, Huitson et al. (2012) presented another set of transmission spectra of HD 189733 b obtained with HST/STIS. In their analysis, Huitson et al. (2012) found excess absorption at a level of (9 ± 1) × 10-4 in the Na i D1 and D2 lines. The excess absorption is concentrated in the line cores, which Huitson et al. (2012) attribute to planetary high-altitude haze or a substantially subsolar sodium abundance of the planet. Both Pont et al. (2008) and Huitson et al. (2012) found clear evidence for starspot occultations in their light curves, which underlines the role of the high level of stellar activity in HD 189733.
Redfield et al. (2008) reported on Na i excess absorption in HD 189733, which is about twice as strong as that observed in HD 209458 b by Snellen et al. (2008). Redfield et al. (2008) used a different convention to quantify the excess absorption; a conversion has been carried out by Snellen et al. (2008). In a reanalysis of the data used by Redfield et al., Jensen et al. (2011) confirmed their results and reported excess absorption at a level of (5.26 ± 1.69) × 10-4 across a 12 Å wide spectral band.
Recently, Wyttenbach et al. (2015) reported on another measurement of excess absorption at a level of (3.2 ± 0.3) × 10-3 in the Na i D1 and D2 lines of HD 189733 b based on transit spectroscopy obtained with HARPS. The quoted number refers to the same 0.75 Å wide bands used earlier by Snellen et al. (2008). Wyttenbach et al. (2015) conclude that the major part of their signal is produced in the line cores and could even quantify the width of the signal, giving a full width at half maximum (FWHM) of (0.52 ± 0.08) Å. Additionally, there seems to be slight blue shift, which may be indicative of a wind in the planetary atmosphere of HD 189733 b blowing from the day to the night side, and is similar to what is observed in the case of HD 209458 b (Snellen et al. 2010).
While transit spectroscopy is a powerful technique for studying the planetary atmosphere, it is only seen in absorption against the stellar disk, whose appearance is, therefore, equally relevant for an appropriate interpretation of the results. A wavelength-dependent change in the brightness of the disk from the center toward the limb has long been observed on the Sun (e.g., Pierce & Slaughter 1977; Neckel & Labs 1994). The center-to-limb variation (CLV) is attributable to a limb-angle dependent viewing geometry, effectively exposing ever higher layers of the solar atmosphere to the observer targeting the limb. As higher layers are usually cooler and emit less light in the optical, the effect is often more specifically dubbed limb darkening. This term mostly, but not always, describes the appearance of the stellar disk in the visual band. At other wavelengths, such as in the X-ray and ultraviolet regime, the solar atmosphere can show limb brightening (e.g., Schlawin et al. 2010; Poppenhaeger et al. 2013; Llama & Shkolnik 2015).
In the analysis of transit light curves of extrasolar planets, the CLV has long been acknowledged as a critical factor (e.g., Müller et al. 2013). In the modeling, the brightness distribution of the stellar disk is usually parametrized by one of many available so-called limb-darkening laws. Among the most frequently applied parameterizations are the linear and quadratic limb-darkening laws, according to which the limb-angle dependent intensity is given by 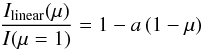 (1)and
(1)and  (2)where a and b are the linear and quadratic limb-darkening coefficients, and μ is the limb angle (see Sect. 2.1). Limb-darkening coefficients for a wide range of stellar parameters, limb-darkening laws, and photometric bands have been tabulated (e.g., Claret 2004).
(2)where a and b are the linear and quadratic limb-darkening coefficients, and μ is the limb angle (see Sect. 2.1). Limb-darkening coefficients for a wide range of stellar parameters, limb-darkening laws, and photometric bands have been tabulated (e.g., Claret 2004).
While the tabulated coefficients usually refer to broad photometric bands, the wavelength dependence of the CLV in the stellar atmosphere can be very strong on shorter scales. In the optical, the wavelength dependence is strongest across the profiles of deep stellar absorption lines, such as the Ca ii H and K or Na i D1 and D2 lines (e.g., Athay et al. 1972). Yan et al. (2015) presented a study on the CLV in the solar Fraunhofer lines observed in solar eclipse spectra reflected by the Moon. The authors clearly detected the CLV of the solar atmosphere in their spectra and argue that the effect becomes most prominent if narrow spectral bands covering the strong (Fraunhofer) lines are used.
In fact, strong modulations in the stellar CLV over small wavelength ranges also dubbed differential CLV (or differential limb darkening) are a known problem in the analysis of the Na i features in extrasolar planets. For instance, Charbonneau et al. (2002) provide a careful discussion on the effect to rule out that their signal is caused by the CLV. Also Sing et al. (2008) discuss the CLV in HD 209458 extensively and present CLV-corrected transit light curves. Among others, the authors conclude that limb darkening in the stellar lines is smaller than in the continuum and that one-dimensional stellar atmospheres can reproduce the observed effects. In fact, many authors, including some of those referenced earlier, have discussed the issue so that the above list is by no means complete.
The treatment of the CLV is further complicated by the availability (or lack thereof) of different model predictions. Claret (2004) give both limb-darkening coefficients derived from (one-dimensional) PHOENIX and ATLAS model atmospheres, which are similar but not identical. Müller et al. (2013) find both sets of coefficients to be consistent with Kepler data. Hayek et al. (2012) compare CLV predictions resulting from one- and three-dimensional model atmospheres to transit light curves of HD 189733 and HD 209458. For the latter, they find a considerably better match with the three-dimensional model. While this is also compatible with their finding for HD 189733, their data remained insufficient for a conclusive result in this case.
In this work, we present the analysis of the CLV in the Ca ii H and K and Na i D1 and D2 lines in HD 189733 and discuss its relevance for searches of atmospheric excess absorption in the Na i lines via transit spectroscopy. In Sects. 2 to 4, we introduce the formalism and models used in our analysis. Our observations and the data analysis are presented in Sects. 5 to 7. Finally, we discuss the results in Sect. 8 and present our conclusions in Sect. 9.
2. Synthetic data
Throughout this work, we present synthetic spectra and simulated light curves of transiting planetary systems. Here, we outline the simulations and input data.
2.1. Limb-angle dependent spectra
The limb angle, θ, is the angle between the outward normal of the stellar atmosphere and the vector pointing from the center of the star toward the observer. Usually its cosine μ = cos(θ) is used to specify the limb angle. With this convention, μ = 0 refers to the limb and μ = 1 to the center of the stellar disk.
All synthetic spectra used in this work are based on Kurucz model atmospheres with solar metallicity (Castelli & Kurucz 2004; Kurucz 1970). The spectra themselves were generated using the spectrum program1 by R.O. Gray (Gray & Corbally 1994), which facilitates the generation of both disk-integrated stellar spectra and limb-angle dependent specific intensities. Based on the assumption of plane-parallel atmospheres and local thermodynamic equilibrium (LTE), spectrum first computes the number densities of electrons and all relevant species in the atmosphere and solves the equation of radiative transfer to obtain a synthetic spectrum. Information on individual spectral lines, viz., their wavelength, the ion, the lower and upper energy levels, and the product of statistical weight and oscillator strength are specified via a line list file. In our calculations, we relied on the line list shipped along with the program.
Whenever we use limb-angle dependent specific intensities, we generate 20 spectra with limb angles between μ = 0 and μ = 1, i.e., a spacing of Δμ = 0.05. To avoid numerical problems at the very edge of the stellar disk (μ = 0), we replace the lower limit by μ = 0.001 in the calculations and assume that the spectrum completely vanishes for μ = 0. The impact of this approximation remains small because the stellar atmosphere is seen at a very steep angle so close to the limb and only contributes a tiny fraction to the total observed flux. Spectra at intermediate limb angles are linearly interpolated based on the spectra on the grid. All spectra are equidistantly sampled on an equidistant wavelength grid with a spacing of 0.01 Å per bin.
2.2. Discretized stellar surface
To simulate the spectra of a stellar disk, potentially partially occulted by a planet, we use a discretized stellar surface with elements defined according to the prescription by Vogt et al. (1987). In particular, we use 1001 latitudinal rings and a total of 250 000 surface elements. In the Vogt et al. discretization, the surface elements have approximately the same size, which is about 5 × 10-5 rad or 0.17 sq. deg in our case.
The spectrum is obtained by summing the contributions of all visible surface elements, assigning to each a spectrum according to its projected area, limb angle, and radial velocity. A transiting planet is implemented by occulting all stellar surface elements covered by the planetary disk. This is equivalent to setting their projected area to zero during occultation.
Given this configuration, the surface element with the largest projected area covers the π × (5 × 10-5)-1 = 62 500th part of the visible stellar disk. Therefore, a Jovian planet occulting one percent of the disk would be sampled by about 625 stellar surface elements, which gives an idea of the statistical uncertainty in the simulations.
3. Transit light curves and their combination
Transit light curves, whether derived from broadband photometry or high-resolution spectroscopy, are among the most important tools to study exoplanets. Below, we briefly discuss the most relevant aspects required in our work.
3.1. The standard planetary system
We present a number of model calculations referring to what we call our standard planetary system, which are used whenever we do not discuss a specific planetary system such as HD 189733. The standard planet represents a typical hot Jupiter. It has one Jovian radius and orbits a star with solar radius in a distance of ten solar radii at an inclination of 90 deg. The orbital period is 2 days. The standard star is a slow rotator with vsin(i) = 0.1 km s-1 seen at an inclination of 90 deg (i.e., equator-on). Assuming the convention that the primary transit occurs at orbital phase zero, the transit lasts from orbital phase −0.018 to + 0.018, and the transit duration is 1.69 h.
3.2. Naming conventions for light curves
We obtain the time-dependent flux, ff(ti), in a spectral band centered on some feature of interest and its equivalent, fr(ti), in the reference band, where the ti refer to the times of our hypothetical measurements. Further, we let tit and toot refer to all measurements in- and out-of-transit. We dub ff(ti) and fr(ti) two light curves. In transit analyses, these are often normalized by their out-of-transit levels, so that  (3)where X represents f or r and the bar indicates the mean value. We refer to nX as the normalized light curve. The difference, d(ti), of the normalized light curves, i.e.,
(3)where X represents f or r and the bar indicates the mean value. We refer to nX as the normalized light curve. The difference, d(ti), of the normalized light curves, i.e.,  (4)traces differential changes in between them. We dub d(ti) the difference curve (DC); this form was used by Charbonneau et al. (2002) in their analysis. To quantify the difference in transit depth, we follow Charbonneau et al. (2002) in defining the in-transit DC excess (DCE)
(4)traces differential changes in between them. We dub d(ti) the difference curve (DC); this form was used by Charbonneau et al. (2002) in their analysis. To quantify the difference in transit depth, we follow Charbonneau et al. (2002) in defining the in-transit DC excess (DCE)  (5)We note that another natural choice for studying differential changes is the ratio, r(ti), of the normalized light curves
(5)We note that another natural choice for studying differential changes is the ratio, r(ti), of the normalized light curves 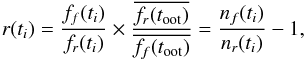 (6)where we subtract one to obtain the same out-of-transit level as for the DC. Yet, the difference between the DC and the ratio curve
(6)where we subtract one to obtain the same out-of-transit level as for the DC. Yet, the difference between the DC and the ratio curve  (7)is small for typical planetary transit light curves with transit depths of a few percent. Therefore, we limit the following discussion to the DC.
(7)is small for typical planetary transit light curves with transit depths of a few percent. Therefore, we limit the following discussion to the DC.
3.3. The appearance of the difference curve
Assume we are given the normalized light curves of a feature, LCf(ti), and a number of normalized reference light curves, LCr,1...n(ti). For instance, these light curves could have been extracted from a series of spectra by integrating the signal in various bands. In this particular case, we assume that LCf(ti) and LCr,1...n(ti) are normalized transit light curves of our standard planetary system (see Sect. 3.1), which we obtain from conventional transit models (Mandel & Agol 2002). The only difference between the feature and reference light curves is the stellar limb darkening. For the sake of simplicity and without loss of generality, we assume the linear limb-darkening law in this demonstration (see Eq. (1)).
 |
Fig. 1 Normalized model transit light curves. |
For the feature light curve, LCf(ti), we specifically assume a value of 0.5 for the linear limb-darkening coefficient, a. Then, we generate two reference light curves: the first, LCr,0.3(ti), using a limb-darkening coefficient of 0.3 and another one, LCr,0.7(ti), assuming a value of 0.7. The resulting model light curves are shown in Fig. 1. Compared to LCr,0.3(ti), the feature shows limb darkening, but it shows limb brightening with respect to LCr,0.7(ti). We emphasize that all of the light curves show limb darkening, and limb brightening is only seen as a relative effect.
In Fig. 2, we show both the DCs obtained by combining the feature light curve, LCf(ti), with either of the reference light curves. The DCs show a distinct behavior, which differs substantially from that of the input transit light curves (cf. Fig. 1). In the case of identical limb darkening for the feature and reference light curve, the DC becomes zero.
 |
Fig. 2 Difference curve, DC(ti), for a limb-darkened (solid, LCf(ti) vs. LCr,0.3(ti)) and a limb-brightened (dashed, LCf(ti) vs. LCr,0.7(ti)) feature. |
When the feature is limb brightened compared to the reference light curve, the DC shows a drop below the out-of-transit level during in- and egress. At the limb of the stellar disk, the planet blocks more light from the feature than it blocks from the reference. In the middle of the transit, with the planet in the center of the stellar disk, the DC shows a peak because the situation is reversed. Compared to the feature, more of the reference light is emitted in the center of the stellar disk, where it is now occulted by the planetary disk. When the feature is limb darkened, the DC is inverted, but otherwise keeps its main characteristics.
4. Differential light curves and the stellar disk
The presence of excess absorption attributable to an exoplanetary atmosphere during transit is often derived by analyzing differential light curves, such as the DC introduced in Sect. 3.2. Usually, the spectral flux is integrated in a band centered on the specific feature under consideration and compared to the flux observed in various reference bands (e.g., Charbonneau et al. 2002; Snellen et al. 2008). Depending on the characteristics of these bands, the limb-angle dependence of the stellar spectrum, i.e., the stellar atmosphere, can imprint a strong signal on the DC totally unrelated to the planetary atmosphere.
 |
Fig. 3 Normalized stellar spectrum around the sodium doublet for two limb angles μ = 0.1 (dashed) and μ = 1.0 (solid) and three effective temperatures. |
4.1. Limb-angle dependence of spectral lines
In Fig. 3, we demonstrate the effective temperature and limb-angle dependence of the Na i D1 and D2 lines using stars with effective temperatures of 4000 K, 5000 K, and 6000 K. Irrespective of limb angle, the width of the Na i D1 and D2 lines increases when the effective temperature decreases. This behavior can primarily be attributed to pressure broadening, viz., to the temperature and pressure dependence of the line damping constants. In solar-like stars, pressure broadening of the Na i D1 and D2 lines is dominated by van der Waals forces (Gray 2008, Fig. 11.4), whose influence is stronger in the denser atmospheres of cooler stars.
At all temperatures, there is a strong dependence of the line profile on the limb angle. In the center of the stellar disk, the line wings are more pronounced than at the limb. At the stellar limb, higher layers with less pressure are seen, where pressure broadening is weaker. Although the limb-angle dependence is more clearly seen in cooler stars, this is mainly attributable to the larger line width. If the wavelength was scaled by the Na i line width, the behavior of the line wings would actually become quite similar. In contrast to the wings, the depth of the line core remains virtually unchanged, which has an immediate and important consequence: compared to the core and the continuum, the line wings of the Na i doublet show limb brightening. In fact, not only the Na i lines, but all spectral lines show distinct CLV.
In Fig. 4, we show the ratio, R(λ), of the specific intensity in the center (μ = 1) and at the limb (μ = 0.05) of a stellar disk with an effective temperature of 5000 K and log (g) = 4.5. In terms of limb darkening (see Sect. 1), this ratio corresponds to  (8)While the (quasi-)continuum sections of the spectrum show a mostly constant ratio, the spectral lines show distinct behavior. Ignoring the sodium doublet for the moment, we find that R(λ) increases for the majority of spectral lines covered in Fig. 4. These lines, therefore, show limb brightening with respect to the continuum, however, a number of lines also show the reverse effect.
(8)While the (quasi-)continuum sections of the spectrum show a mostly constant ratio, the spectral lines show distinct behavior. Ignoring the sodium doublet for the moment, we find that R(λ) increases for the majority of spectral lines covered in Fig. 4. These lines, therefore, show limb brightening with respect to the continuum, however, a number of lines also show the reverse effect.
 |
Fig. 4 Top: ratio of stellar spectra (Teff = 5000 K, log (g) = 4.5) at limb and center (μ = 0.05 and μ = 1.0) shown with a solid line. For comparison, the scaled central spectrum (dashed line). Bottom: normalized specific intensity in the μ = 0.001−1 range in the line core (5889.95 Å, crosses), the line wing (5889 Å, squares), and the quasi-continuum (5864.6 Å, circles). |
Whether a spectral line shows limb brightening or darkening with respect to the continuum depends on its height of formation in the stellar atmosphere. Lines formed in the upper layers become stronger on the limb, where their depth and equivalent width increases because the line of sight resulting from the steeper viewing angle favors higher layers. Spectral lines formed in deeper layers become stronger in the center of the disk, where we look deeper into the atmosphere. While the distribution of spectral line formation in the stellar atmosphere depends on the details of the stratification, it can be said that the height of formation for lines originating from a single ion tends to be higher for lower excitation potentials (e.g., Grossmann-Doerth 1994).
The strongest lines, such as the Na I doublet, are formed over a wide range of depths in the atmosphere. Therefore, they show the most complex behavior of the spectral lines visible in Fig. 4 (top). The line cores show immense optical thickness and are, therefore, formed high up in the atmosphere. In fact, at μ = 0.05 the intensity in the line cores has almost dropped to zero already (Fig. 4, bottom). This corresponds to an effective decrease in the stellar radius or an increase in the planet-to-star radius ratio in the cores of the Na i lines. While the cores, therefore, show strong limb-darkening with respect to the continuum emission, the line wings exhibit the opposite behavior. The wings are limb brightened with the details depending on the exact spectral band chosen. Again, we emphasize that the line wings show only relative limb brightening compared to the continuum. In the bottom panel of Fig. 4, we show the normalized specific intensity of the line core, a point in the line wing, and a point in the surrounding quasi-continuum. The curves clearly demonstrate that the line core shows limb darkening and the line wing shows limb brightening relative to the continuum.
Figure 4 clearly shows that the assumption of a homogeneously limb-darkened stellar disk becomes inappropriate as soon as individual spectral lines are considered. The limb-angle dependence is most prominent in deep and broad lines, such as the Ca ii H and K lines or the Na i doublet lines. The latter are a main focus of the study of exoplanet atmospheres (e.g., Redfield et al. 2008; Charbonneau et al. 2002; Snellen et al. 2008; Huitson et al. 2012).
 |
Fig. 5 Simulated DCs for the Na i lines (D2 in the left column and D1 in the right column) for effective temperatures of 4000 K, 5000 K, and 6000 K. Normalized feature light curves where extracted in four bands with half-widths 0.1 Å, 0.375 Å, 0.75 Å, and 1.5 Å centered the respective sodium line. The resulting DCs are plotted using solid (black), dashed (red), dotted (green), and dash-dotted (blue) lines in the same order. |
4.2. Simulated Na I transit light curves
Using the techniques outlined in Sect. 2, we simulated spectral time series covering a transit of our standard exoplanetary system (see Sect. 3.1). In the simulations, we used a grid of stellar effective temperatures ranging from 4000 K to 7000 K in steps of 500 K; log (g) was 4.5 in all simulations.
We simulated the spectra for 60 equidistant time points between orbital phases of −0.02 and 0.02, where the transit center occurs at phase zero. The temporal cadence of the simulated spectra, therefore, is (0.04 × 2 d)/60 = 1.92 min. The numbers quoted in the following refer to spectra not broadened by instrumental resolution, however, we found its impact remains weak as long the considered spectral bands cover a few spectral resolution elements.
4.2.1. Difference curves with broad feature intervals
In their analysis of the atmosphere of HD 209458 b, Charbonneau et al. (2002) used bands covering the entire sodium-line doublet. In particular, they defined narrow (n), medium (m), and wide (w) bands for the blue and red reference bands and the central band covering the sodium lines.
Charbonneau et al. (2002) detect excess absorption by the planetary atmosphere through a negative excess in what we dubbed the DC (see Sect. 3.2). As the authors point out, the CLV is a potential source of this kind of an excess. However, they verified that it is of no concern in their analysis because the effect remains small (see their Eq. (6)).
Simulated in-transit excess absorption diagnosed by the DC for the narrow (n), medium (m), and wide (w) spectral bands defined by Charbonneau et al. (2002).
We used the spectral bands defined by Charbonneau et al. (2002) and reproduced their DCE estimates (see Sect. 3.2) for our simulations of the standard planetary system. Our results are summarized in Table 1. Clearly, there is an effect related to the CLV, which is stronger for lower effective temperatures for the specified bands. We attribute this trend to the increasing width of the Fraunhofer Na i lines, when effective temperature decreases.
Charbonneau et al. (2002) carried out the analysis for HD 209458 b, which orbits a host star with an effective temperature of 6065 K (Torres et al. 2008). The values given by Charbonneau et al. (2002) read 1.52 × 10-5, 0.39 × 10-5, and 0.47 × 10-5 for the narrow, medium, and wide bands. These values are compatible with the values we derived for a host star with an effective temperature of 6000 K. We attribute the small deviation to the difference in the system geometry and the different model spectra.
Difference curve excesses for narrow reference bands with full widths of 0.75 Å, 1.5 Å, and 3 Å centered on the Na i D1 and D2 lines.
4.2.2. Difference curves with narrow feature intervals
From our simulations, we obtained the feature light curve, ff(ti), by integrating the spectral signal in bands with half-widths of 0.1 Å, 0.375 Å, 0.75 Å, and 1.5 Å, centered on either of the two sodium lines. The reference light curve is defined as the median flux obtained across a broad (5820−5950 Å) wavelength range. The resulting DCs are shown in Fig. 5 for stars with effective temperatures of 4000 K, 5000 K, and 6000 K. The associated DCEs are listed in Table 2. For all stars and bands considered here, we obtain positive DCEs. Therefore, the sodium lines show net brightening during transit.
The actual choice of a reference interval in the simulated spectral region remains quite insignificant for the resulting DCs. Although there is some differential limb darkening even in the continuum, the level of change is much smaller than the deviations seen in the spectral lines. For instance, the DC of the two potential reference intervals 5860−5865 Å and 5920−5940 Å on the blue and red side of the sodium lines shows variation in the ± 2 × 10-5 range for a star with Teff = 4000 K, which is two orders of magnitude smaller than that observed in the Na i lines.
The DCs involving the sodium line show variability on a level of up to 10-3. The behavior is typical for transit light curves obtained from a limb-brightened feature (cf. Sect. 3.3). The details obviously depend on the choice of the extraction bands and CLV of the stellar lines. Nonetheless, the amplitude of the curves shown in Fig. 5 can clearly be sufficient to be relevant for the study of exoplanetary atmospheres, whose signals are expected to be on the order of 10-3−10-4 (e.g., Seager & Sasselov 2000).
4.2.3. Treatment of the CLV-induced in-transit excess
Through the partial occultation of the stellar disk during transit, the stellar CLV is imprinted on the DC. In the cases considered here, it causes apparent net emission in the feature bands covering the Na i D1 and D2 lines. This has to be taken into account in the measurement of in-transit excess absorption due to the planetary atmosphere as has been shown, e.g., by Charbonneau et al. (2002) and Sing et al. (2008). In particular, the corresponding value should be added to the measured transit depth, if we have not previously taken the CLV into account.
As the DC is time dependent, the result of the averaging required to obtain the DCE (see Sect. 3.2) depends on the sampling of the transit. An accurate correction of the CLV-induced effect is only possible, if all boundary conditions like the temporal sampling, instrumental resolution, and sensitivity are taken into account in the modeling.
5. Observation of the center-to-limb variation in HD 189733
In 2012, we obtained high-resolution transit spectroscopy of HD 189733 with UVES. The properties of HD 189733 are summarized in Table 3. We generated synthetic spectra of the star based on a Kurucz model atmosphere with an effective temperature of 5000 K, a surface gravity of log (g) = 4.5, and solar abundances. Again, we used our code to simulate a spectral time series based on the orbital configuration of HD 189733 system from which we derive model light curves to be compared with the observations.
Properties of HD 189733.
5.1. Observations and data reduction
On July 1, 2012, we observed HD 189733 with UVES mounted at the VLT-UT2 (Kueyen). Between 04:06 and 08:40 UT, we obtained 244 spectra, whereof the first 29 were exposed for 30 s and the remaining for 45 s. We applied the dichroic beam splitter (dic2) in the 437 + 760 nm setup. The slit width was 1′′ for the blue and 0.7′′ for the red arm. To optimize the temporal cadence, we used the ultra fast readout option.
To reduce the echelle spectra, we used the UVES-pipeline in version 5.2.0. The pipeline performs bias subtraction, hot-pixel rejection, order definition, order extraction, flat fielding, and the wavelength calibration using ThAr frames. Finally, the echelle orders are merged into a single 1d-spectrum and flux calibrated. In this work, we use the spectra from the blue and lower red chip, which were obtained using optimal extraction.
 |
Fig. 6 Temporal evolution of seeing (top) and air mass (bottom). The vertical dashed lines indicate the duration of the transit. The temporal offset, T0, refers to MJDHJD,UTC = 56 109.26164. |
We obtained reference spectra for flux calibration during our observing night, but found that the spectra calibrated using the master response files2 show a lower degree of large-scale structure not attributable to the stellar spectrum, while the small-scale noise properties of the resulting spectra are identical. The flux obtained with the master response files was generally lower by about 15−20% on the lower red chip, which gives an idea of the involved uncertainties. In our analysis, we prefer to use the spectra calibrated using the master response files.
The blue and red chip are read out separately and, in principle, asynchronously. Analyzing the start times as determined by the header keyword MJD-OBS, we find that, on average, the observation obtained with the blue chip starts 0.83 ± 1.1 s later than on the red chip. In the most extreme case, the observation obtained with the blue chip is delayed by 9 s compared to the red chip. As the difference is, however, larger than 3 s in no more than six cases, the observations can be treated as simultaneous where not explicitly stated otherwise.
The data cover the primary transit plus some pre- and post-transit time. In Fig. 6, we show the temporal evolution of the seeing (header keyword HIERARCH ESO TEL IA FWHM) and the air mass during our observations. The duration of the transit is explicitly indicated. The seeing is between 0.5′′ and 0.6′′ during the first half of the observations and further improves in the second half.
5.2. Accuracy of the flux-calibration
The flux calibration applied by the UVES pipeline takes the exposure time, gain, binning, atmospheric extinction, and air mass3 into account. To verify that reasonable fluxes are produced, we integrated the flux obtained with the individual chips and compare the numbers thus obtained with a model spectrum and a black body. The model spectrum is based on a Kurucz model atmosphere with an effective temperature of 5000 K, a log (g) value of 4.5, and solar metallicity (Castelli & Kurucz 2004; Kurucz 1970). The spectrum was synthesized using the spectrum program (Gray & Corbally 1994). To calculate the blackbody spectrum, we applied a temperature of 5040 K (see Table 3). In Table 4, we list the minimum and maximum observed flux on each chip along with the flux predicted by the Kurucz atmosphere and the black body.
 |
Fig. 7 Temporal evolution of the measured spectral flux on the blue chip (squares) and (scaled) signal in the acquisition images from the blue camera (crosses). Dashed vertical lines indicate the transit duration. |
Measured and predicted fluxes at Earth.
In Fig. 7, we show the measured spectral flux on the blue chip obtained by integrating the flux-calibrated spectrum and the signal measured in the blue-channel acquisition images as a function of time. The latter clearly represents light having missed the slit. Acquisition and spectral signal are strongly anticorrelated. The evolution of the spectral and acquisition signal after the first half of the observation is clearly related to the behavior of the seeing (Fig. 6) with better seeing resulting in more stellar light entering the slit.
Although the spectral signal shows an apparent drop, which is remarkably well aligned with the transit, the depth of this hypothetical transit is about 5% and, therefore, it is too deep to be (solely) caused by the planet, which shows a transit depth of about 3% in the B filter (Bouchy et al. 2005). While the spectral and acquisition signals can be combined to obtain a curve showing a transit of proper depth, the uncertainty in the scaling prevents a meaningful quantitative analysis.
The observed flux and the prediction based on the Kurucz atmosphere agree on the 20% level, which seems reasonable considering the systematic uncertainty in the flux calibration (see Sect. 5.1). The residual variation is largely attributable to slit losses with some residual influence of air mass and atmospheric conditions that are likely also present.
5.3. Wavelength stability
In the red part of the spectrum (λ ≳ 6000 Å), telluric lines yield a radial velocity calibration with an accuracy of about 20 m s-1 (e.g., Balthasar et al. 1982; Caccin et al. 1985; Gray & Brown 2006). We used the telluric lines to study the stability of the wavelength calibration in our data. First, we obtained a nominal telluric transmission spectrum using the Line-By-Line Radiative Transfer Model (LBLRTM) code (Clough et al. 2005). Second, we selected a total of six wavelength intervals between 6800 and 9200 Å4, and third, we determined the (apparent) radial velocity shift of the telluric lines using a cross-correlation.
Figure 8 shows the resulting shift of the telluric oxygen lines between 6864 and 6968 Å. The curve shows a sawtooth-like pattern with an overall amplitude of roughly 1 km s-1, which we found for telluric lines across the entire red spectral arm. We attribute the variation to instrumental effects, mainly changes in the positioning of the stellar disk within the slit, which also manifest in a shift of the location of the echelle orders on the detector and changes in the asymmetry of the acquisition images. The slit width of 0.7′′ in the red arm was, indeed, larger than the seeing disk; the same holds for the blue arm.
 |
Fig. 8 Radial velocity shift of telluric lines between 6864 and 6968 Å. |
To correct for the instrumental shifts, taking its wavelength dependence into account, we used the telluric corrections determined in the six individual bands and interpolated to correct at intermediate wavelengths.
5.4. The Rossiter-McLaughlin effect
The Rossiter-McLaughlin effect is an apparent radial velocity shift caused by a change in the spectral line profile during the planetary transit (e.g., Rossiter 1924; McLaughlin 1924). The Rossiter-McLaughlin curve provides important information about the planetary system, most notably, the relative orientation of the (sky-projected) stellar spin axis and the planetary orbit normal (e.g., Ohta et al. 2005).
In HD 189733, the amplitude of the Rossiter-McLaughlin effect is about 40 m s-1, which is a factor of 25 below the instrumental velocity shifts seen in the telluric lines. To measure the Rossiter-McLaughlin effect, we determined the stellar radial velocity by cross-correlation with a synthetic spectral model in the 6620−6700 Å, 6700−6840 Å, 7780−7820 Å, and 8700−8750 Å bands. The stellar radial velocity was then corrected by subtracting the telluric correction determined in Sect. 5.3 and adding the barycentric correction. The spectral bands used in the cross-correlation were selected because they are close to the telluric bands used to correct the instrumental radial velocity shift, but are themselves only weakly affected by telluric absorption. The resulting curve is shown in Fig. 9 along with a nominal model calculated using the parameters from Triaud et al. (2009), Ohta et al. (2005). The errors were estimated from the scatter of the radial velocity measurements obtained in the individual spectral bands. Note that we did not carry out a fit.
 |
Fig. 9 Rossiter-McLaughlin radial velocity curve along with nominal model with parameters from Triaud et al. (2009; top) and residuals (bottom). |
The Rossiter-McLaughlin effect is clearly seen. Toward the end of the observation run, there seems to be a systematic offset between model and measurement, which may due to a shortcoming of the instrumental correction. Otherwise, the Rossiter-McLaughlin effect is compatible with the curve reported by Triaud et al. (2009). During the transit, we obtain correlated residuals not unlike those seen in previous works (see Winn et al. 2006; Triaud et al. 2009). The residuals seen by Winn et al. (2006) and Triaud et al. (2009) show a remarkable point symmetry with respect to mid-transit time, which is also indicated by our residuals.
5.5. Line profiles and instrumental resolution
Changes in the line profile potentially interfere with all analyses based on individual line characteristics, in particular, the line depth or flux observed around the center of the line. To study the temporal stability of the line profile, we selected a total of 19 sufficiently isolated, telluric spectral lines between 5885 Å and 7265 Å. All the lines were modeled using a Gaussian profile. Assuming that the lines are intrinsically narrow, the instrumental resolution is obtained by the inverse of the FWHM times the wavelength. Figure 10 show the equivalent-width weighted mean instrumental resolution. The temporal evolution of the resolution is anticorrelated with the seeing (see Fig. 6).
 |
Fig. 10 Equivalent-width weighted instrumental resolution obtained from 19 telluric lines between 5885 and 7265 Å. |
According to our analysis, the mean instrumental resolution is about 60 000, but it clearly varies during the observing run. The behavior can likely be attributed to a change in slit illumination, with the seeing disk moving in the slit.
6. Center-to-limb variation observed in the Ca II H and K lines
The Ca ii H and K lines at 3933.66 Å and 3968.47 Å are the widest and strongest spectral lines in the wavelength range covered by our UVES observations. These lines are expected to show a distinct pattern of CLV across their profiles, and their width makes them favorable targets for studying the CLV. Prior to any further analysis, we cross-correlated the observed spectra with a model spectrum to correct for the instrumental radial-velocity shift (see Sect. 5.3). In the following, we adopt the reference continuum bands CH (3891.67−3911.67 Å) and CK (3991.067−4011.067 Å) also used by Melo et al. (2006).
6.1. The line core
The cores of the Ca ii H and K lines are highly sensitive to chromospheric emission (e.g., Baliunas et al. 1995). To obtain the DC, we integrated the spectral signal in 1 Å wide bands centered on the Ca ii H and K lines cores and derived two normalized feature light curves LCK(ti) and LCH(ti). The integration of the signal in the two aforementioned reference bands yields two normalized reference light curves, LCCK(ti) and LCCH(ti). Based on these light curves, we obtained the DC as  (9)where the first term is the mean feature light curve and the second the mean reference light curve. In Fig. 11, we show the resulting DC, which shows a complex temporal pattern of variability. Most prominently, a steep rise is seen at about mid-transit time, which is followed by a decay phase, lasting for the rest of the observation. This behavior in chromospherically sensitive lines is typical of solar and stellar flares (e.g., Fang et al. 1992; Fuhrmeister et al. 2008). Therefore, we attribute it to a flare. Superimposed on the decay phase of the flare is another smaller, yet otherwise similar, event. We interpret this as another, potentially related, flare. Indeed, multiple temporally overlapping flares are frequently observed on active stars (e.g., Lalitha et al. 2013). In the following analysis, we exclude the second half of the DC from our modeling of the CLV.
(9)where the first term is the mean feature light curve and the second the mean reference light curve. In Fig. 11, we show the resulting DC, which shows a complex temporal pattern of variability. Most prominently, a steep rise is seen at about mid-transit time, which is followed by a decay phase, lasting for the rest of the observation. This behavior in chromospherically sensitive lines is typical of solar and stellar flares (e.g., Fang et al. 1992; Fuhrmeister et al. 2008). Therefore, we attribute it to a flare. Superimposed on the decay phase of the flare is another smaller, yet otherwise similar, event. We interpret this as another, potentially related, flare. Indeed, multiple temporally overlapping flares are frequently observed on active stars (e.g., Lalitha et al. 2013). In the following analysis, we exclude the second half of the DC from our modeling of the CLV.
 |
Fig. 11 Top: observed DC extracted from the Ca ii H and K line cores. Bottom: close-up of the first half of the observed DC. The solid line shows a photospheric model DC and the dashed line a chromospheric model DC, assuming homogeneous distribution of the Ca ii H and K core emission. |
To model the observed behavior in the first half of the observation, we derived two synthetic DCs. First, we obtained a photospheric model, representing the DC that would be obtained in the absence of any chromospheric emission from our synthetic spectral time series. By fitting a transit model with quadratic limb darkening (Mandel & Agol 2002) to the synthetic mean feature and reference light curves, we obtained limb-darkening coefficients of af = 0.27 and bf = 0.33 for the feature and ar = 1.08 and br = −0.24 for the reference. The latter are compatible with the values of a = 1.06 and b = −0.2 derived by Claret (2004) for stars like HD 189733 in the Sloan u′-band. Second, we constructed a DC assuming a homogeneous distribution of chromospheric emission across the stellar disk, i.e., zero limb darkening of the feature. The reference light curve was left unchanged. To model the observed DC, we additionally added a second second-order polynomial to the DCs to take the global pattern of variability into account. The actual spatial distribution of chromospheric emission is probably more inhomogeneous as observed on the Sun (Llama & Shkolnik 2015), but we refrain from adopting a more complex model here.
In the bottom panel of Fig. 11, we show the first half of the data along with the our two best-fit photospheric and chromospheric models. In the fitting, only the coefficients of the polynomial were varied. The behavior of the observed DC during ingress is reminiscent of the expected behavior. In particular, an initial decrease followed by an increase toward the mid-transit phase is clearly visible. The behavior is better reproduced by the chromospheric model, assuming homogeneously distributed emission in the Ca ii H and K emission line cores. While this is plausible, there is also variability on a similar scale as observed prior to ingress, which is, therefore, most probably unrelated to the transit. Although the model is plausible, it remains difficult, if not impossible, to distinguish between intrinsic variability and CLV-induced changes in the cores of the Ca ii H and K lines.
 |
Fig. 12 Combined DC of the Ca ii H and K lines wings along with our best-fit second order polynomial model (dashed) and our best-fit model including the synthetic DC. The bottom panel gives the residuals with respect to our DC model. The solid (red) line shows the residuals smoothed by a running mean with a width of eight data points. The vertical lines indicate the transit duration and the three top bars indicate the phase intervals used in the analysis of the spectra. |
 |
Fig. 13 Close-up of the difference between the coadded spectra in the periods r2 and c. The Hϵ line is clearly seen. |
6.2. The line wings
In contrast to the line cores, the wings of the Ca ii H and K lines are not expected to be heavily affected by stellar activity. In Fig. 12, we show the DC derived from the Ca ii H and K lines of HD 189733. Here, our feature light curve was extracted by integrating the spectrum in a region between 3 Å and 5 Å from either line core, while the cores themselves were excluded. A separation of 3 Å from the Ca ii H core also excludes the Hϵ line, which is not unexpectedly prominently seen during the flare (see Fig. 13). We obtained four normalized feature light curves corresponding to the 2 Å wide bands on the blue and red side of the Ca ii H and K line cores and obtained the mean feature light curve by averaging (cf. Eq. (9)).
The DC in the line wings shows the general pattern of variability expected from a limb-brightened feature light curve (see Sect. 3.3). However, there clearly is additional large-scale evolution in the DC, which is reminiscent of the behavior of air mass (see Sect. 5.1). After having estimated the noise from the scatter in the curve, we modeled the curve, first, using a second-order polynomial and, second, using the polynomial plus a synthetic DC. The resulting models are also shown in Fig. 12. For the polynomial alone, we obtained a reduced χ2 value of 1.31. After adding the model DC, we obtained a reduced χ2 value of 1.02. Because we have not added a free parameter, the second model including the synthetic DC is clearly superior. The probability of obtaining a reduced χ2 value of 1.02 or higher from random noise is 40%, which underlines the formal plausibility of the presented model. While there may be some evolution not accounted for by our model in the residuals shown in Fig. 12, in particular, during the first half of the transit, we consider them acceptable, given that no DC parameters were actually fitted (only the underlying polynomial). Finally, we checked that compatible results can be produced using various feature and reference bands to exclude a chance finding based on our particular choice of the integration bands.
6.3. Difference spectra around Ca II H and K
In our next step, we aim to trace back the pronounced signal in the DC to changes directly observable in the spectra. Therefore, we selected the spectra showing the largest differences as indicated by the DCs. In particular, we defined the three orbital phase intervals r1 = −0.011 ± Δp, c = 0.0 ± Δp, and r2 = 0.011 ± Δp with Δp = 0.0027, which results in a length corresponding to 16% of the transit duration. The interval c covers the transit center and r1,2 cover the DC minimum before and after mid-transit time; they are indicated in Fig. 12.
We then coadded all spectra matching the phase requirements, taking their relative radial-velocity shift into account, and then normalized the result by the average of the two mean flux values obtained in the CH and CK reference intervals. We then subtracted the coadded mid-transit spectrum from either of the reference spectra. Finally, we chose similarly phased spectra from our time series of synthetic spectra and carried out the same analysis there to obtain a model.
Figure 13 shows a 5 Å wide excerpt of the difference spectrum obtained by subtracting the mean spectrum in interval c from the r2 spectrum. As a result of the flare, a clear excess is seen in both the core of the Ca ii H and the Hϵ line at 3970.08 Å.
 |
Fig. 14 Top: difference of the normalized spectra obtained in time intervals r1 and c (squares). The solid line shows the sum of our best-fit sinusoidal plus linear model components. Vertical dashed (green) lines indicate the start and vertical dotted (red) lines indicate the end of an echelle order. Bottom: the residuals obtained after subtracting the model shown in the top panel from the data. The solid (red) line shows a smoothed synthetic difference spectrum. |
On larger scales, the difference spectrum shows structure that is not attributable to the star. In the top panel of Fig. 14, we show the difference spectrum resulting from the comparison of the coadded precenter reference spectrum and central spectrum. The difference spectra were rebinned on a 0.5 Å grid to improve visibility. Clearly, the difference spectrum shows a periodic, sine-like signal, whose period of ≈34 Å is compatible with the spacing of the UVES echelle orders in this spectral region for our instrument setup. Therefore, we argue that this signal is probably related to the blaze correction and order merging of the spectra.
Best-fit parameters for fit of difference spectrum.
Close inspection of the synthetic and observed difference spectrum shows that many details are not well reproduced. It must be noted that UVES resolved hundreds of spectral lines in the region, which all show a distinct CLV. To test whether the overall behavior of the observed difference spectrum matches the simulation nonetheless, we smoothed the synthetic difference spectrum using a running mean with a window size of 2.5 Å and compared the smoothed spectrum to the observation. In particular, we fitted the observed difference spectrum using a model, which is the sum of a sinusoidal component, a linear component, and the synthetic difference spectrum, i.e., 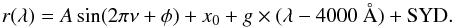 (10)Here, SYD represents the smoothed synthetic difference spectrum. The linear and sinusoidal model components represent changes unrelated to the occultation of the stellar disk. After fixing the period, ν-1, of the sine to 34 Å (the order spacing), we were left with four fit parameters: the constant, x0, the gradient, g, the amplitude, A, and the phase, φ, of the sine. Our best-fit parameters are given in Table 5. During the fit, we excluded the ± 2 Å wide region around the Ca ii H and K line cores and the same region centered on the Hϵ line, which is clearly seen during the flare (see Fig. 13).
(10)Here, SYD represents the smoothed synthetic difference spectrum. The linear and sinusoidal model components represent changes unrelated to the occultation of the stellar disk. After fixing the period, ν-1, of the sine to 34 Å (the order spacing), we were left with four fit parameters: the constant, x0, the gradient, g, the amplitude, A, and the phase, φ, of the sine. Our best-fit parameters are given in Table 5. During the fit, we excluded the ± 2 Å wide region around the Ca ii H and K line cores and the same region centered on the Hϵ line, which is clearly seen during the flare (see Fig. 13).
The solid curve in the top panel of Fig. 14 shows the sum of the linear and sinusoidal components from our best-fit model along with the observed difference spectrum. In the bottom panel, we plot the residuals with respect to the curve shown in the top panel along with the smoothed synthetic spectrum, which is the last model component. While the scatter remains large, the overall behavior follows the expectation.
In Fig. 15, we show the result of the same experiment using the post-center reference spectrum. Again, we fitted the same model to the residuals. As the sinusoidal component is less pronounced here and we argue that it is related to the order merging, we fixed the phase. In this case, we obtain a stronger linear component (see Table 5), which we attribute to a change in the atmospheric transparency not completely removed by the flux calibration.
6.4. Influence of the systematic effects in the difference curve
The analysis of the difference spectra in Sect. 6.3 clearly demonstrated the presence of systematic effects in the spectra. To quantify the impact of these effects on the DC derived in Sect. 6.2, we simulated spectra, including both a sine wave with variable amplitude and a linear term with variable gradient. The phase of the sine was fixed to the value obtained from the fit to the residuals because this is not expected to change for an effect related to the echelle orders. Based on these simulations, we quantify the impact on the DC  (11)Given the measured amplitude of 1.5 × 10-3 of the sine wave, we estimate a resulting change on the order of 10-4 in the DC. The expected change in the DC resulting from the gradient is 54 Å × 10-5 Å-1 = 0.54 × 10-3, where 10-5 Å-1 is on the order of the observed value. The change in the gradient should, however, be slow because it is probably related to a change in air mass. We speculate that the global trend seen in the DC, shown in Fig. 12, is related to this effect.
(11)Given the measured amplitude of 1.5 × 10-3 of the sine wave, we estimate a resulting change on the order of 10-4 in the DC. The expected change in the DC resulting from the gradient is 54 Å × 10-5 Å-1 = 0.54 × 10-3, where 10-5 Å-1 is on the order of the observed value. The change in the gradient should, however, be slow because it is probably related to a change in air mass. We speculate that the global trend seen in the DC, shown in Fig. 12, is related to this effect.
Although there are instrumental effects, we argue that their magnitude remains insufficient to explain the observed DC (see Fig. 12). Furthermore, the temporal association with the transit seen in the DC makes an instrumental origin unlikely. In principle, nonlinearity of the CCD could cause an effect temporally associated with the transit because the star appears necessarily darker when the planet traverses the stellar disk. However, the signal seen in the DC is not proportional to the overall light variation expected during the transit and the signal observed on the CCD is on the order of 1000 ADUs in the region of the Ca ii H and K lines, which is far below the saturation limit of 65 000 ADUs. Therefore, we argue that nonlinearity of the CCD is unlikely to be the origin of the observed change in the DC.
7. Center-to-limb variation observed in the Na I D1 and D2 lines
Our analysis of the Ca ii H and K lines shows flaring activity affecting the line cores from about mid-transit time. To study the effect on the Na i D1 and D2 lines, we created mean spectra in three time intervals covering orbital phases from −0.02 to −0.01, −0.01 to 0.0, and 0.01 to 0.02. While the first two intervals do not cover the flare, the third interval covers its peak phase as observed in the Ca ii H and K lines (cf. Fig. 11). In Fig. 16, we plot the ratios of the averaged spectra in the three intervals. While the Na i D1 and D2 line cores show a clear fill-in during the flare, the ratio of the out-of-flare spectra shows no strong change in the core region. The core is probably also affected by the planetary atmosphere (e.g., Wyttenbach et al. 2015), which we do not consider here. To minimize the impact of the flare on our CLV analysis, we excluded the line core. In particular, we disregarded the central ± 0.3 Å region of the lines, where the line profile is dominated by the central Gaussian component. The region is also indicated in Fig. 16.
 |
Fig. 16 Solid (red) line: ratio of the average peak-flare spectrum (orbital phases 0.01 to 0.02) and the first out-of-flare reference spectrum (phase −0.02 to −0.01). For comparison, the dashed (black) lines shows the ratio of the averaged spectra obtained during the second and first out-of-flare reference phases, which shows no strong change. The dotted (blue) line: scaled stellar spectrum for reference. |
 |
Fig. 17 Region covering the Na i D1 and D2 lines in our first spectrum. Top: shaded (red) regions show the wide reference bands and squared regions the narrow spectral bands. Bottom: close-up of the Na i D1 and D2 lines. The shaded (red) regions have half-width of 0.3, 0.6, 0.9, and 1.5 Å. |
In Fig. 17, we show the observed, flux-calibrated spectrum around the Na i D1 and D2 lines. Note that neither a barycentric correction nor any further normalization was applied to the spectra. From the observed series of spectra, we extract feature light curves using three different feature bands with half-widths of 0.6 Å, 0.9 Å, and 1.5 Å centered on the cores of the sodium lines. These core regions, however, were disregarded by excluding the inner ± 0.3 Å region. We then obtained two feature light curves for both line cores by individually integrating the spectral signal in the blue and red wing.
 |
Fig. 18 Difference curves for Na iD2 (left column) and D1 (right column) for three feature bands with half-widths of 0.6 Å, 0.9 Å, and 1.5 Å (top to bottom). Top panels show the data and the model (solid, red line), and the bottom show the residuals. The line core (± 0.3 Å around the line center) has been excluded. The reference bands were 5840−5860 Å and 5925.875−5945.875 Å. The effect of the CLV is different in the two lines and it is weaker for broader spectral bands. |
In our calculations, we used both wide (20 Å) and narrow reference bands (see Fig. 17). The wide reference bands are defined between 5840−5860 Å and 5925.875−5945.875 Å. To test the influence of the reference bands on the outcome, we defined two further pairs of wide reference bands by shifting both bands toward the Na i D1 and D2 lines in two steps of 10 Å. Additionally, we defined narrow reference bands (5868−5872 Å and 5910.5−5912.5 Å), which contain no strong spectral lines (Fig. 17). To correct for the radial-velocity shift of the individual spectra, we carried out a cross-correlation with a model spectrum in the 5850−5870 Å band and adjusted the start- and end wavelengths of the integration bands according to the radial-velocity shifts thus derived. With this approach, we account for all present shifts, whether they are instrumental or physical in origin.
The resulting DCs are shown in Fig. 18 for both line cores along with model curves obtained from our simulations of spectral time series. Around the center of the transit, we find the behavior of the curves shown in Fig. 18 to be consistent with our model DCs. In particular, the DCs of both sodium lines and all chosen feature bandwidths show a drop during in- and egress phases and a peak at transit center. The synthetic curves show that the CLV effect is not identical for both sodium lines, but a little stronger for the D2 line for the chosen integration bands. This reflects a difference in width and strength of the Na i D1 and D2 lines, with the D2 being a little broader and deeper in stars like HD 189733.
At orbital phase ≈0.03, the observed DCs show a drop for which we currently have no definite explanation. We speculate that this drop might be related to the shift in the curve of the Rossiter-McLaughlin effect seen toward the end of the observation. At this point, the instrumental resolution and radial-velocity shift also show a general change in their behavior (see Fig. 8). Whether the evolution in the DC is ultimately related to an instrumental effect or a true, physical change in the stellar spectrum, e.g., due to the flare or a change on the surface caused by a spot remains unknown.
In Fig. 19, we show the combined DC from both Na i D1 and D2 line cores (0.3−0.6 Å band) up to an orbital phase of 0.03 along with a linear model and a linear model plus our synthetic DC. The curves were produced using the narrow reference band. However, we find little change if other reference bands are used. The error was estimated as the scatter in the observed DC. Clearly, the synthetic model DC explains the general behavior of the observation. In particular, we obtain a χ2 value of 369 using only the linear model and a value of 279 if the full model is used. In both cases, only the two parameters of the linear model were fitted. The profile of the synthetic DC is completely determined by the transit geometry and the stellar model atmosphere. Therefore, we are left with 195 deg of freedom. It seems, however, that the observed DC shows further structure not accounted for by the model. Before and after mid-transit time, there are two drops in the residuals. The structure is, however, not entirely symmetric with the deviation stronger during the first half of the transit.
To study the effect of variable telluric absorption on our measurements, we used the molecfit code to correct our spectra for telluric contamination (Smette et al. 2015; Kausch et al. 2015). The DCs produced using the spectra corrected for telluric absorption do not significantly differ from those that are not corrected for telluric absorption. The main difference is a systematic pattern changing in phase with air mass. The amplitude of this pattern is, however, only 0.5 × 10-3. Formally, we obtained a reduced χ2 value of 1.48 for the CLV model with telluric correction, which is even a little higher than the value of 1.43 obtained without telluric correction. As the CLV-related wave-like pattern remains essentially unaffected, we conclude that variable telluric absorption is unlikely to be the origin of the observed behavior.
 |
Fig. 19 Top: DC observed in the 0.3−0.6 Å band around both Na i D1 and D2 cores with respect to narrow reference intervals. The dashed (red) curve shows a linear fit and the solid (black) line a linear fit plus our synthetic DC model. Bottom: residuals with respect to the synthetic model. The solid (red) curve shows the residuals smoothed using a running mean with a width of eight data points. |
Finally, we verified that the change in instrumental resolution detected in the UVES spectra (see Sect. 5.5) is not responsible for the observed behavior. In particular, we simulated DCs applying instrumental resolutions of 55 000 and 65 000 representing the observed change in resolution (see Sect. 5.5). The resulting change in the DCs remains too small to be of any relevance in the current study.
8. Summary and discussion
We present DCs of the Ca ii H and K and Na i D1 and D2 lines derived from transit spectroscopy of HD 189733 obtained with UVES. Our DCs clearly show the effect of differential CLV in the wings of the Ca ii H and K and Na i D1 and D2 lines of HD 189733.
8.1. The center-to-limb variation
Our analysis of the Ca ii H and K line cores revealed strong variability. Most notably, an increase in the strength of the cores, which we interpret as a stellar flare, was observed at about mid-transit time. We found that the core DC obtained before the flare is better reproduced by a model assuming no limb darkening in the Ca ii H and K line cores than by a model with photospheric limb darkening. This finding is compatible with a homogeneous brightness of the chromospheric core emission across the stellar disk. Yet, the actual spatial distribution is probably more complex (Llama & Shkolnik 2015). The Ca ii H and K emission line cores also show variability before the ingress, which is probably unrelated to the transit. While an earlier ingress either due to planetary material or an extended stellar chromosphere is conceivable (e.g., Czesla et al. 2012; Haswell et al. 2012), intrinsic variability, independent of the transit, appears to be a more plausible interpretation in view of the flare observed later. In any case, it remains difficult to distinguish between effects caused by the transiting planetary disk and intrinsic stellar variability in our data set.
To limit the impact of activity, we focused our analysis on the wings of the Fraunhofer Ca ii H and K and Na i D1 and D2 lines. These are expected to be less strongly influenced by activity, but are still sensitive to the stellar CLV. The shapes of both the DCs based on the Ca ii H and K and Na i D1 and D2 line wings clearly show the behavior expected from the stellar CLV. In particular, we find the line wings to be limb brightened compared to the reference continuum.
The observed DCs are well reproduced by a model composed of a synthetic DC and a low-order polynomial. Including the synthetic DC model clearly improves the fit compared to a low-order polynomial alone. In particular, the reduced χ2 values changed from 1.31 to 1.02 in for the Ca ii H and K lines and from 1.89 to 1.43 for the Na i D1 and D2 lines. Nonetheless, we still obtain some correlated residuals, especially in the modeling of the DC derived from the Na i D1 and D2 lines.
There may be several reasons for these residuals: first, the modeling may be incomplete. Hayek et al. (2012) find better fits to transit light curves with CLV models based on three-dimensional LTE model atmospheres, but our modeling is based on one-dimensional LTE models. Also, non-LTE effects are expected to influence the formation of the strong Fraunhofer lines (e.g., Lind et al. 2011). Because the orbit of HD 189733 b shows only minor misalignment with the stellar spin axis ( °, Triaud et al. 2009), we expect that this kind of an effect should be symmetric with respect to mid-transit time. Therefore, atmospheric model deficiencies can hardly account for all the residuals. Second, there may be instrumental effects. Our data show a complex pattern of instrumental radial velocity shift, and we identified residuals, which we attributed to instrumental effects, in the difference spectra of the Ca ii H and K lines. Clearly, instrumental effects could give rise to residuals on the observed scale. Between orbital phase −0.01 and 0, there seems to be a structure in the residuals of both the Ca ii H and K and Na i D1 and D2 lines, which may have a physical origin. Stellar activity provides viable candidates for this kind of structure.
°, Triaud et al. 2009), we expect that this kind of an effect should be symmetric with respect to mid-transit time. Therefore, atmospheric model deficiencies can hardly account for all the residuals. Second, there may be instrumental effects. Our data show a complex pattern of instrumental radial velocity shift, and we identified residuals, which we attributed to instrumental effects, in the difference spectra of the Ca ii H and K lines. Clearly, instrumental effects could give rise to residuals on the observed scale. Between orbital phase −0.01 and 0, there seems to be a structure in the residuals of both the Ca ii H and K and Na i D1 and D2 lines, which may have a physical origin. Stellar activity provides viable candidates for this kind of structure.
8.2. The influence of stellar activity on the difference curve
Starspots and flares are prominent manifestations of stellar activity. In the following, we briefly discuss their potential impact on the observed DCs. Indeed, starspot occultations have been observed in transit light curves of HD 189733 b earlier (e.g., Pont et al. 2008; Sing et al. 2011), which makes a spot crossing event a plausible scenario. In particular, as we certainly observed HD 189733 in an active phase as evidenced by the tentative flare starting near mid-transit time.
Starspots crossed by the transiting planet cause bumps in the broadband transit light curve because comparably darker regions of the stellar disk are occulted (e.g., Pont et al. 2008; Czesla et al. 2009). For the DC, the height difference of the bump in the feature and reference light curve is relevant. As the wings of the Na i lines become deeper for lower effective temperatures (see Fig. 3), the spot appears darker in the wings of the Na i lines than in the surrounding continuum, given that its spectrum can still be described by an otherwise normal photospheric model. This gives rise to a more pronounced bump in feature light curves covering the Na i line wings and, thus, a net increase in the DC. The same applies to the Ca ii H and K lines. The amplitude of the effect depends on the spectral characteristics and shape of the spot. For a large spot with effective temperature of 4000 K (Pont et al. 2008), we expect that the spot-induced bump can be of the same scale as the amplitude of the actual DC because the change in the profile of the Na i lines is quite pronounced between 4000 K and 5000 K (see Fig. 3).
Also starspots not occulted by the planet affect the DC because they cause an effective wavelength-dependent change in the planet-to-star radius ratio and, thus, alter the normalization of the light curves, which changes the transit depth (Sing et al. 2008; Czesla et al. 2009). While the effect of the starspot crossing is local, unocculted spots modify the entire transit light curve, given that they do not rotate on or off the disk. At least in the case of HD 189733, this seems improbable, because we only observed a little more than one percent of the stellar rotation period.
The flare observed as a rise in the Ca ii H and K emission line cores at about mid-transit time could influence the DC both via chromospheric and photospheric emission. During flares, the strength of chromospheric emission lines including Ca ii H and K and Na i D1 and D2 are expected to increase (e.g., Fuhrmeister & Schmitt 2004). While we exclude the cores in the analysis of the line wings, some contribution could still be present. A fraction of the chromosphere and upper photosphere is thought to be heated to temperatures of ≈10 000 K (Haisch et al. 1991). Effectively, a part of the quiescent photospheric emission would be replaced by emission from a 10 000 K hot spot. The spectra of hot photospheres are dominated by broad Balmer lines, while lines of other ions (including Na i) tend to be narrow. While the exact impact of the flare depends on its location, size, and spectrum, its effect should be temporally limited, and we expect the main contribution to take place during the leading impulsive phase.
8.3. The planetary atmosphere of HD 189733 b seen in Na I D1 and D2
Difference curves have been used to detect planetary excess absorption in the Na i D1 and D2 lines during transit. While there are residuals in our DC not accounted for by our modeling, their temporal behavior is rather untypical for a signal related to the planetary atmosphere (see Fig. 19). In particular, only limited sections before and after mid-transit time show deviations, while the planetary atmosphere should be visible during the entire transit. The presence of residuals of ultimately unknown origin makes it difficult to derive a reliable estimate of the atmospheric excess absorption in the wings of the Na i D1 and D2 lines in the frame of our current analysis.
Detections of in-transit excess absorption in the Na i D1 and D2 lines attributable to the planetary atmosphere have been presented by Redfield et al. (2008), Huitson et al. (2012), and Wyttenbach et al. (2015). Both Huitson et al. (2012) and Wyttenbach et al. (2015) find the bulk of planetary atmospheric absorption concentrated in the cores of the Na i D1 and D2 lines. Wyttenbach et al. derived a FWHM of 0.52 ± 0.08 Å for their signal. As we exclude the inner ± 0.3 Å region around the Na i D1 and D2 line cores in our analysis to minimize contamination by stellar activity, we also exclude about 80% of their signal. In the Na i D1 and D2 lines, they report a relative transit depth of (3.2 ± 0.31) × 10-3 so that the maximum signal we expect is about 0.6 × 10-3. Therefore, we do not regard the lack of an obvious signal related to the planetary atmosphere in our current analysis to be a contradiction of the findings of Wyttenbach et al. (2015). We also do not exclude a contribution by the planetary atmosphere in the DC.
An inspection of Fig. 3 in Wyttenbach et al. (2015) suggests that their curves may also show the effect of the stellar CLV. The curves seem to show a bump in the middle of the transit, which resembles the DCs we obtain for limb-brightened features. In fact, our simulation for their 12 Å wide band indicate a peak-to-peak amplitude of about 0.06% for the DC, which seems to match the distribution of their residuals. In the smaller 0.75 Å band, the expected CLV-induced variation is on the order of 0.4% (see Fig. 18), which is again compatible with their findings. We emphasize, however, that their detection of excess sodium absorption would not be challenged by this. From our models, we obtain a net CLV-induced transit depth of 0.006% in the 12 Å wide band, which is on the order of their error. As this shift would be systematic, the level of sodium absorption derived by Wyttenbach et al. (2015) may be underestimated by this rather small amount.
8.4. The impact of the temporal sampling of the transit
The spectrum of the transited stellar disk evolves continuously as the planet proceeds along its path and therefore, the DC is time dependent. This implies that the temporal sampling of the transit is highly relevant in the analysis of transit spectroscopy. If, for instance, only the central part of the transit of HD 189733 b was covered, the wings of the Na i D1 and D2 and Ca ii H and K lines would actually show net emission. The reverse is true, if only the in- and egress phases were covered. This effect occurs without requiring any change in the physical radius of the planet.
8.5. Relevance of the CLV in large planets
If the planetary atmosphere can be treated as a thin shell enshrouding the planet, it extends the planetary disk seen during transit by a small amount, ΔRp. The area, Aa, of the resulting atmospheric annulus reads  (12)When the strength of the atmospheric absorption is proportional to the atmospheric area, the effect observable in the spectrum is proportional to the planet-to-star radius ratio, p, and the extent of its atmosphere. Therefore, large planet-to-star radius ratios and large atmospheric scale heights are favorable to detect atmospheric absorption.
(12)When the strength of the atmospheric absorption is proportional to the atmospheric area, the effect observable in the spectrum is proportional to the planet-to-star radius ratio, p, and the extent of its atmosphere. Therefore, large planet-to-star radius ratios and large atmospheric scale heights are favorable to detect atmospheric absorption.
A simplified model of the transit light curve with quadratic limb darkening can be obtained for small planets, for which the normalized transit light curve as a function of the limb angle, μ, reads  (13)Here, the limb darkening is parameterized according to Eq. (2) (cf. Müller et al. 2013, Eq. (B.1)). Accordingly, the DC can be approximated by
(13)Here, the limb darkening is parameterized according to Eq. (2) (cf. Müller et al. 2013, Eq. (B.1)). Accordingly, the DC can be approximated by  (14)which depends on the properties of the normalized feature (f) and reference (r) light curves. While this simplified model does not reproduce the in- and egress phases appropriately, Eq. (14) can be used to estimate the value of the DC in the transit center. For the cases discussed in Sect. 3.3, we obtain values of −8.9 × 10-4 for the limb-darkened feature and + 10.4 × 10-4 for the limb-brightened feature, which both agree well with the results obtained from the more elaborate models (cf. Fig. 2).
(14)which depends on the properties of the normalized feature (f) and reference (r) light curves. While this simplified model does not reproduce the in- and egress phases appropriately, Eq. (14) can be used to estimate the value of the DC in the transit center. For the cases discussed in Sect. 3.3, we obtain values of −8.9 × 10-4 for the limb-darkened feature and + 10.4 × 10-4 for the limb-brightened feature, which both agree well with the results obtained from the more elaborate models (cf. Fig. 2).
Equation (14) demonstrates that the amplitude of the CLV-induced effect on the DC is proportional to the squared planet-to-star radius ratio, while the strength of the signal induced by the planetary atmosphere grows linearly with the radius ratio. Additionally, smaller stars, which potentially provide more favorable (i.e., larger) radius ratios also tend to be cooler. In cool stars, however, the CLV-induced variation is also more pronounced. This underlines the importance of an accurate knowledge and modeling of the stellar CLV in the study of planetary atmospheres.
9. Conclusion
We clearly detect the CLV-induced effect in a spectral transit time series of HD 189733, and our findings are generally compatible with predictions from 1D-LTE models. Remaining deviations may be explained by more elaborate modeling of the stellar CLV, stellar activity, instrumental effects, or a combination thereof. The CLV-induced effect is stronger for cooler stars and its relative importance increases for larger planet-to-star radius ratios. Our results demonstrate that the variation in the stellar CLV across individual spectral lines can be detected with transit spectroscopy and that the effect should be taken into account in the study of planetary atmospheres via transmission spectroscopy.
Transiting planets provide a valuable opportunity to resolve the stellar disk, which has been used to study the surface distribution of starspots (e.g., Pont et al. 2008; Huber et al. 2010; Sanchis-Ojeda & Winn 2011). Here we show that the moving planetary disk can also be used to study the spatially resolved stellar spectrum, which is required to constrain three-dimensional hydrodynamic models of the stellar photosphere (Dravins et al. 2015).
Given appropriate modeling, the prominent CLV in the stellar Fraunhofer lines could also be used to reconstruct the planetary path across the stellar disk in terms of the temporal change in the occulted limb angle. In its use of the spectrum, this approach resembles the Rossiter-McLaughlin effect, which is frequently used to study the orbit geometry of exoplanets (e.g., Winn et al. 2006; Triaud et al. 2009). While the strength of this effect depends on the properties of the stellar atmosphere, stellar rotation is not required to see it. Clearly, the CLV in the specific ensemble of stellar spectral lines used to derive the radial velocity shifts should also be taken into account in the modeling of the Rossiter-McLaughlin effect. We speculate that the correlated residuals in the Rossiter-McLaughlin curve obtained by Winn et al. (2006), Triaud et al. (2009), and in this work could be attributable to the stellar CLV.
As noted by Yan et al. (2015), the CLV-induced effect on the light curves derived from transit spectroscopy becomes more pronounced when narrow spectral bands are used for integration in strong spectral lines. Although the use of broader bands reduces the influence of the CLV, a number of studies have found the planetary atmospheric signal to be concentrated in the cores of the line. Therefore, the use of broader bands may not always be desirable. At any rate, an accurate treatment of the stellar CLV is indispensable in the analysis of transit spectroscopy of exoplanets.
See http://www.eso.org/observing/dfo/quality/UVES/qc/SysEffic_qc1.html. We used UV_MRSP_041130_BLUE437 for the blue, UV_GMRE_070511A_master_response_REDL760 for the lower red, and UV_GMRE_090701A_master_response_REDU760 for the upper red chip.
Acknowledgments
T.K. acknowledges support by the DFG program CZ 222/1-1. T.K. and S.K. acknowledge support from the RTG 1351 (“Extrasolar planets and their host stars”). U.W. acknowledges support from the DLR under grant 50OR0105.
References
- Agol, E., Cowan, N. B., Knutson, H. A., et al. 2010, ApJ, 721, 1861 [NASA ADS] [CrossRef] [Google Scholar]
- Athay, R. G., Lites, B. W., White, O. R., & Brault, J. W. 1972, Sol. Phys., 24, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Baliunas, S. L., Donahue, R. A., Soon, W. H., et al. 1995, ApJ, 438, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Balthasar, H., Thiele, U., & Woehl, H. 1982, A&A, 114, 357 [NASA ADS] [Google Scholar]
- Bouchy, F., Udry, S., Mayor, M., et al. 2005, A&A, 444, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, T. M. 2001, ApJ, 553, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Burton, J. R., Watson, C. A., Rodríguez-Gil, P., et al. 2015, MNRAS, 446, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Caccin, B., Cavallini, F., Ceppatelli, G., Righini, A., & Sambuco, A. M. 1985, A&A, 149, 357 [NASA ADS] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2004, ArXiv e-prints [arXiv:astro-ph/0405087] [Google Scholar]
- Charbonneau, D., Brown, T. M., Latham, D. W., & Mayor, M. 2000, ApJ, 529, L45 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Charbonneau, D., Brown, T. M., Noyes, R. W., & Gilliland, R. L. 2002, ApJ, 568, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A. 2004, A&A, 428, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clough, S. A., Shephard, M. W., Mlawer, E. J., et al. 2005, J. Quant. Spec. Radiat. Transf., 91, 233 [Google Scholar]
- Croll, B., Matthews, J. M., Rowe, J. F., et al. 2007, ApJ, 671, 2129 [NASA ADS] [CrossRef] [Google Scholar]
- Czesla, S., Huber, K. F., Wolter, U., Schröter, S., & Schmitt, J. H. M. M. 2009, A&A, 505, 1277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Czesla, S., Schröter, S., Wolter, U., et al. 2012, A&A, 539, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dravins, D., Ludwig, H.-G., Dahlén, E., & Pazira, H. 2015, 18th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, Proc. Conf. held at Lowell Observatory, 8−14 June, 2014, eds G. van Belle, & H. C. Harris., 853 [Google Scholar]
- Fang, C., Hiei, E., Yin, S.-Y., & Gan, W.-Q. 1992, PASJ, 44, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, L., Haswell, C. A., Froning, C. S., et al. 2010, ApJ, 714, L222 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhrmeister, B., & Schmitt, J. H. M. M. 2004, A&A, 420, 1079 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuhrmeister, B., Liefke, C., Schmitt, J. H. M. M., & Reiners, A. 2008, A&A, 487, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gray, D. 2008, The Observation and Analysis of Stellar Photospheres, 3rd edn. (Cambridge University Press) [Google Scholar]
- Gray, D. F., & Brown, K. I. T. 2006, PASP, 118, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, R. O., & Corbally, C. J. 1994, AJ, 107, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Grossmann-Doerth, U. 1994, A&A, 285, 1012 [NASA ADS] [Google Scholar]
- Haisch, B., Strong, K. T., & Rodono, M. 1991, ARA&A, 29, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Haswell, C. A., Fossati, L., Ayres, T., et al. 2012, ApJ, 760, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Hayek, W., Sing, D., Pont, F., & Asplund, M. 2012, A&A, 539, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huber, K. F., Czesla, S., Wolter, U., & Schmitt, J. H. M. M. 2010, A&A, 514, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huitson, C. M., Sing, D. K., Vidal-Madjar, A., et al. 2012, MNRAS, 422, 2477 [NASA ADS] [CrossRef] [Google Scholar]
- Jensen, A. G., Redfield, S., Endl, M., et al. 2011, ApJ, 743, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Kausch, W., Smette, S. N. A., Kimeswenger, S., et al. 2015, A&A, 576, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knutson, H. A., Howard, A. W., & Isaacson, H. 2010, ApJ, 720, 1569 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L. 1970, SAO Sp. Rep., 309 [Google Scholar]
- Lalitha, S., Fuhrmeister, B., Wolter, U., et al. 2013, A&A, 560, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lecavelier Des Etangs, A., Ehrenreich, D., Vidal-Madjar, A., et al. 2010, A&A, 514, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lind, K., Asplund, M., Barklem, P. S., & Belyaev, A. K. 2011, A&A, 528, A103 [Google Scholar]
- Linsky, J. L., Yang, H., France, K., et al. 2010, ApJ, 717, 1291 [NASA ADS] [CrossRef] [Google Scholar]
- Llama, J., & Shkolnik, E. L. 2015, ApJ, 802, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, D. B. 1924, ApJ, 60, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Melo, C., Santos, N. C., Pont, F., et al. 2006, A&A, 460, 251 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. M., Huber, K. F., Czesla, S., Wolter, U., & Schmitt, J. H. M. M. 2013, A&A, 560, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Narita, N., Suto, Y., Winn, J. N., et al. 2005, PASJ, 57, 471 [NASA ADS] [Google Scholar]
- Neckel, H., & Labs, D. 1994, Sol. Phys., 153, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Ohta, Y., Taruya, A., & Suto, Y. 2005, ApJ, 622, 1118 [NASA ADS] [CrossRef] [Google Scholar]
- Pierce, A. K., & Slaughter, C. D. 1977, Sol. Phys., 51, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Pont, F., Knutson, H., Gilliland, R. L., Moutou, C., & Charbonneau, D. 2008, MNRAS, 385, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Poppenhaeger, K., Schmitt, J. H. M. M., & Wolk, S. J. 2013, ApJ, 773, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Redfield, S., Endl, M., Cochran, W. D., & Koesterke, L. 2008, ApJ, 673, L87 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Rossiter, R. A. 1924, ApJ, 60, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Sanchis-Ojeda, R., & Winn, J. N. 2011, ApJ, 743, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Schlawin, E., Agol, E., Walkowicz, L. M., Covey, K., & Lloyd, J. P. 2010, ApJ, 722, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitt, J. H. M. M., Fleming, T. A., & Giampapa, M. S. 1995, ApJ, 450, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Seager, S., & Sasselov, D. D. 2000, ApJ, 537, 916 [NASA ADS] [CrossRef] [Google Scholar]
- Sing, D. K., Vidal-Madjar, A., Désert, J.-M., Lecavelier des Etangs, A., & Ballester, G. 2008, ApJ, 686, 658 [NASA ADS] [CrossRef] [Google Scholar]
- Sing, D. K., Pont, F., Aigrain, S., et al. 2011, MNRAS, 416, 1443 [NASA ADS] [CrossRef] [Google Scholar]
- Sing, D. K., Huitson, C. M., Lopez-Morales, M., et al. 2012, MNRAS, 426, 1663 [NASA ADS] [CrossRef] [Google Scholar]
- Smette, A., Sana, H., Noll, S., et al. 2015, A&A, 576, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Snellen, I. A. G., Albrecht, S., de Mooij, E. J. W., & Le Poole, R. S. 2008, A&A, 487, 357 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Snellen, I. A. G., de Kok, R. J., de Mooij, E. J. W., & Albrecht, S. 2010, Nature, 465, 1049 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Torres, G., Winn, J. N., & Holman, M. J. 2008, ApJ, 677, 1324 [NASA ADS] [CrossRef] [Google Scholar]
- Triaud, A. H. M. J., Queloz, D., Bouchy, F., et al. 2009, A&A, 506, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vidal-Madjar, A., Lecavelier des Etangs, A., Désert, J.-M., et al. 2003, Nature, 422, 143 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Vogt, S. S., Penrod, G. D., & Hatzes, A. P. 1987, ApJ, 321, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, A. J., Donahue, T. M., & Walker, J. C. G. 1981, Icarus, 48, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Johnson, J. A., Marcy, G. W., et al. 2006, ApJ, 653, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, P. L., Maxted, P. F. L., Smalley, B., & Iro, N. 2011, MNRAS, 412, 2376 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, J. T., Marcy, G. W., Butler, R. P., & Vogt, S. S. 2004, ApJS, 152, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Wyttenbach, A., Ehrenreich, D., Lovis, C., Udry, S., & Pepe, F. 2015, A&A, 577, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yan, F., Fosbury, R. A. E., Petr-Gotzens, M. G., Zhao, G., & Pallé, E. 2015, A&A, 574, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhou, G., & Bayliss, D. D. R. 2012, MNRAS, 426, 2483 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Simulated in-transit excess absorption diagnosed by the DC for the narrow (n), medium (m), and wide (w) spectral bands defined by Charbonneau et al. (2002).
Difference curve excesses for narrow reference bands with full widths of 0.75 Å, 1.5 Å, and 3 Å centered on the Na i D1 and D2 lines.
All Figures
 |
Fig. 1 Normalized model transit light curves. |
| In the text | |
 |
Fig. 2 Difference curve, DC(ti), for a limb-darkened (solid, LCf(ti) vs. LCr,0.3(ti)) and a limb-brightened (dashed, LCf(ti) vs. LCr,0.7(ti)) feature. |
| In the text | |
 |
Fig. 3 Normalized stellar spectrum around the sodium doublet for two limb angles μ = 0.1 (dashed) and μ = 1.0 (solid) and three effective temperatures. |
| In the text | |
 |
Fig. 4 Top: ratio of stellar spectra (Teff = 5000 K, log (g) = 4.5) at limb and center (μ = 0.05 and μ = 1.0) shown with a solid line. For comparison, the scaled central spectrum (dashed line). Bottom: normalized specific intensity in the μ = 0.001−1 range in the line core (5889.95 Å, crosses), the line wing (5889 Å, squares), and the quasi-continuum (5864.6 Å, circles). |
| In the text | |
 |
Fig. 5 Simulated DCs for the Na i lines (D2 in the left column and D1 in the right column) for effective temperatures of 4000 K, 5000 K, and 6000 K. Normalized feature light curves where extracted in four bands with half-widths 0.1 Å, 0.375 Å, 0.75 Å, and 1.5 Å centered the respective sodium line. The resulting DCs are plotted using solid (black), dashed (red), dotted (green), and dash-dotted (blue) lines in the same order. |
| In the text | |
 |
Fig. 6 Temporal evolution of seeing (top) and air mass (bottom). The vertical dashed lines indicate the duration of the transit. The temporal offset, T0, refers to MJDHJD,UTC = 56 109.26164. |
| In the text | |
 |
Fig. 7 Temporal evolution of the measured spectral flux on the blue chip (squares) and (scaled) signal in the acquisition images from the blue camera (crosses). Dashed vertical lines indicate the transit duration. |
| In the text | |
 |
Fig. 8 Radial velocity shift of telluric lines between 6864 and 6968 Å. |
| In the text | |
 |
Fig. 9 Rossiter-McLaughlin radial velocity curve along with nominal model with parameters from Triaud et al. (2009; top) and residuals (bottom). |
| In the text | |
 |
Fig. 10 Equivalent-width weighted instrumental resolution obtained from 19 telluric lines between 5885 and 7265 Å. |
| In the text | |
 |
Fig. 11 Top: observed DC extracted from the Ca ii H and K line cores. Bottom: close-up of the first half of the observed DC. The solid line shows a photospheric model DC and the dashed line a chromospheric model DC, assuming homogeneous distribution of the Ca ii H and K core emission. |
| In the text | |
 |
Fig. 12 Combined DC of the Ca ii H and K lines wings along with our best-fit second order polynomial model (dashed) and our best-fit model including the synthetic DC. The bottom panel gives the residuals with respect to our DC model. The solid (red) line shows the residuals smoothed by a running mean with a width of eight data points. The vertical lines indicate the transit duration and the three top bars indicate the phase intervals used in the analysis of the spectra. |
| In the text | |
 |
Fig. 13 Close-up of the difference between the coadded spectra in the periods r2 and c. The Hϵ line is clearly seen. |
| In the text | |
 |
Fig. 14 Top: difference of the normalized spectra obtained in time intervals r1 and c (squares). The solid line shows the sum of our best-fit sinusoidal plus linear model components. Vertical dashed (green) lines indicate the start and vertical dotted (red) lines indicate the end of an echelle order. Bottom: the residuals obtained after subtracting the model shown in the top panel from the data. The solid (red) line shows a smoothed synthetic difference spectrum. |
| In the text | |
 |
Fig. 15 As in Fig. 14 for the time intervals r2 and c. |
| In the text | |
 |
Fig. 16 Solid (red) line: ratio of the average peak-flare spectrum (orbital phases 0.01 to 0.02) and the first out-of-flare reference spectrum (phase −0.02 to −0.01). For comparison, the dashed (black) lines shows the ratio of the averaged spectra obtained during the second and first out-of-flare reference phases, which shows no strong change. The dotted (blue) line: scaled stellar spectrum for reference. |
| In the text | |
 |
Fig. 17 Region covering the Na i D1 and D2 lines in our first spectrum. Top: shaded (red) regions show the wide reference bands and squared regions the narrow spectral bands. Bottom: close-up of the Na i D1 and D2 lines. The shaded (red) regions have half-width of 0.3, 0.6, 0.9, and 1.5 Å. |
| In the text | |
 |
Fig. 18 Difference curves for Na iD2 (left column) and D1 (right column) for three feature bands with half-widths of 0.6 Å, 0.9 Å, and 1.5 Å (top to bottom). Top panels show the data and the model (solid, red line), and the bottom show the residuals. The line core (± 0.3 Å around the line center) has been excluded. The reference bands were 5840−5860 Å and 5925.875−5945.875 Å. The effect of the CLV is different in the two lines and it is weaker for broader spectral bands. |
| In the text | |
 |
Fig. 19 Top: DC observed in the 0.3−0.6 Å band around both Na i D1 and D2 cores with respect to narrow reference intervals. The dashed (red) curve shows a linear fit and the solid (black) line a linear fit plus our synthetic DC model. Bottom: residuals with respect to the synthetic model. The solid (red) curve shows the residuals smoothed using a running mean with a width of eight data points. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


