| Issue |
A&A
Volume 582, October 2015
|
|
|---|---|---|
| Article Number | A117 | |
| Number of page(s) | 8 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201526287 | |
| Published online | 21 October 2015 | |
Numerical simulations of transverse oscillations in radiatively cooling coronal loops
1
Centre for mathematical Plasma Astrophysics, Department of
Mathematics,
KU Leuven, Celestijnenlaan 200B, bus
2400,
3001
Leuven,
Belgium
e-mail:
norbert.magyar@wis.kuleuven.be
2
Babes-Bolyai University Cluj-Napoca, str. Mihail Kogalniceanu nr. 1, 3400
Cluj-Napoca,
Romania
Received: 9 April 2015
Accepted: 18 August 2015
Aims. We aim to study the influence of radiative cooling on the standing kink oscillations of a coronal loop.
Methods. Using the FLASH code, we solved the 3D ideal magnetohydrodynamic equations. Our model consists of a straight, density enhanced and gravitationally stratified magnetic flux tube. We perturbed the system initially, leading to a transverse oscillation of the structure, and followed its evolution for a number of periods. A realistic radiative cooling is implemented. Results are compared to available analytical theory.
Results. We find that in the linear regime (i.e. low amplitude perturbation and slow cooling) the obtained period and damping time are in good agreement with theory. The cooling leads to an amplification of the oscillation amplitude. However, the difference between the cooling and non-cooling cases is small (around 6% after 6 oscillations). In high amplitude runs with realistic cooling, instabilities deform the loop, leading to increased damping. In this case, the difference between cooling and non-cooling is still negligible at around 12%. A set of simulations with higher density loops are also performed, to explore what happens when the cooling takes place in a very short time (tcool ≈ 100 s). In this case, the difference in amplitude after nearly 3 oscillation periods for the low amplitude case is 21% between cooling and non-cooling cases. We strengthen the results of previous analytical studies that state that the amplification due to cooling is ineffective, and its influence on the oscillation characteristics is small, at least for the cases shown here. Furthermore, the presence of a relatively strong damping in the high amplitude runs even in the fast cooling case indicates that it is unlikely that cooling could alone account for the observed, flare-related undamped oscillations of coronal loops. These results may be significant in the field of coronal seismology, allowing its application to coronal loop oscillations with observed fading-out or cooling behaviour.
Key words: Sun: corona / magnetohydrodynamics (MHD) / magnetic fields
© ESO, 2015
1. Introduction
Coronal loops have gained much attention from the scientific community, both observationally and theoretically, since the first observational evidence of transverse magnetohydrodynamic (MHD) oscillations (Aschwanden et al. 1999; Nakariakov et al. 1999), which had been theorized decades before their discovery (Zaitsev & Stepanov 1975; Ryutov & Ryutova 1976; Edwin & Roberts 1983). The study of coronal loop oscillations is important for two main reasons: on the one hand, standing modes are excellent tools for coronal seismology, a technique that determines coronal parameters that are hard to measure by other means. To improve the accuracy of this method, studies focused on increasingly realistic coronal loop models, including several effects that might have an influence on oscillation parameters, such as loop curvature (e.g. Van Doorsselaere et al. 2004; Terradas et al. 2006), density stratification (e.g. Andries et al. 2005b; Dymova & Ruderman 2005), variable cross section (e.g. Verth & Erdélyi 2008; Ruderman et al. 2008), and twisted magnetic field (e.g. Ruderman 2007; Terradas & Goossens 2012). The transverse oscillations have been used for seismology to measure the magnetic field strength (Nakariakov & Ofman 2001; Van Doorsselaere et al. 2007), the density stratification (Andries et al. 2005a), the perpendicular structuring in the magnetic field (Aschwanden et al. 2003) and the Alfvén travel time (Arregui et al. 2007). For a review of coronal seismology, we recommend De Moortel & Nakariakov (2012). On the other hand, since wave heating is a proposed mechanism for the mysteriously high temperature of the corona, ubiquitous propagating waves may contribute to energizing the coronal plasma (for a review of coronal heating, see, e.g. Parnell & De Moortel 2012).
Since their first observation in 1998, there have been numerous theoretical, numerical, and observational works have been done (for a review of coronal loop oscillations, see Ruderman & Erdélyi 2009). In general, the coronal loops are not in a steady state and evolve during the oscillations. Previous studies mostly assume a static background loop. The paper by Aschwanden & Terradas (2008) points out that the intensities of most observed coronal loops in a single extreme-UV waveband vary, as is consistent with a plasma cooling scenario. They suggest that a proper MHD study of oscillating coronal loops should include the density and temperature changes due to the plasma cooling. In the first, zeroth-order analytical study of oscillating, radiatively cooling loops by Morton & Erdélyi (2009), it was shown that cooling leads to damping of the oscillations. However, another study of the phenomenon (Ruderman 2011a), indicates that the cooling leads to an amplification of the oscillations. They found out that neglecting the flow caused by the radiative plasma cooling resulted in the damping behaviour in Morton & Erdélyi (2009).
A common property of observed transverse coronal loop oscillations is that they are damped quickly, usually within a few oscillation periods. It is now generally accepted that the main damping mechanism is resonant absorption (Sakurai et al. 1991; Goossens et al. 1992, 2002; Ruderman & Roberts 2002), transferring energy from the global kink mode to local azimuthal Alfvén modes in the boundary layer of the loop structure, where the two frequencies match (for a review of theoretical results, see Goossens et al. 2011). Less frequently, nearly undamped or even growing transverse oscillations are observed (Wang et al. 2012). Decay-less low amplitude kink oscillations, which are present in loops before and after a high-amplitude flare triggered damped kink oscillations can be explained in terms of a damped linear oscillator excited by a continuous low amplitude harmonic driver (Nisticò et al. 2013; Anfinogentov et al. 2013). Some examples of observed undamped high amplitude coronal loop oscillations can be found in Aschwanden et al. (2002) and Aschwanden & Schrijver (2011). In the latter paper, it was concluded that this could only happen if the thickness of the boundary layer (a radially inhomogeneous outer layer of the coronal loops) is much smaller than the loop radius, in order to minimize the damping due to resonant absorption. It was also evident from the observations that the loop was cooling during the particular undamped oscillation event. It seemed a rather natural explanation that the amplification due to cooling may counterbalance the damping due to resonant absorption, explaining the undamped oscillations, as it was first suggested in Ruderman (2011b). The most elaborate analytical study regarding time-dependent kink oscillations (Ruderman 2011a) considered the simultaneous effects of both damping due to resonant absorption and amplification due to plasma cooling. The conclusion was that, for typical boundary layer thicknesses, the amplification due to plasma cooling can account for the observed undamped oscillations only if the cooling happens quickly, on a timescale close to the oscillation period. However, in the paper, the effects of cooling and resonant damping have been studied under the assumption that both the characteristic cooling time and damping time are much longer than the characteristic oscillation period, when using the WKB method. Thus, it is questionable whether the derived equations remain valid for rapid cooling, i.e. for cooling times near to the oscillation periods. On the other hand, neglected non-linear behavior may change the outcome considerably, for example the Kelvin-Helmholtz instability at the tube boundary (Heyvaerts & Priest 1983; Ofman et al. 1994; Terradas et al. 2008), and the ponderomotive forces for high amplitudes (Terradas & Ofman 2004). The aim of this study is to further investigate the effects of radiative plasma cooling on the fundamental standing kink oscillation by means of numerical analysis.
2. Numerical model
The 3D numerical model consists of a straight, density-enhanced magnetic flux tube (also referred to as loop in what follows) embedded in a background plasma. We aimed to model a coronal active region loop. Initially, the system is permeated by a uniform magnetic field directed along the flux tube, i.e. in the z direction. Gravity is included, and it varies along the flux tube sinusoidally, meaning that it has zero value at the loop centre (z = 0) and maximum/minimum values at footpoints (z = ± L/ 2), in order to mimic the component of gravity parallel to the magnetic field in a semi-circular loop. Thus, we have stratification along the loop according to the hydrostatic equilibrium both inside and outside the loop (Fig. 1): 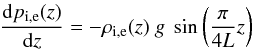 (1)where p is thermal pressure; ρ is mass density; the subscripts i and e denote the interior and exterior plasma, respectively, and g = 274 m/s2 is the Sun’s surface gravity.
(1)where p is thermal pressure; ρ is mass density; the subscripts i and e denote the interior and exterior plasma, respectively, and g = 274 m/s2 is the Sun’s surface gravity.
Owing to stratification, there will be a pressure imbalance at the loop boundary, which leads to a jump in total pressure. This is rapidly equilibrated once the simulation is started, resulting in a slightly increased and stratified magnetic field inside the loop. The perturbation caused by this imbalance has no effect on the long-timescale evolution, even if we do not let the system settle before we trigger the kink mode. We implement a step density profile for the loop. However, the numerical diffusivity means that a thin boundary layer evolves at the interface. The presence of this inhomogeneous layer allows for resonant absorption in the system. Values of the principal physical parameters used in the simulation are given in Table 1.
 |
Fig. 1 Mass density at t = 0: cross section along the axis of the loop (left) and perpendicularly to the loop at its footpoint (right). In the right plot, the mesh (numerical cells) is also shown. |
Values of principal physical parameters used in the simulations.
2.1. Radiative cooling
At low coronal temperatures (below 1 MK), the radiative cooling time is trad ≈ 103 s for typical coronal loops. This is two orders of magnitude shorter than the conductive cooling time, making the radiative loss be the dominant cooling mechanism (Aschwanden & Terradas 2008). We therefore neglect thermal conduction. Potential implications of this are discussed in the Conclusions section. We do not consider any heating mechanisms present during the simulation period.
The cooling module used in the simulation models the radiative loss rate E(T) for an optically thin plasma (Peres et al. 1982): 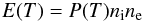 (2)where ni and ne are the ion and electron number density, which are considered to be equal, and P(T) is the plasma emissivity function, which strongly depends on the temperature. In the simulations, the radiative loss rate E(T) is calculated at each time step and is then used in the energy equation:
(2)where ni and ne are the ion and electron number density, which are considered to be equal, and P(T) is the plasma emissivity function, which strongly depends on the temperature. In the simulations, the radiative loss rate E(T) is calculated at each time step and is then used in the energy equation: 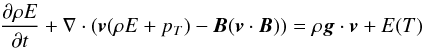 (3)where
(3)where 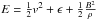 is the specific total energy with ϵ the specific internal energy,
is the specific total energy with ϵ the specific internal energy, 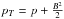 is the total pressure, and the other variables have their usual meaning. The radiative cooling affects the whole system, however the background plasma cools more slowly than our loop structure, owing to its higher temperature and lower density. The used function for P(T) follows the one computed with CHIANTI closely (Landi et al. 2012), shown in Fig. 2, where it can also be seen that for some temperature ranges (e.g. 0.5–2 MK), the emissivity calculated with CHIANTI is four times greater than previously assumed, thus cooling the coronal loops faster than with older emissivity functions. This is due to improvements in atomic models with the inclusion of more accurate atomic data and transition rates, or of lines that were previously unavailable.
is the total pressure, and the other variables have their usual meaning. The radiative cooling affects the whole system, however the background plasma cools more slowly than our loop structure, owing to its higher temperature and lower density. The used function for P(T) follows the one computed with CHIANTI closely (Landi et al. 2012), shown in Fig. 2, where it can also be seen that for some temperature ranges (e.g. 0.5–2 MK), the emissivity calculated with CHIANTI is four times greater than previously assumed, thus cooling the coronal loops faster than with older emissivity functions. This is due to improvements in atomic models with the inclusion of more accurate atomic data and transition rates, or of lines that were previously unavailable.
 |
Fig. 2 Plasma emissivity as a function of temperature, according to Rosner et al. (1978; thin solid line), and to version 7 of the CHIANTI spectral code Landi et al. (2012; thick solid line). The red line represents the piecewise emissivity used in our simulations. Adapted from Reale & Landi (2012). |
For comparison with analytical results, we use a decreased cooling (realistic cooling multiplied by a constant <1 factor) to allow for a slower and linear plasma evolution.
2.2. Perturbation and boundary conditions
Initially, we perturb the transverse component of velocity inside the loop with a pulse v0y = AvvA,ficos(πz/L), which excites a standing kink mode. Here, vA,fi ≈ 0.7 Mm/s is the Alfvén velocity inside the loop, at its footpoints, and Av is the dimensionless, relative amplitude of the perturbation (Av ≪ 1 for linear regime). We focus on modelling standing kink coronal loop oscillations triggered by a flaring event, and not the recently observed ubiquitous small amplitude kink oscillations (Nisticò et al. 2013; Anfinogentov et al. 2013), which are triggered by footpoint excitations.The initial perturbation only acts inside the loop and is constant in radial direction. We note that, because of stratification, the pulse does not correspond exactly to the fundamental kink eigenmode, but higher harmonics are also excited to a small extent (see Andries et al. 2005b). Exploiting the symmetric properties of standing kink waves, only half of the loop in both longitudinal (z axis) and transverse (x axis) direction is modelled, thus reducing the computational time four-fold. For these planes, to simulate the whole loop, symmetric boundary conditions are used, which are the following: In the x–y plane (at the apex), vz,By,Bx change sign, thus are antisymmetric, while the other variables are symmetric. In the y–z plane (the plane cutting the loop in half along it), only vx and Bx are antisymmetric.
 |
Fig. 3 Time-slice plot of the density at the loop apex (z = 0.0), for cooling (left) and non-cooling (right) cases, showing the evolution of the oscillation over time. The colour scale shows the density and is given in units of 10-12 kg/m3. The colour scale is common for the two images. |
 |
Fig. 4 Time-slice plot of the evolution of both the temperature (left) and density (right) at the axis of the loop, over time, for the cooling case. Temperatures are in K, while density is in units of 10-12 kg/m3. The horizontal z axis spans from the loop footpoint (left end) to the apex (right end). |
We emphasize that we do not employ a realistic solar atmosphere model (i.e. with photosphere, chromosphere, and transition region). To mimic coronal loops anchored in the dense photosphere, the loop footpoint is fixed. At this boundary, the line-tying condition is used, setting the velocities in all directions to zero, implying that plasma cannot leave the domain through loop footpoints. To validate our use of the line-tying boundary condition in getting the right behaviour of the downflow at the loop footpoints, we ran simulations with a realistic atmosphere, without transverse velocity perturbations. From the results of these simulations we can state that plasma is not evacuated from the loop structure, but instead accumulates at loop footpoints initially. Furthermore, the thermodynamic properties and the flow inside the loop are not significantly altered by the line-tying condition. (This can be appreciated by comparing Figs. 8 and 10.) The correct condition for the other variables at this boundary is that of a continuation of the hydrostatic equilibrium with constant temperature in the ghost cells. To minimize their influence on the dynamics, the other boundaries are placed at a safe distance from the loop (13 R in the direction of the displacement, i.e. y axis and 4 R for the x axis). At these boundaries, the outflow or open boundary condition is used, which allows waves to leave the domain.
2.3. Numerical method and grid
The 3D ideal MHD problem is solved using the FLASH code, which implements a second-order unsplit Godunov method (Lee & Deane 2009; Lee 2013) and constrained transport for keeping the solenoidal constraint on the magnetic field. We use the “mc” slope limiter and the Roe-type solver. An adaptively refined mesh is used, in order to have high resolution only in the domain of interest, i.e. around the loop, with five levels of refinement. The variable used for triggering mesh refinement (calculated with Löhner’s error estimator) is the density. Initially, the grid consists of 24 × 40 × 32 numerical cells, thus the resolution is bigger in the x–y plane, to resolve the small-scale phenomena that appear around the loop edge, such as instabilities and resonant absorption. In the z direction, the solution is smooth (wavelength close to box length). The effective resolution then (if the whole box was refined), with five levels of refinement, is 1280 × 384 in the x–y plane, which translates into cell sizes of 31.25 km, or 0.02 R. Test simulations with six levels of refinement show an effect on the small scales (instabilites) present in the perpendicular direction, but no relevant changes to oscillation characteristics (period, damping rate).
3. Results and discussion
3.1. Low amplitude perturbations
Initially, we considered relatively low amplitude initial velocity perturbations (Av = 0.02 or v0y = 14 km s-1) in order to remain in the linear regime, which is necessary for comparing our results with available analytical calculations. This also implies that we change from the realistic radiative cooling to a slower cooling by multiplying the radiative loss function with a constant factor to get a cooling time tcool ≈ 1500 s. Simulations were performed both with and without cooling. The perturbation led to a maximum displacement of the loop at the apex of 0.15 R or 225 km, hence a peak-to-peak displacement of 450 km. We let the system evolve until tf = 1200 s, in which we observed approximately six periods of oscillation, with a mean period of 204 s for the non-cooling case, very close to the analytically predicted value for the standing fundamental kink oscillations of a uniform flux tube with densities (inside and outside) equal to the weighted mean density of our stratified loop (Edwin & Roberts 1983; Andries et al. 2005b): 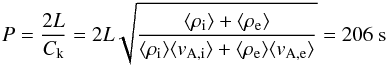 (4)where vA,i,e are the internal and external Alfvén speeds, and the weighting function used to obtain the mean values is
(4)where vA,i,e are the internal and external Alfvén speeds, and the weighting function used to obtain the mean values is 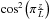 . The weighting function represents the wave energy density distribution along the loop of the fundamental mode (see Andries et al. 2005b). In the non-cooling case, the oscillation is damped due to the energy transfer between the global kink mode and local torsional Alfvén modes, i.e. resonant absorption, resulting in a damping time τD ≈ 1074 s. If we assume that the density varies sinusoidally in the inhomogeneous layer (which is not exactly the case for our data) the theory predicts a damping time (Ruderman & Roberts 2002; Goossens et al. 2002; Arregui et al. 2005):
. The weighting function represents the wave energy density distribution along the loop of the fundamental mode (see Andries et al. 2005b). In the non-cooling case, the oscillation is damped due to the energy transfer between the global kink mode and local torsional Alfvén modes, i.e. resonant absorption, resulting in a damping time τD ≈ 1074 s. If we assume that the density varies sinusoidally in the inhomogeneous layer (which is not exactly the case for our data) the theory predicts a damping time (Ruderman & Roberts 2002; Goossens et al. 2002; Arregui et al. 2005): 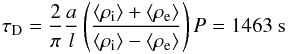 (5)where
(5)where 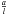 is the total to inhomogeneous layer width ratio. Keeping in mind the uncertainties of the inhomogeneous layer profile and width (for a linear profile with the same width, τD = 927 s), we can just state that the damping time obtained from the simulation lies inside the range of values predicted by the theory (see Soler et al. 2013, 2014).
is the total to inhomogeneous layer width ratio. Keeping in mind the uncertainties of the inhomogeneous layer profile and width (for a linear profile with the same width, τD = 927 s), we can just state that the damping time obtained from the simulation lies inside the range of values predicted by the theory (see Soler et al. 2013, 2014).
 |
Fig. 5 Normalized loop displacement at the apex for both cooling (red dots) and non-cooling (black dots), over time. The red curve represents the best-fit exponential decay, while the blue curve is the analytically predicted amplitude (Ruderman 2011a), both shown for the cooling case. The displacements were obtained by centre-of-mass tracking in the apex cross-section of the loop. |
Now we look at the differences between the two runs, i.e. oscillations in the cooling and non-cooling cases. The obvious difference between the two lies in the longitudinal evolution. More specifically, cooling of the plasma induces a flow inside the loop, which rearranges plasma towards the footpoints. Thus, there is a density increase close to the footpoints and a decrease at the loop tops (see Figs. 3 and 4).
 |
Fig. 6 Sequence of cross-section plots of the density at the loop apex, at different times (written at the left-top of each plot, in seconds), for the high amplitude case. Axis units are in Mm, while density is in units of 10-12 kg/m3. |
This effect can be easily seen from the continuity equation: if we have a time-dependent density (due to cooling), it will give rise to a varying velocity. The resulting flow speeds in the low amplitude run are a few tens of km s-1, which is at the lower boundary of the observed downflow speeds in the range 40–120 km s-1 (Schrijver 2001). As mentioned in Sect. 2.2 there are no outflows throughout the loop footpoints. Simulations that included realistic atmosphere (hyperbolic tangent temperature, see, e.g. Konkol et al. 2010) without velocity perturbations show that plasma evolution near the loop footpoint is approximated well by the simpler line-tying boundary condition (see again Figs. 8 and 10). We could not employ the realistic atmosphere in our study of the oscillations because of disturbances originating in the transition region caused by radiative cooling, which could have altered the oscillation characteristics. Now, we compare our oscillation amplitude evolution with the analytically predicted one from Ruderman (2011a), which includes the effects of both resonant absorption and cooling on the oscillation characteristics. We solved Eq. (98) from the paper numerically for our parameters and obtained the amplitude over time, resulting in a damping time τD ≈ 1090 s. In the analytical studies it is assumed that the hydrostatic formula is valid throughout the evolution, arguing that the flow effect on the density distribution in weak. This implies that the loop footpoint density is considered to be constant and that there is a net outflow of plasma through these footpoints. Thus, the comparison with analytical results should only be qualitative. However, the two evolutions (numerical and analytical) are in a good agreement (Fig. 5).
We can see that the difference in amplitude between the cooling and non-cooling cases is minimal (≈6%), thus the effects of cooling on the oscillation are very small. The efficiency of amplification due to cooling strongly depends on the characteristics of the loop (boundary layer thickness (l), density scale height, etc.), but probably most importantly on its hydrodynamic evolution, as reflected in the cooling time. In our case, the inefficiency might come from the relatively thick boundary layer (l/R ≈ 0.19), created by numerical diffusion. Ruderman (2011a) states that, for typical conditions and cooling times, and for the oscillations of coronal loops to be undamped, the boundary layer should be extremely thin (l/R ≈ 0.02). However, such a thin boundary layer might be very unlikely for oscillating solar coronal loops, as argued in what follows.
3.2. High amplitude perturbations
Now, we consider a higher initial perturbation, with Av = 0.1, thus a velocity perturbation of v0y = 70 km s-1 (5 times bigger than in the low amplitude setup), which leads to an initial displacement of 1.6 Mm, or around one loop radius. The displacement produced by the high perturbation is, however, at the lower boundary of the flare-related, typically observed displacements (see Aschwanden & Schrijver 2011; Terradas et al. 2008). The realistic radiative loss used now leads to a faster cooling (tcool ≈ 800 s), and new features are observed when compared to the previous linear evolution, the most important for the oscillation characteristics being the presence of instabilities at the loop edge, namely the Kelvin-Helmholtz instability, which deforms the loop drastically (see Fig. 6). In Antolin et al. (2014), it is stated that the instability sets in even for low amplitudes. However, in our low amplitude case, the shear instabilities does not evolve, or their growth time is longer than our six-period simulation time. This might be caused by the higher radius-length ratio of our loop or (and) a higher numerical viscosity of the scheme that we use, which might greatly affect the growth rate of the Kelvin-Helmholtz instability.
 |
Fig. 7 Same as in Fig. 5 (cooling with red dots and non-cooling with black dots), but for the high amplitude case. The red curve is the best-fit exponential decay for the non-cooling, low amplitude case (thus showing the added damping due to the presence of the instability). |
From Fig. 7 we see that the damping of high amplitude oscillation is faster than in the low amplitude case. This is an important effect of the instabilities present in the system. The damping is faster for two reasons: firstly, the development of the instability dissipates kinetic energy, and secondly, due to the mixing caused by the instability, a wider inhomogeneous layer develops around the loop, which affects the effectiveness of resonant absorption.
 |
Fig. 8 Time-slice plots showing the evolution of longitudinal flow speed (vz, left) and the density (right) for the cooling case in the high amplitude run, along the loop axis, over time. Flow speed is in Mm/s, while density in units of 10-12 kg/m3. |
Compared to Fig. 5, the effects of cooling on the wave amplitude become measurable after t ≈ tcool, but are not significant when looking at the whole evolution. The best-fit exponential damping time is 805 s for the cooling and 710 s for the non-cooling loop. Thus, the cooling only results in a 12% weaker damping. Another effect is the decrease in the oscillation period for the cooling case, an effect that was shown in analytical studies (Morton & Erdélyi 2009; Ruderman 2011b). For our cooling case, the ratio between the initial oscillation period and the one at the last anti-node (at tf ≈ 1000 s, with the periods measured by hand) is Ptf/Pi ≈ 0.85, which is a smaller deviation than predicted by the linear theory after the same amount of time (Ptf/Pi ≈ 0.57, by solving Eq. (28) from Morton & Erdélyi 2009 with our parameters). This deviation comes from the already mentioned differences between the analytical and numerical studies. This means that in the analytical study, the footpoint density is kept constant so that plasma leaves the loop while in our studies, it accumulates at the footpoint.
Another feature present in the high amplitude runs (due to the realistic radiative cooling) is the different late stage evolution (compare the density evolution from Fig. 4 to that of Fig. 8). At around t = tcool ≈ 750 s, there is a sudden draining of mass towards the footpoints with flow speeds of up to 100 km s-1, (downflow speeds typically observed in the corona), generated by a runaway cooling of the accumulated plasma. However, this effect is of secondary importance for the present study.
As stated above, the displacement observed in the high amplitude setup is still small compared to the typical displacements observed for flare related oscillating coronal loops. Thus, if the instabilities truly develop in oscillating solar coronal loops, for which there is no observational evidence yet (Terradas et al. 2008, but see Antolin et al. 2014 where they claim it could be observed as loop strands), the existence of a very thin inhomogeneous layer for several oscillation periods is highly unlikely, thus implying heavy limitations on the effectiveness of cooling induced amplification.
3.3. High density runs
To extend the scope of our study and conclusions, a series of simulations with fast cooling were run. The faster cooling was achieved by setting the density ratio three times higher than in the previous setups (ρfi/ρfe = 15) while keeping the same temperature and magnetic field strength, resulting in a footpoint density inside the loop of ρfi = 7.5 × 10-12 kg/m3. This results in an increased plasma β inside the loop. The cooling time is extremely short for these runs (tcool ≈ 100 s), cooling the near-MK plasma in the loop to chromospheric temperatures within 200 s. Although it is much faster than the usually observed cooling times in the range 500–2000 s (see, e.g., Aschwanden & Terradas 2008), it is important to see whether such a high energy loss can significantly alter the oscillation characteristics. The resulting flow towards the footpoint is steadily increasing, peaking at 140 km s-1 around tf ≈ 830 s, the end of simulation time. The resulting displacements over time for three cases can be seen in Fig. 9: cooling with both low and high amplitudes (perturbations with the same fraction of footpoint Alfvén speeds as in the previous runs) and non-cooling with low amplitude.
 |
Fig. 9 Normalized displacement amplitudes at the apex over time, for 3 cases: low amplitude perturbation with cooling (red dots), non-cooling (black dots) and high amplitude perturbation with cooling (green dots). The red curve represents the best-fix exponential decay, while the blue curve is the analytically predicted displacement, for the low amplitude with cooling case. The displacements were obtained by centre-of-mass tracking in the apex cross-section of the loop. |
For the low amplitude case, the linear theory (Ruderman 2011a) predicts that the oscillation amplitude should grow in time, in discrepancy with our results which show damping behaviour. However, the effects of the cooling in the low amplitude case are now stronger than for our previous runs, as expected: after ≈750 s, or 3 maximum displacements, the cooling case has a 21% higher amplitude than the non-cooling case. The effect on the oscillation period is also more significant, with the ratio of oscillation periods between the two cases Pcool/Pnocool ≈ 0.6 after the same time.
 |
Fig. 10 Time-slice plots showing the evolution of flow speed (vz, left) and the density (right) with included lower solar atmosphere, for the same conditions as in Fig. 8, along the loop axis, over time. The sawtooth appearance of wave fronts is due to the limited number of snapshots (100). Flow speed is in Mm/s, while density in units of 10-12 kg/m3. |
Looking at the high amplitude run, we still observe a strong damping, despite the fast cooling. This indicates that observed undamped high amplitude kink oscillations of coronal loops are very likely not due solely to plasma cooling.
4. Conclusions
We aimed to perform the first three-dimensional numerical study of a particular and often observed phenomenon: coronal loop oscillations in a cooling coronal loop. For a better estimate of hard-to-measure parameters using coronal seismology, theoretical models must take several physical effects into account that might have an influence on observable oscillation characteristics, and cooling is one of them. We find that, in the linear regime (i.e. small amplitude oscillations and long cooling times), the effect of cooling is negligible. This may be attributable to the relatively thick inhomogeneous layer in our simulations, which arises solely from numerical diffusion. Even if there are differences regarding boundary conditions between the available analytical results and our simulations, the resulting amplitude evolutions are in good agreement.
Increasing the initial velocity perturbation five-fold, resulting in a total displacement that lies at the low end of the observed, flare-related kink oscillations and employing realistic radiative losses shows different evolution than in the linear regime run: instabilities strongly affect the outer layers of the loop, and mixing causes a wider inhomogeneous layer to evolve, which in turn affects resonant absorption. The Kelvin-Helmholtz instability develops where the velocity shear is the strongest, at the edges of the loop perpendicular to the direction of motion. This is important for our study because the growth of such instabilities drains energy from the transverse oscillation, thus leading to increased damping. The effects of cooling appear negligible when looking at the entire evolution even in the high amplitude case, aside from its effect on the period, which is increased because of the lower inertia at the loop apex. With higher density runs, resulting in as short a cooling time as 100 s, the high amplitude run still shows strong damping.
The caveats of our study are the lack of a realistic solar atmosphere and the lack of thermal conduction, without which the present hydrodynamic evolution may not be proper (see e.g. Mariska et al. 1982). Furthermore, a parametric survey of initial plasma properties, such as temperature, would be insightful. It has been shown (Bradshaw & Cargill 2005, 2010) that during the so-called radiative cooling phase, the losses from the transition region lead to enhanced energy loss from the corona in the form of an enthalpy flux. This leads to an enhanced mass loss and could enhance the effects of cooling on the oscillations. In addition, thermal conduction could cool the loops even faster. However, the cooling time in the high density runs is short enough to allow for an appreciation of the effects of a higher energy loss. The presence of damping in the high amplitude runs even with fast energy loss indicates that it is unlikely that cooling alone could explain the observed, flare-related undamped oscillations of coronal loops. These results have implications in the tool of coronal seismology: since the effects of loop cooling with the usually observed cooling times (in our case with tcool ≈ 800 s) on the oscillations are negligible, it can also be applied to observations of flare-related coronal loop oscillations that show similar cooling behaviour.
Acknowledgments
N.M. acknowledges the Fund for Scientific Research-Flanders (FWO-Vlaanderen). T.V.D. was supported by an Odysseus grant, the Belspo IAP P7/08 CHARM network and the GOA-2015-014 (KU Leuven). A.M. and N.M. were supported by a grant of the Romanian National Authority of Scientific Research, Programme for research – Space Technology and Advanced Research – STAR, project number 72/29.11.2013. The software used in this work was developed in part by the DOE NNSA ASC- and DOE Office of Science ASCR-supported Flash Center for Computational Science at the University of Chicago. Visualization was done with the help of VisIt software (Childs et al. 2012).
References
- Andries, J., Arregui, I., & Goossens, M. 2005a, ApJ, 624, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Andries, J., Goossens, M., Hollweg, J. V., Arregui, I., & Van Doorsselaere, T. 2005b, A&A, 430, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anfinogentov, S., Nisticò, G., & Nakariakov, V. M. 2013, A&A, 560, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Antolin, P., Yokoyama, T., & Van Doorsselaere, T. 2014, ApJ, 787, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Arregui, I., Van Doorsselaere, T., Andries, J., Goossens, M., & Kimpe, D. 2005, A&A, 441, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arregui, I., Andries, J., Van Doorsselaere, T., Goossens, M., & Poedts, S. 2007, A&A, 463, 333 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aschwanden, M. J., & Schrijver, C. J. 2011, ApJ, 736, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., & Terradas, J. 2008, ApJ, 686, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Fletcher, L., Schrijver, C. J., & Alexander, D. 1999, ApJ, 520, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., de Pontieu, B., Schrijver, C. J., & Title, A. M. 2002, Sol. Phys., 206, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Nightingale, R. W., Andries, J., Goossens, M., & Van Doorsselaere, T. 2003, ApJ, 598, 1375 [NASA ADS] [CrossRef] [Google Scholar]
- Bradshaw, S. J., & Cargill, P. J. 2005, A&A, 437, 311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bradshaw, S. J., & Cargill, P. J. 2010, ApJ, 717, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Childs, H., Brugger, E., Whitlock, B., et al. 2012, in High Performance Visualization–Enabling Extreme-Scale Scientific Insight, 357 [Google Scholar]
- De Moortel, I., & Nakariakov, V. M. 2012, Roy. Soc. London Philos. Trans. Ser. A, 370, 3193 [Google Scholar]
- Dymova, M. V., & Ruderman, M. S. 2005, Sol. Phys., 229, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Edwin, P. M., & Roberts, B. 1983, Sol. Phys., 88, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Goossens, M., Hollweg, J. V., & Sakurai, T. 1992, Sol. Phys., 138, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Goossens, M., Andries, J., & Aschwanden, M. J. 2002, A&A, 394, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goossens, M., Erdélyi, R., & Ruderman, M. S. 2011, Space Sci. Rev., 158, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Heyvaerts, J., & Priest, E. R. 1983, A&A, 117, 220 [NASA ADS] [Google Scholar]
- Konkol, P., Murawski, K., Lee, D., & Weide, K. 2010, A&A, 521, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Landi, E., Del Zanna, G., Young, P. R., Dere, K. P., & Mason, H. E. 2012, ApJ, 744, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, D. 2013, J. Comput. Phys., 243, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, D., & Deane, A. E. 2009, J. Comput. Phys., 228, 952 [NASA ADS] [CrossRef] [Google Scholar]
- Mariska, J. T., Doschek, G. A., Boris, J. P., Oran, E. S., & Young, Jr., T. R. 1982, ApJ, 255, 783 [NASA ADS] [CrossRef] [Google Scholar]
- Morton, R. J., & Erdélyi, R. 2009, ApJ, 707, 750 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., & Ofman, L. 2001, A&A, 372, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakariakov, V. M., Ofman, L., Deluca, E. E., Roberts, B., & Davila, J. M. 1999, Science, 285, 862 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Nisticò, G., Nakariakov, V. M., & Verwichte, E. 2013, A&A, 552, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ofman, L., Davila, J. M., & Steinolfson, R. S. 1994, Geophys. Res. Lett., 21, 2259 [NASA ADS] [CrossRef] [Google Scholar]
- Parnell, C. E., & De Moortel, I. 2012, Roy. Soc. London Philos. Trans. Ser. A, 370, 3217 [Google Scholar]
- Peres, G., Serio, S., Vaiana, G. S., & Rosner, R. 1982, ApJ, 252, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Reale, F., & Landi, E. 2012, A&A, 543, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosner, R., Tucker, W. H., & Vaiana, G. S. 1978, ApJ, 220, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S. 2007, Sol. Phys., 246, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S. 2011a, A&A, 534, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruderman, M. S. 2011b, Sol. Phys., 271, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S., & Erdélyi, R. 2009, Space Sci. Rev., 149, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S., & Roberts, B. 2002, ApJ, 577, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S., Verth, G., & Erdélyi, R. 2008, ApJ, 686, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Ryutov, D. A., & Ryutova, M. P. 1976, Sov. J. Exper. Theoret. Phys., 43, 491 [Google Scholar]
- Sakurai, T., Goossens, M., & Hollweg, J. V. 1991, Sol. Phys., 133, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J. 2001, Sol. Phys., 198, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Soler, R., Goossens, M., Terradas, J., & Oliver, R. 2013, ApJ, 777, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Soler, R., Goossens, M., Terradas, J., & Oliver, R. 2014, ApJ, 781, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Terradas, J., & Goossens, M. 2012, A&A, 548, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Terradas, J., & Ofman, L. 2004, ApJ, 610, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Terradas, J., Oliver, R., & Ballester, J. L. 2006, ApJ, 650, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Terradas, J., Andries, J., Goossens, M., et al. 2008, ApJ, 687, L115 [Google Scholar]
- Van Doorsselaere, T., Debosscher, A., Andries, J., & Poedts, S. 2004, A&A, 424, 1065 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Doorsselaere, T., Nakariakov, V. M., & Verwichte, E. 2007, A&A, 473, 959 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verth, G., & Erdélyi, R. 2008, A&A, 486, 1015 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, T., Ofman, L., Davila, J. M., & Su, Y. 2012, ApJ, 751, L27 [Google Scholar]
- Zaitsev, V. V., & Stepanov, A. V. 1975, ssled. Geomagn. Aeron. F iz. Solntsa, 37, 3 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Mass density at t = 0: cross section along the axis of the loop (left) and perpendicularly to the loop at its footpoint (right). In the right plot, the mesh (numerical cells) is also shown. |
| In the text | |
 |
Fig. 2 Plasma emissivity as a function of temperature, according to Rosner et al. (1978; thin solid line), and to version 7 of the CHIANTI spectral code Landi et al. (2012; thick solid line). The red line represents the piecewise emissivity used in our simulations. Adapted from Reale & Landi (2012). |
| In the text | |
 |
Fig. 3 Time-slice plot of the density at the loop apex (z = 0.0), for cooling (left) and non-cooling (right) cases, showing the evolution of the oscillation over time. The colour scale shows the density and is given in units of 10-12 kg/m3. The colour scale is common for the two images. |
| In the text | |
 |
Fig. 4 Time-slice plot of the evolution of both the temperature (left) and density (right) at the axis of the loop, over time, for the cooling case. Temperatures are in K, while density is in units of 10-12 kg/m3. The horizontal z axis spans from the loop footpoint (left end) to the apex (right end). |
| In the text | |
 |
Fig. 5 Normalized loop displacement at the apex for both cooling (red dots) and non-cooling (black dots), over time. The red curve represents the best-fit exponential decay, while the blue curve is the analytically predicted amplitude (Ruderman 2011a), both shown for the cooling case. The displacements were obtained by centre-of-mass tracking in the apex cross-section of the loop. |
| In the text | |
 |
Fig. 6 Sequence of cross-section plots of the density at the loop apex, at different times (written at the left-top of each plot, in seconds), for the high amplitude case. Axis units are in Mm, while density is in units of 10-12 kg/m3. |
| In the text | |
 |
Fig. 7 Same as in Fig. 5 (cooling with red dots and non-cooling with black dots), but for the high amplitude case. The red curve is the best-fit exponential decay for the non-cooling, low amplitude case (thus showing the added damping due to the presence of the instability). |
| In the text | |
 |
Fig. 8 Time-slice plots showing the evolution of longitudinal flow speed (vz, left) and the density (right) for the cooling case in the high amplitude run, along the loop axis, over time. Flow speed is in Mm/s, while density in units of 10-12 kg/m3. |
| In the text | |
 |
Fig. 9 Normalized displacement amplitudes at the apex over time, for 3 cases: low amplitude perturbation with cooling (red dots), non-cooling (black dots) and high amplitude perturbation with cooling (green dots). The red curve represents the best-fix exponential decay, while the blue curve is the analytically predicted displacement, for the low amplitude with cooling case. The displacements were obtained by centre-of-mass tracking in the apex cross-section of the loop. |
| In the text | |
 |
Fig. 10 Time-slice plots showing the evolution of flow speed (vz, left) and the density (right) with included lower solar atmosphere, for the same conditions as in Fig. 8, along the loop axis, over time. The sawtooth appearance of wave fronts is due to the limited number of snapshots (100). Flow speed is in Mm/s, while density in units of 10-12 kg/m3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


