| Issue |
A&A
Volume 582, October 2015
|
|
|---|---|---|
| Article Number | A121 | |
| Number of page(s) | 42 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201526067 | |
| Published online | 22 October 2015 | |
Linking dust emission to fundamental properties in galaxies: the low-metallicity picture⋆
1
Institut d’Astrophysique Spatiale, CNRS, UMR 8617,
91405
Orsay,
France
e-mail: aurelie.remyruyer@ias.u-psud.fr; ruyeraurelie.astro@gmail.com
2
Laboratoire AIM, CEA/IRFU/Service d’Astrophysique, Université
Paris Diderot, Bât.
709, 91191
Gif-sur-Yvette,
France
3
Sterrenkundig Observatorium, Universiteit Gent,
Krijgslaan 281 S9, 9000
Gent,
Belgium
4
UK ALMA Regional Centre Node, Jodrell Bank Centre for
Astrophysics, School of Physics & Astronomy, University of
Manchester, Oxford
Road, Manchester
M13 9PL,
UK
5
Laboratoire d’Astrophysique de Marseille – LAM, Université
d’Aix-Marseille & CNRS, UMR 7326, 38 rue F. Joliot-Curie, 13388
Marseille Cedex 13,
France
6
Department of Physics, University of Crete,
71003
Heraklion,
Greece
7
Zentrum für Astronomie der Universität Heidelberg, Institut für
Theoretische Astrophysik, Albert-Ueberle-Str. 2, 69120
Heidelberg,
Germany
8
Center for Cosmology, Department of Physics and Astronomy,
University of California, Irvine, CA
92697,
USA
9
Centre for Astrophysics & Supercomputing, Swinburne
University of Technology, Mail H30,
PO Box 218, Hawthorn
VIC
3122,
Australia
10
Institute of Astronomy, University of Cambridge,
Madingley Road, Cambridge
CB3 0HA,
UK
11
Max-Planck für Extraterrestrische Physik, Giessenbachstr.
1, 85748
Garching-bei-München,
Germany
12
European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748
Garching-bei-München,
Germany
13
Department of Physics and Astronomy, University of
Sussex, Brighton,
BN1 9QH,
UK
14
NASA Herschel Science Center, MS 100-22, California Institute of
Technology, Pasadena,
CA
91125,
USA
15
Instituto di Astrofisica e Planetologia Spaziali, INAF-IAPS,
Via Fosso del Cavaliere
100, 00133
Roma,
Italy
Received: 10 March 2015
Accepted: 14 July 2015
Aims. In this work, we aim to provide a consistent analysis of the dust properties from metal-poor to metal-rich environments by linking them to fundamental galactic parameters.
Methods. We consider two samples of galaxies: the Dwarf Galaxy Survey (DGS) and the Key Insights on Nearby Galaxies: a Far-Infrared Survey with Herschel (KINGFISH), totalling 109 galaxies, spanning almost 2 dex in metallicity. We collect infrared (IR) to submillimetre (submm) data for both samples and present the complete data set for the DGS sample. We model the observed spectral energy distributions (SED) with a physically-motivated dust model to access the dust properties: dust mass, total-IR luminosity, polycyclic aromatic hydrocarbon (PAH) mass fraction, dust temperature distribution, and dust-to-stellar mass ratio.
Results. Using a different SED model (modified black body), different dust composition (amorphous carbon in lieu of graphite), or a different wavelength coverage at submm wavelengths results in differences in the dust mass estimate of a factor two to three, showing that this parameter is subject to non-negligible systematic modelling uncertainties. We find half as much dust with the amorphous carbon dust composition. For eight galaxies in our sample, we find a rather small excess at 500 μm (≤1.5σ). We find that the dust SED of low-metallicity galaxies is broader and peaks at shorter wavelengths compared to more metal-rich systems, a sign of a clumpier medium in dwarf galaxies. The PAH mass fraction and dust temperature distribution are found to be driven mostly by the specific star formation rate, sSFR, with secondary effects from metallicity. The correlations between metallicity and dust mass or total-IR luminosity are direct consequences of the stellar mass-metallicity relation. The dust-to-stellar mass ratios of metal-rich sources follow the well-studied trend of decreasing ratio for decreasing sSFR. The relation is more complex for low-metallicity galaxies with high sSFR, and depends on the chemical evolutionary stage of the source (i.e. gas-to-dust mass ratio). Dust growth processes in the ISM play a key role in the dust mass build-up with respect to the stellar content at high sSFR and low metallicity.
Conclusions. We conclude that the evolution of the dust properties from metal-poor to metal-rich galaxies derives from a complex interplay between star formation activity, stellar mass, and metallicity.
Key words: dust, extinction / evolution / galaxies: dwarf / galaxies: evolution / infrared: ISM / infrared: galaxies
Figures 12 and 13, Tables 4–9, and Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
The processes by which galaxies evolve from primordial environments to present-day galaxies are still widely debated, but the seeds of this evolution lie in the star formation histories of the galaxies, and in their interaction with their environment through gas infall, outflows, or mergers. The interstellar medium (ISM) plays a key role in this evolution since it is the site of stellar birth and the repository of stellar ejecta.
Although interstellar dust represents only ~1% of the total mass of the ISM, it is an important agent in star formation. Dust absorbs the stellar radiation that would otherwise dissociate molecules and thus actively participates in the cooling of the ISM. It is also a catalyser for molecular gas formation by providing a surface where atoms can react (Hasegawa & Herbst 1993; Vidali et al. 2004; Le Bourlot et al. 2012; Bron et al. 2014). The presence of dust can increase the H2 formation rate by about two orders of magnitudes compared to H2 formation without dust (Tielens 2005), thus facilitating star formation.
Dust forms from the available heavy elements in the explosively ejected material from core-collapse supernovæ (SN) and in the quiescent outflows from low-mass stars (Todini & Ferrara 2001; Gomez et al. 2012a,b; Indebetouw et al. 2014; Rowlands et al. 2014; Matsuura et al. 2015). The refractory dust grains may, after their injection into the ISM, grow by accretion or coagulation in dense molecular clouds (Bazell & Dwek 1990; Stepnik et al. 2001, 2003; Köhler et al. 2012, 2015), locking even more heavy elements in the solid phase of the ISM (Savage & Sembach 1996; Whittet 2003). Through destructive processes (such as erosion or sputtering; see Jones et al. 1994, 1996; Serra Díaz-Cano & Jones 2008; Bocchio et al. 2012, 2014), elements are released again into the gas phase. Metallicity, defined as the mass fraction of heavy elements, or “metals”, in the ISM, is thus a key parameter in studying the evolution of galaxies.
Understanding how dust properties evolve as a function of metal enrichment can provide important constraints for galaxy evolution studies. Dwarf galaxies in the local Universe are ideal targets for such a study as many of them have low metallicity and high star formation activity. As such, they present star formation properties and ISM conditions that are the closest analogues to those thought to be present in the primordial environments of the early Universe (Madau et al. 1998).
Previous studies already demonstrated that the dust properties in low-metallicity galaxies were notably different from that of metal-rich sources. Low-metallicity galaxies harbour warmer dust (e.g. Helou 1986; Melisse & Israel 1994; Galliano et al. 2005; Rosenberg et al. 2006; Cannon et al. 2006), lower polycyclic aromatic hydrocarbon (PAH) abundances (e.g. Madden 2000; Boselli et al. 2004; Engelbracht et al. 2005; Wu et al. 2006; O’Halloran et al. 2006; Draine et al. 2007; Galliano et al. 2008; Gordon et al. 2008; Wu et al. 2011; Sandstrom et al. 2012), higher gas-to-dust mass ratios (e.g. Issa et al. 1990; Lisenfeld & Ferrara 1998; Hirashita et al. 2002; James et al. 2002; Draine et al. 2007; Engelbracht et al. 2008; Galliano et al. 2008; Muñoz-Mateos et al. 2009; Bendo et al. 2010; Galametz et al. 2011; Magrini et al. 2011). Submillimetre (submm) excess emission, presently not accounted for by dust models, is observed in numerous dwarf galaxies or low-mass spirals (e.g. Galliano et al. 2003, 2005; Dumke et al. 2004; Bendo et al. 2006; Galametz et al. 2009, 2012, 2014; Zhu et al. 2009; Bot et al. 2010; Grossi et al. 2010, 2015; Dale et al. 2012; Ciesla et al. 2014; Gordon et al. 2014). Low-mass galaxies also show a broadening of the infrared (IR) peak of the SED (e.g. Boselli et al. 2012; Smith et al. 2012a; Ciesla et al. 2014), and a flattening of the far-infrared (FIR) slope (e.g. Boselli et al. 2010; Cortese et al. 2014). However, all of these studies do not extend to very low metallicities and/or have a limited number of sources below ~1/5 Z⊙1 (12 + log (O/H) = 8.0).
In Rémy-Ruyer et al. (2013), we derived the dust properties in a systematic way for a large number of galaxies (109), among which more than half are dwarf galaxies and ~35% have Z ≤ 1/5Z⊙. We confirmed with this significant sample of low-metallicity sources that the dust is warmer at low metallicities and identified several galaxies with submm excess. This study was conducted using only Herschel data and a modified black body to model the dust emission. In Rémy-Ruyer et al. (2014), we confirmed the higher gas-to-dust mass ratios (G/D) at low metallicities using the sample of Rémy-Ruyer et al. (2013), and a semi-empirical spectral energy distribution (SED) model over the whole IR range. We showed that the G/D is actually higher at low metallicities than that expected from a simple description of the dust evolution in the ISM. The large scatter in the observed G/D is intrinsic to the galaxies and reflects a non-universal dust-to-metal mass ratio (see also Dwek 1998; De Cia et al. 2013; Zafar & Watson 2013; Mattsson et al. 2014a). We showed that the metallicity was the main driver of the G/D but that the scatter was controlled by the different SFHs of the sources. Thus metallicity is not the only parameter shaping the dust properties.
As a follow-up of Rémy-Ruyer et al. (2013, 2014), we aim to provide a consistent picture of the evolution of the dust properties from metal-poor to metal-rich galaxies. On the observational side, we present the complete catalogue of IR-to-submm flux densities for the Dwarf Galaxy Survey (DGS). We use a semi-empirical dust SED model, which accounts for starlight intensity mixing in the ISM, to interpret the whole IR-to-submm observed SEDs. In this work, we extend the range of dust properties and look at the dust mass, the total IR (TIR) luminosity, the PAH mass fraction, and the dust temperature distribution. The dust temperature distribution is directly linked to the SED shape and provides valuable insight into the average dust temperature and the broadness of the FIR peak of the SED. We also discuss the evolution of dust-to-stellar mass ratios and link it to the evolution of the G/D observed in Rémy-Ruyer et al. (2014). For the analysis we do not only consider metallicity as our main parameter, but also include the specific star formation rate (SFR) and the stellar mass.
The paper is organised as follows: in Sect. 2, we present the sample used for the study and the whole IR-to-submm data set. Section 3 presents the dust model along with the free parameters (Sects. 3.1 and 3.2), and errors on the best-fit parameters (Sect. 3.3). In this section we also address how the use of a realistic dust model (Sect. 3.4), a different interstellar radiation field (ISRF, Sect. 3.5), a different dust composition (Sect. 3.6), or a different wavelength coverage at 500 μm (Sect. 3.7) impacts the estimated dust properties (especially the dust mass). Section 4 is dedicated to the derived dust properties and their variation with metallicity and star formation activity. In Sect. 5, we discuss our results on the dust-to-stellar mass ratio in the context of galaxy evolution.
The paper also contains several appendices to facilitate the reading of the main body of the paper. Further details are available there. Appendix A presents how we updated Herschel photometry since the studies of Dale et al. (2012) and Rémy-Ruyer et al. (2013). Observing logs are given in Appendix B for the DGS IRAC and IRS Spitzer data. Appendix C compares IRAC and WISE photometry for the DGS sources to other measurements in the literature. Appendix D explains in detail the data reduction and preparation of the IRS spectra. Special cases of SED modelling are discussed in Appendix E.
2. Samples and observations
In this section we present the sample of galaxies and the set of IR-to-submm data used to build their observed dust SEDs. We also derive SFR and specific star formation rates (sSFR) to quantify star formation activity.
2.1. Samples
For this study, we combine two samples of local galaxies observed with Herschel: the Dwarf Galaxy Survey (DGS, Madden et al. 2013) and the Key Insights on Nearby Galaxies: a Far-Infrared Survey with Herschel (KINGFISH, Kennicutt et al. 2011). The DGS is a sample of 48 star-forming dwarf galaxies with low metallicity dedicated to the study of the dust and the gas properties in low-metallicity environments. The DGS sample includes objects among the most metal-poor galaxies in the local Universe, with metallicities ranging from Z ~ 0.03Z⊙ to 0.55 Z⊙ (Fig. 1). Stellar masses range over four orders of magnitudes, from 3 × 106M⊙ to 3 × 1010M⊙ (Madden et al. 2014).
The KINGFISH sample has been built from the Spitzer Infrared Nearby Galaxies Survey (SINGS, Kennicutt et al. 2003), and enables us to span a wider metallicity range by including more metal-rich galaxies. The KINGFISH sample contains 61 galaxies, including mostly spiral galaxies together with several early-type and dwarf galaxies. The metallicities in the KINGFISH sample range from Z ~ 0.07Z⊙ to 1.20 Z⊙. The two samples complement each other very well in terms of metallicities and stellar masses (Fig. 1).
The KINGFISH sources have been classified in terms of “star-forming” or “active galactic nuclei” (AGN) type by Moustakas et al. (2010) using an optical emission-line diagnostic diagram (Baldwin et al. 1981). According to Kennicutt et al. (2011), the detected AGNs are low-luminosity AGNs and none of the galaxies have a dominant AGN, except for NGC 1316. In terms of mid-infrared (MIR) emission line diagnostics, NGC 4725 has a [O iv]/[Ne ii] ratio of ~1 (Dale et al. 2006) and can be considered to be an AGN-dominated source. NGC 4736 has [O iv]/[Ne ii] ~ 0.3 and is an “intermediate” object with a AGN contribution of ~50%. The other KINGFISH AGN sources have [O iv]/[Ne ii] ≲ 0.1 or no detection of the [O iv] 25.9 μm line, equivalent to an AGN fraction ≲10% (Genzel et al. 1998; Tommasin et al. 2010). Except for these three galaxies, we thus do not expect the AGN to significantly impact the IR emission in the KINGFISH galaxies.
The metallicities in both samples have been determined in Madden et al. (2013) and Kennicutt et al. (2011) using the “strong-line” calibration from Pilyugin & Thuan (2005), linking a specific oxygen optical lines ratio2 to the oxygen abundance in terms of 12 + log(O/H). We choose this specific metallicity calibration because it is available and homogeneous for both samples and to avoid any biases using different calibrations. The stellar masses were derived by Madden et al. (2014) for the DGS using the prescription of Eskew et al. (2012) and the IRAC 3.6 μm and 4.5 μm flux densities. We use this prescription for the KINGFISH sample for consistency purposes and to reduce the scatter in the dust-to-stellar mass ratios (as seen in Rémy-Ruyer et al. 2015). When no IRAC observed flux densities are available, we use synthetic flux densities computed from the best-fit SED model (see Sect. 3). Coordinates, distances, and metallicities for the DGS can be found in Madden et al. (2013), and in Kennicutt et al. (2003, 2011) for the KINGFISH sample. Stellar masses are tabulated in Table 4. We have a total of 109 galaxies for this study.
 |
Fig. 1 Metallicity (top), and stellar mass (bottom) distributions of the DGS (purple), KINGFISH (orange) samples. The total distribution is indicated in grey. In the top panel, solar metallicity is indicated here to guide the eye, as well as the 1/50, 1/10, and 1/5 Z⊙ values. |
2.2. Herschel data
The 109 DGS and KINGFISH galaxies have been observed with Herschel in six photometric bands at 70, 100, and 160 μm with the Photodetector Array Camera and Spectrometer (PACS, Poglitsch et al. 2010), and at 250, 350, and 500 μm with the Spectral and Photometric Imaging REceiver (SPIRE, Griffin et al. 2010).
The data reduction and photometry for the DGS and KINGFISH galaxies are presented in Rémy-Ruyer et al. (2013) and Dale et al. (2012), respectively. However, the data reduction techniques and the calibration of the instruments have been updated since the publication of Rémy-Ruyer et al. (2013) and Dale et al. (2012). We, therefore, present the latest updated data. For the DGS data, the Scanamorphos PACS maps are reprocessed with version 23 of Scanamorphos (Roussel 2013), and the SPIRE maps are reprocessed with version 12 of the Herschel Processing Interactive Environment (HIPE – Ott 2010). We find an average difference of 5%, 8%, and 2% at 70, 100, and 160 μm between the updated flux densities and the flux densities of Rémy-Ruyer et al. (2013), and in some extreme cases the difference is as high as 30%. For the SPIRE flux densities, the average difference is 3%, 5%, and 3% at 250, 350, and 500 μm, respectively. The updated PACS and SPIRE flux densities for the DGS galaxies are presented in Table 5.
For the KINGFISH data, we update the flux densities presented in Dale et al. (2012), with an average difference with the Dale et al. (2012) flux densities of 7% at 160 μm, and ~2% for SPIRE wavelengths. Detailed information regarding the update of the DGS and KINGFISH Herschel data can be found in Appendix A. Colour corrections are applied to the SPIRE flux densities in both samples to account for the dependence of the SPIRE beam areas on the FIR spectral shape of the sources (see Appendix A).
2.3. Spitzer data
We collect Spitzer observations for our sample to constrain the warm dust and the PAH emission in MIR wavelengths, with photometric data from the InfraRed Array Camera (IRAC) and the Multiband Imaging Photometer for Spitzer (MIPS), and spectroscopic data from the InfraRed Spectrograph (IRS). Spitzer observations of several DGS sources were already available in the Spitzer database3. New complementary Spitzer observations for 19 DGS galaxies have also been obtained during the cycle 5 program to complete the set of existing Spitzer data (Dust Evolution in Low-Metallicity Environments: P.I. F. Galliano; ID: 50550), and for which only the MIPS data at 24, 70, and 160 μm have been published so far (in Bendo et al. 2012). Thus we only present the IRAC and IRS observations for the DGS sample (observing logs in Appendix B).
Spitzer IRAC and MIPS photometry for the KINGFISH galaxies is taken from Dale et al. (2007). We do not attempt to use the IRS data existing for the KINGFISH galaxies, as the galaxies are very extended and a complete coverage of the sources with IRS is not available (Dale et al. 2009b).
2.3.1. IRAC
The IRAC data at 3.4, 4.5, 5.8, and 8.0 μm is available for the DGS galaxies, and the IRAC maps are retrieved from the NASA/IPAC ISA database for Spitzer data. For three galaxies, HS 1442+4250, SBS 1415+437 and UM 311, only two wavelengths are available (4.5 and 8.0 μm). After subtracting the background and possible contamination from background sources or foreground stars, flux densities are extracted from the maps using aperture photometry. In most cases, we use the same apertures as those used for Herschel photometry. The final IRAC flux densities and the apertures used are given in Table 6.
The IRAC calibration is based on point-source photometry for a 12′′ radius aperture. An additional aperture correction is needed to account for the emission from the wings of the PSF and the scattering of diffuse emission across the IRAC focal plane. This correction is given in the IRAC Instrument Handbook (version 2.0.1 Sect. 4.11.14) and depends on the source aperture radius. Following the recipe given in the IRAC Instrument Handbook, we do not apply this correction to small and compact sources (see Table 6).
The uncertainty on the flux density is computed by summing in quadrature the calibration error, the error from the background determination, and the error from the source flux determination. We adopt a calibration error for the four IRAC bands of 10% as recommended in the IRAC Instrument Handbook5. We consider that galaxies are not detected when the computed flux density is lower than three times its corresponding uncertainty in a given band. The final 3σ upper limit is reported in Table 6.
Photometry with IRAC is available in the literature for 29 DGS sources: Hunt et al. (2006), Dale et al. (2007, 2009a), Engelbracht et al. (2008), Galametz et al. (2009). If we compare our measurements to those from the literature we get a fairly good agreement between them, with some outliers. The details of this comparison and possible explanations for the outliers are given in Appendix C.
2.3.2. IRS
The DGS galaxies have a very rapidly rising continuum in the MIR, and the IRS spectra gives important constraints on the continuum from 20 to 40 μm. Moreover, the spectra can also be used to put constraints on the PAH emission (see Sect. 3.2). Line intensities have been extracted by Cormier et al. (2015) for the [S iv] 10.5 μm, [Ne ii] 12.8 μm, [Ne iii] 15.6 μm, [S iii] 18.7 μm, and 33.5 μm spectral lines, in the compact sources of the DGS.
The IRS spectra for the DGS galaxies have been extracted from the Cornell AtlaS of Spitzer Infrared spectrograph Sources6 (CASSIS v5, Lebouteiller et al. 2011). Most of the DGS galaxies were observed using the staring mode, except for a few extended sources observed with the mapping mode, for which the spectra were reduced manually with cubism (Smith et al. 2007a). We were able to obtain Short-Low (i.e. short wavelength data at low spectral resolution, SL) and Long-Low (i.e. long wavelength data at low spectral resolution, LL) data for 43 galaxies in total. More details about the extraction and the data reduction of the IRS spectra can be found in Appendix D.
It is then necessary to rescale the SL and LL spectra in order to match the photometry. We derive synthetic IRS photometry to correct the two modules and use all of the constraints we have in this wavelength range: the IRAC 5.8 and 8.0 μm, WISE 12 and 22 μm (see Sect. 2.4), and MIPS 24 μm bands. IRAC 5.8, 8.0 and WISE 12 μm are used simultaneously to derive a correction factor for the SL module that depends on the wavelength. However, for the LL module, the two constraints do not sample well the LL spectrum, and the LL correction factor is thus a constant. We use MIPS 24 μm in most cases (or WISE 22 μm when not available). The SL and LL spectra can be treated separately as they are two independent observations. More details about the rescaling of the IRS spectrum can be found in Appendix D. The median correction applied at 5.8 μm, 8.0 μm, 12 μm, and 24 μm are 1.7, 2.0, 1.0, and 1.2, respectively. Note that this correction assumes that the spectral shape of the area observed by the IRS slits likewise describes the expected spectral shape of the full galaxy. This is true for compact sources but can be erroneous for more extended galaxies, except if the region falling within the IRS slits dominates the total emission of the galaxy in the MIR.
To improve the quality of the noisiest spectra (e.g. HS 1304+3529, Fig. D.1, top panel), we smooth the spectra until we reach a signal-to-noise ratio (S/N) of 3 at every wavelength. This smoothing step is applied for 22 DGS galaxies. However, for three galaxies, HS 1236+3937, HS 1442+4250, Tol 0618-402, even with the smoothing step, we cannot reach a S/N of 3 for any point in the spectrum. Thus we do not consider these spectra in the SED modelling. In two galaxies, HS 2352+2733 and UGCA 20, the IRS slits are not centred on the source position, thus we do not present these spectra either. The remaining 38 IRS spectra are shown in Fig. D.3.
2.4. WISE data
The Wide-field Infrared Survey Explorer (WISE, Wright et al. 2010) observed the whole sky at 3.4, 4.6, 12, and 22 μm, and gives an additional constraint at 12 μm, very valuable for probing the MIR range of the observed SED. The InfraRed Astronomical Satellite (IRAS, Neugebauer et al. 1984) also provides a constraint at 12 μm (see Sect. 2.5), but was not able to detect the faintest dwarf galaxies. We also need the 12 and 22 μm constraints to match the IRS spectra to the photometry (Sect. 2.3.2). The WISE flux densities at 3.4 and 4.6 μm are also given for completeness. We only present WISE data for the DGS galaxies, as Spitzer and IRAS already provide the equivalent spectral coverage for the brighter KINGFISH galaxies.
The WISE maps were retrieved from the NASA/IPAC ISA database and the AllWISE database7. Most sources in the DGS are resolved by WISE as the resolution is ~6′′ for the first three bands and 12′′ for the WISE 22 μm band. Profile-fit and standard aperture photometry provided by the WISE database can underestimate the brightness of resolved sources and can suffer from confusion with nearby objects (Sect. 2.2 of the AllWISE explanatory supplement8).
We therefore perform our own aperture photometry on the maps, following the method outlined in Sect. 4.3 of the All WISE explanatory supplement. The apertures are the same as for IRAC and Herschel photometry whenever possible. In some cases, the morphology of the source in the first two bands is quite different from the morphology of the source in the last two bands. These two sets of wavelengths are not tracing the same physical component: old stellar population at 3.4 μm and 4.6 μm on one side, and warm dust at 12 μm and 22 μm on the other side. The NIR morphology may differ from the MIR morphology. In this case we have to use two different apertures if we want to encompass the whole emission of the source and optimise the S/N at all four wavelengths. For the unresolved sources, we use the profile-fit photometry provided by the All WISE database.
The uncertainty comes from the flux determination, from the background estimation, from correlated noise in the maps, and from the calibration and measurement of the zero-point magnitudes (see the AllWISE explanatory supplement). The calibration of WISE has been tied to that of Spitzer IRAC 3.6 μm for WISE1, IRAC 4.5 μm for WISE2, IRS for WISE3, and MIPS 24 μm for WISE4 (see Jarrett et al. 2011), thus we adopt a calibration error of 10% at 3.4 μm and 4.6 μm, 5% at 12 μm, and 7% at 22 μm. As for IRAC photometry, we report upper limits if the detection is below 3σ. The final WISE flux densities and apertures used are given in Table 7. The WISE measurements compare well with other instruments, IRAC at 3.6 μm and 4.5 μm, IRAS at 12 μm, and MIPS at 24 μm. The details of the comparison are given in Appendix C.
 |
Fig. 2 Star formation rates, SFR, (left), specific SFRs, sSFR, (right), for the DGS (crosses) and KINGFISH samples as a function of metallicity, colour coded with Mstar (colour legend in right panel). For the KINGFISH sample, we distinguish the sources that have been classified as “star-forming” (SF, downward triangles) or as “AGN” (stars) by Kennicutt et al. (2011). The distribution of each parameter is indicated on the side of each panel for both samples: solid line for DGS and dashed line for KINGFISH. |
2.5. All-sky survey data from 2MASS and IRAS
We complete our set of Spitzer, WISE and Herschel data by searching the literature for data from 2MASS (Two Microns All Sky Survey, Skrutskie et al. 2006) and IRAS.
The 2MASS data in the J (1.24 μm), H (1.66 μm), and Ks (2.16 μm) bands, for the DGS sample is given in Table 8, and has been compiled from the literature: the NASA/IPAC ISA 2MASS Point Source Catalog9, the 2MASS Extended Objects Final Release, the 2MASS Large Galaxy Atlas (Jarrett et al. 2003), Engelbracht et al. (2008), Dale et al. (2009a). In some cases, the original data is given in magnitudes. To convert this into flux densities, we use the zero-magnitude flux values from Cohen et al. (2003). The 2MASS data for the KINGFISH galaxies is presented in Dale et al. (2007).
We also compile IRAS data for the DGS at 12, 25, 60, and 100 μm from the literature: the NASA/IPAC ISA IRAS Faint Source (v2.0 1990)9 and Point Source (v2.1) Catalogs9, Rice et al. (1988), Sanders et al. (2003), Engelbracht et al. (2008) and is given in Table 8. Note that IRAS is not very sensitive for the low-luminosity dwarf galaxies and that the resolution varies from ~30′′ at 12 μm to ~120′′ at 100 μm. Even for the detected sources, such low resolution implies that several sources may be mixed in the beam and indistinguishable. That is why some of the IRAS fluxes of Table 8 have been noted as unreliable (with the note g). Twenty-five DGS galaxies have IRAS measurements and only 15 are detected in all of the IRAS bands. The KINGFISH IRAS data have been extracted from Sanders et al. (2003) and the IRAS Faint Source (v2.0 1990) and Point Source (v2.1) Catalogs.
DGS and KINGFISH SED parameters.
2.6. Star formation activity
2.6.1. Star formation rates
To estimate the SFR for our sources, we consider two of the most widely used SFR tracers, the far-ultraviolet (FUV) and the Hα luminosities. The observed stellar emission traced either by FUV or Hα has to be corrected for dust attenuation, and this correction is usually made using observational dust tracers such as the TIR or 24 μm luminosities (Kennicutt et al. 2009; Calzetti et al. 2010; Hao et al. 2011; Kennicutt & Evans 2012).
In our sample, we can derive SFR for 90% of the galaxies using Hα+TIR, 88% using Hα+24 μm, 77% using FUV+TIR, and 78% using FUV+24 μm. We thus use the diagnostic based on the observed Hα luminosity, corrected for attenuation using LTIR, and the formula by Kennicutt et al. (2009) for a Kroupa initial mass function (IMF). Moreover, Kennicutt et al. (2009) showed for the Spitzer-SINGS sample that this composite tracer gave the most robust SFR measurements compared to Hα measurements corrected for dust attenuation using the Balmer decrement.
The integrated Hα luminosities for the sample have been taken from the literature (mostly from Moustakas & Kennicutt 2006; Kennicutt et al. 2008, 2009), and are listed in Table 4. Care has been taken in providing Hα luminosities corrected for underlying stellar absorption, for N ii line contamination and foreground Galactic extinction. The same extinction curve was used to correct our sources for foreground Galactic extinction: A(Hα) = 0.6 AB (O’Donnell 1994). The B-band extinction, AB, is taken from the NASA/IPAC Extragalactic Database (NED10) and the measurements of Schlafly & Finkbeiner (2011). For the five galaxies missing either Hα or TIR data, we use the mean of the other SFR estimates. The error on the SFR is derived by taking the standard deviation of all of the SFR estimates when more than one is available, otherwise we use the 20% median error on the SFR in the sample (reported in Table 1).
Lee et al. (2009) cautioned about the use of Hα to derive SFR for galaxies with integrated LHα ≤ 2.5 × 1039 erg s-1 or equivalently SFR ≲ 0.01M⊙ yr-1. Ten galaxies in our sample are below these limits in LHα or SFR. For these very faint galaxies, Hα-SFR will be underestimated, even after correction for dust attenuation (Lee et al. 2009; Meurer et al. 2009). For these ten galaxies, we use the calibration provided by Lee et al. (2009, specifically their Eq. (10)), which converts the non-dust corrected Hα luminosities into dust-corrected SFR, based on the Kennicutt (1998) FUV-SFR. These obtained SFRs are from a calibration assuming a Salpeter IMF (Kennicutt 1998) and we thus convert them into Kroupa IMF-based SFRs using the correction factors tabulated in Table 1 of Kennicutt & Evans (2012). The error on the SFR for these ten galaxies is taken from Table 2 in Lee et al. (2009). The resulting SFRs for these ten galaxies are a factor of 2 larger than the previously estimated SFRs from Hα and TIR. The Hα luminosities and final SFR are given in Table 4, and shown in Fig. 2.
The SFRs in our sample cover four orders of magnitude, with a median SFR of 0.27 M⊙ yr-1 and 0.54 M⊙ yr-1 for the DGS and KINGFISH samples, respectively (see Table 1). We see from Fig. 2 that at a given stellar mass, galaxies with the highest SFRs have the lowest metallicities. This is consistent with the findings of Lara-López et al. (2010), Mannucci et al. (2010), Hunt et al. (2012) on the “fundamental metallicity relation” (FMR) describing the various scaling relations between metallicity, stellar mass, and SFR.
2.6.2. Specific SFR
We also consider the specific SFR, sSFR, i.e. SFR normalised by the stellar mass, to remove scaling effects in our analysis of such a wide variety of environments. The sSFR values are given in Table 4 and plotted as a function of metallicity in Fig. 2.
The median sSFR is one order of magnitude higher in the DGS than in KINGFISH (0.51 Gyr-1 versus 0.04 Gyr-1). In the KINGFISH sample, we distinguish the galaxies according to their nuclear types as defined by Kennicutt et al. (2011): star forming (SF) versus non-thermal emission (AGN). The KINGFISH “AGN” galaxies have the lowest sSFR in Fig. 2, with a median sSFR of 0.01 Gyr-1, versus 0.06 Gyr-1 for the KINGFISH “SF” sample. The stellar masses were estimated on the IRAC 3.6 μm and 4.5 μm flux densities, which might not be appropriate for AGN-type galaxies, possibly overestimating Mstar and thus yielding underestimated sSFR values.
The clear correlation between sSFR and metallicity seen in Fig. 2 follows directly from the FMR. The sSFR can also be interpreted as the amount of star formation occurring today compared to the output of the cumulated past star formation, i.e. the mass of stars already formed, tracing the integrated star formation history. The sSFR value can thus be boosted up by the low stellar mass of the dwarf galaxies even if the present SFR is comparable to that in more metal-rich environments. This is consistent with the so-called “downsizing” effect, i.e. more massive galaxies are more efficient in converting gas into stars than low-mass galaxies (e.g. Sandage 1986; Cowie et al. 1996; Gavazzi & Scodeggio 1996; Boselli et al. 2001; Gavazzi et al. 2002; Brinchmann et al. 2004; Hughes et al. 2013). The less massive galaxies form the bulk of their stellar mass later than more massive systems, and thus undergo a slower metal enrichment. This is consistent with our picture of low-mass, low-metallicity galaxies having a higher sSFR today than their massive metal-rich counterparts.
3. Dust modelling in the DGS and KINGFISH galaxies
In this section, we describe the dust SED model, the parameters, and the derivation of the errors on the best-fit parameters (Sects. 3.1–3.3). In Sect. 3.4, we compare our results with the dust properties derived with a modified black-body model (namely the dust mass and the temperature). In Sects. 3.5 and 3.6, we investigate the effect of a different description for the radiation field and of a different dust composition on the dust properties, respectively. And finally in Sect. 3.7 we show that the 500 μm data point is a necessary constraint to accurately estimate the dust mass and investigate the influence of a potential submm excess.
3.1. Description of the SED model
We adopt the semi-empirical dust SED model presented in Galliano et al. (2011). The model adopts the Galactic grain composition made of silicate grains, carbon grains in the form of graphite, and PAHs. The optical properties are taken from Weingartner & Draine (2001), Laor & Draine (1993) and Draine & Li (2007) respectively. The assumed size distribution is that determined by Zubko et al. (2004) for their BARE-GR-S model, but we allow the relative normalisation of the PAH component to vary for more flexibility. The graphite-to-silicate ratio is kept fixed to the Zubko et al. (2004) value. We assume that the ISRF illuminating the dust grains has the spectral shape of the solar neighbourhood ISRF (Mathis et al. 1983). Only its intensity varies, controlled by the parameter U11. The temperature fluctuations of stochastically heated grains are computed using the transition matrix method (Guhathakurta & Draine 1989).
We assume that the dust properties are uniform, i.e. the size distribution and grain optical properties are constant within the galaxy, and that only the starlight intensity varies. We distribute the mass into different mass elements of uniform illumination with the empirical recommendation from Dale et al. (2001): the distribution of dust mass per starlight intensity can be approximated by a power law of index α, dM/ dU ∝ U− α, with U varying between Umin and Umin+ ΔU. This simply expresses that most of the dust mass should reside in the coldest components, with low starlight intensities U. In most cases, this is flexible enough to reproduce dense and diffuse media, and provides a simple parameterization of the physical conditions in the ISM.
Emission from old stars can also contribute to the IR emission, especially in the NIR. Thus we add a stellar continuum to the dust emission, parameterised by the stellar mass of the galaxy M⋆. This parameter is not designed to estimate the stellar mass, but rather to have a good fit in the NIR (see Galliano et al. 2011, for details).
For each band at a wavelength λi the synthetic luminosity is computed by convolving the model with the spectral response of each band and using the appropriate spectral convention of each instrument. This is done for all of the observational constraints except at SPIRE wavelengths, as the input flux densities are already colour-corrected (see Sect. 2.2).
The fit is performed with the mpcurvefit iterative procedure in idl based on the Levenberg-Marquardt method. This model has been used to model galaxies before by Galametz et al. (2009, 2010, 2011, 2013a), Hony et al. (2010), Meixner et al. (2010), O’Halloran et al. (2010).
3.2. Setting the parameters
The model can be described by six main free parameters:
-
Mdust: the total dust mass,
-
Umin: the minimum of the starlight intensity distribution,
-
ΔU: the difference between the maximum and minimum of the starlight intensity distribution,
-
α: the index of the power law describing the starlight intensity distribution,
-
fPAH: the PAH mass fraction, normalised to the Galactic PAH mass fraction12, and
-
M⋆: the stellar mass.
Units and bounds used for the fitting are described in Galliano et al. (2011). In addition, we vary the mass fraction of very small grains (non-PAH grains with radius a ≤ 10 nm), fvsg, relative to the Galactic value13. It is constrained by the 8−30 μm photometry, plus IRS spectroscopy for the DGS sources, and controls the MIR continuum. We also vary the ionised-to-total PAH mass ratio in the DGS sources, fion, as we have the IRS spectra to constrain this ratio. These two parameters are used to allow for a more flexible and a better fit in the MIR and, in particular, to reproduce the steeply rising continuum of the dwarf galaxies; however, we do not discuss this any further.
 |
Fig. 3 SEDs for a DGS source NGC 4449. The observed SED includes the Herschel data (purple crosses) as well as any available ancillary data (in orange). The different symbols code for the different instruments: Xs for 2MASS bands, stars for Spitzer IRAC and MIPS, diamonds for WISE, and triangles for IRAS. The IRS spectrum is displayed in orange. The total modelled SED in black is the sum of the stellar (green) and dust (red) contributions. The modelled points in the different bands are the filled blue circles. Residuals are shown on the bottom panel. |
From the final best-fit models, we derive the TIR luminosity, LTIR, by integrating the total dust SED between 1 and 1000 μm for each galaxy. We compute the first and second moments of the starlight intensity distribution, ⟨ U ⟩ and (σU)2 as well, corresponding to the mass-averaged starlight intensity and the variance in the starlight intensity distribution, respectively. ⟨ U ⟩ and (σU)2 are given by (see Eqs. (9) to (12) from Galliano et al. 2011)  (1)
(1) (2)where \uav\ can be seen as an indirect measure of the average dust temperature and \sigU\ of the broadness of the FIR peak of the SED.
(2)where \uav\ can be seen as an indirect measure of the average dust temperature and \sigU\ of the broadness of the FIR peak of the SED.
This model is applied to the observed SEDs of DGS and KINGFISH galaxies. An example of fit is given in Fig. 3, the others are shown in Figs. 12 and 13. For four DGS galaxies, there are not enough constraints to properly fit a SED: HS 1236+3937, HS 2352+2733, Tol 0618-402, and UGCA 20. We do not consider KINGFISH galaxies without Herschel detections either: NGC 0584, NGC 1404, DDO 154, and DDO 165. We also remove from the subsequent analysis the three KINGFISH galaxies for which the AGN emission is dominant: NGC 1316, NGC 4725, and NGC 4736 (see Sect. 2.1). Indeed, Ciesla et al. (2015) showed that the emission of an AGN can significantly impact the total IR emission for contribution ≳40%. For the other KINGFISH “AGN” sources, we do not expect the total IR emission to be affected by the AGN contribution on global galaxy scales, and because of the difficulty of accurately constraining low AGN fractions (Ciesla et al. 2015) we do not apply any specific modelling. We have a total of 98 galaxies to which our SED model is applied.
3.2.1. Wavelength coverage
The wavelength coverage is not entirely the same for all of the galaxies. For the DGS galaxies, the observational constraints come from the 2MASS survey and the Spitzer, WISE, IRAS, and Herschel instruments (Sect. 2). For the KINGFISH galaxies, the observational constraints originate from the same instruments (except WISE and Spitzer/IRS). We have complete spectral coverage for 93% of the sources in the 1−5 μm NIR range (five wavelengths14), 87% in the 5−50 μm MIR range (four wavelengths), 90% in the 50−200 μm FIR range (four wavelengths), and 76% in the 200−500 μm submm range (three wavelengths). Ciesla et al. (2014) showed that SPIRE constraints were particularly important to account for the cold dust (see also Sect. 3.7). The 24% of our sample without SPIRE detections are all dwarf galaxies, harbouring particularly warm dust, with a peak of the FIR SED at wavelengths ~30−70 μm, well sampled by constraints until 160 μm. Thus, although heterogeneous, the wavelength coverage achieved in our sample is excellent and we are confident in the parameters derived with these sets of constraints.
When several observations are available at the same wavelength we favour the fluxes obtained with higher resolution data. When IRS constraints are available, we weight the IRS data points for them to contribute equally as the other MIR constraints in the fit. Whenever PAH features are absent from the IRS spectrum, we fix fPAH = 0, and fix fion = 0.5, to reduce the number of free parameters. Some galaxies are not detected at one or several wavelengths, and we impose the best-fit model to be consistent with the upper limits.
3.2.2. Additional features
For 11 DGS galaxies, the observed MIR continuum shape cannot be well reproduced by our model. An example is given in the top panel of Fig. 4 for SBS 1533+574. For these 11 sources, we add to the model an extra modified black-body (modBB) component at MIR wavelengths, with a fixed β = 2.0 and a temperature varying between 80 and 300 K. It can be physically interpreted as a contribution from hot H ii regions to the total emission of the galaxy. As dwarf galaxies have small physical sizes and low dust attenuation, the emission from the energetic H ii regions can indeed affect the total emission from the whole galaxy (da Cunha et al. 2008; Galametz et al. 2010; Hermelo et al. 2013). This is also observed for FIR line emission that is often dominated on galaxy-wide scales by the emission from star-forming regions or diffuse ionised gas in dwarf galaxies (e.g. Cormier et al. 2015). In these cases, the Dale et al. (2001) empirical recipe of dM/ dU ∝ U− α may not be flexible enough to provide a satisfactory fit. Of course, a modBB is not the optimal way of modelling the emission from hot grains in H ii regions (see Galliano et al. 2008; Groves et al. 2008) as these grains are not likely to be in thermal equilibrium, but we adopt this approach as a first approximation.
 |
Fig. 4 SED for SBS1533+574 without (top) and with (bottom) the extra MIR modified black body, shown in yellow. The other colours and the symbols are the same as for Fig. 3. |
This additional component does not significantly impact the total dust mass determination: for each of the 11 cases, dust mass estimates with and without the extra MIR modBB are consistent within errors except for SBS 1533+574. However, in this case the addition of a warm modBB dramatically changes the modelled MIR-to-submm shape of the SED (see Fig. 4). The best-fit MIR modBB temperatures are reported in Table 9. The fits without the MIR modBB are shown in Fig. E.1 for comparison.
Specific modelling was required for five DGS galaxies and is detailed in Appendix E.
 |
Fig. 5 Ratios of the dust masses estimated with a modBB model and with a semi-empirical SED model, MBB/Mdust, for the DGS (crosses) and KINGFISH (downward triangles) samples, as a function of the metallicity. The colour codes the ratio between the dust temperatures estimated from modBB fits and the SED model (assuming TMW = 19.7 K, Planck Collaboration XI 2014, see text for details) TBB/Tdust. |
3.3. Estimating the errors on the best-fit parameters
The errors on the best-fit parameters are estimated by generating 300 random realisations of the observed SEDs within the observational errors, taking special care for errors correlated between different bands (see below). For each galaxy, we perform fits of the 300 random realisations of the SEDs to obtain a distribution for the parameters. Following the method outlined in Rémy-Ruyer et al. (2013), the perturbation to the observed fluxes is the sum of two components:
-
a normal random independent variable representing the measurement errors at each wavelength; and
-
a normal random variable describing the calibration errors that takes the correlation between the wavebands for each instrument (as detailed below) into account.
The errors are taken as the 66.67% confidence level. The best-fit parameters with errors are given in Table 9 for all of the galaxies.
We detail below the decomposition of the calibration errors and eventual correlations between the different bands for all of the instruments, except Herschel as this decomposition has already been presented in Rémy-Ruyer et al. (2013). Taking the correlations in the observational errors into account allows for smaller error bars on the dust parameters.
2MASS:
Jarrett et al. (2003) quote a 2−3% uncertainty on the zero-magnitude flux values. To be conservative, we assume an independent error of 3% in each band.
IRAC:
the total calibration uncertainty used for the DGS and KINGFISH IRAC fluxes is ~10%. This can be decomposed into two parts:
-
Reach et al. (2005) give a 2% uncertainty in all of the IRAC bands. This error is correlated between the four bands.
-
The IRAC Instrument Handbook (Sect. 4.3) also gives a 10% error to account for several systematic effects in the calibration. This error is independent from band to band.
IRS:
the IRS spectra extracted from the CASSIS database provide a decomposition of the total error on the flux densities into three parts:
-
Part of the error is the statistical error on the flux determination, independent for the different wavelengths.
-
Part of the error is systematic and due to the flux difference between the two nod spectra, and is correlated for all of the wavelengths over the SL range on one side and the LL range on the other side.
-
The third component of the error in IRS spectra is the calibration error, and this error is correlated between the two SL and LL modules since the same calibrator star was used for both modules. According to Lebouteiller et al. (2011), the global IRS calibration is better than the 2% level.
MIPS:
for the DGS MIPS photometry, Bendo et al. (2012) used a 4% calibration error at 24 μm (Engelbracht et al. 2007), 10% at 70 μm (Gordon et al. 2007), and 12% at 160 μm (Stansberry et al. 2007). For KINGFISH, the same uncertainties were used by Dale et al. (2007) except for MIPS 70 μm where they adopted a 7% calibration error. According to the MIPS Instrument Handbook, the calibration of the MIPS 160 μm band has been done using the 24 μm and 70 μm observations of asteroids. We can thus consider that the calibration errors for MIPS 24 μm and MIPS 70 μm are both correlated with MIPS 160 μm.
WISE:
WISE calibration has been performed on stars and is tied to Spitzer calibration according to Jarrett et al. (2011). For each wavelength, the correlations between the bands can be summarised this way:
-
The WISE 3.4 μm calibration error is decomposed in an independent part, proper to WISE, of 2.4%, and is correlated with the IRAC 3.6 μm band.
-
Similarly, the WISE 4.6 μm error has an independent part of 2.8% and is correlated with the IRAC 4.5 μm band.
-
The WISE 12 μm error has an independent part of 4.5% and is correlated with the IRS-SL/LL modules.
-
Finally, the WISE 22 μm error has an independent part of 5.7% and is correlated with the MIPS 24 μm band.
IRAS:
according to the IRAS explanatory supplement15, the calibration of IRAS has been tied to the Rieke et al. (1984) ground-based photometric system at 12 μm. The three IRAS bands at 12, 25, and 60 μm have been calibrated using stellar models, and the IRAS 100 μm calibration used asteroids. The relative uncertainties relative to the ground-based 12 μm are 2%, 5%, and 5% for IRAS 12, 25, and 60 μm, respectively; and are independent from band to band. The absolute uncertainty on the 12 μm flux density is 4%, in common and correlated between the three bands. The uncertainty at 100 μm is 10%, and is not correlated with any of the other IRAS bands.
3.4. Comparison with a single modified black body
We conducted a first study of the dust properties in the DGS using a modBB model to describe the dust emission in Rémy-Ruyer et al. (2013). Although very popular in the literature especially when limited data is available, a modBB model assumes a single temperature for the dust grains, and this affects the resulting dust properties. Figure 5 shows the ratios between the dust masses estimated with a modBB model, MBB, and with our semi-empirical SED model, Mdust, for both DGS and KINGFISH samples, as a function of metallicity.
For this comparison, the modBB masses have been updated from Rémy-Ruyer et al. (2013) to be consistent with the updated Herschel data. We also fixed the emissivity index β = 2.0 to be consistent with the effective emissivity index of our dust model. Otherwise, we use the same wavelength range and fitting procedure as in Rémy-Ruyer et al. (2013). The opacity at the reference wavelength, κ(λ0) = 4.5 m2 kg-1 at 100 μm, used to normalise the modBB model is derived from the opacities of the dust composition adopted in the model (Galliano et al. 2011). We find that the modBB model almost systematically underestimates the dust mass compared to a semi-empirical SED model, with a median ratio of 0.48 and ratios sometimes as low as 0.1 (Fig. 5), and that this underestimation does not depend on the metallicity of the source.
We also compare the temperatures derived from a modBB fit, TBB, to the average dust temperatures derived from the SED fits, Tdust. We can estimate Tdust directly by integrating over T = TMW × U1/(4 + β) in Eq. (1), with β = 2.0 for our model. We adopt TMW = 19.7 K from Planck Collaboration XI (2014). We see from the colour coding in Fig. 5 that the more TBB is overestimated compared to Tdust, the more the modBB underestimates the dust mass compared to a more complex dust modelling.
When modelling a galaxy with a broad distribution of equilibrium temperatures, the modBB model tends to average over all temperatures to best fit the peak of the SED. The modBB gets biased towards higher dust temperatures, and thus lower dust masses, as seen in Fig. 5. This also applies, to a smaller extent, in the case where the dust emission is dominated by dust heated by the diffuse ISRF because the two big grain populations (graphite and silicate) do not reach the same equilibrium temperatures.
Other studies have compared dust masses from modBB to those from more complex dust modelling using the Draine & Li (2007) dust SED model (hereafter DL07), and report an underestimation of 10−20% (Magrini et al. 2011; Bianchi 2013). The grain mixture from Zubko et al. (2004) used in our modelling have a slightly different emissivity compared to the DL07 model (i.e. size distribution effect), causing the difference with the results obtained here.
3.5. Influence of the ISRF description
We only describe the starlight intensity distribution with a power-law component only (Dale et al. 2001) and not with an additional diffuse component, as is sometimes done in other studies (Draine et al. 2007; Aniano et al. 2012; Dale et al. 2012). These studies were dedicated to the modelling of metal-rich spirals. Our study is motivated by the modelling of the low-metallicity sources, and adding a diffuse component to the starlight intensity distribution would not be appropriate. Moreover, Galliano et al. (2011) showed on the low-metallicity Large Magellanic Cloud (LMC) that the additional diffuse component was not necessary. Additionally, this diffuse component would add yet another free parameter, which would be difficult to constrain for the few dwarf galaxies not detected beyond 160 μm. We apply this starlight intensity parametrisation to the KINGFIHSH galaxies as well for a consistent and homogeneous modelling approach for the whole sample. Nonetheless, we check that the two descriptions for the starlight intensity distribution (power law only or power law + diffuse) give the same Mdust and ⟨ U ⟩ for the KINGFISH galaxies. We have a median ratio of Mdust(power law+diffuse)/Mdust(power law only) = 1.03 ± 0.15, and ⟨ U ⟩(power law+diffuse)/⟨ U ⟩(power law only) = 1.00 ± 0.12. Given that the average error is 20% on Mdust and 21% on ⟨ U ⟩, we have a good agreement between the two parametrisations of the starlight intensity.
Note that we use the same ISRF for all of the galaxies for consistency, not taking the fact that the ISRF is expected to be harder in low-metallicity galaxies into account (Galliano et al. 2003, 2005; Madden et al. 2006). At fixed energy density, i.e. U, and given that the absorption efficiency, Qabs, is not a strongly varying function of wavelength in the UV/visible regime, the hardness of the radiation field would not greatly impact the emission from the big grains in thermal equilibrium. Under these assumptions, increasing the hardness of the ISRF in dwarf galaxies would only affect the emission spectrum of the stochastically heated grains.
3.6. Influence of the dust composition: amorphous carbons
Several studies suggested that amorphous carbon grains provide a better description of carbonaceous dust in the ISM than graphite. For example, Serra Díaz-Cano & Jones (2008) showed that the erosion of amorphous carbon grains in shocks is more efficient than for graphite grains and matches better the observations of high fractional abundances of carbon in the gas phase of shocked regions. They conclude that even if the carbon dust is in form of graphite when injected in the ISM, it is unlikely that it will remain graphitic as it evolves in the ISM and is subject to erosion or ion irradiation.
We compute another set of dust masses for our sample using amorphous carbons instead of graphite grains in our full SED model, and keeping the same carbon mass budget in the grains. The amorphous carbons optical properties are taken from Zubko et al. (1996) in Galliano et al. (2011). We use exactly the same procedure and options (e.g. additional MIR modBB or not) to be able to directly compare the graphite (noted with [Gr]) and amorphous carbon (noted with [Ac]) dust masses (reported in Table 1).
We find that the amorphous carbon dust masses are about 2.5 times lower than the graphite dust masses. This is because the amorphous carbon dust is more emissive in the submm domain and needs less dust mass to account for the same luminosity. Galliano et al. (2011) showed that this dust composition was better suited for the low-metallicity LMC. However, we do not find any dependence of Mdust[Ac]/Mdust[Gr] on metallicity nor on any other galaxy property. This is because we fixed the dust composition a priori in our models. Regarding the other parameters of the fit, LTIR, σU, and fPAH do not vary significantly between the two dust compositions, while ⟨ U ⟩[Ac]/⟨ U ⟩[Gr] ~ 2.0. At fixed SED shape, i.e. fixed average equilibrium temperature, the radiation field intensity required to heat the amorphous carbon grains is higher as they have a higher emissivity in the submm and absorb more in the UV/visible regime.
In most studies similar to ours where dust SED modelling is used to derive and interpret dust properties (e.g. Draine et al. 2007; Galliano et al. 2008; Galametz et al. 2011; Dale et al. 2012; Cortese et al. 2012a; Ciesla et al. 2014; Rémy-Ruyer et al. 2014), the models mostly use graphite for the carbonaceous component. So to ease the comparison with these various studies, we use Mdust[Gr] in the rest of this paper. As the ratio Mdust[Ac]/Mdust[Gr] is mostly independent of any of the galaxy properties tested here, using Mdust[Ac] instead would systematically shift the trends presented in the following sections without affecting the general conclusions.
3.7. Influence of the wavelength coverage and submm excess
The importance of submm observations longwards of 160 μm has been shown by Gordon et al. (2010), Galametz et al. (2011), Dale et al. (2012), Ciesla et al. (2014). We find that the dust masses estimated without Herschel constraints are overestimated for high-metallicity galaxies (i.e. 12 + log(O/H) ≳ 8.2) and underestimated for lower metallicity galaxies in agreement with the conclusions of the previously mentioned studies.
Excess emission at submm wavelengths (850−870 μm), appearing around 400−500 μm, and presently unaccounted for by the standard dust emission models, has been observed in some low-metallicity systems or low-mass spirals (e.g. Galliano et al. 2003, 2005; Dumke et al. 2004; Bendo et al. 2006; Galametz et al. 2009, 2012, 2014; Zhu et al. 2009; Bot et al. 2010; Grossi et al. 2010, 2015; Dale et al. 2012; Rémy-Ruyer et al. 2013; Ciesla et al. 2014; Gordon et al. 2014). Several hypotheses have been made to explain this excess emission, but so far these remain inconclusive. As the submm excess is not the main focus of this paper, we do not discuss it here. The presence of this submm excess can impact the dust mass, as a large amount of cold dust could be contributing to this submm emission.
We adopt the same definition of the excess as that in Rémy-Ruyer et al. (2013), i.e. an excess is present if the residual at 500 μm is greater than its error bar (1σ criteria). Note that the model used in Rémy-Ruyer et al. (2013), against which the 500 μm emission is compared, is a modBB with a fixed β of 2.0, and that the SPIRE flux densities have been updated to match the latest SPIRE calibration and beam areas for this study (see Sect. 2.2). The findings of Rémy-Ruyer et al. (2013, identification of the galaxies with excess and number of excess sources) are thus not directly comparable to our results.
Eight galaxies exhibit an excess at 500 μm: Haro 11, HS 0052+2536, Mrk 930, NGC 1569, NGC 625, NGC 337, NGC 3049, and NGC 4631. For these eight excess galaxies (except one, NGC 3049) including or omitting the 500 μm point in the fit yields dust mass estimates that are consistent within the errors because the 500 μm excess is quite small (≤1.5σ). However, omitting the 500 μm point in the fit for the entire sample leads to underestimated dust masses (by a factor 2 to 4) for 15% of the 78 galaxies detected at 500 μm because part of the coldest component of the dust is not fully taken into account.
For the purpose of our study, we thus need to include the 500 μm point in the model to get an accurate estimation of the dust mass, and this estimation is not biased for the eight sources with this small submm excess at 500 μm.
4. Dust properties
In this section, we scrutinise the dust properties derived from our realistic dust modelling over the whole IR wavelength range, and present results for Mdust16, LTIR, fPAH, ⟨ U ⟩ and σU. The median error on each parameter along with the spanned range of values and the median values are shown in Table 1 for both samples.
For each parameter, we examine the relation with metallicity expressed as 12 + log(O/H), the star formation activity traced by the sSFR, estimated in Sect. 2.6.2, and the stellar mass Mstar. For simplicity in the notations, we use Z for 12 + log(O/H), even if Z is not strictly equivalent to the oxygen abundance.
We compute Spearman rank correlation coefficients17 for every pair of parameters and present them in Table 2 to determine the most significant relations to investigate. For the 98 galaxies, we determine that the correlation (or anti-correlation) is significant if | ρ | > 0.37 at a significance level of 0.01% (i.e. the probability that the two variables are motonically correlated is greater than 99.99%).
Dust properties: correlations from Spearman rank coefficients.
4.1. Dust mass
The dust masses in our sample cover a range of more than five orders of magnitude. The median value is 4.4 × 105M⊙ for the DGS sample and 1.9 × 107M⊙ for the KINGFISH sample, about two orders of magnitude above the median dust mass for the DGS, in agreement with the findings of Rémy-Ruyer et al. (2013).
The median error on the dust mass is ~20% (Table 1). This error only takes the uncertainties in the observations into account. No systematic modelling uncertainty is included due to the difficulty of determining it. However, with the different tests performed in Sects. 3.4, 3.6, and 3.7 where we changed the model, the dust composition or the submm wavelength coverage, we can say that we have a conservative systematic modelling uncertainty of a factor 2 to 3 on the dust mass estimate.
As seen in Table 2, the stellar mass gives the strongest correlation with the dust mass (ρ(Mdust, Mstar) = 0.92), and not the metallicity: ρ(Mdust, Z) = 0.78. The correlation between stellar mass and metallicity is also stronger than between dust mass and metallicity, ρ(Mstar, Z) = 0.84. This holds whether we consider the full sample, only low-metallicity sources or only metal-rich sources. This simply expresses a scaling effect in which a more massive galaxy also contains more dust (see also Ciesla et al. 2014). The correlation between the dust mass and metallicity is thus a direct consequence of the mass-metallicity relation (Tremonti et al. 2004). This is illustrated in Fig. 6. The best-fit relation gives:  (3)with a dispersion of 0.74 dex from the relation.
(3)with a dispersion of 0.74 dex from the relation.
 |
Fig. 6 Dust masses (top), TIR luminosities (bottom) for the DGS (crosses), and KINGFISH (downward triangles) samples as a function of metallicity, colour coded with Mstar. The best power-law fit is indicated with a black line, and the 1σ dispersion is indicated with dotted lines for the two panels. The distribution of each parameter is indicated on the side of each panel for both samples: solid line for DGS and dashed line for KINGFISH. |
4.2. Total infrared luminosity
4.2.1. Estimating LTIR
Several definitions exist to derive LTIR. We chose to estimate LTIR by integrating the best-fit modelled dust SED, LTIR [SED], (i.e. not including the stellar continuum) between 1 and 1000 μm. Some studies use [8–1100] μm or [3–1100] μm intervals for the integration, but using any of the two other intervals gives equivalent results (see Table 3).
ComparingLFIR and LTIR: we also compare the FIR luminosities, LFIR over the interval [50−650] μm used in Rémy-Ruyer et al. (2013), with LTIR. We find that the LFIR accounts for about 65 ± 13% of the TIR luminosity, and gets lower as the peak of the SED broadens (ρ(LFIR/LTIR, σU)=−0.83). As the peak of the dust SED shifts to shorter wavelengths and broadens, the [50−650] μm FIR interval no longer captures the bulk of the emitted dust luminosity. For very broad SEDs, we can miss up to 70% of the TIR luminosity. The most extreme case is SBS 0335-052 where LFIR/LTIR = 10%, a consequence of its very peculiar SED peaking around 30 μm.
LTIR comparisons.
Prescriptions for the DGS: Galametz et al. (2013b) explored various LTIR calibrations from Spitzer and Herschel bands, using the KINGFISH sample. We test all of the possible relations with 24, 70, 100, and 160 μm, and look at the ratio of the estimated LTIR over the LTIR derived from our best-fit SED18 to determine which relations are the most appropriate for the DGS sample.
We find that for the DGS galaxies, the best monochromatic relation is using 70 μm with a median ratio of 1.13 ± 0.29 (Table 3). Using 70 μm tends to overestimate the LTIR for the DGS, while using 100 μm tends to underestimate the LTIR (Table 3). This is due to the higher F70/F100 colour in dwarf galaxies than in more-metal rich galaxies over which these relations have been calibrated. The best relation using two bands is with 24 and 160 μm. Increasing the number of bands gives similar results, with decreasing scatter. The smallest dispersion using three bands is achieved by combining 24, 70, and 160 μm. Thus, to estimate LTIR for galaxies with similar metallicity and star formation activity, we recommend using the 70 μm, the 24–160 μm, or the 24−70–160 μm calibration depending on the number of available constraints.
Pre-Herschel estimates of the LTIR derived with Spitzer fluxes and the Dale & Helou (2002) formula (LTIR [pre−Herschel]) from Madden et al. (2013) and Kennicutt et al. (2011) are consistent with the LTIR derived here. All of these LTIR comparisons are summarised in Table 3, and show that the TIR luminosity is quite a robust parameter.
4.2.2. LTIR and metallicity
LTIR is presented in Fig. 6 (bottom panel) as a function of metallicity. The LTIR in both samples cover five orders of magnitude, and the low-metallicity dwarf galaxies are about 6.5 times less luminous in the IR than the more metal-rich environments. As for the dust mass, LTIR is strongly correlated with the stellar mass, ρ(LTIR, Mstar) = 0.87, due to scaling effects. The correlation between LTIR and metallicity (ρ(LTIR, Z) = 0.64) is also a consequence of the mass-metallicity relation. As seen in Fig. 6, the relation of LTIR with metallicity is more dispersed than between the dust mass and the metallicity. The best-fit relation gives 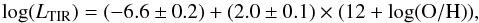 (4)with a dispersion of 0.79 dex from the relation. From the construction of the model, LTIR is directly linked to the product Mdust×⟨ U ⟩ at first order. And while Mdust is correlated with metallicity, ⟨ U ⟩ is anti-correlated with metallicity, which results in a flattened correlation with larger scatter between LTIR and metallicity. LTIR is not correlated with ⟨ U ⟩ (ρ(⟨ U ⟩, LTIR)=−0.05), indicating that the amount of dust primarily drives the luminosity.
(4)with a dispersion of 0.79 dex from the relation. From the construction of the model, LTIR is directly linked to the product Mdust×⟨ U ⟩ at first order. And while Mdust is correlated with metallicity, ⟨ U ⟩ is anti-correlated with metallicity, which results in a flattened correlation with larger scatter between LTIR and metallicity. LTIR is not correlated with ⟨ U ⟩ (ρ(⟨ U ⟩, LTIR)=−0.05), indicating that the amount of dust primarily drives the luminosity.
4.3. PAHs
 |
Fig. 7 The PAH mass fractions for the DGS (purple crosses) and KINGFISH (orange downward triangles) samples as a function of metallicity (left panel) and sSFR (right panel). The parameter fPAH is expressed in units of fPAH⊙, with fPAH⊙ = 4.57%. The distribution of fPAH is indicated on the side for both samples: plain purple line for DGS galaxies and dashed orange line for the KINGFISH sample. In each panel, the best power-law fit is indicated as a solid line, together with the 1σ dispersion as dotted lines. |
Lower PAH abundances in low-metallicity systems than in more metal-rich galaxies have previously been observed (e.g. Madden 2000; Boselli et al. 2004; Engelbracht et al. 2005; Wu et al. 2006; O’Halloran et al. 2006; Draine et al. 2007; Smith et al. 2007b; Gordon et al. 2008; Galliano et al. 2008; Wu et al. 2011; Ciesla et al. 2014). From our model, we obtain an estimate of the mass fraction of PAHs for our sources, including the 19 low-metallicity galaxies with new IRAC and IRS data. We have an average error of 17% on fPAH, and a very good agreement between our fPAH to the PAH mass fraction derived by Dale et al. (2012) for the KINGFISH sample using the Draine & Li (2007) model (median ratio of 1.03 ± 0.24). For the DGS galaxies with featureless IRS continuum, we fit the model to the observations again, leaving fPAH free, and use this value as an upper limit, reported in Table 9.
In our sample, the mass fraction of PAHs covers two orders of magnitude, and are detected over 1.1 dex in metallicity down to ~0.08 Z⊙, expanding the range explored by previous works. From Table 2, fPAH correlates very well with sSFR and metallicity (ρ(fPAH, SFR) = −0.77, and ρ(fPAH, Z) = 0.67, not including the upper limits), with a PAH mass fraction decreasing with decreasing metallicity and increasing sSFR, confirming results from the previously mentioned studies. This is shown in Fig. 7. The best-fit relations of fPAH with metallicity and sSFR yield ![\begin{equation} \left \{ \begin{array}{lcl} {\rm log}(f_{{\rm PAH}}) & = & (-11.0 \pm 0.3) + (1.30 \pm 0.04) \\[1mm] && \times\, (12+{\rm log(O/H)}) \\[2mm] {\rm log}(f_{{\rm PAH}}) & = & (-5.5 \pm 0.1) - (0.53 \pm 0.01) \\[1mm] && \times \,{\rm log}({\rm s}{\it SFR}) \end{array} \right ., \end{equation}](/articles/aa/full_html/2015/10/aa26067-15/aa26067-15-eq103.png) (5)with a dispersion of 0.35 dex around the relation with metallicity, and of 0.38 dex around the relation with sSFR.
(5)with a dispersion of 0.35 dex around the relation with metallicity, and of 0.38 dex around the relation with sSFR.
The lower abundance of PAHs in dwarf galaxies is not controlled by a single parameter, but rather arises from a joint effect of both low metallicity and high sSFR. The higher sSFR results in a harder and more intense galaxy-wide ISRF. Combined with the lower dust attenuation, PAHs are efficiently destroyed by hard UV photons and by shocks and cosmic rays (e.g. Madden et al. 2006; Engelbracht et al. 2008; Micelotta et al. 2011). Because of the small physical size of dwarf galaxies, PAHs are also subject to destruction by SN shock waves on galaxy-wide scales (O’Halloran et al. 2006; Micelotta et al. 2010). In addition, lower C/O ratios in dwarf galaxies (Garnett et al. 1995, 1999) mean that less material is available in the ISM to form the PAHs than to form the oxygen-rich silicate grains, which make the bulk of the dust mass. The deficiency of PAHs in low-metallicity galaxies can also be explained by the delayed injection of carbon dust into the ISM by AGB stars (Galliano et al. 2008).
4.4. Temperature distribution
Rémy-Ruyer et al. (2013) showed that dwarf galaxies harbour warmer dust and present a potentially broad dust SED peak. Warmer dust in dwarf galaxies had been discovered first with IRAS (e.g. Helou 1986; Hunter et al. 1989; Melisse & Israel 1994; Galliano et al. 2003), and this was confirmed later with Spitzer (e.g. Galliano et al. 2005; Rosenberg et al. 2006; Cannon et al. 2006; Galametz et al. 2009). More recent studies have confirmed that low-mass galaxies have broader IR SED peaks (e.g. Boselli et al. 2012; Smith et al. 2012a; Ciesla et al. 2014), or show a flattening of their FIR SED slope compared to more massive systems (Boselli et al. 2010; Cortese et al. 2014). These studies also showed that the most actively star-forming galaxies were those with the warmest dust and the broadest SED peak (Boselli et al. 2010; Ciesla et al. 2014).
 |
Fig. 8 Example of different SED shapes, with increasing broadness around the FIR peak for increasing σU. NGC 0628, NGC 1140, and SBS 1415+437 have log(σU/U⊙) = 0.4, 2.1, and 3.0, respectively. The location of these three galaxies is indicated in Fig. 9. |
 |
Fig. 9 Average starlight intensity ⟨ U ⟩ and σU for the DGS (crosses) and KINGFISH samples. For the KINGFISH sample, we distinguish the sources that have been classified as star forming (SF, downward triangles) or as AGN (stars) by Kennicutt et al. (2011). The average dust equilibrium temperature is shown on the top axis. The colour codes the sSFR of the sources, in units of Gyr-1. We indicate the location of the two most metal-poor galaxies, I Zw 18 and SBS 0335-052, and of the three galaxies of Fig. 8. |
A temperature distribution is necessary to properly describe the dust emission (Sect. 3.4), and this dust temperature distribution is directly linked to the range of starlight intensities, ΔU, to which the dust is exposed. However, to avoid being affected by potential degeneracies between the starlight intensity distribution parameters (ΔU, Umin and α), we consider the standard deviation of the starlight intensity distribution, σU, to describe the range of starlight intensities to which the dust is exposed. Figure 8 illustrates how σU traces the width of the SED peak on three examples. Figure 9 shows the range of starlight intensities to which the dust is exposed, σU, as a function of the average starlight intensity ⟨ U ⟩.
As explained in Sect. 3.2, we added a MIR modBB to get a better match to the observed MIR SED for 11 galaxies. We add a delta function describing this additional single temperature component to the U distribution in Eqs. (1) and (2): δ(U − UMIR,BB), with UMIR,BB = (TMIR,BB/TMW)6. ⟨ U ⟩ covers a range of four orders of magnitude equivalent to ~50 K in dust temperature, from 12 K to 64 K in the DGS; and from 12 K to 30 K in the KINGFISH sample. The median Tdust is 26 K for the DGS and 20 K for the KINGFISH sample, consistent with low-metallicity galaxies harbouring warmer dust than more metal-rich environments (Rémy-Ruyer et al. 2013). The median σU is 290 U⊙ for the DGS and 4 U⊙ for the KINGFISH sample, reflecting the broader SED peak for low-metallicity environments compared to more metal-rich sources.
Both ⟨ U ⟩ and σU strongly correlates with sSFR (Table 2), although the correlation is stronger with σU. The correlation of both parameters with metallicity is weaker than with sSFR (ρ(Z, σU) = −0.52, ρ(Z, ⟨ U ⟩) = −0.47), and is a side effect of the strong correlation between sSFR and metallicity (ρ(Z, SFR) = −0.78). This holds whether we consider the full sample or low-metallicity sources on one side and metal-rich sources on the other side. The sSFR thus seems to be the parameter driving the dust SED shape.
In Fig. 9, we clearly distinguish two clusters of points, one in the lower left corner of the plot, mostly metal-rich KINGFISH galaxies, with low ⟨ U ⟩ and low σU (“cold and narrow” SEDs), and one mainly composed of low-metallicity galaxies, with higher ⟨ U ⟩ and σU (“hot and broad” SEDs). However some high-metallicity sources can be found in the “hot and broad” group, and vice versa. This is due to their higher (or lower) sSFR as shown by the colours on Fig. 9. For example, the spiral galaxy NGC 0628 has the same metallicity as the star-forming dwarf galaxy NGC 1140 (Z = 0.5Z⊙), but very different SED shapes (Fig. 8) because of their different star formation activity: log(sSFR/Gyr-1) = −1.4 for NGC 0628 and −0.8 for NGC 1140. This confirms that the sSFR is the parameter determining the dust SED shape, and that metallicity only plays a secondary role as also noted by da Cunha et al. (2008), Smith et al. (2012a). Low-metallicity sources extend the trend outlined by metal-rich galaxies to warmer temperatures and broader temperature distributions because of their higher star formation activity in a smooth transition rather than in a sharp change. This has been noted by Cortese et al. (2014) in a narrower range of metallicities (0.6 dex).
In more active galaxies, the dust spans a wider temperature range translating into a broader dust SED peak. In a galaxy undergoing an active phase of star formation (e.g. with high sSFR), the ISM will be clumpier as a large number of embedded star-forming clumps are spread all over the galaxy. This clumpier ISM allows for a wider equilibrium temperature distribution of the dust grains, skewed towards higher dust temperatures (and thus higher σU and ⟨ U ⟩). Evidence for this clumpier structure of the ISM in dwarf galaxies can be directly seen from the resolved UV-to-mm observations of the LMC and SMC, and has also been suggested by Cormier et al. (2015) from a detailed study of the DGS FIR fine-structure cooling lines. This irregular ISM structure due to feedback processes related to star formation and supernovae events, results in an ISM in which the dust grains are exposed to a range of stellar populations and thus shows a larger distribution of dust temperatures. The dwarf galaxies in our sample contain warmer dust primarily because they are intensively forming stars. Metallicity has a secondary impact on the dust temperature, as the low dust attenuation enables the dust to heat deeper within the molecular clouds.
In Fig. 9 we have also split the KINGFISH sample into the “SF” and “low-luminosity AGN” groups. The warmest KINGFISH galaxies (i.e. with high ⟨ U ⟩) are mostly the KINGFISH low-luminosity AGNs. It might be possible that, despite a small contribution to the total luminosity, the emission from the central AGN is powerful enough to impact the dust heating on global galaxy scales and to increase the average dust temperature, thus to have an impact on the global shape of the dust SED. Warmer dust in the presence of an AGN has already been seen in Kirkpatrick et al. (2012).
5. Towards a comprehensive view of the dust properties in low-metallicity environments
After studying the different relationships between the dust properties and fundamental galaxy parameters, we now analyse our results in the context of galaxy evolution and attempt to draw a consistent picture of the dust in low-metallicity environments.
 |
Fig. 10 Schematic view of the various correlations between parameters in the DGS and KINGFISH samples. The numbers on the lines are the Spearman correlation coefficients reported from Table 2. The solid lines indicate the dominating correlations between parameters and the dashed lines indicate several secondary correlations of interest. |
 |
Fig. 11 Dust-to-stellar mass ratios for the DGS (crosses) and KINGFISH (downwards triangles) samples as a function of sSFR, colour coded by the gas-to-dust mass ratio (G/D), Mgas/Mdust, from Rémy-Ruyer et al. (2014). The distribution of Mdust/Mstar is indicated on the side for both samples: solid line for DGS and dashed line for KINGFISH. Modelled evolutionary tracks from Asano et al. (2013) are shown, for different star formation timescales (τSF = 0.5, 5 and 50 Gyr), with the red, blue, and purple lines. |
The most famous picture of galaxy evolution is the widely studied mass-metallicity relation. The ISM matter life cycle implies that the metallicity of a galaxy increases as the galaxy evolves through several cycles of star formation, building up its stellar mass (Lequeux et al. 1979; Tremonti et al. 2004; Kirby et al. 2013; Cook et al. 2014; Gonçalves et al. 2014). We saw that the mass-metallicity relation drives all of the extensive quantities, Mdust and LTIR, while the intensive quantities fPAH, ⟨ U ⟩ and σU, are mostly driven by sSFR. This is shown schematically in Fig. 10. From this figure, it is clear that metallicity only plays a secondary role in shaping the dust properties. Our sample, however, is dominated at high metallicities by spiral galaxies and by star-forming, gas-rich dwarf galaxies at low metallicities. The correlations presented here thus may suffer from some selection bias. The dust-to-stellar mass ratio is a normalised (and thus intensive) quantity that enables us to look at the dust mass build up with respect to the stellar mass. Figure 11 shows the dust-to-stellar mass ratios for our sample as a function of sSFR.
The dust-to-stellar mass ratio has been extensively studied previously (e.g. da Cunha et al. 2010; Skibba et al. 2011; Bourne et al. 2012; Cortese et al. 2012b; Smith et al. 2012c). These studies have shown that the dust-to-stellar mass ratio decreases for increasing stellar mass (or metallicity) and decreasing sSFR. We do not find any correlation for the dust-to-stellar mass ratio with metallicity, stellar mass, or sSFR. Considering each sample separately, however, we find a rather weak correlation between the dust-to-stellar mass ratio and metallicity (ρ(Mdust/Mstar, Z) = −0.44) or sSFR (ρ(Mdust/Mstar, sSFR) = 0.47) for the KINGFISH sample, and still no correlations for the DGS sources: ρ(Mdust/Mstar, Z) = 0.18 and ρ(Mdust/Mstar, sSFR) = −0.04. Thus the results for the metal-rich KINGFISH galaxies are in agreement with the findings of the previously mentioned studies. However, the low-metallicity sample does not extend the observed behaviour of the metal-rich galaxies to higher sSFR.
The peculiar behaviour of the dust-to-stellar mass ratios for the low-metallicity DGS galaxies is due to their chemical evolutionary stage. This can be traced by the gas-to-dust-mass ratio (G/D, Rémy-Ruyer et al. 2014), and is shown in colour in Fig. 11. Modelled evolutionary tracks from the chemical evolution model of Asano et al. (2013) are also shown, for different star formation timescales (τSF = 0.5, 5 and 50 Gyr), in Fig. 11. This chemical evolution model, based on models from Hirashita (1999), Inoue (2011), includes dust production by stellar sources (AGB stars and Type II SNe) and by dust growth processes in the ISM. Dust is destroyed by SN shocks. Rémy-Ruyer et al. (2014) showed that this model can successfully reproduce the observed trend between G/D and metallicity, thanks to the dust growth mechanism.
At high sSFR, thus low-metallicity and low stellar masses, the dust content is very low, giving very low Mdust/Mstar and high G/D. The dust production at low metallicity is only controlled by stellar sources. Then when a critical metallicity is reached in the ISM, dust growth by metal accretion on the dust grains in the ISM becomes the major process for building up the dust mass (Asano et al. 2013; Zhukovska 2014), and the dust mass rapidly increases without significant consumption of the gas reservoir or star formation. This rapid increase of the dust mass results in an increase of the dust-to-stellar mass ratio and a decrease of the G/D (Rémy-Ruyer et al. 2014). Thus the large scatter in the dust-to-stellar mass ratio for the highly star-forming galaxies in Fig. 11 is due to their different evolutionary stage, as traced by their G/D. Then dust growth processes saturate when all the available metals are locked up in the grains. In the meantime, star formation continues, consuming the gas reservoir and increasing the stellar mass. This results in a decreasing sSFR, decreasing dust-to-stellar mass ratio and decreasing G/D.
The nucleus type (star forming or AGN) also has an impact in shaping the dust properties (Fritz et al. 2006; Magdis et al. 2014; Ciesla et al. 2015), meaning that the picture drawn from Figs. 10 and 11 is far from being that simple. Metallicity and sSFR are not the only parameters involved in the evolution of the dust properties in galaxies. All of these fundamental parameters can also be affected by inflows and outflows, rendering in practice the relations between stellar mass, star formation, metallicity and dust properties more complex, and can significantly change the position of a galaxy in the Mdust/Mstar– sSFR plot.
Moreover, the dust masses are estimated here with the same dust mixture, using silicates, graphite, and PAH grains, for all of the galaxies, however, amorphous carbon grains could be used instead of graphite grains to model the carbonaceous dust (Galliano et al. 2011; Galametz et al. 2013a; Jones et al. 2013, and see Sect. 3.6). The silicate grain properties used in our model are derived from empirically-normalised astrophysical data, and more realistic types of silicate grains could also be used (Köhler et al. 2014). Changing the dust composition results in different dust properties, e.g. the dust mass or dust temperature as we saw with amorphous carbons in Sect. 3.6. The dust composition can also vary from galaxy to galaxy, which would in turn impact the derived dust masses and observed trends. Thanks to the wealth of spatially resolved dust studies with Herschel, we know now that the dust composition and size distribution also vary within each galaxy (Smith et al. 2012b; Galametz et al. 2012; Mattsson et al. 2014b; Viaene et al. 2014; Ysard et al. 2015). Dust evolves from diffuse to denser regions where bigger grains or aggregates can eventually form (Köhler et al. 2015), thus impacting the SED shape and dust parameters. Studying the impact of a varying dust composition and grain size distribution within and between galaxies on the SED and the derived dust properties is the next step.
6. Conclusion
In this paper, we provided a coherent picture of the evolution of the dust properties from metal-poor to metal-rich environments. Our sample comprises 109 galaxies, spanning almost 2 dex in metallicity, dominated by spiral galaxies at high metallicities and by star-forming, gas-rich dwarf galaxies at low metallicities. Observed SEDs are gathered over the whole IR-to-submm wavelength range, with constraints from 2MASS, Spitzer, WISE, IRAS, and Herschel. The full data set is presented here for the DGS sample of dwarf galaxies. The dust properties (namely, dust mass, TIR luminosity, PAH mass fraction, and dust temperature distribution) are derived in a systematic way using a realistic semi-empirical dust SED model from Galliano et al. (2011), and then compared to fundamental galaxy parameters: stellar mass, metallicity, and sSFR for a final sample of 98 galaxies.
The dust mass is a critical parameter for constraining chemical evolution models. We showed here that different model assumptions could greatly impact the estimated dust mass. A single-temperature modBB model underestimates the dust mass by a factor of 2 compared to a semi-empirical SED model, even with careful matching of the effective optical properties in the modBB. The modBB model overestimates the effective average dust temperature, thus leading to the underestimation of the dust mass, as also shown by Bendo et al. (2015). Changing the carbonaceous component in the dust mixture from graphite grains to amorphous carbon grains results in a decrease of the dust mass estimate by a factor 2.5. Amorphous carbon grains are more emissive than graphite grains, so less dust is needed to account for the same luminosity.
We find an excess at 500 μm for eight galaxies in our sample. The excess is rather small (≤1.5σ) as the transition from thermal dust and submm excess emission observed at longer wavelengths occurs around 500 μm. Including the 500 μm point during the fitting procedure does not result in a drastic overestimation of the dust mass for the excess galaxies. However, leaving the 500 μm data point out of the fit results in an underestimation of the dust mass by a factor 2 to 4 for 15% of the galaxies in our sample because the cold dust component is then not properly constrained. Estimating dust masses is thus subject to non-negligible systematic modelling uncertainties.
We present various ways of estimating LTIR in the DGS sample with mono/polychromatic indicators, using the calibrations presented in Galametz et al. (2013b). For galaxies with similar metallicity and star formation activity, we recommend using the 70, 24–160, or 24−70–160 calibrations of Galametz et al. (2013b).
The dust temperature distribution and PAH mass fraction are primarily driven by the sSFR, with a second order effect from metallicity. In our sample, PAHs are detected down to Z ~ 1/12 Z⊙. Low PAH abundances in dwarf galaxies are a consequence of the high star formation activity and low dust attenuation. This combined effect of sSFR and metallicity is also responsible for the higher average dust temperatures in starbursting low-metallicity dwarf galaxies. We find a median dust temperature (derived from the average starlight intensity ⟨ U ⟩) for the DGS sample of ~26 K, and ~20 K in KINGFISH galaxies. The higher star formation activity results in a clumpier ISM, allowing for a larger range of dust equilibrium temperatures.
The extensive dust properties, Mdust and LTIR, are driven by the mass-metallicity relation, reflecting a scaling effect: the more massive galaxies contain more dust, are more luminous, and are also more metal-rich. However, the dust mass build up with respect to stellar content is not the same in highly star-forming, low-metallicity sources as in more metal rich systems. The dust-to-stellar mass ratios of metal-rich sources follow an increasing trend of Mdust/Mstar with sSFR, previously observed on other samples (da Cunha et al. 2010; Skibba et al. 2011; Cortese et al. 2012b). On the other hand, for the more actively star-forming galaxies (sSFR> 0.1 Gyr-1), the trend is far less clear, with increasing scatter. The peculiar behaviour of the low-metallicity sources is driven by their chemical evolutionary stage: at low metallicity and high star formation activity, the dust production is only dominated by stellar sources. After a critical metallicity is reached, the dust-to-stellar mass ratio rapidly increases because dust growth processes in the ISM dominate the dust production. Then dust growth saturates while star formation goes on, forming stars from the gas reservoir, resulting in a decreasing sSFR and Mdust/Mstar. This completes and confirms our results on the gas-to-dust mass ratios derived in Rémy-Ruyer et al. (2014). Others effects, such as inflows or outflows, presence of an AGN, or varying dust composition between and within galaxies have not been considered here but can also affect our picture of the evolution of the dust properties in galaxies.
Online material
 |
Fig. 12 DGS SEDs: the observed SEDs include the Herschel data (purple crosses) as well as any available ancillary data (in orange). The different symbols refer to the different instruments: Xs for 2MASS bands, stars for Spitzer IRAC and MIPS, diamonds for WISE, and triangles for IRAS. The IRS spectrum is shown in orange. The total modelled SED in black is the sum of the stellar (green) and dust (red) contributions, and eventually of the modified black-body contribution (yellow). The modelled points in the different bands are the filled blue circles. |
 |
Fig. 12 continued. |
 |
Fig. 12 continued. |
 |
Fig. 13 continued. |
 |
Fig. 13 continued. |
DGS and KINGFISH stellar mass and star-formation parameters.
Updated Herschel flux densities for the DGS sample.
Spitzer IRAC flux densities for the DGS sample.
WISE flux densities for the DGS sample.
2MASS and IRAS flux densities from the literature for the DGS sample.
DGS and KINGFISH dust parameters.
Appendix A: Update of the Herschel data
Appendix A.1: PACS
In Rémy-Ruyer et al. (2013), the PACS data for the DGS galaxies were processed either with PhotProject (provided by HIPE) for point sources or with Scanamorphos (version 14, Roussel 2013) for extended sources. The update of Scanamorphos to version 23 implies a significant update on the red band at 160 μm because the PACS distortion flat-field is now taken into account. This effect was already included in PhotProject. For the DGS data, the Scanamorphos maps are thus reprocessed with v23 of the algorithm for the three PACS bands for consistency. The photometry is done with the same method as in Rémy-Ruyer et al. (2013), and using the exact same apertures. There are three changes to note:
-
NGC 1705 – The v14 maps of Scanamorphos for this galaxy presented a non-uniform background, which compelled us to choose the PhotProject maps in Rémy-Ruyer et al. (2013, see note f in their Table 2). This has been corrected in the new version of the maps and so we now consider the Scanamorphos maps for this galaxy.
-
UGC 4483 – The new Scanamorphos maps now manage to do a better job reconstructing the emission for this galaxy at 160 μm, yielding a strong detection (9σ) in the new map. Moreover, this detection at 160 μm is more coherent with the rest of the FIR/submm photometry (detection at 250 μm by SPIRE). So we now consider the Scanamorphos maps for this galaxy and not the PhotProject maps as in Rémy-Ruyer et al. (2013).
-
UM 133 – For this galaxy Rémy-Ruyer et al. (2013) noted that the 70 μm flux density might present some discrepancies with others FIR measurements. Using PhotProject maps instead of Scanamorphos maps yields a 70 μm flux density, which is more consistent with the FIR shape of the SED. So we now consider the PhotProject maps for this galaxy.
The new flux densities for the DGS are presented in Table 5. For the KINGFISH PACS data, we applied a corrective factor of 0.925 to the 160 μm flux densities of Dale et al. (2012; H. Roussel, priv. comm.).
Appendix A.2: SPIRE
There have been two different updates for the SPIRE data: the calibration and the beam model used to compute the beam areas19.
The SPIRE maps for the DGS have been reprocessed with HIPE v12, as in Rémy-Ruyer et al. (2013). We apply the same method as in Rémy-Ruyer et al. (2013) to redo the photometry on the new data, depending whether the source is extended or point-like. For the extended sources, there are two steps to apply before performing aperture photometry: convert the data from point-source calibration to extended-source calibration, via the KPtoE factor20, and convert the data from Jy/beam to Jy/pix, using the beam area. The applied values for the KPtoE factor, given the SPIRE Data Reduction Guide21, are 0.99858, 1.00151, and 0.99933 at 250, 350, and 500 μm, respectively. For the “slightly extended” sources (see Rémy-Ruyer et al. 2013), we do not apply this KPtoE factor. The beam areas depend on the spectral shape of the considered source, which means that the beam areas will be different for each galaxy. To produce the final maps, the SPIRE pipeline assumes a spectral shape with a dependence Fν ∝ ν-1, which corresponds to beam areas of 465, 823, and 1769 arcsec2 at 250 μm, 350 μm, and 500 μm, respectively. These are the beam areas we used for the second step (identical to those used in Rémy-Ruyer et al. 2013) before performing aperture photometry.
To account for the different FIR spectral shapes and thus beam areas, we need to apply a colour correction factor. The colour correction factors, Kcol, have been tabulated in the SPIRE Data Reduction Guide for spectral shapes with Fν ∝ να. For point sources and extended sources, the Kcol are given in Table 6.13 of the SPIRE Data Reduction Guide. For slightly extended sources, we use the point source colour correction times the effective beam area ratios tabulated in Table 6.8 of the SPIRE Data Reduction Guide. Note that this effective beam area ratio is already taken into account in the colour correction for extended sources. The method we use to colour correct our flux densities is the following: we fit a line in logarithmic space to the three SPIRE flux densities to find the spectral slope α. We include PACS 160 μm data if there are some SPIRE non-detections. Once α is determined, we apply the corresponding colour correction factors to the flux densities. We iterate these few steps until α does not vary by more than 0.1%. Usually two iterations are enough.
In Table 5, we give the updated fluxes densities before the colour correction step. On the other hand, the colour-corrected flux densities are those used in the fitting procedure. The colour corrections are of the order of 6%, 4%, and 4% at 250 μm, 350 μm, and 500 μm, respectively, for the DGS.
The SPIRE maps of Dale et al. (2012) for the KINGFISH sample were reduced with HIPE v5, and aperture photometry was performed on the maps to extract the flux densities. Since then, there have been two updates of the calibration with the releases of v7 and v11 of HIPE. To account for the update at v7, we multiply the flux densities from Dale et al. (2012) by 1.0, 1.0067, and 1.022 at 250, 350, and 500 μm respectively. To account for v11 update, we multiply the flux densities by 1.0253, 1.0250, and 1.012522 at 250, 350, and 500 μm, respectively. No KPtoE factor had previously been applied to the flux densities (D. Dale, priv. comm.). Assuming that the KINGFISH sources are all extended, we also apply the KPtoE factor to all of the galaxies. We also convert the fluxes to match the beam areas mentioned previously (465, 823 and 1769 arcsec2). Then these updated flux densities are colour corrected following the method described for the DGS galaxies above. The colour corrections are of the order of ~5% for the three SPIRE wavelengths for the KINGFISH galaxies.
Appendix B: DGS IRAC and IRS observing Logs
DGS Spitzer/IRAC and IRS observing Log.
Appendix C: Quality checks for IRAC and WISE DGS photometry
Appendix C.1: IRAC: Comparison to previous literature measurements
 |
Fig. C.1 Left panels: comparison of our IRAC flux densities to literature IRAC flux densities: F(λ0) /FLIT(λ0) flux density ratios as a function of our IRAC flux density, F(λ0), at 3.6 μm, 4.5 μm, 5.8 μm, and 8.0 μm. The average uncertainties are 17%, 17%, 19%, and 17% at 3.6, 4.5, 5.8, and 8.0 μm. Colours distinguish the reference for the literature measurement. Right panels: ratios of WISE flux densities to other MIR measurements (either IRAC, IRAS, or MIPS) as a function of WISE flux density at 3.4 μm, 4.6 μm, 12 μm, and 22 μm. The average uncertainties are 20%, 22%, 15%, and 12% at 3.4, 4.6, 12, and 22 μm, respectively. On all panels, we show the unit ratio as a solid line as well as the average uncertainties on the ratio in each bands as dashed lines. |
We compare IRAC flux densities previously available in the literature and the flux densities derived in this work. We use the ratios of our IRAC measurement to the literature IRAC flux densities; a ratio of 1 corresponds to a very good agreement. The comparison is presented in Fig. C.1 and shows good agreement between the two measurements, even if some outliers are present:
-
Haro 2 – The comparison to the literature values from Dale et al. (2007) agrees for the first three IRAC bands (ratios of 0.92, 0.96, and 0.93 at 3.6 μm, 4.5 μm, and 5.8 μm, respectively) but not for the IRAC 8.0 μm band where the ratio goes to ~2. Recomputing the flux density with the aperture given in Dale et al. (2007) gives a flux in very close agreement to that we find with our own aperture (ratio of 1.009 at 8.0 μm), and also for the three other IRAC bands. Additionally, we find that Marble et al. (2010) performed photometry for Haro 2 in an IRS-matched aperture and their result is in good agreement with ours (ratio = 1.036 at 8.0 μm).
-
NGC 4861 – UGC 4483 – Tol 1214-277 – Our measurements are systematically larger than the flux densities from Engelbracht et al. (2008). No precise information is given in Engelbracht et al. (2008) about the size of the apertures used for IRAC photometry, so it is difficult to assess whether we are really comparing similar measurements. Nonetheless, a possible explanation for NGC 4861 could be that we include Mrk 39, with which NGC 4861 is interacting in our aperture, and which Engelbracht et al. (2008) may not have included.
Excluding points where one of the two measurements (ours or literature values) is an upper limit, we get a mean ratio of our IRAC measurements to those in the literature of 1.05 ± 0.11 for IRAC 3.6 μm, 1.06 ± 0.11 for IRAC 4.5 μm, 1.02 ± 0.14 for IRAC 5.8 μm, and 1.01 ± 0.11 for IRAC 8.0 μm. This is to be compared to an average uncertainty on the ratios of 17%, 17%, 19%, and 17% at 3.6, 4.5, 5.8, and 8.0 μm. The error on the mean ratio is lower than the average uncertainty on the ratios for all of the bands indicating a good photometric agreement between the two measurements.
Appendix C.2: WISE: Comparison to other MIR measurements
The WISE photometry can be compared to Spitzer IRAC measurements for the first two bands, to IRAS 12 μm and to MIPS 24 μm. WISE, IRAC, IRAS, and MIPS are not calibrated on the same reference spectral shape, so we first apply colour corrections to our flux densities before the comparison. These colour corrections are of the order of <1%, 3%, 4%, 2%, 4%, 5%, <1%, and 9% for WISE 3.4 μm, WISE 4.6 μm, WISE 12 μm, WISE 22 μm, IRAC 3.6 μm, IRAC 4.5 μm, IRAS 12 μm, and MIPS 24 μm, respectively. We remove from the comparison all of the upper limits in any of the bands and we are left with 35 galaxies for WISE1, 37 galaxies for WISE2, 9 galaxies for WISE3, and 32 galaxies for WISE4.
The ratios of WISE flux densities to the corresponding MIR flux densities are shown in Fig. C.1. The median ratios are FWISE3.4/FIRAC3.6 = 0.97 ± 0.12, FWISE4.6/FIRAC4.5 = 0.87 ± 0.17, FWISE12/FIRAS12 = 0.88 ± 0.13, and FWISE22/FMIPS24 = 0.79 ± 0.22. We note that the dispersion is larger for the first two WISE bands for WISE flux densities less than ~1 mJy. The WISE 22 μm flux densities are also systematically lower than MIPS 24 μm flux densities, reflecting the difference in wavelength between the two bands and the steeply rising MIR continuum observed in the SED of dwarf galaxies.
For consistency, we also compare the WISE photometry from the AllWISE database to our measurements on the maps. We confirm that for the brightest and most extended sources, the photometry provided by the database underestimates the emission, and especially at 12 and 22 μm.
Appendix D: DGS IRS spectra
Appendix D.1: IRS data reduction
Two versions of the spectra are available in the CASSIS database (Lebouteiller et al. 2011) for the staring observations: an “optimal” extraction better suited for point sources and a “tapered column” extraction, better suited for partially extended sources. A message advises the user if the “tapered column” extraction or the “optimal” extraction method should be chosen. The chosen extraction for each of the DGS targets, as well as AORkeys, are summarised in Appendix B. CASSIS uses the AdOpt algorithm (Advanced Optimal extraction, Lebouteiller et al. 2010) within the Spectroscopic Modeling Analysis and Reduction Tool (SMART, Higdon et al. 2004). AdOpt enables optimal extraction of spectra using a super-sampled PSF. The pipeline includes steps, such as image cleaning, individual exposure combination, and background subtraction. Specific attention is given to identification and removal of bad pixels and outlier rejection at the image and spectra levels.
Some discrepant fluxes between orders at some wavelengths have to be removed from the spectra. These cut wavelengths are listed in Table D.1. For the extended galaxies, there is a conversion step from MJy/sr to Jy where the IRS spectrum is multiplied by the area over which it has been extracted. The spectra are then rescaled to match the observed photometry.
IRS cut-off wavelengths.
Appendix D.2: Rescaling the spectra to the photometry
 |
Fig. D.1 Example of IRS treatment for HS 1304+3529: the raw spectrum is presented in the top panel. The photometry points are overlaid in filled purple diamonds as well as synthetic photometry as blue open diamonds. The galaxy is not detected at 5.8 μm as indicated by the open purple triangle. Green, orange, and red parts of the spectrum represents the SL2 and LL2, SL3 and LL3, SL1 and LL1 spectra, respectively. The middle panel shows the spectra after cutting off the discrepant wavelengths and rescaling to match the photometry. The spline used to rescale SL is shown in Fig. D.2. The bottom panel shows the spectra smoothed to a S/N of 3. |
 |
Fig. D.2 Example of a spline used to rescale SL in the case of HS 1304+3529. The diamonds represent the ratio between the observed and the synthetic photometry. The spline has been fitted to the blue diamonds, except at 5.8 μm where the galaxy is not detected. The black curve is the final adopted spline, sp(x0), where x0 = 1.9. The orange crosses are the corrections applied to the SL part of the spectrum. |
We describe here the rescaling step of the IRS spectrum in more detail, and how we derive the correction factor for the SL and LL parts of the IRS spectrum.
The correction factor for LL, CLL can be written 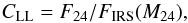 (D.1)
(D.1)
where F24 is the observed 24 μm MIPS flux density (from Bendo et al. (2012)) and FIRS(M24) is the synthetic photometry for the IRS LL, spectrum at 24 μm. Equation (D.1) is adapted for WISE 22 μm when MIPS 24 μm is not available.
Several constraints are available for the SL module, and used simultaneously to derive a correction that smoothly depends on wavelength, CSL(λ). We fit a spline function, using the IDL spline_p procedure, to CSL(I3), CSL(I4), CSL(W3), and CLL. We use CLL here to have a better constraint at the end of the spline. We impose a derivative of 0 at 24 μm to have a smooth function. We also assume that the correction factor CSL(λ) should always be ≥1.0, as the photometry measurement always encompasses more flux than the IRS slit.
CSL(I3), CSL(I4), CSL(W3) are given by  (D.2)
(D.2)
where F5.8, F8.0 and F12 are the observed 5.8 and 8.0 μm IRAC and the 12 μm WISE flux densities (from Tables 6 and 7); and FIRS(I5.8), FIRS(I8.0), and FIRS,SL(W12) are the synthetic photometry for the IRS SL spectrum at 5.8, 8.0, and 12 μm.
Note that there is an overlap between the WISE 12 μm filter and the LL wavelengths. As the LL spectrum has already been corrected, we must find the flux missing in the SL spectrum, i.e. FIRS,SL(W12), to match F12. But the integration over the WISE bandpass is not linear, i.e. FIRS,SL(W12) ≠FIRS(W12) – FIRS,LL(W12). Thus there is no simple way of deriving CSL(W3). Instead, we apply the following method:
-
1.
We generate a grid of potential CSL(W3), {x}, from 0.01 to 10;
-
2.
find the spline going through CSL(I3), CSL(I4), CLL, and each xi, sp(xi);
-
3.
correct the SL spectrum with each sp(xi); and
-
4.
compute the synthetic WISE 12 μm photometry for each corrected total IRS spectrum, FIRS(W12)(sp(xi)).
CSL(W3) is the x0 that gives FIRS(W12)(sp(x0)) = F12.
The final IRS spectrum, FIRS,corr(λSL) and FIRS,corr(λLL), is given by  (D.3)The method presented here is adapted depending on the number of constraints for each galaxy. Upper limits are not considered for the correction of IRS spectrum. An example of this treatment of IRS spectrum is shown in Fig. D.1 along with the spline used to correct the SL spectrum in Fig. D.2. The final IRS spectra for the DGS galaxies are shown in Fig. D.3.
(D.3)The method presented here is adapted depending on the number of constraints for each galaxy. Upper limits are not considered for the correction of IRS spectrum. An example of this treatment of IRS spectrum is shown in Fig. D.1 along with the spline used to correct the SL spectrum in Fig. D.2. The final IRS spectra for the DGS galaxies are shown in Fig. D.3.
In the case of NGC 1140 and NGC 1569, the IRS SL slit only covers a small part of these extended galaxies. We use the ISOCAM spectrum (from Galliano et al. 2003, 2005) for comparison after applying the same rescaling step. The two spectra are consistent with each other and with the general NIR – MIR shape of the SED for both galaxies. Thus we consider that the IRS spectra of these two galaxies are reliable and use them to constrain the SED model.
 |
Fig. D.3 IRS spectra for the DGS galaxies. The SL module is shown in green and the LL module is shown in red. The positions of the [S iv] 10.5 μm, [Ne ii] 12.8 μm, [Ne iii] 15.6 μm, [S iii] 18.7 μm, and 33.5 μm spectral lines are indicated. Line intensities have been extracted by Cormier et al. (2015). |
 |
Fig. D.3 continued. |
 |
Fig. D.3 continued. |
Appendix E: Specific SED modelling
In this Appendix, we detail the specific SED modelling for several DGS sources, and show the SEDs for the galaxies with and without any additional features (addition of a MIR modBB, including extinction, etc.) to show how the fit is improved.
-
Haro 11 – As this galaxy has evident silicate absorption features in the IRS spectrum around 10 μm, we add extinction in our modelling. The output luminosity is modified by
 (E.1)where τ0 is the optical depth, determined from the optical properties and the size distribution of our dust composition. The extinction parameter AV is left varying between 1 and 20, with a best-fit value of AV = 5. The quality of the fit is clearly improved in the NIR-MIR range after introducing AV (see Fig. E.1). Because the stellar continuum is also affected by extinction, the stellar template used for the fit no longer provides a reliable fit of the 2MASS NIR data. Instead, we replace the stellar component by a black body and impose a temperature T ≥ 1000 K. We obtain a best-fit temperature T = 30 000 K, corresponding to a maximum of the black-body emission around 0.1 μm in the UV, a sign of a young stellar population. This is consistent with the results of Adamo et al. (2010) who found a maximum in the cluster formation history ~3.5 Myr ago, and with the UV part of the SED presented in Cormier et al. (2012).
(E.1)where τ0 is the optical depth, determined from the optical properties and the size distribution of our dust composition. The extinction parameter AV is left varying between 1 and 20, with a best-fit value of AV = 5. The quality of the fit is clearly improved in the NIR-MIR range after introducing AV (see Fig. E.1). Because the stellar continuum is also affected by extinction, the stellar template used for the fit no longer provides a reliable fit of the 2MASS NIR data. Instead, we replace the stellar component by a black body and impose a temperature T ≥ 1000 K. We obtain a best-fit temperature T = 30 000 K, corresponding to a maximum of the black-body emission around 0.1 μm in the UV, a sign of a young stellar population. This is consistent with the results of Adamo et al. (2010) who found a maximum in the cluster formation history ~3.5 Myr ago, and with the UV part of the SED presented in Cormier et al. (2012). -
HS 0822+3542 – The observed PACS upper limits at 70 and 100 μm are not consistent with the rest of the MIR to FIR photometry (see Fig. 12). We recommend using the synthetic photometry provided by the model as upper limits for the 70 and 100 μm PACS wavelengths, i.e. F70 ≤ 41 mJy and F100 ≤ 48 mJy. These values are reported in Table 5.
-
HS 2352+2733 – There are only five detected points for this galaxy, and thus not enough constraints to fit a full SED. However, we can get a rough estimate of the dust mass by fitting a modBB with a fixed β = 2.0, through MIPS 24 μm, PACS 70 μm, and PACS 100 μm where the galaxy is detected. We obtain a temperature of T = 52 K and MBB = 1.01 × 104M⊙. This mass can be seen as a lower limit to the real dust mass (see Sect. 3.4). This value is reported in Table 9 and marked with aa.
-
II Zw 40 – This galaxy has an IRS spectrum with very good S/N. However, when compared to other MIR measurements, it seems that the Spitzer IRS-LL spectrum is not consistent with the rest of the MIR – FIR photometry, meaning that for this galaxy, a wavelength dependent correction may also be needed for the IRS LL spectrum. As an alternative, we use the ISOCAM spectrum for this galaxy (from Galliano et al. 2005), which covers a 5.6 to 16.3 μm wavelength range. The ISOCAM spectrum was matched to the broadband photometry by applying the same rescaling process as for the IRS SL spectrum. To properly match the end of the ISOCAM spectrum, we add an extra modBB (β fixed to 2.0 and best-fit temperature T = 113 K).
-
Mrk 153 – This galaxy has a prominent silicate emission feature in its IRS spectrum around 10 μm. This emission feature originates from hot small silicate grains, possibly in the accretion disk around an AGN. We allow the silicate-to-(silicate+graphite) grain mass fraction to vary in our fit and get a ratio of 0.94 (i.e. 1.3 times the Galactic value).
-
SBS 0335-052 – This galaxy has a very surprising SED with an IR peak around 15−30 μm, and an IRS spectrum showing silicate absorption features superimposed on a featureless continuum (see also Thuan et al. 1999; Dale et al. 2001; Houck et al. 2004; Galliano et al. 2008). The silicate absorption feature around 10 μm observed in the IRS spectrum indicates that extinction is present in this galaxy. We add extinction in our model as for Haro 11, and get AV = 1.1. The peculiar shape of the IRS spectrum requires two MIR modified black bodies to obtain a satisfactory fit (β fixed to 2.0 and best-fit temperatures T1 = 273 K and T2 = 123 K, see Fig. E.1).
-
Tol 1214-277 – The MIPS 70 μm point is not consistent with the rest of the photometry: IRS and MIPS 24 μm on one side and PACS 70 and 100 μm on the other side (see Fig. 12). It is another confirmation that this point is discrepant (Rémy-Ruyer et al. 2013), and thus we do not consider it in the modelling.
 |
Fig. E.1 Final SEDs in black compared to the SED without the additional features in blue (MIR modBB, extinction, see text for source per source details). Note how the final SEDs better reproduce the observed IR emission for these galaxies. |
Throughout the paper, we assume (O/H)⊙ = 4.90 × 104, i.e. 12 + log (O/H)⊙ = 8.69 (Asplund et al. 2009).
The query form is available at: http://sha.ipac.caltech.edu
This document is available at http://irsa.ipac.caltech.edu/data/SPITZER/docs/irac/iracinstrumenthandbook
The database is available at http://cassis.astro.cornell.edu/atlas/
The query form is available at: http://sha.ipac.caltech.edu
This document is available at http://wise2.ipac.caltech.edu/docs/release/allwise/expsup/index.html
The catalogue is available at: http://irsa.ipac.caltech.edu
This database is available at http://ned.ipac.caltech.edu/
The Galactic PAH mass fraction is fPAH⊙ = 4.57% from Zubko et al. (2004).
We compute the Galactic mass fraction of non-PAH grains with radius ≤10 nm in Zubko et al. (2004) model: fvsg⊙ = 16%.
This document is available at: http://lambda.gsfc.nasa.gov/product/iras/docs/exp.sup/
For this comparison, we use LTIR integrated over [3–1100] μm to match the interval used in Galametz et al. (2013b).
This factor was denoted K4e/K4p in Rémy-Ruyer et al. (2013).
The SPIRE Data Reduction Guide, v3.0, is available at: http://herschel.esac.esa.int/hcss-doc-12.0/print/spire_drg/spire_drg.pdf#spire_drg
Acknowledgments
The authors would like to thank R. Asano for providing the evolutionary tracks for his model for Fig. 11, and H. Hirashita and T. Takeuchi for interesting discussions on the chemical evolution models. This research was made possible through the financial support of the Agence Nationale de la Recherche (ANR) through the programme SYMPATICO (Program Blanc Projet ANR-11-BS56-0023) and also through the EU FP7 funded project DustPedia (Grant No. 606847). IDL is a postdoctoral researcher of the FWO-Vlaanderen (Belgium). This research has made use of the NASA/IPAC Extragalactic Database (NED) and of the NASA/IPAC Infrared Science Archive, which are operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. PACS has been developed by MPE (Germany); UVIE (Austria); KU Leuven, CSL, IMEC (Belgium); CEA, LAM (France); MPIA (Germany); INAF-IFSI/OAA/OAP/OAT, LENS, SISSA (Italy); IAC (Spain). This development has been supported by BMVIT (Austria), ESA-PRODEX (Belgium), CEA/CNES (France), DLR (Germany), ASI/INAF (Italy), and CICYT/MCYT (Spain). SPIRE has been developed by Cardiff University (UK); Univ. Lethbridge (Canada); NAOC (China); CEA, LAM (France); IFSI, Univ. Padua (Italy); IAC (Spain); SNSB (Sweden); Imperial College London, RAL, UCL-MSSL, UKATC, Univ. Sussex (UK) and Caltech, JPL, NHSC, Univ. Colorado (USA). This development has been supported by CSA (Canada); NAOC (China); CEA, CNES, CNRS (France); ASI (Italy); MCINN (Spain); Stockholm Observatory (Sweden); STFC (UK); and NASA (USA). SPIRE has been developed by a consortium of institutes led by Cardiff Univ. (UK) and including: Univ. Lethbridge (Canada); NAOC (China); CEA, LAM (France); IFSI, Univ. Padua (Italy); IAC (Spain); Stockholm Observatory (Sweden); Imperial College London, RAL, UCL-MSSL, UKATC, Univ. Sussex (UK); and Caltech, JPL, NHSC, Univ. Colorado (USA). This development has been supported by national funding agencies: CSA (Canada); NAOC (China); CEA, CNES, CNRS (France); ASI (Italy); MCINN (Spain); SNSB (Sweden); STFC, UKSA (UK); and NASA (USA).
References
- Adamo, A., Östlin, G., Zackrisson, E., et al. 2010, MNRAS, 407, 870 [NASA ADS] [CrossRef] [Google Scholar]
- Aniano, G., Draine, B. T., Calzetti, D., et al. 2012, ApJ, 756, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Asano, R. S., Takeuchi, T. T., Hirashita, H., & Inoue, A. K. 2013, Earth, Planets, Space, 65, 213 [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bazell, D., & Dwek, E. 1990, ApJ, 360, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Bendo, G. J., Dale, D. A., Draine, B. T., et al. 2006, ApJ, 652, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Bendo, G. J., Wilson, C. D., Warren, B. E., et al. 2010, MNRAS, 402, 1409 [NASA ADS] [CrossRef] [Google Scholar]
- Bendo, G. J., Galliano, F., & Madden, S. C. 2012, MNRAS, 423, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Bendo, G. J., Baes, M., Bianchi, S., et al. 2015, MNRAS, 448, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, S. 2013, A&A, 552, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bocchio, M., Micelotta, E. R., Gautier, A.-L., & Jones, A. P. 2012, A&A, 545, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bocchio, M., Jones, A. P., & Slavin, J. D. 2014, A&A, 570, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Gavazzi, G., Donas, J., & Scodeggio, M. 2001, AJ, 121, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., Lequeux, J., & Gavazzi, G. 2004, A&A, 428, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Ciesla, L., Buat, V., et al. 2010, A&A, 518, L61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Ciesla, L., Cortese, L., et al. 2012, A&A, 540, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bot, C., Ysard, N., Paradis, D., et al. 2010, A&A, 523, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bourne, N., Maddox, S. J., Dunne, L., et al. 2012, MNRAS, 421, 3027 [NASA ADS] [CrossRef] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Bron, E., Le Bourlot, J., & Le Petit, F. 2014, A&A, 569, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calzetti, D., Wu, S.-Y., Hong, S., et al. 2010, ApJ, 714, 1256 [NASA ADS] [CrossRef] [Google Scholar]
- Cannon, J. M., Walter, F., Armus, L., et al. 2006, ApJ, 652, 1170 [NASA ADS] [CrossRef] [Google Scholar]
- Ciesla, L., Boquien, M., Boselli, A., et al. 2014, A&A, 565, A128 [Google Scholar]
- Ciesla, L., Charmandaris, V., Georgakakis, A., et al. 2015, A&A, 576, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cohen, M., Wheaton, W. A., & Megeath, S. T. 2003, AJ, 126, 1090 [NASA ADS] [CrossRef] [Google Scholar]
- Cook, D. O., Dale, D. A., Johnson, B. D., et al. 2014, MNRAS, 445, 899 [NASA ADS] [CrossRef] [Google Scholar]
- Cormier, D., Lebouteiller, V., Madden, S. C., et al. 2012, A&A, 548, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cormier, D., Madden, S. C., Lebouteiller, V., et al. 2015, A&A, 578, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cortese, L., Boissier, S., Boselli, A., et al. 2012a, A&A, 544, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cortese, L., Ciesla, L., Boselli, A., et al. 2012b, A&A, 540, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cortese, L., Fritz, J., Bianchi, S., et al. 2014, MNRAS, 440, 942 [NASA ADS] [CrossRef] [Google Scholar]
- Cowie, L. L., Songaila, A., Hu, E. M., & Cohen, J. G. 1996, AJ, 112, 839 [Google Scholar]
- da Cunha, E., Charlot, S., & Elbaz, D. 2008, MNRAS, 388, 1595 [NASA ADS] [CrossRef] [Google Scholar]
- da Cunha, E., Eminian, C., Charlot, S., & Blaizot, J. 2010, MNRAS, 403, 1894 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, D. A., & Helou, G. 2002, ApJ, 576, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, D. A., Helou, G., Contursi, A., Silbermann, N. A., & Kolhatkar, S. 2001, ApJ, 549, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, D. A., Smith, J. D. T., Armus, L., et al. 2006, ApJ, 646, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, D. A., Gil de Paz, A., Gordon, K. D., et al. 2007, ApJ, 655, 863 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, D. A., Cohen, S. A., Johnson, L. C., et al. 2009a, ApJ, 703, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, D. A., Smith, J. D. T., Schlawin, E. A., et al. 2009b, ApJ, 693, 1821 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dale, D. A., Aniano, G., Engelbracht, C. W., et al. 2012, ApJ, 745, 95 [NASA ADS] [CrossRef] [Google Scholar]
- De Cia, A., Ledoux, C., Savaglio, S., Schady, P., & Vreeswijk, P. M. 2013, A&A, 560, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., Dale, D. A., Bendo, G., et al. 2007, ApJ, 663, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Dumke, M., Krause, M., & Wielebinski, R. 2004, A&A, 414, 475 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dwek, E. 1998, ApJ, 501, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Engelbracht, C. W., Gordon, K. D., Rieke, G. H., et al. 2005, ApJ, 628, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Engelbracht, C. W., Blaylock, M., Su, K. Y. L., et al. 2007, PASP, 119, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Engelbracht, C. W., Rieke, G. H., Gordon, K. D., et al. 2008, ApJ, 678, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Eskew, M., Zaritsky, D., & Meidt, S. 2012, AJ, 143, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Fritz, J., Franceschini, A., & Hatziminaoglou, E. 2006, MNRAS, 366, 767 [Google Scholar]
- Galametz, M., Madden, S., Galliano, F., et al. 2009, A&A, 508, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galametz, M., Madden, S. C., Galliano, F., et al. 2010, A&A, 518, L55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galametz, M., Madden, S. C., Galliano, F., et al. 2011, A&A, 532, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galametz, M., Kennicutt, R. C., Albrecht, M., et al. 2012, MNRAS, 425, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Galametz, M., Hony, S., Galliano, F., et al. 2013a, MNRAS, 431, 1596 [NASA ADS] [CrossRef] [Google Scholar]
- Galametz, M., Kennicutt, R. C., Calzetti, D., et al. 2013b, MNRAS, 431, 1956 [NASA ADS] [CrossRef] [Google Scholar]
- Galametz, M., Albrecht, M., Kennicutt, R., et al. 2014, MNRAS, 439, 2542 [NASA ADS] [CrossRef] [Google Scholar]
- Galliano, F., Madden, S. C., Jones, A. P., et al. 2003, A&A, 407, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galliano, F., Madden, S. C., Jones, A. P., Wilson, C. D., & Bernard, J.-P. 2005, A&A, 434, 867 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galliano, F., Dwek, E., & Chanial, P. 2008, ApJ, 672, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Galliano, F., Hony, S., Bernard, J.-P., et al. 2011, A&A, 536, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garnett, D. R., Skillman, E. D., Dufour, R. J., et al. 1995, ApJ, 443, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Garnett, D. R., Shields, G. A., Peimbert, M., et al. 1999, ApJ, 513, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Gavazzi, G., & Scodeggio, M. 1996, A&A, 312, L29 [NASA ADS] [Google Scholar]
- Gavazzi, G., Boselli, A., Pedotti, P., Gallazzi, A., & Carrasco, L. 2002, A&A, 396, 449 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Genzel, R., Lutz, D., Sturm, E., et al. 1998, ApJ, 498, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Gil de Paz, A., Madore, B. F., & Pevunova, O. 2003, ApJS, 147, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Gomez, H. L., Clark, C. J. R., Nozawa, T., et al. 2012a, MNRAS, 420, 3557 [NASA ADS] [CrossRef] [Google Scholar]
- Gomez, H. L., Krause, O., Barlow, M. J., et al. 2012b, ApJ, 760, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Gonçalves, D. R., Magrini, L., Teodorescu, A. M., & Carneiro, C. M. 2014, MNRAS, 444, 1705 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, K. D., Engelbracht, C. W., Fadda, D., et al. 2007, PASP, 119, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, K. D., Engelbracht, C. W., Rieke, G. H., et al. 2008, ApJ, 682, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, K. D., Galliano, F., Hony, S., et al. 2010, A&A, 518, L89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gordon, K. D., Roman-Duval, J., Bot, C., et al. 2014, ApJ, 797, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Grossi, M., Hunt, L. K., Madden, S., et al. 2010, A&A, 518, L52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grossi, M., Hunt, L. K., Madden, S. C., et al. 2015, A&A, 574, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groves, B., Dopita, M. A., Sutherland, R. S., et al. 2008, ApJS, 176, 438 [NASA ADS] [CrossRef] [Google Scholar]
- Guhathakurta, P., & Draine, B. T. 1989, ApJ, 345, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Hao, C.-N., Kennicutt, R. C., Johnson, B. D., et al. 2011, ApJ, 741, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, T. I., & Herbst, E. 1993, MNRAS, 263, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Helou, G. 1986, ApJ, 311, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Hermelo, I., Lisenfeld, U., Relaño, M., et al. 2013, A&A, 549, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Higdon, S. J. U., Devost, D., Higdon, J. L., et al. 2004, PASP, 116, 975 [NASA ADS] [CrossRef] [Google Scholar]
- Hirashita, H. 1999, ApJ, 522, 220 [NASA ADS] [CrossRef] [Google Scholar]
- Hirashita, H., Tajiri, Y. Y., & Kamaya, H. 2002, A&A, 388, 439 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hony, S., Galliano, F., Madden, S. M., & SAGE Consortium 2010, in BAAS, 42, Am. Astron. Soc. Meet. Abstr., 215, 459.14 [Google Scholar]
- Houck, J. R., Charmandaris, V., Brandl, B. R., et al. 2004, ApJS, 154, 211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hughes, T. M., Cortese, L., Boselli, A., Gavazzi, G., & Davies, J. I. 2013, A&A, 550, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunt, L. K., Thuan, T. X., Sauvage, M., & Izotov, Y. I. 2006, ApJ, 653, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Hunt, L., Magrini, L., Galli, D., et al. 2012, MNRAS, 427, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, D. A., Gallagher, III, J. S., Rice, W. L., & Gillett, F. C. 1989, ApJ, 336, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias-Paramo, J., & Vilchez, J. M. 1997, ApJ, 479, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Indebetouw, R., Matsuura, M., Dwek, E., et al. 2014, ApJ, 782, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, A. K. 2011, Earth, Planets, Space, 63, 1027 [Google Scholar]
- Issa, M. R., MacLaren, I., & Wolfendale, A. W. 1990, A&A, 236, 237 [NASA ADS] [Google Scholar]
- Izotov, Y. I., & Thuan, T. X. 1998, ApJ, 500, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Thuan, T. X., & Lipovetsky, V. A. 1994, ApJ, 435, 647 [NASA ADS] [CrossRef] [Google Scholar]
- James, A., Dunne, L., Eales, S., & Edmunds, M. G. 2002, MNRAS, 335, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Jarrett, T. H., Chester, T., Cutri, R., Schneider, S. E., & Huchra, J. P. 2003, AJ, 125, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Jarrett, T. H., Cohen, M., Masci, F., et al. 2011, ApJ, 735, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. P., Tielens, A. G. G. M., Hollenbach, D. J., & McKee, C. F. 1994, ApJ, 433, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. P., Tielens, A. G. G. M., & Hollenbach, D. J. 1996, ApJ, 469, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. P., Fanciullo, L., Köhler, M., et al. 2013, A&A, 558, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kennicutt, Jr., R. C., 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C., Armus, L., Bendo, G., et al. 2003, PASP, 115, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C., Lee, J. C., Funes, et al. 2008, ApJS, 178, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C., Hao, C.-N., Calzetti, D., et al. 2009, ApJ, 703, 1672 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Calzetti, D., Aniano, G., et al. 2011, PASP, 123, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- Kirby, E. N., Cohen, J. G., Guhathakurta, P., et al. 2013, ApJ, 779, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Kirkpatrick, A., Pope, A., Alexander, D. M., et al. 2012, ApJ, 759, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Köhler, M., Stepnik, B., Jones, A. P., et al. 2012, A&A, 548, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Köhler, M., Jones, A., & Ysard, N. 2014, A&A, 565, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Köhler, M., Ysard, N., & Jones, A. P. 2015, A&A, 579, A15 [Google Scholar]
- Laor, A., & Draine, B. T. 1993, ApJ, 402, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Lara-López, M. A., Cepa, J., Bongiovanni, A., et al. 2010, A&A, 521, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Bourlot, J., Le Petit, F., Pinto, C., Roueff, E., & Roy, F. 2012, A&A, 541, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lebouteiller, V., Bernard-Salas, J., Sloan, G. C., & Barry, D. J. 2010, PASP, 122, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Lebouteiller, V., Barry, D. J., Spoon, H. W. W., et al. 2011, ApJS, 196, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J. C., Gil de Paz, A., Tremonti, C., et al. 2009, ApJ, 706, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Lequeux, J., Peimbert, M., Rayo, J. F., Serrano, A., & Torres-Peimbert, S. 1979, A&A, 80, 155 [NASA ADS] [Google Scholar]
- Lisenfeld, U., & Ferrara, A. 1998, ApJ, 496, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., Pozzetti, L., & Dickinson, M. 1998, ApJ, 498, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Madden, S. C. 2000, New Astron. Rev., 44, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Madden, S. C., Galliano, F., Jones, A. P., & Sauvage, M. 2006, A&A, 446, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Madden, S. C., Rémy-Ruyer, A., Galametz, M., et al. 2013, PASP, 125, 600 [NASA ADS] [CrossRef] [Google Scholar]
- Madden, S. C., Rémy-Ruyer, A., Galametz, M., et al. 2014, PASP, 126, 1079 [CrossRef] [Google Scholar]
- Magdis, G. E., Rigopoulou, D., Hopwood, R., et al. 2014, ApJ, 796, 63 [Google Scholar]
- Magrini, L., Bianchi, S., Corbelli, E., et al. 2011, A&A, 535, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mannucci, F., Cresci, G., Maiolino, R., Marconi, A., & Gnerucci, A. 2010, MNRAS, 408, 2115 [NASA ADS] [CrossRef] [Google Scholar]
- Marble, A. R., Engelbracht, C. W., van Zee, L., et al. 2010, ApJ, 715, 506 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]
- Matsuura, M., Dwek, E., Barlow, M. J., et al. 2015, ApJ, 800, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Mattsson, L., De Cia, A., Andersen, A. C., & Zafar, T. 2014a, MNRAS, 440, 1562 [NASA ADS] [CrossRef] [Google Scholar]
- Mattsson, L., Gomez, H. L., Andersen, A. C., et al. 2014b, MNRAS, 444, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Meixner, M., Galliano, F., Hony, S., et al. 2010, A&A, 518, L71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Melisse, J. P. M., & Israel, F. P. 1994, A&A, 285, 51 [NASA ADS] [Google Scholar]
- Meurer, G. R., Wong, O. I., Kim, J. H., et al. 2009, ApJ, 695, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Micelotta, E. R., Jones, A. P., & Tielens, A. G. G. M. 2010, A&A, 510, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Micelotta, E. R., Jones, A. P., & Tielens, A. G. G. M. 2011, A&A, 526, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moles, M., Marquez, I., Masegosa, J., et al. 1994, ApJ, 432, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Moustakas, J., & Kennicutt, Jr., R. C. 2006, ApJS, 164, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Moustakas, J., Kennicutt, Jr., R. C., Tremonti, C. A., et al. 2010, ApJS, 190, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz-Mateos, J. C., Gil de Paz, A., Boissier, S., et al. 2009, ApJ, 701, 1965 [NASA ADS] [CrossRef] [Google Scholar]
- Neugebauer, G., Habing, H. J., van Duinen, R., et al. 1984, ApJ, 278, L1 [Google Scholar]
- O’Donnell, J. E. 1994, ApJ, 422, 158 [NASA ADS] [CrossRef] [Google Scholar]
- O’Halloran, B., Satyapal, S., & Dudik, R. P. 2006, ApJ, 641, 795 [NASA ADS] [CrossRef] [Google Scholar]
- O’Halloran, B., Galametz, M., Madden, S. C., et al. 2010, A&A, 518, L58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ott, S. 2010, in Astronomical Data Analysis Software and Systems XIX, eds. Y. Mizumoto, K.-I. Morita, & M. Ohishi, ASP Conf. Ser., 434, 139 [Google Scholar]
- Pilyugin, L. S., & Thuan, T. X. 2005, ApJ, 631, 231 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Plana, H., Boulesteix, J., Amram, P., Carignan, C., & Mendes de Oliveira, C. 1998, A&AS, 128, 75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XI. 2014, A&A, 571, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popescu, C. C., & Hopp, U. 2000, A&AS, 142, 247 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pustilnik, S. A., Pramskij, A. G., & Kniazev, A. Y. 2004, A&A, 425, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reach, W. T., Megeath, S. T., Cohen, M., et al. 2005, PASP, 117, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Rémy-Ruyer, A., Madden, S. C., Galliano, F., et al. 2013, A&A, 557, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rémy-Ruyer, A., Madden, S. C., Galliano, F., et al. 2014, A&A, 563, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rémy-Ruyer, A., Madden, S. C., Galliano, F., et al. 2015, A&A, 573, C1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rice, W., Lonsdale, C. J., Soifer, B. T., et al. 1988, ApJS, 68, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Rieke, G., Lada, C., Lebofsky, M., et al. 1984, in BAAS, 16, 906 [Google Scholar]
- Rosenberg, J. L., Ashby, M. L. N., Salzer, J. J., & Huang, J.-S. 2006, ApJ, 636, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Roussel, H. 2013, PASP, 125, 1126 [Google Scholar]
- Rowlands, K., Gomez, H. L., Dunne, L., et al. 2014, MNRAS, 441, 1040 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Sandage, A. 1986, A&A, 161, 89 [NASA ADS] [Google Scholar]
- Sanders, D. B., Mazzarella, J. M., Kim, D.-C., Surace, J. A., & Soifer, B. T. 2003, AJ, 126, 1607 [Google Scholar]
- Sandstrom, K. M., Bolatto, A. D., Bot, C., et al. 2012, ApJ, 744, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Savage, B. D., & Sembach, K. R. 1996, ARA&A, 34, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitt, H. R., Calzetti, D., Armus, L., et al. 2006, ApJS, 164, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Serra Díaz-Cano, L., & Jones, A. P. 2008, A&A, 492, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skibba, R. A., Engelbracht, C. W., Dale, D., et al. 2011, ApJ, 738, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, J. D. T., Armus, L., Dale, D. A., et al. 2007a, PASP, 119, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, J. D. T., Draine, B. T., Dale, D. A., et al. 2007b, ApJ, 656, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, D. J. B., Dunne, L., da Cunha, E., et al. 2012a, MNRAS, 427, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, M. W. L., Eales, S. A., Gomez, H. L., et al. 2012b, ApJ, 756, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, M. W. L., Gomez, H. L., Eales, S. A., et al. 2012c, ApJ, 748, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Stansberry, J. A., Gordon, K. D., Bhattacharya, B., et al. 2007, PASP, 119, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Stepnik, B., Abergel, A., Bernard, J., et al. 2003, A&A, 398, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stepnik, B., Abergel, A., Bernard, J.-P., et al. 2001, in From darkness to light: Origin and evolution of young stellar clusters, eds. T. Montmerle, & P. André, ASP Conf. Ser., 243, 47 [Google Scholar]
- Terlevich, R., Melnick, J., Masegosa, J., Moles, M., & Copetti, M. V. F. 1991, A&AS, 91, 285 [NASA ADS] [Google Scholar]
- Thuan, T. X., Sauvage, M., & Madden, S. 1999, ApJ, 516, 783 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M. 2005, The physics and chemistry of the interstellar medium (Cambridge University Press) [Google Scholar]
- Todini, P., & Ferrara, A. 2001, MNRAS, 325, 726 [NASA ADS] [CrossRef] [Google Scholar]
- Tommasin, S., Spinoglio, L., Malkan, M. A., & Fazio, G. 2010, ApJ, 709, 1257 [NASA ADS] [CrossRef] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Viaene, S., Fritz, J., Baes, M., et al. 2014, A&A, 567, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vidali, G., Roser, J. E., Manicó, G., & Pirronello, V. 2004, J. Geophys. Res. (Planets), 109, 7 [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Whittet, D. C. B. 2003, Astron. Geophys., 44, 35 [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., Charmandaris, V., Hao, L., et al. 2006, ApJ, 639, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, R., Hogg, D. W., & Moustakas, J. 2011, ApJ, 730, 111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ysard, N., Köhler, M., Jones, A., et al. 2015, A&A, 577, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zafar, T., & Watson, D. 2013, A&A, 560, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhu, M., Papadopoulos, P. P., Xilouris, E. M., Kuno, N., & Lisenfeld, U. 2009, ApJ, 706, 941 [NASA ADS] [CrossRef] [Google Scholar]
- Zhukovska, S. 2014, A&A, 562, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zubko, V. G., Mennella, V., Colangeli, L., & Bussoletti, E. 1996, MNRAS, 282, 1321 [NASA ADS] [CrossRef] [Google Scholar]
- Zubko, V., Dwek, E., & Arendt, R. G. 2004, ApJS, 152, 211 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Metallicity (top), and stellar mass (bottom) distributions of the DGS (purple), KINGFISH (orange) samples. The total distribution is indicated in grey. In the top panel, solar metallicity is indicated here to guide the eye, as well as the 1/50, 1/10, and 1/5 Z⊙ values. |
| In the text | |
 |
Fig. 2 Star formation rates, SFR, (left), specific SFRs, sSFR, (right), for the DGS (crosses) and KINGFISH samples as a function of metallicity, colour coded with Mstar (colour legend in right panel). For the KINGFISH sample, we distinguish the sources that have been classified as “star-forming” (SF, downward triangles) or as “AGN” (stars) by Kennicutt et al. (2011). The distribution of each parameter is indicated on the side of each panel for both samples: solid line for DGS and dashed line for KINGFISH. |
| In the text | |
 |
Fig. 3 SEDs for a DGS source NGC 4449. The observed SED includes the Herschel data (purple crosses) as well as any available ancillary data (in orange). The different symbols code for the different instruments: Xs for 2MASS bands, stars for Spitzer IRAC and MIPS, diamonds for WISE, and triangles for IRAS. The IRS spectrum is displayed in orange. The total modelled SED in black is the sum of the stellar (green) and dust (red) contributions. The modelled points in the different bands are the filled blue circles. Residuals are shown on the bottom panel. |
| In the text | |
 |
Fig. 4 SED for SBS1533+574 without (top) and with (bottom) the extra MIR modified black body, shown in yellow. The other colours and the symbols are the same as for Fig. 3. |
| In the text | |
 |
Fig. 5 Ratios of the dust masses estimated with a modBB model and with a semi-empirical SED model, MBB/Mdust, for the DGS (crosses) and KINGFISH (downward triangles) samples, as a function of the metallicity. The colour codes the ratio between the dust temperatures estimated from modBB fits and the SED model (assuming TMW = 19.7 K, Planck Collaboration XI 2014, see text for details) TBB/Tdust. |
| In the text | |
 |
Fig. 6 Dust masses (top), TIR luminosities (bottom) for the DGS (crosses), and KINGFISH (downward triangles) samples as a function of metallicity, colour coded with Mstar. The best power-law fit is indicated with a black line, and the 1σ dispersion is indicated with dotted lines for the two panels. The distribution of each parameter is indicated on the side of each panel for both samples: solid line for DGS and dashed line for KINGFISH. |
| In the text | |
 |
Fig. 7 The PAH mass fractions for the DGS (purple crosses) and KINGFISH (orange downward triangles) samples as a function of metallicity (left panel) and sSFR (right panel). The parameter fPAH is expressed in units of fPAH⊙, with fPAH⊙ = 4.57%. The distribution of fPAH is indicated on the side for both samples: plain purple line for DGS galaxies and dashed orange line for the KINGFISH sample. In each panel, the best power-law fit is indicated as a solid line, together with the 1σ dispersion as dotted lines. |
| In the text | |
 |
Fig. 8 Example of different SED shapes, with increasing broadness around the FIR peak for increasing σU. NGC 0628, NGC 1140, and SBS 1415+437 have log(σU/U⊙) = 0.4, 2.1, and 3.0, respectively. The location of these three galaxies is indicated in Fig. 9. |
| In the text | |
 |
Fig. 9 Average starlight intensity ⟨ U ⟩ and σU for the DGS (crosses) and KINGFISH samples. For the KINGFISH sample, we distinguish the sources that have been classified as star forming (SF, downward triangles) or as AGN (stars) by Kennicutt et al. (2011). The average dust equilibrium temperature is shown on the top axis. The colour codes the sSFR of the sources, in units of Gyr-1. We indicate the location of the two most metal-poor galaxies, I Zw 18 and SBS 0335-052, and of the three galaxies of Fig. 8. |
| In the text | |
 |
Fig. 10 Schematic view of the various correlations between parameters in the DGS and KINGFISH samples. The numbers on the lines are the Spearman correlation coefficients reported from Table 2. The solid lines indicate the dominating correlations between parameters and the dashed lines indicate several secondary correlations of interest. |
| In the text | |
 |
Fig. 11 Dust-to-stellar mass ratios for the DGS (crosses) and KINGFISH (downwards triangles) samples as a function of sSFR, colour coded by the gas-to-dust mass ratio (G/D), Mgas/Mdust, from Rémy-Ruyer et al. (2014). The distribution of Mdust/Mstar is indicated on the side for both samples: solid line for DGS and dashed line for KINGFISH. Modelled evolutionary tracks from Asano et al. (2013) are shown, for different star formation timescales (τSF = 0.5, 5 and 50 Gyr), with the red, blue, and purple lines. |
| In the text | |
 |
Fig. 12 DGS SEDs: the observed SEDs include the Herschel data (purple crosses) as well as any available ancillary data (in orange). The different symbols refer to the different instruments: Xs for 2MASS bands, stars for Spitzer IRAC and MIPS, diamonds for WISE, and triangles for IRAS. The IRS spectrum is shown in orange. The total modelled SED in black is the sum of the stellar (green) and dust (red) contributions, and eventually of the modified black-body contribution (yellow). The modelled points in the different bands are the filled blue circles. |
| In the text | |
 |
Fig. 12 continued. |
| In the text | |
 |
Fig. 12 continued. |
| In the text | |
 |
Fig. 13 KINGFISH SEDs: the colours and symbols are the same as in Fig. 12. |
| In the text | |
 |
Fig. 13 continued. |
| In the text | |
 |
Fig. 13 continued. |
| In the text | |
 |
Fig. C.1 Left panels: comparison of our IRAC flux densities to literature IRAC flux densities: F(λ0) /FLIT(λ0) flux density ratios as a function of our IRAC flux density, F(λ0), at 3.6 μm, 4.5 μm, 5.8 μm, and 8.0 μm. The average uncertainties are 17%, 17%, 19%, and 17% at 3.6, 4.5, 5.8, and 8.0 μm. Colours distinguish the reference for the literature measurement. Right panels: ratios of WISE flux densities to other MIR measurements (either IRAC, IRAS, or MIPS) as a function of WISE flux density at 3.4 μm, 4.6 μm, 12 μm, and 22 μm. The average uncertainties are 20%, 22%, 15%, and 12% at 3.4, 4.6, 12, and 22 μm, respectively. On all panels, we show the unit ratio as a solid line as well as the average uncertainties on the ratio in each bands as dashed lines. |
| In the text | |
 |
Fig. D.1 Example of IRS treatment for HS 1304+3529: the raw spectrum is presented in the top panel. The photometry points are overlaid in filled purple diamonds as well as synthetic photometry as blue open diamonds. The galaxy is not detected at 5.8 μm as indicated by the open purple triangle. Green, orange, and red parts of the spectrum represents the SL2 and LL2, SL3 and LL3, SL1 and LL1 spectra, respectively. The middle panel shows the spectra after cutting off the discrepant wavelengths and rescaling to match the photometry. The spline used to rescale SL is shown in Fig. D.2. The bottom panel shows the spectra smoothed to a S/N of 3. |
| In the text | |
 |
Fig. D.2 Example of a spline used to rescale SL in the case of HS 1304+3529. The diamonds represent the ratio between the observed and the synthetic photometry. The spline has been fitted to the blue diamonds, except at 5.8 μm where the galaxy is not detected. The black curve is the final adopted spline, sp(x0), where x0 = 1.9. The orange crosses are the corrections applied to the SL part of the spectrum. |
| In the text | |
 |
Fig. D.3 IRS spectra for the DGS galaxies. The SL module is shown in green and the LL module is shown in red. The positions of the [S iv] 10.5 μm, [Ne ii] 12.8 μm, [Ne iii] 15.6 μm, [S iii] 18.7 μm, and 33.5 μm spectral lines are indicated. Line intensities have been extracted by Cormier et al. (2015). |
| In the text | |
 |
Fig. D.3 continued. |
| In the text | |
 |
Fig. D.3 continued. |
| In the text | |
 |
Fig. E.1 Final SEDs in black compared to the SED without the additional features in blue (MIR modBB, extinction, see text for source per source details). Note how the final SEDs better reproduce the observed IR emission for these galaxies. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


