| Issue |
A&A
Volume 582, October 2015
|
|
|---|---|---|
| Article Number | A46 | |
| Number of page(s) | 20 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201525924 | |
| Published online | 05 October 2015 | |
Abundance patterns in early-type galaxies: is there a “knee” in the [Fe/H] vs. [α/Fe] relation?
1
Leibniz-Institut für Astrophysik Potsdam (AIP),
An der Sternwarte 16,
14482
Potsdam,
Germany
2
Instituto de Astronomia, Geofísica e Ciẽncias Atmosféricas,
Universidade de São Paulo, Rua do
Matão 1226, 05508-090
São Paulo,
Brasil
3
INAF-Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi
5, 50125
Firenze,
Italy
4
Dark Cosmology Center, University of Copenhagen, Niels Bohr
Institute, Juliane Maries Vej
30, 2100
Copenhagen,
Denmark
5
Centro de Radioastronomía y Astrofísica (CRyA),
Morelia, 58089
Michoacan,
Mexico
6
UPMC-CNRS, UMR7095, Institut d’Astrophysique de
Paris, 75014
Paris,
France
Received: 18 February 2015
Accepted: 18 August 2015
Early-type galaxies (ETGs) are known to be enhanced in α elements, in accordance with their old ages and short formation timescales. In this contribution we aim to resolve the enrichment histories of ETGs. This means we study the abundance of Fe ([Fe/H]) and the α-element groups ([α/Fe]) separately for stars older than 9.5 Gyr ([Fe/H]o, [α/Fe]o) and for stars between 1.5 and 9.5 Gyr ([Fe/H]i, [α/Fe]i). Through extensive simulation we show that we can indeed recover the enrichment history per galaxy. We then analyze a spectroscopic sample of 2286 early-type galaxies from the SDSS selected to be ETGs. We separate out those galaxies for which the abundance of iron in stars grows throughout the lifetime of the galaxy, i.e. in which [Fe/H]o< [Fe/H]i. We call those consistent with self-enrichment, while the others must have experienced some mergers or significant gas accretion. We confirm earlier work where the [Fe/H] and [α/Fe] parameters are correlated with the mass and velocity dispersion of ETGs. We emphasize that the strongest relation is between [α/Fe] and age. This relation falls into two regimes, one with a steep slope for old galaxies and one with a shallow slope for younger ETGs. The vast majority of ETGs in our sample do not show the “knee” in the plot of [Fe/H] vs. [α/Fe] commonly observed in local group galaxies. This implies that for the vast majority of ETGs, the stars younger than 9.5 Gyr are likely to have been accreted or formed from accreted gas. The properties of the intermediate-age stars in accretion-dominated ETGs indicate that mass growth through late (minor) mergers in ETGs is dominated by galaxies with low [Fe/H] and low [α/Fe]. The method of reconstructing the stellar enrichment histories of ETGs introduced in this paper promises to constrain the star formation and mass assembly histories of large samples of galaxies in a unique way.
Key words: galaxies: abundances / galaxies: stellar content / galaxies: elliptical and lenticular, cD
© ESO, 2015
1. Introduction
The stars in massive early-type galaxies (ETGs) have had to form early in the history of the universe for two reasons: 1) Very few of these galaxies have (significant) young stellar populations (e.g., Yi et al. 2005; Trager & Somerville 2009; Thomas et al. 2010) and 2) the ratio of α elements (O, Mg, etc.) to Fe in the atmospheres of these stars is higher than solar (e.g., Peterson 1976; Worthey et al. 1992; Milone et al. 2000), indicating a short timescale for the enrichment of the ISM out of which they formed. The ratio [α/Fe] is a powerful estimator of the duration of star formation (Tinsley 1979; Matteucci & Greggio 1986). Study of the mass dependence of the ages and enhancement ratios of ETGs has led to the classical picture in which the star formation timescales are shorter with increasing galaxy mass (Thomas et al. 2005).
Direct studies of massive galaxies at high redshift support this picture in which at least some ETGs must have “formed the bulk of their mass only a few million years after the big bang” (Nayyeri et al. 2014). On the other hand there is evidence that massive ETGs cannot be described by a stellar population with a single age and abundance pattern (recently, e.g., Lonoce et al. 2014). Indeed, Arimoto & Yoshii (1986) emphasize that this is true in terms not only of an age spread, but also of an abundance spread: “The present analysis shows that such metal-poor stars in the RGB evolution have a strong influence on the integrated colors of the galaxy”.
Recent observational and theoretical work has focused on the question of when and how the late mass growth of early-type galaxies takes place. Two opposite possibilities for such mass growth exist: 1) in situ star formation from gas that was accreted in the initial phase of the galaxies formation and 2) mass growth from later major or minor dry merging. A third possibility with less clear observational signatures is 3) stellar mass growth through star formation from gas that was either accreted during a merger (wet mergers) or in a cold mode from the cosmic web.
Different observational approaches to these questions exist. An important piece of the puzzle is the observation that the progenitors of ETGs at redshifts above z ~ 1 are compact, dense objects (Trujillo et al. 2006; van Dokkum et al. 2008; van der Wel et al. 2008). Naab et al. (2009), Hopkins et al. (2009), and van Dokkum et al. (2010a) show that the cores of today’s ellipticals are consistent with being the dense galaxies observed at high redshift, although van der Wel et al. (2011) make the point that the majority of these distant, dense galaxies should be thought of as disk-like, introducing some tension with the mostly dispersion-dominated cores of today’s early-type galaxies. Overall, the data have led to the notion that (minor) merging over a Hubble time will simultaneously contribute to the mass growth of these objects and to their size growth (Clemens et al. 2009; Naab et al. 2009; van Dokkum et al. 2010a; Oser et al. 2012; Greene et al. 2012, 2013).
Simulations predict that stellar accretion is most important at large radii (Lackner et al. 2012; Navarro-González et al. 2013; Hirschmann et al. 2015). In contrast to earlier notions, simulations even show that no major merger at all is needed to form massive ellipticals (Bournaud et al. 2007). On the other hand, direct measurement of major merging is available in the literature (e.g., Bell et al. 2006; de Ravel et al. 2009; Robaina et al. 2010; Robotham et al. 2014). These studies find that the typical L* galaxy will have undergone one major merger after redshift one (Keenan et al. 2014) and that the higher the mass of a galaxy, the more it grows through major merging. The evolution in the mass function can be combined with the expected growth due to star formation to yield a direct measure of the mass growth due to mergers in ETGs (Walcher et al. 2008; Ownsworth et al. 2014). This leads to estimates of roughly half of the present-day total stellar mass of ETGs being formed in other galaxies prior to their incorporation into the ETG over cosmic time. However, mergers also contribute gas. For example Kormendy et al. (2009) discuss how structural properties can be used to distinguish between dry mergers that would contribute only stars and wet mergers that would in turn contribute gas, thus leading to late star formation and rebuilding of cusps.
The present paper is dedicated to measuring the relative importance of the mass-growth processes from their chemical signature. In particular, other observational approaches cannot hope to distinguish between in situ formation of stars from gas left over from any putative “initial accretion”, on the one hand, and gas subsequently accreted either in a cold mode or through minor mergers, on the other. This distinction is much easier to study from chemical signatures as shown below.
In this contribution we define the stellar enrichment histories (SEH) as the four-dimensional space occupied by the stellar populations in each galaxy and spanned by the parameters age (i.e., time elapsed since formation of those populations), [Fe/H], [α/Fe] and the mass (or luminosity) contribution of these stars. It needs to be kept in mind that we can only address the stellar population within one spatial resolution element (one fiber in our case, the case of SDSS). Because of measurement uncertainties we very strongly bin this space into just two age bins: the old age bin contains all stars older than 9.5 Gyr, the intermediate age bin contains all stars between 1.5 and 9.5 Gyr of age. Within each age bin and for each galaxy we can compute the luminosity-averaged [Fe/H] and [α/Fe] as well as the fractional contribution of the old and intermediate populations to the total luminosity of each galaxy. This principle is illustrated in the upper panel of Fig. 1. For the remainder of this paper we denote the mean [α/Fe] and [Fe/H] of the old stars with the subscript “o” (i.e. we write [Fe/H]o and [α/Fe]o), whereas we denote the mean [α/Fe] and [Fe/H] of the intermediate age stars with the subscript “i” (i.e. we write [Fe/H]i and [α/Fe]i). The “star formation history” (SFH) would simply be the marginalization of the SEH onto the 2-dimensional space of age and luminosity contribution.
The choice of 9.5 Gyr for separating old and intermediate stellar populations in ETGs is of course to some level arbitrary. It can, however, be justified on several grounds as providing the widest age bin for old stars that still makes sense physically. On the one hand simulations such as those of Naab et al. (2009) show the typical mass assembly histories of ETGs in a hierarchical universe. For many of these galaxies there is a change of regime at around 10 Gyr ago, where the mass build-up changes from being dominated by in-situ star formation to accretion of other, smaller galaxies and clumps. Thus this is an age where we expect to maximize the signal from any difference between old and intermediate age population. On the other hand, those alpha-enhanced populations that we can study in detail in the Milky Way are all older than 11 Gyr. This is true for the thick disk (Fuhrmann 2011) and for the bulge (Bensby et al. 2013). As shown later in the present paper (Fig. 12, lower right panel) and in a paper in preparation (Walcher et al., in prep.), this effect is seen in the luminosity-weighted average properties at a lookback time of around 9.5 Gyr as well in the sense that the rate of change of [α/Fe] with time shows a significant change of slope. These 2 or 3 Gyr after the onset of star formation are thus different in the chemical signatures, which helps for the technical as well as scientific arguments of the present paper. Finally, the cosmic star formation density peaks at a lookback time of 10 Gyr, as shown in the recent review by Madau & Dickinson (2014, their Fig. 9). Specifically for ETGs, this is also the time when quiescent galaxies started appearing in large number (see e.g., Arnouts et al. 2007, their Fig. 13).
 |
Fig. 1 Schematic representation of the new parameters introduced in this paper, namely [α/Fe]o and [Fe/H]o. These represent the average [α/Fe] and [Fe/H] of stars older than 9.5 Gyr on a per galaxy basis. The upper panel shows a schematic star formation history, which separates into these two stellar populations. The lower panels depicts on the standard [α/Fe] vs. [Fe/H] diagram familiar for the Milky Way what is expected for the old and intermediate age stars respectively. |
The lower panel of Fig. 1 illustrates basic expectations for the locus the old and intermediate stellar population would occupy in the projection onto the [α/Fe] vs. [Fe/H] plane. As is well known the “knee” in this diagram carries information about the star formation efficiency in the galaxy, where higher star formation efficiency leads to higher overall metallicity before the onset of SNIa enrichment, and thus to a knee that is located at higher [Fe/H] values. The low-[Fe/H] plateau in [α/Fe] can be modulated by the slope of the upper end of the stellar initial mass function, but the data we discuss here do not allow any inference concerning this, thus we neglect this question for the remainder of the paper.
The existence of the knee in the lower panel of Fig. 1 for the Milky Way stars is tied to some causal connection at each time step during the star formation history between the existing stars and the next generation of stars. Although some accretion is needed, if only to solve the g-dwarf question, we generally call this a scenario that is consistent with self-enrichment (SLF). The SLF scenario would predict in our specific case of coarsely resolved enrichment histories for ETGs that the [Fe/H] of the intermediate-age population would always be higher than for the old population and the [α/Fe] of the intermediate-age population would always be lower than that of the old population. On the other hand, as mentioned above we know that mergers contribute a significant percentage of the stars in massive ETGs. The merging stars bear no connection to the pre-existing stars in the ETG and thus could have any [Fe/H] and [α/Fe] properties. The shorthand for this scenario throughout this paper is ACC for accretion.
The mass-metallicity relation (Tremonti et al. 2004; Gallazzi et al. 2005) leads to the expectation that minor, i.e. low mass mergers would contribute stars with sub-solar [Fe/H]. The [α/Fe] of these stars is less certain. However, Sansom & Northeast (2008) show that the high [α/Fe] abundances seen in massive quiescent galaxies do not continue to the lower luminosity quiescent galaxies, as those have generally lower [α/Fe]. Also, lower mass galaxies tend to have prolonged star formation histories, again leading to an expectation of lower [α/Fe] in general. We caution that we currently do not know what the [α/Fe] of intermediate-redshift minor mergers could be. Nevertheless, we are led to an expectation that the intermediate-age stars in ETGs would on average have solar [α/Fe] and [Fe/H] either slightly above or even significantly below the solar value (the blue ellipse in Fig. 1). Indeed, Coelho et al. (2009) found that for the galaxy M32 the metal-poor component of their stellar population fit corresponds to a younger population than the metal-rich one.
Although simple, this picture can be used to provide a framework for interpreting the results in this paper. Complications arise, however, that need to be acknowledged. For example, Pipino et al. (2009) show that semi-analytic models cannot reproduce the [α/Fe]-mass relations yet, owing to inadequate treatment of late mergers, thus clearly implying that we do not have sufficient theoretical understanding of low-mass galaxy evolution in simulations. More generally, Hirschmann et al. (2013) conclud that, while it is clear that accretion, minor merging, major merging, star formation efficiency, and winds must all work together to form those galaxies we see today, their exact interplay is still not sufficiently understood. Simulations thus do not produce a satisfying population of galaxies overall. Observationally, and in the direct context of this contribution, this is illustrated by the recent work of Renzini & Andreon (2014), who concluded from data on the enrichment of the intracluster medium “that even the most massive galaxies must have lost a major fraction of the metals they have produced”.
An uncertainty that much more directly affects our distinction in SLF and ACC ETGs has been spelled out in the works of Arimoto & Yoshii (1986) and Vazdekis et al. (1996). Indeed, it turns out that metallicity may not monotonously increase with age for the most massive ETGs even in absence of accretion events. After a peak in metallicity at a certain age, this metallicity starts declining again because of the late mass loss by the abundant low-metallicity stars still present in the galaxy. Comparison with Fig. 11 of Vazdekis et al. (1996) reveals that the peak in metallicity may be reached very rapidly (within 2 or 3 Gyr after formation of the galaxy). However, the decline in metallicity remains subtle and is of order 0.2 dex in [Z] until redshift zero. We come back to this value in Sect. 6.3.
The present contribution introduces extensions to the method of spectral fitting. We therefore present our algorithm in detail in Sect. 3 and then spend significant space on understanding any possible method-intrinsic effects, such as degeneracies, in Sect. 4. Finally we also verify in detail that the method is applicable to the data at hand in Sect. 5. Readers wishing to read about the scientific results first can jump directly to Sect. 6.
2. Sample
For this paper we are interested in a significant sample of early-type galaxies (ETGs) with high signal-to-noise ratio (S/N) spectra. With ETG we mean a “spectral ETG”, i.e. essentially a galaxy with a spectrum dominated by old stars. Such a sample is easily selected from the MPA/JHU catalogs1 for SDSS DR7 (Abazajian et al. 2009), containing general information about the galaxy’s spectrum (S/N, stellar velocity dispersion), emission lines and absorption indices, as well as photometric information. ETGs in the SDSS have been studied in many contributions to the literature (e.g., Bernardi et al. 2003; Zhu et al. 2010). The specific reason to revisit these spectra is that they provide a large sample of readily available high quality spectra with which to test the power of the new models and the new methodology we apply here. In particular we adopt the following criteria to select our sample:
-
S/N larger than 40;
-
r-band concentration index larger or equal to 2.8;
-
unclassifiable, i.e. with S/N< 3 in all of the BPT diagram emission lines, thus excluding AGN;
-
velocity dispersion between 40 and 375 km s-1;
-
eliminate duplicate observations, keeping the one with higher S/N.
We further estimate stellar masses from absorption indices following the exact same method as Gallazzi et al. (2005). The sample is thus further restricted to those galaxies for which a spectroscopic stellar mass could be obtained (i.e. for which the set of five absorption features, r − i fiber color and z-band model magnitude are available). We use the 16, 50, 84 percentiles of the probability distribution function for the lower 1σ errorbar, the actual value and the upper 1σ error bar, respectively. These masses are normalized to the z-band modelmag and a Chabrier IMF.
These criteria give us a sample of 2286 pure early-type galaxies. This sample has been S/N selected and it would thus be a daunting task to follow through all selection criteria to infer how representative the sample is for all early-type galaxies. We thus refrain from such an exercise. The S/N distribution of our sample is shown in Fig. 2.
 |
Fig. 2 S/N distribution of our sample galaxies. |
3. Stellar population models and fitting procedure
Stellar population models exploring the effects of varying element abundance ratios on specific line indices have been driving our understanding of ETG formation and evolution (e.g., Lee et al. 2009). In particular, studying the dependancies of single elements (e.g., Smith et al. 2009; Worthey et al. 2014) is interesting in its own right, but is currently not possible for the goals of this paper for two reasons: 1) We want to study SEHs in a resolved way and it would be difficult to control physical degeneracies. 2) We need spectral models with a restricted set of free parameters to keep our algorithms mathematically under control. Taking e.g. the recent contribution by Worthey et al. (2014) as a comparison and referring back to Fig. 1 we can highlight one important point of our paper. These authors consider abundance distribution functions (ADFs) within each ETG to address the similar questions to the present contribution, namely how abundance ratios are spread within ETGs. However, due to the nature of the fitting algorithm Worthey et al. (2014) have to parameterize these ADFs, thus leading to a prior assumption on the SEHs possible in the galaxies they analyze. Because knowledge of the real SEHs of ETGs is so scarce we do not believe that putting such a prior is warranted yet. In support of our approach we also highlight that the use of [α/Fe] as a single parameter involving a set of elements is also justified by the findings of Johansson et al. (2012), who find that the correlations of [O/Fe], [Mg/Fe], [C/Fe] with velocity dispersion are identical for ETGs. In general, models capable of predicting the effects of α-elements on the full optical spectrum of stellar populations are starting to become less rare, see Coelho et al. (2007), Koleva et al. (2008b), Walcher et al. (2009), Percival et al. (2009), Vazdekis et al. (2011), Conroy & van Dokkum (2012), Prugniel & Koleva (2012), Vazdekis et al. (2015).
We use an updated version of the differential stellar population models presented in Walcher et al. (2009, hereafter W09) and we refer to that paper for a full description. In brief, to compute the models we combine the simple stellar population (SSP) spectra from fully theoretical stellar population models by Coelho et al. (2007) (based on isochrones from Weiss et al. 2007) with semi-empirical models by Vazdekis et al. (2010) and Falcón-Barroso et al. (2011). Of the Vazdekis et al. (2010) models we only use those with solar metallicity and abundance ratios. The model spectra for non-solar [Fe/H] and [α/Fe] values are then obtained using the C07 models of the same age as a prediction for the effects of varying [Fe/H] and [α/Fe]. We show in W09 that these models yield reliable values for the ages, the [Fe/H] and the [α/Fe] values of Milky Way globular clusters within the range covered by our models.
During the course of the project we realized that the parameter coverage of the Coelho et al. (2007) models (age: 3−12 Gyr, [Fe/H]: −0.5, −0.25, 0.0, 0.2 and [α/Fe]: 0.0, 0.4) lead to “edge effects”, in the sense that when fitting a stellar population older than 12 Gyr and with solar abundance ratios, age-metallicity degeneracy will drive the best-fitting model to have super-solar [Fe/H] and [α/Fe]. We have therefore decided to extrapolate the grid of theoretical models to an age range of 2−13 Gyr, [Fe/H] values of −0.5, −0.25, 0.0, 0.2 and [α/Fe] values of −0.2, 0.0, 0.2, 0.4. The theoretical spectra are interpolated linearly in a multi-dimensional space with the axes: pixel, log(Flux), age, [Fe/H] and [α/Fe] before being applied to the semi-empirical models.
Metallicity is defined as a combination of [Fe/H] and [α/Fe], explicitly for our models [Z] = [Fe/H] + 0.75 * [α/Fe] (see Coelho et al. 2007).
Although we select galaxies for our analysis that have all signs of lacking young stellar populations, we cannot rule out any contribution. In the literature, rejuvenation of ETGs is still a controversial subject with findings related to sample definition, analysis methods and uncertainties related to late, hot phases of stellar evolution ([Fe/H] Yi et al. 2005; Sánchez-Blázquez et al. 2009; Ocvirk 2010; Thomas et al. 2010). We therefore extend our template set by five templates from Vazdekis et al. (2010) with younger ages (1, 0.63, 0.32, 0.1, 0.06 Gyr). These do not have varying [α/Fe] ratios. We include these templates into the fitting in all cases and use them to verify that indeed contributions by younger stellar populations are negligible in the data we analyze.
Full spectrum fitting has survived a number of stringent tests ([Fe/H] Cid Fernandes et al. 2005; Koleva et al. 2008a) and is becoming increasingly popular as a method to derive stellar population properties of galaxies ([Fe/H] Heavens et al. 2000; Cappellari & Emsellem 2004; Cid Fernandes et al. 2013, to cite but a few). For analysis of the spectra using full spectrum fitting we use the software paradise . The underlying algorithm is fully described in Appendix A and the same software was used in our previous papers (Walcher et al. 2006, 2009). In one sentence, paradise fits model template spectra to observed spectra taking into account the uncertainties on each spectral pixel, solving for the kinematics of the stellar population and allowing very flexible masking of wavelength regions due to quality concerns.
4. Analysis of mock galaxy spectra
The goal of this paper is to shed new light on the SEHs of early-type galaxies to understand their formation history. Before we can do so, we must verify that our method is in principle capable of providing us with SEHs. In the present section we describe the creation of mock galaxy spectra and their analysis. As we use the same models for the mock spectra as we then use to analyze these, we can only test the accuracy and intrinsic degeneracies of our method under the assumption that the model is a perfect representation of the data. We performed an independent test of the accuracy of our models as compared to globular cluster spectra in Walcher et al. (2009). In the remainder of the paper we report what we find when fitting the wavelength range 4828 to 5364A. This wavelength range has been shown in W09 to most accurately recover age, [Fe/H] and [alpha/Fe] for bulge globular clusters.
The main conclusion of this section is that we can recover the luminosity-weighted average properties of ETGs and the element abundance patterns of their old stars with good accuracy and precision. Recovering the properties of intermediate-age stars is a more challenging task.
4.1. Mock galaxy spectra
As motivated in the introduction, we analyze the SEHs of our galaxies in three bins of age τ, namely τ ≤ 1.5 Gyr (called young age bin from now on), 1.5 Gyr <τ ≤ 9.5 Gyr (called intermediate-age bin, subscript i), τ> 9.5 Gyr (called old age bin, subscript o). We do not attempt a better time resolution for the reasons given below and because experience with full spectrum fitting shows that three bins in age are a reasonable assumption for the best age resolution one can hope for in the star formation history (compare e.g. Cid Fernandes et al. 2005; Tojeiro et al. 2007). We therefore construct our mock galaxies by separating our SSPs in the three age bins above and assuming a constant SFR within each of these bins. We then go on to neglect the youngest age bin, as any young stars (or hot stars, to be more precise), if present, represent a very small fraction of the light for the large majority of early-type galaxies (90% Thomas et al. 2010).
We then compute a grid of mock galaxies over the following parameter ranges: [Fe/H]i and [Fe/H]o vary between −0.5 and 0.2, [α/Fe]i and [α/Fe]o very between −0.2 and 0.4 and the mass contribution of the intermediate stars to the total stellar mass may vary between 0 and 100%. We note that we thus do not assume an exponentially falling star formation history at any point. On the other hand, for this exercise we divide the SFH of our mock galaxies in two age bins with constant star formation rate. Our grid of models is probably more varied than real early-type galaxies, in particular concerning the contribution of intermediate-age stars, and thus any conclusions we derive from here is applicable to a more restricted set of SFHs as well. All model spectra are convolved with a velocity dispersion of 150 km s-1. We verified that our results do not depend on velocity dispersion, as long as this parameter is correctly determined. One of the advantages of full spectrum fitting is that the velocity dispersion is determined simultaneously with the stellar population analysis, thus avoiding some of the potential pitfalls with the more classical Lick index method. Guided by the S/N distribution of our sample (see Fig. 2), we perturb the spectra assuming Gaussian uncertainties to the lowest S/N ratio of the sample, i.e. 40.
4.2. Recovery of light-weighted mean quantities
We now use paradise to recover the following quantities:
-
V-band light-weighted mean parameters age, [Fe/H], [α/Fe], Z
-
V-band light-weighted mean parameters for old component ageo, [Fe/H]o, [α/Fe]o, Zo
-
V-band light-weighted mean parameters for intermediate component agei, [Fe/H]i, [α/Fe]i, Zi
The mathematical equation defining these values as implemented by paradise is 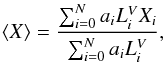 (1)where ai are the weights for N templates with properties Xi as well as V-band luminosities
(1)where ai are the weights for N templates with properties Xi as well as V-band luminosities 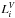 . This equation can also be used to define the same quantities over a restricted range of SSPs that are part of the SEH (e.g. those representing only old or only intermediate-age stars) by suitably restricting the indices over which the sum is computed.
. This equation can also be used to define the same quantities over a restricted range of SSPs that are part of the SEH (e.g. those representing only old or only intermediate-age stars) by suitably restricting the indices over which the sum is computed.
 |
Fig. 3 Simulations of parameter recovery for a randomized coverage of parameter space and a total of 3000 mock galaxies. |
Our results for the overall light-weighted quantities, i.e. when the index i in Eq. (1) runs over all templates, are summarized in Fig. 3.
Koleva et al. (2008b) and Sánchez-Blázquez et al. (2011) study the influence of a metallicity – velocity dispersion degeneracy, implying that when both parameters are fitted simultaneously, the velocity dispersion may be underestimated simultaneously with the metallicity or [Fe/H]. We find the opposite effect in our simulations, i.e. for lower values of [Fe/H] velocity dispersion will be over-estimated slightly (for our fiducial value of 150 km s-1 the overestimate is of order 10 km s-1 at [Fe/H] = −0.3). We observe no dependence on [α/Fe]. Sánchez-Blázquez et al. (2011) emphasize that the effect is larger for young stellar populations, while our study here focusses on old stellar populations. Also, we are not interested in the velocity dispersions here, but in the parameters age, [Fe/H] and [α/Fe]. Any influence of this metallicity – velocity dispersion degeneracy would show up in our study as a bias in [Fe/H] recovery. Indeed, this may be the reason for the slight deviation from a perfect recovery at low metallicities observed in our simulations.
We also explicitly test the influence of either normalizing (rectifying) or not normalizing the spectra with a pseudo-continuum based on a running mean. We find that the fit with non-normalized continuum is formally slightly better, as expected due to the higher information content. We caution, however, that this is true for the ideal case we can test here, i.e. where the model and the “data” ideally match each other. Even a slight problem with flux calibration would potentially bias our results, we thus always normalize spectra from real data below.
 |
Fig. 4 Degeneracies in the overall mean light-weighted values as difference plots. Each Δ is defined as the recovered minus the true value. The dominating degeneracy occurs between age and [Fe/H], while age and [α/Fe] show only weak degeneracy. |
The age-metallicity degeneracy is a long-standing problem in the study of old stellar populations. In the lower left panel in Fig. 4 one can read of that the effect is of order 0.1 dex in [Fe/H] per 2 Gyr. Here we refrain from performing a formal fit to the simulated data. This would only pretend to provide more precise information as it is entirely unclear how the mock galaxy sample would relate to either the sample under study here or the real full galaxy population. Comparison with Thomas et al. (2005, their Fig. 3), Cid Fernandes et al. (2005, their Fig. 6), and Sánchez-Blázquez et al. (2011, their Fig. 7) shows that the trends are qualitatively the same, confirming once more that this effect is physical and does not depend on the fitting algorithm being applied. In particular it is surprisingly independent of whether the fitted stellar population is a SSP or the fitting algorithm allows for a more complex star formation history. To be more precise, the degeneracy is between [Fe/H] and age. There are degeneracies between age and [α/Fe], and between [Fe/H] and [α/Fe], but these are much less pronounced.
A new problem in the analysis of integrated spectra from ETGs are the many lines of evidence for a variation in the initial mass function of galaxies (van Dokkum & Conroy 2010b; Cappellari et al. 2012). Ferré-Mateu et al. (2014) explore how such variations would affect the analysis of the SFHs of ETGs and find that complete neglect of IMF variations would potentially significantly affect the results in particular in terms of the relative contribution of old and intermediate-age stars. Incorporating this caveat into our analysis is at present beyond the scope of this contribution.
As described in Appendix A, paradise performs a bootstrap estimate of errors on the recovered stellar population parameters. Figure 5 verifies that these errorbars are appropriate. Indeed, for correctly estimated Gaussian errorbars, the histogram of the quantity Δ(X) /σX should be a Gaussian with width 1, where Δ(X) = Xmeasured − Xtrue. This is almost exactly the case for age and the widths of the distributions in [Fe/H] and [α/Fe]. There are systematic offsets for [Fe/H] and [α/Fe]. Given the average error bars from the simulations these translate to a systematic overestimation of [Fe/H] by 0.07 dex and an underestimation of [α/Fe] by 0.03 dex. Figure 3 shows that the largest offset of ~0.1 dex occurs at low values of [Fe/H].
 |
Fig. 5 Verification of the uncertainties derived by the fitting routine through bootstrap. Each Δ is defined as the recovered minus the true value, but this time divided by the size of the error bar (denoted σ) as output by the fitting routine. For perfectly Gaussian errors, the distribution should coincide with a Gaussian of width one and normalized to the same total area (dotted line). |
4.3. Can we resolve the enrichment histories?
 |
Fig. 6 Simulations of parameter recovery when splitting the star formation and enrichment history at a fiducial age of 9.5 Gyr. The dashed line in the lower right panel is a formal fit to the points in the data with a slope of ~0.3. |
The term SEH implies the wish to represent the relation between age and abundance for each galaxy. To our knowledge this has not been done in the literature. While de La Rosa et al. (2011) have applied the spectral fitting technique to the SFH, they have not actually resolved the SEH, preferring to quote a single value for the enhancement in α-elements. We thus here investigate in detail, whether our method is able to produce this kind of information reliably. We thus repeat the same plots of input vs. recovered quantities as in Sect. 4.2 for the properties [Fe/H]o, [α/Fe]o, [Fe/H]i, [α/Fe]i. The result is shown in Fig. 6. To economize some space, we do not plot ages and metallicities for the old and intermediate distinction. The reason is that the ages are fixed already by the way we separate the star formation history into bins and its recovered distribution therefore carries no real meaning (although it can vary slightly within the width of that bin). Metallicity on the other hand is only a trivial combination of [Fe/H] and [α/Fe].
Figure 6 looks encouraging concerning the old stars in that clear relations scattering around the one-to-one line exist, with an RMS width of about 0.1 dex. While it may not seem intuitive at first sight that the properties of the older stellar population, which contributes on average less to the total light than the younger or intermediate-age population, would be well-determined from a fit to the integrated spectrum, this is actually in line with the findings of Serra & Trager (2007). These authors found that the SSP-equivalent chemical composition depends mainly on the chemical composition of the older of two constituting stellar populations. It is also in line with theoretical expectations that the effects of [α/Fe] (in particular Mg) are stronger for cooler stars ([Fe/H] Cassisi et al. 2004; Coelho et al. 2007; Sansom et al. 2013).
This would in turn predict that the properties of the younger population are less well traced. Indeed, in the case of [Fe/H]i and [α/Fe]i the slope of the relation is clearly lower than one. A formal fit (the dashed line) yields slopes of ~0.3. To investigate the origin of this slope we have also investigated degeneracies between different quantities after this split into old and intermediate-age population. The same plots as in Fig. 4 for the separation of the SEH into old and intermediate populations shows a much larger scatter, but no noticeable increase in the degeneracies, thus these plots are not shown here in the interest of space. However, and as shown in Fig. 7, the dominating degeneracies are those between [Fe/H]i and [Fe/H]o and between [α/Fe]i and [α/Fe]o.
 |
Fig. 7 The dominating degeneracies in the mean light-weighted values when separating SEHs into intermediate and old stars are those between the same properties of the two stellar generations. Each Δ is defined as the recovered minus the true value. |
At this point we remind the reader of the classification into SLF and ACC galaxies introduced in Sect. 1. Indeed, at specific points in this paper we separate galaxies in two types: 1) Those where [Fe/H]o< [Fe/H]i. For these the [Fe/H] evolution with time is consistent with self-enrichment by SNe Ia and these are therefore termed SLF-ETGs (represented by yellow dots in Figs. 17 to 22 below). 2) Those galaxies where [Fe/H]o> [Fe/H]i. Those are not consistent with self-enrichment and we infer that some accretion of material must have taken place – whether these were mergers, gas accretion or anything else we remain agnostic about (such as winds redistributing elements within a galaxy, see Pipino et al. 2006). Nevertheless, for conciseness we term those merger-accretion or ACC-ETGs (pink color in same figures). A more in-depth discussion of the physical usefulness of this distinction is given in Sect. 8.3.
We now explore how robust such a classification would be to degeneracies. Our input mock galaxy catalogue contains 50% SLF and 50% ACC galaxies. After fitting, 81% of the SLF galaxies would be correctly identified but only 33% of the ACC galaxies. Furthermore, after fitting we would identify 74% of the sample as SLF galaxies and 26% as ACC galaxies. Finally, the number that is probably of most interest is the percentage of galaxies in each half of the parameters space that actually is what it pretends to be: The percentage of galaxies that would be classified as SLF galaxies after fitting and that really are SLF galaxies is 55%, while the percentage of galaxies that would be classified as ACC after fitting and that are really ACC galaxies is 65%. While these numbers are sobering, one should remember that they apply to a sample of mock galaxies that completely fills the parameter space available to our models and at a specified S/N of 40. This does not represent the real distribution of galaxies in this parameter space as we shall see below. In particular we shall explore in an observationally motivated way how our conclusions depend on the exact location of the separation [Fe/H]o< [Fe/H]i + Δ, i.e. how this classification behaves within a range of −0.4 < Δ < 0.4.
 |
Fig. 8 Comparison of the original distribution of parameters (upper row) vs. the one recovered after the fitting process (lower row). We show the two parameter spaces that are of most interest in the remainder of the paper, namely [Fe/H]i vs. [Fe/H]o and [α/Fe]i vs. [α/Fe]o. Left panel: the case in which the total library of mock galaxies is analyzed. Right panel: the case in which only mock galaxies with −0.2 ⟨ [Fe/H]i, [Fe/H]o⟨ 0.0 are analyzed. |
Besides direct classification we use another, more statistically minded method to gauge the distribution of observed galaxies in the planes of [Fe/H]i vs. [Fe/H]o and [α/Fe]i vs. [α/Fe]o, namely the posterior distribution of fitted galaxies. We show the general case in Fig. 8: one starting with a uniform distribution of mock galaxies in parameter space. For reasons to be seen later, another interesting case is the one where all galaxies start out in a narrow range of [Fe/H]i and [Fe/H]o abundances. We have chosen −0.2 < [Fe/H]i, [Fe/H]o< 0.0. Clearly both cases produce significantly different posterior distributions in parameter space that can be used to constrain the real distribution of parameters to some extent – or at least can be used to exclude some real parameter distributions.
In this section we have assessed the uncertainties intrinsic to our method under the assumption that the model is a perfect representation of the data. We have found that these uncertainties exist, but that we can understand, describe and quantify them.
5. Fitting the observed spectra
We now proceed to fit the sample described in Sect. 2 with the method described in Sect. 4. We did not change the setup of the fitting in any way. This means that we fit the spectra with the same models, the same continuum rectification, and all other parameters being equal. There is only a slight difference in the spectra that may affect the fitting procedure to some extent.
This is seen in the stacked fitting residual vectors of all galaxies as shown in Fig. 9. Our sample has been selected to contain emission-line free galaxies as judged by Brinchmann et al. (2004). However, we find that the residuals do contain emission lines of Hβ and [OIII]. We attribute this finding to our excellent stellar population modeling and fitting procedure as well as to conservative estimates of emission line absence. In other words, while to the trained eye emission line residuals in stacked spectra may seem obvious, for an automatic detection procedure it is difficult to attribute a statistical significance to these features per galaxy, given similar-sized residuals in nearby regions of the spectrum. Emission lines affect only small regions of the spectrum and thus should not affect our overall results. In many cases they are masked away by our automatic outlier rejection in paradise (see Appendix A). We have verified that all our simulation results are independent of the potential missing information in the emission line region by applying an appropriate mask in wavelength space to the mock galaxies and rerunning all simulations. We found no difference in the results.
As a side-note we mention the residual absorption feature around 4700 Å. Its origin is unclear, but it does not affect our measurements as it is outside our fitted wavelength range.
We also investigated the presence of any problems with data quality. Given the precision we are claiming to reach here (not much more than one percent in residual) we might be prone to data quality problems at a level not often seen otherwise. Problems might be present in the SDSS data, but also in the stellar templates. We note, however, that Fig. 9 does not indicate such problems. Indeed, the lower panel shows residuals in the observed frame where data problems such as sky emission line residuals should appear. The only obvious sky residual is at the very red end of the wavelength range shown, but way outside our fitted wavelength range. A paper dealing in much more detail with template mismatch vs. data quality is in preparation.
 |
Fig. 9 Mean residual vector and its standard deviation from all galaxies in the sample. The upper plot indicates the residuals in the rest frame of the galaxies, the yellow region has actually not been used to determine the best fit. [OIII] and Hβ emission lines are labelled and clearly visible. The Mgb feature is also indicated for reference, but does not show evidence of specific mismatch. The lower plot shows the observed frame residuals indicating no major concern with the data. |
Another way to assess our fit quality is to compare the cumulative histogram of χ2 obtained from the spectra in our data with the one expected from statistics, i.e. the χ2-distribution. This is done in Fig. 10, assuming 257 degrees of freedom for our fitting procedure, as appropriate after taking into account the number of fitted pixels and the number of free parameters. The distributions do not match perfectly, but they are clearly very similar, both in shape and location. We believe this indicates that the fitting of SDSS spectra is indeed in the realm governed by χ2 statistics, once the models are sophisticated enough and when restricting to a well-known wavelength range.
 |
Fig. 10 Cumulative histogram of χ2 values obtained from the data (solid line) with the χ2 distribution expected from statistics (dotted line) for 257 degrees of freedom. |
In Sect. 4 we used a velocity dispersion of 150 km s-1 for all tests, although the velocity dispersion was left a free parameter in the fitting. Velocity dispersion is clearly different for every observed galaxy. We can, however, feed the SDSS pipeline velocity dispersion as a starting value to paradise , thereby essentially mimicking the fact that we know the velocity dispersion for the simulated galaxies. Indeed, we find that we do recover the velocity dispersion from the SDSS very well, see Fig. 112.
 |
Fig. 11 Comparison between the velocity dispersion from SDSS DR7 and those obtained in this work. |
The output of the fitting are tables with all parameters, such as mean light-weighted age ([Fe/H], [α/Fe]) of the entire spectrum, the same parameters only for the “old” stars (i.e. older than 9.5 Gyr) and for the “intermediate-age” stars (i.e. younger than 9.5 Gyr). Typical errorbars on our parameters are 0.2 Gyr on age and 0.01 dex on [α/Fe] and [Fe/H]. These errorbars reflect random errors and degeneracies, but not model-related errors and systematic problems with the recovery. This can be compared with the typical errors quoted in one of the classical studies of the field. For definiteness we choose Thomas et al. (2005), without prejudice to later or earlier results. They quote typical errors of 1.48 Gyr in age, 0.04 dex in total metallicity, and 0.02 dex in [Fe/H] ratio, although it needs to be said for clarity that these earlier errorbars only take into account the formal uncertainties on the data. Our errorbars also include degeneracies in the stellar population mix. In the more recent paper by Johansson et al. (2012) the uncertainty in [O/Fe] at S/N ~ 40 in the r-band is given as approximately 0.05 dex, but it needs to be kept in mind that this is the uncertainty on a single element, while we group all α-elements together.
Another important point to mention is that none of the derived galaxy ages are older than 13 Gyr, as we show in Sect. 6. While this is predetermined from the range of model spectra in use, there is also no hint of an edge effect in the sense the galaxies that would be older than 13 Gyr cannot be fitted and therefore for those galaxies a higher metallicity would be fitted to compensate. We explicitly tested that this edge effect is present if we restrict our template library to SSPs with ages younger than 13 Gyr.
6. Results
We now discuss our findings in terms of correlations between the parameters we determined ourselves, i.e. ages, [Fe/H] and [α/Fe] and those available for our galaxies i.e. stellar mass M* and velocity dispersion σ.
6.1. The σ-α, M*-α and age-α relations
In Fig. 12 we plot [Fe/H] and [α/Fe] versus velocity dispersion σ, stellar mass M* and mean light-weighted age. We quantify the presence or absence of correlations by means of Spearman rank coefficient tests3 and by means of formal fits to each set of two parameters combinations using the LINFIT module in IDL. The results of the fits are given in Table 1. We confirm correlations between log(σ) as well as log(M*/M⊙) and [α/Fe] as found in previous work (see Sect. 8.1). In Fig. 12 we also see a strong correlation between age and [α/Fe] as well as [Fe/H] in the sense that [α/Fe] decreases for younger light weighted mean age of the galaxy, while [Fe/H] increases.
There seem to be only weak correlations between [Fe/H] and log(σ). However, Johansson et al. (2012) show that when the sample is decomposed into age bins, each age bin by itself shows a strong correlation with log(σ). In the interest of space we refrain from repeating the exercise.
Correlation strengths for light-weighted mean parameters.
Additionally the relation between age and [α/Fe] shows a clear change of slope at age ~9 Gyr. We have fitted the two regimes separately and find that [α/Fe] = −0.01 ± 0.004 + 0.01 ± 0.001 · age for galaxies younger than 9 Gyr, while [α/Fe] = −0.20 ± 0.007 + 0.03 ± 0.001 · age for galaxies older than 9 Gyr. For both regimes the probability of the absence of any correlation is zero.
 |
Fig. 12 Correlations of [Fe/H] and [α/Fe] with velocity dispersion, stellar mass and mean light-weighted age for our sample galaxies. It is clear that the tightest relations are those with age. Note also the change of slope in the relation between age and [α/Fe] ~ 9 Gyr. Average error bars are given in the upper right corner of each panel and spearman rank correlation coefficients are also noted. |
The two rightmost panels of Fig. 12 already indicate a correlation between [α/Fe] and [Fe/H], which we explicitly plot in Fig. 13. We find that early-type galaxies all have on average a total metallicity that is roughly solar. It is the ratio between the abundances of Fe and the α-elements that changes between galaxies.
6.2. Separating the old and intermediate components
We now show results for resolved SEHs, i.e. looking at the abundance ratios of old and intermediate stellar populations separately. Before we do so, as a cautionary remark, it is worth emphasizing that the uncertainty bars include the uncertainties introduced by the degeneracies characterizing galaxy evolution. Thus a direct visual comparison of the size of the error bar and the scatter in the figures is misleading. The size of the error bar indeed denotes the range of possible values for each single galaxy. However, on average, galaxies will tend to be assigned the mean value of that possible range. Scatter in figures is mainly driven by real observational uncertainties and does not represent the degeneracy uncertainties as assessed by paradise . That said, mean uncertainties on our parameters are 0.17 dex for [Fe/H]i, 0.14 dex for [Fe/H]o, 0.12 for [α/Fe]i, and 0.13 for [α/Fe]o.
First we repeat in Fig. 14 the upper panel of Fig. 1, i.e. we show the non-binned average star formation history of all galaxies in our sample. As this is the observable, we show the star formation history in terms of the luminosity contributions of stars of each specified age to the total luminosity of each galaxy. It is noteworthy that several peaks in the star formation history appear, namely at 13 Gyr, 9 Gyr and a somewhat broader one around 6 Gyr. Our SSPs are sampled in steps of 1 Gyr, therefore intermediate ages could in principle be assigned significant weights by paradise . On one hand it is entirely possible that this is an artifact of our fitting procedure, given that such features do not appear in the overall star formation history of the universe (Lilly-Madau plot). On the other hand, the two older episodes of star formation seem entirely compatible with the classical two-infall scenario of chemical evolution (Chiappini et al. 1997) that was originally proposed for the Milky Way. Note that these two oldest peaks also contribute to justifying our separation into old and intermediate-age stars at a lookback time of 9.5 Gyr. We come back to this point below when discussing SLF vs. ACC-ETG percentages.
 |
Fig. 13 Correlation between [Fe/H] vs. [α/Fe] for the luminosity weighted average properties of the ETGs in our sample. The thick solid line is a line of constant, solar metallicity (Z = 0.017). The two dashed line illustrate the extremes of the ETG locus, i.e. for [ Z ] = −0.15 and [ Z ] = 0.18. |
 |
Fig. 14 Average star formation history of all galaxies in the observed sample in terms of the present day contribution of each stellar population to the total luminosity of the galaxy. All galaxies contribute equally to this average, i.e. the total luminosity for each galaxy has been normalized to one before averaging. |
Finally, there is a small peak at less than 1 Gyr which is outside the coverage of our [α/Fe]-enhanced SSP templates. As described in Sect. 3 we include five templates with younger ages, but with solar element ratios only. The total contribution to the light of the population younger than 2 Gyr is however less than 5%. Due to its lower mass to light ratio than the older stellar populations this translates to an even smaller contribution to the total mass of the galaxy. We thus confirm that ETGs harbor very little young stars – maybe even none, if currently unmodeled old and hot stellar populations indeed do play a role (see e.g. Ocvirk 2010).
 |
Fig. 15 Correlations of the [Fe/H]o and [α/Fe]o with the global properties of the sample galaxies σ, M*, and age. Average error bars are given in the upper right corner of each panel and spearman rank correlation coefficients are also noted. |
It is interesting to start the analysis with plotting the properties of the old stellar populations vs. the global parameters of their host galaxies. We refrain from doing so for the intermediate-age populations due to the strong degeneracies we identified in Sect. 4.3 and the lower recovery success for the intermediate component with respect to the old one we identified there. Also, our sample is dominated by galaxies in which the old stellar population contributes more than half of the total light, contributing to possible uncertainties in the properties of the intermediate-age stellar populations. Figure 15 shows that the correlations seen for the global stellar populations do not hold up for the older stars in the galaxies (compare also Table 2). Indeed, while the Spearman rank test indicates a very low probability for the dependence of [α/Fe]o and [Fe/H]o on age to be spurious, inspection of the plot tells another story. There is a cloud of points at older ages, while the galaxies with younger ages show much larger scatter. This can be understood as being caused by difficulties in accurately estimating [α/Fe]o and [Fe/H]o for galaxies with significant intermediate-age populations. We therefore attach no importance to these relations. For σ and M* vs. [α/Fe]o, the Spearman test indicates weak correlation and indicates a high probability (0.68) of no correlation for M* vs. [α/Fe]o. We are thus left with the indication that [Fe/H]o depends positively on mass as parameterized by either σ or M*, but more strongly on the former. This correlation is driven mainly by the presence of objects with low [Fe/H]o at low σ values. Overall these trends are opposite to the average properties, where [α/Fe] depends clearly on mass and [Fe/H] does not.
 |
Fig. 16 Relation between [Fe/H]o vs. [α/Fe]o, the thick line is a line of constant, solar metallicity (Z = 0.017). This is the same as Fig. 13, but only for the stars older than 9.5 Gyr in each galaxy. The old stars in early-type galaxies, have on average high total metallicity, significantly super-solar. Average error bars are shown in the upper right corner. |
The two rightmost panels of Fig. 15 already indicate that the correlation between [α/Fe] and [Fe/H] that is valid on average for early-type galaxies does not hold up when considering the old stars only. Indeed, in Fig. 16 we find that old stars in early-type galaxies have on average super-solar metallicity, where both [Fe/H]o and [α/Fe]o are super-solar. That these properties seem to be independent of mass (see Fig. 15) might be one of the most puzzling findings of this paper.
Correlation strengths old stars only.
6.3. Exploring the possible dichotomy SLF vs. ACC
 |
Fig. 17 Left panels: distribution of mean light-weighted [Fe/H] and [α/Fe] for the old vs. intermediate sub-populations. Galaxies in yellow are those where [Fe/H]o< [Fe/H]i−0.15 (SLF-ETGs), pink where [Fe/H]o> [Fe/H]i+0.15 (ACC-ETGs). Galaxies with uncertain classification are shown in black. Average uncertainties including all degeneracies are shown in the upper left corners. Right panels: age dependence of [Fe/H] and [α/Fe] within each galaxy, i.e. their enrichment history. Galaxies with uncertain classification have been omitted for clarity. |
In Fig. 17 we show the distribution of [Fe/H] and [α/Fe] of the intermediate vs. the old component (left panels). In [Fe/H] galaxies can lie both above the identity line and below it. In [α/Fe], almost all galaxies lie below the identity line, with a few slight outliers that can be thought of as being due to uncertainties. When looking back at Fig. 8 and the discussion in Sect. 4.3, it is obvious that any statement on the distribution in these panels must take into account the uncertainties due to the degeneracies in properties between old and intermediate-age stars. In turns out it is easier to discuss the results in terms of what the data are incompatible with and this is what we do.
 |
Fig. 18 Correlations of [Fe/H] and [α/Fe] with velocity dispersion, stellar mass and mean light-weighted age for our sample galaxies (same as Fig. 12). Colors reproduce the classification from Fig. 17 into SLF-ETGs (yellow) and ACC-ETGs (pink). The mean for each subpopulation is also shown as a large square with black borders. Galaxies that could not be reliably classified are shown as black dots. |
The distribution of points in the upper left panel on Fig. 17 is incompatible with a flat distribution in that plane. I.e. early-type galaxies do not have a random distribution of [Fe/H]i and [Fe/H]o. Rather their distribution is more similar to the right panels in Fig. 8, where the underlying sample had a narrow distribution of [Fe/H]i and [Fe/H]o centered around −0.1 for both.
The distribution of points in the lower left panel of Fig. 17 is equally incompatible with a flat distribution in that plane. I.e. early-type galaxies do not show a random distribution of [α/Fe]i and [α/Fe]o. It seems rather secure that the oldest generation of stars has a high [α/Fe] ratio, higher than 0.1, whereas the intermediate-age stars have a lower ratio of [α/Fe], certainly below 0.1 and going as low as our model permits, i.e. −0.2. Note that [α/Fe] values below zero for late stellar generations are a generic prediction of chemical evolution models in massive galaxies ([Fe/H] Minchev et al. 2013, their Fig. 5). On the other hand low-mass galaxies do not necessarily show low [α/Fe]. Recchi et al. (2001) for example show that stellar winds tend to carry elements produced by SNeIa away, thus leaving behind gas with higher [α/Fe] than expected from the extent of their SFH.
Coming back to the distinction discussed in Sect. 4.3 between ETGs that are compatible with self-enrichment (SLF-ETGs) and mergers/accretion (ACC-ETGs), we wish to identify galaxies that we can reasonable safely assign to any of these categories. SLF-ETGs are those where [Fe/H]o< [Fe/H]i – Δ, and ACC-ETGs are those where [Fe/H]o> [Fe/H]i + Δ. Motivated by the sizes of the error bars quoted in the beginning of Sect. 6.2 and after some testing in the simulations, for definiteness we choose Δ = 0.15. Our results qualitatively do not depend on the exact size of Δ4. We emphasize that this choice of Δ also mitigates concerns over the subtle drop in metallicity at late times shown in the paper by Vazdekis et al. (1996) and discussed in the introduction. We call the remaining galaxies that are neither one nor the other the “gray-ETGs”. Note that for the observational results we include into the class of “gray” galaxies those galaxies that have less than 15% of light in either the old or intermediate stellar populations. This is to account for possible uncertainties in stellar population modeling and in the fitting algorithm.
For the sample of 2286 galaxies analyzed here we find that 29% belong to the ACC-ETG class. 63% are unclassifiable, but most of those would be called ACC-ETGs as well if not for the requirement to have 15% of light at least in the intermediate-age population. Only 8% of the galaxies are bona-fide SLF-ETGs, i.e. consistent with a self-enriching star formation history.
We caution that effects of degeneracies between the properties of the intermediate and old stellar populations, sample selection effects, the uncertainty on the exact boundary to be applied between old and intermediate stellar populations, specific effects of chemical evolution such as the drop in metallicity for young stars in massive ETGs, all contribute to make these numbers indicative only. To indicate the possible size of changes due to at least one of these effects we have recomputed the percentages of SLF and ACC-ETGs for a choice of 8.5 Gyr as the boundary between old and intermediate-age ETGs. We find that this inverts their relative importance, i.e. 30% of the sample would then be SLF ETGs, while only 3% bona-fide ACC-ETGs remain. This high sensitivity of the results to the adopted age boundary is due to a very low [Fe/H] abundance attributed by the fitting code to the spike in the SFH at 9 Gyr. This significantly lowers the average [Fe/H]o abundance, thus increasing the number of SLF-ETGs.
Given the magnitude of this effect, we have to carefully state our arguments for choosing 9.5 Gyr lookback time as our boundary. Indeed, we have argued in the introduction on physical grounds that 9.5 Gyr is a more physical boundary. On technical grounds, we refer to Fig. 14 which shows that the 9 Gyr age bin in the finely sampled SEH has a close significant neighboring age bin at younger age (7 Gyr), while the next significant old age bin (at 13 Gyr) is more distant in look-back time. Generally speaking, it is clear that there are significant degeneracies between the properties of adjacent bins in the reconstructed SEH. We have shown the extent of these degeneracies in Fig. 7 for the coarsest possible choice of SEH, namely an SEH with two age bins. Degeneracies only increase for an SEH with a finer age grid. Degeneracies between the 7 and 9 Gyr age bins shown in Fig. 14 are therefore much more likely than between the 9 and 13 Gyr age bins. This is the technical reason why we believe the results based on a 9.5 Gyr boundary to be more reliable and significant than those we would have obtained based on any other boundary.
Figure 18 repeats Fig. 12 but adding the information about the enrichment history classification. It is immediately clear that on average and for our sample ACC-ETGs are significantly older than SLF-ETGs (compare also Fig. 25). Also, on average SLF-ETGs have lower velocity dispersion and lower [α/Fe] than ACC-ETGs. We come back to these features in the discussion Sect. 8.
6.4. Environment
While nearly out of the focus of this paper, environment is such an important parameter for galaxy evolution that it would be foolish to leave it entirely out. Much work has been done on assessing the correlations between environment and the properties of early-type galaxies and we do not wish to simply repeat this work here, as we strongly expect to confirm it. Rather, in the interest of space, we concentrate only on the correlation of the old stellar population properties [Fe/H]o and [α/Fe]o with environment, taking into account our classification in ACC-ETGs and SLF-ETGs. We are particularly interested to see whether the initial star formation event indeed depends on environment ([Fe/H] Renzini 2006).
As a measure of environmental density we use the one by Tempel et al. (2012), specifically we use the density as derived within 8 Mpc, i.e. their parameter dens8. Their densities are based on luminosity densities around each galaxy calculated in three coordinates, i.e. two projected spatial distances and one based on redshift, the latter however including advanced techniques to suppress peculiar motions such as suppression of the finger-of-god effect. We refer to the original paper for all the details.
Perhaps surprisingly we find in Fig. 19 that the old stellar population may not be affected by environment. This is clearly different from what other authors found for the entire galaxies (Sánchez-Blázquez et al. 2006). It however agrees with inferences made in Thomas et al. (2010). These authors discuss that ETG formation has occurred in two phases, where ETG galaxy formation depended on mass only and not on environment. Rettura et al. (2010) on the other hand argue that while the environment may modulate the timescale of the star formation history for ETGs, the formation epoch is essentially independent of environment and seems to depend on mass only. We here add another piece to the puzzle in saying that for the oldest stars in each galaxy, older than 9.5 Gyr, galaxy formation seems to have been independent of mass and environment, at least for the mass range probed here.
 |
Fig. 19 Environmental density vs. light-weighted [Fe/H] and [α/Fe] (upper panels) and vs. [Fe/H]o and [α/Fe]o of only the old stars in each galaxy. The mean for each subpopulation is also shown as a large square with black borders. |
7. Aperture effects
As discussed in Sect. 1, the cores and the envelopes of ETGs may have assembled in different ways and at different times. Also, winds can redistribute elements within a galaxy (Pipino et al. 2009). Observationally, gradients in element abundances are observed for galaxies in general ([Fe/H] Sánchez et al. 2013; Pérez et al. 2013). However, for ETGs the gradients in age and [α/Fe] are observed to be small or null on average (Mehlert et al. 2003; Rawle et al. 2008; Kuntschner et al. 2010). Not so for the gradient in [Fe/H], which can be significant ([Fe/H] Spolaor et al. 2008). The SDSS uses a single fiber to observe the centers of the target galaxies. The fibers fixed aperture on the sky (3′′) covers a different fraction of the target galaxy, depending on its intrinsic size and redshift. This effect is somewhat counteracted by the effects of seeing, as seeing will also scatter light from larger radii into the fiber area in the focal plane. It is nevertheless clearly important to assess this covering fraction and the potential impact on our results. Proper aperture corrections as demonstrated in Gallazzi et al. (2008) is beyond the scope of the present paper. We also refer to the discussion in Choi et al. (2014) for another angle on the same question, albeit they work on a larger redshift range.
Figure 20 shows the dependence of key physical properties on redshift for our sample. In the uppermost panel the effects of apparent magnitude selection are obvious in that we sample more massive objects at larger distances from Apache Point Observatory. The next panel shows the dependence of the covering fraction on redshift in terms of the ratio between the fiber size and the galaxies effective radius. We use the effective radius from the SDSS pipeline surface brightness profile fit with a de Vaucouleurs profile. It illustrates that two effects nearly cancel each other: on the one hand, the higher the redshift, the larger the area covered by a fiber is physically smaller on the galaxy. On the other hand, the galaxy itself will tend to be more massive and therefore larger. The covering fraction thus depends less on redshift than the stellar mass. The next panel shows the expected non-dependence of [α/Fe] on redshift, given that [α/Fe] varies little with mass and galaxies have flat gradients if any. The final panel shows that [Fe/H] depends in an interesting way on redshift. Because of the stronger gradients and stronger dependence of [Fe/H] on mass it is nontrivial and beyond the scope of the present paper to understand this.
 |
Fig. 20 Dependence of key physical properties of our sample galaxies on redshift. From top to bottom: stellar mass, [α/Fe], age and ratio between radius covered by fiber and effective radius of the galaxy. Colors reproduce the classification from Fig. 17 into SLF-ETGs (yellow) and ACC-ETGs (pink). |
The crucial test, however, is shown in Fig. 21, where we show the dependence of [Fe/H] on covering fraction at a fixed mass (here chosen to be 10.5 < log (stellar mass/M⊙) < 11.0). There is no obvious bias to be seen, besides a potentially spurious tendency to have less [Fe/H]-rich objects at larger covering fraction. We conclude that tests on possible aperture biases are not conclusive enough to endanger any of the fairly general conclusions of this paper.
 |
Fig. 21 Dependence of [Fe/H] on coverage fraction at fixed mass. No bias is obvious. Colors reproduce the classification from Fig. 17 into SLF-ETGs (yellow) and ACC-ETGs (pink). |
Any further investigation of aperture effects, in particular as concerning the resolved SEHs, i.e. the potentially different biases on the old and intermediate-age stars) will have to await analysis of the currently on going integral field spectroscopy surveys such as CALIFA (Sánchez et al. 2012), SAMI (Allen et al. 2015), and Manga (Bundy et al. 2015).
8. Discussion
8.1. Comparison of average quantities to earlier observational work
A simple test is to situate our galaxies on the stellar mass – stellar metallicity relation as defined by Gallazzi et al. (2005) and González Delgado et al. (2014) as done in Fig. 22. The overall match is satisfactory, given the entirely different analysis methods. Note though that we use the same data as for the Gallazzi relation (although our sample is smaller) and we use their stellar masses. Any difference between the two is therefore directly tied to the derivation of the metallicities and abundance ratios. Of particular interest is the difference in slope. Both the Gallazzi et al. (2005) and the González Delgado et al. (2014) relation imply a significant slope at masses around 1011M⊙, where our analysis seems to imply none. This slope is confirmed for the case of ETGs alone in Gallazzi et al. (2006). The absence of a slope in our analysis may point to a sample selection effect at the low mass end of our sample or may be related to the overall offset in total metallicity.
 |
Fig. 22 Locus of our sample galaxies as compared to the mass-metallicity relations of (Gallazzi et al. 2005, solid line, dotted lines are 1σ scatter) and of (González Delgado et al. 2014, dashed line). While there is general agreement, the clear difference in slope within the mass range of our galaxies is interesting and may point to sample selection effects. |
Another interesting difference to earlier studies is the range covered by the [α/Fe] parameter. None of our sample galaxies scatters above 0.3 in its light-weighted average [α/Fe]. While some of the galaxies with higher [α/Fe] in earlier work ([Fe/H] Thomas et al. 2005; Kuntschner et al. 2010; Johansson et al. 2012) may be due to observational scatter, for the stacked spectra of Graves et al. (2010), this does surely not apply. Older models did not take the evolutionary effects of [α/Fe] into account and simplified the corrections for the spectral effects. They would thus underestimate the Mg feature at given α-enhancement (Coelho et al. 2007; Vazdekis et al. 2011). Really pinning down the cause of the offset is out of the scope of the present paper though.
There are many works in the literature reporting correlations between [α/Fe] and either σ or M*. Thomas et al. (2005) find slopes of 0.28 for [α/Fe] vs. log(σ) and 0.06 for [α/Fe] vs. log(M*/M⊙). Trager et al. (2000) on the other hand find a steeper slope of 0.33 for [α/Fe] vs. log(σ), similar to Nelan et al. (2005) who quote 0.31 ± 0.06 for the same slope. Finally, Bernardi et al. (2006) quote a slope of 0.32, while Graves et al. (2007) give 0.36. Our slope of 0.26 seems to lie at the low end of the scatter in the literature, which is probably tied to the lower maximum [α/Fe] reached by our analysis.
A correlation that is more rarely plotted is the one of [α/Fe] and [Fe/H] with age (Fig. 12, right panels). Correlations of age and [α/Fe] were shown in Graves et al. (2010) from stacked spectra (their Fig. 4) and per galaxy in Kuntschner et al. (2010; their Fig. 6)5. In both cases the change of slope at an approximate age of 9 Gyr is visible, while the overall normalization in [α/Fe] seems shifted higher as compared to our results by 0.05 to 0.1 dex. Due to the nature of the stacked spectra in Graves et al. (2010) and the small sample size in Kuntschner et al. (2010) we cannot comment on a comparison of the scatter around the mean relation. Although a direct comparison is difficult because of the different [α/Fe] definition, a change of slope was also seen in Gallazzi et al. (2006), albeit at ages of ~6 Gyr, instead of 9 Gyr. We also note that these results are in contrast to the earlier work of Jørgensen (1999) who found no correlation between [α/Fe] and age.
For the same correlation, it is important to heed the warnings of Thomas et al. (2005), who discuss the importance of degeneracies when using age as a parameter. They find that for index analyses [Fe/H] and [α/Fe] are anti-correlated with age. As our dependency of [α/Fe] on age is positively correlated with age, the observed slope cannot be due to degeneracy. For [Fe/H] we find that the slope of the degeneracy is approximately −0.05 dex/Gyr (see Fig. 4), whereas the slope of the relation is −0.02 dex/Gyr. Furthermore our relation extends over 10 Gyr, which is a much larger range in age than what would arise if all galaxies had the same age and would extend on an age-[Fe/H] relation purely due to a degeneracy. We thus conclude that the age-metallicity degeneracy does not give rise to the observed correlation.
These correlations of [Fe/H] and [α/Fe] with age explain the findings by Sánchez-Blázquez et al. (2006), in which metallicity as measured by different indices (Fe, MgB) seemed to behave differently as a function of age. Fe-sensitive indices are a reasonable proxy of [Fe/H], whereas the MgB indices depend on age, [α/Fe] and [Fe/H], thus likely washing out the pure [α/Fe] signal as a function of age.
We have shown in this paper that the age – [α/Fe] relation can be put on a firm foundation using the advances presented here. Yates et al. (2013) show that even the stellar mass – [α/Fe] relation alone is a good constraint on the delay time distribution of SNe Ia. We suggest that the age – [α/Fe] relation should provide additional interesting constraints, especially when considering the two regimes with different slopes.
Finally, we caution that results such as those in Trager et al. (2008) seem to indicate that while many of the correlations we discuss are true on average over large samples, every single structure or galaxy cluster may have its own peculiar history.
8.2. Comparison between SLF-ETGs and the Milky Way
We have been able to diagnose for the first time the physical properties of old and intermediate stellar populations of ETGs. This means that for the first time we can compare the properties of these sub-populations to measurements otherwise only available for very nearby galaxies, mostly within the local group. We attempt this in Fig. 23, which reproduces the cartoonish expectations of Fig. 1, but this time with real data.
 |
Fig. 23 Comparison of the old and intermediate-age stellar populations in ETGs with the properties of the stars in the Milky Way. There is a fundamental difference in the fact that for ETGs we measure the luminosity weighted average of the properties over all stars in the galaxy. For the Milky Way on the other hand, the averages are over single stars and not all types of stars contribute to the average. |
The two systems in the Milky Way that can be compared to ETGs in a more meaningful way are the thick disk above the plane (where contamination from the thin disk is minimal) and the bulge. For the thick disk we plot the fiducial line [α/Fe] = −0.2 × [Fe/H] + 0.10 from Nidever et al. (2014). We also add the Magnesium abundances of the bulge stars older and younger than 9.5 Gyr from Bensby et al. (2013). These represent bona-fide bulge stars and due to the reliable ages from micro-lensing we are able to apply the same selection as for the old stars in our ETGs. For clarity we have not plotted any values for the thin disk of the Milky Way, which shows continuous star formation until today. It would lie between [Fe/H] = −1 and 0 and around 0.0 in [α/Fe].
 |
Fig. 24 Old and intermediate age stellar populations in ETGs separated by the classification according to their enrichment history. SLF-ETGs (upper panel) are consistent with self-enrichment, while ACC-ETGs must have suffered either strong merging/accretion or strong internal winds. The properties of the merged galaxies can be tentatively read of as the properties of the intermediate age population, i.e. low in [α/Fe] and lower in [Fe/H] than the main body of the galaxy. |
When looking at Fig. 23 it is important to appreciate the difference in the probed stars. For the ETGs analyzed in this work each red dot represents the luminosity weighted average abundance values of all stars older than 9.5 Gyr in the galaxy. For the bulge and the thick disk, each star for which abundances have been measured contributes equally to the locus that is reported in this figure, i.e. we compute a simple mean. We proceed to formulate some basic conclusions that are robust against possible selection effects, given the very different methods to obtain the data in MW and ETGs.
It is immediately clear from the figure that normal, massive ETGs differ wildly in their chemical enrichment history from both the thick disk of the Milky Way and the bulge of the Milky Way. Obviously the initial star formation event in ETGs must have been much more efficient in forming stars than even the stars of the thick disk or the bulge. Our statement is complementary to the findings of Tang et al. (2014) who find that the bulge is closer to ETGs than normal disk stars in its enrichment history. However, here we emphasize that the way in which enrichment proceeds is different, while Tang et al. (2014) find that the result from the enrichment (i.e. the different element abundances) is different. To gain a bit more insight into the variety of manifestations of this fact in our sample of ETGs, we reproduce Fig. 23 for the two classes of ETGs defined in the present paper, namely SLF-ETGs and ACC-ETGs. In Fig. 24 we are particularly interested in the SLF-ETGs which at least are compatible with self-enrichment and a causally connected stellar enrichment history. Indeed, we find for these galaxies that the intermediate age stellar populations follow a relation between [Fe/H]i and [α/Fe]i that is reminiscent of those followed by the thick disk and bulge stars, albeit with a steeper slope and extending to lower values of [α/Fe]i. Very low values of [α/Fe] are indeed expected for the stars formed after a long enrichment history (see [Fe/H] Minchev et al. 2013, their Fig. 5).
If indeed, two different processes (self-enrichment vs. merger/accretion/winds) leave their imprint on the abundances of the intermediate age stars in ETGs, then it is to be expected that both processes act in all galaxies. SLF-ETGs and ACC-ETGs would then mostly differ in which of these two processes dominate, while the other would still play a role. This might be the explanation for the steeper gradient in the [α/Fe]i vs. [Fe/H]i relation as compared to the bulge stars.
While such comparisons between wildly different galaxies that have been analyzed in wildly different ways should be taken with caution, our results are also consistent with those of Sil’chenko (1993), Proctor & Sansom (2002). Both of these author groups find that the bulges of disk galaxies are on average younger and less enhanced in α-elements than ETGs. In particular, Proctor & Sansom (2002) state that spiral bulges show a positive correlation between velocity dispersion and metallicity, as expected from a simple scenario in which mass builds up slowly over a Hubble time, whereas ETGs show an anti-correlation as also found in our data. That our data do not support the presence of a clearly identifiable knee as we are used to from Milky Way data is consistent with this finding of strongly diverging processes in the chemical evolution history of late and early type galaxies.
Finally, we note that we are unable to directly confirm the predictions by Lackner et al. (2012), as in these simulations the accreted stars are ~2.5 Gyr older, and ~0.15 dex more metal poor on average than the stars formed in situ. This does not seem to be compatible with the distribution in [Fe/H] vs. [α/Fe] space we describe here. On the other hand, Navarro-González et al. (2013) point out that it is exactly these older and metal-poor stars that are in the outskirts of galaxies, thus providing a potential way out, as our SDSS spectra overweight the inner parts of galaxies.
8.3. On prolonged star formation in SLF-ETGs and the properties of minor mergers in ACC-ETGs
 |
Fig. 25 Average star formation history of galaxies in the three classes as classified by their enrichment history. The figure shows the present day contribution of each stellar population to the total luminosity of the galaxy. All galaxies contribute equally to the average within each class, i.e. the total luminosity for each galaxy has been normalized to one before averaging. |
Figure 25 shows the star formation histories (i.e. the SEHs marginalized over all abundances) for the three different classes of galaxies introduced in this paper. We remind the reader that there are some caveats to this classification in terms of the exact location of the age boundary used to separate old from intermediate age stars. The following discussion is, however, insensitive to these caveats. A general feature of Fig. 25 is that the percentage of intermediate age stars is much higher in SLF-ETGs than in ACC-ETGs. This would seem to indicate that mass growth through late in-situ star formation can be significant. On the other hand, late mergers only very rarely seem to contribute sufficient mass to significantly change the overall SFH of the ETGs. This behavior has been called quasi-monolithic (or early hierarchical) scenario in the literature (Merlin et al. 2012). For the moment this inference does not contradict a picture in which significant late mass growth occurs through minor mergers, as these are expected to be deposited at larger radii, outside the coverage of the SDSS fiber. Also, this finding is consistent with the recent results of Hahn et al. (2015) in which the authors find from entirely different lines of evidence that most of the ETGs stopped forming stars due to internal processes and not due to external influences. Our data, however, are in tension with simulations such as those by Lackner et al. (2012), in which the authors found that minor mergers contribute between 15% and 40% of the total mass and that the percentage of mass brought in by minor mergers increases with stellar mass. We do not find that accretion increases with stellar mass, but rather that in-situ, prolonged star formation decreases with stellar mass.
If, indeed, the intermediate age stars in ACC-ETGs mostly come from merging over a Hubble time, the properties of these stars should carry information on the properties of the galaxies in which they formed, i.e. on the properties of the minor mergers before the merging. In Fig. 24 the fit results for those stars that contribute to the intermediate age population clearly tend towards the lower boundaries imposed by the model in terms of [Fe/H] and [α/Fe]. In Fig. 4 we showed that the degeneracy between [Fe/H] and [α/Fe] is more mild than for age vs. [Fe/H]. Nevertheless, it does exist and would have the following effect in our case: if the real intermediate age stellar populations of ACC-ETGs were even more [Fe/H]-poor than allowed by our model range, the fit would compensate by lowering the [α/Fe] further. We would thus end up exactly in the lowermost left corner of our model coverage – which is what we see. Our analysis therefore tentatively indicates that the late mass-growth of ACC-ETGs is indeed dominated by low-mass, low-metallicity dwarf galaxies.
8.4. The early star formation event in SLF-ETGs vs. ACC-ETGs
Another interesting feature of Fig. 24 are the properties of the older stars. The [α/Fe]o and [Fe/H]o are both higher for ACC-ETGs than for SLF-ETGs. This implies more efficient, early star formation for ACC-ETGs. Indeed, to reach such high values in both [α/Fe] and [Fe/H] a strong starburst is needed, which may have been sufficient to drive out the remaining gas in the galaxies. Taking the speculation a bit further, one could imagine that ACC-ETGs would be different from SLF-ETGs not in the amount of material brought in by mergers, but rather by the efficiency of their early star formation event.
Figure 18 shows that the velocity dispersions of ACC-ETGs are on average higher than those of SLF-ETGs. This would imply a deeper potential well, which might have two effects: 1) increasing the efficiency of star formation; and 2) increasing the speed needed for wind-driven gas to leave to leave the galaxy. Whether it can be understood through simulations what causes effect 1) to dominate would warrant follow-up work.
9. Conclusions
We have analyzed a spectroscopic sample of 2286 early-type galaxies from the SDSS using state of the art stellar population models and fitting procedures. In particular the models we use predict the effects of age, [Fe/H] and [α/Fe] on the spectra of SSPs over significant wavelength range. This allows us to use the code paradise to fit for the stellar enrichment history of the target galaxies without any prior assumption on any functional form or smoothness of this SEH.
We conduct extensive simulations of our fitting routine and find that we can reliably recover the luminosity-weighted average properties of galaxies. We also find that we can reliably recover the [α/Fe] and [Fe/H] of the stars older and younger than 9.5 Gyr separately. We term those properties [Fe/H]o and [α/Fe]o for the old stars and [Fe/H]i and [α/Fe]i for the intermediate age stars. We introduce a classification of galaxies into those where [Fe/H]o< [Fe/H]i – Δ and term those SLF-ETGs because their enrichment histories are consistent with self-enrichment. ACC-ETGs on the other hand are those where [Fe/H]o> [Fe/H]i + Δ. For this paper we choose Δ = 0.15.
We conclude from our study that:
-
We confirm earlier work in that the [Fe/H] and [α/Fe] parameters are correlated with the mass and velocity dispersion of ETGs. However, we find that the strongest relation is between [α/Fe] and age, as expected from basic chemical evolution6. This relation falls into two regimes, one with steep slope of 0.03 for galaxies with average ages above 9 Gyr and one with a shallower slope of 0.01 for galaxies with average age below 9 Gyr.
-
We empirically find both kinds of galaxies, i.e. SLF-ETGs and ACC-ETGs in our sample. For our sample, bona-fide SLF-ETGs make up only 8% of our sample. However, we find that for all galaxies independent of type [α/Fe]o> [α/Fe]i, as expected from basic chemical evolution. SLF-ETGs are on average younger and less α-enhanced than ACC-ETGs.
-
When studying the old stars in ETGs separately, we observed very high [α/Fe] ratios (above 0.3) and high [Fe/H] ratios (above 0.). On the other hand, and within our uncertainties, we find no evidence for a dependence of the properties of these old stellar populations on any other properties of their host galaxies, be it stellar mass, velocity dispersion or environment.
-
ETGs on average differ strongly in their enrichment histories from any stellar system in the Milky Way, even from the bulge. In particular, the vast majority of them does not show a “knee” in the plot of [Fe/H] vs. [α/Fe], commonly observed in local group galaxies. This implies that for the vast majority of ETGs the old and the intermediate stellar populations are not bound together by a common enrichment history, or in other words, the stars younger than 9.5 Gyr are likely to have been accreted through minor mergers. Whether the accreted material came in the form of stars or gas (that later formed stars) cannot be distinguished easily.
-
The properties of the intermediate age stars in ACC-ETGs indicate that mass growth through late (minor) mergers is dominated by galaxies with low [Fe/H] and low [α/Fe], therefore presumably also low mass galaxies.
-
We have physically and technically motivated the choice of boundary between old and intermediate age stars at 9.5 Gyr. However, the relative percentages of SLF and ACC-ETGs obtained in this paper do depend on that choice and further studies should be undertaken to determine the most physically and technically appropriate value.
This contribution is the first one to attempt to resolve the stellar enrichment history of galaxies from integrated spectra. The method is both powerful and subject to uncertainties and caveats. We expect that further work in the future will allow us to confirm, extend and refine our results. This will allow us to compare the SEHs obtained for nearby galaxies with those of much larger samples, thus providing much needed comparison points and contributing to a united understanding of galaxy formation and evolution across all Hubble types.
There is one object out of 2286 where the SDSS pipeline velocity dispersion is 224.8 km s-1, whereas paradise determines 118.9 km s-1. Visually this object clearly has been correctly fitted by paradise . We only have this one example, which however tentatively indicates that velocity dispersion mismatch would not have been a problem for our analysis.
The Spearman coefficients measure the strength of a potential correlation, where 0 is no correlation, 1 is a strong positive correlation and −1 is a strong anti-correlation. The probabilities on the other hand measure the significance of the correlation, i.e. the probability that the real correlation is zero. Therefore a value of 1 for this probability indicates that we know nothing about the real correlation, while a value of below 0.05 would imply that a correlation indeed exists at the 95% confidence level.
de La Rosa et al. (2011) have shown a correlation between the percentage of mass in old stars and [α/Fe], but that is more difficult to compare to our results.
Acknowledgments
We thank the referee, Alexandre Vazdekis, for a very helpful report, which has helped to significantly improve the presentation of this paper. C.J.W. acknowledges useful discussions with Davor Krajnović, Ivan Minchev, Anne Sansom, Ricardo Schiavon. C.J.W. and P.C. acknowledge support through the Marie Curie Career Integration Grant 303912. S.C. acknowledges support from the European Research Council via an Advanced Grant under grant agreement No. 321323-NEOGAL A.G. acknowledges support from from the European Union FP7/2007-2013 under grant agreement no. 267251 (AstroFIt) and EU Marie Curie Integration Grant “SteMaGE” No. PCIG12-GA-2012-326466 (Call Identifier: FP7-PEOPLE-2012 CIG). Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the US Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, J. T., Croom, S. M., Konstantopoulos, I. S., et al. 2015, MNRAS, 446, 1567 [NASA ADS] [CrossRef] [Google Scholar]
- Arimoto, N., & Yoshii, Y. 1986, A&A, 164, 260 [NASA ADS] [Google Scholar]
- Arnouts, S., Walcher, C. J., Le Fèvre, O., et al. 2007, A&A, 476, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, E. F., Naab, T., McIntosh, D. H., et al. 2006, ApJ, 640, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Yee, J. C., Feltzing, S., et al. 2013, A&A, 549, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernardi, M., Nichol, R. C., Sheth, R. K., Miller, C. J., & Brinkmann, J. 2006, AJ, 131, 1288 [NASA ADS] [CrossRef] [Google Scholar]
- Bernardi, M., Sheth, R. K., Annis, J., et al. 2003, AJ, 125, 1882 [NASA ADS] [CrossRef] [Google Scholar]
- Bournaud, F., Jog, C. J., & Combes, F. 2007, A&A, 476, 1179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Bundy, K., Bershady, M. A., Law, D. R., et al. 2015, ApJ, 798, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., & Emsellem, E. 2004, PASP, 116, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., McDermid, R. M., Alatalo, K., et al. 2012, Nature, 484, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Cassisi, S., Salaris, M., Castelli, F., & Pietrinferni, A. 2004, ApJ, 616, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C., Matteucci, F., & Gratton, R. 1997, ApJ, 477, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, J., Conroy, C., Moustakas, J., et al. 2014, ApJ, 792, 95 [NASA ADS] [CrossRef] [Google Scholar]
- CidFernandes, R., Mateus, A., Sodré, L., Stasińska, G., & Gomes, J. M. 2005, MNRAS, 358, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., Pérez, E., García Benito, R., et al. 2013, A&A, 557, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clemens, M. S., Bressan, A., Nikolic, B., & Rampazzo, R. 2009, MNRAS, 392, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Coelho, P., Barbuy, B., Meléndez, J., Schiavon, R. P., & Castilho, B. V. 2005, A&A, 443, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coelho, P., Bruzual, G., Charlot, S., et al. 2007, MNRAS, 382, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Coelho, P., Mendes de Oliveira, C., & Cid Fernandes, R. 2009, MNRAS, 396, 624 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., & van Dokkum, P. 2012, ApJ, 747, 69 [NASA ADS] [CrossRef] [Google Scholar]
- de La Rosa, I. G., La Barbera, F., Ferreras, I., & de Carvalho, R. R. 2011, MNRAS, 418, L74 [NASA ADS] [CrossRef] [Google Scholar]
- de Ravel, L., Le Fèvre, O., Tresse, L., et al. 2009, A&A, 498, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falcón-Barroso, J., Sánchez-Blázquez, P., Vazdekis, A., et al. 2011, A&A, 532, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferré-Mateu, A., Sánchez-Blázquez, P., Vazdekis, A., & de la Rosa, I. G. 2014, ApJ, 797, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhrmann, K. 2011, MNRAS, 414, 2893 [NASA ADS] [CrossRef] [Google Scholar]
- Gallazzi, A., Charlot, S., Brinchmann, J., White, S. D. M., & Tremonti, C. A. 2005, MNRAS, 362, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Gallazzi, A., Charlot, S., Brinchmann, J., & White, S. D. M. 2006, MNRAS, 370, 1106 [NASA ADS] [CrossRef] [Google Scholar]
- Gallazzi, A., Brinchmann, J., Charlot, S., & White, S. D. M. 2008, MNRAS, 383, 1439 [NASA ADS] [CrossRef] [Google Scholar]
- González Delgado, R. M., Cid Fernandes, R., García-Benito, R., et al. 2014, ApJ, 791, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Graves, G. J., Faber, S. M., Schiavon, R. P., & Yan, R. 2007, ApJ, 671, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Graves, G. J., Faber, S. M., & Schiavon, R. P. 2010, ApJ, 721, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, J. E., Murphy, J. D., Comerford, J. M., Gebhardt, K., & Adams, J. J. 2012, ApJ, 750, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, J. E., Murphy, J. D., Graves, G. J., et al. 2013, ApJ, 776, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Hahn, C., Blanton, M. R., Moustakas, J., et al. 2015, ApJ, 806, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Heavens, A. F., Jimenez, R., & Lahav, O. 2000, MNRAS, 317, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschmann, M., Naab, T., Davé, R., et al. 2013, MNRAS, 436, 2929 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschmann, M., Naab, T., Ostriker, J. P., et al. 2015, MNRAS, 449, 528 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Bundy, K., Murray, N., et al. 2009, MNRAS, 398, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Johansson, J., Thomas, D., & Maraston, C. 2012, MNRAS, 421, 1908 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, I. 1999, MNRAS, 306, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Keenan, R. C., Foucaud, S., De Propris, R., et al. 2014, ApJ, 795, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Koleva, M., Prugniel, P., Ocvirk, P., Le Borgne, D., & Soubiran, C. 2008a, MNRAS, 385, 1998 [NASA ADS] [CrossRef] [Google Scholar]
- Koleva, M., Gupta, R., Prugniel, P., & Singh, H. 2008b, in Pathways Through an Eclectic Universe, eds. J. H. Knapen, T. J. Mahoney, & A. Vazdekis, ASP Conf. Ser., 390, 302 [Google Scholar]
- Kormendy, J., Fisher, D. B., Cornell, M. E., & Bender, R. 2009, ApJS, 182, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Kuntschner, H., Emsellem, E., Bacon, R., et al. 2010, MNRAS, 408, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Lackner, C. N., Cen, R., Ostriker, J. P., & Joung, M. R. 2012, MNRAS, 425, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Lawson, C. L., & Hanson, R. J. 1974, Solving least squares problems, Prentice-Hall Series in Automatic Computation (Englewood Cliffs: Prentice-Hall) [Google Scholar]
- Lee, H.-c., Worthey, G., Dotter, A., et al. 2009, ApJ, 694, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Lonoce, I., Longhetti, M., Saracco, P., Gargiulo, A., & Tamburri, S. 2014, MNRAS, 444, 2048 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F., & Greggio, L. 1986, A&A, 154, 279 [NASA ADS] [Google Scholar]
- Mehlert, D., Thomas, D., Saglia, R. P., Bender, R., & Wegner, G. 2003, A&A, 407, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merlin, E., Chiosi, C., Piovan, L., et al. 2012, MNRAS, 427, 1530 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A., Barbuy, B., & Schiavon, R. P. 2000, AJ, 120, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., Chiappini, C., & Martig, M. 2013, A&A, 558, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Naab, T., Johansson, P. H., & Ostriker, J. P. 2009, ApJ, 699, L178 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro-González, J., Ricciardelli, E., Quilis, V., & Vazdekis, A. 2013, MNRAS, 436, 3507 [NASA ADS] [CrossRef] [Google Scholar]
- Nayyeri, H., Mobasher, B., Hemmati, S., et al. 2014, ApJ, 794, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Nelan, J. E., Smith, R. J., Hudson, M. J., et al. 2005, ApJ, 632, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Nidever, D. L., Bovy, J., Bird, J. C., et al. 2014, ApJ, 796, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Ocvirk, P. 2010, ApJ, 709, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Ocvirk, P., Pichon, C., Lançon, A., & Thiébaut, E. 2006, MNRAS, 365, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Oser, L., Naab, T., Ostriker, J. P., & Johansson, P. H. 2012, ApJ, 744, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Ownsworth, J. R., Conselice, C. J., Mortlock, A., et al. 2014, MNRAS, 445, 2198 [NASA ADS] [CrossRef] [Google Scholar]
- Percival, S. M., Salaris, M., Cassisi, S., & Pietrinferni, A. 2009, ApJ, 690, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez, E., Cid Fernandes, R., González Delgado, R. M., et al. 2013, ApJ, 764, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, R. C. 1976, ApJ, 210, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Pipino, A., Matteucci, F., & Chiappini, C. 2006, ApJ, 638, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Pipino, A., Devriendt, J. E. G., Thomas, D., Silk, J., & Kaviraj, S. 2009, A&A, 505, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Proctor, R. N., & Sansom, A. E. 2002, MNRAS, 333, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Prugniel, P., & Koleva, M. 2012, in IAU Symp. 284, eds. R. J. Tuffs, & C. C. Popescu, 16 [Google Scholar]
- Rawle, T. D., Smith, R. J., Lucey, J. R., & Swinbank, A. M. 2008, MNRAS, 389, 1891 [NASA ADS] [CrossRef] [Google Scholar]
- Recchi, S., Matteucci, F., & D’Ercole, A. 2001, MNRAS, 322, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Renzini, A. 2006, ARA&A, 44, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Renzini, A., & Andreon, S. 2014, MNRAS, 444, 3581 [NASA ADS] [CrossRef] [Google Scholar]
- Rettura, A., Rosati, P., Nonino, M., et al. 2010, ApJ, 709, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Rix, H.-W., & White, S. D. M. 1992, MNRAS, 254, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Robaina, A. R., Bell, E. F., van der Wel, A., et al. 2010, ApJ, 719, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Robotham, A. S. G., Driver, S. P., Davies, L. J. M., et al. 2014, MNRAS, 444, 3986 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, S. F., Kennicutt, R. C., Gil de Paz, A., et al. 2012, A&A, 538, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez, S. F., Rosales-Ortega, F. F., Jungwiert, B., et al. 2013, A&A, 554, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez-Blázquez, P., Gorgas, J., Cardiel, N., & González, J. J. 2006, A&A, 457, 787 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez-Blázquez, P., Gibson, B. K., Kawata, D., Cardiel, N., & Balcells, M. 2009, MNRAS, 400, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Blázquez, P., Ocvirk, P., Gibson, B. K., Pérez, I., & Peletier, R. F. 2011, MNRAS, 415, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Sansom, A. E., & Northeast, M. S. 2008, MNRAS, 387, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Sansom, A. E., de Castro Milone, A., Vazdekis, A., & Sánchez-Blázquez, P. 2013, MNRAS, 435, 952 [NASA ADS] [CrossRef] [Google Scholar]
- Serra, P., & Trager, S. C. 2007, MNRAS, 374, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Sil’chenko, O. K. 1993, Astron. Lett., 19, 283 [NASA ADS] [Google Scholar]
- Smith, R. J., Lucey, J. R., Hudson, M. J., & Bridges, T. J. 2009, MNRAS, 398, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Spolaor, M., Forbes, D. A., Proctor, R. N., Hau, G. K. T., & Brough, S. 2008, MNRAS, 385, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Tang, B., Worthey, G., & Davis, A. B. 2014, MNRAS, 445, 1538 [NASA ADS] [CrossRef] [Google Scholar]
- Tempel, E., Tago, E., & Liivamägi, L. J. 2012, A&A, 540, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thomas, D., Maraston, C., Bender, R., & Mendes de Oliveira, C. 2005, ApJ, 621, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, D., Maraston, C., Schawinski, K., Sarzi, M., & Silk, J. 2010, MNRAS, 404, 1775 [NASA ADS] [Google Scholar]
- Tinsley, B. M. 1979, ApJ, 229, 1046 [NASA ADS] [CrossRef] [Google Scholar]
- Tojeiro, R., Heavens, A. F., Jimenez, R., & Panter, B. 2007, MNRAS, 381, 1252 [NASA ADS] [CrossRef] [Google Scholar]
- Trager, S. C., & Somerville, R. S. 2009, MNRAS, 395, 608 [NASA ADS] [CrossRef] [Google Scholar]
- Trager, S. C., Faber, S. M., Worthey, G., & González, J. J. 2000, AJ, 120, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Trager, S. C., Faber, S. M., & Dressler, A. 2008, MNRAS, 386, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., Feulner, G., Goranova, Y., et al. 2006, MNRAS, 373, L36 [NASA ADS] [CrossRef] [Google Scholar]
- van der Wel, A., Holden, B. P., Zirm, A. W., et al. 2008, ApJ, 688, 48 [NASA ADS] [CrossRef] [Google Scholar]
- van der Wel, A., Rix, H.-W., Wuyts, S., et al. 2011, ApJ, 730, 38 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., & Conroy, C. 2010b, Nature, 468, 940 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., Franx, M., Kriek, M., et al. 2008, ApJ, 677, L5 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., Whitaker, K. E., Brammer, G., et al. 2010a, ApJ, 709, 1018 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Casuso, E., Peletier, R. F., & Beckman, J. E. 1996, ApJS, 106, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Sánchez-Blázquez, P., Falcón-Barroso, J., et al. 2010, MNRAS, 404, 1639 [NASA ADS] [Google Scholar]
- Vazdekis, A., Falcón-Barroso, J., Sánchez-Blázquez, P., et al. 2011, in Galaxy Formation (online at http://astro.dur.ac.uk/Gal2011), 17 [Google Scholar]
- Vazdekis, A., Coelho, P., Cassisi, S., et al. 2015, MNRAS, 449, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Walcher, C. J., Böker, T., Charlot, S., et al. 2006, ApJ, 649, 692 [NASA ADS] [CrossRef] [Google Scholar]
- Walcher, C. J., Lamareille, F., Vergani, D., et al. 2008, A&A, 491, 713 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walcher, C. J., Coelho, P., Gallazzi, A., & Charlot, S. 2009, MNRAS, L275 [Google Scholar]
- Walcher, J., Groves, B., Budavári, T., & Dale, D. 2011, Ap&SS, 331, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, A., Ferguson, J., & Salaris, M. 2007, in IAU Symp. 241, eds. A. Vazdekis, & R. Peletier, 43 [Google Scholar]
- Worthey, G., Faber, S. M., & Gonzalez, J. J. 1992, ApJ, 398, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Worthey, G., Tang, B., & Serven, J. 2014, ApJ, 783, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Yates, R. M., Henriques, B., Thomas, P. A., et al. 2013, MNRAS, 435, 3500 [NASA ADS] [CrossRef] [Google Scholar]
- Yi, S. K., Yoon, S.-J., Kaviraj, S., et al. 2005, ApJ, 619, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, G., Blanton, M. R., & Moustakas, J. 2010, ApJ, 722, 491 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Fitting procedure
To derive the star formation histories of composite stellar population spectra we use a full spectrum fitting software called paradise . This software is based on algorithms described in Rix & White (1992) and an earlier version was used previously in e.g. Walcher et al. (2006, 2009, and references therein). Since then a number of new features have been added and we describe here the entire algorithm for the sake of definiteness.
-
Read in observed spectra and the corresponding standard deviations. Rebin to logarithmic wavelength basis if original spectra are in linear. The set of observed spectra is considered to be in row-stacked spectrum format, with one axis being wavelength and the other axis allowing to fit any reasonable number of spectra sequentially.
-
Read in template spectra, rebin to same wavelength solution as object spectrum. Template spectra can be chosen freely, those used in this paper are described in Sect. 3. Spectra should come with a description file containing information such as age, mass, luminosity, [Fe/H], [α/Fe].
-
Specified pieces of the spectra can be masked from the fit, either in restframe (e.g. emission lines) or in observed frame (e.g. telluric features).
-
The continuum of the object and the templates can either be left untouched, or taken out. In the second case the continuum can be determined through a set of Legendre polynomials or through a running mean with to-be-specified width. The continuum can be subtracted or the spectra can be divided by it. For continuum computation reasons, a separate restframe mask can be supplied.
-
Use an initial template to obtain a reasonable value for the velocity and velocity dispersion of the object through a χ2-biased random walk. The line-of-sight velocity distribution is assumed to be Gaussian. This losvd is applied to all template spectra.
-
Apply a non-negative least squares algorithm (nnls, Lawson & Hanson 1974) to perform the inversion onto the stellar population model (see Walcher et al. 2006, for details on this step).
-
Finally, repeat χ2-biased random walk to yield a best estimate for the kinematic parameters, starting from the best fit values obtained before.
-
The nnls routine has the feature of preferring some templates over others, leading to spurious non-continuous star formation histories. Therefore one can choose to repeat the stellar population inversion many times, where the object spectrum is noised assuming Gaussian noise and the variance vector, the order of the templates is reshuffled and a certain percentage of the template set spectra is not considered anymore. This is what we call the stellar population bootstrap. The stellar population bootstrap allows also to derive useful rms uncertainties on any of the stellar population parameters output by the code. In practice we find that after 100 bootstrap runs and using 80% of the initial template set we at the same time obtain smooth SFHs and useful errorbars. We believe this approach to be a straightforward alternative to regularization (Ocvirk et al. 2006; Cappellari & Emsellem 2004).
-
It is often unclear to what extent stellar population uncertainties can bias the velocity dispersion measurements. To address this, the code has the capability to repeat the kinematic fit after each step of the stellar population bootstrap. We call this the kinematics bootstrap. This feature is not used in the current paper.
-
Finally the code puts out the fiducial best fit spectrum, the continuum it used to normalize the object spectrum, the associated errorbar, and residual. It also provides the user with two tables, one with the fiducial values of the fit and the other with the results of the bootstrap. Finally, the variance vector on the best fit derived from the bootstrap procedure is also provided. In this paper we generally use the stellar population parameters obtained from the bootstrap as these come with errorbars. Within the errorbars, these are consistent with the fiducial values.
For a review of other available spectral fitting codes, the reader is referred to Walcher et al. (2011) and the website http://www.sedfitting.org
A general note on averaging may also be useful for the reader: when quoting the mean [Fe/H] and [α/Fe] abundances, it is not trivial to determine the most appropriate way to do the averaging. One could either 1) average on the “square bracket quantities”; or 2) average on actual element abundance ratios; or 3) average on actual masses of Fe atoms M(Fe) and of Hydrogen atoms M(H) (alpha elements and Fe respectively for the case of [α/Fe]). We have decided to stick with possibility one for an observational reason: interpolating linearly two stars with [Fe/H] = −1 and [Fe/H] = 0 exactly reproduces a star with [Fe/H] = −0.5 (tested using stellar spectra from Coelho et al. 2005). Because we can thus observationally not distinguish between these last two situations, we shall use an averaging procedure in which they both correspond to the same result. In this way we avoid inconsistencies and degeneracies. When attempting to compare our results to simulations, one will have to do the same to their derived quantities.
All Tables
All Figures
 |
Fig. 1 Schematic representation of the new parameters introduced in this paper, namely [α/Fe]o and [Fe/H]o. These represent the average [α/Fe] and [Fe/H] of stars older than 9.5 Gyr on a per galaxy basis. The upper panel shows a schematic star formation history, which separates into these two stellar populations. The lower panels depicts on the standard [α/Fe] vs. [Fe/H] diagram familiar for the Milky Way what is expected for the old and intermediate age stars respectively. |
| In the text | |
 |
Fig. 2 S/N distribution of our sample galaxies. |
| In the text | |
 |
Fig. 3 Simulations of parameter recovery for a randomized coverage of parameter space and a total of 3000 mock galaxies. |
| In the text | |
 |
Fig. 4 Degeneracies in the overall mean light-weighted values as difference plots. Each Δ is defined as the recovered minus the true value. The dominating degeneracy occurs between age and [Fe/H], while age and [α/Fe] show only weak degeneracy. |
| In the text | |
 |
Fig. 5 Verification of the uncertainties derived by the fitting routine through bootstrap. Each Δ is defined as the recovered minus the true value, but this time divided by the size of the error bar (denoted σ) as output by the fitting routine. For perfectly Gaussian errors, the distribution should coincide with a Gaussian of width one and normalized to the same total area (dotted line). |
| In the text | |
 |
Fig. 6 Simulations of parameter recovery when splitting the star formation and enrichment history at a fiducial age of 9.5 Gyr. The dashed line in the lower right panel is a formal fit to the points in the data with a slope of ~0.3. |
| In the text | |
 |
Fig. 7 The dominating degeneracies in the mean light-weighted values when separating SEHs into intermediate and old stars are those between the same properties of the two stellar generations. Each Δ is defined as the recovered minus the true value. |
| In the text | |
 |
Fig. 8 Comparison of the original distribution of parameters (upper row) vs. the one recovered after the fitting process (lower row). We show the two parameter spaces that are of most interest in the remainder of the paper, namely [Fe/H]i vs. [Fe/H]o and [α/Fe]i vs. [α/Fe]o. Left panel: the case in which the total library of mock galaxies is analyzed. Right panel: the case in which only mock galaxies with −0.2 ⟨ [Fe/H]i, [Fe/H]o⟨ 0.0 are analyzed. |
| In the text | |
 |
Fig. 9 Mean residual vector and its standard deviation from all galaxies in the sample. The upper plot indicates the residuals in the rest frame of the galaxies, the yellow region has actually not been used to determine the best fit. [OIII] and Hβ emission lines are labelled and clearly visible. The Mgb feature is also indicated for reference, but does not show evidence of specific mismatch. The lower plot shows the observed frame residuals indicating no major concern with the data. |
| In the text | |
 |
Fig. 10 Cumulative histogram of χ2 values obtained from the data (solid line) with the χ2 distribution expected from statistics (dotted line) for 257 degrees of freedom. |
| In the text | |
 |
Fig. 11 Comparison between the velocity dispersion from SDSS DR7 and those obtained in this work. |
| In the text | |
 |
Fig. 12 Correlations of [Fe/H] and [α/Fe] with velocity dispersion, stellar mass and mean light-weighted age for our sample galaxies. It is clear that the tightest relations are those with age. Note also the change of slope in the relation between age and [α/Fe] ~ 9 Gyr. Average error bars are given in the upper right corner of each panel and spearman rank correlation coefficients are also noted. |
| In the text | |
 |
Fig. 13 Correlation between [Fe/H] vs. [α/Fe] for the luminosity weighted average properties of the ETGs in our sample. The thick solid line is a line of constant, solar metallicity (Z = 0.017). The two dashed line illustrate the extremes of the ETG locus, i.e. for [ Z ] = −0.15 and [ Z ] = 0.18. |
| In the text | |
 |
Fig. 14 Average star formation history of all galaxies in the observed sample in terms of the present day contribution of each stellar population to the total luminosity of the galaxy. All galaxies contribute equally to this average, i.e. the total luminosity for each galaxy has been normalized to one before averaging. |
| In the text | |
 |
Fig. 15 Correlations of the [Fe/H]o and [α/Fe]o with the global properties of the sample galaxies σ, M*, and age. Average error bars are given in the upper right corner of each panel and spearman rank correlation coefficients are also noted. |
| In the text | |
 |
Fig. 16 Relation between [Fe/H]o vs. [α/Fe]o, the thick line is a line of constant, solar metallicity (Z = 0.017). This is the same as Fig. 13, but only for the stars older than 9.5 Gyr in each galaxy. The old stars in early-type galaxies, have on average high total metallicity, significantly super-solar. Average error bars are shown in the upper right corner. |
| In the text | |
 |
Fig. 17 Left panels: distribution of mean light-weighted [Fe/H] and [α/Fe] for the old vs. intermediate sub-populations. Galaxies in yellow are those where [Fe/H]o< [Fe/H]i−0.15 (SLF-ETGs), pink where [Fe/H]o> [Fe/H]i+0.15 (ACC-ETGs). Galaxies with uncertain classification are shown in black. Average uncertainties including all degeneracies are shown in the upper left corners. Right panels: age dependence of [Fe/H] and [α/Fe] within each galaxy, i.e. their enrichment history. Galaxies with uncertain classification have been omitted for clarity. |
| In the text | |
 |
Fig. 18 Correlations of [Fe/H] and [α/Fe] with velocity dispersion, stellar mass and mean light-weighted age for our sample galaxies (same as Fig. 12). Colors reproduce the classification from Fig. 17 into SLF-ETGs (yellow) and ACC-ETGs (pink). The mean for each subpopulation is also shown as a large square with black borders. Galaxies that could not be reliably classified are shown as black dots. |
| In the text | |
 |
Fig. 19 Environmental density vs. light-weighted [Fe/H] and [α/Fe] (upper panels) and vs. [Fe/H]o and [α/Fe]o of only the old stars in each galaxy. The mean for each subpopulation is also shown as a large square with black borders. |
| In the text | |
 |
Fig. 20 Dependence of key physical properties of our sample galaxies on redshift. From top to bottom: stellar mass, [α/Fe], age and ratio between radius covered by fiber and effective radius of the galaxy. Colors reproduce the classification from Fig. 17 into SLF-ETGs (yellow) and ACC-ETGs (pink). |
| In the text | |
 |
Fig. 21 Dependence of [Fe/H] on coverage fraction at fixed mass. No bias is obvious. Colors reproduce the classification from Fig. 17 into SLF-ETGs (yellow) and ACC-ETGs (pink). |
| In the text | |
 |
Fig. 22 Locus of our sample galaxies as compared to the mass-metallicity relations of (Gallazzi et al. 2005, solid line, dotted lines are 1σ scatter) and of (González Delgado et al. 2014, dashed line). While there is general agreement, the clear difference in slope within the mass range of our galaxies is interesting and may point to sample selection effects. |
| In the text | |
 |
Fig. 23 Comparison of the old and intermediate-age stellar populations in ETGs with the properties of the stars in the Milky Way. There is a fundamental difference in the fact that for ETGs we measure the luminosity weighted average of the properties over all stars in the galaxy. For the Milky Way on the other hand, the averages are over single stars and not all types of stars contribute to the average. |
| In the text | |
 |
Fig. 24 Old and intermediate age stellar populations in ETGs separated by the classification according to their enrichment history. SLF-ETGs (upper panel) are consistent with self-enrichment, while ACC-ETGs must have suffered either strong merging/accretion or strong internal winds. The properties of the merged galaxies can be tentatively read of as the properties of the intermediate age population, i.e. low in [α/Fe] and lower in [Fe/H] than the main body of the galaxy. |
| In the text | |
 |
Fig. 25 Average star formation history of galaxies in the three classes as classified by their enrichment history. The figure shows the present day contribution of each stellar population to the total luminosity of the galaxy. All galaxies contribute equally to the average within each class, i.e. the total luminosity for each galaxy has been normalized to one before averaging. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


