EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 581 (September 2015) A&A, 581 (2015) A20 Full HTML
Free Access
Issue
A&A
Volume 581, September 2015
Article Number A20
Number of page(s) 11
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201526648
Published online 26 August 2015

© ESO, 2015

1. Introduction

With the success of the Kepler space telescope in the past few years for detecting several planets around main sequence binaries, the formation and dynamical evolution of these objects are now among the most outstanding questions in exoplanetary science. A survey of the currently known Kepler’s circumbinary planetary systems1 indicates that, as expected, in all these systems, the binaries are close with orbital periods ranging from 7 to 41 days. The planets in these systems are Saturn-sized or slightly smaller and revolve around their host binaries in orbits with periods from 50 to 300 days. Also, dynamical analyses of these objects have indicated that several of these planets are close to the boundary of orbital stability (see Dvorak 1986; Holman & Wiegert 1999), and they are all between two major n:1 mean-motion resonances (MMR).

The proximity of the orbits of some of the circumbinary planets (CBPs) to the stability limit raised the question of whether planet formation can proceed efficiently in these regions. Several attempts have been made to answer this question (Meschiari 2012; Paardekooper et al. 2012; Marzari et al. 2013; Dunhill & Alexander 2013; Rafikov 2013; Lines et al. 2014; Bromley & Kenyon 2015). However, in situ formation does not appear to be possible. The lack of success in growing planetesimals to larger sizes in the vicinity of the stability boundary, combined with the fact that, as indicated by observations, the orbits of the currently known CBPs are almost all coplanar with the orbit of their host binaries, has strongly suggested that these planets formed at large distances (where the perturbing effect of the binary on the disk is negligible and planet formation can proceed in the same way as around single stars) and ended up in their current orbits either through planet migration (as a result of planet-disk interaction), planet-planet scattering, or a combination of both (Pierens & Nelson 2007, 2008b).

The first study of planet migration in circumbinary disks was carried out by Nelson (2003), who show that in low eccentricity binaries (ebin ≤ 0.2), massive, Jovian-type bodies will be captured in a 4:1 MMR with the binary, and when the binary is more eccentric, these planets may be captured in stable orbits farther out (see also Pierens & Nelson 2008b). In a subsequent study, Pierens & Nelson (2007) extended previous analyses to less massive planets (as low as 20 MEarth) and show that migrating CBPs may stop near the edge of the inner disk cavity. They suggest that CBPs should be predominantly found in that area, because in low eccentric binaries, the inner edge of the disk cavity, caused by the tidal effect of the binary on the disk material, almost coincides with the boundary of orbital stability. The predictions made by these authors agreed with the orbital architecture of the first few Kepler CBPs. More general cases in which accretion and multiple planets were also considered were then studied by the same authors (Pierens & Nelson 2008a,b).

The earliest attempt to explain the orbital architecture of Kepler CBPs using planet migration was by Pierens & Nelson (2013). Considering a locally isothermal disk, where the disk thermodynamics is modeled by prescribing a given temperature profile, and assuming a closed boundary condition at the edge of the cavity (i.e., no mass accretion onto the central binary), these authors applied their model to the systems of Kepler 16, 34, and 35 and showed that the planets in these systems can migrate and reside in a stable orbit. However, the values of the semimajor axes of the final orbits of planets in their models did not agree well with their observed values. In a recent paper (Kley & Haghighipour 2014), we showed that the limitation of the models by Pierens & Nelson (2013) are due to their two simplifying assumptions: considering that a disk is locally isothermal and has a close boundary condition. A more realistic model requires the radiative effects to be taken into account and the disk material to flow through the inner edge of the disk into the disk cavity. The latter has also been shown in numerical simulations by Artymowicz & Lubow (1996) and Günther & Kley (2002), where the results indicate that despite the appearance of a cavity in the center of a circumbinary disk, material can still flow inside and onto the central binary.

In Kley & Haghighipour (2014), we presented an improved and extended disk model that included a detailed balance of viscous heating and radiative cooling from the surface of the disk (D’Angelo et al. 2003), as well as additional radiative diffusion in the plane of the disk (Kley & Crida 2008). For a planet embedded in the disk, the improved thermodynamics can have dramatic effects on the planet orbital dynamics such that it can even reverse the direction of migration for low-mass planets (Kley & Crida 2008; Kley et al. 2009). In addition, we considered an open boundary condition and allowed free in-flow of material from the disk into the central cavity. This enabled us to construct models with net mass in-flow through the disk. We showed that when our model is applied to circumbinary planetary systems with low eccentricity or circular binaries (e.g., Kepler 38), it removes the discrepancy observed in the model by Pierens & Nelson (2013) and allows the planet to reside in close proximity to the boundary of orbital stability between two n:1 MMRs.

In our previous study, we considered the system of Kepler-38 because this system represents one of the CBP systems with an almost circular binary. As mentioned above, in such systems, the boundary of the stability of planetary orbits coincides with the outer edge of the disk inner cavity. The latter raises the question of how the results will change if the binary is eccentric. In a circumbinary disk around an eccentric binary, the inner cavity will be more eccentric. The inner cavity is developed due to the tidal effect of the binary, and its outer edge will no longer coincide with the stability boundary becausethe latter will also change with the binary eccentricity. In this paper, we address these issues by applying our disk model to the circumbinary system of Kepler-34. The central binary in this system has an eccentricity of 0.52, and the orbital eccentricity of its CBP is 0.18. It has been suggested that the formation history of this system may have been different from the more circular cases such as Kepler-16 and Kepler-38 (Georgakarakos & Eggl 2015).

This paper is organized as follows. In the next section we briefly describe our hydrodynamic model. In Sect. 3, we present the structure of the disk without an embedded planet. In Sect. 4, the results for the migration of a single planet are presented, which is followed in Sect. 5 by a study of the dynamics of a pair of embedded planets. In Sect. 6, we summarize and discuss our results.

2. The hydrodynamic model

As mentioned in the introduction, the target of our investigation is the system of Kepler-34, and we tailored our simulations to that particular system. Our overall methodology is identical to the one used in our previous study of the Kepler-38 system (Kley & Haghighipour 2014), so we only give a short outline here.

2.1. Basic disk setup

To model the evolution of a disk around a binary star, we assume that the disk is vertically thin and the system is coplanar, an assumption that is justified by the observations of Kepler CBPs. We then perform two-dimensional (2D) hydrodynamical simulations in the plane of the binary. To simulate the evolution of the disk, the viscous hydrodynamic equations are solved in a polar coordinate system (r,φ) with its origin at the center of mass of the binary.

When using the polar coordinate system, a hole remains in the center in which the binary orbits. As pointed out in previous studies (Pierens & Nelson 2013; Kley & Haghighipour 2014), the location of the inner boundary of the grid can affect the outcome of the simulations. Given that the semi-major axis of the central binary of Kepler-34 is abin = 0.23 AU, we consider the radial extent of the disk (r) to be from 0.34 AU to 5.0 au. Accordingly, the inner radius of the grid will be about 1.5 abin, as suggested by the studies mentioned above. The polar angle φ varies in an entire annulus of [0,360°]. This domain is covered by a grid of 256 × 256 grid cells that are centrally condensed in the radial direction and equidistant in azimuth. In all models, we evolve the vertically integrated hydrodynamical equations for the surface density Σ and the velocity components (ur,uφ).

When simulating locally isothermal disks, we do not evolve the energy equation and instead use an isothermal equation of state for the pressure. When considering radiative models, a vertically averaged energy equation is used that evolvesthe temperature of the midplane (Müller & Kley 2012). Radiative effects are included in two ways. First, a cooling term is considered to account for the radiative loss from the disk surface (D’Angelo et al. 2003). Second, we include diffusive radiative transport in the midplane of the disk using flux-limited diffusion (Kley & Crida 2008; Müller & Kley 2013). In the radiative simulations, the full, vertically averaged dissipation is taken into account (Müller & Kley 2012).

To calculate the necessary height of the disk H at a position r following Günther & Kley (2002) and Kley & Haghighipour (2014), the individual distances from the two central stars were taken into account. The equation of state of the gas in the disk is given by the ideal gas law using a mean molecular weight of μ = 2.35 (in atomic mass units) and an adiabatic exponent of γ = 1.4. For the shear viscosity, we used the α-parametrization with α = 0.01 or 0.004 depending on the model, and we set the bulk viscosity to zero. For the Rosseland opacity, we used an analytic formula provided by Lin & Papaloizou (1985) and the flux limiter as in Kley (1989).

The calculation of the gravitational force acting by the binary and planets on the disk was done in the same way as in Kley & Haghighipour (2014). Here we used a smoothing length of 0.6H for the planet, where the local scale height takes both stars of the binary into account. In some of the simulations, we added a second planet. The integration of the hydrodynamical equations (explicit/implicit 2nd-order scheme) and the N-body integrator (4th-order Runge Kutta) were performed again identically to Kley & Haghighipour (2014). To calculate the force from the disk acting on the planet, we excluded parts of the Hill sphere of the planet using a tapering function as given in Kley & Haghighipour (2014). We calculated the orbital parameters of the planet using Jacobian coordinates, assuming the planet orbits a star with mass Mbin = M1 + M2, at the binary barycenter.

2.2. Initial setup and boundary conditions

Table 1

Binary parameter and the observed planetary parameter of the Kepler-34 system used in the simulations.

In our models, the disk initial surface density is chosen to have a Σ(r) = Σ0r−1/2 profile where r is the distance from the center of mass of the binary. For this reference surface density, following our earlier results (Kley & Haghighipour 2014), we chose two different values, a higher mass model with Σ0 = 3000 g/cm2 and a lower mass model with a quarter of this value, Σ0/ 4 = 775 g/cm2. We chose the initial temperature of the disk to vary with r as T(r) ∝ r-1 such that, assuming a central star of Mbin, the vertical thickness of the disk will always maintain the condition H/r = 0.05. For the radiative model, the temperature profile is determined self-consistently. The initial angular velocity of the disk at a distance r from the barycenter is chosen to be equal to the Keplerian velocity at that distance, and the radial velocity is set to zero.

The parameters of the central binary have been adopted from Welsh et al. (2012) and are quoted in Table 1, together with the planetary data. Owing to the interaction of the binary with the disk (and planet), these parameters will slowly vary during a simulation. However, during the course of our simulations the change is very small. Even for the longest runs that stretch over 10 000 yr (equivalent to over 1.3 × 105 binary orbits) the relative change of the semi-major axis and the eccentricity of the binary is 3 × 10-3 and 6 × 10-3, respectively. For the models with an embedded planet, we consider the planet to have a mass of mp = 2.1 × 10-4M1 which is equivalent to mp = 0.22 MJup or about 73 Earth masses (see Table 1). At the beginning of each simulation, we start the binary at its periastron.

The boundary conditions of the simulations are constructed such that at the outer boundary of the disk, rmax = 5.0 au and the surface density remains constant and equal to its initial value. This is achieved by using a damping boundary condition where the density is relaxed toward its initial value, Σ(rmax), and the radial velocity is damped toward zero, using the procedure specified in de Val-Borro et al. (2006). The angular velocity at the outer boundary is also kept equal to its initial Keplerian value. For the temperature, we use a reflecting condition such that there will be no artificial radiative flux through the outer boundary for the radiative model. These conditions at the outer boundary lead to a disk with zero eccentricity at rmax. As a result, rmax has to be large enough such that the inner regions are not influenced.

At the inner boundary (rmin), we consider a boundary condition such that the in-flow of disk material onto the binary is allowed. This means, for the radial boundary grid cells at rmin, we choose a zero-gradient mass out-flow condition, where the material can freely leave the grid and flow onto the binary. No mass in-flow into a grid is allowed at rmin. The zero-gradient condition is also applied to the angular velocity of the material since the effect of the binary means that no well-defined Keplerian velocity can be found that could be used otherwise. This zero-gradient condition for the angular velocity implies a physically more realistic zero-torque boundary. With these boundary conditions, the disk can reach a quasi-stationary state in which there will be a constant mass flow through the disk (Kley & Haghighipour 2014).

3. Structure of the circumbinary disk

Before we study the evolution of planets within the circumbinary disk around Kepler-34, we analyze the disk’s dynamics due to the effect of the central binary. For this purpose, we simulated the dynamics of the disk in our reference model (see Table 2) with a zero-mass planet. In the simulations the inner boundary of the disk is open to mass flow into the central cavity, and at the outer boundary the density is relaxed to its initial values. Starting from the initial setup, mass flows out into the inner cavity and the binary’s torques change the disk’s density profile. However, caused by the relaxation outer boundary condition it eventually settles into a new final quasi-stationary state, where its mass remains constant, and there is a constant mass accretion rate onto the central binary. This behavior is similar to our previous simulations for the Kepler-38 system (Kley & Haghighipour 2014). We constructed our disk model for a locally isothermal equation of state where we do not evolve the energy equation but instead leave the temperature of the disk at its initial value. This procedure has the advantage of making the simulations much faster since no heating and cooling of the disk have to be considered.

Table 2

Parameters of the locally isothermal disk reference model without a planet.

thumbnail Fig. 1

Azimuthally averaged surface density (top) and disk eccentricity (bottom) for our locally isothermal reference model. Shown here are the profiles at different evolutionary times (in years); the red curve denotes the initial setup.

3.1. Disk structure

During this time, the surface density slowly evolves away from its initial profile until it settles in a new equilibrium state. This is shown in the upper panel of Fig. 1 where the azimuthally averaged radial surface density profile is shown at different evolutionary times. The equilibration time takes only a few hundred years. After this time, the surface density profiles will no longer change considerably. Because of the tidal action of the binary on the disk, a central gap is formed with a surface density that is many orders of magnitude lower than inside the disk. The inner edge of the disk, which we can define very approximately as that radius at which the surface density is about half the maximum value, lies here at around r ≈ 1.25 AU. This is about five times larger than abin and, as such, larger than the stability region of massless particle trajectories around binary stars as given by Artymowicz & Lubow (1994). Our result is in good agreement with Pierens & Nelson (2013) and our own results on Kepler-38 (Kley & Haghighipour 2014). The larger inner gap is caused by the high eccentricity of the binary disk in this case. Outside of about r = 3 AU, the surface density profile remains at the initial value.

As was shown by Pierens & Nelson (2013), circumbinary disks can attain significant eccentricities. We calculate the eccentricity of the disk by treating each grid cell as an individual particle with a mass and velocity equal to the mass and velocity of the cell (Kley & Dirksen 2006). To calculate a radial dependence for the disk eccentricity, edisk(r), we average over the angular direction. In our simulations, the disk eccentricity becomes very high, with edisk about 0.3 to 0.5, in the gap region of the disk, as shown in the lower panel of Fig. 1. In the inner, nearly evacuated regions, the disk eccentricity can be even higher. Near the maximum of the density (at r = 1.7), the eccentricity is around 0.15, and it drops slowly farther out. At radial distances r> 3.0 AU, the disk eccentricity becomes lower than about 0.01.

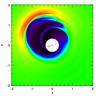thumbnail Fig. 2

Two-dimensional density structure of our isothermal reference disk model around the central binary star. The graph shows only a local view around the binary. The entire computational grid, however, extends from r = 0.34 AU to r = 5.0 AU. The white inner region lies inside the computational domain and is not covered by the grid. The positions of the primary and secondary stars are indicated by the gray dots. The Roche lobe of the secondary is also shown. The central cross marks the origin of the coordinate system. which coincides with the center of mass of the binary.

In Fig. 2, we show the 2D surface density distribution for the isothermal disk models. We note that this figure shows only the inner part of the computational domain around the central binary. The Roche lobe of the secondary star is shown as well. As shown here, an eccentric central binary strongly perturbs the disk and produces time varying patterns and a very large eccentric inner gap. At the same time, the disk features a strong asymmetric maximum in the surface density.

To test the sensitivity of the results to changes in the inner boundary condition, we performed a comparison model with a closed inner boundary and found no significant differences in the results concerning the gap structure. The width of the gap and the disk eccentricity were the same. Only the value of the maximum density was slightly higher in the closed boundary model.

thumbnail Fig. 3

Azimuthally averaged surface density (top) and eccentricity (bottom) for locally isothermal disks, with H/r = 0.05, around the two systems, Kepler-34 and Kepler-38. The figure shows the profiles for the final equilibrium state without any embedded planet. The radial coordinate has been scaled by the binary separation which is 0.23 AU for Kepler-34 and 0.15 AU for Kepler-38. The results for Kepler-38 have been taken from Kley & Haghighipour (2014).

To study the influence of the binary parameters on the disk structure, we compare the averaged disk structure for the Kepler-34 system and the Kepler-38 system in Fig. 3. These two systems are different in mass ratio and eccentricity, where for the Kepler-38 system, q = 0.26 and e = 0.10. It is clear that the combination of a higher mass ratio and a higher binary eccentricity creates a much larger variation in the surface density profile and a higher disk eccentricity. This difference will have a profound effect on the dynamical evolution of embedded planets as shown in Sect. 4.

thumbnail Fig. 4

Evolution of the argument of periapses of the disk with respect to the inertial frame. Results of two different estimates are shown for comparison. Red corresponds to estimates using the maximum of the 2D density distribution (see Fig. 2), and blue is for estimates using the mass-weighted mean value of the inner disk.

3.2. Disk precession

As outlined above, the surface distribution around the central binary becomes clearly eccentric. To analyze the disk dynamics without a planet, we further analyzed the precession rate of this eccentric mode. In principle, the argument of periapse of the disk, ϖdisk, can be calculated in the same manner as the disk eccentricity, as a mass-weighted average over the disk integrating over all annuli (Kley & Dirksen 2006). However, when calculating the integral over the entire disk from rmin to rmax, the result showed a nearly constant value for ϖdisk. However, animations of the surface density distribution, as shown for a single snapshot in Fig. 2, indicated a clear precession of the inner disk regions. For that reason, we decided to restrict the range of integration to the inner disk alone and used a radial range extending from rmin = 0.34 to r = 2. As an additional indicator for the precession, we calculated the disk’s line of periapses from the maximum of the density distribution in the disk. The two methods resulted in similar results as shown in Fig. 4 where the time evolution of ϖdisk is displayed for the reference model without an embedded planet.

thumbnail Fig. 5

Evolution of the argument of periapses of the binary with respect to the inertial frame. The red curve corresponds to the case where the backreaction of the disk onto the binary has been articifially switched off such that the motion of the binary is not influenced by the presence of the disk. The blue curve correponds to the reference model as shown in Fig. 2.

The above-mentioned averaging method gives strong fluctuations whenever the angle crosses zero because individual rings may have values close to zero or close to 360°. The density maximum method, on the other hand, is noisier owing to the disk dynamics, which results in the “thicker” curves. The overall agreement of the two methods confirms that the disk experiences a precession. In the initial phase of the simulations, the precession rate adjusts to the changing density profile, and in the final equilibrium state the disk experiences a precession with a rate of about 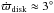\hbox{$\dot{\varpi}_{\rm disk} \approx 3^\circ$}/yr. In comparision to the orbital period of the binary, Pbin = 28 d, this indicates a very slow precession rate. Similar slow precession rates have been found for disks around massive planets (Kley & Dirksen 2006), as well as the inner disks in close binary systems such as Cataclysmic binaries (Kley et al. 2008). The reason that Pierens & Nelson (2013) did not find precession of the disk in their models is probably related to an integration over the whole disk.

In this paper, we do not investigate further details of our disk dynamics, but only briefly comment on the feedback the disk can have on the central binary. In Fig. 5, we show the precession rate for the binary as induced by the disk. As expected, without the disk feedback, the binary orbit does not precess. However, including the disk’s feedack leads to a very slow prograde precession of about 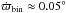\hbox{$\dot{\varpi}_\mathrm{bin} \approx 0.05^\circ$}/yr in the orbit of the binary. Here, the total mass of the disk is about 0.015 M⊙. During the time that the orbit of the binary developed precession, the disk yielded a slow decrease in the orbit of the binary with a rate of about 4 × 10-7 au/yr.

thumbnail Fig. 6

Evolution of the semi-major axis (top) and eccentricity (bottom) of an embedded planet in an isothermal disk (reference model) that was first brought into an equilibrium. In the two simulations, the planet was started at different distances from the center of mass of the binary. In the first simulation (shown in red), the planet started at a distance of a0 = 1.75 au, and in the second simulation (shown in green and blue) it started as a0 = 2.0 au. In the simulation shown in red, the planet is immediately released and evolves with the disk. In the second simulation, the planet’s orbit is held constant during the first 600 yrs (in blue) and then released (green lines). In both simulations, the planet migrates inward with a rate of about 0.1 au/100 yrs. Both models result in unstable evolution when the planet has reached a distance of about 1.35 au. The dashed horizontal lines shows the observed semi-major axis and eccentricity of Kepler-34 b.

4. Planet migration

In this section, we analyze the evolution of embedded planets in the disk around Kepler-34. Similar to our previous study of Kepler-38 (Kley & Haghighipour 2014), we first study migration for our standard isothermal disk model because these are numerically faster. Subsequently, we study planets in radiative disks, as well.

4.1. Migration in the standard disk model

To study the evolution of the system with an embedded planet, we start our simulations with a planet initially placed at different distances (semi-major axes, a0) from the center of mass (barycenter) of the binary and in a circular orbit. The planet’s evolution is determined by the gravitational action of the disk and the central binary. As mentioned earlier, during the evolution of the planet, its orbital elements are calculated using Jacobian coordinates with respect to the barycenter of the central binary. The planet mass is fixed to 73 Earth masses (the observed value), and there is no accretion onto the planet. As a reference, we present the orbital parameters of the planet Kepler-34 b in Table 1, as inferred from the observations.

Figure 6 shows the evolution of the planet through the disk for the reference model. We present here the results of two simulations that were carried out for different initial conditions of the planet from the center of mass of the binary. In the first model, the planet is started directly after insertion. Initially, it rapidly migrates inward until it has reached a distance of about 1.4 au at around 300 yr into the evolution. After this, the inward migration proceeds at a slower pace because the planet has reached the eccentric inner hole of the disk. Upon reaching a distance of 1.3 au, the eccentricity of the planet has increased to about 0.3, and its orbit becomes unstable. To examine whether this outcome might have been caused by too small an initial separation of the planet, so that the system could not reach equilibrium, we started a second model with the planet initially embedded farther out at r0 = 2.0 au. During the first 600 years, the semi-major axis of the planet was held constant (Fig. 6), which gave enough time to the disk to adjust to the presence of the planet. The planet was then released, and it migrated due to the effect of the disk torque acting on it. The planet drifted inward with the same speed as in the first model, about 0.1 au/100 yr, and the orbit became unstable after the planet reached the same position as before. This implies that the outcome of the migration process does not depend on the history of the system and is determined solely by the physical parameters of the disk. In the following we analyze whether reducing migration speed can stabilize the orbit.

4.2. Planet migration in disks with lower mass

To investigate whether it was the very rapid inward migration of the planet in our standard model that resulted in its unstable evolution, we performed additional isothermal disk simulations with a reduced disk mass but otherwise identical parameter. The results are shown in Fig. 7. Here, the standard model is shown with the same color as in Fig. 6 and the blue line to a model with half the disk mass. The reduction of the disk mass resulted in a slower inward migration with slightly reduced eccentricity, but the model became unstable again.

thumbnail Fig. 7

Evolution of the semi-major axis (top) and eccentricity (bottom) of an embedded planet in isothermal disk models with half the disk mass. The red curve refers to the original model and is identical to the one shown in Fig. 6.

thumbnail Fig. 8

Evolution of the semi-major axis (top) and eccentricity (bottom) of an embedded planet in disks with lower surface densities (1/4 of the reference model) and reduced viscosities (α = 0.004). The red graph corresponds to the isothermal model and the blue refers to the radiative disk. In the two simulations, the planet is started in a circular orbit at a distance of a0 = 2.0 au from the center of mass of the binary. In the simulation shown in red, the planet is included in the disk from the very beginning of the simulation, and it begins to migrate simultaneously with the disk evolution starting from its initial density profile. In the simulation shown in blue, the disk is first relaxed to the radiative equilibrium, and then the planet is embedded in it. The dashed horizontal lines refer to the observed parameter of the Kepler-34 planet.

thumbnail Fig. 9

Graphs of the azimuthally averaged radial surface density of the isothermal and radiative disk models of Fig. 8 with an embedded planet. The density distributions are taken near the final state of the evolutions shown in Fig. 8. The big colored dot in each graph represents the semi-major axis of the planet at these times. For illustrative purposes, we have moved the circles close to their corresponding curves.

4.3. Planet migration in disks with lower viscosity and with radiation

In addition to the disk mass, we also varied the viscosity and thermodynamics of the disk to investigate its influence on the migration process. Figure 8 shows the semi-major axis and eccentricity of the planet embedded in a disk with a lower surface density (1/4 of the reference model) and a reduced disk viscosity (α = 0.004). We compare a locally isothermal model with a radiative one. In the isothermal model, the planet migrates inward at a constant rate that is about five times slower than in the reference model. When the planet reaches a distance slightly inside of r = 1.3 au, it reverses its direction and migrates outward until it finally settles at a distance of about 1.35 au. In the radiative case, the planet migrates inward initially at a fast pace, but then it continues its inward migration much more slowly than the isothermal model. The overall evolution of the planet in this case is similar to the isothermal one. The final orbit of the planet is only slightly farther away at approximately 1.5 au. Given the similarity of the isothermal and radiative results, we decided to continue our study in the rest of the paper by using primarily the isothermal approximation in order to cut down on unnecessary computation time.

The interesting outward migration of the planet near the end of its evolution can be understood in terms of the interaction of the eccentric disk with the migrating planet. During the inward migration of the planet, the eccentricity of the planet’s orbit remains small. We noticed that when the planet approaches the inner, more eccentric regions of the disk, the disk becomes more circular which allows further inward migration of the planet. Once the planet reaches the inner hole of the disk, the eccentricities of the disk and the planet increase again, causing the planet to move into the disk periodically. Subsequently, the planet turns around and moves slightly outward, as shown in Fig. 8.

The final position of the planet in the two models is illustrated in Fig. 9 where the radial surface density distribution is plotted together with the location of the planet. In both cases, the planet’s final orbit is near the inner edge of the disk where the density slope is positive. As shown here, the final position of the planet lies just inside of the peak density. This can be compared to the case of Kepler-38 where the central binary is on an almost circular orbit, and the planet ends up in a position closer to the inner binary where the density drops to less than 20% of its maximum value (Kley & Haghighipour 2014).

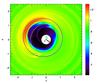thumbnail Fig. 10

2D surface density distribution for the isothermal disk model near the final state of its evolution. The gray dots refer to the positions of the two binary stars and the planet. The Roche lobe of the system of the secondary star and planet are also shown. The blue dashed line refers to the orbit of the planet, and the blue arrow points to the periapse of the planetary orbit. The red arrow points to the periapse of the inner, eccentric disk, while the green arrow points to the periapse of the binary. The white dashed circle refers to the observed semi-major axis of the planet with a radius of 1.09 AU.

Figure 10 shows the 2D density distribution of the disk near the final state of planet migration, along with the positions of the binary and planet. Also shown here are the directions of the periapses of the binary, the disk, and the planet. It also shows the orbit of the planet and the observed semi-major axis of the planet in the Kepler-34 system. For the observed orbit, we chose to plot the semi-major axis instead of the true ellipse because its orientation is not constant with respect to the binary. This figure suggests that the disk’s and the planet’s orbits are aligned such that their corresponding periapses always point in the same direction. The analysis of the time evolution of the system supports this conjecture and confirms that in the equilibrium state, the planet and disk precess exactly at the same rate of about 3°/yr (i.e., with the same rate as the disk without the planet) see Fig. 4. We also ran a test simulation that continued this model but with a very low disk mass so that the planet would no longer feel the disk. Interestingly, in this case the planet precessed with the same rate as before, indicating that the presence of the disk does not have a significant influence on this process. This result seems to imply that the precession rate of the inner disk equals that of small massless particles, a result that will be analyzed in our subsequent studies.

The strict alignment of the planetary orbit with that of the eccentric inner disk implies that near apocenter, the planet is always positioned outside of the maximum density of the disk, as indicated in Fig. 10. That means that a comparison between the semi-major axis of the planet and the radial location of the maximum of the azimuthally averaged density (see Fig. 9) can give the wrong impression that the planet orbits inside the density maximum.

thumbnail Fig. 11

Evolution of the semi-major axis (top) and eccentricity (middle) of two embedded planets. The simulation was continued from the isothermal model shown in Fig. 8 (red line) by adding an additional planet with the same mass at 2.0 AU. The green curve corresponds to the original model with the new planet added at t ≈ 2300 yrs. The red curves correspond to the (original) inner planet and the blue curves is for the (additional) outer planet. The bottom panel shows the period ratio (outer/inner) of the two planets.

5. Evolution with two planets

As shown in previous sections, a single, embedded planet in a disk around Kepler 34 stops its migration well outside the observed orbit of Kepler-34 b. This large deviation from the observed orbit is caused mainly by the wide, eccentric inner hole of the disk that does not allow the planet to migrate closer to the star. One possible solution to this discrepancy would be to consider an additional planet in the system located initially at a larger distance in the disk. During its inward migration, this outer planet, while still embedded in the disk, will interact with the inner planet scattering it farther inward and closer to the central binary.

To examine this scenario, we carried out simulations, starting from the single-planet models displayed in Fig. 8, with an additional planet with the same mass as that of Kepler-34 b. This planet was added to simulations at different evolutionary times and was allowed to migrate owing to its interaction with the disk. All simulations led to similar results. We show a sample of these simulations for an isothermal model in Fig. 11. In the first phase (from t ≈ 400 to t ≈ 2300), the final part of the simulation of Fig. 8 where we have shifted the time axis. Then, at t ≈ 2300, the second planet is added. This new planet migrates inward with an initial rate similar to that of the original planet. At t ≈ 3200, the migration rate suddenly changes to a slower rate. At the same time, the inner planet begins to move inward at a similar pace, and its eccentricity is slightly increased. The period ratio Pouter/Pinner (lower panel) indicates a capture into the 7:4 resonance, which is confirmed by an analyses of the resonant angles. During its subsequent evolution, the system remains in resonance, and eventually the eccentricity of the inner planet reaches high values and the system becomes unstable. A similar process in the radiative case of Fig. 8 shows that in that simulation, the two planets end up in a 3:2 resonance, and again the system becomes unstable. We also carried out simulations where we varied the mass of the additional planet, the disk mass, and the time of second planet insertion. We found that, in general, the system goes through similar evolutionary paths: the two planets are captured in different resonances (2:1, 3:2 or 5:3), and they ultimately scatter each other in unstable orbits.

In the previous section, we noted that the evolution of two planets embedded in the disk always resulted in their mutual scattering and unstable configurations. Despite this instability, we found that after a scattering event, one of the planets remained at a location close to the observed orbit of Kepler-34 b. This motivated us to continue the simulation in one of this cases with a reduced disk mass to examine whether the resulted configuration could remain stable. A lower disk mass is to be expected in the final phase of planet evolution, and our mass reduction somewhat mimics that state of disk dissipation.

Figure 12 shows the results of one of these simulations. Here, we again started the simulation from the isothermal case of Fig. 8, now at an earlier time. The evolution of the initial single planet is shown again. At t ≈ 3500 yr into the simulation, the second planet was added at 2.0 au and evolved with the original planet. At around t ≈ 7000 yr, the system entered a 3:2 MMR, followed brieflyby a non-destructive scattering event where the outer planet ended up near its starting position at 2 au, and the inner planet moved slightly inward, close to the observed location of Kepler-34 b. Had we stopped the simulation at this point, we would have had a perfect match with the observations for the inner planet. However, the subsequent evolution (with the disk still present) led to an inward migration of the outer planet and a slight outward motion of the inner planet (see Appendix A). At around t ≈ 15 000, the planets were captured again into the 3:2 resonance, which at t ≈ 16 000, resulted in a violent scattering event.

To study the effect of disk dissipation, we restarted the above-mentioned simulation just before the final scattering event and after t ≈ 15 000, with one tenth of the original disk mass. For this phase, the evolution of the outer planet is shown in light blue and that of the inner planet is in purple. The bottom panel shows the period ratio in purple as well. During this low disk mass phase, the inward migration of the outer planet continues with a very low rate, while the inner planet remains at its location. Eventually the planets are captured in a 3:2 MMR; however, the system remains stable as is indicated by the low values of the planets’ eccentricities.

thumbnail Fig. 12

Evolution of the semi-major axis (top), eccentricity (middle), and period ratios of two embedded planets in the disk. The simulation was continued from the isothermal model shown in Fig. 8 (red line) that is shown in green here. At t ≈ 3500 yr, a second planet was added (blue line) at 2.0 au. At t ≈ 7000 yr, the planets entered a 3:2 mean-motion resonance and experienced a scattering event. At a later time (t ≈ 16 000), the original evolution with the two planets eventually became unstable. At around t ≈ 15 000, the disk mass was reduced by a factor of 10, and the simulation was continued (shown in purple for the outer planet and in light blue for the inner one).

6. Summary and discussion

Using 2D hydrodynamical simulations, we studied the evolution of planets embedded in a circumbinary disk for the parameters of the Kepler-34 system. The stellar binary consists of two stars of nearly equal masses (~1 M⊙) orbiting each other in a relatively high eccentric orbit with ebin = 0.52. These orbital characteristics of Kepler-34 make this system much more dynamic than some of the other systems that host CBPs.

Our investigation followed that of Kepler-38 (Kley & Haghighipour 2014) where we adopted a two-step approach. We first studied the structure of a circumbinary disk without a planet, and then included a planet in the disk and followed its subsequent evolution. We considered locally isothermal disks, as well as more realistic disks that include viscous dissipation, vertical cooling, and radiative diffusion. In the following, we briefly present our most important results.

As shown in Fig. 1, a highly eccentric stellar binary generates a large inner hole in the disk with high eccentricity. As a result, around an eccentric binary such as Kepler-34, the maximum value of the density distribution lies at farther distances (around 7 abin) than in systems with circular binaries such as Kepler-38 (at about 5 abin). Our simulations also showed that the inner region of the disk will precess in a prograde sense. For the system of Kepler-34, the rate of this precession is about ϖdisk = 3°/yr. In turn, the disk that has a total mass of 0.015 M⊙ within 5 au (our reference model), induces a slow prograde precession on the binary with a rate of ϖbin = 0.05°/yr.

To study the evolution of an embedded planet in a disk around Kepler-34, we added a planet with a mass of 0.22 MJup (the observed value of the mass of Kepler-34 b) to the system and allowed the planet to migrate in the disk as a result of disk torques acting on it. In our reference disk model, the planet migration was so rapid that its orbit became unstable by the time it had reached a distance of about 1.35 au from the barycenter of the binary. When reducing the mass of the disk to 25% and considering a lower viscosity (α = 0.004), the orbit of the planet became stable. Here, isothermal and radiative models resulted in qualitatively similar evolutions. The planet migrated inward to a distance of about 1.3 au from the center and then moved out to settle into an equilibrium state of about 1.35 au for the isothermal and 1.5 au for the radiative models. A test simulation, in which the planet started inside the hole of the disk, at the observed distance of 1.09 au, showed that the planet moves outward and settles approximately at the same location as well (see Appendix).

Results of our simulations indicated that the final location of the planet is robust and determined by the size and shape (eccentricity) of the disk inner hole. The final distance of the planet from the binary’s barycenter is greater than the observed semi-major axis of Kepler-34 b, but its eccentricity is in good agreement with its observed value. In this final state, the precession rate of the planet orbit becomes equal to the disk precession rate where they enter into a state of apsidal corotation with an alignment of their periapses. As a result, the planet always orbits outside the disk’s eccentric hole, avoiding moving farther into the disk. These results seem to indicate that in an eccentric binary such as Kepler-34, the evolution of the disk makes it difficult for the planet to reach close distances from the binary. The final position of the planet is determined by the size of the disk inner hole which becomes larger for eccentric binaries.

The difficulty in reaching close orbits for a planet in an eccentric disk combined with the discovery of the circumbinary planetary system of Kepler-47 with multiple planets motivated us to assume that Kepler-34 may contain (or might have contained) at least one additional planet. To investigate the evolution of multiple planets in the disk, we added an additional planet in an exterior orbit to our single-planet disk models and followed the combined evolution of both planets. For isothermal and radiative disks, these typically resulted in a capture of the two planets in low-order, mean-motion resonances with period ratios of 2:1, 3:2, 5:3, and 7:4. In all cases, the inward migration of the resonantly coupled pair resulted in unstable configurations when the inner planet reached a distance of about 1.1 to 1.2 au from the binary’s barycenter. In these simulations, one planet was typically ejected from the system, and the second one was scattered into an orbit with a much larger semi-major axis.

Upon reducing the disk mass by a factor of 10, we found that the planet orbits could stabilize with their subsequent evolution resulting in a system where the inner planet has a semimajor axis close to its observed value. This suggested that a model in which a pair of planets are driven toward the binary just before disk dispersal represent a possible scenario for explaining the orbital configuration of the Kepler-34 system. In this case, it may be interesting to search for additional planets in the system.

As we have shown in this study, the evolution of planets in a disk depends crucially on the structure of the inner hole of the disk, which itself depends on the binary eccentricity. The detailed dependence on disk parameters, such as viscosity and disk mass, will be investigated in more detail in future studies.

We note that in the models presented in this paper, we restricted ourselves to flat two-dimensional disks. Given the flatness of the observed circumbinary systems, this is a realistic assumption. However, a more comprehensive study of the dynamical evolution of these systems requires full 3D simulations of radiative disks around binary star systems.

Acknowledgments

N.H. acknowledges support from the NASA ADAP grant NNX13AF20G, and the Alexander von Humboldt Foundation. N.H. would also like to thank the Computational Physics Group at the University of Tübingen for their kind hospitality during the course of this project.

References

  1. Artymowicz, P., & Lubow, S. H. 1994, ApJ, 421, 651 [NASA ADS] [CrossRef] [Google Scholar]
  2. Artymowicz, P., & Lubow, S. H. 1996, ApJ, 467, L77 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bromley, B. C., & Kenyon, S. J. 2015, ApJ, 806, 98 [NASA ADS] [CrossRef] [Google Scholar]
  4. D’Angelo, G., Henning, T., & Kley, W. 2003, ApJ, 599, 548 [NASA ADS] [CrossRef] [Google Scholar]
  5. de Val-Borro, M., Edgar, R. G., Artymowicz, P., et al. 2006, MNRAS, 370, 529 [NASA ADS] [CrossRef] [Google Scholar]
  6. Doyle, L. R., Carter, J. A., Fabrycky, D. C., et al. 2011, Science, 333, 1602 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
  7. Dunhill, A. C., & Alexander, R. D. 2013, MNRAS, 435, 2328 [NASA ADS] [CrossRef] [Google Scholar]
  8. Dvorak, R. 1986, A&A, 167, 379 [NASA ADS] [Google Scholar]
  9. Georgakarakos, N., & Eggl, S. 2015, ApJ, 802, 94 [NASA ADS] [CrossRef] [Google Scholar]
  10. Günther, R., & Kley, W. 2002, A&A, 387, 550 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  11. Holman, M. J., & Wiegert, P. A. 1999, AJ, 117, 621 [NASA ADS] [CrossRef] [Google Scholar]
  12. Kley, W. 1989, A&A, 208, 98 [NASA ADS] [Google Scholar]
  13. Kley, W., & Crida, A. 2008, A&A, 487, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Kley, W., & Dirksen, G. 2006, A&A, 447, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Kley, W., & Haghighipour, N. 2014, A&A, 564, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Kley, W., Papaloizou, J. C. B., & Ogilvie, G. I. 2008, A&A, 487, 671 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Kley, W., Bitsch, B., & Klahr, H. 2009, A&A, 506, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Kostov, V. B., McCullough, P. R., Carter, J. A., et al. 2014, ApJ, 784, 14 [NASA ADS] [CrossRef] [Google Scholar]
  19. Lin, D. N. C., & Papaloizou, J. 1985, in Protostars and Planets II, eds. D. C. Black, & M. S. Matthews, 981 [Google Scholar]
  20. Lines, S., Leinhardt, Z. M., Paardekooper, S., Baruteau, C., & Thebault, P. 2014, ApJ, 782, L11 [NASA ADS] [CrossRef] [Google Scholar]
  21. Marzari, F., Thebault, P., Scholl, H., Picogna, G., & Baruteau, C. 2013, A&A, 553, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Meschiari, S. 2012, ApJ, 761, L7 [NASA ADS] [CrossRef] [Google Scholar]
  23. Müller, T. W. A., & Kley, W. 2012, A&A, 539, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Müller, T. W. A., & Kley, W. 2013, A&A, 560, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Nelson, R. P. 2003, MNRAS, 345, 233 [NASA ADS] [CrossRef] [Google Scholar]
  26. Orosz, J. A., Welsh, W. F., Carter, J. A., et al. 2012a, ApJ, 758, 87 [NASA ADS] [CrossRef] [Google Scholar]
  27. Orosz, J. A., Welsh, W. F., Carter, J. A., et al. 2012b, Science, 337, 1511 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  28. Paardekooper, S.-J., Leinhardt, Z. M., Thébault, P., & Baruteau, C. 2012, ApJ, 754, L16 [NASA ADS] [CrossRef] [Google Scholar]
  29. Pierens, A., & Nelson, R. P. 2007, A&A, 472, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Pierens, A., & Nelson, R. P. 2008a, A&A, 478, 939 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Pierens, A., & Nelson, R. P. 2008b, A&A, 483, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Pierens, A., & Nelson, R. P. 2013, A&A, 556, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Rafikov, R. R. 2013, ApJ, 764, L16 [NASA ADS] [CrossRef] [Google Scholar]
  34. Schwamb, M. E., Orosz, J. A., Carter, J. A., et al. 2013, ApJ, 768, 127 [NASA ADS] [CrossRef] [Google Scholar]
  35. Welsh, W. F., Orosz, J. A., Carter, J. A., et al. 2012, Nature, 481, 475 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]

Appendix A: Evolution of a close-in planet

To test the robustness of the final position of a migrating planet in an eccentric disk around the Kepler-34 binary, we performed additional simulations where the planet was started inside the inner hole of the circumbinary disk. In Fig. A.1, we show the evolution of a planet in two systems. In the first system shown in red, the planet starts at r0 = 2.0 au as displayed already in Fig. 8. In the second case, shown in blue, the planet starts at r0 = 1.09 au inside the hole of the disk. In both cases, the initial eccentricity of the planet was set to e0 = 0. In the second system, the starting position of the planet lies at the present observed location of Kepler-34 b.

The simulations show that the planet starting inside the inner hole of the disk does not remain at its orbit but moves slowly outward. In both systems, the final position of the planet is the same, at ~1.35 AU from the binary barycenter. The inner planet that moves out shows large oscillations in its eccentricity, causing variations to appear in its semi-major axis. When running simulations for long times, these variations seem to become smaller. The outward migration in the second system can be understood by the interaction of an eccentric disk with the orbiting planet. During one orbit of the planet, because of the oscillations in its semi-major axis, it enters periodically into the eccentric disk where it experiences a positive net torque that drives the planets outward.

thumbnail Fig. A.1

Evolution of the semi-major axis of two the planets in an isothermal disk. The red curve corresponds to the model displayed in Fig. 8. The blue curve corresponds to a planet that has started with an initial position of a0 = 1.09 inside the inner hole of the disk.

All Tables

Table 1

Binary parameter and the observed planetary parameter of the Kepler-34 system used in the simulations.

In the text
Table 2

Parameters of the locally isothermal disk reference model without a planet.

In the text

All Figures

thumbnail Fig. 1

Azimuthally averaged surface density (top) and disk eccentricity (bottom) for our locally isothermal reference model. Shown here are the profiles at different evolutionary times (in years); the red curve denotes the initial setup.

In the text
thumbnail Fig. 2

Two-dimensional density structure of our isothermal reference disk model around the central binary star. The graph shows only a local view around the binary. The entire computational grid, however, extends from r = 0.34 AU to r = 5.0 AU. The white inner region lies inside the computational domain and is not covered by the grid. The positions of the primary and secondary stars are indicated by the gray dots. The Roche lobe of the secondary is also shown. The central cross marks the origin of the coordinate system. which coincides with the center of mass of the binary.

In the text
thumbnail Fig. 3

Azimuthally averaged surface density (top) and eccentricity (bottom) for locally isothermal disks, with H/r = 0.05, around the two systems, Kepler-34 and Kepler-38. The figure shows the profiles for the final equilibrium state without any embedded planet. The radial coordinate has been scaled by the binary separation which is 0.23 AU for Kepler-34 and 0.15 AU for Kepler-38. The results for Kepler-38 have been taken from Kley & Haghighipour (2014).

In the text
thumbnail Fig. 4

Evolution of the argument of periapses of the disk with respect to the inertial frame. Results of two different estimates are shown for comparison. Red corresponds to estimates using the maximum of the 2D density distribution (see Fig. 2), and blue is for estimates using the mass-weighted mean value of the inner disk.

In the text
thumbnail Fig. 5

Evolution of the argument of periapses of the binary with respect to the inertial frame. The red curve corresponds to the case where the backreaction of the disk onto the binary has been articifially switched off such that the motion of the binary is not influenced by the presence of the disk. The blue curve correponds to the reference model as shown in Fig. 2.

In the text
thumbnail Fig. 6

Evolution of the semi-major axis (top) and eccentricity (bottom) of an embedded planet in an isothermal disk (reference model) that was first brought into an equilibrium. In the two simulations, the planet was started at different distances from the center of mass of the binary. In the first simulation (shown in red), the planet started at a distance of a0 = 1.75 au, and in the second simulation (shown in green and blue) it started as a0 = 2.0 au. In the simulation shown in red, the planet is immediately released and evolves with the disk. In the second simulation, the planet’s orbit is held constant during the first 600 yrs (in blue) and then released (green lines). In both simulations, the planet migrates inward with a rate of about 0.1 au/100 yrs. Both models result in unstable evolution when the planet has reached a distance of about 1.35 au. The dashed horizontal lines shows the observed semi-major axis and eccentricity of Kepler-34 b.

In the text
thumbnail Fig. 7

Evolution of the semi-major axis (top) and eccentricity (bottom) of an embedded planet in isothermal disk models with half the disk mass. The red curve refers to the original model and is identical to the one shown in Fig. 6.

In the text
thumbnail Fig. 8

Evolution of the semi-major axis (top) and eccentricity (bottom) of an embedded planet in disks with lower surface densities (1/4 of the reference model) and reduced viscosities (α = 0.004). The red graph corresponds to the isothermal model and the blue refers to the radiative disk. In the two simulations, the planet is started in a circular orbit at a distance of a0 = 2.0 au from the center of mass of the binary. In the simulation shown in red, the planet is included in the disk from the very beginning of the simulation, and it begins to migrate simultaneously with the disk evolution starting from its initial density profile. In the simulation shown in blue, the disk is first relaxed to the radiative equilibrium, and then the planet is embedded in it. The dashed horizontal lines refer to the observed parameter of the Kepler-34 planet.
In the text
thumbnail Fig. 9

Graphs of the azimuthally averaged radial surface density of the isothermal and radiative disk models of Fig. 8 with an embedded planet. The density distributions are taken near the final state of the evolutions shown in Fig. 8. The big colored dot in each graph represents the semi-major axis of the planet at these times. For illustrative purposes, we have moved the circles close to their corresponding curves.

In the text
thumbnail Fig. 10

2D surface density distribution for the isothermal disk model near the final state of its evolution. The gray dots refer to the positions of the two binary stars and the planet. The Roche lobe of the system of the secondary star and planet are also shown. The blue dashed line refers to the orbit of the planet, and the blue arrow points to the periapse of the planetary orbit. The red arrow points to the periapse of the inner, eccentric disk, while the green arrow points to the periapse of the binary. The white dashed circle refers to the observed semi-major axis of the planet with a radius of 1.09 AU.

In the text
thumbnail Fig. 11

Evolution of the semi-major axis (top) and eccentricity (middle) of two embedded planets. The simulation was continued from the isothermal model shown in Fig. 8 (red line) by adding an additional planet with the same mass at 2.0 AU. The green curve corresponds to the original model with the new planet added at t ≈ 2300 yrs. The red curves correspond to the (original) inner planet and the blue curves is for the (additional) outer planet. The bottom panel shows the period ratio (outer/inner) of the two planets.

In the text
thumbnail Fig. 12

Evolution of the semi-major axis (top), eccentricity (middle), and period ratios of two embedded planets in the disk. The simulation was continued from the isothermal model shown in Fig. 8 (red line) that is shown in green here. At t ≈ 3500 yr, a second planet was added (blue line) at 2.0 au. At t ≈ 7000 yr, the planets entered a 3:2 mean-motion resonance and experienced a scattering event. At a later time (t ≈ 16 000), the original evolution with the two planets eventually became unstable. At around t ≈ 15 000, the disk mass was reduced by a factor of 10, and the simulation was continued (shown in purple for the outer planet and in light blue for the inner one).

In the text
thumbnail Fig. A.1

Evolution of the semi-major axis of two the planets in an isothermal disk. The red curve corresponds to the model displayed in Fig. 8. The blue curve corresponds to a planet that has started with an initial position of a0 = 1.09 inside the inner hole of the disk.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.