| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A62 | |
| Number of page(s) | 16 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201526200 | |
| Published online | 02 September 2015 | |
Modelling the observed properties of carbon-enhanced metal-poor stars using binary population synthesis
1 Argelander Institut für Astronomie, Auf dem Hügel 71, 53121 Bonn, Germany
e-mail: cabate@uni-bonn.de
2 Department of Astrophysics/IMAPP, Radboud University Nijmegen, PO Box 9010, 6500 GL Nijmegen, The Netherlands
3 Institute of Astronomy, Madingley Road, Cambridge CB3 0HA, UK
4 Research School of Astronomy & Astrophysics, Mount Stromlo Observatory, Weston Creek ACT 2611, Australia
5 Department of Physics and JINA-CEE, 225 Nieuwland Science Hall, Notre Dame, IN 46656, USA
6 Deptartment of Astronomy & Space Science, Chungnam National University, 305-764 Daejeon, Republic of Korea
Received: 27 March 2015
Accepted: 5 July 2015
The stellar population in the Galactic halo is characterised by a large fraction of carbon-enhanced metal-poor (CEMP) stars. Most CEMP stars have enhanced abundances of s-process elements (CEMP-s stars), and some of these are also enriched in r-process elements (CEMP-s/r stars). In one formation scenario proposed for CEMP stars, the observed carbon excess is explained by invoking wind mass transfer in the past from a more massive thermally-pulsing asymptotic giant branch (AGB) primary star in a binary system.In this work we generate synthetic populations of binary stars at metallicity Z = 0.0001 ([Fe/H] ≈ − 2.3), with the aim of reproducing the observed fraction of CEMP stars in the halo. In addition, we aim to constrain our model of the wind mass-transfer process, in particular the wind-accretion efficiency and angular-momentum loss, and investigate under which conditions our model populations reproduce observed distributions of element abundances.We compare the CEMP fractions determined from our synthetic populations and the abundance distributions of many elements with observations. Several physical parameters of the binary stellar population of the halo are uncertain, in particular the initial mass function, the mass-ratio distribution, the orbital-period distribution, and the binary fraction. We vary the assumptions in our model about these parameters, as well as the wind mass-transfer process, and study the consequent variations of our synthetic CEMP population.The CEMP fractions calculated in our synthetic populations vary between 7% and 17%, a range consistent with the CEMP fractions among very metal-poor stars recently derived from the SDSS/SEGUE data sample. The resulting fractions are more than a factor of three higher than those determined with default assumptions in previous population-synthesis studies, which typically underestimated the observed CEMP fraction. We find that most CEMP stars in our simulations are formed in binary systems with periods longer than 10 000 days. Few CEMP stars have measured orbital periods, but all that do have periods up to a few thousand days. Our results are consistent only if this small subpopulation represents the short-period tail of the underlying period distribution. The results of our comparison between the modelled and observed abundance distributions are significantly different for CEMP-s/r stars and for CEMP-s stars without strong enrichment in r-process elements. For the latter, our simulations qualitatively reproduce the observed distributions of carbon, sodium, and heavy elements such as strontium, barium, europium, and lead. Contrarily, for CEMP-s/r stars our model cannot reproduce the large abundances of neutron-rich elements such as barium, europium, and lead. This result is consistent with previous studies, and suggests that CEMP-s/r stars experienced a different nucleosynthesis history to CEMP-s stars.
Key words: stars: abundances / stars: chemically peculiar / binaries: general / Galaxy: halo / stars: Population II / stars: low-mass
© ESO, 2015
1. Introduction
The population of old metal-poor stars observed in the Galactic halo carries information about the conditions under which the Milky Way was formed. In the past three decades, the HK survey (Beers et al. 1985, 1992), the Hamburg/ESO survey (HES; Christlieb et al. 2001, 2008), and the SDSS/SEGUE survey (York et al. 2000; Gunn et al. 2006; Yanny et al. 2009) have collected spectra of a large sample of very metal-poor stars (VMP, that is, stars with abundances of iron1[Fe/H] ≲ −2), and have made it possible to investigate their dynamical and chemical properties. These studies reveal a large proportion of carbon-enhanced metal-poor (CEMP) stars. According to the original nomenclature proposed by Beers & Christlieb (2005), CEMP stars have [C/Fe] > +1. More recently a number of authors have adopted the criterion [C/Fe] > +0.7 to define CEMP stars (e.g. Aoki et al. 2007; Lee et al. 2013; Yong et al. 2013). The fraction of CEMP stars among metal-poor stars is observed to rise with increasing distance from the Galactic plane (Frebel et al. 2006; Carollo et al. 2012). A strong increase in the cumulative fraction of CEMP stars with decreasing metallicity has been confirmed by many studies, from about 3% at [Fe/H] < −1 to around 75% at [Fe/H] < − 4 (e.g. Cohen et al. 2005; Marsteller et al. 2005; Frebel et al. 2006; Lucatello et al. 2006; Carollo et al. 2012; Aoki et al. 2013; Lee et al. 2013; Yong et al. 2013; Placco et al. 2014).
CEMP stars are usually classified into four categories according to the observed abundances of barium and europium, two elements associated with the slow (s-) and rapid (r-) neutron-capture process, respectively.
-
CEMP-s stars exhibit enhanced abundances of s-elements, and are defined by [Ba/Fe] > +0.5 and [Ba/Eu] > 0. CEMP-s stars account for at least 80% of all observed CEMP stars (Aoki et al. 2007). A number of authors adopt slightly different criteria, e.g. [Ba/Fe] > +1 and/or [Ba/Eu] > +0.5 (Beers & Christlieb 2005; Jonsell et al. 2006; Masseron et al. 2010).
-
CEMP-s/r stars 2 are CEMP-s stars that also enriched in europium and r-elements, [Eu/Fe] > +1.
-
CEMP-r stars are a rare CEMP subclass enriched in elements produced purely by the r-process, and are defined by the criteria [Eu/Fe] > +1 and [Ba/Eu] < 0.
-
CEMP-no stars do not exhibit peculiar enhancements in the elements heavier than iron (Aoki et al. 2002).
The formation scenario of CEMP stars is still uncertain, and different categories of CEMP stars are likely to have different formation channels. Several mechanisms have been proposed to explain the large carbon abundances, for example: (a) the gas cloud in which these stars were formed was already enriched in carbon produced by zero-metallicity and/or rapidly rotating stars (Mackey et al. 2003; Meynet et al. 2006, 2010; Maeder et al. 2014) or expelled by the faint supernovae associated with the first generation of stars (Umeda & Nomoto 2003, 2005; Nomoto et al. 2013); and (b) the carbon-enhanced material was accreted from the envelope of a thermally-pulsing asymptotic giant branch (AGB) primary star in a binary system onto the presently observed low-mass companion. The mass-transfer scenario provides a natural explanation for the chemical abundances of CEMP-s stars because carbon and s-elements are produced during AGB nucleosynthesis, and the observed fraction of CEMP-s stars with a binary companion is consistent with the hypothesis of all CEMP-s stars being in binary systems (Lucatello et al. 2006; Starkenburg et al. 2014). By contrast, many CEMP-no stars show no indication of a binary companion (Norris et al. 2013; Hansen et al., in prep.), and they exhibit low abundances of s-elements, whereas large enhancements of s-elements are normally produced in AGB stellar models, except in some models of mass M∗> 3 M⊙. The origin of CEMP-s/r stars is also an open issue. Current stellar models indicate that in AGB stars the density of free neutrons is not sufficiently large for the r-process to take place, hence the enhancement of r-elements in CEMP-s/r stars remains unexplained.
A number of authors have simulated populations of very metal-poor stars with the aim of reproducing the observed fraction of CEMP stars. The largest uncertainties in these models include the amount of carbon and s-elements produced by AGB nucleosynthesis as a function of the stellar mass and metallicity, the shape of the initial mass function (IMF) of the early Galaxy, the binary fraction, the efficiency of the mass-transfer process, and the range of separations in which it occurs. Lucatello et al. (2005) and Komiya et al. (2007) argue that the IMF in the early Galaxy was weighted towards intermediate-mass stars to account for the large fraction of CEMP stars at low metallicity. Suda et al. (2013) and Lee et al. (2014) suggest that the transition between the early (top-heavy) and the present-day IMF occurred over the metallicity range between [Fe/H] = −2.5 and [Fe/H] = −1.5. However, Pols et al. (2012) show that, with an IMF biased towards intermediate-mass stars, many nitrogen-enhanced metal-poor stars are produced, whereas very few are observed.
Izzard et al. (2009) and Abate et al. (2013) model the CEMP population at metallicity Z = 10-4 (that is [Fe/H] ≈ − 2.3) with their population-synthesis models, adopting the solar-neighbourhood IMF proposed by Kroupa et al. (1993), and varying a set of uncertain physical parameters related to the mechanism of mass transfer, nucleosynthesis, and mixing processes. They typically find CEMP fractions between 2% and 4%, while the observed values found by different authors at [Fe/H] ≤ −2 vary between 9% and 25% (Marsteller et al. 2005; Frebel et al. 2006; Lucatello et al. 2006; Lee et al. 2013). However, their AGB evolution models are based on detailed models that do not allow for third dredge-up in AGB stars of mass below approximately 1.2 M⊙. To increase the CEMP/VMP fraction, Izzard et al. (2009) and Abate et al. (2013) artificially allow for third dredge-up in AGB stars down to mass 0.8 M⊙ in their models (as proposed by Izzard et al. 2004 using independent arguments), and show that in this way it is possible to raise the modelled CEMP/VMP ratio to ≳10%.
The most recent detailed models of AGB evolution and nucleosynthesis of Stancliffe & Glebbeek (2008), Karakas (2010) and Lugaro et al. (2012) find third dredge-up in stars of mass down to 0.9 M⊙ at metallicity Z = 10-4. In the models of Karakas (2010) and Lugaro et al. (2012), the nucleosynthesis products of stars are computed on a grid of 16 initial masses in the range [0.9, 6] M⊙, taking into account 320 isotopes from 1H up to 210Po. In our recent work (Abate et al. 2015a,b, Papers I and II hereafter) we include the results of these detailed calculations in our model of binary evolution and nucleosynthesis, and study in detail the chemical compositions for a sample of 67 CEMP-s stars. We compare the surface abundances of each CEMP-s star with a grid of model binary stars, and determine the best fit to the observed abundances. From this comparison we conclude that our models reproduce reasonably well the chemical properties of CEMP-s stars with [Eu/Fe] < + 1 (for brevity, “r-normal CEMP-s” stars hereafter), but not CEMP-s/r stars, possibly indicating different nucleosynthesis histories for the two categories. Also, our models typically predict orbital periods longer than those observed, suggesting that wind mass transfer should be more efficient at close separations.
In this paper we extend our recent work on CEMP stars, and analyse the properties of the population of CEMP stars at [Fe/H] ≈ − 2.3 as a whole, through a comparison with synthetic populations. Our purpose is to answer the following questions:
-
1.
Is it possible to reproduce the observed CEMP/VMP ratio withour model of binary population synthesis that includes the latestdetailed AGB models of Karakas (2010) andLugaro et al. (2012)?
-
2.
Can we constrain our model of the wind mass-transfer process, and in particular the wind-accretion efficiency and angular-momentum loss?
-
3.
Under which conditions does our model reproduce the observed abundance distributions of elements associated with AGB nucleosynthesis?
The paper is organised as follows. In Sect. 2 we describe the most important characteristics of our model and the selection criteria that we adopt to compare the results of our synthetic population with the observations. In Sect. 3 we present the results of our models, which are further discussed in Sect. 4. Our conclusions are presented in Sect. 5.
2. Models
In this work we use the binary population synthesis code binary_c/nucsyn described by Izzard et al. (2004, 2006, 2009) to simulate populations of stars at low metallicity, and compare them with a sample of observed stars. In this section we summarise the physical parameters of our model (Sect. 2.1), the assumptions made in our grid of binary models (Sect. 2.2), and describe the method used to select the simulated stars according to their luminosity (Sect. 2.3).
2.1. Input physics
Physical parameters adopted in our binary population models.
In our default model set A we adopt the same input physics as in model set A of Papers I and II. We briefly list our most important assumptions below. Table 1 provides an overview of our alternative model sets, in which we varied some of these assumptions.
-
The Reimers (1975) equation multiplied by afactor of η = 0.5 is used to compute the wind mass-loss rate up to the AGB. The prescription of Vassiliadis & Wood (1993) describes mass loss during the AGB phase, with minimum and maximum wind velocities vw = 5 km s-1 and vw = 15 km s-1, respectively.
-
We adopt the approximation of a spherically-symmetric wind (Abate et al. 2013, Eq. (4)) to compute the angular momentum carried away by the ejected material, and calculate the wind-accretion rate according to a wind Roche-lobe overflow (WRLOF) model described by Eq. (9) of Abate et al. (2013). Our model sets B and C are as in Paper II. In both model sets the expelled material carries away a multiple γ = 2 of the average specific orbital angular momentum of the binary system. In model set B we adopt an enhanced Bondi-Hoyle-Lyttleton (BHL) model of wind accretion computed with Eq. (6) of Boffin & Jorissen (1988) and αBHL = 10, whereas in model set C our default WRLOF prescription is adopted (Paper II).
-
The algorithms that we use to compute the nucleosynthesis of the star through the first and second dredge-ups are based on the results of Karakas et al. (2002) and Karakas & Lattanzio (2007); we refer the interested reader to Izzard et al. (2004, 2006, 2009) for a thorough description.
-
The amount of material dredged up during the AGB phase is computed with algorithms tuned to reproduce the detailed models of Karakas (2010) at metallicity Z = 10-4, as described in Paper I. The chemical composition of the intershell region of the AGB star is tabulated as a function of the mass of the star at the beginning of the AGB phase, the evolution along the AGB, and the mass of the partial mixing zone, MPMZ, a free parameter of our model. In the detailed AGB models of Karakas (2010), the partial mixing zone (PMZ) is the site in which protons from the envelope are partially mixed with material of the intershell region. The protons react with the 12C nuclei and form a 13C pocket, in which free neutrons are produced and become available for the s-process. We refer the reader to Karakas (2010) and Lugaro et al. (2012) for a detailed explanation of the numerical treatment of the PMZ, and to Paper I for a description of our implementation in our population-synthesis code.
-
We assume efficient thermohaline mixing, that is, the accreted material is instantaneously mixed with the accreting star. The calculations of Stancliffe et al. (2007) suggest this approximation is reasonable in many cases, even though Stancliffe & Glebbeek (2008) and Stancliffe (2009) show that other processes, such as gravitational settling, may in some circumstances reduce the effect of thermohaline mixing. To account for the possibility of inefficient thermohaline mixing, in model set D the accreted material remains on the stellar surface until mixed in by convection.
-
In our models we assume the metallicity of the detailed nucleosynthesis models by Lugaro et al. (2012), i.e. Z = 10-4. We adopt the same initial composition as Papers I and II based on the chemical evolution models of Kobayashi et al. (2011) for the isotopes up to 76Ge. For heavier isotopes we assume the solar abundance distribution of Asplund et al. (2009) scaled down to Z = 10-4.
2.2. Population synthesis
Each of our simulated populations consists of N binary stars uniformly distributed in the log 10M1 − M2 − log 10a parameter space, where M1,2 are the masses of the primary and the secondary star, respectively, and a is the orbital separation. Seven different values of the PMZ mass are taken into account. The adopted grid resolution is N = NM1 × NM2 × Na × NPMZ, where NM1 = 100, NM2 = 32, Na = 80 and NPMZ = 7. A finer grid with higher resolution does not change our results.
The initial parameters vary in the following ranges:
-
M1,i is in the interval [0.5, 8.0] M⊙. Stars of mass below 0.5 M⊙ are not expected to be visible with the current magnitude limitation of the observational surveys, as explained in Sect. 2.3. Massive stars that end their evolution as supernovae are not considered.
-
M2,i is uniformly spaced in [0.1, 0.9] M⊙. More massive stars have already evolved to a white dwarf after 10 Gyr, thus they are excluded because they do not contribute to the fraction of CEMP stars. By definition, initially M2,i ≤ M1,i, therefore the initial mass ratio qi = M2,i/M1,i is always 0 <qi ≤ 1.
-
We consider circular orbits with ai between 50 and 5 × 106R⊙. Binary stars outside the considered range do not become CEMP stars in our models, either because they are too close and they merge when the primary star becomes a red giant, or because they are too wide to interact. However, binary stars at closer separations are observed. For example, Kouwenhoven et al. (2007) analyse the binary population of the stellar association Scorpius OB2 in the range [5, 5 × 106] R⊙. We assume that all stars are formed in binary systems with separations in this range. When calculating the CEMP fraction, we take into account that our grid investigates a fraction of the total population of binary stars. For example, with a flat distribution in log 10ai our grid covers 83% of the observed range, thus the model CEMP fraction is multiplied by this factor. For different ai distributions we compute the corresponding corrections. Binary systems with wider separations than 5 × 106R⊙ and single stars could in principle be taken into account by decreasing the binary fraction.
-
When the stellar mass is M∗< 3 M⊙ we adopt the following values of MPMZ: 0, 2 × 10-4, 5 × 10-4, 6.6 × 10-4, 1 × 10-3, 2 × 10-3, 4 × 10-3 M⊙. MPMZ is always zero for M∗ ≥ 3 M⊙.
Following Izzard et al. (2009) and Abate et al. (2013), stars are counted according to the sum 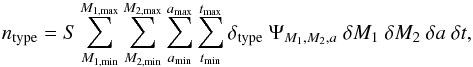 (1)where
(1)where
-
S is the star-formation rate, assumed to be constant for ages between tmin and tmax.
-
tmin = 10 Gyr corresponds to the approximate minimum age of the Galactic halo, while tmax = 13.7 Gyr is the age of the Universe; δt is the timestep.
-
The volume unit in the parameter space is δM1·δM2·δa.
-
δtype = 1 when the star belongs to a specific type, and zero otherwise. Model stars are classified as follows: VMP stars are all stars older than tmin that have not become white dwarfs; CEMP stars are VMP stars with [C/Fe] > + 0.7 ; CEMP-s stars are CEMP stars with [Ba/Fe] > + 0.5.
-
ΨM1,M2,a is the inital distribution of M1, M2, and a. We assume Ψ to be separable,
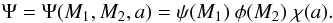 (2)In our default model set A the primary mass distribution ψ(M1,i) is the IMF proposed by Kroupa et al. (1993), the secondary mass distribution φ(M2,i) is flat in qi, and the separation distribution χ(a) is flat in log a.
(2)In our default model set A the primary mass distribution ψ(M1,i) is the IMF proposed by Kroupa et al. (1993), the secondary mass distribution φ(M2,i) is flat in qi, and the separation distribution χ(a) is flat in log a.
Some of the assumed parameters in our model are uncertain and not well-constrained by observational data, in particular: the IMF of the primary star, the binary fraction, the distribution of the mass ratios and separations in binary systems, and the age of the halo. To determine how each of these uncertainties affects our results we modify our default model set A by varying one parameter at a time. Table 1 lists some of the model sets that we tested, and their differences with respect to our default model set A.
2.3. Selection criteria
In the papers by Izzard et al. (2009) and Abate et al. (2013), the synthetic stars are selected from the simulations when their surface gravities are below the threshold log 10(g/ cm s-2) = 4.0. This criterion essentially restricts the analysis to giant stars, and is based on the implicit assumption that all giant stars of the halo are visible. Here we replace this criterion with a more realistic selection, based on the apparent magnitudes of the stars, including in the analysis the main-sequence stars that are sufficiently luminous to be visible.
To calculate the number of stars that are visible as a function of their luminosity, N(L), we follow the method adopted by van Oirschot et al. (2014). The main steps are summarised as follows.
-
1.
Our model computes the luminosity, L, the effective temperature, Teff, and surface gravity, log 10g, of each simulated star. The absolute visual magnitude, MV, is calculated from the luminosity as described by Torres (2010, Eq. (10)). The bolometric correction is computed as a function of Teff and log 10g of the star, adopting the values published by Bessell et al. (1998, Table 1).
-
2.
The apparent V magnitude of a star is computed as a function of the distance from the Sun, d, and the Galactic latitude, b. Similarly to van Oirschot et al. (2014), the extinction of stellar light is taken into account according to the Galactic-dust distribution proposed by Toonen & Nelemans (2013) and the prescription of Sandage (1972). For b ≠ 0, one has
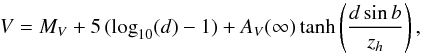 (3)where zh = 120 pc is
the scale height of Galactic dust, and AV(∞) is:
(3)where zh = 120 pc is
the scale height of Galactic dust, and AV(∞) is: 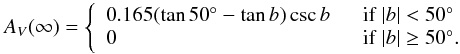
-
3.
For each simulated star of luminosity L and corresponding absolute magnitude MV, we compute the volume in which the star has apparent magnitude Vmin<V<Vmax. In our simulations, Vmin and Vmax are set consistently with the detection limits of the observational data. We compare our synthetic populations with two different data sets, which have different magnitude ranges:
-
i)
The observations of the SDSS/SEGUE survey (for brevity,SEGUE), which include the effective temperatures, surfacegravities, and carbon abundances forabout 13 000 very metal-poor stars with −2.5 ≤ [Fe/H] < − 2.0 observed at medium resolution (Lee et al. 2013). The formal g-magnitude range of the SEGUE survey is 14 <g< 20.3; however, Yanny et al. (2009) state that reliable atmospheric parameter measurements are possible only within the range 14 <g< 19. We convert the limits in the g-band to 13.5 <V< 18.5 with the empirical photometric relation (Windhorst et al. 1991),
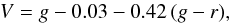 (4)where we adopt (g −
r)max = 1.2, as derived
from Fig. 7 of Lee et al. (2013).
(4)where we adopt (g −
r)max = 1.2, as derived
from Fig. 7 of Lee et al. (2013).
-
ii)
A sample of 378 very metal-poor stars with −2.8 ≤ [Fe/H] ≤ − 1.8, both carbon-normal and carbon-enhanced, mostly based on the SAGA database (Suda et al. 2008, 2011, last updates in January 2015). This is the sample adopted in Paper II, and includes high-resolution measurements of the surface abundances of many elements. The apparent V magnitudes of the stars in this sample vary between Vmin = 6 and Vmax = 16.5, hence we adopt this range in our simulations.
-
i)
 (5)where r⊙ = 8 kpc is the distance of the Sun from the Galactic centre (e.g. Moni Bidin et al. 2012), α is the minor-to-major axis ratio, and n is the exponent of the density profile. For α and n we adopt the best-fit values determined by Jurić et al. (2008) in their three-dimensional density map of the Galactic halo: α = 0.64 and n = −2.8.
(5)where r⊙ = 8 kpc is the distance of the Sun from the Galactic centre (e.g. Moni Bidin et al. 2012), α is the minor-to-major axis ratio, and n is the exponent of the density profile. For α and n we adopt the best-fit values determined by Jurić et al. (2008) in their three-dimensional density map of the Galactic halo: α = 0.64 and n = −2.8.
To speed up the calculations we initially calculate N(L,Teff,log 10g) for a grid of luminosities, temperatures, and gravities. The intervals of these parameters in the grid are chosen to reproduce the ranges of variation of these parameters in the binary stars of our simulations (namely: [−3, 5], [3000, 8000] and [−1, 6] for log 10(L/L⊙), Teff/K and log 10(g/ cm s-2), respectively). The values of N(L,Teff,log 10g) are stored in two tables, one for each magnitude range considered.
Each star in our simulation is counted by multiplying the value ntype computed with Eq. (1) by N(L,Teff,log 10g). The value of N(L,Teff,log 10g) is determined by interpolating L,Teff, and log 10g within our tables. This step is repeated for all the synthetic populations generated with different model sets.
Finally, we note that in our models most horizontal-branch stars have large effective temperatures, up to 10 000 K. In the range −2.8 ≤ [Fe/H] ≤ − 1.8, the SEGUE and SAGA databases contain only a few horizontal-branch stars hotter than 6000 K, possibly because hotter stars are selected against. In our simulations these stars are typically not very numerous because the time spent on the horizontal branch is short compared to the total stellar lifetime. However, including them in our analysis modifies the model distribution of surface gravities between approximately 2.5 dex and 3.5 dex, as noted also by Izzard et al. (2009). For this reason we exclude from our simulations all stars with Teff> 6000 K that have evolved further than the turnoff. This selection has a negligible effect on the computed fraction of CEMP stars.
3. Results
3.1. Comparison with the results of Abate et al. (2013)
We now compare the CEMP-to-VMP fraction, FC, computed with our default model set A and model set Cq of Abate et al. (2013). These two model sets adopt the same assumptions about the distributions of initial parameters, the wind-accretion efficiency, and the mechanism of angular-momentum loss. However, the selection criteria used in these model sets are different (Sect. 2.3). In model set A4 the same definitions are used as in model set Cq to select VMP stars, namely log 10(g/ cm s-2) < 4.0 and t∗ ≥ 10 Gyr, and the criterion [C/Fe] > + 1 is used to select CEMP stars. Because model set Cq was computed assuming a range of initial separations different from the present work, namely between 3 R⊙ and 105R⊙, the CEMP/VMP ratio of model Cq has been recalculated to take into account this difference.
 |
Fig. 1 Distribution of M1,i computed with model set A4 (solid, blue line) and model set Cq of Abate et al. (2013; dashed, red line). The bins are equally spaced and the width in M1,i/M⊙ of each bin is 0.1. The y-axis indicates the number of CEMP stars in each bin, arbitrarily rescaled. |
CEMP/VMP ratio, FC, calculated with model sets A1 and A4, with set Cq of Abate et al. (2013), and determined for observed stars from the SEGUE sample and the SAGA database.
CEMP star fraction computed from the SEGUE data in the range −2.5 < [Fe/H] ≤ 2, and computed with our different model sets.
With these assumptions, the only difference between model sets A4 and Cq is in the adopted set of AGB evolution models. The AGB model of Abate et al. (2013) was tuned to reproduce the evolution of AGB stars as predicted by the detailed models of Karakas et al. (2002) and Karakas & Lattanzio (2007). In these models, AGB stars of mass below approximately 1.2 M⊙ did not experience third dredge-up, and consequently did not contribute to the formation of CEMP stars. On the other hand, Stancliffe & Glebbeek (2008) and the recent work of Karakas (2010), on which our AGB model is based, show that AGB stars of mass down to 0.9 M⊙ undergo third dredge-up. Consequently, in our model set A4 CEMP stars are formed in a wider range of M1,i. The distributions of M1,i computed with model sets A4 and Cq are compared in Fig. 1. Model set A4 peaks for M1,i in the range [0.9, 1.1] M⊙, in which set Cq does not produce CEMP stars. With the adopted solar-neighbourhood IMF low-mass stars are much more commo, consequently model set A4 predicts a CEMP fraction of 7.9%, i.e. a factor 3.3 larger than set Cq, as shown in Table 2.
Model set A1 differs from model set A4 in that the model stars are selected according to their luminosity, as described in Sect. 2.3. With model set A1 we find a CEMP/VMP ratio of 8.0%. Comparison with the result of model set A4 indicates that the selection criterion has a small impact on the total fraction of CEMP stars because in our synthetic population the fraction of CEMP stars is very similar among stars above and below the threshold of log 10(g/ cm s-2) = 4. If we reduce the minimum abundance of carbon in the definition of CEMP stars, and adopt [C/Fe] > + 0.7 (our default assumption in this paper), the CEMP/VMP ratio increases to 8.5% (model set A, Table 3). This occurs because our model produces very few stars with + 0.7 < [C/Fe] ≤ + 1.0, whereas 94% of the model CEMP stars have [C/Fe] > + 1, and the average carbon abundance in the synthetic CEMP population is [C/Fe] = + 1.9.
Table 2 compares the model predictions with the observed CEMP/VMP ratio derived from the SEGUE and SAGA data sets. The CEMP fraction among SEGUE stars is taken from Table 4 of Lee et al. (2013) for stars with iron abundance in the range −2.5 < [Fe/H] ≤ − 2 and with [C/Fe] > + 1. A more detailed comparison between the results of our model sets and the SEGUE sample is performed in the next section. The CEMP fraction in the SAGA sample is approximately 24%, almost four times larger than the value determined for SEGUE stars. We discuss this discrepancy in Sect. 4.
3.2. The fraction of CEMP stars
We now compare the CEMP fraction observed in the SEGUE sample with the results of our simulations. We select stars according to the method explained in Sect. 2.3, with Vmin = 13.5, Vmax = 18.5 and a carbon abundance in CEMP stars [C/Fe] > + 0.7.
Table 3 summarises the results obtained with different model sets. The observed fractions and relative uncertainties are computed from the data reported by Lee et al. (2013, Table 6) for stars in the range −2.5 ≤ [Fe/H] ≤ − 2. For consistency with the assumptions of Lee et al. (2013), a minimum observational uncertainty of 1% is adopted, and stars are defined as giant, turnoff, and dwarf if their surface gravities are log 10(g/ cm s-2) < 3.5, 3.5 ≤ log 10(g/ cm s-2) < 4.2 and log 10(g/ cm s-2) ≥ 4.2, respectively. The CEMP/VMP ratios computed among giants, turnoff, and dwarf stars are indicated as FC,gia, FC,TO, FC,dwa (Cols. 3–5). The proportions of giant, turnoff and dwarf stars among CEMP stars are indicated as Fgia,CEMP, FTO,CEMP, Fdwa,CEMP, respectively (Cols. 6–8). The quoted uncertainties in the models convey only Poisson statistics. In this section we compare the observed and model fractions calculated with our default model set A, while the comparison of the results with different model sets is the subject of the next section.
Fractions of CEMP stars derived from the SAGA database and computed with our models.
Our total CEMP/VMP fractions underestimate those observed by a factor of 1.2 − 1.4. We note a large difference between the observed and modelled proportions of the three evolutionary stages among CEMP stars. In our models almost half of the CEMP stars are on the main sequence. By contrast, in the observed sample the CEMP dwarf stars count for approximately 1.6%, while giants and turnoff stars count for approximately 50% each. This discrepancy is also evident from the comparison between the log 10g distribution of the observed CEMP stars of the SEGUE sample and the results of model set A (Fig. 2). The positions of the peaks of the two distributions differ by approximately 0.5 dex. If we artificially decrease the log 10g of our model CEMP stars by 0.5 dex to mimic a hypothetical systematic offset we obtain fractions of giant, turnoff, and dwarf stars among CEMP stars of 35.4%, 60.5% and 4.1%, respectively. However, with such a systematic offset we find that approximately 3% of the modelled CEMP stars have log 10(g/ cm s-2) < 1, while far fewer SEGUE stars are observed at such low gravity (Lee et al. 2013).
An offset in the model-vs.-observed surface gravities can also be identified in Fig. 3, in which the temperature-gravity distribution of our synthetic population (red-scaled distribution) is compared to SEGUE stars with iron abundances in the range −2.4 ≤ [Fe/H] < − 2.2. The surface gravity of the main sequence and of the turnoff point in the synthetic population appear to be shifted by several times 0.1 dex with respect to the observed sample. The reason for such a discrepancy is currently unclear. One possible explanation is that in our simulations we overestimate the upper limit in V magnitude and, as a consequence, in our selection procedure we take into account stars that in reality are too faint to be detected. However, Table 4 shows that, even if Vmax is reduced by 2 mag, the proportion of dwarfs among CEMP stars decreases only by a factor of two. To reproduce the observed dwarf fraction a far lower Vmax is necessary, which is inconsistent with the characteristics of the SEGUE survey. An alternative explanation of this discrepancy is that the surface gravities determined from the SEGUE spectra are systematically underestimated. However, the algorithms to determine the surface parameters of SEGUE stars are calibrated on a set of stars with available high-resolution spectroscopy, and systematic errors that shift log 10g by more than −0.3 dex are considered highly unlikely (Lee et al. 2013).
 |
Fig. 2 Distribution of log 10(g/ cm s-2) as derived from the SEGUE sample of CEMP stars with −2.5 ≤ [Fe/H] ≤ − 2 (histogram with Poisson errors) and computed with our default model set A (solid line). The 0.2 dex bins are equally spaced in log 10(g/ cm s-2). In this and the similar plots that follow the area under the graph (which is the total number of stars) is normalised such that it is the same for both the observations and our model stars. |
 |
Fig. 3 Teff − log 10g probability distribution of all stars in our simulation computed with model set A. Darker colours indicate regions of higher probability. The grey solid and magenta dotted lines show the isochrones computed with detailed stellar-evolution models at 10 Gyr and 13.7 Gyr, respectively. The isochrones computed for the same ages with a detailed model that includes gravitational settling are shown as light-blue dashed and blue dot-dashed lines, respectively. The black dotted lines indicate the ranges of Teff and log 10g in which Lee et al. (2013) select the SEGUE stars. Black circles indicate all SEGUE stars with −2.4 ≤ [Fe/H] < − 2.2. |
Figure 3 shows that there is also a discrepancy between the effective temperatures of the modelled and observed stars. To reliably estimate [C/Fe], Lee et al. (2013) restrict the SEGUE sample to stars with 4400 K ≤ Teff ≤ 6700 K because in this range their technique is robust. However, in our models most of the turnoff stars have Teff> 6700 K, up to ≈8000 K, regardless of the predicted abundance of carbon, whereas in the SEGUE sample there are very few turnoff stars with Teff> 6700 K (which are not plotted in Fig. 3). Such a discrepancy is at least partly explained by an inaccuracy in our model temperatures. Our code calculates the effective temperature from the luminosity and the radius of the star, which are computed with fitting formulae based on the detailed stellar models of Pols et al. (1998). For a 0.8 M⊙ star at the turnoff point these fitting formulae reproduce the luminosity and radius of the detailed model within a factor of 1.15 and 0.98, respectively. However, because with binary˙c the luminosity is higher and the radius is smaller than in the detailed model, the combination of these two factors gives a higher effective temperature than in the detailed model. Figure 3 shows two isochrones, for 10 Gyr and 13.7 Gyr (grey solid and magenta dotted lines), which were constructed using the same version of the STARS code (Eggleton 1971, subsequently updated by many authors, e.g. Pols et al. 1995) as adopted in the detailed models of Pols et al. (1998). These isochrones bracket the age range of our synthetic population. The offset between our population-synthesis results and these isochrones yields an estimate of the error in temperature because of inaccuracies in the fitting formulae.
The discrepancy between modelled and observed temperatures decreases if efficient gravitational settling is included in the models. Two isochrones including settling are shown in Fig. 3 (light-blue dashed and blue dot-dashed lines, for 10 Gyr and 13.7 Gyr, respectively), which were constructed using a recent version of the STARS code (Stancliffe & Glebbeek 2008; Stancliffe & Eldridge 2009). Settling decreases the turnoff temperature of the 10 Gyr isochrone by approximately 300 K, that is, the same shift caused by a 3 Gyr difference in age. The 13.7 Gyr isochrone with settling has a turnoff temperature of about 6400 K, which is not much hotter than the average turnoff temperature of the observed stars (≈6000 K). Although the effects of gravitational settling on the structure and composition of metal-poor stars are not fully explored (Richard et al. 2002a,b; Stancliffe & Glebbeek 2008), these results suggest that the discrepancy in effective temperature can be reduced by including settling in our models.
The effective temperature of giant stars is underestimated both by the population synthesis models and by the isochrones. This discrepancy can also be resolved by calibrating the mixing-length parameter in the detailed models (as done for example by Spada et al. 2013, in the Yonsei-Yale isochrone sets), and it does not affect any of the results presented in this work.
In the observed sample the CEMP/VMP ratio is found to increase significantly with luminosity, that is, FC is smaller among dwarf stars and larger among giants, although this relation is reversed at lower metallicity (Fe/H < −3, Lee et al. 2013). In our models we find smaller variations of the CEMP/VMP ratio among the different classes of stars. The smallest CEMP/VMP ratio is calculated among dwarf stars and the largest among turnoff stars. Turnoff and giant CEMP stars in the models have very similar mass distributions: the CEMP fraction is smaller among the giants as an effect of the first dredge-up, which depletes part of the carbon at the surface. Consequently, a turnoff CEMP star with carbon abundance close to the threshold [C/Fe] = +0.7 has [C/Fe] < +0.7 after the dredge-up. This effect is small because in our model thermohaline mixing already dilutes the accreted material throughout the entire star. If we inhibit thermohaline mixing in our models the difference between FC,gia and FC,TO increases (Table 3, model set D).
The reason for the discrepancy between the predictions of our models and the observations is still unclear. One possible explanation is related to the method adopted by Lee et al. (2013) to compute FC. Stars for which only an upper limit to [C/Fe] is available or stars with a poor carbon measurement (i.e. if the correlation coefficient between the observed and synthetic spectrum is lower than 0.7) are counted among carbon-normal very metal-poor stars. Carbon lines are more difficult to detect in the spectra of warm stars, which are therefore clearly identified as CEMP stars only if carbon is very enhanced. As a consequence, the CEMP/VMP ratio computed for turnoff stars is somewhat biased towards lower values, although this effect is probably small (Lee et al. 2014). This bias is not expected to be significant for the observed dwarf stars, which are typically cooler than turnoff stars. The fact that the observed FC,dwa is approximately a factor of ten lower than FC,TO and FC,gia suggests some effect prevents the detection of dwarf CEMP stars. It is still unclear whether this is a physical effect, which should be stronger for carbon-rich dwarfs than for carbon-normal ones, or a bias introduced during the spectral analysis.
3.3. CEMP fractions computed adopting different sets of initial parameters
The characteristics of our synthetic CEMP populations depend on our assumptions about the mass-transfer process, the extent to which the accreted material is diluted, and the properties of the stellar population, such as its age, and the initial distributions of masses and separations.
The differences in the CEMP/VMP ratios between model sets A–C are mainly due to the range of periods at which the secondary star accretes material from the AGB primary star, as shown in Fig. 4. Model sets B and C have a larger fraction of CEMP stars than set A because of the more efficient mechanism of angular-momentum loss which allows binary systems to interact at longer initial periods. The largest range of initial periods is accessible to model set C because it combines the model of efficient angular-momentum loss with the WRLOF model of wind accretion. Similar results are found by Abate et al. (2013). In binary systems that are initially very wide (Pi > 106 days) only relatively massive primary stars (M1,i > 1.5 M⊙) transfer significant amounts of mass. Such stars are rare according to the solar-neighbourhood IMF adopted in our models. Consequently the increase in FC in models B and C is rather modest.
The relative proportion of giant, turnoff, and dwarf stars depends essentially on the mass distribution of the CEMP stars. All model sets produce the majority of CEMP stars with masses after accretion between 0.75 M⊙ and 0.9 M⊙. However, the initial mass distribution of the CEMP stars and the distribution of the accreted masses differ between model sets. In wide binary systems (P > 104 days) our WRLOF model typically predicts larger accretion efficiencies than our enhanced Bondi-Hoyle-Lyttleton model. Hence, at large separations secondary stars on average accrete more mass with model sets A and C than does model set B, and are initially less massive. As a consequence, the proportion of CEMP stars formed from systems with initial secondary masses less than 0.7 M⊙ is 41% with model sets A and C, while it is 24% with model set B.
 |
Fig. 4 Initial period distribution computed with model sets A–C (solid, dot-dashed and dashed line, respectively). The 0.2 dex bins are equally spaced in log 10(Pi/ days). |
In our model set D we inhibit the thermohaline mixing, consequently the material accreted by the secondary stars remains on the surface until it is mixed in by convection. As a result, the range of initial periods in which CEMP stars are formed increases (by roughly a factor of 25) because even a tiny amount of mass transferred from the AGB primary star on top of a dwarf or turnoff star is sufficient to enhance carbon. Consequently, the fractions FC,TO and FC,dwa both increase, as does the overall CEMP/VMP ratio.
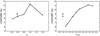 |
Fig. 5 Left:FC calculated with model sets that assume a power-law initial mass-ratio distribution, φ(q) ∝ qγq, with different values of γq. Right: FC of model sets that assume a log-normal initial-period distribution with different values of the mean, μlog P, and fixed standard deviation, σlog P = 2.3. The filled circles show the value of FC computed with our default model set A. |
Our knowledge of the initial properties of the halo stellar population is very uncertain and difficult to constrain. To determine how robust our results are to changes in the age, the IMF, and the initial distributions of separations and mass ratios of our models, we simulate populations of VMP binary stars with a variety of model sets that adopt different assumptions. The CEMP/VMP ratio typically varies between 7% and 12%, with the exception of model IL05, while the proportion of different stellar types among CEMP stars is roughly constant. Below we briefly summarise the results obtained with the different model sets.
-
Variations in the IMF (model sets IK01 and IL05). With the IMF proposed byKroupa (2001) primary stars above one solar massare favoured compared to the default IMF because the IMF slopeis slightly shallower; therefore, with model set IK01 there is a small increase in FC. Compared to the default IMF, the IMF suggested by Lucatello et al. (2005) produces more stars with M ≥ 0.9 M⊙ (which can contribute to the formation of CEMP stars) than stars with M< 0.9 M⊙ (which do not form CEMP stars), therefore IL05 is the model that predicts the largest CEMP/VMP ratio.
-
Variations in the initial mass-ratio distribution (model sets Qp4 and Q1). Model set Qp4, with φ(q) ∝ q-0.4, favours systems with low mass ratios, q = M2,i/M1,i. Binary systems with low-mass secondary stars (M2,i< 0.5 M⊙) do not contribute significantly to the CEMP fraction, either because the secondary stars need to accrete large amounts of mass, or they are not sufficiently luminous to be detected. As a consequence, FC decreases. On the contrary, model set Q1, with φ(q) ∝ q, favours equal mass ratios; therefore, binary systems with relatively massive secondary stars are more common, which need to accrete a small amount of mass to become sufficiently luminous CEMP stars. Consequently, FC increases. In the left panel of Fig. 5 we show the value of FC computed with five model sets that assume different γq in a power-law distribution of the initial mass-ratio, φ(q) ∝ qγq. The maximum CEMP/VMP ratio is found with γq = 1, i.e. with model set Q1.
-
Variations in the initial-period distribution (model sets SDM and S3). Because the initial-period distribution of halo binary stars is poorly constrained, we test a variety of models with log-normal period distributions in which we vary the mean, μlog P, while we adopt a fixed standard deviation, σlog P = 2.3, i.e. the value determined by Duquennoy & Mayor (1991) for a solar-neighbourhood population of binaries with G-dwarf primaries. The CEMP/VMP ratio computed with these models is shown in the right panel of Fig. 5 as a function of μlog P. The maximum is found with model set SDM, that is, the Duquennoy & Mayor (1991) distribution with μlog P = 4.8. With model set SDM, the initial period distribution peaks at orbital periods between 5 × 104 and 105 days, which is approximately the range where our WRLOF model of wind accretion is most efficient in forming CEMP stars. Because the average orbital period in the sample of 15 observed CEMP-s stars analysed in Paper I is approximately 1500 days, we assume μlog P = 3 in our model set S3. The CEMP/VMP ratio decreases compared to model SDM because model S3 predicts more close binary systems that undergo a common-envelope phase and do not form CEMP stars. On the other hand, model set S3 predicts a larger CEMP/VMP ratio than our default model set A (with a flat log P-distribution) because it has fewer very wide systems that do not interact. If a log-normal period distribution (as in model SDM) is combined with a mass-ratio distribution that favours equal masses (as in model Q1), a CEMP/ VMP fraction of approximately 15% is produced, i.e. almost the same fraction as assuming an IMF weighted towards relatively large masses, M ≳ 0.9 M⊙.
-
Variations in the minimum age of the synthetic population (model sets T8 and T12). A change in the minimum age of the stellar population in the halo by ± 2 Gyr has a small effect on FC, as also found by Izzard et al. (2009). This is mainly because of the difference in lifetime between the stars that accreted mass during the evolution and the stars that did not. As we discuss in more detail in Sect. 3.5, for a minimum age of the halo of tmin = 10 Gyr, stars of mass 0.9 M⊙ and above have already become white dwarfs, whereas CEMP stars that (after accretion) have masses up to about 0.95 M⊙ may still be visible. That is, only CEMP stars can be detected in the mass range [0.9,0.95] M⊙ for this age (Fig. 7). With tmin = 8 Gyr, CEMP stars up to about 1.05 M⊙ are still visible, whereas normally at this age stars more massive than 0.95 M⊙ have already become white dwarfs, that is, the difference in the maximum mass of visible stars increases. As a result, the CEMP fraction increases. On the other hand, with tmin = 12 Gyr such a difference in mass decreases (the maximum masses are approximately 0.88 M⊙ and 0.91 M⊙ for normal stars and CEMP stars, respectively), and so does the CEMP fraction.
3.4. Orbital periods of the CEMP stars
 |
Fig. 6 Cumulative orbital-period (Pf) distributions for SAGA CEMP stars with −2.8 ≤ [Fe/H] ≤ − 1.8 (shaded area). The lower limit of the observed distribution is determined assuming that all CEMP stars are binaries, whereas to determine the upper limit we assume that only CEMP-s stars are in binaries. Our model sets A and IL05 are shown as solid and dotted lines, respectively. The 0.2 dex bins of the model distributions are equally spaced in log 10(Pf/days). |
We now compare the orbital-period distribution predicted by our models with the observed sample of 15 binary CEMP stars with measured periods studied in Paper I. We exclude from this sample the stars CS 22964–161 A and B because they have most likely been polluted by a third star whose period is unknown (Thompson et al. 2008), LP 625–55 because it only has a lower limit on the orbital period, and CS 29497–034 which has [Fe/H] = −2.96. Our models produce most CEMP stars in orbits longer than a few thousand days, whereas the observed systems have orbital periods shorter than 4600 days. However, in the SAGA sample, only 11 out of 94 CEMP stars with −2.8 ≤ [Fe/H] ≤ − 1.8 have measured orbital periods, thus they may not be representative of the period distribution of the entire sample. To compare the observations with the results of our models, Fig. 6 shows the observed and modelled cumulative period distributions. The implicit assumptions made in deriving the observed cumulative distribution are (i) that all CEMP stars are formed in binaries, most of which have unknown periods, and (ii) that the SAGA sample is complete for Porb ≤ 4600 days. The first assumption is probably correct for CEMP-s stars, which are mostly found in binary systems, but it is unlikely to be valid for CEMP-no stars (Lucatello et al. 2006; Norris et al. 2013; Starkenburg et al. 2014; Hansen et al., in prep.). For this reason we plot the cumulative period distribution as a range (shaded area in Fig. 6), in which the lower limit corresponds to the hypothesis that all 94 CEMP stars in the SAGA sample are binaries, while the upper limit corresponds to the hypothesis that only the 71 CEMP-s stars in the sample are binaries. The solid and dotted lines in Fig. 6 represent the cumulative period distributions predicted with models A and IL05, respectively, which bracket the distributions found with all the other models.
Under the above assumptions, our models are consistent with the observations in the range between approximately 600 and 5000 days, and they seemingly predict an excess of CEMP stars with periods between a few tens and a few hundreds of days. On the other hand, the models do not reproduce the single observed CEMP star3 at Pf< 10 days. However, the assumption that the unknown periods of all other CEMP stars in our sample are longer than about 5000 days may be incorrect; in reality at least some of these stars are likely to have shorter periods (e.g. Starkenburg et al. 2014). In addition, the comparison in Fig. 6 is based on the implicit assumption that our models reproduce the observed CEMP fraction. However, the CEMP/VMP ratio determined for the SAGA sample is larger than predicted by a factor of 1.5 up to 3, depending on the model set (Table 4). Hence, given all the uncertainties, the results of this comparison are inconclusive.
3.5. Masses of CEMP stars
Our models predict that approximately 90% of the CEMP stars have masses between 0.75 M⊙ and 0.95 M⊙, with the peak of the distribution around 0.85 M⊙. In Fig. 7 we compare the mass distributions computed with model set A for CEMP and carbon-normal stars (solid and dot-dashed lines, respectively). The distribution of CEMP stars is shifted towards higher mass by about 0.05 M⊙ compared to the distribution of carbon-normal stars. This difference is a consequence of the mass-accretion process. A single star of mass 0.85 M⊙ ascends the giant branch after approximately 10.8 Gyr, and about 0.4 Gyr later it becomes a white dwarf. By contrast, if a star with an initial mass of 0.75 M⊙ accretes 0.1 M⊙ from a binary companion and becomes a CEMP star, its life is longer than a normal 0.85 M⊙ star because until mass accretion occurs the CEMP star evolves as a lower-mass star, i.e. more slowly. Currently, no mass measurements of CEMP stars are available for comparison with our models, but future observations that aim to detect very metal-poor stars in eclipsing binary systems may allow the determination of whether the predicted difference in mass is correct.
 |
Fig. 7 Mass distribution of CEMP stars (solid line) and C-normal stars (dot-dashed line) computed with model set A. Bins of width 0.025 dex are equally spaced in M∗/M⊙. |
 |
Fig. 8 Panels a)–d): abundance distributions of sodium, light-s elements, heavy-s elements and lead, respectively. The 0.2 dex bins are equally spaced in [El/Fe]. The histograms represent CEMP and CEMP-s/r stars from our database (light and dark grey, respectively), with Poisson errors. Models with MPMZ = 0,2 × 10-4 M⊙, 2 × 10-3 M⊙, 4 × 10-3 M⊙ are shown as dotted, dashed, solid, dot-dashed lines, respectively. |
3.6. Abundance distributions
The SAGA database includes the observed abundances of many elements. We compare the abundance distributions derived from the observations with those of our models. This comparison is qualitative because the observed sample is inhomogeneous and incomplete, but it can provide indications to constrain our models. The magnitude limits adopted in the models are Vmin = 6 and Vmax = 16.5, consistent with the magnitude range of the very metal-poor stars in the observed sample. In the first part of this section we study the consequences of adopting different masses of the partial mixing zone (Sect. 3.6.1) while in the second part we compare the predictions of different model sets (Sect. 3.6.2).
3.6.1. The effect of MPMZ
The mass of the partial mixing zone is a free parameter in our models. To understand its impact on the chemical properties of a population of CEMP stars we compare the element distributions computed with default model set A and four different values of MPMZ: no PMZ, and MPMZ equal to 2 × 10-4 M⊙, 2 × 10-3 M⊙ and 4 × 10-3 M⊙. Figures 8a–d show the abundance distributions of sodium, light-s elements, heavy-s elements4, and lead. The histograms represent the distributions of the observed CEMP stars and the subsample of CEMP-s/r stars (light and dark grey, respectively). CEMP-s/r stars are plotted separately because their history of nucleosynthesis is probably different from CEMP stars with low abundances of europium and r-elements (e.g. Jonsell et al. 2006; Sneden et al. 2008; Lugaro et al. 2009; Bisterzo et al. 2012; Abate et al. 2015a,b). Our models do not include the r-process, therefore in CEMP-s/r stars we do not expect to reproduce the abundances of elements with a strong r-process component. However, the r-process is responsible for the production of many neutron-capture elements, including some amounts of elements traditionally associated with the s-process. In Paper II we show that CEMP-s/r stars have different abundance distributions than r-normal CEMP-s stars (i.e. with [Eu/Fe] < + 1). In particular, the abundances of neutron-rich elements such as barium, lanthanum, cerium, and lead are typically strongly enhanced and the [hs/ls] ratio is larger than is observed in r-normal CEMP-s stars and than predicted by our models, in line with the results of previous studies (e.g. Bisterzo et al. 2012; Lugaro et al. 2012).
In the models with a small PMZ (MPMZ = 0 and 2 × 10-4 M⊙), the majority of CEMP stars have normal, non-enhanced abundances of sodium (Fig. 8a). This is because the abundance of sodium produced in AGB nucleosynthesis is sensitive to both the mass of the star and of its PMZ. With no PMZ, or only a small PMZ, only relatively massive AGB stars produce significant amounts of sodium. In the modelled population, most CEMP stars are formed in systems with a low-mass primary star, hence the distribution peaks around the initial abundance. On the other hand, with a relatively large PMZ (MPMZ = 2 − 4 × 10-3 M⊙), low-mass AGB stars also produce significant amounts of sodium; consequently the modelled distribution qualitatively reproduces the observations.
The distributions of light-s and heavy-s elements (Figs. 8b and c) do not vary significantly as a function of MPMZ, because low-mass AGB stars (below ≈2 M⊙) experience episodes of proton ingestion from the convective envelope in the He-flash induced convection zone (Lugaro et al. 2012), and some amounts of s-elements are produced regardless of the PMZ5. Because low-mass primary stars dominate our synthetic binary population, the distributions of light-s and heavy-s elements in CEMP stars are quite similar. By contrast, the abundance of lead is related more strongly to the PMZ mass, as shown in Fig. 8d, and the distributions obtained with small and large MPMZ are shifted by about 0.5 dex. Models with MPMZ ≥ 2 × 10-3 M⊙ are in better agreement with the observed distribution; however, none of the models can reproduce the 11 observed CEMP stars with [Pb/Fe] ≥ + 2.8. Nine of these stars are CEMP-s/r stars, and the discrepancy with the models may indicate that lead in these extremely enriched stars was not produced purely by the s-process. We note that the observed abundances are determined assuming local thermodynamic equilibrium. It has been shown that departures from this approximation can greatly impact the abundances of giants and metal-poor stars (e.g. Bergemann et al. 2012). In particular, positive corrections of 0.3–0.5 dex are to be expected for the lead abundances of stars in the metallicity range of our observed sample (Mashonkina et al. 2012). If we assume an average correction of 0.4 dex, 21 CEMP-s stars (of which 16 are CEMP-s/r) would have [Pb/Fe] ≥ 2.8 and cannot be reproduced by any of our models.
The results of the comparison between models with different partial mixing zones, as well as the results of Papers I and II, suggest that to reproduce the chemical properties of the observed sample our models require a relatively large MPMZ. Therefore, in the following we adopt MPMZ = 2 × 10-3 M⊙ in our model sets.
 |
Fig. 9 Panels a)–d): distributions of [C/Fe], [Sr/Fe], [La/Fe], and [Eu/Fe], respectively. Model sets A, B, D, and IL05 are shown with solid, dot-dashed, dotted, and dashed lines, respectively. Light and dark grey histograms represent the observed CEMP and CEMP-s/r stars in the SAGA database. The 0.2 dex bins are equally spaced in [El/Fe]. |
3.6.2. Abundance distributions with different model sets
Our modelled abundance distributions depend mostly on the distributions of the primary and secondary stellar mass of our synthetic CEMP stars; the former determines the amount of each element produced by AGB nucleosynthesis, while the latter essentially determines how much mass is accreted and consequently the abundance enhancement. We compare the results of our default model set A with three model sets: model set B, in which the M2,i distribution of CEMP stars is more peaked towards relatively massive secondary stars (M2,i> 0.7 M⊙), model set IL05, in which a significant proportion of CEMP stars are formed in binary systems with a primary star initially above 1.2 M⊙, and model set D, in which thermohaline mixing is inhibited and therefore the abundances of the accreted material are not diluted in turnoff and dwarf CEMP stars. The CEMP fractions observed in the SAGA database and computed with these four model sets are shown in Table 4. In model sets A, B, and IL05, the CEMP/VMP ratios are higher than the corresponding sets in Table 3 because for the comparison with SAGA stars we adopt lower magnitude limits in our simulations, thus the fainter dwarf stars are selected against. These fainter stars have a larger proportion of carbon-normal stars, so the CEMP/VMP ratios increase. On the other hand, in model set D, among the fainter dwarf stars the CEMP stars are more frequent because of the lack of dilution, thus FC decreases.
Figures 9a–d show the abundance distributions of carbon, strontium, lanthanum, and europium. We find similar trends for all elements. Compared to the default model A, model set IL05 favours more massive primary stars, which typically produce larger abundances of carbon and s-elements for MPMZ = 2 × 10-3 M⊙. Also, in model set IL05 more CEMP stars are formed with M2,i ≤ 0.6 M⊙, which accrete large amounts of material from the primary star. Consequently, the abundance distributions of model set IL05 are weighted towards large enhancements. On the contrary, model set B favours relatively massive secondary stars, M2,i ≥ 0.7 M⊙, which accrete small amounts of material that is more strongly diluted. Consequently, model set B predicts abundance distributions that peak at lower [El/Fe] than our default model A. With model set D, dwarfs form a clearly distinct group of stars. Because the accreted material is not efficiently mixed throughout the entire star, these stars have a chemical composition very similar to that of the polluting stars, and hence the largest enhancements.
The distributions of lanthanum and europium (respectively, a heavy-s and an r-element) in Figs. 9c and d show that the abundances observed in CEMP-s/r stars are outside the range that can be produced by our models. If we exclude the CEMP-s/r stars from the sample, our models qualitatively reproduce the observed distributions. This discrepancy is observed also in the distributions of [hs/Fe] and [Pb/Fe] (Figs. 8c and d). By contrast, the distributions of carbon, sodium, strontium, and light-s elements do not differ significantly between CEMP-s/r stars and r-normal CEMP-s stars. These results suggest that there is a relation between the strongly enhanced abundances of the heavy-s elements and the r-elements in the population of CEMP-s/r stars, in line with our conclusions in Paper II.
The origin of the r-enhancement in CEMP-s/r stars is uncertain. If we start our simulations with an initially enhanced abundance of r-elements to mimic the effect of a primordial enrichment independent of the abundances of s-elements, as suggested e.g. by Bisterzo et al. (2012), our models fail to reproduce the stars with the lowest [Eu/Fe] without improving the results obtained for CEMP-s/r stars. Figure 10 shows the observed abundances of europium and barium in the CEMP stars of our sample, together with the synthetic abundances computed with our default model set A (red distribution), assuming an initial enhancement of [r/ Fe] ini = 1 (grey distribution). The observations exhibit a clear linear correlation between the abundances of barium and europium. Our model set A qualitatively reproduces this correlation for r-normal CEMP-s stars, that is, to the left of the vertical dotted line at [Eu/Fe] = +1. As discussed by Lugaro et al. (2012), an initial enhancement of [r/ Fe] ini ≤ 0.4 dex is essentially washed out by the europium produced by the s-process in the AGB nucleosynthesis. If we adopt [r/ Fe] ini = +1, europium increases while barium does not change, and the observed correlation is not reproduced. If we adopt [r/ Fe] ini = + 2 to reproduce the most r-rich CEMP-s/r stars, then the abundances of the r-elements in our synthetic CEMP stars all end up in one bin around this value.
 |
Fig. 10 Distribution of [Ba/Fe] vs. [Eu/Fe]. The red distribution represents our default model A. The grey distribution is computed with an initial enhancement of [r/ Fe] ini = 1. The dotted lines indicate the thresholds [Ba/Fe] = + 0.5 and [Eu/Fe] = 1 that define CEMP-s and CEMP-s/r stars, respectively. The crosses indicate the observed CEMP-s stars with [Eu/Fe] < + 1. CEMP-s/r are shown as blue circles. The + symbol in the top-left corner shows the average observed uncertainty. |
 |
Fig. 11 As Fig. 10 for [Ba/Fe] vs. [C/Fe]. The vertical line represents the threshold [C/Fe] = + 0.7. In the bottom-right corner the average observed uncertainty is shown as a + symbol. |
Figure 11 shows the distribution of [Ba/Fe] vs. [C/Fe] computed with model set A. An apparent correlation exists between carbon and barium in the observed CEMP-s stars, regardless of the r-enhancement, although there is considerable scatter in the data. In the binary scenario for the formation of CEMP stars this correlation is a direct consequence of nucleosynthesis in AGB stars. The amounts of carbon and barium produced by an AGB star are correlated, and depend only on the stellar mass (for a fixed PMZ). The observed correlation is qualitatively reproduced by our model, although a fraction of the CEMP stars have a barium abundance systematically larger than the model predictions. This discrepancy is not removed even with higher masses of the PMZ, and suggests that, for a given amount of carbon, our AGB models should produce a larger amount of barium.
The observed correlation between carbon and barium breaks down for CEMP-no stars, whose carbon abundances are spread over two orders of magnitude, and are not well reproduced by our models. This discrepancy may arise within the mass-transfer scenario because a large abundance of carbon, combined with a small abundance of barium, can be obtained in models of massive AGB stars (M > 2.8 M⊙) with no PMZ, and massive stars are relatively rare in our population. However, about half of the CEMP-no stars in our sample have [Ba/Fe] < 0, and with our model it is not possible to reproduce their abundances. The formation scenario of CEMP-no stars is currently uncertain. Masseron et al. (2010) show that there is a clear continuity from CEMP-s to CEMP-no in the abundance trends of several elements, including C+N, O, Mg, 12C /13C and C/N, pointing towards the scenario of mass transfer from an AGB star. On the other hand, the study of Starkenburg et al. (2014) indicates that CEMP-no stars are not found in binary systems more often than carbon-normal stars or, alternatively, they belong to very wide binaries. Although the hypothesis of wide separations is consistent with our results, the evidence that with our models most of the CEMP-no stars are not reproduced in the carbon-barium space may be an indication that their observed carbon enhancement is not related with AGB nucleosynthesis but rather is the result of contributions from first-generation stars.
4. Discussion
In this paper we have simulated populations of binary stars at metallicity Z = 10-4 ([Fe/H ≈ −2.3) to investigate the mass-transfer scenario for the formation of CEMP stars. A comparison with similar studies (e.g. Izzard et al. 2009; Abate et al. 2013) shows that our default model set A predicts a CEMP/VMP ratio more than three times larger than previous models adopting default initial assumptions. In the default model adopted in Abate et al. (2013), AGB stars of mass below 1.2 M⊙ do not undergo third dredge-up, whereas in our models (based on the detailed calculations of Karakas 2010) the minimum mass for third dredge-up in AGB stars is 0.9 M⊙. Therefore, the range of primary masses that contribute to the formation of CEMP stars is larger and, as a consequence, the CEMP/VMP ratio predicted in our models increases. In our simulations we adopt a selection criterion based on the luminosity of the stars, instead of a simple cut-off in surface gravity as in Abate et al. (2013). As a result, the proportion of dwarf stars in the CEMP population increases to approximately 50%, but the total CEMP/VMP ratio remains essentially the same.
If we adopt a solar-neighbourhood IMF, our CEMP/VMP ratio, FC, is approximately 8% for [C/Fe] > +1, consistent with the observed value of the SEGUE sample in the range −2.5 < [Fe/H] ≤ −2.0. Therefore, a change of the IMF towards relatively large primary masses (as suggested, e.g. by Lucatello et al. 2005; and Suda et al. 2013) is not necessary to reproduce the observed CEMP/VMP ratio. However, the proportion of dwarf CEMP stars predicted in our models is much larger than observed in the SEGUE sample at −2.5 < [Fe/H] ≤ −2.0. Also, the total number of dwarf stars observed at this metallicity in the SEGUE sample is a factor of four to five lower than the number of turnoff and giant stars. These differences may suggest that our simulations include stars that in reality are too faint to be detected, or that the observed surface gravities are possibly underestimated by a few tenths of a dex.
The CEMP/VMP ratio observed in the SEGUE sample increases by almost a factor of two if the minimum carbon abundance in the definition of CEMP stars is reduced from [C/Fe] = + 1.0 to [C/Fe] = + 0.7. By contrast, this causes only a small difference in our models. In Paper II we showed that most carbon-normal VMP stars from the SAGA database exhibit carbon abundances within approximately 0.4 dex from the average value of [C/Fe] = + 0.3. Assuming that carbon-normal VMP stars in the SEGUE sample have the same distribution of carbon abundances, and considering that an observational error of 0.3 dex is associated with carbon abundances in SEGUE stars, one explanation of the large increase in the observed CEMP fraction between [C/Fe] = + 0.7 and [C/Fe] = + 1.0 is that we are observing the tail of the carbon-abundance distribution of carbon-normal very metal-poor stars.
The CEMP/VMP ratio calculated among stars in the SAGA database is very different from the SEGUE sample. In the range −2.8 ≤ [Fe/H] ≤ − 1.8 we find FC = 28%, adopting [C/Fe] min = + 0.7, almost a factor of three larger than the value calculated for SEGUE stars. A discrepancy of about a factor of three is also found with most of our model sets, which predict CEMP/VMP ratios around 10%. Another remarkable difference with the SEGUE sample is that the CEMP fraction from the SAGA sample increases towards stars of higher log 10g. A possible explanation of these discrepancies is that the SAGA sample is a compilation of all very metal-poor stars currently available in the literature. Hence, it is an inhomogeneous and incomplete sample, and is possibly biased towards chemically peculiar stars. However, the large differences between the results obtained with the SEGUE and SAGA samples point out the general problem that the measured fractions depend significantly on the observed sample considered. Consequently, the results of the comparisons with population synthesis models are as yet inconclusive.
In our simulations we assume a binary fraction of unity in the range of orbital separations between 5 R⊙ and 5 × 106R⊙. For comparison, Kouwenhoven et al. (2007) find that, with 3σ confidence, the binary fraction in the young stellar association Scorpius OB2 is at least 0.7, and probably close to unity for stars of spectral type A and B in the same range of separations. However, the binary fraction of the stellar population of the Galactic halo is poorly constrained (Carney et al. 2001, 2005; Rastegaev 2010; Gao et al. 2014; Aoki et al. 2015). Recent results suggest that among stars with [Fe/H] < − 1.1 the binary fraction is at least 50% and possibly increasing with decreasing metallicity (Gao et al. 2014; Yuan et al. 2015).
All our model sets predict that CEMP stars are formed in initially wide binary systems with orbital periods typically longer than 1000 days up to approximately 106 days. About 80% of the simulated CEMP stars have periods longer than 5000 days, which is approximately the longest period currently observed. The median of the observed period distribution is approximately 500 days, consistent with the average orbital period estimated by Starkenburg et al. (2014) for a different sample of CEMP-s stars, whereas for the synthetic distributions it is about 20 000 days. This indicates that, if the distribution determined from the CEMP stars with measured orbital periods is representative of the entire CEMP population, our simulations significantly underestimate the observed CEMP/VMP ratio. A similar discrepancy between the observed periods and model predictions also exists at higher metallicity for the barium stars, which are likely formed by the same wind-accretion process as CEMP stars (e.g. Boffin & Jorissen 1988; Jorissen et al. 1998). For barium stars, the observed sample of orbital periods is complete, and only a few systems are known with periods longer than 104 days. The discrepancy between the observed and modelled periods suggests that in our models binary systems need to efficiently lose angular momentum, and transfer mass more efficiently at short separations, as also discussed by Izzard et al. (2010) and in Papers I and II.
The comparison between the observed and synthetic abundance distributions provides constraints on our nucleosynthesis model and on the properties of the progenitor systems. The chemical composition of a modelled CEMP star depends essentially on the mass of the primary star, which determines the elements produced by AGB nucleosynthesis, and on the initial mass of the secondary star, which determines the amount of material that needs to be accreted so that after 10 Gyr the star is luminous enough to be visible and enriched in carbon. Most model sets predict similar distributions of M1,i and M2,i, consequently the abundance distributions are similar.
The modelled abundance distributions of most elements do not show a strong dependence on the mass of the partial mixing zone, MPMZ. The production of s-elements is sensitive to MPMZ, especially for stars with M1,i ≥ 1.5 M⊙, while most CEMP stars in our simulations are formed from binary systems with M1,i ≤ 1.2 M⊙. By contrast, in Papers I and II we find that primary masses above 1.4 M⊙ are necessary to reproduce the detailed chemical composition of most observed CEMP-s stars of our sample. Systems with primary mass between 1.5 M⊙ and 2.5 M⊙ are required to reproduce the element-to-element ratios observed in CEMP-s stars that exhibit abundant heavy-s elements and large [hs/ls] and [Pb/hs] values. These chemical properties are observed mostly in CEMP-s/r stars, and also in some r-normal CEMP-s stars. The discrepancy between the results of the population-synthesis simulations and the detailed analysis of Papers I and II may hint that nucleosynthesis models of low-mass AGB stars (M ≲ 1.2 M⊙) should produce, in some circumstances, higher abundances of heavy-s elements and lead.
We note that the observed abundances are normally determined under the assumption of local thermodynamic equilibrium, which is not always fulfilled in the layers of the stellar atmosphere where spectral lines are formed (e.g. Mihalas & Athay 1973). The departure from local thermodynamic equilibrium in real stars introduces a bias in the abundance determination of most elements, including carbon, iron, strontium, barium, and lead. For example, Mashonkina et al. (2012) show that a positive correction of about 0.3–0.5 dex for metal-poor stars should be applied to the observed lead abundances. This correction increases for increasing temperature, and for decreasing metallicity and surface gravity. Positive corrections are typically required also for barium and europium (Mashonkina et al. 2012; Niemczura et al. 2014). Although the magnitudes of the corrections are of the order of the observational uncertainties (≲0.2 dex), they suggest that our models should produce higher abundances of heavy elements for a given amount of carbon.
Our default model set A predicts abundance distributions of light elements (e.g. carbon and sodium) and light-s elements that are qualitatively consistent with the observed distributions in all CEMP stars. In contrast, the abundance distributions of heavy-s elements, lead, and europium are reproduced only in r-normal CEMP stars, whereas in CEMP-s/r stars the abundances of these elements are outside the range of our model predictions. Similarly, a clear correlation between the abundances of barium and europium is observed in all CEMP-s stars. Our model reproduces such a correlation in CEMP stars with [Eu/Fe] < + 1, while in CEMP-s/r stars the observed enhancements of barium and europium are too large. Consistent results are found in the detailed analysis of CEMP-s stars performed in Papers I and II. In Paper I we find that to reproduce the large abundances of heavy-s elements observed in CEMP-s/r stars, our models typically overestimate the abundances of carbon, sodium, magnesium, and light-s elements. Paper II shows that in r-normal CEMP-s stars the abundances of most elements are reproduced on average within the observed uncertainty, whereas in CEMP-s/r stars the abundances of both heavy-s and r-elements are systematically underestimated.
Although enhanced abundances of r-elements are also observed in carbon-normal stars with no evidence of duplicity (e.g. Barklem et al. 2005; Roederer et al. 2014a,b; Hansen et al., in prep.), our results suggest that the s- and r-processes responsible for the abundances observed in CEMP-s/r stars may have occurred in the same astrophysical site. Consequently, these results indicate that under some conditions AGB stars may be able to reach the large densities necessary to activate the r-process, in contrast to what is currently found in the AGB models. Detailed models of AGB stars at extremely low or zero metallicity show that large neutron densities (1012 − 1016cm-3, Campbell & Lattanzio 2008; Herwig et al. 2011) may be reached as a result of proton ingestion in the helium-flash region. Lugaro et al. (2009) propose a speculative scenario in which extremely low-metallicity (Z< 10-5) AGB stars may be able to produce both s- and r-elements. Further evolutionary and nucleosynthetic calculations are needed to test quantitatively if this scenario may also work at metallicity Z ≈ 10-4, and if the predicted abundances reproduce the chemical compositions of observed CEMP-s/r stars.
5. Conclusions
In conclusion, in our synthetic population of very metal-poor binary stars we find a CEMP fraction that varies between 7% and 17%, depending on the initial assumptions. Our default model set predicts a CEMP/VMP fraction of 8.5% for [C/Fe] > + 0.7. This fraction is more than three times larger than the results obtained by Izzard et al. (2009) and Abate et al. (2013) with the same population-synthesis code and default initial assumptions. This difference results from the updates that we included in the model of AGB nucleosynthesis. With the default models adopted in the previous work, AGB stars below 1.2 M⊙ did not undergo third dredge-up, whereas in our updated models AGB stars experience third dredge-up down to 0.9 M⊙. Hence, the range of primary masses that can form a CEMP star is increased.
The observed fraction of CEMP stars depends significantly on the sample that is taken into account. In the most recent study of the SDSS/SEGUE stellar survey a CEMP fraction of 11.5% is found for stars with −2.5 < [Fe/H] ≤ −2. Considering the large uncertainties associated at low metallicity with the initial distributions of masses and separations in binary systems, the CEMP/VMP ratio predicted with our models is consistent with the observed value, although the models predict many more dwarf CEMP stars than are observed.
There are currently few measured orbital periods for CEMP stars, and therefore it is difficult to provide strong constraints on our model of angular-momentum loss and wind-accretion efficiency. Future observations of the orbital periods of additional CEMP stars will allow us to gain insight into the mass-transfer process at low metallicity. At present, the orbital periods of most of our synthetic stars are on average ten times longer than the typical observed periods. This indicates that our models should produce more CEMP stars in binary systems below a few times 103 days, or, alternatively, that most CEMP stars have periods longer than 104 days.
The population of synthetic CEMP stars qualitatively reproduces the abundance distributions of carbon, sodium, and light-s elements observed in all CEMP stars. On the other hand, the observed distributions of heavy-s elements, lead, and europium are reproduced only in r-normal CEMP-s stars, whereas in CEMP-s/r stars the abundances of these elements are underestimated. The correlation between the abundances of barium and europium observed in all CEMP stars indicate that the enhancements in s- and r-elements are not independent. This suggests that both the s- and r-processes may be active in the same astrophysical site.
Possible formation scenarios for this peculiar CEMP star with period 3.14 days, HE 0024–2523, are discussed, for example, by Lucatello et al. (2003) and in Paper I.
The nucleosynthetic signature of a proton-ingestion event is uncertain because one-dimensional stellar-evolution models do not adequately treat the physics of these inherently three-dimensional phenomena (see e.g. Stancliffe et al. 2011; Herwig et al. 2014).
Acknowledgments
We thank the referee for her/his helpful and supportive comments on our paper. C.A. is grateful to P. van Oirschot for many useful discussions on the stellar distribution in the Galactic halo and to the Netherlands Organisation for Scientific Research (NWO) for funding support under grant 614.000.901. R.J.S. is the recipient of a Sofja Kovalevskaja Award from the Alexander von Humboldt Foundation. R.G.I. is grateful to the Alexander von Humboldt Foundation and the Science and Technology Facilities Council (STFC) for funding support. A.I.K. is supported through an Australian Research Council Future Fellowship (FT110100475). T.C.B. acknowledges partial support for this work from grants PHY 08-22648; Physics Frontier Center/Joint Institute for Nuclear Astrophysics (JINA), and PHY 14-30152; Physics Frontier Center/JINA Center for the Evolution of the Elements (JINA-CEE), awarded by the US National Science Foundation. Y.S.L. acknowledges partial support by the 2014 Research Fund of the Chungnam National University.
References
- Abate, C., Pols, O. R., Izzard, R. G., Mohamed, S. S., & de Mink, S. E. 2013, A&A, 552, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abate, C., Pols, O. R., Karakas, A. I., & Izzard, R. G. 2015a, A&A, 576, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abate, C., Pols, O. R., Izzard, R. G., & Karakas, A. I. 2015b, A&A, 581, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aoki, W., Norris, J. E., Ryan, S. G., Beers, T. C., & Ando, H. 2002, ApJ, 567, 1166 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W., Beers, T. C., Christlieb, N., et al. 2007, ApJ, 655, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W., Beers, T. C., Lee, Y. S., et al. 2013, AJ, 145, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W., Suda, T., Beers, T. C., & Honda, S. 2015, AJ, 149, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Barklem, P. S., Christlieb, N., Beers, T. C., et al. 2005, A&A, 439, 129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beers, T. C., & Christlieb, N. 2005, ARA&A, 43, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Beers, T. C., Preston, G. W., & Shectman, S. A. 1985, AJ, 90, 2089 [NASA ADS] [CrossRef] [Google Scholar]
- Beers, T. C., Preston, G. W., & Shectman, S. A. 1992, AJ, 103, 1987 [NASA ADS] [CrossRef] [Google Scholar]
- Bergemann, M., Lind, K., Collet, R., Magic, Z., & Asplund, M. 2012, MNRAS, 427, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Bessell, M. S., Castelli, F., & Plez, B. 1998, A&A, 333, 231 [NASA ADS] [Google Scholar]
- Bisterzo, S., Gallino, R., Straniero, O., Cristallo, S., & Käppeler, F. 2012, MNRAS, 422, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Boffin, H. M. J., & Jorissen, A. 1988, A&A, 205, 155 [NASA ADS] [Google Scholar]
- Campbell, S. W., & Lattanzio, J. C. 2008, A&A, 490, 769 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carney, B. W., Latham, D. W., Laird, J. B., Grant, C. E., & Morse, J. A. 2001, AJ, 122, 3419 [NASA ADS] [CrossRef] [Google Scholar]
- Carney, B. W., Aguilar, L. A., Latham, D. W., & Laird, J. B. 2005, AJ, 129, 1886 [NASA ADS] [CrossRef] [Google Scholar]
- Carollo, D., Beers, T. C., Bovy, J., et al. 2012, ApJ, 744, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Christlieb, N., Green, P. J., Wisotzki, L., & Reimers, D. 2001, A&A, 375, 366 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Christlieb, N., Schörck, T., Frebel, A., et al. 2008, A&A, 484, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cohen, J. G., Shectman, S., Thompson, I., et al. 2005, ApJ, 633, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] [Google Scholar]
- Eggleton, P. P. 1971, MNRAS, 151, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Frebel, A., Christlieb, N., Norris, J. E., et al. 2006, ApJ, 652, 1585 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, S., Liu, C., Zhang, X., et al. 2014, ApJ, 788, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., Siegmund, W. A., Mannery, E. J., et al. 2006, AJ, 131, 2332 [NASA ADS] [CrossRef] [Google Scholar]
- Helmi, A. 2008, A&ARv, 15, 145 [CrossRef] [Google Scholar]
- Herwig, F., Pignatari, M., Woodward, P. R., et al. 2011, ApJ, 727, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F., Woodward, P. R., Lin, P.-H., Knox, M., & Fryer, C. 2014, ApJ, 792, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Izzard, R. G., Tout, C. A., Karakas, A. I., & Pols, O. R. 2004, MNRAS, 350, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Izzard, R. G., Dray, L. M., Karakas, A. I., Lugaro, M., & Tout, C. A. 2006, A&A, 460, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izzard, R. G., Glebbeek, E., Stancliffe, R. J., & Pols, O. R. 2009, A&A, 508, 1359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izzard, R. G., Dermine, T., & Church, R. P. 2010, A&A, 523, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jonsell, K., Barklem, P. S., Gustafsson, B., et al. 2006, A&A, 451, 651 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jorissen, A., Van Eck, S., Mayor, M., & Udry, S. 1998, A&A, 332, 877 [NASA ADS] [Google Scholar]
- Jurić, M., Ivezić, Ž., Brooks, A., et al. 2008, ApJ, 673, 864 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Karakas, A. I. 2010, MNRAS, 403, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A., & Lattanzio, J. C. 2007, PASA, 24, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A. I., Lattanzio, J. C., & Pols, O. R. 2002, PASA, 19, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, C., Karakas, A. I., & Umeda, H. 2011, MNRAS, 414, 3231 [NASA ADS] [CrossRef] [Google Scholar]
- Komiya, Y., Suda, T., Minaguchi, H., et al. 2007, ApJ, 658, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Kouwenhoven, M. B. N., Brown, A. G. A., Portegies Zwart, S. F., & Kaper, L. 2007, A&A, 474, 77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, Y. S., Beers, T. C., Masseron, T., et al. 2013, AJ, 146, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, Y. S., Suda, T., Beers, T. C., & Stancliffe, R. J. 2014, ApJ, 788, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Lucatello, S., Gratton, R., Cohen, J. G., et al. 2003, AJ, 125, 875 [NASA ADS] [CrossRef] [Google Scholar]
- Lucatello, S., Gratton, R. G., Beers, T. C., & Carretta, E. 2005, ApJ, 625, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Lucatello, S., Beers, T. C., Christlieb, N., et al. 2006, ApJ, 652, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Lugaro, M., Campbell, S. W., & de Mink, S. E. 2009, PASA, 26, 322 [NASA ADS] [Google Scholar]
- Lugaro, M., Karakas, A. I., Stancliffe, R. J., & Rijs, C. 2012, ApJ, 47, 1998 [Google Scholar]
- Mackey, J., Bromm, V., & Hernquist, L. 2003, ApJ, 586, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., Przybilla, N., Nieva, M.-F., et al. 2014, A&A, 565, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marsteller, B., Beers, T. C., Rossi, S., et al. 2005, Nucl. Phys. A, 758, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Mashonkina, L., Ryabtsev, A., & Frebel, A. 2012, A&A, 540, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masseron, T., Johnson, J. A., Plez, B., et al. 2010, A&A, 509, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., Ekström, S., & Maeder, A. 2006, A&A, 447, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., Hirschi, R., Ekstrom, S., et al. 2010, A&A, 521, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mihalas, D., & Athay, R. G. 1973, ARA&A, 11, 187 [NASA ADS] [CrossRef] [Google Scholar]
- MoniBidin, C., Carraro, G., Méndez, R. A., & Smith, R. 2012, ApJ, 751, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Niemczura, E., Smalley, B., & Pych, W. 2014, Determination of Atmospheric Parameters of B-, A-, F- and G-Type Stars: Lectures from the School of Spectroscopic Data Analyses, GeoPlanet: Earth and Planetary Sciences (Berlin: Springer Verlag) [Google Scholar]
- Nomoto, K., Kobayashi, C., & Tominaga, N. 2013, ARA&A, 51, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J. E., Yong, D., Bessell, M. S., et al. 2013, ApJ, 762, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Placco, V. M., Frebel, A., Beers, T. C., & Stancliffe, R. J. 2014, ApJ, 797, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Pols, O. R., Tout, C. A., Eggleton, P. P., & Han, Z. 1995, MNRAS, 274, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Pols, O. R., Schröder, K.-P., Hurley, J. R., Tout, C. A., & Eggleton, P. P. 1998, MNRAS, 298, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Pols, O. R., Izzard, R. G., Stancliffe, R. J., & Glebbeek, E. 2012, A&A, 547, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rastegaev, D. A. 2010, AJ, 140, 2013 [NASA ADS] [CrossRef] [Google Scholar]
- Reimers, D. 1975, Mem. Soc. Roy. Sci. Liège, 8, 369 [Google Scholar]
- Richard, O., Michaud, G., & Richer, J. 2002a, ApJ, 580, 1100 [NASA ADS] [CrossRef] [Google Scholar]
- Richard, O., Michaud, G., Richer, J., et al. 2002b, ApJ, 568, 979 [Google Scholar]
- Roederer, I. U., Cowan, J. J., Preston, G. W., et al. 2014a, MNRAS, 445, 2970 [NASA ADS] [CrossRef] [Google Scholar]
- Roederer, I. U., Preston, G. W., Thompson, I. B., et al. 2014b, AJ, 147, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A. 1972, ApJ, 178, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C., Cowan, J. J., & Gallino, R. 2008, ARA&A, 46, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spada, F., Demarque, P., Kim, Y.-C., & Sills, A. 2013, ApJ, 776, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Stancliffe, R. J. 2009, MNRAS, 394, 1051 [NASA ADS] [CrossRef] [Google Scholar]
- Stancliffe, R. J., & Eldridge, J. J. 2009, MNRAS, 396, 1699 [NASA ADS] [CrossRef] [Google Scholar]
- Stancliffe, R. J., & Glebbeek, E. 2008, MNRAS, 389, 1828 [Google Scholar]
- Stancliffe, R. J., Glebbeek, E., Izzard, R. G., & Pols, O. R. 2007, A&A, 464, L57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stancliffe, R. J., Dearborn, D. S. P., Lattanzio, J. C., Heap, S. A., & Campbell, S. W. 2011, ApJ, 742, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Starkenburg, E., Shetrone, M. D., McConnachie, A. W., & Venn, K. A. 2014, MNRAS, 441, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Suda, T., Katsuta, Y., Yamada, S., et al. 2008, PASJ, 60, 1159 [NASA ADS] [Google Scholar]
- Suda, T., Yamada, S., Katsuta, Y., et al. 2011, MNRAS, 412, 843 [NASA ADS] [Google Scholar]
- Suda, T., Komiya, Y., Yamada, S., et al. 2013, MNRAS, 432, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, I. B., Ivans, I. I., Bisterzo, S., et al. 2008, ApJ, 677, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Toonen, S., & Nelemans, G. 2013, A&A, 557, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Torres, G. 2010, AJ, 140, 1158 [NASA ADS] [CrossRef] [Google Scholar]
- Umeda, H., & Nomoto, K. 2003, Nature, 422, 871 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Umeda, H., & Nomoto, K. 2005, ApJ, 619, 427 [NASA ADS] [CrossRef] [Google Scholar]
- van Oirschot, P., Nelemans, G., Helmi, A., et al. 2014, Proc. IAU Symp., 298, 431 [NASA ADS] [Google Scholar]
- Vassiliadis, E., & Wood, P. R. 1993, ApJ, 413, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Windhorst, R. A., Burstein, D., Mathis, D. F., et al. 1991, ApJ, 380, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Yanny, B., Rockosi, C., Newberg, H. J., et al. 2009, AJ, 137, 4377 [NASA ADS] [CrossRef] [Google Scholar]
- Yong, D., Norris, J. E., Bessell, M. S., et al. 2013, ApJ, 762, 27 [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, Jr., J. E., et al. 2000, AJ, 120, 1579 [Google Scholar]
- Yuan, H., Liu, X., Xiang, M., et al. 2015, ApJ, 799, 135 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
CEMP/VMP ratio, FC, calculated with model sets A1 and A4, with set Cq of Abate et al. (2013), and determined for observed stars from the SEGUE sample and the SAGA database.
CEMP star fraction computed from the SEGUE data in the range −2.5 < [Fe/H] ≤ 2, and computed with our different model sets.
Fractions of CEMP stars derived from the SAGA database and computed with our models.
All Figures
 |
Fig. 1 Distribution of M1,i computed with model set A4 (solid, blue line) and model set Cq of Abate et al. (2013; dashed, red line). The bins are equally spaced and the width in M1,i/M⊙ of each bin is 0.1. The y-axis indicates the number of CEMP stars in each bin, arbitrarily rescaled. |
| In the text | |
 |
Fig. 2 Distribution of log 10(g/ cm s-2) as derived from the SEGUE sample of CEMP stars with −2.5 ≤ [Fe/H] ≤ − 2 (histogram with Poisson errors) and computed with our default model set A (solid line). The 0.2 dex bins are equally spaced in log 10(g/ cm s-2). In this and the similar plots that follow the area under the graph (which is the total number of stars) is normalised such that it is the same for both the observations and our model stars. |
| In the text | |
 |
Fig. 3 Teff − log 10g probability distribution of all stars in our simulation computed with model set A. Darker colours indicate regions of higher probability. The grey solid and magenta dotted lines show the isochrones computed with detailed stellar-evolution models at 10 Gyr and 13.7 Gyr, respectively. The isochrones computed for the same ages with a detailed model that includes gravitational settling are shown as light-blue dashed and blue dot-dashed lines, respectively. The black dotted lines indicate the ranges of Teff and log 10g in which Lee et al. (2013) select the SEGUE stars. Black circles indicate all SEGUE stars with −2.4 ≤ [Fe/H] < − 2.2. |
| In the text | |
 |
Fig. 4 Initial period distribution computed with model sets A–C (solid, dot-dashed and dashed line, respectively). The 0.2 dex bins are equally spaced in log 10(Pi/ days). |
| In the text | |
 |
Fig. 5 Left:FC calculated with model sets that assume a power-law initial mass-ratio distribution, φ(q) ∝ qγq, with different values of γq. Right: FC of model sets that assume a log-normal initial-period distribution with different values of the mean, μlog P, and fixed standard deviation, σlog P = 2.3. The filled circles show the value of FC computed with our default model set A. |
| In the text | |
 |
Fig. 6 Cumulative orbital-period (Pf) distributions for SAGA CEMP stars with −2.8 ≤ [Fe/H] ≤ − 1.8 (shaded area). The lower limit of the observed distribution is determined assuming that all CEMP stars are binaries, whereas to determine the upper limit we assume that only CEMP-s stars are in binaries. Our model sets A and IL05 are shown as solid and dotted lines, respectively. The 0.2 dex bins of the model distributions are equally spaced in log 10(Pf/days). |
| In the text | |
 |
Fig. 7 Mass distribution of CEMP stars (solid line) and C-normal stars (dot-dashed line) computed with model set A. Bins of width 0.025 dex are equally spaced in M∗/M⊙. |
| In the text | |
 |
Fig. 8 Panels a)–d): abundance distributions of sodium, light-s elements, heavy-s elements and lead, respectively. The 0.2 dex bins are equally spaced in [El/Fe]. The histograms represent CEMP and CEMP-s/r stars from our database (light and dark grey, respectively), with Poisson errors. Models with MPMZ = 0,2 × 10-4 M⊙, 2 × 10-3 M⊙, 4 × 10-3 M⊙ are shown as dotted, dashed, solid, dot-dashed lines, respectively. |
| In the text | |
 |
Fig. 9 Panels a)–d): distributions of [C/Fe], [Sr/Fe], [La/Fe], and [Eu/Fe], respectively. Model sets A, B, D, and IL05 are shown with solid, dot-dashed, dotted, and dashed lines, respectively. Light and dark grey histograms represent the observed CEMP and CEMP-s/r stars in the SAGA database. The 0.2 dex bins are equally spaced in [El/Fe]. |
| In the text | |
 |
Fig. 10 Distribution of [Ba/Fe] vs. [Eu/Fe]. The red distribution represents our default model A. The grey distribution is computed with an initial enhancement of [r/ Fe] ini = 1. The dotted lines indicate the thresholds [Ba/Fe] = + 0.5 and [Eu/Fe] = 1 that define CEMP-s and CEMP-s/r stars, respectively. The crosses indicate the observed CEMP-s stars with [Eu/Fe] < + 1. CEMP-s/r are shown as blue circles. The + symbol in the top-left corner shows the average observed uncertainty. |
| In the text | |
 |
Fig. 11 As Fig. 10 for [Ba/Fe] vs. [C/Fe]. The vertical line represents the threshold [C/Fe] = + 0.7. In the bottom-right corner the average observed uncertainty is shown as a + symbol. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


