| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A43 | |
| Number of page(s) | 16 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201525874 | |
| Published online | 31 August 2015 | |
Three-dimensional simulations of near-surface convection in main-sequence stars
IV. Effect of small-scale magnetic flux concentrations on centre-to-limb variation and spectral lines⋆
1 Max-Planck-Institut für Sonnensystemforschung, Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany
e-mail: beeck@mps.mpg.de
2 Institut für Astrophysik, Universität Göttingen, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
Received: 12 February 2015
Accepted: 20 April 2015
Context. Magnetic fields affect the local structure of the photosphere of stars. They can considerably influence the radiative properties near the optical surface, flow velocities, and the temperature and pressure profiles. This has an impact on observables such as limb darkening and spectral line profiles.
Aims. We aim at understanding qualitatively the influence of small magnetic flux concentrations in unipolar plage regions on the centre-to-limb variation of the intensity and its contrast and on the shape of spectral line profiles in cool main-sequence stars.
Methods. We analyse the bolometric and continuum intensity and its angular dependence of 24 radiative magnetohydrodynamic simulations of the near-surface layers of main-sequence stars with six different sets of stellar parameters (spectral types F to early M) and four different average magnetic field strengths (including the non-magnetic case). We also calculated disc-integrated profiles of three spectral lines.
Results. The small magnetic flux concentrations formed in the magnetic runs of simulations have a considerable impact on the intensity and its centre-to-limb variation. In some cases, the difference in limb darkening between magnetic and non-magnetic runs is larger than the difference between the spectral types. Spectral lines are not only broadened owing to the Zeeman effect, but are also strongly affected by the modified thermodynamical structure and flow patterns. This indirect magnetic impact on the line profiles is often bigger than that of the Zeeman effect.
Conclusions. The effects of the magnetic field on the radiation leaving the star can be considerable and is not restricted to spectral line broadening and polarisation by the Zeeman effect. The inhomogeneous structure of the magnetic field on small length scales and its impact on (and spatial correlation with) the local thermodynamical structure and the flow field near the surface influence the measurement of the global field properties and stellar parameters. These effects need to be taken into account in the interpretation of observations.
Key words: magnetic fields / magnetohydrodynamics (MHD) / radiative transfer / stars: magnetic field / stars: low-mass / line: profiles
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Many cool main-sequence stars have substantial surface magnetic fields (see Reiners 2012, for a review). These fields are believed to be generated by a hydrodynamic dynamo in the deeper parts of the convection zone and are transported to the surface layers by buoyancy and convective flows (see Charbonneau 2010, for a review). Knowledge of the global geometry and strength of stellar surface magnetic fields and their dependence on stellar parameters is important in order to understand the underlying nature of the dynamo processes in stars of different internal structure (e. g. Donati 2011). Moreover, the magnetic field is an important noise source for many astronomical observations (such as exo-planet detection, see e. g. Jeffers et al. 2013), which makes a deeper understanding of its properties and the impact on observables essential.
The presence of stellar magnetic fields is often indirectly detected by means of activity indicators (such as chromospheric S-index, X-ray flux) or photometric variability, which is mainly attributed to the rotational variation of the projected starspot area. Fast rotators in general tend to be more magnetically active (see Reiners et al. 2014, and references therein). Moreover, at least some stars were found to exhibit activity cycles analogous to the 11-year solar activity cycle (Baliunas et al. 1995).
In some cases, it is possible to measure the surface magnetic field by spectroscopic or spectropolarimetric means, which exploit the action of the Zeeman effect on spectral line profiles in the integrated (Stokes-I) and circularly polarised (Stokes-V) light. While line broadening in Stokes-I gives an estimate of the unsigned average magnetic field of a star, Stokes-V measurements are sensitive to the polarity of the field so that they pick up only the uncancelled net flux (signed average field). For main-sequence stars of spectral types F, G, and K, there exist only a few (Stokes-I) magnetic field measurements, as the magnetic line broadening owing to the Zeeman effect is usually much smaller than the rotational broadening in these stars (see Reiners 2012, and references therein). For M dwarfs, such measurements are somewhat more feasible as the rotational velocities required for the generation of measurable magnetic fields are smaller. Some M dwarfs are found to be completely covered with a magnetic field in the kG regime, with local values of up to ~7 kG (Shulyak et al. 2014).
Disc-centre (μ = 1) intensities.
For rapidly rotating stars, it is possible to infer the large-scale geometry of the magnetic field with spectropolarimetry: Zeeman-Doppler imaging (ZDI) exploits the latitude-dependent time dependence of the Zeeman-effect signature in polarised light caused by the Doppler effect due to the stellar rotation. ZDI reveals large-scale magnetic geometries which are often quite unlike the solar one (Morin et al. 2010).
Owing to their interaction with the convective flows, stellar surface magnetic fields are expected to be highly structured and inhomogeneous on spatial scales as small as the scale of the convection, as it is known for the Sun: the magnetic flux at the solar surface is mainly concentrated in sunspots, pores, and smaller magnetic structures in the intergranular lanes. In these magnetic flux concentrations, the magnetic forces cause local modifications of the thermodynamical structure and the convective flows in the photospheric layers, which result, e.g. in a modulation of the local intensity emerging from magnetic flux concentrations. These modifications should be taken into account in spectroscopic and spectropolarimetric measurements of stellar magnetic fields as they will have a considerable influence on the shape of the local spectral line profiles. Basri et al. (1990) and Saar & Solanki (1992) analysed the significant impact of multicomponent atmospheres and magnetic field gradients on spectral lines and the consequences for stellar magnetic field measurements. More recently, Rosén & Kochukhov (2012) showed that ZDI of the magnetic field for a star with cool (dark) magnetic spots can fail if one does not simultaneously reconstruct the temperature. Three-dimensional MHD simulations of the near-surface convection as presented in this paper series provide a realistic and self-consistent structure of the magnetic field and stellar atmosphere and consequently can help to considerably improve stellar magnetic field measurements.
In Beeck et al. (2013a, hereafter Paper I), we presented non-magnetic 3D simulations of six main-sequence stars (spectral types F3V to M2V). In Beeck et al. (2013b, hereafter Paper II), we analysed the impact of the convective flows and the surface structure caused by them on the limb darkening and on the shapes of the profiles of three spectral lines. In Beeck et al. (2015, hereafter Paper III) we investigated a grid of MHD simulations with the same stellar parameters as the non-magnetic simulations analysed in Paper I and Paper II. The magnetic simulation runs include a unipolar magnetic field with an average field strength of up to 500 G. In this paper, we analyse the impact of the magnetic field on the intensity field and spectral line profiles in the grid of simulations introduced in Papers I and III.
2. Methods
The grid of six non-magnetic and 18 magnetic simulations was run with the 3D radiative RMHD code MURaM (Vögler 2003; Vögler et al. 2005). It comprises six sets of stellar parameters (Teff, log g), which roughly follow the (zero-age) main-sequence and correspond to stars of spectral types F3V, G2V, K0V, K5V, M0V, and M2V (see Paper I for more details). The metallicity was assumed to be solar (abundances by Anders & Grevesse 1989) in all cases. The code uses the OPAL equation of state (Rogers et al. 1996; Rogers 1994) and ATLAS9 opacities (Kurucz 1993), which were binned into four opacity bins (τ-sorting applying an averaged 3D atmosphere of the hydrodynamical run of each simulation as reference; for more details see Paper I). For each set of stellar parameters, there is one non-magnetic simulation and three magnetic simulations with average vertical field strengths of 20, 100, and 500 G (for more details, see Paper III). Table 1 lists the gravitational acceleration and the effective temperature of all 24 simulations considered.
The spectral line synthesis was done with the forward module of the code Spinor (Frutiger 2000; Frutiger et al. 2000). Whenever averaged spectral line profiles are considered, the average is a spatial average over the 512 × 512 horizontal pixels (of the simulation boxes) as well as a temporal average over six snapshots which are taken several minutes apart from each other. These averaged line profiles were calculated for 10 different values of μ (cosine of the angle ϑ between line of sight and stellar surface). For the disc-integrated line profiles considered, we used a numerical integration which takes into account differential rotation according to 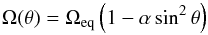 (1)where Ω is the local angular velocity of the star, Ωeq its value at the stellar equator, θ the latitude and α a parameter describing the differential rotation.
(1)where Ω is the local angular velocity of the star, Ωeq its value at the stellar equator, θ the latitude and α a parameter describing the differential rotation.
In all cases considered here, the star was assumed to be homogeneous on large scales as we use (six snapshots of) a local-box simulation for the line synthesis of the disc-integrated line profile. For more details, see Paper II and references therein. The simulation snapshots were taken with a cadence of a few minutes from the relaxed phase of the run (see Paper III).
 |
Fig. 1 Vertically emerging bolometric intensity of a snapshot of the 500 G runs of the G2V (left) and M2V (right) simulations. The grey scale saturates at ± 2.5 standard deviations from the mean intensity. Intensity maps of further simulations are given in Paper I (Fig. 2) and Paper III (Fig. 1). |
3. Intensity field
3.1. Disc-centre intensity
Figure 1 shows maps of the vertically emerging bolometric intensity from snapshots of the 500 G runs of the solar (G2V) and the M2V-star simulation. As shown in Paper III, the dark and bright structures in the intergranular lanes coincide with locations of strong concentrations of magnetic flux, while the granular upflows are only weakly magnetised. The high magnetic field strength in the flux concentrations causes a local depression of the optical surface, which either results in bright structures if the depth of the depression is comparable or larger than its horizontal extent (efficient side-wall heating) or dark structures if its depth is small compared to the horizontal size. The smaller superadiabaticity in M dwarfs compared to hotter main-sequence stars is responsible for smaller typical depth-to-radius ratio of these local depressions. Consequently in F-, G-, and K-type dwarfs, there are only a few dark magnetic structures in the 500 G runs and none at all in the 100 G runs whereas the M-star photospheres are dominated by dark magnetic structures at 500 G and show many of them already at 100 G (for more details see Paper III).
Table 1 lists the mean bolometric intensities at the disc centre (i.e. μ = cosϑ = 1) along with its relative rms contrast and the extrema of a time-resolved sequence of intensity snapshots spanning several minutes for each of the 24 simulations considered. The disc-centre intensity is almost unaffected by the magnetic field in the F-, G-, and K-star simulations although the radiative flux (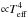 ) increases significantly owing to magnetic limb brightening (see Sect. 3.2). In the M-star simulations, the disc-centre intensity is reduced in the 500 G runs with respect to the non-magnetic runs, whereas the radiative flux is unaffected (M0V) or only marginally reduced (M2V).
) increases significantly owing to magnetic limb brightening (see Sect. 3.2). In the M-star simulations, the disc-centre intensity is reduced in the 500 G runs with respect to the non-magnetic runs, whereas the radiative flux is unaffected (M0V) or only marginally reduced (M2V).
 |
Fig. 2 Intensity histograms of the G2V (left panels) and M2V (right panels) simulations. In both representations (upper panels: linear; lower panels: logarithmic), the histogram bins are linearly equidistant with a bin size of 0.01. |
In the F3V and G2V stars, the rms contrast is slightly reduced by the magnetic field while minimum and maximum intensity are somewhat increased as (moderately) bright magnetic regions replace the darkest regions in the intergranular lanes. In the K stars, the contrast is increasing with increasing B0. Here, the bright magnetic regions are much more prominent than in the hotter stars. This is also reflected in the maximum value of the intensity, which is strongly enhanced in the magnetic K-star simulations to values up to 20 standard deviation above the mean intensity. The reason for this particular brightness of the bright magnetic regions is the weak dependence of the opacity on temperature between 4000 and 5000 K, which renders the location of the photospheric transition more sensitive to density than to temperature. Consequently, the partial evacuation in the magnetic flux concentrations shifts the optical surface to particularly high temperatures in these stars. A similar effect has been observed in vertical vortices in the non-magnetic K-star simulations (see Paper II). From K5V to M2V, the bright magnetic regions become less bright (and less frequent) with decreasing effective temperature along our model sequence and the maximum intensity decreases (in terms of standard deviations above the mean). Our findings are in agreement with the results published by Steiner et al. (2014), who also find the highest contrast of bright magnetic structures in the early K star of their sequence of simulations and decreasing contrasts for hotter as well as cooler stars.
In the K-star and M-star simulations, the global intensity minima decrease from B0 = 20 G to B0 = 500 G, owing to the formation of dark magnetic regions. These dark regions become more pronounced with lower effective temperature as the depth of the optical surface depression becomes smaller compared to the horizontal size of the flux concentrations (see Paper III). Dark magnetic structures become dominating in the M-star simulations and significantly reduce the mean disc-centre intensity in the 500 G runs with respect to the non-magnetic runs of these stars.
 |
Fig. 3 Relation between the magnetic field strength B(τR = 1) at the optical surface and the vertical bolometric intensity Ibol(μ = 1) normalised with its mean value. The field is binned in steps of 200 G. Error bars give the 1σ scatter within the bins. For bins with fewer than 1000 pixels (~0.06% of the total area considered), the symbol size is scaled with the logarithm of the number of pixels. |
Figure 2 shows histograms of the vertically emerging intensity (normalised to the mean) for all four runs of the G2V and the M2V stars. The bright magnetic features produce high-intensity tails in the histograms in all magnetic runs of both stars. In the solar case, these bright features have the highest area fraction and intensity in the 100 G run and are considerably weaker at B0 = 20 G and B0 = 500 G. The dark magnetic structures are responsible for low-intensity tails in the histograms of the M2V-star simulations with B0 = 100 G and B0 = 500 G as well in the 500 G run of the G2V star. As pointed out in Paper III, the appearance of bright and dark magnetic structures does not only depend on spectral type, but also on the amount of magnetic flux available (and hence on B0). Compared to the overall spread of the intensity distribution the dark structures are much more prominent in the M2V star simulations than in the G2V star (cf. Table 1).
 |
Fig. 4 Continuum intensity in a passband between 400 and 410 nm of the six simulations with B0 = 500 G viewed at an angle of 60° with respect to the vertical (i.e. μ = 0.5). |
 |
Fig. 5 Limb darkening for the G2V (left) and M2V (right) simulations without magnetic field (diamonds and dotted curves) and with B0 = 500 G (squares and solid curves) in narrow passbands near 400, 600, 800, and 2000 nm. The temporal scatter is considerably smaller than the symbol size. |
Figure 3 shows a binned scatter plot of the vertical bolometric intensity (normalised to its mean value) as a function of the magnetic field at the optical surface for all magnetic runs of the F3V, G2V, K5V, and M2V stars. In all runs (with the notable exception of the 500 G run of the M2V star), the mean intensity of the first bin (B(τR = 1) < 200 G), is close to the mean intensity of the whole box, while the intensity of regions with a surface magnetic field strength between 200 and 1000 G on average falls somewhat below this value. This has purely kinematic reasons: the magnetic flux is concentrated in the dark intergranular lanes, which stay dark as long as the field is too weak to considerably influence the thermodynamical structure and the flow patterns. At a higher field strength (B(τR = 1) > 1 kG), many of the curves have a positive slope, indicating that regions of high magnetic field strength have, on average, an increasing intensity with increasing field strength. This is the case for all runs for the F3V and G2V stars. In these two models, the 20 G runs show the highest intensities at a given field strength. The intensity of highly magnetised regions in the 500 G runs is somewhat lower than in the 20 G and 100 G runs and the scatter of intensity values (indicated by the error bars, which give the 1σ scatter) within each bin increases somewhat. This can be attributed to the formation of a few dark magnetic structures among the still dominant component of bright structures. In the K5V simulation with B0 = 500 G as well as in the 100 G and 500 G runs of the M2V simulations, the slope of the binned scatter plots stays negative in the kG regime indicating that dark regions are dominant in these simulation runs. Only at very high field strengths of B(τR = 0) > 3 kG does the average intensity tend to increase with increasing field strength in these models. This is, however, produced by very few surface elements, which correspond to localised bright points with very small area coverage.
3.2. Centre-to-limb variation of intensity and contrast
Figure 4 shows maps of the continuum intensity near 400 nm of the 500 G runs at an inclined viewing angle of μ = cosϑ = 0.5. The snapshots are the same as in Fig. 1 of Paper III (and for G2V and M2V the same as in Fig. 1 in this paper). The differences between the different spectral types are mainly caused by the different depth of the depressions in the optical surface caused by the magnetic flux concentrations, but also by the different impact of the flux concentrations on the local density and temperature structures. In the F3V star, the depressions are deepest (in terms of pressure scale heights as well as in terms of granule sizes, see Paper III) and the evacuation in the upper part of the magnetic flux concentration is strongest. Consequently, the intergranular lanes and the centres of the magnetic flux concentrations are hidden from view behind granules while the granules which are seen through the highly evacuated upper parts of magnetic structures appear brightened. Moreover, the granules show dark edges where the optical path through the cool layers above the optical surface is particularly long (“limb darkening” of single granules). With decreasing effective temperature the corrugation of the optical surface as well as the typical depth of the depressions caused by the magnetic flux concentrations decrease (see Paper III) and the appearance of I(μ = 0.5) changes. In the G-, K-, and M-star simulations, only a part of the granules seen through flux concentrations are brightened significantly. These small scale brightenings are observed on the Sun as “faculae” (see Keller et al. 2004, and references therein). In the M stars, especially M2V, the dark magnetic structures are still visible at μ = 0.5 and the faculae are less bright (in terms of the standard deviation of the intensity) than in the K- and G-type stars.
 |
Fig. 6 Centre-to-limb variation of the rms intensity contrast for the G2V (left) and M2V (right) simulations without magnetic field (diamonds and dotted curves) and with B0 = 500 G (squares and solid curves) in narrow passbands near 400, 600, 800, and 2000 nm. The temporal scatter is considerably smaller than the symbol size. We note the logarithmic scale of the ordinates. |
Figure 5 shows the centre-to-limb variation of the continuum intensity in four narrow wavelength passbands for the G2V- and the M2V-star simulations, comparing the non-magnetic runs (dotted curves) with the 500 G runs. In both cases, the limb darkening is reduced in the magnetic runs compared to the non-magnetic runs, i.e. the magnetic field effectively brightens the limb. This limb brightening is produced by the faculae (cf. Fig. 4). The effect is stronger at higher effective temperature as the faculae become more prominent and have a higher filling factor. In the G2V-star simulation, the difference in limb darkening between the non-magnetic and the 500 G runs is even larger than the difference between the non-magnetic runs of different spectral types.
 |
Fig. 7 Limb darkening in the Johnson UX, B, V, R, and I passband filters (Johnson & Morgan 1951; Bessell 1990) in the G2V star. Analogous plots for the F3V and the M0V star are given in Fig. A.1. Left panel: limb darkening of the non-magnetic (hydro.) and 500 G runs. Right panel: relative difference between both runs. |
In Fig. 6, the centre-to-limb variation of the relative intensity fluctuations (“intensity contrast”) is plotted as a function of μ = cosϑ for the non-magnetic and 500 G runs of the solar (G2V) and M2V-star simulations. In the solar case, the intensity contrast at the disc centre does not significantly differ between non-magnetic case and 500 G case (cf. Table 1). Near the limb the effect of the faculae leads to a strongly enhanced intensity contrast: while in the non-magnetic case, the contrast monotonically drops from the disc centre to the limb, it reaches a maximum in the 500 G runs around μ = 0.3 in all wavelength passbands considered. In the M2V-star simulations, the magnetic field affects the intensity contrast at all disc positions: the contrast is roughly twice (near the limb: three times) as high in the magnetic run as in the non-magnetic run. Unlike the solar case, the intensity contrast does not strongly increase from the disc centre towards the limb in the 500 G run as the faculae are less pronounced.
 |
Fig. 8 Local vertical spectral line profiles for the K0V simulation with B0 = 500 G. Left panel: intensity image with four positions marked. Right panels: local profiles of the Fe i line at 617.3 nm (top) and the Ti i line at 2223 nm (bottom) at (μ = 1); the four different colours correspond to the four points marked in the left panel. |
Figure 7 shows the limb darkening in the non-magnetic and the 500 G runs of the G2V star in the Johnson UX, B, V, R, and I passbands (left panel) and the difference between the two runs in per cent (right panel). The highest relative deviations are in the UX band near the limb, where the magnetic run is more than 30% brighter than the non-magnetic run. For some real stars, limb darkening can be inferred from eclipses (in binaries) or exoplanet transits. Possibly, the limb darkening can be used as an indicator for small scale magnetic structures (faculae) on such stars even in cases where the field is too small to be detected spectroscopically. In the same way as for the continuum passbands (see Fig. 5), the magnetic limb brightening becomes weaker with decreasing effective temperature along our model sequence in the Johnson passbands (see Fig. A.1).
4. Spectral line profiles
4.1. Spectral line profiles at the disc centre
In Paper II, we analysed the effects of the convective velocity field and its spatial correlation with the thermodynamical quantities on a set of three spectral lines (Fe i at 616.5 nm, Fe i at 617.3 nm, and Ti i at 2223.3 nm). Here, we investigate the impact of the local magnetic field structure and its correlation with thermodynamical quantities and with the convective flows on these lines. In the presence of a magnetic field, all three lines are split into their Zeeman components. The effective Landé factors are quite different: while the Fe i line at 617.3 nm was chosen for its large effective Landé factor of geff = 2.5, the Fe i line at 616.5 nm is rather insensitive to the magnetic field (geff = 0.69). The third line, Ti i at 2223.3 nm, has an effective Landé factor of geff = 1.66. However, as it is in the infrared, the broadening or splitting due to the Zeeman effect is expected to be larger in comparison to the line width than in the optical Fe i lines.
Figure 8 shows a snapshot of the K0V-star simulation with B0 = 500 G. Four pixels are marked for which vertical local spectral line profiles of the Ti i line and the Fe i line at 617.3 nm are plotted in the two right panels. Point 1 is located in an upflow region with negligible magnetic field strength. The corresponding line profiles are shifted somewhat to the blue. Especially for the Fe i line at 617.3 nm, this shift affects the line wings more strongly than the core, resulting in a strong asymmetry. As the wings of these photospheric lines form very close to the surface, while the line core forms somewhat higher in the stellar atmosphere, this asymmetry reflects the deceleration of the (overshooting) upflow as discussed in Paper II. Point 2 is located in a downflow with low field strength. The corresponding line profiles are shifted to the red, with an asymmetry (especially in the Fe i line at 617.3 nm) indicating an acceleration along the downflow. We note that the continuum flux is lower in Point 2 and that the depth of the line profiles is smaller. In the average spectrum, Point 2 consequently has a lower weight than Point 1 for these lines.
 |
Fig. 9 Decomposition of four line profiles (at μ = 1) into differently magnetised components. The black curve shows the average line profile, while the coloured curves show the line averaged over areas where B(τR = 1) is in the specified ranges. Each line is normalised to its own continuum. The numbers in parentheses give the weight of the components in the composite spectrum (i.e. average continuum flux times area fraction). |
The other two points in Fig. 8 are situated in magnetised regions: Points 3 in a bright (hot) magnetic structure and Point 4 in the centre of a dark (cool) magnetic structure. The corresponding spectral line profiles are split into two components by virtue of the Zeeman effect. The components are asymmetric owing to the vertical gradient of the magnetic field: as the field rapidly decreases with height in the photosphere (see Paper III), the cores of the Zeeman components are less strongly shifted away from the line centre than their wings. In comparison to Point 1, the equivalent width (EW) of the Fe i line at 617.3 nm (upper right panel of Fig. 8) is larger in Point 3 and smaller in Point 4, caused by the (moderate) temperature sensitivity of the corresponding line opacity. As the continuum is also higher in Point 3 than in Point 4, the weight of the local line profile from Point 3 will be higher in the spatially averaged line profile than that of Point 4.
In contrast to the Fe i line at 617.3 nm, the Ti i line (lower right panel in Fig. 8) has a strongly reduced EW in the bright magnetic structure (Point 3) with respect to Points 1 and 2. The Ti i line is very sensitive to temperature around 4000 K, owing to ionisation and to depopulation of the lower level of the transition. Therefore, the line opacity is considerably reduced in hot magnetic structures of this star. This effect will be referred to as “line weakening” in the following discussion. The same phenomenon also exists in the Fe i lines but at a higher temperature (around 6000 K), which is more relevant for the G2V- and F3V-star simulations. In the dark magnetic structure (Point 4), the EW of the Ti i line is somewhat larger than in Points 1 and 2. In summary, dark (cool) and bright (hot) magnetic structures can produce crucially different local spectral line profiles. As shown in Sect. 3.1, the relative importance of dark and bright magnetic structures depends on the average field strength and the stellar parameters.
Figure 9 shows horizontally averaged profiles of the Fe i line at 617.3 nm for the 500 G runs of the F3V- and the K0V-star simulations and of the Ti i line for the 500 G runs of the K0V- and the M2V-star simulations. The thick black curves represent the line profiles averaged over the entire area of the simulation box, while the four coloured curves are the profiles averaged over surface components with different magnetic field ranges at the optical surface. The numbers in parentheses give the weight of the individual components in the average line profile. The profile of the Fe i line at 617.3 nm has a strongly extended red wing in the F3V simulations. As the decomposition into distinct surface components illustrates, this red wing is produced mainly by the flow velocities in the area components with intermediate field strengths of 250 to 2000 G: these components mainly represent short-lived, dynamic magnetic flux concentrations in a convective collapse phase in this star (see Paper III). This results in an (on average) increased downflow velocity in the optical depth range where this spectral line is forming. Additionally, the Zeeman effect broadens the line profiles emerging from these surface components, shifting its red wing even further towards longer wavelengths. The regions with high magnetic field strengths of >2 kG do not contribute much to the average spectrum because of line weakening, which affects the Fe i lines in the G2V and F3V atmospheres (while it does not play a great role for K0V, cf. Fig. 8).
 |
Fig. 10 Centre-to-limb variation of the equivalent width, FWHM, and the effective Doppler shifts of the line core and wings (from left to right) of the Fe i line at 617.3 nm in all four simulation runs of the F3V star. The colour code is the same for all panels, see legend in the left panel. |
In the K0V simulation, the flow velocities are much lower and the magnetic flux concentrations are less dynamic. Consequently, the Doppler shift of the line components is weaker. As the temperature is lower, less line weakening occurs in the Fe i line at 617.3 nm and the substantially broadened line profile emerging from the strongly magnetised area components produces extended wings in the averaged (disc-centre) line profile. For the Ti i line, these wings are even more pronounced as the Zeeman splitting is stronger in the infrared (with respect to the line width). Owing to line weakening, however, the equivalent width of the line profiles stemming from the magnetised area is somewhat reduced. In the M2V simulation, line weakening does not play a role for the lines considered. The line width is larger here for all surface components owing to the higher photospheric pressure, rendering the extended wings more difficult to see in the pressure-broadened line profile.
 |
Fig. 11 Difference of equivalent width, FWHM, line core shift, and line wing shift (from left to right) between simulations with B0 = 500 G and the respective non-magnetic simulations for the three spectral lines as a function of μ. |
4.2. Centre-to-limb-variation of spectral line profiles
In Paper II, the variation of the equivalent width (EW), the full width at half maximum (FWHM), and the Doppler shifts of the cores and wings of spectral lines (in particular of the Fe i line at 617.3 nm) as a function of viewing angle μ = cosϑ were analysed for the non-magnetic simulations. Here, we show the effect of the magnetic field on the centre-to-limb variation of the line profiles. As discussed above for the vertical (i.e. disc-centre) spectral line profiles, the magnetic field has a substantial impact on the line profile shape parameters. Figure 10 shows this for the Fe i line at 617.3 nm for the example of the F3V star. The EW decreases with increasing B0 at all disc positions (i.e. for all values of μ). This is mostly caused by line weakening in the magnetic flux concentrations (cf. Fig. 8). The centre-to-limb variation of the FWHM does not differ much between the non-magnetic and the 20 G and 100 G runs. At B0 = 500 G, however, the FWHM near the limb is considerably smaller than in the non-magnetic run. This is a result of the stronger corrugation of the optical surface in the magnetic run, which hides from view the part of the granular flows receding from the observer as well as the cool downflows and thus reduces the broadening induced by variations of the line-of-sight velocity and temperature. The centre-to-limb variations of the effective Doppler shifts of the line differ considerably between the runs. At the disc centre, the line wings1 are strongly shifted to the red in the 500 G runs owing to the higher downflow velocities at constant optical depth (cf. Fig. 9) in this run in comparison to the non-magnetic runs. Near the limb, however, the stronger corrugation in the 500 G run results in an effective blue shift, as the receding flows are mostly hidden behind the granules. As the effect of the magnetic field on the shifts of line cores and wings is qualitatively and quantitatively different, the magnetic field also has a strong impact on the line bisectors.
 |
Fig. 12 Doppler shift of the line profile cores (solid curves) and wings (dashed curves) of the three spectral lines in the F3V simulations as function of υrotsini. In all cases, i = 60° and α = 0.2 was assumed. |
Figure 11 shows the difference in EW, FWHM, line core shift, and line wing shift between the 500 G runs and the non-magnetic runs as a function of μ for all spectral types and all three spectral lines (for the Fe i line at 617.3 nm in the F3V star this corresponds to the difference between the blue and the black curve in Fig. 10). The differences in EW and FWHM are given as relative difference in per cent, while the Doppler shifts are given as absolute differences in km s-1. For both Fe i lines, the EW is smaller with magnetic field than without in the G2V and F3V simulations (cf. Fig. 10) owing to line weakening in the bright magnetic flux concentrations. In the other stars, line weakening does not play an important role for these lines. Here, the EW is unaffected in the magnetically insensitive Fe i line at 616.5 nm while it is increased in the magnetically sensitive line at 617.3 nm owing to broadening by the Zeeman effect, which reduces the degree of saturation of the line. For the Ti i line, line weakening also affects the EW in the K0V star at disc centre. We note that the EW of this line is very small in the F3V simulation, particularly near the disc centre (see Paper II) and only regions with exceptional temperature gradients and high density contribute substantially to the average profile, which might explain why the impact of the magnetic field on the EW of this line is not similar or stronger than in the G2V star as expected.
The FWHM follows a similar trend: for the hotter stars, the FWHM tends to be smaller with magnetic field while, in the cooler stars, it is almost unchanged in the magnetically insensitive line and strongly enhanced in the magnetically sensitive lines. This again is showing the relative importance of line weakening and Zeeman broadening. As the line weakening affects mainly the contributions from downflows, it reduces the FWHM.
The effective Doppler shifts in the lines show an impact of the magnetic field which is almost independent of the sensitivity of the line to the magnetic field. The disc centres of the F3V and G2V stars show strongly redshifted line wings and slightly redshifted line cores in the 500 G runs (relative to the non-magnetic runs) in both Fe i lines. As shown earlier, this is caused by a strongly enhanced red wing, resulting from the larger filling factor of downflows (see Paper III) and the higher downflow speed at the optical depth range where these lines form. The Zeeman effect only slightly enhances this effect by broadening the spectral line originating from the magnetised downflows. Consequently, the relative redshifts in line wings and cores are somewhat higher in the 617.3 nm line than in the 616.5 nm. Towards the limb, these two stars show a small relative blueshift of line wings and cores with respect to the non-magnetic runs (which is probably due to the stronger corrugation of the optical surface). In the cooler stars, the impact of the magnetic field on the Doppler shifts of the line cores and wings and on their dependence on μ is much weaker since the convective velocities (particularly in the magnetic flux concentrations) are considerably smaller.
4.3. Disc-integrated spectral line profiles
Applying the numerical method outlined in Paper II, disc-integrated spectral line profiles were calculated using the angle dependent spectral line profiles from the local simulation boxes. So far, we do not include any large-scale surface inhomogeneities (such as active regions), but assume the stars to be homogeneous on large scales (i.e. having the properties of the 3D simulation with a constant B0 across the entire disc). The disc integration includes the rotation of the star, which follows the simple law given in Eq. (1) and thus introduces three parameters: the equatorial velocity of the rotation, υrot, the inclination, i, of the rotation axis with respect to the line of sight, and the differential rotation parameter, α.
 |
Fig. 13 Disc-integrated profiles of the Fe i line at 617.3 nm without rotation (left) and with υrot sini = 7.5 km s-1 (differential, α = 0.2, i = 60°; right) for G2V simulations. The grey line represents the profile of the non-magnetic run (hydro.), the blue curve is the profile of the 500 G run, the red curve is calculated using the thermodynamic structure of the 500 G run but assuming B ≡ 0 G for the line calculation (see text for further explanation). Dashed curves give the bisectors of the profiles with λ−λc values magnified by a factor of 5 for clarity. We note the different scales of ordinate and abscissa. |
As shown in Figs. 10 and 11, the 500 G runs of the hottest two stars of our sequence show redshifted line wings and (to a lesser extent) redshifted line cores at the disc centre. In the disc-integrated spectral line profiles, there is still a relative redshift with respect to the non-magnetic simulations, but the shift is considerably smaller. These effective Doppler shifts turn out to be sensitive to the rotational velocity as the spectral line profiles get distorted by the rotational broadening (cf. Paper II). Figure 12 illustrates this for the F3V star (where the shifts are largest) with the assumption of i = 60° and α = 0.2. In all three spectral lines, the line core moves redwards with increasing rotational velocity and the line wings move bluewards. Although this is the case in the non-magnetic and the magnetic runs alike, the effect becomes stronger with magnetic field: in the 500 G runs, the redshift in the line core reaches values around 1.5 km s-1 at a υrotsini of 15 km s-1.
From the above (Sects. 4.1 and 4.2) it is evident that the magnetic field has an impact on the spectral line profiles not only by virtue of the Zeeman effect, but also owing to the local modifications of the thermodynamical structure and the flow patterns caused by the magnetic flux concentrations. In order to disentangle these two effects, the spectral line synthesis for the 500 G runs was carried out again ignoring the magnetic field for the line synthesis. The result is indicated by the red curve in Fig. 13 for the example of the Fe i line at 617.3 nm and the G2V-star simulation. For comparison, the line profile of the non-magnetic simulation (grey) and of the full synthesis of the 500 G run (blue) are shown as well. Without rotation, the difference between the grey and red curves, which is exclusively caused by the modifications in thermodynamical structure and flows, is approximately equal in magnitude to the change induced by the Zeeman effect (difference between blue and red curves). While the local structure modifications shift the line somewhat to the red and reduce its equivalent width and FWHM, as discussed above (cf. Fig.11), the Zeeman effect broadens the line, as expected. This broadening, however, is not exactly symmetric. The magnetic field is predominantly located in downflows and is thus correlated with a Doppler shift leading to a more broadened red wing. As a result the Zeeman effect increases the C-shape of the profile of this spectral line as can be seen in the bisectors (dashed curves in the figure). In the other stars and in the Ti i line a qualitatively similar impact on the bisectors is visible (see Figs. A.2 and A.3), albeit less pronounced.
At a moderate rotational velocity of 7.5 km s-1 (see right panel of Fig. 13), the broadening due to the Zeeman effect is already very small compared to the rotational broadening. Consequently, the effect of the modified flows and thermodynamical structure on the line is overall much larger than the Zeeman effect.
This calculation has been carried out for all simulations and all spectral lines (more plots are given in Appendix A). We find the locally modified thermodynamics and flows to have a major impact on the line profiles in the F-, G-, and K-type stars. Only in the M-star simulation is the effect of thermodynamics significantly smaller than that of the Zeeman effect. This has several reasons. Firstly, line weakening does not play a role here for the spectral lines considered. Secondly, the absolute contrast of the temperature is smaller than in the hotter stars. Thirdly, the convective velocities are generally smaller; in particular, there are no large downflow velocities in the magnetic structures as they are found in the hotter stars.
5. Concluding remarks
We have shown that the intensity, its contrast and centre-to-limb variation as well as spectral line profile shapes are strongly influenced be a moderate local magnetic field. In unipolar regions with an average magnetic field of up to 500 G, the magnetic flux is strongly concentrated in localised structures of reduced or enhanced intensity. F-, G-, and K-type stars show more magnetic flux concentrations of enhanced intensity under these conditions, whereas M-type stars have prominent dark pore-like structures. These structures generally become bright near the limb and thus reduce the limb darkening (magnetic limb brightening). Moreover, the intensity contrast is enhanced, particularly near the limb. The influence on spectral line profiles is not only caused by the action of the Zeeman effect on the magnetically sensitive lines, but also by the presence of the magnetic flux concentrations which substantially deviate in their thermodynamical structure and flow patterns from the non-magnetised surroundings. Moreover, the height dependence of the magnetic field and the flow velocity as well as convective collapse events (resulting in strong downflows in magnetic flux concentrations) add asymmetries to the full-disc spectral line profiles, which can strongly depend on the rotation velocity of star.
For the synthesis of spectral lines as well as for the calculation of the limb darkening, we have implicitly made the assumption that the stars are completely covered with a unipolar field, which is homogeneous on large scales2. As the solar example as well as ZDI results show, stellar magnetic fields are not only structured on small scales, but also possess global structure (e.g. active latitudes, star spot groups, polar fields). Even though a homogeneously magnetised star as we implicitly assume does probably not exist in reality, the results presented in this paper illustrate that the impact even of a moderate magnetic field on observable quantities is expected to be significant. For Stokes-I measurements the Zeeman-effect signature can be largely obliterated by the effect of the deviating atmospheric structure in the magnetised regions. Consequently, magnetic field measurements for stars (at least for solar-like stars) have to be taken with caution because the magnetic field is usually considered to have no impact on the spectral lines apart from the Zeeman effect. The comparison of magnetically sensitive and insensitive lines (see e.g. Robinson 1980) only helps to a certain extent, as this does not account for the correlation of the magnetic field with, e.g. the velocity field, which can modify the impact of the Zeeman effect.
In this paper, we do not consider spectral line profiles in polarised light. The line weakening discussed here does also affect the other Stokes components of the spectral lines. Moreover, a strong line-of-sight velocity variation in the magnetised surface components (as we have found it at least for the F3V star) will also affect the Stokes-V signal and reduce the resolution of ZDI (which makes use of the line-of-sight velocity to obtain information on the spatial distribution of the magnetic flux).
Great progress has been made in the detection and measurement of stellar magnetic fields in recent years. To improve the methods it will be important to include the various effects of the magnetic field on the stellar atmospheres resulting from its 3D structure.
Online material
Appendix A: Additional figures
In Fig. 7 in Sect. 3.2, the magnetic limb brightening is given in the Johnson passbands UX, B, V, R, and I for the G2V star. Figure A.1 shows the limb brightening for the F3V and M0V simulations. The magnetic limb brightening is largest for the F3V star and becomes smaller towards lower effective temperatures as the faculae become less bright and less frequent (cf. Fig. 4).
In Fig. 13 in Sect. 4.3, disc-integrated profiles of the Fe i line at 617.3 nm are given for the G2V simulations without magnetic field (grey curves) and with B0 = 500 G (blue and red curves) where the magnetic field has been ignored for the spectral line synthesis for the red curves in order to disentangle the effect of the modified atmospheric structure from that of the Zeeman effect. Here, we give analogous plots for further simulations for the same spectral line (Fig. A.2) and for the Ti i line at 2223 nm (Fig. A.3).
As Fig. A.2 illustrates, the Fe i line is significantly affected by line weakening in the F3V star. Similar to the G2V-star case, the line is shifted to the red (in particular its wings) by the modified convective flows. The Zeeman effect has
a relatively small impact on the spectral line profile. In the K stars, the thermodynamic modifications seem less important than the Zeeman effect without rotation (left panels). In the rotating case (right panel), both effects are of similar magnitude. As they are of opposite sign, the apparent broadening of the line by the Zeeman effect is reduced by the modifications in the atmosphere structure. In the M stars (here, only the M0V is shown), the impact of the modified thermodynamics and flows is very small. For these stars, systematic errors in Stokes-I measurements of the magnetic field caused by differences in atmospheric structure between magnetised and unmagnetised regions will probably be the small.
Figure A.3 shows the same plots as Fig. A.2 but for the Ti i line and only for the K- and M-type stars. Although the line weakening is stronger for this line in the K-type stars (cf. Fig. 8), possibly leading to an underestimation of the unsigned average field from Stokes-I measurements, the general detection of magnetic field is probably more feasible in this line as the broadening due to the Zeeman effect is larger and leads to extended line wings. The line profiles from the M-star simulations are almost unaffected by the modifications of the thermodynamical atmosphere structure.
Acknowledgments
The authors acknowledge research funding by the Deutsche Forschungsgemeinschaft (DFG) under the grant SFB 963/1, project A16. A.R. has received research funding from the DFG under DFG 1664/9-2.
References
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Baliunas, S. L., Donahue, R. A., Soon, W. H., et al. 1995, ApJ, 438, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Basri, G., Valenti, J. A., & Marcy, G. W. 1990, ApJ, 360, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Beeck, B., Cameron, R. H., Reiners, A., & Schüssler, M. 2013a, A&A, 558, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beeck, B., Cameron, R. H., Reiners, A., & Schüssler, M. 2013b, A&A, 558, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beeck, B., Schüssler, M., Cameron, R. H., & Reiners, A. 2015, A&A, 581, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bessell, M. S. 1990, PASP, 102, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, P. 2010, Liv. Rev. Sol. Phys., 7, 3 [Google Scholar]
- Donati, J.-F. 2011, in IAU Symp. 271, eds. N. H. Brummell, A. S. Brun, M. S. Miesch, & Y. Ponty, 23 [Google Scholar]
- Frutiger, C. 2000, Diss. ETH, 13896 [Google Scholar]
- Frutiger, C., Solanki, S. K., Fligge, M., & Bruls, J. H. M. J. 2000, A&A, 358, 1109 [NASA ADS] [Google Scholar]
- Jeffers, S. V., Barnes, J. R., Jones, H., & Pinfield, D. 2013, in EPJ Web Conf., 47, 9002 [Google Scholar]
- Johnson, H. L., & Morgan, W. W. 1951, ApJ, 114, 522 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, C. U., Schüssler, M., Vögler, A., & Zakharov, V. 2004, ApJ, 607, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. 1993, ATLAS9 Stellar Atmosphere Programs and 2 km s-1 grid. Kurucz CD-ROM No. 13, Cambridge, Mass.: Smithsonian Astrophysical Observatory [Google Scholar]
- Morin, J., Donati, J.-F., Petit, P., et al. 2010, MNRAS, 407, 2269 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Reiners, A. 2012, Liv. Rev. Sol. Phys., 9, 1 [Google Scholar]
- Reiners, A., Schüssler, M., & Passegger, V. M. 2014, ApJ, 794, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Robinson, Jr., R. D. 1980, ApJ, 239, 961 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, F. J. 1994, in The Equation of State in Astrophysics, eds. G. Chabrier & E. Schatzman, IAU Colloq, 147, 16 [Google Scholar]
- Rogers, F. J., Swenson, F. J., & Iglesias, C. A. 1996, ApJ, 456, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Rosén, L., & Kochukhov, O. 2012, A&A, 548, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saar, S. H., & Solanki, S. K. 1992, in Cool Stars, Stellar Systems, and the Sun, eds. M. S. Giampapa & J. A. Bookbinder, A&A Conf. Ser., 26, 259 [Google Scholar]
- Shulyak, D., Reiners, A., Seemann, U., Kochukhov, O., & Piskunov, N. 2014, A&A, 563, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steiner, O., Salhab, R., Freytag, B., et al. 2014, PASJ, 66, 5 [Google Scholar]
- Vögler, A. 2003, Ph.D. Thesis, Georg-August-Universität Göttingen [Google Scholar]
- Vögler, A., Shelyag, S., Schüssler, M., et al. 2005, A&A, 429, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Vertically emerging bolometric intensity of a snapshot of the 500 G runs of the G2V (left) and M2V (right) simulations. The grey scale saturates at ± 2.5 standard deviations from the mean intensity. Intensity maps of further simulations are given in Paper I (Fig. 2) and Paper III (Fig. 1). |
| In the text | |
 |
Fig. 2 Intensity histograms of the G2V (left panels) and M2V (right panels) simulations. In both representations (upper panels: linear; lower panels: logarithmic), the histogram bins are linearly equidistant with a bin size of 0.01. |
| In the text | |
 |
Fig. 3 Relation between the magnetic field strength B(τR = 1) at the optical surface and the vertical bolometric intensity Ibol(μ = 1) normalised with its mean value. The field is binned in steps of 200 G. Error bars give the 1σ scatter within the bins. For bins with fewer than 1000 pixels (~0.06% of the total area considered), the symbol size is scaled with the logarithm of the number of pixels. |
| In the text | |
 |
Fig. 4 Continuum intensity in a passband between 400 and 410 nm of the six simulations with B0 = 500 G viewed at an angle of 60° with respect to the vertical (i.e. μ = 0.5). |
| In the text | |
 |
Fig. 5 Limb darkening for the G2V (left) and M2V (right) simulations without magnetic field (diamonds and dotted curves) and with B0 = 500 G (squares and solid curves) in narrow passbands near 400, 600, 800, and 2000 nm. The temporal scatter is considerably smaller than the symbol size. |
| In the text | |
 |
Fig. 6 Centre-to-limb variation of the rms intensity contrast for the G2V (left) and M2V (right) simulations without magnetic field (diamonds and dotted curves) and with B0 = 500 G (squares and solid curves) in narrow passbands near 400, 600, 800, and 2000 nm. The temporal scatter is considerably smaller than the symbol size. We note the logarithmic scale of the ordinates. |
| In the text | |
 |
Fig. 7 Limb darkening in the Johnson UX, B, V, R, and I passband filters (Johnson & Morgan 1951; Bessell 1990) in the G2V star. Analogous plots for the F3V and the M0V star are given in Fig. A.1. Left panel: limb darkening of the non-magnetic (hydro.) and 500 G runs. Right panel: relative difference between both runs. |
| In the text | |
 |
Fig. 8 Local vertical spectral line profiles for the K0V simulation with B0 = 500 G. Left panel: intensity image with four positions marked. Right panels: local profiles of the Fe i line at 617.3 nm (top) and the Ti i line at 2223 nm (bottom) at (μ = 1); the four different colours correspond to the four points marked in the left panel. |
| In the text | |
 |
Fig. 9 Decomposition of four line profiles (at μ = 1) into differently magnetised components. The black curve shows the average line profile, while the coloured curves show the line averaged over areas where B(τR = 1) is in the specified ranges. Each line is normalised to its own continuum. The numbers in parentheses give the weight of the components in the composite spectrum (i.e. average continuum flux times area fraction). |
| In the text | |
 |
Fig. 10 Centre-to-limb variation of the equivalent width, FWHM, and the effective Doppler shifts of the line core and wings (from left to right) of the Fe i line at 617.3 nm in all four simulation runs of the F3V star. The colour code is the same for all panels, see legend in the left panel. |
| In the text | |
 |
Fig. 11 Difference of equivalent width, FWHM, line core shift, and line wing shift (from left to right) between simulations with B0 = 500 G and the respective non-magnetic simulations for the three spectral lines as a function of μ. |
| In the text | |
 |
Fig. 12 Doppler shift of the line profile cores (solid curves) and wings (dashed curves) of the three spectral lines in the F3V simulations as function of υrotsini. In all cases, i = 60° and α = 0.2 was assumed. |
| In the text | |
 |
Fig. 13 Disc-integrated profiles of the Fe i line at 617.3 nm without rotation (left) and with υrot sini = 7.5 km s-1 (differential, α = 0.2, i = 60°; right) for G2V simulations. The grey line represents the profile of the non-magnetic run (hydro.), the blue curve is the profile of the 500 G run, the red curve is calculated using the thermodynamic structure of the 500 G run but assuming B ≡ 0 G for the line calculation (see text for further explanation). Dashed curves give the bisectors of the profiles with λ−λc values magnified by a factor of 5 for clarity. We note the different scales of ordinate and abscissa. |
| In the text | |
 |
Fig. A.1 Same as Fig. 7 but for the F3V and the M0V star. |
| In the text | |
 |
Fig. A.2 Same as Fig. 13, but for the F3V, K0V, K5V and M0V simulations. |
| In the text | |
 |
Fig. A.3 Same as Fig. A.2, but for the Ti i line at 2223 nm and for the K- and M-star simulations. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


