| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A78 | |
| Number of page(s) | 6 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201525621 | |
| Published online | 07 September 2015 | |
Coexisting fast and slow propagating waves of the extreme-UV intensity in solar coronal plasma structures⋆
1 Key Laboratory of Solar Activity, National Astronomical Observatories, Chinese Academy of Sciences, 100012 Beijing, PR China
e-mail: yuzong@nao.cas.cn; zjun@nao.cas.cn; wangjx@nao.cas.cn
2 Physics Department, University of Warwick, Coventry CV4 7AL, UK
e-mail: V.Nakariakov@warwick.ac.uk
3 Central Astronomical Observatory of the Russian Academy of Sciences at Pulkovo, 196140 St Petersburg, Russia
Received: 7 January 2015
Accepted: 12 July 2015
Context. From 06:15 UT to 08:15 UT on 2011 June 2, a toroidal filament located at the joint of two active regions, 11226 and 11227, appeared to perform two eruptions. During this phenomenon, fast and slow magnetoacoustic waves were detected to propagate simultaneously along a funnel coronal loop system of AR 11227.
Aims. We aim to understand the relationship between fast and slow magnetoacoustic waves during their propagations and measure their properties, such as the propagating speed, path, amplitude, and period observed in the extreme ultraviolet (EUV) wavebands.
Methods. We analyse time sequences of EUV images acquired by the Atmospheric Imaging Assembly onboard the Solar Dynamics Observatory. By creating time-distance maps along selected directions, we measure the speeds and localisation of EUV intensity waves in different EUV wavebands. We determine the periods of the waves with wavelet analysis.
Results. The fast and slow magnetoacoustic waves, apparently propagating along the same path, are found to have different properties. Their apparent propagation speeds, travel distances, and periods are about 900 km s-1 and 100 km s-1, 145 Mm and 36 Mm, and 2 min and 3 min, respectively.
Key words: Sun: corona / Sun: oscillations / methods: observational
The movie is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
As basic physical phenomena, waves of any kind carry important information about the physical systems supporting them, and hence provide a foundation for spectroscopic or seismological diagnostics techniques. Uchida (1970), Zajtsev & Stepanov (1975), and Roberts et al. (1984) proposed the technique of magnetohydrodynamic (MHD) coronal seismology, based upon the study of the plasma of the solar corona by MHD waves and oscillations. Observational discoveries of several kinds of MHD waves and oscillations in the corona, provided by the commissioning of high-resolution extreme-UV (EUV) imagers, led to the rapid development of this diagnostics technique (see De Moortel & Nakariakov 2012; Liu & Ofman 2014, for recent reviews) and stimulated further progress in the observational study.
Both standing and propagating MHD waves are confidently detected in the corona, and identified in terms of MHD wave theory. Propagating waves of emission intensity perturbations are clearly distinguished as slow waves (e.g. Ofman et al. 1997; DeForest & Gurman 1998; De Moortel et al. 2000; Ofman & Wang 2008; Krishna Prasad et al. 2012b, 2014), at the speeds lower than a few hundred km s-1, and fast waves (e.g. Williams et al. 2002; Liu et al. 2011, 2012; Shen & Liu 2012; Yuan et al. 2013), at the speeds exceeding several hundred km s-1. In particular, slow waves are routinely detected in the 1 MK plasmas of magnetic fans and polar plumes. Typically, these perturbations propagate at an apparent sub-sonic speed, e.g. lower than 150 km s-1 for the 171 Å waveband. The departure of the apparent speed from the sound speed value is attributed to projection effects. Usually, the phase speed remains constant with the distance along the wave path (e.g. Yuan & Nakariakov 2012). Su (2014) showed that the periods are nearly equal in the observational channels and correspond to different temperatures, while the wavelengths increase with temperature. In the majority of analysed cases the speed depends on the temperature of the plasma (e.g. Robbrecht et al. 2001; Marsh et al. 2009; Krishna Prasad et al. 2011, 2012a; Kiddie et al. 2012; Gupta 2014). The slowly propagating disturbances of the coronal EUV emission are observed with very stable periods, ranging from a few minutes to several tens of minutes. The direction of the slow wave propagation is usually associated with the direction of the magnetic field. Slow wave amplitudes are observed to decay rapidly with the distance from their source. The waves are usually detected at the heights below several tens of Mm, but are also found at much larger heights (e.g. Ofman et al. 1997). Observational properties of coronal slow waves are comprehensively reviewed in De Moortel (2006, 2009).
Fast waves, seen as rapidly propagating disturbances of the EUV or white light emission intensity, are detected less frequently. The waves appear in the form of quasi-periodic wave trains (Yuan et al. 2013). The characteristic periods are about one minute or shorter. The speed of the propagating fast EUV disturbances is typically over several hundred km s-1, and varies with height (Yuan et al. 2013). The waves are continuously detected at the heights from the bottom of the corona up to 300 Mm, which is much higher than the slow EUV disturbances. The fast EUV disturbances are observed to propagate along the apparent direction of the magnetic field, similar to slow waves.
The observational properties of coronal slow waves are well consistent with theoretical models for slow magnetoacoustic waves (Ofman et al. 2000; Nakariakov et al. 2000), which account for the effects of stratification, dissipation, and weak non-linearity. Rapid damping of these waves is associated with the effect of thermal conduction along the magnetic field (De Moortel & Hood 2004). The monochromaticity was demonstrated to be caused by thermal structure of the lower regions of the atmosphere (Botha et al. 2011), see also (Suematsu et al. 1982). The recently established blue-red asymmetry in the spectral signatures of slowly propagating EUV intensity perturbations (e.g. De Pontieu & McIntosh 2010) was shown to be consistent with the in-phase behaviour of velocity and density perturbations in upwardly propagating slow magnetoacoustic waves (Verwichte et al. 2010). Recent theoretical efforts address the forward-modelling to construct observational signatures of the waves (see e.g. De Moortel et al. 2015).
Modelling of fast magnetoacoustic waves requires accounting for the non-uniformity of the plasma across the magnetic field, as well as the gravitational stratification, and hence needs to be at least 2D. Indeed, fast waves can propagate along the magnetic field only because of the wave-guiding effect caused by refraction or reflection at the field-aligned non-uniformity (Roberts et al. 1983; Van Doorsselaere et al. 2008). Numerical simulations demonstrated the consistence of observed fast wave dynamics with MHD wave theory (Liu et al. 2012). A more detailed study of dispersive formation of fast wave trains in plasma funnels strengthened this interpretation (Pascoe et al. 2013). Recent studies showed convincing consistence of numerical and observational results (Nisticò et al. 2014).
Slow and fast magnetoacoustic waves are both natural modes of the medium, and hence in the simplest case of linear propagation, do not interact with each other, excluding the case of β ≈ 1. In other words, these waves can simultaneously propagate along the same path in the corona without affecting each other, but could be coupled in the vicinity of the footpoint of the waveguiding plasma non-uniformity (see, e.g. Terradas et al. 2011). However, so far the coexistence of slow and fast waves in the same coronal structure has not been established.
The Atmosphere Imaging Assembly (AIA; Lemen et al. 2012) onboard the Solar Dynamics Observatory (SDO; Pesnell 2012) with superior temporal and spatial resolution and the signal-to-noise ratio provides us with a prime opportunity to study waves of EUV intensity, propagating along coronal plasma structures. In this paper, we report the first simultaneous observations of fast and slow magnetoacoustic waves propagating along the same path. In Sects. 2 and 3 we introduce the used data and analysis methods, and describe the main results. Section 4 summarises our conclusions and gives their discussion.
 |
Fig. 1 Panel a): Hα image made at 06:26 UT on 2011 June 2 by Kanzelhöhe Solar Observatory. A toroidal filament marked by “F” located at the joint of the ARs 11226 and 11227 (1″ ≈ 725 km) The contours are the line-of-sight magnetic flux density of + 300, +100 G (white) and −300, −100 G (black) measured with SDO/HMI; panel b): image made with the use of two SDO/AIA EUV wavebands, 171 Å and 304 Å, respectively. Slow and fast waves of EUV intensity are detected along the funnel loop system indicated by the arrow in panel b). The solid box in panels a) and b) shows the region zoomed in panels c) and d). The dashed box denotes the region shown in Fig. 6a. Panels c) and d) are SDO/AIA EUV 304 Å images, showing the double eruption processes of the toroidal filament. Panel e): solar X-ray flux recorded by GOES 15 in 1.0–8.0 Å (red) and 0.5−4.0 Å (blue). Two pink regions mark the start and end time of two flares, i.e. C1.4 and C3.7 in ARs 11226, and 11227, respectively. |
 |
Fig. 2 Panels a)–c) are running difference images based on the observations in EUV 193 Å by SDO/AIA. The arrows in panels a) and c) mark the wavefront of the EUV waves. The red line OP is the slit for making the time-distance images of panel e). Panel d) is a running difference image made with LASCO C2. The slopes of dashed lines, green lines, and red lines give the propagating speeds of the expanding erupted filament, EUV waves, and reflected EUV waves during the toroidal filament eruptions. |
 |
Fig. 3 Panels a)–c) are SDO/AIA EUV 171 Å original and two running difference images. Panel d) is a time-distance image showing the brightness changes along the red dot-dashed curve AB marked in panels a)–c). The section of AB located between the small blue block and triangle denotes the propagating range of the fast waves. The red curve shows the time variation of EUV brightness difference at the distance of 100 Mm from point A. Panel e) is the time-distance map along the fan-like region “CD” positioned along the funnel loop system in panel a) and Fig. 1b. The red and blue curves show the time variations of EUV brightness difference at the distances of 1 Mm and 75 Mm from point C, respectively. The short red and blue dashed lines denote the diagonal structures corresponding to the slow and fast mode waves, respectively. In panel e) the signals are shown in relative brightness (RB). |
2. Data and analysis
On 2011 June 2, there were two conjoint active regions (ARs) 11226 (S22E02) and 11227 (S19E14) in the southern visible hemisphere (see Fig. 1a). A toroidal filament (marked by “F” in the figure) was located at the joint of the two β-type ARs. From 06:15 UT to 08:15 UT, it erupted two times (see Figs. 1c and d) in association with two C-class flares, i.e., C1.4 and C3.7, respectively, which is recorded by the GOES 15 satellite in the soft X-ray waveband (see Fig. 1e). During the first filament eruption, the filament was first ignited from its northeast, and then its most eastern part fired up. In contrast, the second eruption was more violent. Shown in Fig. 1d, all parts of the toroidal filament erupted. At 07:24 UT and 08:12 UT, the Large Angle and Spectrometric Coronagraph-2 (LASCO C2) onboard the Solar and Heliospheric Observatory observed the appearances of a partial coronal mass ejection (CME) and a halo CME (see Fig. 2d). The EUV waves related to these two CMEs are clearly displayed by the running difference images in 193 Å (see Figs. 2a and c). Along with the development of the EUV waves, most of coronal loops of these two neighbouring ARs were disturbed. In this study, we focus on a funnel loop system of AR 11227 labelled “Funnel” in Fig. 1b, located east of the toroidal filament. This coronal structure shows interesting wave dynamics. The data for the analysis are the EUV 171 Å and 193 Å observations acquired by SDO/AIA with the time cadence and spatial resolution of 12 s and 1.̋2 (1″ ≈ 725 km), respectively. A Solar Software (SSW) standard routine (aia_prep.pro) was used to process the raw data from Level 1.0 to Level 1.5. Then another SSW routine, drot_map.pro, was used to de-rotate and co-align different SDO/AIA images. Then, a time-distance map was made to measure parameters of the waves, such as the speed, period, and location along the funnel.
3. Simultaneously propagating fast and slow waves
Figure 2e shows a time-distance map made in the 193 Å channel of SDO/AIA along the curved slice “OP” (see Fig. 2b) during the time from 06:15 UT to 08:15 UT. The map demonstrates the developments of two eruptions, seen as two distinct diagonal features propagating upwards at about 06:30 UT and 07:40 UT. The eruptions were located in the lower corona, up to the distances about 145 Mm along the path OP. The speeds of the upward motion were 239 ± 9 km s-1 and 255±38 km s-1, respectively. Global EUV waves were excited simultaneously with the eruptions. Their speeds along the slit OP were 305±8 km s-1 and 560±42 km s-1, respectively. Both these EUV waves reached the same position at about 250 Mm along the path OP, where they experienced reflection from an AR in the northern hemisphere. Interestingly, the apparent speeds of the reflected waves were 118±39 km s-1 and 120±16 km s-1, which are much lower than those of the original EUV waves.
At about 180 Mm on the east from the origins of the low-coronal eruptions and the epicentres of the EUV waves, there were also detected quasi-periodic wave motions propagating upwards along the funnel loop system. The wave motions are clearly exhibited by the movie made by the running difference images in the 171 Å and 193 Å wavebands of AIA. We visualise this phenomenon by making time-distance maps for slits situated along and across the funnel. Positioning of the slits is shown in Figs. 3a−c as “CD” and “AB”, respectively. Figure 3d shows the time-distance map made for the slit “AB” directed across the apparent direction of the magnetic field. The red curve in Fig. 3d gives the EUV brightness variation at the position of about 100 Mm off the point “A” along the perpendicular slit “AB”. The fan-shaped slit “CD” , marked by the semi-transparent structure (Fig. 3a), coincides with a pie-piece sector of the funnel structure in Fig. 1b. The wave evolution with the distance from the source is clearly shown in the time-distance map along “CD”. The signal was averaged in the azimuthal direction, i.e. for the pixels that are at the same distance from the origin point C. A similar approach was employed, e.g. by De Moortel et al. (2000, 2002) in the analysis of coronal slow magnetoacoustic waves.
The quasi-periodic wave patterns of the variations of 171 Å emission intensity, shown in Fig. 3, belong to two distinct types, fast and slow. The fast compressive wave motions appear as a series of well-pronounced bright and dark strips occurring in turn in the running difference images (see Figs. 3b and c). The red dot-dashed line “AB” in Figs. 3a−c, highlights the shape of the consecutive wave fronts of the fast wave disturbance across the direction of the wave propagation. The structure of the fast perturbation across the direction of the wave propagation is highly non-uniform. The propagating fast wave motions occur as two consecutive wave trains occurring in the time intervals 06:30–06:40 UT and 07:35–07:55 UT; see the signal taken along “CD” at 100 Mm from the point C. Besides the strong signals in the fast wave trains, there is also a relatively weak signal seen at about 07:25–07:35 UT (shown by the pair of white arrows in Fig. 3e). The fast waves are detected up to the distance of 145 Mm from the point C. The apparent phase speeds of the two main wave trains are estimated as 776±167 km s-1 and 978±133 km s-1, respectively. The errors are estimated as the standard deviation of the ten independent measurements. The speed remains constant (within the error bars) at all distances along the observational slit. The times of the two main wave trains coincide with the times of the low-coronal eruptions and global EUV waves (cf. Figs. 2e and 3e).
We found in our wavelet analysis that the main power of the fast waves is in the vicinity of the 2-min period; see Figs. 4a, b. The amplitude of the fast perturbations is about 20% relative to the background in 171 Å.
 |
Fig. 4 Wavelet spectra of the variations of EUV intensity at two different distances along the slit CD (see Fig. 3a). Panels a) and c) show the wavelet spectra of the signals at the distances of about 75 Mm and 1 Mm, respectively. Panels b) and d) show the corresponding global wavelet spectra (solid curves), and the 95% global confidence level (dashed curves). |
 |
Fig. 5 Time-distance maps along the fan-like region “CD” (see Fig. 3a), based on running difference images at 193 Å, 211 Å, and 335 Å, respectively. |
 |
Fig. 6 Panels a) and b) are 304Å and 171Å images taken by SDO/AIA at 07:24 UT on 2011 June 2. In panel b), the red dotted lines indicate the propagation range of the fast mode waves along the funnel. L1 and L2, denoted by the green and light blue dotted lines, respectively, are the loop systems overlapping before or after the funnel in the image. Panel c) is a time-distance map showing the intensity change along slice MN shown in blue in panel b). The blue circles in both panels b) and c) are located at the same spatial position of slice MN. Digits 1 and 2 mark the start times of the C1.4 and C3.7 flares in ARs 11226 and 11227, respectively. The temporal evolution of the 304Å and 171Å emission is illustrated by a running difference movie available online. The field-of-view of the movie is the same as that in panels a) and b). The time delay in the 304Å and 171Å difference movie are 1 min and 12 s (based on their available maximum temporal resolution), respectively. |
In addition to the fast wave motions, near the footpoint of the funnel loop system, there are slow compressive wave motions along the same path. They are clearly seen in the bottom part of the time-distance map, Fig. 3e; see also the signal taken at about 1 Mm from point C. In contrast with the fast waves, the slow waves are persistent over the whole two-hour time interval analysed. Thus, the slow waves do not show the apparent correlation with the events of lower coronal eruptions and global EUV waves. The brightness variation relative to the background is of about 7% in 171 Å, which is lower than that in the fast waves. The phase speed of the slow waves is estimated as 79±10 km s-1, about ten times lower than that of the fast waves. The wavelet spectral power of the slow waves (Figs. 4c, d) concentrates in the vicinity of the 3-min period. The slow waves are seen to propagate up to about 40 Mm before experiencing an apparent decay.
The coexisting fast and slow waves in the funnel loop system are also observed in the 193 Å, 211 Å, and 335 Å wavebands (see Fig. 5). The first fast wave train is detected at 193 Å, while not at 211 Å and 335 Å. The second fast wave train is well seen at 193 Å, 211 Å, and 335 Å. The phase speeds of fast waves are of the same order of magnitude, of about 1000 km s-1 within the error bars in all observational channels. Slow waves are also clearly seen at 193 Å. Their phase speeds measured in this channel are systematically higher than measured at 171 Å. With the increase in the temperature associated with the AIA waveband, the relative amplitudes of both fast and slow waves become weaker.
4. Discussion and conclusions
Analysis of EUV emission of the solar corona demonstrated the simultaneous presence of EUV emission disturbances propagating at fast and slow speeds. There is a possibility that the fast and slow waves spatially coincide in observations because of the projection effect, while actually the fast wave train propagates either in front or behind the slow waves. However, theoretical modelling shows that both kinds of waves propagate along the magnetic field. The slow waves are intrinsically almost field aligned, while fast waves propagate along the funnel axis because of refraction. In particular, Fig. 6 of Nisticò et al. (2014) shows that the most significant perturbation of the density in the fast wave is guided by the enhancement of the plasma density along the magnetic field (the region shown by the red box in that figure). There is also a possibility that the fast wave train propagates across the field because of refraction (Pascoe et al. 2013). However, in the observed geometry, it would correspond to the situation when the fast wave train refracts in vertical direction perpendicular to the funnel, i.e. along the line of sight (LoS). In this case, the fast wave train would have an infinite (or very high) projected phase speed in the plane of the sky, which is not consistent with our findings. Moreover, it is not clear why in this case there is no fast wave train guided by the funnel itself, while those wave trains are revealed by all simulations of this phenomenon.
Another option is that the fast wave train is guided by another funnel, which overlaps in the images with the funnel shown in Fig. 3a. Figure 6a shows that there are two funnel-like loop systems L1 and L2, which could overlap with the funnel that guides the slow waves. However, only a small section of L1 overlaps with the funnel, near its footpoint. Therefore, it is not clear how the fast waves guided along L1 would appear in the higher section of the funnel. Also, the fast waves guided by L1 would be seen propagating across the funnel in the images. Hence, theses waves should be detected in slice AB, but Fig. 3b does not show such propagating patterns. Likewise, system L2 does not show any propagating patterns either. Figure 6b shows the dynamics of system L2. It is evident that L2 displaces only slightly during the first eruption and changes tremendously during the second eruption. However, the two fast wave trains seen in Fig. 3c in the funnel do not show an obviously difference between each other in either the propagating directions or in relative intensity. Moreover, during the time interval 07:40 UT to 07:52 UT, system L2 is displaced from the funnel, and hence cannot be responsible for the fast wave trains. Thus, it is not likely that the fast wave trains arrived at the funnel along L2.
There is also a hypothetical possibility that the fast wave trains propagate along the field in another, invisible funnel situated higher or lower, i.e. the slow-waveguiding funnel. This type of assumed, fast-waveguiding funnel should be almost totally overlapping with the slow-waveguiding funnel in the plane of the sky. Consequently, both the slow-waveguiding funnel and the fast-waveguiding funnel should begin at almost the same origin. In this case, it is not clear why the waves excited very close to each other would choose to propagate along different paths of similar physical properties. Thus, we are inclined to disregard this interpretation too.
Thus, it is quite likely that both the slow and fast waves we observed propagate along the same path, however, this conclusion could be rigorously confirmed only if stereoscopic high-cadence observations were available.
The disturbances of both kinds propagate along the apparent direction of the magnetic field, highlighted by a fan-like coronal plasma structure. The projected speeds are about 900 km s-1, and 80 km s-1, respectively. Relative amplitudes of the disturbance during the fast and slow mode wave propagations are about 20% and 7% percents, respectively. Average periods of the disturbances of both kinds, determined by the global wavelet transform, are about 3 min. The fast waves are seen to appear in the form of two distinct wave trains that coincide in time with the eruption of filaments.
The observed properties of the waves are consistent with the properties of fast and slow waves of the EUV intensity disturbances previously detected in the corona. In particular, the slow waves are interpreted as slow magnetoacoustic waves (see Nakariakov et al. 2000; De Moortel 2009; Su et al. 2013; Sych et al. 2009). A possible cause of these waves is the leakage of chromospheric oscillations (see e.g. Suematsu et al. 1982; Botha et al. 2011). In the low-β plasma of the solar corona, slow magnetoacoustic waves propagate along the magnetic field. Usually, propagating slow waves are situated at low heights, and are not associated with any energy releases, such as flares or eruptions. All these features are consistent with our findings in this study.
In contrast with the well-understood slow disturbances, recently discovered fast disturbances (Liu et al. 2011) are shown to be fast magnetoacoustic waves excited by impulsive energy releases (Ofman et al. 2011). The wave-train nature of the fast waves was established in Yuan et al. (2013), and was demonstrated to be consistent with dispersive evolution of broadband fast magnetoacoustic pulses guided by a field-aligned plasma non-uniformity (Roberts et al. 1984; Nakariakov et al. 2004; Pascoe et al. 2013; Nisticò et al. 2014). Locally the fast modes of the non-uniformity are oblique, but collectively they propagate along the field because of refraction or reflection. The visual inspection of the fast waves signals in Fig. 3e shows that in the trains the periods slightly decrease. This behaviour is consistent with theoretical modelling (Nakariakov et al. 2004). The apparent independence of the speed of the fast EUV disturbance on the temperature also supports this interpretation. Thus we conclude that the observed fast wave trains are of fast magnetoacoustic nature.
The observed phenomenology can be interpreted as the simultaneous excitation of both kinds of magnetoacoustic waves, fast and slow, guided by a field-aligned plasma non-uniformity. To the best of our knowledge, it is the first observational detection of this phenomenon in the imaging data. Following Van Doorsselaere et al. (2011a), we can use the combination of fast and slow speeds for estimating the plasma β. Assuming that β is small, we find that the slow wave propagates at the sound speed, Cs. Fast wave trains formed by a plasma waveguide, propagate at the speed close to the local Alfvén speed CA(Pascoe et al. 2013). Thus, using the measurements of the speeds of the fast and slow disturbances, we find that Cs ≈ 80 km s-1/ cos α, where α is the angle between the wave vector and the LoS. Likewise, the Alfvén speed is CA ≈ 900 km s-1/ cos α. Using the definition of the plasma-β as the ratio of the gas and magnetic pressures, we can express it through the characteristic speeds, 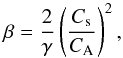 (1)where γ is the adiabatic index. Thus, we obtain the estimation γβ = 2(Cs/CA)2 ≈ 0.015. In the solar corona, the value of γ is usually found in the range from 1 to 5/3, for the isothermal and adiabatic cases, respectively. In particular, seismological estimations performed by Van Doorsselaere et al. (2011b) yielded γ ≈ 1.1. Thus, we obtain that β ranges from 0.009 to 0.015. In addition, our results provide further confirmation that fast compressive wave trains detected in the corona propagate along the magnetic field and are formed by dispersion caused by the plasma non-uniformity. In the case of whether the fast and slow waves propagated along two different paths that overlap along the LoS, the above estimations should be modified: the estimated plasma β would correspond to the average value between both waveguiding structures.
(1)where γ is the adiabatic index. Thus, we obtain the estimation γβ = 2(Cs/CA)2 ≈ 0.015. In the solar corona, the value of γ is usually found in the range from 1 to 5/3, for the isothermal and adiabatic cases, respectively. In particular, seismological estimations performed by Van Doorsselaere et al. (2011b) yielded γ ≈ 1.1. Thus, we obtain that β ranges from 0.009 to 0.015. In addition, our results provide further confirmation that fast compressive wave trains detected in the corona propagate along the magnetic field and are formed by dispersion caused by the plasma non-uniformity. In the case of whether the fast and slow waves propagated along two different paths that overlap along the LoS, the above estimations should be modified: the estimated plasma β would correspond to the average value between both waveguiding structures.
Online material
Movie of Fig. 6 Access here
Acknowledgments
SDO data and images are courtesy of NASA/SDO and the AIA and HMI science teams. The discussion with Dr. Wei Liu, Dr. Jiangtao Su, Dr. Hui Zhao, Dr. Leping Li and Dr. Nisticò Giuseppe is very appreciated. The work is supported by the National Natural Science Funds for Distinguished Young Scholar (11025315), the National Basic Research Program of China under grant 2011CB811403 and Y07024A900, National Natural Science Foundations of China (11533008, 11373004, 11322329, 11303050, 11203037, 11221063, and 11303049), the Young Researcher Grant of National Astronomical Observatories and the CAS Project KJCX2-EW-T07; the Marie Curie PIRSES-GA-2011-295272 “RadioSun project”, the European Research Council under the SeismoSun Research Project No. 321141, and the STFC consolidated grant ST/L000733/1.
References
- Botha, G. J. J., Arber, T. D., Nakariakov, V. M., & Zhugzhda, Y. D. 2011, ApJ, 728, 84 [NASA ADS] [CrossRef] [Google Scholar]
- De Moortel, I. 2006, Roy. Soc. London Phil. Trans. Ser. A, 364, 461 [Google Scholar]
- De Moortel, I. 2009, Space Sci. Rev., 149, 65 [NASA ADS] [CrossRef] [Google Scholar]
- De Moortel, I., & Hood, A. W. 2004, A&A, 415, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Moortel, I., & Nakariakov, V. M. 2012, Roy. Soc. London Phil. Trans. Ser. A, 370, 3193 [Google Scholar]
- De Moortel, I., Ireland, J., & Walsh, R. W. 2000, A&A, 355, L23 [NASA ADS] [Google Scholar]
- De Moortel, I., Ireland, J., Walsh, R. W., & Hood, A. W. 2002, Sol. Phys., 209, 61 [NASA ADS] [CrossRef] [Google Scholar]
- De Moortel, I., Antolin, P., & Van Doorsselaere, T. 2015, Sol. Phys., 290, 399 [NASA ADS] [CrossRef] [Google Scholar]
- De Pontieu, B., & McIntosh, S. W. 2010, ApJ, 722, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- DeForest, C. E., & Gurman, J. B. 1998, ApJ, 501, L217 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, G. R. 2014, A&A, 568, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kiddie, G., De Moortel, I., Del Zanna, G., McIntosh, S. W., & Whittaker, I. 2012, Sol. Phys., 279, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Krishna Prasad, S., Banerjee, D., & Gupta, G. R. 2011, A&A, 528, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krishna Prasad, S., Banerjee, D., & Singh, J. 2012a, Sol. Phys., 281, 67 [NASA ADS] [Google Scholar]
- Krishna Prasad, S., Banerjee, D., Van Doorsselaere, T., & Singh, J. 2012b, A&A, 546, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krishna Prasad, S., Banerjee, D., & Van Doorsselaere, T. 2014, ApJ, 789, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., & Ofman, L. 2014, Sol. Phys., 289, 3233 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., Title, A. M., Zhao, J., et al. 2011, ApJ, 736, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., Ofman, L., Nitta, N. V., et al. 2012, ApJ, 753, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Marsh, M. S., Walsh, R. W., & Plunkett, S. 2009, ApJ, 697, 1674 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., Verwichte, E., Berghmans, D., & Robbrecht, E. 2000, A&A, 362, 1151 [NASA ADS] [Google Scholar]
- Nakariakov, V. M., Arber, T. D., Ault, C. E., et al. 2004, MNRAS, 349, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Nisticò, G., Pascoe, D. J., & Nakariakov, V. M. 2014, A&A, 569, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ofman, L., & Wang, T. J. 2008, A&A, 482, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ofman, L., Romoli, M., Poletto, G., Noci, G., & Kohl, J. L. 1997, ApJ, 491, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Ofman, L., Nakariakov, V. M., & Sehgal, N. 2000, ApJ, 533, 1071 [Google Scholar]
- Ofman, L., Liu, W., Title, A., & Aschwanden, M. 2011, ApJ, 740, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Pascoe, D. J., Nakariakov, V. M., & Kupriyanova, E. G. 2013, A&A, 560, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pesnell, W. D. 2012, Sol. Phys., 281, 507 [NASA ADS] [Google Scholar]
- Robbrecht, E., Verwichte, E., Berghmans, D., et al. 2001, A&A, 370, 591 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roberts, B., Edwin, P. M., & Benz, A. O. 1983, Nature, 305, 688 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, B., Edwin, P. M., & Benz, A. O. 1984, ApJ, 279, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., & Liu, Y. 2012, ApJ, 753, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Su, J. T. 2014, ApJ, 793, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Su, J. T., Liu, Y., Liu, S., et al. 2013, ApJ, 762, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Suematsu, Y., Shibata, K., Neshikawa, T., & Kitai, R. 1982, Sol. Phys., 75, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Sych, R., Nakariakov, V. M., Karlicky, M., & Anfinogentov, S. 2009, A&A, 505, 791 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Terradas, J., Andries, J., & Verwichte, E. 2011, A&A, 527, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Uchida, Y. 1970, PASJ, 22, 341 [NASA ADS] [Google Scholar]
- Van Doorsselaere, T., Brady, C. S., Verwichte, E., & Nakariakov, V. M. 2008, A&A, 491, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Doorsselaere, T., De Groof, A., Zender, J., Berghmans, D., & Goossens, M. 2011a, ApJ, 740, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Van Doorsselaere, T., Wardle, N., Del Zanna, G., et al. 2011b, ApJ, 727, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Verwichte, E., Marsh, M., Foullon, C., et al. 2010, ApJ, 724, L194 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, D. R., Mathioudakis, M., Gallagher, P. T., et al. 2002, MNRAS, 336, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, D., & Nakariakov, V. M. 2012, A&A, 543, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yuan, D., Shen, Y., Liu, Y., et al. 2013, A&A, 554, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zajtsev, V. V., & Stepanov, A. V. 1975, Issledovaniia Geomagnetizmu Aeronomii i Fizike Solntsa, 37, 11 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1 Panel a): Hα image made at 06:26 UT on 2011 June 2 by Kanzelhöhe Solar Observatory. A toroidal filament marked by “F” located at the joint of the ARs 11226 and 11227 (1″ ≈ 725 km) The contours are the line-of-sight magnetic flux density of + 300, +100 G (white) and −300, −100 G (black) measured with SDO/HMI; panel b): image made with the use of two SDO/AIA EUV wavebands, 171 Å and 304 Å, respectively. Slow and fast waves of EUV intensity are detected along the funnel loop system indicated by the arrow in panel b). The solid box in panels a) and b) shows the region zoomed in panels c) and d). The dashed box denotes the region shown in Fig. 6a. Panels c) and d) are SDO/AIA EUV 304 Å images, showing the double eruption processes of the toroidal filament. Panel e): solar X-ray flux recorded by GOES 15 in 1.0–8.0 Å (red) and 0.5−4.0 Å (blue). Two pink regions mark the start and end time of two flares, i.e. C1.4 and C3.7 in ARs 11226, and 11227, respectively. |
| In the text | |
 |
Fig. 2 Panels a)–c) are running difference images based on the observations in EUV 193 Å by SDO/AIA. The arrows in panels a) and c) mark the wavefront of the EUV waves. The red line OP is the slit for making the time-distance images of panel e). Panel d) is a running difference image made with LASCO C2. The slopes of dashed lines, green lines, and red lines give the propagating speeds of the expanding erupted filament, EUV waves, and reflected EUV waves during the toroidal filament eruptions. |
| In the text | |
 |
Fig. 3 Panels a)–c) are SDO/AIA EUV 171 Å original and two running difference images. Panel d) is a time-distance image showing the brightness changes along the red dot-dashed curve AB marked in panels a)–c). The section of AB located between the small blue block and triangle denotes the propagating range of the fast waves. The red curve shows the time variation of EUV brightness difference at the distance of 100 Mm from point A. Panel e) is the time-distance map along the fan-like region “CD” positioned along the funnel loop system in panel a) and Fig. 1b. The red and blue curves show the time variations of EUV brightness difference at the distances of 1 Mm and 75 Mm from point C, respectively. The short red and blue dashed lines denote the diagonal structures corresponding to the slow and fast mode waves, respectively. In panel e) the signals are shown in relative brightness (RB). |
| In the text | |
 |
Fig. 4 Wavelet spectra of the variations of EUV intensity at two different distances along the slit CD (see Fig. 3a). Panels a) and c) show the wavelet spectra of the signals at the distances of about 75 Mm and 1 Mm, respectively. Panels b) and d) show the corresponding global wavelet spectra (solid curves), and the 95% global confidence level (dashed curves). |
| In the text | |
 |
Fig. 5 Time-distance maps along the fan-like region “CD” (see Fig. 3a), based on running difference images at 193 Å, 211 Å, and 335 Å, respectively. |
| In the text | |
 |
Fig. 6 Panels a) and b) are 304Å and 171Å images taken by SDO/AIA at 07:24 UT on 2011 June 2. In panel b), the red dotted lines indicate the propagation range of the fast mode waves along the funnel. L1 and L2, denoted by the green and light blue dotted lines, respectively, are the loop systems overlapping before or after the funnel in the image. Panel c) is a time-distance map showing the intensity change along slice MN shown in blue in panel b). The blue circles in both panels b) and c) are located at the same spatial position of slice MN. Digits 1 and 2 mark the start times of the C1.4 and C3.7 flares in ARs 11226 and 11227, respectively. The temporal evolution of the 304Å and 171Å emission is illustrated by a running difference movie available online. The field-of-view of the movie is the same as that in panels a) and b). The time delay in the 304Å and 171Å difference movie are 1 min and 12 s (based on their available maximum temporal resolution), respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


