EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 581 (September 2015) A&A, 581 (2015) A69 Full HTML
Free Access
Issue
A&A
Volume 581, September 2015
Article Number A69
Number of page(s) 9
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/201425440
Published online 03 September 2015

© ESO, 2015

1. Introduction

LQ Hya (HD 82558, GL 355) is a young, chromospherically active BY Dra-type star with a spectral classification of K2V (Cutispoto 1991). BY Dra-type stars are typically K or M class with strong Ca ii H and K emission lines. LQ Hya is considered a young solar analogue, with an estimated mass of 0.8 ± 0.1 M⊙ and an age of 51.9 ± 17.5 Myr (Tetzlaff et al. 2011). It is a rapid rotator, with a rotation period ~1.6 days. It is located at a distance of about 18.3 pc.

Flare activity on LQ Hya has been studied by Covino et al. (2001), Montes et al. (1999), and Ambruster & Fekel (1990). These observations show that LQ Hya has a high level of chromospheric activity. LQ Hya is a single star, as evidenced by a constant radial velocity (Fekel et al. 1986b). Photometric variability was proposed by Eggen (1984), and later confirmed by Fekel et al. (1986a), where a variation in magnitude of 0.1 was measured along with a rotation period of .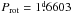

LQ Hya has slight, if any, observable surface differential rotation. The differential rotation rate k is defined to be ΔΩ/Ω0 where Ω0 is the angular rotation velocity at the equator and ΔΩ is the difference between the equatorial and polar region rotation. Estimates from photometry based on observed variations in the photometric period indicate a differential rotation coefficient of the order of k = 0.025 (You 2007), while estimates from Doppler imaging (DI) are even smaller, where k = 0.0057 (Kovári et al. 2004). An even smaller value for k of 0.002 was obtained from Zeeman Doppler imaging (ZDI) results (Donati et al. 2003a). For comparison, surface differential rotation in the Sun is k ≈ 0.2. With only weak differential rotation, the dynamo is expected to be of α2-type, or α2Ω-type where magnetic field generation is dominated by turbulent convective effects, and any contribution from the differential rotation is minor (Krause & Rädler 1980).

Possible activity cycle periods have been recovered from photometry by several groups ranging from 3.2 years (Messina & Guinan 2003) to up to 12.4 years (Oláh et al. 2009). The most commonly reported cyclicity is of 6–7 years (Jetsu 1993; Strassmeier et al. 1997; Cutispoto 1998b; Oláh et al. 2000; Alekseev 2003; Messina & Guinan 2003).

Jetsu (1993) found evidence of short-lived active longitudes. When two such active longitudes were present, they were found to be a phase of φ = 0.25 apart. Berdyugina et al. (2002) used 20 years of photometric data, and reported a persistent non-axisymmetric starspot distribution consistent with two alternating active longitudes with a phase difference of φ = 0.5. The timescale of this flip-flop phenomenon was claimed to be of the order of 5.2 yrs. Such results are consistent with observations of other rapid rotators, such as II Peg (Berdyugina & Tuominen 1998; Lindborg et al. 2013) and AB Dor (Järvinen et al. 2005). More recently, Lehtinen et al. (2012b) found no such stable active longitudes for longer timescales than 6 months, with the exception for years between 2003–2009 and before 1985. Possible flip-flop phenomena in the light curve were reported where the main photometric minima switched phase by φ ≈ 0.5 with the weaker secondary minima. Similarly, Olspert et al. (2015a) found no active longitudes in the photometry, and coherent structures were short-lived, with the exception of 2005–2008.

There are DI temperature maps of LQ Hya for January 1991 (Strassmeier et al. 1993), March 1995 (Rice & Strassmeier 1998), and November–December 1996 and April–May 2000 (Kovári et al. 2004). The maps by Strassmeier et al. (1993) were retrieved from single-line inversion solutions, and show a spot temperature of ΔTspot = 500 K cooler than the unspotted surface. They reported spots at both mid- to low-latitudes and some polar features, but the appearance of the latter was highly dependent on the strength of the spectral line used for the inversion. Rice & Strassmeier (1998) made use of multiple spectral lines in the same inversion, and found bands of features around the equator with ΔTspot = 600 K and a weaker polar spot than that previously reported by Strassmeier et al. (1993). The band of spots occupied lower latitudes and it was postulated that it coincided with the star being at a less active state in the activity cycle than for the January 1991 maps, although the spot temperature difference was greater. The two seasons of maps calculated by Kovári et al. (2004) reveal changes probably related to the spot cycle. They retrieved no polar spot, and spots were largely confined to mid- and low-latitudes.

ZDI of LQ Hya ranges from December 1991 (Donati 1999) to December 2001 (Donati et al. 2003b). ZDI maps of LQ Hya over a 5-year period by Donati (1999) revealed a shifting spot structure and the concentration of the magnetic field had only a weak correlation with respective brightness maps. Another 5-year period was covered by Donati et al. (2003b) to construct an 11-year time-series of ZDI results. McIvor et al. (2004) selected two years of dense observation coverage and found that the magnetic field topology differences between high and low activity states of LQ Hya were quite different from magnetic field structures at solar maximum and minimum. Near maximum, in 2000, LQ Hya resembled a tilted dipole, with two open field emergences at mid-latitudes separated by approximately φ = 0.5. A year later, in December 2001, the field resembled an aligned dipole with contributions from east to west arcades. McIvor et al. (2004) concluded that the magnetic structure underwent rapid changes in less than a year.

2. Observations

Table 1

Summary of observations.

Our observations were made over a 5-year period using the high resolution échelle-spectrograph SOFIN at the 2.56 m Nordic Optical Telescope at La Palma, Spain. The spectral resolution was R ≈ 70 000. A total of 7 observing seasons were used within this time period. The observations are summarized in Table 1. The date, signal-to-noise ratio (S/N), and phase of each individual observation for each season are available in Table 2.

Phase coverage fφ was quantified by assuming a phase range of φ ± 0.05 for each observation. Vogt et al. (1987) studied the robustness of the DI method against phase gaps and concluded that poor phase coverage may affect spot shape and location, but does not introduce spurious spots. This was further tested by Rice & Strassmeier (2000) where large phase gaps produced warmer starspots and smoother temperature maps. Lindborg et al. (2014) examined the changes in observational data by repeating an inversion of a season with higher phase coverage, eliminating all but 5, and found the spot coverage increased slightly. And so we conclude that phase coverage for the temperature maps in this report is sufficient for drawing some basic conclusions, with 50% or better phase coverage for all seasons (see Table 1). The total observations cover just over 4 years, which is a few years shy of the oft-cited cycle of about 6–7 years (e.g., Jetsu 1993; Cutispoto 1998a; Alekseev 2003).

Table 3

Adopted parameters for individual lines.

The spectral regions 6172.8–6174.3 Å, 6174.7–6178.0 Å, and 6179.6–6181.2 Å were used for the images Oct.98, Mar.99, May.99, and Nov.00. Due to changes in the instrument setup, the regions 6410.9–6412.8 Å, 6419.0–6422.5 Å, and 6430.2–6431.8 Å were used for Oct.99, Feb.02, and Nov.02. To transform the observing times into rotation phases φ, we used the ephemeris derived by Jetsu (1993): 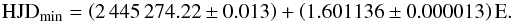(1)Later reported rotation periods are different (e.g. Kovári et al. 2004; Cutispoto et al. 2001; O’Neal et al. 2001), but these values are well within the variability in the rotation period determined by You (2007).

3. Doppler imaging

DI requires a selection of relatively unblended absorption lines. Since the S/N was considerably lower than ideal, it was particularly important to use multiple lines and weight each phase in our DI procedure to mitigate the effects of noise in each inversion. The lines were not added, and so there was no corresponding improvement in the discrepancy between the model and observations.

Stellar model atmospheres were taken from the MARCS database (Gustafsson et al. 2008). The main lines are Fe i and Ni i absorption lines. The full list of spectral lines can be found in Table 3.

The continuum was determined in two steps. The spectral orders were first normalized by a polynomial continuum fit of the third degree, as part of the standard spectrum reduction. This procedure does not take into account line blending and the possible absence of a real continuum within a spectral interval. An additional continuum correction for each wavelength interval was made by comparing the seasonal average observed profile and a synthetic line profile. Near-continuum points were used for a first or second degree polynomial fit to correct the normalized flux level.

3.1. Stellar and spectral parameters

A summary of relevant stellar parameters used in this paper are listed in Table 4. The inversion is sensitive to the value for vsini, and so we determined it by using a model with no spots and testing values 25 − 28 km s-1 and taking the value giving the smallest deviation from the mean observed line profile. The best fit was achieved with vsini = 26.5 km s-1. With regards to metallicity, we use solar values and make individual adjustments to the log (gf) values of specific lines, listed in Table 3. Adjustments are minor, and not particularly of interest as the idea is to study the variability in the spectral lines and not determine stellar parameters to high accuracy. These minor changes to values are required to reduce systematic errors caused by discrepancies between the model and the observations. We use i = 65°, but in reality values ±10° have only a minor impact on the results.

Spectral parameters for the model were obtained from the Vienna Atomic Line Database (Kupka et al. 1999). A total of 38 spectral lines were used for the images Oct.98, Mar.99, May.99, and Nov.00, and 21 lines for the images Oct.99, Feb.02, and Nov.02.

3.2. Inversion procedure

We use the inversion method developed by Piskunov (1991) and further described by Lindborg et al. (2011). This method uses Tikhonov regularization to stabilize the otherwise ill-posed inversion problem. In order not to extrapolate, we limit the solution to the temperature range of atmospheric models used in the calculations, in a similar way as described by Hackman et al. (2001). The limits imposed in this study restricted the temperature to values between 3400 − 5500 K. This range comfortably accommodates the observed Teff = 5000 K for LQ Hya and allows for spot temperatures to be at least 1000 K cooler than the mean temperature of the star. Previous DI results have shown spots as cool as 4200 K (Kovári et al. 2004), 4400 K (Rice & Strassmeier 1998), and 4700 K (Strassmeier et al. 1993) so the temperature range should be more than sufficient to accommodate even the coolest spots.

Table 4

Chosen stellar parameters.

thumbnail Fig. 1

Top: temperature map in equirectangular projection. The phase is defined in Eq. (1), and phases of observations are marked by vertical dashed lines. Bottom: normalized flux of the spectral region used for the inversion. Points are observations with error, the solid red line is the model calculated from the DI solution. The phase of each observation is listed to the right of the lines.

thumbnail Fig. 2

Same as in Fig. 1 for the March 1999 observing season.

thumbnail Fig. 3

Same as in Fig. 1 for the May–June 1999 observing season.

Line profiles were calculated using plane-parallel stellar atmosphere models and log g = 4.0 for temperatures between 3400 − 5500 K. The surface grid resolution used for the inversion was 40 × 80 in latitude and longitude, respectively. The inversion was run for 30 iterations, at which point a sufficient convergence was reached.

4. Results

thumbnail Fig. 4

Same as in Fig. 1 for the October 1999 observing season. A different spectral region was used due to different instrument setup.

thumbnail Fig. 5

Same as in Fig. 1 for the November 2000 observing season.

The Oct.98 map (Fig. 1) shows clear artifacts, mainly arches and hot spots in the temperature maps. Due to the low phase coverage and S/N, the latitude of spots and spot temperatures should be viewed with some skepticism. Mar.99 (Fig. 2) has slightly poorer phase coverage, artifacts, and little evidence for spots within the observed phases, as those that appear to coincide with poorer S/N. May.99 (Fig. 3) has decent phase coverage and S/N, with evenly spaced observations, and minimal appearance of ovals, arches, or hot and cool spot pairings. Oct.99 (Fig. 4) has poor phase coverage but S/N is improved. Spots at certain phases are distinctly visible in the spectral line profiles as consistent deep bumps in multiple lines. So while information regarding latitude and spot shape cannot be inferred from this map, the phase of spots is likely physical and the amplitude of the bump supports a large temperature difference between the spot and the mean temperature ⟨ T ⟩. Nov.00 (Fig. 5) has a lower S/N and poorer phase coverage and shows similar evidence of artifacts as Oct.99. However, the spot phases and mean temperatures are still meaningful due to the proximity of spots to the observed phases, but unlike the previous season, the noisier spectra make it difficult to determine if the spot temperature is due to artifacts or physical. Feb.02 (Fig. 6) has the best phase coverage of all the observing seasons, and Nov.02 (Fig. 7) has the highest S/N. These two are therefore the most reliable maps.

5. Discussion

The inversions are sensitive to phase coverage and S/N. Lower values in either of these for an observing season introduce artifacts in the temperature maps. Certain quantities are more meaningful in these cases than others. Phases of spots can be confirmed by examining the spectral lines corresponding to each map. Bumps similarly visible in multiple spectral lines are possible evidence for the presence of a real spot. The mean temperature ⟨ T ⟩ is calculated over the visible surface of the star and as such, any effects from noise or low phase coverage should cancel out with the appearance of both cooler and hotter regions.

However, spot temperatures are sensitive to phase coverage and noise. Hot regions in the temperature maps may be physical, but are also possibly artifacts related either to noise or poor phase coverage. The spot latitude should also be taken with a grain of salt, particularly with spots below the equator. The lower the phase coverage, the less information there is available for the inversion program to distinguish latitudes of spots as being above or below the equator. The inversion method may also interpret sudden changes in spots during the observing season as spots at lower latitudes. A spot at a low latitude would only appear during a limited phase range, and sudden spot changes at higher latitudes would have similarly limited phase ranges. For spots close to the equator, noise or errors from the continuum level can create artifacts. Arches and ovals that appear in the temperature maps are also artifacts, usually related to noise or poor phase coverage. Due to the limitations imposed by the inversion method and the resolution of the maps, it is not possible to determine if a spot is a single feature or a composite of multiple spots located near each other.

thumbnail Fig. 6

Same as in Fig. 1 for the February–March 2002 observing season. This is the same spectral region as in Fig. 4.

thumbnail Fig. 7

Same as in Fig. 1 for the November 2002 observing season. This is the same spectral region as in Fig. 4.

Table 5

Spot coverage, mean temperature, and spot temperature difference from the mean.

For the spot coverage analysis, all surface elements having Teff ≤ 4500 K were regarded as spots. Table 5 contains the mean temperature, coolest spot temperature, and spot coverage for each season. Figure 8 illustrates these values in relation to the photometry. Results that are less certain due to either low S/N or phase coverage are represented by smaller symbols. We tested the robustness of the inversion against phase gaps by taking the observing season with the best phase coverage, February–March 2002, and used only 5 observations from the 18 available. The comparison between these two maps is presented in Table 6. While ⟨ T ⟩ is pretty consistent, reducing the phase coverage increased the spot coverage from 1.9% to 9.3% and decreased the minimum temperature of the map. Therefore, we can conclude that the spot coverage may be overestimated by a similar factor in the low phase coverage maps.

Table 6

Observing season February–March 2002 with original and reduced phase coverage obtained by selecting 5 out of 18 observations.

Spot coverage is low for most seasons, but increases for seasons October 1999 and November 2000. These seasons somewhat coincide with an observed decrease in photometric magnitude (Lehtinen et al. 2012b). Even accounting for a low phase coverage, there is a minimum in ⟨ T ⟩ and a corresponding increase in spot coverage, although the spot coverage is less reliable due to the tendency for there to be higher temperature contrasts in images with lower phase coverage.

thumbnail Fig. 8

Top-left: photometric magnitude from Lehtinen et al. (2012a). Top-right: mean temperature of DI maps. Bottom-left: greatest temperature difference from the mean. Bottom-right: percentage of surface less than or equal to 4500 K. Symbol sizes are proportional to the S/N and phase coverage.

thumbnail Fig. 9

Longitudinal spot distribution from October 1998 to November 2002. Temperature is averaged over all latitudes for the Doppler images. Also plotted are the photometric minimum epochs from Lehtinen et al. (2012a) and Olspert et al. (2015b).

Figure 9 shows the longitudinal spot distributions by averaging over the latitudinal direction. This mimics the results one could obtain from photometric observations, where only phase and magnitude of the star at a particular point of time is observed. We have marked the primary and secondary minimum epochs retrieved from light curves from both Lehtinen et al. (2012a) and from Olspert et al. (2015a) using the Continuous Period Search (CPS) and Carrier Fit (CF) methods, respectively. Many seasons show good agreement with the photometry. For instance, in February–March 2002 both the results from Lehtinen et al. (2012b) and Olspert et al. (2015a) agree with each other and match the recovered phases of spot locations in the Doppler images. The photometric studies coinciding with our DI seasons reveal an especially chaotic spot activity with non-persistent phase jumps. No coherent active longitudes are seen during this epoch. The period used to phase our observations in longitude is not optimally describing the rotation of the spot structures, evidenced by the upward trend in the global CF fit results. This is indicative of spot structures moving more slowly than the adopted rotation period of the star. The trend is disrupted at several points, and it would appear that the Prot from Jetsu (1993) is not coherent for the length of time of this study. Olspert et al. (2015a) find occurrences of flip-flop type events (sudden switches in the phase of the primary and secondary minima) coinciding with our observing seasons of October 1999 and November 2000. We find no evidence of active longitudes (phases with persistent spots over multiple observing seasons), and our spot phases are not in agreement with the ones listed in Berdyugina et al. (2002), and any similar conversion of spot phases into primary and secondary minima reveals no tendency for these spot structures to be consistently spaced approximately 180° apart.

We compare our maps to previous DI results. We average the temperature distribution over longitude in Fig. 10 to facilitate this, keeping in mind that the spot latitude is less reliable for October 1998, October 1999, and November 2000. There is a somewhat bimodal distribution with a dark band at or near the equator for most seasons as well as a second dark band near the pole. This is exaggerated for observing seasons with poorer phase coverage.

Early DI results by Strassmeier et al. (1993) for January and February 1991 show spots at mid-latitudes and polar features when using specific single spectral lines. However, temperature maps from observations during March, 1995 by Rice & Strassmeier (1998) have a band of spots centered around the equator and a slight polar feature. The reliable maps of this study show similar weak high-latitude spots, but no bands.

Our observations coincide approximately with DI by Kovári et al. (2004) and the ZDI by Donati et al. (2003b), time-wise. Kovári et al. (2004) observe an increase in spot coverage from November and December 1996 to April and May 2000. Our temperature maps show a similar increase in the spot coverage around October 1999. In contrast to the April and May 2000 maps, our October 1999 and November 2000 maps have no band of spots, although there are several cool spots located near the equator, but the latitude is not reliable in these two maps.

Donati (1999) and Donati et al. (2003b) published ZDI maps spanning over 10 years. The spot occupancy results, roughly comparable to temperature maps, are sensitive to the phase coverage of an observing season. Because of this, more reliable seasons have higher spot occupancy and so it is difficult to make a comparison between spot occupancy maps and our temperature maps with regards to an activity cycle. The bimodal distribution of spots near the pole and near the equator is in agreement with our results.

Fekel et al. (1986b) proposed that tidal forces in binary systems would have a chaotic influence upon spot evolution and thus single stars would have more stable light curves resulting from slow spot evolution over several hundred rotations than binary stars. Henry et al. (1995) disagreed, postulating that the Roche lobe would instead have a stabilizing influence. Recent results and this report support the latter. Studies of RS CVn stars in binary systems such as II Peg seem to display more stable behaviour (Hackman et al. 2012), whereas single stars such as HD 116956 and FK Com displayed more chaotic behaviour (Lehtinen et al. 2011; Hackman et al. 2013). LQ Hya fits in this latter group, and the DI results support this. There is no appearance of long-lived structures even within the 4-year time span of maps in this report.

thumbnail Fig. 10

Latitudinal spot distribution from October 1998 to November 2002. Temperature is averaged over all longitudes for the Doppler images.

6. Summary

We have a total of 7 observing seasons from 1998–2002. Observing seasons February–March 2002 and November 2002 are the most reliable, whereas poor phase coverage and a higher S/N make the maps for October 1999 and November 2000 the least reliable. We consider the mean temperature the most reliable result of all maps when taking phase coverage and S/N into consideration. There is a general decrease in the mean temperature during the months of October 1999 and November 2000, before increasing again by February 2002.

We compare the Doppler images to photometry. LQ Hya does not have a consistent spot structure over a long period of time, unlike other studied objects such as II Peg. There is no evidence of active longitudes over multiple observing seasons, and this is consistent with recent findings using photometry (Lehtinen et al. 2012b; Olspert et al. 2015a). Spots possibly have a bimodal distribution (Fig. 10), and the spot coverage (areas with temperatures ≤4500 K) ranges from covering a small amount to a third of the star. The cycle length cannot be inferred from only 4 years of observations. The spot activity is chaotic with flip-flop events in photometry unfortunately occurring during the seasons with the least reliable maps.

Online material

Table 2

All observations.

Acknowledgments

Financial support from the Academy of Finland Centre of Excellence ReSoLVE No. 272157 (MJK) and from the Vilho, Yrjö and Kalle Väisälä Foundation (EC) is gratefully acknowledged.

References

  1. Alekseev, I. Y. 2003, Astron. Rep., 47, 430 [Google Scholar]
  2. Ambruster, C., & Fekel, F. 1990, BAAS, 22, 857 [NASA ADS] [Google Scholar]
  3. Berdyugina, S. V., & Tuominen, I. 1998, A&A, 336, L25 [NASA ADS] [Google Scholar]
  4. Berdyugina, S. V., Pelt, J., & Tuominen, I. 2002, A&A, 394, 505 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Covino, S., Panzera, M. R., Tagliaferri, G., & Pallavicini, R. 2001, A&A, 371, 973 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Cutispoto, G. 1991, A&AS, 89, 435 [NASA ADS] [CrossRef] [Google Scholar]
  7. Cutispoto, G. 1998a, A&AS, 127, 207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Cutispoto, G. 1998b, A&AS, 131, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Cutispoto, G., Messina, S., & Rodonò, M. 2001, A&A, 367, 910 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Donati, J.-F. 1999, MNRAS, 302, 457 [NASA ADS] [CrossRef] [Google Scholar]
  11. Donati, J.-F., Collier Cameron, A., & Petit, P. 2003a, MNRAS, 345, 1187 [NASA ADS] [CrossRef] [Google Scholar]
  12. Donati, J.-F., Collier Cameron, A., Semel, M., et al. 2003b, MNRAS, 345, 1145 [NASA ADS] [CrossRef] [Google Scholar]
  13. Eggen, O. J. 1984, AJ, 89, 1358 [NASA ADS] [CrossRef] [Google Scholar]
  14. Fekel, F. C., Bopp, B. W., Africano, J. L., et al. 1986a, AJ, 92, 1150 [NASA ADS] [CrossRef] [Google Scholar]
  15. Fekel, F. C., Moffett, T. J., & Henry, G. W. 1986b, ApJS, 60, 551 [NASA ADS] [CrossRef] [Google Scholar]
  16. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Hackman, T., Jetsu, L., & Tuominen, I. 2001, A&A, 374, 171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Hackman, T., Mantere, M. J., Lindborg, M., et al. 2012, A&A, 538, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Hackman, T., Pelt, J., Mantere, M. J., et al. 2013, A&A, 553, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Henry, G. W., Eaton, J. A., Hamer, J., & Hall, D. S. 1995, ApJS, 97, 513 [NASA ADS] [CrossRef] [Google Scholar]
  21. Järvinen, S. P., Berdyugina, S. V., Tuominen, I., Cutispoto, G., & Bos, M. 2005, A&A, 432, 657 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Jetsu, L. 1993, A&A, 276, 345 [NASA ADS] [Google Scholar]
  23. Kovári, Z., Strassmeier, K. G., Granzer, T., et al. 2004, A&A, 417, 1047 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Krause, F., & Rädler, K.-H. 1980, Mean-field magnetohydrodynamics and dynamo theory (Oxford: Pergamon Press) [Google Scholar]
  25. Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
  26. Lehtinen, J., Jetsu, L., Hackman, T., Kajatkari, P., & Henry, G. W. 2011, A&A, 527, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Lehtinen, J., Jetsu, L., Hackman, T., Kajatkari, P., & Henry, G. W. 2012a, VizieR Online Data Catalog, J/A+A/542/A38 [Google Scholar]
  28. Lehtinen, J., Jetsu, L., Hackman, T., Kajatkari, P., & Henry, G. W. 2012b, A&A, 542, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Lindborg, M., Korpi, M. J., Hackman, T., et al. 2011, A&A, 526, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Lindborg, M., Mantere, M. J., Olspert, N., et al. 2013, A&A, 559, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Lindborg, M., Hackman, T., Mantere, M. J., et al. 2014, A&A, 562, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. McIvor, T., Jardine, M., Collier Cameron, A., Wood, K., & Donati, J.-F. 2004, MNRAS, 355, 1066 [NASA ADS] [CrossRef] [Google Scholar]
  33. Messina, S., & Guinan, E. F. 2003, A&A, 409, 1017 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Montes, D., Saar, S. H., Collier Cameron, A., & Unruh, Y. C. 1999, MNRAS, 305, 45 [NASA ADS] [CrossRef] [Google Scholar]
  35. Oláh, K., Kolláth, Z., & Strassmeier, K. G. 2000, A&A, 356, 643 [NASA ADS] [Google Scholar]
  36. Oláh, K., Kolláth, Z., Granzer, T., et al. 2009, A&A, 501, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Olspert, N., Käpylä, M. J., Pelt, J., et al. 2015a, A&A, 577, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Olspert, N., Kapyla, M. J., Pelt, J., et al. 2015b, VizieR Online Data Catalog, J/A+A/577/A120 [Google Scholar]
  39. O’Neal, D., Neff, J. E., Saar, S. H., & Mines, J. K. 2001, AJ, 122, 1954 [NASA ADS] [CrossRef] [Google Scholar]
  40. Piskunov, N. E. 1991, in The Sun and Cool Stars. Activity, Magnetism, Dynamos, eds. I. Tuominen, D. Moss, & G. Rüdiger (Berlin: Springer Verlag), IAU Colloq., 130, Lect. Notes Phys. 380, 309 [Google Scholar]
  41. Rice, J. B., & Strassmeier, K. G. 1998, A&A, 336, 972 [NASA ADS] [Google Scholar]
  42. Rice, J. B., & Strassmeier, K. G. 2000, A&AS, 147, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Strassmeier, K. G., Rice, J. B., Wehlau, W. H., Hill, G. M., & Matthews, J. M. 1993, A&A, 268, 671 [NASA ADS] [Google Scholar]
  44. Strassmeier, K. G., Bartus, J., Cutispoto, G., & Rodono, M. 1997, A&AS, 125, 11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Tetzlaff, N., Neuhäuser, R., & Hohle, M. M. 2011, MNRAS, 410, 190 [NASA ADS] [CrossRef] [Google Scholar]
  46. Vogt, S. S., Penrod, G. D., & Hatzes, A. P. 1987, ApJ, 321, 496 [NASA ADS] [CrossRef] [Google Scholar]
  47. You, J. 2007, A&A, 475, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1

Summary of observations.

In the text
Table 3

Adopted parameters for individual lines.

In the text
Table 4

Chosen stellar parameters.

In the text
Table 5

Spot coverage, mean temperature, and spot temperature difference from the mean.

In the text
Table 6

Observing season February–March 2002 with original and reduced phase coverage obtained by selecting 5 out of 18 observations.

In the text
Table 2

All observations.

In the text

All Figures

thumbnail Fig. 1

Top: temperature map in equirectangular projection. The phase is defined in Eq. (1), and phases of observations are marked by vertical dashed lines. Bottom: normalized flux of the spectral region used for the inversion. Points are observations with error, the solid red line is the model calculated from the DI solution. The phase of each observation is listed to the right of the lines.
In the text
thumbnail Fig. 2

Same as in Fig. 1 for the March 1999 observing season.
In the text
thumbnail Fig. 3

Same as in Fig. 1 for the May–June 1999 observing season.
In the text
thumbnail Fig. 4

Same as in Fig. 1 for the October 1999 observing season. A different spectral region was used due to different instrument setup.
In the text
thumbnail Fig. 5

Same as in Fig. 1 for the November 2000 observing season.
In the text
thumbnail Fig. 6

Same as in Fig. 1 for the February–March 2002 observing season. This is the same spectral region as in Fig. 4.
In the text
thumbnail Fig. 7

Same as in Fig. 1 for the November 2002 observing season. This is the same spectral region as in Fig. 4.
In the text
thumbnail Fig. 8

Top-left: photometric magnitude from Lehtinen et al. (2012a). Top-right: mean temperature of DI maps. Bottom-left: greatest temperature difference from the mean. Bottom-right: percentage of surface less than or equal to 4500 K. Symbol sizes are proportional to the S/N and phase coverage.

In the text
thumbnail Fig. 9

Longitudinal spot distribution from October 1998 to November 2002. Temperature is averaged over all latitudes for the Doppler images. Also plotted are the photometric minimum epochs from Lehtinen et al. (2012a) and Olspert et al. (2015b).
In the text
thumbnail Fig. 10

Latitudinal spot distribution from October 1998 to November 2002. Temperature is averaged over all longitudes for the Doppler images.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.