| Issue |
A&A
Volume 580, August 2015
|
|
|---|---|---|
| Article Number | A88 | |
| Number of page(s) | 21 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201525794 | |
| Published online | 07 August 2015 | |
Search for associations containing young stars (SACY)
VI. Is multiplicity universal? Stellar multiplicity in the range 3–1000 au from adaptive-optics observations⋆,⋆⋆,⋆⋆⋆
1 European Southern Observatory, Alonso de Cordova 3107, 19001 Vitacura Casilla, Santiago 19 Chile
e-mail: pe210@exeter.ac.uk
2 School of Physics, University of Exeter, Stocker Road, Exeter, EX4 4QL, UK
3 Centro de Astrobiología, ESAC Campus, Apdo. 78, 28691 Villanueva de la Cañada ( Madrid), Spain
4 Departamento de Física y Astronomía, Facultad de Ciencias, Universidad de Valparaíso, Av. Gran Bretaña 1111, 5030 Casilla, Valparaíso, Chile
5 Laboratório Nacional de Astrofísica/ MCT, Rua Estados Unidos 154, 37504-364 Itajubá (MG), Brazil
6 Laboratoire d’Astrophysique, Observatoire de Grenoble, BP 53, 38041 Grenoble Cedex 9, France
Received: 3 February 2015
Accepted: 28 May 2015
Context. Young loose nearby associations are unique samples of close (<150 pc), young (≈5–100 Myr) pre-main-sequence (PMS) stars. A significant number of members of these associations have been identified in the SACY (search for associations containing young stars) collaboration. We can use the proximity and youth of these members to investigate key ingredients in star formation processes, such as multiplicity.
Aims. With the final goal of better understanding multiplicity properties at different evolutionary stages of PMS stars, we present the statistics of identified multiple systems from 113 confirmed SACY members. We derive multiplicity frequencies, mass-ratio, and physical separation distributions in a consistent parameter space, and compare our results to other PMS populations and the field.
Methods. We have obtained adaptive-optics assisted near-infrared observations with the Nasmyth Adaptive Optics System and Near-Infrared Imager and Spectrograph (NACO), ESO/VLT, and the Infrared Camera for Adaptive optics at Lick observatory (IRCAL), Lick Observatory, for at least one epoch of all 113 SACY members. We have identified multiple systems using co-moving proper-motion analysis for targets with multi-epoch data, and using contamination estimates in terms of mass-ratio and physical separation for targets with single-epoch data. We have explored ranges in projected separation and mass-ratio of a [3–1000 au], and q [0.1–1], respectively.
Results. We have identified 31 multiple systems (28 binaries and 3 triples). We derive a multiplicity frequency (MF) of MF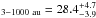 % and a triple frequency (TF) of TF
% and a triple frequency (TF) of TF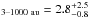 % in the separation range of 3–1000 au. We do not find any evidence for an increase in the MF with primary mass. The estimated mass-ratio of our statistical sample (with power-law index γ = −0.04 ± 0.14) is consistent with a flat distribution (γ = 0).
% in the separation range of 3–1000 au. We do not find any evidence for an increase in the MF with primary mass. The estimated mass-ratio of our statistical sample (with power-law index γ = −0.04 ± 0.14) is consistent with a flat distribution (γ = 0).
Conclusions. Analysis from previous work using tight binaries indicated that the underlying multiple system distribution of the SACY dataset and the young star-forming region Taurus are statistically similar, supporting the idea that these two populations formed in a similar way. In this work, we show further similarities (but also hints of discrepancies) between the two populations: flat mass-ratio distributions and statistically similar MF and TF values. We also compared the SACY sample to the field (in the separation range of 19–100 au), finding that the two distributions are indistinguishable, suggesting a similar formation mechanism.
Key words: stars: pre-main sequence / stars: variables: T Tauri, Herbig Ae/Be / techniques: high angular resolution / stars: statistics / binaries: visual
Based on observations obtained using the instruments NACO at the VLT (077.C-0483, 081.C-0825, 088.C-0506, 089.C-0207) and the adaptive optics facilities at the Lick Observatory (UCO 3 m).
Appendices are available in electronic form at http://www.aanda.org
Table B.1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/580/A88
© ESO, 2015
1. Introduction
The multiplicity of a stellar population holds a huge amount of information about the birth, evolution, and eventual fate of the population itself and its individual members. Thus, comprehensively characterising these properties has implications across many fields such as star formation, N-body dynamics, and supernovae rates. Multiplicity surveys of solar-type stars (e.g. Duquennoy & Mayor 1991; Raghavan et al. 2010; Tokovinin 2014) have made use of a combination of techniques (from small physical separations to large: spectroscopy, interferometry including sparse aperture masking (SAM) speckle imaging, adaptive optics (AO) assisted imaging, and classical direct imaging) to probe and characterise multiple systems with periods between ~1–1010 days (with a peak at ≈105 day). As a result, they show that almost 50% of solar-type stars (0.9–1.5 M⊙) have one or more companion. Considering the high-mass end of the initial mass function (IMF), the O-type stars, the percentage increases up to ≈100% (Sana et al. 2014). In other words, these massive stars form almost exclusively in multiple systems.
Such surveys are volume-limited, making use of the high number of main sequence (MS) field stars that are nearby to produce robust statistics (e.g. in the case of Tokovinin 2014, 90% completeness, considering their spatial density, for d< 70 pc). However, the history of this population is not well constrained as it comprises stars born at different times and in a range of environments. As a result, they must have undergone quite different dynamical processing (Parker et al. 2009). Therefore, the information regarding the multiplicity properties as a direct output from star formation has been smeared out during its somewhat unreproducible dynamical history. To study a more pristine population one has to consider the observations of younger stars (<100 Myr) in their nurseries, which usually provide smaller datasets. Such studies are usually performed in nearby star-forming regions (SFRs) like e.g. Taurus (Leinert et al. 1993; Kraus et al. 2011; Daemgen et al. 2015), Ophiuchus/L1688 (Ratzka et al. 2005), Chamaeleon I (Lafrenière et al. 2008), IC 348: (Duchêne 1999), or the Orion Nebula Cluster (ONC) (Reipurth et al. 2007). However, as King et al. (2012b) demonstrated, the amount of overlapping cluster-to-cluster parameter space limits the number of systems that one is able to statistically compare (typically <100).
All SACY targets observed and analysis in this work.
Summary of the properties and frequency of visual multiple systems identified for the SACY associations studied in this work.
Young associations have also been studied owing to their proximity (<150 pc) and youth (≲100 Myr). There are a handful of studies focused on the stellar multiplicity in these populations (see e.g. Brandeker et al. 2003, 2006). The results of these works lead to varying conclusions about the nature of the stars in such associations. As an example, Brandeker et al. (2003) found a very high frequency of stellar multiple systems in TW Hydrae, and an absence of systems (with separations >20 au) in η Chamaeleontis, with an extremely small likelihood (<10-4) that the two populations share the same parental multiplicity distribution. It is still unclear whether this is due to dependencies on purely initial density (Moraux et al. 2007) or additional environmental effects (Becker et al. 2013).
There have also been some studies focused on the substellar multiplicity in these associations (Masciadri et al. 2005; Lafrenière et al. 2007; Nielsen & Close 2010; Evans et al. 2012; Chauvin et al. 2010; Biller et al. 2013). In addition to such surveys, many individual objects have been imaged with the aim to disentangle the planetary/brown dwarf nature of their companions and further understand their circumstellar discs (Chauvin et al. 2004; Huélamo et al. 2011).
However, a detailed statistical analysis of the abundance and characteristics of multiple systems in young associations compared to those identified in SFRs is still missing. Such an analysis was very complex until recently, posing a compromise between the publicly available data and the ability to probe the same parameter space. Motivated by this, in 2006 we started an homogeneous observational campaign to derive the multiplicity of young loose associations.
We aim to characterise the multiplicity properties of these associations across a large parameter space (a ~ 0.1–104 au) by combining a range of observational techniques. We have already derived the spectroscopic multiple system fraction (the tightest multiple systems, semi-major axis (a) ≲ 1 au) of our sample (Elliott et al. 2014). We found that the derived multiplicity fraction is compatible with that of the field and nearby SFRs, as one would expect due to the lack of dynamical processing for systems with such high binding energy, that have statistically similar primordial abundances. We are now extending our analysis to wider binaries, using AO imaging.
Adaptive optics imaging allows us to identify and characterise multiple systems across a huge parameter space for targets that belong to nearby associations. As an example, for an average member of our sample (d = 70 pc, age = 30 Myr, M1 = 1 M⊙), an instrument such as NAOS-CONICA at the VLT (point spread function, PSF, full-width half maximum, FWHM, of 0.07 ″ at 2.2 μm, with a strehl ratio of 1), is sensitive to companions at separations [a ~ 3–1000 au] in the [M2 ~ 0.01–1 M⊙] mass range. As mentioned previously, the peak of field stars period distribution is at 105 day which, considering a secondary of 0.1 M⊙, corresponds to a semi-major axis of ~40 au assuming a circular orbit. Therefore, our observing campaign should yield a high number of multiple systems when a large enough sample is observed. In addition, the observations must have sufficient temporal coverage to discard that a visual pair is just a chance alignment through a proper motion analysis (as orbital motion is negligible in the majority of cases).
The manuscript is organised as follows: Sect. 2.1 describes the target selection. Section 3 details the observations, data reduction, and the sensitivity limits, as well as the literature analysis. Section 4 outlines the methods used to identify bound multiple systems and the uncertainty estimations. Section 5 describes how we derived the multiplicity properties of our sample. Section 6 presents the statistical analysis of the built distributions and comparisons to other populations. Section 7 states the main conclusions of this work and prospects.
2. Sample definition
The search for associations containing young stars (SACY) dataset contains ≈2000 stars located all over the sky. The stars are defined as members of distinct moving groups by the convergence method (see census of Torres et al. 2006). The kinematic properties of the stars are derived from the parallax, the proper motion (PM) and the radial velocity (RV) values.
The starting point for our sample selection was based on the census by Torres et al. (2006). For the southern targets two additional criteria were followed: (i) we only consider stars with spectral types later than G5, in order to increase the contrast between the primary and the possible companion candidate; and (ii) the right ascension (RA) should be obtainable from Paranal Observatory when our service observations were conducted (periods 77, 81, 88, and 89). The northern targets also followed criterion (i) and were also observed according to their visibility during the two runs at the Lick Observatory in 2008 and 2009.
Later on, the membership of several targets was revised based on new data (e.g. new RV values derived from high-resolution spectra, Elliott et al. (2014). This revision allowed us to eliminate contamination within the sample from interlopers. From the 201 SACY targets observed originally with AO, 113 are now confirmed SACY members, while 88 have been rejected.
The bulk of this work is focused on the 113 confirmed SACY members, and the specific details of the sample are provided below (summarised in Table 1). However, for completeness with our original observations, we also provide details on the 88 non-SACY targets, including their observational parameters and a summary of the identified multiple systems, in Tables B.1 and C.1, respectively.
2.1. Filtered coherent sample for this work
Table 1 provides the census of the 113 confirmed SACY members (once the additional data from Elliott et al. 2014 have been included to identify interlopers) studied in this work. We have included two K magnitude values: the one from the 2MASS survey, K (2MASS), and our estimated K (M1). From our observations (with a narrow field of view that does not allow for a robust flux calibration), we can only obtain relative photometry and therefore we use 2MASS magnitudes for calibration. We denoted our estimated magnitude, K (M1), and it only differs from the original 2MASS value in the case of a detection of a new companion (previously unresolved) within the 2MASS PSF. The typical PSF width for 2MASS is ≈2 ′′ and, in some cases, multiple components can be found within this angular distance. To estimate the photometry of the primary and components we weighted the 2MASS value according to the observed flux ratio. In the next sections, the primary masses have been calculated using this value, and the age value included in Table 2 with the evolutionary tracks of Baraffe et al. (1998).
Finally, we note that all the targets in this sample have PM values from the UCAC4 catalogue (Zacharias et al. 2012). Precise PMs will allow us to determine whether identified companions are co-moving with the primary source.
3. Observations and data reduction
3.1. Southern targets: NACO data
We had four sets of observations in service mode dedicated to collecting data on SACY sources with NAOS-CONICA, an adaptive optics system and near-IR camera at the Very Large Telescope (VLT). The first epoch of data was taken between March–August 2006 (077.C-0483), and 76 targets were observed (seeing ≈0.9″). The 40 objects (out of the 76) identified to have potential companions were re-observed (seeing ≈0.7″) between March–June 2008 (081.C-0825). We had two additional programs to observe other members of the SACY associations in 2011 and 2012 (088.C-0506, and 089.C-0207), and we observed 60 and 25 targets (seeing ≈1.0″), respectively (see Table A.1 for details on individual sources).
All the targets are bright enough (V< 16 mag or K< 13 mag) to be used as AO reference stars. For the majority of the stars, we used the visible wave-front sensor (VIS WFS). For the reddest objects we used the IR WFS with the N90C10 dichroic, which sends 90% of the light to NAOS and 10% to the infrared detector. Since all the sources are very bright in the near-IR, the observations with the VIS WFS were performed with intermediate- and narrow-band filters to avoid saturation of the primary star. The first selection of filters was IB 2.21 (λ0, Δλ = 2.21, 0.06μm) and NB 2.17 (λ0, Δλ = 2.17, 0.023μm). During the observations, the IB 2.21 filter showed strong optical ghosts that prevented us from detecting companions in some particular regions of the detector. Therefore, we replaced it with the IB 2.27 (λ0, Δλ = 2.27, 0.06μm) filter. The observations with the IR WFS were performed with the broad-band Ks filter (λ0, Δλ = 2.18, 0.35μm). All the observations from 2006 and 2008 used the S27 objective, which provides a field of view (FOV) of 27.6″ × 27.6″. The data from 2011 and 2012 used the S13 objective, with a FOV of 14′′ × 14′′.
We observed each object using a jitter sequence to remove the sky contribution and to correct for bad pixels. The sky emission was estimated from the median image of all offsets positions. The average total exposure time for each source was ≈12 min. We reduced the data using the recommended eclipse ESO software (Devillard 1997) and the esorex driven interface gasgano. Dark subtraction, bad pixel correction, and flat-field correction were applied to each frame prior to aligning and stacking.
To derive accurate astrometry of the potential companions, we derived the plate scale and orientation on the infrared detector, using archival observations of the astrometric field θ1 Ori C (McCaughrean & Stauffer 1994), and the astrometric binaries IDS 2150 and IDS 22141 (van Dessel & Sinachopoulos 1993); see Chauvin et al. (2012) for details. The values measured in different epochs are listed in Table 3. For each target, we have adopted the plate scale and orientation closest to the date of observation.
A summary of the NACO observations is provided in Table 4.
3.2. Northern targets: lick data
To observe the 40 northern targets in our sample, we used the adaptive optics facility at the Lick Observatory Shane 3 m telescope (Gavel et al. 2002) between 14–18 July 2008 and 8–9 July 2009.
In 2008 the conditions were relatively good, although not photometric, with an average seeing between 0.8″ and 1.1″ in the visible, at the zenith. The targets were all bright enough to be used as a reference for the wave-front sensor. All of the targets were observed using the Ks filter, which provides the best compromise between the AO performances and the sensitivity to faint and red companions.
When a clear companion was detected in the images, an additional H-band (and sometimes J-band) image was acquired to provide colour information. All observations were performed using a dither pattern to efficiently remove cosmic rays, bad pixels and accurately compute the sky. The data were processed using Eclipse, including dark subtraction, flatfield correction, sky subtraction, frame registration, and stacking. A Hipparcos binary (HIP 66225, Gontcharov 2006) was observed every night to be used as an astrometric calibrator and derive an accurate plate scale and plate position angle on the sky (see Table 3).
The 2009 observations aimed at obtaining second epoch images of the 21 targets with companion candidates detected in the first epoch images. Conditions were poorer, with a seeing of ≈1.5′′ and some cirrus. As we were most interested in deriving accurate astrometry, the observations were performed in a single band (using the Ks filter). The same observing strategy (five point dither pattern) and processing steps were applied. The same astrometric reference was used to calibrate the plate scale and position angle of the camera (see Table 3).
A description of the Lick data used in this work is included in Table 4.
Detector plate scales (s ± σs) and true north orientations (t ± σt).
Summary of all AO-imaging data used in this work.
3.3. Archival data and literature search
We queried the ESO archive for related NACO data for objects that were observed only once in our service campaigns. This way, we could utilise a second epoch to determine if the detected companion candidates are co-moving. In total 64 objects had multi-epoch observations. In addition to this, we queried the CDS for object-type determinations and multiplicity flags for all 201 targets studied in this work, (see Table A.1). For objects previously identified as multiple systems, we checked whether the companions’ properties were within the parameter space of our observations, which in turn, tests the completeness of our work. As a result, we did not find any previously identified systems in this parameter space which we failed to detect.
3.4. Observational detection limits
Figure 1 shows the average contrast in the selected filters as a function of the angular separation from the primary star for both the NACO (using the S13 and S27 objectives) and Lick data. On average, we reach ΔKs = 7 mag and ΔKs = 4 mag at an angular separation of 0.5″, for the NACO and Lick data, respectively. For an age of 30 Myr (the average age of the SACY associations) and a primary mass of 1.0 M⊙, these differences in magnitude correspond to masses of ~15 MJup and ~0.10 M⊙ (dashed lines in Fig. 1), using the evolutionary tracks from Baraffe et al. (1998).
 |
Fig. 1 Average sensitivity limit in all filters for both NACO and Lick data. The limits were computed from the 3σ root-mean squared (rms) of the PSF radial profile for each target, and then averaged within each filter. The Ks filter for the NACO data is given for the S13 and S27 objective. The dashed lines represent our mass limits at 0.̋5, according to Baraffe et al. (1998) evolutionary tracks, assuming an average age of 30 Myr and a primary mass of 1 M⊙. |
4. Identifying multiple systems
In order to identify multiple systems in our sample, we have followed the next procedure: first, we have identified all the point sources within the FOV of each target. Then, we have determined the astrometry and photometry of these sources, and used these parameters to determine whether the identified point sources are bound companions or background objects. We provide all the details in the next subsections.
4.1. Initial source detection
Combining the NACO data and Lick data, we have imaged a total of 201 young targets. In order to identify companions in our images, we first need to identify all possible point sources in the FOV. We used the source extraction software SExtractor (Bertin & Arnouts 1996) to perform the source identification. Only detections of sources with five or more pixels with values ≥3σ were considered (where σ is the standard deviation of the background signal).
We visually checked each image to (i) confirm whether the detection was from a true point source as opposed to, for example, an optical ghost and (ii) search for potential severely blended binaries (with component separations ~4 pixel) that had been detected as one source. With the catalogues of point sources for each observation we then modelled the PSFs using the software PSFEx in conjunction with SExtractor. For the majority of observations, the primary targets were used to model the PSF. In the case that the primary target was resolved into a close binary, either additional components in the FOV (as close to the centre of the image as possible) were used, or another bright target observed during the same night with the same instrumental setup and as close in time as possible. Figure 2 shows a typical example of a blended object originally detected as a single source. The centre and the photometric aperture as derived by SExtractor are represented by the black circle and black ellipse, respectively. Through the modelling of the PSF we were able to extract the astrometry and photometry for the two components, whose centres and FWHMs are shown by the red crosses and dashed circles, respectively.
 |
Fig. 2 Section of the NACO image for target CD-30 3394B, showing two partially resolved components. The black solid-lined ellipse is the aperature applied by SExtractor and the black filled circle the centre of the ellipse. The red crosses and black dashed circles indicate the centre and FWHM of the model PSF extracted from the primary CD-30 3394A, using PSFEx for each source. |
4.2. Relative photometry
Our observations did not include photometric calibrator fields and, therefore, we can only perform relative photometry in our images. However, the vast majority of our targets were imaged in the Ks band, so we can make use of the available 2MASS Ks values (Skrutskie et al. 2006). In the cases where we discovered multiple components within the original PSF of 2MASS, we weighted the magnitudes according to the flux ratios of the components. These values are provided in the fifth column of Table 1, as K(M1), and have been used to compute the mass ratio of the multiple systems using evolutionary tracks (Baraffe et al. 1998), and the age estimation from Table 2.
4.3. Relative astrometry
For every point source detected in each observation, we calculated the angular separation from the primary in detector coordinates and then applied the appropriate pixel scale and true north correction value (Table 3). In the case of non-blended sources, we have used the parameters from the aperture extraction, while for severely blended sources we have used the ones coming from PSF modelling. We have performed both types of extractions (aperture and PSF) on a small number of targets and confirmed that, for non-blended sources, the resultant photometry and astrometry is consistent within the uncertainties. We then have employed a different method to determine whether the detected point sources are bound companions or not, depending on the availability of multiple epochs.
4.3.1. Uncertainties
The main source of uncertainty comes from the temporal and spatial variability of the atmospheric conditions. The uncertainties for the angular separation, ρ(x,y) ± σρ, and position angle, θ(x,y) ± σθ, were derived using Eqs. (1) and (2), using the appropriate plate-scale and true north correction values. ![\begin{equation} \label{eq:ang_sep} \sigma_\rho = \Bigg[\bigg(\frac{\partial \rho}{\partial x}\sigma_\mathrm{x}\bigg)^2+\bigg(\frac{\partial \rho}{\partial y}\sigma_\mathrm{y}\bigg)^2\Bigg]^{\frac{1}{2}}, \end{equation}](/articles/aa/full_html/2015/08/aa25794-15/aa25794-15-eq96.png) (1)where σx = xσs, σy = yσs and σs is the uncertainty in the plate scale, and
(1)where σx = xσs, σy = yσs and σs is the uncertainty in the plate scale, and ![\begin{equation} \label{eq:pa} \sigma_\theta = \Bigg[\bigg(\frac{\partial \theta}{\partial x}\sigma_\mathrm{x}\bigg)^2+\bigg(\frac{\partial \theta}{\partial y}\sigma_\mathrm{y}\bigg)^2+\sigma_{\mathrm{t}}^2\Bigg]^{\frac{1}{2}}, \end{equation}](/articles/aa/full_html/2015/08/aa25794-15/aa25794-15-eq100.png) (2)where σt is the uncertainty in the true north correction. Table B.1 shows the parameters and their uncertainties of the multiple systems identified for each observation.
(2)where σt is the uncertainty in the true north correction. Table B.1 shows the parameters and their uncertainties of the multiple systems identified for each observation.
4.3.2. Multi-epoch data
To assess whether a pair of point sources are bound, and not a projection effect, we computed their relative motion and compared it to the motion one would expect for a background object. The PM values were taken from UCAC4 (Zacharias et al. 2012). We then combined this with the parallactic motion, and produced the total relative motion one would expect to see if the point source were a background, stationary object (see Chauvin et al. 2005). An example is shown in Fig. 3. We would expect a bound companion to show negligible movement with respect to the primary between our multi-epoch observations, and this is our criterion for binary identification. In those cases in which the PM of the source did not produce significant motion, given the time difference between observations, we used the criterion described in Sect. 4.3.3.
 |
Fig. 3 Relative movement of four point sources, in RA and Dec, for two observations of GSC 08350-01924. The black dotted line and black markers represent the motion one would expect from a background (BKG) source with respect to the primary, and the shaded area represents the error space. The dark blue marker represents a source showing no significant relative motion, consistent with a bound (BND) companion at 0.3″. The other coloured markers represent three background sources detected at separations of 10.5, 13.2 and 14.2″ from the primary. |
4.3.3. Single-epoch data
For those targets with only one epoch of data (NACO data using S13 camera) we could use their properties, to provide statistical constraints on how likely is the source to be bound. One way to do that is to estimate the potential contamination from background sources given the target’s galactic co-ordinates, and the limiting magnitude of the observations. However, galactic models such as Robin et al. (2003) have a limited resolution and, given our small FOV (13″ × 13″), this method only provides a very rough estimate of the level of contamination. To avoid this limitation and provide more realistic estimations, we decided to use our available multi-epoch data to assist in the classification of our single-epoch data.
We classified our own multi-epoch detections as either bound companions or background sources from PM analysis, see Sect. 4.3.2). We then used two additional sources of data. Firstly, Wahhaj et al. (2013), a high-contrast direct imaging survey for giant planets. We converted the H-band photometry into mass-ratios using the evolutionary tracks of Baraffe et al. (2003) and the ages quoted in the work. Secondly, we used the data from Daemgen et al. (2015), a multiplicity survey in Taurus conducted in Ks-band. From these two works, we only used sources classified by PM analysis (in total, 246 classified sources).
We then pseudo-randomly split this classified data: 2/3 as a training set, 1/3 a test set. Using support vector machines (SVM)1, we determined the optimum soft-boundary in the physical separation-mass-ratio space that splits bound and background sources. On average, we reached a completeness and contamination rate of >80% and <10% respectively, when classifying our test set. With this classifier we then calculated the probability that our single-epoch sources are bound (Pbnd) or background (Pbkg). In this instance, there are only two labels: either bound or background and as a result, Pbnd = 1−Pbkg. We repeated this procedure 1000 times and took the median result to account for the variations induced by different training and test datasets. The individual probabilities (Pbnd) of these companion candidates with their respective properties are shown in Table 5.
A summary of the properties of multiple systems identified in this work.
To test whether this technique produces realistic probabilities, we calculated the bound probabilities for the 35 companions already confirmed by PM analysis. The median bound probability was ≈99%.
Figure 4 shows the graphical result of this procedure. There is a clear trend towards high mass-ratio, closely-separated sources being bound (as one would expect), and only very few bound sources lie in the parameter space mainly populated by background sources.
5. Results
We have identified 31 potential multiple systems (28 binaries and 3 triples) from 113 confirmed SACY targets. Of these 31 systems, 7 have been confirmed by PM analysis and 24 have a bound-probability ≥95%2 (see Sect. 4.3.3). The details of the observational properties from individual observations are listed in Table B.1. A summary of the physical properties of the multiple systems is included in Table 5.
We have followed the multiple component designations described in Tokovinin (2005), where systems are described by individual components and super components. For example, a triple system composed of a binary system orbiting the primary (brightest) star would have the following designations: “A, B, *” and “Ba, Bb, B” following increasing hierarchy. In such cases, there are two entries in Table 5, one to describe “A, Ba” and the other “Ba, Bb”.
The analysis presented in the following subsections considers the 31 identified multiple systems from 8 SACY associations (outlined in Table 2). We note that have also identified 28 multiple systems in the sample of non-SACY members. A summary of these systems’ properties can be found in Appendix C.
We have defined two ranges of physical separations in our analysis, derived from the sample sensitivities shown in Fig. 5. The first, 3–1000 au, is the most extensive, considering 109 from the 113 observed targets, and including all the 34 companion detections (28 binaries and 3 triples). We define another as 10–1000 au, which will allow us to compare our results with other studies. For this parameter space, we again consider 109 observed targets but only 27 companions detections (25 binaries and 1 triple).
5.1. Multiplicity frequencies
The frequency of multiple systems in a population can be computed in a number of ways, see Reipurth & Zinnecker (1993). In this paper we consider the following quantities: multiplicity frequency (MF), companion star frequency (CSF) and triple frequency (TF).
We have identified 31 multiple systems from observations of 113 confirmed SACY targets. Therefore, we estimate a raw multiplicity frequency (MFraw) of 27.4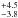 %, and a raw companion star frequency (CSFraw) of 30.1
%, and a raw companion star frequency (CSFraw) of 30.1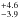 %. However, as mentioned previously, these frequencies include companions that would not be detected around all of the targets due to different contrasts and distances (see Fig. 5). When we remove these targets, we derive a multiplicity frequency of MF
%. However, as mentioned previously, these frequencies include companions that would not be detected around all of the targets due to different contrasts and distances (see Fig. 5). When we remove these targets, we derive a multiplicity frequency of MF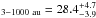 % in the separation range 3–1000 au. All of our companion detections are above 95% sensitivity curve and therefore we do not disregard any of them in our calculation.
% in the separation range 3–1000 au. All of our companion detections are above 95% sensitivity curve and therefore we do not disregard any of them in our calculation.
5.1.1. Higher-order multiple systems
Considering the higher-order systems separately (three triple systems) we derive a triple frequency of TF % in the separation range of 3–1000 au. It is interesting to note that two of the three triple systems identified in this work have secondary components at very small separations (4.8 and 5.2 au) that are only detectable due to the small distance to the systems (31 and 17 pc).
% in the separation range of 3–1000 au. It is interesting to note that two of the three triple systems identified in this work have secondary components at very small separations (4.8 and 5.2 au) that are only detectable due to the small distance to the systems (31 and 17 pc).
5.1.2. Multiplicity frequency and primary mass
We analysed the effect of the primary mass on the multiplicity frequency within our sample for the 109 systems in the separation range 3–1000 au. We binned our data according to the Freedman-Diaconis rule, which is suited for non-Gaussian distributions (bin width ≈0.1 M⊙). The results are shown in Fig. 6. The large uncertainties for masses of 0.25, 0.35, and 0.45 M⊙ are a result of the low-number fractions 0/1, 0/1, and 1/1, respectively.
 |
Fig. 4 Probability of identifying a bound system from 100–0% in intervals of 10% from blue to red in physical separation-mass-ratio parameter space. The circles and crosses represent the training and test set, respectively. Blue markers represent bound companions, and red markers unbound companions. |
 |
Fig. 5 Top panel: physical projected separations versus mass-ratio for identified multiple systems. The filled red markers represent binary companions, the other coloured markers are components of triple systems with matching colours for the secondary and tertiary. The size of the marker is proportional the companion’s mass. The grey lines represent the sensitivity limits for the individual targets. The red and black lines represent the 90% and 95% detections limits for the whole sample, respectively. Bottom panel: 95% detection limits for four studies, red: this work, blue: Daemgen et al. (2015), green: Kraus et al. (2011) and brown: Raghavan et al. (2010), used for analysis in Sect. 6. |
5.2. Mass-ratios
We calculated the mass-ratios (q) of our multiple systems in two ways, to test the effect of using primary mass values derived with different methods. We note that, in the case of triple systems composed of a primary component A and an outer orbiting binary (Ba, Bb), the mass-ratio of the component Ba is derived as be MBa/MA:
-
(i)
We derived primary mass values (M1) from absolute magnitudes using kinematic distances (D) and ages with the evolutionary tracks of Baraffe et al. (1998). We then calculated the companion masses from ΔK values and computed the mass-ratios (the normalised cumulative distribution function (CDF) is shown by the red line in Fig. 7).
-
We used the ΔK values of our components for a range of K1 values, which is equivalent to a range of model-based M1 values for the given age of the system (0.8–1.2 M⊙, according to the evolutionary tracks of Baraffe et al. 1998). To obtain the uncertainty, we calculated the standard deviation of the mass-ratio as a function of the primary mass for a given system. We then computed 100 mass-ratio distributions composed of pseudo-random realisations of each mass-ratio value and its uncertainty. We binned the data in 0.01 steps and took the average and standard deviation producing a smoothed, normalised CDF, shown by the black dots and shaded areas (dark and light: 1σ and 3σ) of Fig. 7, respectively.
The values and uncertainties used in further analysis (shown in Table 5) are obtained using method (ii) in order provide realistic uncertainties given that, at this time, the masses are model based.
 |
Fig. 6 Primary mass versus multiplicity frequency for systems in the separation range 3–1000 au. The data is binned according to the Freedman-Diaconis rule. The fractions are shown by each mass bin. |
 |
Fig. 7 Left panel: normalised frequency of mass-ratios. The dashed line represents a power-law function with index γ = 0. Right panel: the cumulative frequency distribution of mass-ratios using the two methods outlined in Sect. 5.2. Method (i) The red line represent the derived mass ratios. Method (ii) The black dots, dark and light blue-coloured area represent the average, 1σ and 3σ variation in frequency from 100 realisations of the mass ratio, respectively. |
The mass distribution is usually described using a power law index, γ. We derive a value of γ = −0.04 ± 0.14 using linear regression of 1000 pseudo-random realisations of the mass-ratio distribution considering their respective uncertainties.
5.3. Physical separations
We calculated the physical separations of the multiple systems using the kinematic distances shown in Table 1, and the average angular separation from our observations. The top panel of Fig. 5 shows the physical separation versus mass-ratio for the 31 SACY multiple systems, considering both multiple-epoch and single-epoch observations with probabilities ≥95%). The size of the markers represents the companion’s mass. In addition to this, the detection limits are shown for each multiple system (grey lines) and 90% and 95% detection limits for the entire observed sample in red and black, respectively. This calculation demonstrates the powerful nature of the SACY dataset when observed with AO-imaging: we can probe very small physical projected separations across our sample down to low mass-ratios.
In addition to this, we generated separation distributions in two ranges. Firstly, 10–1000 au, for SACY, Taurus (Kraus et al. 2011; Daemgen et al. 2015, hereafter K11 and D15) and the field (Raghavan et al. 2010, hereafter R10), see Fig. 8. Secondly, 19–100 au, for SACY, Taurus (only K11) and the field (see Fig. 9). The first separation range was chosen to maximise the number of comparable systems due to different observational techniques. The second, to make the same comparison that was made in King et al. (2012a).
First of all, we created 90% sensitivity curves for each study in terms of mass-ratio and physical separation (shown by the coloured lines in the bottom panel of Fig. 5), using the available published data. In the case of R10, we used the sensitivity curve from Fig. 11 of that paper. Then, we defined the master sensitivity curve as the upper boundary of all the individual curves (shown by the black solid line in the bottom panel of Fig. 5). We then only consider systems with parameters above this curve.
To perform this analysis we used kernel density estimations (KDEs), see Scott (2009) for details. This technique minimises potential problems with the bin size and the phase. The results for the two separation ranges are shown in the left panels of Figs. 8 and 9. The plots shows the KDE from SACY in red, Taurus in blue and green, and the field in gold with 95% confidence intervals (CIs) shown by the respective-coloured shaded areas. The CIs were calculated by considering the distribution of densities for each physical separation from 105 bootstrap iterations of the KDE. To see the differences between the distributions more clearly we have plotted them in the form of cumulative frequency distributions (CDFs) in the right panels of Figs. 8 and 9.
The low-density nature of Taurus makes it very interesting to compare it to our associations, as they most likely formed in a low-density environment too. We use the work of K11 and D15 since the samples are complementary. The statistical sample defined in D15 consists of 10 members from the extended Taurus region (~20 Myr) and 5 from the young Taurus region (~2 Myr), totalling 15 multiple systems. That of K11 only considers the young region and in our defined parameter space, this produces a sample of 50 multiple systems for comparison.
The field represents a far more processed population of stars from a range of initial environments and, therefore, provides a mixed sample of evolved multiple systems. The number of comparable systems in the field within our defined parameter range is 123.
 |
Fig. 8 Left: red, green, blue and gold shaded areas represent the 68% confidence intervals for the kernel density estimation (KDE) for SACY, Taurus (K11), Taurus (D15) and the field (R10) respectively. The multiple systems considered are all above the master sensitivity curve defined in the bottom panel of Fig. 5 and in the separation range 10–1000 au. Right: the cumulative distribution frequencies for the same systems. |
Firstly, we tested the effect of primary mass on the separation distribution as the studies we are considering probe slightly different primary mass ranges.
We performed a set of simulations using 10 000 synthetic binaries with primary masses between 0.2–1.4 M⊙. We performed two sets of simulations which differed by their mass-ratio distribution. In the first case, we considered the mass-ratio distribution as uniform across all primary masses. In the second simulation we adopt the information from Fig. 5 of K11 as priors. In the range M1: 0.7–1.4 M⊙ the mass-ratio distribution as uniform. For the range M1: 0.2–0.7 M⊙ there is a preference for more equal mass-ratio systems for lower primary masses. We created a probability function for the secondary masses, and pseudo-randomly chose mass-ratio values from this distribution.
The period values were drawn from the log-normal distribution defined in Raghavan et al. (2010), μ = 5.03 and σ = 2.28 log (day). We then fitted the separation distributions with log-normal distribution and evaluated their parameters. When comparing the two sets of simulations, we see that the peaks of the separation distributions are shifted to smaller separations for the lightest primary masses: mean values of 30 au in the first case, and 60 au in the second case. However, this difference is not significant given the separation range we are considering (10–1000 au) There is also no significant difference resulting from the mass-ratio distributions.
Based on this result, we have compared separations distributions of field stars in the mass range of 0.7–1.4 M⊙, and SACY objects in the mass range of 0.2–1.2 M⊙.
 |
Fig. 9 Left: red, green and gold shaded areas represent the 68% confidence intervals for the kernel density estimation (KDE) of multiple systems for SACY, Taurus (K11) and the field (R10), respectively. The multiple systems considered are all above the master sensitivity curve defined in the bottom panel of Fig. 5 and in the separation range 19–100 au. Right: the cumulative distribution frequencies for the same systems. |
Our comparison between the three populations is shown in Fig. 8. The shape of the SACY distribution differs from those of the other populations at a 1σ level (68% CIs are represented by the coloured filled areas in left panel of Fig. 8). The distribution departs in form from the other populations at ≈50–100 au. Potentially, this departure for wider systems is the result of a bias in the way we classify our objects as bound, favouring close-in systems, using the method described in Sect. 4.3.3. However, to check this, we included companions regardless of their probabilities and the resultant distribution still differed from the other populations at a 1σ level for the widest systems.
6. Discussion
The SACY sample offers a unique opportunity to study multiplicity among young stars down to very small physical separations. Currently, it is not known whether all these associations shared a common origin, due to limitations on the accuracy of their galactic motion3. Whether these associations share a common origin or not, it is likely that these groups resulted from sparse star formation whereby fewer than 100 stars were formed in each group. Therefore by studying these targets we are obtaining crucial information regarding this mode of star formation. In this analysis we present the results assuming a common formation mechanism, i.e. grouping the data together in some cases from all associations and looking for relationships in physical parameters (i.e. primary mass, physical separation).
6.1. Frequency of multiple systems
The triple frequency is TF % in the separation range 3–1000 au. If we consider the range 10–1000 au, we derive the value TF
% in the separation range 3–1000 au. If we consider the range 10–1000 au, we derive the value TF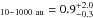 %. The value from Daemgen et al. (2015) in Taurus, TF
%. The value from Daemgen et al. (2015) in Taurus, TF %, is comparable within the uncertainties.
%, is comparable within the uncertainties.
The multiplicity frequency for SACY is MF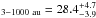 % in the separation range 3–1000 au across the primary mass range 0.2–1.2 M⊙. To compare this result to the work of Daemgen et al. (2015) in the Taurus SFR, we consider the separation range 10–1000 au and derive a multiplicity frequency of MF
% in the separation range 3–1000 au across the primary mass range 0.2–1.2 M⊙. To compare this result to the work of Daemgen et al. (2015) in the Taurus SFR, we consider the separation range 10–1000 au and derive a multiplicity frequency of MF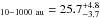 %. The multiplicity frequency for Taurus in that parameter space is MF
%. The multiplicity frequency for Taurus in that parameter space is MF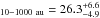 %, so the two values agree very well within the uncertainties. However, if we limit the primary mass of our targets the result is slightly different, as discussed below.
%, so the two values agree very well within the uncertainties. However, if we limit the primary mass of our targets the result is slightly different, as discussed below.
As shown by King et al. (2012b,a), collating studies from Taurus, ρ-Ophiuchus, Chamaeleon I, IC 348 and the ONC, and additionally the work of Kraus et al. (2011), Daemgen et al. (2015) studying Taurus, the multiplicity frequency of Taurus is marginally higher (≈1σ) than that of other SFRs. In order to make a comparison between Taurus (Daemgen et al. 2015), SACY and the field (Raghavan et al. 2010) we have selected targets in the separation range 10–1000 au and the primary mass range ≥0.7 M⊙. In the case of SACY the primary mass range is 0.7–1.2 M⊙ for Taurus and the field it is 0.7–1.4 M⊙. The resultant multiplicity frequencies (MF10−1000 au,M1 ≥ 0.7) are shown in the bottom panel of Fig. 10. The result of SACY (23.2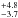 %) agrees with the field (28.9
%) agrees with the field (28.9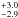 %) and marginally disagrees with Taurus (37.9
%) and marginally disagrees with Taurus (37.9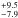 %) at ≈1σ level. Based on these results, within this range, there is marginal evidence that the Taurus region has a higher frequency of multiple systems then SACY and the field. This result further supports the idea that Taurus has a higher MF value than other SFRs and associations. Kroupa & Bouvier (2003) showed how environments such as Taurus are insufficient at binary disruption and, therefore, their high MF values are due to their binary populations being more pristine than that of heavily processed populations. We would therefore expect, assuming similar primordial multiple system distributions, to see the same effect in the SACY associations. Currently, owing to the small dataset, we cannot say conclusively whether this property is shared or not. There is no disagreement between SACY and the field, which, assuming common primordial multiple distributions, suggests that few multiple systems have been destroyed by dynamical processing in this range.
%) at ≈1σ level. Based on these results, within this range, there is marginal evidence that the Taurus region has a higher frequency of multiple systems then SACY and the field. This result further supports the idea that Taurus has a higher MF value than other SFRs and associations. Kroupa & Bouvier (2003) showed how environments such as Taurus are insufficient at binary disruption and, therefore, their high MF values are due to their binary populations being more pristine than that of heavily processed populations. We would therefore expect, assuming similar primordial multiple system distributions, to see the same effect in the SACY associations. Currently, owing to the small dataset, we cannot say conclusively whether this property is shared or not. There is no disagreement between SACY and the field, which, assuming common primordial multiple distributions, suggests that few multiple systems have been destroyed by dynamical processing in this range.
 |
Fig. 10 Age versus multiplicity frequency. Top panel: in the separation and primary mass range 3–1000 au and 0.2–1.2 M⊙, respectively. Bottom panel: in the separation and primary mass range range 10–1000 au and 0.7–1.4 M⊙, respectively. Data from (Daemgen et al. 2015, Taurus) and (Raghavan et al. 2010, the field) are shown by the star and diamond marker, respectively. Argus (ARG) has been omitted as only 1 object was observed. |
In contrast to the general trend of high multiplicity in low-density SFRs and associations, Brandeker et al. (2006) found an absence of multiple systems with separations >20 au in the young (6–8 Myr, Jilinski et al. 2005) cluster η Chamaeleontis. This survey of 17 targets used NACO observations similar to those presented here, probing similar targets and mass-ratio systems. They found a probability <10-4 that η Chamaeleontis and TW Hydrae share the same parent multiple system distribution. Although η Chamaeleontis is denser than the associations presented in this work, the authors conducted analysis to disregard dynamical processing as the cause of such a result, finding a collision time scale 3000 times that of the cluster age. The frequency of spectroscopic systems (SBs) in η Chamaeleontis is statistically similar to that of the SACY associations (Riviere-Marichalar et al. 2015), ≈10%. The physical separations of these SBs are so tight that they should be free of dynamical processing and therefore similarities between regions support the idea of statistically similar binary populations. However, the discs in η Chamaeleontis are long-lived (Sicilia-Aguilar et al. 2009), considering its age, with respect to other young regions. Therefore, at this time, it is still not clear whether the differences in multiplicity frequency between this cluster and other low-density SFRs and associations, are the result of dynamical processing or stem from environment-dependent star formation.
However, since there is a general trend of high multiplicity frequency with low-density environments, it is likely that, at least in some part, it stems from the lack of dynamical processing compared to stars in populations such as the field (Lada & Lada 2003).
What is the effect of the primary mass on the frequency?
It is common in many populations to observe an increase in multiplicity frequency with primary mass (see Fig. 12 of Raghavan et al. 2010). We also noted the same relationship among the tightest multiple systems, i.e. spectroscopic binaries (Elliott et al. 2014). However, this is considering a very large mass range, from spectral types O-M. We have investigated whether this relationship is also observable within our sample of stars (primary mass range 0.2–1.2 M⊙.)
Figure 6 shows the result of binning our data in terms of primary mass for the 109 targets with ≥95% sensitivity from Fig. 5). There is no observed trend of increasing multiplicity frequency with primary mass. There is a slight disagreement between some mass bins (≈1σ) but only in the case of very low numbers (≤3). The most reliable mass bins (with more than 10 objects) show no tendency of higher frequency with primary mass. This is in agreement with the results of Kraus et al. (2011) and Daemgen et al. (2015) within the same primary mass range.
6.2. The impact of a flat mass-ratio distribution
Duchêne & Kraus (2013) compiled observations and discussed how random pairing from the IMF (Chabrier 2003) does not agree with the derived observational mass-ratio distributions for primary masses of ~1–10 M⊙. The mass-ratio power-law index is a much steeper function of the mass for lower-mass primaries (≤0.5 M⊙).
The mass-ratio distribution derived for the SACY sample (power-law index γ = −0.04 ± 0.14), agrees with the compilation of observational results in Duchêne & Kraus (2013), in the primary mass range of ≈0.2–1.2 M⊙ (see left panel of Fig. 7). The derived γ values in this range are very close to 0, i.e. flat distributions. With our current observations we are not sensitive to more extreme mass-ratio systems (smaller than 0.2) at close-separations. To investigate whether the power-law index continues to be flat in this primary mass range, we need to observe our sample with more sensitive techniques, such as extreme high-contrast imaging or sparse-aperture masking (Evans et al. 2012). We aim to perform this analysis in future work.
6.3. Is there dynamical evolution within the SACY sample?
Another great advantage of the SACY sample is the range of pre-main-sequence (PMS) ages that we can probe (~10–100 Myr). This allows us to search for any potential dynamical evolution within the sample on these time scales.
Figure 10 shows the multiplicity frequency for systems in the separation range 3–1000 au. If we consider the youngest and oldest associations, ϵ-Cha (ECH) and AB Dor (ABD), we do not see significant differences in the multiplicity frequency. Given the number of observations we have at this time, we are limited by the small dataset. To investigate this further, we need to observe more systems in each association to build up larger samples. Given that there is only one association that does not agree with the other seven, we assume a statistically similar primordial multiple system distribution for all associations.
Although the parameters of such systems may evolve on a time scale of 10–100 Myr (see below) it is very unlikely that the systems will be entirely destroyed. Most of the destruction of multiple systems occurs very early on, within a few crossing times of the clusters (<1 Myr, Parker et al. 2009) and, therefore, at the age of the associations studied here this process has long ended.
As mentioned above, we can also investigate the relationship between the projected physical separation and the age of the systems. Although the frequency of systems has not significantly evolved, it is possible that we can observe significant differences in the system parameters. To check this, we performed a KS test for three sets of ages: a) <30; b) 30–50; and c) >50 Myr. The age groups were comprised of 7, 23, 6 companions, respectively. The KS test produced one significant result; the distributions of b) and c) are very unlikely to be resultant from two different parental distributions (KS statistic: 0.18, p-value: 0.99). This statistical similarity implies there is no significant dynamical evolution of the physical separations on this time scale (30–100 Myr). Owing to the insignificant results from the other KS tests we cannot discern whether or not the other age-grouped samples agree or not.
6.4. Comparing physical separation distributions
The current understanding of binary formation invokes two formation channels; (i) fragmentation of the proto-stellar core, systems ≥100 au (Bodenheimer & Burkert 2001) (ii) via gravitational instability and fragmentation of the proto-stellar accretion disc of the primary star, systems ≤100 au (Toomre 1964). If one of these two formation channels is dominant, one would expect to see a relative over- or under-abundance of systems between the two separation ranges, assuming that within our age range there is no significant evolution of the physical separations (see Sect. 6.3).
Therefore, one interpretation of the over-abundance of multiple systems with separations <100 au, a total of 21 systems, compared to wider systems, a total of 8, is that formation channel (ii) is dominant for multiple systems in our sample.
Another interpretation is that the original density of the SACY associations was much higher than the present day density. This high-density environment would have dynamically processed many of the wider systems >100 au early-on and, therefore, would lead to an observed relative under-abundance in this separation range. However, this original density would have to be extremely high to account for such extreme processing. In addition to this, the MF value of SACY is large and similar to that of Taurus which is an indication that the binary population has not been heavily processed.
6.5. Universality of multiple systems
Using a compilation of multiplicity surveys, King et al. (2012a,b, K12a,b hereafter) claimed that binary (multiple system) formation is not the same everywhere, and that star formation is not a single universal process. This conclusion was partly based on the significant differences found in the CDF between young populations and field stars, in the separation range of 19–100 au. They claim that, in this particular separation range, these systems should not be dynamically processed and therefore their CDFs should be indistinguishable, independent of their age and initial environment. However, Marks et al. (2014) dispute many of the results and claims of K12b. They argue that if different initial densities are considered for the analysed SFRs, then the resultant multiple system properties are compatible with a single universal star formation process. In fact, the separation range 19–100 au is potentially not pristine, and in the case of Taurus, the comparable pristine range is only ≈20–30 au.
For the sake of comparison, we have also produced a separation distribution in the range 19–100 au, comparing 16 SACY systems, 23 Taurus systems, and 48 field systems. The results are shown in Fig. 9. We note that we excluded data from D15, as in this separation range only seven systems were available for comparison.
We find that the SACY and field distributions are statistically indistinguishable within the CIs. We also performed a KS test which produced a p-value of 0.995, which is highly significant, this means it is very unlikely that the two distributions are realisations of different parent distributions. If the separation range of 19–100 au is considered a pristine range, this result is a strong indication that the stars born in the field and those born in associations form in a similar way.
In the case of Taurus, the distribution shows a different shape, and has a p-value of 0.30 and 0.24 when compared to SACY and the field, respectively. However, the p-values are not significant and therefore we cannot rule out that it is a realisation of the same parent distribution.
SACY and Taurus share many similar multiplicity properties (similar MF10−1000au and TF10−1000au values, a flat mass-ratio distribution).
However, their respective separation distributions differ in both the 10–1000 au and the 19–100 au range and additionally their MF10−1000 au, M1 ≥ 0.7 are marginally discrepant. If one population had been more heavily dynamically processed than the other, we would expect to see differences in both their MF values and their separation distributions. We do see tentative differences in both quantities, implying that Taurus has experienced less dynamical processing than the SACY associations.
At this time, the significance of the differences between the populations is still low (≈1σ), and therefore further data and analysis is still needed to clarify whether these differences are physical or merely an effect of the small dataset. One way to approach this problem is to focus on imaging a large number of targets in a pristine separation range. However, calculating this pristine range can be problematic because of unknown initial densities. Once again, the recently launched ESA mission, gaia, will put important constraints on the galactic velocities of members with accurate astrometry. This will provide much better constraints on the initial densities of such associations.
7. Conclusions
In this work we have presented multiplicity statistics of the SACY associations from AO-observations. We have derived multiplicity properties of our sample from observations of 113 targets in the mass range 0.2–1.2 M⊙. We compared these derived properties to other populations searching for statistical similarities and/or differences.
This study and previous work (Elliott et al. 2014) form part of a larger project to characterise the multiplicity properties of the SACY associations across a large and continuous parameter space, using spectroscopy, sparse-aperture masking (SAM), speckle imaging, AO-imaging and classical direct imaging.
Our observed sample consisted of 201 targets: 113 confirmed SACY members and 88 targets belonging to other populations (both from the field and PMS regions). As discussed in Sect. 3, these 88 targets were not included in our analysis. The parameters from individual observations can be found in Table B.1, and a summary of the identified multiple systems in Table C.1.
From the multiplicity study of the 113 confirmed SACY members our main conclusions can be summarised as follows:
-
1.
We have identified 31 multiple systems (28 binaries,3 triples) from observations of 113 targets.
-
1.
Out of these 31 systems, 7 were identified from co-moving proper motion analysis, and 24 from contamination likelihood based on the component’s parameters (with probabilities ≥0.95).
-
1.
The multiplicity frequency and triple frequency for SACY, in the separation range 3–1000 au, are MF
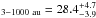 % and TF
% and TF %, respectively.
%, respectively. -
2.
In the separation range 10–1000 au and for primary masses ≥0.7 M⊙ the multiplicity frequency (MF10−1000 au,M1 ≥ 0.7) of SACY (23.2
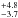 %) is similar to the field (28.9
%) is similar to the field (28.9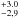 %) and discrepant at a 1σ level to Taurus (37.9
%) and discrepant at a 1σ level to Taurus (37.9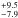 %).
%). -
3.
The multiplicity frequency is not a function of the primary mass, within the primary mass range of 0.2–1.2 M⊙.
-
4.
There is no evidence of dynamical destruction of multiple systems in the age range of 10–100 Myr.
-
5.
There is evidence that the multiple systems’ physical separations do not evolve significantly on the time scale 30–100 Myr.
-
6.
The mass-ratio distribution (power-law index γ = −0.04 ± 0.14) is compatible with a uniform distribution (γ = 0).
-
7.
The SACY and the field separation distributions are indistinguishable in the separation range 19–100 au, suggesting a similar formation mechanism (if we assume this separation range is free of dynamical processing).
A detailed analysis of the statistical properties of the SACY associations in the context of star formation will be presented in a future paper. It will include Elliott et al. (2014), this paper, and (Torres et al. 2008) in addition to collating all the available published information and data from the literature (e.g. Evans et al. 2012). We can then compare a significant number of these young systems across a larger parameter space, and make our analysis much more comprehensive.
Online material
Appendix A: All sources observed in this work
All targets analysed in this work.
Appendix B: Individual detections in this work
Table B.1 is available in electronic form at the CDS.
Appendix C: Non SACY targets
A summary of the properties of non-SACY multiple systems identified in this work.
See Chap. 9 of Ivezić et al. (2014) for many applications of this technique in classification of astronomical objects such as differentiating variable and non-variable MS-stars using photometric colours.
The GAIA mission (Lindegren et al. 2008) will provide extremely precise astrometry for members of such associations, with expected accuracies of 7–25 μas.
Acknowledgments
The authors would like to thank the anonymous referee for the thorough work put into improving the content and direction of this manuscript. Thanks go to Dr. Tokovinin for providing assistance and insightful discussions regarding the analysis of multiple systems in addition to tabular data. Thanks also go to Sebastian Daemgen for assistance with the multiplicity data of Taurus and to Simon Murphy for the discussion of stellar ages. This research has been funded by Spanish grants AYA2010-21161-C02-02 and AYA2012-38897-C02-01. A. Bayo acknowledges financial support from the Proyecto Fondecyt de Iniciación 11140572. This paper has made use of the SIMBAD database and VizieR catalogue access tool, CDS, Strasbourg, France. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infra-red Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. The following ESO observations were utilised in this work: 077.C-0483, 081.C-0825, 088.C-0506 and 089.C-0207.
References
- Aarnio, A. N., Weinberger, A. J., Stassun, K. G., Mamajek, E. E., & James, D. J. 2008, AJ, 136, 2483 [NASA ADS] [CrossRef] [Google Scholar]
- Alcalá, J. M., Spezzi, L., Chapman, N., et al. 2008, ApJ, 676, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, E., & Francis, C. 2012, Astron. Lett., 38, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 1998, A&A, 337, 403 [NASA ADS] [Google Scholar]
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. 2003, in Brown Dwarfs, ed. E. Martín, IAU Symp., 211, 41 [Google Scholar]
- Becker, C., Moraux, E., Duchêne, G., Maschberger, T., & Lawson, W. 2013, A&A, 552, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergfors, C., Brandner, W., Janson, M., et al. 2010, A&A, 520, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biller, B. A., Liu, M. C., Wahhaj, Z., et al. 2013, ApJ, 777, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Bodenheimer, P., & Burkert, A. 2001, in The Formation of Binary Stars, eds. H. Zinnecker, & R. Mathieu, IAU Symp., 200, 13 [Google Scholar]
- Brandeker, A., Jayawardhana, R., & Najita, J. 2003, AJ, 126, 2009 [NASA ADS] [CrossRef] [Google Scholar]
- Brandeker, A., Jayawardhana, R., Khavari, P., Haisch, Jr., K. E., & Mardones, D. 2006, ApJ, 652, 1572 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Chauvin, G., Lagrange, A.-M., Dumas, C., et al. 2004, A&A, 425, L29 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Chauvin, G., Lagrange, A.-M., Dumas, C., et al. 2005, A&A, 438, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chauvin, G., Lagrange, A.-M., Bonavita, M., et al. 2010, A&A, 509, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chauvin, G., Lagrange, A.-M., Beust, H., et al. 2012, A&A, 542, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daemgen, S., Bonavita, M., Jayawardhana, R., Lafrenière, D., & Janson, M. 2015, ApJ, 799, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Devillard, N. 1997, The Messenger, 87, 19 [NASA ADS] [Google Scholar]
- Dommanget, J., & Nys, O. 2000, A&A, 363, 991 [NASA ADS] [Google Scholar]
- Dommanget, J., & Nys, O. 2002, VizieR Online Data Catalog: I/274 [Google Scholar]
- Duchêne, G. 1999, A&A, 341, 547 [NASA ADS] [Google Scholar]
- Duchêne, G., & Kraus, A. 2013, ARA&A, 51, 269 [Google Scholar]
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] [Google Scholar]
- Elliott, P., Bayo, A., Melo, C. H. F., et al. 2014, A&A, 568, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, T. M., Ireland, M. J., Kraus, A. L., et al. 2012, ApJ, 744, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Gavel, D. T., Max, C. E., Olivier, S. S., et al. 2002, in Adaptive Optics Systems and Technology II, eds. R. K. Tyson, D. Bonaccini, & M. C. Roggemann, SPIE Conf. Ser., 4494, 336 [Google Scholar]
- Gliese, W., & Jahreiß, H. 1991, Preliminary Version of the Third Catalogue of Nearby Stars, Tech. Rep. (Greenbelt, MD: Goddard Space Flight Center) [Google Scholar]
- Gontcharov, G. A. 2006, Astron. Astrophys. Trans., 25, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Huélamo, N., Lacour, S., Tuthill, P., et al. 2011, A&A, 528, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivezić, Ž., Connolly, A., Vanderplas, J., & Gray, A. 2014, Statistics, Data Mining and Machine Learning in Astronomy (Princeton University Press) [Google Scholar]
- Jilinski, E., Ortega, V. G., & de la Reza, R. 2005, ApJ, 619, 945 [NASA ADS] [CrossRef] [Google Scholar]
- King, R. R., Goodwin, S. P., Parker, R. J., & Patience, J. 2012a, MNRAS, 427, 2636 [NASA ADS] [CrossRef] [Google Scholar]
- King, R. R., Parker, R. J., Patience, J., & Goodwin, S. P. 2012b, MNRAS, 421, 2025 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, A. L., & Hillenbrand, L. A. 2007, ApJ, 662, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, A. L., Ireland, M. J., Martinache, F., & Hillenbrand, L. A. 2011, ApJ, 731, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., & Bouvier, J. 2003, MNRAS, 346, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Lafrenière, D., Doyon, R., Marois, C., et al. 2007, ApJ, 670, 1367 [NASA ADS] [CrossRef] [Google Scholar]
- Lafrenière, D., Jayawardhana, R., Brandeker, A., Ahmic, M., & van Kerkwijk, M. H. 2008, ApJ, 683, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Leinert, C., Zinnecker, H., Weitzel, N., et al. 1993, A&A, 278, 129 [NASA ADS] [Google Scholar]
- Lindegren, L., Babusiaux, C., Bailer-Jones, C., et al. 2008, in IAU Symp. 248, eds. W. J. Jin, I. Platais, & M. A. C. Perryman, 217 [Google Scholar]
- López-Santiago, J., Montes, D., Crespo-Chacón, I., & Fernández-Figueroa, M. J. 2006, ApJ, 643, 1160 [NASA ADS] [CrossRef] [Google Scholar]
- Malogolovets, E. V., Balega, Y. Y., Rastegaev, D. A., Hofmann, K.-H., & Weigelt, G. 2007, Astrophys. Bull., 62, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Mamajek, E. E., Meyer, M. R., & Liebert, J. 2006, AJ, 131, 2360 [NASA ADS] [CrossRef] [Google Scholar]
- Marks, M., Leigh, N., Giersz, M., et al. 2014, MNRAS, 441, 3503 [NASA ADS] [CrossRef] [Google Scholar]
- Masciadri, E., Mundt, R., Henning, T., Alvarez, C., & Barrado y Navascués, D. 2005, ApJ, 625, 1004 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, B. D., Wycoff, G. L., Hartkopf, W. I., Douglass, G. G., & Worley, C. E. 2001, AJ, 122, 3466 [Google Scholar]
- McCaughrean, M. J., & Stauffer, J. R. 1994, AJ, 108, 1382 [NASA ADS] [CrossRef] [Google Scholar]
- Messina, S., Desidera, S., Turatto, M., Lanzafame, A. C., & Guinan, E. F. 2010, A&A, 520, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montes, D., López-Santiago, J., Gálvez, M. C., et al. 2001, MNRAS, 328, 45 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Moraux, E., Lawson, W. A., & Clarke, C. 2007, A&A, 473, 163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nielsen, E. L., & Close, L. M. 2010, ApJ, 717, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, R. J., Goodwin, S. P., Kroupa, P., & Kouwenhoven, M. B. N. 2009, MNRAS, 397, 1577 [NASA ADS] [CrossRef] [Google Scholar]
- Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ratzka, T., Köhler, R., & Leinert, C. 2005, A&A, 437, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reipurth, B., & Zinnecker, H. 1993, A&A, 278, 81 [NASA ADS] [Google Scholar]
- Reipurth, B., Guimarães, M. M., Connelley, M. S., & Bally, J. 2007, AJ, 134, 2272 [NASA ADS] [CrossRef] [Google Scholar]
- Riedel, A. R., Finch, C. T., Henry, T. J., et al. 2014, AJ, 147, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Riviere-Marichalar, P., Elliott, P., Rebollido, I., et al. 2015, A&A, submitted [Google Scholar]
- Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sana, H., Le Bouquin, J.-B., Lacour, S., et al. 2014, ApJS, 215, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Sartori, M. J., Lépine, J. R. D., & Dias, W. S. 2003, A&A, 404, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlieder, J. E., Lépine, S., & Simon, M. 2012, ApJ, 144, 109 [Google Scholar]
- Scott, D. W. 2009, Multivariate density estimation: theory, practice, and visualization (John Wiley & Sons), 383 [Google Scholar]
- Shkolnik, E. L., Hebb, L., Liu, M. C., Reid, I. N., & Collier Cameron, A. 2010, ApJ, 716, 1522 [NASA ADS] [CrossRef] [Google Scholar]
- Sicilia-Aguilar, A., Bouwman, J., Juhász, A., et al. 2009, ApJ, 701, 1188 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Song, I., Zuckerman, B., & Bessell, M. S. 2012, AJ, 144, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Tokovinin, A. 2005, Highlights of Astronomy, ASP Conf., 13, 992 [Google Scholar]
- Tokovinin, A. 2014, AJ, 147, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Toomre, A. 1964, ApJ, 139, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, C. A. O., Quast, G. R., da Silva, L., et al. 2006, A&A, 460, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Torres, C. A. O., Quast, G. R., Melo, C. H. F., & Sterzik, M. F. 2008, Young Nearby Loose Associations, 2, 757 [Google Scholar]
- Turon, C., Creze, M., Egret, D., et al. 1993, Bulletin d’Information du Centre de Donnees Stellaires, 43, 5 [NASA ADS] [Google Scholar]
- van Dessel, E., & Sinachopoulos, D. 1993, A&AS, 100, 517 [NASA ADS] [Google Scholar]
- Wahhaj, Z., Liu, M. C., Nielsen, E. L., et al. 2013, ApJ, 773, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Finch, C. T., Girard, T. M., et al. 2012, VizieR Online Data Catalog: I/1322 [Google Scholar]
- Zuckerman, B., Song, I., & Bessell, M. S. 2004, ApJ, 613, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Zuckerman, B., Rhee, J. H., Song, I., & Bessell, M. S. 2011, ApJ, 732, 61 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Summary of the properties and frequency of visual multiple systems identified for the SACY associations studied in this work.
A summary of the properties of non-SACY multiple systems identified in this work.
All Figures
 |
Fig. 1 Average sensitivity limit in all filters for both NACO and Lick data. The limits were computed from the 3σ root-mean squared (rms) of the PSF radial profile for each target, and then averaged within each filter. The Ks filter for the NACO data is given for the S13 and S27 objective. The dashed lines represent our mass limits at 0.̋5, according to Baraffe et al. (1998) evolutionary tracks, assuming an average age of 30 Myr and a primary mass of 1 M⊙. |
| In the text | |
 |
Fig. 2 Section of the NACO image for target CD-30 3394B, showing two partially resolved components. The black solid-lined ellipse is the aperature applied by SExtractor and the black filled circle the centre of the ellipse. The red crosses and black dashed circles indicate the centre and FWHM of the model PSF extracted from the primary CD-30 3394A, using PSFEx for each source. |
| In the text | |
 |
Fig. 3 Relative movement of four point sources, in RA and Dec, for two observations of GSC 08350-01924. The black dotted line and black markers represent the motion one would expect from a background (BKG) source with respect to the primary, and the shaded area represents the error space. The dark blue marker represents a source showing no significant relative motion, consistent with a bound (BND) companion at 0.3″. The other coloured markers represent three background sources detected at separations of 10.5, 13.2 and 14.2″ from the primary. |
| In the text | |
 |
Fig. 4 Probability of identifying a bound system from 100–0% in intervals of 10% from blue to red in physical separation-mass-ratio parameter space. The circles and crosses represent the training and test set, respectively. Blue markers represent bound companions, and red markers unbound companions. |
| In the text | |
 |
Fig. 5 Top panel: physical projected separations versus mass-ratio for identified multiple systems. The filled red markers represent binary companions, the other coloured markers are components of triple systems with matching colours for the secondary and tertiary. The size of the marker is proportional the companion’s mass. The grey lines represent the sensitivity limits for the individual targets. The red and black lines represent the 90% and 95% detections limits for the whole sample, respectively. Bottom panel: 95% detection limits for four studies, red: this work, blue: Daemgen et al. (2015), green: Kraus et al. (2011) and brown: Raghavan et al. (2010), used for analysis in Sect. 6. |
| In the text | |
 |
Fig. 6 Primary mass versus multiplicity frequency for systems in the separation range 3–1000 au. The data is binned according to the Freedman-Diaconis rule. The fractions are shown by each mass bin. |
| In the text | |
 |
Fig. 7 Left panel: normalised frequency of mass-ratios. The dashed line represents a power-law function with index γ = 0. Right panel: the cumulative frequency distribution of mass-ratios using the two methods outlined in Sect. 5.2. Method (i) The red line represent the derived mass ratios. Method (ii) The black dots, dark and light blue-coloured area represent the average, 1σ and 3σ variation in frequency from 100 realisations of the mass ratio, respectively. |
| In the text | |
 |
Fig. 8 Left: red, green, blue and gold shaded areas represent the 68% confidence intervals for the kernel density estimation (KDE) for SACY, Taurus (K11), Taurus (D15) and the field (R10) respectively. The multiple systems considered are all above the master sensitivity curve defined in the bottom panel of Fig. 5 and in the separation range 10–1000 au. Right: the cumulative distribution frequencies for the same systems. |
| In the text | |
 |
Fig. 9 Left: red, green and gold shaded areas represent the 68% confidence intervals for the kernel density estimation (KDE) of multiple systems for SACY, Taurus (K11) and the field (R10), respectively. The multiple systems considered are all above the master sensitivity curve defined in the bottom panel of Fig. 5 and in the separation range 19–100 au. Right: the cumulative distribution frequencies for the same systems. |
| In the text | |
 |
Fig. 10 Age versus multiplicity frequency. Top panel: in the separation and primary mass range 3–1000 au and 0.2–1.2 M⊙, respectively. Bottom panel: in the separation and primary mass range range 10–1000 au and 0.7–1.4 M⊙, respectively. Data from (Daemgen et al. 2015, Taurus) and (Raghavan et al. 2010, the field) are shown by the star and diamond marker, respectively. Argus (ARG) has been omitted as only 1 object was observed. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


